随着我国汽车、高速列车、航空航天等高端装备制造业的飞速发展,对构件制造提出了更高的要求,亟需实现高性能、轻量化、高精度、能源高效利用以及资源节约与环境友好等目标。在汽车制造领域,轻量化是实现“节能减排”的最主要途径之一;在飞机制造领域,结构轻量化可显著提升经济效益和并优化材料性能[1~4]。轻量化主要通过以下3个途径实现:轻质材料的广泛应用、先进的制造工艺和结构优化设计。其中,轻质高强金属的广泛应用是实现构件轻量化的有效途径之一[5~7]。环境保护政策和温室气体排放标准的日益严格,推动了运输行业对产品减量的需求,采用铝、镁合金等轻质材料并结合电脉冲辅助成形方法已成为实现结构轻量化的有效方法。5182-O铝合金因其优异的强度-重量比、良好的加工性能和耐腐蚀性能,已成为一种重要的轻质金属材料[8~12]。为了进一步提高5182-O铝合金的应用效率和性能,深入了解其在不同应力状态下的屈服演化行为及各向异性特征尤为重要。这不仅涉及材料的成形工艺设计,更直接影响到产品的可靠性和安全性。
在塑性力学领域,对材料屈服行为的研究是理解其塑性变形机制的关键。5182-O铝合金作为一种典型的fcc结构合金,其屈服行为受到晶粒取向、微观结构和应力状态的共同影响[13~17]。因此,在不同应力状态下表征5182-O铝合金的屈服演化行为,对预测和控制其在复杂工况下的性能具有重要意义。相对于主应力函数,pDrucker函数具有以下优势:可灵活表征不同应力状态下的强度差异;具有较高的计算效率。Lou等[18]将Drucker[19]提出的屈服函数进一步修改为考虑压力敏感性的pDrucker函数,该函数能够准确地模拟剪切和平面应力之间的强度差异直至材料发生断裂。Hou等[20]指出,需要通过解析求解屈服函数中的参数以模拟屈服面的演变。Shang等[21]将逆向工程方法的标定结果作为神经网络模型的输入集,并结合pDrucker函数对材料大应变条件下的塑性行为进行了预测。Shen等[22]通过扩展非关联Hill48模型,使其能准确表征材料在较宽温度范围内受动态应变老化显著影响的各向异性流动行为。Zhang和Lou[23]提出了一种各向异性-差分硬化函数以模拟不同应力状态下材料硬化行为的差异。
晶体塑性模拟能够从微观角度揭示材料的塑性变形机制。通过模拟合金内部的位错运动、晶粒间相互作用以及织构演变,可以预测材料在宏观尺度上的力学响应。Engler和Aretz[24]将多晶塑性模型与屈服函数结合到一个多级建模框架中,用以描述各向异性铝合金的力学响应特性。Guo等[25]研究了初始晶粒取向、晶粒尺寸和几何形状对微深拉工艺中孪晶诱导塑性(TWIP)钢塑性各向异性的影响。Tang等[26]建立了一种基于多晶塑性的热-机械-动态再结晶耦合的方法,以研究轻金属在热变形过程中的织构和晶粒尺寸。Liu等[27]提出了多尺度计算方案以分析铝合金的复杂塑性行为。Wang等[28]通过各向异性Drucker、Hill48和Yld91屈服函数及晶体塑性有限元模型(CPFEM)的研究实现了多尺度仿真。因此结合实验和晶体塑性模拟,可以更全面地理解5182-O铝合金的屈服行为,为材料的设计和加工提供理论支持。
本工作采用多应力状态实验与逆向工程方法相结合,分析了不同应力状态和各向异性对5182-O铝合金塑性流动行为的影响。然后通过pDrucker屈服函数的解析计算对5182-O铝合金塑性行为的差异进行表征并与实验结果对比。进一步通过晶体塑性模拟和代表性体积单元(RVE)计算,研究了应力状态和晶粒取向对孔洞演化的影响。本工作通过宏观本构模型与微观晶体塑性模拟的协同分析,对5182-O铝合金的塑性力学特性进行了系统表征和分析。
1 力学性能实验
1.1 不同应力状态及各向异性条件下的实验方法
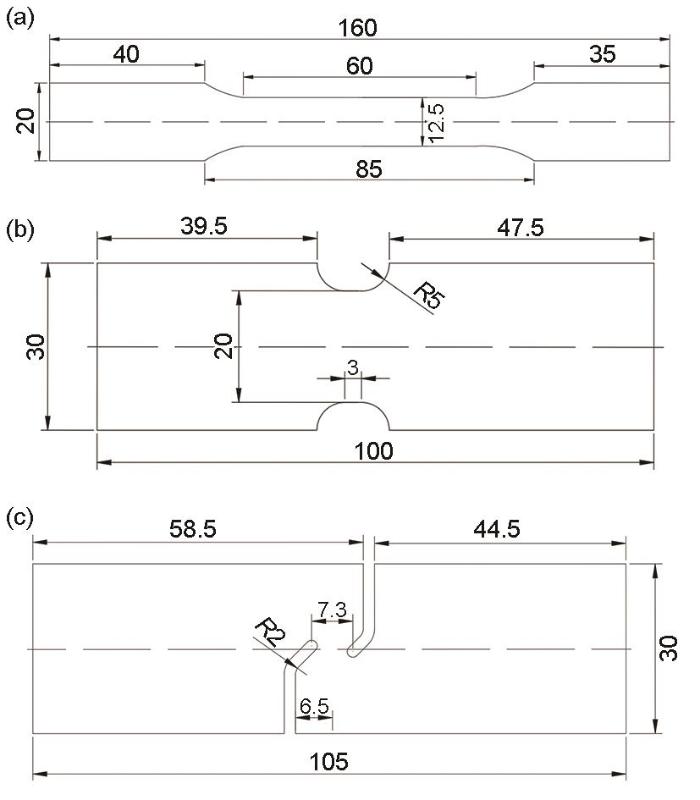
本工作以5182-O铝合金为研究对象,研究了其在不同应变下的塑性行为的变化。采用激光切割从1.25 mm厚的板材切取单向拉伸(UT)、平面应变拉伸(PST)和剪切(SS)试样,具体尺寸如图1所示。为系统评估5182-O铝合金板材的各向异性,分别沿板材的轧制方向(RD)、轧向的45°方向(DD)和90°方向(TD)制备拉伸试样,制备出的试样分别命名为UT0、UT45、UT90、SS0和PST0试样。加工后试样尺寸误差小于0.14 mm,满足测试要求。采用TSE万能试验机进行拉伸实验,应变速率均为0.001 s-1 (通过将UT、PST和SS试样的加载速率分别设置为1.8、0.5和0.5 mm/min实现)。在每种条件下,实验重复3次以上以确保实验的可重复性。
图1
图1
试样形状及尺寸示意图
Fig.1
Schematics of shape and size of the specimens for mechanical tests (unit: mm)
(a) uniaxial tension (UT) specimen
(b) plane strain tension (PST) specimen
(c) shear (SS) specimen
图2
图2
数字图像相关(DIC)三维全场应变测量分析系统照片
Fig.2
Photo of three-dimensional full-field strain measurement and analysis system based on digital image correlation (DIC) (Insets are contour diagram of strain and equipment photo for taking pictures)
表1 DIC分析系统的参数
Table 1
| Item | Parameter | Item | Parameter |
|---|---|---|---|
| Software | XTOP | Standard ranging | 630 mm |
| Image resolution | 2448 × 2048 | Depth of field | ≤ 300 mm |
| Optical zoom | 35x | Subset size (pixels) | 31 |
| Camera format | 400 mm × 300 mm | Analysis step size (pixels) | 6 |
试样采用标准金相方法抛光。采用配有电子背散射衍射(EBSD)系统的Quanta 250FEG扫描电镜(SEM)观察电解抛光后试样的断口形貌,加速电压为20 V,扫描步长为0.2 μm。EBSD数据由开源MATLAB软件工具箱MTEX进行分析。
1.2 实验结果与分析
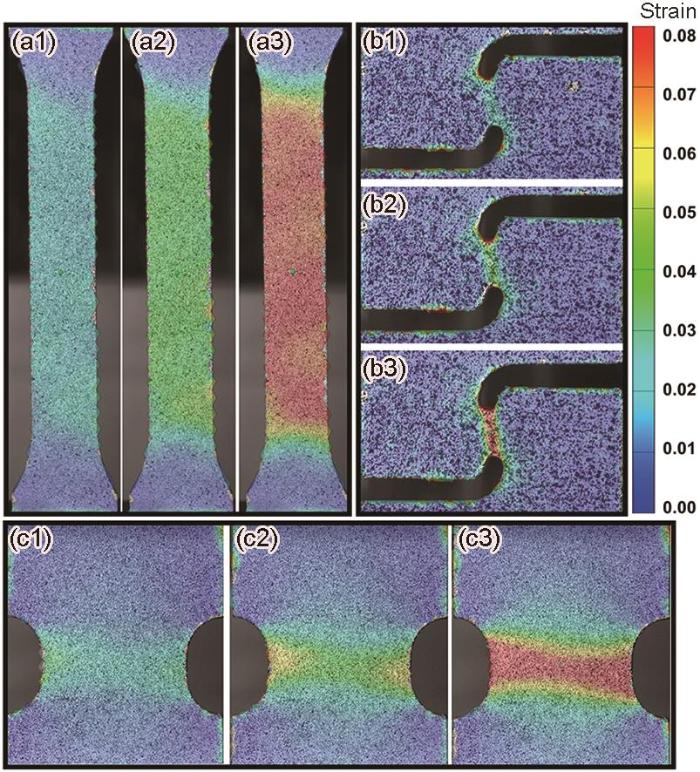
图3为UT0试样、SS0试样和PST0试样在0.02、0.04和0.08应变下的应变云图。可以看出,随着应变的增大,变形主要集中在各试样的最小横截面区域。PST0试样的中心点位置可近似为理想平面应变状态,通过设置平行段使得应变不会在缺口位置过于集中。SS0试样的几何设计可确保变形主要发生在试样中间的狭长区域,因此选取狭长区域中间点的剪切应力状态作为表征依据。
图3
图3
试样在不同应变下的DIC测试应变云图
Fig.3
Strain contours of the specimens under strains of 0.02 (a1-c1), 0.04 (a2-c2), and 0.08 (a3-c3) from DIC testing for UT0 specimen (a1-a3), SS0 specimen (b1-b3), and PST0 specimen (c1-c3)
式中,
图4
图4
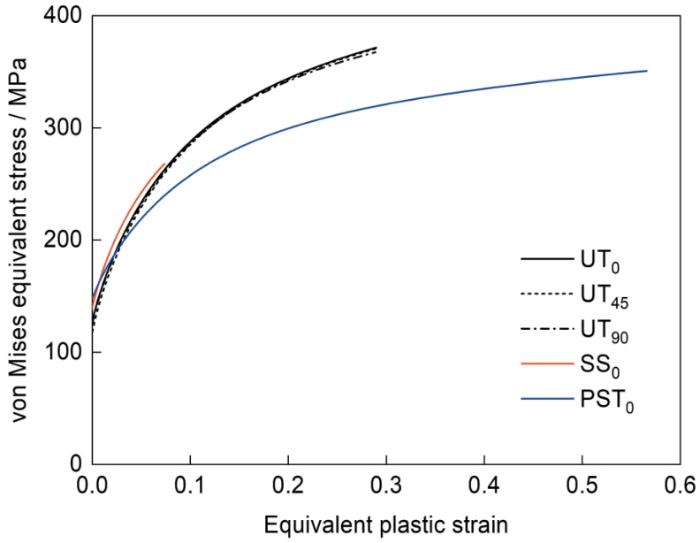
三种应力状态下的von Mises等效应力-等效塑性应变曲线
Fig.4
von Mises equivalent stress-equivalent plastic strain curves under different stress states (0, 45, and 90 represent 0°, 45°, and 90° directions relative to the rolling direction, respectively)
表2 不同硬化行为的标定参数
Table 2
| Specimen | K | ɛ0 | n | A | B | C |
|---|---|---|---|---|---|---|
| UT0 | 559.60 | 0.0071 | 0.3289 | 373.36 | 130.60 | 12.46 |
| UT45 | 504.10 | 0.0047 | 0.3544 | 422.50 | 160.10 | 12.03 |
| UT90 | 446.20 | 0.0046 | 0.3463 | 452.21 | 181.70 | 11.67 |
| SS0 | 398.15 | 0.0116 | 0.2658 | 357.59 | 165.62 | 10.53 |
| PST0 | 466.92 | 0.0070 | 0.2696 | 366.24 | 143.10 | 15.60 |
如图4所示,5182-O铝合金的各向异性硬化效应不明显,但其在不同应力状态下的硬化行为存在显著差异。图5为UT0、PST0和SS0试样断口形貌的SEM像。可以看出,3种试样中均存在清晰的混合凹痕和撕裂边缘,表明5182-O铝合金的断裂模式为延性断裂。凹痕的形成机制源于微孔洞的形核、生长和聚结,而撕裂边缘则是由微孔洞的聚结或连接所致。如图5a所示,UT0试样断口处的孔洞尺寸和分布均匀且规整,这是由于其主要承受单向拉伸应力。如图5b所示,PST0试样断口的凹坑更大、更深,并且倾向于合并在一起形成杯锥状凹坑。如图5c所示,SS0试样的断口形貌较为平整,这是由于SS0试样受到剪切应力,主要沿着剪切面发生原子或分子间的相对滑移,因此其变形和断裂主要集中在剪切面上。
图 5
图 5
不同试样断口形貌的SEM像
Fig.5
SEM images showing fracture morphologies of UT0 (a), PST0 (b), and SS0 (c) specimens
2 屈服函数标定实验结果
2.1 pDrucker屈服函数解析计算
针对材料在各向异性和不同应力状态条件下的建模问题,可采用插值方法与屈服函数相结合的方法描述塑性变形过程中屈服面形状的演变行为。由于需计算不同应变下合金的校准屈服面,因此对硬化行为进行准确表征非常重要。在数值模拟过程中,为获得更高的精度,需输入不同应变水平下的校准参数作为材料特性,这将增加每个应变水平参数下的标定工作量,且需输入的材料参数也随之增加。目前,解析方法被广泛用于表征屈服面随塑性应变的变化,为模拟各向异性硬化行为,通常将方程中的等效应力(
式中,σij 为应力分量,i = x、y、z,j = x、y、z;
式中, s ′为线性变换应力张量, s ′ = L ′ σ,其中 σ 为应力张量; L ′为构建的线性变换矩阵,应力张量和线性变换矩阵表达式如下:
式中,
在平面内应力状态下,
式中,
因此经线性转换,平面应力状态下的
(1) 各向异性参数。在单向拉伸下,η = 1/3和
假定计算得出的流动曲线与沿RD的单向拉伸的流动曲线一致,则
联立公式
(2) 应力状态参数。根据各向同性形式中的
式中,下标SS θ 和PST θ 分别表示沿θ方向的剪切和平面应变拉伸。需要注意的是,在相同应力状态下,θ不同时
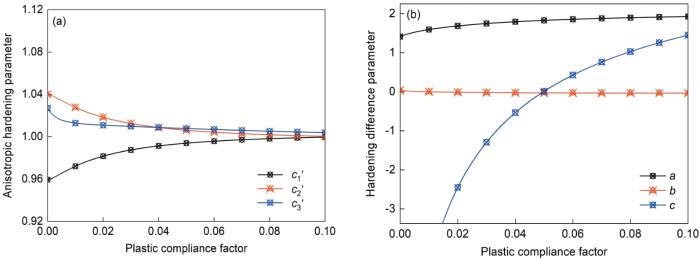
图6展示了扩展为各向异性的pDrucker函数对5182-O铝合金在3种应力状态下的各向异性参数和硬化差异参数的标定结果。随着pDrucker函数参数的增加,
图6
图6
3种应力状态下5182-O铝合金的pDrucker函数参数的演变
Fig.6
Evolutions of pDrucker function parameters of 5182-O aluminum alloys under three stress states
(a) anisotropic hardening parameters (
(b) hardening difference parameters (a, b, and c)
2.2 各向异性验证
通过
图 7
图 7
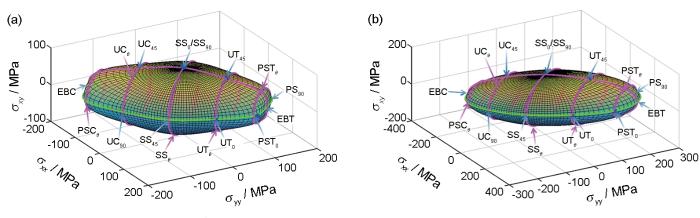
不同等效塑性应变下5182-O铝合金的3D屈服面和实验结果对比
Fig.7
Comparisons of 3D yield surfaces and experimental results of 5182-O aluminum alloys under different
(a)
图8
图8
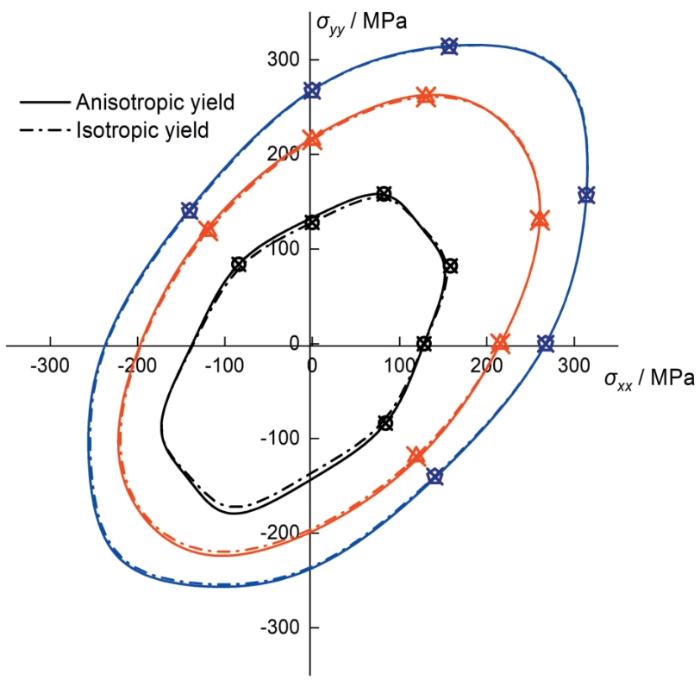
各向同性和各向异性屈服面演化的对比
Fig.8
Comparisons of isotropic and anisotropic yield surface evolutions (Blue, red, and black lines and open symbols represent calculated and experimental yield surfaces under 0.02, 0.04, and 0.08 strains, respectively)
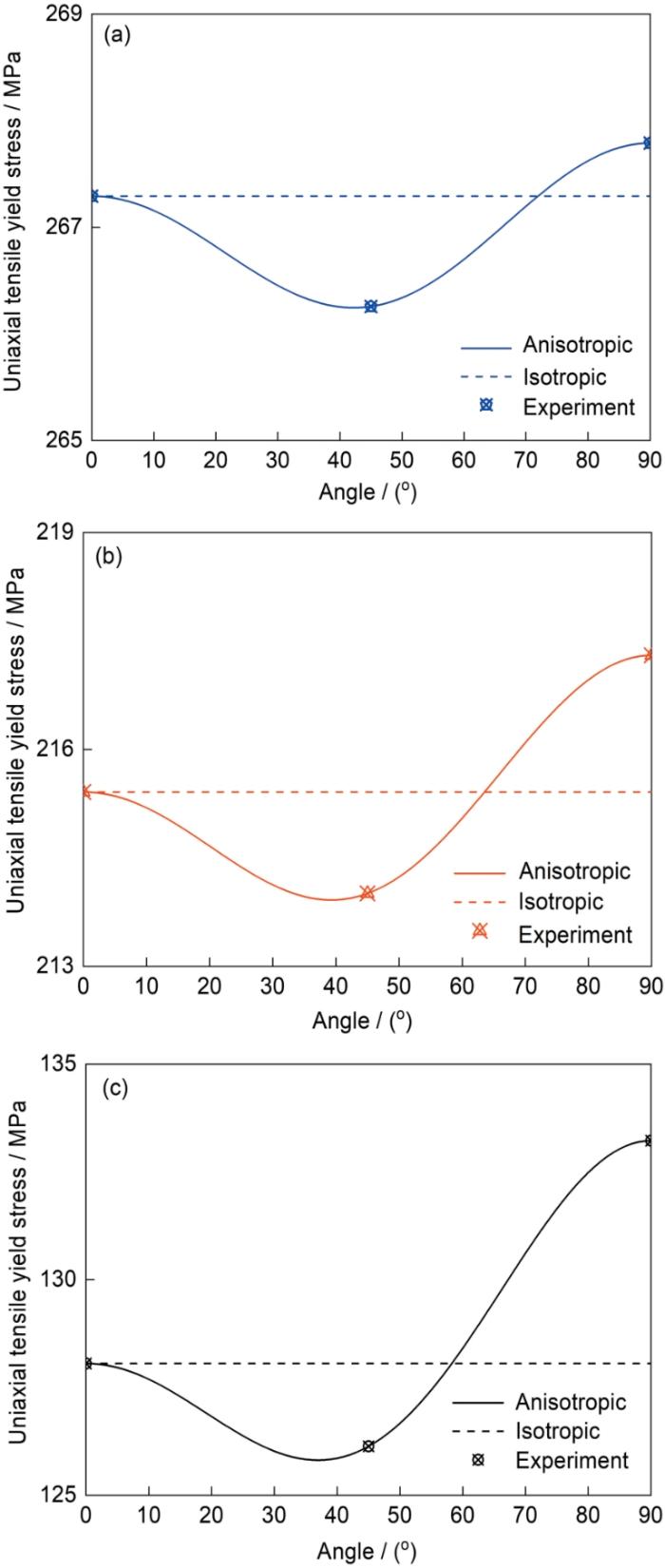
通过提取图7中单向拉伸时的屈服应力数据,在图9中评估了各向异性形式单向拉伸下各向异性硬化行为的预测效果。由图可知,在单向拉伸状态下,不同加载方向的屈服应力呈现出特定的变化规律。具体而言,从RD到DD屈服应力逐渐减小,而从DD到TD则逐渐增大。然而,随着应变的增加,不同θ下的屈服应力有所不同。当
图9
图9
单向拉伸状态下5182-O铝合金各向异性屈服强度的演化
Fig.9
Evolutions of anisotropic yield strengths of 5182-O aluminum alloys under uniaxial tension
(a)
图10
3 晶体塑性模拟分析
3.1 晶体塑性模型
假设铝合金塑性变形过程中的主要变形机理为位错滑移,则晶体变形包括由晶格旋转引起的弹性变形和位错滑移引起的塑性变形。变形梯度张量( F )的乘法分解如下[30]:
式中, Fe为弹性变形张量, Fp为塑性变形张量。
速度梯度( L )可分解为弹性速度梯度( Le)和塑性速度梯度( Lp)形式:
单位向量 sα 和 mα 分别表示沿滑移方向和滑移平面法线方向的α滑移系。在塑性变形后晶体发生扭曲和旋转,变形后的向量(
考虑滑移机制, Lp可表示为:
式中,k为滑移系总数,
基于Schmid定律选择幂律模型表征晶体材料的应变硬化行为[32]:
式中,
应变强化效应采用以下增量表达形式:
式中,
硬化模量反映了变形过程中由位错增殖和交互作用引起的滑移阻力增加。目前,多数硬化模型都采用如下的简化假设[28]:
式中,hβ 为潜硬化模量,q为常数,h0为初始硬化模量,δαβ 为滑移系硬化参数,γ为滑移系统的累积剪切应变,τs为由大塑性流动引起的剪切应力,τ0为屈服应力,t为时间。
式中,E为弹性模量,v为Poisson比,G为剪切模量。
表3 晶体的塑性本构模型参数
Table 3
| Parameter | Unit | Value |
|---|---|---|
| C11 | MPa | 91040 |
| C12 | MPa | 51084 |
| C44 | MPa | 25900 |
| h0 | MPa | 80.6659 |
| τs | MPa | 46.3126 |
| τ0 | MPa | 33.6519 |
| q | 1 | |
| s-1 | 0.001 |
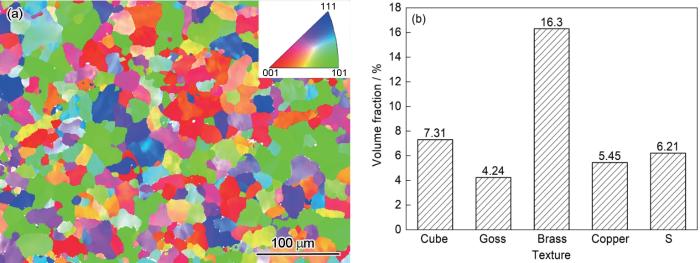
图11为AA5182-O铝合金初始态织构的EBSD分析。由图可知,合金中显微组织取向呈随机分布;合金中主要包含Cube、Goss、Brass、Copper和S织构,晶粒取向以[001]和[101]为主。
图11
图11
5182-O铝合金初态取向织构的EBSD分析
Fig.11
Inverse pole figure (a) and volume fraction distributions (b) of initial orientation texture for 5182-O aluminum alloy
3.2 代表性体积单元建模
考虑到多晶材料晶体结构的空间周期性,选择受周期性边界条件影响的RVE模型进行模拟计算。本工作采用的有限元模型含有80660个单元(C3D8),初始孔洞体积分数(
式中,Vvoid和VRVE分别为孔洞和代表性体积单元的归一化体积分数。
图12
图12
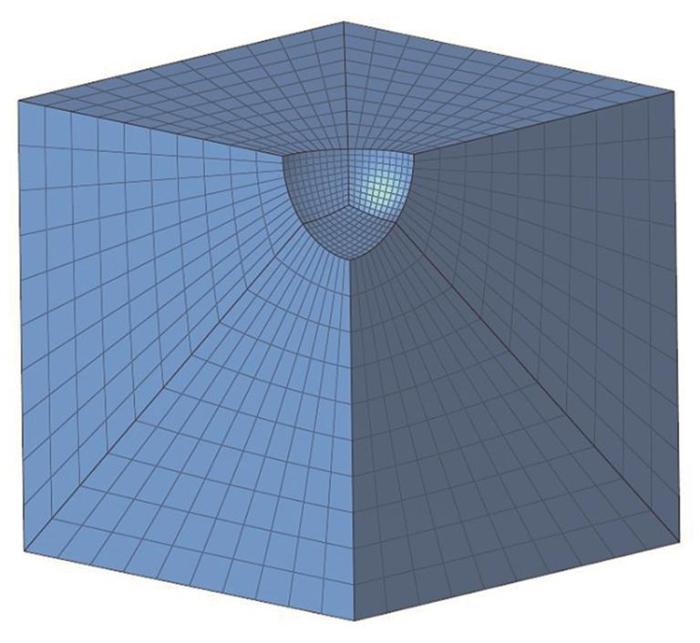
1/8代表性体积单元(RVE)有限元网格模型
Fig.12
Finite element mesh model of 1/8 representative volume element (RVE)
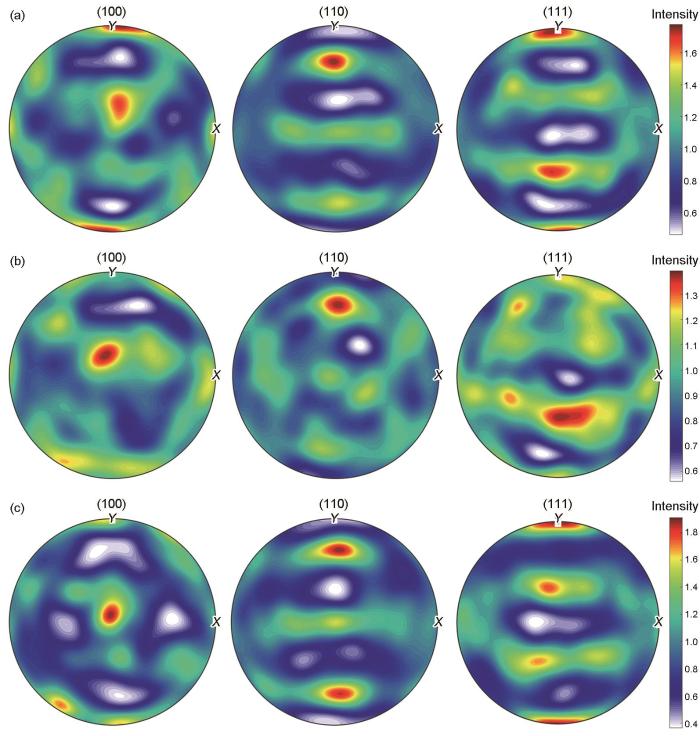
基于晶体塑性有限元方法,通过ABAQUS软件进行数值模拟。首先从EBSD数据得到取向分布函数(ODF);然后,采用最小二乘法对ODF进行离散化处理,获得特定数量晶粒的取向数据,用以表征初始态5182-O铝合金的典型织构特征。图13为5182-O铝合金初始态及晶粒数量为400和500时的取向织构的极图。晶粒数量为400时能够初步反映初始织构特征;当晶粒数量大于500时,能够充分反映初始取向的织构特征。因此,综合考虑计算时间和计算精度,将晶体塑性有限元模型中的晶粒数量确定为500。RVE模型由500个晶粒组成,能够充分反映初始取向的织构特性。通过Miller指数的形式将提取的取向信息分配给材料,作为CPFEM的初始条件,并采用3D Voronoi镶嵌技术对空间分布和晶粒形态进行分析。为探究微观结构对孔洞生长的影响,分别建立含有孔洞的单晶和多晶模型,如图14所示。
图13
图13
5182-O铝合金初始取向及晶粒数量为400和500晶时取向织构的极图
Fig.13
Pole figures of textures for 5182-O aluminum alloys
(a) initial orientation (b) 400 grain orientation (c) 500 grain orientation
图14
图14
微观结构的横截面模型
Fig.14
Cross-section models of the microstructure
(a) single crystals with holes (b) polycrystals with holes
3.3 边界条件与应力状态
式中,x为节点对的当前位置,x0为节点对的初始位置,完全周期性边界条件表明每对节点(M–, M+)在周期性位移场(uper)中保持相同的值,即
由于
式中,I为应力不变量。
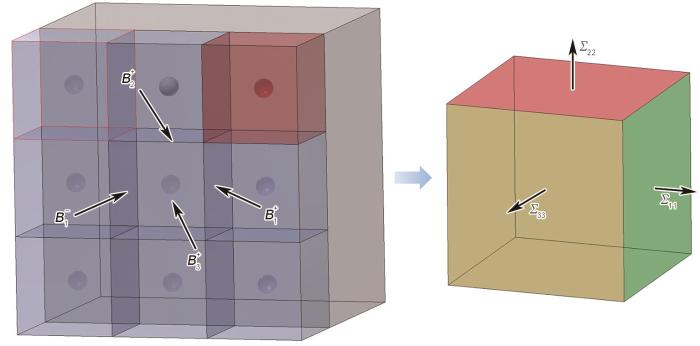
受完全周期性边界条件约束的RVE模型受到对角线三轴宏观应力状态的影响,其中宏观剪切应力被忽略,如图15所示。施加宏观载荷时要求变形过程中Cauchy应力比(β1 = Σ11 / Σ33和β2 = Σ22 / Σ33)保持不变,其中Σ11、Σ22和Σ33为指定宏观Cauchy应力张量( Σ )的对角线分量。平均应力(Σm)和
图15
图15
RVE模型的宏观应力状态
Fig.15
Macroscopic stress states of RVE model (
假设宏观Cauchy应力分量满足Σ11
通过恒定β1和β2,可在变形过程中得到η和
3.4 RVE模拟结果分析
为深入探究单晶中晶体取向对孔洞生长行为的影响,选取图11b所示的5个关键取向织构进行RVE模拟,并且对单向拉伸和单向压缩应力状态进行模拟。
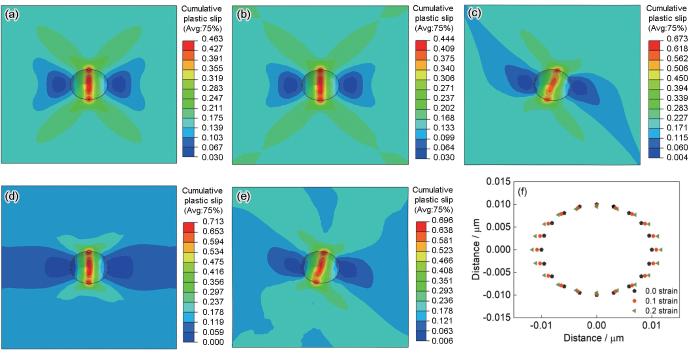
以归一化孔洞体积分数的演变作为等效应变的函数。图16和17分别为单向拉伸和单向压缩状态下应变为0.2时5182-O铝合金的累积塑性滑移云图和应变为0.0~0.2时剖面图。对比2种应力状态下的云图可以看出,最大累积塑性滑移都发生在孔洞中间位置,Copper织构和S织构的孔洞变形最明显,其次是Brass织构。Cube织构和Goss织构的累积塑性滑移云图类似,且由图16f可知,随着应变的增加,孔洞的剖面轮廓逐渐被拉长,导致归一化孔洞体积分数逐渐增加;图17f中剖面轮廓表明,归一化孔洞体积分数随着应变的增加逐渐减小。不同织构导致在相同应变下的累积塑性滑移云图有明显的区别,这验证了单晶中孔洞生长表现出的显著取向依赖性。
图16
图16
单向拉伸、0.2应变条件下5182-O铝合金的累积塑性滑移云图和应变为0.0~0.2时剖面图
Fig.16
Contour maps of cumulative plastic slips of 5182-O aluminum alloy at 0.2 strain under uniaxial tension (a-e) and cross-sectional profile at strains of 0.0-0.2 (f)
(a) Cube texture (b) Goss texture (c) Brass texture (d) Copper texture (e) S texture
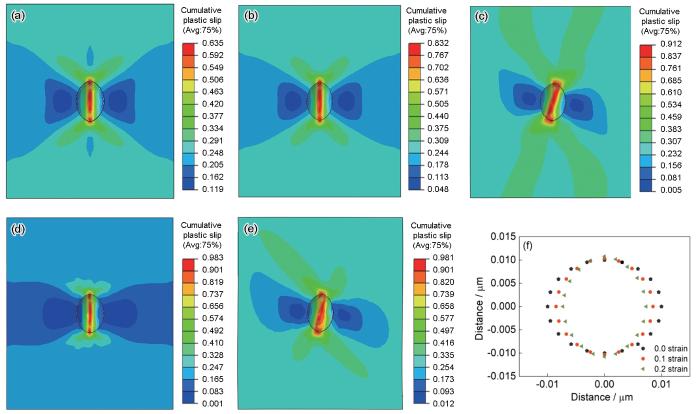
图17
图17
单向压缩、0.2应变条件下5182-O铝合金的累积塑性滑移云图和应变为0.0~0.2时剖面图
Fig.17
Contour maps of cumulative plastic slips of 5182-O aluminum alloy at 0.2 strain under uniaxial compression (a-e) and cross-sectinal profile at strains of 0.0-0.2 (f)
(a) Cube texture (b) Goss texture (c) Brass texture (d) Copper texture (e) S texture
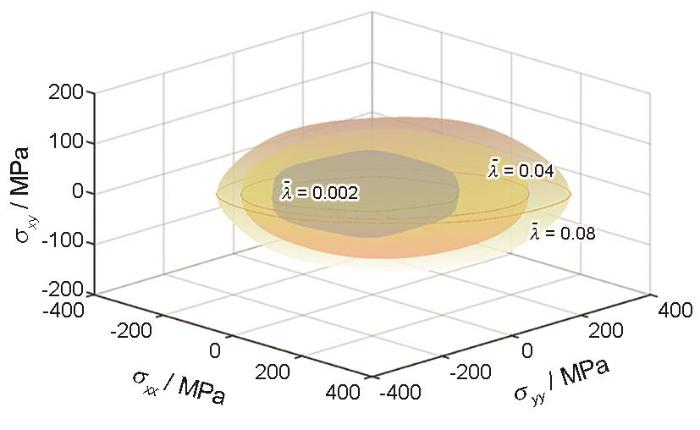
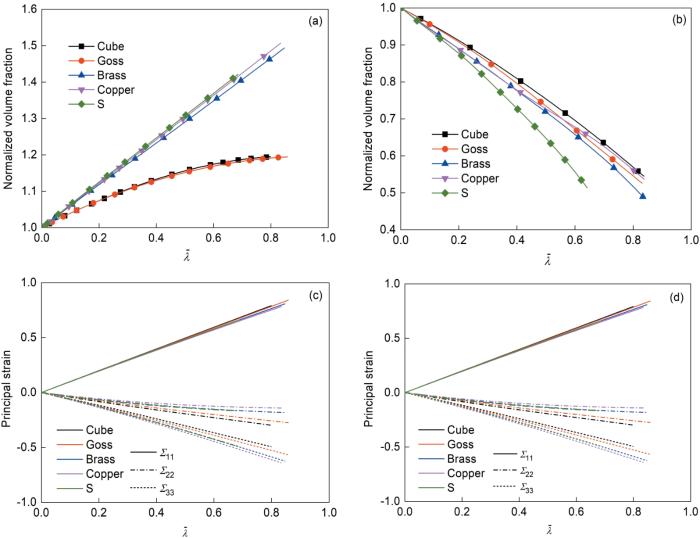
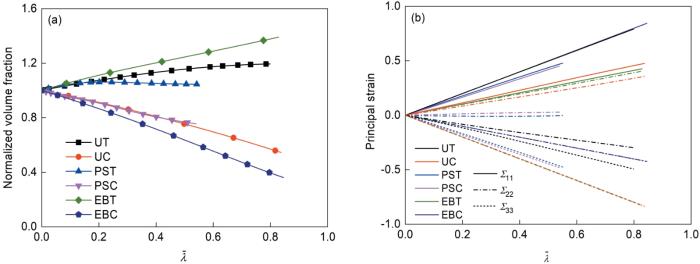
图18为归一化体积分数和主应变随等效塑性应变的变化曲线。由图可知,随着
图18
图18
5182-O铝合金中归一化体积分数和主应变随等效塑性应变的演变
Fig.18
Evolutions of normalized volume fractions (a, b) and principal strains (c, d) with
(a, c) uniaxial tensile stress state (η = 1/3) (b, d) uniaxial compressive stress state (η = -1/3)
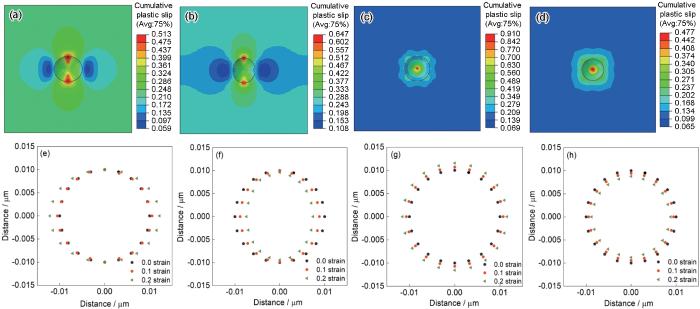
图19为5182-O铝合金在0.2应变条件下,不同应力状态对应的累积塑性滑移云图和剖面图。等轴双压和等轴双拉试样的应力三轴度分别为-2/3和2/3。图19f显示了Cube织构在单晶模拟中的累积塑性滑移随应变的演变。平面应变的孔洞形状演变为扁圆形,而双轴应变下孔洞形状演变为圆形。模拟结果表明,在4种应力状态下,塑性变形均始于孔洞内表面的中心区域。然而,剪切带的传播和孔洞形状的演变在很大程度上取决于应力三轴度。在平面应变条件下,随着塑性变形的进行,最初形成的剪切带迅速扩散至孔洞侧表面,随后第二剪切带快速萌生并传播到中心区域外表面。因此,塑性变形集中在相邻孔洞间的垂直韧带上,材料其余部分保持弹性变形状态,导致孔洞形貌演变为椭圆形。在双轴应力条件下,剪切带优先在孔洞内表面的中间区域形成,且孔洞生长过程中的材料主体保持弹性变形状态。因此,在孔洞生长过程中,孔洞形貌保持为相对球形。图20为不同应力状态下5182-O铝合金中归一化体积分数和主应变随等效塑性应变的变化曲线。由图可知,在双轴应力状态下,由于塑性变形和相应的孔洞扩展局限于剪切带,在相对较低的等效塑性应变下的孔洞扩展速率比较快。
图19
图19
不同应力状态下应变为0.2时5182-O铝合金的累积塑性滑移云图和剖面图
Fig.19
Contour maps of cumulative plastic slips for 5182-O aluminum alloys with 0.2 strain under different stress states (a-d) and cross-sectional profiles (e-h)
(a, e) plane strain tension (b, f) plane strain compression (c, g) equiaxed double tension (d, h) equiaxed double compression
图20
图20
不同应力状态下5182-O铝合金中归一化体积分数和主应变随等效塑性应变的演变
Fig.20
Evolutions of normalized volume fractions (a) and principal strains (b) with
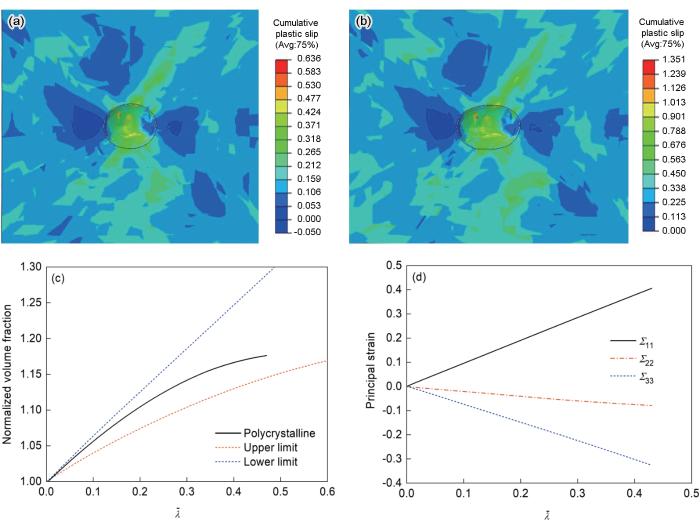
由前文可知,500个晶粒可以充分反映初始取向的织构特性。提取的500个晶粒取向以Miller指数的形式分配给材料属性作为CPFEM的初始取向,多晶中孔洞演变的模拟结果如图21所示。与单晶相比,多晶的孔洞生长受晶粒形貌、晶粒取向分布、孔洞相对位置以及孔洞尺寸等因素的影响。多晶在单向拉伸状态下的孔洞生长的模拟结果如图21a和b所示,随着
图21
图21
不同等效塑性应变下多晶5182-O铝合金的累积塑性滑移云图及归一化体积分数和主应变随等效应变的演变
Fig.21
Contour maps of cumulative plastic slips (a, b) and evolutions of normalized volume fractions (c) and principal strains (d) with
(a)
4 结论
(1) 5182-O铝合金的屈服行为表现出明显的应力状态敏感性。合金的屈服强度及塑性演化特征会随着应力状态的变化而发生非线性变化。不同应力状态下5182-O铝合金的最大强度差异约为8%,各向异性的强度差异均低于1%,因此对于各向异性和应力状态导致的硬化差异应合理建模。
(2) 利用逆向工程方法结合实验数据可得到不同应力状态和各向异性条件下合金的塑性行为,以此作为pDrucker屈服函数的解析依据。在非关联流动准则下解析pDrucker函数的参数,能够准确描述不同应力状态下塑性响应的差异和演变,扩展的各向异性形式函数在RD、DD和TD上有比较高的预测精度。
(3) 塑性模拟Copper织构和S织构的孔洞变形最明显,这验证了单晶中的孔洞生长表现出很强的取向依赖性。不同应力状态下的塑性变形均起始于孔洞内表面的中心区域,但是剪切带的传播和孔洞形状的演变取决于应力三轴度。多晶孔洞的不规则演变导致归一化体积分数曲线的斜率逐渐变缓,表明晶粒取向与孔洞演变间存在密切联系。
参考文献
Research state of lightweight material and manufacture processes in automotive industry
[J].
汽车轻量化材料及制造工艺研究现状
[J].
Recent development and prospects for giant plane aluminum alloys
[J].
大飞机用铝合金的研究现状及展望
[J].
Overview of research and development for aluminum matrix composites driven by aerospace equipment demand
[J].Tianwen-1 is China's first planetary probe. Its core, the rover Zhurong, undertook the task of tour and survey, and had extended the mission over the designed 90-Martian-day period limit on Mars. The rover was equipped with various silicon-carbide-particle-reinforced aluminum matrix composites for its bearing structure, motion system, and detectors to meet design requirements, such as lightweight, wear resistance, impact resistance, and dimensional stability. The use of these composites has set a new record for the proportion of aluminum matrix composites used in Chinese spacecraft. This paper discusses the research and development process of the four types of aluminum matrix composites used for the rover Zhurong: property simulation, material design, preparation, and processing. Additionally, the paper introduces new research and development paradigms based on material genetic engineering and the use of synchrotron radiation or neutron scattering facilities. The future development of aluminum matrix composites for high-tech equipment is also discussed.
航天装备牵引下的铝基复合材料研究进展与展望
[J].天问一号是我国第一个行星探测器,其核心祝融号火星车承担着星面巡视和探测重任,已圆满完成预定90个火星日的探测并进入拓展任务。火星车上使用了多种SiC颗粒增强铝基复合材料,分别满足承载结构、运动机构、探测器结构的轻量化、耐磨损、耐冲击、尺寸稳定等苛刻服役要求,用量刷新了我国航天器铝基复合材料占比记录。本文介绍了针对火星车需求的4种铝基复合材料的研发历程,尤其是性能仿真、材料成分设计与制备加工等。在此基础上,针对未来飞行器等先进装备更苛刻服役工况对材料性能的更高要求,对低成本、高效制备和快速响应的需求,介绍了基于材料基因工程思想与大科学装置的研发新模式,展望了铝基复合材料未来的发展方向。
Electrical energy storage for transportation-approaching the limits of, and going beyond, lithium-ion batteries
[J].
A review on forming techniques for manufacturing lightweight complex-shaped aluminium panel components
[J].
On material substitution in automotive BIWs—From steel to aluminum body sides
[J].
A review on mechanical joining of aluminium and high strength steel sheets by plastic deformation
[J].
Effect of post-aging on microstructure and mechanical properties of an ultrafine-grained 6061 aluminum alloy
[J].Al-Mg-Si alloys are widely used in automotive body panels and parts of the engine owing to their low density, medium strength, high specific strength, good corrosion resistance and other characteristics. Currently, there are many studies on the precipitation behavior of undeformed Al-Mg-Si aluminum alloy, but there is a lack of research on the precipitation evolution and precipitation strengthening mechanism of ultra-fine grained 6061 aluminum alloy at different post-aging temperatures. In this study, the microstructure and mechanical properties of an ultrafine grain 6061 aluminum alloy produced by combining the equal channel angular pressing (ECAP) and post aging methods was comparatively evaluated via TEM, XRD, microhardness tests, and tensile tests. The results indicated that the average grain size of the alloy after two ECAP passes was refined to 210 nm. The average grain size of the alloy after the ECAP pass at 80oC and 20 min post aging was 278 nm; moreover, the fine needle β'', L phase, and Q' phase precipitates at nanoscale were dispersed in the matrix. Furthermore, the tensile and yield strengths were 514 and 483 MPa, respectively, while maintaining a remarkably uniform elongation of 15.1%. These results indicate that numerous dislocations introduced by ECAP in the matrix provide a location for the nucleation of the precipitate, which accelerates the precipitation kinetics during the post aging process. The high strength and toughness of the ECAP alloy after low temperature post aging can be attributed to the grain refinement strengthening, dislocation strengthening, and nanoprecipitation strengthening. Thus, the evolution of the aging precipitates during the ECAP and post aging alloy was analyzed.
后时效对超细晶6061铝合金微观结构与力学性能的影响
[J].采用TEM、XRD、显微硬度实验和拉伸实验,利用等通道转角挤压(ECAP)和后时效相结合制备出超细晶6061铝合金,对其微观结构和力学性能进行了对比研究。结果表明,经过两道次ECAP后,合金的平均晶粒尺寸细化到210 nm。两道次ECAP + 80℃、20 min低温后时效,合金的平均晶粒尺寸为278 nm,基体中弥散分布细小的针状β''、L相和Q'相纳米级析出物,拉伸强度和屈服强度分别达到514和483 MPa,并保持了15.1%的均匀伸长率。ECAP在基体中引入的大量位错促进了析出相的形核,加速了时效过程中的析出动力学;ECAP低温后时效,合金的高强度和高韧性与细晶强化、位错强化和纳米析出相强化有关。基于实验结果,分析了合金ECAP和后时效过程中时效相的演变过程。
Recent development in aluminium alloys for the automotive industry
[J].
Microstructure and properties of 5182 aluminum alloy automobile body sheet
[D].
汽车车身用5182铝合金板组织与性能研究
[D].
Fracture behavior of a rapidly solidified thin-strip continuous cast AA5182 Al-Mg alloy with the Portevin-Le Chatelier effect under varying strain rates
[J].
Portevin-Le Chatelier effect in heterogeneous microstructural condition produced by friction-stir processing of Al-Mg alloy
[J].
Effects of initial grain size and strengthening phase on thermal deformation and recrystallization behavior of GH4096 superalloy
[J].GH4096 alloy were used for disks and shafts of advanced gas turbine engines owing to its excellent properties such as resistance to creep, fatigue, and corrosion as well as microstructure stability up to about 700oC. In this study, GH4096, a hard-to-deform disk superalloy, was processed through an advanced cast and wrought route to avoid the expensive power metallurgy (P/M) route. Many types of full-scale disk forgings possessing homogeneous fine-grained microstructures were successfully carried out, and the ultrasonic inspectability was comparative to that of the alloy produced by the P/M route. The effects of the initial grain size and strengthening phase on hot deformation behavior and dynamic recrystallization (DRX) were studied by OM, SEM, EBSD, and TEM under different deformation parameters. The results showed that as the initial grain size decreased within the temperature range of 1050-1120oC, the flow peak stresses decreased and the fractions of DRX increased. With an increase in the initial grain size, the thermal deformation temperature required for complete dynamic recrystallization decreased, and also the critical strain of dynamic recrystallization decreased. The initial grain size and the strain did not affect the recrystallized grain size when deformed at a sub-solvus temperature. The thermal deformation constitutive equations related to the initial grain sizes were established and the activation energies of thermal deformation related to the original grain sizes were calculated. The effect of γ' phase size on the thermal deformation behavior in as-cast microstructure was studied. In the sub-solvus temperature range, the thermal deformation resistance could be effectively reduced with the increase in the size of γ' phase, the critical strain of DRX was decreased, and the DRX fraction was also increased. The dynamic recrystallization mechanisms related to the γ' phase and initial grain size were also discussed. DRX nucleation takes place at the sub-grains near original grain boundaries for samples with larger initial grain size deformed at sub-solvus temperature. For samples with fine initial grain size, the interface slip of incoherent γ' phase is the significant dynamic softening mechanism during the sub-solvus temperature deformation. For as-cast samples, the main dynamic softening mechanism is original grain boundary bowing out DRX nucleation and coarse second-phase-induced DRX nucleation.
初始晶粒尺寸和强化相对GH4096高温合金热变形行为和再结晶的影响
[J].以镍基变形高温合金GH4096为研究对象,进行了不同组织状态下的热压缩实验,分析了该合金热变形流变行为特点,并采用OM、SEM、EBSD和TEM等手段研究了热压缩过程中初始晶粒尺寸(晶界面积和数量)和强化相对动态再结晶行为及组织演变的影响。结果表明:在1050~1120℃温度范围内,随着初始晶粒尺寸的减小,峰值流变应力降低,动态再结晶分数增加,实现完全动态再结晶所需热变形温度降低,发生动态再结晶的临界应变降低;在亚固溶温度下热变形时,动态再结晶晶粒尺寸与初始晶粒尺寸和变形量没有相关性;计算了与初始晶粒尺寸相关的热变形激活能,并建立了与热变形前的初始晶粒尺寸相关的热变形本构方程;研究了铸态组织中强化相γ'相形态对热变形行为的影响,在亚固溶温度下热变形时,随着强化相γ'相尺寸的增加,可一定程度降低热变形峰值流变应力,降低动态再结晶的临界应变,提高动态再结晶分数。分析讨论了GH4096合金不同组织状态下的主导动态软化机制。
The Portevin-Le Chatelier effect in nickel-base superalloys: Origins, consequences and comparison to strain ageing in other alloy systems
[J].
Mechanical behaviors and deformation constitutive equations of CrFeNi medium-entropy alloys under tensile conditions from 77 K to 1073 K
[J].Concentrated multicomponent alloys (CMCAs) or high/medium-entropy alloys (HEAs/MEAs) possess outstanding comprehensive properties, causing them to have the potential to be the next generation of structural materials. Phenomena occurring under dynamic tensile loading or high/low temperature of such alloys have been hardly investigated. However, its understanding is essentially needed in their application in automotive, aerospace, and military industries. Meanwhile, the suitable constitutive equations of CMCAs under such cases have been rarely investigated. In this work, the thermodynamic behavior of equiatomic CrFeNi MEA with single-phase fcc structure has been systematically investigated at strain rates from 10-3 s-1 to 1800 s-1 and temperatures from 77 K to 1073 K. The results showed that as the deformation temperature decreased from 1073 K to 77 K, the yield stress was improved significantly from 125 MPa to 415 MPa. Meanwhile, the uniform elongation increased from 2% to 82%. The abnormal uniform elongation appearing at 673 K was closely related to dynamic strain aging. As the strain rate increased from 10-3 s-1 to 1800 s-1 at a constant temperature of 77 K, the strength increased significantly (e.g., the yield stress increased from 415 MPa to 595 MPa), and the uniform elongation remained unchanged, still maintaining 68% at 1800 s-1. After deformation, there were no second phases attributed to a large Ni amount in the alloys. Some deformation twins appeared at 77 K. Based on the experimental results, the relationship between yield stress and temperatures/strain rates could be successfully revealed using the ZA model. Moreover, regression analysis and constraint optimization established two phenomenological constitutive models (JC and KHL models) and three physically-based constitutive models (PB model, ZA model, and NNL model). JC and PB models had the highest and lowest description accuracy, respectively. Besides, the JC model was hard to describe the case that the work hardening decreased due to the change of temperature or strain rates, and the PB model was unsuitable in characterizing the complex work hardening behaviors.
CrFeNi中熵合金在宽温域拉伸条件下的力学行为与变形本构方程
[J].
A critical review on the Portevin-Le Chatelier effect in aluminum alloys
[J].
Spatio-temporal characteristics of plastic instability in AA5182-O during biaxial deformation
[J].
Strength modeling of sheet metals from shear to plane strain tension
[J].
Relation of experiments to mathematical theories of plasticity
[J].
A non-quadratic pressure-sensitive constitutive model under non-associated flow rule with anisotropic hardening: Modeling and validation
[J].
Analysis of electric pulse-assisted forming based on neural network plastic evolution model
[J].
An evolving plasticity model considering anisotropy, thermal softening and dynamic strain aging
[J].
Characterization and modelling of evolving plasticity behaviour up to fracture for FCC and BCC metals
[J].
A virtual materials testing approach to calibrate anisotropic yield functions for the simulation of earing during deep drawing of aluminium alloy sheet
[J].
Analysis of size dependent earing evolution in micro deep drawing of TWIP steel by using crystal plasticity modeling
[J].
A polycrystal plasticity based thermo-mechanical-dynamic recrystallization coupled modeling method and its application to light weight alloys
[J].
Multi-scale modelling of evolving plastic anisotropy during Al-alloy sheet forming
[J].
Multi-scale numerical investigation of deep drawing of 6K21 aluminum alloy by crystal plasticity and a stress-invariant based anisotropic yield function under non-associated flow rule
[J].
A six-component yield function for anisotropic materials
[J].
Investigation on intragranular and intergranular void growth and their competition in polycrystalline materials
[J].
In-situ EBSD-DIC simulation of microstructure evolution of aluminum alloy welds
[J].
Crystal plasticity quantification of anisotropic tensile and fatigue properties in laser powder bed fused Inconel 718 superalloy
[J].
Modelling of the plastic behavior of Cu crystal with twinning-induced softening and strengthening effects
[J].Dislocation slip and twinning are the main deformation mechanisms dominating plastic behavior of crystalline materials, such as twinning-induced plasticity steel, Cu, Mg, and their alloys. The influence of twinning and interaction between dislocations and twins on the plastic deformation of crystal materials is complex. On the one hand, a sudden stress drop in the stress-strain curve during twin nucleation, propagation, and growth (TNPG) of crystal materials, i.e., the twinning softening effect, is evident. On the other hand, the interaction between twins and dislocations demonstrates the strengthening effect of plastic deformation. Polycrystalline materials are used in engineering applications, and twin nucleation corresponds to different strains in each grain. Therefore, determining the influence of twin softening and strengthening effects on plastic deformation of polycrystalline materials is difficult. In this work, a crystal plastic finite element model of Cu, considering the twinning softening effect, was developed to describe the TNPG process based on the crystal plasticity theory. The method was used to reveal the influence of twins' activation and their interaction with dislocations on strain hardening during the tension of Cu single crystal and polycrystal. The results show that twinning has an evident orientation effect. Under twinning favorable orientation, a sudden stress drop in the stress-strain curve caused by twinning propagation during plastic deformation of Cu single crystal is evident, and the total plastic deformation can be divided into three stages: slip, twinning, and interaction between dislocations and twins. Compared with Cu single crystal, the stress-strain curve changes smoothly and the strain hardening rate is higher during the tension of Cu polycrystal. Meanwhile, the dislocation density is concentrated at the grain boundary, and twins are easy to form at the grain boundary during the plastic deformation of Cu polycrystal.
孪生诱发软化与强化效应的Cu晶体塑性行为模拟
[J].基于晶体塑性理论,考虑孪生软化效应建立了描述孪晶形核、增殖和长大的位错密度基晶体塑性有限元模型。应用该模型揭示了不同晶体取向Cu单晶拉伸变形过程中位错滑移、孪生激活及其交互作用下的宏观塑性行为演化规律,进一步分析了Cu多晶拉伸变形过程中晶粒间交互作用对孪生软化、应变硬化等宏观塑性行为的影响。结果表明:孪生具有明显的取向效应,在孪生主导塑性条件下,Cu单晶塑性变形过程中孪晶增殖导致应力-应变曲线存在明显的应力突降现象,其塑性变形分为滑移、孪生及位错与孪晶交互作用3个阶段;此外,随着饱和孪晶体积分数增加,Cu单晶塑性变形过程中第3阶段的应变硬化率也随之提升。进一步模拟Cu多晶拉伸变形的塑性行为可知,在晶粒间交互作用下孪晶形核、增殖和长大过程中不会出现应力突降现象,与Cu单晶相比整个塑性变形过程具有更高的应变硬化率;Cu多晶塑性变形过程中位错密度在晶界处出现集中现象,孪晶也容易在晶界处形成。
Deformation mechanisms of additively manufactured Hastelloy-X: A neutron diffraction experiment and crystal plasticity finite element modeling
[J].
Dislocation density based model for plastic deformation and globularization of Ti-6Al-4V
[J].