Multiaxial isothermal and thermomechanical fatigue behavior of 316H stainless steel welded joint and life prediction
1
2026
... 过去十几年间,人类对可靠且可持续的能源的迫切需求极大地激发了对先进核能系统的兴趣,其中包括第四代反应堆和聚变反应堆.然而,先进核能系统中的结构材料必须承受恶劣的环境,其特点是高温、复杂应力,尤其是强辐照.在此背景下,焊接作为不可或缺的制造工艺被广泛应用于核能结构系统,例如反应堆压力容器(RPV)的内表面堆焊、反应堆压力容器与蒸汽发生器之间的连接以及主管道的焊接等.焊接过程中,快速冷却和热循环会导致材料内部产生复杂的微观结构,进而影响焊接部件的结构完整性和力学性能,因此焊接接头或焊缝金属往往被认为是结构部件中最薄弱的部分,在服役过程中比母材更早发生失效.值得注意的是,焊接接头的整体性能实质上由母材和焊缝金属的综合作用所决定.因此,有效地评价焊接接头的服役行为需要深入揭示母材与焊缝金属的组织演化规律及其差异机制[1,2]. ...
Tracking martensitic substructure evolution in the heat-affected zone of P91 steel: Integrating CSLM observation and post-mortem microstructural analysis
1
2025
... 过去十几年间,人类对可靠且可持续的能源的迫切需求极大地激发了对先进核能系统的兴趣,其中包括第四代反应堆和聚变反应堆.然而,先进核能系统中的结构材料必须承受恶劣的环境,其特点是高温、复杂应力,尤其是强辐照.在此背景下,焊接作为不可或缺的制造工艺被广泛应用于核能结构系统,例如反应堆压力容器(RPV)的内表面堆焊、反应堆压力容器与蒸汽发生器之间的连接以及主管道的焊接等.焊接过程中,快速冷却和热循环会导致材料内部产生复杂的微观结构,进而影响焊接部件的结构完整性和力学性能,因此焊接接头或焊缝金属往往被认为是结构部件中最薄弱的部分,在服役过程中比母材更早发生失效.值得注意的是,焊接接头的整体性能实质上由母材和焊缝金属的综合作用所决定.因此,有效地评价焊接接头的服役行为需要深入揭示母材与焊缝金属的组织演化规律及其差异机制[1,2]. ...
Bubble formation in helium-implanted nanostructured ferritic alloys at elevated temperatures
1
2021
... 持续的辐照损伤会产生饱和点缺陷(空位和间隙原子),在扩散、温度、应力以及晶界、位错和界面等微观结构的综合作用下,这些点缺陷往往会演变成位错环以及孔洞等纳米级的辐照缺陷.其中,由于核嬗变形成的He不溶于材料,且会与空位团簇结合形成He泡,同时引发辐照硬化和氦脆化,进而可能导致金属沿晶断裂,因此辐照He泡受到了研究人员的广泛关注[3,4].316L钢的原位He+辐照实验表明,更高的辐照剂量和温度会促进He泡的形核与生长[5].He泡的生长粗化研究往往通过对预辐照试样进行退火处理后的He泡观察.Chen等[6]研究发现,在经He+辐照的FeCrAl合金退火过程中,由于点缺陷迁移和He泡的长大合并,He泡尺寸增大、密度降低.此外,Ostwald熟化被认为是气泡生长的另一种机制[7].He泡对力学性能的影响也是核材料领域的研究重点.Judge等[8]通过透射电子显微镜(TEM)观察到沿晶界和界面排列的He泡,并将沿晶断裂与沿晶界分布的He泡直接关联起来.Miura等[9]通过微拉伸实验发现,沿晶界发生的脆性断裂与He浓度、He泡间距和基体硬化程度相关. ...
Helium irradiation-induced ultrahigh hardening in niobium
1
2022
... 持续的辐照损伤会产生饱和点缺陷(空位和间隙原子),在扩散、温度、应力以及晶界、位错和界面等微观结构的综合作用下,这些点缺陷往往会演变成位错环以及孔洞等纳米级的辐照缺陷.其中,由于核嬗变形成的He不溶于材料,且会与空位团簇结合形成He泡,同时引发辐照硬化和氦脆化,进而可能导致金属沿晶断裂,因此辐照He泡受到了研究人员的广泛关注[3,4].316L钢的原位He+辐照实验表明,更高的辐照剂量和温度会促进He泡的形核与生长[5].He泡的生长粗化研究往往通过对预辐照试样进行退火处理后的He泡观察.Chen等[6]研究发现,在经He+辐照的FeCrAl合金退火过程中,由于点缺陷迁移和He泡的长大合并,He泡尺寸增大、密度降低.此外,Ostwald熟化被认为是气泡生长的另一种机制[7].He泡对力学性能的影响也是核材料领域的研究重点.Judge等[8]通过透射电子显微镜(TEM)观察到沿晶界和界面排列的He泡,并将沿晶断裂与沿晶界分布的He泡直接关联起来.Miura等[9]通过微拉伸实验发现,沿晶界发生的脆性断裂与He浓度、He泡间距和基体硬化程度相关. ...
TEM study of the nucleation of bubbles induced by He implantation in 316L industrial austenitic stainless steel
1
2015
... 持续的辐照损伤会产生饱和点缺陷(空位和间隙原子),在扩散、温度、应力以及晶界、位错和界面等微观结构的综合作用下,这些点缺陷往往会演变成位错环以及孔洞等纳米级的辐照缺陷.其中,由于核嬗变形成的He不溶于材料,且会与空位团簇结合形成He泡,同时引发辐照硬化和氦脆化,进而可能导致金属沿晶断裂,因此辐照He泡受到了研究人员的广泛关注[3,4].316L钢的原位He+辐照实验表明,更高的辐照剂量和温度会促进He泡的形核与生长[5].He泡的生长粗化研究往往通过对预辐照试样进行退火处理后的He泡观察.Chen等[6]研究发现,在经He+辐照的FeCrAl合金退火过程中,由于点缺陷迁移和He泡的长大合并,He泡尺寸增大、密度降低.此外,Ostwald熟化被认为是气泡生长的另一种机制[7].He泡对力学性能的影响也是核材料领域的研究重点.Judge等[8]通过透射电子显微镜(TEM)观察到沿晶界和界面排列的He泡,并将沿晶断裂与沿晶界分布的He泡直接关联起来.Miura等[9]通过微拉伸实验发现,沿晶界发生的脆性断裂与He浓度、He泡间距和基体硬化程度相关. ...
In-situ TEM observation of the evolution of dislocation loops and helium bubbles in a pre helium irradiated FeCrAl alloy during annealing
1
2020
... 持续的辐照损伤会产生饱和点缺陷(空位和间隙原子),在扩散、温度、应力以及晶界、位错和界面等微观结构的综合作用下,这些点缺陷往往会演变成位错环以及孔洞等纳米级的辐照缺陷.其中,由于核嬗变形成的He不溶于材料,且会与空位团簇结合形成He泡,同时引发辐照硬化和氦脆化,进而可能导致金属沿晶断裂,因此辐照He泡受到了研究人员的广泛关注[3,4].316L钢的原位He+辐照实验表明,更高的辐照剂量和温度会促进He泡的形核与生长[5].He泡的生长粗化研究往往通过对预辐照试样进行退火处理后的He泡观察.Chen等[6]研究发现,在经He+辐照的FeCrAl合金退火过程中,由于点缺陷迁移和He泡的长大合并,He泡尺寸增大、密度降低.此外,Ostwald熟化被认为是气泡生长的另一种机制[7].He泡对力学性能的影响也是核材料领域的研究重点.Judge等[8]通过透射电子显微镜(TEM)观察到沿晶界和界面排列的He泡,并将沿晶断裂与沿晶界分布的He泡直接关联起来.Miura等[9]通过微拉伸实验发现,沿晶界发生的脆性断裂与He浓度、He泡间距和基体硬化程度相关. ...
Helium bubble evolution and hardening in 316L by post-implantation annealing
1
2018
... 持续的辐照损伤会产生饱和点缺陷(空位和间隙原子),在扩散、温度、应力以及晶界、位错和界面等微观结构的综合作用下,这些点缺陷往往会演变成位错环以及孔洞等纳米级的辐照缺陷.其中,由于核嬗变形成的He不溶于材料,且会与空位团簇结合形成He泡,同时引发辐照硬化和氦脆化,进而可能导致金属沿晶断裂,因此辐照He泡受到了研究人员的广泛关注[3,4].316L钢的原位He+辐照实验表明,更高的辐照剂量和温度会促进He泡的形核与生长[5].He泡的生长粗化研究往往通过对预辐照试样进行退火处理后的He泡观察.Chen等[6]研究发现,在经He+辐照的FeCrAl合金退火过程中,由于点缺陷迁移和He泡的长大合并,He泡尺寸增大、密度降低.此外,Ostwald熟化被认为是气泡生长的另一种机制[7].He泡对力学性能的影响也是核材料领域的研究重点.Judge等[8]通过透射电子显微镜(TEM)观察到沿晶界和界面排列的He泡,并将沿晶断裂与沿晶界分布的He泡直接关联起来.Miura等[9]通过微拉伸实验发现,沿晶界发生的脆性断裂与He浓度、He泡间距和基体硬化程度相关. ...
Intergranular fracture in irradiated Inconel X-750 containing very high concentrations of helium and hydrogen
1
2015
... 持续的辐照损伤会产生饱和点缺陷(空位和间隙原子),在扩散、温度、应力以及晶界、位错和界面等微观结构的综合作用下,这些点缺陷往往会演变成位错环以及孔洞等纳米级的辐照缺陷.其中,由于核嬗变形成的He不溶于材料,且会与空位团簇结合形成He泡,同时引发辐照硬化和氦脆化,进而可能导致金属沿晶断裂,因此辐照He泡受到了研究人员的广泛关注[3,4].316L钢的原位He+辐照实验表明,更高的辐照剂量和温度会促进He泡的形核与生长[5].He泡的生长粗化研究往往通过对预辐照试样进行退火处理后的He泡观察.Chen等[6]研究发现,在经He+辐照的FeCrAl合金退火过程中,由于点缺陷迁移和He泡的长大合并,He泡尺寸增大、密度降低.此外,Ostwald熟化被认为是气泡生长的另一种机制[7].He泡对力学性能的影响也是核材料领域的研究重点.Judge等[8]通过透射电子显微镜(TEM)观察到沿晶界和界面排列的He泡,并将沿晶断裂与沿晶界分布的He泡直接关联起来.Miura等[9]通过微拉伸实验发现,沿晶界发生的脆性断裂与He浓度、He泡间距和基体硬化程度相关. ...
Micro-mechanical investigation for effects of helium on grain boundary fracture of austenitic stainless steel
1
2015
... 持续的辐照损伤会产生饱和点缺陷(空位和间隙原子),在扩散、温度、应力以及晶界、位错和界面等微观结构的综合作用下,这些点缺陷往往会演变成位错环以及孔洞等纳米级的辐照缺陷.其中,由于核嬗变形成的He不溶于材料,且会与空位团簇结合形成He泡,同时引发辐照硬化和氦脆化,进而可能导致金属沿晶断裂,因此辐照He泡受到了研究人员的广泛关注[3,4].316L钢的原位He+辐照实验表明,更高的辐照剂量和温度会促进He泡的形核与生长[5].He泡的生长粗化研究往往通过对预辐照试样进行退火处理后的He泡观察.Chen等[6]研究发现,在经He+辐照的FeCrAl合金退火过程中,由于点缺陷迁移和He泡的长大合并,He泡尺寸增大、密度降低.此外,Ostwald熟化被认为是气泡生长的另一种机制[7].He泡对力学性能的影响也是核材料领域的研究重点.Judge等[8]通过透射电子显微镜(TEM)观察到沿晶界和界面排列的He泡,并将沿晶断裂与沿晶界分布的He泡直接关联起来.Miura等[9]通过微拉伸实验发现,沿晶界发生的脆性断裂与He浓度、He泡间距和基体硬化程度相关. ...
Evolution of helium bubbles in SLM 316L stainless steel irradiated with helium ions at different temperatures
1
2022
... 焊接过程中形成的复杂微观结构也会导致He泡演化与对应的母材有所差异.Fu等[10]比较了在700 ℃下1 × 1017 ion/cm2辐照剂量下,固溶态316L和增材制造(AM) 316L钢中的He泡.结果发现,AM 316L钢中的He泡数密度较低,尺寸较大,表明AM 316L钢中的本征微观组织(相界面和位错等)抑制了He泡的形核与生长.白菊菊等[11]认为,位错线对He原子以及间隙子的捕获是导致GH3535合金焊缝中He泡尺寸大于母材的重要原因.本研究团队前期研究[12]也表明,焊缝金属中因为高位错密度偏置吸收间隙原子,导致缺陷复合效应降低,造成空位浓度过饱和,从而导致焊缝金属中He泡尺寸明显大于316H钢母材.然而,由于现有实验观测技术在空间和时间分辨率方面的限制,He泡的生长动力学及其与材料微观组织之间的关联仍不明确. ...
Effect of He ion irradiation on the GH3535 weld metal at high temperature
2
2024
... 焊接过程中形成的复杂微观结构也会导致He泡演化与对应的母材有所差异.Fu等[10]比较了在700 ℃下1 × 1017 ion/cm2辐照剂量下,固溶态316L和增材制造(AM) 316L钢中的He泡.结果发现,AM 316L钢中的He泡数密度较低,尺寸较大,表明AM 316L钢中的本征微观组织(相界面和位错等)抑制了He泡的形核与生长.白菊菊等[11]认为,位错线对He原子以及间隙子的捕获是导致GH3535合金焊缝中He泡尺寸大于母材的重要原因.本研究团队前期研究[12]也表明,焊缝金属中因为高位错密度偏置吸收间隙原子,导致缺陷复合效应降低,造成空位浓度过饱和,从而导致焊缝金属中He泡尺寸明显大于316H钢母材.然而,由于现有实验观测技术在空间和时间分辨率方面的限制,He泡的生长动力学及其与材料微观组织之间的关联仍不明确. ...
... 式中,和分别为基体中产生空位和He原子的恒定值.的取值参考He+辐照实验过程中He原子的产生速率,约2.0 × 10-6 s-1.但对于空位的产生速率,尚未见明确的计算模型.此外,针对本工作研究对象316H钢及其焊缝金属,前期研究工作中的速率理论计算[12]表明,位错作为“偏置缺陷阱”吸收间隙原子和空位的数量不相等,高位错密度的焊缝金属偏置吸收间隙原子的情况下会导致空位过剩,即焊缝中的空位浓度会高于母材.因此,本工作参考Aagesen等[50]的工作,将基体中空位的产生速率设置为 = (6~15),并讨论该参数对He泡演化的影响,从而揭示316H钢母材和焊缝金属中空位浓度差异条件下He泡的演化机制.此外,白菊菊等[11]研究表明,焊缝中存在的大量位错线扩散通道,能够促进He泡长大.为了描述316H钢母材和焊缝金属中扩散的差异,有效扩散系数(Deff)根据下式进行修正[51]: ...
GH3535合金焊缝高温氦离子辐照效应
2
2024
... 焊接过程中形成的复杂微观结构也会导致He泡演化与对应的母材有所差异.Fu等[10]比较了在700 ℃下1 × 1017 ion/cm2辐照剂量下,固溶态316L和增材制造(AM) 316L钢中的He泡.结果发现,AM 316L钢中的He泡数密度较低,尺寸较大,表明AM 316L钢中的本征微观组织(相界面和位错等)抑制了He泡的形核与生长.白菊菊等[11]认为,位错线对He原子以及间隙子的捕获是导致GH3535合金焊缝中He泡尺寸大于母材的重要原因.本研究团队前期研究[12]也表明,焊缝金属中因为高位错密度偏置吸收间隙原子,导致缺陷复合效应降低,造成空位浓度过饱和,从而导致焊缝金属中He泡尺寸明显大于316H钢母材.然而,由于现有实验观测技术在空间和时间分辨率方面的限制,He泡的生长动力学及其与材料微观组织之间的关联仍不明确. ...
... 式中,和分别为基体中产生空位和He原子的恒定值.的取值参考He+辐照实验过程中He原子的产生速率,约2.0 × 10-6 s-1.但对于空位的产生速率,尚未见明确的计算模型.此外,针对本工作研究对象316H钢及其焊缝金属,前期研究工作中的速率理论计算[12]表明,位错作为“偏置缺陷阱”吸收间隙原子和空位的数量不相等,高位错密度的焊缝金属偏置吸收间隙原子的情况下会导致空位过剩,即焊缝中的空位浓度会高于母材.因此,本工作参考Aagesen等[50]的工作,将基体中空位的产生速率设置为 = (6~15),并讨论该参数对He泡演化的影响,从而揭示316H钢母材和焊缝金属中空位浓度差异条件下He泡的演化机制.此外,白菊菊等[11]研究表明,焊缝中存在的大量位错线扩散通道,能够促进He泡长大.为了描述316H钢母材和焊缝金属中扩散的差异,有效扩散系数(Deff)根据下式进行修正[51]: ...
Microstructural and mechanical responses of 316H and weld metal under Helium irradiation at 550 oC
8
2025
... 焊接过程中形成的复杂微观结构也会导致He泡演化与对应的母材有所差异.Fu等[10]比较了在700 ℃下1 × 1017 ion/cm2辐照剂量下,固溶态316L和增材制造(AM) 316L钢中的He泡.结果发现,AM 316L钢中的He泡数密度较低,尺寸较大,表明AM 316L钢中的本征微观组织(相界面和位错等)抑制了He泡的形核与生长.白菊菊等[11]认为,位错线对He原子以及间隙子的捕获是导致GH3535合金焊缝中He泡尺寸大于母材的重要原因.本研究团队前期研究[12]也表明,焊缝金属中因为高位错密度偏置吸收间隙原子,导致缺陷复合效应降低,造成空位浓度过饱和,从而导致焊缝金属中He泡尺寸明显大于316H钢母材.然而,由于现有实验观测技术在空间和时间分辨率方面的限制,He泡的生长动力学及其与材料微观组织之间的关联仍不明确. ...
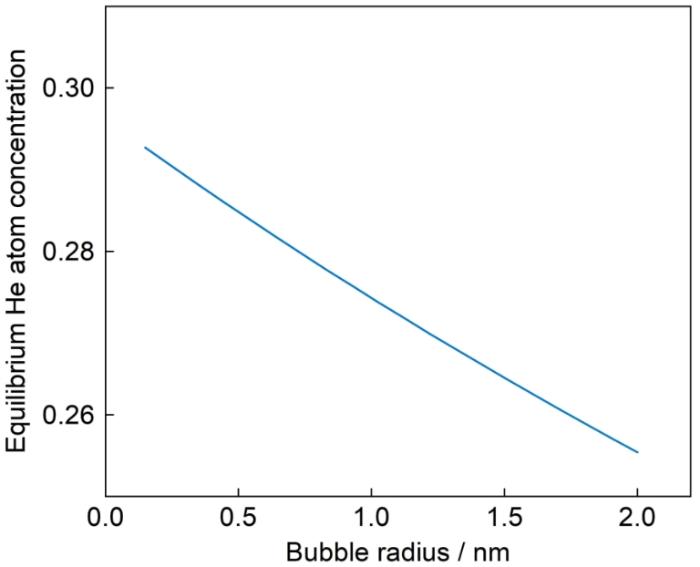
... 图2显示了550 ℃下基于Van der Waals状态方程得出的奥氏体不锈钢He泡中He原子的热力学平衡浓度,所采用的奥氏体不锈钢相关的热力学参数见表2[12,32~34].可见,随着He泡尺寸的增大,He泡中He原子的平衡浓度呈现下降趋势. ...
... He泡相场模拟中所用的热力学参数[12,32~34] ...
... Thermodynamic parameters used in phase field simulation[12,32-34] ...
... [
12]
3.2 × 10-19 | J | | [12] | 6.4 × 10-19 | J |
| Ω[32] | 1.17 × 10-29 | m3 |
| bv[33] | 0.039 | nm3·atom-1 |
| a[33] | 0.0034 | J·m3·mol-2 |
| γs[34] | 1.82 | J·m-2 |
Note:Va—molar fraction, —vacancy formation energy, —He atom formation energy, Ω—atomic volume, bv—Van der Waals constant of He, a—constant for intermolecular attraction, γs—surface tension ...
... [
12]
6.4 × 10-19 | J | | Ω[32] | 1.17 × 10-29 | m3 |
| bv[33] | 0.039 | nm3·atom-1 |
| a[33] | 0.0034 | J·m3·mol-2 |
| γs[34] | 1.82 | J·m-2 |
Note:Va—molar fraction, —vacancy formation energy, —He atom formation energy, Ω—atomic volume, bv—Van der Waals constant of He, a—constant for intermolecular attraction, γs—surface tension ...
... 本工作所涉及的参数主要包括He泡相场模型中的热力学参数、辐照参数以及晶体塑性模型中的力学行为参数.He泡形核与演化的热力学参数均从He泡相场模拟的文献或原子尺度计算的文献中获得(表2[12,32~34]).对于辐照参数,为了保证He泡内部不产生辐照点缺陷,辐照空位和He原子产生项的表达式为: ...
... 式中,和分别为基体中产生空位和He原子的恒定值.的取值参考He+辐照实验过程中He原子的产生速率,约2.0 × 10-6 s-1.但对于空位的产生速率,尚未见明确的计算模型.此外,针对本工作研究对象316H钢及其焊缝金属,前期研究工作中的速率理论计算[12]表明,位错作为“偏置缺陷阱”吸收间隙原子和空位的数量不相等,高位错密度的焊缝金属偏置吸收间隙原子的情况下会导致空位过剩,即焊缝中的空位浓度会高于母材.因此,本工作参考Aagesen等[50]的工作,将基体中空位的产生速率设置为 = (6~15),并讨论该参数对He泡演化的影响,从而揭示316H钢母材和焊缝金属中空位浓度差异条件下He泡的演化机制.此外,白菊菊等[11]研究表明,焊缝中存在的大量位错线扩散通道,能够促进He泡长大.为了描述316H钢母材和焊缝金属中扩散的差异,有效扩散系数(Deff)根据下式进行修正[51]: ...
Molecular dynamics modeling of helium bubbles in austenitic steels
1
2018
... 随着计算机模拟技术的发展,研究人员从原子尺度、纳米尺度和微米尺度开展了大量工作,以揭示He泡的形核、生长和粗化过程.原子模拟表明,间隙He原子迁移能低,易于扩散,且由于结合能高,会与空位结合形成He-空位团簇[13].因此,这些He-空位团簇可作为辐照金属中He泡的形核位点.但由于势函数的限制,分子动力学(MD)在研究He泡的生长和演化方面并未获得大量应用.近年来,介观尺度的相场方法被广泛应用于研究微观结构演变及其对力学性能的影响.基于相场方法,研究人员开展了大量关于核燃料中裂变气体气泡的研究.Stan等[14]和Hu等[15]基于气体原子浓度场(ci)构建了核燃料中气泡的演化,并在随后的研究中进一步引入空位浓度场(cv),该模型能够研究气泡的形核与生长,并有效地模拟了气泡在晶界处的偏聚,但相场能量方程中对气泡的描述较为简单.Millett等[16,17]在热力学框架中引入缺陷形成能,并在控制方程中引入缺陷的产生与复合、湮灭以及晶界的影响.模拟结果表明,气泡的演化经历3个不同的阶段:孕育期,形核和生长期,粗化期;模拟的气泡稳定生长的动力学规律与传统的Johnson-Mehl-Avarami理论吻合较好.Li等[18]采用类似的热力学框架,并基于Kim-Kim-Suzuki (KKS)相场模型研究了UO2中晶内裂变气泡的演化,发现气泡数密度的对数与直径的对数呈线性关系,与实验结果吻合良好.由于气泡内部存在较大的内压,弹性作用在气泡的演化过程中起着重要作用,在最近的研究中,研究人员在相场模型中进一步引入缺陷的弹性相互作用[19,20].Jiang等[21]研究发现,弹性应变能在He泡演化初期影响较小,在后期则会抑制He泡的生长. ...
Models and simulations of nuclear fuel materials properties
1
2007
... 随着计算机模拟技术的发展,研究人员从原子尺度、纳米尺度和微米尺度开展了大量工作,以揭示He泡的形核、生长和粗化过程.原子模拟表明,间隙He原子迁移能低,易于扩散,且由于结合能高,会与空位结合形成He-空位团簇[13].因此,这些He-空位团簇可作为辐照金属中He泡的形核位点.但由于势函数的限制,分子动力学(MD)在研究He泡的生长和演化方面并未获得大量应用.近年来,介观尺度的相场方法被广泛应用于研究微观结构演变及其对力学性能的影响.基于相场方法,研究人员开展了大量关于核燃料中裂变气体气泡的研究.Stan等[14]和Hu等[15]基于气体原子浓度场(ci)构建了核燃料中气泡的演化,并在随后的研究中进一步引入空位浓度场(cv),该模型能够研究气泡的形核与生长,并有效地模拟了气泡在晶界处的偏聚,但相场能量方程中对气泡的描述较为简单.Millett等[16,17]在热力学框架中引入缺陷形成能,并在控制方程中引入缺陷的产生与复合、湮灭以及晶界的影响.模拟结果表明,气泡的演化经历3个不同的阶段:孕育期,形核和生长期,粗化期;模拟的气泡稳定生长的动力学规律与传统的Johnson-Mehl-Avarami理论吻合较好.Li等[18]采用类似的热力学框架,并基于Kim-Kim-Suzuki (KKS)相场模型研究了UO2中晶内裂变气泡的演化,发现气泡数密度的对数与直径的对数呈线性关系,与实验结果吻合良好.由于气泡内部存在较大的内压,弹性作用在气泡的演化过程中起着重要作用,在最近的研究中,研究人员在相场模型中进一步引入缺陷的弹性相互作用[19,20].Jiang等[21]研究发现,弹性应变能在He泡演化初期影响较小,在后期则会抑制He泡的生长. ...
Phase-field modeling of gas bubbles and thermal conductivity evolution in nuclear fuels
1
2009
... 随着计算机模拟技术的发展,研究人员从原子尺度、纳米尺度和微米尺度开展了大量工作,以揭示He泡的形核、生长和粗化过程.原子模拟表明,间隙He原子迁移能低,易于扩散,且由于结合能高,会与空位结合形成He-空位团簇[13].因此,这些He-空位团簇可作为辐照金属中He泡的形核位点.但由于势函数的限制,分子动力学(MD)在研究He泡的生长和演化方面并未获得大量应用.近年来,介观尺度的相场方法被广泛应用于研究微观结构演变及其对力学性能的影响.基于相场方法,研究人员开展了大量关于核燃料中裂变气体气泡的研究.Stan等[14]和Hu等[15]基于气体原子浓度场(ci)构建了核燃料中气泡的演化,并在随后的研究中进一步引入空位浓度场(cv),该模型能够研究气泡的形核与生长,并有效地模拟了气泡在晶界处的偏聚,但相场能量方程中对气泡的描述较为简单.Millett等[16,17]在热力学框架中引入缺陷形成能,并在控制方程中引入缺陷的产生与复合、湮灭以及晶界的影响.模拟结果表明,气泡的演化经历3个不同的阶段:孕育期,形核和生长期,粗化期;模拟的气泡稳定生长的动力学规律与传统的Johnson-Mehl-Avarami理论吻合较好.Li等[18]采用类似的热力学框架,并基于Kim-Kim-Suzuki (KKS)相场模型研究了UO2中晶内裂变气泡的演化,发现气泡数密度的对数与直径的对数呈线性关系,与实验结果吻合良好.由于气泡内部存在较大的内压,弹性作用在气泡的演化过程中起着重要作用,在最近的研究中,研究人员在相场模型中进一步引入缺陷的弹性相互作用[19,20].Jiang等[21]研究发现,弹性应变能在He泡演化初期影响较小,在后期则会抑制He泡的生长. ...
Phase-field simulation of irradiated metals: Part I: Void kinetics
3
2011
... 随着计算机模拟技术的发展,研究人员从原子尺度、纳米尺度和微米尺度开展了大量工作,以揭示He泡的形核、生长和粗化过程.原子模拟表明,间隙He原子迁移能低,易于扩散,且由于结合能高,会与空位结合形成He-空位团簇[13].因此,这些He-空位团簇可作为辐照金属中He泡的形核位点.但由于势函数的限制,分子动力学(MD)在研究He泡的生长和演化方面并未获得大量应用.近年来,介观尺度的相场方法被广泛应用于研究微观结构演变及其对力学性能的影响.基于相场方法,研究人员开展了大量关于核燃料中裂变气体气泡的研究.Stan等[14]和Hu等[15]基于气体原子浓度场(ci)构建了核燃料中气泡的演化,并在随后的研究中进一步引入空位浓度场(cv),该模型能够研究气泡的形核与生长,并有效地模拟了气泡在晶界处的偏聚,但相场能量方程中对气泡的描述较为简单.Millett等[16,17]在热力学框架中引入缺陷形成能,并在控制方程中引入缺陷的产生与复合、湮灭以及晶界的影响.模拟结果表明,气泡的演化经历3个不同的阶段:孕育期,形核和生长期,粗化期;模拟的气泡稳定生长的动力学规律与传统的Johnson-Mehl-Avarami理论吻合较好.Li等[18]采用类似的热力学框架,并基于Kim-Kim-Suzuki (KKS)相场模型研究了UO2中晶内裂变气泡的演化,发现气泡数密度的对数与直径的对数呈线性关系,与实验结果吻合良好.由于气泡内部存在较大的内压,弹性作用在气泡的演化过程中起着重要作用,在最近的研究中,研究人员在相场模型中进一步引入缺陷的弹性相互作用[19,20].Jiang等[21]研究发现,弹性应变能在He泡演化初期影响较小,在后期则会抑制He泡的生长. ...
... 图7对He泡演化进行了定量分析.根据占比分数曲线可以将He泡演化分为3个阶段:Ⅰ 形核孕育阶段,Ⅱ 形核生长阶段,Ⅲ 粗化阶段.在形核孕育阶段,基本观察不到He泡;随着辐照过程的进行,基体的空位和He浓度达到形核条件,He泡占比和数量迅速增加,迅速消耗基体中过饱和空位与He原子,因此在形核生长阶段的后期基本不再形核,从而进入粗化阶段;在粗化阶段,He泡占比增加速率减缓,已存在的He泡持续吸收空位生长,He泡尺寸持续变大.相邻较近的He泡还会合并长大,且较大的He泡会以较小的He泡为代价发生Ostwald熟化,因此粗化阶段He泡数量有所下降.此外,根据Millett[16,17]等和Ding等[56]的研究结果,辐照过程中空洞与He泡的形核生长可以用经典的Johnson-Mehl-Avrami-Kolmogorov (JMAK)方程描述: ...
... 式中,p表示He泡占比,p0表示形核生长阶段结束时的He泡占比,kp和np为特征常数,为形核生长的起始时间.从图7的拟合曲线可以看出,相场模拟的形核生长阶段的动力学完全符合经典JMAK理论,其中np = 3,表明在第Ⅱ阶段He泡持续形核与长大,与Millet等[16,17]的研究结果一致,进一步验证了模型的合理性. ...
Phase-field simulation of irradiated metals: Part II: Gas bubble kinetics
5
2011
... 随着计算机模拟技术的发展,研究人员从原子尺度、纳米尺度和微米尺度开展了大量工作,以揭示He泡的形核、生长和粗化过程.原子模拟表明,间隙He原子迁移能低,易于扩散,且由于结合能高,会与空位结合形成He-空位团簇[13].因此,这些He-空位团簇可作为辐照金属中He泡的形核位点.但由于势函数的限制,分子动力学(MD)在研究He泡的生长和演化方面并未获得大量应用.近年来,介观尺度的相场方法被广泛应用于研究微观结构演变及其对力学性能的影响.基于相场方法,研究人员开展了大量关于核燃料中裂变气体气泡的研究.Stan等[14]和Hu等[15]基于气体原子浓度场(ci)构建了核燃料中气泡的演化,并在随后的研究中进一步引入空位浓度场(cv),该模型能够研究气泡的形核与生长,并有效地模拟了气泡在晶界处的偏聚,但相场能量方程中对气泡的描述较为简单.Millett等[16,17]在热力学框架中引入缺陷形成能,并在控制方程中引入缺陷的产生与复合、湮灭以及晶界的影响.模拟结果表明,气泡的演化经历3个不同的阶段:孕育期,形核和生长期,粗化期;模拟的气泡稳定生长的动力学规律与传统的Johnson-Mehl-Avarami理论吻合较好.Li等[18]采用类似的热力学框架,并基于Kim-Kim-Suzuki (KKS)相场模型研究了UO2中晶内裂变气泡的演化,发现气泡数密度的对数与直径的对数呈线性关系,与实验结果吻合良好.由于气泡内部存在较大的内压,弹性作用在气泡的演化过程中起着重要作用,在最近的研究中,研究人员在相场模型中进一步引入缺陷的弹性相互作用[19,20].Jiang等[21]研究发现,弹性应变能在He泡演化初期影响较小,在后期则会抑制He泡的生长. ...
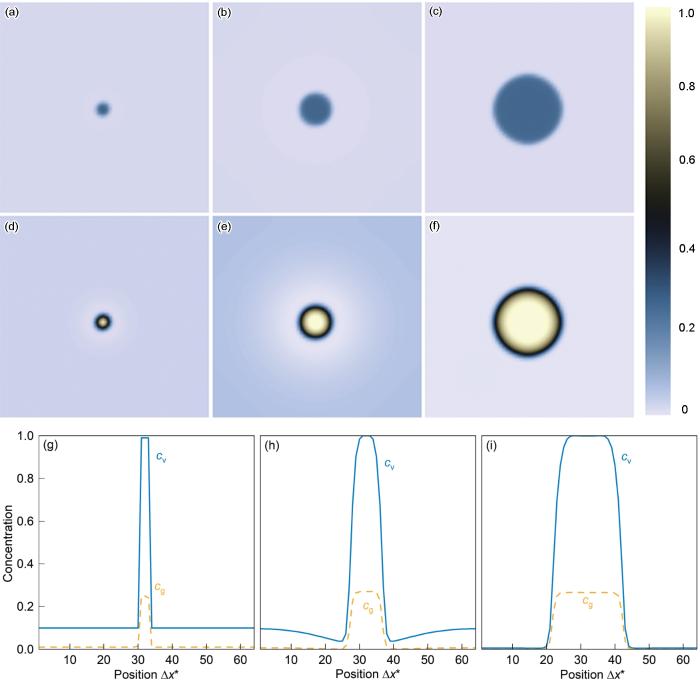
... 对于He泡相场的第一个验证案例,一个直径为0.3 nm的团簇在模拟开始时被放置在模拟体系的中心,模拟体系尺寸为9.6 nm × 9.6 nm,如图5a所示,图中t* 表示无量纲时间.周围的基体设置过饱和的空位和He原子,以支持He泡的生长.空位和He的初始浓度分别设置为0.1和0.01,远高于热平衡浓度.图5a~c和d~f分别为He和空位浓度场的演化过程.由于从He泡周围的基体中不断吸收He原子和空位,He泡尺寸逐渐增大.Millett等[17]指出,He泡尺寸的增大主要受空位向He泡中的扩散控制.图5g~i进一步展示了He和空位沿中心线的浓度分布.可以看出,He泡在早期阶段包含高于平衡浓度的He原子(图5h),表明He泡处于高压状态.同时在He泡长大的过程中,在He泡界面附近形成明显的空位浓度的不均匀分布,这意味着空位不断向He泡中扩散支持He泡的长大.随着尺寸的增加,He泡内的He浓度下降(图5i),这与式(5)的理论结果保持一致.图5i中He泡内部的He平衡浓度为0.265,与Wen等[33]的计算结果一致. ...
... 图7对He泡演化进行了定量分析.根据占比分数曲线可以将He泡演化分为3个阶段:Ⅰ 形核孕育阶段,Ⅱ 形核生长阶段,Ⅲ 粗化阶段.在形核孕育阶段,基本观察不到He泡;随着辐照过程的进行,基体的空位和He浓度达到形核条件,He泡占比和数量迅速增加,迅速消耗基体中过饱和空位与He原子,因此在形核生长阶段的后期基本不再形核,从而进入粗化阶段;在粗化阶段,He泡占比增加速率减缓,已存在的He泡持续吸收空位生长,He泡尺寸持续变大.相邻较近的He泡还会合并长大,且较大的He泡会以较小的He泡为代价发生Ostwald熟化,因此粗化阶段He泡数量有所下降.此外,根据Millett[16,17]等和Ding等[56]的研究结果,辐照过程中空洞与He泡的形核生长可以用经典的Johnson-Mehl-Avrami-Kolmogorov (JMAK)方程描述: ...
... 式中,p表示He泡占比,p0表示形核生长阶段结束时的He泡占比,kp和np为特征常数,为形核生长的起始时间.从图7的拟合曲线可以看出,相场模拟的形核生长阶段的动力学完全符合经典JMAK理论,其中np = 3,表明在第Ⅱ阶段He泡持续形核与长大,与Millet等[16,17]的研究结果一致,进一步验证了模型的合理性. ...
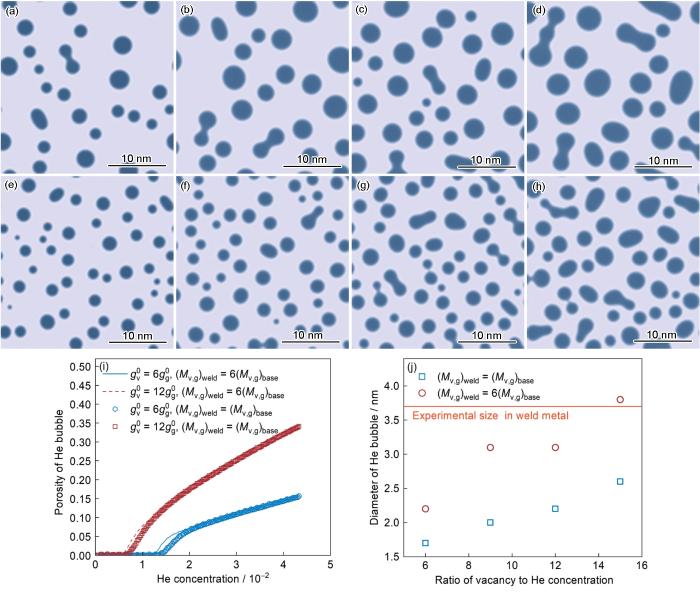
... 为了进一步揭示焊缝金属中He泡尺寸明显增加的物理机制,本工作计算了不同空位与He原子比例下的He泡演化(图11a~d),同时还计算了不考虑316H钢和焊缝金属扩散差异时的He泡演化(图11e~h).首先,在任一扩散条件下(图11a~d或图11e~h),随着空位相对He浓度的比例增高,He泡的尺寸均表现出明显的增大趋势.这表明,由位错优先吸收间隙原子而导致的空位过剩,是促进He泡长大的一个驱动力,更多的空位向He泡中扩散可以显著促进He泡的形核与生长,最终高空位浓度的体系具有更高的He泡占比(图11i),这与Millett等[17]的研究结果一致.此外,考虑316H与焊缝金属扩散差异时,焊缝中由高位错密度引起的扩散加速,显著地促进了He泡尺寸的增加(图11j).同时,对比图11i中不同扩散条件下的He泡占比演化可以看出,扩散能力的提高并没有改变最终的He泡占比.较快的扩散一方面可以使He泡快速达到形核条件,另一方面可以在生长的过程中使得He泡快速地吸收空位和He原子实现He泡的快速生长.扩散较慢时,形核时间较迟,因此有更多的区域可以满足形核条件,导致He泡数量较多(图11a和e),在生长过程中又由于扩散的限制难以通过快速合并和粗化实现He泡的生长,因此相同空位和He原子比例下,扩散较慢时的He泡尺寸较小.综上所述,单一地考虑扩散或空位与He原子的比例均不能有效地解释焊缝金属中He泡尺寸明显增大,其是由焊缝中高密度位错造成的空位浓度过剩和快速扩散共同主导的. ...
Phase-field simulations of intragranular fission gas bubble evolution in UO2 under post-irradiation thermal annealing
2
2013
... 随着计算机模拟技术的发展,研究人员从原子尺度、纳米尺度和微米尺度开展了大量工作,以揭示He泡的形核、生长和粗化过程.原子模拟表明,间隙He原子迁移能低,易于扩散,且由于结合能高,会与空位结合形成He-空位团簇[13].因此,这些He-空位团簇可作为辐照金属中He泡的形核位点.但由于势函数的限制,分子动力学(MD)在研究He泡的生长和演化方面并未获得大量应用.近年来,介观尺度的相场方法被广泛应用于研究微观结构演变及其对力学性能的影响.基于相场方法,研究人员开展了大量关于核燃料中裂变气体气泡的研究.Stan等[14]和Hu等[15]基于气体原子浓度场(ci)构建了核燃料中气泡的演化,并在随后的研究中进一步引入空位浓度场(cv),该模型能够研究气泡的形核与生长,并有效地模拟了气泡在晶界处的偏聚,但相场能量方程中对气泡的描述较为简单.Millett等[16,17]在热力学框架中引入缺陷形成能,并在控制方程中引入缺陷的产生与复合、湮灭以及晶界的影响.模拟结果表明,气泡的演化经历3个不同的阶段:孕育期,形核和生长期,粗化期;模拟的气泡稳定生长的动力学规律与传统的Johnson-Mehl-Avarami理论吻合较好.Li等[18]采用类似的热力学框架,并基于Kim-Kim-Suzuki (KKS)相场模型研究了UO2中晶内裂变气泡的演化,发现气泡数密度的对数与直径的对数呈线性关系,与实验结果吻合良好.由于气泡内部存在较大的内压,弹性作用在气泡的演化过程中起着重要作用,在最近的研究中,研究人员在相场模型中进一步引入缺陷的弹性相互作用[19,20].Jiang等[21]研究发现,弹性应变能在He泡演化初期影响较小,在后期则会抑制He泡的生长. ...
... 式中,插值函数区分了基体和He泡中不同的本征应变,基体中的本征应变是由于过饱和点缺陷造成的晶格错配引起的,而He泡中的本征应变则与He泡中的压力相关[18].和分别为与空位和He原子相关的晶格膨胀系数;和,分别为空位和He原子在基体中的平衡空位浓度;δij 为Kronecker函数.为He泡引起的本征应变,定义如下[31]: ...
Formation mechanism of gas bubble superlattice in UMo metal fuels: Phase-field modeling investigation
1
2016
... 随着计算机模拟技术的发展,研究人员从原子尺度、纳米尺度和微米尺度开展了大量工作,以揭示He泡的形核、生长和粗化过程.原子模拟表明,间隙He原子迁移能低,易于扩散,且由于结合能高,会与空位结合形成He-空位团簇[13].因此,这些He-空位团簇可作为辐照金属中He泡的形核位点.但由于势函数的限制,分子动力学(MD)在研究He泡的生长和演化方面并未获得大量应用.近年来,介观尺度的相场方法被广泛应用于研究微观结构演变及其对力学性能的影响.基于相场方法,研究人员开展了大量关于核燃料中裂变气体气泡的研究.Stan等[14]和Hu等[15]基于气体原子浓度场(ci)构建了核燃料中气泡的演化,并在随后的研究中进一步引入空位浓度场(cv),该模型能够研究气泡的形核与生长,并有效地模拟了气泡在晶界处的偏聚,但相场能量方程中对气泡的描述较为简单.Millett等[16,17]在热力学框架中引入缺陷形成能,并在控制方程中引入缺陷的产生与复合、湮灭以及晶界的影响.模拟结果表明,气泡的演化经历3个不同的阶段:孕育期,形核和生长期,粗化期;模拟的气泡稳定生长的动力学规律与传统的Johnson-Mehl-Avarami理论吻合较好.Li等[18]采用类似的热力学框架,并基于Kim-Kim-Suzuki (KKS)相场模型研究了UO2中晶内裂变气泡的演化,发现气泡数密度的对数与直径的对数呈线性关系,与实验结果吻合良好.由于气泡内部存在较大的内压,弹性作用在气泡的演化过程中起着重要作用,在最近的研究中,研究人员在相场模型中进一步引入缺陷的弹性相互作用[19,20].Jiang等[21]研究发现,弹性应变能在He泡演化初期影响较小,在后期则会抑制He泡的生长. ...
Three-dimensional phase-field simulations of intragranular gas bubble evolution in irradiated U-Mo fuel
1
2018
... 随着计算机模拟技术的发展,研究人员从原子尺度、纳米尺度和微米尺度开展了大量工作,以揭示He泡的形核、生长和粗化过程.原子模拟表明,间隙He原子迁移能低,易于扩散,且由于结合能高,会与空位结合形成He-空位团簇[13].因此,这些He-空位团簇可作为辐照金属中He泡的形核位点.但由于势函数的限制,分子动力学(MD)在研究He泡的生长和演化方面并未获得大量应用.近年来,介观尺度的相场方法被广泛应用于研究微观结构演变及其对力学性能的影响.基于相场方法,研究人员开展了大量关于核燃料中裂变气体气泡的研究.Stan等[14]和Hu等[15]基于气体原子浓度场(ci)构建了核燃料中气泡的演化,并在随后的研究中进一步引入空位浓度场(cv),该模型能够研究气泡的形核与生长,并有效地模拟了气泡在晶界处的偏聚,但相场能量方程中对气泡的描述较为简单.Millett等[16,17]在热力学框架中引入缺陷形成能,并在控制方程中引入缺陷的产生与复合、湮灭以及晶界的影响.模拟结果表明,气泡的演化经历3个不同的阶段:孕育期,形核和生长期,粗化期;模拟的气泡稳定生长的动力学规律与传统的Johnson-Mehl-Avarami理论吻合较好.Li等[18]采用类似的热力学框架,并基于Kim-Kim-Suzuki (KKS)相场模型研究了UO2中晶内裂变气泡的演化,发现气泡数密度的对数与直径的对数呈线性关系,与实验结果吻合良好.由于气泡内部存在较大的内压,弹性作用在气泡的演化过程中起着重要作用,在最近的研究中,研究人员在相场模型中进一步引入缺陷的弹性相互作用[19,20].Jiang等[21]研究发现,弹性应变能在He泡演化初期影响较小,在后期则会抑制He泡的生长. ...
Effects of grain boundaries on the evolution of radiation-induced bubbles in polycrystalline tungsten: A phase-field simulation
2
2024
... 随着计算机模拟技术的发展,研究人员从原子尺度、纳米尺度和微米尺度开展了大量工作,以揭示He泡的形核、生长和粗化过程.原子模拟表明,间隙He原子迁移能低,易于扩散,且由于结合能高,会与空位结合形成He-空位团簇[13].因此,这些He-空位团簇可作为辐照金属中He泡的形核位点.但由于势函数的限制,分子动力学(MD)在研究He泡的生长和演化方面并未获得大量应用.近年来,介观尺度的相场方法被广泛应用于研究微观结构演变及其对力学性能的影响.基于相场方法,研究人员开展了大量关于核燃料中裂变气体气泡的研究.Stan等[14]和Hu等[15]基于气体原子浓度场(ci)构建了核燃料中气泡的演化,并在随后的研究中进一步引入空位浓度场(cv),该模型能够研究气泡的形核与生长,并有效地模拟了气泡在晶界处的偏聚,但相场能量方程中对气泡的描述较为简单.Millett等[16,17]在热力学框架中引入缺陷形成能,并在控制方程中引入缺陷的产生与复合、湮灭以及晶界的影响.模拟结果表明,气泡的演化经历3个不同的阶段:孕育期,形核和生长期,粗化期;模拟的气泡稳定生长的动力学规律与传统的Johnson-Mehl-Avarami理论吻合较好.Li等[18]采用类似的热力学框架,并基于Kim-Kim-Suzuki (KKS)相场模型研究了UO2中晶内裂变气泡的演化,发现气泡数密度的对数与直径的对数呈线性关系,与实验结果吻合良好.由于气泡内部存在较大的内压,弹性作用在气泡的演化过程中起着重要作用,在最近的研究中,研究人员在相场模型中进一步引入缺陷的弹性相互作用[19,20].Jiang等[21]研究发现,弹性应变能在He泡演化初期影响较小,在后期则会抑制He泡的生长. ...
... 然而,相场方法在He泡研究中的进一步推广和应用仍面临一些挑战.仅有少数基于相场方法的研究涉及结构材料及其焊缝金属中的He泡[21,22],对于这类材料,He泡的演变以及材料的力学响应都是关键问题,高温下He泡内部的高压可能导致塑性变形[23].因此,相场模型中需要充分考虑弹塑性框架.晶体塑性方法可以有效地揭示焊缝金属微观组织和力学性能之间的关联[24~26],如焊缝微观组织不均匀性对拉伸性能的影响[22]以及局部位错密度差异导致的性能梯度[24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
Phase field simulation of bubble evolution dynamics in Fe-Cr alloys
2
2024
... 然而,相场方法在He泡研究中的进一步推广和应用仍面临一些挑战.仅有少数基于相场方法的研究涉及结构材料及其焊缝金属中的He泡[21,22],对于这类材料,He泡的演变以及材料的力学响应都是关键问题,高温下He泡内部的高压可能导致塑性变形[23].因此,相场模型中需要充分考虑弹塑性框架.晶体塑性方法可以有效地揭示焊缝金属微观组织和力学性能之间的关联[24~26],如焊缝微观组织不均匀性对拉伸性能的影响[22]以及局部位错密度差异导致的性能梯度[24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
... [22]以及局部位错密度差异导致的性能梯度[24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
Fe-Cr合金气泡演化动力学的相场法模拟
2
2024
... 然而,相场方法在He泡研究中的进一步推广和应用仍面临一些挑战.仅有少数基于相场方法的研究涉及结构材料及其焊缝金属中的He泡[21,22],对于这类材料,He泡的演变以及材料的力学响应都是关键问题,高温下He泡内部的高压可能导致塑性变形[23].因此,相场模型中需要充分考虑弹塑性框架.晶体塑性方法可以有效地揭示焊缝金属微观组织和力学性能之间的关联[24~26],如焊缝微观组织不均匀性对拉伸性能的影响[22]以及局部位错密度差异导致的性能梯度[24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
... [22]以及局部位错密度差异导致的性能梯度[24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
Gas bubble evolution in polycrystalline UMo fuels under elastic-plastic deformation: A phase-field model with crystal-plasticity
4
2021
... 然而,相场方法在He泡研究中的进一步推广和应用仍面临一些挑战.仅有少数基于相场方法的研究涉及结构材料及其焊缝金属中的He泡[21,22],对于这类材料,He泡的演变以及材料的力学响应都是关键问题,高温下He泡内部的高压可能导致塑性变形[23].因此,相场模型中需要充分考虑弹塑性框架.晶体塑性方法可以有效地揭示焊缝金属微观组织和力学性能之间的关联[24~26],如焊缝微观组织不均匀性对拉伸性能的影响[22]以及局部位错密度差异导致的性能梯度[24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
... He的主要特征是在材料中不溶解.然而,He可以在固体中自由扩散,并向空位团簇、位错和晶界等缺陷阱处迁移.聚集的He最初会形成He泡的形核位点,并在后续的辐照过程中生长和粗化,形成大尺寸He泡.本工作采用具有2个浓度场(无量纲的位点分数,即:原子数/晶格位点数)的相场模型,即空位浓度场cv( r, t)和He浓度场cg( r, t) (其中, r 为空间,t为时间).此外,模型中还引入了一个非守恒序参数ηb( r, t),用于在空间上区分He泡与基体.基于非守恒序参数,相场模型可以定义2种稳定相,ηb = 0代表基体,ηb = 1代表He泡.相场变量在空间和时间尺度上演化是以自由能降低为驱动力,整个模拟体系朝着稳定状态发展.因此,He泡演变相场模型的关键是根据相场变量构建包含He泡的体系自由能,根据Hu和Beeler[23]的研究,He泡相场模拟体系的总自由能泛函(F)可以表示为各相自由能、界面能以及弹性应变能的总和: ...
... 此外,可以看出,弹性常数的差异也会对弹性应变能密度分布产生影响.在Jiang等[36]的工作中,He泡的弹性模量被赋予一个极小值,意味着在变形过程中He泡中的弹性应变能可以忽略不计.而在Hu和Beeler[23]的工作中,认为He泡具有弹性模量,根据Van der Waals状态方程,He泡内部的体模量可根据下式进行计算[33]: ...
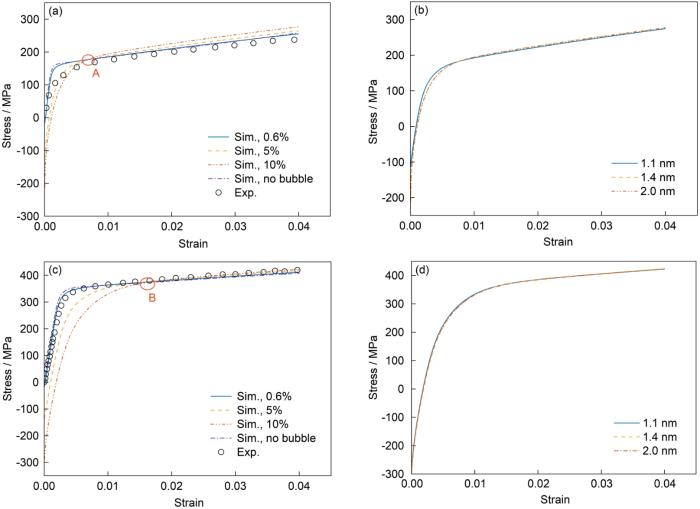
... 图13给出了550 ℃不同He泡占比和尺寸条件下316H钢母材和焊缝金属的应力-应变曲线,同时图13a和c中还给出了不含He泡体系的316H钢母材和焊缝金属的实验与模拟结果.本工作重点研究He泡微观组织对316H钢母材和焊缝金属微观变形的影响,在辐照材料的拉伸模拟过程中未考虑辐照缺陷对屈服强度的影响.通过对比可见,基于晶体塑性模拟的应力-应变曲线与实验结果表现出良好的一致性.焊缝金属在快速凝固和冷却过程中的凝固收缩、热收缩以及膨胀会引入残余应力,形成高密度的位错,因此,原始焊缝金属的屈服强度明显高于316H钢母材,550 ℃下焊缝金属和316H钢母材的屈服强度分别约为350和150 MPa.对比不含He泡与含He泡的应力-应变曲线(图13a和c),随着He泡占比的增加,应力-应变曲线弹性段的斜率(即弹性模量)有所下降,这是因为模型中He泡的弹性常数远小于基体的弹性常数.由于He泡内压造成的晶格错配会导致在模拟开始时存在负值的残余应力,因此在外加应变为0时,整体应力为负值,且随着He泡占比的增加,负值的偏移量越大,这与Hu和Beeler[23]的研究结果一致.He泡占比为0.6%、5%和10%时,316H钢母材中负值的偏移量分别为-16、-122和-211 MPa;焊缝金属中负值的偏移量分别为-16、-135和-286 MPa.在He泡占比为0.6%时,316H钢母材和焊缝金属整体的应力响应与不含He泡体系的应力响应基本没有区别.随着He泡占比增加至5%和10%,在应变初期(图13a中A,图13a中B处),整体的应力响应明显低于不含He泡体系的应力响应,表明He泡的内压和外应变共同主导了这一阶段的应力/应变行为.He泡内部的高压在宏观上表现为一个压缩性的“预应力”或“本征应变”,因此在拉伸初期,外加的拉伸应力需要先抵消这部分内压的影响,导致宏观应力较低.在应变后期,应力响应与不含He泡体系的应力响应仅有微小的差别,其数值略大于不含He泡体系的应力,这是因为He泡内压导致He泡附近发生塑性变形而造成应变硬化.在应变后期,外应变主导作用会明显大于He泡内压的作用.对比316H钢母材与焊缝金属可以发现,焊缝金属中负值的偏移量大于316H钢母材,这是由于316H钢母材的屈服强度较低,在相同的He泡内压条件下会发生较大的塑性变形,从而降低了He泡对应力-应变曲线的影响.而焊缝金属屈服强度较高,难以发生塑性变形,He泡对应力的影响被完整地保留下来.从图13a和c中的A点和B点也可以看出,在316H钢母材中,He泡对应力-应变曲线起主导作用的外应变区间为0~0.6%;而在焊缝金属中,He泡对应力-应变曲线起主导作用的外应变区间为0~1.6%.此外,从图13b可以看出,He泡尺寸在4%的外应变范围内对应力-应变曲线基本没有影响. ...
Grain size and shape dependent crystal plasticity finite element model and its application to electron beam welded SS316L
4
2023
... 然而,相场方法在He泡研究中的进一步推广和应用仍面临一些挑战.仅有少数基于相场方法的研究涉及结构材料及其焊缝金属中的He泡[21,22],对于这类材料,He泡的演变以及材料的力学响应都是关键问题,高温下He泡内部的高压可能导致塑性变形[23].因此,相场模型中需要充分考虑弹塑性框架.晶体塑性方法可以有效地揭示焊缝金属微观组织和力学性能之间的关联[24~26],如焊缝微观组织不均匀性对拉伸性能的影响[22]以及局部位错密度差异导致的性能梯度[24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
... [24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
... 晶体塑性模型中的参数(表3)包括临界分切应力和位错模型中的参数.临界分切应力模型中的参数根据316系列不锈钢晶体塑性的文献[24,39,53]确定.位错模型中的4组参数则根据Sedighiani等[54]提出的由宏观应力-应变曲线拟合的方法确定. ...
... Parameters used in crystal plasticity model
Table 3| Parameter | Value | Unit |
|---|
| KHP[39] | 1.1 | MPa· |
| dgrain | 50 (base), 100 (weld) | μm |
| ρ | 1 × 1012 (base), 6 × 1013 (weld) | m-2 |
| [24] | 1 × 10-3 | s-1 |
| n[53] | 5 | - |
| kmul | 0.03 (base), 0.02 (weld) | - |
| Rcp | 2 × 10-9 | nm |
| βp | 0.015 (base), 0.01 (weld) | – |
| krecov | 200 | – |
| C11, C12, C44 | 157, 114, 99 | GPa |
| μ[39] | 88 - 3 × 10-5T2 - 5.6 × 10-3T | GPa |
Note:KHP—Hall-Petch constant; dgrain—grain size; ρ—dislocation density; —initial plastic shear rate; n—stress exponent; kmul—dislocation multiplication constant; Rcp—critical capture radius; βp—dislocation trapping constant; krecov—dislocation recover constant; C11, C12, C44—elastic constants; μ—shear modulus; base—316H base metal, weld—316H weld metal, T—temperature ...
Micro-mechanics investigation of heterogeneous deformation fields and crack initiation driven by the local stored energy density in austenitic stainless steel welded joints
1
2024
... 然而,相场方法在He泡研究中的进一步推广和应用仍面临一些挑战.仅有少数基于相场方法的研究涉及结构材料及其焊缝金属中的He泡[21,22],对于这类材料,He泡的演变以及材料的力学响应都是关键问题,高温下He泡内部的高压可能导致塑性变形[23].因此,相场模型中需要充分考虑弹塑性框架.晶体塑性方法可以有效地揭示焊缝金属微观组织和力学性能之间的关联[24~26],如焊缝微观组织不均匀性对拉伸性能的影响[22]以及局部位错密度差异导致的性能梯度[24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
Interpretation of mechanical properties gradient in laser-welded joints: Experiments and grain morphology-dependent crystal plasticity modeling
2
2024
... 然而,相场方法在He泡研究中的进一步推广和应用仍面临一些挑战.仅有少数基于相场方法的研究涉及结构材料及其焊缝金属中的He泡[21,22],对于这类材料,He泡的演变以及材料的力学响应都是关键问题,高温下He泡内部的高压可能导致塑性变形[23].因此,相场模型中需要充分考虑弹塑性框架.晶体塑性方法可以有效地揭示焊缝金属微观组织和力学性能之间的关联[24~26],如焊缝微观组织不均匀性对拉伸性能的影响[22]以及局部位错密度差异导致的性能梯度[24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
... ,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
A microstructure-based study of irradiation hardening in stainless steel: Experiment and phase field modeling
1
2022
... 然而,相场方法在He泡研究中的进一步推广和应用仍面临一些挑战.仅有少数基于相场方法的研究涉及结构材料及其焊缝金属中的He泡[21,22],对于这类材料,He泡的演变以及材料的力学响应都是关键问题,高温下He泡内部的高压可能导致塑性变形[23].因此,相场模型中需要充分考虑弹塑性框架.晶体塑性方法可以有效地揭示焊缝金属微观组织和力学性能之间的关联[24~26],如焊缝微观组织不均匀性对拉伸性能的影响[22]以及局部位错密度差异导致的性能梯度[24].通过引入不同区域典型组织特征,晶体塑性模型可以准确预测焊接接头的宏观力学响应以及微观变形行为[25,26].因此,相场与晶体塑性的耦合可以实现“辐照-微观组织-应力”多物理场耦合.最近,相场与晶体塑性耦合的方法已被用于研究辐照材料中位错环和He泡等辐照缺陷对应力-应变响应的影响[27].尽管如此,由于He泡内气体压力、应力或应变与热力学或动力学性质之间的相互作用尚不明确,发展能够耦合关键物理过程(He泡演化热力学及动力学过程、微观变形行为)的、更具物理基础的相场模型是亟须解决的问题.此外,实验数据与相场模拟结果之间的直接对比非常有限,而这对于参数和模拟结果的验证至关重要.一些相场模型模拟的是模型合金中的微观结构演变,未能模拟特定结构材料中的He泡演化,也未能揭示母材与焊缝金属中He泡演化的差异机制.因此,将模型应用于真实的、具有复杂微观结构的工程材料,有助于将相场方法发展成为能够预测材料在辐照环境下的服役行为的有力工具. ...
A quantitative phase-field model of gas bubble evolution in UO2
1
2020
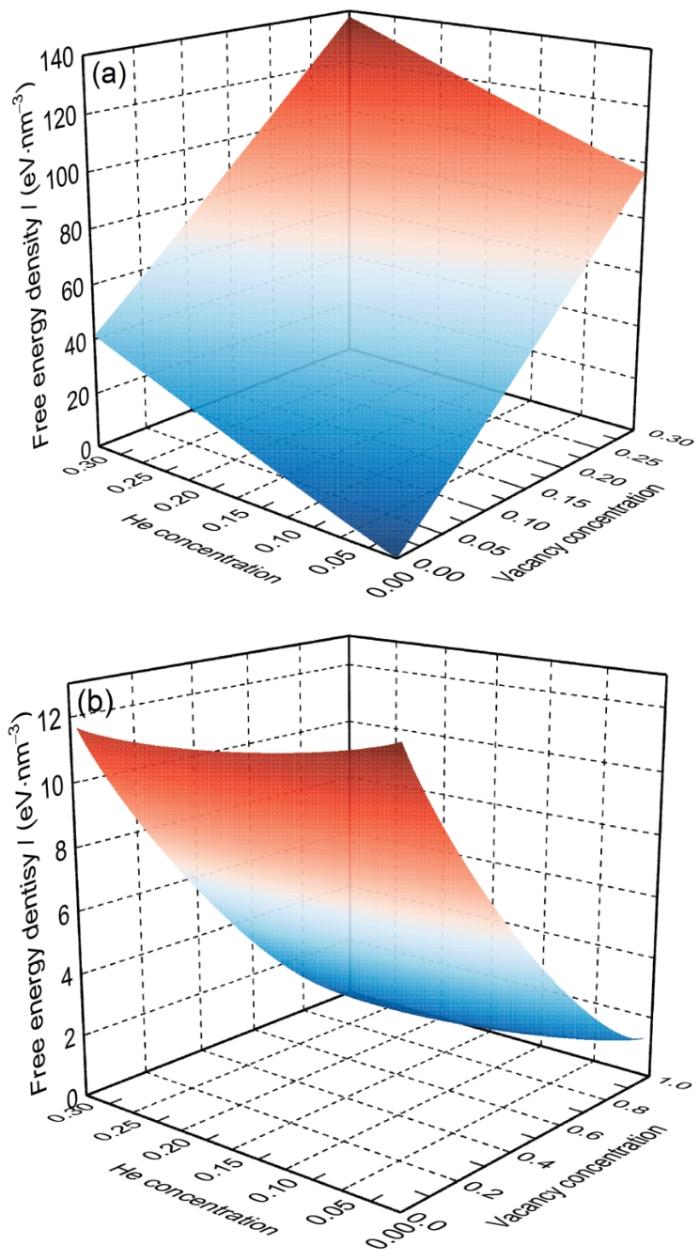
... 根据统计热力学理论,fmatrix和fbubble可以分别由以下公式描述[28,29]: ...
Phase-field simulation of radiation-induced bubble evolution in recrystallized U-Mo alloy
1
2022
... 根据统计热力学理论,fmatrix和fbubble可以分别由以下公式描述[28,29]: ...
A phase field study of the thermal migration of gas bubbles in UO2 nuclear fuel under temperature gradient
2
2020
... 式中,和分别为空位和He原子的形成能;NA为Avogadro常数;R为气体常数;Va为摩尔体积;T为热力学温度;为He泡中He原子的最大浓度,可以根据Van der Waals常数(bv)计算而得[30]:,其中,Ω为原子体积;和分别为He泡中空位和He原子的平衡浓度.根据王亚峰等[31]的研究,He泡中的空位平衡浓度为1,但模拟过程中为了数值的稳定性,取0.99.He原子的平衡浓度则由Van der Waals状态方程推导得出[30]: ...
... [30]: ...
Xe gas bubbles evolution in UO2 fuels—A phase field simulation
3
2019
... 式中,和分别为空位和He原子的形成能;NA为Avogadro常数;R为气体常数;Va为摩尔体积;T为热力学温度;为He泡中He原子的最大浓度,可以根据Van der Waals常数(bv)计算而得[30]:,其中,Ω为原子体积;和分别为He泡中空位和He原子的平衡浓度.根据王亚峰等[31]的研究,He泡中的空位平衡浓度为1,但模拟过程中为了数值的稳定性,取0.99.He原子的平衡浓度则由Van der Waals状态方程推导得出[30]: ...
... 式中,插值函数区分了基体和He泡中不同的本征应变,基体中的本征应变是由于过饱和点缺陷造成的晶格错配引起的,而He泡中的本征应变则与He泡中的压力相关[18].和分别为与空位和He原子相关的晶格膨胀系数;和,分别为空位和He原子在基体中的平衡空位浓度;δij 为Kronecker函数.为He泡引起的本征应变,定义如下[31]: ...
... 图8a对比了He泡形核后基于不同方法计算的He泡内压演化,包括EOS状态方程[31]、毛细压力方程[34]以及应力应变求解.3种计算方法下的He泡内压演化均呈现出先快速下降后逐渐饱和的演化趋势,表明了He泡演化相场模型的自洽性.相场模拟得到的最终He泡平均内压约为3 GPa,该数值与分子动力学模拟结果[57]一致.在形核阶段,小尺寸的He泡中高密度的He原子导致极高的内压,随着辐照过程的进行,He泡尺寸的增加导致He泡内部的He浓度下降并接近稳定状态(图8b),He泡内压随之下降并稳定.以上结果表明,本工作所构建的相场模型可以表征辐照条件下He泡的形核与生长过程. ...
UO2核燃料中Xe气泡演化的相场模型与分析
3
2019
... 式中,和分别为空位和He原子的形成能;NA为Avogadro常数;R为气体常数;Va为摩尔体积;T为热力学温度;为He泡中He原子的最大浓度,可以根据Van der Waals常数(bv)计算而得[30]:,其中,Ω为原子体积;和分别为He泡中空位和He原子的平衡浓度.根据王亚峰等[31]的研究,He泡中的空位平衡浓度为1,但模拟过程中为了数值的稳定性,取0.99.He原子的平衡浓度则由Van der Waals状态方程推导得出[30]: ...
... 式中,插值函数区分了基体和He泡中不同的本征应变,基体中的本征应变是由于过饱和点缺陷造成的晶格错配引起的,而He泡中的本征应变则与He泡中的压力相关[18].和分别为与空位和He原子相关的晶格膨胀系数;和,分别为空位和He原子在基体中的平衡空位浓度;δij 为Kronecker函数.为He泡引起的本征应变,定义如下[31]: ...
... 图8a对比了He泡形核后基于不同方法计算的He泡内压演化,包括EOS状态方程[31]、毛细压力方程[34]以及应力应变求解.3种计算方法下的He泡内压演化均呈现出先快速下降后逐渐饱和的演化趋势,表明了He泡演化相场模型的自洽性.相场模拟得到的最终He泡平均内压约为3 GPa,该数值与分子动力学模拟结果[57]一致.在形核阶段,小尺寸的He泡中高密度的He原子导致极高的内压,随着辐照过程的进行,He泡尺寸的增加导致He泡内部的He浓度下降并接近稳定状态(图8b),He泡内压随之下降并稳定.以上结果表明,本工作所构建的相场模型可以表征辐照条件下He泡的形核与生长过程. ...
Parameters of the vacancy formation and self-diffusion in the iron
6
2023
... 图2显示了550 ℃下基于Van der Waals状态方程得出的奥氏体不锈钢He泡中He原子的热力学平衡浓度,所采用的奥氏体不锈钢相关的热力学参数见表2[12,32~34].可见,随着He泡尺寸的增大,He泡中He原子的平衡浓度呈现下降趋势. ...
... He泡相场模拟中所用的热力学参数[12,32~34] ...
... Thermodynamic parameters used in phase field simulation[12,32-34] ...
... [
32]
7.06 | cm3·mol-1 | | [12] | 3.2 × 10-19 | J |
| [12] | 6.4 × 10-19 | J |
| Ω[32] | 1.17 × 10-29 | m3 |
| bv[33] | 0.039 | nm3·atom-1 |
| a[33] | 0.0034 | J·m3·mol-2 |
| γs[34] | 1.82 | J·m-2 |
Note:Va—molar fraction, —vacancy formation energy, —He atom formation energy, Ω—atomic volume, bv—Van der Waals constant of He, a—constant for intermolecular attraction, γs—surface tension ...
... [
32]
1.17 × 10-29 | m3 | | bv[33] | 0.039 | nm3·atom-1 |
| a[33] | 0.0034 | J·m3·mol-2 |
| γs[34] | 1.82 | J·m-2 |
Note:Va—molar fraction, —vacancy formation energy, —He atom formation energy, Ω—atomic volume, bv—Van der Waals constant of He, a—constant for intermolecular attraction, γs—surface tension ...
... 本工作所涉及的参数主要包括He泡相场模型中的热力学参数、辐照参数以及晶体塑性模型中的力学行为参数.He泡形核与演化的热力学参数均从He泡相场模拟的文献或原子尺度计算的文献中获得(表2[12,32~34]).对于辐照参数,为了保证He泡内部不产生辐照点缺陷,辐照空位和He原子产生项的表达式为: ...
The effect of stress on the migration of He gas bubbles under a thermal gradient in Fe by phase-field modeling
5
2022
... Thermodynamic parameters used in phase field simulation
[12,32-34]Table 2| Parameter | Value | Unit |
|---|
| Va[32] | 7.06 | cm3·mol-1 |
| [12] | 3.2 × 10-19 | J |
| [12] | 6.4 × 10-19 | J |
| Ω[32] | 1.17 × 10-29 | m3 |
| bv[33] | 0.039 | nm3·atom-1 |
| a[33] | 0.0034 | J·m3·mol-2 |
| γs[34] | 1.82 | J·m-2 |
Note:Va—molar fraction, —vacancy formation energy, —He atom formation energy, Ω—atomic volume, bv—Van der Waals constant of He, a—constant for intermolecular attraction, γs—surface tension ...
... [
33]
0.0034 | J·m3·mol-2 | | γs[34] | 1.82 | J·m-2 |
Note:Va—molar fraction, —vacancy formation energy, —He atom formation energy, Ω—atomic volume, bv—Van der Waals constant of He, a—constant for intermolecular attraction, γs—surface tension ...
... 此外,可以看出,弹性常数的差异也会对弹性应变能密度分布产生影响.在Jiang等[36]的工作中,He泡的弹性模量被赋予一个极小值,意味着在变形过程中He泡中的弹性应变能可以忽略不计.而在Hu和Beeler[23]的工作中,认为He泡具有弹性模量,根据Van der Waals状态方程,He泡内部的体模量可根据下式进行计算[33]: ...
... 式中,Bb为体模量,a为度量分子间引力的唯象参数,Vm为描述He泡内He原子体积状态的变量.本工作采用与Wen等[33]类似的处理方法,根据式(10)计算得出Bb约为20 GPa.因此,取,其中,为He泡内部的弹性常数,为基体的弹性常数 ...
... 对于He泡相场的第一个验证案例,一个直径为0.3 nm的团簇在模拟开始时被放置在模拟体系的中心,模拟体系尺寸为9.6 nm × 9.6 nm,如图5a所示,图中t* 表示无量纲时间.周围的基体设置过饱和的空位和He原子,以支持He泡的生长.空位和He的初始浓度分别设置为0.1和0.01,远高于热平衡浓度.图5a~c和d~f分别为He和空位浓度场的演化过程.由于从He泡周围的基体中不断吸收He原子和空位,He泡尺寸逐渐增大.Millett等[17]指出,He泡尺寸的增大主要受空位向He泡中的扩散控制.图5g~i进一步展示了He和空位沿中心线的浓度分布.可以看出,He泡在早期阶段包含高于平衡浓度的He原子(图5h),表明He泡处于高压状态.同时在He泡长大的过程中,在He泡界面附近形成明显的空位浓度的不均匀分布,这意味着空位不断向He泡中扩散支持He泡的长大.随着尺寸的增加,He泡内的He浓度下降(图5i),这与式(5)的理论结果保持一致.图5i中He泡内部的He平衡浓度为0.265,与Wen等[33]的计算结果一致. ...
The capillarity equation at the nanoscale: Gas bubbles in metals
6
2015
... 图2显示了550 ℃下基于Van der Waals状态方程得出的奥氏体不锈钢He泡中He原子的热力学平衡浓度,所采用的奥氏体不锈钢相关的热力学参数见表2[12,32~34].可见,随着He泡尺寸的增大,He泡中He原子的平衡浓度呈现下降趋势. ...
... He泡相场模拟中所用的热力学参数[12,32~34] ...
... Thermodynamic parameters used in phase field simulation[12,32-34] ...
... [
34]
1.82 | J·m-2 | Note:Va—molar fraction, —vacancy formation energy, —He atom formation energy, Ω—atomic volume, bv—Van der Waals constant of He, a—constant for intermolecular attraction, γs—surface tension ...
... 本工作所涉及的参数主要包括He泡相场模型中的热力学参数、辐照参数以及晶体塑性模型中的力学行为参数.He泡形核与演化的热力学参数均从He泡相场模拟的文献或原子尺度计算的文献中获得(表2[12,32~34]).对于辐照参数,为了保证He泡内部不产生辐照点缺陷,辐照空位和He原子产生项的表达式为: ...
... 图8a对比了He泡形核后基于不同方法计算的He泡内压演化,包括EOS状态方程[31]、毛细压力方程[34]以及应力应变求解.3种计算方法下的He泡内压演化均呈现出先快速下降后逐渐饱和的演化趋势,表明了He泡演化相场模型的自洽性.相场模拟得到的最终He泡平均内压约为3 GPa,该数值与分子动力学模拟结果[57]一致.在形核阶段,小尺寸的He泡中高密度的He原子导致极高的内压,随着辐照过程的进行,He泡尺寸的增加导致He泡内部的He浓度下降并接近稳定状态(图8b),He泡内压随之下降并稳定.以上结果表明,本工作所构建的相场模型可以表征辐照条件下He泡的形核与生长过程. ...
1
1983
... He泡相场中弹性自由能密度的构建是基于Khachaturyan[35]发展的微弹性理论: ...
Three-dimensional phase-field modeling of porosity dependent intergranular fracture in UO2
1
2020
... 此外,可以看出,弹性常数的差异也会对弹性应变能密度分布产生影响.在Jiang等[36]的工作中,He泡的弹性模量被赋予一个极小值,意味着在变形过程中He泡中的弹性应变能可以忽略不计.而在Hu和Beeler[23]的工作中,认为He泡具有弹性模量,根据Van der Waals状态方程,He泡内部的体模量可根据下式进行计算[33]: ...
Effect of grain structure and strain rate on dynamic recrystallization and deformation behavior: A phase field-crystal plasticity model
1
2020
... 在晶体塑性理论框架中,塑性应变由位错滑移引起,塑性应变率张量()可表示为所有激活滑移系上的剪切速率之和[37,38]: ...
OXFORD-UMAT: An efficient and versatile crystal plasticity framework
1
2025
... 在晶体塑性理论框架中,塑性应变由位错滑移引起,塑性应变率张量()可表示为所有激活滑移系上的剪切速率之和[37,38]: ...
Prediction of irradiation hardening in austenitic stainless steels: Analytical and crystal plasticity studies
4
2019
... 在316系列奥氏体不锈钢中,临界分切应力主要与固溶元素的摩擦应力(),位错相互作用形成局部阻碍产生的切应力(),以及晶界阻碍位错运动形成的切应力()相关[39]: ...
... 晶体塑性模型中的参数(表3)包括临界分切应力和位错模型中的参数.临界分切应力模型中的参数根据316系列不锈钢晶体塑性的文献[24,39,53]确定.位错模型中的4组参数则根据Sedighiani等[54]提出的由宏观应力-应变曲线拟合的方法确定. ...
... Parameters used in crystal plasticity model
Table 3| Parameter | Value | Unit |
|---|
| KHP[39] | 1.1 | MPa· |
| dgrain | 50 (base), 100 (weld) | μm |
| ρ | 1 × 1012 (base), 6 × 1013 (weld) | m-2 |
| [24] | 1 × 10-3 | s-1 |
| n[53] | 5 | - |
| kmul | 0.03 (base), 0.02 (weld) | - |
| Rcp | 2 × 10-9 | nm |
| βp | 0.015 (base), 0.01 (weld) | – |
| krecov | 200 | – |
| C11, C12, C44 | 157, 114, 99 | GPa |
| μ[39] | 88 - 3 × 10-5T2 - 5.6 × 10-3T | GPa |
Note:KHP—Hall-Petch constant; dgrain—grain size; ρ—dislocation density; —initial plastic shear rate; n—stress exponent; kmul—dislocation multiplication constant; Rcp—critical capture radius; βp—dislocation trapping constant; krecov—dislocation recover constant; C11, C12, C44—elastic constants; μ—shear modulus; base—316H base metal, weld—316H weld metal, T—temperature ...
... [
39]
88 - 3 × 10-5T2 - 5.6 × 10-3T | GPa | Note:KHP—Hall-Petch constant; dgrain—grain size; ρ—dislocation density; —initial plastic shear rate; n—stress exponent; kmul—dislocation multiplication constant; Rcp—critical capture radius; βp—dislocation trapping constant; krecov—dislocation recover constant; C11, C12, C44—elastic constants; μ—shear modulus; base—316H base metal, weld—316H weld metal, T—temperature ...
Modeling dislocation storage rates and mean free paths in face-centered cubic crystals
1
2008
... 式中,μ为剪切模量,μ(300K)表示300 K下的剪切模量,b为Burgers矢量模,aαβ 为描述不同滑移系(α、β)位错交互作用强度的系数[40],和分别为可动位错和不可动位错密度,KHP为材料的Hall-Petch常数,dgrain为晶粒尺寸,M为Taylor因子(fcc结构取3.06). ...
Crystal plasticity-based constitutive modelling of irradiated bcc structures
1
2012
... 位错密度的演化采用如下公式进行计算[41]: ...
Free energy of a nonuniform system. I. Interfacial free energy
1
1958
... He泡相场演化的控制方程包括控制空位和He原子扩散的Cahn-Hilliard方程[42,43]和控制界面迁移的Allen-Cahn方程[44]: ...
On spinodal decomposition
1
1961
... He泡相场演化的控制方程包括控制空位和He原子扩散的Cahn-Hilliard方程[42,43]和控制界面迁移的Allen-Cahn方程[44]: ...
A microscopic theory for domain wall motion and its experimental verification in Fe-Al alloy domain growth kinetics
1
1977
... He泡相场演化的控制方程包括控制空位和He原子扩散的Cahn-Hilliard方程[42,43]和控制界面迁移的Allen-Cahn方程[44]: ...
A nucleation algorithm for the coupled conserved-nonconserved phase field model
1
2016
... 尽管式(21)~(23)构建了He泡演化的动力学方程,但在相场模型中,形核并不是一个自发现象.相场模型中有两种常用的方法描述形核现象[45]:一是通过在演化方程中加入随机噪声项,模拟相场变量的热起伏,从而引发均匀形核,形核后则关闭噪声项;二是基于经典形核理论确定形核的概率与位置,显式地在相场模型中引入晶核. ...
A phase-field model for void and gas bubble superlattice formation in irradiated solids
1
2022
... 在显式形核算法中,在每个模拟时间步针对每一个模拟单元计算形核速率和形核概率,通过比较形核概率与随机数(Rn)来确定模拟体系内某一位置是否发生形核,当PnRn时,则在该模拟时间步引入晶核[46]: ...
Applications of semi-implicit Fourier-spectral method to phase field equations
1
1998
... 本工作采用耦合晶体塑性的相场模型对辐照条件下316H钢母材和其焊缝金属中He泡的演化开展研究.图4为相场与晶体塑性耦合计算流程.其中,相场控制方程采用Chen和Shen[47]提出的半隐式Fourier谱方法求解,在He泡的演化过程中,模拟体系始终保持应力平衡状态, (其中,σij 和rj 分别表示应力张量分量和空间矢量分量).本工作采用Moulinec和Suquet[48]提出的Fourier谱方法求解力学平衡方程.对于晶体塑性本构模型,则在Moulinec和Suquet[48]提出的框架中进一步引入塑性应变,基于Newton-Raphson (N-R)迭代法快速求解塑性应变,具体算法见文献[49]. ...
A numerical method for computing the overall response of nonlinear composites with complex microstructure
2
1998
... 本工作采用耦合晶体塑性的相场模型对辐照条件下316H钢母材和其焊缝金属中He泡的演化开展研究.图4为相场与晶体塑性耦合计算流程.其中,相场控制方程采用Chen和Shen[47]提出的半隐式Fourier谱方法求解,在He泡的演化过程中,模拟体系始终保持应力平衡状态, (其中,σij 和rj 分别表示应力张量分量和空间矢量分量).本工作采用Moulinec和Suquet[48]提出的Fourier谱方法求解力学平衡方程.对于晶体塑性本构模型,则在Moulinec和Suquet[48]提出的框架中进一步引入塑性应变,基于Newton-Raphson (N-R)迭代法快速求解塑性应变,具体算法见文献[49]. ...
... [48]提出的框架中进一步引入塑性应变,基于Newton-Raphson (N-R)迭代法快速求解塑性应变,具体算法见文献[49]. ...
An elasto-viscoplastic formulation based on fast Fourier transforms for the prediction of micromechanical fields in polycrystalline materials
1
2012
... 本工作采用耦合晶体塑性的相场模型对辐照条件下316H钢母材和其焊缝金属中He泡的演化开展研究.图4为相场与晶体塑性耦合计算流程.其中,相场控制方程采用Chen和Shen[47]提出的半隐式Fourier谱方法求解,在He泡的演化过程中,模拟体系始终保持应力平衡状态, (其中,σij 和rj 分别表示应力张量分量和空间矢量分量).本工作采用Moulinec和Suquet[48]提出的Fourier谱方法求解力学平衡方程.对于晶体塑性本构模型,则在Moulinec和Suquet[48]提出的框架中进一步引入塑性应变,基于Newton-Raphson (N-R)迭代法快速求解塑性应变,具体算法见文献[49]. ...
Phase-field modeling of fission gas bubble growth on grain boundaries and triple junctions in UO2 nuclear fuel
1
2019
... 式中,和分别为基体中产生空位和He原子的恒定值.的取值参考He+辐照实验过程中He原子的产生速率,约2.0 × 10-6 s-1.但对于空位的产生速率,尚未见明确的计算模型.此外,针对本工作研究对象316H钢及其焊缝金属,前期研究工作中的速率理论计算[12]表明,位错作为“偏置缺陷阱”吸收间隙原子和空位的数量不相等,高位错密度的焊缝金属偏置吸收间隙原子的情况下会导致空位过剩,即焊缝中的空位浓度会高于母材.因此,本工作参考Aagesen等[50]的工作,将基体中空位的产生速率设置为 = (6~15),并讨论该参数对He泡演化的影响,从而揭示316H钢母材和焊缝金属中空位浓度差异条件下He泡的演化机制.此外,白菊菊等[11]研究表明,焊缝中存在的大量位错线扩散通道,能够促进He泡长大.为了描述316H钢母材和焊缝金属中扩散的差异,有效扩散系数(Deff)根据下式进行修正[51]: ...
The kinetics of static recovery by dislocation climb
1
2022
... 式中,和分别为基体中产生空位和He原子的恒定值.的取值参考He+辐照实验过程中He原子的产生速率,约2.0 × 10-6 s-1.但对于空位的产生速率,尚未见明确的计算模型.此外,针对本工作研究对象316H钢及其焊缝金属,前期研究工作中的速率理论计算[12]表明,位错作为“偏置缺陷阱”吸收间隙原子和空位的数量不相等,高位错密度的焊缝金属偏置吸收间隙原子的情况下会导致空位过剩,即焊缝中的空位浓度会高于母材.因此,本工作参考Aagesen等[50]的工作,将基体中空位的产生速率设置为 = (6~15),并讨论该参数对He泡演化的影响,从而揭示316H钢母材和焊缝金属中空位浓度差异条件下He泡的演化机制.此外,白菊菊等[11]研究表明,焊缝中存在的大量位错线扩散通道,能够促进He泡长大.为了描述316H钢母材和焊缝金属中扩散的差异,有效扩散系数(Deff)根据下式进行修正[51]: ...
Self-diffusion in grain boundaries and dislocation pipes in Al, Fe, and Ni and application to AlN precipitation in steel
1
2014
... 式中,Dbulk为在基体中的扩散系数,Dpipe为沿位错线的扩散系数,ρ为材料内部位错密度.基于Stechauner和Kozeschnik[52]针对fcc Fe中基体和位错线扩散系数的研究结果,焊缝金属中位错密度为6 × 1013 m-2时的有效扩散系数为316H钢母材中位错密度为1 × 1012 m-2时的6倍,本工作对间隙原子的扩散和空位的扩散采用同样的处理,即,(Mv)weld = 6(Mv)base,(Mg)weld = 6(Mg)base,(Mv)weld和(Mv)base分别表示焊缝金属和316H钢母材中空位的化学迁移率,(Mg)weld和(Mg)base分别表示焊缝金属和316H钢母材中He原子化学迁移率,为简化表达,后文写成(Mv,g)weld与(Mv,g)base.除上述两组参数外,He泡相场模型中316H钢母材和焊缝金属的参数均保持一致. ...
Effect of δ-ferrite decomposition on the tensile properties of one modified 316H stainless steel: Experimental investigations and crystal plastic finite element simulations
2
2024
... 晶体塑性模型中的参数(表3)包括临界分切应力和位错模型中的参数.临界分切应力模型中的参数根据316系列不锈钢晶体塑性的文献[24,39,53]确定.位错模型中的4组参数则根据Sedighiani等[54]提出的由宏观应力-应变曲线拟合的方法确定. ...
... Parameters used in crystal plasticity model
Table 3| Parameter | Value | Unit |
|---|
| KHP[39] | 1.1 | MPa· |
| dgrain | 50 (base), 100 (weld) | μm |
| ρ | 1 × 1012 (base), 6 × 1013 (weld) | m-2 |
| [24] | 1 × 10-3 | s-1 |
| n[53] | 5 | - |
| kmul | 0.03 (base), 0.02 (weld) | - |
| Rcp | 2 × 10-9 | nm |
| βp | 0.015 (base), 0.01 (weld) | – |
| krecov | 200 | – |
| C11, C12, C44 | 157, 114, 99 | GPa |
| μ[39] | 88 - 3 × 10-5T2 - 5.6 × 10-3T | GPa |
Note:KHP—Hall-Petch constant; dgrain—grain size; ρ—dislocation density; —initial plastic shear rate; n—stress exponent; kmul—dislocation multiplication constant; Rcp—critical capture radius; βp—dislocation trapping constant; krecov—dislocation recover constant; C11, C12, C44—elastic constants; μ—shear modulus; base—316H base metal, weld—316H weld metal, T—temperature ...
An efficient and robust approach to determine material parameters of crystal plasticity constitutive laws from macro-scale stress-strain curves
1
2020
... 晶体塑性模型中的参数(表3)包括临界分切应力和位错模型中的参数.临界分切应力模型中的参数根据316系列不锈钢晶体塑性的文献[24,39,53]确定.位错模型中的4组参数则根据Sedighiani等[54]提出的由宏观应力-应变曲线拟合的方法确定. ...
On the coarsening mechanisms of helium bubbles—Ostwald ripening versus migration and coalescence
1
1991
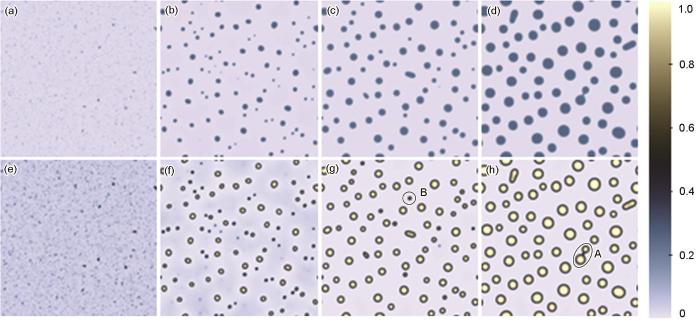
... He泡相场的第二个验证案例模拟了辐照过程中He泡的演化过程,模拟体系尺寸为38.4 nm × 38.4 nm.图6展示了He泡的动力学演化过程,其中图6a~d为He浓度场的演化,图6e~h为空位浓度场的演化.随着He+的持续注入和空位浓度的增加,He泡在过饱和空位和He浓度条件下均匀形核.在过饱和基体中空位和He原子的净通量作用下,He泡持续生长.在后期,He泡通过两种典型机制发生粗化:合并粗化(图6h中A处)和Ostwald熟化(图6g中B处),这与实验结果[55]保持一致. ...
Effect of damage rate on the kinetics of void nucleation and growth by phase field modeling for materials under irradiations
1
2016
... 图7对He泡演化进行了定量分析.根据占比分数曲线可以将He泡演化分为3个阶段:Ⅰ 形核孕育阶段,Ⅱ 形核生长阶段,Ⅲ 粗化阶段.在形核孕育阶段,基本观察不到He泡;随着辐照过程的进行,基体的空位和He浓度达到形核条件,He泡占比和数量迅速增加,迅速消耗基体中过饱和空位与He原子,因此在形核生长阶段的后期基本不再形核,从而进入粗化阶段;在粗化阶段,He泡占比增加速率减缓,已存在的He泡持续吸收空位生长,He泡尺寸持续变大.相邻较近的He泡还会合并长大,且较大的He泡会以较小的He泡为代价发生Ostwald熟化,因此粗化阶段He泡数量有所下降.此外,根据Millett[16,17]等和Ding等[56]的研究结果,辐照过程中空洞与He泡的形核生长可以用经典的Johnson-Mehl-Avrami-Kolmogorov (JMAK)方程描述: ...
An atomistic assessment of helium behavior in iron
1
2014
... 图8a对比了He泡形核后基于不同方法计算的He泡内压演化,包括EOS状态方程[31]、毛细压力方程[34]以及应力应变求解.3种计算方法下的He泡内压演化均呈现出先快速下降后逐渐饱和的演化趋势,表明了He泡演化相场模型的自洽性.相场模拟得到的最终He泡平均内压约为3 GPa,该数值与分子动力学模拟结果[57]一致.在形核阶段,小尺寸的He泡中高密度的He原子导致极高的内压,随着辐照过程的进行,He泡尺寸的增加导致He泡内部的He浓度下降并接近稳定状态(图8b),He泡内压随之下降并稳定.以上结果表明,本工作所构建的相场模型可以表征辐照条件下He泡的形核与生长过程. ...
An in situ study on the effect of grain boundaries on helium bubble formation in dual beam irradiated FeCrAl alloy
1
2023
... 图10a和c分别定量对比了不同He浓度下,316H钢母材和焊缝金属He泡尺寸演化的相场模拟与实验结果.可见,相场模拟预测的He泡尺寸与实验结果吻合良好.316H钢母材与焊缝金属中He泡尺寸演化规律类似,但316H钢母材中He泡的形核要晚于焊缝金属(图9a1和c1).在辐照初期低He浓度下,He泡形核后尺寸会快速增加,随着辐照损伤增加,尺寸增加变缓.模拟预测的He泡尺寸在辐照初期快速增加的现象也与相关的实验结果[58]一致.图10b和d分别对比了316H钢母材和焊缝金属在He浓度为0.04时,He泡平均直径分布的相场模拟与实验结果.对于316H钢母材,相场模拟的平均直径分布的峰值为2.0 nm,实验结果平均直径分布的峰值为1.6 nm;对于焊缝金属,相场模拟的平均直径分布的峰值为3.5 nm,实验结果平均直径分布的峰值为3.5 nm.综上所述,由相场模拟得出的He泡尺寸演化和He泡尺寸分布均与实验结果具有较好的一致性. ...
A comparative study on the microstructural evolution and mechanical behavior of 316LN stainless steel welds made using hot-wire tungsten inert gas and activated tungsten inert gas process
1
2024
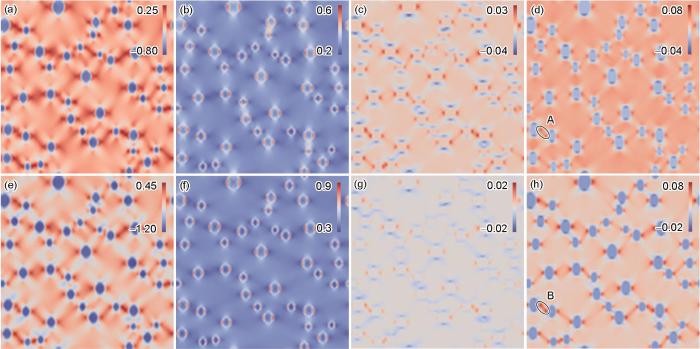
... 以He泡占比为10%的模拟体系进一步研究拉伸过程中的应力(S22)和塑性应变()分布,图14给出了外应变为0.04%和4%时316H钢母材和焊缝金属中的S22及对应的分布.总体而言,相比于基体中的应力,He泡与基体界面周围出现了显著的应力集中,相应地,应力集中处也发生了较大的塑性变形,特别是在两个相邻He泡中间形成了较为明显的变形带.由于He泡内部存在较高的内压,尽管在很小的外应变条件下(0.04%),基体中仍产生了较为明显的塑性变形(图14c和g),焊缝金属(图14g)中塑性变形程度要低于316H钢母材(图14c),这是由于焊缝金属中的高位错密度对位错滑移产生更大的阻碍.塑性变形会在一定程度上减轻局部的应力集中,因此,316H钢母材中He泡界面处的应力集中要小于焊缝金属.外应变为0.04%条件下,316H钢母材和焊缝金属He泡界面处的应力分别约为250和450 MPa;同时,He泡内部由于内压仍处于负的应力状态,这与图13应力-应变曲线中负的应力值是自洽的.随着外应变增加至4%,He泡界面处的应力集中进一步增加,316H钢母材和焊缝金属中的应力分别约为600和900 MPa.此时,塑性变形更加明显,316H钢母材基体中塑性变形程度大于焊缝金属,其原因与外应变0.04%时一致.但焊缝金属中He泡之间的塑性变形带(图14h中B处)的变形程度明显大于316H钢母材中塑性变形带(图14d中A处),焊缝金属中为0.058,316H钢母材中为0.044,表明焊缝金属在变形过程中发生了更加明显的变形局域化现象.316H钢母材的初始位错密度较低,在变形过程中,位错可以在晶粒内较为均匀地增殖和滑移,同时产生明显的加工硬化效应,这种加工硬化能力使得变形能够更均匀地分布于整个材料中.而焊缝金属中初始位错密度较高,材料加工硬化能力低[59],塑性变形过程中位错相互湮灭形成“软化”的通道,后续的位错滑移则集中在“软化”通道中,导致显著的塑性变形带(图14h中B处),与辐照材料中的位错通道的形成机制类似[60].综上所述,He泡的存在改变了拉伸过程中材料内部的局部应力状态与塑性变形行为,在应力集中的界面附近将诱发裂纹的形核,而相邻He泡则为裂纹扩展提供了优先路径,最终加速材料的失效. ...
Crystal plasticity investigation of the microstructural factors influencing dislocation channeling in a model irradiated bcc material
1
2016
... 以He泡占比为10%的模拟体系进一步研究拉伸过程中的应力(S22)和塑性应变()分布,图14给出了外应变为0.04%和4%时316H钢母材和焊缝金属中的S22及对应的分布.总体而言,相比于基体中的应力,He泡与基体界面周围出现了显著的应力集中,相应地,应力集中处也发生了较大的塑性变形,特别是在两个相邻He泡中间形成了较为明显的变形带.由于He泡内部存在较高的内压,尽管在很小的外应变条件下(0.04%),基体中仍产生了较为明显的塑性变形(图14c和g),焊缝金属(图14g)中塑性变形程度要低于316H钢母材(图14c),这是由于焊缝金属中的高位错密度对位错滑移产生更大的阻碍.塑性变形会在一定程度上减轻局部的应力集中,因此,316H钢母材中He泡界面处的应力集中要小于焊缝金属.外应变为0.04%条件下,316H钢母材和焊缝金属He泡界面处的应力分别约为250和450 MPa;同时,He泡内部由于内压仍处于负的应力状态,这与图13应力-应变曲线中负的应力值是自洽的.随着外应变增加至4%,He泡界面处的应力集中进一步增加,316H钢母材和焊缝金属中的应力分别约为600和900 MPa.此时,塑性变形更加明显,316H钢母材基体中塑性变形程度大于焊缝金属,其原因与外应变0.04%时一致.但焊缝金属中He泡之间的塑性变形带(图14h中B处)的变形程度明显大于316H钢母材中塑性变形带(图14d中A处),焊缝金属中为0.058,316H钢母材中为0.044,表明焊缝金属在变形过程中发生了更加明显的变形局域化现象.316H钢母材的初始位错密度较低,在变形过程中,位错可以在晶粒内较为均匀地增殖和滑移,同时产生明显的加工硬化效应,这种加工硬化能力使得变形能够更均匀地分布于整个材料中.而焊缝金属中初始位错密度较高,材料加工硬化能力低[59],塑性变形过程中位错相互湮灭形成“软化”的通道,后续的位错滑移则集中在“软化”通道中,导致显著的塑性变形带(图14h中B处),与辐照材料中的位错通道的形成机制类似[60].综上所述,He泡的存在改变了拉伸过程中材料内部的局部应力状态与塑性变形行为,在应力集中的界面附近将诱发裂纹的形核,而相邻He泡则为裂纹扩展提供了优先路径,最终加速材料的失效. ...