最新录用 | 当期目录 | 过刊浏览 | 热点文章 | 虚拟专辑 | 阅读排行 | 下载排行 | 引用排行 | 期刊订阅

金属学报, 2023, 59(2): 277-288 DOI: 10.11900/0412.1961.2021.00241

研究论文

CrFeNi中熵合金在宽温域拉伸条件下的力学行为与变形本构方程

王凯1, 晋玺1, 焦志明2, 乔珺威,1

1.太原理工大学 材料科学与工程学院 太原 030024

2.太原理工大学 机械与运载工程学院 太原 030024

Mechanical Behaviors and Deformation Constitutive Equations of CrFeNi Medium-Entropy Alloys Under Tensile Conditions from 77 K to 1073 K

WANG Kai1, JIN Xi1, JIAO Zhiming2, QIAO Junwei,1

1.College of Materials Science and Engineering, Taiyuan University of Technology, Taiyuan 030024, China

2.College of Mechanical and Vehicle Engineering, Taiyuan University of Technology, Taiyuan 030024, China

通讯作者: 乔珺威，qiaojunwei@tyut.edu.cn，主要从事亚稳态金属材料力学与物理性能的研究

责任编辑: 肖素红

收稿日期: 2021-06-10   修回日期: 2021-09-18  

基金资助: 国家自然科学基金项目(52271110)
爆炸科学与技术国家重点实验室开放项目(KFJJ20-13M)

Corresponding authors: QIAO Junwei, professor, Tel: 13643467172, E-mail:qiaojunwei@tyut.edu.cn

Received: 2021-06-10   Revised: 2021-09-18  

Fund supported: National Natural Science Foundation of China(52271110)
Opening Project of the State Key Laboratory of Explosion Science and Technology(KFJJ20-13M)

作者简介 About authors

王 凯，男，1996年生，硕士生

摘要

系统地研究了单相fcc结构等原子比CrFeNi中熵合金在应变速率10-3~1800 s-1，变形温度77~1073 K的拉伸力学行为。结果表明，在准静态应变速率(10-3 s-1)下，随着变形温度从1073 K降低到77 K，该合金的屈服应力从125 MPa提高到415 MPa，同时均匀延伸率由2%提高到82%。在673 K拉伸时材料表现出反常的均匀延伸率，这与变形过程中发生了动态应变时效相关。在恒定温度77 K下，随着应变速率从10-3 s-1提高到1800 s-1，合金的强度显著提高，屈服应力从415 MPa提高到595 MPa，同时均匀延伸率保持不变，在1800 s-1应变速率下仍可保持在68%。基于经典的ZA模型，构建了屈服应力-温度/应变速率之间的本构关系，结果表明，ZA模型可以很好地拟合和预测CrFeNi中熵合金在不同温度和应变速率下的屈服应力。基于实验结果，通过回归分析和约束优化建立了2种唯象本构模型(JC模型和KHL模型)和3种基于物理基础的本构模型(PB模型、ZA模型和NNL模型)。对比发现，JC模型和PB模型分别具有最高和最低的描述准确性。

关键词： 中熵合金; 力学行为; 高应变速率; 高/低温; 本构模型

Abstract

Concentrated multicomponent alloys (CMCAs) or high/medium-entropy alloys (HEAs/MEAs) possess outstanding comprehensive properties, causing them to have the potential to be the next generation of structural materials. Phenomena occurring under dynamic tensile loading or high/low temperature of such alloys have been hardly investigated. However, its understanding is essentially needed in their application in automotive, aerospace, and military industries. Meanwhile, the suitable constitutive equations of CMCAs under such cases have been rarely investigated. In this work, the thermodynamic behavior of equiatomic CrFeNi MEA with single-phase fcc structure has been systematically investigated at strain rates from 10-3 s-1 to 1800 s-1 and temperatures from 77 K to 1073 K. The results showed that as the deformation temperature decreased from 1073 K to 77 K, the yield stress was improved significantly from 125 MPa to 415 MPa. Meanwhile, the uniform elongation increased from 2% to 82%. The abnormal uniform elongation appearing at 673 K was closely related to dynamic strain aging. As the strain rate increased from 10-3 s-1 to 1800 s-1 at a constant temperature of 77 K, the strength increased significantly (e.g., the yield stress increased from 415 MPa to 595 MPa), and the uniform elongation remained unchanged, still maintaining 68% at 1800 s-1. After deformation, there were no second phases attributed to a large Ni amount in the alloys. Some deformation twins appeared at 77 K. Based on the experimental results, the relationship between yield stress and temperatures/strain rates could be successfully revealed using the ZA model. Moreover, regression analysis and constraint optimization established two phenomenological constitutive models (JC and KHL models) and three physically-based constitutive models (PB model, ZA model, and NNL model). JC and PB models had the highest and lowest description accuracy, respectively. Besides, the JC model was hard to describe the case that the work hardening decreased due to the change of temperature or strain rates, and the PB model was unsuitable in characterizing the complex work hardening behaviors.

Keywords： medium-entropy alloy; mechanical behavior; high strain rate; high/low temperature; constitutive equation

PDF (3876KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王凯, 晋玺, 焦志明, 乔珺威. CrFeNi中熵合金在宽温域拉伸条件下的力学行为与变形本构方程[J]. 金属学报, 2023, 59(2): 277-288 DOI:10.11900/0412.1961.2021.00241

WANG Kai, JIN Xi, JIAO Zhiming, QIAO Junwei. Mechanical Behaviors and Deformation Constitutive Equations of CrFeNi Medium-Entropy Alloys Under Tensile Conditions from 77 K to 1073 K[J]. Acta Metallurgica Sinica, 2023, 59(2): 277-288 DOI:10.11900/0412.1961.2021.00241

自2004年多主元合金(也称高/中熵合金)问世以来，广大学者对多主元合金的性能进行了广泛的研究。由于其宽泛的组分可调性[1]，多主元合金具有优异的综合性能，例如在室温和低温下高的强度和断裂韧性[2]、良好的焊接性能[3]、优异的深加工性能[4]和优异的抗氢脆性能[5]等。多主元合金卓越的加工硬化能力和强塑性结合使其有望成为下一代冲击防护结构材料[6]。然而，冲击防护领域通常需要材料能够在高/低温、高应变速率载荷耦合的条件下仍然保持优异的性能，而目前对于多主元合金在高/低温、高应变速率下的力学行为研究相对较少，且大多集中于室温/低温准静态拉压或室温/低温动态压缩[2,7~15]。例如，Gludovatz等[15]研究了单相fcc结构CrCoNi中熵合金在77、200和298 K下的拉伸力学行为，发现随着温度的降低，材料的强塑性同时提高，这是因为变形机制由室温下的平面滑移位错运动诱导强化转化为低温下的变形孪晶诱导强化，孪晶的出现使合金持续稳定地发生加工硬化。Senkov等[10]研究了TiZrNbHfTa难熔高熵合金在不同温度和应变速率下的压缩力学性能和组织演化，结果表明，温度低于873 K时，存在着显著的加工硬化现象；温度达到1073 K时，合金的晶粒尺寸减小，晶界处有第二相生成，晶界的强度较低，成为裂纹源；温度达到1273 K后，合金组织转变为动态再结晶生成的细晶粒；合金的屈服强度不高，在1173 K下仅有200 MPa。Ma等[8]研究了fcc + bcc双相结构AlCrCuFeNi2高熵合金的准静态和动态压缩力学性能，该合金的铸态组织为双相共晶结构，随着应变的增加，材料的强度显著提高。同时，基于经典的JC模型，很好地模拟了该合金在高应变速率下的力学行为。Song等[9]研究了fcc结构V10Cr10Fe45Co35高熵合金在低温和室温下的准静态和动态压缩力学行为，发现随着温度的降低或应变速率的增加，材料的屈服应力均提高，同时塑性保持不变；在室温下，合金会发生马氏体相变，同时随着应变的增加，会有孪晶的出现；在低温下，马氏体的体积分数高于室温，然而低温动态压缩过程中没有孪晶的出现，这是因为绝热温升导致的堆垛层错增加不足以使材料的堆垛层错能达到孪晶诱导塑性机制发生的堆垛层错能区间。值得注意的是，拉伸和压缩的不对称性广泛存在于各种合金中[16~18]，单纯的压缩性能研究并不能完全反映材料在高应变速率下的力学性能，还需要进一步地通过拉伸实验来检测多主元合金能否在高应变速率下承担起冲击防护的重任。本工作以单相fcc结构CrFeNi中熵合金为研究对象，研究其在宽温范围和宽应变速率范围内的拉伸力学行为。

近年来，随着汽车、航空航天和军工等领域的发展，材料在极端载荷(例如：高/低温、高应变速率、强辐射)作用下的塑性变形行为引起了广泛关注。在材料受到碰撞、冲击或爆炸的变形过程中，应变、应变速率和温度变化显著。为了精确地描述金属的变形行为，需要恰当的本构模型来描述应力随温度和应变速率演化的复杂情形。目前已经发展出许多先进的本构模型，主要包括2类：唯象本构模型[19~22]和基于物理基础的本构模型[23~25]。对于这2类模型，材料常数确定的简单性和材料变形行为表征的准确性是决定其适用性的2个关键决定因素。研究人员系统研究了几种典型的唯象本构模型和基于物理基础的本构模型对bcc结构钢[26]和fcc结构纯金属[27]流动应力的描述和预测能力。目前对fcc结构多主元合金本构模型的研究较少，且大多研究均使用JC本构模型进行拟合[28,29]，基于其他几种经典的本构模型的单相fcc结构多主元合金本构模型的研究很少，同时这些模型在较宽的温度和应变速率范围内对多主元合金流变行为预测的适用性尚不清楚。同时，fcc结构纯金属与fcc结构多主元合金的应变硬化对应变速率和温度的依赖性有很大的差异[13,30]。因此，本工作还研究了不同本构模型对单相fcc结构中熵合金流变行为的描述能力。

1 实验方法

使用WK-Ⅱ型非自耗真空电弧炉对原子比为1∶1∶1的CrFeNi中熵合金进行熔炼，利用水冷铜模吸铸出尺寸为80 mm × 22 mm × 2 mm的样品，随后在1473 K下对样品进行2 h均匀化退火，然后在室温下进行冷轧，轧下量为70%，最后在1373 K下进行10 min再结晶退火。利用PANAlytical型X射线衍射仪(XRD)对拉伸断裂前后试样进行相结构分析，扫描范围为40°~80°，扫描速率为2°/min。使用JSM-7100F场发射扫描电镜(SEM)进行电子背向散射衍射(EBSD)检测。使用400~2000号砂纸对变形前后样品进行粗磨，然后使用50 nm的Al2O3抛光液进行抛光，最后进行电解抛光，电解抛光液为10%HClO4 + 90%C2H5OH (体积分数)，电压为15 V，在室温下抛光10~15 s。EBSD拍摄电压为25 V，电流为14 mA，扫描步长为1 μm。

选择Instron5969力学试验机进行准静态拉伸实验，变形温度为77~1073 K，应变速率为10-3~10-1 s-1，拉伸试样的标距段尺寸为10 mm × 2 mm × 0.6 mm。进行低温(77 K)准静态(10-3~10-1 s-1)拉伸前，将样品浸泡在盛满液氮的容器中至少10 min，保证试样的温度达到液氮温度后开始拉伸实验，保证整个拉伸过程中样品完全浸泡在液氮中。进行高温(473、673、873和1073 K)准静态拉伸(10-3 s-1)前，在试样前方放置激光加热装置，同时用热电偶测量试样表面温度，当温度达到所需温度后保温1 min后开始拉伸实验。低温动态拉伸(应变速率1800 s-1，变形温度77 K)试样的标距段尺寸为10 mm × 4 mm × 0.6 mm，实验设备选择分离式Hopkinson拉杆，示意图如图1所示。该装置主要由空心圆柱冲击器、入射杆、透射杆、加压室和数据采集系统(DH5922D动态信号测试分析系统)组成。子弹、入射杆、透射杆均为高强钢，杆的直径为19 mm。通过控制气压来控制应变速率，以期得到103量级应变速率下材料的动态拉伸性能。试样置于入射杆和透射杆之间。从加压室释放的气体推动套筒式子弹向右运动，冲击入射杆端头的法兰，在入射杆中形成向左传播的拉伸加载波。利用贴于入射杆表面的应变片记录入射信号和反射信号，利用贴于透射杆上的应变片记录透射信号。应变信号经动态应变仪放大，由示波器存储和记录，最终由端口传入计算机进行处理。利用一维应力波理论计算相应的动态应力(σ)、应变(ε)和应变速率(ε˙)[31]：

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   分离式Hopkinson拉杆示意图

Fig.1   Schematic of the split Hopkinson tensile bar


ε˙=dεdt=-2CbεrLs
(1)
ε=-2CbLs∫0tεr(t)dt
(2)
σ=EAbAsεr(t)
(3)

式中，t为时间；εr为应变片记录的反射脉冲；Ab为拉伸试样的标距段横截面积；Ls为拉伸试样的标距段长度；E为入射杆和透射杆的弹性模量，在本工作中为190 GPa；As为入射杆和透射杆的横截面积，为283.53 mm2；Cb为入射杆和透射杆中弹性纵波传递速率，约为4900 m/s。

2 实验结果与讨论

2.1 变形前合金的微观结构

图2a为CrFeNi中熵合金经过70%冷轧和1373 K退火10 min后的EBSD相图。可以看出，样品仅包含fcc相，这与先前的研究结果[32]一致。图2d给出的XRD谱进一步证实了该合金的相结构为单相fcc结构，晶格常数为0.3607 nm。图2b为相应的EBSD反极图。可以看出，该合金在经过1373 K退火10 min之后内部晶粒为取向随机的等轴晶。图2e统计了晶粒尺寸分布，其平均晶粒尺寸(包括孪晶界)约为6.2 μm。图2c为EBSD带衬度图。可以看到有一些退火孪晶(Σ3孪晶界)的存在，如黄色线所示。图2f统计了取向差角分布。可见，Σ3退火孪晶体积分数约为2.5%。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   CrFeNi中熵合金经70%冷轧和1373 K退火10 min后的EBSD分析

Fig.2   EBSD analyses of CrFeNi medium-entropy alloy (MEA) after 70% cold rolling followed by annealing at 1373 K for 10 min

(a) EBSD phase map

(b) EBSD inverse pole figure (IPF)

(c) EBSD band contrast map with Σ3 twin boundary showed by yellow lines

(d) XRD spectrum (a—lattice constant)

(e) grain size distribution map (Dave—avearge grain size)

(f) misorientation angle distribution map


2.2 合金的力学性能

图3a显示了77~1073K下，应变速率为10-3 s-1时CrFeNi中熵合金的拉伸工程应力-应变曲线。可以看出，合金在873 K及以下温度变形时表现出明显的应变硬化，而1073 K变形时发生明显的软化现象。图3b总结了不同温度下的屈服应力、均匀延伸率和极限抗拉强度。随着温度从77 K增加到1073 K，屈服应力从415 MPa降低到了125 MPa，其中1073 K时的屈服应力与873 K时的屈服应力十分接近，在CoCrFeMnNi高熵合金和与之相似组分的三元/四元等原子比合金的高温拉伸下也有类似的现象[30]。同时，随着温度从77 K增加到1073 K，材料的均匀延伸率从82%降低到2%。其中在673 K下出现了一个反常现象，相比于473 K，673 K下的均匀延伸率较高，这一结果与Liang等[33]在孪晶诱导塑性(TWIP)钢中发现的结果以及Wang等[34]在相变诱导塑性(TRIP)中锰钢中观察到的结果相类似，反常的塑性可能是因为变形过程中发生了动态应变时效。相应的真应力-应变曲线如图3c所示。673 K下的真实抗拉强度为552 MPa，略低于473 K下的真实抗拉强度580 MPa。图3d为相应的加工硬化率曲线。可以看出，77 K下拉伸试样的加工硬化率在应变大于0.2时会有一个不降反升的趋势(即加工硬化率回复现象)，这表明在应变大于0.2之后，材料内部可能有额外的变形机制。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   在应变速率为10-3 s-1及不同变形温度下CrFeNi中熵合金的力学性能

Fig.3   Mechanical properties of CrFeNi MEA at different deformation temperatures and strain rate of 10-3 s-1

(a) quasi-static tensile engineering stress-strain curves

(b) yield stress (YS), ultimate tensile strength (UTS), and uniform elongation (UE)

(c) true stress-strain curves

(d) corresponding work hardening rate-true strain curves


图4a展示了77 K时，不同应变速率下CrFeNi中熵合金的拉伸工程应力-应变曲线。图4b为相应的力学性能指标。随着应变速率从10-3 s-1增加到1800 s-1，该合金的屈服应力从415 MPa增长到了595 MPa，同时其均匀延伸率仍然保持68%。图4c和d分别为相应的真应力-应变曲线和加工硬化率曲线。可以看出，当真应变超过0.2时，动态拉伸下样品的加工硬化率有明显的回升，回升幅度显著高于准静态拉伸下的幅度。综上可以推知，当应变超过0.2后，在低温准静态和低温动态下拉伸的试样内部中均可能存在额外的变形机制。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   在77 K及不同变形速率下CrFeNi中熵合金的力学性能

Fig.4   Mechanical properties of CrFeNi MEA at different strain rates and temperature of 77 K

(a) cryogenic tensile engineering stress-strain curves

(b) YS, UTS, and UE

(c) true stress-strain curves

(d) corresponding work hardening rate-true strain curves


Zerilli-Armstrong (ZA)模型是一个基于热激活位错运动理论的基于物理基础的本构模型，常常被用来预测不同应变速率/温度下材料的屈服应力(σy)[13]，可表达如下[23]：

σy=β0ε0.5exp(-β1T+β2Tlnε˙)+σG
(4)

式中，β0、β1和β2为材料参数；ε取0.002；ε˙取10-3 s-1；T为热力学温度；σG是绝热应力，可以认作是当前CrFeNi合金的晶界强化效应。本工作使用CoCrNi合金的晶界强化因子(265 MPa∙μm1/2[35])，根据Hall-Petch关系可以近似计算出σG约为106 MPa。利用温度为77、298和473 K时准静态拉伸下的屈服应力和温度为77 K，应变速率为1800 s-1的拉伸屈服应力拟合 式(4)中的各个参数，来源于最佳拟合的β0、β1和β2值分别为9347 MPa、1.0 × 10-3 K-1以及2.94 × 10-4 K-1。利用 式(4)预测了不同条件下的屈服应力，预测结果如图5所示。可以看出，当前的本构模型成功地预测了宽温域和宽应变速率范围内材料的屈服应力变化规律。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   CrFeNi中熵合金不同温度和不同应变速率下的屈服应力预测结果与实验值对比

Fig.5   Yield stresses, fitting curves, and comparisons between predicted results from ZA models and experimental results at different temperatures and strain rates

(a) experimental yield stress and corresponding fit curve at 10-3 s-1 from ZA model

(b) experimental yield stress and corresponding fit curve at 77 K from ZA model

(c) comparisons between predicted results from ZA model and experimental results of yield stress at 10-3 s-1

(d) comparisons between predicted results from ZA model and experimental results of yield stress at 77 K


2.3 变形后微结构演化

据报道，具有18%Cr和8%Ni (质量分数)的奥氏体不锈钢在变形过程中容易发生相变[36]。图6显示了在77、298、473、673、873和1073 K变形后CrFeNi中熵合金的XRD谱。所有可识别的峰均为fcc相的衍射峰。在温度为77 K时，不同应变速率下拉伸后样品的XRD谱与之类似。因此，变形过程中没有发生相变，这意味着在本工作的温度和应变速率范围内，CrFeNi中熵合金在变形过程中没有析出强化或者相变强化。这是因为该合金中含有大量的Ni元素，Ni元素是一种奥氏体稳定元素，抑制了析出动力学，稳定了奥氏体[37]。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   不同温度拉伸断裂后CrFeNi中熵合金的XRD谱

Fig.6   XRD spectra of CrFeNi MEA after tension at different temperatures


图7显示了CrFeNi中熵合金不同温度拉伸断裂后具有Σ3孪晶界的EBSD带衬度图。在77 K变形试样中可以观察到高密度的孪晶界，对比变形前样品的EBSD带衬度图(图2c)可以看出，77 K变形样品中的大部分孪晶界为变形孪晶界。在其他变形温度下，EBSD带衬度图中只能看到少量的孪晶界。随着温度的升高，材料内部的堆垛层错能显著增加，对变形孪晶有一定的抑制作用[38]。因此，在298~1073 K变形后的样品中观察到的孪晶界应该是拉伸变形以前就存在的退火孪晶界。由于这些预先存在的退火孪晶界数量有限，且尺寸较大，因此在变形过程中孪晶的影响可以忽略不计。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   CrFeNi中熵合金不同温度拉伸断裂后的EBSD带衬度图

Fig.7   EBSD band contrast maps of CrFeNi MEA after tension with Σ3 twin boundary (yellow lines)

(a) 77 K (b) 298 K (c) 473 K (d) 673 K (e) 873 K (f) 1073 K


一般认为，马氏体或变形孪晶的形成是与堆垛层错能相关的形核与生长的过程[38]。为研究CrFeNi等原子比中熵合金的堆垛层错能随温度的演化规律，基于Curtze等[39]的研究，构建了这一演化规律，如下表达式[40]：

Γ=34.096+0.10656T
(5)

式中，Γ为堆垛层错能。可以看出，该合金在0 K时的堆垛层错能就已经达到34 mJ/m2，远远超过了传统TWIP钢或TRIP钢中发生马氏体相变的临界堆垛层错能(15 mJ/m2)[41]。因而，在当前CrFeNi等原子比中熵合金中无法发生马氏体相变。在变形过程中产生变形孪晶的堆垛层错能范围为15~45 mJ/m2[41]，当变形温度为103 K时，CrFeNi中熵合金的堆垛层错能就已经超过了这一范围，因而在准静态拉伸过程中，只有温度为77 K时才会有变形孪晶的出现。

2.4 本构关系

高/中熵合金的塑性变形行为与施加的应变速率、温度和塑性应变密切相关。因此，用本构模型准确描述和预测与应变速率和温度相关的流动应力具有重要意义。Xu和Huang[42]基于2个唯象本构模型(JC和KHL模型)和5个基于物理基础的本构模型(PB、NNL、ZA、VA和RK模型)比较系统地描述了钨基复合材料的塑性变形行为。本工作选取5个比较具有代表性的模型来描述CrFeNi中熵合金的应力演化，通过物理定义或实验数据拟合确定模型常数的初始值，然后结合回归分析和约束优化程序对这些值进行优化，以尽量减少预测结果和实验结果之间的误差。

2.4.1 Johnson-Cook本构模型

JC本构模型的基本形式为[22]：

σ=A+Bεpn1+Clnε˙ε˙01-T-TmTm-Trm
(6)

式中，εp为等效塑性应变；Tr为室温；Tm为合金熔点(通过混合定律计算)，本工作CrFeNi中熵合金的熔点为1895 K；ε˙0为参考应变速率，取2000 s-1；A、B、n、C和m都为常数，拟合优化后得到的参数值为A = 216.1、B = 1490.5、n = 1.0157、C = 0.0276和m = 1。实验值与JC模型拟合值之间的对比如图8a和b所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   准静态加载和低温加载下实验数据和唯象本构模型(JC和KHL模型)结果的对比

Fig.8   Comparisons of experimental data and phenomenological constitutive model description under quasit-static loading (a, c) and cryogenic loading (b, d) (ε˙—strain rate, T—temperature)

(a, b) JC model (c, d) KHL model


2.4.2 Khan-Huang-Liang本构模型

在KHL本构模型中，σ可以表示为[20]：

σ=A+B(1-lnε˙lnε˙0)n1εn0(ε˙ε˙*)CTm-TTm-Trm
(7)

式中，ε˙*是参考应变速率，取106 s-1；n1和n0为常数。拟合优化后得到的参数值为A = 416.2、B = 1741.7、n1 = -0.4432、n0 = 1.0619、C = 0.0047和m = 1.7708，实验值与KHL模型拟合值之间的对比如图8c和d所示。

2.4.3 Zerilli-Armstrong本构模型

对fcc结构金属而言，ZA本构模型可表示为[23]：

σ=βε1/2exp(-c1T+c2Tlnε˙)+σG
(8)

式中，β、c1和c2是给定材料的相关参数。拟合优化后得到的参数值为β = 1854.278、c1 = -0.000877和c2 = 0.000347，实验值与ZA模型拟合值之间的对比如图9a和b所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

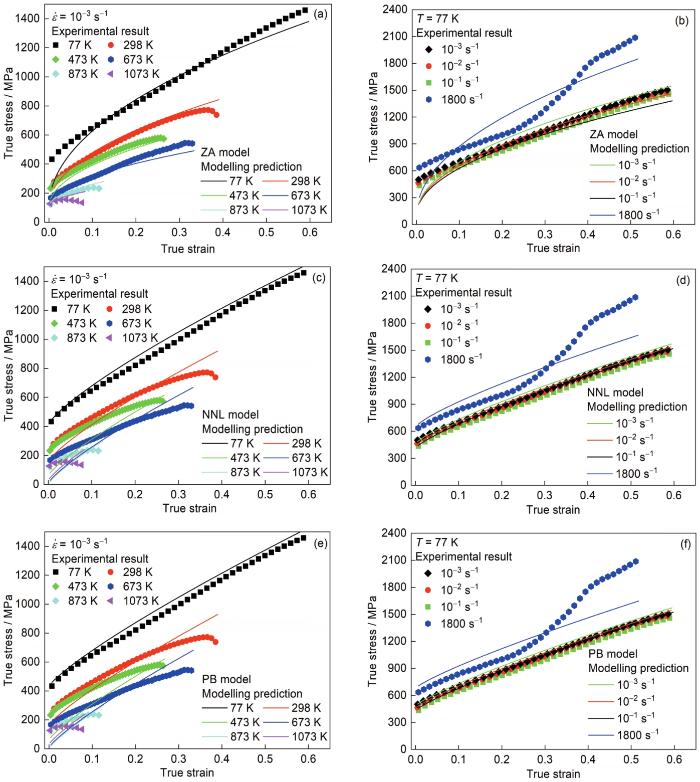
图9   准静态加载和低温加载下实验数据和基于物理基础的本构模型(ZA、NNL和PB模型)结果的对比

(a, b) ZA model (c, d) NNL model (e, f) PB model

Fig.9   Comparisons of experimental data and physically-based constitutive model description under quasit-static loading (a, c, e) and cryogenic loading (b, d, f)


2.4.4 Nemat-Nasser-Li本构模型

σ可以拆分为热激活应力和非热激活应力2部分的贡献，在NNL本构模型中[25]，热应力(τ*)与非热应力(τμ)分别表示为：

τμ=a1εn
(9)
τ*=τ01--kTG0lnε˙ε˙0+ln(1+a(T)ε12)1q1p⋅1+aTε12          (T≤Tc)
(10)

式中，a1和τ0为给定材料的相关参数；ε˙0取2000 s-1；k / G0为代表材料的温度敏感性的一个参数(通常将其认作一个整体进行计算)；Tc为临界温度，可表示为：

Tc=-G0klnε˙ε˙0+lnf(ε, T)-1
(11)

f是ε和T的函数：

f(ε, T)=1+aTε12
(12)

a(T)是一个经验函数，它有助于定义材料的应变硬化：

aT=a01-TTm2
(13)

式中，a0为给定材料的相关参数；常数q和p一般分别取1.5和0.5，所以σ的最终表达式为：

σ=a1εn+τ01--kTG0lnε˙ε˙0+ln(1+a(T)ε12)2321+aTε12        
(14)

拟合优化后得到的参数值为a1 = 1602.8、n = 0.8109、τ0 = 653、k / G0 = 0.0000849、a0 = 0.1581，实验值与NNL模型拟合值之间的对比如图9c和d所示。

2.4.5 PB本构模型

PB本构模型与NNL本构模型非常类似，均将热应力和非热应力区分计算[24]。σ可以表示为：

σ=τ*+τμ
(15)

τ*可由下式计算：

τ*=σ^[1-(-kTG0lnε˙ε˙0)1q]1p               (T≤Tc)
(16)

式中，σ^是在没有热激活的情况下克服势垒的阈值应力，Tc为：

Tc=-G0kln(ε˙ / ε˙0)
(17)

在温度大于临界温度时，τ*为0。τμ通常会用以下幂函数来表示：

τμ=aεn
(18)

综合 式(16)和(18)便可得到PB本构模型的流动应力函数：

σ=τ*+τμ=aεn+σ^[1-(-kTG0lnε˙ε˙0)1q]1p
(19)

拟合优化后得到的参数值为a1 = 1675.5、n = 0.8321、τ0 = 690.6、k / G0 = 0.0000853，实验值与PB模型拟合值之间的对比如图9e和f所示。

2.4.6 描述能力

模型对塑性变形的描述能力(描述误差，Error(%))可以通过下式来定量计算：

Error%=1h∑i=1hσexpi-σmodeliσexpi×100%
(20)

式中，σexpi和σmodeli分别是第i个来源于实验和模型的应力，h为数据点的个数。基于 式(20)，计算了不同温度和不同应变速率下模型的描述结果与实验数据的描述误差，如图10所示。可以看出，在温度恒定、应变速率变化的情况下模型的描述值和实验值的偏差普遍比恒定应变速率、不同温度下的偏差小。同时，JC模型和PB模型分别具有最低和最高的描述误差。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   不同本构模型对实验数据的描述误差

Fig.10   Description errors of experimental data for each constitutive model (strain rate—description error of experimental data obtained at constant temperatures and different strain rates; temperature—description error of experimental data obtained at constant strain rates and different temperatures; average—description error of all experimental data)


观察1073 K下的准静态拉伸实验曲线和描述曲线可知，JC模型无法拟合加工硬化随温度/应变速率变化而降低或不变的加工硬化行为，而KHL模型可以拟合这样的加工硬化行为。这是因为KHL模型考虑了流动应力的软化效应(见 式(7))，并改进了温度依赖项[27]。KHL模型的优势在于其描述热软化和随应变的增加而降低的加工硬化率的能力。

在本工作研究的基于物理基础的本构模型中，PB模型是唯一通过附加项的形式定义加工硬化行为的模型，这是该模型的主要缺点。加工硬化率(dσ / dε)与特定塑性应变下的温度和应变速率无关。从图9e和f中模型曲线之间的等距现象可以清楚地观察到这一点。因此，PB模型并不适合描述材料(特别是fcc结构金属)复杂的加工硬化行为，但它可以较好地模拟应力-应变曲线的温度和应变速率效应，如图9e和f所示。ZA模型定义了一个恒定的流动应力非热分量，它与应变、应变速率或温度无关。模型只在热应力中考虑加工硬化现象，热应力定义为温度和应变速率的函数。与此相反，NNL模型考虑了材料在两组分中的加工硬化；通过引入函数f，将热应力与不同变形水平下的应变速率和温度联系起来，而非热应力则采用幂律形式。

综上所述，PB模型不适合描述材料复杂的加工硬化行为，因为其加工硬化率与温度和应变速率无关。KHL模型能较好地表征热软化和随着应变的增加加工硬化率降低的情况。描述能力上，这5种模型对随应变速率演化的加工硬化行为的描述能力优于对随温度演化的加工硬化行为的描述能力。

3 结论

(1) 在恒定应变速率10-3 s-1下，变形温度越低，CrFeNi中熵合金的强度越高，塑性越好。77 K下强塑性同步提高，主要是因为随着温度降低，堆垛层错能降低，有利于变形孪晶的出现。673 K下表现出的反常均匀延伸率与变形过程中发生了动态应变时效相关。

(2) 在恒定温度77 K下，应变速率越高，材料的屈服应力越高，塑性保持不变。在1800 s-1的超高应变速率下，屈服应力为595 MPa，均匀延伸率仍可保持在68%。

(3) 基于经典的ZA模型，构建了屈服应力与温度和应变速率的预测模型，表达式为：σy = 418 × exp(-0.001T + 0.000294Tlnε˙) + 106。该模型成功地预测了不同温度和应变速率下单相fcc结构CrFeNi中熵合金的屈服应力。

(4) 建立了2个唯象本构模型和3个基于物理基础的本构模型来表征单相fcc结构等原子比CrFeNi中熵合金的加工硬化行为。JC模型和PB模型分别具有最高和最低的描述准确性。由于其加工硬化率与温度和应变速率无关，因此PB本构模型不适合描述材料复杂的加工硬化行为。JC模型无法拟合加工硬化率随着温度/应变速率变化而降低的情形。KHL模型能较好地表征热软化和随着应变的增加加工硬化率降低的情况。描述能力上，这5种模型对随应变速率演化的加工硬化行为的描述能力优于对随温度演化的加工硬化行为的描述能力。

参考文献

Zhang Y, Zuo T T, Tang Z, et al.

Microstructures and properties of high-entropy alloys

[J]. Prog. Mater. Sci., 2014, 61: 1

DOI      URL     [本文引用: 1]

Gludovatz B, Hohenwarter A, Catoor D, et al.

A fracture-resistant high-entropy alloy for cryogenic applications

[J]. Science, 2014, 345: 1153

DOI      PMID      [本文引用: 2]

High-entropy alloys are equiatomic, multi-element systems that can crystallize as a single phase, despite containing multiple elements with different crystal structures. A rationale for this is that the configurational entropy contribution to the total free energy in alloys with five or more major elements may stabilize the solid-solution state relative to multiphase microstructures. We examined a five-element high-entropy alloy, CrMnFeCoNi, which forms a single-phase face-centered cubic solid solution, and found it to have exceptional damage tolerance with tensile strengths above 1 GPa and fracture toughness values exceeding 200 MPa·m(1/2). Furthermore, its mechanical properties actually improve at cryogenic temperatures; we attribute this to a transition from planar-slip dislocation activity at room temperature to deformation by mechanical nanotwinning with decreasing temperature, which results in continuous steady strain hardening. Copyright © 2014, American Association for the Advancement of Science.

Wu Z, David S A, Feng Z, et al.

Weldability of a high entropy CrMnFeCoNi alloy

[J]. Scr. Mater., 2016, 124: 81

DOI      URL     [本文引用: 1]

Bae J W, Moon J, Jang M J, et al.

Deep drawing behavior of CoCrFeMnNi high-entropy alloys

[J]. Metall. Mater. Trans., 2017, 48A: 4111

[本文引用: 1]

Zhao Y K, Lee D H, Seok M Y, et al.

Resistance of CoCrFeMnNi high-entropy alloy to gaseous hydrogen embrittlement

[J]. Scr. Mater., 2017, 135: 54

DOI      URL     [本文引用: 1]

Li Z Z, Zhao S T, Ritchie R O, et al.

Mechanical properties of high-entropy alloys with emphasis on face-centered cubic alloys

[J]. Prog. Mater. Sci., 2019, 102: 296

DOI      URL     [本文引用: 1]

Eleti R R, Bhattacharjee T, Shibata A, et al.

Unique deformation behavior and microstructure evolution in high temperature processing of HfNbTaTiZr refractory high entropy alloy

[J]. Acta Mater., 2019, 171: 132

DOI      URL     [本文引用: 1]

Ma S G, Jiao Z M, Qiao J W, et al.

Strain rate effects on the dynamic mechanical properties of the AlCrCuFeNi2 high-entropy alloy

[J]. Mater. Sci. Eng., 2016, A649: 35

[本文引用: 1]

Song H, Kim D G, Kim D W, et al.

Effects of strain rate on room- and cryogenic-temperature compressive properties in metastable V10Cr10Fe45Co35 high-entropy alloy

[J]. Sci. Rep., 2019, 9: 6163

DOI      PMID      [本文引用: 1]

Quasi-static and dynamic compressive properties of an FCC-based metastable HEA (composition; V10Cr10Fe45Co35 (at.%)) showing both Transformation Induced Plasticity (TRIP) and TWinning Induced Plasticity (TWIP) were investigated at room and cryogenic temperatures. During the quasi-static and dynamic compression at room temperature, the FCC to BCC TRIP occurred inside FCC grains, and resulted in very high strain-hardening rate and consequently maximum compressive strength over 1.6 GPa. The dynamic compressive strength was higher by 240 MPa than the quasi-static strength because of strain-rate-hardening effect, and kept increasing with a high strain-hardening rate as the twinning became activated. The cryogenic-temperature strength was higher than the room-temperature strength as the FCC to BCC TRIP amount increased by the decrease in stability of FCC phase with decreasing temperature. Under dynamic loading at cryogenic temperature, twins were not formed because the increase in SFE due to adiabatic heating might not be enough to reach the TWIP regime. However, the dynamically compressed specimen showed the higher strength than the quasi-statically compressed specimen as the strain-rate-hardening effect was added with the TRIP.

Senkov O N, Scott J M, Senkova S V, et al.

Microstructure and elevated temperature properties of a refractory TaNbHfZrTi alloy

[J]. J. Mater. Sci., 2012, 47: 4062

DOI      URL     [本文引用: 1]

Zhang T W, Jiao Z M, Wang Z H, et al.

Dynamic deformation behaviors and constitutive relations of an AlCoCr1.5Fe1.5NiTi0.5 high-entropy alloy

[J]. Scr. Mater., 2017, 136: 15

DOI      URL    

Moon J, Hong S I, Seol J B, et al.

Strain-rate sensitivity of high-entropy alloys and its significance in deformation

[J]. Mater. Res. Lett., 2019, 7: 503

DOI      URL    

Zhang T W, Ma S G, Zhao D, et al.

Simultaneous enhancement of strength and ductility in a NiCoCrFe high-entropy alloy upon dynamic tension: Micromechanism and constitutive modeling

[J]. Int. J. Plast., 2020, 124: 226

DOI      URL     [本文引用: 2]

Zhang S, Wang Z, Yang H J, et al.

Ultra-high strain-rate strengthening in ductile refractory high entropy alloys upon dynamic loading

[J]. Intermetallics, 2020, 121: 106699

DOI      URL    

Gludovatz B, Hohenwarter A, Thurston K V S, et al.

Exceptional damage-tolerance of a medium-entropy alloy CrCoNi at cryogenic temperatures

[J]. Nat. Commun., 2016, 7: 10602

DOI      PMID      [本文引用: 2]

High-entropy alloys are an intriguing new class of metallic materials that derive their properties from being multi-element systems that can crystallize as a single phase, despite containing high concentrations of five or more elements with different crystal structures. Here we examine an equiatomic medium-entropy alloy containing only three elements, CrCoNi, as a single-phase face-centred cubic solid solution, which displays strength-toughness properties that exceed those of all high-entropy alloys and most multi-phase alloys. At room temperature, the alloy shows tensile strengths of almost 1 GPa, failure strains of similar to 70% and K-JIc fracture-toughness values above 200 MPa m(1/2); at cryogenic temperatures strength, ductility and toughness of the CrCoNi alloy improve to strength levels above 1.3 GPa, failure strains up to 90% and K-JIc values of 275 MPa m(1/2). Such properties appear to result from continuous steady strain hardening, which acts to suppress plastic instability, resulting from pronounced dislocation activity and deformation-induced nano-twinning.

Zhang F, Zhou J Q.

Tension-compression asymmetry and twin boundaries spacings effects in polycrystalline Ni nanowires

[J]. J. Appl. Phys., 2016, 120: 044303

[本文引用: 1]

Habib S A, Khan A S, Gnäupel-Herold T, et al.

Anisotropy, tension-compression asymmetry and texture evolution of a rare-earth-containing magnesium alloy sheet, ZEK100, at different strain rates and temperatures: Experiments and modeling

[J]. Int. J. Plast., 2017, 95: 163

DOI      URL    

He J Y, Wang Q, Zhang H S, et al.

Dynamic deformation behavior of a face-centered cubic FeCoNiCrMn high-entropy alloy

[J]. Sci. Bull., 2018, 63: 362

DOI      URL     [本文引用: 1]

Khan A S, Sung Suh Y, Kazmi R.

Quasi-static and dynamic loading responses and constitutive modeling of titanium alloys

[J]. Int. J. Plast., 2004, 20: 2233

DOI      URL     [本文引用: 1]

Khan A S, Liang R Q.

Behaviors of three BCC metal over a wide range of strain rates and temperatures: Experiments and modeling

[J]. Int. J. Plast., 1999, 15: 1089

DOI      URL     [本文引用: 1]

Liang R Q, Khan A S.

A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures

[J]. Int. J. Plast., 1999, 15: 963

DOI      URL    

Johnson G R, Cook W H.

A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures

[J]. Eng. Fract. Mech., 1983, 21: 541

[本文引用: 2]

Zerilli F J, Armstrong R W.

Dislocation-mechanics-based constitutive relations for material dynamics calculations

[J]. J. Appl. Phys., 1987, 61: 1816

DOI      URL     [本文引用: 3]

Klepaczko J R, Rusinek A, Rodríguez-Martínez J A, et al.

Modelling of thermo-viscoplastic behaviour of DH-36 and Weldox 460-E structural steels at wide ranges of strain rates and temperatures, comparison of constitutive relations for impact problems

[J]. Mech. Mater., 2009, 41: 599

DOI      URL     [本文引用: 1]

Netat-Nasser S, Li Y L.

Flow stress of f.c.c. polycrystals with application to OFHC Cu

[J]. Acta Mater., 1998, 46: 565

DOI      URL     [本文引用: 2]

Xu Z J, Huang F L.

Comparison of physically based constitutive models characterizing armor steel over wide temperature and strain rate ranges

[J]. Modell. Simul. Mater. Sci. Eng., 2012, 20: 015005

[本文引用: 1]

Xu Z J, Huang F L.

Comparison of constitutive models for FCC metals over wide temperature and strain rate ranges with application to pure copper

[J]. Int. J. Impact Eng., 2015, 79: 65

DOI      URL     [本文引用: 2]

Park J M, Moon J, Bae J W, et al.

Strain rate effects of dynamic compressive deformation on mechanical properties and microstructure of CoCrFeMnNi high-entropy alloy

[J]. Mater. Sci. Eng., 2018, A719: 155

[本文引用: 1]

Bobbili R, Madhu V.

A modified Johnson-Cook model for FeCoNiCr high entropy alloy over a wide range of strain rates

[J]. Mater. Lett., 2018, 218: 103

DOI      URL     [本文引用: 1]

Wu Z, Bei H, Pharr G M, et al.

Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures

[J]. Acta Mater., 2014, 81: 428

DOI      URL     [本文引用: 2]

Meyers M A. Dynamic Behavior of Materials[M]. New York: John Wiley & Sons Inc., 1994: 305

[本文引用: 1]

Wang K, Wang X J, Zhang T W, et al.

Tuning Cr-rich nanoprecipitation and heterogeneous structure in equiatomic CrFeNi medium-entropy stainless alloys

[J]. J. Iron Steel Res. Int., 2022, 29: 529

DOI      URL     [本文引用: 1]

Liang Z Y, Luo Z C, Huang M X.

Temperature dependence of strengthening mechanisms in a twinning-induced plasticity steel

[J]. Int. J. Plast., 2019, 116: 192

DOI      URL     [本文引用: 1]

Wang X G, Huang M X.

Temperature dependence of Lüders strain and its correlation with martensitic transformation in a medium Mn transformation-induced plasticity steel

[J]. J. Iron Steel Res. Int., 2017, 24: 1073

DOI      URL     [本文引用: 1]

Yoshida S, Bhattacharjee T, Bai Y, et al.

Friction stress and Hall-Petch relationship in CoCrNi equi-atomic medium entropy alloy processed by severe plastic deformation and subsequent annealing

[J]. Scr. Mater., 2017, 134: 33

DOI      URL     [本文引用: 1]

Reed R P.

The spontaneous martensitic transformations in 18% Cr, 8% Ni steels

[J]. Acta Metall., 1962, 10: 865

DOI      URL     [本文引用: 1]

Wei D X, Li X Q, Schönecker S, et al.

Development of strong and ductile metastable face-centered cubic single-phase high-entropy alloys

[J]. Acta Mater., 2019, 181: 318

DOI      URL     [本文引用: 1]

Christian J W, Mahajan S.

Deformation twinning

[J]. Prog. Mater. Sci., 1995, 39: 1

DOI      URL     [本文引用: 2]

Curtze S, Kuokkala V T, Oikari A, et al.

Thermodynamic modeling of the stacking fault energy of austenitic steels

[J]. Acta Mater., 2011, 59: 1068

DOI      URL     [本文引用: 1]

Wang K. Microstructure control and dynamic tension deformation behavior of CrFeNi medium entropy alloys[D]. Taiyuan: Taiyuan University of Technology, 2021

[本文引用: 1]

王 凯. CrFeNi中熵合金的组织调控与动态拉伸变形行为[D]. 太原: 太原理工大学, 2021

[本文引用: 1]

De Cooman B C, Estrin Y, Kim S K.

Twinning-induced plasticity (TWIP) steels

[J]. Acta Mater., 2018, 142: 283

DOI      URL     [本文引用: 2]

Xu Z J, Huang F L.

Thermomechanical behavior and constitutive modeling of tungsten-based composite over wide temperature and strain rate ranges

[J]. Int. J. Plast., 2013, 40: 163

DOI      URL     [本文引用: 1]

/

〈 〉


版权所有 © 《金属学报》编辑部
地址: 沈阳市文化路72号, 中国科学院金属研究所(110016)
电话: +86- 024-23971286 　E-mail: jsxb@imr.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发 技术支持：support@magtech.com.cn