金属基复合材料(metal matrix composites,MMC)集成了金属基体和增强相在模量、强度、导热、线膨胀和耐磨性能等方面的优势,且可以通过增强相种类、含量和形态来调控其性能,因此广泛应用于航空航天、电子及光学仪器等领域[1,2]。目前MMC主要采用陶瓷作为增强相,大量硬脆性陶瓷颗粒弥散分布在基体中,导致微观组织不均匀,这不仅使变形过程中模具寿命短、变形精度难以保证,而且容易导致工件表面产生复杂缺陷。石墨烯具有独特的结构,其力学和物理性能远高于陶瓷增强相,是制备高性能MMC的理想增强相之一。由于获得单层或寡层石墨烯较为困难,目前多以石墨烯纳米片(graphene nanoplatelets,GNPs)为原料,通过粉末冶金、原位合成、等离子烧结和压力浸渗等方法获得GNPs/金属基复合材料[3~6]。经过近十年的发展,GNPs/金属基复合材料突破了分散与损伤控制、规模制备等技术瓶颈,显示出比陶瓷相更优异的增强效果。如Zhang等[7]通过粉末冶金及多道搅拌摩擦加工制备了1%GNPs/2009Al复合材料(质量分数),其屈服强度和抗拉强度分别达398和514 MPa,与SiC含量10%~15% (体积分数)的铝基复合材料性能相当。随着复合材料强韧化理论的发展,近期研究[8~11]表明,GNPs增强相空间分布特征,即GNPs构型对复合材料综合性能的影响更为明显,因此实现石墨烯分布构型的调控设计成为金属基复合材料研究的热点之一。
目前,对GNPs/金属基复合材料的研究主要集中在制备工艺及材料性能等方面。文献[12~14]采用不同方法制备了GNPs/铝基、铁基和钛基复合材料,并对其力学性能进行了研究,发现随着石墨烯体积分数的增加,弹性模量、拉伸强度以及断裂应变均有所增加。周霞和刘霄霞[15]采用分子动力学方法,对单层GNPs增强镁基复合材料的力学性能进行了预测。除力学性能外,石墨烯良好的导热性能和极低的热膨胀特性使其成为制备具有高热传导和低膨胀性能的新型复合材料理想的纳米增强相之一。Mandal等[16]采用粉末熔融增材制造技术制备了石墨烯增强316L不锈钢金属基复合材料,当温度升高到1100℃时,复合材料热膨胀系数为19.3 × 10-6 ℃-1,与基体热膨胀系数相比降低了6.2%。研究[17~19]表明,均匀分布的GNPs/铝基复合材料,当GNPs含量较低时,复合材料的导热性能增强效果良好,而当GNPs含量过高时,增强效果反而有所降低。此外,GNPs的分布形式对复合材料的力学性能及热性能有很大影响。Chu等[20,21]采用真空抽滤法制备了平行层状排列的35%GNPs/Cu复合材料(体积分数),其热导率高达525 W/(m·K),相对于纯 Cu 提升了50%,但其热膨胀系数相比于纯Cu降低了64%。常庆民等[9]指出GNPs在基体中的均匀性将会影响复合材料力学性能,采用改进的Hummer法制备出氧化石墨烯,在采用静电自组装技术得到的复合材料中没有大规模的石墨烯团聚现象,而且力学性能显著提升。Wang等[10]在石墨烯薄片表面制备了垂直排列的GNPs,结果表明,当石墨烯含量为3.3% (体积分数)时,复合材料的导热系数提高了96.8%。Evans等[11]利用三层均质理论对纳米复合材料的有效导热系数进行了预测,结果表明,颗粒聚集可以显著提高纳米复合材料的导热系数。
有限元模拟是一种能满足新型GNPs/Al复合材料设计需求的重要研究方法,特别是在非均匀材料的模拟计算中。微观力学模型通常采用代表性体积元(representative volume element,RVE),可有效提高复杂微观结构的模拟精度。
由于GNPs较大的比表面积以及片层与片层之间的相互作用,因此在复合材料中极易出现团聚现象,GNPs在基体中的分散问题一直面临着极大的挑战。因此,本工作首先采用三维热力耦合有限元法分析了GNPs/2009Al复合材料分布形式对热膨胀系数的影响,进而分析了几何构型(包括均匀构型、层状构型以及网络构型)对热膨胀系数的影响。
1 有限元计算
1.1 几何模型
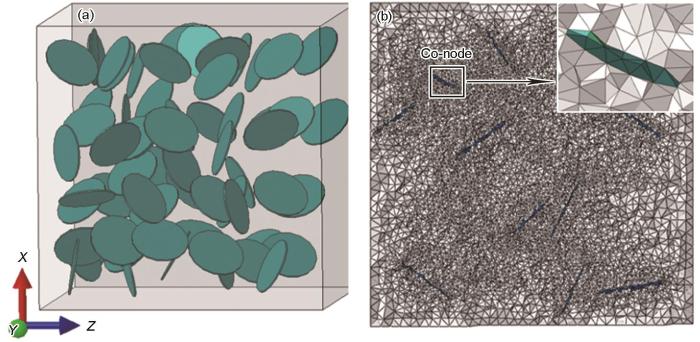
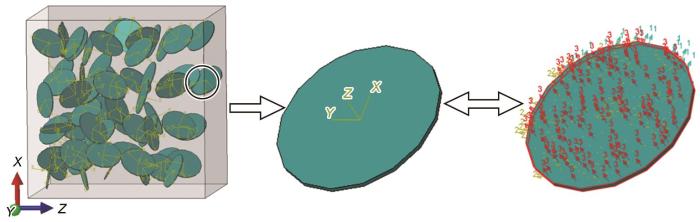
图1
图1
石墨烯纳米片(GNPs)/2009Al复合材料的代表性体积元(RVE)模型
Fig.1
Representative volume element (RVE) model of graphene nanoplatelets (GNPs)/2009Al composites
(a) whole model (b) meshing (Inset shows the local mesh refinement)
1.2 材料属性
式中,smn (m, n = 1, …, 6)为柔度系数,且smn = snm;εi 为正应变,σi 为正应力,γij 为剪应变,τij 为剪应力(i, j = 1, 2, 3)。考虑温度载荷的作用时,材料的力-热本构关系表示为[24]:
式中,σij 表示应力张量分量,εkl 表示应变张量分量,αkl 表示热膨胀系数分量,ΔT表示温差,Sijkl 表示柔度张量分量。
如果是正交各向异性材料,则有3个正交的特性对称面,
式中,σ11、σ22和σ33分别表示X、Y和Z方向的应力分量;ε11、ε22和ε33分别表示X、Y和Z方向的应变分量。此时,独立系数变成12个,包括9个柔度系数,3个热膨胀系数。横观各向同性是正交各向异性的特例,材料的3个正交性能对称面中,有一个是各向同性的。其柔度矩阵( S )变为:
可见,横观各向同性材料仅包含5个独立的柔度系数,即s11、s12、s22、s23和s66。横观各向同性材料的柔度系数与弹性常数的关系为:
式中,Ei 是在第i主方向上的弹性模量;Gij 是i-j平面上的剪切模量;νij 是主向i的作用力σi 在主向j引起横向变形的Poisson比,即j方向应变与i方向应变之比的负值。综上所述,表征横观各向同性材料的热力学性能需要5个独立的弹性常数和3个热膨胀系数,即E1、E2、ν12、ν23、G21、α11、α22和α33。
图2
| Property | Parameter | GNPs[25] | 2009Al[26] | Unit |
|---|---|---|---|---|
| Elastic property | E1 = E2 | 943600 | 69000 | MPa |
| E3 | 19500 | 69000 | MPa | |
| ν12 | 0.14 | 0.35 | ||
| ν13 | -0.09 | 0.35 | ||
| ν23 | -0.09 | 0.35 | ||
| G12 | 414180 | 25555 | MPa | |
| G13 = G23 | 5010 | 25555 | MPa | |
| Thermal expansion coefficient | α1 = α2 | -5 | 23.2 | 10-6oC-1 |
| α3 | 0.75 | 23.2 | 10-6oC-1 |
1.3 边界条件及载荷
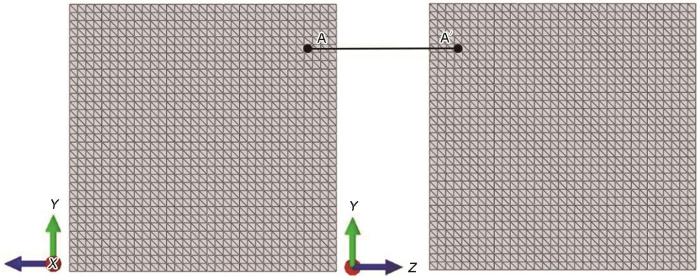
复合材料通常可以看作是三维空间中晶胞模型的周期性排列。因此,为了准确模拟复合材料在微观条件下的热膨胀行为,判断复合材料的热膨胀性能,不仅要保证增强体和基体的几何连续性,还需要在相对的边界表面上施加周期性位移边界条件。应用位移边界条件的前提是保证相对面上网格节点的分布完全一致,如图3所示。
图3
式中,
对于平行六面体的周期性微元,
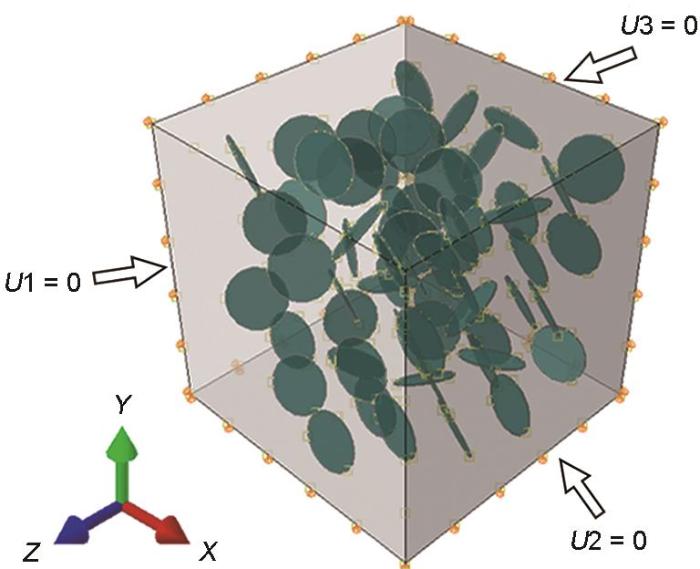
图4
图4
边界条件
Fig.4
Boundary conditions (U1, U2, and U3 are displacements in the x, y, and z directions, respectively)
1.4 热膨胀原理及计算方法
为了计算复合材料等效热膨胀系数,采用顺序耦合法,首先对模型进行传热分析,然后将得到的温度场结果作为应力分析的温度载荷,从而获得由温度引起的应力与应变的变化。其中,传热分析中整个模型的初始温度为25℃,然后设置温度载荷为26℃,使模型温度上升1℃。线膨胀系数(α)为[25]:
式中,L为初始长度,dL / dT为单位温度发生的长度变化。根据材料力-热本构方程,该模型的总应变(ε)满足:
式中,εF为外载荷引起的应变,εT为温度引起的应变。本工作分析只有温度载荷,εF= 0。因此,等效热膨胀系数为εT / ΔT。通过提取模型中所有节点的热应变,计算平均热应变与温度差的比值即可获得等效热膨胀系数。
2 结果与分析
2.1 GNPs分布形式的影响
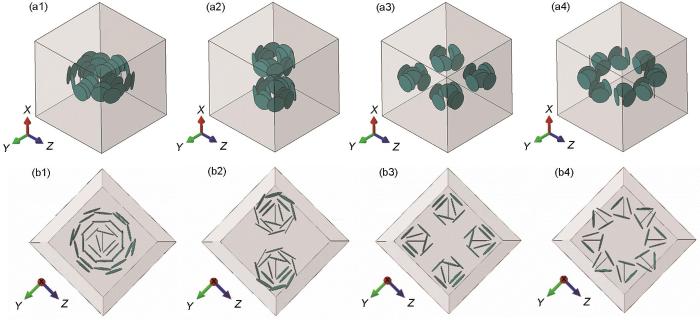
图5
图5
GNPs不同分布形式的复合材料RVE
Fig.5
Axial views (a1-a4) and cross-sectional views (b1-b4) of RVE with different GNPs distributions
(a1, b1) one cluster (a2, b2) two clusters (a3, b3) four clusters (a4, b4) eight clusters
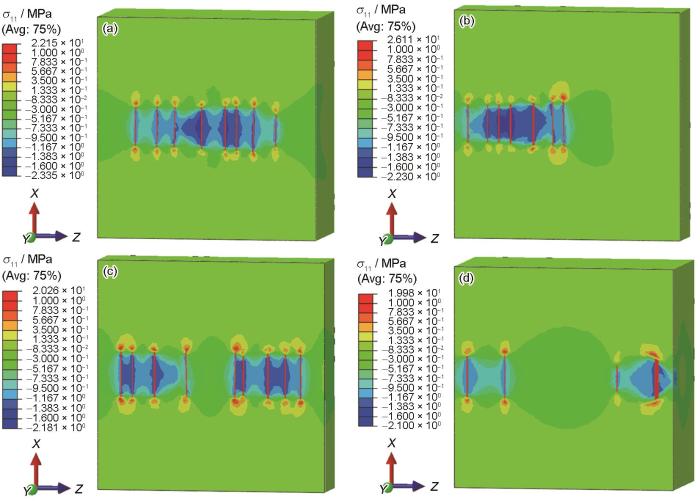
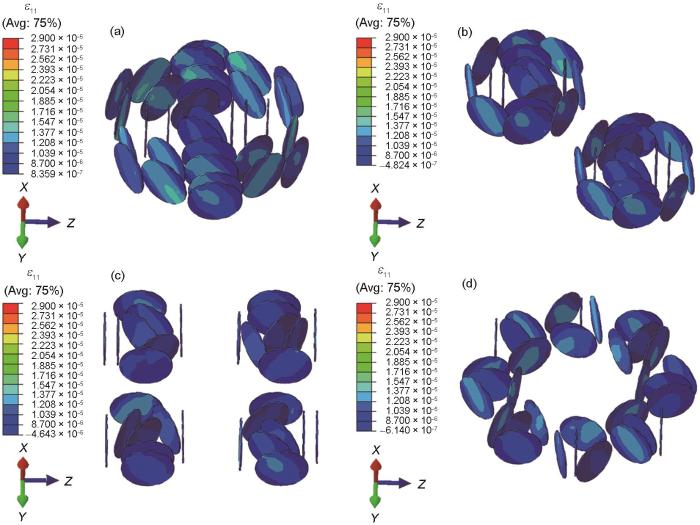
图6所示为不同GNPs分布形式下GNPs/2009Al复合材料沿X轴方向的应力(σ11)分布。由于GNPs和2009Al基体的热力学性能存在差异,在热载荷的作用下,GNPs和2009Al基体产生了不均匀的内应力。很明显,GNPs承受拉应力,基体承受压应力。GNPs拉应力约为20 MPa,GNPs附近区域基体的应力约为2 MPa,远离GNPs区域基体的应力更低。此外,沿X轴方向基体与GNPs界面处应力最高,而且是拉应力。这是因为2009Al基体热膨胀系数大,而沿着GNPs高度方向的热膨胀系数为负,温度升高使GNPs具有沿着其高度方向收缩的趋势。2009Al基体的膨胀作用力与GNPs的收缩作用力方向相反,使得界面处产生应力突变。从图6还可以看出,GNPs分布形式对应力的影响不大,当GNPs分布形式为聚集2簇时其应力最高,其他3种分布形式的应力接近。
图6
图6
不同GNPs分布形式下GNPs/2009Al复合材料X方向的应力(σ11)分布
Fig.6
X-direction stress (σ11) distributions of GNPs/2009Al composites with different GNPs distributions
(a) one cluster (b) two clusters (c) four clusters (d) eight clusters
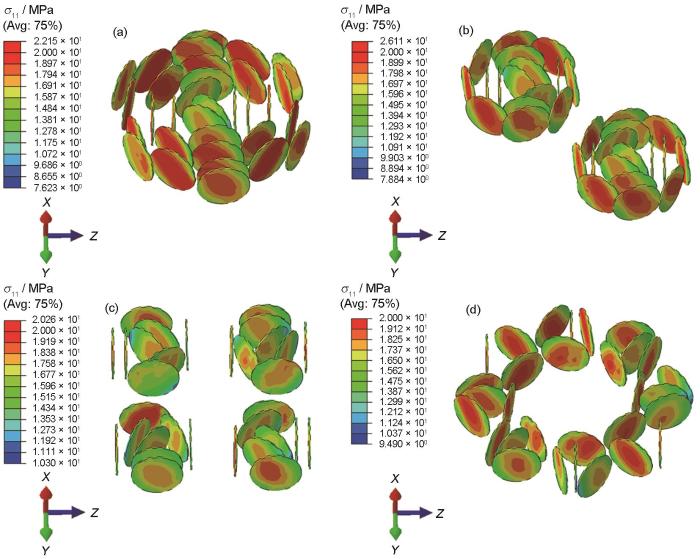
图7
图7
不同分布形式下GNPs的σ11分布
Fig.7
σ11 distributions of GNPs with different GNPs distributions
(a) one cluster (b) two clusters (c) four clusters (d) eight clusters
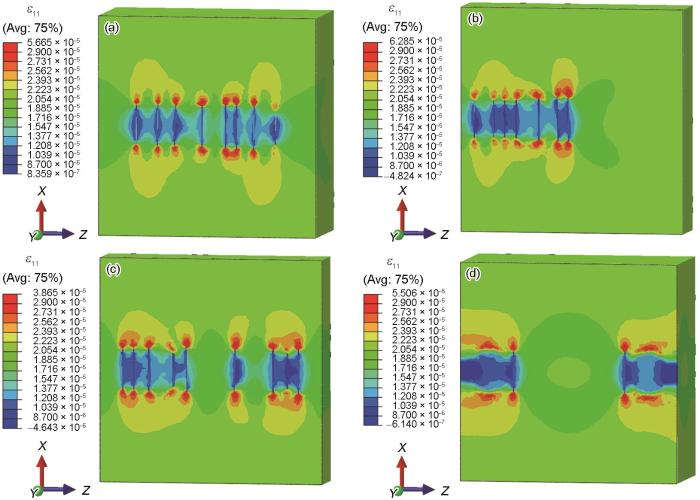
图8所示为不同GNPs分布形式下GNPs/2009Al复合材料沿X轴方向的应变(ε11)分布。可以明显地发现,GNPs及附近的基体产生的拉应变以及压应变非常小,远离GNPs的基体内产生的拉应变较大。由于GNPs的热膨胀系数很小,GNPs及其附近的基体产生的应变绝对值远低于2009Al基体产生的应变。同样,在沿X轴方向的GNPs与基体交接处出现较大的应变梯度,此处的应变比GNPs的应变高将近2个数量级。同样,当GNPs分布形式为聚集2簇时其最大应变高于其他几种分布形式。
图8
图8
不同GNPs分布形式下GNPs/2009Al复合材料X方向的应变(ε11)分布
Fig.8
X-direction strain (ε11) distributions of GNPs/2009Al composites with different GNPs distributions
(a) one cluster (b) two clusters (c) four clusters (d) eight clusters
图9
图9
不同GNPs分布形式下GNPs的ε11分布
Fig.9
ε11 distributions of GNPs with different GNPs distributions
(a) one cluster (b) two clusters (c) four clusters (d) eight clusters
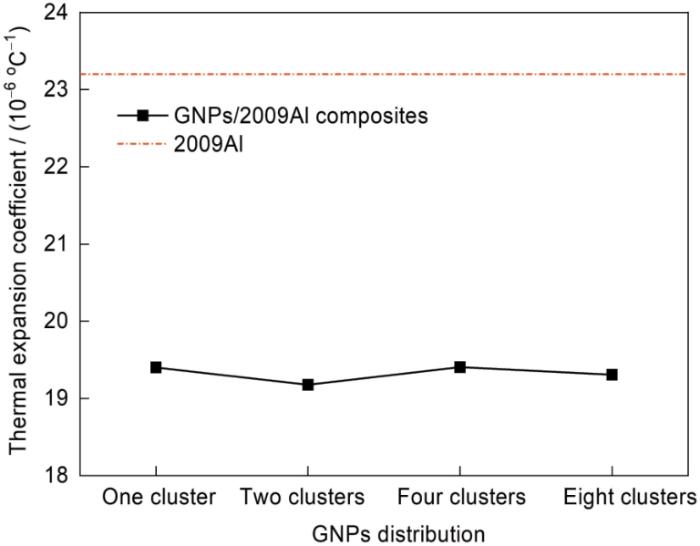
通过
图10
图10
GNPs分布形式对GNPs/2009Al复合材料热膨胀系数的影响
Fig.10
Effects of GNPs distribution on thermal expansion coefficient of GNPs/2009Al composites
2.2 GNPs几何构型的影响
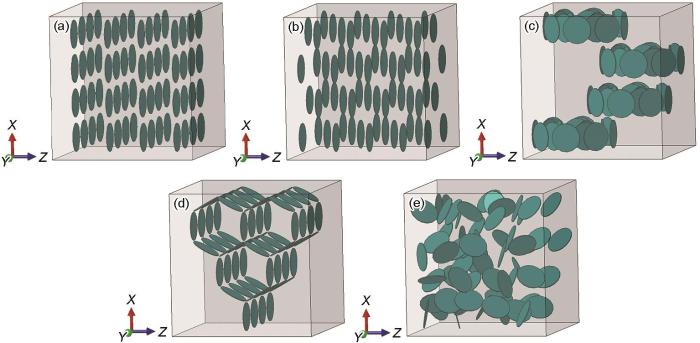
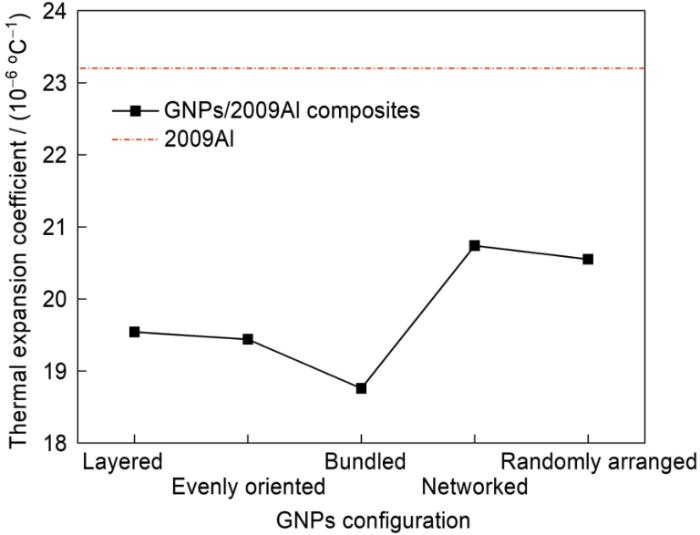
为了研究GNPs几何构型对热膨胀系数的影响,建立了5种典型构型的复合材料REV模型,分别为层状分布、均匀分布、集聚分布、网孔分布和随机分布,如图11所示。
图11
图11
典型GNPs几何构型复合材料的RVE模型
Fig.11
Schematics of RVE model with five GNPs configurations
(a) layered (b) evenly oriented (c) bundled (d) networked (e) randomly arranged
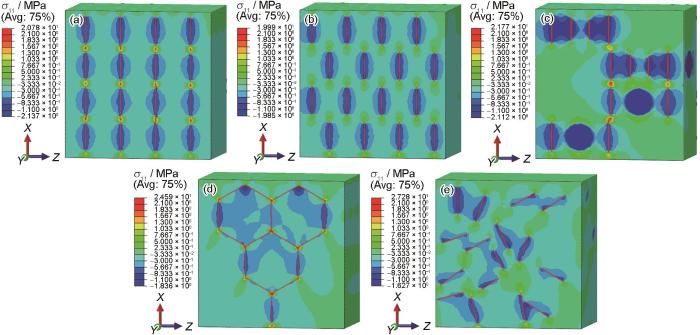
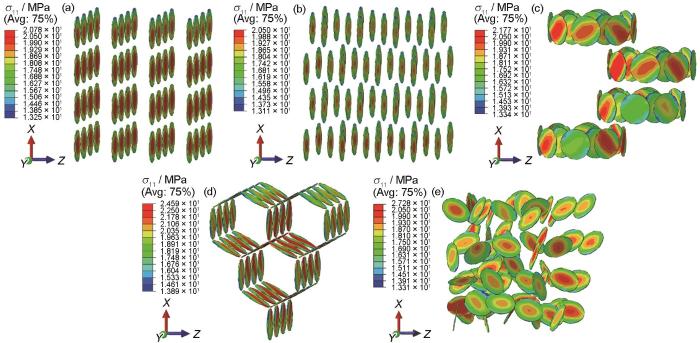
图12
图12
不同GNPs构型GNPs/2009Al复合材料的σ11分布
Fig.12
σ11 distributions of GNPs/2009Al composite with different GNPs configurations
(a) layered (b) evenly oriented (c) bundled (d) networked (e) randomly arranged
图13
图13
不同GNPs构型GNPs/2009Al复合材料GNPs的σ11分布
Fig.13
σ11 distributions of GNPs with different GNPs configurations
(a) layered (b) evenly oriented (c) bundled (d) networked (e) randomly arranged
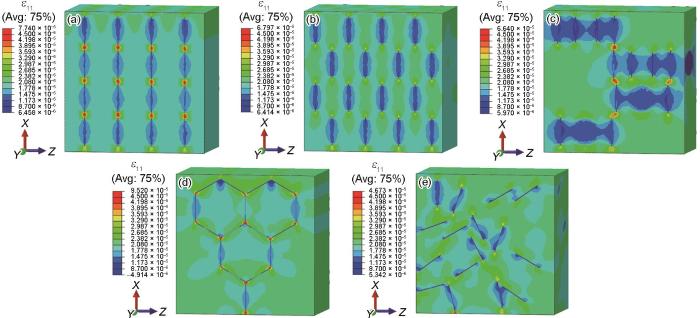
图14显示了5种GNPs构型对应的2009Al基体的真应变分布。在集聚分布的基体中,蓝色区域面积最大。层状分布和均匀分布次之。蓝色区域面积最小的为随机分布和网孔分布。这说明GNPs的聚集分布抑制了2009Al基体的热膨胀,其余分布形式的GNPs抑制作用不明显。
图14
图14
不同GNPs构型GNPs/2009Al复合材料的ε11分布
Fig.14
ε11 distributions of GNPs/2009Al composites with different GNPs configurations
(a) layered (b) evenly oriented (c) bundled (d) networked (e) randomly arranged
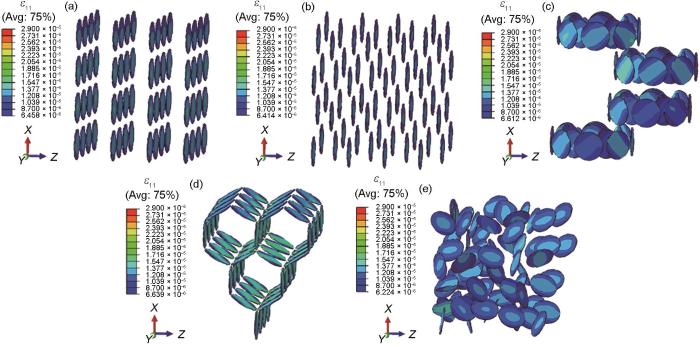
图15显示了5种构型GNPs的ε11分布。可以看出,GNPs所产生的应变均为拉应变。集聚分布以及网状分布下,蓝色区域面积较大,而其他3种构型蓝色区域面积较小。说明2009Al基体对该构型的GNPs收缩趋势的抑制作用较大。
图15
图15
不同构型GNPs的ε11分布
Fig.15
ε11 distributions of GNPs with different configurations
(a) layered (b) evenly oriented (c) bundled (d) networked (e) randomly arranged
在不同几何构型中可以发现,随机分布和网孔分布的复合材料中会出现大部分GNPs与热膨胀方向呈一定角度排列的现象。这也是随机分布和网孔分布形式下基体蓝色区域面积较小的原因。当GNPs排列方向与特定热膨胀方向存在一定的角度时,由于GNPs具有方向性的负热膨胀,从而导致GNPs沿高度方向的收缩无法充分抑制特定方向的热膨胀。
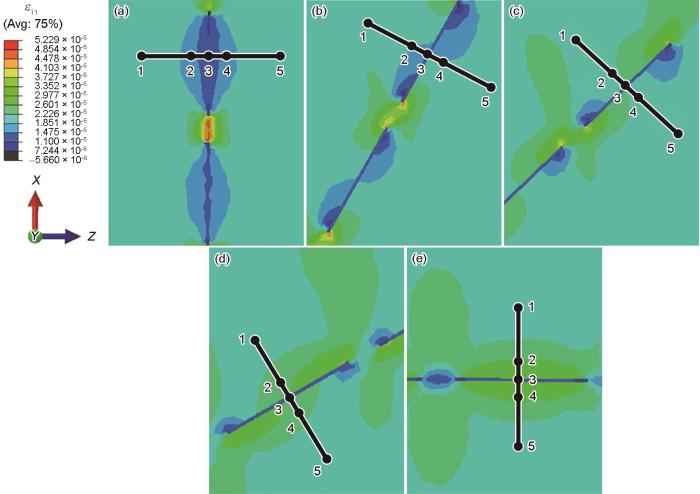
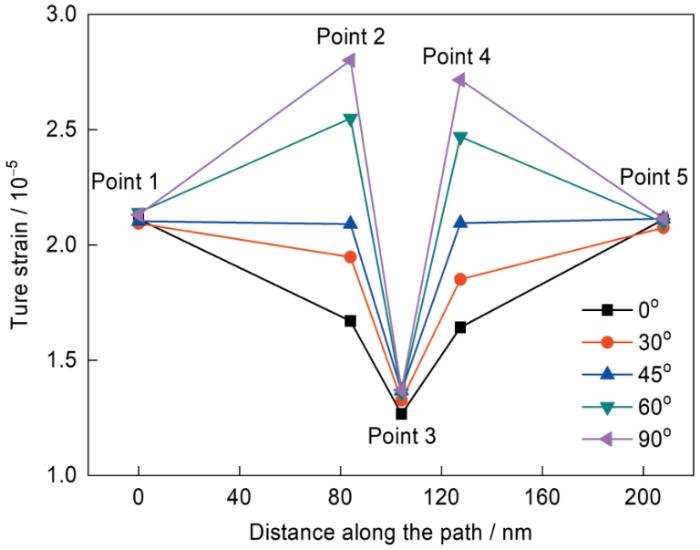
如图16所示,选取GNPs的不同排列方式来分析其排列方向对复合材料热膨胀特性的影响。GNPs高度方向与X轴方向的夹角分别为0°、30°、45°、60°和90°,在GNPs及其侧面两边分别布置点路径,点1~5依次经过基体、GNPs、基体。
图16
图16
不同角度的点路径示意图
Fig.16
Schematics of point paths at different angles
(a) 0° (b) 30° (c) 45° (d) 60° (e) 90°
图17所示为各点应变的变化趋势。随着角度的变化,点1、3和5的应变变化较小。点1和5的变化规律是由于GNPs对距离较远的Al基体影响较小。而点3的变化规律是由于其自身具有较低的热膨胀系数和较高的弹性模量,使其不容易发生形变。相反,点2和4的应变随着夹角增大而增大。这是由于GNPs在受热后,会沿着倾斜方向收缩,导致GNPs对附近Al基体的热膨胀抑制作用减弱。
图17
通过
图18
图18
GNPs构型对GNPs/2009Al复合材料热膨胀系数的影响
Fig.18
Effect of GNPs configurations on thermal expansion coefficient of GNPs/2009Al composites
2.3 GNPs体积分数的影响
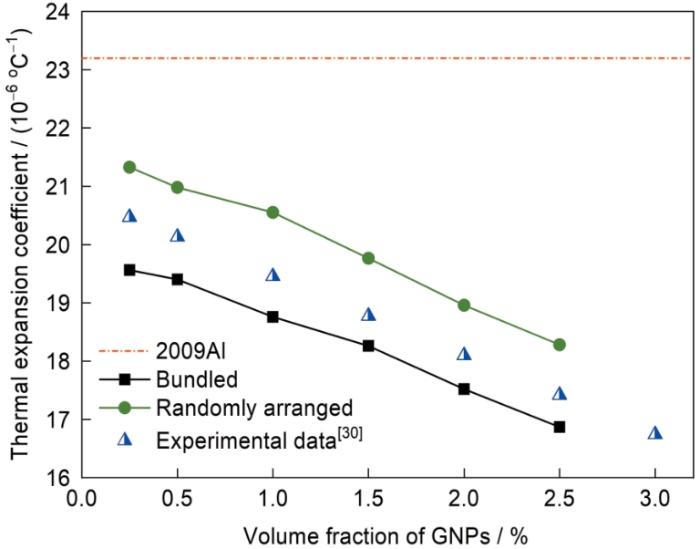
研究[28,29]表明,增强体体积分数的增加对提高复合材料的性能起着重要作用。本工作通过建立不同GNPs体积分数(0.25%、0.5%、1%、1.5%、2%、2.5%)的复合材料热膨胀模型,探讨了GNPs体积分数对其热膨胀特性的影响。图19为GNPs/2009Al复合材料的热膨胀系数随 GNPs的体积分数的变化。可以看出,随着GNPs体积分数的增加,实验与模拟的复合材料的热膨胀系数都逐渐减小。当GNPs体积分数为2.5%时,对于集聚分布的GNPs,GNPs/2009Al复合材料的热膨胀系数降低到16.87 × 10-6 ℃-1,比2009Al基体的热膨胀系数降低约27%。然而,GNPs在制备过程中的搅拌,使得其大部分随机分散在Al基体中;在随机分布的GNPs构型下,复合材料的热膨胀系数为18.28 × 10-6 ℃-1,相比于基体,降低了21.2%,与Bhouri等[30]的实验结果接近,误差范围在5.2%以内,验证了该热膨胀模型的准确性。
图19
图19
GNPs/2009Al复合材料热膨胀系数随GNPs体积分数的变化
Fig.19
Thermal expansion coefficients of GNPs/2009Al composites as a function of volume fraction of GNPs
3 结论
(1) 由于GNPs和2009Al基体热膨胀系数和力学性能存在较大差异,在受热变形时,界面处产生较大的应力突变。GNPs的分布形式对复合材料热膨胀系数的影响较小。
(2) GNPs构型对复合材料的热膨胀系数有显著的影响。GNPs集聚分布对复合材料的热膨胀有较强的抑制作用,使其热膨胀系数降低到18.76 × 10-6 ℃-1。除此之外,GNPs随机分布和网孔分布对其抑制作用较小。
(3) GNPs的体积分数对复合材料热膨胀系数产生很大的影响。随着体积分数的增加,复合材料的热膨胀系数明显降低。当GNPs体积分数为2.5%时,GNPs集聚分布的GNPs/2009Al复合材料热膨胀系数降低到16.87 × 10-6 ℃-1,比基体降低约27%。
参考文献
Opportunities and challenges for metal matrix composites in the context of equipment upgrading
[J].
装备升级换代背景下金属基复合材料的发展机遇和挑战
[J].
Progress in high throughput fabrication and characterization of metal matrix composites
[J].The "material genetic engineering" plan, based on the large data, is to investigate the high throughput design, fabrication and characterization techniques with the aim to shift the material research from traditional mode to high throughput mode with low cost and fast response speed, and to accelerate the research and development of new materials and achieve the goal of "double reduction halves". As the metal matrix composites (MMCs) exhibit multi-components and a thermodynamically non-equilibrium state during fabrication, some key issues occur and need to be addressed including: (1) for high throughput fabrication, currently developed high throughput technologies based on thermodynamically equilibrium conditions, such as spray printing and multi-node diffusion methods, are not applicable for MMCs; (2) for high throughput characterization, there is a lack of multi- dimensional, field and scale acquisition technique for the composition, morphology, microstructure and property of MMCs. In order to solve these problems, the progress on the research and development of high throughput fabrication and characterization techniques of MMCs was reviewed, especially, in the field of gradient reinforced MMCs and their high throughput combination characterization methods, which may promote the application of high throughput fabrication and characterization techniques in MMCs. Finally, the bottlenecks and prospects in the high throughput fabrication and characterization of MM Cs are proposed.
金属基复合材料高通量制备及表征技术研究进展
[J].“材料基因工程”计划是以大数据作为支撑,采用高通量设计、制备和表征技术,促使材料研究从传统的试错模式转向低成本、快速响应的新模式,从而加快新材料的研发速度,实现研发成本和周期“双减半”的目标。金属基复合材料由于组分复杂、制备过程为热力学非平衡状态,带来一些新的问题需要解决,包括:(1) 高通量制备方法方面,针对合金块体样品开发的喷印合成法、多元结扩散法等基于热力学平衡理论的高通量制备技术无法直接用于金属基复合材料构件块体坯料的制造;(2) 高通量表征技术方面,缺乏针对金属基复合材料单一样品成分、形貌、组织、结构和性能的多维、多场、多尺度同步采集技术,以及针对阵列样品成分、形貌、组织与结构的快速表征技术。鉴于上述问题,本文综述了金属基复合材料高通量制备及表征技术发展现状及已取得的进展,特别是在增强体呈梯度分布的金属基复合材料制备技术与高通量组合表征方法上取得的突破,推动了高通量制备及表征技术在金属基复合材料领域的应用。最后指出了金属基复合材料高通量计算、制备方法和表征技术方面存在的瓶颈问题,并对高通量制备与表征技术的发展进行了展望。
Enhanced mechanical properties of Al5083 alloy with graphene nanoplates prepared by ball milling and hot extrusion
[J].
Microstructure evolution and properties of graphene nanoplatelets reinforced aluminum matrix composites
[J].
Microstructures and mechanical properties of TA15 titanium alloy and graphene reinforced TA15 composites prepared by spark plasma sintering
[J].Titanium alloys and titanium-based composites are widely used in the field of aerospace owing to their advantages such as low density and high specific strength. Graphene has been found to significantly improve the mechanical properties of metal matrix composites at a lower content due to high modulus, fracture strength, and specific surface area. To achieve excellent mechanical properties, TA15 titanium alloy was fabricated via spark plasma sintering (SPS), and the effects of sintering temperature, sintering time, and sintering pressure on the densification, microstructure, and mechanical properties of the obtained alloys were investigated. The results indicate that the sintering parameters exert trivial effect on the phase composition of the sintered TA15 titanium alloy. The microstructure of the sintered alloy is mainly determined by the sintering temperature, and the prolonged sintering time will cause microstructure coarsening. Meanwhile, the sintering pressure does not have obvious effect on the sintered microstructure. Furthermore, higher sintering temperature, longer sintering time, and accurate increase in sintering pressure contribute to the densification process of TA15 titanium alloy. At room and high temperatures, the comprehensive mechanical properties exhibited by the sintered TA15 titanium alloy are determined by density and microstructure. The dense TA15 titanium alloy can be fabricated via SPS under the sintering conditions of 900oC, 50 MPa, and 5 min. Such alloy exhibits optimally comprehensive mechanical properties at room and high temperatures. Additionally, 0.5% (mass fraction) graphene reinforced TA15 composites were fabricated by SPS under the sintering conditions of 900oC, 50 MPa, and 7 min. When compared with TA15 titanium alloy, the compression yield strength and ultimate compressive strength of composites have significantly improved at room and high temperatures.
放电等离子烧结TA15钛合金及石墨烯增强TA15复合材料微观组织与力学性能
[J].采用放电等离子烧结(SPS)方法制备了TA15钛合金,并研究了烧结温度、烧结时间以及烧结压力参数对合金致密化、微观组织与力学性能的影响。结果表明:在烧结温度为800~1200℃、烧结时间为3~7 min、烧结压力为20~50 MPa的烧结条件下,烧结参数对TA15钛合金的物相组成影响不大;合金的微观组织主要由烧结温度决定,并且延长烧结时间会使微观组织发生一定的粗化,而烧结压力对微观组织没有明显的影响。升高烧结温度、延长烧结时间以及适当地增加烧结压力,有助于TA15钛合金致密化过程的进行。烧结态TA15钛合金的室温及高温压缩力学性能由合金的致密度和微观组织共同决定。采用SPS工艺在900℃及50 MPa的烧结条件下,5 min即可获得致密的TA15钛合金,并具有最佳的室温及高温综合力学性能。此外,在900℃、50 MPa和7 min的烧结条件下,采用SPS制备了0.5% (质量分数)石墨烯增强TA15复合材料,与TA15钛合金相比,复合材料室温与高温压缩屈服强度及极限抗压强度得到了明显提高。
Effect of ball milling time on graphene nanosheets reinforced Al6063 composite fabricated by pressure infiltration method
[J].
High efficiency dispersal and strengthening of graphene reinforced aluminum alloy composites fabricated by powder metallurgy combined with friction stir processing
[J].
Progress on graphene/copper composites focusing on reinforcement configuration design: A review
[J].Copper matrix composites have extensive application prospects in electronics and electrical engineering because of their excellent functional and mechanical properties. Graphene has excellent properties and a two-dimensional structure, making it an ideal reinforcement material. Compared with other reinforcements such as particles and whiskers, graphene has better performance matching with copper. Moreover, its distribution in the copper matrix can be controlled well, which can significantly improve the comprehensive properties of the composite. Therefore, controlling the distribution of graphene using novel fabrication processes is essential. This review focuses on the configuration of graphene distributed in a copper matrix (uniform configuration, layered configuration, and network configuration) and the corresponding fabrication processes. The effects of different graphene configurations on the properties of various copper matrix composites are discussed. New ideas for graphene configuration design, future development trends, and potential applications of graphene/copper matrix composites with unique configurations are anticipated.
基于增强相构型设计的石墨烯/Cu复合材料研究进展
[J].铜基复合材料具有优异的功能特性及力学性能,在电子、电工等领域具有广阔的应用前景。作为一类理想的增强相,石墨烯具有优异的综合性能以及二维结构特征。相比于其他如颗粒增强相、晶须增强相,石墨烯与Cu的性能匹配性更好,同时其在Cu基体中的分布结构具有更强的可设计性,可显著改善铜基复合材料的综合性能,因此利用新工艺实现石墨烯分布构型的调控设计成为当今铜基复合材料研究的热点。本文总结了近年来石墨烯在Cu基体中分布的构型(均匀构型、层状构型以及网络构型)及其相应的制备工艺,讨论了石墨烯构型对于铜基复合材料性能的影响,并展望了石墨烯构型设计的新思路,以及特殊构型石墨烯/Cu复合材料未来的发展趋势以及应用领域。
Preparation and properties of graphene reinforced aluminum matrix composites
[J].
石墨烯增强铝基复合材料的制备及性能研究
[J].
Enhanced through-plane thermal conductivity and mechanical properties of vertically aligned graphene nanoplatelet@graphite flakes reinforced aluminum composites
[J].
Effect of aggregation and interfacial thermal resistance on thermal conductivity of nanocomposites and colloidal nanofluids
[J].
In-situ synthesis of graphene decorated with nickel nanoparticles for fabricating reinforced 6061Al matrix composites
[J].
Single-layer graphene oxide reinforced metal matrix composites by laser sintering: Microstructure and mechanical property enhancement
[J].
Mechanical properties and microstructures of reduced graphene oxide reinforced titanium matrix composites produced by spark plasma sintering and simple shear extrusion
[J].
Mechanical properties and strengthening mechanism of graphene nanoplatelets reinforced magnesium matrix composites
[J].To improve the mechanical properties of Mg alloys and broaden their application fields, high performance Mg matrix nanocomposites have received more and more attention nowadays. Therefore, the research on the basic mechanical properties and strengthening mechanism of new Mg matrix composites at nanoscale has important theoretical and practical significance. The mechanical properties of pristine single-layer graphene nanoplatelets (GNPs) and single-side and double-side nickel-coated GNP (Ni-GNP, Ni-GNP-Ni) reinforced Mg composites (GNP/Mg, Ni-GNP/Mg, Ni-GNP-Ni/Mg) are studied under uniaxial tension by molecular dynamics (MD) simulations. Meanwhile, their tensile properties are also compared with those of double-side nickel-coated GNP with vacancy defects (Ni-defected GNP-Ni) and double-side nickel-coated multilayer GNPs (Ni-nGNPs-Ni) reinforced Mg-based composites. The simulated results show that the mechanical properties of Mg matrix composites are improved significantly by the addition of GNPs. Compared with single crystal Mg, the tensile strength and elastic modulus of GNP/Mg nanocomposites at 300 K and 1×109 s-1 are increased by 32.60% and 37.91%, respectively; while the tensile strength and elastic modulus of Ni-GNP-Ni/Mg composites are increased by 46.79% and 54.53%, separately. In addition, there is a larger increase in the elastic modulus and tensile strength but a smaller increase in the fracture strain for Ni-defected GNP-Ni/Mg composites, while there is a larger increase in the tensile strength and fracture strain but a smaller increase in the elastic modulus for Ni-GNP/Mg composites as compared with those of GNP/Mg composites. The elastic modulus, tensile strength and fracture strain of Ni-GNP-Ni/Mg composites decreases with increase in temperature, showing a temperature softening effect, but the variation in the elastic modulus of the composites is insensitive to temperature. With increasing of the layers or volume fractions of GNPs in Ni-nGNPs-Ni, the elastic modulus, tensile strength and fracture strain of the composites are all increased significantly, and the composites show excellent comprehensive mechanical properties. It is concluded that the main strengthening mechanisms for Ni-GNP-Ni/Mg nanocomposites are strong interface bonding, effective load transfer from the Mg matrix to the Ni-GNP-Ni and dislocation strengthening by analysis of the evolution of atomic structure.
石墨烯纳米片增强镁基复合材料力学性能及增强机制
[J].
Microstructural and thermal expansion behaviour of graphene reinforced 316L stainless steel matrix composite prepared via powder bed fusion additive manufacturing
[J].
Microstructure and thermal conductivity of graphene-Al composite
[J].
石墨烯铝基复合材料的组织和导热性能
[J].
Material properties of graphene/aluminum metal matrix composites fabricated by friction stir processing
[J].
Microstructure and thermal conductivity of Al-graphene composites fabricated by powder metallurgy and hot rolling techniques
[J].
Largely enhanced thermal conductivity of graphene/copper composites with highly aligned graphene network
[J].
Thermal properties of graphene/metal composites with aligned graphene
[J].
Numerical simulation of temperature dependence of tensile mechanical properties for single graphene sheet
[J].
石墨烯拉伸力学性能温度相关性的数值模拟
[J].
Fabrication and properties of graphite flakes/metal composites for thermal management applications
[J].
Effect of architecture on mechanical properties of carbon/carbon composites
[J].
Study on the mechanical and thermal properties of 3D braided composites with graphene nanoplatelets/carbon nanotubes reinforced resin matrix
[D].
石墨烯/碳纳米管强化树脂基3D编织复合材料力-热性能研究
[D].
The Study on fabrication and properties of high strength and high thermal conductivity graphite/aluminium composites material
[D].
高强度高导热镀层石墨铝复合材料的制备与性能研究
[D].
A unified periodical boundary conditions for representative volume elements of composites and applications
[J].
Analysis of thermo-elastic and physical properties of recycled 2017 aluminium alloy/Gp composites: Thermal management application
[J].
Thermal expansion anisotropy in extruded SiC particle reinforced 2080 aluminum alloy matrix composites
[J].
Numerical homogenization and experimental study of the influence of graphite content and voids on the coefficients of thermal expansion of 2017 aluminium matrix composites
[J].