The discovery of superconductivity
1
1996
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
The 2021 room-temperature superconductivity roadmap
0
2022
2
2019
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
... [3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
1
2017
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
Ein neuer effekt bei eintritt der supraleitf?higkeit
1
1933
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
Superconducting materials classes: Introduction and overview
2
2015
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
... ,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
Microscopic theory of superconductivity
3
1957
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
... [7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
... Fermi能级处电子的态密度D(Ef)对Tc的影响体现在简化的BCS公式[7]中: ...
Possible high Tc superconductivity in the Ba-La-Cu-O system
1
1986
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
From quantum matter to high-temperature superconductivity in copper oxides
0
2015
Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-O compound system at ambient pressure
0
1987
Superconductivity above 130 K in the Hg-Ba-Ca-Cu-O system
1
1993
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
Iron-based layered superconductor La[O1 - x F x ]FeAs (x = 0.05-0.12) with Tc = 26 K
1
2008
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
High-temperature superconductivity in iron-based materials
0
2010
Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3
1
2012
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
Superconductivity in an infinite-layer nickelate
1
2019
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
Signatures of superconductivity near 80?K in a nickelate under high pressure
1
2023
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
Signature of superconductivity in pressurized La4Ni3O10
0
2024
Superconductivity in trilayer nickelate La4Ni3O10 under pressure
0
2023
Discovery of high-Tc superconductivity in a nickelate
1
2023
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
液氮温区镍氧化物高温超导体的发现
1
2023
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
Colloquium: Room temperature superconductivity: The roles of theory and materials design
1
2023
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
Searching for new unconventional high temperature superconductors
0
2021
Spin fluctuations and uncoventional superconducting pairing
1
2021
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
自旋涨落与非常规超导配对
1
2021
... 材料的超导电性一直是凝聚态物理和材料领域的研究热点之一[1~4].超导材料的零电阻特性和完美抗磁特性[5]使得超导体在许多领域具有广阔的应用前景[3,6],如高效的电力转换、无损的电力输出、超强磁铁、高灵敏度传感器材料等.但是,超导的形成机制依然是理论和实验研究的重大难题之一,尤其是如何突破温度的限制,使得超导体能够在高温(如≥ 40 K,BCS (Bardeen-Cooper-Schrieffer)理论预测的极限温度[7])甚至室温下获得应用,是科学人员一直在攻克的难题.在过去30余年里,科学人员对不能用传统BCS理论[7]解释的非常规超导体进行了广泛研究.目前,常压下铜基超导体的临界温度(Tc)在20~133 K范围[8~11],铁基超导体的Tc在26~77 K范围[12~14].铜基超导体因其Tc可以超过77 K (液氮沸点),因此在某些领域获得了的应用[3,6].近年,镍基超导体[15~19]成为新的研究热点.Sun等[16]报道了一种镍氧化物La3Ni2O7单晶在14 GPa压力下表现出超导电性,超导转变温度为80 K,是继铜基超导体之后再次在氧化物体系中发现的液氮温区的超导体.然而,由于非常规超导体的形成机制尚不明晰,目前仍存在争议[20~22],在关于超导转变温度研究上亟待突破. ...
Superconductivity at 39?K in magnesium diboride
1
2001
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Metallic hydrogen: A high-temperature superconductor?
2
1968
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
... [24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Hydrogen dominant metallic alloys: High temperature superconductors?
2
2004
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
... ,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity
1
2014
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Pressure and high-Tc superconductivity in sulfur hydrides
0
2016
Conventional superconductivity at 203 Kelvin at high pressures in the sulfur hydride system
1
2015
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Dynamics and superconductivity in compressed lanthanum superhydride
1
2018
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures
0
2019
Superconductivity at 250 K in lanthanum hydride under high pressures
1
2019
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
High-temperature superconductivity in hydrides: Experimental evidence and details
1
2022
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Superconductive hydrogen-rich compounds under high pressure
1
2021
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Anomalous high-temperature superconductivity in YH6
2
2021
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
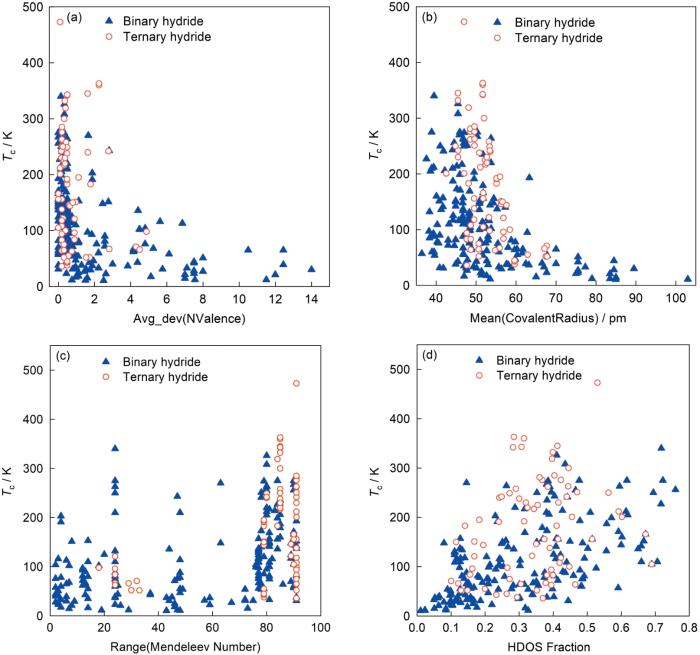
... 在金属氢化物超导体中,Range(Mendeleev Number)表示氢化物中元素MN最大的数(即H的MN数92)减去元素MN最小的数.图4c展示了Tc与Range(Mendeleev Number)的关系.从图中的趋势可以看出,MN较小的金属元素有助于提高氢化物超导体的Tc.这是因为MN较小的金属元素通常具有较低的电负性、较大的原子半径及较低的价电子数,如Y、La等元素.这些金属元素可能更容易与H元素形成超氢化物,有助于提高Tc.这与文献[34,35,53,54]报道的高Tc氢化物超导体大都是钇或镧基超氢化物相一致. ...
RETRACTED: Synthesis of yttrium superhydride superconductor with a transition temperature up to 262 K by catalytic hydrogenation at high pressures
2
2021
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
... 在金属氢化物超导体中,Range(Mendeleev Number)表示氢化物中元素MN最大的数(即H的MN数92)减去元素MN最小的数.图4c展示了Tc与Range(Mendeleev Number)的关系.从图中的趋势可以看出,MN较小的金属元素有助于提高氢化物超导体的Tc.这是因为MN较小的金属元素通常具有较低的电负性、较大的原子半径及较低的价电子数,如Y、La等元素.这些金属元素可能更容易与H元素形成超氢化物,有助于提高Tc.这与文献[34,35,53,54]报道的高Tc氢化物超导体大都是钇或镧基超氢化物相一致. ...
Synthesis of ThH4, ThH6, ThH9 and ThH10: A route to room-temperature superconductivity
1
1902
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Superconductivity at 161 K in thorium hydride ThH10: Synthesis and properties
1
2020
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Predicted high-temperature superconductivity in cerium hydrides at high pressures
1
2019
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
High-temperature superconducting phases in cerium superhydride with a Tc up to 115 K below a pressure of 1 megabar
1
2021
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Superconductive sodalite-like clathrate calcium hydride at high pressures
1
2012
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
Superconductivity above 200 K discovered in superhydrides of calcium
1
2022
... 因此,科研人员将目光转向了可以用理论解释的常规超导体上.但是在传统BCS理论框架下,很难在非氢化物常规超导体的Tc上取得突破.例如,目前Tc最高的非氢化物常规超导体为MgB2,常压下测得其Tc为39 K[23].为寻求更高Tc的超导材料,Ashcroft[24,25]提出以H元素为主要成分的化合物有望实现这个目标.这是因为H是元素周期表中最轻的元素,根据Tc (M为元素质量),所以氢化物可以实现高的Tc.此外,H原子提供了高Tc所必要的高频声子以及强的电声耦合作用.在氢化物中通过其他元素对H原子的化学压缩,可以实现超导的临界压力降低[24,25].需要强调的是,氢化物超导体是唯一先通过理论预测、后被实验验证的超导材料.其中2个最为典型的例子为氢化物超导体H3S[26~28]和LaH10[29~31].这重新激发了研究者对寻找高Tc超导体的浓厚兴趣[32,33].随着超导理论的完善和计算能力的提升,许多氢化物超导体体系被理论预测并在实验中成功合成,如Y-H[34,35]、Th-H[36,37]、Ce-H[38,39]、Ca-H[40,41]等体系. ...
A perspective on conventional high-temperature superconductors at high pressure: Methods and materials
1
2020
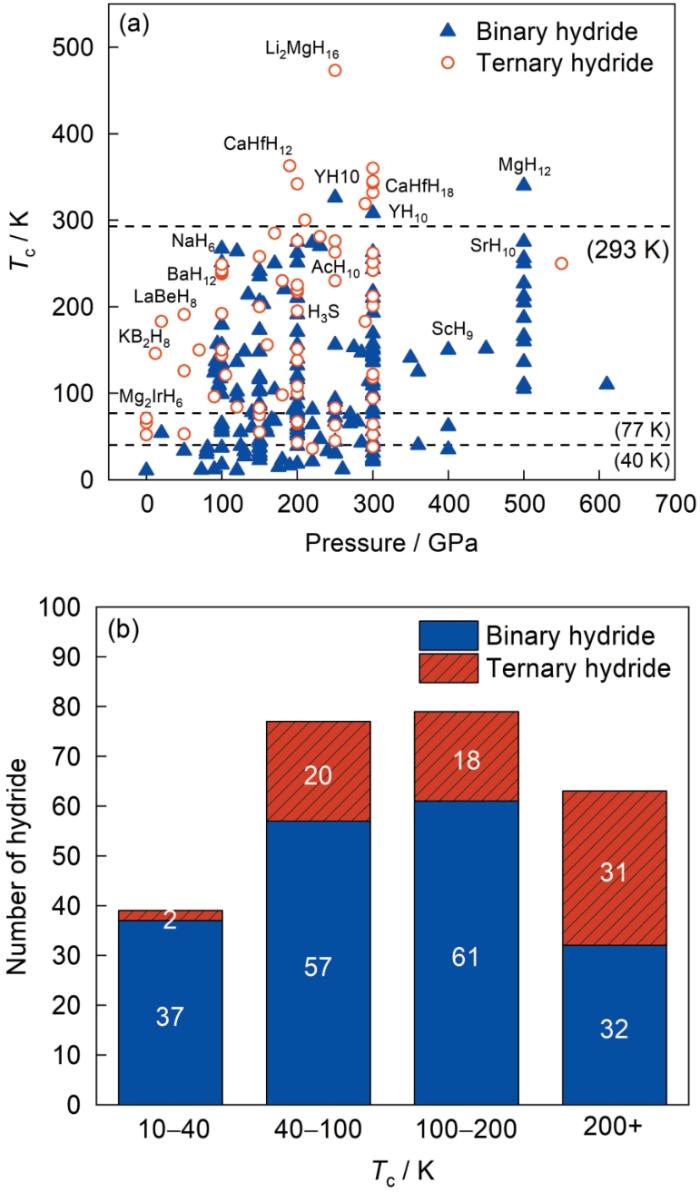
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
Route to a superconducting phase above room temperature in electron-doped hydride compounds under high pressure
6
2019
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
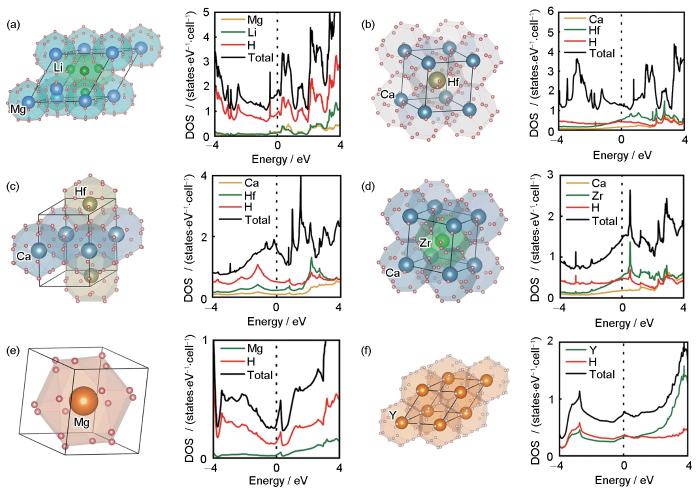
... 为了比较构建的随机森林机器学习预测模型和Belli等[59]提出的经验 公式(3),作为例子,本工作仅针对数据集中6个Tc最高的氢化物超导材料的Tc进行了预测,具体对比结果见表2[43,59,60,70,89].它们的晶体结构和电子态密度见图5.可见,随机森林机器学习预测模型最优,其性能要远优于Belli经验 公式(3).从表2[43,59,60,70,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... [43,59,60,70,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... 针对数据集中6个Tc最高的氢化物超导材料的模型预测[43,59,60,70,89] ...
... Model predictions for the six hydride superconductors with the highest Tc in the dataset[43,59,60,70,89] ...
... K
Tc (Expt.) K | | Li2MgH16 | 250 | 0.53 | 91 | 47.0 | 0.10 | 319.3 | 298.3 | 473.0[43] |
| CaHfH12 | 190 | 0.28 | 85 | 51.6 | 2.24 | 324.9 | 198.3 | 363.0[60] |
| CaHfH18 | 300 | 0.41 | 85 | 45.5 | 1.62 | 339.0 | 332.0 | 345.0[60] |
| CaZrH12 | 300 | 0.31 | 85 | 51.6 | 0.49 | 308.2 | 192.6 | 343.0[60] |
| MgH12 | 500 | 0.72 | 24 | 39.5 | 0.14 | 300.5 | 522.4 | 340.0[70] |
| YH10 | 250 | 0.41 | 80 | 45.6 | 0.33 | 312.5 | 259.6 | 326.0[89] |
| MAE | - | - | - | - | - | 47.6 | 125.3 | - |
| RMSE | - | - | - | - | - | 68.4 | 140.3 | - |
Note: RF—random forest, HDOS—hydrogen fraction of the total density of states at the Fermi energy ...
Phase diagram and superconductivity of calcium borohyrides at extreme pressures
0
2020
Structural diversity and superconductivity in S-P-H ternary hydrides under pressure
0
2022
Hot hydride superconductivity above 550 K
0
2022
Metal borohydrides as ambient-pressure high-Tc superconductors
0
2023
High-pressure Mg-Sc-H phase diagram and its superconductivity from first-principles calculations
0
2022
Ternary superconducting hydrides in the La-Mg-H system
0
2024
Enhancement of superconducting properties in the La-Ce-H system at moderate pressures
0
2023
Superconducting ternary hydrides: Progress and challenges
1
2024
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
Phonon-mediated high-temperature superconductivity in the ternary borohydride KB2H8 under pressure near 12 GPa
2
2021
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
... [52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
Design principles for high-temperature superconductors with a hydrogen-based alloy backbone at moderate pressure
3
2022
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
... [53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
... 在金属氢化物超导体中,Range(Mendeleev Number)表示氢化物中元素MN最大的数(即H的MN数92)减去元素MN最小的数.图4c展示了Tc与Range(Mendeleev Number)的关系.从图中的趋势可以看出,MN较小的金属元素有助于提高氢化物超导体的Tc.这是因为MN较小的金属元素通常具有较低的电负性、较大的原子半径及较低的价电子数,如Y、La等元素.这些金属元素可能更容易与H元素形成超氢化物,有助于提高Tc.这与文献[34,35,53,54]报道的高Tc氢化物超导体大都是钇或镧基超氢化物相一致. ...
Stoichiometric ternary superhydride LaBeH8 as a new template for high-temperature superconductivity at 110 K under 80 GPa
2
2023
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
... 在金属氢化物超导体中,Range(Mendeleev Number)表示氢化物中元素MN最大的数(即H的MN数92)减去元素MN最小的数.图4c展示了Tc与Range(Mendeleev Number)的关系.从图中的趋势可以看出,MN较小的金属元素有助于提高氢化物超导体的Tc.这是因为MN较小的金属元素通常具有较低的电负性、较大的原子半径及较低的价电子数,如Y、La等元素.这些金属元素可能更容易与H元素形成超氢化物,有助于提高Tc.这与文献[34,35,53,54]报道的高Tc氢化物超导体大都是钇或镧基超氢化物相一致. ...
Pressure-induced high-Tc superconductivity in the ternary clathrate system Y-Ca-H
2
2022
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
... [55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
Room-temperature superconductivity in Yb/Lu substituted clathrate hexahydrides under moderate pressure
1
2022
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
Prediction of ambient pressure conventional superconductivity above 80 K in hydride compounds
1
2024
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
Feasible route to high-temperature ambient-pressure hydride superconductivity
1
2024
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
Strong correlation between electronic bonding network and critical temperature in hydrogen-based superconductors
12
2021
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
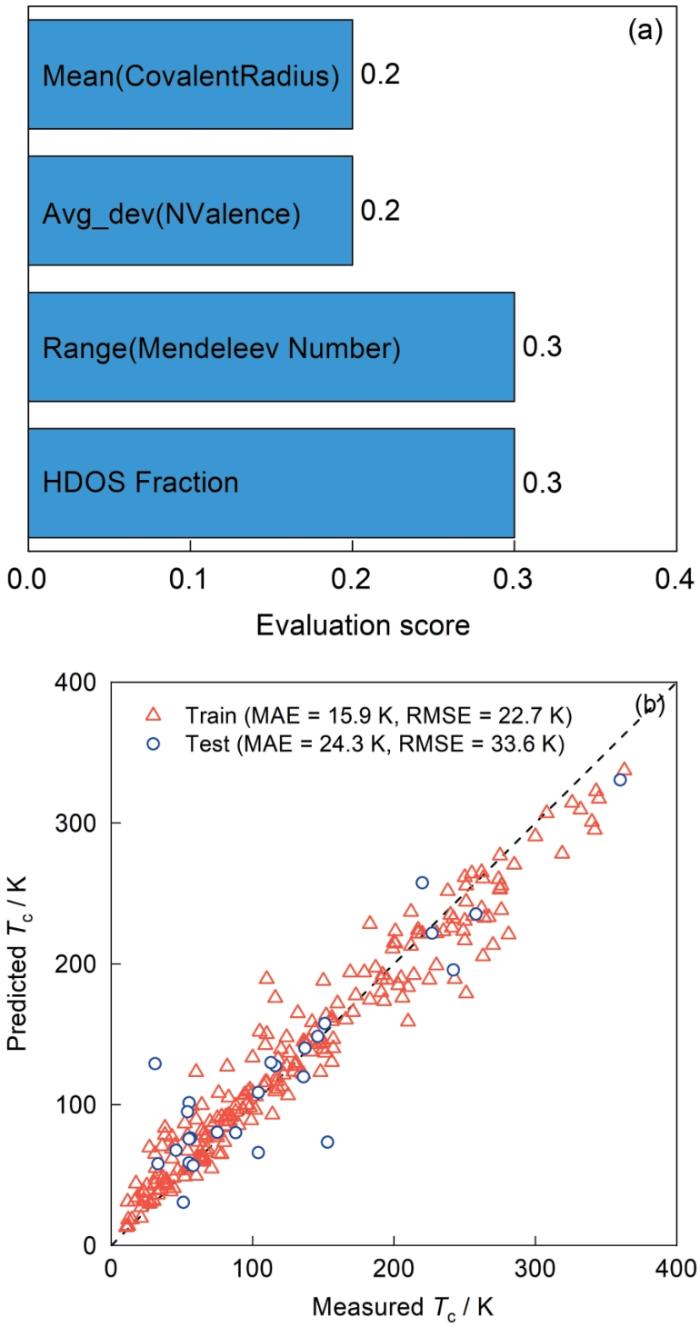
... 为了建立准确、可靠的机器学习模型,选取相关的重要特征是极为必要的.考虑的特征不仅应该能够唯一地表示每种材料,还应该容易计算,以便对新材料进行快速预测.本工作获取特征的方式有3种.第一,使用MATMINER软件包[80]获取.该软件包是一个很好的资源库,可以快速地生成特征,特别适用材料科学领域.同时,下载了材料的一系列广谱特征,如共价半径、原子质量、价电子数、配位数、Mendeleev数等.此外,还捕获了构成元素的s、p、d、f壳层中价电子的平均数量.第二,针对收集的氢化物超导体的晶体结构进行键长和配位数的计算,得到了键长(最短、最长及平均)和配位数特征.第三,引入具有物理意义的特征.受Belli等[59]和Liu等[78]工作的启发,本工作通过第一性原理计算得到最高饱和轨道和最低不饱和轨道之间的能级间隔ΔE[78]、Fermi能级处体系的总态密度(TDOS)、Fermi能级处H的态密度占比(HDOS Fraction)、氢化物中H原子的原子比例(Hf)等.通过这3种方式,本工作最终获得了共计133个特征. ...
... 式中,λ是电声耦合系数.但是,Belli等[59]发现在部分氢化物超导材料中,Tc与体系总的电子态密度似乎没有太大的关联.与之相比,他们发现与Tc相关性更强的是HDOS[59].从图4d中可以看出,Tc确实与HDOS存在着很强的正相关性,即HDOS越大,Tc通常也越高.这也与本工作中通过随机森林算法获得的特征重要性评价一致,表现出HDOS特征的重要性值最高(图3a).需要强调的是,HDOS特征也蕴含了压强的信息.即随着压强的改变,材料的结构与DOS也随之变化.尽管Tc与压强的关系十分密切,但是在机器学习过程中,压强特征因重要性低而被筛选掉,而HDOS特征则因为具有更高的重要性而被保留下来.基于HDOS,Belli等提出了一个预测Tc的经验公式[59]: ...
... [59].从图4d中可以看出,Tc确实与HDOS存在着很强的正相关性,即HDOS越大,Tc通常也越高.这也与本工作中通过随机森林算法获得的特征重要性评价一致,表现出HDOS特征的重要性值最高(图3a).需要强调的是,HDOS特征也蕴含了压强的信息.即随着压强的改变,材料的结构与DOS也随之变化.尽管Tc与压强的关系十分密切,但是在机器学习过程中,压强特征因重要性低而被筛选掉,而HDOS特征则因为具有更高的重要性而被保留下来.基于HDOS,Belli等提出了一个预测Tc的经验公式[59]: ...
... [59]: ...
... 式中,φ是电子局域函数网络的描述符,Hf为H在氢化物中的原子分数.该经验公式是通过拟合178种超导材料(包含纯H和二元氢化物)获得的,预测精度约为60 K[59]. ...
... 为了比较构建的随机森林机器学习预测模型和Belli等[59]提出的经验 公式(3),作为例子,本工作仅针对数据集中6个Tc最高的氢化物超导材料的Tc进行了预测,具体对比结果见表2[43,59,60,70,89].它们的晶体结构和电子态密度见图5.可见,随机森林机器学习预测模型最优,其性能要远优于Belli经验 公式(3).从表2[43,59,60,70,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... ,59,60,70,89].它们的晶体结构和电子态密度见图5.可见,随机森林机器学习预测模型最优,其性能要远优于Belli经验 公式(3).从表2[43,59,60,70,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... ,59,60,70,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... 针对数据集中6个Tc最高的氢化物超导材料的模型预测[43,59,60,70,89] ...
... Model predictions for the six hydride superconductors with the highest Tc in the dataset[43,59,60,70,89] ...
... Tc (Belli)[59] ...
Generic rules for achieving room-temperature superconductivity in ternary hydrides with clathrate structures
11
2023
... 尽管如此,对氢化物超导体的研究仍面临着一些问题和挑战.例如,目前发现的大多数氢化物超导体都需要在高压条件下才能稳定存在,而且电声耦合的强度也依赖于高压.为了降低所需要的压力,研究者将重心转向三元或多元氢化物上,因为它们具有进一步提高Tc并降低金属化压强的潜力[42~51].目前理论预测的最高Tc的氢化物超导材料为Sun等[43]预测的Li2MgH16,250 GPa下Tc高达473 K.目前已预测了一些可以在中低压区实现高Tc的氢化物超导材料.如,Gao等[52]预测KB2H8在12 GPa下Tc为134~146 K[52].Zhang等[53]预测了一系列具有萤石型结构框架的AXH8 (A = Sc、Ca、Y、Sr、La、Ba,X = Be、B、Al)氢化物超导体,其中LaBeH8被预测在20 GPa下可以声子稳定,预测Tc约为185 K[53].之后不久,LaBeH8被Song等[54]首次在实验上成功合成,在80 GPa下测得的Tc为110 K.Zhao等[55]研究了Y-Ca-H的体系结构和超导性,发现了4种笼型结构三元氢化物,经过计算,Y3CaH24的超导转变温度在150 GPa下为242~258 K[55].Du等[56]通过将重稀土元素Yb/Lu加入类钠盐的六氢化物中,得到一系列可以在中压下稳定的高Tc氢化物超导体,其中Y3LuH24在120 GPa下Tc为283 K,YLuH12在140 GPa下Tc为275 K,YLu3H24在110 GPa下Tc为288 K.最近,Sanna等[57]理论预测了Mg2XH6 (X = Rh、Ir、Pd、Pt)常压超导家族,预测的常压下超导转变温度在45~80 K之间.同时期内,Dolui等[58]也独立地理论预测Mg2IrH6为常压超导材料,并提出了可能的实验合成路径.此外,一些学者对高Tc的成因进行了相关性研究.比如Belli等[59]利用第一性原理计算分析了100多种二元氢化物超导体的电子和结构特性,发现Tc与电子键合之间存在很强的相关性,并建立了一个基于电子局域函数网络的描述符来预测Tc.Liu等[60]提出了实现高Tc氢化物超导的2种规则(即最优价电子数规则和最优原子占据规则),并在此基础上预测了CaHfH12在300 GPa下Tc为360 K,CaZrH12在200 GPa下Tc为290 K. ...
... Stanev等[74]曾在自己的工作中提到“3个‘黄金描述符’将60个已知的Tc > 10 K的超导体限制在了特征空间的3个小岛上:平均价电子数、轨道半径差和金属电负性差”.选择这3个描述符是因为它们在二元、三元化合物的分类上以及稳态、亚稳态晶体的预测方面获得的成功[74].Liu等[60]发现在金属氢化物超导体中,要使金属原子为H原子有效提供电子,那么金属原子应该具有价电子数3.由此可见,价电子数对氢化物超导是一个重要的特征.而在本工作开发的氢化物超导体Tc机器学习预测模型中,[Avg_dev(NValence)]被随机森林算法选为一个重要的特征.从图4a可以看出,高Tc氢化物超导体大多集中在Avg_dev(NValence) = 0~1的区域内.此外,通过绘制Tc与金属氢化物超导体中金属原子价电子数平均值的关系图,发现高Tc金属氢化物超导体大都分布在金属原子价电子数平均值为3的区域,这与Liu等[60]发现的最优价电子数规则高度一致. ...
... [60]发现的最优价电子数规则高度一致. ...
... 原子半径影响原子间的距离和相互作用强度,从而影响晶体结构和电子结构.对超导材料来说,晶体结构的变化会影响其中电子的相互作用方式,从而影响电子的运动和配对.在金属氢化物超导体中为了实现高的Tc,需要对H原子施加尽可能高的化学挤压,那么金属元素的原子半径需要在给定的晶格下使金属原子最大地填充晶格.这就是Liu等[60]提出的最优原子占据规则.此外,在Stanev等[74]和Hutcheon等[77]开发的机器学习模型中,平均原子半径亦作为一个重要的特征.图4b绘制了Tc与平均共价半径的关系.可见,高Tc氢化物超导体的平均共价半径一般在40~55 pm范围内. ...
... 为了比较构建的随机森林机器学习预测模型和Belli等[59]提出的经验 公式(3),作为例子,本工作仅针对数据集中6个Tc最高的氢化物超导材料的Tc进行了预测,具体对比结果见表2[43,59,60,70,89].它们的晶体结构和电子态密度见图5.可见,随机森林机器学习预测模型最优,其性能要远优于Belli经验 公式(3).从表2[43,59,60,70,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... ,60,70,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... 针对数据集中6个Tc最高的氢化物超导材料的模型预测[43,59,60,70,89] ...
... Model predictions for the six hydride superconductors with the highest Tc in the dataset[43,59,60,70,89] ...
... K
Tc (Expt.) K | | Li2MgH16 | 250 | 0.53 | 91 | 47.0 | 0.10 | 319.3 | 298.3 | 473.0[43] |
| CaHfH12 | 190 | 0.28 | 85 | 51.6 | 2.24 | 324.9 | 198.3 | 363.0[60] |
| CaHfH18 | 300 | 0.41 | 85 | 45.5 | 1.62 | 339.0 | 332.0 | 345.0[60] |
| CaZrH12 | 300 | 0.31 | 85 | 51.6 | 0.49 | 308.2 | 192.6 | 343.0[60] |
| MgH12 | 500 | 0.72 | 24 | 39.5 | 0.14 | 300.5 | 522.4 | 340.0[70] |
| YH10 | 250 | 0.41 | 80 | 45.6 | 0.33 | 312.5 | 259.6 | 326.0[89] |
| MAE | - | - | - | - | - | 47.6 | 125.3 | - |
| RMSE | - | - | - | - | - | 68.4 | 140.3 | - |
Note: RF—random forest, HDOS—hydrogen fraction of the total density of states at the Fermi energy ...
... [
60]
| CaZrH12 | 300 | 0.31 | 85 | 51.6 | 0.49 | 308.2 | 192.6 | 343.0[60] |
| MgH12 | 500 | 0.72 | 24 | 39.5 | 0.14 | 300.5 | 522.4 | 340.0[70] |
| YH10 | 250 | 0.41 | 80 | 45.6 | 0.33 | 312.5 | 259.6 | 326.0[89] |
| MAE | - | - | - | - | - | 47.6 | 125.3 | - |
| RMSE | - | - | - | - | - | 68.4 | 140.3 | - |
Note: RF—random forest, HDOS—hydrogen fraction of the total density of states at the Fermi energy ...
... [
60]
| MgH12 | 500 | 0.72 | 24 | 39.5 | 0.14 | 300.5 | 522.4 | 340.0[70] |
| YH10 | 250 | 0.41 | 80 | 45.6 | 0.33 | 312.5 | 259.6 | 326.0[89] |
| MAE | - | - | - | - | - | 47.6 | 125.3 | - |
| RMSE | - | - | - | - | - | 68.4 | 140.3 | - |
Note: RF—random forest, HDOS—hydrogen fraction of the total density of states at the Fermi energy ...
Eliashberg theory: A short review
1
2020
... 综上氢化物超导材料的研究发展可见理论预测的重要性.第一性原理方法(如Eliashberg理论[61,62]、McMillan-Allen-Dynes公式[63~65]及超导密度泛函理论[66~68])可以准确预测氢化物超导体的Tc,但计算量很大.尤其是在强电声耦合超导体[69]中,电声耦合矩阵计算十分昂贵.因此,开发准确且高效的氢化物超导转变温度预测模型是十分必要的.随着数据库和人工智能方法的快速发展,数据驱动和机器学习方法也逐渐被应用于超导领域. ...
Interactions between electrons and lattice vibrations in a superconductor
1
1960
... 综上氢化物超导材料的研究发展可见理论预测的重要性.第一性原理方法(如Eliashberg理论[61,62]、McMillan-Allen-Dynes公式[63~65]及超导密度泛函理论[66~68])可以准确预测氢化物超导体的Tc,但计算量很大.尤其是在强电声耦合超导体[69]中,电声耦合矩阵计算十分昂贵.因此,开发准确且高效的氢化物超导转变温度预测模型是十分必要的.随着数据库和人工智能方法的快速发展,数据驱动和机器学习方法也逐渐被应用于超导领域. ...
McMillan's equation and the Tc of superconductors
1
1972
... 综上氢化物超导材料的研究发展可见理论预测的重要性.第一性原理方法(如Eliashberg理论[61,62]、McMillan-Allen-Dynes公式[63~65]及超导密度泛函理论[66~68])可以准确预测氢化物超导体的Tc,但计算量很大.尤其是在强电声耦合超导体[69]中,电声耦合矩阵计算十分昂贵.因此,开发准确且高效的氢化物超导转变温度预测模型是十分必要的.随着数据库和人工智能方法的快速发展,数据驱动和机器学习方法也逐渐被应用于超导领域. ...
Transition temperature of strong-coupled superconductors reanalyzed
0
1975
Transition temperature of strong-coupled superconductors
1
1968
... 综上氢化物超导材料的研究发展可见理论预测的重要性.第一性原理方法(如Eliashberg理论[61,62]、McMillan-Allen-Dynes公式[63~65]及超导密度泛函理论[66~68])可以准确预测氢化物超导体的Tc,但计算量很大.尤其是在强电声耦合超导体[69]中,电声耦合矩阵计算十分昂贵.因此,开发准确且高效的氢化物超导转变温度预测模型是十分必要的.随着数据库和人工智能方法的快速发展,数据驱动和机器学习方法也逐渐被应用于超导领域. ...
Density-functional theory for superconductors
1
1988
... 综上氢化物超导材料的研究发展可见理论预测的重要性.第一性原理方法(如Eliashberg理论[61,62]、McMillan-Allen-Dynes公式[63~65]及超导密度泛函理论[66~68])可以准确预测氢化物超导体的Tc,但计算量很大.尤其是在强电声耦合超导体[69]中,电声耦合矩阵计算十分昂贵.因此,开发准确且高效的氢化物超导转变温度预测模型是十分必要的.随着数据库和人工智能方法的快速发展,数据驱动和机器学习方法也逐渐被应用于超导领域. ...
Ab initio theory of superconductivity. II. Application to elemental metals
0
2005
Ab initio theory of superconductivity. I. Density functional formalism and approximate functionals
1
2005
... 综上氢化物超导材料的研究发展可见理论预测的重要性.第一性原理方法(如Eliashberg理论[61,62]、McMillan-Allen-Dynes公式[63~65]及超导密度泛函理论[66~68])可以准确预测氢化物超导体的Tc,但计算量很大.尤其是在强电声耦合超导体[69]中,电声耦合矩阵计算十分昂贵.因此,开发准确且高效的氢化物超导转变温度预测模型是十分必要的.随着数据库和人工智能方法的快速发展,数据驱动和机器学习方法也逐渐被应用于超导领域. ...
Designing high-TC superconductors with BCS-inspired screening, density functional theory, and deep-learning
2
2022
... 综上氢化物超导材料的研究发展可见理论预测的重要性.第一性原理方法(如Eliashberg理论[61,62]、McMillan-Allen-Dynes公式[63~65]及超导密度泛函理论[66~68])可以准确预测氢化物超导体的Tc,但计算量很大.尤其是在强电声耦合超导体[69]中,电声耦合矩阵计算十分昂贵.因此,开发准确且高效的氢化物超导转变温度预测模型是十分必要的.随着数据库和人工智能方法的快速发展,数据驱动和机器学习方法也逐渐被应用于超导领域. ...
... 在数据驱动方面,Shipley等[70]利用晶体结构预测方法搜索了整个元素周期表10~50 GPa下稳定的二元氢化物,对最佳超导候选材料进行了高通量计算,发现了36种Tc超过100 K的声子稳定的高压氢化物超导体.Choudhary和Garrity[69]针对常规超导体开发了一个高通量计算工作流,计算了超过1000个材料的Tc,建立了一个系统的BCS超导数据库,并基于此开发了深度学习预测模型.Saha等[71]基于现有氢化物超导体的结构框架,通过元素替换方式获得了139个新的氢化物超导体,并基于此创建了Superhydra数据库,目前仅限于在200 GPa下的二元氢化物.Sommer等[72]建立了“3DSC”超导数据库,其中包括Tc和结构数据,以便进行机器学习.Cerqueira等[73]对7000多个常规超导候选材料的Tc进行了高通量第一性原理计算,发现了许多之前尚未报道的新超导材料. ...
High-throughput discovery of high-temperature conventional superconductors
6
2021
... 在数据驱动方面,Shipley等[70]利用晶体结构预测方法搜索了整个元素周期表10~50 GPa下稳定的二元氢化物,对最佳超导候选材料进行了高通量计算,发现了36种Tc超过100 K的声子稳定的高压氢化物超导体.Choudhary和Garrity[69]针对常规超导体开发了一个高通量计算工作流,计算了超过1000个材料的Tc,建立了一个系统的BCS超导数据库,并基于此开发了深度学习预测模型.Saha等[71]基于现有氢化物超导体的结构框架,通过元素替换方式获得了139个新的氢化物超导体,并基于此创建了Superhydra数据库,目前仅限于在200 GPa下的二元氢化物.Sommer等[72]建立了“3DSC”超导数据库,其中包括Tc和结构数据,以便进行机器学习.Cerqueira等[73]对7000多个常规超导候选材料的Tc进行了高通量第一性原理计算,发现了许多之前尚未报道的新超导材料. ...
... 为了比较构建的随机森林机器学习预测模型和Belli等[59]提出的经验 公式(3),作为例子,本工作仅针对数据集中6个Tc最高的氢化物超导材料的Tc进行了预测,具体对比结果见表2[43,59,60,70,89].它们的晶体结构和电子态密度见图5.可见,随机森林机器学习预测模型最优,其性能要远优于Belli经验 公式(3).从表2[43,59,60,70,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... ,70,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... 针对数据集中6个Tc最高的氢化物超导材料的模型预测[43,59,60,70,89] ...
... Model predictions for the six hydride superconductors with the highest Tc in the dataset[43,59,60,70,89] ...
... K
Tc (Expt.) K | | Li2MgH16 | 250 | 0.53 | 91 | 47.0 | 0.10 | 319.3 | 298.3 | 473.0[43] |
| CaHfH12 | 190 | 0.28 | 85 | 51.6 | 2.24 | 324.9 | 198.3 | 363.0[60] |
| CaHfH18 | 300 | 0.41 | 85 | 45.5 | 1.62 | 339.0 | 332.0 | 345.0[60] |
| CaZrH12 | 300 | 0.31 | 85 | 51.6 | 0.49 | 308.2 | 192.6 | 343.0[60] |
| MgH12 | 500 | 0.72 | 24 | 39.5 | 0.14 | 300.5 | 522.4 | 340.0[70] |
| YH10 | 250 | 0.41 | 80 | 45.6 | 0.33 | 312.5 | 259.6 | 326.0[89] |
| MAE | - | - | - | - | - | 47.6 | 125.3 | - |
| RMSE | - | - | - | - | - | 68.4 | 140.3 | - |
Note: RF—random forest, HDOS—hydrogen fraction of the total density of states at the Fermi energy ...
Mapping superconductivity in high-pressure hydrides: The Superhydra project
1
2023
... 在数据驱动方面,Shipley等[70]利用晶体结构预测方法搜索了整个元素周期表10~50 GPa下稳定的二元氢化物,对最佳超导候选材料进行了高通量计算,发现了36种Tc超过100 K的声子稳定的高压氢化物超导体.Choudhary和Garrity[69]针对常规超导体开发了一个高通量计算工作流,计算了超过1000个材料的Tc,建立了一个系统的BCS超导数据库,并基于此开发了深度学习预测模型.Saha等[71]基于现有氢化物超导体的结构框架,通过元素替换方式获得了139个新的氢化物超导体,并基于此创建了Superhydra数据库,目前仅限于在200 GPa下的二元氢化物.Sommer等[72]建立了“3DSC”超导数据库,其中包括Tc和结构数据,以便进行机器学习.Cerqueira等[73]对7000多个常规超导候选材料的Tc进行了高通量第一性原理计算,发现了许多之前尚未报道的新超导材料. ...
3DSC—A dataset of superconductors including crystal structures
1
2023
... 在数据驱动方面,Shipley等[70]利用晶体结构预测方法搜索了整个元素周期表10~50 GPa下稳定的二元氢化物,对最佳超导候选材料进行了高通量计算,发现了36种Tc超过100 K的声子稳定的高压氢化物超导体.Choudhary和Garrity[69]针对常规超导体开发了一个高通量计算工作流,计算了超过1000个材料的Tc,建立了一个系统的BCS超导数据库,并基于此开发了深度学习预测模型.Saha等[71]基于现有氢化物超导体的结构框架,通过元素替换方式获得了139个新的氢化物超导体,并基于此创建了Superhydra数据库,目前仅限于在200 GPa下的二元氢化物.Sommer等[72]建立了“3DSC”超导数据库,其中包括Tc和结构数据,以便进行机器学习.Cerqueira等[73]对7000多个常规超导候选材料的Tc进行了高通量第一性原理计算,发现了许多之前尚未报道的新超导材料. ...
Sampling the materials space for conventional superconducting compounds
1
2024
... 在数据驱动方面,Shipley等[70]利用晶体结构预测方法搜索了整个元素周期表10~50 GPa下稳定的二元氢化物,对最佳超导候选材料进行了高通量计算,发现了36种Tc超过100 K的声子稳定的高压氢化物超导体.Choudhary和Garrity[69]针对常规超导体开发了一个高通量计算工作流,计算了超过1000个材料的Tc,建立了一个系统的BCS超导数据库,并基于此开发了深度学习预测模型.Saha等[71]基于现有氢化物超导体的结构框架,通过元素替换方式获得了139个新的氢化物超导体,并基于此创建了Superhydra数据库,目前仅限于在200 GPa下的二元氢化物.Sommer等[72]建立了“3DSC”超导数据库,其中包括Tc和结构数据,以便进行机器学习.Cerqueira等[73]对7000多个常规超导候选材料的Tc进行了高通量第一性原理计算,发现了许多之前尚未报道的新超导材料. ...
Machine learning modeling of superconducting critical temperature
4
2018
... 在机器学习预测方面,Stanev等[74]使用随机森林(random forest,RF)机器学习方法[75]对SuperCon数据库[76]中超过12000条的超导数据进行了训练,探索了超导电性与材料化学/结构特性之间的联系.Hutcheon等[77]针对二元氢化物EH n (其中E为除H元素以外的其他元素,如La、Mg等),将E元素的van der Waals半径、原子序数、原子质量、原子每个轨道上的电子数及H含量作为描述符,构建了一个基于神经网络的机器学习模型,模型均方根误差为34 K.Liu等[78]对轨道属性、电子壳层信息等具有物理意义的特征进行了排列组合,得到了140多个特征,对SuperCon数据库的Tc数据进行了回归预测,得出材料的超导转变温度上限与电子轨道杂化存在着很强的联系.Wines和Choudhary[79]使用第一性原理计算预测了900多种氢化物材料的Tc,发现了125种稳定的结构,并开发了图神经网络Tc预测模型,大大缩减了预测成本. ...
... Stanev等[74]曾在自己的工作中提到“3个‘黄金描述符’将60个已知的Tc > 10 K的超导体限制在了特征空间的3个小岛上:平均价电子数、轨道半径差和金属电负性差”.选择这3个描述符是因为它们在二元、三元化合物的分类上以及稳态、亚稳态晶体的预测方面获得的成功[74].Liu等[60]发现在金属氢化物超导体中,要使金属原子为H原子有效提供电子,那么金属原子应该具有价电子数3.由此可见,价电子数对氢化物超导是一个重要的特征.而在本工作开发的氢化物超导体Tc机器学习预测模型中,[Avg_dev(NValence)]被随机森林算法选为一个重要的特征.从图4a可以看出,高Tc氢化物超导体大多集中在Avg_dev(NValence) = 0~1的区域内.此外,通过绘制Tc与金属氢化物超导体中金属原子价电子数平均值的关系图,发现高Tc金属氢化物超导体大都分布在金属原子价电子数平均值为3的区域,这与Liu等[60]发现的最优价电子数规则高度一致. ...
... [74].Liu等[60]发现在金属氢化物超导体中,要使金属原子为H原子有效提供电子,那么金属原子应该具有价电子数3.由此可见,价电子数对氢化物超导是一个重要的特征.而在本工作开发的氢化物超导体Tc机器学习预测模型中,[Avg_dev(NValence)]被随机森林算法选为一个重要的特征.从图4a可以看出,高Tc氢化物超导体大多集中在Avg_dev(NValence) = 0~1的区域内.此外,通过绘制Tc与金属氢化物超导体中金属原子价电子数平均值的关系图,发现高Tc金属氢化物超导体大都分布在金属原子价电子数平均值为3的区域,这与Liu等[60]发现的最优价电子数规则高度一致. ...
... 原子半径影响原子间的距离和相互作用强度,从而影响晶体结构和电子结构.对超导材料来说,晶体结构的变化会影响其中电子的相互作用方式,从而影响电子的运动和配对.在金属氢化物超导体中为了实现高的Tc,需要对H原子施加尽可能高的化学挤压,那么金属元素的原子半径需要在给定的晶格下使金属原子最大地填充晶格.这就是Liu等[60]提出的最优原子占据规则.此外,在Stanev等[74]和Hutcheon等[77]开发的机器学习模型中,平均原子半径亦作为一个重要的特征.图4b绘制了Tc与平均共价半径的关系.可见,高Tc氢化物超导体的平均共价半径一般在40~55 pm范围内. ...
Random forests
1
2001
... 在机器学习预测方面,Stanev等[74]使用随机森林(random forest,RF)机器学习方法[75]对SuperCon数据库[76]中超过12000条的超导数据进行了训练,探索了超导电性与材料化学/结构特性之间的联系.Hutcheon等[77]针对二元氢化物EH n (其中E为除H元素以外的其他元素,如La、Mg等),将E元素的van der Waals半径、原子序数、原子质量、原子每个轨道上的电子数及H含量作为描述符,构建了一个基于神经网络的机器学习模型,模型均方根误差为34 K.Liu等[78]对轨道属性、电子壳层信息等具有物理意义的特征进行了排列组合,得到了140多个特征,对SuperCon数据库的Tc数据进行了回归预测,得出材料的超导转变温度上限与电子轨道杂化存在着很强的联系.Wines和Choudhary[79]使用第一性原理计算预测了900多种氢化物材料的Tc,发现了125种稳定的结构,并开发了图神经网络Tc预测模型,大大缩减了预测成本. ...
MDR SuperCon Datasheet Ver
1
... 在机器学习预测方面,Stanev等[74]使用随机森林(random forest,RF)机器学习方法[75]对SuperCon数据库[76]中超过12000条的超导数据进行了训练,探索了超导电性与材料化学/结构特性之间的联系.Hutcheon等[77]针对二元氢化物EH n (其中E为除H元素以外的其他元素,如La、Mg等),将E元素的van der Waals半径、原子序数、原子质量、原子每个轨道上的电子数及H含量作为描述符,构建了一个基于神经网络的机器学习模型,模型均方根误差为34 K.Liu等[78]对轨道属性、电子壳层信息等具有物理意义的特征进行了排列组合,得到了140多个特征,对SuperCon数据库的Tc数据进行了回归预测,得出材料的超导转变温度上限与电子轨道杂化存在着很强的联系.Wines和Choudhary[79]使用第一性原理计算预测了900多种氢化物材料的Tc,发现了125种稳定的结构,并开发了图神经网络Tc预测模型,大大缩减了预测成本. ...
Predicting novel superconducting hydrides using machine learning approaches
2
2020
... 在机器学习预测方面,Stanev等[74]使用随机森林(random forest,RF)机器学习方法[75]对SuperCon数据库[76]中超过12000条的超导数据进行了训练,探索了超导电性与材料化学/结构特性之间的联系.Hutcheon等[77]针对二元氢化物EH n (其中E为除H元素以外的其他元素,如La、Mg等),将E元素的van der Waals半径、原子序数、原子质量、原子每个轨道上的电子数及H含量作为描述符,构建了一个基于神经网络的机器学习模型,模型均方根误差为34 K.Liu等[78]对轨道属性、电子壳层信息等具有物理意义的特征进行了排列组合,得到了140多个特征,对SuperCon数据库的Tc数据进行了回归预测,得出材料的超导转变温度上限与电子轨道杂化存在着很强的联系.Wines和Choudhary[79]使用第一性原理计算预测了900多种氢化物材料的Tc,发现了125种稳定的结构,并开发了图神经网络Tc预测模型,大大缩减了预测成本. ...
... 原子半径影响原子间的距离和相互作用强度,从而影响晶体结构和电子结构.对超导材料来说,晶体结构的变化会影响其中电子的相互作用方式,从而影响电子的运动和配对.在金属氢化物超导体中为了实现高的Tc,需要对H原子施加尽可能高的化学挤压,那么金属元素的原子半径需要在给定的晶格下使金属原子最大地填充晶格.这就是Liu等[60]提出的最优原子占据规则.此外,在Stanev等[74]和Hutcheon等[77]开发的机器学习模型中,平均原子半径亦作为一个重要的特征.图4b绘制了Tc与平均共价半径的关系.可见,高Tc氢化物超导体的平均共价半径一般在40~55 pm范围内. ...
Upper limit of the transition temperature of superconducting materials
6
2023
... 在机器学习预测方面,Stanev等[74]使用随机森林(random forest,RF)机器学习方法[75]对SuperCon数据库[76]中超过12000条的超导数据进行了训练,探索了超导电性与材料化学/结构特性之间的联系.Hutcheon等[77]针对二元氢化物EH n (其中E为除H元素以外的其他元素,如La、Mg等),将E元素的van der Waals半径、原子序数、原子质量、原子每个轨道上的电子数及H含量作为描述符,构建了一个基于神经网络的机器学习模型,模型均方根误差为34 K.Liu等[78]对轨道属性、电子壳层信息等具有物理意义的特征进行了排列组合,得到了140多个特征,对SuperCon数据库的Tc数据进行了回归预测,得出材料的超导转变温度上限与电子轨道杂化存在着很强的联系.Wines和Choudhary[79]使用第一性原理计算预测了900多种氢化物材料的Tc,发现了125种稳定的结构,并开发了图神经网络Tc预测模型,大大缩减了预测成本. ...
... 为了建立准确、可靠的机器学习模型,选取相关的重要特征是极为必要的.考虑的特征不仅应该能够唯一地表示每种材料,还应该容易计算,以便对新材料进行快速预测.本工作获取特征的方式有3种.第一,使用MATMINER软件包[80]获取.该软件包是一个很好的资源库,可以快速地生成特征,特别适用材料科学领域.同时,下载了材料的一系列广谱特征,如共价半径、原子质量、价电子数、配位数、Mendeleev数等.此外,还捕获了构成元素的s、p、d、f壳层中价电子的平均数量.第二,针对收集的氢化物超导体的晶体结构进行键长和配位数的计算,得到了键长(最短、最长及平均)和配位数特征.第三,引入具有物理意义的特征.受Belli等[59]和Liu等[78]工作的启发,本工作通过第一性原理计算得到最高饱和轨道和最低不饱和轨道之间的能级间隔ΔE[78]、Fermi能级处体系的总态密度(TDOS)、Fermi能级处H的态密度占比(HDOS Fraction)、氢化物中H原子的原子比例(Hf)等.通过这3种方式,本工作最终获得了共计133个特征. ...
... [78]、Fermi能级处体系的总态密度(TDOS)、Fermi能级处H的态密度占比(HDOS Fraction)、氢化物中H原子的原子比例(Hf)等.通过这3种方式,本工作最终获得了共计133个特征. ...
... 使用基于密度泛函理论的VASP[81,82]软件计算电子态密度和ΔE.选用广义梯度近似下的Perdew-Burke-Ernzerhof (PBE)[83]电子交换关联泛函.平面波截断能设置为600 eV.结构优化和态密度计算分别使用了波矢k点间距为0.3 × 2π nm-1和0.2 × 2π nm⁻¹的格点.ΔE的具体计算公式如下[78]: ...
... 针对关键特征筛选,首先利用递归特征消除算法,将特征数量从初始的133个减少至55个.随后进行第二次递归特征消除计算,将55个特征再次降低至11个.这11个特征分别是:Fermi能级处的TDOS、Fermi能级处的HDOS Fraction、平均键长[Mean(length)]、平均配位数[Mean(cn)]、3个Mendeleev数特征[Mean(Mendeleev Number)、Range(Mendeleev Number)及Min(Mendeleev Number)]、平均族序数[Mean(column)]、平均共价半径[Mean(CovalentRadius)]、最小电负性[Min(Electronegativity)],及价电子数的标准差[Avg_dev(NValence)].需要指出的是,Liu等[78]提出的ΔE因其重要性值较低而并未保留下来.这说明尽管ΔE与超导材料Tc的上限存在很强的相关性[78],但是ΔE对Tc本身并不是一个重要的特征. ...
... [78],但是ΔE对Tc本身并不是一个重要的特征. ...
Data-driven design of high pressure hydride superconductors using DFT and deep learning
1
2024
... 在机器学习预测方面,Stanev等[74]使用随机森林(random forest,RF)机器学习方法[75]对SuperCon数据库[76]中超过12000条的超导数据进行了训练,探索了超导电性与材料化学/结构特性之间的联系.Hutcheon等[77]针对二元氢化物EH n (其中E为除H元素以外的其他元素,如La、Mg等),将E元素的van der Waals半径、原子序数、原子质量、原子每个轨道上的电子数及H含量作为描述符,构建了一个基于神经网络的机器学习模型,模型均方根误差为34 K.Liu等[78]对轨道属性、电子壳层信息等具有物理意义的特征进行了排列组合,得到了140多个特征,对SuperCon数据库的Tc数据进行了回归预测,得出材料的超导转变温度上限与电子轨道杂化存在着很强的联系.Wines和Choudhary[79]使用第一性原理计算预测了900多种氢化物材料的Tc,发现了125种稳定的结构,并开发了图神经网络Tc预测模型,大大缩减了预测成本. ...
Matminer: An open source toolkit for materials data mining
1
2018
... 为了建立准确、可靠的机器学习模型,选取相关的重要特征是极为必要的.考虑的特征不仅应该能够唯一地表示每种材料,还应该容易计算,以便对新材料进行快速预测.本工作获取特征的方式有3种.第一,使用MATMINER软件包[80]获取.该软件包是一个很好的资源库,可以快速地生成特征,特别适用材料科学领域.同时,下载了材料的一系列广谱特征,如共价半径、原子质量、价电子数、配位数、Mendeleev数等.此外,还捕获了构成元素的s、p、d、f壳层中价电子的平均数量.第二,针对收集的氢化物超导体的晶体结构进行键长和配位数的计算,得到了键长(最短、最长及平均)和配位数特征.第三,引入具有物理意义的特征.受Belli等[59]和Liu等[78]工作的启发,本工作通过第一性原理计算得到最高饱和轨道和最低不饱和轨道之间的能级间隔ΔE[78]、Fermi能级处体系的总态密度(TDOS)、Fermi能级处H的态密度占比(HDOS Fraction)、氢化物中H原子的原子比例(Hf)等.通过这3种方式,本工作最终获得了共计133个特征. ...
Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set
1
1996
... 使用基于密度泛函理论的VASP[81,82]软件计算电子态密度和ΔE.选用广义梯度近似下的Perdew-Burke-Ernzerhof (PBE)[83]电子交换关联泛函.平面波截断能设置为600 eV.结构优化和态密度计算分别使用了波矢k点间距为0.3 × 2π nm-1和0.2 × 2π nm⁻¹的格点.ΔE的具体计算公式如下[78]: ...
Ab initio molecular dynamics for liquid metals
1
1993
... 使用基于密度泛函理论的VASP[81,82]软件计算电子态密度和ΔE.选用广义梯度近似下的Perdew-Burke-Ernzerhof (PBE)[83]电子交换关联泛函.平面波截断能设置为600 eV.结构优化和态密度计算分别使用了波矢k点间距为0.3 × 2π nm-1和0.2 × 2π nm⁻¹的格点.ΔE的具体计算公式如下[78]: ...
Generalized gradient approximation made simple
1
1996
... 使用基于密度泛函理论的VASP[81,82]软件计算电子态密度和ΔE.选用广义梯度近似下的Perdew-Burke-Ernzerhof (PBE)[83]电子交换关联泛函.平面波截断能设置为600 eV.结构优化和态密度计算分别使用了波矢k点间距为0.3 × 2π nm-1和0.2 × 2π nm⁻¹的格点.ΔE的具体计算公式如下[78]: ...
VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code
1
2021
... 式中,E1代表氢化物中某一原子的最高占据轨道能量,E2表示H原子的s轨道能量;PDOS和DOS分别为各原子的轨道分辨投影态密度和总的态密度;n1和n2表示原子个数.利用了vaspkit软件[84]提取了VASP计算的态密度信息,然后进行了更密格点的插值. ...
Scikit-learn: Machine learning in python
1
2011
... 本工作主要使用SCIKIT-LEARN (sklearn)库[85]提供的随机森林算法.随机森林算法是一种基于决策树的集成学习算法,不论是在分类还是在回归方面都表现出良好的性能.它的优点是计算量小,适用于较少数据集的机器学习.最重要的是,随机森林算法可以评估每个特征对目标变量的重要性,这对关键特征筛选、提高机器学习模型泛化能力非常有用.本工作所用随机森林算法的超参数见表1.其中,n-estimators决定决策树的数量,增加树的数量可以提高模型的准确性和稳定性,但同时也会增加计算成本和过拟合风险.max-depth为决策树的最大深度,限制树的最大深度可以防止过拟合,但也可能导致欠拟合,如果没有特别指定,树会一直生长直到叶节点都是纯叶节点或者达到max-depth指定的最大深度.min-samples-split为分割内部节点所需的最小样本数,增加这个值可以使得树更加平滑,减少过拟合风险,但是可能导致模型变得过于简单.min-samples-leaf为叶节点最小样本数,这个参数控制着树的复杂度,增加它的值可以使模型更加稳定,但可能导致过拟合. ...
A chemical scale for crystal-structure maps
2
1984
... Mendeleev数由Pettifor[86,87]在1984年首次提出,是晶体中每个化学元素分配的排列数,目的是使具有相似行为的化学元素归为一类[86,88].在Pettifor图中,元素被排列成一条线或曲线,这条线上的元素按照它们的化合物形成能力进行排序.Pettifor图中位置接近的元素通常意味着具有相似的化合物形成能力.元素的电负性和原子半径也是排列元素时考虑的因素之一,这些物理化学性质影响元素之间的相互作用,从而影响化合物的形成和性质.换句话说,MN根据元素的电子结构和化学性质改变元素的顺序,使具有相似性质的元素彼此靠近. ...
... [86,88].在Pettifor图中,元素被排列成一条线或曲线,这条线上的元素按照它们的化合物形成能力进行排序.Pettifor图中位置接近的元素通常意味着具有相似的化合物形成能力.元素的电负性和原子半径也是排列元素时考虑的因素之一,这些物理化学性质影响元素之间的相互作用,从而影响化合物的形成和性质.换句话说,MN根据元素的电子结构和化学性质改变元素的顺序,使具有相似性质的元素彼此靠近. ...
The structures of binary compounds. I. Phenomenological structure maps
1
1986
... Mendeleev数由Pettifor[86,87]在1984年首次提出,是晶体中每个化学元素分配的排列数,目的是使具有相似行为的化学元素归为一类[86,88].在Pettifor图中,元素被排列成一条线或曲线,这条线上的元素按照它们的化合物形成能力进行排序.Pettifor图中位置接近的元素通常意味着具有相似的化合物形成能力.元素的电负性和原子半径也是排列元素时考虑的因素之一,这些物理化学性质影响元素之间的相互作用,从而影响化合物的形成和性质.换句话说,MN根据元素的电子结构和化学性质改变元素的顺序,使具有相似性质的元素彼此靠近. ...
Data-driven atomic environment prediction for binaries using the Mendeleev number: Part 1. Composition AB
1
2004
... Mendeleev数由Pettifor[86,87]在1984年首次提出,是晶体中每个化学元素分配的排列数,目的是使具有相似行为的化学元素归为一类[86,88].在Pettifor图中,元素被排列成一条线或曲线,这条线上的元素按照它们的化合物形成能力进行排序.Pettifor图中位置接近的元素通常意味着具有相似的化合物形成能力.元素的电负性和原子半径也是排列元素时考虑的因素之一,这些物理化学性质影响元素之间的相互作用,从而影响化合物的形成和性质.换句话说,MN根据元素的电子结构和化学性质改变元素的顺序,使具有相似性质的元素彼此靠近. ...
Potential high-Tc superconducting lanthanum and yttrium hydrides at high pressure
5
2017
... 为了比较构建的随机森林机器学习预测模型和Belli等[59]提出的经验 公式(3),作为例子,本工作仅针对数据集中6个Tc最高的氢化物超导材料的Tc进行了预测,具体对比结果见表2[43,59,60,70,89].它们的晶体结构和电子态密度见图5.可见,随机森林机器学习预测模型最优,其性能要远优于Belli经验 公式(3).从表2[43,59,60,70,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... ,89]也可以看到,高Tc氢化物超导体一般具有高的HDOS或Range(MN).图5表明,6个Tc最高的氢化物超导材料都是具有笼型结构的超氢化物. ...
... 针对数据集中6个Tc最高的氢化物超导材料的模型预测[43,59,60,70,89] ...
... Model predictions for the six hydride superconductors with the highest Tc in the dataset[43,59,60,70,89] ...
... K
Tc (Expt.) K | | Li2MgH16 | 250 | 0.53 | 91 | 47.0 | 0.10 | 319.3 | 298.3 | 473.0[43] |
| CaHfH12 | 190 | 0.28 | 85 | 51.6 | 2.24 | 324.9 | 198.3 | 363.0[60] |
| CaHfH18 | 300 | 0.41 | 85 | 45.5 | 1.62 | 339.0 | 332.0 | 345.0[60] |
| CaZrH12 | 300 | 0.31 | 85 | 51.6 | 0.49 | 308.2 | 192.6 | 343.0[60] |
| MgH12 | 500 | 0.72 | 24 | 39.5 | 0.14 | 300.5 | 522.4 | 340.0[70] |
| YH10 | 250 | 0.41 | 80 | 45.6 | 0.33 | 312.5 | 259.6 | 326.0[89] |
| MAE | - | - | - | - | - | 47.6 | 125.3 | - |
| RMSE | - | - | - | - | - | 68.4 | 140.3 | - |
Note: RF—random forest, HDOS—hydrogen fraction of the total density of states at the Fermi energy ...