再结晶织构源于不同织构组分在形核和长大过程中的竞争。形变金属内的应变储能及取向梯度分布依赖于形变晶粒取向,在高储能和高取向梯度位置形核的织构组分具有形核和长大动力学优势[1 ~3 ] 。不同织构组分形核点位相毗邻时,优势织构组分会消耗毗邻织构组分的形核点位和长大空间,在强化自身的同时弱化其他织构组分[4 ~7 ] 。因此,毗邻织构组分的竞争关系决定了再结晶织构的形成与发展,改变形核与长大动力学以及侵入毗邻形变晶粒的能力是再结晶织构调控的关键。
晶界偏析元素可降低晶界可动性,延缓再结晶晶粒的形核和长大速率,从而影响再结晶织构组分间的竞争关系。添加晶界偏析元素可以弱化无取向硅钢γ (<111>//ND,ND为轧面法向)再结晶织构,强化α (<110>//RD,RD为轧制方向)和λ (<100>//ND)再结晶织构[8 ~12 ] 。在对Fe-Si合金和Fe-Si-Sn合金再结晶行为的准原位电子背散射衍射(EBSD)研究[13 ] 中发现,偏析元素通过延缓γ 形变晶粒再结晶,使毗邻α 形变晶粒获得再结晶形核和长大的时机。而γ 再结晶晶粒需要达到临界尺寸以上,才能侵入毗邻α 形变晶粒[14 ] 。这些实验研究表明,优先形核的γ 晶粒长大过程涉及向γ 形变晶粒内生长和侵入毗邻形变晶粒2个阶段,晶界偏析元素可以抑制其获得向毗邻较低储能形变晶粒入侵的能力。
针对偏析元素干预再结晶织构发展的机制也进行了一些研究。亚晶长大是再结晶形核的重要机制,只有亚晶长大至临界尺寸且具有大角晶界时才完成再结晶晶粒形核过程[15 ] 。基于位错攀移机制,Cram等[16 ] 认为晶界偏析元素与空位结合可提高位错攀移和亚晶界迁移的激活能,延缓亚晶长大进而抑制再结晶形核。基于溶质拖拽机制,晶界偏析元素通过降低亚晶界的迁移速率延缓再结晶形核,Buk-en和Kozeschnik[17 ] 结合亚晶长大机制和溶质拖拽理论给出了偏析干预下再结晶晶粒形核动力学模型。再结晶晶粒的长大动力学则由应变储能驱动下溶质拖拽晶界迁移过程控制,溶质拖拽下的晶界迁移行为可由Cahn[18 ] 模型描述。传统基于形核和长大动力学的再结晶织构模型,处理织构组分间竞争行为时采用空间平均场假设,即再结晶晶粒在空间随机分布并消耗其周围均匀分布的形核点位和形变基体[19 ~21 ] 。然而,γ 再结晶晶粒的长大过程呈现明显的阶段性,空间平均场假设不适于偏析干预下的再结晶织构竞争。目前,尚无偏析干预下γ 与α 等主要再结晶织构组分间竞争关系的定量模型,晶界偏析元素对再结晶织构竞争行为的干预规律尚不清晰。
Fe-3%Si (质量分数,下同)合金是研究体心立方(bcc)结构金属再结晶行为的常用模型材料,添加偏析元素Sb可以显著改变γ 与α 等主要再结晶织构组分间的竞争关系。本工作以无Sb和含Sb的Fe-3%Si合金为模型材料,对偏析干预下的再结晶织构竞争进行了实验和模拟研究。通过引入γ 再结晶晶粒长大与毗邻形变织构和临界入侵半径间的定量关系,构建了偏析干预下再结晶织构竞争关系模型,据此解析了偏析干预下再结晶织构的竞争规律及调控方法。
1 研究方法
实验采用含0.04%Sb (质量分数,下同)和不含Sb的2种Fe-3%Si铸锭,经相同工艺制得厚度为2.3 mm的常化板,在室温下轧至0.46 mm厚,总压下率为80%。将冷轧板在N2 保护下于850℃退火至部分和完全初次再结晶状态。利用X-Pert型X射线衍射仪(XRD)对冷轧和初次再结晶样品不同层的宏观织构进行表征。定义厚度参数S = 2a / d (其中,a 为距中心层的距离,d 为板材厚度),S = 0.5为亚表层,S = 0为中心层。冷轧和部分再结晶样品经92%C2 H5 OH + 8%HClO4 (体积分数)溶液电解抛光,利用JSM-7001F扫描电子显微镜(SEM)配备的HKL Channel5 EBSD系统进行微观织构表征,加速电压为15 kV,步长为0.6 μm。EBSD表征后的部分再结晶样品进一步在真空炉中进行850℃退火,真空度< 1 × 10-4 Pa。真空退火后样品直接进行EBSD观测,以实现初次再结晶过程的准原位分析。
偏析干预下的再结晶织构竞争关系模型主要由再结晶形核长大动力学和空间竞争2部分构成。在形核长大动力学方面,基于亚晶长大形核和溶质拖拽理论构建时间分辨的形核率模型,再结晶晶粒在形变晶粒的晶界形核、再结晶晶粒取向及形核动力学依赖于形变晶粒取向和应变储能;晶粒长大过程由应变储能和晶界能共同驱动。在空间竞争关系方面,再结晶晶粒优先在其形核基体中各向同性长大,当晶粒长大至临界入侵尺寸后进入毗邻形变晶粒。
2 实验结果
2.1 形变与再结晶织构
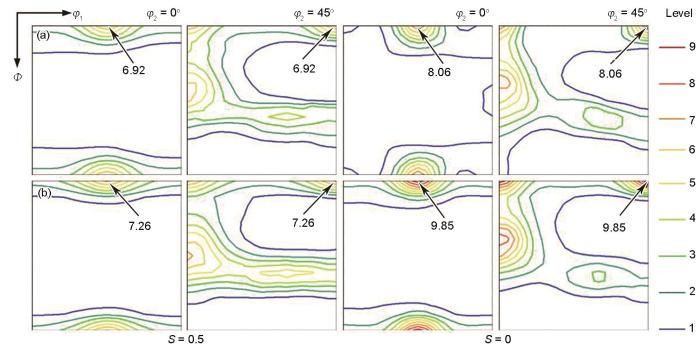
图1 为冷轧板亚表层和中心层取向分布函数(ODF)的φ 2 = 0°和45° (φ 2 为Euler角)截面图。可见,Sb元素对冷轧织构组分和强度均无显著影响,2种成分冷轧板的亚表层和中心层织构组分构成相同,均为强点位于{111}<110>的γ 织构和强点位于{001}<110>和{112}<110>的α 织构。与亚表层相比,中心层γ 织构减弱,α 织构增强,主要织构组分强点不变。
图1
图1
无Sb和含Sb的Fe-3%Si冷轧板亚表层和中心层取向分布函数(ODF)的φ 2 = 0°和45° (φ 2 为Euler角)截面图
Fig.1
Constant φ 2 = 0° and 45° sections of ODFs at subsurface (S = 0.5) and center (S = 0) layers in cold rolled Fe-3%Si sheets without (a) and with (b) Sb addition (ODF—orientation distribution function; φ 1 , φ 2 , Φ— Euler angles; S —thickness parameter)
图2 为再结晶板亚表层和中心层取向分布函数的φ 2 = 0°和45°截面图。可见,2种成分再结晶板亚表层和中心层织构均由较强的γ 和η (<100>//RD)织构及较弱的α 和λ 织构组成,γ 和η 织构强点分别位于{111}<112>和{110}<001>,α 和λ 织构分布均匀。与无Sb样品相比,含Sb样品亚表层和中心层织构组分和强点均未发生变化,但γ 和η 织构强度减弱。
图2
图2
无Sb和含Sb的Fe-3%Si再结晶板亚表层和中心层ODF的φ 2 = 0°和45°截面图
Fig.2
Constant φ 2 = 0° and 45° sections of ODFs at subsurface and center layers in recrystallized Fe-3%Si sheets without (a) and with (b) Sb addition
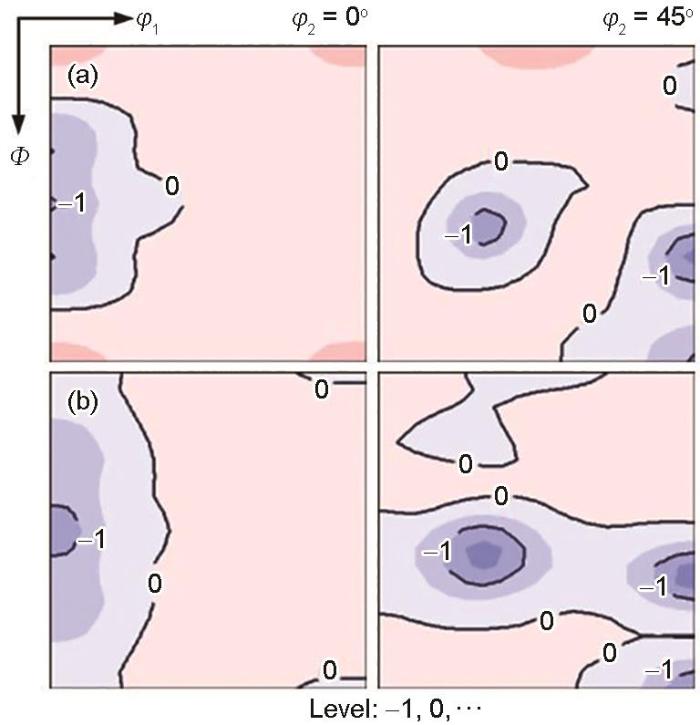
将无Sb和含Sb样品再结晶织构取向密度相减,可清晰呈现晶界偏析元素对再结晶织构的影响。图3 给出了添加Sb元素导致的再结晶织构变化。可见,不论亚表层还是中心层,γ 和Goss ({110}<001>)再结晶织构组分减弱,α 和λ 再结晶织构组分增强。一般情况下,γ 与Goss、α 和λ 组分间存在如下竞争关系:Goss弱化将导致γ 增强,α 和λ 增强导致γ 减弱。但图3 中γ 和Goss弱化而α 和λ 增强,表明晶界偏析元素显著削弱了γ 相对于α 和λ 再结晶织构组分的竞争力。与亚表层相比,中心层γ 形变织构更弱,但晶界偏析元素对γ 再结晶织构组分的弱化作用却稍强,这表明晶界偏析元素对中心层γ 竞争力的削弱作用更显著。
图3
图3
添加Sb后Fe-3%Si再结晶板亚表层和中心层ODF变化的φ 2 = 0°和45°截面图
Fig.3
Difference of ODFs in constant φ 2 = 0° and 45° sections at subsurface (a) and center (b) layer in Fe-3%Si recrystallized sheets between without and with Sb addition
2.2 偏析干预下再结晶织构的竞争
图4 给出了冷轧板主要织构组分的EBSD取向成像图和几何必需位错(GND)密度成像图。可见,无Sb和含Sb样品中γ 形变晶粒内部均分布有剪切带,亚表层γ 形变晶粒内的剪切带更为密集。亚表层γ 形变晶粒有更高的几率相互毗邻,中心层γ 形变晶粒则倾向于被α 形变晶粒包围。由于轧制变形下γ 取向晶粒的Taylor因子高于α 取向晶粒,γ 取向晶粒具有更高的位错累积速率[22 ] 。对γ 和α 形变晶粒内平均GND密度进行统计可知,无Sb和含Sb样品中,γ 形变晶粒内平均GND密度分别为7.41 × 1014 和7.68 × 1014 m-2 ,α 形变晶粒内的平均GND密度分别为2.87 × 1014 和3.12 × 1014 m-2 。本工作中Sb元素添加量仅为0.04%,其对形变过程中的位错累积无明显影响。
图4
图4
无Sb和含Sb的Fe-3%Si冷轧板EBSD取向成像图和几何必需位错(GND)密度成像图
Fig.4
EBSD orientation image maps (a, c) and GND density maps (b, d) in cold rolled Fe-3%Si sheets without (a, b) and with (c, d) Sb addition (GND—geometrically necessary dislocation, ND—normal direction, RD—rolling direction)
为了分析晶界偏析元素对再结晶竞争行为的影响,图5 给出了部分再结晶和再结晶基本完成时的EBSD取向成像图。可见,再结晶早期,γ 再结晶晶粒主要形核于{111}<110>取向形变晶粒的晶界区域,{111}<112>形变晶粒基本被剪切带形核的Goss取向占据,α 形变晶粒基本未发生再结晶。含Sb样品中{111}<110>形变晶粒的再结晶程度低于无Sb样品,表明γ 晶粒的形核和长大被Sb元素延缓。无Sb样品再结晶基本完成时,B1 区域左侧γ 再结晶晶粒显著长大,并且成功侵入A1 区域α 形变晶粒。B1 区域右侧γ 再结晶晶粒长大有限,未侵入A1 区域α 形变晶粒。A1 区域右侧α 形变晶粒内α 和λ 再结晶晶粒成功形核并长大,最终A1 区域内γ 再结晶晶粒面积分数为0.59。含Sb元素样品再结晶基本完成时,B2 区域内γ 再结晶晶粒尺寸显著长大,但γ 再结晶晶粒向A2 区域α 形变晶粒的入侵极为有限,最终A2 区域内γ 再结晶晶粒面积分数为0.27。当γ 再结晶晶粒毗邻γ 形变晶粒时(C1 和C2 区域),不论是否含偏析元素,γ 再结晶晶粒均未越过原始晶界。上述结果表明,当γ 再结晶晶粒与α 形变晶粒毗邻时,晶界偏析元素可以有效抑制γ 再结晶晶粒向α 形变晶粒的入侵。
图5
图5
无Sb和含Sb的Fe-3%Si冷轧板部分再结晶和完全再结晶时的EBSD取向成像图
Fig.5
EBSD orientation image maps in partially (a, c) and just completely recrystallized (b, d) Fe-3%Si sheets without (a, b) and with (c, d) Sb addition (Grain boundaries of deformed grains are represented by white dotted lines. A1 and A2 indicate α deformed regions before recrystallization. B1 , B2 , C1 , and C2 indicate γ deformed regions before recrystallization)
为进一步分析γ 再结晶晶粒侵入α 形变晶粒的过程,图6 给出了再结晶早期和再结晶中期入侵过程的EBSD取向成像图。可见,优先形核的再结晶晶粒向毗邻α 形变晶粒的入侵滞后于其向形核基体的生长。由图6a 和c 可知,晶界区域优先形核的再结晶晶粒首先在其形核基体内长大,与毗邻的α 形变晶粒形成平直晶界。随再结晶进程发展,优先形核的再结晶晶粒尺寸持续增大,部分尺寸较大的再结晶晶粒成功侵入毗邻α 形变晶粒。通过测量图6b 和d 中入侵α 形变晶粒的γ 晶粒与原始晶界交线的长度,得到无Sb和含Sb样品中成功入侵α 形变晶粒的γ 晶粒最小尺寸分别为9.2和10.4 μm。
图6
图6
无Sb和含Sb的Fe-3%Si冷轧板再结晶早期和中期主要织构组分EBSD取向成像图
Fig.6
EBSD orientation image maps of early (a, c) and middle (b, d) recrystallization stages without (a, b) and with (c, d) Sb addition (Grain boundaries of deformed grains are represented by white dotted lines. Invading and non-invading γ recrystallized grains are indicated by black and white arrows, respectively)
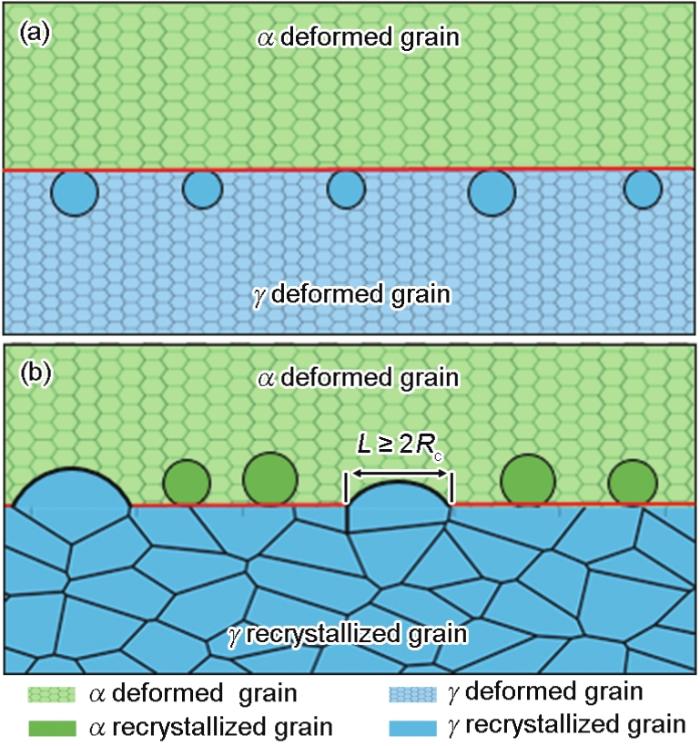
图7 给出了γ 再结晶晶粒入侵α 形变晶粒过程的示意图。再结晶早期,γ 再结晶晶粒形核于γ 形变晶粒的晶界区域并在γ 形变晶粒内长大。在后续退火过程中,γ 再结晶晶粒在应变储能和晶界能驱动下持续长大,与毗邻的α 形变晶粒形成平直晶界。当γ 再结晶晶粒长大至临界尺寸2R c (R c 为临界入侵半径),并且该γ 再结晶晶粒毗邻的α 形变晶粒晶界区域未再结晶时,γ 再结晶晶粒可成功侵入α 形变晶粒并继续长大。
图7
图7
γ 再结晶晶粒入侵α 形变晶粒过程的示意图
Fig.7
Schematics for the invasion process of γ recrystallized grains into adjacent α deformed grains
(a) γ grain nucleation
(b) γ recrystallized grain invasion into α defor-med grains (L —grain size, R c —critical invasion radius)
3 偏析干预下再结晶织构竞争关系模型
实验研究表明,优先形核长大的γ 晶粒在达到临界尺寸后可入侵毗邻的低储能形变晶粒,偏析元素通过抑制入侵导致γ 再结晶织构组分弱化。本工作以bcc金属再结晶过程中主要织构组分γ 与α 间的竞争为对象,构建了包含毗邻取向关系和临界入侵条件的偏析干预下再结晶织构竞争关系模型。
3.1 形核与长大
再结晶形核采用亚晶长大机制,亚晶半径随时间的演变规律为[23 ] :
r ( t ) = r 0 + ∫ 0 t M S G s u b P d t (1)
式中,r (t )为t 时刻的亚晶半径,r 0 为初始亚晶半径,M S G s u b P 为形核基体应变储能。亚晶初始半径和储能与形变基体内的位错密度(ρ )相关[24 ,25 ] :
r 0 = 7.1 ρ (2)
P = 0.5 G b 2 ρ (3)
式中,G 为剪切模量,b 为Burgers矢量模。当亚晶长大至临界形核半径(r c )时,再结晶晶粒形核。r c 为[23 ] :
r c = 2 γ g b P (4)
式中,γ gb 为大角度晶界的晶界能。t 时刻达到临界形核半径的亚晶分数(F sub (t ))以及单位晶界面积的再结晶形核率(N ˙ r e ( t ))可表示为[17 ] :
F s u b ( t ) = e x p ( - π r ¯ ( t ) 2 4 r c 2 ) (5)
N ˙ r e t = 1 π r c 2 ( 1 - B ( t ) ) F ˙ s u b ( t ) (6)
式中,r ¯ ( t )为平均亚晶尺寸,B (t )为已再结晶的晶界面积分数,F ˙ s u b ( t )为单位时间内达到临界形核半径的亚晶分数。再结晶晶粒在应变储能和晶界能驱动下的长大动力学可分别表示为[26 ,27 ] :
d R E t = M S G g b P d t (7)
d R G B ( t ) = M S G g b γ g b 8 9 R ¯ - 1 R (8)
式中,M S G g b R 和R ¯ R E (t )为储能驱动晶界迁移导致的晶粒半径增量,dR GB (t )为晶界能驱动晶界迁移导致的晶粒半径增量。则初次再结晶过程中的晶粒长大动力学为:
d R t = 1 - X r e d R E t + X r e d R G B ( t ) (9)
式中,dR (t )为应变储能和晶界能共同导致的晶粒半径增量,X re 为再结晶体积分数。依据溶质拖拽理论,偏析干预下的界面迁移率可表示为[18 ] :
M S G i = 1 M f r e e i + α i C 0 m m a t r i x m s o l u t e - 1 (10)
α i = δ i N V ( k b T ) 2 E s e g i D C i s i n h E s e g i k b T - E s e g i k b T (11)
式中,M S G i M f r e e i αi 为中间变量,C 0 为晶界偏析元素质量分数,m matrix 和m solute 分别为基体平均摩尔质量和偏析元素摩尔质量,δ i N V 为单位体积原子数,k b 为Bolzmann常数,T 为热力学温度,E s e g i D C i i 为该物理量在晶界或亚晶界中的值。
3.2 再结晶晶粒入侵毗邻形变晶粒
优先形核的γ 晶粒在后续退火过程中持续长大,当γ 晶粒半径达到R c 后成功入侵α 形变晶粒,在α 形变晶粒内形成一个半径为R c 的再结晶晶粒。R c 反比于应变储能[28 ] :
R c ≥ K P α (12)
式中,Pα 为α 晶粒应变储能,K 为比例系数。在纯净金属中K 为2γ gb ,存在杂质时R c 将增大[14 ] 。单位面积γ 形变晶粒的晶界上,半径达到R c 的γ 再结晶晶粒总数为N R c ( t )。当γ 再结晶晶粒与α 形变晶粒毗邻时,t 时刻成功入侵α 形变晶粒的γ 再结晶晶粒数(N γ α / γ ( t ))为:
N γ α / γ t = ( 1 - B α / γ ( t ) ) ( N R c ( t ) - N R c t - d t ) (13)
式中,Bα / γ γ 晶粒毗邻的α 形变晶粒晶界再结晶面积分数。
3.3 再结晶分数
γ 和α 形变晶粒抽象为厚度为h 的板状晶粒。对于α 形变晶粒,其与γ 形变晶粒的毗邻关系有3类:(1) 双侧与γ 形变晶粒毗邻;(2) 单侧与γ 形变晶粒毗邻;(3) 不与γ 形变晶粒毗邻。分别计算γ 形变晶粒和具有不同毗邻关系的α 形变晶粒的再结晶行为,并进行加权平均获得多晶体中的织构竞争结果,权重为多晶体中γ 形变晶粒和具有不同毗邻关系的α 形变晶粒的几率。
再结晶γ 晶界面积分数(Bγ (t ))和γ 形变晶粒内的再结晶分数(X γ t ))为:
B γ t = π ∑ N j γ R j γ ( t ) 2 (14)
X γ ( t ) = 2 π 3 h ∑ N j γ R j γ ( t ) 3 (15)
式中,N j γ R j γ ( t )分别为γ 再结晶晶粒的数量和半径,j 为第j 个时间步内形核的再结晶晶粒。当α 形变晶粒与γ 晶粒相毗邻时,α 晶界再结晶面积分数(Bα / γ t ))为:
B α / γ t = π ∑ N j α R j α t 2 + π ∑ N γ , j α / γ R γ , j α / γ ( t ) 2 (16)
式中,N j α R j α ( t )分别为α 再结晶晶粒的数量和半径,N γ , j α / γ R γ , j α / γ ( t )分别为入侵α 形变晶粒的γ 再结晶晶粒的数量和半径。当α 形变晶粒与α 晶粒相毗邻时,α 晶界再结晶面积分数Bα / α t )为:
B α / α t = π ∑ N j α R j α t 2 (17)
α 形变晶粒的再结晶分数(X α t ))由α 形变晶粒晶界区域再结晶晶粒的形核长大以及γ 再结晶晶粒向α 形变晶粒的入侵共同决定:
X α ( t ) = 2 π 3 h ( ∑ ( N j α R j α t 3 + N γ , j α / γ R γ , j α / γ ( t ) 3 ) ) (18)
入侵α 形变晶粒的γ 再结晶晶粒的体积分数(X γ α / γ ( t ))为:
X γ α / γ ( t ) = 2 π 3 h ∑ N γ , j α / γ R γ , j α / γ ( t ) 3 (19)
4 模拟与讨论
4.1 偏析干预下 γ
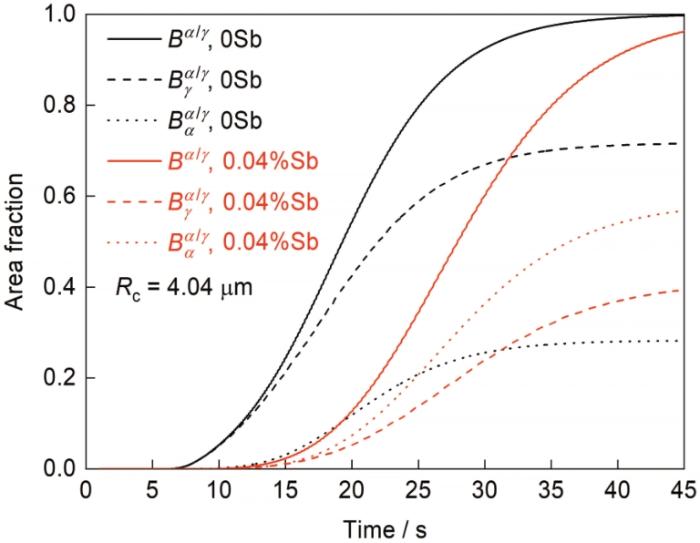
针对图5 中γ 再结晶晶粒入侵A1 区域和A2 区域内α 形变晶粒的行为进行了模拟计算。计算采用时间循环迭代方式进行,记录并更新每个时间步的晶核数量和晶粒尺寸,时间步长dt 需保证每步计算的再结晶分数增量小于1%,以减小误差。A1 区域内的α 形变晶粒两侧均与γ 晶粒毗邻,A2 区域内的α 形变晶粒可以拆分为两侧均与γ 晶粒毗邻和单侧与γ 晶粒毗邻的混合。γ 和α 形变晶粒位错密度取自图4 的实测值,A1 和A2 区域α 晶粒的平均厚度h 分别为45和35 μm,偏析元素含量C 0 分别为0和0.04%。α -Fe晶界能为(1.11 ± 0.209) J/m2 [29 ] ,计算所需其他参数见表1 [23 ,26 ,30 ~35 ] 。计算求得A1 和A2 区域内的γ 再结晶晶粒占比分别为0.77~0.58和0.39~0.16,实测值0.59和0.27处于相应区间内。本工作建模过程忽略了偏析元素对界面能的影响,而理论上微量晶界偏析元素倾向使界面能有所降低,这可能导致稍许高估偏析干预效果。因此,计算与实测符合良好,表明构建的模型可以描述偏析干预下毗邻织构组分竞争关系。在4.2~4.4节中,取α -Fe平均晶界能1.11 J/m2 进行相关计算。
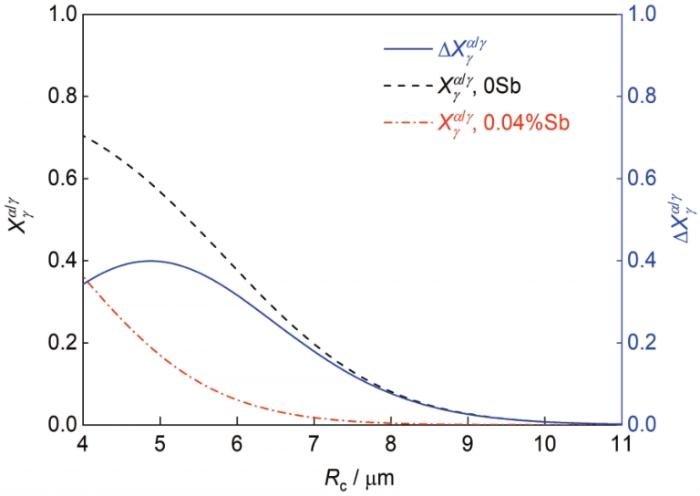
4.2 临界入侵半径对偏析干预效果的影响
为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为。γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同。图8 给出了X γ α / γ R c 的变化。可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm。晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量。偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值。R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强。R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱。
图8
图8
入侵α 形变晶粒的γ 再结晶晶粒分数随临界入侵半径(R c )的变化
Fig.8
Volume fraction of γ recrystallized grains invading into α deformed grains (X γ α / γ ) as a function of R c without and with Sb addition (ΔX γ α / γ
4.3 形变织构对偏析干预效果的影响
偏析干预效果与形变织构密切相关。假设形变基体内仅有γ 和α 2种形变晶粒且在空间上随机毗邻,图9 给出了入侵行为随形变γ 织构分数的变化。可见,随γ 形变织构增加,入侵γ 再结晶晶粒分数和偏析抑制入侵效果均先增强后减弱,在γ 形变织构含量为50%时达到峰值。在统计上,γ 再结晶织构向α 形变织构的入侵,正比于γ 再结晶形核点位数量以及γ 形核点位与α 形变晶粒的毗邻几率。当γ 形变织构较少时,入侵行为由γ 再结晶形核点位数量主导,其随γ 形变织构增加而增强。当γ 形变织构超过50%时,入侵行为由γ 形核点位与α 形变晶粒相毗邻的几率主导,毗邻几率随初始γ 织构增加而减小。当然,形变织构的空间分布影响毗邻概率,形变晶粒离散或聚集分布会提高或降低毗邻概率,进而强化或弱化偏析干预效果。在本工作中,亚表层γ 形变晶粒倾向于聚集,而中心层γ 形变晶粒倾向于被α 形变晶粒包围,使得偏析元素在中心层呈现更强的γ 再结晶织构弱化效果。
图9
图9
入侵α 形变晶粒的γ 再结晶晶粒体积分数随γ 形变织构分数的变化
Fig.9
Volume fraction of γ recrystallization texture invading into α deformed grains as a function of γ deformation texture fraction
4.4 偏析干预下 α
图10 给出了α 形变晶粒再结晶过程中被γ 晶粒入侵(B γ α / γ ) 和自身形核占据(B α α / γ ) 的晶界面积分数。可见,偏析元素延迟了α 形变晶粒晶界区域完成再结晶的时间。无Sb元素时,γ 再结晶晶粒在α 再结晶晶粒形核前就可成功入侵α 形变晶粒,随后γ 再结晶晶粒借助先发优势,高效率消耗α 形变晶粒。含Sb元素时,γ 晶粒入侵孕育期延长,并且入侵时α 再结晶晶粒已开始形核和长大,随后α 再结晶晶粒有效消耗α 形变晶粒。偏析干预下α 形变晶粒晶界区域再结晶动力学的计算结果,提供了调控再结晶竞争关系的时间窗口,可以指导再结晶织构优化控制设计。
图10
图10
α 形变晶粒晶界区域再结晶动力学
Fig.10
Recrystallization kinetics at grain boundary region of α deformed grains (B α / γ α -deformed grain, B γ α / γ γ -recrystallized grain in the grain boundary of α -deformed grain, B α α / γ α -recrystallized grain in the grain boundary of α -deformed grain)
本工作提出的偏析干预下再结晶织构竞争关系模型,是基于再结晶形核与长大动力学以及晶界偏析元素的拖拽效应,故适用于不同晶体结构的金属材料。γ 和α 织构间的竞争是轧制bcc金属板带再结晶织构发展的主要问题,也是形变金属材料再结晶过程中高低应变储能织构组分间竞争的共性问题。通过输入具体偏析元素在特定形变金属材料中的D C i E s e g i
5 结论
(1) 晶界偏析元素干预不同织构组分间的竞争关系。通过延长入侵孕育期和延缓入侵速率抑制γ 再结晶晶粒向α 形变晶粒内发展,从而削弱γ 再结晶织构组分、强化α 等相对低储能织构组分。
(2) 通过引入毗邻形变织构和临界入侵半径,构建了偏析干预下再结晶形核和长大过程中织构竞争关系模型,实现了偏析干预再结晶织构竞争的定量描述和预测。
(3) 随临界入侵半径增大和γ 形核点位增加,晶界偏析元素干预效果先增强后减弱。通过改变临界入侵半径和形变织构特征及其空间分布,可以有效调控基于晶界偏析元素的再结晶织构特征。
参考文献
View Option
[1]
Wauthier-Monnin A Chauveau T Castelnau O et al The evolution with strain of the stored energy in different texture components of cold-rolled IF steel revealed by high resolution X-ray diffraction
[J]. Mater. Charact. , 2015 , 104 : 31
DOI
URL
[本文引用: 1]
[2]
Hawezy D Birosca S Disparity in recrystallization of α - & γ -fibers and its impact on cube texture formation in non-oriented electrical steel
[J]. Acta Mater. , 2021 , 216 : 117141
DOI
URL
[3]
Sanjari M He Y L Hilinski E J et al Texture evolution during skew cold rolling and annealing of a non-oriented electrical steel containing 0.9wt% silicon
[J]. J. Mater. Sci. , 2017 , 52 : 3281
DOI
URL
[本文引用: 1]
[4]
Sebald R Gottstein G Modeling of recrystallization textures: Interaction of nucleation and growth
[J]. Acta Mater. , 2002 , 50 : 1587
DOI
URL
[本文引用: 1]
[5]
Fu Q Sha Y H Zhang F et al Correlative effect of critical parameters for η recrystallization texture development in rolled Fe81 Ga19 sheet: Modeling and experiment
[J]. Acta Mater. , 2019 , 167 : 167
DOI
URL
[6]
Sánchez-Araiza M Godet S Jacques P J et al Texture evolution during the recrystallization of a warm-rolled low-carbon steel
[J]. Acta Mater. , 2006 , 54 : 3085
DOI
URL
[7]
Okuda K Rollett A D Monte Carlo simulation of elongated recrystallized grains in steels
[J]. Comput. Mater. Sci. , 2005 , 34 : 264
DOI
URL
[本文引用: 1]
[8]
Shimanaka H Irie T Matsumura K et al A new non-oriented Si-steel with texture of {100}<ovw >
[J]. J. Magn. Magn. Mater. , 1980 , 19 : 63
DOI
URL
[本文引用: 1]
[9]
Vodopivec F Marinšek F Grešovnik F et al Effect of antimony of energy losses in non-oriented 1.8 Si, 0.3 Al electrical sheets
[J]. J. Magn. Magn. Mater. , 1991 , 97 : 281
DOI
URL
[10]
Lee S De Cooman B C Effect of phosphorus on the magnetic losses of non-oriented 2%Si steel
[J]. ISIJ Int. , 2012 , 52 : 1162
DOI
URL
[11]
Godec M Jenko M Mast R et al Texture measurements on electrical steels alloyed with tin
[J]. Vacuum , 2001 , 61 : 151
DOI
URL
[12]
Chang S K Huang W Y Texture effect on magnetic properties by alloying specific elements in non-grain oriented silicon steels
[J]. ISIJ Int. , 2005 , 45 : 918
DOI
URL
[本文引用: 1]
[13]
Mavrikakis N Saikaly W Calvillo P R et al How Sn addition influences texture development in single-phase Fe alloys: Correlation between local chemical information, microstructure and recrystallisation
[J]. Mater. Charact. , 2022 , 190 : 112072
DOI
URL
[本文引用: 1]
[14]
Duggan B J Tse Y Y Crystal growth in deformed metals by an impingement and spheroidisation process
[J]. Acta Mater. , 2004 , 52 : 387
DOI
URL
[本文引用: 2]
[15]
Bailey J E Hirsch P B The recrystallization process in some polycrystalline metals
[J]. Proc. R. Soc. , 1962 , 267A : 11
[本文引用: 1]
[16]
Cram D G Fang X Y Zurob H S et al The effect of solute on discontinuous dynamic recrystallization
[J]. Acta Mater. , 2012 , 60 : 6390
DOI
URL
[本文引用: 1]
[17]
Buken H Kozeschnik E Modeling static recrystallization in Al-Mg alloys
[J]. Metall. Mater. Trans. , 2021 , 52A : 544
[本文引用: 2]
[18]
Cahn J W The impurity-drag effect in grain boundary motion
[J]. Acta Metall. , 1962 , 10 : 789
DOI
URL
[本文引用: 2]
[19]
Crumbach M Goerdeler M Gottstein G Modelling of recrystallisation textures in aluminium alloys: I. Model set-up and integration
[J]. Acta Mater. , 2006 , 54 : 3275
DOI
URL
[本文引用: 1]
[20]
Raabe D A texture-component Avrami model for predicting recrystallization textures, kinetics and grain size
[J]. Modell. Simul. Mater. Sci. Eng. , 2007 , 15 : 39
DOI
URL
[21]
Raabe D Multiscale recrystallization models for the prediction of crystallographic textures with respect to process simulation
[J]. J. Strain Anal. Eng. Des. , 2007 , 42 : 253
DOI
URL
[本文引用: 1]
This paper discusses the most relevant multiscale models for predicting crystallographic textures formed during the primary static recrystallization of metals. Two main groups of approaches are presented, namely those which spatially discretize the grains and the interface motion associated with recrystallization and those which treat these phenomena in an Avrami-type statistical fashion. The article gives a concise review of the methods, placing particular attention on their strengths and weaknesses in the context of process modelling, of conceptual aspects, and of the data sets required as input for practically applying the models to the prediction of crystallographic textures in the course of metallurgical processes.
[22]
Hutchinson B Deformation microstructures and textures in steels
[J]. Philos. Trans. R. Soc. , 1999 , 357 : 1471
[本文引用: 1]
[23]
Zurob H S Bréchet Y Dunlop J Quantitative criterion for recrystallization nucleation in single-phase alloys: Prediction of critical strains and incubation times
[J]. Acta Mater. , 2006 , 54 : 3983
DOI
URL
[本文引用: 7]
[24]
Witcomb M J Dislocation cell structure relation d = Kρ -1/2 : The stacking fault energy dependence of K
[J]. Phys. Status Solidi , 1974 , 22A : 299
[本文引用: 1]
[25]
Huang X Jensen D J Hansen N Effect of grain orientation on deformation structure and recrystallization behaviour of tensile strained copper
[A]. 4th International Conference on Recrystallization and Related Phenomena [C]. Tsukuba : JIM , 1999 : 161
[本文引用: 1]
[26]
Buken H Kozeschnik E A model for static recrystallization with simultaneous precipitation and solute drag
[J]. Metall. Mater. Trans. , 2017 , 48A : 2812
[本文引用: 7]
[27]
Després A Mithieux J D Sinclair C W Modelling the relationship between deformed microstructures and static recrystallization textures: Application to ferritic stainless steels
[J]. Acta Mater. , 2021 , 219 : 117226
DOI
URL
[本文引用: 1]
[28]
Montaño-Zuñiga I M Sepulveda-Cervantes G Lopez-Hirata V M et al Numerical simulation of recrystallization in BCC metals
[J]. Comput. Mater. Sci. , 2010 , 49 : 512
DOI
URL
[本文引用: 1]
[29]
Ratanaphan S Olmsted D L Bulatov V V et al Grain boundary energies in body-centered cubic metals
[J]. Acta Mater. , 2015 , 88 : 346
DOI
URL
[本文引用: 1]
[30]
Yong Q L The Second Phase in Steel Materials [M]. Beijing : Metallurgical Industry Press , 2006 : 65
[本文引用: 6]
雍岐龙 钢铁材料中的第二相 [M]. 北京 : 冶金工业出版社 , 2006 : 65
[本文引用: 6]
[31]
Lee H H Jung J Yoon J I et al Modelling the evolution of recrystallization texture for a non-grain oriented electrical steel
[J]. Comput. Mater. Sci. , 2018 , 149 : 57
DOI
URL
[本文引用: 1]
[32]
Mavrikakis N Detlefs C Cook P K et al A multi-scale study of the interaction of Sn solutes with dislocations during static recovery in α -Fe
[J]. Acta Mater. , 2019 , 174 : 92
DOI
[本文引用: 1]
The properties of engineering materials can be improved by optimising the microstructural developments during annealing processes. Here, we investigate the effect of Sn on the recovery annealing of cold rolled Fe-3%Si alloys. We use a multiscale approach combining micro hardness, electron back scattering diffraction (EBSD), and dark field X-ray microscopy (DFXM): a recent, non-destructive synchrotron-based technique that allows 3D mapping of orientation and lattice strain within individual grains embedded in bulk samples. Micro hardness results show that the Sn solute has a strong effect on the recovery kinetics. These results are compared to a physical kinetic model suggesting that Sn limits the softening. This observation is further discussed by a complementary atomistic modelling that demonstrates solute-dislocation interaction around edge dislocations. In situ DFXM experiments reveal the 3D microstructural evolution upon annealing at the grain level with high angular resolution. The DFXM observations show that Sn slows the recovery kinetics within individual grains, in agreement with the other microscopic investigations. Furthermore, the DFXM results provide a direct observation of strain fields around dislocation loops in an embedded single grain, which is argued to remain static due to solute effect during recovery. (C) 2019 Acta Materialia Inc. Published by Elsevier Ltd.
[33]
Faulkner R G Song S H Flewitt P E J Determination of impurity-point defect binding energies in alloys
[J]. Mater. Sci. Technol. , 1996 , 12 : 904
DOI
URL
[本文引用: 1]
[34]
Lejček P Grain boundary segregation of antimony in α -iron: Prediction and experimental data
[J]. J. Alloys Compd. , 2004 , 378 : 85
DOI
URL
[本文引用: 1]
[35]
Pérez A R A Torres D N Dyment F Sb diffusion in α -Fe
[J]. Appl. Phys. , 2005 , 81 : 787
[本文引用: 5]
The evolution with strain of the stored energy in different texture components of cold-rolled IF steel revealed by high resolution X-ray diffraction
1
2015
... 再结晶织构源于不同织构组分在形核和长大过程中的竞争.形变金属内的应变储能及取向梯度分布依赖于形变晶粒取向,在高储能和高取向梯度位置形核的织构组分具有形核和长大动力学优势[1 ~3 ] .不同织构组分形核点位相毗邻时,优势织构组分会消耗毗邻织构组分的形核点位和长大空间,在强化自身的同时弱化其他织构组分[4 ~7 ] .因此,毗邻织构组分的竞争关系决定了再结晶织构的形成与发展,改变形核与长大动力学以及侵入毗邻形变晶粒的能力是再结晶织构调控的关键. ...
Disparity in recrystallization of α - & γ -fibers and its impact on cube texture formation in non-oriented electrical steel
0
2021
Texture evolution during skew cold rolling and annealing of a non-oriented electrical steel containing 0.9wt% silicon
1
2017
... 再结晶织构源于不同织构组分在形核和长大过程中的竞争.形变金属内的应变储能及取向梯度分布依赖于形变晶粒取向,在高储能和高取向梯度位置形核的织构组分具有形核和长大动力学优势[1 ~3 ] .不同织构组分形核点位相毗邻时,优势织构组分会消耗毗邻织构组分的形核点位和长大空间,在强化自身的同时弱化其他织构组分[4 ~7 ] .因此,毗邻织构组分的竞争关系决定了再结晶织构的形成与发展,改变形核与长大动力学以及侵入毗邻形变晶粒的能力是再结晶织构调控的关键. ...
Modeling of recrystallization textures: Interaction of nucleation and growth
1
2002
... 再结晶织构源于不同织构组分在形核和长大过程中的竞争.形变金属内的应变储能及取向梯度分布依赖于形变晶粒取向,在高储能和高取向梯度位置形核的织构组分具有形核和长大动力学优势[1 ~3 ] .不同织构组分形核点位相毗邻时,优势织构组分会消耗毗邻织构组分的形核点位和长大空间,在强化自身的同时弱化其他织构组分[4 ~7 ] .因此,毗邻织构组分的竞争关系决定了再结晶织构的形成与发展,改变形核与长大动力学以及侵入毗邻形变晶粒的能力是再结晶织构调控的关键. ...
Correlative effect of critical parameters for η recrystallization texture development in rolled Fe81 Ga19 sheet: Modeling and experiment
0
2019
Texture evolution during the recrystallization of a warm-rolled low-carbon steel
0
2006
Monte Carlo simulation of elongated recrystallized grains in steels
1
2005
... 再结晶织构源于不同织构组分在形核和长大过程中的竞争.形变金属内的应变储能及取向梯度分布依赖于形变晶粒取向,在高储能和高取向梯度位置形核的织构组分具有形核和长大动力学优势[1 ~3 ] .不同织构组分形核点位相毗邻时,优势织构组分会消耗毗邻织构组分的形核点位和长大空间,在强化自身的同时弱化其他织构组分[4 ~7 ] .因此,毗邻织构组分的竞争关系决定了再结晶织构的形成与发展,改变形核与长大动力学以及侵入毗邻形变晶粒的能力是再结晶织构调控的关键. ...
A new non-oriented Si-steel with texture of {100}<ovw >
1
1980
... 晶界偏析元素可降低晶界可动性,延缓再结晶晶粒的形核和长大速率,从而影响再结晶织构组分间的竞争关系.添加晶界偏析元素可以弱化无取向硅钢γ (<111>//ND,ND为轧面法向)再结晶织构,强化α (<110>//RD,RD为轧制方向)和λ (<100>//ND)再结晶织构[8 ~12 ] .在对Fe-Si合金和Fe-Si-Sn合金再结晶行为的准原位电子背散射衍射(EBSD)研究[13 ] 中发现,偏析元素通过延缓γ 形变晶粒再结晶,使毗邻α 形变晶粒获得再结晶形核和长大的时机.而γ 再结晶晶粒需要达到临界尺寸以上,才能侵入毗邻α 形变晶粒[14 ] .这些实验研究表明,优先形核的γ 晶粒长大过程涉及向γ 形变晶粒内生长和侵入毗邻形变晶粒2个阶段,晶界偏析元素可以抑制其获得向毗邻较低储能形变晶粒入侵的能力. ...
Effect of antimony of energy losses in non-oriented 1.8 Si, 0.3 Al electrical sheets
0
1991
Effect of phosphorus on the magnetic losses of non-oriented 2%Si steel
0
2012
Texture measurements on electrical steels alloyed with tin
0
2001
Texture effect on magnetic properties by alloying specific elements in non-grain oriented silicon steels
1
2005
... 晶界偏析元素可降低晶界可动性,延缓再结晶晶粒的形核和长大速率,从而影响再结晶织构组分间的竞争关系.添加晶界偏析元素可以弱化无取向硅钢γ (<111>//ND,ND为轧面法向)再结晶织构,强化α (<110>//RD,RD为轧制方向)和λ (<100>//ND)再结晶织构[8 ~12 ] .在对Fe-Si合金和Fe-Si-Sn合金再结晶行为的准原位电子背散射衍射(EBSD)研究[13 ] 中发现,偏析元素通过延缓γ 形变晶粒再结晶,使毗邻α 形变晶粒获得再结晶形核和长大的时机.而γ 再结晶晶粒需要达到临界尺寸以上,才能侵入毗邻α 形变晶粒[14 ] .这些实验研究表明,优先形核的γ 晶粒长大过程涉及向γ 形变晶粒内生长和侵入毗邻形变晶粒2个阶段,晶界偏析元素可以抑制其获得向毗邻较低储能形变晶粒入侵的能力. ...
How Sn addition influences texture development in single-phase Fe alloys: Correlation between local chemical information, microstructure and recrystallisation
1
2022
... 晶界偏析元素可降低晶界可动性,延缓再结晶晶粒的形核和长大速率,从而影响再结晶织构组分间的竞争关系.添加晶界偏析元素可以弱化无取向硅钢γ (<111>//ND,ND为轧面法向)再结晶织构,强化α (<110>//RD,RD为轧制方向)和λ (<100>//ND)再结晶织构[8 ~12 ] .在对Fe-Si合金和Fe-Si-Sn合金再结晶行为的准原位电子背散射衍射(EBSD)研究[13 ] 中发现,偏析元素通过延缓γ 形变晶粒再结晶,使毗邻α 形变晶粒获得再结晶形核和长大的时机.而γ 再结晶晶粒需要达到临界尺寸以上,才能侵入毗邻α 形变晶粒[14 ] .这些实验研究表明,优先形核的γ 晶粒长大过程涉及向γ 形变晶粒内生长和侵入毗邻形变晶粒2个阶段,晶界偏析元素可以抑制其获得向毗邻较低储能形变晶粒入侵的能力. ...
Crystal growth in deformed metals by an impingement and spheroidisation process
2
2004
... 晶界偏析元素可降低晶界可动性,延缓再结晶晶粒的形核和长大速率,从而影响再结晶织构组分间的竞争关系.添加晶界偏析元素可以弱化无取向硅钢γ (<111>//ND,ND为轧面法向)再结晶织构,强化α (<110>//RD,RD为轧制方向)和λ (<100>//ND)再结晶织构[8 ~12 ] .在对Fe-Si合金和Fe-Si-Sn合金再结晶行为的准原位电子背散射衍射(EBSD)研究[13 ] 中发现,偏析元素通过延缓γ 形变晶粒再结晶,使毗邻α 形变晶粒获得再结晶形核和长大的时机.而γ 再结晶晶粒需要达到临界尺寸以上,才能侵入毗邻α 形变晶粒[14 ] .这些实验研究表明,优先形核的γ 晶粒长大过程涉及向γ 形变晶粒内生长和侵入毗邻形变晶粒2个阶段,晶界偏析元素可以抑制其获得向毗邻较低储能形变晶粒入侵的能力. ...
... 式中,Pα 为α 晶粒应变储能,K 为比例系数.在纯净金属中K 为2γ gb ,存在杂质时R c 将增大[14 ] .单位面积γ 形变晶粒的晶界上,半径达到R c 的γ 再结晶晶粒总数为N R c ( t ).当γ 再结晶晶粒与α 形变晶粒毗邻时,t 时刻成功入侵α 形变晶粒的γ 再结晶晶粒数(N γ α / γ ( t ))为: ...
The recrystallization process in some polycrystalline metals
1
1962
... 针对偏析元素干预再结晶织构发展的机制也进行了一些研究.亚晶长大是再结晶形核的重要机制,只有亚晶长大至临界尺寸且具有大角晶界时才完成再结晶晶粒形核过程[15 ] .基于位错攀移机制,Cram等[16 ] 认为晶界偏析元素与空位结合可提高位错攀移和亚晶界迁移的激活能,延缓亚晶长大进而抑制再结晶形核.基于溶质拖拽机制,晶界偏析元素通过降低亚晶界的迁移速率延缓再结晶形核,Buk-en和Kozeschnik[17 ] 结合亚晶长大机制和溶质拖拽理论给出了偏析干预下再结晶晶粒形核动力学模型.再结晶晶粒的长大动力学则由应变储能驱动下溶质拖拽晶界迁移过程控制,溶质拖拽下的晶界迁移行为可由Cahn[18 ] 模型描述.传统基于形核和长大动力学的再结晶织构模型,处理织构组分间竞争行为时采用空间平均场假设,即再结晶晶粒在空间随机分布并消耗其周围均匀分布的形核点位和形变基体[19 ~21 ] .然而,γ 再结晶晶粒的长大过程呈现明显的阶段性,空间平均场假设不适于偏析干预下的再结晶织构竞争.目前,尚无偏析干预下γ 与α 等主要再结晶织构组分间竞争关系的定量模型,晶界偏析元素对再结晶织构竞争行为的干预规律尚不清晰. ...
The effect of solute on discontinuous dynamic recrystallization
1
2012
... 针对偏析元素干预再结晶织构发展的机制也进行了一些研究.亚晶长大是再结晶形核的重要机制,只有亚晶长大至临界尺寸且具有大角晶界时才完成再结晶晶粒形核过程[15 ] .基于位错攀移机制,Cram等[16 ] 认为晶界偏析元素与空位结合可提高位错攀移和亚晶界迁移的激活能,延缓亚晶长大进而抑制再结晶形核.基于溶质拖拽机制,晶界偏析元素通过降低亚晶界的迁移速率延缓再结晶形核,Buk-en和Kozeschnik[17 ] 结合亚晶长大机制和溶质拖拽理论给出了偏析干预下再结晶晶粒形核动力学模型.再结晶晶粒的长大动力学则由应变储能驱动下溶质拖拽晶界迁移过程控制,溶质拖拽下的晶界迁移行为可由Cahn[18 ] 模型描述.传统基于形核和长大动力学的再结晶织构模型,处理织构组分间竞争行为时采用空间平均场假设,即再结晶晶粒在空间随机分布并消耗其周围均匀分布的形核点位和形变基体[19 ~21 ] .然而,γ 再结晶晶粒的长大过程呈现明显的阶段性,空间平均场假设不适于偏析干预下的再结晶织构竞争.目前,尚无偏析干预下γ 与α 等主要再结晶织构组分间竞争关系的定量模型,晶界偏析元素对再结晶织构竞争行为的干预规律尚不清晰. ...
Modeling static recrystallization in Al-Mg alloys
2
2021
... 针对偏析元素干预再结晶织构发展的机制也进行了一些研究.亚晶长大是再结晶形核的重要机制,只有亚晶长大至临界尺寸且具有大角晶界时才完成再结晶晶粒形核过程[15 ] .基于位错攀移机制,Cram等[16 ] 认为晶界偏析元素与空位结合可提高位错攀移和亚晶界迁移的激活能,延缓亚晶长大进而抑制再结晶形核.基于溶质拖拽机制,晶界偏析元素通过降低亚晶界的迁移速率延缓再结晶形核,Buk-en和Kozeschnik[17 ] 结合亚晶长大机制和溶质拖拽理论给出了偏析干预下再结晶晶粒形核动力学模型.再结晶晶粒的长大动力学则由应变储能驱动下溶质拖拽晶界迁移过程控制,溶质拖拽下的晶界迁移行为可由Cahn[18 ] 模型描述.传统基于形核和长大动力学的再结晶织构模型,处理织构组分间竞争行为时采用空间平均场假设,即再结晶晶粒在空间随机分布并消耗其周围均匀分布的形核点位和形变基体[19 ~21 ] .然而,γ 再结晶晶粒的长大过程呈现明显的阶段性,空间平均场假设不适于偏析干预下的再结晶织构竞争.目前,尚无偏析干预下γ 与α 等主要再结晶织构组分间竞争关系的定量模型,晶界偏析元素对再结晶织构竞争行为的干预规律尚不清晰. ...
... 式中,γ gb 为大角度晶界的晶界能.t 时刻达到临界形核半径的亚晶分数(F sub (t ))以及单位晶界面积的再结晶形核率(N ˙ r e ( t ))可表示为[17 ] : ...
The impurity-drag effect in grain boundary motion
2
1962
... 针对偏析元素干预再结晶织构发展的机制也进行了一些研究.亚晶长大是再结晶形核的重要机制,只有亚晶长大至临界尺寸且具有大角晶界时才完成再结晶晶粒形核过程[15 ] .基于位错攀移机制,Cram等[16 ] 认为晶界偏析元素与空位结合可提高位错攀移和亚晶界迁移的激活能,延缓亚晶长大进而抑制再结晶形核.基于溶质拖拽机制,晶界偏析元素通过降低亚晶界的迁移速率延缓再结晶形核,Buk-en和Kozeschnik[17 ] 结合亚晶长大机制和溶质拖拽理论给出了偏析干预下再结晶晶粒形核动力学模型.再结晶晶粒的长大动力学则由应变储能驱动下溶质拖拽晶界迁移过程控制,溶质拖拽下的晶界迁移行为可由Cahn[18 ] 模型描述.传统基于形核和长大动力学的再结晶织构模型,处理织构组分间竞争行为时采用空间平均场假设,即再结晶晶粒在空间随机分布并消耗其周围均匀分布的形核点位和形变基体[19 ~21 ] .然而,γ 再结晶晶粒的长大过程呈现明显的阶段性,空间平均场假设不适于偏析干预下的再结晶织构竞争.目前,尚无偏析干预下γ 与α 等主要再结晶织构组分间竞争关系的定量模型,晶界偏析元素对再结晶织构竞争行为的干预规律尚不清晰. ...
... 式中,dR (t )为应变储能和晶界能共同导致的晶粒半径增量,X re 为再结晶体积分数.依据溶质拖拽理论,偏析干预下的界面迁移率可表示为[18 ] : ...
Modelling of recrystallisation textures in aluminium alloys: I. Model set-up and integration
1
2006
... 针对偏析元素干预再结晶织构发展的机制也进行了一些研究.亚晶长大是再结晶形核的重要机制,只有亚晶长大至临界尺寸且具有大角晶界时才完成再结晶晶粒形核过程[15 ] .基于位错攀移机制,Cram等[16 ] 认为晶界偏析元素与空位结合可提高位错攀移和亚晶界迁移的激活能,延缓亚晶长大进而抑制再结晶形核.基于溶质拖拽机制,晶界偏析元素通过降低亚晶界的迁移速率延缓再结晶形核,Buk-en和Kozeschnik[17 ] 结合亚晶长大机制和溶质拖拽理论给出了偏析干预下再结晶晶粒形核动力学模型.再结晶晶粒的长大动力学则由应变储能驱动下溶质拖拽晶界迁移过程控制,溶质拖拽下的晶界迁移行为可由Cahn[18 ] 模型描述.传统基于形核和长大动力学的再结晶织构模型,处理织构组分间竞争行为时采用空间平均场假设,即再结晶晶粒在空间随机分布并消耗其周围均匀分布的形核点位和形变基体[19 ~21 ] .然而,γ 再结晶晶粒的长大过程呈现明显的阶段性,空间平均场假设不适于偏析干预下的再结晶织构竞争.目前,尚无偏析干预下γ 与α 等主要再结晶织构组分间竞争关系的定量模型,晶界偏析元素对再结晶织构竞争行为的干预规律尚不清晰. ...
A texture-component Avrami model for predicting recrystallization textures, kinetics and grain size
0
2007
Multiscale recrystallization models for the prediction of crystallographic textures with respect to process simulation
1
2007
... 针对偏析元素干预再结晶织构发展的机制也进行了一些研究.亚晶长大是再结晶形核的重要机制,只有亚晶长大至临界尺寸且具有大角晶界时才完成再结晶晶粒形核过程[15 ] .基于位错攀移机制,Cram等[16 ] 认为晶界偏析元素与空位结合可提高位错攀移和亚晶界迁移的激活能,延缓亚晶长大进而抑制再结晶形核.基于溶质拖拽机制,晶界偏析元素通过降低亚晶界的迁移速率延缓再结晶形核,Buk-en和Kozeschnik[17 ] 结合亚晶长大机制和溶质拖拽理论给出了偏析干预下再结晶晶粒形核动力学模型.再结晶晶粒的长大动力学则由应变储能驱动下溶质拖拽晶界迁移过程控制,溶质拖拽下的晶界迁移行为可由Cahn[18 ] 模型描述.传统基于形核和长大动力学的再结晶织构模型,处理织构组分间竞争行为时采用空间平均场假设,即再结晶晶粒在空间随机分布并消耗其周围均匀分布的形核点位和形变基体[19 ~21 ] .然而,γ 再结晶晶粒的长大过程呈现明显的阶段性,空间平均场假设不适于偏析干预下的再结晶织构竞争.目前,尚无偏析干预下γ 与α 等主要再结晶织构组分间竞争关系的定量模型,晶界偏析元素对再结晶织构竞争行为的干预规律尚不清晰. ...
Deformation microstructures and textures in steels
1
1999
... 图4 给出了冷轧板主要织构组分的EBSD取向成像图和几何必需位错(GND)密度成像图.可见,无Sb和含Sb样品中γ 形变晶粒内部均分布有剪切带,亚表层γ 形变晶粒内的剪切带更为密集.亚表层γ 形变晶粒有更高的几率相互毗邻,中心层γ 形变晶粒则倾向于被α 形变晶粒包围.由于轧制变形下γ 取向晶粒的Taylor因子高于α 取向晶粒,γ 取向晶粒具有更高的位错累积速率[22 ] .对γ 和α 形变晶粒内平均GND密度进行统计可知,无Sb和含Sb样品中,γ 形变晶粒内平均GND密度分别为7.41 × 1014 和7.68 × 1014 m-2 ,α 形变晶粒内的平均GND密度分别为2.87 × 1014 和3.12 × 1014 m-2 .本工作中Sb元素添加量仅为0.04%,其对形变过程中的位错累积无明显影响. ...
Quantitative criterion for recrystallization nucleation in single-phase alloys: Prediction of critical strains and incubation times
7
2006
... 再结晶形核采用亚晶长大机制,亚晶半径随时间的演变规律为[23 ] : ...
... 式中,G 为剪切模量,b 为Burgers矢量模.当亚晶长大至临界形核半径(r c )时,再结晶晶粒形核.r c 为[23 ] : ...
... 针对图5 中γ 再结晶晶粒入侵A1 区域和A2 区域内α 形变晶粒的行为进行了模拟计算.计算采用时间循环迭代方式进行,记录并更新每个时间步的晶核数量和晶粒尺寸,时间步长dt 需保证每步计算的再结晶分数增量小于1%,以减小误差.A1 区域内的α 形变晶粒两侧均与γ 晶粒毗邻,A2 区域内的α 形变晶粒可以拆分为两侧均与γ 晶粒毗邻和单侧与γ 晶粒毗邻的混合.γ 和α 形变晶粒位错密度取自图4 的实测值,A1 和A2 区域α 晶粒的平均厚度h 分别为45和35 μm,偏析元素含量C 0 分别为0和0.04%.α -Fe晶界能为(1.11 ± 0.209) J/m2 [29 ] ,计算所需其他参数见表1 [23 ,26 ,30 ~35 ] .计算求得A1 和A2 区域内的γ 再结晶晶粒占比分别为0.77~0.58和0.39~0.16,实测值0.59和0.27处于相应区间内.本工作建模过程忽略了偏析元素对界面能的影响,而理论上微量晶界偏析元素倾向使界面能有所降低,这可能导致稍许高估偏析干预效果.因此,计算与实测符合良好,表明构建的模型可以描述偏析干预下毗邻织构组分竞争关系.在4.2~4.4节中,取α -Fe平均晶界能1.11 J/m2 进行相关计算. ...
... Fe-3%Si合金再结晶行为模拟用参数[23 ,26 ,30 ~35 ] ...
... List of parameters for simulating recrystallization behavior of Fe-3%Si alloy[23 ,26 ,30 -35 ] ...
... [
23 ]
Grain boundary width, δ gb 1 × 10-9 m [26 ] Sub-grain boundary width, δ sub δ gb m This work Number of atoms per unit volume, N V 8.45 × 1028 m-3 Binding energy of Sb to sub-grain boundary, E s e g s u b -0.43 eV [32 ,33 ] Binding energy of Sb to grain boundary, E s e g g b -0.67 eV [34 ] Sb bulk diffusion coefficient, D B 1.3 × 10 - 5 e x p ( - 3.37 × 10 - 19 k b T ) m2 ·s-1 [35 ] Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work <strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
... 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
Dislocation cell structure relation d = Kρ -1/2 : The stacking fault energy dependence of K
1
1974
... 式中,r (t )为t 时刻的亚晶半径,r 0 为初始亚晶半径,M S G s u b P 为形核基体应变储能.亚晶初始半径和储能与形变基体内的位错密度(ρ )相关[24 ,25 ] : ...
Effect of grain orientation on deformation structure and recrystallization behaviour of tensile strained copper
1
1999
... 式中,r (t )为t 时刻的亚晶半径,r 0 为初始亚晶半径,M S G s u b P 为形核基体应变储能.亚晶初始半径和储能与形变基体内的位错密度(ρ )相关[24 ,25 ] : ...
A model for static recrystallization with simultaneous precipitation and solute drag
7
2017
... 式中,r ¯ ( t )为平均亚晶尺寸,B (t )为已再结晶的晶界面积分数,F ˙ s u b ( t )为单位时间内达到临界形核半径的亚晶分数.再结晶晶粒在应变储能和晶界能驱动下的长大动力学可分别表示为[26 ,27 ] : ...
... 针对图5 中γ 再结晶晶粒入侵A1 区域和A2 区域内α 形变晶粒的行为进行了模拟计算.计算采用时间循环迭代方式进行,记录并更新每个时间步的晶核数量和晶粒尺寸,时间步长dt 需保证每步计算的再结晶分数增量小于1%,以减小误差.A1 区域内的α 形变晶粒两侧均与γ 晶粒毗邻,A2 区域内的α 形变晶粒可以拆分为两侧均与γ 晶粒毗邻和单侧与γ 晶粒毗邻的混合.γ 和α 形变晶粒位错密度取自图4 的实测值,A1 和A2 区域α 晶粒的平均厚度h 分别为45和35 μm,偏析元素含量C 0 分别为0和0.04%.α -Fe晶界能为(1.11 ± 0.209) J/m2 [29 ] ,计算所需其他参数见表1 [23 ,26 ,30 ~35 ] .计算求得A1 和A2 区域内的γ 再结晶晶粒占比分别为0.77~0.58和0.39~0.16,实测值0.59和0.27处于相应区间内.本工作建模过程忽略了偏析元素对界面能的影响,而理论上微量晶界偏析元素倾向使界面能有所降低,这可能导致稍许高估偏析干预效果.因此,计算与实测符合良好,表明构建的模型可以描述偏析干预下毗邻织构组分竞争关系.在4.2~4.4节中,取α -Fe平均晶界能1.11 J/m2 进行相关计算. ...
... Fe-3%Si合金再结晶行为模拟用参数[23 ,26 ,30 ~35 ] ...
... List of parameters for simulating recrystallization behavior of Fe-3%Si alloy[23 ,26 ,30 -35 ] ...
... [
26 ]
Sub-grain boundary width, δ sub δ gb m This work Number of atoms per unit volume, N V 8.45 × 1028 m-3 Binding energy of Sb to sub-grain boundary, E s e g s u b -0.43 eV [32 ,33 ] Binding energy of Sb to grain boundary, E s e g g b -0.67 eV [34 ] Sb bulk diffusion coefficient, D B 1.3 × 10 - 5 e x p ( - 3.37 × 10 - 19 k b T ) m2 ·s-1 [35 ] Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work <strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
... [
26 ]
Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work <strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
... 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
Modelling the relationship between deformed microstructures and static recrystallization textures: Application to ferritic stainless steels
1
2021
... 式中,r ¯ ( t )为平均亚晶尺寸,B (t )为已再结晶的晶界面积分数,F ˙ s u b ( t )为单位时间内达到临界形核半径的亚晶分数.再结晶晶粒在应变储能和晶界能驱动下的长大动力学可分别表示为[26 ,27 ] : ...
Numerical simulation of recrystallization in BCC metals
1
2010
... 优先形核的γ 晶粒在后续退火过程中持续长大,当γ 晶粒半径达到R c 后成功入侵α 形变晶粒,在α 形变晶粒内形成一个半径为R c 的再结晶晶粒.R c 反比于应变储能[28 ] : ...
Grain boundary energies in body-centered cubic metals
1
2015
... 针对图5 中γ 再结晶晶粒入侵A1 区域和A2 区域内α 形变晶粒的行为进行了模拟计算.计算采用时间循环迭代方式进行,记录并更新每个时间步的晶核数量和晶粒尺寸,时间步长dt 需保证每步计算的再结晶分数增量小于1%,以减小误差.A1 区域内的α 形变晶粒两侧均与γ 晶粒毗邻,A2 区域内的α 形变晶粒可以拆分为两侧均与γ 晶粒毗邻和单侧与γ 晶粒毗邻的混合.γ 和α 形变晶粒位错密度取自图4 的实测值,A1 和A2 区域α 晶粒的平均厚度h 分别为45和35 μm,偏析元素含量C 0 分别为0和0.04%.α -Fe晶界能为(1.11 ± 0.209) J/m2 [29 ] ,计算所需其他参数见表1 [23 ,26 ,30 ~35 ] .计算求得A1 和A2 区域内的γ 再结晶晶粒占比分别为0.77~0.58和0.39~0.16,实测值0.59和0.27处于相应区间内.本工作建模过程忽略了偏析元素对界面能的影响,而理论上微量晶界偏析元素倾向使界面能有所降低,这可能导致稍许高估偏析干预效果.因此,计算与实测符合良好,表明构建的模型可以描述偏析干预下毗邻织构组分竞争关系.在4.2~4.4节中,取α -Fe平均晶界能1.11 J/m2 进行相关计算. ...
6
2006
... 针对图5 中γ 再结晶晶粒入侵A1 区域和A2 区域内α 形变晶粒的行为进行了模拟计算.计算采用时间循环迭代方式进行,记录并更新每个时间步的晶核数量和晶粒尺寸,时间步长dt 需保证每步计算的再结晶分数增量小于1%,以减小误差.A1 区域内的α 形变晶粒两侧均与γ 晶粒毗邻,A2 区域内的α 形变晶粒可以拆分为两侧均与γ 晶粒毗邻和单侧与γ 晶粒毗邻的混合.γ 和α 形变晶粒位错密度取自图4 的实测值,A1 和A2 区域α 晶粒的平均厚度h 分别为45和35 μm,偏析元素含量C 0 分别为0和0.04%.α -Fe晶界能为(1.11 ± 0.209) J/m2 [29 ] ,计算所需其他参数见表1 [23 ,26 ,30 ~35 ] .计算求得A1 和A2 区域内的γ 再结晶晶粒占比分别为0.77~0.58和0.39~0.16,实测值0.59和0.27处于相应区间内.本工作建模过程忽略了偏析元素对界面能的影响,而理论上微量晶界偏析元素倾向使界面能有所降低,这可能导致稍许高估偏析干预效果.因此,计算与实测符合良好,表明构建的模型可以描述偏析干预下毗邻织构组分竞争关系.在4.2~4.4节中,取α -Fe平均晶界能1.11 J/m2 进行相关计算. ...
... Fe-3%Si合金再结晶行为模拟用参数[23 ,26 ,30 ~35 ] ...
... List of parameters for simulating recrystallization behavior of Fe-3%Si alloy[23 ,26 ,30 -35 ] ...
... [
30 ]
Boltzmann's constant, k b 1.38 × 10-23 J·K-1 Burgers vector modulus, b 0.25 × 10-9 m [30 ] Mobility of free grain boundary, M f r e e g b 9 × 10 - 8 e x p ( - 1.99 × 10 - 19 k b T ) m4 ·J-1 ·s-1 [31 ] Mobility of free sub-grain boundary, M f r e e s u b 0.2M f r e e g b m4 ·J-1 ·s-1 [23 ] Grain boundary width, δ gb 1 × 10-9 m [26 ] Sub-grain boundary width, δ sub δ gb m This work Number of atoms per unit volume, N V 8.45 × 1028 m-3 Binding energy of Sb to sub-grain boundary, E s e g s u b -0.43 eV [32 ,33 ] Binding energy of Sb to grain boundary, E s e g g b -0.67 eV [34 ] Sb bulk diffusion coefficient, D B 1.3 × 10 - 5 e x p ( - 3.37 × 10 - 19 k b T ) m2 ·s-1 [35 ] Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work <strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
... [
30 ]
Mobility of free grain boundary, M f r e e g b 9 × 10 - 8 e x p ( - 1.99 × 10 - 19 k b T ) m4 ·J-1 ·s-1 [31 ] Mobility of free sub-grain boundary, M f r e e s u b 0.2M f r e e g b m4 ·J-1 ·s-1 [23 ] Grain boundary width, δ gb 1 × 10-9 m [26 ] Sub-grain boundary width, δ sub δ gb m This work Number of atoms per unit volume, N V 8.45 × 1028 m-3 Binding energy of Sb to sub-grain boundary, E s e g s u b -0.43 eV [32 ,33 ] Binding energy of Sb to grain boundary, E s e g g b -0.67 eV [34 ] Sb bulk diffusion coefficient, D B 1.3 × 10 - 5 e x p ( - 3.37 × 10 - 19 k b T ) m2 ·s-1 [35 ] Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work <strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
... 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
6
2006
... 针对图5 中γ 再结晶晶粒入侵A1 区域和A2 区域内α 形变晶粒的行为进行了模拟计算.计算采用时间循环迭代方式进行,记录并更新每个时间步的晶核数量和晶粒尺寸,时间步长dt 需保证每步计算的再结晶分数增量小于1%,以减小误差.A1 区域内的α 形变晶粒两侧均与γ 晶粒毗邻,A2 区域内的α 形变晶粒可以拆分为两侧均与γ 晶粒毗邻和单侧与γ 晶粒毗邻的混合.γ 和α 形变晶粒位错密度取自图4 的实测值,A1 和A2 区域α 晶粒的平均厚度h 分别为45和35 μm,偏析元素含量C 0 分别为0和0.04%.α -Fe晶界能为(1.11 ± 0.209) J/m2 [29 ] ,计算所需其他参数见表1 [23 ,26 ,30 ~35 ] .计算求得A1 和A2 区域内的γ 再结晶晶粒占比分别为0.77~0.58和0.39~0.16,实测值0.59和0.27处于相应区间内.本工作建模过程忽略了偏析元素对界面能的影响,而理论上微量晶界偏析元素倾向使界面能有所降低,这可能导致稍许高估偏析干预效果.因此,计算与实测符合良好,表明构建的模型可以描述偏析干预下毗邻织构组分竞争关系.在4.2~4.4节中,取α -Fe平均晶界能1.11 J/m2 进行相关计算. ...
... Fe-3%Si合金再结晶行为模拟用参数[23 ,26 ,30 ~35 ] ...
... List of parameters for simulating recrystallization behavior of Fe-3%Si alloy[23 ,26 ,30 -35 ] ...
... [
30 ]
Boltzmann's constant, k b 1.38 × 10-23 J·K-1 Burgers vector modulus, b 0.25 × 10-9 m [30 ] Mobility of free grain boundary, M f r e e g b 9 × 10 - 8 e x p ( - 1.99 × 10 - 19 k b T ) m4 ·J-1 ·s-1 [31 ] Mobility of free sub-grain boundary, M f r e e s u b 0.2M f r e e g b m4 ·J-1 ·s-1 [23 ] Grain boundary width, δ gb 1 × 10-9 m [26 ] Sub-grain boundary width, δ sub δ gb m This work Number of atoms per unit volume, N V 8.45 × 1028 m-3 Binding energy of Sb to sub-grain boundary, E s e g s u b -0.43 eV [32 ,33 ] Binding energy of Sb to grain boundary, E s e g g b -0.67 eV [34 ] Sb bulk diffusion coefficient, D B 1.3 × 10 - 5 e x p ( - 3.37 × 10 - 19 k b T ) m2 ·s-1 [35 ] Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work <strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
... [
30 ]
Mobility of free grain boundary, M f r e e g b 9 × 10 - 8 e x p ( - 1.99 × 10 - 19 k b T ) m4 ·J-1 ·s-1 [31 ] Mobility of free sub-grain boundary, M f r e e s u b 0.2M f r e e g b m4 ·J-1 ·s-1 [23 ] Grain boundary width, δ gb 1 × 10-9 m [26 ] Sub-grain boundary width, δ sub δ gb m This work Number of atoms per unit volume, N V 8.45 × 1028 m-3 Binding energy of Sb to sub-grain boundary, E s e g s u b -0.43 eV [32 ,33 ] Binding energy of Sb to grain boundary, E s e g g b -0.67 eV [34 ] Sb bulk diffusion coefficient, D B 1.3 × 10 - 5 e x p ( - 3.37 × 10 - 19 k b T ) m2 ·s-1 [35 ] Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work <strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
... 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
Modelling the evolution of recrystallization texture for a non-grain oriented electrical steel
1
2018
... List of parameters for simulating recrystallization behavior of Fe-3%Si alloy
[23 ,26 ,30 -35 ] Table 1 Parameter Value Unit Ref. Temperature, T 1123 K Shear modulus, G 87.88 - 0.02467T GPa [30 ] Boltzmann's constant, k b 1.38 × 10-23 J·K-1 Burgers vector modulus, b 0.25 × 10-9 m [30 ] Mobility of free grain boundary, M f r e e g b 9 × 10 - 8 e x p ( - 1.99 × 10 - 19 k b T ) m4 ·J-1 ·s-1 [31 ] Mobility of free sub-grain boundary, M f r e e s u b 0.2M f r e e g b m4 ·J-1 ·s-1 [23 ] Grain boundary width, δ gb 1 × 10-9 m [26 ] Sub-grain boundary width, δ sub δ gb m This work Number of atoms per unit volume, N V 8.45 × 1028 m-3 Binding energy of Sb to sub-grain boundary, E s e g s u b -0.43 eV [32 ,33 ] Binding energy of Sb to grain boundary, E s e g g b -0.67 eV [34 ] Sb bulk diffusion coefficient, D B 1.3 × 10 - 5 e x p ( - 3.37 × 10 - 19 k b T ) m2 ·s-1 [35 ] Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work
<strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
A multi-scale study of the interaction of Sn solutes with dislocations during static recovery in α -Fe
1
2019
... List of parameters for simulating recrystallization behavior of Fe-3%Si alloy
[23 ,26 ,30 -35 ] Table 1 Parameter Value Unit Ref. Temperature, T 1123 K Shear modulus, G 87.88 - 0.02467T GPa [30 ] Boltzmann's constant, k b 1.38 × 10-23 J·K-1 Burgers vector modulus, b 0.25 × 10-9 m [30 ] Mobility of free grain boundary, M f r e e g b 9 × 10 - 8 e x p ( - 1.99 × 10 - 19 k b T ) m4 ·J-1 ·s-1 [31 ] Mobility of free sub-grain boundary, M f r e e s u b 0.2M f r e e g b m4 ·J-1 ·s-1 [23 ] Grain boundary width, δ gb 1 × 10-9 m [26 ] Sub-grain boundary width, δ sub δ gb m This work Number of atoms per unit volume, N V 8.45 × 1028 m-3 Binding energy of Sb to sub-grain boundary, E s e g s u b -0.43 eV [32 ,33 ] Binding energy of Sb to grain boundary, E s e g g b -0.67 eV [34 ] Sb bulk diffusion coefficient, D B 1.3 × 10 - 5 e x p ( - 3.37 × 10 - 19 k b T ) m2 ·s-1 [35 ] Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work
<strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
Determination of impurity-point defect binding energies in alloys
1
1996
... List of parameters for simulating recrystallization behavior of Fe-3%Si alloy
[23 ,26 ,30 -35 ] Table 1 Parameter Value Unit Ref. Temperature, T 1123 K Shear modulus, G 87.88 - 0.02467T GPa [30 ] Boltzmann's constant, k b 1.38 × 10-23 J·K-1 Burgers vector modulus, b 0.25 × 10-9 m [30 ] Mobility of free grain boundary, M f r e e g b 9 × 10 - 8 e x p ( - 1.99 × 10 - 19 k b T ) m4 ·J-1 ·s-1 [31 ] Mobility of free sub-grain boundary, M f r e e s u b 0.2M f r e e g b m4 ·J-1 ·s-1 [23 ] Grain boundary width, δ gb 1 × 10-9 m [26 ] Sub-grain boundary width, δ sub δ gb m This work Number of atoms per unit volume, N V 8.45 × 1028 m-3 Binding energy of Sb to sub-grain boundary, E s e g s u b -0.43 eV [32 ,33 ] Binding energy of Sb to grain boundary, E s e g g b -0.67 eV [34 ] Sb bulk diffusion coefficient, D B 1.3 × 10 - 5 e x p ( - 3.37 × 10 - 19 k b T ) m2 ·s-1 [35 ] Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work
<strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
Grain boundary segregation of antimony in α -iron: Prediction and experimental data
1
2004
... List of parameters for simulating recrystallization behavior of Fe-3%Si alloy
[23 ,26 ,30 -35 ] Table 1 Parameter Value Unit Ref. Temperature, T 1123 K Shear modulus, G 87.88 - 0.02467T GPa [30 ] Boltzmann's constant, k b 1.38 × 10-23 J·K-1 Burgers vector modulus, b 0.25 × 10-9 m [30 ] Mobility of free grain boundary, M f r e e g b 9 × 10 - 8 e x p ( - 1.99 × 10 - 19 k b T ) m4 ·J-1 ·s-1 [31 ] Mobility of free sub-grain boundary, M f r e e s u b 0.2M f r e e g b m4 ·J-1 ·s-1 [23 ] Grain boundary width, δ gb 1 × 10-9 m [26 ] Sub-grain boundary width, δ sub δ gb m This work Number of atoms per unit volume, N V 8.45 × 1028 m-3 Binding energy of Sb to sub-grain boundary, E s e g s u b -0.43 eV [32 ,33 ] Binding energy of Sb to grain boundary, E s e g g b -0.67 eV [34 ] Sb bulk diffusion coefficient, D B 1.3 × 10 - 5 e x p ( - 3.37 × 10 - 19 k b T ) m2 ·s-1 [35 ] Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work
<strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
Sb diffusion in α -Fe
5
2005
... 针对图5 中γ 再结晶晶粒入侵A1 区域和A2 区域内α 形变晶粒的行为进行了模拟计算.计算采用时间循环迭代方式进行,记录并更新每个时间步的晶核数量和晶粒尺寸,时间步长dt 需保证每步计算的再结晶分数增量小于1%,以减小误差.A1 区域内的α 形变晶粒两侧均与γ 晶粒毗邻,A2 区域内的α 形变晶粒可以拆分为两侧均与γ 晶粒毗邻和单侧与γ 晶粒毗邻的混合.γ 和α 形变晶粒位错密度取自图4 的实测值,A1 和A2 区域α 晶粒的平均厚度h 分别为45和35 μm,偏析元素含量C 0 分别为0和0.04%.α -Fe晶界能为(1.11 ± 0.209) J/m2 [29 ] ,计算所需其他参数见表1 [23 ,26 ,30 ~35 ] .计算求得A1 和A2 区域内的γ 再结晶晶粒占比分别为0.77~0.58和0.39~0.16,实测值0.59和0.27处于相应区间内.本工作建模过程忽略了偏析元素对界面能的影响,而理论上微量晶界偏析元素倾向使界面能有所降低,这可能导致稍许高估偏析干预效果.因此,计算与实测符合良好,表明构建的模型可以描述偏析干预下毗邻织构组分竞争关系.在4.2~4.4节中,取α -Fe平均晶界能1.11 J/m2 进行相关计算. ...
... Fe-3%Si合金再结晶行为模拟用参数[23 ,26 ,30 ~35 ] ...
... List of parameters for simulating recrystallization behavior of Fe-3%Si alloy[23 ,26 ,30 -35 ] ...
... [
35 ]
Sb cross grain boundary diffusion coefficient, D C g b 2D B m2 ·s-1 [26 ] Sb cross sub-grain boundary diffusion coefficient, D C s u b D C g b m2 ·s-1 This work <strong>4.2</strong> 临界入侵半径对偏析干预效果的影响 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...
... 为探讨R c 对偏析干预效果的影响,模拟计算了不同R c 下γ 再结晶晶粒对α 形变晶粒的入侵行为.γ 和α 形变晶粒位错密度取自图4 的统计结果,其他参数与表1 [23 ,26 ,30 ~35 ] 相同.图8 给出了X γ α / γ R c 的变化.可见,不论是否含有晶界偏析元素,X γ α / γ R c 的增大持续下降,含Sb和无Sb下入侵行为被完全禁止的R c 分别为8.5和10.5 μm.晶界偏析元素对入侵行为的抑制效果,用α 形变晶粒内γ 再结晶晶粒体积分数的差值 (ΔX γ α / γ ) 衡量.偏析干预效果随R c 的增大先增强后减弱,在R c = 5 μm时达到峰值.R c 较小时,γ 再结晶晶粒长大至R c 的过程主导入侵行为,随R c 增大晶界偏析元素对入侵前γ 再结晶晶粒长大过程的抑制越充分,偏析干预越强.R c 高于峰值时,α 形变晶粒的再结晶形核和长大主导γ 再结晶晶粒的入侵行为,随R c 增大α 形变晶粒再结晶形核和长大越充分,可供γ 再结晶晶粒入侵的晶界面积减小,偏析干预减弱. ...