最新录用 | 当期目录 | 过刊浏览 | 热点文章 | 虚拟专辑 | 阅读排行 | 下载排行 | 引用排行 | 期刊订阅

金属学报, 2020, 56(7): 1047-1056 DOI: 10.11900/0412.1961.2019.00344

铝电解槽中局部阴极电流增大对电解质-铝液两相流场的影响

王富强1,2, 刘伟2, 王兆文,1

1.东北大学冶金学院 沈阳 110819

2.沈阳铝镁设计研究院有限公司 沈阳 110001

Effect of Local Cathode Current Increasing on Bath-Metal Two-Phase Flow Field in Aluminum Reduction Cells

WANG Fuqiang1,2, LIU Wei2, WANG Zhaowen,1

1. School of Metallurgy, Northeastern University, Shenyang 110819, China

2. Shenyang Aluminum and Magnesium Engineering and Research Institute Co. , Ltd. , Shenyang 110001, China

通讯作者: 王兆文，zhaowenw@mail.neu.edu.cn，主要从事熔盐电解理论及应用的研究

责任编辑: 肖素紅

收稿日期: 2019-10-15   修回日期: 2020-05-06   网络出版日期: 2020-07-11

基金资助: 国家自然科学基金项目.  51434005
国家自然科学基金项目.  51529401

Corresponding authors: WANG Zhaowen, professor, Tel: (024)83686464, E-mail:zhaowenw@mail.neu.edu.cn

Received: 2019-10-15   Revised: 2020-05-06   Online: 2020-07-11

Fund supported: National Natural Science Foundation of China.  51434005
National Natural Science Foundation of China.  51529401

作者简介 About authors

王富强，男，1981年生，教授级高级工程师，博士生

摘要

采用数值模拟方法建立了三维非稳态电解质-铝液两相流500 kA全槽模型，并通过铝液流速和电解质/铝液的界面变形测试数据验证了模型的准确性。在此基础上模拟并定量评估了6种实际电解生产中存在的局部阴极电流增大60%对铝液流场和界面变形产生的影响程度。结果表明，局部阴极电流增大并不能改变全槽的铝液流场和界面变形的整体趋势，只是局部位置的铝液流速和界面变形幅度略有差异，其中A2A3阴极电流增大有利于抑制B侧中部的界面隆起，极距平均改善幅度为3.0%。分别通过增大电解槽两端部，中部和A、B两侧的部分阴极电流比例对比分析了两相流场变化规律。结果表明，适当增加电解槽两端部的阴极电流有利于抑制界面变形，尤其是A1~A4和A21~A34阴极电流增加28%可将界面隆起最大值降低2.4 mm，B7~B18的极距平均拉高9.5%。该研究为母线优化和改善电解槽磁流体稳定性提供了一条新思路。

关键词： 铝电解槽 ; 两相流场 ; 局部阴极电流增大 ; 界面变形 ; 数值模拟 ; 优化

Abstract

The stability of the magnetohydrodynamics (MHD) of aluminum reduction cell is determined by the bath-metal two-phase flow field. So, konwing how to optimize the metal flow field and restrain the bath/metal interface deformation is the key to maintain the stable and efficient operation of cell. Many previous works on the bath-metal flow field are based on the static electromagnetic force stirring the melt, however, it should be have some deviation from the actual cell state. A three dimensional bath-metal two-phase quasi-steady flow model (based on transient electromagnetic force) for full 500 kA aluminum reduction cell was built by means of numerical simulation in this work, and validated by metal velocity and bath/metal interface deformation measurement in industrial cells. The effects of 60% increase of local cathode current on melt flow distribution and interface deformation were simulated and evaluated according to abnormal 6 cases in realistic electrolytic process. It was found that the increase of local cathode current has little effects on the general pattern of flow field and interface deformation in cell, but the amplitude of local metal velocity and interface deformation would be changed in certain extent. The increase of local cathode current in A2~A3 could decrease the interface height in middle cell of downstream side (side B), with anode cathode distance (ACD) increasing by 3.0%. But the other 5 cases could deteriorate the low ACD zone further in side B, especially the increase of local cathode current in A10A11, with average ACD decreasing by 4.6% in B12~B20. The solution is to cut cathode flexes partially in abnormal position to decrease the effect on the bath-metal two-phase flow. According to the evaluation results, it is found that the uneven distribution of cathode current may be helpful to decrease the interface deformation and improve the MHD stability of cell. Based on this finding, the bath-metal two-phase flow field was changed by increasing the proportion of cathode current at the two ends of cell, the middle part of cell and side A and side B respectively, and then was analyzed in this work. The simulation results show that it is beneficial to restrain the interface deformation by increasing the cathode current at both ends of cell properly, and it is also helpful to solve the cooling problem at cell ends. In particular, when the cathode currents at A1~A4 and A21~A24 increase by 28%, the distribution trend of melt flow field remains unchanged basically, and the maximum of metal velocity under A19~A20 increases by 10%, and the maximum of interface height decreases by 2.4 mm, and the average of ACD under B7~B18 increases by 9.5%. It provides a valuable reference for optimizing the busbar design and improving the cell MHD stability.

Keywords： aluminum reduction cell ; two-phase flow field ; local cathode current increase ; interface deformation ; numerical simulation ; optimization

PDF (2520KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王富强, 刘伟, 王兆文. 铝电解槽中局部阴极电流增大对电解质-铝液两相流场的影响. 金属学报[J], 2020, 56(7): 1047-1056 DOI:10.11900/0412.1961.2019.00344

WANG Fuqiang, LIU Wei, WANG Zhaowen. Effect of Local Cathode Current Increasing on Bath-Metal Two-Phase Flow Field in Aluminum Reduction Cells. Acta Metallurgica Sinica[J], 2020, 56(7): 1047-1056 DOI:10.11900/0412.1961.2019.00344

众所周知，铝液高速流动和电解质-铝液界面变形直接关系到铝电解槽内磁流体的稳定程度，是决定槽电压、电流效率、能耗和槽寿命的关键因素之一[1]。在电解生产中经常出现局部阴极电流异常的情况，可能会对电解质-铝液的两相流场产生不利影响，而铝厂普遍缺乏可靠的技术手段来综合评估电解槽磁流体稳定性变化的程度，进而无法制定合理的应对措施，以致影响电流效率、能耗等各项技术指标。

受制于工业实验的成本高、周期长等缺点，国内外电解铝行业的学者大多采用数值模拟技术研究铝电解槽的各类物理场问题。早期学者们基于Navier-Stokes方程提出了多种简化理论[2,3]，用以近似模拟电磁场作用下电解质和铝液的二维单相稳态流场[4,5]，例如熔体区的3个分区思想[6]、浅水模型[7,8,9]等，对界面形状的模拟则根据简单的静力平衡和界面处压强连续原理[5]进行计算。随着计算机软件和硬件的快速发展，越来越多的学者利用数值模拟软件来研究铝电解槽的两相流动问题，例如ESTER/PHOENICS[10,11]、MHD-Valdis[12,13]、CFX[14,15,16,17,18,19]和Fluent[20,21,22,23,24,25,26]等。在流场模型建立过程中，常用的方法是将静态磁场和静态电场先耦合成静态电磁力，然后再将其导入磁流体(magnetohydrodynamics，MHD)模型中作为动量源项搅拌熔液[16,17,18,19,20,21]，采用标准k-ε湍流模型(k为湍动能，m2/s2；ε为湍流耗散率，m2/s3)来计算电解质和铝液的流动问题[15,16,17,18,19,20,21,22,23,24,25,26]，基于电解质和铝液密度存在差异而互不相溶的特点采用界面追踪法(volume of fluid，VOF)来模拟电解质/铝液的界面变形问题[16,17,18,19,20,21,22,23,24,25,26]。然而，在实际的电解生产过程中，由于铝液流动产生的电解质/铝液界面变形会使各阳极下的极距(anode cathode distance，ACD)时刻变化，进而产生了动态电场和动态电磁力[26]，这与许多模型中设置的静态磁场耦合静态电场产生的静态电磁力必然存在一定偏差。在数学模型的验证方面，大部分研究主要测量铝液流场[15,16,17,18,27]，但对界面变形模拟结果的测试验证鲜见报道。就数学模型的工业应用方面，李宝宽课题组[20,21,23]和Dupuis等[13,28]对平底阴极和异型阴极的两相流场进行了对比，但只是从模拟结果上比较了二者在铝液流速和界面变形上的区别。Bojarevics等[12]研究了A4阴极钢棒不导电(切断)对磁流体稳定性的影响，但并未给出解决方案，对实际电解生产的指导意义有限。

本工作搭建了500 kA铝电解槽三维非稳态电解质-铝液两相流全槽模型，通过静态磁场耦合动态电场形成动态电磁力计算电解槽内电解质-铝液的两相流场，并在500 kA工业槽上测试铝液流速和界面变形数据，验证了数学模型的准确性；针对电解生产中存在的局部阴极电流偏大的现象进行数值模拟，量化了其对两相流场的影响，并提出了应对措施，同时也对如何改善异常槽况下的磁流体稳定性提供了一条解决思路。

1 模型简述

1.1 物理模型及物性参数

以500 kA铝电解槽为研究对象，选取电解质、铝液、阴极炭块和阴极钢棒为计算域，全槽共48块单阳极、24组阴极，其中ACD为0.045 m，电解质高度0.18 m，铝液高度0.24 m。其中，电解槽的A (side A)、B (side B)两侧，烟道端(duct end，DE)和出铝端(tapping end，TE)均依据炉帮形状设置；水平轴X和Y的原点取在电解槽的中心位置，Z轴原点位于铝液的上表面。物性参数及物理模型分别见表1和图1。

表1   物性参数

Table 1  Material properties

Material

Density

kg·m-3

Viscosity

Pa·s

Conductivity

S·m-1

Bath2.13×1032.51×10-30.23×103
Metal2.30×1031.18×10-34.17×106

新窗口打开| 下载CSV


图1

新窗口打开| 下载原图ZIP| 生成PPT

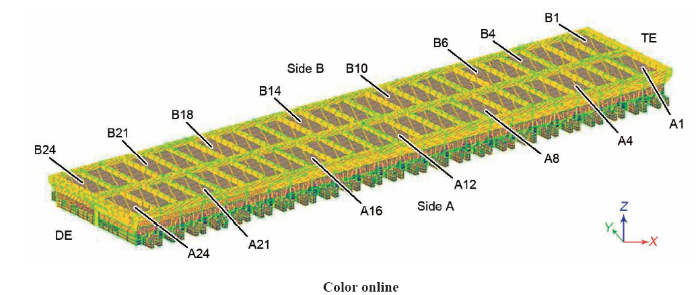
图1   电解质-铝液两相流物理模型

Fig.1   Bath-metal two-phase flow physical model (TE—tapping end, DE—duct end)


由于气泡主要影响阳极区域的电解质流场，与电解质中的Al2O3扩散及浓度分布直接相关，对铝液流场和界面变形影响较小[29]，因此，本工作将重点研究动态电磁力这一影响铝液流场和界面变形的主要因素，暂不考虑阳极气泡的作用。

1.2 数学模型

1.2.1 两相流VOF模型

在电解槽中，由于电解质和铝液密度差较大且互不掺混，呈自然分层状态，因此选用VOF模型模拟计算域内的各相体积分数，跟踪界面形状。

连续性方程：

∂∂tαbρb+∇·αbρbub=0
(1)
∂∂tαmρm+∇·αmρmum=0
(2)
αb+αm=1
(3)

式中，t为时间，s；α、ρ和u分别为体积分数(%)、密度(kg/m3)和速度(m/s)；下标b和m分别代表电解质相和铝液相。

动量方程：

∂∂tρu+∇·ρuu=-∇P+∇·μ∇u+∇uT+ρg+F
(4)
ρ=αbρb+αmρm
(5)
μ=αbμb+αmμm
(6)

式中，μ为黏度，kg/(m·s)；P为压力，Pa；g为重力加速度，m/s2；F为力的源项，N/m3。

根据电解质与铝液之间的表面张力系数计算得出Weber数We范围为0.001~0.06，远小于1，因此在模拟计算中还应考虑界面张力的影响。

1.2.2 湍流模型

估算Reynolds数Re约为5728，属于湍流，故选用标准k-ε模型，分别求解湍动能和湍流耗散率。其控制方程为：

αqρq∂k∂t+uq·∇k=∇·αqμtσk∇k+αqGk-αqρqε+Sk
(7)
αqρq∂ε∂t+uq·∇ε=∇·αqμtσε∇ε+αqC1εεkGk-αqC2ερqε2k+Sε
(8)

式中，下标q表示电解质相b或铝液相m；μt为有效湍流黏度，kg/(m·s)；Gk为平均速度梯度引起的湍动能，kg/(m·s3)；Sk为湍动能的源项，kg/(m·s3)；Sε为湍动能耗散率的源项，kg/(m·s3)；σk和σε分别为k和ε的Prandtl数Pr；C1ε和C2ε均为常数，分别为1.44和1.92。

1.2.3 磁流体MHD模型

先根据母线配置计算出静态磁场并导入MHD模块中；动态的电场随着电解质和铝液流动、界面形状波动而相应变化，由MHD模块自动计算。由于电解槽中的电解质和铝液流速不高，熔体流动引起的感应电流强度和磁感应强度可忽略[30]，因此，根据Maxwell方程，静态磁场耦合动态电场形成动态电磁力的计算过程可简化为：

j=σE
(9)
f=j×B
(10)

式中，j为电流密度，A/m2；σ为电导率，S/m；E为电场强度，V/m；B为磁通密度，T；f为电磁力，N。

1.3 边界条件

在阳极底部输入电流密度，阴极钢棒截面设置为零电势。电解质上表面为自由边界，阳极侧面、炉膛及阴极炭块表面均设置为无滑移壁面。

2 正常槽况下电解质-铝液两相流场模拟及验证

2.1 电解质-铝液两相流场模拟

正常槽况下分别取铝液中心层流速分布和电解质/铝液界面变形来分析电解质-铝液的两相流场的运动规律，分别如图2和3所示。界面变形范围见表2。可以看出，铝液中心层的流速最大值0.19 m/s，整个流场分成2个对称大漩涡，其中TE侧为顺时针漩涡，DE侧为逆时针，且DE侧的流速和漩涡范围均略大于TE侧；B侧2个角部(B1和B24)还存在局部反向小漩涡，但影响区域仅限于角极。界面隆起区域主要集中在B侧中部(B7~B18)，然后分别朝两端和A侧逐渐降低，界面隆起最大值0.031 m；界面凹陷区域主要集中在A侧中部和B侧的2个角部，尤以B24角部凹陷最明显，界面凹陷最大值0.047 m。由表2可知，统计界面变形范围基本符合正态分布，全槽97.7%区域的界面变形介于±0.03 m之内，界面隆起超过0.03 m的区域仅占0.1%，界面凹陷低于0.03 m的仅占2.2%。

图2

新窗口打开| 下载原图ZIP| 生成PPT

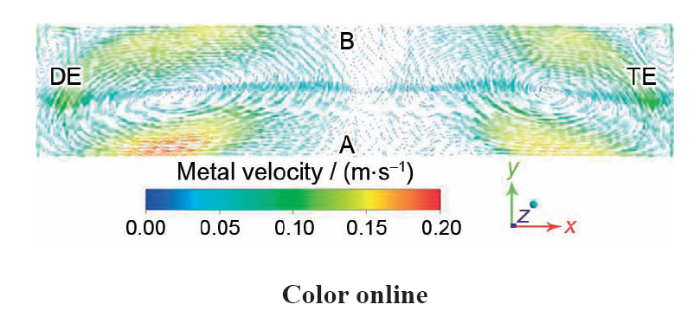
图2   正常槽况下铝液流速分布模拟结果

Fig.2   Simulated metal velocity distribution of normal state


表2   正常槽况下界面变形范围分布

Table 2  Interface deformation range distribution of normal state

Range / mRatio / %
-0.05~-0.040.3
-0.04~-0.032.0
-0.03~-0.027.0
-0.02~-0.0121.8
-0.01~08.4
0~0.0123.9
0.01~0.0223.8
0.02~0.0312.8
0.03~0.040.1

新窗口打开| 下载CSV


由上述分析可知，B侧中部界面隆起显著，易出现极距偏低的情况，因此，如何抑制该区域的界面隆起是改善电解槽磁流体稳定性的主要方向。

2.2 电解质-铝液两相流场结果验证

根据上述模拟结果制定测试方案，采用铁棒溶蚀法[31]对正常槽况下的铝液层中心流速进行测试，并测量多点铝液高度来计算电解质/铝液界面变形，以验证两相流场模拟结果的准确性。铝液流速测点位置及测点的流速方向见图4，铝液流场及界面变形的模拟值与测试值对比分别见图5和6。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   正常槽况下电解质/铝液界面变形模拟结果

Fig.3   Simulated bath/metal interface deformation of normal state


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   铝液流速测点位置及流速方向

Fig.4   Positions of metal velocity measure points and flow direction


图5

新窗口打开| 下载原图ZIP| 生成PPT

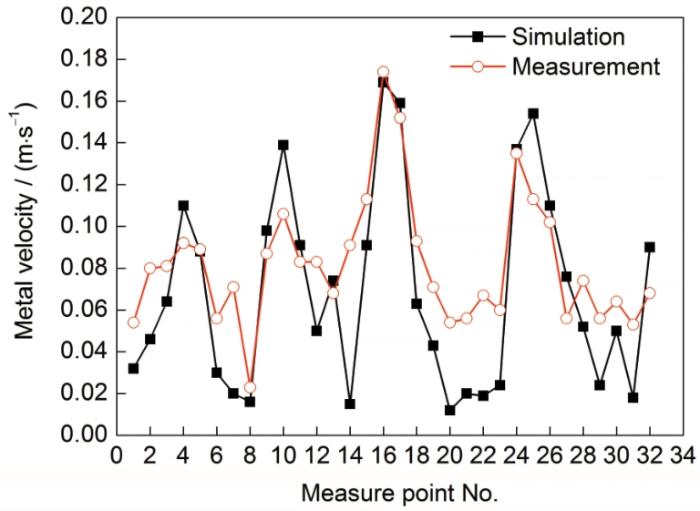
图5   铝液流速模拟值与测试值对比

Fig.5   Comparisons between simulation and measurement metal velocity


从图5可以看出，在铝液流速测试中，全槽共选取32个测点。测量铝液流速最大值0.174 m/s，位于A21~A22阳极之间(测点16)，对应测点位置的模拟值为0.170 m/s，偏差约3%；各测点的流速测试平均值0.082 m/s，与相应位置的模拟平均值0.068 m/s接近；且各测点的流速方向与模拟值相同，测试所得流场整体呈现出2个对称大漩涡，与模拟的流场分布趋势一致。

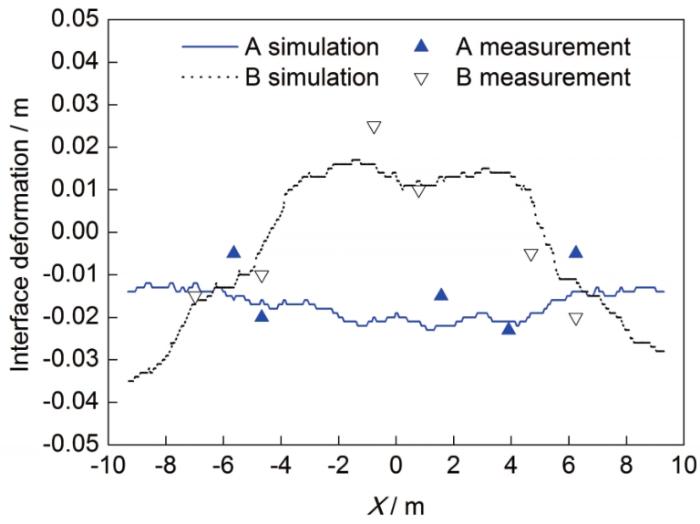
界面变形的测点位于阳极间缝，与(靠近A、B两侧大面)第一根阳极钢爪平齐，多点测量铝液高度，测量值取平均后计算得到各测点电解质/铝液的界面变形。测量结果显示，B侧中部的界面变形明显高于A侧和端部，且变化趋势与模拟结果较吻合(图6)。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   界面变形的模拟值与测试值对比

Fig.6   Comparisons between simulation and measurement interface deformation


由上述对比分析可知，铝液流场和界面变形的测试结果均与模拟结果相吻合，说明本次研究选用的数学模型正确，计算结果真实可靠。

3 局部阴极电流增大对电解质-铝液两相流场的影响

在上述已验证模型基础上，可以适当改变边界条件，以考察两相流场的变化规律，为量化各类异常槽况对电解槽磁流体稳定性的影响和寻求解决办法提供技术支持。例如，个别阴极钢棒温度偏高，阴极电流偏大(个别偏大幅度>40%)，尤其以A侧居多；此种现象对电解槽磁流体稳定性的影响程度一直缺乏定量评估，也缺乏合理的解决方案，往往选择直接割断异常位置处的阴极软带，给异常槽后续的平稳生产带来较大困难。

针对这一现场问题，本次研究假设A侧6根立柱母线下对应的A2A3、A6A7、A10A11、A14A15、A18A19和A22A23阴极电流分别增大60%，以考察其对两相流场的影响程度。6种异常槽况的铝液流速和界面变形模拟结果见表3和图7 (图中方框即为阴极电流增大位置)。

表3   6种不同槽况下两相流场的模拟结果对比

Table 3  Comparisons of two-phase flow field simulations for 6 cases after increasing the local cathode current by 60%

CaseLocationMetal velocity / (m·s-1)Interface deformation / m
Max.Aver.Min.Max.
1A2A30.2150.064-0.0460.031
2A6A70.1840.068-0.0450.032
3A10A110.1840.072-0.0530.032
4A14A150.1790.071-0.0540.031
5A18A190.1990.067-0.0440.031
6A22A230.2060.067-0.0470.031

新窗口打开| 下载CSV


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   局部阴极电流增大后的两相流场模拟结果

Fig.7   Simulated two-phase flow fields after increasing the local cathode current for case 1 (a1, b1), case 2 (a2, b2), case 3 (a3, b3), case 4 (a4, b4), case 5 (a5, b5), case 6 (a6, b6) (The current increase locations are shown in square frames)

(a1~a6) metal velocity (b1~b6) interface deformation


以正常槽况下每块阳极下的极距为基准，6种异常槽况下A、B两侧每块对应阳极下的极距变化幅度见图8。极距变化幅度计算公式如下：

ACD_Ri=ACD_CiACD_Ni×100%
(11)

式中，i为阳极编号，全槽分A、B两侧，共48块阳极；ACD_Ri为第i块阳极下的极距变化幅度，%；ACD_Ni为正常槽况下第i块阳极下的极距，m；ACD_Ci为异常槽况算例下对应第i块阳极下的极距，m。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   A侧和B侧极距(ACD)变化幅度

Fig.8   Anode cathode distance (ACD) changement ratios at side A (a) and side B (b)


从图7a1和b1可以看出，A2A3阴极电流增大后，A3A4处靠近A侧的铝液流速明显增大，而B2~B4的高流速区域面积减小。A1A2、A8~A17界面上升，极距略有降低；A3~A7、A19~A24界面凹陷加剧，极距相应增大，见图8a。B1~B3和B20处界面上升，其中B1B2极距降幅达11.6%；B21~B24界面小幅回落，极距平均增幅1.9%；B5~B19界面高度显著降低，极距平均增幅3.0% (图8b)，电解槽B侧中部极距偏低的趋势有所改善。

从图7a2和b2可知，A6A7阴极电流增大后，A6~A8处的铝液流速略有增大，且高流速区域扩大。A5~A8处界面凹陷加剧(极距最大增幅达12%)；A10~A17界面上升，极距平均降幅3.5%，见图8a。B7~B11的界面小幅回落，极距平均增幅2.4%；B12~B20界面隆起加剧，极距平均降幅3.1%，其中B18最低降幅达7% (图8b)，B侧中部极距呈轻微恶化的趋势。

如图7a3和b3所示，A10A11阴极电流增大后，正对A10A11处的槽中心位置铝液流速显著增大，可能与该位置流速原本偏低有直接关系。A9~A12界面凹陷加剧，极距最大降幅达14.8%；A1~A3、A21~A24的界面凹陷略有加剧趋势，而A5~A8、A13~A20的界面略有上升，见图8a。B8~B11界面显著回落，极距最大增幅达10.2%；但B4~B7、B12~B20界面隆起加剧，极距平均降幅4.1% (图8b)，B侧中部界面隆起偏大的趋势进一步恶化。

从图7a4和b4中可知，A14A15阴极电流增大后，A14A15处及槽中心位置的铝液流速明显增大。A11~A16界面凹陷加剧，极距最大降幅达15.7%；A1~A4、A22~A24的界面高度小幅降低，A5~A10、A17~A21的界面上升(A8和A18极距最高降幅达6.2%)，见图8a。B10B11、B14~B17界面显著回落，极距上升，(B10)极距最高升幅达6.4%；但B1~B8、B12B13、B18~B23界面隆起加剧，极距平均降幅2.8%，其中B6和B20最大降幅达7.2% (图8b)，磁流体稳定性减弱。

如图7a5和b5所示，A18A19阴极电流增大后，A18A19处靠A侧的铝液流速略有增大。A15~A19界面凹陷加剧，极距最大降幅达13.8%；A6~A10、A20~A24的界面上升(A21极距最高降幅达6.1%)，见图8a。B14~B17界面显著回落，极距上升，(B17)极距最高升幅达8.9%；但B4~B13、B19~B23界面隆起加剧，其中B20极距最大降幅达9.7% (图8b)，磁流体稳定性降低。

从图7a6和b6可以看出，A22A23阴极电流增大后，A19~A21处靠A侧的铝液流速略增大。A1~A5、A17~A21的界面进一步凹陷，极距相应增大；A8~A10、A22~A24的界面升高，极距减小，尤其在DE侧最为明显(A24极距降幅达8.3%)，见图8a。B14~B19界面显著回落，极距增大，其中B17极距增幅达7.4%；但B6~B8、B10~B13、B20~B24的界面继续上升，极距相应降低，其中B11~B14平均极距降幅2.6%，B22极距降幅最高达6.5%，见图8b。因此，B侧中部极距偏低的趋势略有加剧。

由上述分析可知，局部位置的阴极电流增大60%不会影响铝液流速和界面变形的整体趋势，但会改变局部位置的铝液流速和界面变形。其中A2A3的阴极电流增大反而对B侧中部极距偏低的趋势有一定改善作用，但其余5处局部阴极电流增大都会恶化电解槽的磁流体稳定性。造成这一反差的原因应该与全槽流场和界面变形整体分布有关，与邻列对电解槽TE侧磁场影响最小也有一定关系。

针对A2A3阴极电流增大的情况，应密切关注原铝中的Fe、Si含量是否异常，换极时要探摸该区域的阴极炭块表面是否出现破损，持续跟踪钢棒温度和熔体区槽壳温度；若电流无继续增大趋势，Fe、Si含量正常，且阴极炭块表面无破损，建议密切关注，暂不处理。对于其它5种局部阴极电流增大的情况，也应密切关注槽况，并适当割断部分阴极软带以减少该处电流量；割断阴极软带的数量必须通过两相流场的复核计算来确定，应随着所处位置不同、对两相流场影响程度的大小而各异。

4 电解质-铝液两相流场的优化

由上述异常槽况的分析可知，A侧局部(A2A3)阴极钢棒电流偏大反而有利于抑制B侧中部界面隆起。因此，不均匀的阴极电流分布有可能是改善电解槽磁流体稳定性的有效途径。针对这一发现，本工作分别增大电解槽两端部，中部以及A、B两侧的部分阴极钢棒电流，对比分析两相流场的变化规律和极距的改善程度，为提高电解槽磁流体稳定性指明优化方向。表4列出了9个对比算例的两相流场模拟结果，各算例的B侧极距变化幅度见图9，部分算例的铝液流速和界面变形模拟结果见图10。

表4   9种对比槽况下两相流场的模拟结果汇总

Table 4  Summary of two-phase flow field simulation results for 9 cases used to compare

CaseLocationCurrent increaseMetal velocity / (m·s-1)Interface deformation / m
%Max.Aver.Min.Max.
11AB: 1~4, 21~24①100.2010.065-0.0450.030
12AB: 1~4, 21~24200.2090.064-0.0530.029
13AB: 5~20②50.1770.067-0.0440.032
14B: 1~4, 21~24③140.1910.067-0.0490.031
15B: 1~4, 21~24280.1960.067-0.0560.030
16B: 1~4, 21~24420.1970.067-0.0610.030
17A: 1~4, 21~24④140.1970.065-0.0440.029
18A: 1~4, 21~24280.2070.063-0.0410.029
19A: 1~4, 21~24420.2150.061-0.0410.030

Note: ① "AB: 1~4, 21~24" means that 10% increase of cathode current at A1~A4, A21~A24, B1~B4 and B21~B24; ② "AB: 5~20" means that 5% increase of cathode current at A5~A20 and B5~B20; ③ "B: 1~4, 21~24" means that 14% increase of cathode current at B1~B4 and B21~B24; ④ "A: 1~4, 21~24" means that 14% increase of cathode current at A1~A4 and A21~A24

新窗口打开| 下载CSV


图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   Case 11~case 19的B侧极距变化幅度

Fig.9   ACD changement ratios at side B for case 13~case 16 (a) and case 11, case 12, case 17~case 19 (b)


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   Case 11、case 12和case 17~case 19的两相流场模拟结果

Fig.10   Simulated two-phase flow fields for case 11 (a1, b1), case 12 (a2, b2), case 17 (a3, b3), case 18 (a4, b4), case 19 (a5, b5) (The current increase locations are shown in square frames) (a1~a5) metal velocity (b1~b5) interface deformation


由表4可知，算例case 11~case 13对比了分别增大电解槽两端部和中部的阴极钢棒电流对两相流场的影响。与正常槽况相比，case 13增大电解槽中部阴极(AB: 5~20)电流5%后，虽然界面最大凹陷深度减小，但最大隆起高度增加1 mm，且B侧(B13~B18)极距分布的均匀性显著恶化，极距(B16)最大降幅达6.5%，如图9a所示；再加上中部阴极电流增大，使得电解槽中部熔体区散热压力增大，而两端部更加趋冷，不利于全槽热场的均匀分布。

而case 11和case 12恰好相反，两端部阴极电流(AB: 1~4、21~24)分别增大10%和20%后，界面最大隆起高度分别减小1.4和1.8 mm，且B7~B18的极距略有增大，其平均增幅分别为5.1%和6.6%，详见图9b；与此同时，两端部阴极电流增大有利于提高电解槽两端部区域的发热量，弱化端部效应对电解槽热平衡差异性的影响，改善全槽热场分布的均匀性。因此，提高端部阴极的电流比例，有助于同时改善电解槽磁流体稳定性和热平衡均匀性。

Case 14~case16将电解槽B侧两端部的阴极电流比例分别提高到14%、28%和42%，发现界面最大凹陷深度显著增大，虽然界面最大隆起高度略有降低，但B侧的极距分布进一步恶化，具体表现在B4~B7和B16~B21处，且极距恶化程度随着阴极电流比例升高而加剧，如图9a所示。因此，增加B侧两端部的阴极电流会显著恶化电解槽磁流体的稳定性。

Case 17~case 19将电解槽A侧两端部的阴极电流比例分别提高到14%、28%和42%，发现界面最大凹陷深度分别减小3.0、5.5和6.1 mm，最大隆起高度分别降低2.0、2.4和1.6 mm，界面变形得到有效抑制；且B侧极距分布的均匀性显著改善，B7~B18的极距平均增幅分别为6.6%、9.5%和10.1%，如图9b所示。由此可知，电解槽磁流体稳定性随着A侧两端部阴极电流比例的增大而上升。

对比5个改善磁流体稳定性算例(case 11、case 12和case 17~case19)的模拟结果发现，电解槽两端部阴极电流增大，并不会改变两相流场的基本规律(图10)，只是局部铝液流速略有增大。通过对比可知，仅增大A侧两端部阴极电流(case 17~case 19)对抑制B7~B18界面隆起的效果更明显。尽管case 19中B7~B18极距平均增幅最大，但case 18中B7~B18的极距分布和增幅更均匀；case 19中A19A20处靠A侧边部的铝液流速增幅14%，界面隆起最大值降低1.6 mm，而case 18中相同位置的铝液流速增幅只有10%，界面隆起最大值降低2.4 mm；并且case 18中A1~A4和A21~A24阴极电流仅增大28%，有限的阴极电流增幅在不引起该区域阴极钢棒过热的情况下可显著提高电解槽两端部的热收入，有效改善电解槽热平衡分布的均匀性。由此可知，case 18改善电解槽磁流体稳定性和全槽热平衡均匀性的作用最明显。

5 结论

(1) 正常槽况下的铝液流场存在2个大漩涡，A侧流速略高于B侧；槽两端及A侧的电解质/铝液界面凹陷，B侧中部(B7~B18)界面隆起。铝液流速和界面变形测试数据表明，测试结果与两相流场模拟结果吻合度较好，证明了数学模型的可靠性。

(2) A侧的局部阴极电流增大60%不会改变电解质-铝液两相流场的整体趋势，但对局部位置的铝液流速和界面变形有一定程度的影响。其中A2A3阴极电流增大有利于抑制B侧中部的界面隆起，极距平均改善幅度为3.0%；A侧其它5处局部阴极电流增大都会进一步恶化B侧中部极距偏低的趋势，其中A10A11阴极电流增大后B12~B20平均极距降幅4.6%，应割断异常位置的部分阴极软带以再平衡区域阴极电流分布。

(3) 与均匀的阴极电流分布相比，适当增加电解槽两端部的阴极电流比例有助于抑制界面变形和解决电解槽端部易偏冷的问题，尤其是A侧A1~A4和A21~A34阴极电流增加28%可有效改善B7~B18 (界面隆起最大值降低2.4 mm，极距平均增幅9.6%)极距偏低的趋势。该发现对电解槽磁流体设计和优化具有一定的参考价值。

参考文献

Liu Y X, Li J, et al. Modern Aluminum Electrolysis [M]. Beijing: Metallurgical Industry Press, 2008: 338

[本文引用: 1]

(刘业翔, 李 劼等. 现代铝电解 [M]. 北京: 冶金工业出版社, 2008: 338)

[本文引用: 1]

Urata N, Arita Y, Ikeuchi H.

Magnetic field and flow pattern of liquid aluminum in the reduction cells

[A]. Light Metals [C]. Warrendale: Metallurgical Society of AIME, 1975: 233

[本文引用: 1]

Mori K, Shiota K, Urata N, et al.

Surface oscillation of liquid metal in aluminum reduction cells

[A]. Light Metals [C]. Warrendale: Metallurgical Society of AIME, 1976: 77

[本文引用: 1]

Arita Y, Ikeuchi H.

Numerical calculation of bath and metal convection patterns and their interface profile in Al reduction cells

[A]. Light Metals [C]. Warrendale: Metallurgical Society of AIME, 1981: 357

[本文引用: 1]

Tarapore E D.

Magnetic fields in aluminum reduction cells and their influence on metal pad circulation

[A]. Light Metals [C]. Warrendale: Metallurgical Society of AIME, 1979: 541

[本文引用: 2]

Ai D K.

The hydrodynamics of the hall-héroult cell an overview

[A]. Light Metals [C]. Warrendale: Metallurgical Society of AIME, 1985: 593

[本文引用: 1]

Moreau R, Evans J W.

An analysis of the hydrodynamics of aluminum reduction cells

[J]. J. Electrochem. Soc., 1984, 131: 2251

[本文引用: 1]

Moreau R J, Ziegler D.

The moreau-evans hydrodynamic model applied to actual hall-héroult cells

[J]. Metall. Trans., 1988, 19B: 737

[本文引用: 1]

Zikanov O, Thess A, Davidson P A, et al.

A new approach to numerical simulation of melt flows and interface instability in hall-héroult cells

[J]. Metall. Mater. Trans., 2000, 31B: 1541

[本文引用: 1]

Potočnik V, Laroche F.

Comparison of measured and calculated metal pad velocities for different prebake cell designs

[A]. Light Metals [C]. Warrendale: TMS, 2001: 419

[本文引用: 1]

Severo D S, Gusberti V, Schneider A F, et al.

Comparison of various methods for modeling the metal-bath interface

[A]. Light Metals [C]. Warrendale: TMS, 2008: 413

[本文引用: 1]

Bojarevics V, Sira S.

MHD stability for irregular and disturbed aluminium reduction cells

[A]. Light Metals [C]. Warrendale: TMS, 2014: 685

[本文引用: 2]

Dupuis M, Bojarevics V.

Influence of the cathode surface geometry on the metal pad current density

[A]. Light Metals [C]. Warrendale: TMS, 2014: 479

[本文引用: 2]

Severo D S, Schneider A F, Pinto E C V, et al.

Modeling magneto-hydrodynamics of aluminum electrolysis cells with ANSYS and CFX

[A]. Light Metals [C]. Warrendale: TMS, 2005: 475

[本文引用: 1]

Zhou P, Zhou N J, Mei C, et al.

Numerical calculation and industrial measurements of metal pad velocities in hall-héroult cells

[J]. Trans. Nonferrous Met. Soc. China, 2003, 13: 208

[本文引用: 3]

Li M, Zhou J M, Wang C H.

Coupled simulation of multiple physical fields in a 300 kA aluminum electrolysis cell

[J]. Chin. J. Process Eng., 2007, 7: 354

[本文引用: 5]

(李 茂, 周孑民, 王长宏.

300 kA铝电解槽电、磁、流多物理场耦合仿真

[J]. 过程工程学报, 2007, 7: 354)

[本文引用: 5]

Zhou J M, Li M, Jiang S J.

Two-phase simulation and its interface tracking of fluid flow in aluminum electrolysis cell

[J]. J. Cent. South Univ. (Sci. Technol.), 2007, 38: 267

[本文引用: 5]

(周孑民, 李 茂, 蒋胜矩.

铝电解槽磁流体的两相模拟及其界面追踪

[J]. 中南大学学报(自然科学版), 2007, 38: 267)

[本文引用: 5]

Liu W, Li J, Lai Y Q, et al.

Development and application of electro-magneto-flow mathematic model of aluminum reduction cells

[J]. Chin. J. Nonferrous Met., 2008, 18: 909

[本文引用: 5]

(刘 伟, 李 劼, 赖延清等.

铝电解槽电磁流场的数学建模与应用

[J]. 中国有色金属学报, 2008, 18: 909)

[本文引用: 5]

Xu Y J.

A study of multi-physical fields coupled modeling and structure optimization of large-scale energy-saving aluminum reduction cells

[D]. Changsha: Central South University, 2010

[本文引用: 4]

(徐宇杰.

铝电解槽内熔体运动数学建模及应用研究

[D]. 长沙: 中南大学, 2010)

[本文引用: 4]

He Z, Li B K, Wang F, et al.

Impact of the novel cathode convex on the electrolyte/aluminum interface wave in a reduction cell

[J]. J. Northeastern Univ. (Nat. Sci.), 2011, 32: 704

[本文引用: 5]

(贺 铸, 李宝宽, 王 芳等.

电解槽内异型凸台对电解质/铝液界面波动的影响

[J]. 东北大学学报(自然科学版), 2011, 32: 704)

[本文引用: 5]

He Z, Xia T, Xiong W, et al.

Mathematical models for the novel cathode convexes in a reduction cell

[J]. J. Metall., 2013, 2013: 196891

[本文引用: 5]

Hua J S, Droste C, Einarsrud K E, et al.

Revised benchmark problem for modeling of metal flow and metal heaving in reduction cells

[A]. Light Metals [C]. Warrendale: TMS, 2014: 691

[本文引用: 3]

Wang Q, Li B K, He Z, et al.

Simulation of magnetohydrodynamic multiphase flow phenomena and interface fluctuation in aluminum electrolytic cell with innovative cathode

[J]. Metall. Mater. Trans., 2014, 45B: 272

[本文引用: 4]

Zhan S Q.

Numerical simulation and application of multiphase flow dynamics behavior in melts of aluminum reduction cells

[D]. Changsha: Central South University, 2015

[本文引用: 3]

(詹水清.

铝电解槽熔体内多相流体动力学行为的数值模拟及应用研究

[D]. 长沙: 中南大学, 2015)

[本文引用: 3]

Hua J S, Rudshaug M, Droste C, et al.

Modelling of metal flow and metal pad heaving in a realistic reference aluminum reduction cell

[A]. Light Metals [C]. Warrendale: TMS, 2016: 339

[本文引用: 3]

Hua J S, Rudshaug M, Droste C, et al.

Numerical simulation of multiphase magnetohydrodynamic flow and deformation of electrolyte-metal interface in aluminum electrolysis cells

[J]. Metall. Mater. Trans., 2018, 49B: 1246

[本文引用: 4]

Liu W, Zhou D F, Liu Y F, et al.

Simulation and measurements on the flow field of 600 kA aluminum reduction pot

[A]. Light Metals [C]. Warrendale: TMS, 2015: 479

[本文引用: 1]

Dupuis M, Pagé M.

Modeling gravity wave in 3D with openfoam in an aluminum reduction cell with regular and irregular cathode surfaces

[A]. Light Metals [C]. Warrendale: TMS, 2016: 909

[本文引用: 1]

Feng Y Q, Schwarz M P, Yang W, et al.

Two-phase CFD model of the bubble-driven flow in the molten electrolyte layer of a hall-héroult aluminum cell

[J]. Metall. Mater. Trans., 2015, 46B: 1959

[本文引用: 1]

Mei C. Simulation and Optimization of Nonferrous Metallurgy Furnace [M]. Beijing: Metallurgical Industry Press, 2001: 74

[本文引用: 1]

(梅 炽. 有色冶金炉窑仿真与优化 [M]. 北京: 冶金工业出版社, 2001: 74)

[本文引用: 1]

Bradley B F, Dewing E W, Rogers J N.

Metal pad velocity measurements by the iron rod method

[A]. Light Metals [C]. Warrendale: Metallurgical Society of AIME, 1984: 541

[本文引用: 1]

/

〈 〉


版权所有 © 《金属学报》编辑部
地址: 沈阳市文化路72号, 中国科学院金属研究所(110016)
电话: +86- 024-23971286 　E-mail: jsxb@imr.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发 技术支持：support@magtech.com.cn