六重对称合金枝晶生长场变量扩散元胞自动机模型

doi:10.11900/0412.1961.2023.00174

六重对称合金枝晶生长场变量扩散元胞自动机模型

汤思璠¹^,², 魏晶晶¹, 岳怡心¹, 李鹏宇¹, 姚曼¹, 王旭东^,¹^,²

1 大连理工大学材料科学与工程学院大连 116024

2 大连理工大学辽宁省凝固控制与数字化制备技术重点实验室大连 116024

Field-Variable Diffusion Cellular Automaton Model for Dendritic Growth with Sixfold Symmetry Alloys

TANG Sifan¹^,², WEI Jingjing¹, YUE Yixin¹, LI Pengyu¹, YAO Man¹, WANG Xudong^,¹^,²

1 School of Materials Science and Engineering, Dalian University of Technology, Dalian 116024, China

2 Key Laboratory of Solidification Control and Digital Preparation Technology (Liaoning Province), Dalian University of Technology, Dalian 116024, China

通讯作者: 王旭东，hler@dlut.edu.cn，主要从事连铸过程模型化与质量控制、凝固过程的微观组织预测研究

责任编辑: 李海兰

收稿日期: 2023-04-18 修回日期: 2023-06-10

基金资助:

国家自然科学基金项目(51974056)
国家自然科学基金项目(51474047)

Corresponding authors: WANG Xudong, associate professor, Tel:(0411)84707347, E-mail:hler@dlut.edu.cn

Received: 2023-04-18 Revised: 2023-06-10

Fund supported:

National Natural Science Foundation of China(51974056)
National Natural Science Foundation of China(51474047)

作者简介 About authors

汤思璠，女，1998年生，博士生

摘要

在合金凝固枝晶生长元胞自动机(CA)模型中，正方形元胞、邻胞构造、尖锐界面模型固有特性引起的各向异性，给枝晶择优取向生长的模拟研究带来了诸多限制，特别是难以模拟六重对称合金的枝晶生长行为。本工作在借鉴相场弥散界面模型中相场变量梯度能项建模与求解方法的基础上，构建和推导了考虑元胞状态变量的场变量梯度泛函及场变量扩散方程，提出了一种新的场变量扩散元胞自动机(FCA)模型。模型考虑了成分过冷和Gibbs-Thomson效应，采用“浓度势法”处理溶质扩散和再分配，依据杠杆定理处理界面凝固的生长动力学，通过引入场变量扩散项修正界面元胞的生长速率，并利用不同条件下Mg-6%Al (质量分数)合金的枝晶生长结果对模型进行了验证。在正方形网格离散方式下，六重对称Mg-6%Al合金的枝晶尖端稳态特征和生长动力学与LGK模型的预测结果基本吻合，模型能够呈现多重合金枝晶形貌的对称性以及枝晶的随机择优取向生长，还原凝固过程的枝晶臂生长、竞争和粗化等行为。

关键词： 场变量扩散; 元胞自动机; 六重对称; 枝晶生长; 随机择优取向

Abstract

The cellular automaton (CA) model exhibits a notable disadvantage of substantial anisotropy, triggered by the square cells, adjacent cell structures, and intrinsic features of the sharp interface model. This disadvantage leads to limitations in simulating dendritic growth with random preferred orientations during the solidification of alloys, particularly in the context of sixfold symmetric alloys. In the present study, drawing inspiration from the processing concept of diffuse interfaces and the gradient energy term in the phase field model, a function concerning the gradient of the field variable associated with the cell state is constructed and the diffusion equation for the field variable is derived. Consequently, a novel field-variable diffusion CA (FCA) model is proposed, which addresses the growth kinetics of the solid-liquid interface in accordance with the lever rule. The proposed model considers constitutional supercooling and the Gibbs-Thomson effect, employing the concentration potential method to manage solute diffusion and redistribution. The growth rate of interface cells is modulated by introducing a field-variable diffusion term. The analysis reveals that within the square-grid discretization mode, the model demonstrates validation under various conditions, focusing on the steady-state characteristics of the dendritic tip and growth kinetics of the sixfold symmetric Mg-6%Al (mass fraction) alloy. The findings are consistent with the predictions of the LGK model, suggesting that the FCA model can effectively emulate dendritic morphology with multifold symmetry and random preferred orientations, and elucidate critical dendritic arm behaviors, such as competitive dendritic growth and coarsening.

Keywords： field variable diffusion; cellular automaton; six-fold symmetry; dendritic growth; random preferred orientation

PDF (2869KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

汤思璠, 魏晶晶, 岳怡心, 李鹏宇, 姚曼, 王旭东. 六重对称合金枝晶生长场变量扩散元胞自动机模型[J]. 金属学报, 2025, 61(6): 941-952 DOI:10.11900/0412.1961.2023.00174

TANG Sifan, WEI Jingjing, YUE Yixin, LI Pengyu, YAO Man, WANG Xudong. Field-Variable Diffusion Cellular Automaton Model for Dendritic Growth with Sixfold Symmetry Alloys[J]. Acta Metallurgica Sinica, 2025, 61(6): 941-952 DOI:10.11900/0412.1961.2023.00174

合金凝固组织的形态、尺寸和分布等特征主导着材料的最终性能，理解枝晶的形成与演化机制是控制凝固过程的关键。合金凝固过程中的枝晶生长行为是涉及多物理场、非均相和时变性的复杂非线性问题，数值模拟可以精确量化枝晶生长过程中的各种现象及演化规律，是认识凝固微观组织形成机制的重要途径。枝晶生长模拟属于介观尺度的运动界面问题，主要有弥散界面模型和尖锐界面模型2种计算方法。弥散界面模型认为界面是具有一定厚度的边界层，各种物理性质在边界层内连续变化，代表性方法是相场(phase field，PF)法。PF法避免了追踪固-液界面的繁琐过程，易于处理复杂边界形貌^[1,2]和运动界面^[3,4]等问题，但PP法计算网格尺度较小，计算量巨大，与宏观尺度的耦合计算十分困难。尖锐界面模型则不考虑界面厚度，界面两侧的物理属性是突变的，代表性方法是元胞自动机(cellular automaton，CA)法。CA模型方法简单，易于实现且计算效率高，广泛应用于许多领域的跨尺度研究^[5~8]。

在经典的CA模型中，枝晶形貌与生长动力学出现了强烈的各向异性，这是模型计算中无法忽视的关键问题。在枝晶生长模拟中主要表现为两方面：(1) 枝晶对称次数受元胞几何形状的影响十分显著，二维正方形元胞易于模拟四重对称的枝晶形貌^[9~11]，而正六边形元胞则用于模拟六重对称的枝晶形貌^[12~14]；(2) 难以模拟具有不同随机择优取向的枝晶生长，即，无强制手段干预时枝晶通常沿网格坐标轴方向生长。由元胞几何特征、邻胞构造与捕获规则等因素导致的各向异性，导致CA模型计算结果偏离实际行为和现象^[15]，成为限制CA模型应用和发展的障碍。

鉴于以上原因，CA凝固组织模拟的一项重要内容即在于弱化甚至消除网格依赖性对生长动力学和择优生长方向的影响，代表性研究包括随机性方法(random zig-zag^[16])和确定性方法(角点生长算法^[17,18]、虚拟界面跟踪法^[10,19]、偏心算法^[20~23]、坐标系变换^[24]及定义多层邻居元胞^[25]、类6重对称的邻胞设置^[26]等) 2类。上述修正算法在不同程度上弱化了枝晶形貌的各向异性，通常用于模拟单一的四重或六重对称枝晶形貌，难以拓展至多维、多相的合金凝固过程模拟。因此，构建能够实现不同对称次数、不同择优取向枝晶生长的通用CA模型，对于拓展CA方法在合金凝固领域的应用是十分必要的。

借鉴相场弥散界面模型相场变量梯度能项的处理思路，本工作将表征元胞状态的场变量及其梯度项引入CA模型，构造场变量梯度泛函推导其扩散方程，以此对枝晶生长动力学进行修正，建立了场变量扩散元胞自动机(field variable diffusion cellular automaton，FCA)模型。以Mg-6%Al (质量分数，下同)合金六重对称的枝晶生长过程为对象，模拟计算不同条件下镁合金的枝晶形貌及演化特征，考察场变量扩散CA生长模型弱化各向异性的能力，对模型计算结果的准确性和适用性进行验证。

1 场变量梯度扩散方程推导

1.1 CA模型场变量引入的背景和思路

在相场模型中，相场变量用于描述变量在空间中的分布及特征，系统会自发地从场变量非均匀分布状态(非平衡态)向均匀分布状态(平衡态)转变，状态分布的空间变化速率和特征可以用场变量的梯度描述。与热量、质量和动量的扩散行为类似，相场变量同样是在梯度方向的变化速率最大，沿其梯度减小的方向扩散，使系统向梯度趋于零的状态发展。因此，尽管在相场模型中无捕获环节，但扩散界面梯度能项的界面能驱动着相场变量的扩散，主导枝晶生长动力学和形貌演化，在很大程度上避免了各向异性的影响。受此启发，在枝晶生长CA模型中，表征元胞固、液状态的固相分数( $f_{S}$ )在0~1内连续变化，因此，尝试考虑在CA模型中引入该场变量的梯度项，弱化枝晶生长的各向异性和网格依赖性。

1.2 二维场变量扩散CA模型推导

首先，根据元胞的固相分数定义一个场变量 $u (x, y)$ ，如式(1)所示。为简化数值计算流程和运算量，对场变量做二值化处理，使用 $u$ 代替 $f_{S}$ 。

u (x, y) = \{\begin{array}{l} 0 (f_{S} < 1) \\ 1 (f_{S} \geq 1) \end{array}

(1)

然后，构造二维计算域S中场变量 $u (x, y)$ 的梯度泛函E(u)，如式(2)所示。

E (u) = \frac{D}{p} \iint_{S}^{} {|\nabla u|}^{p} d x d y = \frac{D}{p} \iint_{S}^{} F (u_{x}, u_{y}) d x d y

(2)

式中， $\nabla u$ 为 $u (x, y)$ 的梯度， $\nabla u = (u_{x}, u_{y})$ ；D为常系数；参数 $1 \leq p \leq 2$ ； $|\nabla u| = \sqrt[]{(u_{x})^{2} + (u_{y})^{2}}$ 为 $\nabla u$ 的模； $F (u_{x}, u_{y}) = {|\nabla u|}^{p}$ 为被积函数。随着场变量 $u (x, y)$ 的演化， ${|\nabla u|}^{p}$ 在域内积分不断降低，即，E(u)不断减小。

采用梯度下降法^[27]求解式(2)， $E (u)$ 的值沿负梯度方向下降最快，故场变量 $u (x, y)$ 的变化量应满足：

\frac{\partial u}{\partial τ} = - g r a d (E (u))

(3)

式中， $τ$ 为引入的“时间变量”， $g r a d (E (u))$ 为泛函 $E (u)$ 的梯度，如式(4)所示。

g r a d (E (u)) = \frac{\partial F}{\partial u} - \frac{d}{d x} (\frac{\partial F}{\partial u_{x}}) - \frac{d}{d y} (\frac{\partial F}{\partial u_{y}})

(4)

联立式(2)~(4)，得到场变量 $u (x, y)$ 的演化方程，如式(5)所示。

\frac{\partial u}{\partial τ} = D d i v ({|\nabla u|}^{p - 2} \nabla u)

(5)

当 $p$ = 2时，式(5)可简化为各向同性线性扩散方程，如式(6)所示。

\frac{\partial u}{\partial τ} = D \nabla \cdot (\nabla u) = D (u_{x x} + u_{y y})

(6)

采用显示差分格式对场变量扩散方程进行离散，为了提高差分格式的精度，运用九点差分格式离散二维场变量扩散方程，如式(7)：

u_{i, j}^{N} = (1 - 4 F_{0}) u_{i, j}^{I} + \frac{2}{3} F_{0} (u_{i - 1, j}^{I} + u_{i + 1, j}^{I} + u_{i, j - 1}^{I} +

u_{i, j + 1}^{I}) + \frac{1}{3} F_{0} (u_{i + 1, j + 1}^{I} + u_{i + 1, j - 1}^{I} + u_{i - 1, j - 1}^{I} +

u_{i - 1, j + 1}^{I})

(7)

式中，i、j分别为直角坐标系中x、y坐标轴方向的元胞索引；F₀ = $D Δ t / {(Δ x)}^{2}$ ， $Δ t$ 和 $Δ x$ 分别为时间步长和空间步长(即网格尺寸)，为满足稳定性条件，取 $F_{0}$ = 0.24；上标 $N$ 和 $I$ 分别代表场变量 $u$ 迭代后的结果和初始值，初值 $u^{I}$ 设置如下：固相元胞为1，液相元胞和界面元胞为0。

以上即为二维场变量扩散CA模型的推导过程及解析表达式。 $u^{N}$ 的值域在0~1之间。凝固初期，元胞及周围邻胞均为液相胞或界面胞，故等式右边 $u^{I}$ 项均为0， $u^{N}$ 即为最小值0；随着凝固的进行，邻胞逐渐转变为固相胞， $u^{N}$ 逐渐增大；当元胞及周围邻胞全部凝固为固相胞， $u^{N}$ 即为最大值1。通过引入场变量扩散项 $u^{N}$ ，根据邻胞的凝固状态动态校正其生长方向和速率，进而调整和追踪固-液界面的推进状态、形貌和位置等信息。

1.3 各向异性算例与结果讨论

生长动力学计算是所有相变数值计算模型的核心，CA模型生长动力学和各向异性主要有2方面影响因素：固相元胞捕获规则、界面元胞固相分数的增长。在本工作中，引入场变量扩散项 $u_{i, j}^{N}$ 调节界面元胞的生长速率，当不考虑其他物理场或边界条件的各向异性时，恒定的生长速率应产生各向同性形状，即二维平面内圆形或三维空间中的球体，需对模型进行定量验证，评估其弱化各向异性的能力。

建立具有固定生长速率 $v_{s e t}$ = 0.1的二维CA模型，元胞有液相、界面及固相3种状态，分别对应于 $f_{S}$ = 0，0 < $f_{S}$ < 1及 $f_{S} \geq 1$ 。当界面胞的 $f_{S}$ 增至1后，元胞转变为固相胞，之后，该固相胞捕获周围邻域内的液相元胞，并将液相胞转化为界面胞。初始时刻，计算域中心放置一个固相胞A，A的液相邻胞都被转变为界面元胞。原始CA模型的界面元胞固相分数增量( $Δ f_{S}$ )为：

Δ f_{S} = v_{s e t}

(8)

采用式(7)中的场变量扩散项对界面元胞的固相分数增量进行修正：

Δ f_{S} = v_{s e t} \cdot u_{i, j}^{N}

(9)

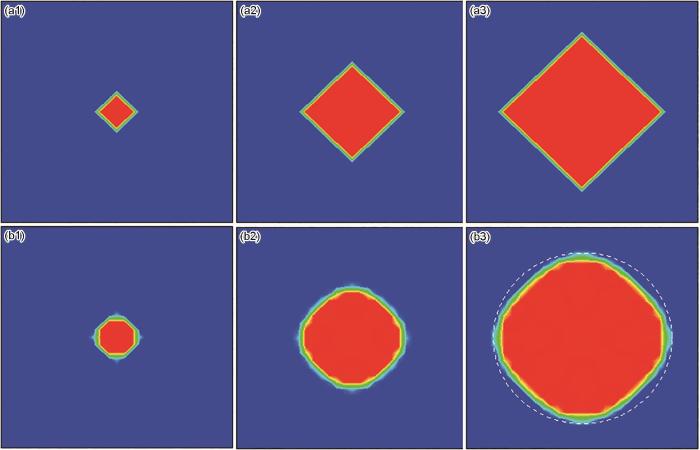
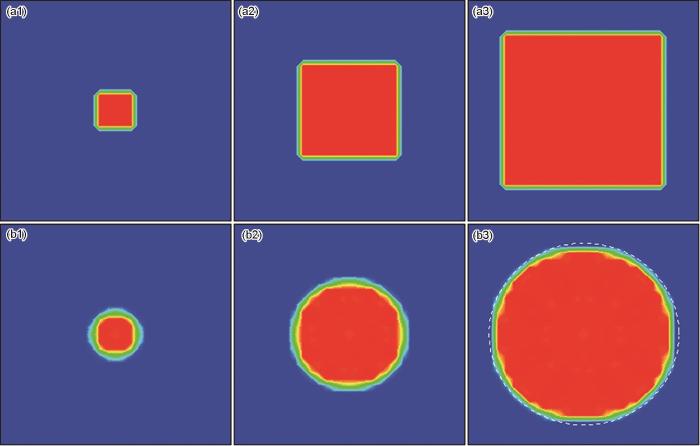
图1和2分别为采用Von Neumann型和Moore型邻胞，二维CA模型在不同迭代次数下得到的演化形貌，图中的白色虚线圆为参考曲线，元胞数目251 × 251。其中，图1a1~a3和图2a1~a3为原始的CA模型的模拟结果，迭代次数分别为20、60和100次；图1b1~b3和图2b1~b3为FCA模型模拟结果，迭代次数分别为120、260和400次。可以看出，与原始的二维CA模型相比，引入场变量扩散项可以得到近似圆形的演化形貌，且Moore型邻胞的模拟结果优于Von Neumann型邻胞。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 Von Neumann型邻胞2种模型模拟结果

Fig.1 Morphologies simulated by two cellular automaton (CA) models using Von Neumann neighborhood

(a1-a3) original CA model with 20 iterations (a1), 60 iterations (a2), and 100 iterations (a3) (b1-b3) field variable diffusion (FCA) model with 120 iterations (b1), 260 iterations (b2), and 400 iterations (b3)

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 Moore型邻胞2种模型模拟结果

Fig.2 Morphologies simulated by the two CA models using Moore neighborhood

(a1-a3) original CA model with 20 iterations (a1), 60 iterations (a2), and 100 iterations (a3) (b1-b3) FCA model with 120 iterations (b1), 260 iterations (b2), and 400 iterations (b3)

FCA模型显著弱化了原始CA模型中的各向异性，近似实现了各向同性的界面演化。值得一提的是，引入场变量扩散项虽然增加了计算量，但计算流程简洁，可以通过算法优化及并行计算加快计算速率，也易于扩展至三维模型。

2 场变量扩散二元合金枝晶生长CA模型

基于推导的场变量扩散方程，建立了溶质传输驱动的二元合金枝晶生长CA模型。模型包括场变量扩散、溶质传输、生长动力学计算、元胞状态转变、捕获规则等模块。采用“浓度势法”处理溶质扩散和再分配，利用杠杆定律处理界面凝固/重熔的生长动力学，并将场变量扩散项引入CA模型对界面胞的生长速率进行修正。模型的基本假设如下：(1) 热量传输速率比溶质传输速率高3~4个数量级，因此忽略枝晶生长中的传热；(2) 不考虑熔体流动；(3) 忽略动力学过冷，不考虑固相线斜率、液相线斜率及平衡分配系数(k)随温度和生长速率的变化；(4) 凝固过程中，局部固-液界面达到平衡状态，即在局部固-液界面处，液相平衡溶质浓度( $C_{L}^{*}$ )与固相平衡浓度( $C_{S}^{*}$ )满足：k = $C_{S}^{*}$ / $C_{L}^{*}$ 。

2.1 溶质控制方程

不考虑液体中的自然对流和强迫对流，液体和固体中扩散的控制方程可以描述为：

\frac{\partial C_{m}}{\partial t} = \nabla \cdot (D_{m} \nabla C_{m})

(10)

式中，t为时间，s； $C$ 为溶质浓度(质量分数，%)； $D_{m}$ 为溶质扩散系数，m²/s；下标 $m$ 代表固相(S)或液相(L)。由于固-液界面形状复杂且不断发生变化，界面两侧溶质浓度分布不连续，溶质传输计算中固相和液相的浓度需分开处理，导致计算相对繁琐。

因此，采用浓度势^[28]的方法进行计算，定义浓度势( $P$ )：液相元胞P = $C_{L}$ ，固相元胞P = $C_{S} / k$ ，界面元胞P = $C_{L}$ 。式(10)可以改写为式(11)：

\frac{\partial C_{e}}{\partial τ} = \nabla \cdot (\bar{D} \nabla P)

(11)

式中， $C_{e}$ 为元胞的等效浓度，质量分数，%， $C_{e}$ = $f_{S} C_{S} + (1 - f_{S}) C_{L}$ ； $\bar{D}$ 为等效的溶质扩散系数。如果离散计算涉及2个元胞α和β，则 $\bar{D}$ 定义如下：

\bar{D} = \frac{f_{S}^{α} D_{S} + (1 - f_{S}^{α}) D_{L} + f_{S}^{β} D_{S} + (1 - f_{S}^{β}) D_{L}}{2}

(12)

式中， $f_{S}^{α}$ 和 $f_{S}^{β}$ 分别为元胞α和β $的$ 固相分数。采用浓度势的处理方法，可将整个计算域的溶质传输作为一个单相处理，极大简化了计算流程。

2.2 固-液界面曲率及界面能各向异性计算

凝固过程中固-液界面处始终维持局部平衡状态：k = $C_{S}^{*}$ / $C_{L}^{*}$ 。考虑到成分过冷、界面曲率及界面能各向异性等因素， $C_{L}^{*}$ 的计算公式如下：

C_{L}^{*} = C_{0} + \frac{T - T_{L}}{m_{L}} + \frac{Γ \cdot K \cdot f (φ, θ)}{m_{L}}

(13)

式中， $T$ 为界面处的实际温度，K； $T_{L}$ 为初始熔体浓度 $C_{0}$ 对应的液相线温度，K； $m_{L}$ 为液相线斜率，K/% (%为质量分数)； $Γ$ 为Gibbs-Thomson系数，K∙m； $K$ 为固-液界面处的平均曲率， $m^{- 1}$ ； $φ$ 为固-液界面的法向与水平方向的夹角，rad； $θ$ 为枝晶的优先生长方向，rad； $f (φ, θ)$ 为界面能各向异性函数。K^[29]、 $φ$ 、 $f (φ, θ)$ 计算公式见式(14)~(16)。

K = \frac{2 \frac{\partial f_{S}}{\partial x} \frac{\partial f_{S}}{\partial y} \frac{\partial^{2} f_{S}}{\partial x \partial y} - {(\frac{\partial f_{S}}{\partial x})}^{2} \frac{\partial^{2} f_{S}}{\partial y^{2}} - {(\frac{\partial f_{S}}{\partial y})}^{2} \frac{\partial^{2} f_{S}}{\partial x^{2}}}{{[{(\frac{\partial f_{S}}{\partial x})}^{2} + {(\frac{\partial f_{S}}{\partial y})}^{2}]}^{3 / 2}}

(14)

φ = \{\begin{matrix} \begin{array}{l} c o s^{- 1} (\frac{\partial f_{S} / \partial x}{{({(\frac{\partial f_{S}}{\partial x})}^{2} + {(\frac{\partial f_{S}}{\partial y})}^{2})}^{1 / 2}}) \\ (\frac{\partial f_{S}}{\partial y} \geq 0) \end{array} \\ \begin{array}{l} 2 π - c o s^{- 1} (\frac{\partial f_{S} / \partial x}{{({(\frac{\partial f_{S}}{\partial x})}^{2} + {(\frac{\partial f_{S}}{\partial y})}^{2})}^{1 / 2}}) \\ (\frac{\partial f_{S}}{\partial y} < 0) \end{array} \end{matrix}

(15)

f (φ, θ) = 1 + δ c o s (n (φ - θ))

(16)

式中， $δ$ 为界面能各向异性强度， $n$ 为各向异性模数。

2.3 固相分数计算

在局部固-液界面平衡凝固假设条件下，可以通过杠杆定律计算得到整个界面元胞的固相分数，因此 $f_{S}$ 的计算为：

f_{S} = \frac{C_{L}^{*} - C_{e}}{C_{L}^{*} (1 - k)}

(17)

由式(13)可知，不同时间步长内局部界面的曲率差异导致 $C_{L}^{*}$ 不同。因此，综合考虑场变量扩散项及动力学各向异性等因素， $Δ f_{S}$ 的计算公式为：

Δ f_{S} = \frac{1}{1 - k} (\frac{C_{e}^{p r e}}{C_{L}^{* p r e}} - \frac{C_{e}}{C_{L}^{*}}) \cdot f_{k} (φ, θ) \cdot γ \cdot u^{N}

(18)

式中，上标 $p r e$ 代表上一时间步长的变量值；γ为生长速率调节系数； $u^{N}$ 是场变量扩散项； $f_{k} (φ, θ)$ 为生长各向异性函数，定义为：

f_{k} (φ, θ) = 1 + δ_{k} c o s (n (φ - θ))

(19)

式中， $δ_{k}$ 为生长动力学系数。局部固-液界面曲率不同而产生的Gibbs-Thomson效应，导致界面平衡成分的差异，在液相中产生浓度梯度，引起溶质扩散。这些相互作用关系使得高曲率部位熔化而低曲率部位凝固，从而驱动了枝晶的粗化过程^[30]。当( $C_{e}^{p r e}$ / $C_{L}^{* p r e}$ - $C_{e}$ / $C_{L}^{*}$ ) > 0时，界面元胞的 $Δ f_{S}$ > 0，局部固-液界面发生凝固；当( $C_{e}^{p r e}$ / $C_{L}^{* p r e}$ - $C_{e}$ / $C_{L}^{*}$ ) < 0时，局部固-液界面发生熔化( $Δ f_{S}$ < 0)。因此，由于耦合了界面曲率和溶质扩散对界面凝固/熔化相变动力学的作用，理论上FCA模型能够模拟枝晶的凝固及重熔行为。

2.4 捕获规则

FCA模型采用场变量扩散项修正生长速率，故无须限制枝晶形貌、生长方向和捕获规则，元胞捕获时也不再做随机处理。枝晶在生长时采用最简单的捕获规则，即，刚凝固的固相元胞将Moore型邻域内的液相元胞全部捕获，并将液相元胞转变为界面元胞。

2.5 计算流程

采用显式有限差分格式求解溶质传输控制方程， $Δ t$ 必须满足稳定性条件，即：

Δ t < \frac{Δ x^{2}}{4.0 D_{L}}

(20)

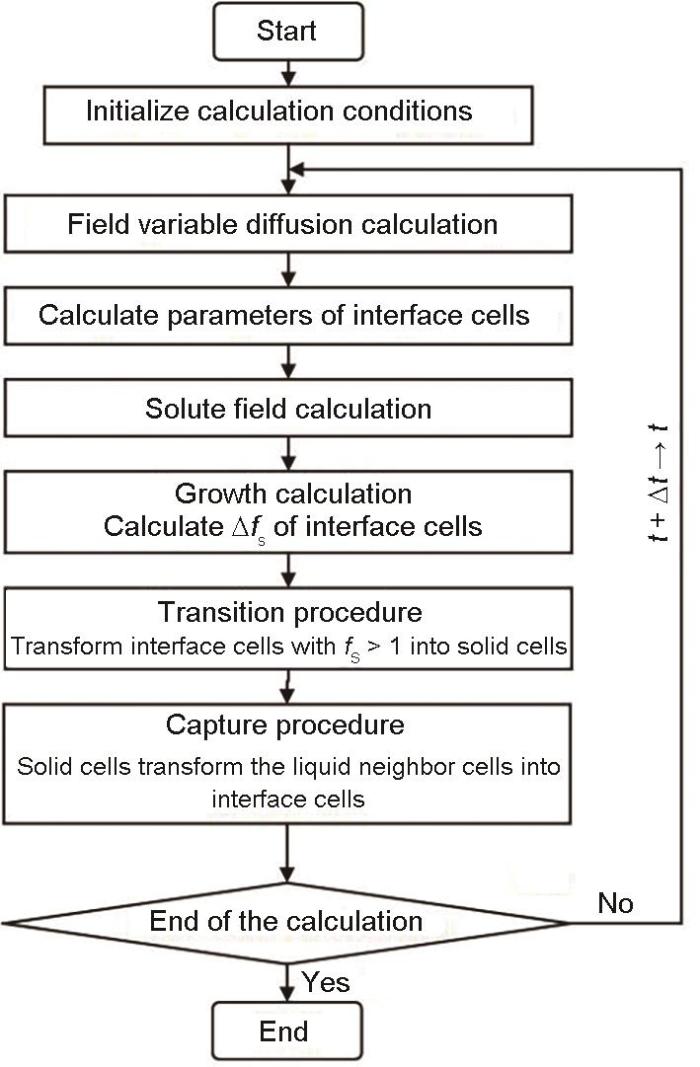
图3显示了FCA模型的流程图。FCA模型首先进行场变量模块计算，得到的场变量扩散项 $u^{N}$ 用于后续的生长动力学计算过程。生长计算和元胞状态转变过程仅针对界面细胞进行，最后对新凝固的固相元胞进行捕获模块的计算。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 场变量扩散枝晶生长CA模型计算流程

Fig.3 Flowchart of the CA model for dendritic growth based on field variable diffusion (t—time, Δt—time step, f_S—solid fraction, $Δ f_{S}$ —solid fraction increment)

3 模型验证

基于以上建立的模型与计算程序，对等温凝固条件下单个枝晶生长的结果进行验证和分析。从随机择优取向和生长动力学2方面，模拟了具有六重对称特征的Mg-6%Al合金的枝晶形貌，模拟中使用的材料物性参数及计算参数如表1^[13]所示。由于热量传输速率远大于溶质传递速率，因此将模拟区域设置为均匀温度场，只研究溶质扩散对枝晶生长的影响。模拟开始时，在计算域中心随机放置一个晶核。计算域元胞数目为551 × 551， $Δ x$ = 1 μm， $Δ t$ = 0.13 ms。

表1 计算采用的Mg-6%Al合金热物性参数^[13]

Table 1 Thermophysical properties of Mg-6%Al alloy used in the calculations^[13]

Parameter	Value	Unit
Diffusivity of alloy elements in liquid $D_{L}$	1.8 × 10^-9	m²·s^-1
Diffusivity of alloy elements in solid $D_{S}$	1.0 × 10^-13	m²·s^-1
Liquidus temperature $T_{L}$	901	K
Partition coefficient $k$	0.4	-
Liquidus slope $m_{L}$	-5.5	K·%^-1 (% for mass fraction)
Gibbs-Thomson coefficient $Γ$	2.0 × 10^-7	K·m
Kinetic anisotropy $δ_{k}$	0.5	-
Thermodynamic anisotropy δ	0.03	-
Accommodation coefficient γ	1.25	-
Degree of anisotropy $n$	6	-

新窗口打开| 下载CSV

3.1 六重对称枝晶生长模拟

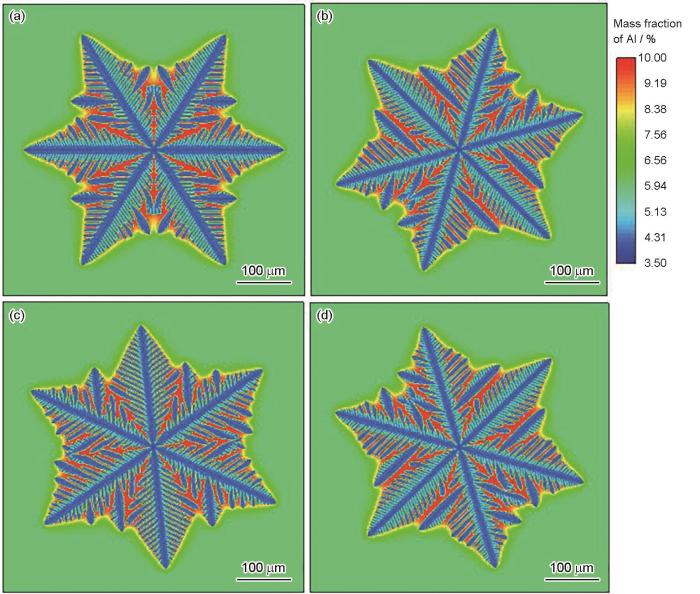
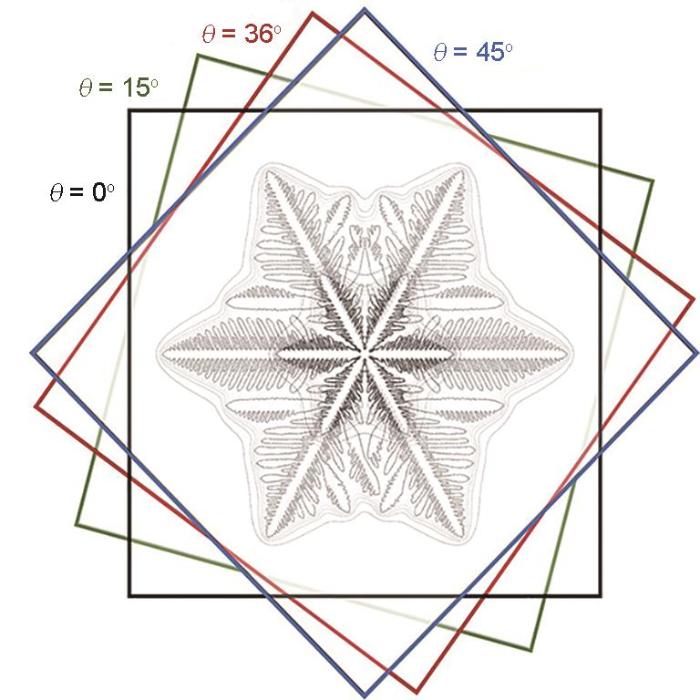
图4为择优取向为0º、15º、36º及45º的Mg-6%Al合金在凝固时间为0.455 s时的枝晶形貌。计算域元胞数目551 × 551， $Δ x$ = 1 μm，温度场均匀分布，过冷度 $Δ T$ = 20 K。图中4个枝晶的主枝晶臂方向均与设定的生长角度相同，且枝晶尺寸基本一致。需要指出的是，模型同样适用于四重、多重等不同对称次数枝晶生长行为的模拟，前期工作^[31]对3 K过冷度Al-4%Cu合金四重对称枝晶形貌和不同择优取向的枝晶形貌进行了模拟，结果表明，所有枝晶的偏转方向均与预设生长角度相符，各枝晶形貌及分支间夹角基本一致。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同择优取向的Mg-6%Al在凝固时间为0.455 s时的枝晶形貌

Fig.4 Simulated dendrites of Mg-6%Al alloy with different preferred orientations at the solidification time of 0.455 s

(a) 0° (b) 15° (c) 36° (d) 45°

枝晶生长过程是非线性的，对生长动力学的变化非常敏感。为此，提取0.195和0.455 s时刻的枝晶形貌，将图4b~d中的枝晶顺时针分别旋转15º、36º和45º，对比4个不同择优生长取向下的枝晶形貌，结果如图5所示。可以看出，不同择优生长角度的枝晶形貌基本重合，但由于二次枝晶和三次枝晶于枝晶间液相溶质富集的影响，生长速率不同，导致二次枝晶臂粗壮程度略有差异。总体来看，不同时刻下主枝晶臂的生长速率和尺寸基本一致，模型实现了正方形网格离散方式下，六重对称枝晶形貌的模拟，不同择优取向下枝晶形貌的各向异性显著降低。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同择优生长方向的枝晶形貌对比

Fig.5 Comparison of dendritic morphologies with different preferred orientations (θ)

3.2 枝晶尖端生长速率与半径

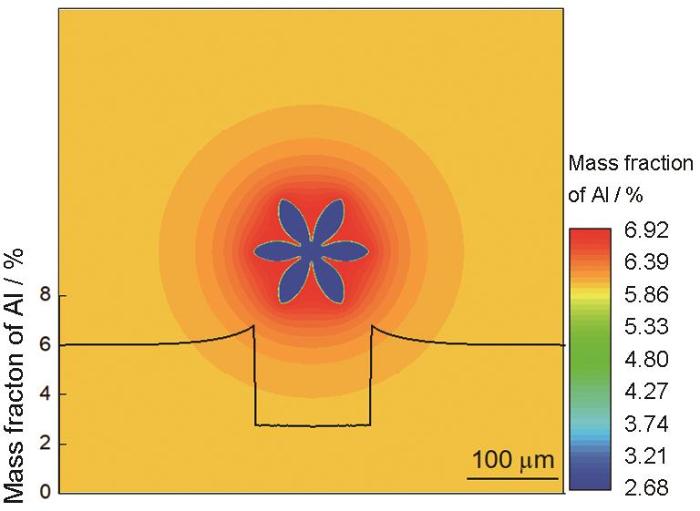
图6为过冷度为5 K、凝固时间为2.08 s的计算条件下，模拟得到的合金枝晶形貌及浓度场分布，元胞数目551 × 551， $Δ x$ = 1 μm，下方的黑色曲线为 $x$ 方向主枝晶臂的溶质浓度。可以看出，枝晶形貌及浓度场的分布都是对称的。在主枝晶臂方向，固相溶质浓度基本相同，固-液界面浓度处突然增加，形成了溶质富集的边界层，随后逐渐降低至初始浓度。由于过冷度较小，未出现二次枝晶臂。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 Mg-6%Al合金枝晶形貌模拟与水平方向主枝晶臂浓度

Fig.6 Simulated dendrite morphology and concentration of the horizontal main dendrite arms for Mg-6%Al alloy

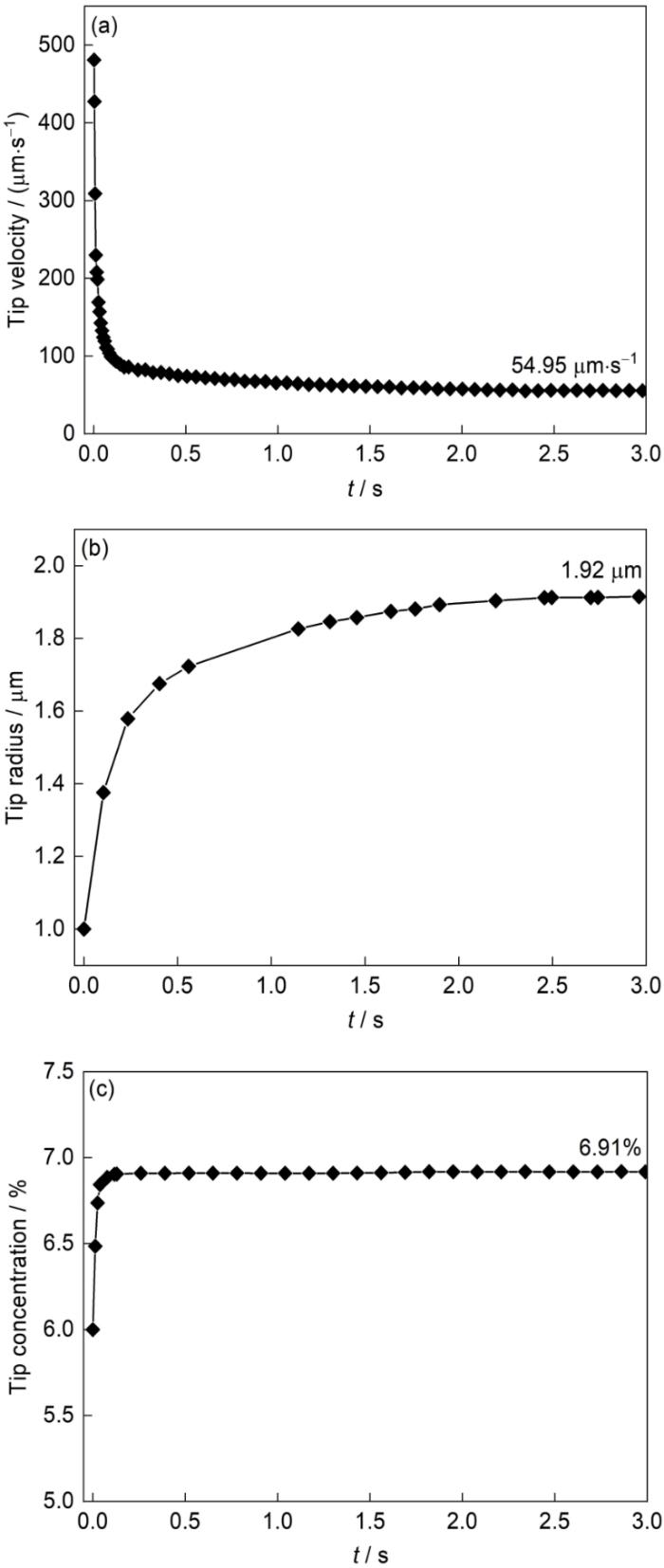
图7为Mg-6%Al在过冷度为5 K下，枝晶尖端半径、生长速率和溶质浓度随时间的变化关系。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 Mg-6% Al合金枝晶尖端特征参数随时间变化

Fig.7 Simulated curves of dendrite tip parameters against time for Mg-6% Al alloy with 5 K under-cooling

(a) tip growth velocity

(b) tip radius

等温凝固过程中，固-液界面的运动是由界面前沿溶质浓度差异引起的溶质扩散所驱动的。初始阶段，液相溶质浓度为初始浓度，固-液界面前沿溶质富集的程度较低，溶质浓度低且过冷度较高，因此，枝晶尖端以相对较高的速率开始生长，如图7a所示；随着凝固进行，枝晶逐渐增长，枝晶尖端半径也随之增大，如图7b所示，由溶质再分配释放的溶质富集在固-液界面，固相排出的溶质在固-液界面前沿不断积累，且枝晶生长所排出的溶质速率大于溶质扩散速率，枝晶尖端前沿的浓度迅速增加，导致合金液相线温度降低，过冷度减小，故生长速率降低，如图7c所示；最后溶质在界面前沿的释放与通过扩散的传输达到动态平衡，枝晶尖端逐渐达到稳态生长阶段。枝晶尖端生长速率在3.0 s时稳定在54.95 μm/s，此时尖端半径为1.92 μm。

3.3 枝晶尖端稳态特征与LGK模型预测结果对比

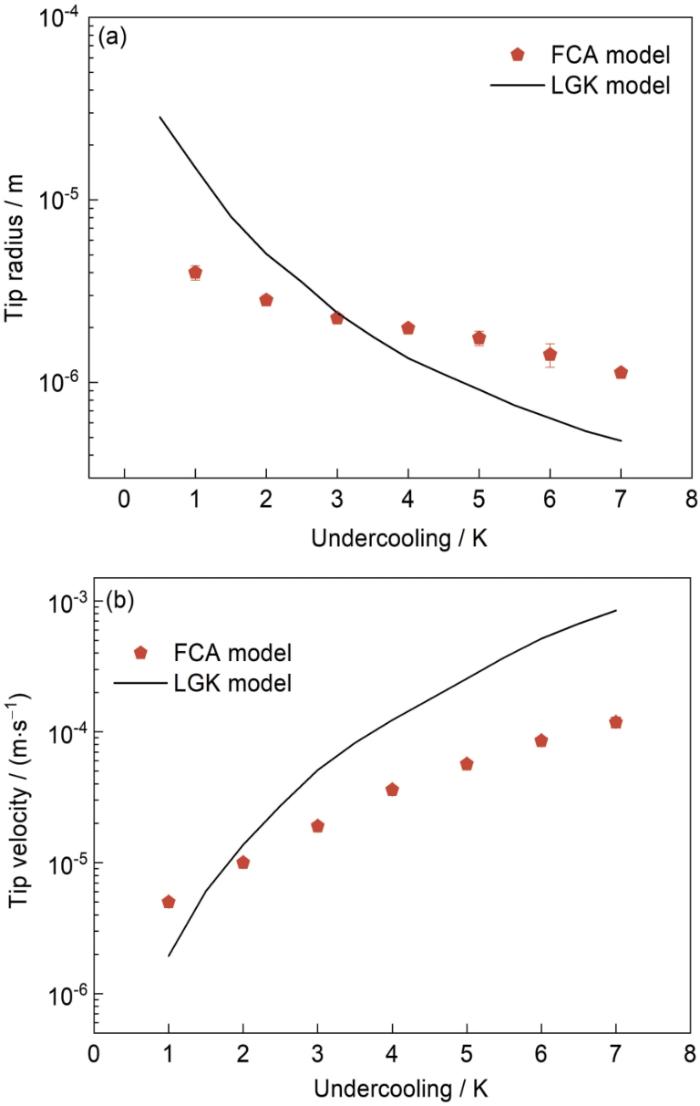
图8为Mg-6%Al合金在不同过冷度下，模拟得到的枝晶尖端特征与Lipton-Glicksman-Kurz (LGK)模型^[32]计算数据的对比结果。两模型预测的生长速率和尖端半径随过冷度变化的趋势相似，即随着过冷度的增大，枝晶尖端稳态生长速率逐渐增加，尖端半径逐渐减小，且2者数量级均为10^-5。刘龙飞^[33]基于LGK模型，探讨了过冷度对Mg-Al合金凝固时枝晶尖端生长半径及生长速率的影响，当过冷度从0.5 K增加至5 K时，枝晶尖端生长速率从2 × 10^-5 m/s增加到8 × 10^-5 m/s，尖端半径从1 × 10^-5 m降低至2 × 10^-6 m，研究结果与本工作结果在同一数量级，尖端半径和生长速率随过冷度的变化趋势一致。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 Mg-6%Al合金枝晶尖端半径和速率与LGK预测结果对比

Fig.8 Comparisons of dendrite tip radius (a) and tip growth velocity (b) from the FCA and Lipton-Glicksman-Kurz (LGK) models for the Mg-6%Al alloy

尖端半径在较低和较高过冷度下存在一定偏差，而尖端生长速率在较高过冷度下存在差异。当过冷度较小时，生长速率低，生长排出的溶质有充足的时间扩散；在枝晶生长到相同长度时，相比于较低的过冷度，过冷度较高时枝晶臂粗化的程度更加明显，导致高过冷度下枝晶尖端平均曲率降低，枝晶半径减小。本工作模型计算结果与LGK模型预测结果在同一数量级，需要说明的是，LGK模型仅求解枝晶尖端形状，未考虑枝晶臂演化和界面曲率对生长速率的影响，枝晶尖端半径的计算和确定方法本身就存在一定偏差，故低过冷度下本模型计算得到的尖端生长速率高于LGK模型；随着过冷度增大，情况相反，本模型计算的尖端生长速率小于LGK模型，Beltran-Sanchez等^[11]和Luo等^[34]也得到了同样的结论。

4 计算结果及讨论

为验证模型对六重对称合金枝晶生长模拟的适用性，分别对等温凝固和连续冷却下的Mg-6%Al合金的枝晶形貌进行模拟，首先模拟了等温凝固条件下单个等轴枝晶的生长，然后模拟了多个等轴晶的枝晶生长过程。对于Mg-6%Al合金来说，热扩散速率(α_T约为10^-5)远远大于溶质在液相中的扩散速率(D_L约为10^-9)，因此可以认为在枝晶尺度上热量扩散保持平衡态，即等轴晶生长过程中计算域的温度是均匀的。

4.1 等温凝固条件下单个等轴枝晶生长

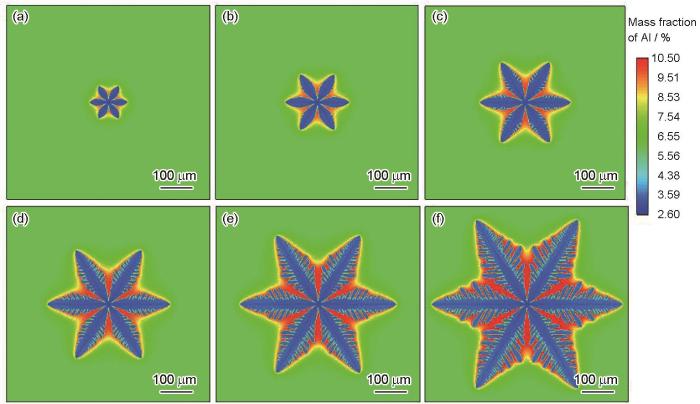
图9显示了Mg-6%Al合金枝晶形貌随时间的演化，计算域元胞数目650 × 650， $Δ x$ = 1 μm，时间步长为0.8 ms，计算域温度均匀分布，过冷度 $Δ T$ = 8 K。从图中可以看出，枝晶各个分支呈60°夹角，且每个分支大小一致。由于过冷度较小，虽有少量二次枝晶产生，未出现三次枝晶。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 Mg-6%Al合金枝晶形貌及溶质浓度随时间演化

Fig.9 Evolutions of dendrite morphologies and solution concentrations of Mg-6%Al alloy with time

(a) 0.16 s (b) 0.28 s (c) 0.40 s (d) 0.52 s (e) 0.64 s (f) 0.76 s

在枝晶生长过程中，枝晶臂粗化，溶质扩散区域逐渐增大。枝晶尖端排出的溶质沿其生长方向和周围两侧扩散，而枝晶臂粗化排出的溶质只能向两侧扩散，故枝晶尖端溶质浓度低于主枝晶臂两侧浓度，进而获得了较大的过冷度，生长速率加快。在枝晶根部，枝晶臂交汇造成溶质富集，枝晶生长受到抑制，根部出现“颈缩”现象。需要指出，如果利用经典的正方形元胞CA模型计算六重枝晶的生长行为，不仅计算中的处理十分繁琐，且不同择优取向枝晶的生长速率也会出现较大的差异。Fu等^[35]利用正方形元胞CA模型模拟了AZ91D合金的枝晶形貌，结果表明处于不同方向的主枝晶臂生长速率不一致，且主枝晶臂之间的夹角也不相等，与实际均匀温度场下的枝晶形貌不符。与之相比，本模型模拟得到的6个枝晶臂长度相等，侧枝角度对称，与相场法得到的结果^[36]基本一致。

4.2 连续冷却条件下多等轴枝晶生长

模拟了连续冷却条件下Mg-6%Al合金多个等轴晶的枝晶生长过程，计算域网格数目650 × 650， $Δ x$ = 1 μm，时间步长为0.8 ms，温度场均匀分布，初始过冷度 $Δ T$ = 12 K，降温速率9 K/s。图10a1~a4和图10b1~b4分别为随机设置8个和30个晶核，Mg-6%Al合金等轴晶形貌及溶质浓度随时间的演化。晶核数目为8时，在凝固初期(0.48 s)，枝晶生长速率较快，主枝晶臂沿其择优取向生长，并且主枝晶臂的两侧产生二次枝晶臂；随着凝固的进行(2.64 s)，枝晶周围液相溶质富集，相邻枝晶溶质场的相互作用变得越来越强，使一些枝晶臂偏离其择优取向生长，六重对称的枝晶形貌发生了明显的变化。凝固5.60 s时，溶质在枝晶臂间熔体内进一步富集，导致溶质扩散及尖端生长受到明显抑制。凝固后期(10.00 s)，枝晶生长速率进一步降低，Gibbs-Thomson效应导致枝晶臂粗化。晶核数目为30时的枝晶生长规律与8个时基本相同，但由于枝晶的相互阻碍作用较强，二次枝晶臂的发展被抑制。Yin和Felicelli^[17]采用正六边形元胞CA模型模拟得到Mg-8.9%Al的枝晶形貌，主枝晶臂只能沿着与x轴正方向呈60°夹角的方向生长，但无法实现枝晶偏转。本模型采用正方形元胞模拟得到六重对称合金枝晶形貌，与相场法得到的镁合金多枝晶生长形貌和溶质场分布结果^[37]大致相符。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 Mg-6%Al合金等轴晶形貌及溶质浓度分布随时间演化

Fig.10 Evolutions of simulated equiaxed dendrite morphologies and solution concentrations of Mg-6%Al alloy with dendrite numbers (N) and time

(a1) N = 8, 0.48 s (a2) N = 8, 2.64 s (a3) N = 8, 5.60 s (a4) N = 8, 10.00 s

(b1) N = 30, 0.48 s (b2) N = 30, 2.64 s (b3) N = 30, 5.60 s (b4) N = 30, 10.00 s

4.3 定向凝固条件下柱状枝晶生长

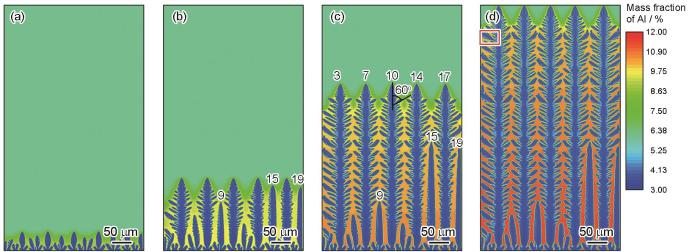
图11显示了Mg-6%Al合金定向凝固过程中柱状晶形貌随时间的演化。计算域元胞数目400 × 800， $Δ x$ = 1 μm，时间步长为0.8 ms，计算域底部初始过冷度为15 K，从底部到顶部温度梯度为10000 K/m，抽拉速率0.001 m/s。19个具有不同择优生长取向的晶核布置在计算域底部。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 Mg-6%Al合金定向凝固柱状晶形貌随时间的模拟结果

Fig.11 Simulated columnar dendritic morphologies during directional solidification of a Mg-6%Al alloy with time

(a) 0.16 s (b) 0.56 s (c) 1.04 s

(d) 1.44 s (The outlined region illustrates the local “necking” phenomenon during dendrite growth)

凝固初期，所有枝晶均沿其择优生长方向发展，与温度梯度方向相近的主枝晶臂生长速率较快，如图11a所示。随着凝固的进行，出现“竞争生长”现象。择优取向与温度梯度方向相近的枝晶继续生长，主枝晶臂两侧出现了不同程度的侧向分支；由于相邻枝晶的影响，择优取向不利的主枝晶臂生长均受到抑制，与吴孟武和熊守美^[13]模拟镁合金定向凝固不同温度梯度和凝固速率下柱状晶的竞争生长观察的现象一致。最终仅有5个枝晶的主枝晶臂继续生长，二次枝晶臂的发展也较完全，且与主枝晶臂间的夹角为60º。由于3^#、17^#枝晶与边界间距较大，溶质浓度较低，在朝向边界的方向均发展出了三次枝晶臂。图11b和c标示出了择优生长方向与温度梯度方向一致的枝晶编号。可以看出，9^#、15^#、19^#枝晶虽然取向有利，但在生长过程中受到相邻枝晶二次枝晶臂的阻挡，仍然被逐渐“淘汰”。如图11d红色方框所示，二次枝晶生长过程中，溶质富集在枝晶根部，产生“颈缩”现象。

5 结论

(1) 通过引入考虑元胞状态变量的场变量梯度泛函及场变量扩散方程，建立了基于场变量扩散的二元合金枝晶生长CA模型，采用“浓度势法”处理溶质扩散和再分配，依据杠杆定理处理界面凝固的生长动力学，引入场变量的扩散方程修正界面元胞的生长速率。对界面元胞的生长行为进行修正，旨在针对具有六重对称合金的枝晶生长及任意择优取向的枝晶生长过程进行模拟。采用“浓度势法”处理溶质扩散和再分配，依据杠杆定理处理界面凝固的生长动力学，引入场变量的扩散方程修正界面元胞的生长速率。

(2) 以Mg-6%Al合金为对象，利用模型对不同凝固条件下的枝晶形貌、稳态特征等进行计算和分析验证。模拟计算结果显示，Mg-6%Al合金稳态生长阶段，模型计算的枝晶尖端生长速率、尖端半径随过冷度的变化趋势与LGK模型预测结果大致相符。

(3) 等温凝固和连续冷却条件下，模型计算的主枝晶臂、二/三次枝晶及其形貌均沿着各自择优取向生长，可反映出凝固前沿溶质富集、枝晶根部“缩颈”以及由Gibbs-Thomson效应导致的枝晶臂粗化等行为。

(4) 定向凝固条件下，择优取向与温度梯度相近的主枝晶臂生长速率高，计算中可观察到枝晶的竞争、淘汰和“缩颈”等现象。

(5) 建立的场变量扩散元胞自动机枝晶生长模型，显著弱化了CA模型枝晶形貌模拟的各向异性，实现了二维平面正方形网格离散方式下，六重对称合金和任意择优取向枝晶生长形貌的计算模拟，原理清晰、易于并行，为元胞自动机法推广至合金凝固组织的三维和跨尺度模拟研究提供参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Kobayashi

Modeling and numerical simulations of dendritic crystal growth

[J]. Physica, 1993, 63D: 410