水口吹Ar技术是目前一种主流的用以减缓或者防止浸入式水口结瘤,去除夹杂物,改善板坯质量,提高生产效率的关键性结晶器冶金技术之一。然而,吹Ar过程中结晶器内气泡的尺寸和数量不仅影响气泡对夹杂物的去除效果以及钢液洁净度,也影响凝固坯壳对气泡的捕获。结晶器内Ar气泡的尺寸不仅与连铸工艺参数有关,也与气泡间的相互作用有关。研究Ar气泡在结晶器内的运动行为及其分布是连铸过程中需重点监控的指标之一。
由于连铸过程极其复杂以及高温环境的限制,大多数学者采用水模型实验或者数值模拟的方法研究Ar气泡的运动行为。倪冰等[1]的水模型实验结果表明,在不同吹气流量条件下,气泡的算术平均直径为2.6 mm,在上回流区、射流区和下回流区气泡的算术平均直径依次略微减小。而Ramos-Banderas等[2]的研究表明,在较大吹Ar量条件下,气泡的聚合效应强于气泡的破碎效应,较大吹Ar量下气泡的尺寸更大。Wu等[3]发现,当气体流量增加时,气泡数量也增加,气泡以更高的速率上浮,气体流量对气泡数量的影响比水流量的影响更加显著。刘崇林等[4]统计了整个结晶器内的气泡尺寸和数量浓度。结果表明,较大的气泡在水口附近上浮,较小的气泡在距离水口较远的区域上浮。王波等[5]的水模型研究表明,拉速是影响气泡运动行为的主要因素,其次是吹气量。Vikas等[6]发现气泡穿透深度主要取决于水流速和水口倾角。Lee等[7]也研究了吹Ar量和拉速对进入水口的初始气泡尺寸的影响规律。
Liu等[8~13]通过双Euler模型和群体平衡模型研究了结晶器内气泡的聚合和破碎行为,主要研究了钢液的流场、含气率分布和气泡尺寸分布等规律。Thomas和Sengupta[14]利用双Euler模型对结晶器内气-液两相流动、传热和传质进行了研究,分析了结晶器内部复杂的多相流动现象,预测了吹Ar对钢液流动、过热度耗散和板坯成分的影响。杨伟栋等[15]利用双向耦合Euler-Lagrange模型模拟了结晶器内钢水的流场,发现在结晶器水口出口处气泡破裂的概率最高,大量的Ar气泡从结晶器水口流出时会破碎分解成小气泡。结晶器水口出口上部区域的气泡聚合率高,水口出口下部区域气泡数量大大减少,且气泡聚合率较低。气泡距离水口出口的最远距离主要取决于气泡尺寸。金小礼等[16]发现弯月面处的枝晶是阻碍气泡上浮,导致气泡被凝固坯壳捕获的一个主要原因。宫佳睿等[17]针对连铸结晶器内Ar气泡的瞬态运动和捕捉行为,利用耦合流动-传热凝固-气泡运动的大涡模拟模型研究了结晶器内钢液的非稳态湍流场和Ar气泡的瞬态运动特征。结果表明,凝固坯壳对结晶器内钢液流场有较大影响,小尺寸的气泡更容易运动到液相穴较深的区域,从而易被凝固坯壳捕获;且随着拉速增大,气泡的穿透深度增加。Miki和Thomas[18]利用Euler-Lagrange模型分析了Marangoni力对气泡运动行为的影响。此外,Yuan等[19,20]建立了考虑分子级别的受力和水平方向以及竖直方向受力的凝固坯壳捕获气泡的力平衡模型。
虽然水模型研究能从总体上揭示结晶器内的气泡运动行为,但考虑到实际钢液的自身特性和水模型比例等因素,实验结果可能无法准确预测熔池内的实际情况,导致某些细节和特性无法很好地被模拟或捕捉到。同时,上述研究在模拟及分析Ar气泡的运动时,很少会考虑Ar气泡破碎和碰撞的相互作用或者考虑凝固坯壳对气泡的捕获,多数研究仅考虑了其中1种情况,鲜有学者同时考虑这2种情况下Ar气泡的运动与分布。然而,无论是Ar气泡的相互作用或者凝固坯壳对气泡的捕获,都对结晶器内Ar气泡的运动与分布有着重要影响。本工作在研究影响Ar气泡的运动与分布行为的过程中将同时基于以上2种情况进行建模及分析,研究了拉速、吹Ar量、水口倾角和水口浸入深度这4种主要工艺参数对结晶器内Ar气泡运动行为的影响,得出了提高钢液洁净度和板坯质量的合适参数。
1 数学模型
1.1 基本假设
(1) 钢液视为不可压缩流体,且各相定义为均相物质,钢液的热物性参数为常数;(2) 不考虑结晶器内自由液面波动和保护渣对钢液流动的影响,忽略结晶器振动和结晶器锥度对钢液流动的影响;(3) 气泡物性参数各向同性,气泡视为刚性球体,气泡间的碰撞属于完全弹性碰撞,即气泡间的碰撞没有能量损失,忽略钢液温度和钢液静压强对气泡的影响。
1.2 控制方程
1.2.1 流动控制方程
连续方程[21]:
式中,ρ为钢液密度;vj 为钢液在xj 方向上的速度分量。
动量方程[22]:
式中,下标i = 1、2、3分别表示x、y、z方向的分量;vi 为钢液的速度分量;t为时间;p为压强;μeff为有效黏度系数;gi 为重力加速度;FTi 为热浮力;Smi 为动量方程源项;Fbli 为气泡运动产生的动量源项。
本工作采用低Reynolds数(Re) k-ε (其中,k为湍流动能,ε为湍流耗散率)模型[23]求解湍流方程,湍动能和湍流耗散方程如下:
式中,μ为钢液黏度;μτ 为湍流黏度;C1、C2、σk,σε 为经验常数,其值分别为1.44、1.92、1.00、1.30;f1和f2为湍流耗散率中的系数;D和E为湍流动能方程和湍流耗散率方程中的附加项;Gk 为平均速度梯度产生的湍动能生成项;Sk 和Sε 分别为湍流动能方程和湍流耗散率方程中的源项[24]。
1.2.2 凝固传热控制方程
本工作采用热焓-多孔介质法计算结晶器内钢液的凝固和熔化,能量方程[21]为:
式中,λ为钢液导热系数;T为温度;Se为能量方程源项[24];H为钢液总焓,其表达式如下:
式中,fL为液相率;Lh为钢液的凝固潜热;h为显焓,其表达式如下:
式中,href为参考温度下的热焓;Tref为参考温度;cp 为定压比热容。
定义液相率为:
式中,TS和TL分别为钢液的固相线温度和液相线温度。
1.2.3 离散相控制方程 (1) 气泡受力方程
采用Lagrange方法描述气泡在钢液中的运动行为,根据Newton第二定律,其控制方程可表示为:
式中, xb为气泡空间位置矢量; vb为气泡速度;mb为气泡质量; Fbl为气泡运动产生的动量源项; Fl、 Fd、 Fg、 Fb、 Fp、 Fvm分别为气泡所受到的升力、曳力、重力、浮力、压力梯度力和虚拟质量力,各受力的表达式及系数依据文献[15]确定,其中升力和曳力模型方程均通过UDF程序编写。
(2) 气泡破碎方程
对于给定的流体湍流强度,可通过下式计算湍流区中的气泡最大稳定尺寸(dmax)[22]:
式中,We为气泡破裂临界Weber数,对于空气-水体系一般取1.3,对于钢液-Ar体系一般取0.53[22];γb为气泡与流体间的表面张力系数,本工作取1.4。
当气泡尺寸d > dmax时,气泡发生破裂。本工作假设气泡破裂后生成2个等尺寸及等速度的子气泡。依据动量守恒定律可确定破裂后的子气泡的相关参数,即:
式中,r、m、 u 分别为气泡的半径、质量、速度,下标1、2表示气泡破裂之后产生的2个子气泡。气泡破裂后,其中1个子气泡的球心位于母气泡球心位置,另1个子气泡随机出现在母气泡周围任意位置。为了避免气泡破裂后立即发生聚合,假定2个子气泡球心的距离为2个子气泡半径之和的1.1倍[22]。
(3) 气泡碰撞方程
当2个气泡在流体内运动并相互靠近时,若2个气泡的半径之和大于或者等于2个气泡的距离,则认为气泡发生碰撞。
当气泡发生碰撞后,气泡间是相互聚合还是直接弹开,这与气泡碰撞聚合Weber数(Wecr)、等效直径(de)及碰撞系数(B)等都有关,相应的公式为:
式中,R1和R2分别为2个气泡的半径; ur为2个气泡的相对速度;b为2个气泡的球心连线在与 ur垂直平面上的投影长度;d1和d2分别为2个气泡的直径;re为等效半径。
本工作依据偏心碰撞模型[6],通过以下2个判据判断气泡聚合还是弹开,即:
(i) 当de ≤ 2.3 mm时,若Wecr(1 - B2) < 0.16 + B / 24,则相互聚合,否则直接弹开;(ii) 当de > 2.3 mm时,若| ur| < 0.11 m/s,则相互聚合,否则直接弹开。
当2个气泡发生碰撞并聚合为1个大气泡时,该大气泡的速度( u3)根据动量守恒可表示为:
当2个气泡发生碰撞并弹开后,2个气泡碰撞前后球心连线方向上的动量守恒,因此碰撞后2个气泡的速度可表示为:
图1
图1
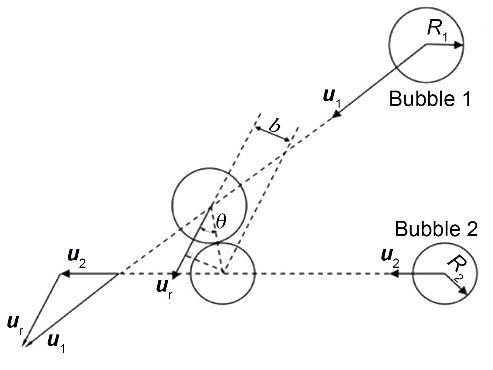
气泡偏心碰撞模型示意图[15] (0 < B < 1,其中B为碰撞系数)
Fig.1
Schematic of eccentric collision model of bubbles[15] (0 < B < 1, B—collision coefficient, R1—radius of Bubble 1, R2—radius of Bubble 2, ur—relative velocity of two bubbles, b—projection length of the line connecting the centers of two bubbles on the vertical plane with respect to the ur, θ—angle between the line connecting the centers of two bubbles and ur, u1—velocity of Bubble 1, u2—velocity of Bubble 2)
(4) 气泡捕获模型
1.3 边界条件
(1) 入口:由钢液质量守恒定律可确定钢液在水口处的入口速度。气泡随着钢液一起运动,初始速度与钢液一致。入口处钢液的湍动能(kin)和湍流耗散率(εin)分别为:
(2) 结晶器液面设置为自由滑移边界;气泡上浮到液面即认为进入渣层。传热条件设置为绝热。
(3) 结晶器和二冷区壁面均为无滑移壁面,壁面速度为拉坯速度,方向沿拉坯方向;气泡碰壁通过捕获模型判断是反弹还是捕获。
结晶器壁面冷却条件采用热流边界条件,其热流密度通过以下关系式确定:
式中,q为结晶器热流密度;β为经验常数;l为结晶器有效长度;vp为拉速。
二冷区壁面采用对流换热边界条件,其传热系数通过以下关系式确定:
式中,hT为传热系数;W为喷水密度;tw为铸坯表面冷却水温度;α为与二冷区冷却相关的系数。
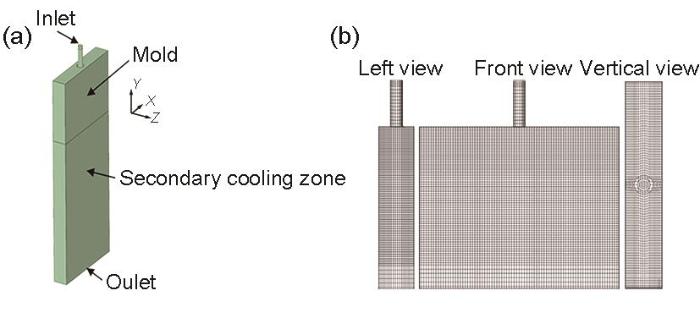
1.4 几何参数
图2
表1 模拟计算主要参数
Table 1
| Process parameter | Symbol | Value | Unit |
|---|---|---|---|
| Mold length, width, and thickness | Lm × Wm × Tm | 800 × 1300 × 230 | mm3 |
| Nozzle diameter | din | 80 | mm |
| Nozzle outlet height and width | Hout × Wout | 83 | mm2 |
| Nozzle angle | dθ | -10, -15, -20 | (°) |
| Nozzle immersion depth | dim | 130, 180, 230 | mm |
| Casting speed | vp | 1.2, 1.4, 1.6 | m·min-1 |
| Degree of superheat | Tsub | 15 | K |
| Initial particle diameter of argon bubbles | dinit | 1 | mm |
| Ar blowing rate | Qb | 5, 10, 20 | L·min-1 |
| Density of molten steel | ρ | 7020 | kg·m-3 |
| Viscosity of molten steel | μ | 0.0067 | Pa·s-1 |
| Specific heat capacity at constant pressure | cp | 750 | J·kg-1·K-1 |
| Thermal conductivity | λ | 30 | W·m-1·K-1 |
| Coefficient of thermal expansion | γt | 0.0001 | K-1 |
| Latent heat | Lh | 270 | kJ·kg-1 |
| Argon-liquid steel surface tension coefficient | γb | 1.4 | N·m-1 |
| Bubble density | ρb | 0.56 | kg·m-3 |
| Solidus temperature | TS | 1730 | K |
| Liquidus temperature | TL | 1786 | K |
1.5 网格无关性验证
为保证计算结果的精确性,对网格进行了无关性验证。对4种不同数量的网格(A、B、C、D)进行了误差分析,误差结果如表2所示。结果表明,随着网格数量的增加,误差逐渐减小。考虑到计算资源与计算成本,在不影响计算精度的前提下,选择B网格进行模拟计算。
表2 4种不同网格数量的网格无关性验证
Table 2
| Case | Total cell number | (| Vj - VD| / | VD|) / % | (|Tj - TD| / |TD|) / % | (|Lj - LD| / |LD|) / % |
|---|---|---|---|---|
| A | 353680 | 1.800 | 1.38 | 2.909 |
| B | 405784 | 1.648 | 1.36 | 1.075 |
| C | 457888 | 0.379 | 0.65 | 0.506 |
| D | 536044 | - | - | - |
1.6 模型验证方法
2 结果与讨论
2.1 气泡模型验证
图3
图4
图5
2.2 结晶器内的钢液流动与气泡运动行为
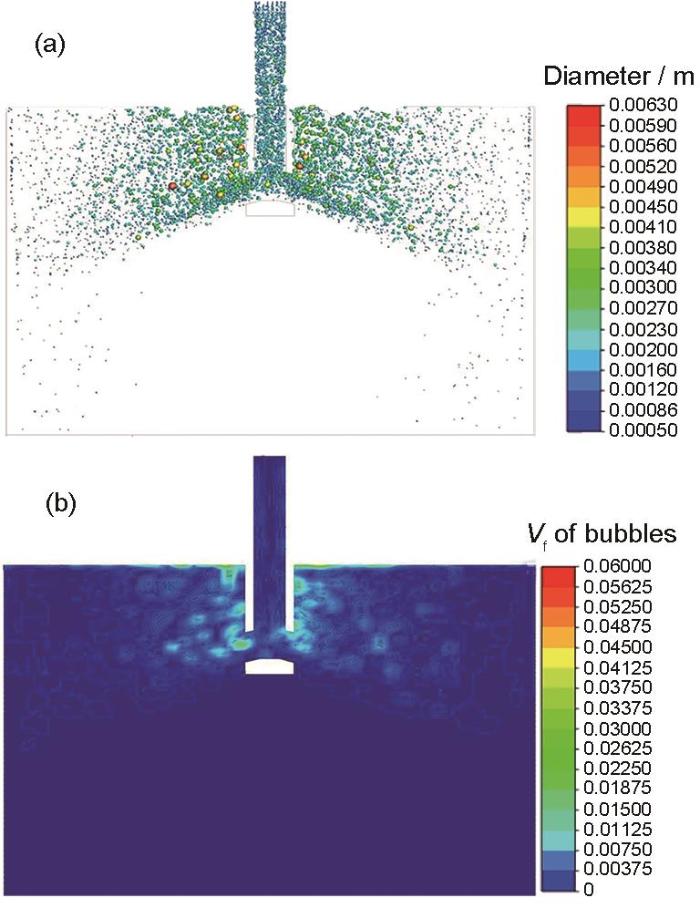
图6[26]为在水流量3.16 m3/h、Ar气量0.074 m3/h、水口底部形状凹形、水口插入深度78 mm的条件下,结晶器内气泡分布的水模型实验结果[26]。图7为在拉速1.4 m/min、吹Ar量10 L/min、水口倾角-15°、水口插入深度180 mm的条件下,数值模拟得到的Ar在结晶器内的气泡和含气率分布。可见,气泡运动和分布的模拟结果基本符合水模型实验规律,数值模拟结果可以正确地反映气泡在结晶器内的分布。后续研究结晶器内不同工艺参数下气泡的分布、含气率、数量和粒径以及被捕获的气泡量和不同直径气泡的捕获占比,其计算条件均以此为基准,分别改变拉速、吹Ar量、水口倾角、水口插入深度,且其他条件均保持不变,以达到控制变量的目的。从图7中可以看出,由于气泡破碎和气泡碰撞-聚合,使得结晶器内各个区域的含气率不同,气泡直径大小不同。大气泡主要在水口附近上浮,中等尺寸气泡在远离水口区域上浮,小气泡主要在窄面附近上浮,这符合实际连铸结晶器生产过程中气泡的直径分布,与宫佳睿等[17]没有考虑结晶器内气泡相互作用的单一粒径模型相比,本工作的聚合-破碎模型更具优越性且符合实际,故考虑气泡破碎与气泡碰撞是有必要的。
图6
图7
图7
结晶器内的Ar气泡分布和含气率分布
Fig.7
Distribution of Ar bubbles (a) and gas volume fraction (b) of the mold (The casting speed is 1.4 m/min, the Ar blowing rate is 10 L/min, the nozzle angle is -15°, and the nozzle immersion depth is 180 mm. Vf—volume fraction)
图8为拉速1.4 m/min、吹Ar量10 L/min、水口倾角-15°、水口插入深度180 mm条件下,结晶器中心截面上的速度和流场分布。可以看出,钢液从结晶器水口流出,冲击结晶器窄面后形成典型的上、下两股返流区域。钢液流股速度在水口底部和水口出口最大,钢液加速冲击到水口底部并发生转向,然后分成左右2个方向运动到结晶器窄面。与此类似,图9为在拉速1.4 m/min、吹Ar量10 L/min、水口倾角-15°、水口插入深度180 mm的条件下气泡在结晶器内不同时刻的运动轨迹。可见,气泡从水口的透气砖进入水口后,气泡在水口内发生碰撞、聚合或者弹开。气泡随着钢液流股运动至水口底部,随后分成2个方向从水口出口运动至结晶器内,之后在结晶器内运动。
图8
图8
结晶器中心截面上的速度和流场分布
Fig.8
Velocity distribution (a) and flow field distribution (b) on center section of mold (The casting speed is 1.4 m/min, the Ar blowing rate is 10 L/min, the nozzle angle is -15°, and the nozzle immersion depth is 180 mm)
图9
图9
Ar气泡在结晶器内不同时刻(t)的运动轨迹
Fig.9
Trajectories of Ar bubbles in the mold at different time (t) (The casting speed is 1.4 m/min, the Ar blowing rate is 10 L/min, the nozzle angle is -15°, and the nozzle immersion depth is 180 mm)
(a)
2.3 不同工艺参数下的气泡运动特征
2.3.1 拉速对气泡分布的影响
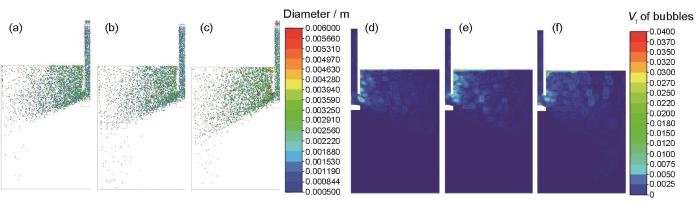
图10为吹Ar量10 L/min、水口倾角-15°、水口插入深度180 mm条件下,不同拉速下结晶器内的气泡分布和含气率分布。由图10a~c可知,当拉速为1.2 m/min时,钢液流股对气泡的冲击力较小,气泡之间很容易发生碰撞和聚合,此时大尺寸的气泡相对较多,小尺寸的气泡相对较少。气泡在浮力作用下会发生上浮,大多数尺寸较大的气泡在水口附近上浮,少量尺寸较小的气泡在远离水口附近上浮,而更小尺寸的气泡跟随钢液流股运动到结晶器深处。当拉速增大到1.6 m/min时,钢液流股对气泡的冲击增大,钢液的湍流耗散率增加,此时气泡很难发生聚合,更容易发生破碎。少量的较大尺寸气泡会在水口附近上浮,更多的较大尺寸气泡会在远离水口区域及窄面附近上浮。这是因为当拉速增大时,气泡受到钢液流股的裹挟较大,很容易运动到窄面,然后在合力的作用下上浮,其中也有少部分尺寸较小的气泡跟随钢液流股运动到结晶器深处,容易被初生凝固坯壳捕获,从而导致严重的铸坯质量缺陷。
图10
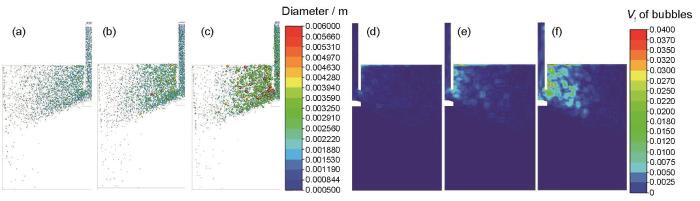
图10
不同拉速下结晶器内的气泡与含气率分布
Fig.10
Distributions of bubbles (a-c) and gas volume fractions (d-f) of the mold with different casting speeds (The Ar blowing rate is 10 L/min, the nozzle angle is -15°, and the nozzle immersion depth is 180 mm)
(a, d) 1.2 m/min (b, e) 1.4 m/min (c, f) 1.6 m/min
从图10d~f可以明显看出,随着拉速增加,气泡在结晶器内的分布更加弥散,气泡的主要运动范围为从水口附近到窄面附近,但相应的气泡体积分数却不断减少。这是由于拉速增大,钢液的湍动能和湍流耗散率均增大,气泡很难聚合。而且已经在水口内部聚合的气泡,运动到水口出口时则由于较大的湍流耗散率,使得气泡发生了破碎,气泡的直径变小,导致水口附近的气泡和随着钢液流股运动的气泡的体积均有所减小,所以钢液中的气泡分布更加弥散,有助于捕捉夹杂物。但由于气泡的直径减小,更小的气泡会运动到结晶器深处从而更加容易被凝固坯壳捕获,造成铸坯质量缺陷,所以只能适当增大拉速。
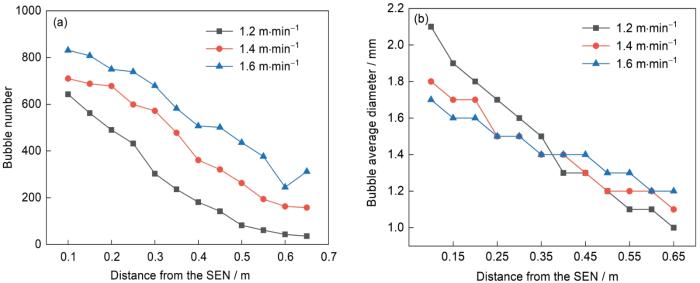
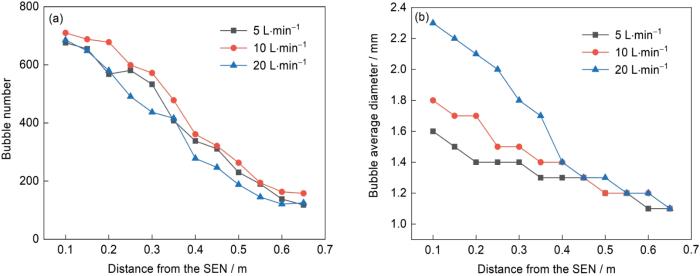
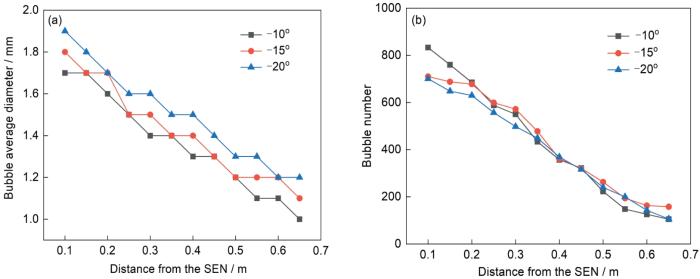
图11为不同拉速下结晶器内的气泡数目和平均直径。由图可知,在不同拉速下,随着离开水口出口的距离不断增加,气泡数量和气泡平均直径不断减少。当拉速为1.2 m/min时,水口附近的气泡数量最少,气泡平均直径最大,约为2.1 mm;窄面附近的气泡数量也最少,气泡平均直径最小,约为1.0 mm。当拉速为1.6 m/min时,水口附近的气泡数量最多,气泡平均直径最小,约为1.7 mm;窄面附近的气泡数量也最多,气泡平均直径最大,约为1.2 mm。这是因为拉速较小时,湍动能和湍流耗散率均较小,气泡更加容易聚合而不容易破碎,此时水口附近的气泡数量较少,尺寸较大。而且气泡聚合后形成的大部分大尺寸气泡在水口附近上浮,由于钢液流股的冲击较小,大尺寸气泡难以运动到窄面附近,仅有少量的小尺寸气泡可以运动到窄面附近,所以此时窄面附近的气泡数量也较少,窄面附近的气泡平均直径相对较小。当拉速较大时,大尺寸气泡容易发生破碎从而形成中等尺寸的气泡和小尺寸气泡,气泡每次发生破碎,气泡数目便会增加,所以此时水口附近的气泡数量较多。而中等尺寸的气泡由于钢液流股的冲击较大,一部分继续发生破碎,一部分则会跟随钢液流股运动到窄面附近发生上浮。这样窄面附近不仅有小尺寸气泡,还有一部分跟随钢液流股运动来的中等尺寸气泡,所以窄面附近的气泡平均直径相对较大。
图11
图11
不同拉速下结晶器内气泡数量和平均直径
Fig.11
Numbers (a) and average diameters (b) of bubbles in the mold with different casting speeds (SEN—submerged entry nozzle)
图12
图12
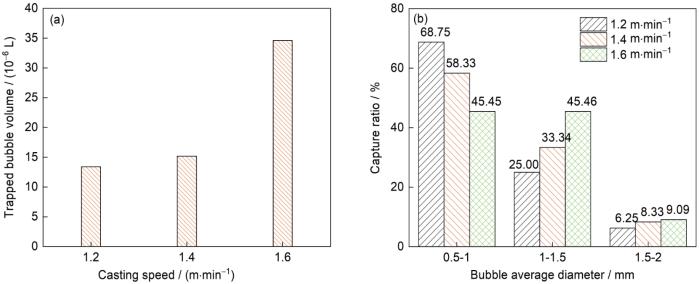
不同拉速下结晶器内的被捕获气泡量和不同直径气泡的捕获占比
Fig.12
Trapped bubble volumes (a) and capture ratio of bubbles with different diameters (b) of the mold with different casting speeds
由图12b可知,当拉速为1.2 m/min时,被凝固坯壳捕获的气泡中小尺寸(0.5~1.0 mm)气泡的占比最大。随着拉速增大,凝固坯壳对气泡的捕获体积不断增大,被捕获的气泡中各个尺寸的气泡占比也不断变化。拉速较小时,大量的气泡在水口内发生聚合后便在水口附近上浮,仅有小尺寸气泡和少量的大、中等尺寸气泡能够运动到结晶器窄面和窄面附近,所以此时被凝固坯壳捕获的基本是小尺寸气泡,而中等尺寸的气泡和大尺寸气泡被捕获的较少,所以此时小尺寸气泡的捕获占比最大。当拉速增大时,由于钢液流股冲击较大,气泡更加容易被钢液流股带到结晶器窄面。此时中等尺寸(1.0~1.5 mm)的气泡一部分发生破碎形成小气泡,另一部分则跟随钢液流股运动到窄面和窄面附近,此时窄面附近的气泡平均直径增加,中等尺寸气泡占比增加,凝固坯壳捕获中等尺寸气泡的数量增多,所以此时捕获的中等尺寸气泡的占比较大。而单一粒径模型研究[18]表明,随着拉速增大,小气泡的捕获占比增大。因此,考虑气泡碰撞、破碎和聚合是有必要的,能更好地揭示结晶器内气泡运动的基本规律。但拉速变化时,凝固坯壳对大尺寸气泡的捕获占比影响不大。主要是因为无论是较大的拉速还是较小的拉速,大气泡主要集中在水口出口处,并随即上浮到达液面。当拉速增大时,大气泡很难形成,即使气泡间的碰撞形成了大尺寸气泡,但是随着钢液流股的冲击,在运动的过程中大气泡也会破碎成中等尺寸的气泡。所以可以明显看出,较小和较大的拉速对大气泡的捕获占比影响均很小,其主要影响小尺寸和中等尺寸气泡的捕获占比。
2.3.2 吹Ar量对气泡分布的影响
图13为拉速1.4 m/min、水口倾角-15°、水口插入深度180 mm条件下,不同吹Ar量下结晶器内的气泡分布和含气率分布。可见,当吹Ar量较小时,气泡与气泡之间的碰撞概率较低,总体而言气泡尺寸较小,分散较为广泛,钢液中的含气率也较小。大量的小尺寸气泡可以运动到结晶器窄面附近。虽然小气泡对夹杂物的黏附效果更好,但是小尺寸气泡也更容易运动到结晶器深处,从而被凝固坯壳捕获,影响铸坯质量。当吹Ar量增大时,钢液中的含气率较大,气泡之间的碰撞概率较大,更多的气泡参与碰撞-聚合,所以总体而言气泡的尺寸较大,钢液中的含气率也增大。随着吹Ar量继续增大,水口内部及水口出口附近基本都是大气泡,水口附近的含气率很高。这是因为大气泡的体积较大,浮力更大,更容易上浮。由于大气泡对夹杂物的捕获效果不如小气泡,因此过大的吹Ar量并不能达到很好的捕获夹杂物效果。
图13
图13
不同吹Ar量下结晶器内的气泡分布和含气率分布
Fig.13
Distributions of bubbles (a-c) and gas volume fractions (d-f) of mold with different Ar blowing rates (The casting speed is 1.4 m/min, the nozzle angle is -15°, and the nozzl immesion depth is 180 mm)
(a, d) 5 L/min (b, e) 10 L/min (c, f) 20 L/min
图14是不同吹Ar量下结晶器内的气泡数量和平均直径分布。如图14a所示,吹Ar量从5 L/min增加到10 L/min时,随着吹Ar量增加,气泡数量增多,气泡的平均直径不断增大。当吹Ar量从10 L/min增加到20 L/min时,气泡数量有所减少,但气泡的平均直径不断增大。这是因为吹Ar量增大时,气泡数量增加,气泡间容易发生碰撞-聚合,所以气泡的平均直径增加。但继续增加吹Ar量,气泡间的碰撞频率会大幅度增加,碰撞-聚合发生的次数更多,此时由于吹Ar量增大而增加的气泡数量,会因为气泡间的碰撞-聚合而削弱减少,但碰撞-聚合后气泡的平均直径会增加,这从图13d~f的含气率分布可以明显看出。吹Ar量对气泡尺寸的影响规律与Ramos-Banderas等[2]的测试结果相一致。
图14
图14
不同吹Ar量下结晶器内的气泡数量和平均直径
Fig.14
Numbers (a) and average diameters (b) of bubbles in the mold with different Ar blowing rates
如图14b所示,在不同吹Ar量下,水口出口附近气泡的平均直径相差较大。在远离水口区域,当气泡距离水口出口0.4 m时,气泡的平均直径的差值开始减小。当气泡到达窄面及窄面附近时,气泡的平均直径基本没有差异,均在0.001 mm左右。这主要是因为虽然随着吹Ar量增加,气泡之间的碰撞概率增大,气泡更加容易聚合,水口附近的气泡平均直径最大。由于大气泡更加容易上浮,所以较大的气泡很快就在水口出口附近开始上浮,当气泡运动到结晶器窄面附近时,大尺寸气泡基本全部上浮,只剩下小尺寸气泡。所以增加吹Ar量,只会影响水口附近的气泡直径,对窄面附近的气泡直径无太大影响。
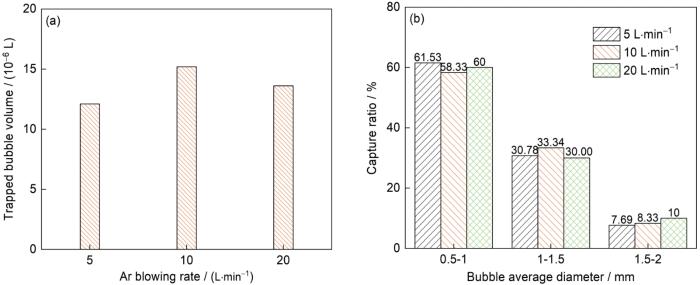
图15是不同吹Ar量下结晶器内被凝固坯壳捕获的气泡体积和不同直径气泡的捕获占比。可见,在3个吹Ar量下,被凝固坯壳捕获的气泡数量的差异不明显。吹Ar量从5 L/min增加到10 L/min时,气泡被凝固坯壳捕获的体积略有增大。吹Ar量从10 L/min增加到20 L/min时,气泡被凝固坯壳捕获的体积又略有减少。这与结晶器内气泡数量变化有关。当吹Ar量增加时,结晶器内气泡数量增加,气泡随着钢液流股运动,更多的气泡被带到结晶器窄面,容易被凝固坯壳捕获,所以被凝固坯壳捕获的气泡体积增加。吹Ar量继续增大,气泡间的碰撞频率大幅度增加,碰撞-聚合发生的次数更多,此时由于吹Ar量增大而增加的气泡数量,会因为气泡间的碰撞-聚合而被削弱减少,跟随钢液流股运动被带到结晶器窄面的气泡减少,所以此时被凝固坯壳捕获的气泡体积有所减少。
图15
图15
不同吹Ar量下结晶器内的气泡捕获量和不同直径气泡的捕获率
Fig.15
Trapped bubble volumes (a) and capture ratios of bubbles with different diameters (b) of the mold with different Ar blowing rates
同样,增大吹Ar量后,被凝固坯壳捕获的相同尺寸气泡的占比也变化不大。被捕获的气泡中,小尺寸气泡的占比最大。这是因为如图15b所示,随着吹Ar量增大,虽然水口附近的气泡直径增加,但对窄面附近的气泡直径没有太大影响,大气泡基本都在水口出口附近上浮,能够到达结晶器窄面的大部分都是小尺寸气泡和部分中等尺寸气泡,所以增加吹Ar量对被凝固坯壳捕获的气泡尺寸的影响较小。
2.3.3 水口倾角对气泡分布的影响
图16为拉速1.4 m/min、吹Ar量10 L/min、水口插入深度180 mm的条件下,不同水口倾角结晶器内的气泡和含气率分布。如图所示,随着水口向下倾角增加,气泡的分布规律有明显变化。依据本工作计算结果和文献[22,27]可知,当水口向下倾角较小时,钢液从入口冲击到水口底部发生转向到达水口出口时,其产生的湍动能和湍流耗散率较大,导致在水口内部大量已聚合的大气泡发生了破碎并形成小气泡,所以水口附近很难见到较大尺寸的气泡,水口附近的含气率也较低,并且大量的小尺寸气泡会运动到结晶器窄面,此时气泡分布较弥散,但以小尺寸气泡为主。随着水口向下倾角增加,水口底部到水口出口钢液转向所产生的湍动能较小,气泡不容易发生破碎,在水口内部碰撞并聚合的大气泡则在水口附近上浮,此时水口附近的含气率最大。因此,如图17a所示,随着水口向下倾角不断增大,在水口附近和窄面附近气泡的平均直径均会不断增大。当水口倾角为-10°时,水口附近气泡的平均直径约为1.0 mm,当水口倾角为-20°时,水口附近气泡的平均直径约为1.2 mm。故在其他工艺参数相同的条件下,水口向下倾角较小时产生的气泡大部分为小尺寸气泡;水口向下倾角较大时产生的气泡不容易破碎,大部分为中等尺寸的气泡和大尺寸气泡。
图16
图16
不同水口倾角结晶器内的气泡分布和含气率分布
Fig.16
Distributions of bubbles (a-c) and gas volume fractions (d-f) of the mold with different nozzle angles (The casting speed is 1.4 m/min, the nozzle angle is 15°, and the nozzle immesion depth is 180 mm)
(a, d) -10° (b, e) -15° (c, f) -20°
图17
图17
不同水口倾角下结晶器内的气泡平均直径和气泡数量
Fig.17
Average diameters (a) and numbers (b) of bubbles in the mold with different nozzle angles
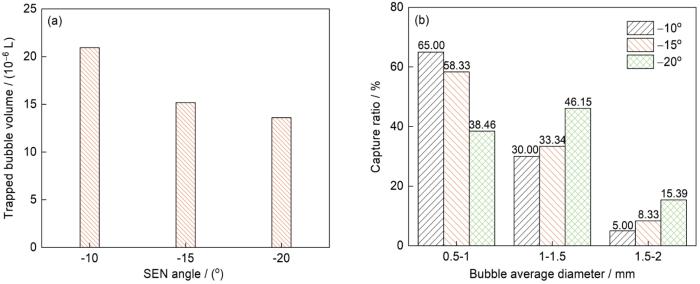
由图18可见,随着水口向下倾角增加,气泡被凝固坯壳捕获的体积减小,凝固坯壳中所捕获的气泡平均直径增大。特别是水口向下倾角从10°增加到15°后,被捕获的气泡体积显著减少。当水口倾角为-10°时,被捕获的气泡中小气泡的占比最大,达到65%;当水口倾角为-20°时,被捕获的气泡中,中等尺寸气泡占比最大,达到46.15%。如前所述,当水口倾角为-10°时,钢液流股运动到水口底部发生转向时产生的湍动能最大,此时气泡急剧破碎,流向结晶器内部的气泡数量显著增加,且小气泡更容易运动到结晶器深处被凝固坯壳捕获,所以此时小气泡的捕获占比最大,故水口向下倾角不宜过小。随着水口向下倾角的继续增大,结晶器内的气泡数量减少,气泡直径增大,在水口附近上浮去除的气泡数量增多,因此被凝固坯壳捕获的气泡体积有所减少。同时,如前文所述,虽然不断增加的大气泡主要在水口附近上浮,但是仍有部分由大气泡破碎而成的中等尺寸气泡会随着钢液流股运动到结晶器窄面,此时结晶器窄面及窄面附近的气泡平均直径较大,故随着水口向下倾角增加,凝固坯壳捕获气泡的平均直径也会随之增大。可见,水口倾角对凝固壳捕获气泡的行为有明显影响,适当增大水口向下倾角可以减少凝固坯壳对气泡的捕获体积。
图18
图18
不同水口倾角下结晶器内气泡被捕获量和不同直径气泡的捕获占比
Fig.18
Trapped bubble volumes (a) and capture ratios of bubbles with different diameters (b) of the mold with different nozzle angles
2.3.4 水口浸入深度对气泡分布的影响
图19为拉速1.4 m/min、吹Ar量10 L/min、水口倾角-15°的条件下,不同水口浸入深度下结晶器内的气泡和含气率分布。由图可知,随着水口浸入深度增加,气泡随着钢液流股裹挟运动的距离不断减小。当水口浸入深度为130 mm时,跟随钢液主流股的气泡从水口出口运动至结晶器宽面3/4处。当水口浸入深度为230 mm时,气泡主要在结晶器水口附近上浮,大尺寸和中等尺寸的气泡只能运动到水口出口与窄面的中间位置。这主要是因为水口浸入深度较小时,如图19a和b所示,水口附近气泡较小,Ar气泡可更好地随着钢液流股运动,因此气泡分布较为弥散且此时钢液中的含气率较小。而水口浸入深度较大时,水口附近气泡尺寸较大,由于大尺寸和中等尺寸的气泡比小尺寸气泡更容易上浮,因此气泡从水口出口流出时,很快就会上浮,此时可以明显看出,水口附近的含气率较大。这说明过大的水口浸入深度使得气泡不能很好地跟随钢液流股运动,不利于对夹杂物的裹挟上浮,同时容易加剧水口附近的液面波动,可能导致产生卷渣。
图19
图19
不同水口浸入深度下结晶器内的气泡分布和含气率
Fig.19
Distributions of bubbles (a-c) and gas volume fractions (d-f) of the mold with different nozzle immersion depths (The casting speed is 1.4 m/min, the Ar blowing rate is 10 L/min, and the nozzle angle is -15°)
(a, d) 130 mm (b, e) 180 mm (c, f) 230 mm
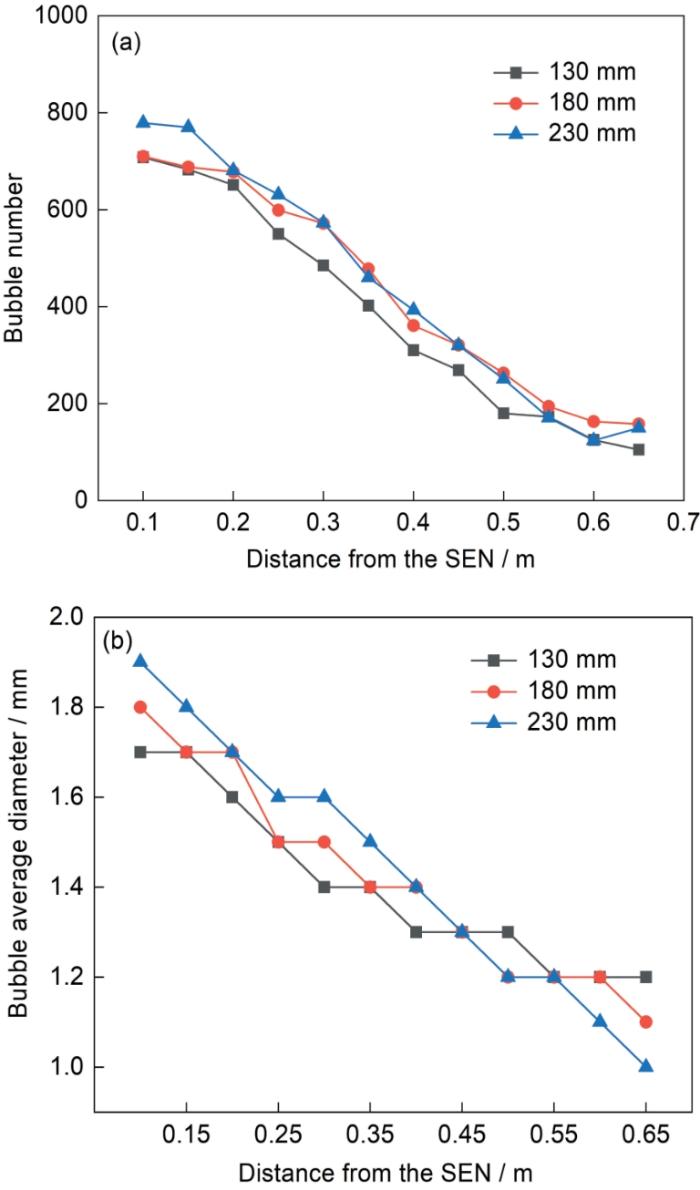
图20为不同水口浸入深度下结晶器内的气泡数量和气泡平均直径。随着水口浸入深度增加,结晶器内水口附近的气泡数量略有增加。当水口浸入深度在130 mm时,窄面附近的气泡平均直径最大,约为1.2 mm;当水口浸入深度在230 mm时,水口附近的气泡平均气泡直径最大,约为1.9 mm。当水口浸入深度为180 mm时,结晶器内的气泡直径介于其他2个浸入深度之间。如前所述,当水口浸入深度过大时,气泡并不能很好地随钢液流股运动,尤其是大气泡,当运动到水口出口时基本已经上浮,所以水口附近的气泡数量偏多,但气泡平均粒径较大。当水口浸入深度较小时,气泡可以很好地跟随钢液流股运动,在远离水口区域及窄面附近气泡分布得较为均匀,但水口浸入深度也不能过小,从气泡去除夹杂物的可能性看,一是气泡主要分布在结晶器的上方,不利于气泡分布的弥散性;二是窄面及窄面附近的气泡尺寸较大,气泡不易去除窄面附近的夹杂物,故水口浸入深度应有一个合适的深度。
图20
图20
不同水口浸入深度下结晶器内的气泡数量和平均直径
Fig.20
Numbers (a) and average diameters (b) of bubbles in the mold with different nozzle immersion depths
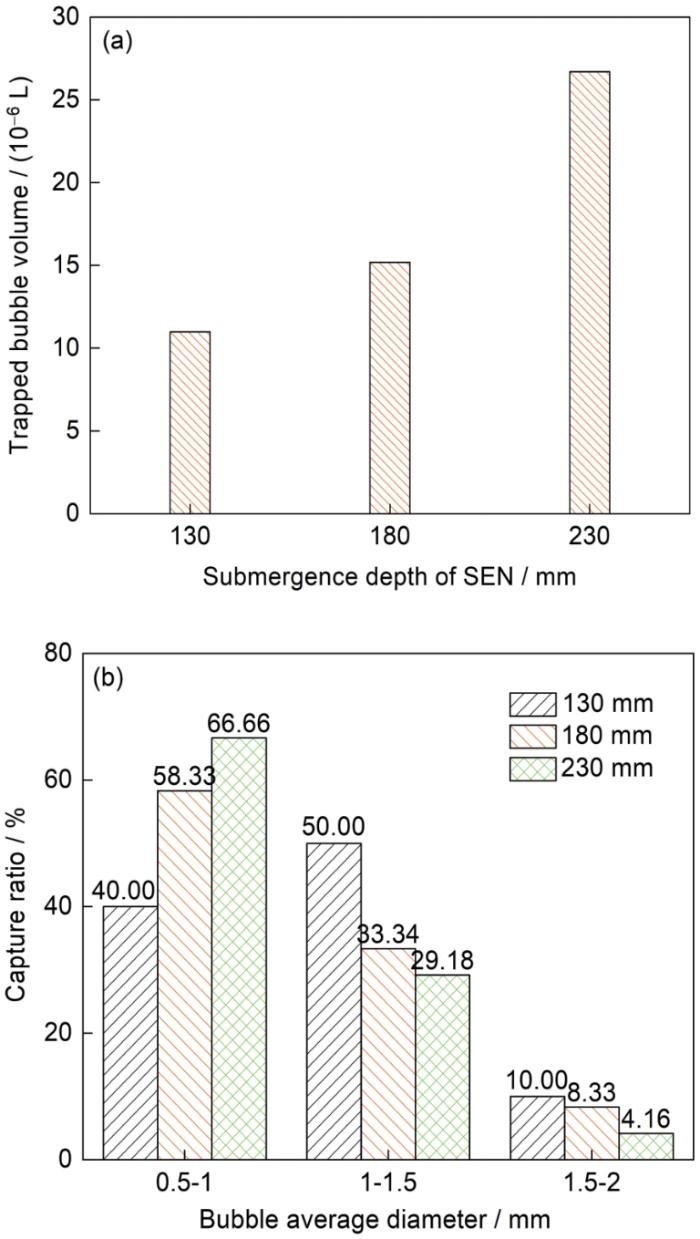
如图21所示,随着水口浸入深度增加,被凝固坯壳捕获的气泡数量增多,小尺寸气泡的捕获占比逐渐增大,大尺寸气泡的捕获占比逐渐减小。当水口浸入深度在230 mm时,凝固坯壳对小气泡的捕获占比最大,约有66.66%。与前文中结晶器内气泡的平均粒径分布规律一致,当水口浸入深度过大时,大尺寸气泡基本在水口出口流出时直接上浮,而小气泡则跟随钢液流股运动到结晶器窄面附近,所以被凝固坯壳捕获的气泡中小尺寸气泡的占比最大。而且水口浸入深度越大,小气泡越容易运动到结晶器深处,从而被凝固坯壳捕获,此时凝固坯壳对气泡的捕获量更多。当水口浸入深度超过180 mm后,被捕获的气泡数量会显著增多。因此水口浸入深度不宜过大,否则容易造成凝固坯壳质量缺陷。
图21
图21
不同水口浸入深度下结晶器内被气泡捕获数量和不同直径气泡的捕获占比
Fig.21
Trapped bubble volumes (a) and capture ratios of bubbles with different diameters (b) in the mold with different nozzle immersion depths
3 结论
(1) 气泡间的碰撞、聚合和破碎是影响结晶器内气泡直径的主要原因,结晶器内的工艺参数是影响气泡分布的主要因素。大尺寸气泡主要在水口附近上浮,中等尺寸气泡在远离水口区域上浮,小尺寸气泡主要在窄面附近上浮,其中一部分小气泡会运动到结晶器深处被凝固坯壳捕获,造成铸坯质量缺陷。
(2) 拉速是影响钢液洁净度和凝固坯壳质量的关键参数。适当增加拉速可以提高气泡在结晶器内的分布弥散性,气泡的平均直径较小,气泡的数量较多,有利于气泡黏附夹杂物,提高结晶器内钢液的洁净度,但拉速过大则会增大凝固坯壳对气泡的捕获数量。基于以上考虑,选取拉速为1.4 m/min较为合理。
(3) 吹Ar量主要影响结晶器内的气泡数量和气泡直径,对凝固坯壳捕获气泡的行为影响较小。适当增加吹Ar量可以增加结晶器内的气泡数量,水口附近的气泡直径略微增大,但对窄面附近的气泡直径影响较小;当吹Ar量过大时,结晶器内的气泡数量降低,水口附近的气泡直径显著增加。从结晶器内气泡的弥散分布和小气泡对夹杂物的较好裹挟效果考虑,选取10 L/min吹Ar量较为合理。
(4) 水口倾角对结晶器内气泡数量、气泡直径和窄面处凝固坯壳对气泡的捕获有较大影响。水口向下倾角太小,小气泡数量增加,这有利于对夹杂物的黏附去除,但也增加了凝固坯壳对气泡的捕获,影响凝固坯壳的质量;水口向下倾角过大,气泡不容易发生破碎,小气泡数量减少,大气泡数量增加,不利于气泡对夹杂物的黏附去除,但可以减少凝固坯壳对气泡的捕获,因此本工作推荐选取-15°水口倾角较为合理。
(5) 水口浸入深度主要影响结晶器内气泡的分布。当水口浸入深度较小时,气泡在结晶器内的分布较为弥散,但主要分布在结晶器上方;水口浸入深度过大时,大尺寸气泡和中等尺寸气泡集中在水口附近上浮,小气泡到达结晶器深处,不利于气泡的弥散分布,同时增加了凝固坯壳对气泡的捕获。浸入深度为180 mm较为合适。
参考文献
Water model study on bubble behavior in slab continuous casting mold
[J].
板坯连铸结晶器水模内气泡运动的实验研究
[J].
Dynamics of two-phase downwards flows in submerged entry nozzles and its influence on the two-phase flow in the mold
[J].
Experimental investigation of trajectories, velocities and size distributions of bubbles in a continuous-casting mold
[J].
Mathematical simulation on gas bubble movement in the water model for the slab caster mould
[J].
板坯结晶器水模型内气泡运动行为的数学模拟
[J].
Study on water modeling of slab continuous casting mould with argon blowing
[J].
吹氩板坯连铸结晶器水模型实验研究
[J].
Experimental simulation and mathematical modeling of air bubble movement in slab caster mold
[J].
Effect of refractory properties on initial bubble formation in continuous-casting nozzles
[J].
Large-Eddy simulation of transient horizontal gas-liquid flow in continuous casting using dynamic subgrid-scale model
[J].
Multiple size group modeling of polydispersed bubbly flow in the mold: An analysis of turbulence and interfacial force models
[J].
Population balance modeling of polydispersed bubbly flow in continuous-casting using multiple-size-group approach
[J].
Transient asymmetric flow and bubble transport inside a slab continuous-casting mold
[J].
Euler-Euler-Lagrangian modeling for two-phase flow and particle transport in continuous casting mold
[J].
Modeling of bubble behaviors and size distribution in a slab continuous casting mold
[J].
The visualization of defect formation during casting processes
[J].
Study on multiphase transport phenomena in continuous casting mold with argon blowing considering bubble coalescence and breakup
[D].
考虑气泡聚合和破碎的吹氩连铸结晶器内多相传输现象的研究
[D].
Physical simulation of Ar bubble behavior in the solid/liquid interface of continuous casting billet
[J].
Ar气泡在连铸坯固/液界面处运动行为的物理模拟研究
[J].
Transient movement and capture behavior of dispersed argon bubbles in continuous casting mold
[J].
连铸结晶器内弥散氩气泡的瞬态运动和捕捉行为
[J].
Modeling of inclusion removal in a tundish
[J].
Transient study of turbulent flow and particle transport during continuous casting of steel slabs
[D].
Study of transient flow and particle transport in continuous steel caster molds: Part II. Particle transport
[J].
Numerical simulation of molten steel flow, heat transfer, solidification, and inclusion migration in mold with vertical electromagnetic brake
[D].
立式电磁制动结晶器内钢液流动、传热凝固与夹杂物迁移的数值模拟研究
[D].
Fundamental research of suppressing metal liquid surface deformation and fluctuation by magnetic pressure
[D].
磁压控制金属液面变形和波动行为的基础研究
[D].
The coupled simulation of electromagnetic field, steel flow and solidification in soft-contact mold
[D].
软接触结晶器内电磁场及钢液流动凝固的数值模拟
[D].
Numerical simulation of flow and solidification in continuous casting process with mold electromagnetic stirring
[J].
Modeling of motion and interaction of discrete phases in continuous casting mold
[D].
连铸结晶器内离散相运动行为及相互作用的模拟
[D].
Numerical and physical simulation of argon gas injection in a continuous slab casting mold
[D].
板坯连铸结晶器内钢液吹氩过程数学物理模拟
[D].