钛合金是一种高强度的结构合金，具有高强度、高比刚度、耐蠕变性及较好的抗疲劳性能等特点，被广泛应用于航天航空、化工、海洋工业及生物医药等领域。钛合金的性能由其微观组织决定，根据热加工方法的不同，合金的组织存在差异。在α + β型钛合金中，常见的典型微观组织有等轴组织、片层组织、网篮组织和双态组织。这4种组织中，在相同强度等级下，片层组织的断裂韧性最好，有更好的抗疲劳裂纹扩展能力，更符合损伤容限设计的要求^[1]，得到了科研工作者的广泛关注，并进行了大量的理论实验研究和计算模拟。

Yoder等^[2,3]观察到Ti-6Al-4V合金中的α集束尺寸对疲劳裂纹的生长有一定的影响，研究认为由于片层组织中裂纹的分叉，在同时进行β退火和轧制退火时，裂纹的开裂速率显著降低。Hall和Hammond^[4]通过实验观测到片状α的厚度大于0.2 μm时，裂纹可显著偏离α/β界面。Banerjee等^[5]通过激光沉积方法制备了Ti-8Al-xV梯度成分合金，并观测析出的晶界α与β基体的取向关系，研究结果表明一些片状α从晶界附近形核，并向晶粒内生长，而另一些则从晶界α直接向晶粒内生长。Chong等^[6]讨论了双片层组织，发现在双相区的800~960℃温度区间进行热处理时，会获得不同的组织参数，得出转变β相的厚度随温度的增加而变宽，退火后水淬可得到此双片层α组织。马英杰等^[7]的研究表明，α相片层的厚度对近门槛阶段的裂纹扩展速率影响较大。α相越薄，裂纹扩展门槛值越高，团簇的尺寸就越小，α相长宽比越大及厚度越薄时，裂纹扩展速率越低。杨梅等^[8]对片层组织的生长机制进行了定量研究，包括界面能各向异性和热处理温度对片层生长的影响。结果表明，在高温热处理条件下，温度越高，α相沿长度方向生长越慢，片层的宽度和厚度越大；对于不同界面能各向异性，当界面能各向异性越强时，生成的α相越宽，残余β相宽度也越大。Wang等^[9]应用相场方法进一步对钛合金中的片层与网篮生长相互竞争机制进行了探讨，同时还研究了初生α相生长及织构等。Sun等^[10]采用相场模型对多晶Ti-6Al-4V合金的片层组织生长机制进行了二维尺度的讨论，同时还分析了片层α侧枝的形成。Huang等^[11]通过深冷处理分析了处理时间对Ti-6Al-4V合金组织和力学性能的影响，结果表明，试样的典型组织为片层组织，随着处理时间的延长，层状α相厚度减小、变细，提高了拉伸性能和抗裂纹扩展能力，导致低温处理后材料的拉伸强度、屈服强度和延伸率迅速上升。王刚等^[12]在二维尺度下模拟了双相区温度时的界面能各向异性和温度对α相形貌的影响。关于α片层与片层分叉现象，Shi等^[13~15]在考虑α/β相界面能和弹性能各向异性条件下，采用相场方法模拟了Ti-Mo体系片层分支的过程，说明了片层分叉是从α片层惯习面的凸出部分开始生长的。

针对复杂的钛合金微观组织，由于三维信息的不足，未能获得晶界、晶界α、α片层、α侧枝等全面的相对取向关系，无法用于实际的片层组织调控和性能调控。本工作主要应用相场模型对片层组织侧枝的生长机制进行三维尺度的研究，定量研究界面能各向异性对钛合金的片层α组织形貌的影响，并分析实验观察到的片层α侧枝的形成机理。

相场理论基于渐变界面模型而被提出，常见的相场模型是基于Ginzburg和Landau^[16]提出的用于处理超导电性的模型，模型包含了复杂的序参量与梯度向量。之后Allen等^[17]和Cahn等^[18]进行了优化，基于热力学方程同时考虑到非均匀体系中扩散界面，构建出当前广泛使用的瞬时微观结构演化模型。通常将相场模型分为2类：微观相场模型和连续相场模型。连续相场模型有2种，即分别应用于液-固相变和固态相变的相场模型。用于液-固界面的相场模型^[19,20]是引入一个相场变量用以区分液相和固相，比如场变量为0表示液相，场变量为1表示固相，介于0~1之间则表示液-固界面。该方法有效避免了跟踪界面。用于固态相变的相场模型需要引入的场变量主要包含成分序参量和结构序参量。此类相场模型最早是以Wang和Chen^[21,22]以Khachaturyan微观理论^[23]为基础引入微观组织的，可以应用于固态相变、马氏体相变和有序金属间化合物析出等。

在相场模型中，主要包含2个动力学方程，分别是Ginzburg-Landau控制的非保守场变量ηkr,t和φkr,t随时间的变化(r为空间位置，t为时间)，称为Allen-Cahn方程，如 式(1)，及Cahn-Hilliard控制的保守场变量(成分场xB)随时间的演化方程，如 式(2)^[24]。

式中，η表示结构场变量，φ表示相的体积分数，角标k表示体系中的k相；L为正的动力学系数，与界面迁移率μ有关；F为体系总自由能；f₀为相的体自由能；κ为梯度能系数，与场变量有关；V_m为体系的摩尔体积；M为动力参数，是场变量和成分的函数；ε为应变。

为解决界面厚度与界面能的限制问题，Kim-Kim-Suzuki (KKS)新模型^[25]将2者完全分离，使得相场方法不受材料体系的尺度限制，为多相体系和大规模的相场模拟奠定了基础。本工作为包含多个序参量的相场模型，任何一种晶粒结构位向向量可以用一组连续的序参量{η₁(r, t), η₂(r, t),…, η_p (r, t)}来表示，其中η_i (r, t) (i = 1, 2, 3, …, p)为不同晶粒的晶向场变量，下标i表示第i个组元，p表示可能的晶向数。体系中的总自由能可以写为：

式中，f0'为局域自由能密度；被积函数第二项为梯度能，界面能与梯度能系数κ成正比；V表示系统总体积。 式(3)可以应用于任何非均匀材料体系^[24]。

相场模型需要输入热动力学参数，如各相的Gibbs自由能、晶格常数、界面能、各向异性的弹性常数、动力学参数(原子迁移率)等^[26]。其中体系的Gibbs自由能等这些随温度和成分变化的数据可通过CALPHAD方法获得^[27]。对于片层生长的相场模型需要耦合KKS模型，即在相变过程中，将结构场变量与成分场变量耦合。将局域摩尔自由能G_m写成温度T、成分X_i (i代表Al和V元素, X_i 表示原子浓度)和序参量η(r, t)的函数，如 式(4)。

式中，p(η) = η(10 - 15η + 6η² )为插值函数；ω为双势阱高度，表征α与β两相平衡状态间的能垒；GmαX,T和GmβX,T分别为α和β相的摩尔自由能。局域摩尔自由能为复合能量、理想混合自由能和过剩自由能3者的总和。详见Pandat数据库。

为解决界面能与界面厚度受限的问题，KKS模型^[25]将体系总的Gibbs自由能写成：

式中，积分第一项gmT,xi,η为合金的体化学自由能，xi为组分i的质量浓度。第二项∑i=1n-1κi2∇ηi2和第三项ε2∇xi2分别为结构序参量和成分序参量对应的梯度能，表征结构和成分非均匀性对界面能的贡献。故，结构场变量η和浓度场变量X_k 的控制方程演化为 式(6)和(7)。

式中，Mki(T,Xi,η)为溶质的化学迁移率，化学迁移率与原子迁移率有关(式(8))^[28]；Mlp为原子迁移率；δjl和δlk表示Kronecker delta函数；下标i、j、k表示组元；l表示界面厚度。另外，式中的热力学和动力学数据分别来自Thermo-Calc和DICTRA数据库^[24]。

采用式(4)~(7)这4个相场方程模拟片层α的生长机制，考虑到梯度能系数影响梯度能量，而梯度能系数κij是一个三维二阶张量，可写成：

式中，k_x 、k_y 、k_z 均为正常数，表示三维方向上界面能的各向异性；κ0为正常数。给定初始参数，在x、y、z 3个方向上采用反周期边界条件^[29]求解微分方程，即可得到片层α的演化过程。

选取包含256Δx × 256Δx × 256Δx单元的立方体系，单元长度为Δx = 5 × 10^-8 m，故体系总的边长相当于12.8 μm。设置非共格界面能参数γ = 0.5 J/m²，自由能归一化参数为G₀ = 5 × 10⁴ J/mol，迁移率归一化参数为M₀ = 1.0 × 10^-18 mol·m²/(s·J)，时间步长dt = 0.1 s，无量纲参数为k˜=0.001814，L˜=2.0，ω˜=0.00036。

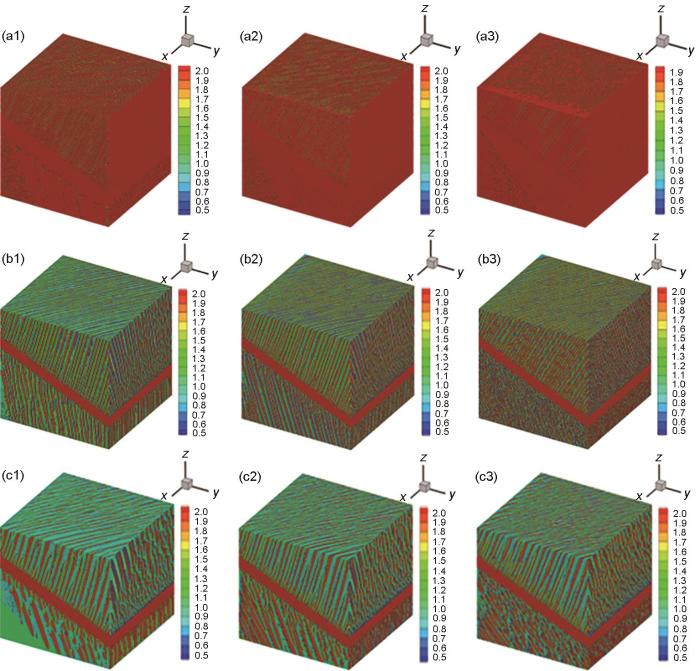
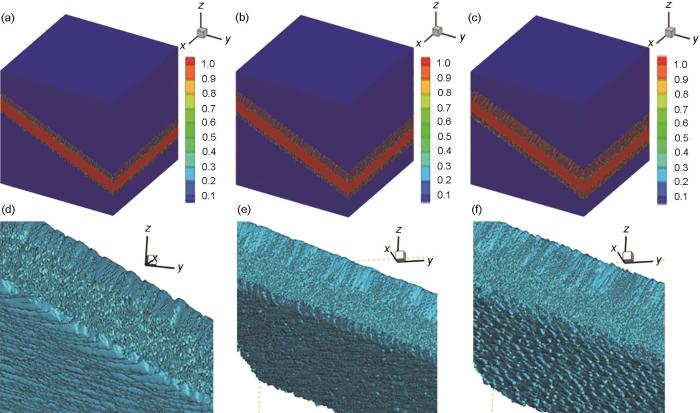
为了得到较好的断裂性能和裂纹扩展能力，更容易满足疲劳损伤容限设计的要求，钛合金的热加工方法通常采用在β单相区退火的热处理制度。其中，温度、界面能、冷却速率和弹性能等因素都会影响片层α组织的形貌。如图1的模拟结果表明，Ti-6Al-4V合金在820℃时能较好观察到片层组织及片层α侧枝的生长演化情况，且片层形貌较为规律，不同的界面能各向异性对应的形貌差异足够明显，故在进行相场模拟时将该体系置于热处理温度为820℃的条件下时效。通过相场模型模拟钛合金双相区的时效过程，忽略弹性作用，探索界面能各向异性对片层α形貌的影响。初始组织建立为α/β晶界有一层晶界α相，通过随机噪声在α/β界面处进行干扰，得出非平直界面的初始模型。此时α相的平衡成分是：X_Al = 0.105，X_V = 0.023；整个体系的平均成分是Ti-6Al-4V。设置片层α与2个β晶粒间的旋转矩阵角度分别为θ₁ = -40°，θ₂ = 20°，为研究界面能各向异性对片层组织的影响，用k_x:k_y:k_z 3者的比值表征x、y和z 3个方向上界面能各向异性的强弱，分别讨论各向异性比为(1) 0.4:0.1:1.0，(2) 0.6:0.1:1.0，(3) 0.8:0.1:1.0 这3种条件下片层α相的生长及片层侧枝的形貌。模拟结果中的颜色标尺为相应图中的序参量的数值。

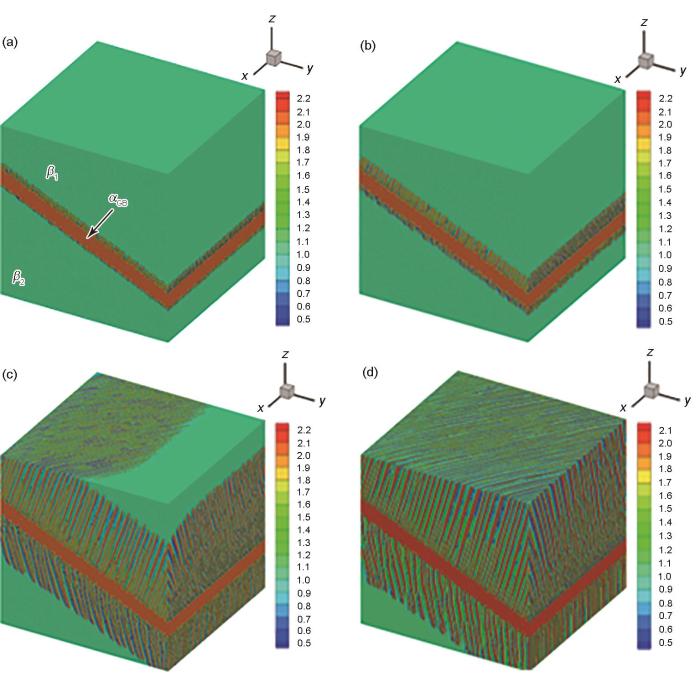
由于在较高的温度下成分和结构起伏会造成界面失稳，使得片层α在界面突起形核，并向相应的β晶粒内生长。图2为热处理温度在820℃、界面能各向异性比k_x:k_y:k_z = 0.6:0.1:1.0时，不同时刻下片层组织形貌的生长情况。可见，片层组织从晶界开始向两侧生长，其生长方向沿片层长度方向而垂直于厚度方向，并且其向β₁内的生长速率要高于向β₂内的生长速率。而β₁与β₂晶粒之间只有旋转矩阵角度不同，由此可见旋转矩阵角度对片层α的生长也有一定的影响。本工作所得结论与前期研究^[10]讨论过的旋转矩阵角度对片层α生长的影响基本一致。即在合理范围内，α/β相界角度相差越大，片层α越易形成且生长速率越快。另外，随时间的推移，片层α组织逐渐长大，当不同方向界面上的α片层相遇时，片层停止生长，直到片层α铺满整个晶粒，系统基本达到平衡。可观测到，三维片层的生长特征极为规律，排列整齐，目前尚未有片层交叉相互拦截的形态。从演化的形貌可见，生成的组织中存在残余的β基体、晶界α (grain boundary allotriomorphs，以下简称α_GB相)与片层α，这3种物质共存。

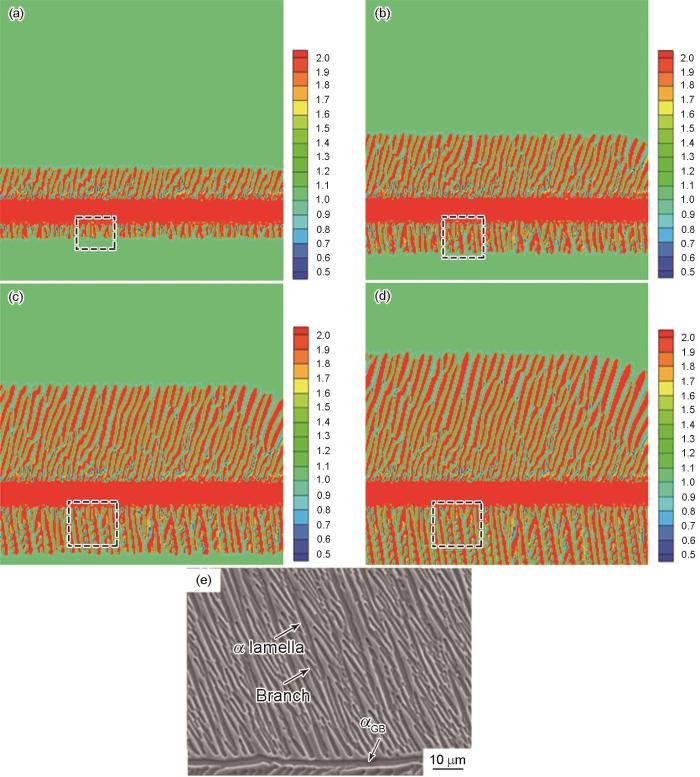
为清晰观察片层侧枝的生长情况，图3a~d展示了t = 100、200、300和400 s时z-x面上(y = 252.85Δx)的片层演化形貌，将片层α的生长过程进行展示。可以看出，三维片层α的生长规律与Sun等^[10]研究的二维情况基本一致。前期α片层的形态整体呈粗大棒状，之后逐渐细化，变得细长。随时间演化，在已生成的主片层上会出现类似侧枝形状的小片层，如图3中矩形虚线框所示。小侧枝从片层演化初始就存在^[10]，图3b显示，在t = 200 s时，片层α侧枝的形貌已经比较明显，之后随着主片层的生长而生长，变得越来越密集。实验结果如图3e^[10]所示，将模拟结果与其进行比较得出，从平面上观测三维模拟钛合金的片层及片层侧枝的生长和二维实验的结果是一致的。即片层α从晶界α开始向β晶粒内生长，片层侧枝广泛分布在主片层上，且在主片层根部侧枝形貌就已经存在。

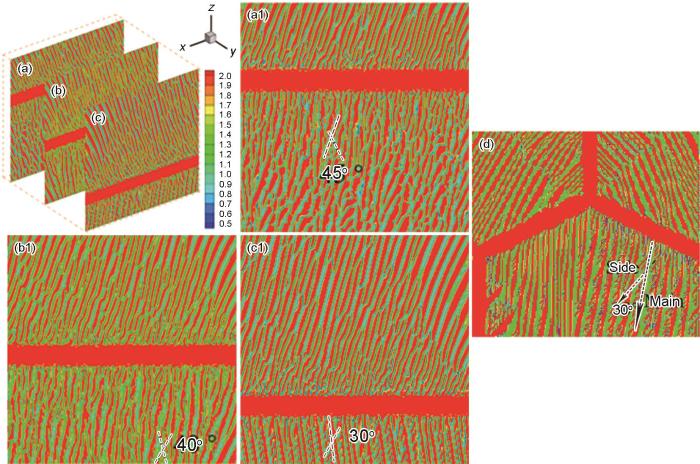
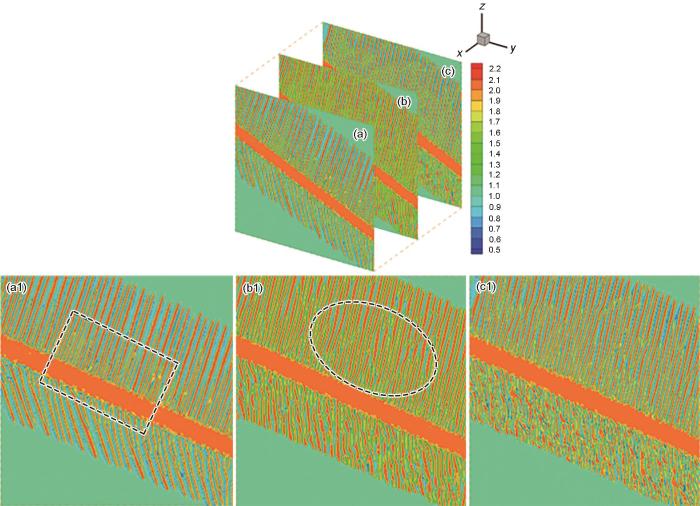
在三维视图下，在晶粒不同位置处，侧枝的形貌不同，但比二维下的形态更短小，侧枝的生长方向与二维尺度下的相比也存在差异，从晶粒的z-x切面形貌来看，侧枝从主片层以一定的角度冒出，之后有朝着主片层的取向生长的趋势，中间存在明显的生长方向的转变。另外，当侧枝明显时，与相应的主片层侧枝的角度与二维视图下的角度相同^[30]，大致呈30°，而当处于侧枝不明显的晶粒位置时，与相应主片层的角度较为随机，并且角度范围较大，无明显规律，如图4所示。

在研究三维条件下片层的生长过程时发现，片层α组织在β晶粒的不同位置生长的速度也不相同。图5说明相同时间步下(t = 500 s)，晶粒不同位置处片层α的生长情况。以x方向切片可见，靠近晶粒的最大边界处时，片层α组织生长得较为规律，且易观察到小侧枝的存在(图5a)。而且，由图5b1可知，片层在生长的过程中出现了断续和扭折的现象，如虚线圆圈中所示。本模拟条件无外加应力，因此可推断片层仅在热处理作用下即可发生扭折与断裂现象。在x = 255.8Δx切面上，片层的生长是比较整齐的，未出现片层断裂或扭转形貌；而在x = 128.5Δx和x = 1.2Δx切面上，片层均出现了生长间断的现象。因此，在相同的条件下，三维尺度下β晶粒内部的片层生长动力学过程也不完全相同。

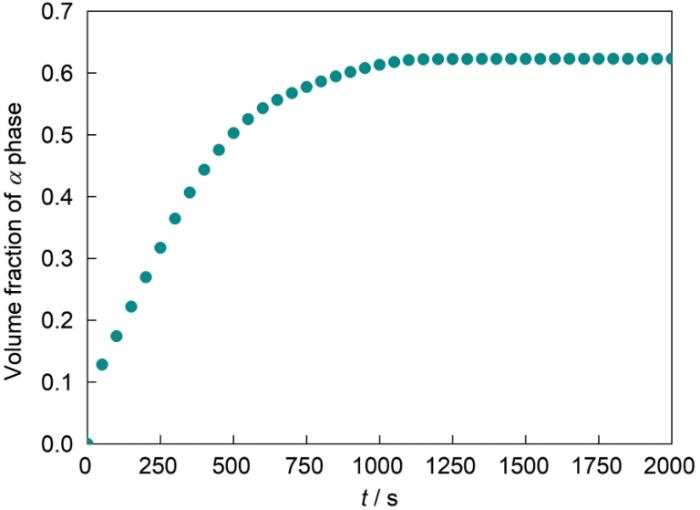
图6为α相体积分数随时间的演化规律。可见，片层α在生长过程中基本保持匀速，在t = 600 s的附近生长速率开始变缓，直到t = 1100 s时基本达到平衡。α相的平衡体积分数大约为62%。

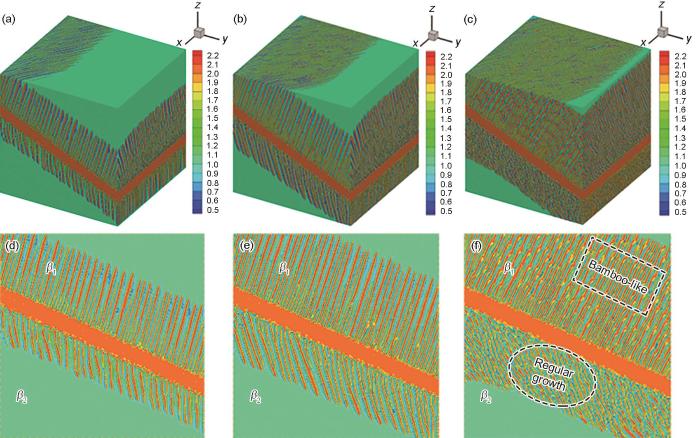
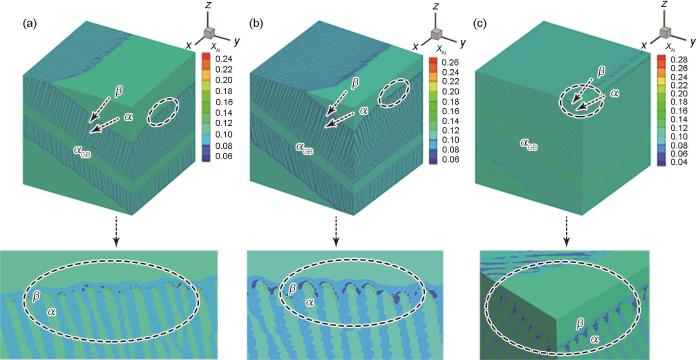
为探索界面能各向异性对片层α生长动力学的影响作用，选取820℃温度下界面能各向异性比分别为k_x:k_y:k_z =0.4:0.1:1.0、0.6:0.1:1.0和0.8:0.1:1.0探索片层α生长过程。如图7所示，不同界面能各向异性条件下片层α生长形貌显著不同。由模拟结果可看出，k_x:k_y:k_z =0.4:0.1:1.0条件下，各片层间距比较大，数量较少，可以明显观察到主片层α的侧枝形貌。片层基本呈棒状，侧枝也有一定的宽度；在k_x:k_y:k_z = 0.6:0.1:1.0条件下，片层α组织更密，排列更整齐。侧枝的宽度较小，呈针状。故界面能较大片层组织越易生长，与先前的研究结果一致。但各向异性比为0.8:0.1:1.0时(图7c)，界面能各向异性过大，β₂晶粒中片层断裂为几段，之后分别生长，形成该生长方向上各个片层堆挤生长的形貌，看起来较为杂乱，但是总体上保持一个方向生长，如虚线圆圈中所示；而在β₁晶粒中的片层则出现了竹节状形貌(bamboo-like)，如图7f中虚线方框所示。如果不考虑片层形貌，从整体生长趋势来说，界面能各向异性为0.8:0.1:1.0的条件下，片层α组织沿片层长度方向的生长速率更快，故界面能大的生长速率快。再次验证了界面能与梯度项系数有关，在合理范围内，界面能系数越大，梯度能系数越大，α相生长越快^[30]。相似地，主片层生长得慢，侧枝相应地就小而稀疏。

图7d~f是z-y切面的放大图。界面能各向异性不同时，片层α组织的形貌不相同，这是因为3种不同界面能条件下α在x方向上界面能不同导致的。界面能各向异性会影响片层α生长的动力学过程，界面能不同会引起片层α生长速度的差异。

有研究^[31]表明，同时考虑弹性能和界面能各向异性时，对单个α相进行模拟，片层更尖、生长速率更大。但本工作所考虑的温度范围内，扩散速率较高，显著降低了弹性能的作用，故可忽略弹性能的贡献。

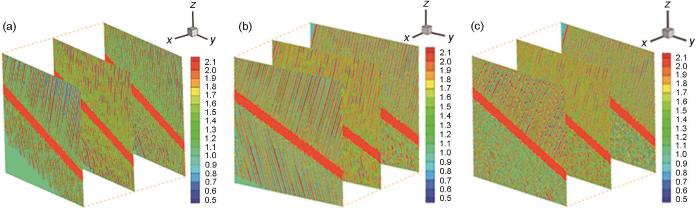
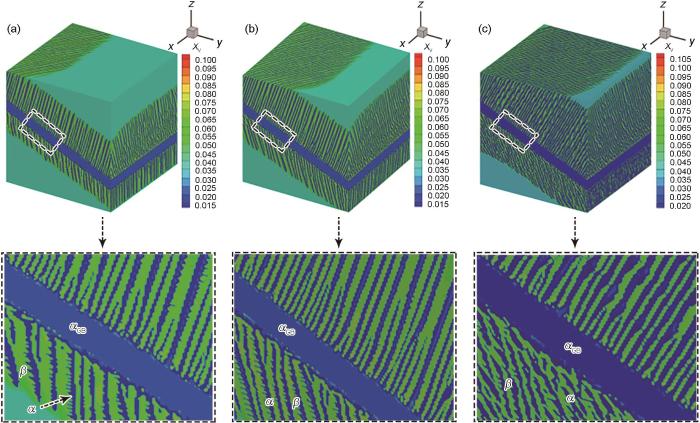
为深入研究界面能对片层α形貌在晶粒内具体的影响，保持不同界面能各向异性条件下，在晶粒不同位置的z-y切面上片层的生长形貌如图8和9所示。图8为不同界面能各向异性在相同时间下(t = 1000 s)按z-y切面方向切出的切面整体示意图。图9为图8切面片层形貌的二维平面图。对比图9a1~a3可以看出，当界面能各向异性变大时，片层侧枝的形状变得越细。且当k_x 为0.4时，相界上侧β₁晶粒内有部分主片层上也出现小侧枝，而在k_x 为0.6或0.8时不存在。另外，k_x 为0.8时伸入β₁晶粒生长的片层在靠近边界处出现竹节形形貌，而不是一般粗度均匀的棒状。此时存在主片层将分叉出的小片层吞并，使得该部分的片层转变为较粗状的竹节形。

图10展示了在820℃生长100 s时不同界面能各向异性条件下的溶质分布。由图可见，Al在α相中的浓度高于β相。对于Al，在α的生长过程中，基体β内的Al向α扩散，片层β侧Al的含量较α侧的低。从图10a~c可见界面能各向异性不同条件下Al的浓度场对比，在k_x 为0.4和0.6的界面能各向异性条件下，α和β内Al的含量差异明显，分布明显不均，但在k_x 为0.8时，Al分布较均匀。从图10的局部放大图(椭圆虚线区域)可见，在片层生长过程中，片层头部Al的浓度较高，同时头部β侧的Al浓度明显低于α侧。这是因为片层头部优先生长，基体中的Al含量还较高，会有更多的Al扩散到α中，造成该部位Al浓度较大。另外，也可能由于界面能各向异性使得片层形状的不同导致浓度分布不均。当片层形状规则且排列整齐密集时，Al在α中的扩散足够充分，则浓度就相对均匀；否则，扩散不充分浓度差异就较大。

图11所示为不同界面能各向异性条件下V的溶质分布。观察片层生长期间V的浓度场，可见：在α相内V的含量很低但分布均匀，在β相内分布不均，浓度比α相内的高。原因在于在片层α生长过程中，V要向β相内扩散，在片层α组织之间的残余β相内造成局部堆积，导致V浓度较高。同时，在晶界附近可观测到在α_GB内部V含量高于片层α内的V含量，推测是因为α_GB内部部分不与基体和残余β相接触，V无法向外扩散，相应的α_GB内的V浓度就较高，形成熟知的富V区域，如图10局部放大图所示。

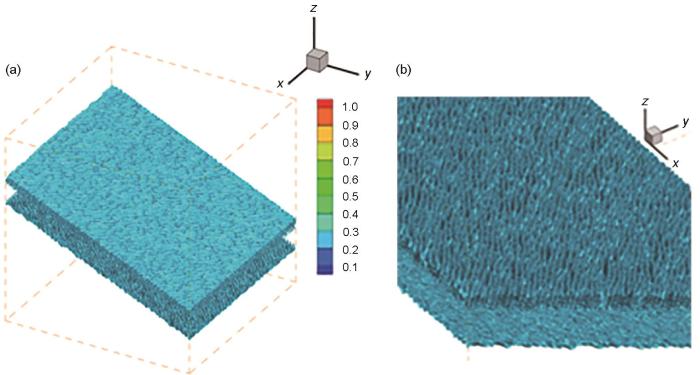
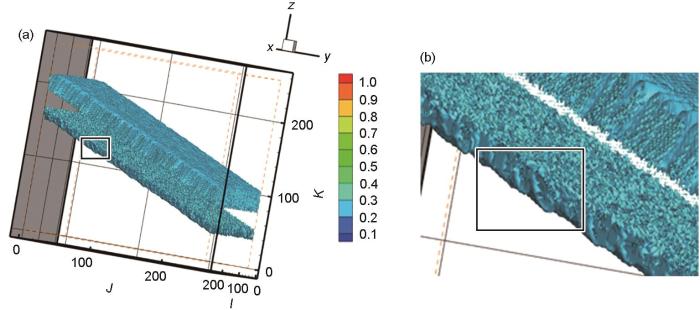
为了更清晰地了解片层形貌生长的过程，对模拟结果采用三维透视方法进行观察，图12展示了界面能各向异性k_x:k_y:k_z = 0.6:0.1:1.0情况下在t = 50 s时的片层状态。生长初期，片层组织较小，只能大致看出片层的生长趋势，从晶界处开始生长^[32]，形成排列整齐且相互之间具有一定间隙的片层组。另外，由于初始设置的2个β晶粒取向不同，导致晶界两侧的片层生长角度不同，生长速度也不相同。随时间演化，当t = 100 s时，晶界下侧有生成小侧枝的趋势，相应的片层形貌如图13中的矩形框所示。由图13b可见侧枝所在的主片层形貌呈粗大的棒状，从主片层冒出的侧枝头部近似呈三角状和锥状。这种方法更加直观地展现了片层在某一时刻的形貌，并且更易推测出下一时刻的生长趋势。

从三维透视图片层生长情况可见，在不同界面能各向异性条件下，片层α组织的生长情况存在一定的差异。图14简要说明在x方向上界面能不同的片层形貌结果(k_x 不同)。对比得出，主要差别在于片层的疏密程度和生长速度，整体的生长方向基本无异。单片层的宽度逐渐变宽。

另外，在三维片层组织中，通过观察晶粒不同位置处片层与片层侧枝形貌，可得出侧枝与主片层间的随机角度关系，图15为热处理温度820℃和界面能各向异性比k_x:k_y:k_z = 0.6:0.1:1.0条件下，在t = 2000 s时的片层组织及片层侧枝的二维z-y切面形貌。由于片层具有一定的厚度，为确定同一个主片层上形成的片层侧枝取向是否相同，通过对三维晶粒的z-y切面图进行观测，分别测量同一个主片层上靠近根部、中部和尖部3个片层侧枝与主片层沿各自长度方向形成的角度。从测量结果来看，同一个主片层从根部到尖部生成的侧枝与主片层的夹角角度存在差异，而且相同片层组织在晶粒不同位置处侧枝与主片层的夹角也在变化。模拟结果既存在实验中能观测到的30°左右的角，也存在随机角度的侧枝夹角，具体的角度变化暂无明显规律。由此可见，从三维尺度对片层α及片层侧枝进行观察，能看到比二维扫描图片更细节的形貌。

(1) 片层沿片层长度方向的生长速率随界面能各向异性的增加而增加。片层α侧枝同主片层的生长情况基本一致，但片层α侧枝在晶粒内不同位置处的形貌均不相同。

(2) 三维片层组织表现出比二维片层组织更丰富的细节，即片层侧枝与主片层的夹角不完全是30°，而是随机的角度，无明显的规律。

(3) 随着x方向和z方向界面能各向异性降低(k_x:k_y:k_z 从0.4:0.1:1.0到0.8:0.1:1.0)，片层α从粗大棒状转变为细长针状，且排列由稀疏变密集，单片层厚度逐渐变宽，溶质元素分布由不均匀趋于均匀。