基于上述研究背景,本工作采用第一性原理方法,利用Russell-Brown模量强化模型,研究了合金化及微观组织参数如沉淀相体积分数、颗粒尺寸等对α + β双相钛合金沉淀强化的影响,研究对象包括二元Ti-xM (M = Al、V、Cr、Mn、Fe、Co、Ni、Zr、Nb、Mo、Ta、W;x为原子分数,%,下同)以及高强高韧Ti55521合金。
1 计算方法与模型
1.1 Russell-Brown模型
根据Russell-Brown模型,沉淀强化引起的强度增量(
式中,
式中,
由
1.2 微观组织参数对模量强化的影响
为考虑微观组织对沉淀强化的影响,本工作利用沉淀相尺寸
设沉淀相为半径
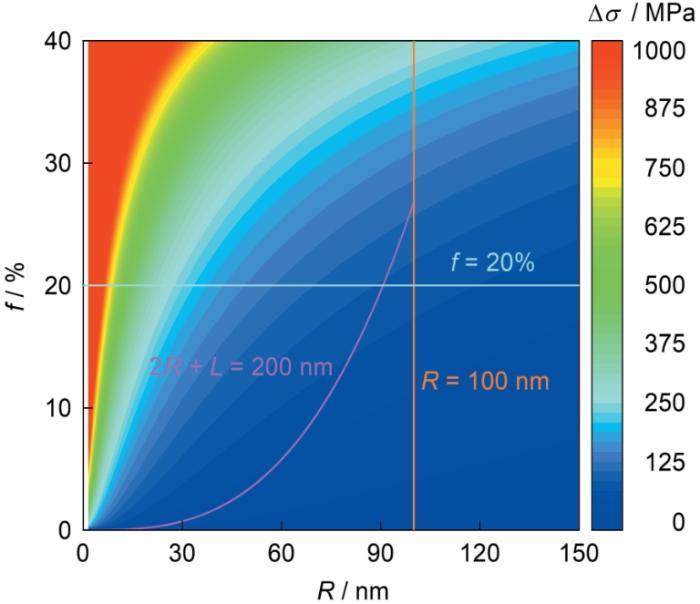
图1
图1
基体内均匀分布的球形沉淀相示意图
Fig.1
Schematic representation of the spherical precipitation particle distributed homogenously in the matrix (R—radius of precipitate, L—spacing between precipitation phase particles)
即,
结合式(
1.3 弹性常数及弹性模量
由上述可知,沉淀相及基体的弹性剪切模量是计算模量强化的关键参数。高强高韧钛合金中的bcc结构基体β相有3个独立的弹性常数
式中,
式中,
可获得独立弹性常数
高强高韧钛合金中的强化相为hcp结构的α相,有5个独立的弹性常数,
其中,
式中,
利用上述关系式,可求出六方晶系的5个独立弹性常数。通过计算得到的单晶弹性常数,根据Hill平均[16]进一步计算多晶弹性模量(如体模量B、Young's模量Y、剪切模量G等)。
1.4 计算参数
本工作采用基于密度泛函理论(density functional theory,DFT)[17]的精确muffin-tin轨道(exact muffin-tin orbitals,EMTO)第一性原理方法[15,18]计算弹性常数及弹性模量。在电子自洽计算过程中,单电子Kohn-Sham方程采用Green函数技术求解,其中,有效势采用最优重叠muffin-tin近似处理,但在计算总能量时,引入全电荷密度修正[15]。单电子有效势中的电子交换关联泛函采用Perdew等[19]广义梯度近似描述。电子波函数采用精确muffin-tin轨道展开,基组中包含spdf轨道成分。将Al-3s23p1、Ti-3p64s23d2、V-3p64s23d3、Cr-3p64s13d5、Mn-3p64s23d5、Fe-3p64s23d6、Co-3p64s23d7、Ni-3p63d84s2、Zr-4p65s24d2、Nb-4p65s24d3、Mo-4p65s14d5、Ta-5s25p65d3、W-5s25p65d4作为价电子处理。对于α和β相,简约Brillouin区均匀
2 结果与讨论
2.1 晶格常数
2.1.1 纯Ti
表1 纯Ti α和β相的晶格常数(a、c)与实验值和其他理论值的比较[20~24]
Table 1
2.1.2 二元钛合金
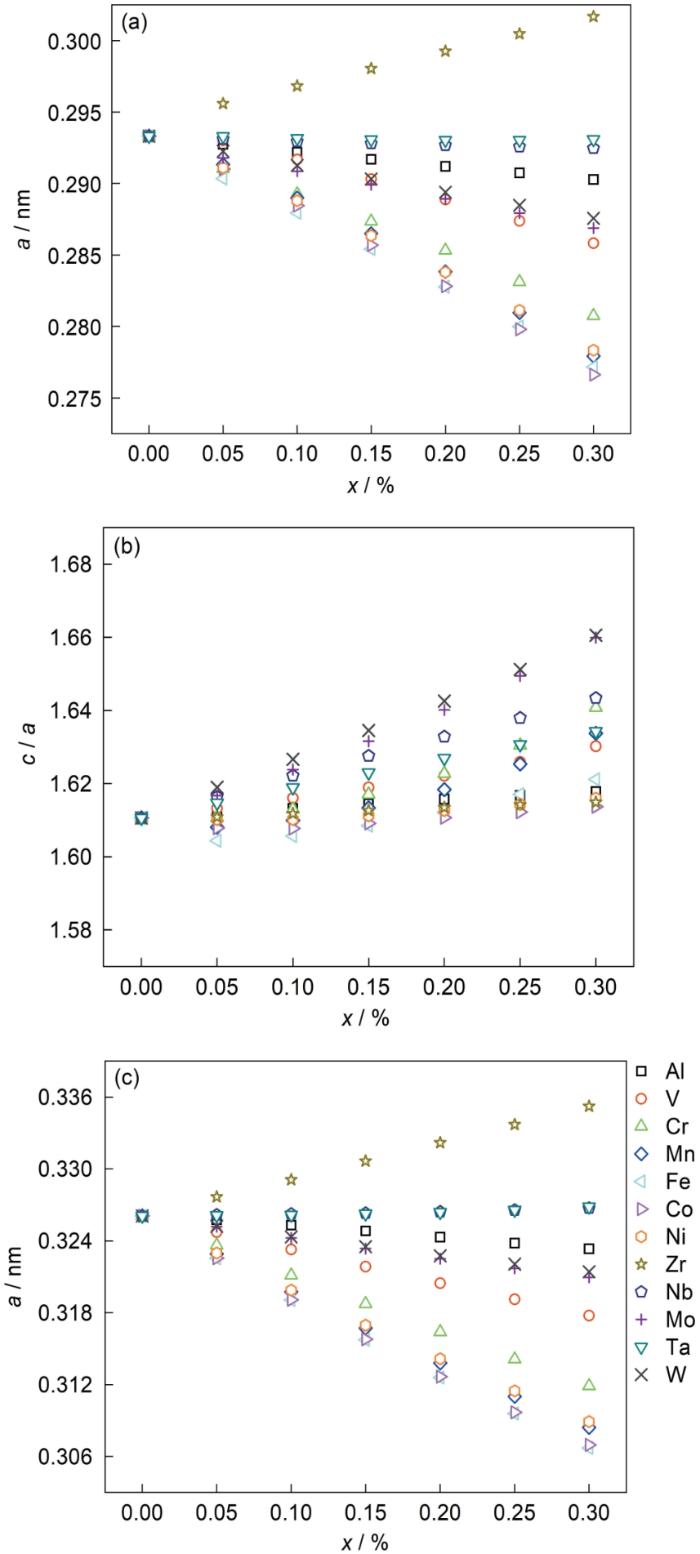
图2
图2
二元钛合金Ti-xM (M = Al、V、Cr、Mn、Fe、Co、Ni、Zr、Nb、Mo、Ta、W)的晶格常数随成分x的变化
Fig.2
Lattice parameters of binary Ti-xM (M = Al, V, Cr, Mn, Fe, Co, Ni, Zr, Nb, Mo, Ta, W) against the composition x (atomic fraction)
(a) a of the α phase
(b)
(c) a of the β phase
2.2 弹性性质
2.2.1 纯Ti
表2 纯Ti中α和β相的弹性常数与实验值和其他理论值的比较[20~22,28~30] (GPa)
Table 2
| Phase | Method | ||||||
|---|---|---|---|---|---|---|---|
| α | EMTO | 201.6 | 44.2 | 54.4 | 222.6 | 49.3 | 78.7 |
| VASP[20] | 204.0 | 59.1 | 77.0 | 192.9 | 45.9 | 72.5 | |
| VASP[21] | 176.6 | 84.5 | 77.0 | 190.2 | 41.5 | 46.1 | |
| VASP[22] | 171.6 | 86.6 | 72.6 | 190.6 | 41.1 | 42.5 | |
| Exp.[28] | 176.1 | 86.9 | 68.3 | 190.5 | 50.8 | 44.6 | |
| Exp.[29] | 162.4 | 92.0 | 68.5 | 180.7 | 46.6 | 35.2 | |
| Exp.[30] | 155.0 | 91.0 | 79.0 | 173.0 | 65.0 | 32.0 | |
| β | EMTO | 102.2 | 103.6 | - | - | 65.9 | - |
| VASP[20] | 76.6 | 121.9 | - | - | 30.0 | - | |
| VASP[22] | 87.8 | 112.2 | - | - | 39.8 | - |
2.2.2 二元钛合金
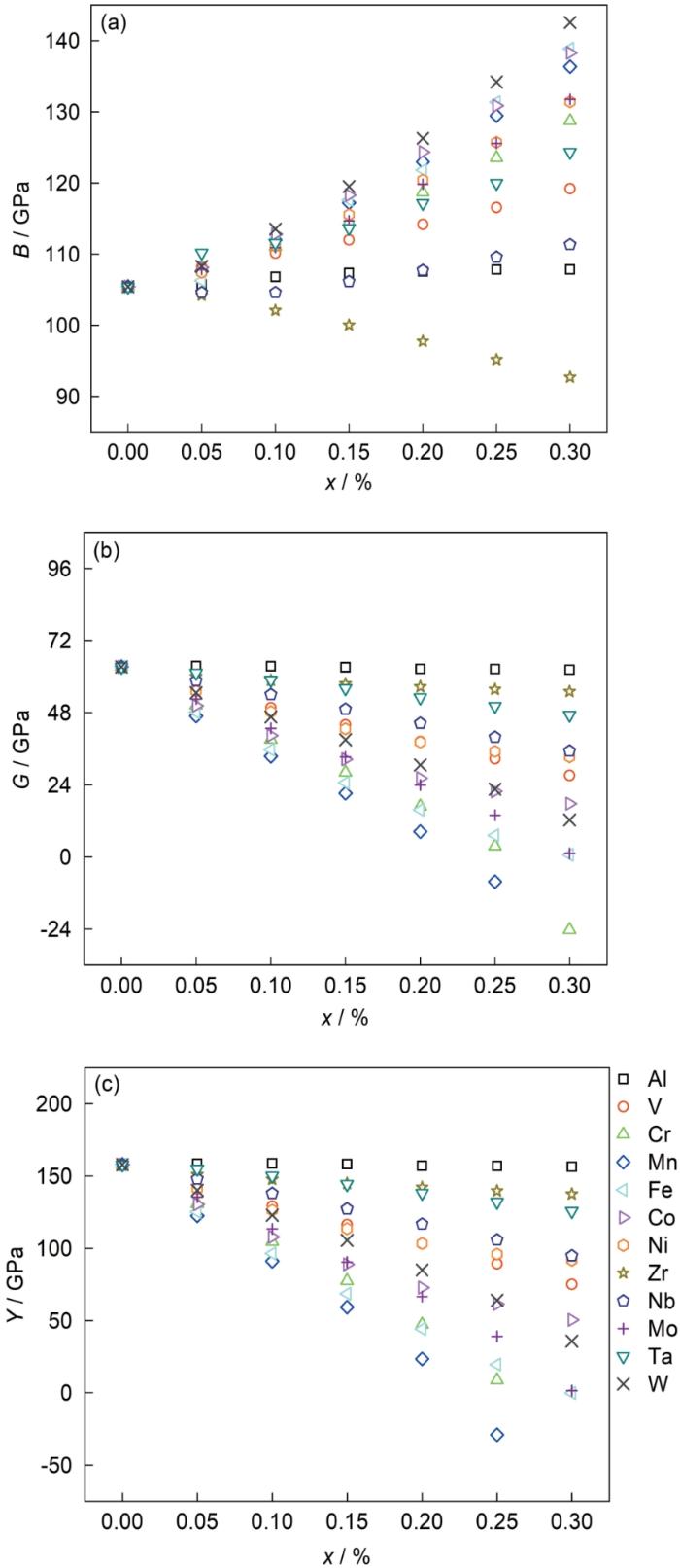
图3
图3
二元钛合金Ti-xM (M = Al、V、Cr、Mn、Fe、Co、Ni、Zr、Nb、Mo、Ta、W)的α相多晶弹性模量随x的变化
Fig.3
Polycrystalline elastic moduli of the α phase of binary Ti-xM (M = Al, V, Cr, Mn, Fe, Co, Ni, Zr, Nb, Mo, Ta, W) against x
(a) bulk modulus (B)
(b) shear modulus (G)
(c) Young's modulus (Y)
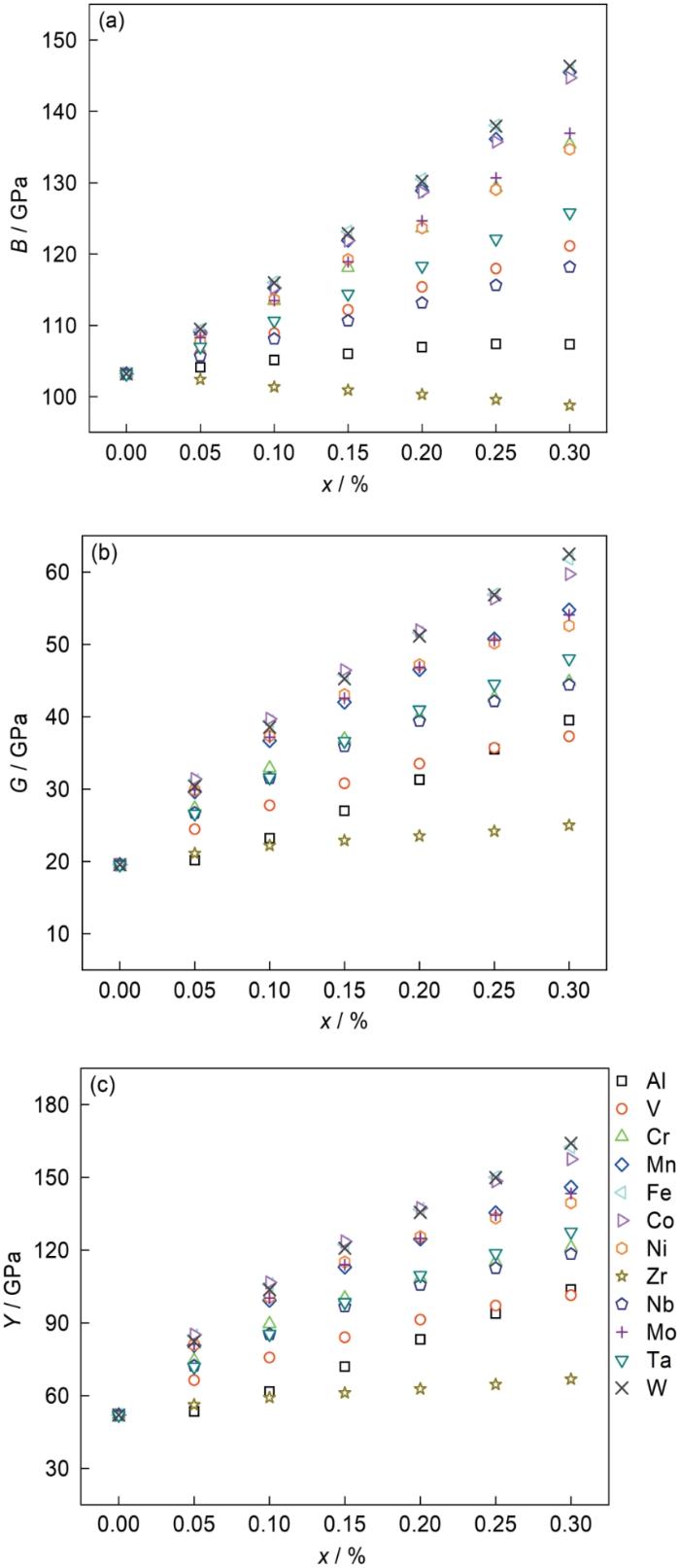
图4
图4
二元钛合金Ti-xM (M = Al、V、Cr、Mn、Fe、Co、Ni、Zr、Nb、Mo、Ta、W)的β相多晶弹性模量随x的变化
Fig.4
Polycrystalline elastic moduli of the β phase of binary Ti-xM (M = Al, V, Cr, Mn, Fe, Co, Ni, Zr, Nb, Mo, Ta, W) against x
(a) bulk modulus
(b) shear modulus
(c) Young's modulus
表3
二元Ti-xM合金剪切模量
Table 3
| M | α | β | |
|---|---|---|---|
| Al | 0.87 ± 1.29 | 38.84 ± 4.57 | 107.37 ± 18.26 |
| V | -116.97 ± 0.42 | 103.95 ± 3.96 | -142.15 ± 15.85 |
| Cr | -254.92 ± 11.39 | 161.50 ± 6.75 | -255.07 ± 26.99 |
| Mn | -279.12 ± 3.47 | 198.59 ± 9.37 | -270.81 ± 37.46 |
| Fe | -225.56 ± 8.13 | 227.59 ± 9.73 | -288.98 ± 38.94 |
| Co | -167.85 ± 8.85 | 240.66 ± 7.59 | -353.45 ± 30.36 |
| Ni | -110.81 ± 5.70 | 216.68 ± 6.73 | -353.20 ± 26.90 |
| Zr | -19.07 ± 0.35 | 38.28 ± 3.52 | -61.30 ± 14.07 |
| Nb | -90.08 ± 0.76 | 148.00 ± 5.10 | -212.12 ± 20.40 |
| Mo | -200.39 ± 1.61 | 207.58 ± 9.16 | -308.80 ± 36.65 |
| Ta | -48.13 ± 1.72 | 145.14 ± 4.63 | -161.78 ± 18.53 |
| W | -162.35 ± 1.68 | 215.07 ± 8.60 | -239.50 ± 34.42 |
2.2.3 多元合金
钛合金一般为复杂成分多元合金。在钛合金设计过程中,需要对成分进行优化迭代,若每次迭代均进行第一性原理计算,成本较高。因此,需要发展弹性模量的高通量计算方法。本工作尝试利用二元钛合金的弹性模量估算多元钛合金的弹性模量。
表3中,弹性模量拟合公式中的一次项系数可以表征各元素对弹性模量的影响。据此,可定义弹性模量的Mo当量系数,即:
其中,
表4
不同合金元素在α及β相中的剪切模量Mo当量系数(
Table 4
| Phase | Al | V | Cr | Mn | Fe | Co | Ni | Zr | Nb | Ta | W |
|---|---|---|---|---|---|---|---|---|---|---|---|
| α | -0.004 | 0.584 | 1.272 | 1.393 | 1.126 | 0.838 | 0.553 | 0.095 | 0.450 | 0.240 | 0.810 |
| β | 0.187 | 0.501 | 0.778 | 0.957 | 1.096 | 1.159 | 1.044 | 0.184 | 0.713 | 0.699 | 1.036 |
弹性模量Mo当量意味着,含量为
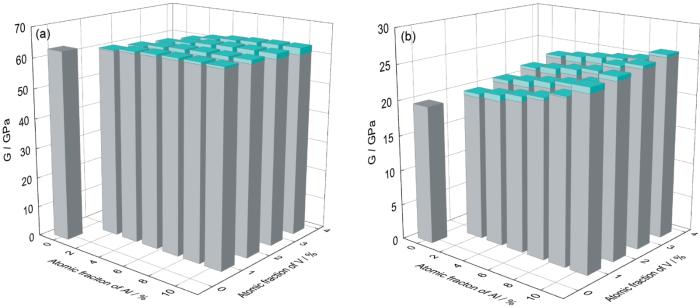
图5
图5
Ti-Al-V合金α相和β相剪切模量EMTO-CPA计算值(灰色方柱)以及该计算值与采用模量Mo当量方法的估算值的绝对误差(青色方柱)
Fig.5
Shear moduli of α phase (a) and β phase (b) of Ti-Al-V alloy from direct EMTO-CPA calculations (gray column) and the error of the shear modulus evaluated with modulus Mo-equivalency (cyan column)
直接计算与采用弹性模量Mo当量估算得到的弹性模量的差别主要来自2个方面:其一,没有考虑多元合金中不同合金元素原子间的相互作用对弹性模量的影响;其二,对于β相,弹性模量和成分间的关系为二次曲线,弹性模量Mo当量系数仅考虑一次项系数,忽略了二次项系数的贡献。在x较小时,二次项
2.3 双相钛合金的模量强化
2.3.1 二元合金
利用2.2节中计算得到的α及β相的弹性模量,本工作首先研究了二元Ti-xM (M = V、Cr、Mn、Fe、Co、Ni、Nb、Mo、Ta、W)合金中的模量强化。由于以上元素为β相稳定元素,在β相中有较高固溶度,在α相中固溶度极低。经长期时效后,这些元素集中在β相中,在α相中的含量较少。因此,在计算过程中将α相视为纯Ti,合金元素都集中在β相中。
作为代表性合金,图6给出了β相成分为Ti-5%Mo合金模量强化强度增量(
图6
图6
β相成分为5%Mo的Ti-Mo合金中,模量强化强度增量(
Fig.6
Strength increment (
(iii) 若保持沉淀相
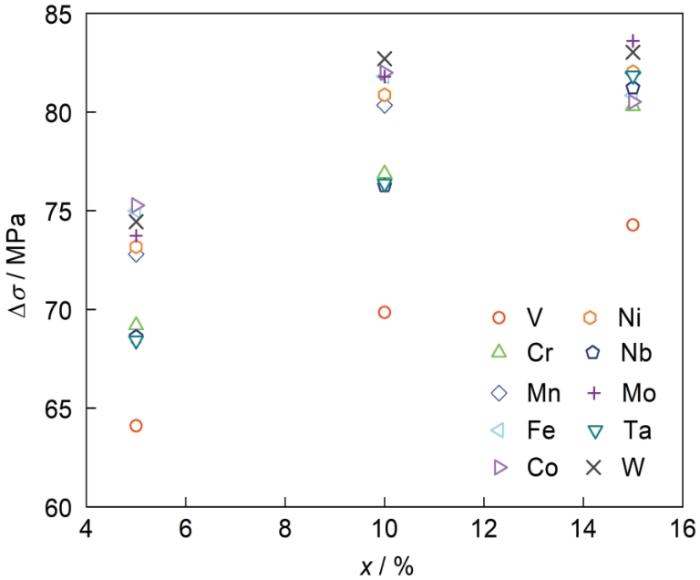
其他二元钛合金沉淀强化强度增量随沉淀相
图7
图7
在沉淀相R = 100 nm、f = 20%时,二元α + β双相Ti-xM (M = V、Cr、Mn、Fe、Co、Ni、Nb、Mo、Ta、W)合金的模量强化强度增量
Fig.7
2.3.2 高强高韧Ti55521合金中的模量强化
表5 不同热处理条件下,Ti55521合金中的元素分配、α相体积分数及颗粒尺寸[31],以及根据实验获得的α、β相成分计算得到的剪切模量
Table 5
| State | Phase | Element partition / (atomic fraction, %) | f / % | R / nm | G / GPa | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ti | Al | Mo | V | Cr | Fe | Cal. | Mo Eq. | ||||
| TMP | α | 86.9 | 9.2 | 1.3 | 2.2 | 0.3 | 0.1 | 22 ± 3 | 35 | 60.08 | 56.40 |
| β | 81.2 | 8.4 | 3.2 | 5.2 | 1.1 | 0.9 | - | - | 34.97 | 35.20 | |
| Aged I | α | 86.5 | 11.3 | 0.2 | 1.5 | 0.3 | 0.2 | 38 ± 6 | 225 | 61.99 | 59.20 |
| β | 75.3 | 6.5 | 4.8 | 8.4 | 3.2 | 1.8 | - | - | 41.15 | 42.52 | |
| Aged II | α | 86.47 | 12 | 0.1 | 1.2 | 0.2 | 0.03 | 50 ± 3 | 425 | 62.96 | 60.41 |
| β | 76.1 | 5.8 | 4.3 | 7.8 | 4.5 | 1.5 | - | - | 40.91 | 42.23 | |
Ahmed等[31]的实验测试表明,随时效时间延长,Ti55521合金的屈服强度单调增加(见表6),与沉淀强化强度增量的变化趋势并不相同。需要指出的是,本工作重点考虑的是沉淀强化引起的强度变化。事实上,合金的屈服强度还包括基体的强度。从TMP状态到Aged I状态,基体β相中β稳定元素含量有较大幅度增加,基体强度也显著增加,因此,虽然沉淀强化强度增量
表6
不同热处理制度下沉淀强化强度增量Ti55521合金的
Table 6
| State | ||
|---|---|---|
| TMP | 237.8 ± 42.8 | 980 ± 15 |
| Aged I | 161.1 ± 80.3 | 1080 ± 18 |
| Aged II | 364.3 ± 148.3 | 1200 ± 12 |
3 结论
(1) 采用EMTO方法结合CPA,计算了二元钛合金Ti-xM (M = Al、V、Cr、Mn、Fe、Co、Ni、Zr、Nb、Mo、Ta、W)的弹性性质。结果显示,除Zr之外,α和β相的体模量均随着合金元素含量x的增加而增加。α相的Young's模量和剪切模量均降低,相反β相的Young's模量和剪切模量均升高。
(2) 提出用弹性模量Mo当量估算多元钛合金α及β的弹性模量。测试计算表明,Ti-Al-V及Ti55521合金的弹性模量估算值与第一性原理方法直接计算值误差均不超过5%。
(3) 采用Russell-Brown模量强化模型,研究了α + β双相钛合金中的沉淀强化。结果表明,根据β稳定元素对二元合金模量强化的贡献,钛合金中的β稳定元素可分为3类:I类元素包括Co、Fe、W、Mo、Ni、Mn,模量强化作用较强;II类元素包括Cr、Nb、Ta,强化作用居中;III类元素为V,强化作用最弱。随x增加,沉淀强化作用均有所增强,但I类与II类元素的沉淀强化效果差别逐渐消失;热机械处理高强高韧Ti55521合金经短时时效后,沉淀强化作用减弱,但长时时效后,沉淀强化效果增强。
参考文献
An overview on the use of titanium in the aerospace industry
[J].
Perspectives on titanium science and technology
[J].
Research progress in dwell fatigue service reliability of titanium alloys for pressure shell of deep-sea submersible
[J].Service reliability of deep-sea submersible pressure shells is critical for ensuring the safety of the submersibles. To manufacture pressure shells for deep-sea submersibles, titanium alloys have emerged as key materials owing to their exceptional service performances in the deep-sea environment. Herein, use of titanium alloys in deep submersibles is introduced. Then, the latest research on the primary failure modes of titanium alloys, including creep at room temperature, low cycle fatigue, and dwell fatigue, based on the types of titanium alloys used in deep-sea submersibles is reviewed. Additionally, the main factors that affect dwell fatigue, including the micromechanism of dwell fatigue damage and dwell fatigue model, are summarized. This work can serve as a reference for the development of new titanium alloys with high strength and low dwell effect. Finally, specific issues related to the service reliability evaluation of titanium alloy components used in the deep sea are outlined, and future research focuses are presented.
深潜器耐压壳用钛合金保载疲劳服役可靠性研究进展
[J].
Toughening high strength titanium alloys through fine tuning phase composition and refining microstructure
[J].Titanium alloys are key materials for applications in major engineering areas, such as aerospace and marine equipment. Studies on structural titanium alloys focus on strengthening and toughening the alloys, especially the latter. The mainstream structural titanium alloys comprise both α and β phases. The optimization of the strength and toughness balance relies on the control of the compositions, volume fractions, and morphologies of both phases. In this study, some recent advances along the above line are reviewed, focusing on studies on the composition design, plastic-deformation mechanism, and microstructure tuning. Rational design of the compositions of both phases improved the deformation coordination within the α phase and across the α/β interface, suppressed the precipitation of brittle ω and α2 phases, and resulted in improved plasticity and toughness through the α-deformation twin and β-deformation-triggered phase transformation. The multiscale microstructure enhanced the strength and toughness of the titanium alloy. Using the abovementioned approaches, a series of titanium alloys with an improved strength-toughness combination were developed and fabricated. Finally, an attempt was made to predict the prospect of technology development in the field of high-strength and high-toughness titanium alloys for various applications.
高强韧钛合金组成相成分和形态的精细调控
[J].
A comparative study of the mechanical properties of high-strength β-titanium alloys
[J].
Precipitation processes in the beta-titanium alloy Ti-5Al-5Mo-5V-3Cr
[J].
Progress report on recent advances in physical metallurgy: (C) The quantitative relationship between microstructure and properties in two-phase alloys
[J].
The strength of a precipitation hardened AlZnMg alloy
[J].
A dispersion strengthening model based on differing elastic moduli applied to the iron-copper system
[J].
First-principles study of phase stability and elastic properties of binary Ti-xTM (TM= V, Cr, Nb, Mo) and ternary Ti-15TM-yAl alloys
[J].
Density functional theory investigations of titanium γ-surfaces and stacking faults
[J].
Selecting non-isothermal heat treatment schedules for precipitation hardening systems: An example of coupled process-property optimization
[J].
The elastic behaviour of a crystalline aggregate
[J].
Anisotropic lattice distortions in random alloys from first-principles theory
[J].
Generalized gradient approximation made simple
[J].
First-principles study of the phase stability and elastic properties of Ti-X alloys (X = Mo, Nb, Al, Sn, Zr, Fe, Co, and O)
[J].
Generalized stacking fault energies and critical resolved shear stresses of random α-Ti-Al alloys from first-principles calculations
[J].
First-principles calculations for development of low elastic modulus Ti alloys
[J].
Thermodynamics of the solid solution of hydrogen in β-titanium alloys: β-TiMo and β-Ti/Re
[J].
Neutron diffraction study of the deuterides of Ti-Mo alloy
[J].
First-principles investigations of lattice parameters, bulk moduli and phase stabilities of Ti1- x V x and Ti1- x Nb x alloys
[J].
Ti1- x V x 及Ti1- x Nb x 合金晶格参数、体模量及相稳定性的第一原理研究
[J].利用基于密度泛函理论的第一原理精确Muffin-Tin轨道(EMTO)方法结合相干势近似(CPA), 研究了Ti1-xVx与Ti1-xNbx合金中α(α'), ω及β相的晶格常数、体模量及相稳定性随成分的变化. 结果表明, Ti-V合金中随着V含量的增加, α(α')相晶格参数aα$减小, cα/aα略有增加, ω相晶格参数aω及cω/aω同时减小, β相晶格参数aβ减小; Ti-Nb合金中随Nb含量的增加, aα几乎不变, cα/aα增加, aω增加, cω/aω减小, aβ几乎不变. 随V及Nb含量的增加, ω与β相的晶格错配度线性增加. V和Nb均能提高三相的体模量, 且增加 β相对于其它两相的稳定性.
Single-crystal elastic moduli and the hcp→bcc transformation in Ti, Zr, and Hf
[J].
Empirical tight-binding model for titanium phase transformations
[J].