真空自耗电弧熔炼(vacuum arc remelting,VAR)是目前钛合金铸锭的主要生产方法。该方法在真空环境下通过电弧使自耗电极熔化,金属熔液落入下方水冷铜坩埚中形成熔池,进而凝固成铸锭。这其中金属液凝固过程中产生的溶质宏观偏析是一种最为常见的铸锭缺陷,且难以通过后续热处理消除。掌握宏观偏析形成机理及规律是实现相关调控及工艺优化的重要前提,一直是本领域研究者关注的重要课题。
凝固过程中的溶质再分配是引起宏观偏析的重要原因。当前对钛合金中不同元素凝固分配系数与自耗熔炼铸锭宏观偏析的关系已开展了大量研究。Mitchell等[1 ] 测定了Ti-6242、Ti-17和Ti-1023钛合金中Al、V、Fe、Mo、Cr、Sn、Zr等元素的分配系数(k ),发现实际铸锭中元素的k 与二元相图中的平衡数值存在明显差异,并指出Fe和Cr是2种最易偏析的元素。赵永庆等[2 ,3 ] 分析了多种钛合金铸锭中Cu、Fe、Cr的偏析分布,发现Fe和Cu元素沿径向存在严重的偏析,并指出这与2者的k 远偏离1相关。Yang等[4 ] 测量了Ti-1023合金中偏析最严重的Fe元素的空间分布,并分析了熔炼电流的影响,发现大电流下宏观偏析更为严重。
熔体流动是引起宏观偏析的另一个重要因素。VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究。Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上。Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动。Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变。Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响。Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响。上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为。Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响。樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析。除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律。
上述关于宏观偏析行为的研究均针对一次VAR熔炼的铸锭开展。实际钛合金VAR熔炼中,为保证铸锭的均匀性、减少夹杂,通常采用三次熔炼工艺。初次熔炼时将海绵钛和中间合金一起压制成电极,电极熔化后在坩埚中形成一次铸锭;再将一次铸锭当做二次熔炼的电极,将电极熔化形成二次铸锭;最后用二次铸锭做为第三次熔炼电极,制备三次铸锭。三次熔炼过程中采用的坩埚直径不断增加,形成的铸锭直径也相应增大。由于VAR铸锭中宏观偏析的存在,当把铸锭做为电极进行再次熔炼时,势必涉及电极成分均匀性对后续铸锭偏析的影响问题。Zagerbelnyy[15 ] 认为,绝大多数情况下电极成分的均匀性对铸锭成分的影响微乎其微。然而也有研究[16 ,17 ] 指出,采用与铸锭偏析分布相反的布料方式压制电极可以减轻偏析。实际生产过程中,通常将上次熔炼铸锭底部与头部颠倒后做为下次电极,这一方式的偏析程度要轻于铸锭直接正置的情况。当前关于宏观偏析在多次熔炼中是否存在传递,以及传递的原因、规律和影响程度都缺乏清晰的理解。
本工作采用数值模拟手段,研究宏观偏析在三次VAR过程中的传递行为,分析二次及三次熔炼时前次铸锭放置方式对后续铸锭宏观偏析的影响,并通过实验测定成分分布,检验模拟的可靠性。
1 模型描述
1.1 数学模型
本研究采用Swaminathan等[18 ] 和Voller等[19 ] 提出的合金连续介质模型来描述凝固过程,并在其中耦合自感应电磁力和搅拌电磁力。假定熔池中熔体流动为层流,采用Boussinesq近似[20 ,21 ] 。模型中连续性方程、能量守恒方程、溶质守恒方程与文献[13 ,18 ,19 ]中类似,不再赘述;动量方程中加入了电磁力源项,并且考虑了旋转速度,具体形式如下。
∂ ρ v ∂ t + ∇ ∙ ρ V v = - ∂ p ∂ x + ∇ ∙ μ l ρ ρ l ∇ v - μ l K ρ ρ l v +
ρ l g β T T - T r e f + β S c l - c r e f + F a (1)
∂ ρ u ∂ t + ∇ ∙ ρ V u = - ∂ p ∂ y + ∇ ∙ μ l ρ ρ l ∇ u -
μ l K ρ ρ l u + ρ u θ 2 y + F r (2)
∂ ρ u θ ∂ t + ∇ ∙ ρ V u θ = 1 y ∂ ∂ x y μ l ∂ u θ ∂ x +
1 y 2 ∂ ∂ y y 3 μ l ∂ ∂ x u θ y - ρ u u θ y + F θ (3)
式中,t 为时间,x 为横坐标(轴向),y 为纵坐标(径向),v 为轴向速率,u 为径向速率,uθ 为切向速率, V ρ 为合金密度,p 为压力,μ l 为液相黏度,K 为渗透率,ρ l 为液相密度,g 为重力加速度,β T 为温度膨胀系数,β S 为溶质膨胀系数,T 为合金的瞬时温度,T ref 为参考温度,c l 为元素的瞬时浓度,c ref 为元素的参考浓度;F a 、F r 和F θ
真空自耗电弧熔炼过程中,电源、坩埚、铸锭、自耗电极形成一个闭合回路,熔炼电流与其自身产生的磁场相互作用,形成自感电磁力,自感电磁力的计算包括3步。
J = σ E (4)
式中, J σ 为电导率, E [22 ] 报道,金属液体在磁场中运动产生的感应电流远小于熔炼电流,因此 式(4)忽略了感应电流。根据 E φ )之间的关系, 式(4)可改写为:
J = - σ ∇ φ (5)
∇ ∙ σ ∇ φ = 0 (6)
通过求解 式(6)即可获得铸锭内电势场分布,进而得到电流密度。
对于轴对称铸锭而言,自感磁场主要为旋转(azimuthal)分量(Bθ )[22 ] ,计算公式如下:
B θ = μ 0 y ∫ 0 R i n g o t y J x d y (7)
式中,Bθ 为磁通密度,μ 0 为真空磁导率,R ingot 为铸锭半径,Jx 为轴向电流密度。
F = J × B (8)
轴向和径向的Lorentz力(F a 和F r )表达式为:
F a = B θ J y (9)
F r = - B θ J x (10)
外加稳弧线圈通电产生的电磁场即为搅拌磁场,其与熔炼电流相互作用产生的Lorentz力称为搅拌电磁力。搅拌电磁力使熔池水平面产生旋转,旋转流动会产生向心力使熔池竖直面内形成中心向上、侧壁向下的对流。搅拌电磁力的计算公式为:
F θ = B e x t , x J y (11)
式中,B ext, x
1.2 计算条件及参数
本工作通过Fluent软件二次开发实现上述模型求解,通过用户自定义标量(User Defined Scalar)方程计算φ ,通过用户自定义函数(User Defined Functions)实现电流密度、磁通密度以及电磁力计算,并将电磁力以源项宏加入动量方程,通过动网格技术实现熔炼过程中铸锭的连续增长。考虑到圆柱形VAR铸锭的对称性,可将三维铸锭用二维轴对称模型代替。
铸锭的侧壁和底部边界均为无滑移边界,铸锭顶部边界类型设置为速度入口,动网格在顶部生长模拟熔炼过程中铸锭的生长,动网格抬升速率设置为实际熔炼速率。在熔炼过程中,铸锭上表面的热量主要来自于电弧的作用,电弧产生的等效温度可以表示为[23 ] :
T i n l e t = T l i q + Δ T I a r c , D i n g o t (12)
式中,T inlet 为熔池表面的温度;T liq 为液相线温度;I arc 为熔炼电流;D ingot 为铸锭直径;ΔT (I arc , D ingot )为熔化过热,可以通过下面的经验公式得出[24 ] :
Δ T I a r c , D i n g o t = 400 e x p ( - 12 D i n g o t I a r c ) (13)
铸锭底部设为对流换热边界,换热系数设为500 W/(m2 ·K)。铸锭侧壁与外界的热交换分成2个区域处理:侧壁上部与坩埚直接接触,可设为对流换热边界,换热系数设为800 W/(m2 ·K);铸锭下部由于凝固收缩,侧壁与坩埚壁之间会形成间隙,此时铸锭热量主要以辐射形式向外界散失。通过临界温度(T c )来判断铸锭侧壁与坩埚的接触情况,当侧壁温度小于T c 时认为形成间隙,T c 设为合金固相线温度以下100 K[10 ] 。为简化处理,可将辐射散热用对流换热等效,等效对流换热系数(h gap )计算公式如下[10 ] :
h g a p = γ T i n g o t 4 - T w a l l 4 1 ε 1 + 1 ε 2 - 1 T i n g o t - T w a l l (14)
式中,T ingot 为铸锭壁面的温度;T wall 为坩埚内壁的温度,假定为300 K;γ 为Stefan-Boltzmann常数(值为5.67 × 10-8 W/(m2 ·K4 ));ε 1 和ε 2 分别为铸锭壁和坩埚内壁的热辐射系数,分别取0.4和0.6。
对于电势场边界,铸锭底部和侧壁电势均设置为零,在铸锭顶部设置电流密度(j (y ))沿径向呈Gaussian分布,公式如下[15 ] :
j ( y ) = K A ∙ I a r c π R a r c 2 ∙ e x p - K B y 2 R a r c 2 (15)
式中,R arc 为电极半径,K A 和K B 是Gaussian分布系数。
本工作首先以Ti-4.25%V (质量分数,下同)二元模型合金为例,详细分析三次熔炼过程中宏观偏析的传递行为;而后针对实际TC4合金(Ti-4.25%V-6.35%Al)三次熔炼过程进行模拟,进一步检验二元模型合金偏析传递规律的普适性,并通过模拟成分分布与实验测量值的对比,检验模拟可靠性。在二元模型合金模拟时并未加入搅拌磁场,从而使研究聚焦到偏析传递问题,更方便进行分析讨论。计算中所用到的参数如表1 所示。
1.3 三次熔炼方案
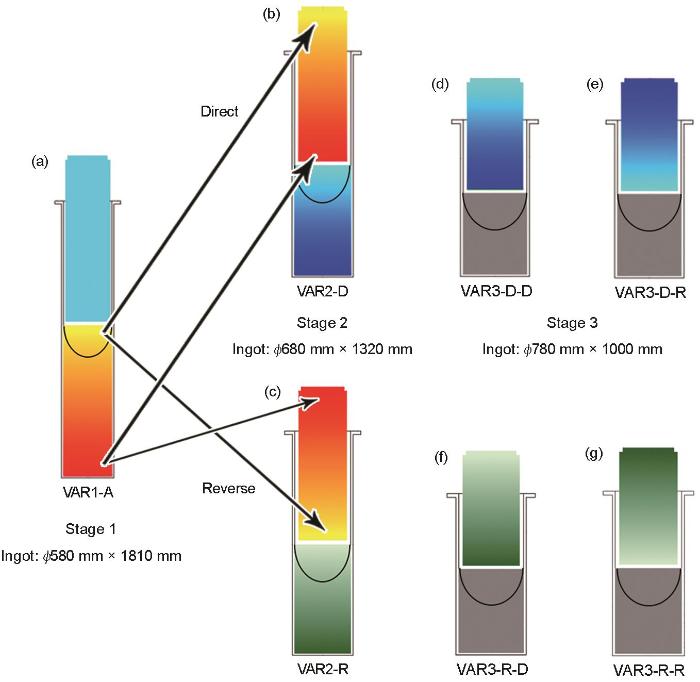
本工作分别采用成分均匀分布电极、前次熔炼铸锭正置做电极、前次熔炼铸锭反置做电极3种方案。采用均匀分布电极时,熔炼过程中铸锭顶部新增熔体的成分设为体系平均成分;而采用前次铸锭做电极时,下次熔炼过程中铸锭顶部新增熔体成分设为前次铸锭相应部位的成分。
三次熔炼铸锭尺寸(直径×高度)分别为580 mm × 1810 mm、680 mm × 1320 mm和780 mm × 1000 mm。三次铸锭直径与实际生产一致,为减小计算量,将第三次熔炼铸锭高度从实际值减为1000 mm,第一、二次铸锭高度根据总体积守恒计算获得。第一次熔炼中假定各种原料在电极中均匀分布,电极熔化的熔体成分始终保持合金名义成分,将此次熔炼命名为VAR1-A (末尾字母A代表average),如图1a 所示。第二次熔炼时的电极放置设置2种方案:(1) 一次铸锭正置,即直接将一次熔炼铸锭底部做为二次熔炼电极的底部,如图1b 所示,此情况命名为VAR2-D (数字2代表熔炼次数,末尾字母D代表direct);(2) 一次铸锭反置,即一次铸锭的顶部作为二次熔炼电极的底部,如图1c 所示,将此方案命名为VAR2-R (字母R代表reverse)。
图1
图1
三次真空自耗电弧熔炼(VAR)过程中电极放置方案示意图
Fig.1
Schematics of electrode placement in the triple vacuum arc remelting (VAR) process (The first smelting uses a homogeneous electrode, denoted by A. When the previous ingot is placed upright as an electrode, it is represented by D; when the previous ingot is placed upside down as an electrode, it is represented by R)
(a) VAR1-A (b) VAR2-D (c) VAR2-R
(d) VAR3-D-D (e) VAR3-D-R (f) VAR3-R-D (g) VAR3-R-R
第三次熔炼时设置4种方案:(1) 将VAR2-D铸锭正置做电极,命名为VAR3-D-D,如图1d 所示;(2) 将VAR2-D铸锭反置做电极,命名为VAR3-D-R,如图1e 所示;(3) 将VAR2-R铸锭正置做电极,命名为VAR3-R-D,如图1f 所示;(4) 将VAR2-R铸锭反置做电极,命名为VAR3-R-R,如图1g 所示。
此外,设置对照组,使用成分均匀的电极直接进行二次熔炼和三次熔炼,分别命名为VAR2-A、VAR3-A。二元模型合金三次熔炼电流分别为: 21 kA (第一次熔炼)、29 kA (第二次熔炼)、36 kA (第三次熔炼)。
2 二元模型合金偏析传递模拟
2.1 第一次熔炼过程中的熔体流动及偏析行为
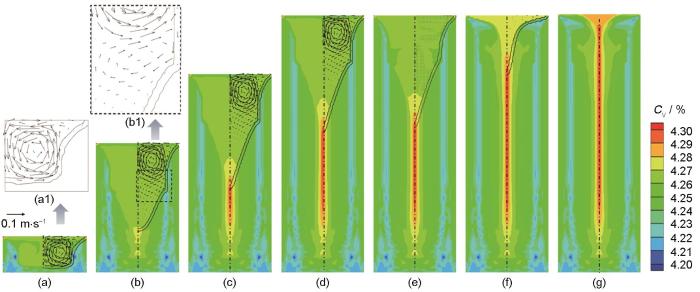
图2 是第一次熔炼过程中溶质分布随时间的演化结果,右半部分溶质场内加入了熔池轮廓和流场。从图2a 可以看出,在熔炼初始阶段(1000 s),熔池较浅,熔池中熔体沿熔池中心向下、侧壁向上流动,这是典型的电磁力主导对流[8 ,25 ] ,此对流将熔池底部固/液界面前沿凝固排出的溶质沿侧壁向上带到熔池内部,造成底部固/液界面处的溶质贫乏,从而在铸锭底部中心两侧形成了明显的负偏析区域(底部蓝色区域)。到4300 s时,如图2b 所示,随着熔池深度加大,熔池上部仍为电磁力控制的中心向下、侧壁向上的对流;而在熔池下部区域,形成了浮力控制的侧壁向下、中心向上的微弱流动,从放大图(图2b1 )可以清晰观察到这一浮力控制对流。这种熔池上部与下部相反的流动模式与Davidson 等[8 ] 报道的较大熔炼电流下的熔池稳态流动结果一致。此时熔池下部浮力对流将熔池侧壁的溶质带到熔池底部,从而使底部形成正偏析;浮力对流区上方是电磁力控制的沿侧壁向上的流动,它将侧壁凝固排出的溶质带到熔池上方。因此在向下流动与向上流动的分界线附近,形成了显著的负偏析。在随后熔炼过程中(4300~8800 s),熔池深度基本恒定,熔池上部保持电磁力控制对流,下部为热浮力控制对流,已凝固铸锭形成了显著的中心正偏析和两侧负偏析条带,如图2b~d 所示。最后小电流保温阶段(9000~12500 s),熔池内电磁力基本消失,整个区域重新形成浮力控制的微弱流动,最终冒口部位形成正偏析,如图2e~g 所示。
图2
图2
第一次熔炼过程中溶质场及流场演化
Fig.2
Solute distributions and liquid phase flow vectors in the ingot at different time during the first smelting process (Two solid lines represent the weld pool outlines, the same below. C V —mass fraction of vanadium element)
(a) 1000 s (b) 4300 s (c) 6700 s (d) 8800 s (e) 9000 s (f) 10800 s (g) 12500 s
(a1, b1) enlarged views of liquid phase flow vectors in Fig.2a (a1) and Fig.2b (b1), respectively
2.2 第二、三次熔炼过程中的偏析传递
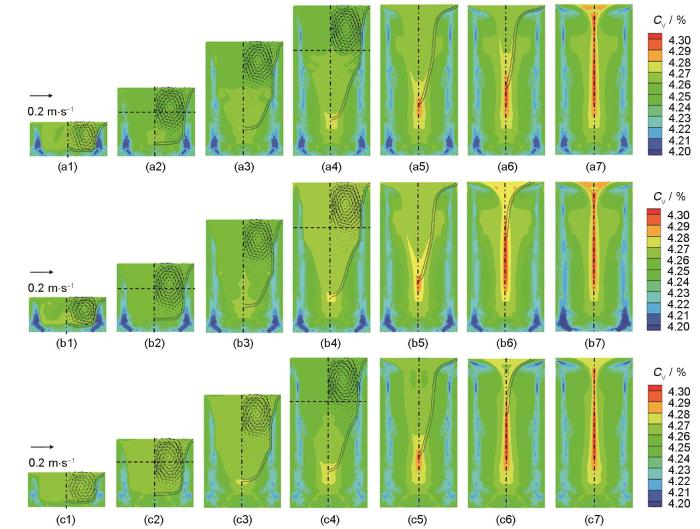
第二次熔炼过程中溶质及熔池内流场演化如图3 所示,其中包含了VAR2-A、VAR2-D和VAR2-R 3种情况。可以看出,3种情况下熔池内液相对流均与第一次熔炼过程类似,初始阶段均为电磁力完全控制对流,随着熔池加深,熔池底部出现弱的浮力对流。这表明电极成分差异对熔池内流动没有影响。这是由于Ti-V体系中液相密度随浓度变化较小,溶质浮力较弱,而电磁力在起主导作用,3种情况下电磁力相同,因此熔池对流类似。
图3
图3
第二次熔炼时的溶质场及流场演化
Fig.3
Solute distributions and liquid phase flow vectors in the ingot at 1000 s (a1-c1), 2200 s (a2-c2), 3800 s (a3-c3), 5080 s (a4-c4), 6520 s (a5-c5), 8520 s (a6-c6), and 9440 s (a7-c7) during the second smelting process (a1-a7) VAR2-A (b1-b7) VAR2-D (c1-c7) VAR2-R
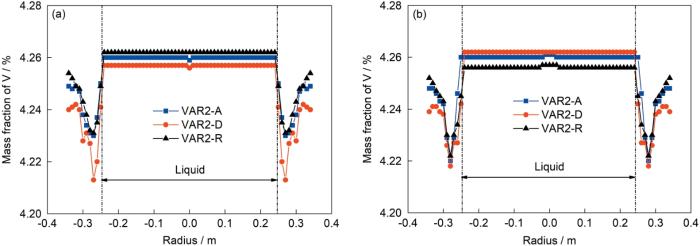
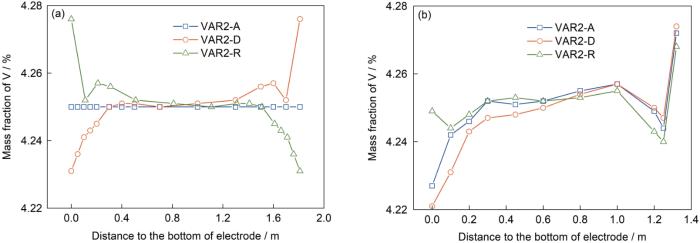
从图3 中还可以看出,3种电极情况下,强烈的对流使得熔池内液相成分都呈现出较为均匀的分布,但3种情况下熔池内液相的平均成分存在差异。初始阶段(1000~2200 s),一次铸锭正置做电极(VAR2-D)时熔池内液相浓度最低(图中呈现深绿色),而一次铸锭反置做电极(VAR2-R)时熔池内液相浓度最高(图中呈现浅绿色),均匀成分电极情况(VAR2-A)介于2者中间。为进一步定量对比,提取了2200 s时熔池中间高度处(2200 s结果中水平线位置)的径向浓度分布,3种电极情况的结果对比如图4a 所示。可以看到,VAR2-D的液相浓度最低,而VAR2-R的液相浓度最高。液相成分的差异将导致凝固形成固相的成分不同。VAR2-D情况下,初始熔池内平均液相浓度低,导致铸锭底部形成了负偏析程度较重的固相;而VAR2-R情况下,初始熔池内平均液相浓度高,相应的铸锭底部负偏析较轻。随着熔炼的进行,5080 s时熔炼达到铸锭最大高度,可以发现此时VAR2-D情况下的熔池液相浓度为3者中最高(图中呈现浅绿色),而VAR2-R情况下熔池液相成分最低(图中呈现深绿色)。图4b 为5080 s时3种情况熔池中间高度处的径向浓度分布对比,从中可以更清楚地看到这一点。在随后的小电流保温阶段,残余液相在弱的浮力控制对流下完成凝固。5080 s时残余液相浓度越高,凝固完成后铸锭中心的正偏析程度越重,因此最终VAR2-D情况下铸锭中心(特别是顶部中心)正偏析程度最大,而VAR2-R情况下中心正偏析程度最轻,如图3c7 所示。
图4
图4
第二次熔炼过程中不同时刻下径向浓度分布曲线
Fig.4
Radial concentration distribution curves at different time during the second remelting process (The extracted concentration positions are shown by horizontal lines in Fig.3)
(a) comparisons of the three electrode placement results at 2200 s
(b) comparisons of the three electrode placement results at 5080 s
上述3种电极情况下,熔池液相平均浓度的差异是由电极沿轴向的成分差异引起的。图5a 为3种电极内径向平均浓度随电极高度(即轴向)的分布曲线。可以看出,VAR2-D的电极底部平均浓度最低,而VAR2-R的电极底部平均浓度最高。由于电极底部最先熔化进入坩埚,因此第二次熔炼初始阶段,VAR2-D的熔池内液相浓度最低,而VAR2-R的熔池内液相浓度最高。在电极末端的情况正好相反,VAR2-D的电极底部平均浓度最高,相应的熔炼末期VAR2-D的熔池内液相浓度最高。上述电极中沿轴向的成分分布差异造成了二次铸锭沿轴向的成分差异。如图5b 所示,VAR2-D铸锭底部径向平均成分最低、顶部径向平均成分最高;而VAR2-R铸锭底部平均成分最高、顶部平均成分最低。总体来看,VAR2-R铸锭偏析最轻、成分最为均匀。
图5
图5
第二次熔炼时电极及铸锭中径向平均浓度随高度变化曲线
Fig.5
Radial average concentrations in the second remelting electrode (a) and ingot (b) varied with height
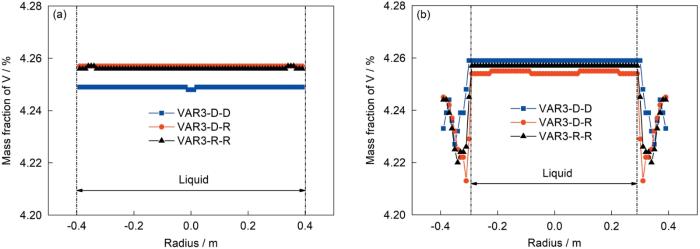
上述分析表明,一次铸锭做二次熔炼电极时,其沿轴向的成分分布对二次铸锭的宏观偏析具有较大影响。实际上,一次铸锭除轴向成分不均匀外,其径向成分也存在明显的不均匀,如图2 所示,一次铸锭径向中心浓度高、侧壁浓度低。第二次熔炼过程中,当一次铸锭做电极被熔化后,熔体刚落入二次铸锭熔池上表面时,同样会形成沿径向的浓度差异。但由于熔池上方强烈的液相流动,会将这一径向浓度差异快速消除,使得熔池内绝大部分位置的径向成分基本均匀,图4 清楚地表明了这一点。虽然最终二次铸锭也呈现出中心浓度高、侧壁浓度低的径向成分偏析,但这是由于二次熔炼时固/液界面前沿的溶质再分配及液相对流所致,而并非一次铸锭的径向浓度差异引起。综上所述,在熔池上方有强烈对流时,一次铸锭的径向成分不均匀对二次铸锭的宏观偏析无影响。而一次铸锭沿轴向的成分不均匀会传递给二次铸锭。
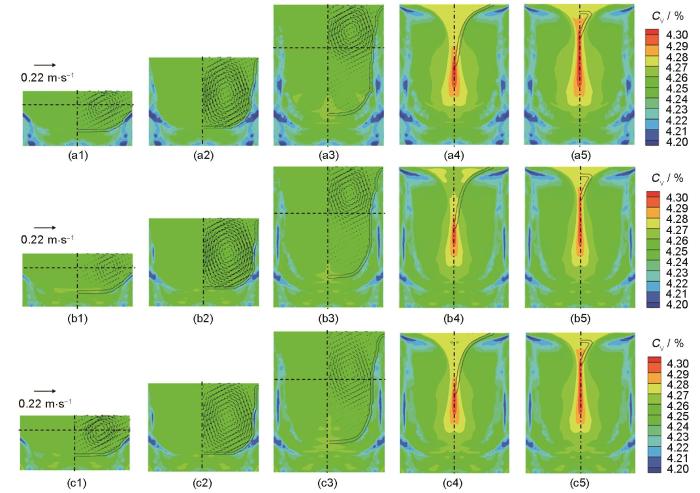
第三次熔炼过程中的溶质偏析传递行为与第二次熔炼类似。图6 以VAR3-D-D、VAR3-D-R和VAR3-R-R 3种电极放置情况为例,展示了第三次熔炼过程中溶质场及流场演化。可以看出,熔池内强烈的对流使得熔池内绝大部分位置的径向成分基本均匀,从1300和3800 s时熔池中部沿水平方向的浓度分布曲线(图7 )可以更清楚地看到这一点。因此二次铸锭的径向成分不均匀也不会传递给三次铸锭。
图6
图6
第三次熔炼时的溶质场及流场演化
Fig.6
Solute distributions and liquid phase flow vectors in the ingot at 1300 s (a1-c1), 2300 s (a2-c2), 3800 s (a3-c3), 8350 s (a4-c4), and 9400 s (a5-c5) during the third smelting process (a1-a5) VAR3-D-D (b1-b5) VAR3-D-R (c1-c5) VAR3-R-R
图7
图7
第三次熔炼过程中不同时刻下径向浓度分布曲线
Fig.7
Radial concentration distribution curves at different time during the third remelting process (The extracted concentration positions are shown by the horizontal lines in Fig.6)
(a) comparison of the three electrode placement results at 1300 s
(b) comparison of the three electrode placement results at 3800 s
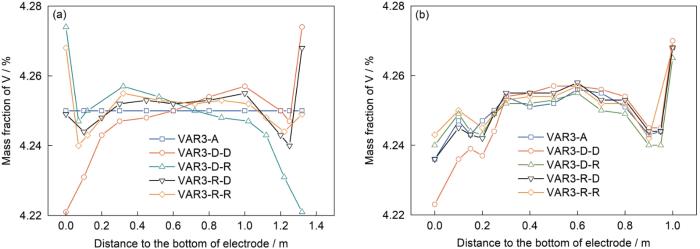
但二次铸锭沿轴向的成分不均匀会传递给三次铸锭。第三次熔炼时5种电极放置方案中电极径向平均浓度沿轴向的分布情况如图8a 所示。可以看出,在电极底部,VAR3-D-D情况下的平均成分最低。因此,第三次熔炼初始阶段,VAR3-D-D情况下熔池内液相成分最低,这从图6 和7a 可以看出;此时,形成的三次铸锭底部负偏析程度也最重,如图8b 所示。
图8
图8
第三次熔炼时电极及铸锭中径向平均浓度随高度变化曲线
Fig.8
Radial average concentrations in the third remelting electrode (a) and ingot (b) varied with height
从图8 还可以看出,三次熔炼中不同电极的顶部平均成分也存在明显差异(图8a ),但最终铸锭顶部偏析程度基本相同(图8b ),无显著差异。造成这一现象的原因在于,第三次熔炼铸锭的半径比二次熔炼时增大,在熔速基本相当的情况下,单位时间热输入增加,铸锭熔池深度加大,且三次铸锭高度降低,因而熔炼到最大高度时(3800 s),熔池在整个铸锭中的体积占比显著增加,如图6 所示,此时熔池体积占比超过铸锭总体积一半以上。在熔炼末期,电极末端熔化进入熔池的同时,熔池内还保留有大量电极中前端熔化形成的液相,熔池上方强烈的对流使得2种液相充分混合,从而削弱了末端电极成分偏析带来的影响。而熔炼初期,由于熔池内液相仅由电极底部熔化而来,不同电极情况下,电极之间底部成分的差异在初始熔池液相中充分体现,进而带来了铸锭底部偏析的差异。
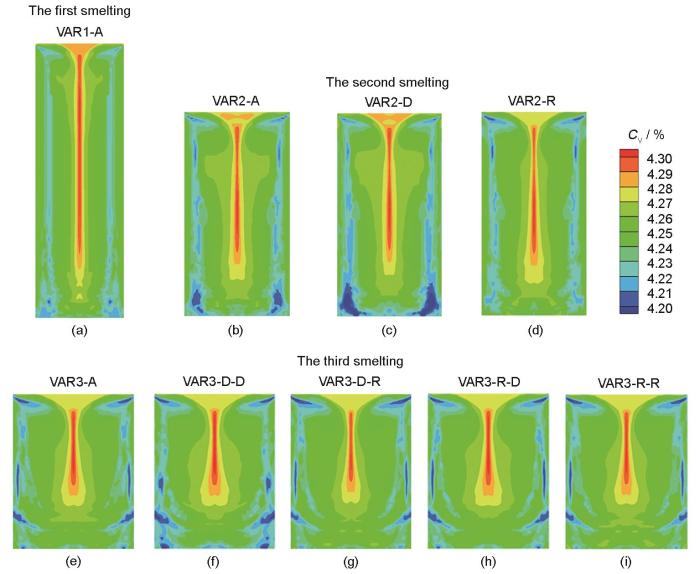
2.3 不同熔炼方案宏观偏析对比
图9 为模拟的各种电极情况下铸锭完全凝固后的成分分布。可以看出,第二次熔炼过程中电极正置情况下(VAR2-D)铸锭底部负偏析和顶部正偏析程度最大。与第二次熔炼相比,第三次熔炼时,采用不同电极放置方案获得的铸锭之间宏观偏析差异性较小,仅VAR3-D-D情况下铸锭底部负偏析程度相对较重,其他情况铸锭底部负偏析程度相近。
图9
图9
全部三次熔炼铸锭最终成分分布对比
Fig.9
Comparisons of final concentration distributions of all triple remelting ingots
(a) VAR1-A (b) VAR2-A (c) VAR2-D (d) VAR2-R
(e) VAR3-A (f) VAR3-D-D (g) VAR3-D-R (h) VAR3-R-D (i) VAR3-R-R
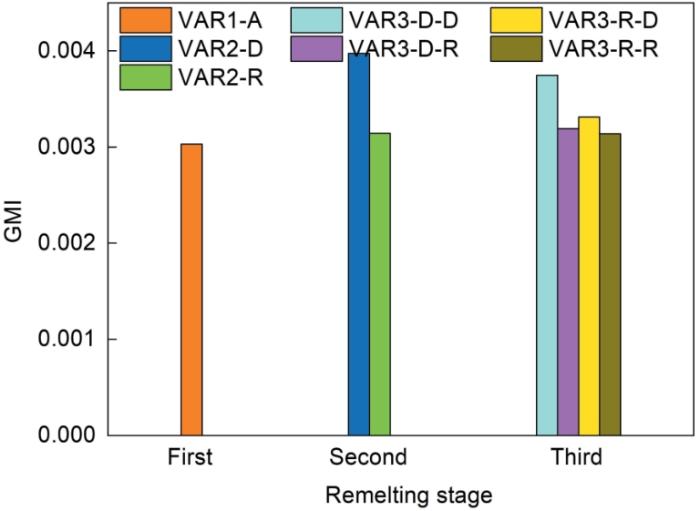
为定量地反映铸锭整体偏析程度,可采用Zagrebelnyy和Krane[25 ] 定义的整体宏观偏析指数(global macrosegregation index,GMI):
G M I = 1 V i n g o t ∫ C - C 0 C 0 d V 1 / 2 (16)
式中,V ingot 为铸锭的总体积,C 为每个单元内浓度,C 0 为体系平均浓度。GMI值为0代表整个铸锭完全无偏析,GMI值越大代表整体偏析越重。
图10 为不同电极情况下铸锭GMI对比。可以看出,如果三次熔炼过程中始终保持前次铸锭正置做电极(VAR3-D-D),则最终第三次熔炼铸锭的GMI最高,表明整体偏析程度最重。而如果在第二次或第三次熔炼中,至少有一次将铸锭反置做电极(VAR3-D-R、VAR3-R-D),则第三次熔炼铸锭的GMI显著降低,整体偏析程度显著减轻。但进一步增加到两次反置(VAR3-R-R),偏析程度进一步减轻有限。这是由于一方面采用反置电极进行第二次熔炼得到的铸锭底部和顶部成分差异已经弱于一次铸锭底部和顶部的成分差异(对比图9a 和d ),因此二次铸锭做三次熔炼电极时,反置与否引起的偏析差异较小;另一方面,第三次熔炼时较深的熔池使得电极底部与顶部之间的成分差异在流动作用下被削弱,从而减轻了电极放置方向的影响。
图10
图10
各次熔炼铸锭的整体宏观偏析指数(GMI)对比
Fig.10
Comparisons of the global macrosegregation index (GMI) of each remelting ingot
3 TC4 合金偏析传递模拟及实验验证
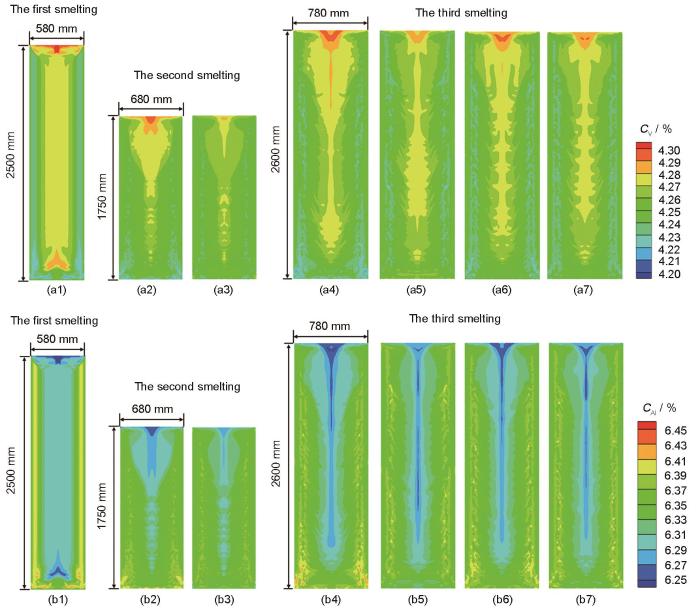
采用TC4合金实际三次熔炼的铸锭尺寸和电流工艺进行模拟,第三次熔炼的电极由两根二次铸锭头/尾焊接而成。采用不同电极放置方案下的铸锭成分分布结果如图11 所示,其中标出了各次熔炼的铸锭尺寸。可以看出,Al元素分布(图11a1~a7 )呈现中心负偏析、侧壁正偏析,与V元素分布(图11b1~b7 )恰好相反。这是因为V元素平衡分配系数小于1,而Al元素平衡分配系数大于1。在固/液界面前沿,液相中Al贫乏,这些贫Al的液相被铸锭侧壁向下对流带到熔池底部,从而形成中心负偏析、侧壁正偏析。此外,从图11 中还可看出,在第二次熔炼中,直接将一次铸锭正置作电极(VAR2-D)偏析比一次铸锭反置作电极(VAR2-R)严重;在第三次熔炼中连续两次正置电极(VAR3-D-D)得到的铸锭偏析要大于其他3种电极放置方案的结果。
图11
图11
TC4合金三次熔炼铸锭中V、Al成分分布的模拟结果
Fig.11
Simulation results of V element (a1-a7) and Al element (b1-b7) concentration distributions in triple remelting ingot of TC4 alloy (C Al —mass fraction of aluminum element) (a1, b1) VAR1-A (a2, b2) VAR2-D (a3, b3) VAR2-R (a4, b4) VAR3-D-D (a5, b5) VAR3-D-R (a6, b6) VAR3-R-D (a7, b7) VAR3-R-R
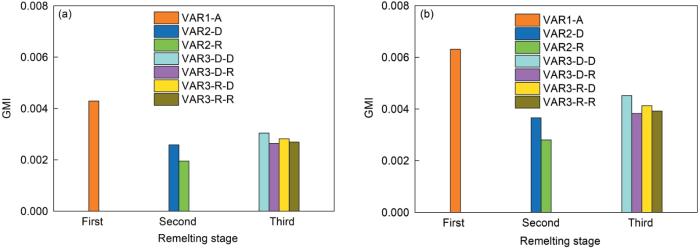
进一步对V元素和Al元素的GMI进行对比,如图12 所示。可以看出,第二次熔炼时一次铸锭反置作电极(VAR2-R)得到的铸锭V元素和Al元素的GMI均比正置情况要小;三次熔炼过程中始终保持前次铸锭正置做电极(VAR3-D-D)铸锭的GMI最高,偏析程度最重,相比之下,在第二次或第三次熔炼中,至少有一次将铸锭反置做电极(VAR3-D-R、VAR3-R-D)时GMI降低,但进一步增加到两次反置(VAR3-R-R)时的GMI与有一次反置的情况差异不大。这与第2节中模拟得到的偏析传递规律一致,进一步验证了这一偏析传递规律的普适性。
图12
图12
TC4合金不同熔炼方案下铸锭中V元素和Al元素的GMI
Fig.12
GMI of V element (a) and Al element (b) in TC4 alloy ingot under different melting schemes
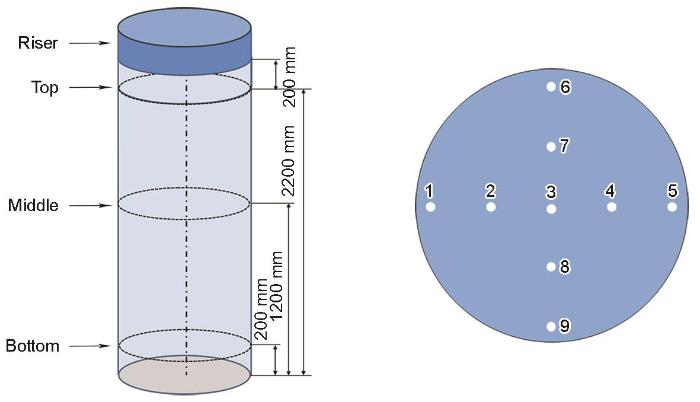
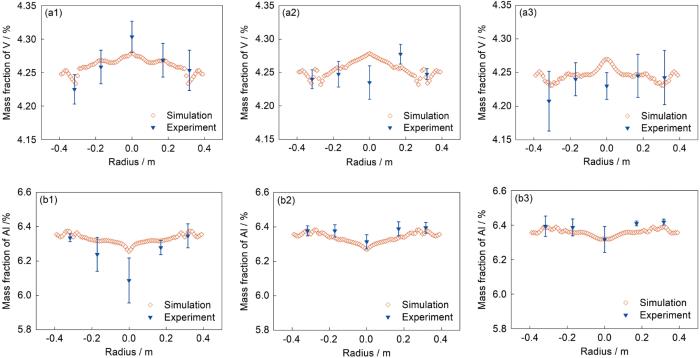
对实际生产第三次熔炼铸锭,从头部、中部、底部3个不同的水平面上由中心到边缘取样9个点,如图13 所示,采用电感耦合等离子体原子发射光谱法测量Al元素和V元素成分。对相同工艺三批次生产的铸锭随机选择3根进行成分测定,取平均值作为最终结果,并计算方差。根据实验中铸锭头部、中部、底部取样点的高度位置,提取了模拟中相应高度处的径向浓度分布曲线,与实验结果进行对比。模拟结果与实验测量结果对比如图14 所示。可以发现2者基本吻合。在铸锭头部,Al元素浓度实验测量值要比模拟结果整体偏低,且越靠近中心部位,测量值偏低的程度越大,如图14b1 所示。造成这一差异的原因在于,实际熔炼末期存在小电流保温过程,此时铸锭头部的熔池发生长时间缓慢凝固,且越靠近中心的液相凝固时间越长,在这一过程中,由于Al蒸气压高,为易挥发元素,因此熔池液相中Al浓度会由于挥发而下降;且液相存在时间越长的部位(中心处) Al挥发越严重,Al浓度越低。由于模拟中并未考虑Al挥发造成的液相成分变化,从而使模拟结果与实验测量值存在一定差异。但这并不影响本工作模拟中揭示的凝固偏析形成及传递规律。此外,V元素浓度模拟结果在铸锭心部与实验值对比存在一定差异,其原因是:模拟用到的凝固模型只考虑了由铸锭外侧向中心生长的柱状晶,未考虑液相内形核的等轴晶;而实际铸锭熔炼过程中,熔炼进行一段时间后熔池中心部位温度梯度下降,导致固/液界面前方液相中形成等轴晶,与液相相比,等轴晶中贫V,这些等轴晶随着液相漂移到熔池底部中心,从而导致中心处的V浓度降低。考虑铸锭中心等轴晶游离的研究工作还有待进一步开展。综上所述,因模型假设忽略了Al元素挥发和液相中的等轴晶游离,使模拟结果和实验值在个别位置存在一定偏差,但基本偏析规律符合实际情况。
图13
图13
铸锭取样方式
Fig.13
Ingot sampling procedure and positions 1-9
图14
图14
TC4合金三次熔炼最终铸锭中不同部位径向V浓度分布和Al浓度分布的模拟结果与实验结果对比
Fig.14
Comparisons between the simulation and the experimental results of radial V element (a1-a3) and Al element (b1-b3) concentration distributions in the top (a1, b1), middle (a2, b2), and bottom (a3, b3) parts of the final ingot of TC4 alloy after triple remelting
4 结论
(1) 前次铸锭的径向成分不均匀会由于对流作用而基本消除,对下一次熔炼铸锭的宏观偏析无影响;而前次铸锭的轴向成分不均匀会传递给下一次熔炼的铸锭,这一传递对下次铸锭底部影响最显著,而在铸锭顶部,当熔池较深时,熔池内强烈的对流使得前次铸锭末端与中前端熔化的液相充分混合,从而削弱前次铸锭轴向成分差异的影响。
(2) 三次熔炼中,如果始终保持铸锭正置作电极,铸锭宏观偏析最重;如至少有一次将铸锭反置作电极,可显著减轻宏观偏析;但增加到两次反置,偏析进一步减轻的程度有限。
(3) 模拟所得铸锭宏观偏析与实验结果基本吻合,验证了本工作所用模型以及对于三次熔炼中宏观偏析传递行为研究的准确性。
参考文献
View Option
[1]
Mitchell A Kawakami A Cockcroft S L Segregation in titanium alloy ingots
[J]. High Temp. Mater. Processes , 2007 , 26 : 59
[本文引用: 1]
[2]
Zhao Y Q Liu J L Zhou L Analysis on the segregation of typical β alloying elements of Cu, Fe and Cr in Ti alloys
[J]. Rare Met. Mater. Eng. , 2005 , 34 : 531
[本文引用: 1]
赵永庆 , 刘军林 , 周 廉 典型β 型钛合金元素Cu,Fe和Cr的偏析规律
[J]. 稀有金属材料与工程 , 2005 , 34 : 531
[本文引用: 1]
[3]
Liu J L Zhao Y Q Zhou L Segregation of Ti-2.5Cu, Ti-3Fe and Ti-3Cr alloy ingots
[J]. Rare Met. Mater. Eng. , 2004 , 33 : 731
[本文引用: 1]
刘军林 , 赵永庆 , 周 廉 Ti-2. 5Cu,Ti-3Fe,Ti-3Cr合金铸锭的偏析
[J]. 稀有金属材料与工程 , 2004 , 33 : 731
[本文引用: 1]
[4]
Yang Z J Kou H C Li J S et al Macrosegregation behavior of Ti-10V-2Fe-3Al alloy during vacuum consumable arc remelting process
[J]. J. Mater. Eng. Perform. , 2011 , 20 : 65
[本文引用: 1]
[5]
Zhao X H Li J S Yang Z J et al Numerical simulation of fluid flow caused by buoyancy forces during vacuum arc remelting process
[J]. J. Shanghai Jiaotong Univ. (Sci.) , 2011 , 16 : 272
[本文引用: 1]
[6]
Zhao X H Li J S Yang Z J et al Numerical simulation of temperature field in vacuum arc remelting Ti alloy
[J]. Spec. Cast. Nonferrous Alloys , 2010 , 30 : 1001
[本文引用: 1]
赵小花 , 李金山 , 杨治军 等 钛合金真空自耗电弧熔炼过程中温度场的数值模拟
[J]. 特种铸造及有色合金 , 2010 , 30 : 1001
[本文引用: 1]
[7]
Kou H C Zhang Y J Yang Z J et al Liquid metal flow behavior during vacuum consumable arc remelting process for titanium
[J]. Int. J. Eng. Technol. , 2012 , 12 : 50
[本文引用: 1]
[8]
Davidson P A He X Lowe A J Flow transitions in vacuum arc remelting
[J]. Mater. Sci. Technol. , 2000 , 16 : 699
[本文引用: 3]
[9]
Davidson P A Kinnear D Lingwood R J et al The role of Ekman pumping and the dominance of swirl in confined flows driven by Lorentz forces
[J]. Eur. J. Mech. , 1999 , 18B : 693
[本文引用: 1]
[10]
Chapelle P Ward R M Jardy A et al Lateral boundary conditions for heat transfer and electrical current flow during vacuum arc remelting of a zirconium alloy
[J]. Metall. Mater. Trans. , 2009 , 40B : 254
[本文引用: 3]
[11]
Shevchenko D M Ward R M Liquid metal pool behavior during the vacuum arc remelting of Inconel 718
[J]. Metall. Mater. Trans. , 2009 , 40B : 263
[本文引用: 1]
[12]
Patel A Fiore D On the modeling of vacuum arc remelting process in titanium alloys
[J]. IOP Conf. Ser.: Mater. Sci. Eng. , 2016 , 143 : 012017
[本文引用: 1]
[13]
Fan K Wu L C Li J J et al Numerical simulation of macrosegregation caused by buoyancy driven flow during VAR process for titanium alloys
[J]. Rare Met. Mater. Eng. , 2020 , 49 : 871
[本文引用: 2]
樊 凯 , 吴林财 , 李俊杰 等 钛合金VAR过程中自然对流下的宏观偏析行为模拟
[J]. 稀有金属材料与工程 , 2020 , 49 : 871
[本文引用: 2]
[14]
Revil-Baudard M Jardy A Combeau H et al Solidification of a vacuum arc-remelted zirconium ingot
[J]. Metall. Mater. Trans. , 2014 , 45B : 51
[本文引用: 1]
[15]
Zagrebelnyy D V Modeling macrosegregation during the vacuum arc remelting of Ti-10V-2Fe-3Al alloy
[D]. West Lafayette : Purdue University , 2007
[本文引用: 2]
[16]
Lv Y F Meng X J Li S K An overview of β fleck in TB6 alloy
[J]. Rare Met. Mater. Eng. , 2008 , 37 (): 544
[本文引用: 1]
吕逸帆 , 孟祥军 , 李士凯 TB6合金β 斑研究概述
[J]. 稀有金属材料与工程 , 2008 , 37 (): 544
[本文引用: 1]
[17]
Chen Z Q Gao Q Liu X et al Control of iron segregation in Ti-1023 titanium alloy
[J]. Titanium Ind. Prog. , 2003 , 20 (4-5 ): 56
[本文引用: 1]
陈战乾 , 高 颀 , 刘 新 等 Ti-1023合金铸锭铁偏析控制
[J]. 钛工业进展 , 2003 , 20 (4-5 ): 56
[本文引用: 1]
[18]
Swaminathan C R Voller V R A general enthalpy method for modeling solidification processes
[J]. Metall . Trans., 1992 , 23B : 651
[本文引用: 2]
[19]
Voller V R Cross M Markatos N C An enthalpy method for convection/diffusion phase change
[J]. Int. J. Numer. Methods Eng. , 1987 , 24 : 271
[本文引用: 2]
[20]
Bellet M Combeau H Fautrelle Y et al Call for contributions to a numerical benchmark problem for 2D columnar solidification of binary alloys
[J]. Int. J. Therm. Sci. , 2009 , 48 : 2013
[本文引用: 1]
[21]
Prakash C Voller V On the numerical solution of continuum mixture model equations describing binary solid-liquid phase change
[J]. Numer. Heat Transfer , 1989 , 15B : 171
[本文引用: 1]
[22]
Chapelle P Jardy A Bellot J P et al Effect of electromagnetic stirring on melt pool free surface dynamics during vacuum arc remelting
[J]. J. Mater. Sci. , 2008 , 43 : 5734
[本文引用: 2]
[23]
Kondrashov E N Musatov M I Maksimov A Y et al Calculation of the molten pool depth in vacuum arc remelting of alloy Vt3-1
[J]. J. Eng. Thermophys. , 2007 , 16 : 19
[本文引用: 1]
[24]
Bellot J P Ablitzer D Foster B et al Dissolution of hard-alpha inclusions in liquid titanium alloys
[J]. Metall. Mater. Trans. , 1997 , 28B : 1001
[本文引用: 1]
[25]
Zagrebelnyy D Krane M J M Segregation development in multiple melt vacuum arc remelting
[J]. Metall. Mater. Trans. , 2009 , 40B : 281
[本文引用: 2]
Segregation in titanium alloy ingots
1
2007
... 凝固过程中的溶质再分配是引起宏观偏析的重要原因.当前对钛合金中不同元素凝固分配系数与自耗熔炼铸锭宏观偏析的关系已开展了大量研究.Mitchell等[1 ] 测定了Ti-6242、Ti-17和Ti-1023钛合金中Al、V、Fe、Mo、Cr、Sn、Zr等元素的分配系数(k ),发现实际铸锭中元素的k 与二元相图中的平衡数值存在明显差异,并指出Fe和Cr是2种最易偏析的元素.赵永庆等[2 ,3 ] 分析了多种钛合金铸锭中Cu、Fe、Cr的偏析分布,发现Fe和Cu元素沿径向存在严重的偏析,并指出这与2者的k 远偏离1相关.Yang等[4 ] 测量了Ti-1023合金中偏析最严重的Fe元素的空间分布,并分析了熔炼电流的影响,发现大电流下宏观偏析更为严重. ...
Analysis on the segregation of typical β alloying elements of Cu, Fe and Cr in Ti alloys
1
2005
... 凝固过程中的溶质再分配是引起宏观偏析的重要原因.当前对钛合金中不同元素凝固分配系数与自耗熔炼铸锭宏观偏析的关系已开展了大量研究.Mitchell等[1 ] 测定了Ti-6242、Ti-17和Ti-1023钛合金中Al、V、Fe、Mo、Cr、Sn、Zr等元素的分配系数(k ),发现实际铸锭中元素的k 与二元相图中的平衡数值存在明显差异,并指出Fe和Cr是2种最易偏析的元素.赵永庆等[2 ,3 ] 分析了多种钛合金铸锭中Cu、Fe、Cr的偏析分布,发现Fe和Cu元素沿径向存在严重的偏析,并指出这与2者的k 远偏离1相关.Yang等[4 ] 测量了Ti-1023合金中偏析最严重的Fe元素的空间分布,并分析了熔炼电流的影响,发现大电流下宏观偏析更为严重. ...
典型β 型钛合金元素Cu,Fe和Cr的偏析规律
1
2005
... 凝固过程中的溶质再分配是引起宏观偏析的重要原因.当前对钛合金中不同元素凝固分配系数与自耗熔炼铸锭宏观偏析的关系已开展了大量研究.Mitchell等[1 ] 测定了Ti-6242、Ti-17和Ti-1023钛合金中Al、V、Fe、Mo、Cr、Sn、Zr等元素的分配系数(k ),发现实际铸锭中元素的k 与二元相图中的平衡数值存在明显差异,并指出Fe和Cr是2种最易偏析的元素.赵永庆等[2 ,3 ] 分析了多种钛合金铸锭中Cu、Fe、Cr的偏析分布,发现Fe和Cu元素沿径向存在严重的偏析,并指出这与2者的k 远偏离1相关.Yang等[4 ] 测量了Ti-1023合金中偏析最严重的Fe元素的空间分布,并分析了熔炼电流的影响,发现大电流下宏观偏析更为严重. ...
Segregation of Ti-2.5Cu, Ti-3Fe and Ti-3Cr alloy ingots
1
2004
... 凝固过程中的溶质再分配是引起宏观偏析的重要原因.当前对钛合金中不同元素凝固分配系数与自耗熔炼铸锭宏观偏析的关系已开展了大量研究.Mitchell等[1 ] 测定了Ti-6242、Ti-17和Ti-1023钛合金中Al、V、Fe、Mo、Cr、Sn、Zr等元素的分配系数(k ),发现实际铸锭中元素的k 与二元相图中的平衡数值存在明显差异,并指出Fe和Cr是2种最易偏析的元素.赵永庆等[2 ,3 ] 分析了多种钛合金铸锭中Cu、Fe、Cr的偏析分布,发现Fe和Cu元素沿径向存在严重的偏析,并指出这与2者的k 远偏离1相关.Yang等[4 ] 测量了Ti-1023合金中偏析最严重的Fe元素的空间分布,并分析了熔炼电流的影响,发现大电流下宏观偏析更为严重. ...
Ti-2. 5Cu,Ti-3Fe,Ti-3Cr合金铸锭的偏析
1
2004
... 凝固过程中的溶质再分配是引起宏观偏析的重要原因.当前对钛合金中不同元素凝固分配系数与自耗熔炼铸锭宏观偏析的关系已开展了大量研究.Mitchell等[1 ] 测定了Ti-6242、Ti-17和Ti-1023钛合金中Al、V、Fe、Mo、Cr、Sn、Zr等元素的分配系数(k ),发现实际铸锭中元素的k 与二元相图中的平衡数值存在明显差异,并指出Fe和Cr是2种最易偏析的元素.赵永庆等[2 ,3 ] 分析了多种钛合金铸锭中Cu、Fe、Cr的偏析分布,发现Fe和Cu元素沿径向存在严重的偏析,并指出这与2者的k 远偏离1相关.Yang等[4 ] 测量了Ti-1023合金中偏析最严重的Fe元素的空间分布,并分析了熔炼电流的影响,发现大电流下宏观偏析更为严重. ...
Macrosegregation behavior of Ti-10V-2Fe-3Al alloy during vacuum consumable arc remelting process
1
2011
... 凝固过程中的溶质再分配是引起宏观偏析的重要原因.当前对钛合金中不同元素凝固分配系数与自耗熔炼铸锭宏观偏析的关系已开展了大量研究.Mitchell等[1 ] 测定了Ti-6242、Ti-17和Ti-1023钛合金中Al、V、Fe、Mo、Cr、Sn、Zr等元素的分配系数(k ),发现实际铸锭中元素的k 与二元相图中的平衡数值存在明显差异,并指出Fe和Cr是2种最易偏析的元素.赵永庆等[2 ,3 ] 分析了多种钛合金铸锭中Cu、Fe、Cr的偏析分布,发现Fe和Cu元素沿径向存在严重的偏析,并指出这与2者的k 远偏离1相关.Yang等[4 ] 测量了Ti-1023合金中偏析最严重的Fe元素的空间分布,并分析了熔炼电流的影响,发现大电流下宏观偏析更为严重. ...
Numerical simulation of fluid flow caused by buoyancy forces during vacuum arc remelting process
1
2011
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
Numerical simulation of temperature field in vacuum arc remelting Ti alloy
1
2010
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
钛合金真空自耗电弧熔炼过程中温度场的数值模拟
1
2010
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
Liquid metal flow behavior during vacuum consumable arc remelting process for titanium
1
2012
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
Flow transitions in vacuum arc remelting
3
2000
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
... 图2 是第一次熔炼过程中溶质分布随时间的演化结果,右半部分溶质场内加入了熔池轮廓和流场.从图2a 可以看出,在熔炼初始阶段(1000 s),熔池较浅,熔池中熔体沿熔池中心向下、侧壁向上流动,这是典型的电磁力主导对流[8 ,25 ] ,此对流将熔池底部固/液界面前沿凝固排出的溶质沿侧壁向上带到熔池内部,造成底部固/液界面处的溶质贫乏,从而在铸锭底部中心两侧形成了明显的负偏析区域(底部蓝色区域).到4300 s时,如图2b 所示,随着熔池深度加大,熔池上部仍为电磁力控制的中心向下、侧壁向上的对流;而在熔池下部区域,形成了浮力控制的侧壁向下、中心向上的微弱流动,从放大图(图2b1 )可以清晰观察到这一浮力控制对流.这种熔池上部与下部相反的流动模式与Davidson 等[8 ] 报道的较大熔炼电流下的熔池稳态流动结果一致.此时熔池下部浮力对流将熔池侧壁的溶质带到熔池底部,从而使底部形成正偏析;浮力对流区上方是电磁力控制的沿侧壁向上的流动,它将侧壁凝固排出的溶质带到熔池上方.因此在向下流动与向上流动的分界线附近,形成了显著的负偏析.在随后熔炼过程中(4300~8800 s),熔池深度基本恒定,熔池上部保持电磁力控制对流,下部为热浮力控制对流,已凝固铸锭形成了显著的中心正偏析和两侧负偏析条带,如图2b~d 所示.最后小电流保温阶段(9000~12500 s),熔池内电磁力基本消失,整个区域重新形成浮力控制的微弱流动,最终冒口部位形成正偏析,如图2e~g 所示. ...
... [8 ]报道的较大熔炼电流下的熔池稳态流动结果一致.此时熔池下部浮力对流将熔池侧壁的溶质带到熔池底部,从而使底部形成正偏析;浮力对流区上方是电磁力控制的沿侧壁向上的流动,它将侧壁凝固排出的溶质带到熔池上方.因此在向下流动与向上流动的分界线附近,形成了显著的负偏析.在随后熔炼过程中(4300~8800 s),熔池深度基本恒定,熔池上部保持电磁力控制对流,下部为热浮力控制对流,已凝固铸锭形成了显著的中心正偏析和两侧负偏析条带,如图2b~d 所示.最后小电流保温阶段(9000~12500 s),熔池内电磁力基本消失,整个区域重新形成浮力控制的微弱流动,最终冒口部位形成正偏析,如图2e~g 所示. ...
The role of Ekman pumping and the dominance of swirl in confined flows driven by Lorentz forces
1
1999
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
Lateral boundary conditions for heat transfer and electrical current flow during vacuum arc remelting of a zirconium alloy
3
2009
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
... 铸锭底部设为对流换热边界,换热系数设为500 W/(m2 ·K).铸锭侧壁与外界的热交换分成2个区域处理:侧壁上部与坩埚直接接触,可设为对流换热边界,换热系数设为800 W/(m2 ·K);铸锭下部由于凝固收缩,侧壁与坩埚壁之间会形成间隙,此时铸锭热量主要以辐射形式向外界散失.通过临界温度(T c )来判断铸锭侧壁与坩埚的接触情况,当侧壁温度小于T c 时认为形成间隙,T c 设为合金固相线温度以下100 K[10 ] .为简化处理,可将辐射散热用对流换热等效,等效对流换热系数(h gap )计算公式如下[10 ] : ...
... [10 ]: ...
Liquid metal pool behavior during the vacuum arc remelting of Inconel 718
1
2009
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
On the modeling of vacuum arc remelting process in titanium alloys
1
2016
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
Numerical simulation of macrosegregation caused by buoyancy driven flow during VAR process for titanium alloys
2
2020
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
... 本研究采用Swaminathan等[18 ] 和Voller等[19 ] 提出的合金连续介质模型来描述凝固过程,并在其中耦合自感应电磁力和搅拌电磁力.假定熔池中熔体流动为层流,采用Boussinesq近似[20 ,21 ] .模型中连续性方程、能量守恒方程、溶质守恒方程与文献[13 ,18 ,19 ]中类似,不再赘述;动量方程中加入了电磁力源项,并且考虑了旋转速度,具体形式如下. ...
钛合金VAR过程中自然对流下的宏观偏析行为模拟
2
2020
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
... 本研究采用Swaminathan等[18 ] 和Voller等[19 ] 提出的合金连续介质模型来描述凝固过程,并在其中耦合自感应电磁力和搅拌电磁力.假定熔池中熔体流动为层流,采用Boussinesq近似[20 ,21 ] .模型中连续性方程、能量守恒方程、溶质守恒方程与文献[13 ,18 ,19 ]中类似,不再赘述;动量方程中加入了电磁力源项,并且考虑了旋转速度,具体形式如下. ...
Solidification of a vacuum arc-remelted zirconium ingot
1
2014
... 熔体流动是引起宏观偏析的另一个重要因素.VAR熔池内的液相流动行为,难以通过实验直接观测,目前主要通过理论分析及数值模拟手段开展研究.Zhao等[5 ,6 ] 基于有限元模拟分析了VAR过程中热浮力引起的自然对流行为,结果表明,热浮力作用下熔池流动沿侧壁向下、中心向上.Kou等[7 ] 进一步耦合电磁场计算,分析了Lorentz力对于VAR熔池内熔体流动的影响规律,发现自感应Lorentz力可改变熔体流动方向,形成中心向下、侧壁向上的流动.Davidson等[8 ,9 ] 计算分析了热浮力、自感电磁力和搅拌电磁力引起的对流模式以及3者之间的竞争关系,发现熔池中熔体流动规律会因3种力的竞争而发生改变.Chapelle等[10 ] 模拟了搅拌电磁力引起的熔池表面运动,并分析了其对铸锭表面质量的影响.Shevchenko和Ward[11 ] 计算了电弧运动对熔池液相流动的影响.上述关于熔池运动的模拟研究中并未耦合溶质传输,无法直接反映流动造成的成分偏析行为.Patel和Fiore[12 ] 模拟了TC4合金VAR过程中Fe和O元素的偏析行为,分析了搅拌磁场强度对偏析的影响.樊凯等[13 ] 通过模拟,分析了热浮力和溶质浮力引起的自然对流在TC4合金宏观偏析形成中的作用机制,发现抑制自然对流可最大程度减轻宏观偏析.除钛合金以外,还有研究[14 ] 通过模拟方法分析了锆合金VAR过程中热浮力和溶质浮力引起的宏观偏析规律. ...
Modeling macrosegregation during the vacuum arc remelting of Ti-10V-2Fe-3Al alloy
2
2007
... 上述关于宏观偏析行为的研究均针对一次VAR熔炼的铸锭开展.实际钛合金VAR熔炼中,为保证铸锭的均匀性、减少夹杂,通常采用三次熔炼工艺.初次熔炼时将海绵钛和中间合金一起压制成电极,电极熔化后在坩埚中形成一次铸锭;再将一次铸锭当做二次熔炼的电极,将电极熔化形成二次铸锭;最后用二次铸锭做为第三次熔炼电极,制备三次铸锭.三次熔炼过程中采用的坩埚直径不断增加,形成的铸锭直径也相应增大.由于VAR铸锭中宏观偏析的存在,当把铸锭做为电极进行再次熔炼时,势必涉及电极成分均匀性对后续铸锭偏析的影响问题.Zagerbelnyy[15 ] 认为,绝大多数情况下电极成分的均匀性对铸锭成分的影响微乎其微.然而也有研究[16 ,17 ] 指出,采用与铸锭偏析分布相反的布料方式压制电极可以减轻偏析.实际生产过程中,通常将上次熔炼铸锭底部与头部颠倒后做为下次电极,这一方式的偏析程度要轻于铸锭直接正置的情况.当前关于宏观偏析在多次熔炼中是否存在传递,以及传递的原因、规律和影响程度都缺乏清晰的理解. ...
... 对于电势场边界,铸锭底部和侧壁电势均设置为零,在铸锭顶部设置电流密度(j (y ))沿径向呈Gaussian分布,公式如下[15 ] : ...
An overview of β fleck in TB6 alloy
1
2008
... 上述关于宏观偏析行为的研究均针对一次VAR熔炼的铸锭开展.实际钛合金VAR熔炼中,为保证铸锭的均匀性、减少夹杂,通常采用三次熔炼工艺.初次熔炼时将海绵钛和中间合金一起压制成电极,电极熔化后在坩埚中形成一次铸锭;再将一次铸锭当做二次熔炼的电极,将电极熔化形成二次铸锭;最后用二次铸锭做为第三次熔炼电极,制备三次铸锭.三次熔炼过程中采用的坩埚直径不断增加,形成的铸锭直径也相应增大.由于VAR铸锭中宏观偏析的存在,当把铸锭做为电极进行再次熔炼时,势必涉及电极成分均匀性对后续铸锭偏析的影响问题.Zagerbelnyy[15 ] 认为,绝大多数情况下电极成分的均匀性对铸锭成分的影响微乎其微.然而也有研究[16 ,17 ] 指出,采用与铸锭偏析分布相反的布料方式压制电极可以减轻偏析.实际生产过程中,通常将上次熔炼铸锭底部与头部颠倒后做为下次电极,这一方式的偏析程度要轻于铸锭直接正置的情况.当前关于宏观偏析在多次熔炼中是否存在传递,以及传递的原因、规律和影响程度都缺乏清晰的理解. ...
TB6合金β 斑研究概述
1
2008
... 上述关于宏观偏析行为的研究均针对一次VAR熔炼的铸锭开展.实际钛合金VAR熔炼中,为保证铸锭的均匀性、减少夹杂,通常采用三次熔炼工艺.初次熔炼时将海绵钛和中间合金一起压制成电极,电极熔化后在坩埚中形成一次铸锭;再将一次铸锭当做二次熔炼的电极,将电极熔化形成二次铸锭;最后用二次铸锭做为第三次熔炼电极,制备三次铸锭.三次熔炼过程中采用的坩埚直径不断增加,形成的铸锭直径也相应增大.由于VAR铸锭中宏观偏析的存在,当把铸锭做为电极进行再次熔炼时,势必涉及电极成分均匀性对后续铸锭偏析的影响问题.Zagerbelnyy[15 ] 认为,绝大多数情况下电极成分的均匀性对铸锭成分的影响微乎其微.然而也有研究[16 ,17 ] 指出,采用与铸锭偏析分布相反的布料方式压制电极可以减轻偏析.实际生产过程中,通常将上次熔炼铸锭底部与头部颠倒后做为下次电极,这一方式的偏析程度要轻于铸锭直接正置的情况.当前关于宏观偏析在多次熔炼中是否存在传递,以及传递的原因、规律和影响程度都缺乏清晰的理解. ...
Control of iron segregation in Ti-1023 titanium alloy
1
2003
... 上述关于宏观偏析行为的研究均针对一次VAR熔炼的铸锭开展.实际钛合金VAR熔炼中,为保证铸锭的均匀性、减少夹杂,通常采用三次熔炼工艺.初次熔炼时将海绵钛和中间合金一起压制成电极,电极熔化后在坩埚中形成一次铸锭;再将一次铸锭当做二次熔炼的电极,将电极熔化形成二次铸锭;最后用二次铸锭做为第三次熔炼电极,制备三次铸锭.三次熔炼过程中采用的坩埚直径不断增加,形成的铸锭直径也相应增大.由于VAR铸锭中宏观偏析的存在,当把铸锭做为电极进行再次熔炼时,势必涉及电极成分均匀性对后续铸锭偏析的影响问题.Zagerbelnyy[15 ] 认为,绝大多数情况下电极成分的均匀性对铸锭成分的影响微乎其微.然而也有研究[16 ,17 ] 指出,采用与铸锭偏析分布相反的布料方式压制电极可以减轻偏析.实际生产过程中,通常将上次熔炼铸锭底部与头部颠倒后做为下次电极,这一方式的偏析程度要轻于铸锭直接正置的情况.当前关于宏观偏析在多次熔炼中是否存在传递,以及传递的原因、规律和影响程度都缺乏清晰的理解. ...
Ti-1023合金铸锭铁偏析控制
1
2003
... 上述关于宏观偏析行为的研究均针对一次VAR熔炼的铸锭开展.实际钛合金VAR熔炼中,为保证铸锭的均匀性、减少夹杂,通常采用三次熔炼工艺.初次熔炼时将海绵钛和中间合金一起压制成电极,电极熔化后在坩埚中形成一次铸锭;再将一次铸锭当做二次熔炼的电极,将电极熔化形成二次铸锭;最后用二次铸锭做为第三次熔炼电极,制备三次铸锭.三次熔炼过程中采用的坩埚直径不断增加,形成的铸锭直径也相应增大.由于VAR铸锭中宏观偏析的存在,当把铸锭做为电极进行再次熔炼时,势必涉及电极成分均匀性对后续铸锭偏析的影响问题.Zagerbelnyy[15 ] 认为,绝大多数情况下电极成分的均匀性对铸锭成分的影响微乎其微.然而也有研究[16 ,17 ] 指出,采用与铸锭偏析分布相反的布料方式压制电极可以减轻偏析.实际生产过程中,通常将上次熔炼铸锭底部与头部颠倒后做为下次电极,这一方式的偏析程度要轻于铸锭直接正置的情况.当前关于宏观偏析在多次熔炼中是否存在传递,以及传递的原因、规律和影响程度都缺乏清晰的理解. ...
A general enthalpy method for modeling solidification processes
2
1992
... 本研究采用Swaminathan等[18 ] 和Voller等[19 ] 提出的合金连续介质模型来描述凝固过程,并在其中耦合自感应电磁力和搅拌电磁力.假定熔池中熔体流动为层流,采用Boussinesq近似[20 ,21 ] .模型中连续性方程、能量守恒方程、溶质守恒方程与文献[13 ,18 ,19 ]中类似,不再赘述;动量方程中加入了电磁力源项,并且考虑了旋转速度,具体形式如下. ...
... ,18 ,19 ]中类似,不再赘述;动量方程中加入了电磁力源项,并且考虑了旋转速度,具体形式如下. ...
An enthalpy method for convection/diffusion phase change
2
1987
... 本研究采用Swaminathan等[18 ] 和Voller等[19 ] 提出的合金连续介质模型来描述凝固过程,并在其中耦合自感应电磁力和搅拌电磁力.假定熔池中熔体流动为层流,采用Boussinesq近似[20 ,21 ] .模型中连续性方程、能量守恒方程、溶质守恒方程与文献[13 ,18 ,19 ]中类似,不再赘述;动量方程中加入了电磁力源项,并且考虑了旋转速度,具体形式如下. ...
... ,19 ]中类似,不再赘述;动量方程中加入了电磁力源项,并且考虑了旋转速度,具体形式如下. ...
Call for contributions to a numerical benchmark problem for 2D columnar solidification of binary alloys
1
2009
... 本研究采用Swaminathan等[18 ] 和Voller等[19 ] 提出的合金连续介质模型来描述凝固过程,并在其中耦合自感应电磁力和搅拌电磁力.假定熔池中熔体流动为层流,采用Boussinesq近似[20 ,21 ] .模型中连续性方程、能量守恒方程、溶质守恒方程与文献[13 ,18 ,19 ]中类似,不再赘述;动量方程中加入了电磁力源项,并且考虑了旋转速度,具体形式如下. ...
On the numerical solution of continuum mixture model equations describing binary solid-liquid phase change
1
1989
... 本研究采用Swaminathan等[18 ] 和Voller等[19 ] 提出的合金连续介质模型来描述凝固过程,并在其中耦合自感应电磁力和搅拌电磁力.假定熔池中熔体流动为层流,采用Boussinesq近似[20 ,21 ] .模型中连续性方程、能量守恒方程、溶质守恒方程与文献[13 ,18 ,19 ]中类似,不再赘述;动量方程中加入了电磁力源项,并且考虑了旋转速度,具体形式如下. ...
Effect of electromagnetic stirring on melt pool free surface dynamics during vacuum arc remelting
2
2008
... 式中, J σ 为电导率, E [22 ] 报道,金属液体在磁场中运动产生的感应电流远小于熔炼电流,因此 式(4) 忽略了感应电流.根据 E φ )之间的关系, 式(4) 可改写为: ...
... 对于轴对称铸锭而言,自感磁场主要为旋转(azimuthal)分量(Bθ )[22 ] ,计算公式如下: ...
Calculation of the molten pool depth in vacuum arc remelting of alloy Vt3-1
1
2007
... 铸锭的侧壁和底部边界均为无滑移边界,铸锭顶部边界类型设置为速度入口,动网格在顶部生长模拟熔炼过程中铸锭的生长,动网格抬升速率设置为实际熔炼速率.在熔炼过程中,铸锭上表面的热量主要来自于电弧的作用,电弧产生的等效温度可以表示为[23 ] : ...
Dissolution of hard-alpha inclusions in liquid titanium alloys
1
1997
... 式中,T inlet 为熔池表面的温度;T liq 为液相线温度;I arc 为熔炼电流;D ingot 为铸锭直径;ΔT (I arc , D ingot )为熔化过热,可以通过下面的经验公式得出[24 ] : ...
Segregation development in multiple melt vacuum arc remelting
2
2009
... 图2 是第一次熔炼过程中溶质分布随时间的演化结果,右半部分溶质场内加入了熔池轮廓和流场.从图2a 可以看出,在熔炼初始阶段(1000 s),熔池较浅,熔池中熔体沿熔池中心向下、侧壁向上流动,这是典型的电磁力主导对流[8 ,25 ] ,此对流将熔池底部固/液界面前沿凝固排出的溶质沿侧壁向上带到熔池内部,造成底部固/液界面处的溶质贫乏,从而在铸锭底部中心两侧形成了明显的负偏析区域(底部蓝色区域).到4300 s时,如图2b 所示,随着熔池深度加大,熔池上部仍为电磁力控制的中心向下、侧壁向上的对流;而在熔池下部区域,形成了浮力控制的侧壁向下、中心向上的微弱流动,从放大图(图2b1 )可以清晰观察到这一浮力控制对流.这种熔池上部与下部相反的流动模式与Davidson 等[8 ] 报道的较大熔炼电流下的熔池稳态流动结果一致.此时熔池下部浮力对流将熔池侧壁的溶质带到熔池底部,从而使底部形成正偏析;浮力对流区上方是电磁力控制的沿侧壁向上的流动,它将侧壁凝固排出的溶质带到熔池上方.因此在向下流动与向上流动的分界线附近,形成了显著的负偏析.在随后熔炼过程中(4300~8800 s),熔池深度基本恒定,熔池上部保持电磁力控制对流,下部为热浮力控制对流,已凝固铸锭形成了显著的中心正偏析和两侧负偏析条带,如图2b~d 所示.最后小电流保温阶段(9000~12500 s),熔池内电磁力基本消失,整个区域重新形成浮力控制的微弱流动,最终冒口部位形成正偏析,如图2e~g 所示. ...
... 为定量地反映铸锭整体偏析程度,可采用Zagrebelnyy和Krane[25 ] 定义的整体宏观偏析指数(global macrosegregation index,GMI): ...