最新录用 | 当期目录 | 过刊浏览 | 热点文章 | 虚拟专辑 | 阅读排行 | 下载排行 | 引用排行 | 期刊订阅

金属学报, 2022, 58(2): 175-183 DOI: 10.11900/0412.1961.2020.00443

研究论文

Fe-C-Ni体系膨胀应变能对马氏体转变的影响

陈维1,2, 陈洪灿1,2, 王晨充3, 徐伟3, 罗群,1,2, 李谦1,2, 周国治1,2

1.上海大学 材料科学与工程学院 省部共建高品质特殊钢冶金与制备国家重点实验室 上海 200444

2.上海大学 材料科学与工程学院 上海市钢铁冶金新技术应用开发重点实验室 上海 200444

3.东北大学 轧制技术及连轧自动化国家重点实验室 沈阳 110819

Effect of Dilatational Strain Energy of Fe-C-Ni System on Martensitic Transformation

CHEN Wei1,2, CHEN Hongcan1,2, WANG Chenchong3, XU Wei3, LUO Qun,1,2, LI Qian1,2, CHOU Kuochih1,2

1.State Key Laboratory of Advanced Special Steel, School of Materials Science and Engineering, Shanghai University, Shanghai 200444, China

2.Shanghai Key Laboratory of Advanced Ferrometallurgy, School of Materials Science and Engineering, Shanghai University, Shanghai 200444, China

3.State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, China

通讯作者: 罗 群，qunluo@shu.edu.cn，主要从事合金相变热力学研究

收稿日期: 2020-11-04   修回日期: 2021-03-09  

基金资助: 国家自然科学基金项目.  U1808208.  51734002
上海大学省部共建高品质特殊钢冶金与制备国家重点实验室自主课题项目.  SKLASS2020-Z01
上海市科学技术委员会项目.  19DZ2270200

Corresponding authors: LUO Qun, associate professor, Tel:(021)66136577, E-mail:qunluo@shu.edu.cn

Received: 2020-11-04   Revised: 2021-03-09  

作者简介 About authors

陈维，男，1994年生，硕士

摘要

为探究马氏体转变膨胀应变能对马氏体转变起始温度(Ms)的影响以及实现对Ms的准确预测，采用热膨胀相变仪测定了Fe-C-Ni合金的膨胀曲线，通过三切线法得到Ms与奥氏体转变起始温度。采用OM观察和XRD技术分析了成分对马氏体转变后组织和晶格参数的影响规律。通过考虑C成分与Ni成分交互作用，修正了马氏体转变膨胀应变能模型。以马氏体转变化学驱动力(同成分bcc相与fcc相的Gibbs自由能差)与非化学驱动力(奥氏体的剪切应变能、奥氏体的膨胀应变能、马氏体的缺陷储能和奥氏体与马氏体的界面能)之和为0作为判据，计算了Fe-C-Ni体系的Ms。结果表明，C含量与Ni含量的增加会促进转变后bcc相的晶格膨胀，Ni含量的增加会使形成的马氏体的板条变细小。在C含量(原子分数)小于1.0%，Ni含量(原子分数)小于20%的Fe-C-Ni合金中，计算得到膨胀应变能在非化学驱动力中的平均占比为41.3%。使用修正后的模型计算Fe-C-Ni体系的Ms，预测误差为4.1%。

关键词： Fe-C-Ni体系 ; 马氏体转变起始温度 ; 膨胀应变能 ; 热力学计算

Abstract

Ultrahigh-strength steels have been widely used in critical engineering structures in military and civilian applications owing to the combination of ultrahigh strength and excellent toughness. The martensitic transformation start temperature (Ms) is an important parameter for designing alloys; it describes the thermodynamic stability and transformation behavior of austenite, affecting the strength and toughness of the alloy. To explore the influence of dilatational strain energy during martensitic transformation on Ms and calculate Ms in the Fe-C-Ni system, the dilatational curves of Fe-C-Ni alloys are measured using a dilatometer. Three tangents method is used to calculate Ms and austenitic transformation start temperature. The influence of composition on microstructure and lattice parameters after martensitic transformation was analyzed using OM and XRD. The dilatational strain energy model in the nonchemical driving force of martensitic transformation is modified considering the interaction between C and Ni components. The Ms of Fe-C-Ni system was calculated using a thermodynamic model in which the sum of martensitic transformation chemical driving force (the difference of Gibbs free energy between fcc and bcc phases) and nonchemical driving force (shearing strain energy of austenite, dilatational strain energy of austenite, dislocation stored energy of martensite, and interfacial energy of austenite and martensite) is zero. These results show that increasing C and Ni contents promote lattice expansion of the bcc phase after transformation whereas increasing Ni content reduces the martensite lath. The average proportion of dilatational strain energy of austenite in nonchemical driving force is approximately 41.3% in Fe-C-Ni alloys with atomic fractions of C < 1.0% and Ni < 20%. The prediction error of Ms in the Fe-C-Ni system is 4.1% using the modified model.

Keywords： Fe-C-Ni system ; martensitic transformation start temperature ; dilatational strain energy ; thermodynamic calculation

PDF (2219KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

陈维, 陈洪灿, 王晨充, 徐伟, 罗群, 李谦, 周国治. Fe-C-Ni体系膨胀应变能对马氏体转变的影响. 金属学报[J], 2022, 58(2): 175-183 DOI:10.11900/0412.1961.2020.00443

CHEN Wei, CHEN Hongcan, WANG Chenchong, XU Wei, LUO Qun, LI Qian, CHOU Kuochih. Effect of Dilatational Strain Energy of Fe-C-Ni System on Martensitic Transformation. Acta Metallurgica Sinica[J], 2022, 58(2): 175-183 DOI:10.11900/0412.1961.2020.00443

以淬火-配分钢(quenching and partitioning steel，Q&P钢)为代表的先进高强钢通过淬火-配分工艺调整亚稳奥氏体的稳定性、形貌及分布，使其获得超高强度和高塑性[1~3]。而马氏体转变起始温度(Ms)是综合描述奥氏体热稳定性和相变行为的重要参数，因此对Ms的准确预测是实现组织和性能调控的基础[4~7]。

目前Ms的预测模型主要有3种：经验模型[8~10]、热力学模型[11~15]和神经网络模型[16~20]。经验模型和神经网络模型依赖大量的实验数据，常存在过度拟合、成分范围有限和未触及转变机理等问题。而热力学模型结合了相变过程中能量变化的理论分析与实验分析2部分，使得模型在解释马氏体转变机理与预测多组元合金的Ms时具有独特优势[21]。

在热力学模型中，马氏体发生转变的总驱动力(ΔGγ→M)需满足ΔGγ→M = ΔGγ→α + ΔGα→M ≤ 0，其中ΔGγ→α 表示化学驱动力；ΔGα→M表示非化学驱动力，当温度降低至Ms时ΔGγ→M为0[11]。化学驱动力是奥氏体与铁素体的Gibbs自由能差，可通过CALPHAD方法简便而准确获得。对于非化学驱动力，研究者们有不同的表示方法。如Hsu[11]认为非化学驱动力主要由屈服强度(σs)相关的剪切应变能(2.1σs)、位错与孪晶储能以及其他能量(共约900 J/mol)组成。Olson等[13,14]和Ghosh等[15]提出一种描述马氏体热成核的方法，主要关注添加不同合金元素引起的晶格摩擦功的变化。Celada-Casero等[4]在此基础上考虑了晶粒尺寸效应引起的奥氏体强化对Ms的影响。Ishida[22,23]认为非化学驱动力主要包括剪切应变能、弹性应变能和界面能，在计算时主要考虑了奥氏体屈服强度对剪切应变能的影响，忽略了后2项能量。

可见，目前对非化学驱动力的构成尚未有定论，且研究者们对膨胀应变能和位错储存能部分缺少定量分析。Luo等[12]在前人工作的基础上，定量评估了剪切应变能、膨胀应变能、缺陷储能和界面能，发现非化学驱动力中膨胀应变能和位错储存能是主要贡献项。但在计算膨胀应变能时，仅仅考虑了合金成分对膨胀系数贡献的线性加和部分，尚未考虑合金成分之间的相互作用。而对于添加了Cr、Mn、Mo等元素的低合金钢，加入Cr与Mn、Cr与Mo交互作用参数，可以提高热膨胀系数预测值准确性[24]。因此，本工作通过热膨胀相变仪测定了Fe-C-Ni三元合金的膨胀曲线，考虑了C、Ni元素的交互作用对膨胀应变能的影响，计算了Fe-C-Ni合金的Ms，并且定量分析了膨胀应变能对非化学驱动力的贡献。

1 实验方法和计算方法

1.1 样品制备

实验采用CXZG-0.5型真空感应熔炼炉和WK-II型非自耗真空电弧熔炼炉对Fe-C-Ni合金进行熔炼，熔炼过程采用高纯Ar气进行保护。第1步使用CXZG-0.5型真空感应熔炼炉熔炼Fe-C中间合金。选用纯度为99.98%的纯Fe，放入石墨坩埚，加热至纯Fe熔化，使C元素渗入Fe液之中，保温5 min后在铜模中浇铸成型，翻转重熔3次。通过CS600型碳硫分析仪测得其C含量为7.0% (原子分数)。第2步使用WK-II型非自耗真空电弧熔炼炉熔炼Fe-C-Ni合金，原料为99.98%的纯Fe、第1步熔炼好的Fe-C合金以及99.99%的纯Ni。熔炼时加热至合金完全熔化后保持5 min，每个合金进行3次翻转重熔。铸锭质量为50 g，测定成分时分别从铸锭顶部、中心及底部取样。采用Optima7300DV型电感耦合等离子体原子发射光谱分析仪测定其Ni含量，采用CS600型碳硫分析仪测定其中的C含量，发现不同部位的成分差异不超过0.1% (原子分数)，合金的实测成分如表1所示。

表1   Fe-C-Ni合金的成分 (atomic fraction / %)

Table 1  Compositions of Fe-C-Ni alloys

Steel numberNiCFe
118.330.49Bal.
29.140.47Bal.
34.320.48Bal.
415.620.86Bal.
57.940.88Bal.
64.090.97Bal.

新窗口打开| 下载CSV


1.2 膨胀曲线测定与表征

实验采用DIL805A型热膨胀仪。将试样线切割成直径4 mm、长10 mm的圆柱体。在圆柱侧面焊上热电偶后装入夹具，实验过程保持仪器内部真空度在1 × 10-4 Pa以下。以10 K/s的升温速率加热至1174 K进行奥氏体化，并保温5 min，使转变充分且成分均匀。降温时采用N2作为冷却气体，以50 K/s的速率冷却至室温。

将膨胀曲线测定后的样品经冷镶、砂纸打磨、抛光、5% (体积分数)的硝酸-酒精溶液浸润后通过DYJ-908BD型光学显微镜(OM)进行显微组织观察；另一份样品经砂纸打磨、抛光后，采用D8 Advance型X射线衍射仪(XRD)分析转变后的相组成。XRD检测条件为Cu靶，扫描范围30°~100°，扫描速率2°/min。

1.3 计算方法

根据马氏体转变的热力学判据ΔGγ→M|Ms = ΔGγ→α + ΔGα→M = 0计算Ms[11]。

1.3.1 化学驱动力计算

化学驱动力可通过体心立方(bcc)相与面心立方(fcc)相的Gibbs自由能差来计算。而亚点阵模型一般用于描述化学计量比相、规则溶液、间隙固溶体和金属间化合物的Gibbs自由能[25]，是CALPHAD方法中的重要模型。Fe-C-Ni合金的双亚点阵模型为(Fe, Ni) a (C, Va) c (Va表示空位，a和c分别表示(Fe, Ni)亚点阵和(C, Va)亚点阵所占的位置分数[25])。bcc结构中a∶c = 1∶3；fcc结构中a∶c = 1∶1。亚点阵模型中亚点阵表示晶体点阵中的某一原子位置，并认为晶格是由几个亚点阵相互穿插构成，粒子在每个亚点阵中随机混合。对于磁性材料而言，还需要添加磁性部分对Gibbs自由能的贡献(Gmag)，则体系的摩尔Gibbs自由能(Gsys)可表示为[25]：

Gsys=Gref+Gid+Gex+Gmag
(1)

式中，Gref表示各假想配比组成的Gibbs自由能线性叠加；Gid表示组态熵对自由能的贡献；Gex表示不同亚点阵原子之间的相互作用所引起的过剩自由能。各部分Gibbs自由能的表达式如式(2)~(5)所示[25]：

Gref=yFe'yC″GFe:C°+yFe'yVa″GFe:Va°+yNi'yC″GNi:C°+
yNi'yVa″GNi:Va°                                        
(2)
Gid=RT[a(yFe'lnyFe'+yNi'lnyNi')+
c(yC″lnyC″+yVa″lnyVa″)]
(3)
Gex=yFe'yNi'(yC″LFe,  Ni:C+yVa″LFe,  Ni:Va)+      
yC″yVa″(yFe'LFe:C, Va+yNi'LNi:C, Va)
(4)
Gmag=RTln(β+1)ƒ(τ)
(5)

式中，yi'、yi″分别表示i原子在第1个与第2个亚点阵中的点阵分数；Gi:j°为ia jc假想化合物的Gibbs自由能；Li,  j:k为相互作用参数；R为理想气体常数；β为Bohr磁子中每摩尔原子的平均磁通量；T为热力学温度；f(τ)为磁性热容多项式，τ = T / TC，TC表示Curie温度。在特定温度下bcc相与fcc相的Gibbs自由能(Gbcc和Gfcc)之差即为此温度下马氏体转变的化学驱动力，其表达式为：

ΔGγ→α=Gbcc-Gfcc
(6)

1.3.2 非化学驱动力计算

马氏体实际转变温度低于ΔGγ→α = 0时的温度(T0)，主要是由于存在非化学因素阻碍了相变的发生。非化学驱动力可表示为由于非化学因素影响使相变需要额外消耗的能量[11,14,15,26~28]。主要包括：① 由奥氏体切变转变为马氏体所消耗的能量，即奥氏体的剪切应变能(ΔGshγ)；② 由奥氏体转变为马氏体产生体积膨胀，造成周围组织受挤压应变所消耗的能量，即奥氏体的膨胀应变能(ΔGdilγ)；③ 形成马氏体亚结构(如高密度的位错与孪晶)所需的能量，即马氏体的缺陷储能(ΔGstorM)；④ 由于发生马氏体转变而形成新界面所需的能量，即奥氏体与马氏体的界面能(ΔGinter)。因此，非化学驱动力可表示为：

ΔGα→M=ΔGshγ+ΔGdilγ+ΔGstorM+ΔGinter
(7)

其中，ΔGinter通过下式计算[29]：

ΔGinter=2σVmr
(8)

式中，σ是形成单位面积奥氏体与马氏体两相界面所消耗的能量，r为所形成的马氏体的曲率半径,Vm是马氏体的摩尔体积。取σ = 1.0 J/m2、r = 2 × 10-7 m、Vm = 7.09 × 10-6 m3/mol，可计算得ΔGinter约为70.9 J/mol[29]。

根据Luo等[12]对非化学驱动力模型的建立，有：

ΔGα→M=12bdσsVm+32E(ΔLL)2Vm+Gb2ρVm+70.9
(9)

式中，b是不全位错Burgers矢量模；d是密排面的面间距；E为奥氏体的弹性模量；ΔL / L为马氏体转变时的线膨胀率；G为马氏体的剪切模量；ρ为马氏体的位错密度。

ΔGinter相对于ΔGα→M (约1500 J/mol)占比小，研究者在处理ΔGinter时通常将其忽略不计或者作为常数项来处理。如Hsu[11]对ΔGinter采用了定值，而Ishida[22,23]则直接忽略了ΔGinter的影响。在本工作中，优先考虑对非化学驱动力主要贡献项：膨胀应变能和位错储能。因此，也将ΔGinter作为常数项(70.9 J/mol)来处理。

2 膨胀应变能模型

2.1 膨胀应变能的产生

膨胀应变能是马氏体转变的主要影响因素之一，在非化学驱动力中占有主要地位[12]。Fe-C-Ni合金从奥氏体的fcc结构转变为马氏体的体心四方(bct)结构会产生体积膨胀，这一现象很容易被膨胀仪检测到[30,31]。产生这种现象主要有2个原因：① bcc结构的致密度为0.68，而fcc结构的致密度为0.74，fcc结构更致密，导致转变为bcc结构时发生体积膨胀；② C在铁素体中的最大溶解度为0.0218% (质量分数)，而在奥氏体中的最大溶解度为2.11% (质量分数)。在奥氏体通过切变的方式发生转变时，由于反应速率快、温度低，使C原子来不及扩散，C原子仍然留在6个Fe原子所组成的八面体中心，使晶格短轴伸长，长轴缩短。因此，晶格里会固溶过多的C而形成过饱和固溶体，从而产生体积膨胀[32]。马氏体转变需要额外克服周围奥氏体组织的约束做功，而这部分损耗的能量即为马氏体转变的膨胀应变能，这也是马氏体转变必须克服的阻力之一。

2.2 膨胀应变能模型

Hsu等[11,33]计算CeO2-ZrO2体系马氏体转变膨胀应变能(ΔGdil)时采用了下式：

ΔGdil=E9(1-ν)(ΔVV)2Vm
(10)

式中，ν为Poisson比，ΔV / V为体积膨胀率。而体积膨胀率可通过下式转变为方便实验测定的线膨胀率(ΔL / L)[31]：

ΔVV=3ΔLL+3ΔLL2+ΔLL3
(11)

将式(11)代入式(10)，由于式(11)中的2次项(3(ΔL / L)2)与3次项((ΔL / L)3)经平方后小于10-4，对计算结果影响较小，因此忽略其影响。在Fe-C-Ni合金中取ν = 1 / 3[11]，则ΔGdil可表示为：

ΔGdil=32E(∆LL)2Vm
(12)

2.3 膨胀应变能模型的重要参数

膨胀应变能中的E和ΔL / L是影响膨胀应变能计算结果的主要参数，其余参数如Vm一般取定值7.5 cm3/mol[11]。纯Fe奥氏体的E随T的变化关系可表示为[34]：

E=214×[1-(T-300)×4.7×10-4]
(13)

而考虑合金成分的影响，Fe-C-Ni合金在Ms处的E可表示为[35]：

E=208.2-7.53xC-1.75xNi (14)式中，xi 为i元素的原子分数。同样地，ΔL / L也与T有关，拟合Fe-Ni膨胀曲线的实验数据[12]，ΔL / L可由下式表示：

ΔL / L=(1.37-0.84×10-3T)×100%
(15)

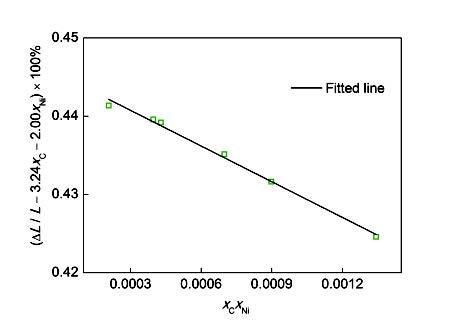
ΔL / L也与成分相关，为了简化模型，可根据实验数据直接拟合在Ms处的实际参数。如Luo等[12]通过对Fe-C、Fe-Ni二元体系的数据分析，外推Fe-C-Ni三元体系在马氏体转变时的ΔL / L，如下式所示：

ΔL / L=(1.55+3.24xC+2.00xNi)×100%
(16)

但是该方程尚未考虑C与Ni的交互作用对ΔL / L的贡献，这正是本工作修正的部分。

3 实验结果与分析

3.1 马氏体转变线膨胀曲线与表征结果

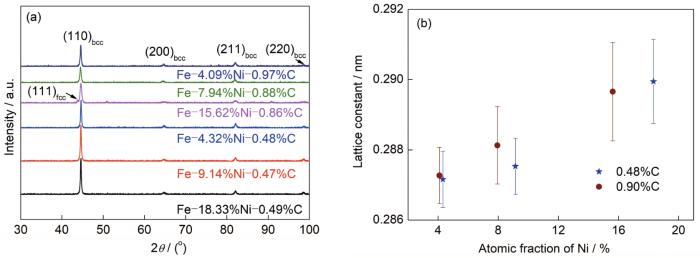
图1是平均C含量(原子分数)为0.48%和0.90%时，不同Ni含量的Fe-C-Ni合金的膨胀曲线。可以看出，Ni含量较大的合金膨胀曲线随温度变化的斜率更小，说明Ni含量的增加会降低Fe-C-Ni合金的热膨胀系数。此外，在图中使用三切线法得到Ms与奥氏体转变起始温度(As)。在C含量一定时，随着Ni含量的增加Ms与As都会降低，相对于Ms，As受Ni含量的影响更小。对比图1a和b可以发现，C含量的增加使Ms降低，而相对于Ms，C含量对As的影响较小。从热力学角度来看，非化学驱动力的增加使相变需要更大的驱动力才可以发生，因此需要更低的温度来提供更大的驱动力。而造成非化学驱动力增加的主要原因包括：① 固溶强化效应提高了σs，增加了奥氏体的剪切应变能；② C和Ni含量的增加使晶格畸变更大，使马氏体转变的膨胀量增加，造成奥氏体的膨胀应变能增加；③ C和Ni含量的增加会造成马氏体的位错密度增加，从而提高马氏体的缺陷储能。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   不同C含量的Fe-C-Ni合金的膨胀曲线

(a) 0.48%C (b) 0.90%C

Fig.1   Dilatation curves of Fe-C-Ni alloys with different atomic fractions of C (Ms—martensitic transformation start temperature, As—austenitic transformation start temperature)


图2是不同成分Fe-C-Ni合金经膨胀曲线测定后显微组织的OM像。从图2c和f可以看到清晰的板条结构，在图2b和e中板条结构相对细小，而在图2a和d中只能看到细小的线条状相。由此可见，Fe-C-Ni合金在50 K/s冷速下形成的马氏体主要为板条状的位错型马氏体，其亚结构主要为高密度的位错。随着Ni含量的增加，板条变得越来越细小。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   不同成分Fe-C-Ni合金显微组织的OM像

(a) Fe-18.33%Ni-0.49%C (b) Fe-9.14%Ni-0.47%C (c) Fe-4.32%Ni-0.48%C

(d) Fe-15.62%Ni-0.86%C (e) Fe-7.94%Ni-0.88%C (f) Fe-4.09%Ni-0.97%C

Fig.2   OM images of Fe-C-Ni alloys with different atomic fractions of C and Ni


图3a是不同成分Fe-C-Ni合金的XRD谱。XRD谱中观察不到残余奥氏体的衍射峰，说明马氏体转变较为完全。计算的Fe-C-Ni合金bcc结构的晶格常数如图3b所示。C含量(原子分数)从0.48%增加至0.90%时，Fe-C-Ni合金的晶格常数变化不大。而随着Ni含量(原子分数)从4.09%增加至18.33%，合金的晶格常数增加明显。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   Fe-C-Ni合金的XRD谱和计算的Fe-C-Ni合金bcc相的晶格常数

Fig.3   XRD spectra of Fe-C-Ni alloys (a) and calculated lattice constants of bcc phase in Fe-C-Ni alloys (b)


3.2 马氏体转变线膨胀率随成分和温度的变化关系

在图1中，转变前奥氏体相与转变后马氏体相的膨胀曲线大致为线性的，通过对膨胀曲线的线性外推，可计算任意温度的相变线膨胀率。取在Ms处的相变线膨胀率数据，引入C、Ni的交互作用参数，通过对Fe-C-Ni实验数据的拟合，如图4，有：

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   Fe-C-Ni体系马氏体相变线膨胀率(ΔL / L)模型拟合曲线

Fig.4   Fitting line of linear dilatational ratio (ΔL / L) of martensitic transformation vs the product of atomic fraction of C and Ni (xCxNi) by Eq.(17)


∆L / L=(0.445+3.24xC+2.00xNi-15.20xCxNi)×
100%                                                     
(17)

式中，C、Ni元素的系数来自于对Fe-C与Fe-Ni二元合金马氏体转变线膨胀研究，如Fe-C合金ΔL / L = (1.10 + 3.24xC) × 100%，Fe-Ni合金ΔL / L = (0.63 + 2.00xNi) × 100%[12]。常数项表示计算式对纯Fe线膨胀率的外推值，可见其都小于纯Fe的实验线膨胀率1.55%[31]。所以，采用纯Fe的实验值对常数项进行了修正：

∆L / L=(1.55+3.24xC+2.00xNi-15.20xCxNi)×100%                                                  
(18)

3.3 Fe-C-Ni体系 Ms 的计算

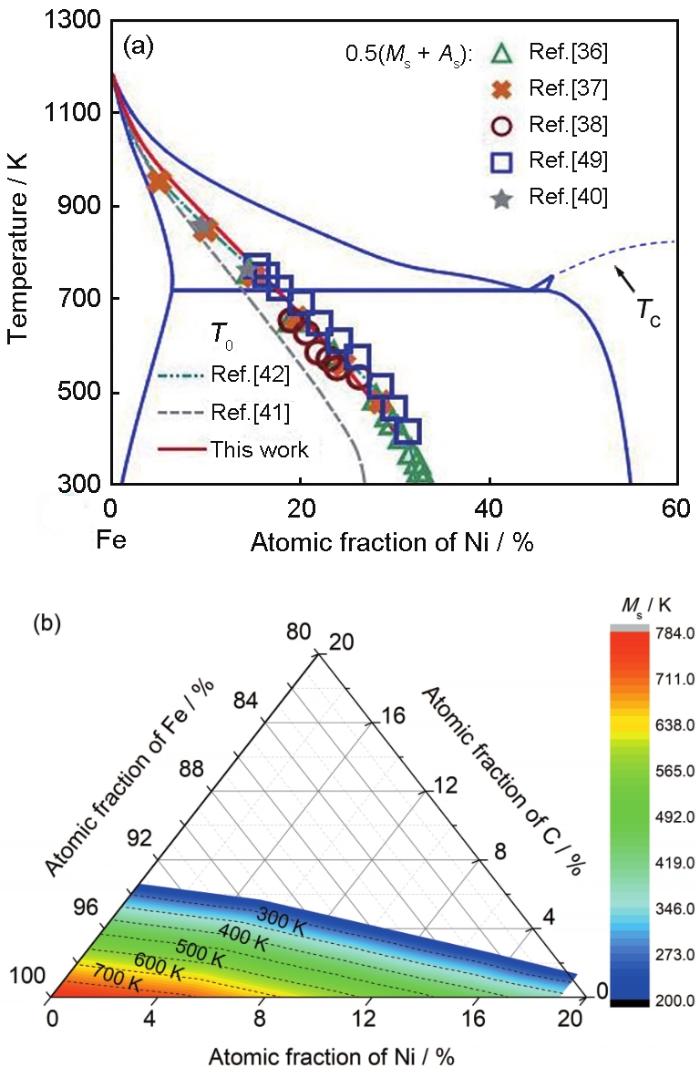
在Fe-C-Ni体系中，T0可通过实验值0.5(Ms + As)近似表示[29]。图5a将实验值0.5(Ms + As)[36~40]与T0计算值(本工作与文献[41,42])进行比较。可以看到，采用Gabriel等[41]数据在Ni含量(原子分数)大于15%时会低于实验值80~130 K，而Ghosh和Olson[42]所优化的数据库(kMART)的计算结果与实验值较为吻合。因此，在Gabriel等[41]工作的基础上，根据实验数据重新优化了bcc相与fcc相的磁性参数，计算结果如图5a中红色实线所示。计算值在Ni含量(原子分数)为5%~15%时会略高于实验值25~40 K，其余成分范围内吻合较好。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   Fe-Ni体系实验值0.5(Ms + As)[36~40]与T0温度预测值(本工作与文献[41,42])比较以及计算的Fe-C-Ni体系Ms (Ms—马氏体转变起始温度，As—奥氏体转变起始温度，T0—化学驱动力为0时的温度)

Fig.5   Comparison between 0.5(Ms + As)[36-40] with the predicted T0 (this work and Refs.[41,42]) in Fe-Ni system (T0—temperature of chemical driving force is equal to 0， TC—Curie temperature) (a) and calculated Ms in Fe-C-Ni system (b)


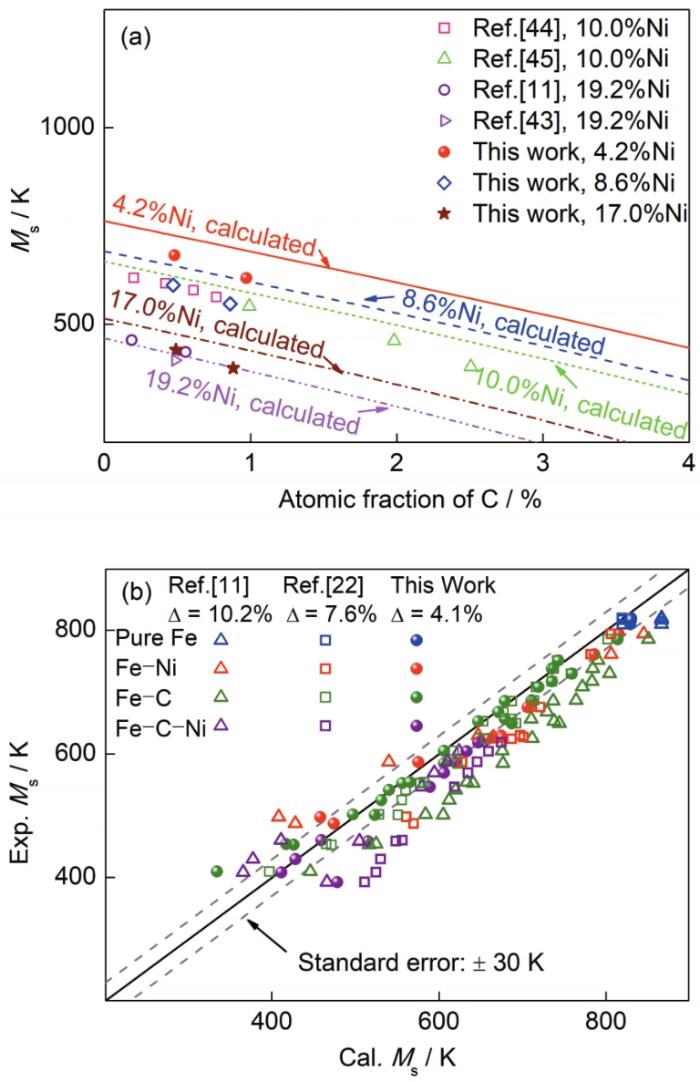
将式(18)代入式(12)，得到添加C、Ni交互作用的膨胀应变能模型。计算Fe-C-Ni体系成分为C含量(原子分数)为0~6.7%、Ni含量(原子分数)为0~19%的Ms等值线，计算结果如图5b所示，其中Ms随C含量的增加而下降的速度比随Ni含量快。

图6a为不同Ni含量的Fe-C-Ni合金Ms的计算值与实验值(本工作和文献[11,43~45])的对比。可以看到，本工作的计算值较实验值偏高。其可能原因为：① 工艺条件的原因。本工作的膨胀相变实验，采用1174 K保温5 min。相较于Izumiyama等[46]在1274 K保温2 h、Magee等[43]在1204 K保温1 h，本实验保温温度较低，时间较短。研究表明在高于Ms较多的温度下保温，会促进Ms升高[47]，部分原因是高温和保温时间增加会促进C原子的扩散，使其脱离位错逃逸，从而降低母相的奥氏体强度，使非化学驱动力的阻碍作用降低，导致合金在较高的温度下就可发生转变[48]。② T0的计算值在Ni含量(原子分数)为5%~15%时会略高于实验值25~40 K，如图5a，因此在计算Ms时会偏高。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   不同Ni含量的Fe-C-Ni合金Ms计算值与本工作和文献[11,43~45]实验值及3种模型对Fe-C-Ni合金Ms的计算值(本工作与文献[11,22])和实验值对比(实验数据来源：Fe-C[11,50~53]、Fe-Ni[36,46,54~56]、Fe-C-Ni[11,43,44,54])

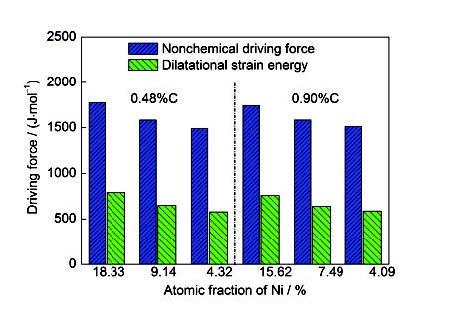
Fig.6   Calculated and experimental (this work and Refs.[11,43-45]) Ms in Fe-C-Ni alloys with different Ni contents (a) and comparison of experimental and calculated (this work and Refs.[11,22]) Ms by three models(experimental data from: Fe-C[11,50-53], Fe-Ni[36,46,54-56], and Fe-C-Ni[11,43,44,54]) (b)


图6b使用Ishida[22]给出的经验方程和Hsu等[11,49]的模型计算了Fe-C-Ni合金的Ms。在Luo等[12]模型的基础上，本模型考虑了C、Ni交互作用。将以上3种模型计算的Ms值与文献报道的Fe-C[11,50~53]、Fe-Ni[36,46,54~56]和Fe-C-Ni[11,43,44,54]体系Ms实验值进行对比，结果显示本工作修正后的模型计算精度更高。相较于Ishida方程[22]的计算误差7.6%、Hsu模型[11,49]的10.2%，本工作计算精度提高至4.1%。

图7计算了1~6试样在Ms处的非化学驱动力与膨胀应变能。可以看到，在C含量一定时，Ni含量越高的合金非化学驱动力与膨胀应变能越高，其中膨胀应变能在非化学驱动力中的平均占比约为41.3%。此外，在300~850 K的温度范围内，Fe-C-Ni合金的位错储存能约为436~750 J/mol，剪切应变能约为60~162 J/mol，膨胀应变能约为510~832 J/mol，可知膨胀应变能在非化学驱动力的计算中占有重要地位，对Ms计算值的影响较大。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   Fe-C-Ni合金在Ms处的非化学驱动力与膨胀应变能

Fig.7   Nonchemical driving force and dilatational strain energy of Fe-C-Ni alloys at Ms


4 结论

(1) 通过XRD方法检测Fe-C-Ni合金试样经膨胀相变实验后的物相，主要为马氏体与少量残余奥氏体，C含量与Ni含量的增加会促进转变后bcc相的晶格膨胀；OM像中可观察到清晰的板条马氏体，且Ni含量的增加会使板条更细小。

(2) 通过热膨胀相变仪测定了Fe-C-Ni合金的膨胀曲线，马氏体转变膨胀率会随C与Ni含量的增加而增加；考虑C、Ni交互作用对线膨胀率的影响，建立了马氏体转变时的线膨胀率-成分定量关系：ΔL / L = (1.55 + 3.24xC + 2.00xNi – 15.20xCxNi) × 100%。

(3) 优化膨胀应变能计算模型，结合Fe-C-Ni体系奥氏体和马氏体转变的化学驱动力，热力学预测了Fe-C-Ni体系的Ms，计算相对误差为4.1%，标准差为± 30 K。

(4) 计算了C含量(原子分数)小于1.0%，Ni含量(原子分数)小于20%的Fe-C-Ni合金中，马氏体转变时的膨胀应变能与非化学驱动力，膨胀应变能平均占比为41.3%，对Ms的计算起主要作用。

参考文献

Jin X J , Gong Y , Han X H , et al .

A review of current state and prospect of the manufacturing and application of advanced hot stamping automobile steels

[J]. Acta Metall. Sin., 2020, 56: 411

[本文引用: 1]

金学军, 龚 煜, 韩先洪 等 .

先进热成形汽车钢制造与使用的研究现状与展望

[J]. 金属学报, 2020, 56: 411

[本文引用: 1]

Tian Y Q , Tian G , Zheng X P , et al .

C and Mn elements characterization and stability of retained austenite in different locations of quenching and partitioning bainite steels

[J]. Acta Metall. Sin., 2019, 55: 332

田亚强, 田 耕, 郑小平 等 .

淬火配分贝氏体钢不同位置残余奥氏体C、Mn元素表征及其稳定性

[J]. 金属学报, 2019, 55: 332

Wang C Y , Chang Y , Yang J , et al .

The combined effect of hot deformation plus quenching and partitioning treatment on martensite transformation of low carbon alloyed steel

[J]. Acta Metall. Sin., 2015, 51: 913

[本文引用: 1]

王存宇, 常 颖, 杨 洁 等 .

热变形和淬火配分处理的复合作用对低碳合金钢马氏体相变机制的影响

[J]. 金属学报, 2015, 51: 913

[本文引用: 1]

Celada-Casero C , Sietsma J , Santofimia M J .

The role of the austenite grain size in the martensitic transformation in low carbon steels

[J]. Mater. Des., 2019, 167: 107625

[本文引用: 2]

Santofimia M J , Zhao L , Petrov R , et al .

Microstructural development during the quenching and partitioning process in a newly designed low-carbon steel

[J]. Acta Mater., 2011, 59: 6059

Zhang B , Peng Y H , Lu X , et al .

Study of γ→ε martensite transformation of Fe-24Mn-Ge alloys

[J]. Acta Metall. Sin., 2001, 37: 1238

张 斌, 彭颖红, 陆 兴 等 .

Fe-Mn-Ge合金γ→ε马氏体相变的研究

[J]. 金属学报, 2001, 37: 1238

Hu L , Wang X , Yi X H , et al .

Influence of inter-pass temperature on residual stress in multi-layer and multi-pass butt-welded 9%Cr heat-resistant steel pipes

[J]. Acta Metall. Sin., 2018, 54: 1767

[本文引用: 1]

胡 磊, 王 学, 尹孝辉 等 .

层间温度对9%Cr热强钢管道多层多道焊接头残余应力的影响

[J]. 金属学报, 2018, 54: 1767

[本文引用: 1]

Lee S J , Park K S .

Prediction of martensite start temperature in alloy steels with different grain sizes

[J]. Metall. Mater. Trans., 2013, 44A: 3423

[本文引用: 1]

Finkler H , Schirra M .

Transformation behaviour of the high temperature martensitic steels with 8-14% chromium

[J]. Steel Res., 1996, 67: 328

van Bohemen S M C , Santofimia M J , Sietsma J .

Experimental evidence for bainite formation below MS in Fe-0.66C

[J]. Scr. Mater., 2008, 58: 488

[本文引用: 1]

Hsu T Y .

An approximate approach for the calculation of MS in iron-base alloys

[J]. J. Mater. Sci., 1985, 20: 23

[本文引用: 22]

Luo Q , Chen H C , Chen W , et al .

Thermodynamic prediction of martensitic transformation temperature in Fe-Ni-C system

[J]. Scr. Mater., 2020, 187: 413

[本文引用: 7]

Olson G B , Cohen M .

A general mechanism of martensitic nucleation: Part II. FCC→BCC and other martensitic transformations

[J]. Metall. Trans., 1976, 7A: 1905

[本文引用: 1]

Olson G B , Cohen M .

A general mechanism of martensitic nucleation: Part I. General concepts and the FCC→HCP transformation

[J]. Metall. Trans., 1976, 7A: 1897

[本文引用: 2]

Ghosh G , Olson G B .

Kinetics of f.c.c.→b.c.c. heterogeneous martensitic nucleation-II. Thermal activation

[J]. Acta Metall. Mater., 1994, 42: 3371

[本文引用: 3]

Lu Q , Liu S L , Li W , et al .

Combination of thermodynamic knowledge and multilayer feedforward neural networks for accurate prediction of MS temperature in steels

[J]. Mater. Des., 2020, 192: 108696

[本文引用: 1]

Wang C C , Shen C G , Huo X J , et al .

Design of comprehensive mechanical properties by machine learning and high-throughput optimization algorithm in RAFM steels

[J]. Nucl. Eng. Technol., 2020, 52: 1008

Eyercioglu O , Kanca E , Pala M , et al .

Prediction of martensite and austenite start temperatures of the Fe-based shape memory alloys by artificial neural networks

[J]. J. Mater. Process. Technol., 2008, 200: 146

Wang C C , Shen C G , Cui Q , et al .

Tensile property prediction by feature engineering guided machine learning in reduced activation ferritic/martensitic steels

[J]. J. Nucl. Mater., 2020, 529: 151823

You W , Fang H S , Bai B Z .

Predicting the martensitic transformation start temperature using back-propagation artificial neural networks

[J]. Acta Metall. Sin., 2003, 39: 630

[本文引用: 1]

由 伟, 方鸿生, 白秉哲 .

用反向传播人工神经网络预测低碳低合金钢的马氏体转变开始温度

[J]. 金属学报, 2003, 39: 630

[本文引用: 1]

Yang F X , Zheng W S , He Y L , et al .

Thermodynamic calculation of martensitic transformation start temperature in Fe-C-Mn-Si-Cr alloys

[J]. Shanghai Met., 2016, 38(1): 1

[本文引用: 1]

杨飞翔, 郑伟森, 何燕霖 等 .

Fe-C-Mn-Si-Cr的马氏体开始转变点的热力学计算

[J]. 上海金属, 2016, 38(1): 1

[本文引用: 1]

Ishida K .

Calculation of the effect of alloying elements on the Ms temperature in steels

[J]. J. Alloys Compd., 1995, 220: 126

[本文引用: 6]

Ishida K .

Effect of alloying elements on the critical driving force of martensitic transformation in iron alloys

[J]. Scr. Metall., 1977, 11: 237

[本文引用: 2]

Xie H J , Wu X C , Min Y A .

Influence of chemical composition on phase transformation temperature and thermal expansion coefficient of hot work die steel

[J]. J. Iron Steel Res. Int., 2008, 15: 56

[本文引用: 1]

Lukas H L , Fries S G , Sundman B . Computational Thermodynamics: the Calphad Method [M]. Cambridge: Cambridge University Press, 2007: 79

[本文引用: 4]

van Bohemen S M C , Morsdorf L .

Predicting the Ms temperature of steels with a thermodynamic based model including the effect of the prior austenite grain size

[J]. Acta Mater., 2017, 125: 401

[本文引用: 1]

Wang B H , Bai B Z , Ma H F , et al .

Yield ratio of Nb-Ti micro-alloyed Mn-series low carbon bainitic steel with different tempering temperature

[J]. Chin. J. Rare Met., 2019, 43: 151

王宝华, 白秉哲, 马海峰 等 .

回火温度对Nb-Ti微合金化Mn系低碳贝氏体钢屈强比的影响

[J]. 稀有金属, 2019, 43: 151

Ji Y P , Ren H P , Peng J , et al .

Growth restriction effect of solutes on refinement of solidification structure in iron-based binary alloys

[J]. Chin. J. Rare Met., 2020, 44: 886

[本文引用: 1]

计云萍, 任慧平, 彭 军 等 .

铁基二元合金凝固细化中溶质的生长抑制作用

[J]. 稀有金属, 2020, 44: 886

[本文引用: 1]

Nakada N , Kusunoki N , Kajihara M , et al .

Difference in thermodynamics between ferrite and martensite in the Fe-Ni system

[J]. Scr. Mater., 2017, 138: 105

[本文引用: 3]

He Y M , Zhang J X , Wang Y H , et al .

The expansion behavior caused by deformation-induced martensite to austenite transformation in heavily cold-rolled metastable austenitic stainless steel

[J]. Mater. Sci. Eng., 2019, A739: 343

[本文引用: 1]

Moyer J M , Ansell G S .

The volume expansion accompanying the martensite transformation in iron-carbon alloys

[J]. Metall. Trans., 1975, 6A: 1785

[本文引用: 3]

Ren X B , Wang X T .

Carbon ordering in Fe-1.83C martensite II. Crystal structure of long-period ordered phase

[J]. Acta Metall. Sin., 1994, 30: 337

[本文引用: 1]

任晓兵, 王笑天 .

Fe-

1.83C马氏体中碳的有序化Ⅱ. 长周期有序相的晶体结构 [J]. 金属学报, 1994, 30: 337

[本文引用: 1]

Hsu T Y , Li L , Jiang B H .

Thermodynamic calculation of the equilibrium temperature between the tetragonal and monoclinic phases in CeO2-ZrO2

[J]. Mater. Trans., 1996, 37: 1281

[本文引用: 1]

Fields R J , Weerasooriya T , Ashby M F .

Fracture-mechanisms in pure iron, two austenitic steels, and one ferritic steel

[J]. Metall. Trans., 1980, 11A: 333

[本文引用: 1]

Field D M , Baker D S , Van Aken D C .

On the prediction of α-martensite temperatures in medium manganese steels

[J]. Metall. Mater. Trans., 2017, 48A: 2150

[本文引用: 1]

Kaufman L , Cohen M .

The martensitic transformation in the iron-nickel system

[J]. JOM, 1956, 8(10): 1393

[本文引用: 6]

Scheil E , Saftig E .

Messung der umwandlungswärme bei der martensitbildung an eisen-nickel-legierungen mit hilfe eines trockeneiskalorimeters

[J]. Arch. Eisenhüttenwes., 1960, 31: 623

Yeo R B G .

Effect of some alloying elements on the transformation of Fe-22.5PctNi alloys

[J]. Trans. Metall. Soc. AIME, 1963, 227: 884

Ishida K , Nishizawa T .

Ferrite/austenite stabilizing parameter of alloying elements in steel at 200-500oC

[J]. Trans. Jpn. Inst. Met., 1974, 15: 217

Campbell C E .

Systems design of high-performance stainless steels

[D]. Evanston: Northwestern University, 1997

[本文引用: 3]

Gabriel A , Gustafson P , Ansara I .

A thermodynamic evaluation of the C-Fe-Ni system

[J]. Calphad, 1987, 11: 203

[本文引用: 5]

Ghosh G , Olson G B .

Computational thermodynamics and the kinetics of martensitic transformation

[J]. J. Phase Equilib., 2001, 22: 199

[本文引用: 4]

Magee C L , Davies R G .

The structure, deformation and strength of ferrous martensites

[J]. Acta Metall., 1971, 19: 345

[本文引用: 7]

Rao M M , Winchell P G .

Growth rate of bainite form low-carbon iron-nickel-carbon austenite

[J]. Trans. Metall. Soc. AIME, 1967, 239: 956

[本文引用: 3]

Steven W , Haynes A G .

Temperature of formation of martensite and bainite in low-alloy steel

[J]. J. Iron Steel Inst., 1956, 183: 349

[本文引用: 3]

Izumiyama M , Tsuchiya M , Yunoshin I .

Effects of alloying element on supercooled A3 transformation of iron

[J]. Sci. Rep. Res. Inst., Tohoku Univ., 1970, 22A: 105

[本文引用: 4]

Li P Y , Wang Y S , Meng F Y , et al .

Effect of heat treatment temperature on martensitic transformation and superelasticity of the Ti49Ni51 shape memory alloy

[J]. Materials, 2019, 12: 2539

[本文引用: 1]

Ning B Q , Yan Z S , Fu J C , et al .

Austenitic stability process of T91 steel held isothermally above Ms

[J]. J. Mater. Sci. Eng., 2011, 29: 21

[本文引用: 1]

宁保群, 严泽生, 付继成 等 .

Ms点以上保温时T91钢的奥氏体稳定化过程

[J]. 材料科学与工程学报, 2011, 29: 21

[本文引用: 1]

Hsu T Y , Li J , Zeng Z P .

Effect of solution strengthening of austenite on martensitic transformation in Fe-Ni-C alloys

[J]. Acta Metall. Sin., 1986, 22(6): 46

[本文引用: 2]

徐祖耀, 李 箭, 曾振鹏 .

Fe-Ni-C合金中奥氏体固溶强化对马氏体相变的影响

[J]. 金属学报, 1986, 22(6): 46

[本文引用: 2]

Greninger A B .

The martensite thermal arrest in iron-carbon alloys and plain carbon steels

[J]. Trans. ASM, 1942, 30: 1

[本文引用: 3]

Wilson E A .

The γ→α transformation in iron and its dilute alloys

[J]. Scr. Metall., 1970, 4: 309

Morozov O P .

Règles cinétiques et structurales de transformation de l'austénite dans les aciers

[J]. Fiz. Met. Metalloved., 1984, 57: 142

Mirzaev D A , Shtejnberg M M , Ponomareva T N , et al .

Effect of cooling rate on martensite point position: Carbon steels

[J]. Fiz. Met. Metalloved., 1979, 47: 125

[本文引用: 3]

Goodenow R H , Hehemann R F .

Transformation in iron and Fe-9pct Ni alloys

[J]. Trans. Metall. Soc. AIME, 1965, 233: 1777

[本文引用: 6]

Winchell P G , Cohen M .

The strength of martensite

[J]. Trans. Amer. Soc. Met., 1962, 55: 347

Mirzaev D A , Morozov O P , Shtejnberg M M .

On the relation between γ➝α transformations in iron and iron alloys

[J]. Fiz. Met. Metalloved., 1973, 36: 560

[本文引用: 3]

/

〈 〉


版权所有 © 《金属学报》编辑部
地址: 沈阳市文化路72号, 中国科学院金属研究所(110016)
电话: +86- 024-23971286 　E-mail: jsxb@imr.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发 技术支持：support@magtech.com.cn