奥氏体不锈钢在焊接接头热影响区的应力腐蚀开裂是核电材料的主要失效形式之一[1],对核电设备的安全稳定运行造成严重威胁。近期,在日本的压水堆核电站中检测到稳压器喷淋管316不锈钢焊接接头的应力腐蚀裂纹并引起了业界的高度关注[2]。除了腐蚀环境和材料敏化特性外,拉伸应力尤其是焊接产生的残余拉应力被认为是导致奥氏体不锈钢应力腐蚀开裂的一个关键因素。热-弹-塑性有限元计算方法作为与实验测量手段同等重要的获取残余应力的方法,已被广泛应用于预测焊接接头的残余应力。由于具有fcc晶体结构和较低的层错能,奥氏体不锈钢具有较强的加工硬化倾向,在多层多道焊接过程中容易累积较大的塑性应变;另一方面,由于动态回复、再结晶和晶粒长大等因素对材料位错的影响[3],材料累积的应变硬化在一定温度范围内被快速清除[4],这一现象被称为“退火软化”效应[5](annealing effect)。因此,建立合理的加工硬化和退火软化材料模型对奥氏体不锈钢焊接残余应力的高精度预测具有重要科学理论意义和工程实用价值。需要指出的是,本工作中的“退火”与热处理过程的“退火”概念是有区别的,在本研究中仅用于描述焊接过程中材料应变硬化的回复现象。
早期的焊接数值模拟研究一般未考虑退火软化效应的影响,因而倾向采用屈服面大小不变的塑性模型(如理想弹塑性模型和移动硬化模型)进行有限元分析[6]。近10多年来,研究者们在热-弹-塑性有限元计算方法中通常采用各向同性硬化模型和混合硬化模型来考虑材料的加工硬化。同时,开发了多种退火模型来考虑焊接过程中的退火软化现象。Xu等[7,8]和Muránsky等[9,10]分别研究了加工硬化模型对316LN不锈钢平板槽焊接头残余应力预测精度的影响,结果表明,混合硬化模型的焊接残余应力模拟结果与实验测量结果吻合良好,采用各向同性硬化模型会高估残余应力,而移动硬化模型会低估残余应力。随后,Deng等[11]针对304不锈钢平板对接接头,Wang等[12]针对10Ni5CrMoV钢平板对接接头,耿鲁阳等[13]针对13MnNiMoR钢厚管对接接头进行了类似的研究,并得出了相似的结论。然而,这些研究均采用了仅与温度相关的退火模型,退火温度为800~1400℃,未考虑退火时间等因素对焊接残余应力计算精度的影响。
在阶跃退火模型中,通常假定当材料达到预设温度(即退火温度)时完全清除累积的应变硬化,由于模型简单而获得广泛使用。邓德安等[5]利用数值模拟方法研究了阶跃退火温度对304不锈钢焊接残余应力计算精度的影响,认为在采用各向同性硬化模型时将阶跃退火温度设定为1000℃比较合理。乔东虓[4]采用Gleeble设备和数字图像相关(DIC)技术研究了304L不锈钢和Alloy 82镍基合金等材料在不同温度下短时间退火处理对应变硬化的影响,实验结果表明预加载的304L不锈钢试样在600~1000℃保温数分钟时应变硬化得到部分或全部清除,而在1075℃以上保温数秒即可达到完全退火状态。基于实验数据[4],Yu等先后开发了基于等效退火参数(EAP)的动态退火模型[14]和Yu-Qiao-Feng (YQF)动态退火模型[15]。EAP动态退火模型根据等效退火参数分为2个阶段进行描述,但其控制方程存在不连续的问题。YQF模型考虑了退火温度、时间和初始硬化程度的影响,计算结果与实验数据吻合良好,但模型相对复杂。乔东虓[4]采用各向同性硬化模型和EAP动态退火模型的组合模型对核电安全端异种钢接头的焊接残余应力和累积塑性应变进行了数值模拟,结果表明动态退火模型具有较高的计算精度。然而,目前尚未见到阐明退火模型对焊接残余应力和累积塑性应变形成过程与机理的影响的详细报道。
本工作基于通用有限元软件Abaqus开发了一种新的动态退火模型。以壁厚为74 mm的316不锈钢管-管对接接头为研究对象,采用2D轴对称模型计算了对接接头的温度场和焊接残余应力,并与实验测量结果进行了对比与验证。此外,基于数值模拟方法研究了应变硬化模型(各向同性硬化模型和Chaboche混合硬化模型)和退火模型(阶跃退火模型和动态退火模型)对Satoh数值实验应力和累积塑性应变形成过程的影响,以及对管-管对接接头焊接残余应力的影响。
1 实验方法
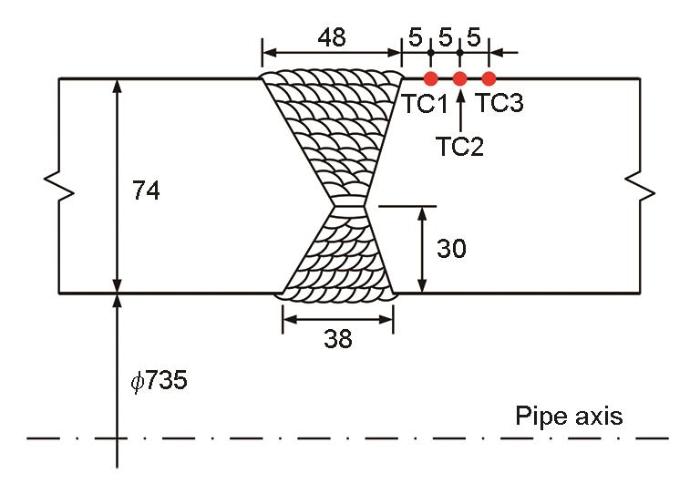
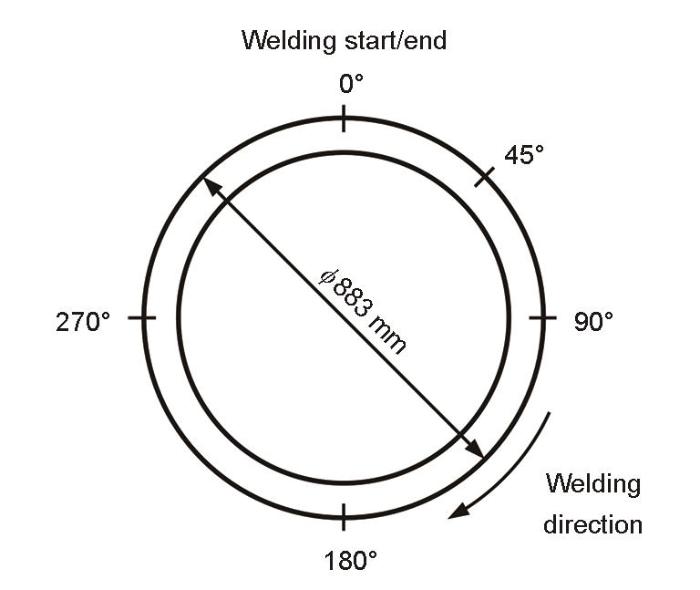
实验所用材料为316奥氏体不锈钢,其主要化学成分(质量分数,%)为:C 0.06,Si 0.54,Mn 0.87,P < 0.04,S < 0.03,Ni 12.2,Cr 16.8,Mo 2.13,Fe余量。焊接接头的坡口尺寸和焊道布置如图1所示,焊接始终端和焊接方向如图2所示。圆管外径与壁厚之比约为12,圆管长度为1 m。采用手工电弧焊(SMAW)进行焊接,焊接参数为:焊接电流140~170 A,电压27 V,焊接速率180~200 mm/min,焊接线能量1.26~1.38 kJ/mm,层间温度低于150℃。焊接填充材料采用D316L焊条,其主要化学成分(质量分数,%)为:C 0.02,Si 0.40,Mn 1.34,P < 0.04,S < 0.03,Ni 12.7,Cr 18.2,Mo 2.45,Fe余量。焊接时采用K型热电偶测量焊接热循环数据[16],测量点(TC1、TC2和TC3)分布在圆管45º截面的外壁,如图1所示。焊接实验方法参见文献[17]。
图1
图1
坡口尺寸和焊道布置示意图
Fig.1
Schematic of the multipass butt-welded pipe joint and the locations of thermocouple (TC1, TC2, and TC3) (unit: mm)
图2
图2
焊接始终端和焊接方向示意图
Fig.2
Schematic of welding start/end location and welding direction of the welded joint
焊接完成后,采用切片法(SM)测量管-管对接接头表面的残余应力,采用固有应变法(IS)测量接头内部的残余应力,测量点在圆管180º截面,如图3所示。其中,切片法将接头切割成小块并采用应变片测量切割过程的释放应变,通过理论计算得到残余应力[18]。切片法的测量精度较高,但只能测量接头表面的残余应力。固有应变法切取接头内部的片状试样并测量其固有应变,通过有限元计算反求出残余应力[19]。另外,从管-管对接接头中切取弧长为250 mm (约为圆周的1/10)的局部接头,采用深孔法(DHD)测量沿焊缝中心线的残余应力分布,如图3所示。深孔法首先在工件上钻一个直径约为3 mm的通孔(即参考孔),然后加工一个包含参考孔的套孔(直径约为10 mm),通过测量加工套孔前后参考孔的孔径变化来计算残余应力[20]。管-管对接接头残余应力的实验测量结果见文献[16,17]。
图3
图3
焊接残余应力测量位置示意图
Fig.3
Schematic of the locations for residual stress measurements in the welded joint
2 数值模拟方法
2.1 有限元计算方法
本工作采用顺序耦合的热-弹-塑性有限元计算方法,首先计算焊接温度场,然后基于温度场计算结果进行应力分析。在温度场计算中,采用单元激活功能“Model Change”模拟焊道填充,采用瞬间热源对焊道整体加热模拟焊接热输入。瞬间热源的热流密度(
式中,th为热源加载时间(s),A为焊道面积(mm2),η为焊接热效率,U为电压(V),I为电流(A),v为焊接速率(mm/s)。根据实际焊接线能量和焊接热循环测量数据对参数进行设定和调整。在本工作中,热源加载时间设定为5 s,焊接热效率平均值为0.68。温度场计算所考虑的焊接参数和层间温度与实验一致。
2.2 应变硬化与退火模型
在热-弹-塑性有限元模型中,本工作详细考虑了材料的高温热物理性能和力学性能参数。316不锈钢的热物理性能参数和力学性能参数见文献[21]。由于化学成分和材料性能相近,对于D316L填充材料采用了与316不锈钢相同的材料参数。
2.2.1 应变硬化模型
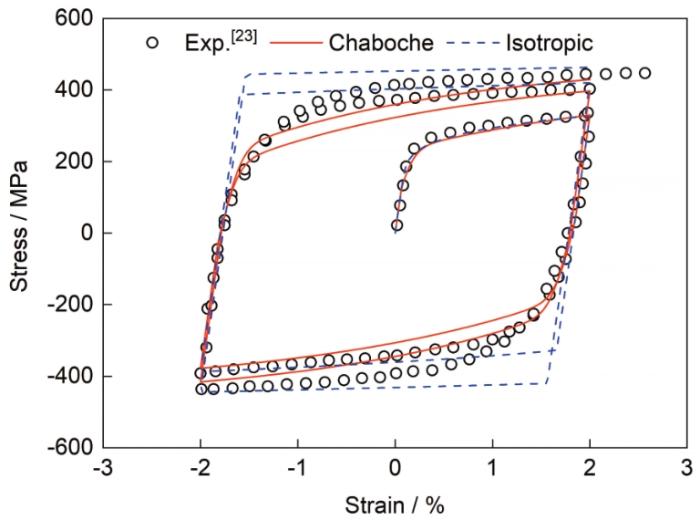
本工作采用非线性各向同性硬化和Chaboche混合硬化2种模型来模拟材料的塑性行为,并计算了厚壁多层多道316不锈钢管-管对接接头的残余应力。对于各向同性硬化模型,材料的屈服强度(σs)通过Ludwik公式确定[24]:
式中,σ0为比例极限(MPa),
式中,Qinf为屈服面最大扩张量(MPa);σ为应力张量(MPa);β、Ci和γi为材料参数。
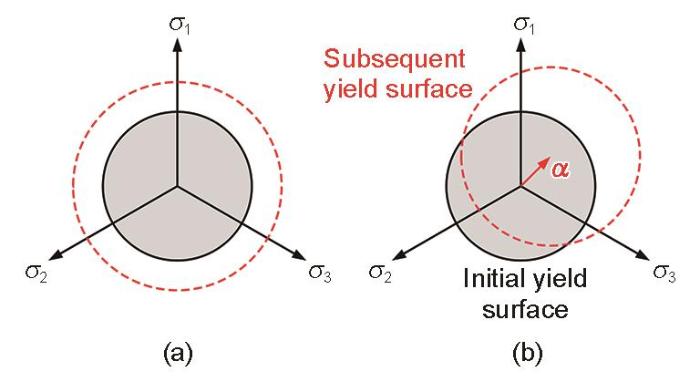
图4展示了各向同性硬化模型和混合硬化模型的屈服面变化过程。在各向同性硬化模型中,屈服面的大小随塑性应变的累积或清除而变化,而屈服面的中心在应力空间的位置保持不变;在混合硬化模型中,屈服面的大小和中心位置均会发生变化。
图4
图4
各向同性硬化模型和Chaboche混合硬化模型的屈服面示意图
Fig.4
Schematics of the initial and subsequent yield surfaces in the isotropic strain hardening model (a) and the Chaboche mixed isotropic-kinematic strain-hardening model (b) (σ1, σ2, and σ3 are principal stresses; α—back stress)
表1 316LN不锈钢的各向同性硬化参数和Chaboche混合硬化参数[9]
Table 1
| T / oC | Isotropic hardening model | Chaboche mixed isotropic-kinematic hardening model | |||||||
|---|---|---|---|---|---|---|---|---|---|
| σ0 / MPa | K / MPa | m | Qinf / MPa | β | C1 / MPa | C2 / MPa | γ1 | γ2 | |
| 20 | 125.6 | 519.2 | 0.24 | 153.4 | 6.9 | 156435 | 6134 | 1410.85 | 47.19 |
| 275 | 97.6 | 475.5 | 0.28 | 154.7 | 6.9 | 100631 | 5568 | 1410.85 | 47.19 |
| 550 | 90.9 | 444.9 | 0.32 | 150.6 | 6.9 | 64341 | 6227 | 1410.85 | 47.19 |
| 750 | 71.4 | 259.4 | 0.26 | 57.9 | 6.9 | 56232 | 4108 | 1410.85 | 47.19 |
| 900 | 66.2 | 47.0 | 0.06 | 0 | 6.9 | 0.05 | 292 | 1410.85 | 47.19 |
| 1000 | 31.8 | 0 | 0 | 0 | 6.9 | 0 | 0 | 1410.85 | 47.19 |
| 1100 | 19.7 | 0 | 0 | 0 | 6.9 | 0 | 0 | 1410.85 | 47.19 |
| 1400 | 2.1 | 0 | 0 | 0 | 6.9 | 0 | 0 | 1410.85 | 47.19 |
图5
2.2.2 退火模型
本工作中,对于阶跃退火模型,假定当材料达到退火温度(TA)以上时完全清除累积塑性应变和背应力。由于阶跃退火模型忽略了退火时间的影响,而现有的动态退火模型如YQF退火模型[15]形式相对复杂。因此开发了新的动态退火模型,考虑了退火温度和时间对材料应变硬化的影响。
新的动态退火模型采用Johnson-Mehl-Avrami公式[26]计算材料应变硬化的回复程度,即退火因子(f):
表2 304L不锈钢的动态退火模型材料参数
Table 2
| T / oC | fA | b | n |
|---|---|---|---|
| 600 | 0.10 | 0.05 | 0.59 |
| 680 | 0.20 | 0.19 | 0.50 |
| 750 | 0.30 | 0.54 | 0.34 |
| 825 | 0.40 | 0.79 | 0.26 |
| 900 | 0.84 | 0.32 | 0.33 |
| 1000 | 1.00 | 0.68 | 0.37 |
在新的退火模型中,累积塑性应变增量(
式中,ΔH为von Mises等效塑性应变的增量,代表由于单元塑性变形产生的应变硬化;累积硬化量H'为新增硬化(1 - f )ΔH的累积值;Δf为退火因子的增量。
在焊接有限元计算中,可以在每个增量步内基于叠加原理将焊接热循环处理成一系列等温过程。对于等温过程,新模型的材料参数与时间无关。因此,退火因子对时间的导数可以表示为:
根据式(
图6
图6
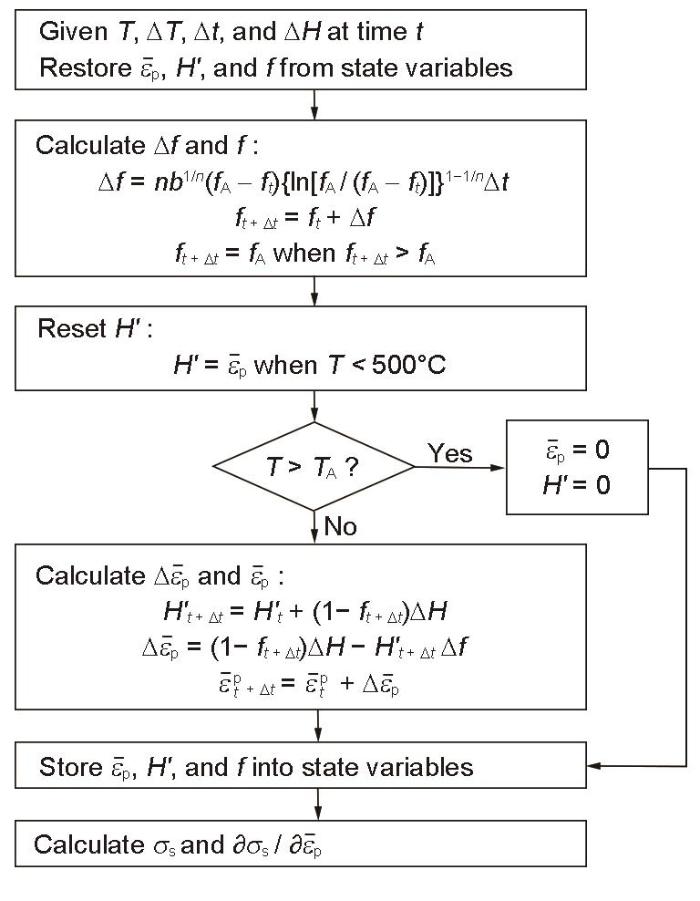
新开发的动态退火模型的UHARD子程序流程图
Fig.6
Flowchart of the UHARD subroutine of the new time-temperature-dependent annealing model (t—time, ΔH—increment of the von Mises equivalent plastic strain,
图7
2.3 Satoh数值实验
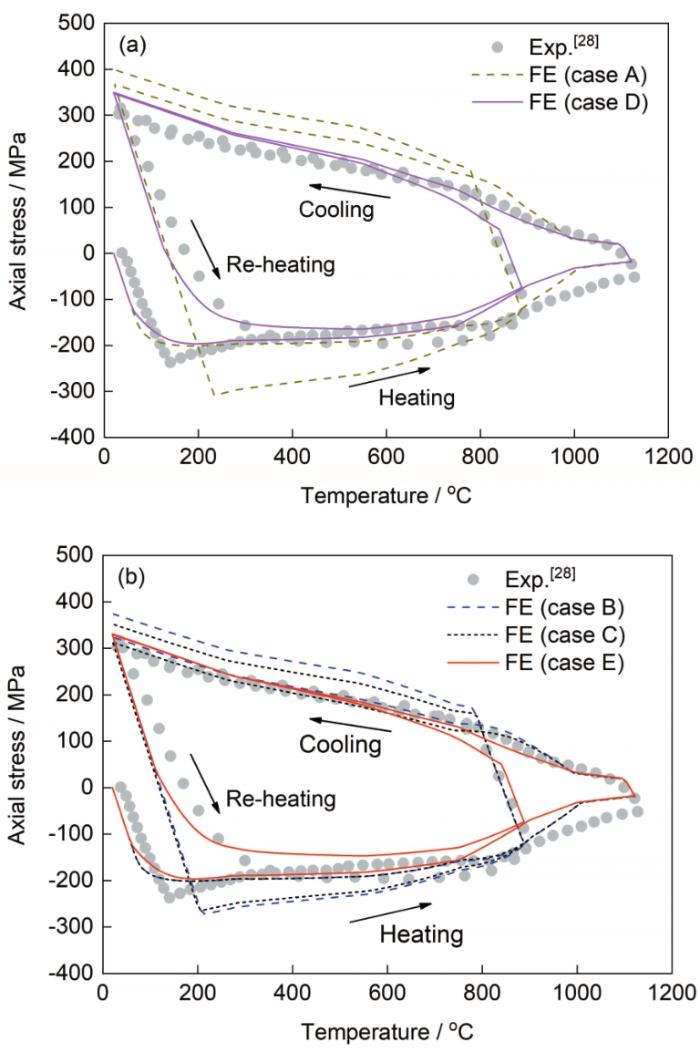
在Satoh数值实验中,试件的初始温度为20℃,第1次热循环的最高温度为1122℃,第2次热循环的最高温度为888℃,加热速率为90℃/s,冷却速率为10℃/s。Satoh数值实验的热循环参数与实验条件[28]一致。
2.4 厚壁管-管对接接头数值模拟
图8
图8
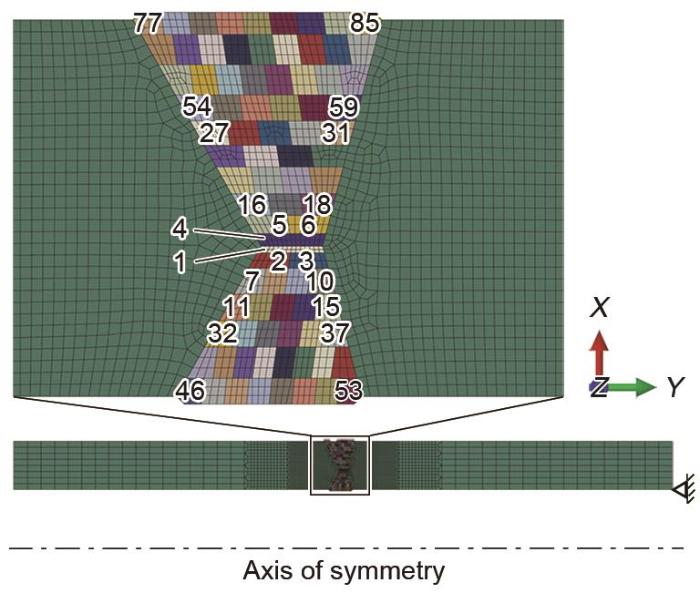
316不锈钢对接接头的有限元网格
Fig.8
Finite element (FE) mesh and the number of welding passes of the 316 stainless steel butt-welded pipe joint (Numbers show the welding passes)
Satoh数值实验和管-管对接接头的有限元计算案例如表3所示。由于缺少循环加载条件下的退火软化实验数据,本工作未考虑采用Chaboche混合硬化模型和动态退火模型的组合模型的计算案例。用于数值计算的计算机CPU为i7-7700K (4.2 GHz),RAM为32 GB。单个案例的计算总时间约为11 h。
表3 有限元计算案例
Table 3
| Case | Strain hardening model | Annealing model |
|---|---|---|
| A | Isotropic | Neglected |
| B | Isotropic | Single-stage model with TA = 1000℃ |
| C | Isotropic | New time-temperature-dependent model |
| D | Chaboche mixed isotropic-kinematic | Neglected |
| E | Chaboche mixed isotropic-kinematic | Single-stage model with TA = 1000℃ |
3 模拟结果
3.1 Satoh数值实验结果
图9
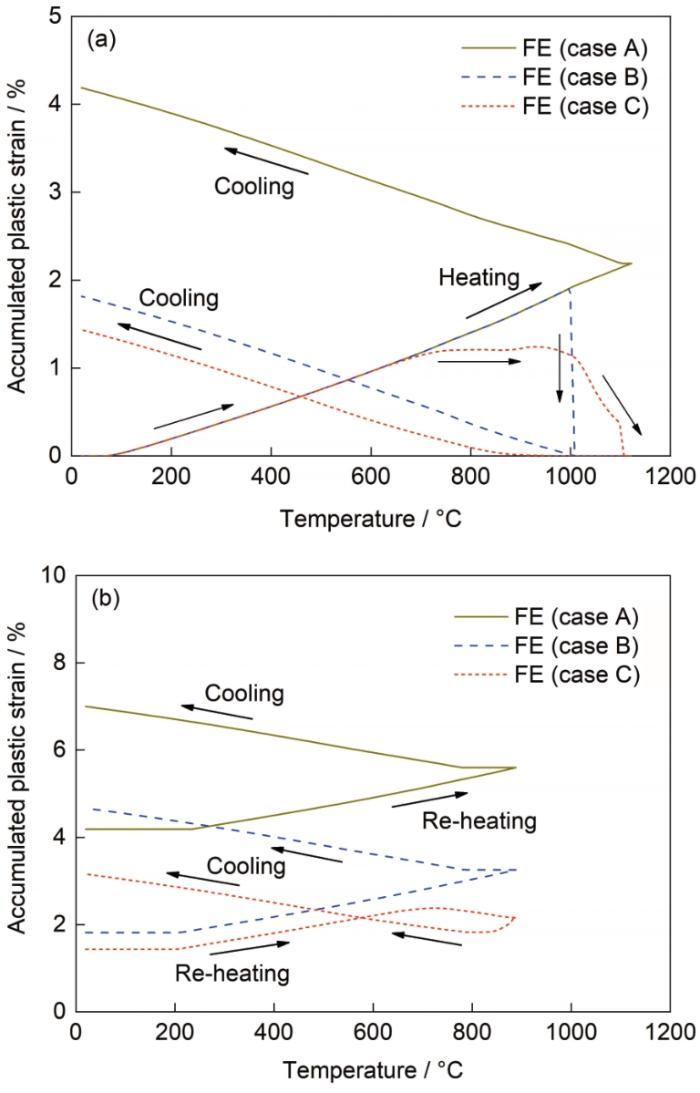
图10a和b分别对比了在第1次和第2次热循环中Cases A~C的累积塑性应变的形成过程。在图10a中,由于没有考虑退火软化效应,Case A的累积塑性应变在热循环过程中近似线性增加。由于采用了1000℃的阶跃退火温度,Case B的累积塑性应变在热循环温度达到1000℃时完全清零,并在温度低于1000℃时重新增加。Case C采用了动态退火模型,其累积塑性应变在700~1000℃基本保持不变,此时材料的应变硬化和退火软化达到一种动态平衡。当温度进一步升高时,退火软化效应逐渐占主导,Case C的累积塑性应变在1000~1100℃近似线性降低,并在1100℃以上完全清零。在冷却阶段,Case C的累积塑性应变在温度低于900℃左右时重新增加。在第1次热循环结束时,Case A的累积塑性应变计算结果为4.2%,Case B为1.8%,Case C为1.4%。
图10
图10
Satoh数值实验第1次和第2次热循环中累积塑性应变的形成过程
Fig.10
Evolutions of the simulated accumulated plastic strain during the first (a) and second (b) thermal cycles in the numerical Satoh test
在图10b中,Case A的累积塑性应变在第2次热循环中仍然近似线性增加。试件在加热/冷却开始阶段处于弹性状态,其塑性应变保持不变。由于第2次热循环的峰值温度低于Case B所采用的阶跃退火温度,Case B的累积塑性应变同样近似线性增加。由于动态退火模型对材料应变硬化的部分清除,Case C的累积塑性应变在较高温度有一定降低。在第2次热循环结束时,Case A的累积塑性应变计算结果为7.0%,Case B为4.7%,Case C为3.2%。
Satoh数值实验结果表明,不考虑退火软化效应的应力计算结果明显高于实验结果。在多次热循环过程中,采用各向同性硬化模型的计算结果与实验结果的差值会进一步增大。考虑退火软化效应可以有效提高残余应力计算精度,退火模型对累积塑性应变计算结果具有显著影响。对于各向同性硬化模型,采用阶跃退火模型时在第1次热循环中具有较高的残余应力计算精度,但在多重热循环过程中可能得到偏高的计算结果。与阶跃退火模型相比,采用本研究新开发的动态退火模型的计算精度更高。另外,由于Satoh实验具有明显的压缩-拉伸应力循环特征,考虑Bauschinger效应的混合硬化模型可以更精确地预测Satoh实验多重热循环过程的应力演变过程。
3.2 焊接温度场结果
图11
3.3 焊接残余应力结果
图12展示了各个计算案例(Cases A~E)的周向残余应力分布云图。由于焊接过程中材料的冷却收缩在沿焊接方向受到强拘束,对接接头的盖面层及其附近区域产生了很高的周向拉应力,拉应力峰值位于最后一道的热影响区。在Case A中,由于采用各向同性硬化模型且没有考虑退火软化效应,其拉应力峰值达到643 MPa。Case B和Case C均采用了各向同性硬化模型,其中Case B采用了退火温度为1000℃的阶跃退火模型,而Case C采用了本研究新开发的动态退火模型。Case B和Case C的周向残余应力分布差异不显著,Case B的周向拉应力峰值为576 MPa,Case C为555 MPa。Case D采用了混合硬化模型且没有考虑退火软化效应,其周向拉应力峰值为564 MPa,与Case A相比明显更低。由于采用了混合硬化模型且考虑了退火软化效应,Case E的周向拉应力峰值为454 MPa,低于Cases A~D的计算结果。另外,Case E的高拉伸应力区域也相对较小。
图12
图12
316不锈钢对接接头的周向残余应力分布
(a) case A (b) case B (c) case C(d) case D (e) case E
Fig.12
Distributions of hoop residual stresses in the 316 stainless steel butt-welded pipe joint
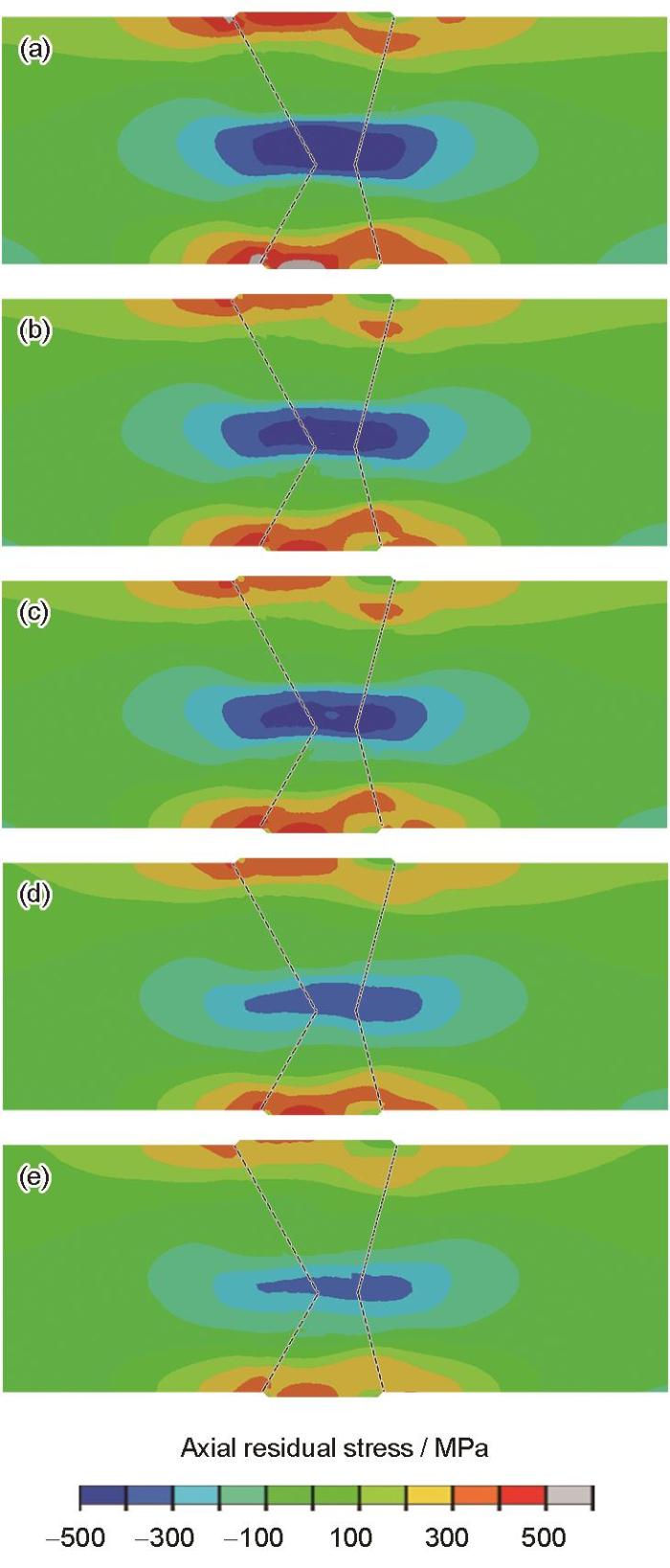
图13
图13
316不锈钢对接接头的轴向残余应力分布
(a) case A (b) case B (c) case C(d) case D (e) case E
Fig.13
Distributions of axial residual stresses in the 316 stainless steel butt-welded pipe joint
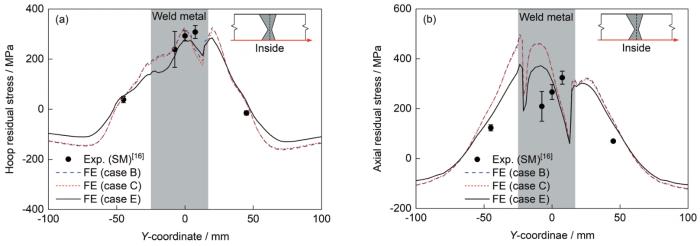
图14为316不锈钢管-管对接接头外表面(如插图所示)的焊接残余应力模拟结果和切片法测量值[16]的对比结果,图中仅展示了考虑退火软化效应的3个案例(Case B、Case C和Case E)的计算结果。总体而言,外表面周向残余应力呈现“几”字形分布特征,在焊缝及附近区域产生了较高的拉伸残余应力。外表面周向残余应力峰值位于最后一道(即第85道)的热影响区,其中采用各向同性硬化模型(Case B和Case C)的峰值相同,约为450 MPa,而采用混合硬化模型(Case E)的峰值为390 MPa。在焊缝区域,Case B和Case C的周向应力模拟结果与切片法测量值吻合良好,而Case E的模拟结果与测量值相比偏低。对于外表面的轴向残余应力,Case E的模拟结果与切片法测量值相对比较吻合,而Case B和Case C的模拟结果与测量值相比偏高。
图14
图15
图16
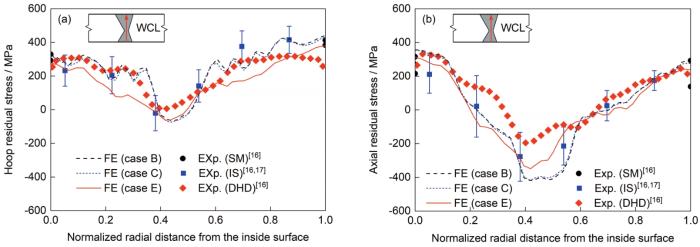
图16
316不锈钢对接接头沿焊缝中心线的周向和轴向残余应力模拟结果与实验测量值[16,17]对比
Fig.16
Comparisons of simulated results and measurements[16,17] of hoop (a) and axial (b) residual stresses along the weld centerline (WCL) of the 316 stainless steel butt-welded pipe joint (Insets show the locations of the WCL; IS—inherent strain method, DHD—deep-hole drilling)
3.4 累积塑性应变结果
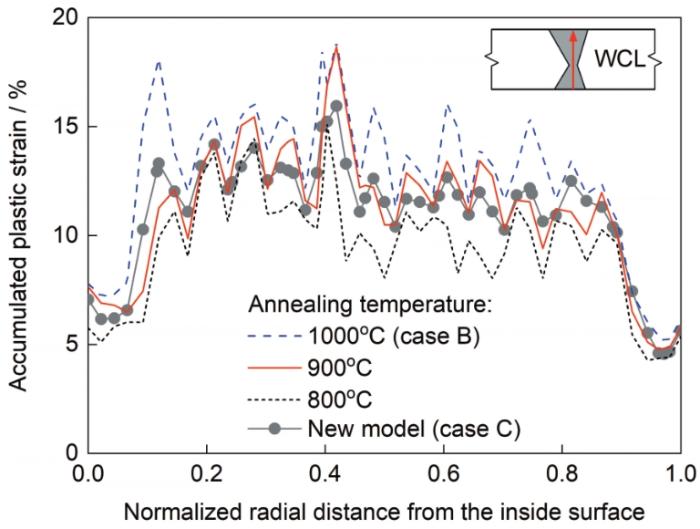
图17对比了采用阶跃退火模型的Case B沿焊缝中心线的累积塑性应变计算结果和采用新开发的动态退火模型的Case C的计算结果,并增加了阶跃退火温度分别为800和900℃的计算案例作为对比,计算案例均采用各向同性硬化模型。结果显示,采用阶跃退火模型的累积塑性应变分布存在较大的“锯齿状”波动。而动态退火模型(Case C)考虑了一定温度范围内的应变硬化回复过程以及时间因素的影响,其累积塑性应变分布相对比较平缓。Case C的累积塑性应变模拟结果在圆管壁厚中心区域为10%~15%,在内、外表面约为5%。与Case C的累积塑性应变计算结果相比,阶跃退火温度为1000℃ (Case B)的计算结果平均相对偏高约16%,而阶跃退火温度为800℃的计算结果平均相对偏低约14%。当阶跃退火温度为900℃时,沿焊缝中心线的累积塑性应变计算结果与Case C的计算结果比较吻合。因此,在焊接数值模拟中采用阶跃退火模型时,考虑到工程应用通常倾向采用保守估计,因此,在焊接数值模拟中采用阶跃退火模型时,建议将316奥氏体不锈钢的退火温度设定为900~1000℃。
图17
图17
316不锈钢对接接头沿焊缝中心线的累积塑性应变模拟结果对比
Fig.17
Comparisons of simulated results of the accumulated plastic strain along the WCL of the 316 stainless steel butt-welded pipe joint (Inset shows the location of the WCL)
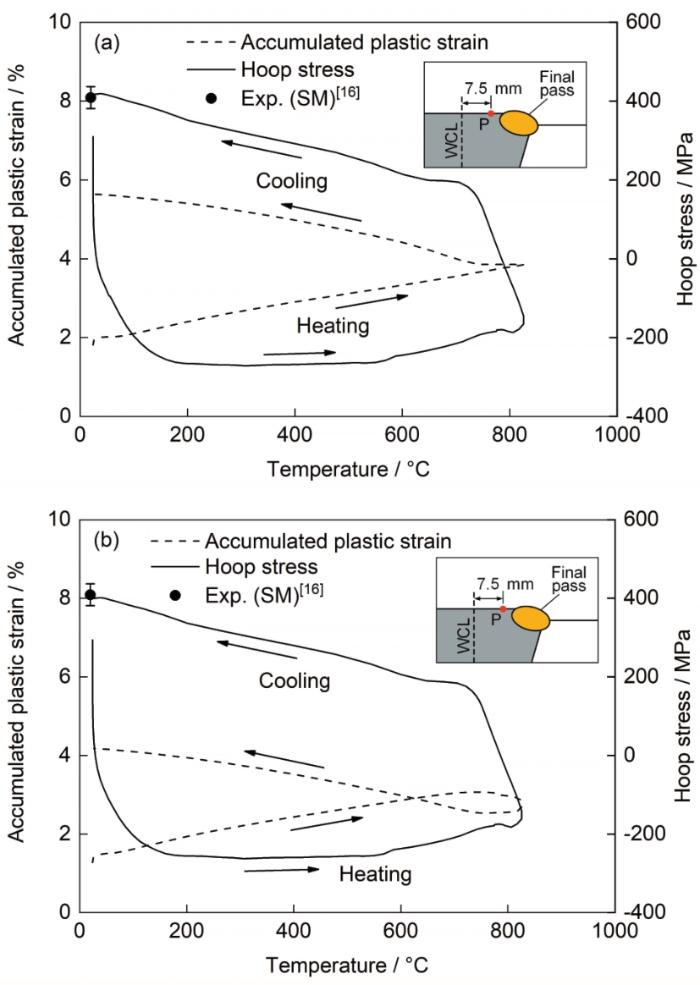
图18展示了在最后一道(即第85道)焊接热循环中Case B和Case C在特征点P的累积塑性应变和周向应力形成过程,并与切片法应力测量值[16]进行了对比。选取的特征点P位于最后一道的热影响区,距离焊缝中心线7.5 mm,如图18中插图所示。Case B和Case C在点P的周向应力和累积塑性应变形成过程分别与图9b和图10b中Satoh数值实验的计算结果基本一致,说明Satoh数值实验可以有效分析焊缝和热影响区的残余应力和累积塑性应变的形成机理。Case B和Case C的周向应力形成过程的差别较小,焊接完成后,Case B的周向残余应力模拟结果为417 MPa,Case C为400 MPa,2者均与切片法测量值吻合良好。结果表明,退火模型对累积塑性应变的形成过程有显著影响,而对焊接残余应力形成过程的影响相对有限。
图18
图18
最后一道焊接热循环中点P的累积塑性应变和周向应力形成过程的模拟结果
(a) case B (b) case C
Fig.18
Evolutions of the simulated accumulated plastic strain and the hoop stress at point P during the final welding thermal cycle (Insets show the locations of point P)
4 分析讨论
表4 316不锈钢对接接头残余应力模拟结果与测量值[16,17]的平均差异
Table 4
| Case | Hoop residual stress / MPa | Axial residual stress / MPa | ||||
|---|---|---|---|---|---|---|
| FE-SM | FE-IS | FE-DHD | FE-SM | FE-IS | FE-DHD | |
| A | 79 | 28 | 58 | 94 | -23 | -85 |
| B | 19 | -6 | 26 | 43 | -18 | -83 |
| C | 13 | -11 | 18 | 39 | -15 | -83 |
| D | 30 | -35 | -22 | 37 | -6 | -84 |
| E | -15 | -72 | -56 | 4 | -3 | -83 |
在表4中,“FE-SM”为残余应力模拟结果与切片法测量值的对比,其余类似。以切片法测量值为基准,对于没有考虑退火软化效应的Case A和Case D,由于采用了各向同性硬化模型,Case A的模拟结果偏高80~90 MPa;而Case D采用了Chaboche混合硬化模型,其模拟结果偏高30~40 MPa。这说明退火软化效应对于焊接残余应力计算精度有显著影响,其中,对各向同性硬化模型的影响较大,而对混合硬化模型的影响相对较小。Case B和Case C均采用了各向同性硬化模型,其中Case B采用了阶跃退火模型,而Case C采用了新开发的动态退火模型。2者的模拟结果与切片法测量值相比均偏高10~40 MPa,说明通过采用合适的退火模型,各向同性硬化模型可以获得较高的焊接残余应力计算精度,但模拟结果偏保守。由于采用了Chaboche混合硬化模型且考虑了退火软化效应,Case E的模拟结果与切片法测量值相比误差相对较小,说明混合硬化模型具有更高的应力计算精度。总体而言,应变硬化模型的选择以及是否考虑退火软化效应对于残余应力计算精度的影响都非常显著,而退火模型的影响相对较小。
对于有限元计算,采用2D轴对称模型模拟虽然可以较好地反映对接接头稳定区的焊接残余应力分布,但由于对模型和热源的简化处理,大尺寸管-管对接接头的2D轴对称模型模拟结果与3D模型相比可能有一定差别[21]。为了提高残余应力计算精度,需要采用考虑移动热源的3D有限元模型进行计算,但由于计算规模增大以及需要更多的计算增量步,计算时间会大幅增加。对于焊道数较多的焊接接头,采用3D模型进行热-弹-塑性有限元计算将耗费大量的计算资源和时间。另一方面,采用深孔法测试的局部接头在预先切割过程中应力会重新分布,与完整对接接头的残余应力分布相比可能存在一定差异,而轴向应力更容易受到局部拘束条件变化的影响。另外,深孔法实际测量的是套孔(直径约为10 mm)区域内的平均应力值。
本工作新开发的动态退火模型考虑了温度和时间因素的影响,计算结果与实验数据[4]吻合良好(如图7所示),与仅考虑温度因素的阶跃退火模型相比能够更真实地反映材料的退火软化行为。图10和18的模拟结果均显示,新开发的动态退火模型有效反映了材料的应变硬化在加热至700~1100℃时得到部分清除的现象。然而,虽然不同退火模型的累积塑性应变模拟结果存在一定差异,但对材料屈服强度的影响有限。总体而言,采用阶跃退火模型的Case B和采用动态退火模型的Case C的残余应力整体分布差别不显著,说明对于厚大构件,退火模型中时间因素对于焊接残余应力计算精度的影响有限,而温度因素的影响可能更显著,采用仅与温度相关的阶跃退火模型也可以获得较好的残余应力预测结果。
需要注意的是,在图12中,Case C的周向拉应力峰值(555 MPa)与Case B (576 MPa)相比更低。在图14a中,在对接接头外壁最后一道(第85道)的焊缝区域,Case C的周向残余应力最小值(302 MPa)与Case B (319 MPa)相比更低。在图15a中,在内壁最后一道(第53道)的焊缝区域,Case C的周向残余应力最小值(174 MPa)与Case B (190 MPa)相比更低。在图18中,在外壁最后一道的热影响区,Case C的周向残余应力(400 MPa)与Case B (417 MPa)相比更低。这些结果均说明在最后一道的焊缝和热影响区,采用动态退火模型和阶跃退火模型的残余应力计算结果存在约20 MPa的差异。因此,对于焊道数较少的中厚板焊接接头,退火模型对焊接残余应力和累积塑性应变计算精度的影响还需要进一步的研究。
由于各向同性硬化模型的参数可根据单轴拉伸实验进行定义,而对于混合硬化模型则需要开展循环加载实验,因此,在解决工程问题时推荐采用各向同性硬化模型和阶跃退火模型的组合模型。当具有材料退火软化实验数据时,采用动态退火模型可以提高累积塑性应变和焊接残余应力的计算精度。在应力计算精度要求较高的情况下,建议采用混合硬化模型并考虑退火软化效应。另外,通过测量循环加载条件下的退火软化实验数据,可以完善现有的动态退火模型,并与混合硬化模型相结合进一步提高焊接残余应力的计算精度。
5 结论
(1) 新开发的动态退火模型考虑了温度和时间因素的影响,计算结果与实验数据吻合良好,具有较高的计算精度。退火模型对累积塑性应变的形成过程有显著影响。对于厚大构件的焊接数值模拟,采用动态退火模型和阶跃退火模型获得的残余应力整体分布的差别不显著,但在最后一道的焊缝和热影响区存在约20 MPa的差异。
(2) 退火软化效应对累积塑性应变和焊接残余应力的计算精度有显著影响,当采用各向同性硬化模型时,不考虑退火软化效应的残余应力计算结果与切片法测量结果对比具有较大的误差(80~90 MPa)。退火软化效应对于Chaboche混合硬化模型的焊接残余应力计算结果的影响相对较小(30~40 MPa)。
(3) 当采用合适的退火模型时,各向同性硬化模型的焊接残余应力计算精度较高且结果偏保守(10~40 MPa)。由于各向同性硬化参数容易获取,对于工程应用推荐采用各向同性硬化模型和阶跃退火模型的组合模型。而采用Chaboche混合硬化模型的焊接残余应力计算结果与实验结果更吻合,其计算精度更高。
(4) 对于316不锈钢而言,当采用阶跃退火模型时,建议将退火温度设定为900~1000℃。
参考文献
Microstructure and local properties of a domestic safe-end dissimilar metal weld joint by using hot-wire GTAW
[J].
国产核电安全端异种金属焊接件的微观结构及局部性能研究
[J].
Results of the investigation on the welded joint in the pressurizer spray line piping of the unit 3 of the Oi nuclear power plant (Data set)
[R].
大飯発電所3号機加圧器スプレイライン配管溶接部の調査結果 (データ集)
[R].
Recovery, recrystallization, and grain-growth structures
[A].
Strain hardening recovery and its influence on welding residual stresses in reactor safe-end in power plants
[D].
核电安全端焊接中应变硬化回复及其对残余应力的影响
[D].
Influence of annealing temperature on calculation accuracy of welding residual stress in a SUS304 stainless steel joint
[J].
退火温度对SUS304不锈钢焊接残余应力计算精度的影响
[J].
Improvement and validation of weld residual stress modelling procedure
[R].
Temperature and residual stress simulations of the NeT single-bead-on-plate specimen using SYSWELD
[J].
Effect of material hardening model on welding residual stresses of 316L stainless steel
[J].
材料硬化模型对316L不锈钢焊接残余应力的影响
[J].
The effect of plasticity theory on predicted residual stress fields in numerical weld analyses
[J].
The influence of constitutive material models on accumulated plastic strain in finite element weld analyses
[J].
Influence of material model on prediction accuracy of welding residual stress in an austenitic stainless steel multi-pass butt-welded joint
[J].
Numerical simulation of residual stress in 10Ni5CrMoV steel weldments
[J].
Simulation of residual stress in butt girth welding of ultra-thick 13MnNiMoR steel cylinder by different material hardening models
[J].
不同材料硬化模型模拟13MnNiMoR钢超厚圆筒对接环焊接残余应力
[J].
High temperature dynamics strain hardening behavior in stainless steels and nickel alloys
[A].
High-temperature deformation constitutive law for dissimilar weld residual stress modeling: Effect of thermal load on strain hardening
[A].
Annual report on the integrity assessment of flawed components with structural discontinuity
[R].
複雑形状部機器配管健全性実証事業に関する報告書
[R].
Sensitivity analysis of residual stress simulation of dissimilar metal joint of safe end nozzle and key issues for standard procedure to maintenance rules
[A].
Residual stress measurements
[A].
Inherent strain method for residual stress measurement and welding distortion prediction
[A].
Measurement of residual stresses in the dissimilar metal weld joint of a safe-end nozzle component
[A].
Influence of size factor on calculation accuracy of welding residual stress of stainless steel pipe by 2D axisymmetric model
[J].
尺寸因素对2D轴对称模型计算不锈钢管焊接残余应力精度的影响
[J].
Effect of creep on prediction accuracy and calculating efficiency of residual stress in post weld heat treatment
[J].
蠕变对焊后热处理残余应力预测精度和计算效率的影响
[J].
Influence of viscoplasticity, hardening, and annealing effects during the welding of a three-pass slot weld (NET-TG4 round robin)
[J].
A review of some plasticity and viscoplasticity constitutive theories
[J].
Mathematical models of anisothermal phase transformations in steels, and predicted plastic behaviour
[J].
Transient thermal stresses of weld heat-affected zone by both-ends-fixed bar analogy
[J].
Simulation numérique du soudage-acier 316L-validation sur cas tests de complexité croissante
[D].
Influence of solid-state phase transformation on residual stress in P92 steel welded joint
[J].
固态相变对P92钢焊接接头残余应力的影响
[J].
Influence of multi-thermal cycle and constraint condition on residual stress in P92 steel weldment
[J].
多重热循环和约束条件对P92钢焊接残余应力的影响
[J].
On the mechanics of residual stresses in girth welds
[J].