中子辐照条件下，Fe-Cr合金中可生成嬗变气体He、辐照空位和间隙原子等缺陷及缺陷团簇^[1,2]。由于气体原子在固体中的溶解度极低，因此，在气体易扩散的较高温度，气体易与空位结合形成气泡。气泡会导致核材料发生尺寸变化、肿胀效应及脆性断裂，影响反应堆的长期服役安全^[3~5]。因此，理解气泡的形成和演化对材料的肿胀和辐照性能的影响，对Fe-Cr合金设计具有重要意义。

辐照过程中观察到的气泡根据形态和位置主要分为2种：晶内气泡和晶间气泡。晶内气泡均匀分布于晶粒内部，尺寸较小(纳米量级)；晶间气泡位于晶界，通常尺寸较大(微米量级)，对材料的肿胀影响较大^[6~8]。Millett等^[6]和Aagesen等^[7]研究了晶界裂变气泡的演化，发现基体中产生的裂变产物通过扩散输运到晶界，气泡在晶界或三叉晶界处形核长大并相互连通，形成气泡渗透网络与燃料表面连接，从而将裂变气体释放。裂变气体的释放降低了燃料和包壳空隙的导热性，导致燃料内部温度升高，压力增加，加速包壳性能的降低。对于特殊的气泡——He泡，是由于嬗变反应产生的He气与空位团簇结合而产生。He泡的存在会导致金属材料的韧-脆转变温度显著升高，使材料的塑性降低，即高温氦脆^[9]。然而，目前应对高温氦脆的有效措施还很少，是核反应堆结构材料面临的巨大挑战。近年来研究^[10,11]表明，He团簇扩散系数随着温度的降低和Cr浓度的增加而减小，因此Cr元素的添加可能会一定程度上抑制He泡的形成，增强材料的抗辐照性能，缓解材料的塑性损失。因此，建立特定材料性质的气泡微观结构的演化模型，可以更好地理解气泡演化对性能的影响。有诸多学者对辐照过程中缺陷和裂变气体的输运特性进行了研究，其中包括团簇动力学(速率理论)^[12]和动力学Monte Carlo以及相场模拟^[13~15]等方法。团簇动力学可以研究团簇浓度随时间的演化，但是无法获得材料微观结构与空间的相关性；动力学Monte Carlo克服了分子动力学时间的限制，但必须提前预知模拟系统的演化速率。相场模拟采用空间连续和时间相关的相场变量来描述介观尺度的微观结构，采用扩散界面模型来描述微观界面，求解时避免了对微观结构演化时界面的显性追踪，对于复杂的微观结构形态不需要先验假设，因此被广泛用于研究辐照过程中缺陷和气泡的演化^[16~18]。

本工作基于辐照条件下气泡的物理现象，采用相场法模拟了辐照环境下裂变产物引起的气泡微观结构演化。首先研究了单个气泡的形核与长大过程，然后分别考虑了材料成分(Cr含量)和位错应力场对气泡动力学演化的影响，揭示了气泡形核生长过程中的演化行为。该模型可以进一步扩展到研究温度、辐照剂量及气体重溶对气泡演化的影响。

相场法可以方便地处理无势垒的形核问题，如有序化转变、相分离及缺陷处的非均匀形核等。本工作借鉴了非均匀形核和相分离这2种思想对气泡的形成进行描述。对于单个气泡的演化，在模拟体系中预置一个空位团簇来实现气泡的非均匀形核，而对于多个气泡的演化，由于空位和气体原子过饱和，其浓度远远高于2者在基体中的溶解度，采用热起伏实现均匀形核。

气体在基体中的溶解度较低，空位团簇吸收空位和气体原子长大形成气泡。因而，采用气体浓度(C_g)和空位浓度(C_v)来描述气泡的演化，该模型包括2相：固溶有过饱和点缺陷(空位、气体原子)的基体相、由空位和气体原子簇聚形成的气泡相。在整个模拟体系中，C_v(r, t)和C_g(r, t)在时间(t)和空间(r，r为空间位置)上连续变化。本工作旨在研究气泡的演化过程，假设Fe-Cr合金为均一的固溶基体，将模拟体系中的各相和界面的自由能表示为总自由能泛函(F)^[19]：

式中，f(C_v, C_g)为体系的化学自由能密度，f^elast为弹性能密度，V为模拟单元的体积；后2项为梯度项，表示界面能的贡献，κ_v和κ_g分别为空位和气体原子的梯度能因子。

由于实际辐照体系的复杂性，想要精确地计算体系的化学自由能是十分困难的。因而，通过体系中各相的热力学平衡特点来构造化学自由能。参考Hu等^[19]给出的自由能形式，假设空位和气体原子在基体中的溶解度很低，并且2者存在很强的结合力。气泡中空位平衡浓度为Cveq = 1，气体原子平衡浓度由Van der Waals气体状态方程决定。f(C_v, C_g)由下式给出：

式中，f_v、f_g、b₃、b₂、b₁、b₀均为常数；Cg0和Cv0分别为气体原子和空位在基体中的溶解度。f_b由气泡相和基体相的平衡性质决定，如平衡浓度、平衡浓度下的自由能以及气泡的成核势垒等。本工作中，气泡相的平衡性质参考了文献[19~21]中He气相的状态方程和化学自由能。

由于空位、气体原子、位错等微观缺陷处的局域不均匀性，在缺陷处形成本征应力-应变场，其弹性相互作用会影响空位和气体原子的分布。采用无应力应变概念描述沿位错的局部晶格失配^[22,23]，由此产生的弹性相互作用是空位和气体原子迁移的驱动力之一。f^elast为：

式中，C_ijkl 是与位置相关的弹性张量；εijel和εklel为弹性应变分量，εijel=εij-εij*，其中ε_ij 为总应变，εij*为本征应变。该模型的本征应变由4部分组成：空位引起的本征应变(εijvac)、气体原子引起的本征应变(εijgas)、位错引起的本征应变(εijdis)和气泡引起的本征应变(εijbub)，εij*=εijvac+εijgas+εijbub+εijdis。本征应变与空位和气体原子引起的晶格失配有关，即εijvac=εvac0Cvδij和εijgas=εgas0Cgδij，其中εvac0和εgas0分别表示由空位和气体原子引起晶格参数的膨胀系数，δ_ij 为Kronecker-Delta函数。假设无应力晶格参数(a)随空位浓度的变化遵循Vegard定律。利用Van der Waals气体状态方程描述气泡内部气体压力与气体原子浓度之间的关系，进而定义气泡内部的本征应变，εijbub=(P-2γsR)/C11，其中P为气泡内压力，C₁₁为基体的弹性常数，γ_s为表面张力，R为气泡半径。

通过本征应变考虑了位错对弹性能的贡献，位错引起的本征应变表示为^[24]：

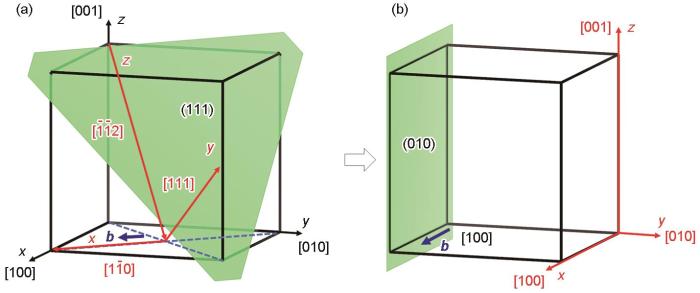
式中，b_i 和n_j 分别为滑移面的Burgers向量和法向量的分量，d为滑移面的面间距。在(111)滑移面上引入一对位错偶极子(由2个刃型位错构成)，分别取晶体的[11¯0]、[111]、[1¯_{1¯2]方向为模型的x、y、z轴，插入(111)平面上的刃型位错的Burgers矢量为b=a02[11¯0]，其中a0为晶格常数。在新坐标系下位错所在平面变为(010)，Burgers矢量方向变为[100]，如图1所示。}

由于弹性模量和本征应变与组分和位置的相关性，演化方程完全耦合了力学平衡方程的解：

式中，σ_ij 为作用在j面上的第i个应力分量，x_i 表示位置。

空位浓度场和气体原子浓度场随时间和空间演化的动力学方程由Cahn-Hilliard方程描述，可表示为：

式中，M_v和M_g分别为空位和气体原子的迁移率，本工作中假设不考虑同一成分的基体中空位和气体原子的迁移率差异；g˙v(r, t)和g˙g(r, t)分别表示空位和气体原子的产生率，ζ_v(r, t)和ζ_g(r, t)分别表示空位和气体原子的热涨落随机项。而对于不同Cr含量的基体，其迁移率可通过迁移能与成分之间的关系来区分。空位和气体原子的迁移率可由扩散系数(D_i )表示为：

式中，T为温度，k_B为Boltzmann常数，D₀为扩散常数，Eim表示空位和气体原子的迁移能。

空位的迁移不仅涉及跳跃原子的位移，还涉及与空位和跳跃原子最临近的其他原子的协调运动。这种协调运动可以看作是一种特殊的应变波动， Flynn^[25]基于这一行为推导了Eim的经验公式：

式中，C₁₂、C₄₄为均一基体的弹性模量，基体弹性模量随Fe、Cr浓度的变化遵循Vegard定律；χ为经验常数，在fcc结构中为0.022。

式中，g˙i0=0.01(i=v,g)；C_v(r, t) = 1 (即气泡相)处点缺陷产生速率为0。

采用半隐式Fourier谱方法对浓度场的演化方程进行求解。时间步长为Δt，第n + 1步迭代格式为：

式中，{C_i }kn为第n步迭代，{} _k 表示变换到Fourier空间，k=k12+k22， k= (k₁, k₂)为Fourier空间矢量。

考虑特征长度(l₀)和特征时间(t₀)，采用以下形式对模型中的各参数进行无量纲化处理：

式中，带星号的符号为各参数的无量纲量。

模拟区域大小为256 × 256网格点，边界条件为周期性边界条件。当模拟单个气泡的演化时，将单一的圆形空位团簇植入含空位和气体原子的基体中，基体中空位和气体原子浓度均为6.69 × 10^-4。由于间隙原子的扩散速率远大于空位，本工作假设间隙原子对气泡演化的影响较小，由于空位和间隙原子复合引起的空位浓度变化可以忽略不计。本工作中所使用的参数如表1所示。

首先以不含Cr的纯Fe为例，研究了持续辐照条件下无溶质和应力场影响下的气泡生长过程，这种条件下空位缺陷团簇捕获空位和气体，可作为气泡的非均质形核位置。通过在演化方程中引入辐照产生项使基体中持续产生空位和气体原子，来描述持续辐照过程。图2a1~a3和图2b1~b3分别为空位和气体原子浓度场演化结果。空位团簇作为非均匀形核位点，吸收周边空位和气体形核长大，气体原子填充空位团簇形成气泡。在演化初期，气体原子在空位团簇周围聚集，沿气泡内表面扩散，气泡中的气体浓度迅速增加。当气泡中气体浓度达到平衡浓度，气体压力和空洞弹性应力达到相对平衡。平衡气体浓度的情况下气泡持续吸收空位和气体长大。

图2c1~c3为不同演化时间下空位和气体浓度沿气泡横截面中心线的分布。空位团簇作为气泡的异质形核位置，随着演化时间的延长，气泡内气体浓度增加，当演化时间达到2500t₀时，气体浓度达到平衡值且不再增加。对于半径为R的气泡，气泡内的气体平衡浓度可以通过气体状态方程求得。在此过程中假设气泡的内部压力与表面张力平衡，此时P = 2γ_s / R。Van der Waals状态方程可用于真实气体气泡的近似，基于该方程可得：

式中，cgeb为气泡中的气体平衡浓度，与R、T、P、γ_s及Van der Waals常数b相关；Ω为基体原子的体积。依据上式可得，在一定温度下，当气泡内的压力与表面张力平衡且为恒定值时，气泡内的平衡浓度将保持不变。因此气泡内气体平衡浓度趋于稳定值是与Van der Waals状态方程的推导^[14,26]是一致的。事实上，气泡的演化与气泡中气体原子的数量及气泡的半径密切相关，且存在临界气泡半径和临界气体含量。临界气泡是包含一定数量空位和气体原子的团簇，并且属于体系中的最低自由能构型，此时空位和气体的加入均会引起体系能量的升高。当气泡内气体含量大于临界气体含量时，气泡会不断吸引空位长大。而当气泡内气体含量小于临界气体含量，并且气泡的半径大于临界气泡半径时，此时气泡通过向基体中发射空位使半径缩小。本工作通过引入辐照产生项，在基体中不断引入空位和气体原子，使气泡内的气体含量大于临界值，从而使气泡持续生长，未出现缩小的现象。

气泡的演化也可以表现为空位和气体原子的弹性相互作用。空位的本征应变为负值，气体原子的本征应变为正值。当气泡的本征应变为正值时，通过弹性相互作用吸引空位并排斥气体原子，而气泡的本征应变为负值时，则吸引气体原子排斥空位。如果气泡的本征应变为零，则气泡对空位和气体原子的弹性效应为中性。图2d1~d3所示为气泡演化时间为10t₀时的应力场分布，σ_xx 和σ_yy 为气泡的正应力，σ_xy 为切应力。气泡内部应力为正，外部应力为负，此时气泡的压力大于气泡的平衡压力，气泡处于非平衡状态，气泡倾向于吸引更多的空位而长大来缓解这种状态。因此，通过吸收空位和气体原子而长大，期间气泡内的气体浓度趋于稳定，达到临界尺寸后，会转变为欠压空洞。当气体吸收达到稳定极限时，气泡通过空位吸收开始长大，此时气泡呈现出空洞的性质，该规律与气泡的临界生长模型^[27,28]相一致。

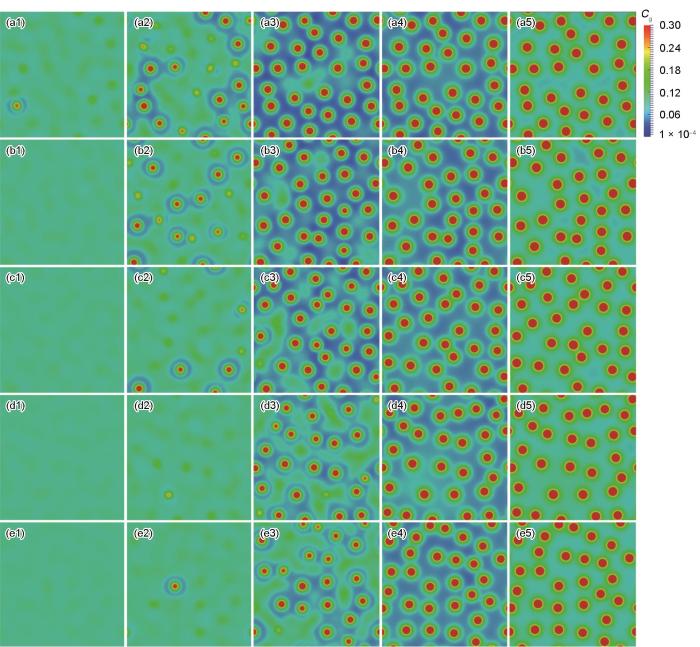
选择不同Cr含量的合金成分，Fe-0Cr、Fe-3Cr、Fe-7Cr、Fe-11Cr和Fe-13Cr (质量分数，%)，模拟辐照条件下气泡的演化。在模型中引入空位与气体原子浓度的随机扰动，模拟基体中气泡的随机形核与长大。由于空位和气体原子协同演化，因此模拟演化统一采用气体原子浓度表征，其演化结果如图3所示。

对比不同Cr含量合金中的气泡演化过程发现，Fe-0Cr合金中的气泡最先形核，在演化时间为1400t₀时即有气泡析出。随着Cr浓度的提高，气泡的形核孕育时间延长，Cr浓度越高，气泡析出越滞后。在演化时间为5000t₀时所有合金都形成了大量均匀分布的球形气泡。在相同的温度和空位、气体产生速率条件下，Fe-0Cr合金的形核孕育时间最短，长大最快。Cr浓度的增加，一定程度上延缓了气泡的形核，该延缓作用与Cr浓度增加影响了空位和气体原子的扩散有关。

依据 式(10)，扩散迁移能与平衡晶格常数有关，溶质Cr和溶剂Fe的固溶体相晶格常数可依据Vegard定律确定，Fe-Cr固溶体晶格常数既与两组元晶格常数差有关又与2者组分有关。图4给出了不同Cr含量合金中空位迁移能和扩散系数及晶格常数的变化。随Cr含量增加，迁移能提高，空位和气体原子扩散系数下降，迁移速率降低，延缓了气泡的形核。Cr的添加还表现出对气体原子或气体-空位团簇的束缚作用^[29]，气体原子或气体-空位的迁移率降低，一定程度上抑制了气泡的长大和粗化。然而，由于Cr与Fe原子半径相近(Cr：0.118 nm，Fe：0.117 nm)，因而固溶体晶格常数随组分变化较小，Cr浓度的提升对抑制或延缓气泡形核的能力有限。

进一步对不同Cr含量合金中气泡的面积分数和平均半径进行了统计，如图5所示。可见，形核孕育期随Cr含量增加而延长，孕育期后，形成大量稳定的气泡核心，不同Cr含量合金中，随演化时间增加气泡面积分数和平均半径都迅速增加。气泡达到一定尺寸后，生长速率逐渐变得缓慢。随着Cr含量的增加，气泡的面积分数和平均半径略有减小，各合金的气泡尺寸相差不大，高低Cr含量合金中的气泡均未严重粗化。

非均质形核是固相材料相变形核的主要形核机制，因而表面、晶界、相界的表面能或位错核心的弹性应变能易于诱导特定溶质在此处优先聚集，成为择优形核位点。在低燃耗情况下，表/界面通常作为空位和气体的阱，气体和空位在阱处湮灭。位错容纳空位和气体缺陷能力有限，晶内位错处的空位和气体短程扩散即可簇聚，因而易于形核长大。位错偶极子构型稳定，是晶内常见的位错组态，因而本工作通过引入位错偶极子应力场，考察非均质形核下空洞和气泡的协同演化规律。

在气泡演化的相场模型中引入如图6a所示位置的位错偶极子，其所在的平面为(010)，图6b1~b3分别为位错偶极子的应力分布，σ₁₁和σ₂₂为正应力，σ₁₂为切应力。由于气体原子和空位只有正应变而无切应变，因此位错应力场的切应力与气体原子和空位无相互作用，只有正应力会产生影响。如图6b1和b2所示σ₁₁和σ₂₂的正应力分布，左边的刃型位错上方应力为正，为拉应力，下方为负，为压应力，而右边的刃型位错的应力分布相反，同时σ₁₁和σ₂₂拉应力场与压应力场分布位置相同，因而σ₁₁和σ₂₂对气体原子和空位的弹性作用是相似的。

图7所示为位错应力作用下Fe-0Cr和Fe-13Cr合金的气泡演化结果。气体原子优先在位错上方聚集，以松弛位错应力场，同时吸引空位。从图7a1~a5和b1~b5可见，气泡优先在拉应力(应力为正)的区域形核，然后沿着位错偶极子周围继续形核。在位错应力场位置形成的气泡优先吸收周围的空位和气体而长大，因而在位错周围一定区域存在空位和气体原子浓度的贫化区。其主要原因是位错应力场与气体原子和空位的弹性相互作用使空位和气体优先在应力场附近聚集，同时应力场导致体系中气体原子和空位浓度非均匀分布，因而表现出优先形核和粗化的差异。位错应力场的引入明显促进了气泡的形核与演化，与未引入应力场的模拟结果相比其形核时间提前了约1000t₀。图7c和d分别为位错应力场作用下Fe-0Cr和Fe-13Cr合金中气泡的面积分数和平均半径。可见，Fe-0Cr合金中气泡面积分数由未引入应力场时的8.1%增加到9.2%，Fe-13Cr合金由7.6%增加到11.4%。对比Fe-0Cr与Fe-13Cr合金中位错偶极子应力场作用下的气泡演化，发现Fe-13Cr合金中气泡的形核时间明显推迟。弹性应变能的引入使体系的驱动力增加，进而驱使空位和气体原子快速迁移演化以释放应变能，气泡形成后由位错产生的应变能被松弛，整个体系的自由能降低。

(1) 建立了持续辐照条件下气泡演化的相场模型，气泡的生长过程实质上是通过吸引空位和气体原子以达到体系的平衡态的过程。气泡可以通过空位团簇与位错非均匀形核，通过吸收空位和气体原子而生长。首先吸收气体原子使气泡中的气体浓度增加，当气泡中气体浓度达到平衡浓度时，气泡主要通过吸收空位来实现自身的生长。在气泡长大的后期，气泡中的空位饱和度很高，气泡的压力低于相同半径气泡的平衡压力，此时气泡表现为空洞的性质。

(2) 气泡的生长动力学与气泡内气体的含量、材料的成分和应力场的作用密切相关， Cr元素的加入会降低气体原子的扩散速率，随着合金中Cr含量的增加，气泡的形核孕育期延长，并一定程度上延缓了气泡的粗化。

(3) 位错应力场的存在将使气泡优先在拉应力区域附近形成，并促进了气泡的形核过程，使材料的力学性能被加速破坏。