钢是含有C、Si、Mn、S、P等元素的合金材料,在钢液凝固过程中,钢中溶质元素在固相和液相之间会重新再分配,在枝晶间富集或消耗,这会导致微米尺度的成分变化,即枝晶间溶质的微观偏析。影响金属枝晶间微观偏析的因素包括溶质元素在固/液界面的平衡分配系数、冷却速率、反扩散强度以及枝晶粗化等,其中固相中溶质元素反扩散强度和枝晶粗化是2个不容忽视的影响因素。部分学者[3~7]对金属凝固过程中溶质微观偏析的影响因素做了研究,例如:徐达鸣等[3]通过建立合金枝晶凝固过程中任意固相反扩散条件下的溶质再分布模型,研究了溶质在枝晶中的反扩散效应与溶质扩散能力、枝晶间距、固相体积分数以及溶质分配系数等物性参数之间的关系;Zhao等[4]建立了Al-Si-Mg合金的微观偏析模型,研究固相反扩散强度对合金凝固路径的影响;冯科等[5]通过建立半解析模型,研究了固相反扩散和枝晶粗化对液相溶质富集的影响;He等[6]通过在凝固过程中施加磁场,研究了枝晶粗化现象对微观偏析的影响;Zhang等[7]采用元胞自动机(CA)模型研究了枝晶粗化过程中局部凝固、界面形状变化以及溶质扩散之间的关系。因此,研究钢液凝固过程中溶质元素的微观偏析行为,需考虑固相反扩散和枝晶粗化对溶质微观偏析的影响。
鉴于此,本工作研究了高强度贝氏体轨道钢的凝固过程,针对该钢的凝固特点,考虑钢液凝固过程中δ/γ相变以及枝晶臂粗化对溶质微观偏析的影响,建立高强度贝氏体轨道钢凝固过程中溶质微观偏析模型,分析冷却速率和溶质含量对凝固过程中溶质元素微观偏析行为、凝固前沿特征温度(ZST、ZDT)的影响规律,研究结果对于高强度贝氏体轨道钢的连铸生产具有重要指导意义。
1 贝氏体轨道钢凝固过程中微观偏析模型建立
1.1 偏析模型建立
式中,CL,i 为凝固前沿平衡液相中溶质元素i的含量,%;C0,i 为钢液中溶质元素i实际初始含量,%;ki 为溶质元素i在固/液界面的平衡分配系数;fS为固相率;βi 为反向扩散系数,βi = 2αi,其中αi 为溶质元素i的凝固参数,表达式为:
式中,DS,i 为溶质元素i在固相中的扩散系数,m2/s;τS为局部凝固时间,s;X为微观偏析的尺寸,m,通常取值为二次枝晶臂间距的一半。τS表达式为:
式中,TL和TS分别为钢的液相线温度和固相线温度,℃;CR为冷却速率,℃/s。
考虑枝晶臂粗化对溶质元素微观偏析的影响,通过增加附加项αC对αi 进行修正,如下式所示[25]:
表1 元素的平衡分配系数、扩散系数和液相线斜率[26]
Table 1
| Element | mi / (oC·%-1) | ||||
|---|---|---|---|---|---|
| C | 0.19 | 0.0127exp(-81382.6 / (RT)) | 0.34 | 0.076exp(-134563.8 / (RT)) | 78.0 |
| Si | 0.77 | 8.0exp(-248959.7 / (RT)) | 0.52 | 0.3exp(-251470.3 / (RT)) | 7.6 |
| Mn | 0.76 | 0.76exp(-224440.3 / (RT)) | 0.78 | 0.055exp(-249378.2 / (RT)) | 4.9 |
| P | 0.23 | 2.9exp(-230130.9 / (RT)) | 0.13 | 0.001exp(-182849.4 / (RT)) | 34.4 |
| S | 0.05 | 4.56exp(-214649.3 / (RT)) | 0.04 | 2.4exp(-223516.8 / (RT)) | 38.0 |
| Cr | 0.95 | 2.4exp(-239796.3 / (RT)) | 0.86 | 0.0012exp(-219000.9 / (RT)) | 1.0 |
| Ni | 0.83 | 1.6exp(-240005.6 / (RT)) | 0.95 | 0.34exp(-282391.5 / (RT)) | 4.7 |
| Mo | 0.80 | 3.47exp(-241386.3 / (RT)) | 0.59 | 0.068exp(-246867.6 / (RT)) | 2.6 |
1.2 二次枝晶臂间距计算
二次枝晶臂间距与冷却速率和合金成分有关,本工作采用Won和Thomas[22]拟合回归得到的计算式:
式中,wC为钢中C元素初始含量,%;L为二次枝晶臂间距,m。
1.3 固相线和液相线温度
TL和不同固相率固/液界面处温度由下式计算[27]:
1.4 铁素体(δ)/奥氏体(γ) 凝固方式
钢液在凝固过程中存在2种相,一种是bcc结构的铁素体相(δ),另一种是fcc结构的奥氏体相(γ)[28]。由于溶质元素在不同相中的凝固参数不同,导致不同凝固方式下溶质元素分配系数存在差异。当钢中C含量(质量分数)介于0.095%~0.53%之间时,钢液先以δ相析出,随着凝固的进行,固相占比逐渐增加,残余液相中的C含量不断富集并超过0.53%时,残余液相将以γ相析出[29]。因此,钢中C含量介于0.095%~0.53%之间时,钢液凝固存在一个凝固方式转变点。为确定此固相率,模型计算起始时钢液以L→δ模式凝固,随固相率增加的同时计算残余液相中C含量,当残余液相中C含量CL,C达到0.53%时,此刻的临界固相率即为凝固方式转变时的固相率,记为
式中,
1.5 固相线温度的迭代
在模型建立过程中,TS是本模型计算的关键,而TS又通过CL,i 确定。本模型采用初始值迭代法来确定贝氏体轨道钢的TS。初始TS由经验公式计算确定,并代入模型计算得到凝固结束时的CL,i,然后通过
式中,C0,M 为元素M的初始含量。
2 偏析模型验证
2.1 枝晶间溶质元素分布
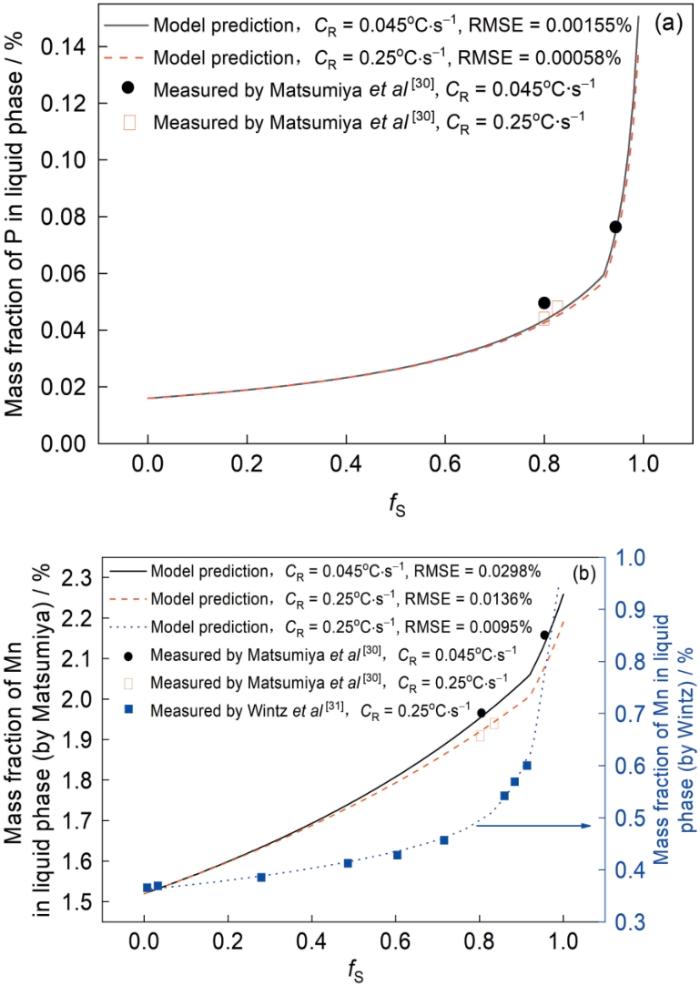
图1
2.2 凝固特征温度
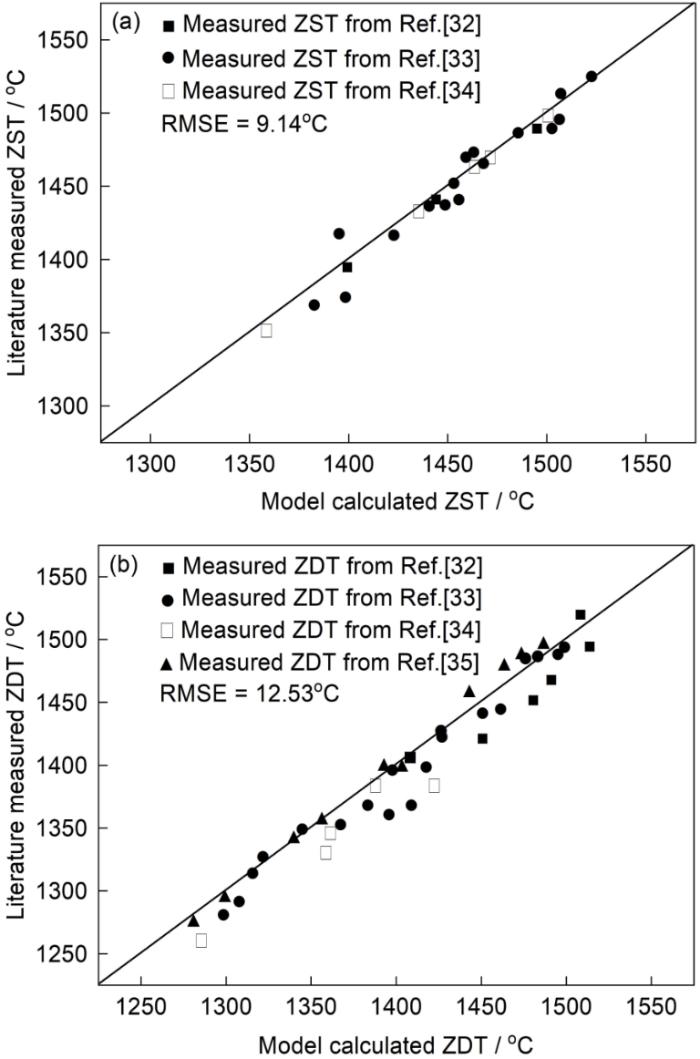
图2
3 计算结果与讨论
3.1 枝晶间溶质元素分布
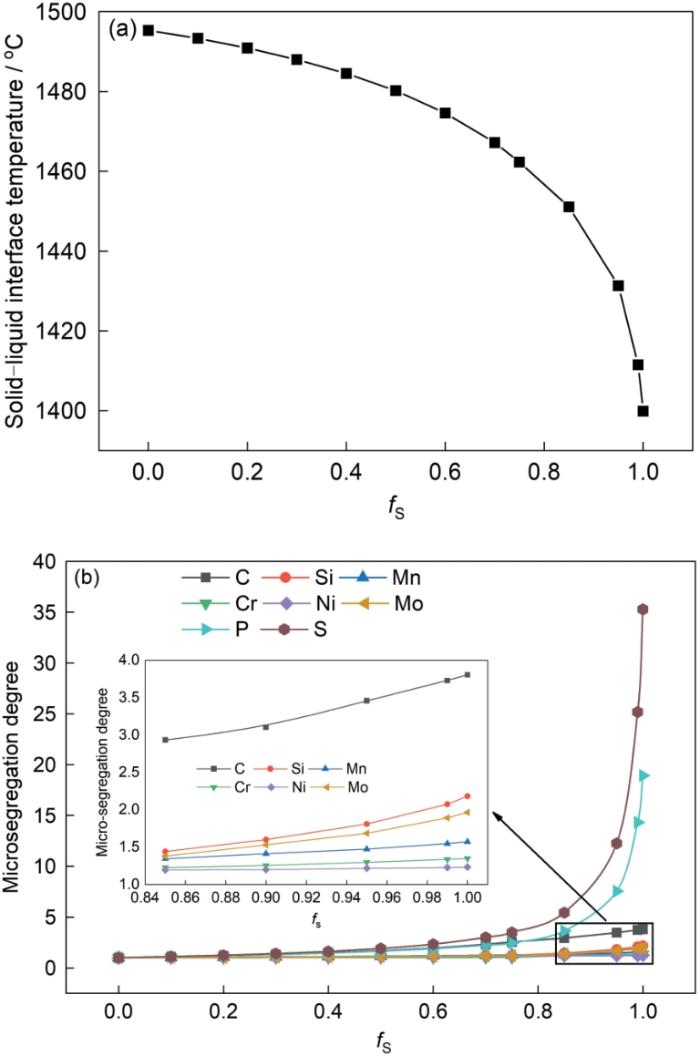
以贝氏体轨道钢为研究对象,其主要化学成分(质量分数)为:C 0.21%,Si 0.9%,Mn 2.29%,P 0.022%,S 0.015%,Cr 0.92%,Ni 0.62%,Mo 0.37%,Fe余量。贝氏体轨道钢采用大方坯生产,钢液凝固过程中采用弱冷,在计算中采用冷速为0.1℃/s。为直观表示溶质元素的偏析程度,采用偏析度(残余液相中元素含量与初始钢液中元素含量之比)来表示凝固过程中溶质元素的偏析情况。由图3a可知,固/液界面处温度随fS增加而呈降低趋势。由图3b可知,贝氏体轨道钢在凝固过程中,S、P、C元素微观偏析较为严重。随着fS的增加,各溶质元素偏析度均有增加。当fS在0~0.75区间内时,各溶质元素微观偏析程度较低。当fS超过0.75以后,各溶质元素偏析度增加更为明显,其中S、P偏析度上升趋势最明显。在凝固末期fS达到1.0时,溶质元素偏析度达到最大,其中,S元素约为35.3,P元素约为18.9,C元素约为3.8,Si等其余元素次之。
图3
图3
凝固过程中固/液界面温度和溶质元素偏析度变化
Fig.3
Changes of solid-liquid interface temperature (a) and segregation degree of solute elements (b) during solidification (Inset in Fig.3b shows the locally enlared curves)
3.2 C元素的影响
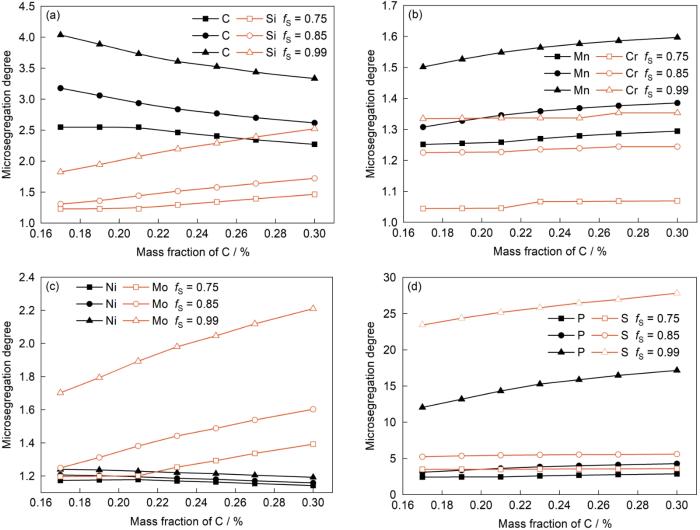
C是钢中的重要元素,其在凝固过程中形成的偏析显著影响钢的性能,因而有必要研究C含量对溶质微观偏析的影响。研究[36~38]表明, 钢的脆性温度区间一般取ZST (fS = 0.75)与ZDT (fS = 0.99)之间的温度区间。因此将铸坯凝固末期作为研究重点,分别取fS为0.75、0.85和0.99时,对各溶质元素的偏析度进行计算。图4为冷却速率为0.1℃/s时不同固相率下C元素含量(其余溶质元素含量保持不变,参照3.1节)对贝氏体轨道钢中各元素在枝晶间微观偏析度的影响。可见,在钢液中初始C含量C0,C相同时,随着fS的增加,各溶质元素偏析度均增加。而当fS相同时,随着C0,C的增加,各溶质元素的微观偏析程度和变化趋势不尽相同。当fS为0.75时,C0,C由0.17%增加到0.21%,各溶质元素偏析度变化趋势较为平稳;在C0,C超过0.21%后,P、S、Si、Mo和Cr元素偏析度呈现上升趋势。这是因为C0,C越高,随着凝固的进行,枝晶间残余液相中C含量越高,使得钢液的凝固方式转变更早进行,P、S、Si、Mo和Cr在γ相中的固溶度远小于在δ相中的固溶度,并且P、S、Si、Mo和Cr在γ/L界面的平衡分配系数(kγ/L)均小于在δ/L界面的平衡分配系数(kδ/L),因此更易富集而导致偏析度增加。当fS为0.99时,随着C0,C的增加,Si、Mn、Cr和Mo元素偏析度均有增加,但始终维持在较低水平;而C0,C对S、P元素影响较大,偏析度上升趋势显著。这是因为随着凝固的进行,C0,C的增加使得钢液的凝固方式转变更早进行,更多残余钢液以γ相析出,而Si、Mn、Cr、Mo、S和P的kγ/L比kδ/L小,且S、P在固/液界面的平衡分配系数(kγ/L和kδ/L)均小于Si、Mn、Cr、Mo的固/液界面的平衡分配系数,所以当fS为0.99时,随着C0,C的增加,Si、Mn、Cr、Mo、S、P的偏析度均有不同程度增加,且S、P的偏析度增加更明显。由图4c可知,随着C0,C的增加,Ni元素偏析度呈现降低趋势。这是由于随着凝固的进行,C0,C的增加使残余钢液更早地以γ相析出,Ni元素的kγ/L大于kδ/L,从而使得钢液凝固溶质再分配过程中Ni元素微观偏析度降低。
图4
图4
不同固相率下C含量对溶质元素微观偏析度的影响
Fig.4
Effects of C content on the microsegregation degree of C and Si (a), Mn and Cr (b), Ni and Mo (c), P and S (d) at different fS
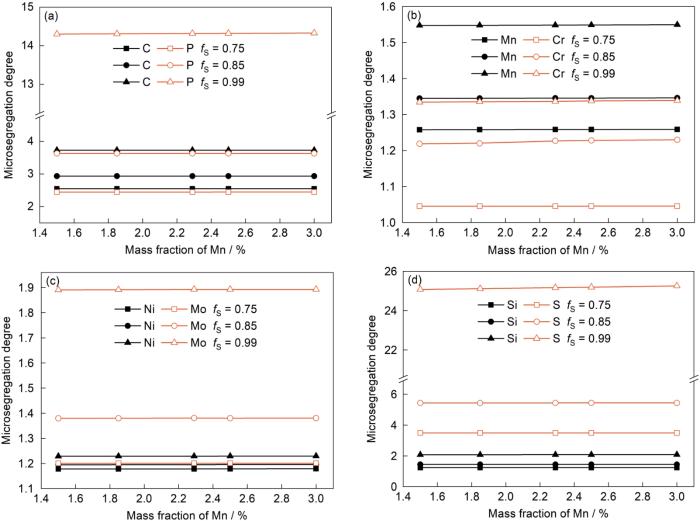
3.3 Mn元素的影响
Mn显著影响贝氏体轨道钢的性能,且是贝氏体轨道钢中易偏析的大原子合金元素,因而控制钢中Mn含量和分布很关键。图5为冷却速率为0.1℃/s,fS分别为0.75、0.85和0.99时Mn元素含量(其余溶质元素含量保持不变,参照3.1节)对贝氏体轨道钢中各元素在枝晶间微观偏析度的影响。可见,在钢液中初始Mn含量C0,Mn相同时,随着fS的增加,各溶质元素偏析度均增加。在fS相同时,随着C0,Mn增加,其余溶质元素偏析度均变化不大。由图5a可知,当fS为0.75时,C元素偏析度稍大于P元素;当fS为0.99时,P元素偏析度明显大于C元素。这是由于C元素的kδ/L小于P元素,而C元素的kγ/L大于P元素。当fS为0.75时,钢液以δ相析出时,C元素偏析度大于P元素;而当fS为0.99时,钢液以γ相析出时,P元素偏析度大于C元素,且该现象与Mn含量无关。
图5
图5
不同固相率下Mn含量对溶质元素微观偏析度的影响
Fig.5
Effects of Mn content on the microsegregation degree of C and P (a), Mn and Cr (b), Ni and Mo (c), Si and S (d) at different fS
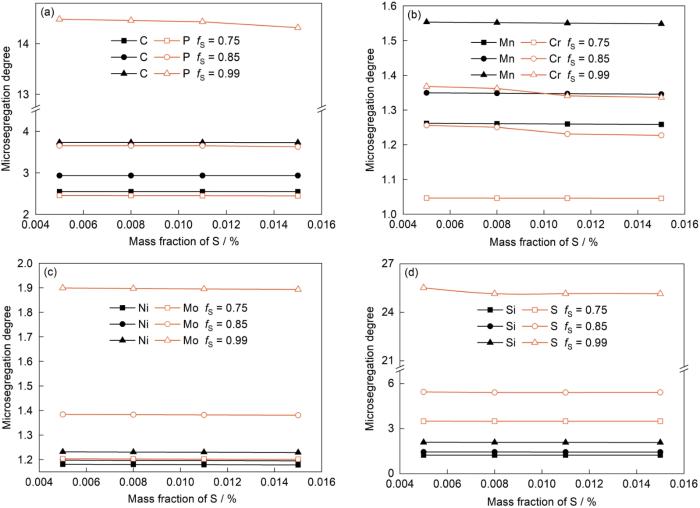
3.4 S元素的影响
在通常情况下S是有害元素,其含量和分布影响钢的热加工性能。图6为冷却速率为0.1℃/s,fS分别为0.75、0.85和0.99时S元素含量(其余溶质元素含量保持不变,参照3.1节)对贝氏体轨道钢中各元素在枝晶间微观偏析度的影响。可见,在钢液中初始S含量C0,S相同时,随着fS的增加,各溶质元素偏析度均增加。当fS相同时,随着C0,S的增加,各溶质元素偏析度变化不大。由图6d可知,当fS为0.99时,C0,S由0.005%增加到0.015%,S元素偏析度有略微降低。这是因为C0,S越高,在凝固末期枝晶间残余液相中S含量越高,因而使得固相线温度降低,凝固温度区间(TL- TS) 增大,钢液凝固时间延长,S元素扩散时间变长,因此S元素偏析度有略微降低。由图6a可知,当fS为0.75时,C元素偏析度稍大于P元素;在固相率为0.99时,P元素偏析度明显大于C元素,具体原因与3.3节所述相同。
图6
图6
不同固相率下S含量对溶质元素微观偏析度的影响
Fig.6
Effects of S content on the microsegregation degree of C and P (a), Mn and Cr (b), Ni and Mo (c), Si and S (d) at different fS
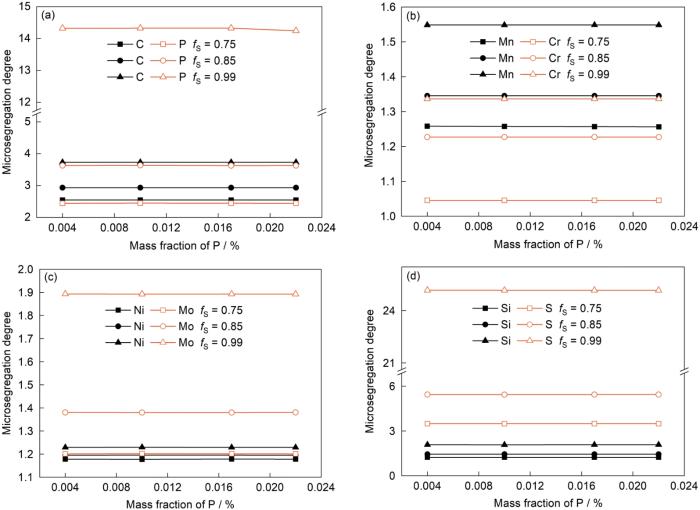
3.5 P元素的影响
P是钢中易偏析元素,有必要研究P含量对钢微观偏析的影响。图7为冷却速率为0.1℃/s,fS分别为0.75、0.85和0.99时P元素含量(其余溶质元素含量保持不变,参照3.1节)对贝氏体轨道钢中各元素在枝晶间微观偏析度的影响。可见,在钢液中初始P含量C0,P相同时,随着fS的增加,各溶质元素偏析度均增加。当fS相同时,随着C0,P的增加,各溶质元素偏析度变化不大。由图7a可知,当fS为0.99时,C0,P由0.004%增加到0.022%,P元素偏析度有略微降低。这是因为C0,P越高,在凝固末期枝晶间残余液相中P含量越高,因而使得固相线温度降低,凝固温度区间(TL- TS) 增大,钢液凝固时间延长,P元素扩散时间变长,因此P元素偏析度有略微降低。由图7a可知,当fS为0.75时,C元素偏析度稍大于P元素;在固相率为0.99时,P元素偏析度明显大于C元素,具体原因与3.3节所述相同。
图7
图7
不同固相率下P含量对溶质元素微观偏析度的影响
Fig.7
Effects of P content on the microsegregation degree of C and P (a), Mn and Cr (b), Ni and Mo (c), Si and S (d) at different fS
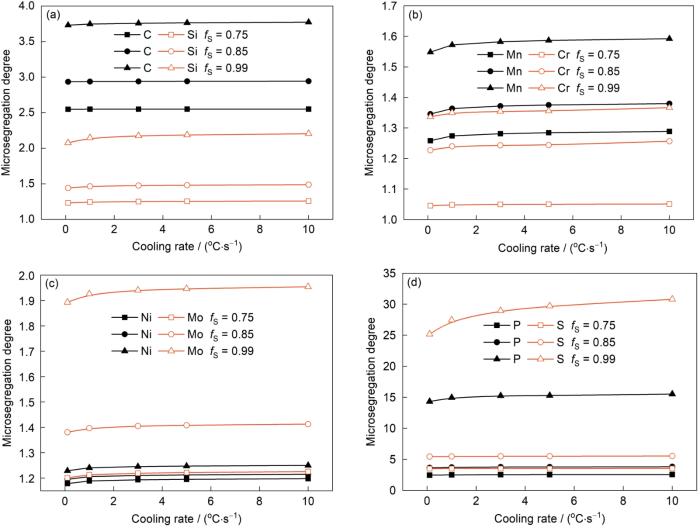
3.6 冷却速率的影响
图8为冷却速率对贝氏体轨道钢在不同固相率时枝晶间溶质元素微观偏析度的影响。可见,在冷却速率相同时,随着fS的增加,各溶质元素偏析度均增加。在不同fS时,随着冷却速率的增加,钢中各溶质元素偏析度变化趋势存在一定差异。当fS为0.75和0.85时,随着冷却速率的增加,C、Si、S和P元素偏析度变化不大,Mn、Cr、Ni和Mo元素偏析度略有增加。当fS为0.99时,随着冷却速率的增加,Si、Mn、Cr、Ni、Mo、P和S元素偏析度均有不同程度的增加。可见,冷却速率对溶质元素微观偏析产生一定影响。这是由于冷却速率的变化会改变二次枝晶臂间距,进而影响溶质扩散的距离;亦会影响凝固时间,进而影响溶质在固相中反扩散时间;此外,还影响αi,进而影响βi。冷却速率的变化使得多种影响溶质微观偏析的因素发生变化,进而影响溶质元素的微观偏析规律。此外,不同溶质元素的固/液界面平衡分配系数和反扩散系数存在差异,使得随着冷却速率的增加,钢中各溶质元素偏析度变化趋势存在一定差异。
图8
图8
不同固相率下冷却速率对溶质元素微观偏析度的影响
Fig.8
Effects of cooling rate on the microsegregation degree of C and Si (a), Mn and Cr (b), Ni and Mo (c), P and S (d) at different fS
3.7 凝固特征温度的变化
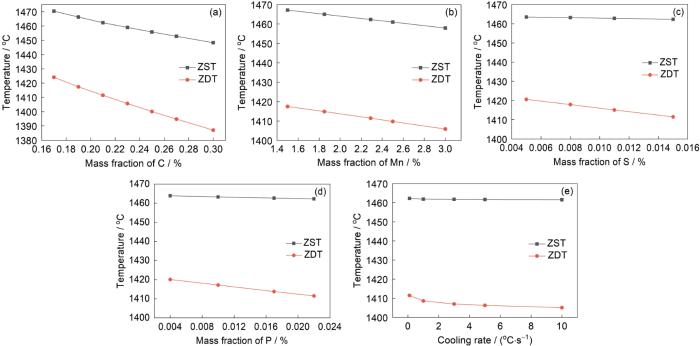
溶质元素微观偏析和钢液冷却强度均影响钢的凝固前沿特征温度,如图9所示。由图9a和b可知,随着C、Mn含量的增加,ZST和ZDT均有明显降低。其中Mn含量变化对ZST和ZDT影响差别不大,而C含量变化对ZDT影响大于ZST。由图9c和d可知,随着P、S含量的增加,ZST变化不大,而ZDT有明显降低趋势。从图6d可以看出,当fS为0.99时,虽然初始S含量越高,会使得其最终偏析度略有降低。但是初始S含量越高,凝固末期枝晶间残余液相中S富集量也更高,故导致ZDT降低趋势更为显著。P元素对特征温度的影响原因与S元素同理。由图9e可知,随着冷却速率的增加,ZST变化不大,ZDT呈现明显降低趋势。这是因为冷却速率对钢凝固末期溶质元素微观偏析影响更显著,随着冷速的增加,S、P等元素微观偏析加剧,在凝固末期易形成低熔点化合物,从而造成ZDT降低。
图9
图9
溶质元素含量和冷却速率对凝固特征温度的影响
Fig.9
Effects of C content (a), Mn content (b), S content (c), P content (d), and cooling rate (e) on solidification characteristic temperatures
4 结论
(1) 考虑钢液凝固过程中δ/γ相变和枝晶粗化的影响,建立了贝氏体轨道钢连铸凝固过程中的溶质微观偏析模型,并验证了其准确性。利用该模型的模拟结果分析了溶质元素含量和冷却速率对溶质微观偏析、凝固前沿特征温度(ZST和ZDT)的影响。
(2) 贝氏体轨道钢凝固过程中S、P元素微观偏析较为严重,C、Si等元素次之。在固相率为0.99时,随着S、P元素含量增加,其微观偏析度略有降低。
(3) 钢中C元素含量对其余溶质元素的微观偏析影响显著,它主要是通过影响钢的凝固方式进而影响溶质微观偏析。S、P元素微观偏析受C含量和冷却速率影响明显,其余元素影响较小;而Mn、P和S元素含量对其余溶质元素微观偏析影响不大。当固相率不同时,冷却速率对溶质元素微观偏析的影响存在一定差异;当固相率为0.99时,随冷却速率增加,Si、Mn、Cr、Ni、Mo、P和S元素偏析度均有不同程度的增加。
(4) C、Mn元素含量的增加使ZST和ZDT均降低,C元素含量对ZDT的影响大于ZST,Mn元素含量对ZST和ZDT影响的差别不大;随冷却速率、P和S元素含量增加,ZST变化不大,ZDT明显降低。
参考文献
Research progress of bainitic steel used for railway crossing
[J].
铁路辙叉用贝氏体钢研究进展
[J].
Current development situation of bainitic rails at home and abroad
[J].
国内外贝氏体钢轨的研发现状
[J].
Micro-/macro-scopic modeling of solutal mass transport in dendrite solidification with partial solid back diffusion
[J].
任意固相反扩散条件下枝晶凝固溶质传输微观/宏观模型化
[J].通过对合金枝晶凝固中有任意固相反扩散条件下微观溶质再分布的模型化,扩展了作者提出的合金凝固传输及宏观偏析连续介质模型本文微观/宏观统一模型提出的归一化固相反扩散集合参数除了包括合金的团相扩散系数外,还包含了生长枝晶尺度及几何形态参数、凝固速率和溶质分配系数等影响因素模型的数值计算结果表明,在相同的凝固条件下不同的合金固相扩散能力可对其铸锭的宏观偏析行为产生明显的影响
Influences of initial compositions, dendrite morphologies and solid-back diffusion on solidification path of Al-Si-Mg alloys
[J].
The microsegregation mathematical model for binary alloy based on coarsening and back-diffusion
[J].
基于枝晶粗化和反向扩散的二元合金微观偏析数学模型
[J].
Enhanced dendrite coarsening and microsegregation in Al-Cu alloy under a steady magnetic field
[J].
Interaction of local solidification and remelting during dendrite coarsening—Modeling and comparison with experiments
[J].
A transient simulation and dynamic spray cooling control model for continuous steel casting
[J].
Optimal control of secondary cooling for medium thickness slab continuous casting
[J].
Study on a mathematical model of microsegregation in continuously cast slab
[J].
连铸坯中微观偏析的模型研究
[J].对导致连铸坯中内裂纹形成的微观偏析进行了模型研究, 模型中考虑了铁素体(δ)凝固向奥氏体(γ)凝固的转化以及MnS的析出, 讨论了钢中C, Mn, S和P对凝固过程中晶间偏析、零强度温度(ZST)、零塑性温度(ZDT)的影响, 结果表明, 钢中碳含量对凝固前支晶间的微的有显著影响, 碳含量在0.1%~0.2%之间, P的偏析显著增加, S的偏析由于受到Mn的掏而随碳含量变化不大.
Analysis of surface and internal cracks in continuously cast beam blank
[J].
Effect of carbon and sulfur in continuously cast strand on longitudinal surface cracks
[J].
Critical strain for internal crack formation in continuous casting
[J].
Effects of deformation on the microstructures and mechanical properties of carbide-free bainitic steel for railway crossing and its hydrogen embrittlement characteristics
[J].
A novel bainitic steel comparable to maraging steel in mechanical properties
[J].
Research on heat treatment of bainitic steel crossing
[J].A comparison study is performed on the heat-treatment processes of a new bainitic steel containing Al used for railway crossing. Microstructures and properties obtained by air cooling, fast cooling before bainite transformation starting temperature (BS) followed by air cooling and isothermal quenching are analyzed. Results show that the microstructure obtained by isothermal quenching is the finest and possesses the best comprehensive properties. However, higher production cost is caused by isothermal quenching and it is not available in actual production limited by the large size of railway crossing. Based on the character of isothermal quenching process, a three-step cooling method is designed, which consists of fast cooling before BS point, then slow cooling in furnace between BS and martensite transformation starting temperature (MS) and eventually followed by air cooling. It is found that the microstructure, strength and toughness obtained by the three-step cooling method are almost the same as that of isothermal quenching. The cooling curves of the bulk samples close to the actual size of rail crossing under different cooling ways are measured and find that oil cooling can achieve the required cooling rate and easy to realize in actual production.
贝氏体钢辙叉热处理工艺研究
[J].
Effects of tempering on the microstructure and properties of a high-strength bainite rail steel with good toughness
[J].
Variation law of typical inclusions in bainitic steel production process
[J].
贝氏体钢生产流程中典型夹杂物变化规律
[J].
Prediction on the spatial distribution of the composition of inclusions in a heavy rail steel continuous casting bloom
[J].
Microscale experimental and modeling wear studies of rail steels
[J].
Corrosion behavior of multiphase bainitic rail steels
[J].
Simple model of microsegregation during solidification of steels
[J].
Mathematical analysis of solute redistribution during solidification with diffusion in solid phase
[J].
Solute redistribution during solidification with rapid solid state diffusion
[J].
A unified model of microsegregation and coarsening
[J].
Study on solute microsegregation model inmushy zone during continuous casting
[J].
钢连铸过程中两相区溶质微观偏析模型研究
[J].
Research on internal crack susceptibility of continuous-casting bloom based on micro-segregation model
[J].The solidification and cooling of liquid steel in continuous casting process is a complicated non-equilibrium phenomenon. During steel solidification process, the micro-segregation of solute elements between liquid steel and solidified shell will vary with their temperature-dependent diffusion coefficients and equilibrium distribution coefficients. Due to non-uniform cooling pattern in the continuous casting process of steel blooms, the fluctuation of cooling rate in bloom will have a great influence on micro-segregation degree of the elements. The micro-segregation behavior of solute elements in steel solidification process is responsible for the variation of characteristic temperatures such as zero strength temperature (ZST), zero ductility temperature (ZDT) and liquid impenetrable temperature (LIT), which make up the brittle temperature range in steel solidification. During continuous casting process of steel, internal cracks created by thermal and mechanical deformation tend to occur in this range. To prevent the occurrence of these cracks in continuous casting bloom, it is essential to better understand about the internal crack susceptibility concerning micro-segregation behavior in the non-uniform cooling process. In this work, a micro-segregation analytical model for YQ450NQR1 steel continuous casting bloom is established to study the inter-dendritic segregation behavior of main solute elements C, Si, Mn, P and S at various cooling rates, the results show that P and S are more likely to segregate compared with C, Si and Mn and the increase of cooling rate weakens the micro-segregation degree of C, Si, Mn, P and S. Based on the micro-segregation model established above, ZST, ZDT and LIT for YQ450NQR1 steel are calculated and the influences of cooling rate on ZST, ZDT and LIT are analyzed. It reveals that ZST, ZDT and LIT of YQ450NQR1 steel bloom decrease accordingly with the increase of cooling rate. On this basis, the index of internal crack susceptibility (IICS) is defined to quantitatively characterize the internal crack susceptibility of the bloom. The results show that the internal crack susceptibility becomes larger while the IICS value approaches to 1. Furthermore, an internal crack susceptibility model is obtained concerning IICS and cooling rate (CR) and the validation is performed to certify the model′s suitability in quantitatively predicting internal crack susceptibility of YQ450NQR1 steel continuous casting bloom in the non-uniform cooling process.
基于微观偏析模型的连铸方坯内裂纹敏感性研究
[J].
Variation of equilibrium partition coefficient of solutes in steel 45 during solidification and phase transformation
[J].
45钢凝固相变过程中溶质平衡分配系数的变化
[J].以45钢为研究对象,建立了多元凝固体系溶质平衡分配系数的热力学计算模型,利用FactSage Equilib模块计算得到了45钢凝固相变过程以及各溶质分配系数的变化。结果表明:45钢凝固路径先后经过L- δ、L- γ固- 液两相区,MnS在固相中析出;依据相区间和温度的变化,回归得到了45钢中溶质C、Si、Mn、P、S平衡分配系数变化公式;溶质C、Si、Mn、P、S平均平衡分配系数分别为0307、0737、0695、018、0021,其中S偏析趋势最强烈,P次之,C偏析趋势较P小,Si和Mn基本相当,偏析较小。
A microsegregation model in the two-phase region of an ND steel continuous casting billet
[J].
ND钢连铸坯两相区内的微观偏析模型
[J].
Mathematical analysis of segregations in continuously-cast slabs
[J].
Experimental study and modeling of the precipitation of non-metallic inclusions during solidification of steel
[J].
Mechanical behavior of carbon steels in the temperature range of mushy zone
[J].
Influence of the carbon content of 0.015 to 1% and of the structure on the high-temperature strength and toughness behavior of structural steels after solidification from the melt
[J].
Hot ductility and strength of strand cast steels up to their melting points [C]. Open Hearth Proceedings
[A].
Chemistry effects on the crack susceptibility of structural steels during continuous casting
[J].
Microsegregation of solute elements in solidifying mushy zone of steel and its effect on longitudinal surface cracks of continuous casting strand
[J].
钢凝固两相区溶质元素的微观偏析及其对连铸坯表面纵裂纹的影响
[J].以Ueshima的正六边形横断面枝晶模型为原型, 采用有限差分方法建立了钢凝固过程伴随δ/γ相变的两相区溶质微观偏析模型, 确立了在冷却速率为10 ℃/s非平衡凝固条件下钢的脆性温度区间, 研究分析了各溶质元素在该温度区内的偏析特点及对脆性温度区间Δθ<sub>B</sub>与热应变的影响规律, 定量计算了不同P, S含量下脆性温度区热应变随C含量的变化规律, 揭示了P, S含量的增加使连铸坯出现表面纵裂纹几率提高的机理.
Influence of solute segregation on crack susceptibility at solidification front of continuous casting strand
[J].
溶质偏析对连铸坯凝固前沿裂纹敏感性影响的研究
[J].