蠕变是指材料在低于屈服强度的应力作用下,其应变随时间而不断增加的流动塑性变形现象,会导致材料变形并最终失效。过去学界认为蠕变主要发生在高温环境中,随着对金属材料研究的不断深入,在中低温也发现了许多金属材料的蠕变现象。随着各国对核电站效率的提升和安全性要求的提高,近年来学界对锆合金的蠕变现象越发重视,在实验探究和计算机模拟研究方面都进行了许多工作。目前在实验研究中主要采用单轴拉伸或者纳米压痕等方法对Zr及锆合金进行蠕变机理的研究。Guguloth等[8,9]研究了Zr-2.5Nb合金的拉伸蠕变行为,认为蠕变速率主要受扩散导致的位错攀移的影响,而β-(Nb, Zr)析出物起到了提高材料抗蠕变性能的作用。Kozar等[10]对Zr-2合金进行了反应堆内的监测蠕变实验,认为在各应力区间会分别激活不同的蠕变机制,并且认为这一结论与Nichols[11]提出的蠕变理论相吻合。在实验研究的同时,还有许多学者采用计算模拟的方法研究锆合金的蠕变行为。汪秉忠等[12]利用有限元方法模拟了锆合金包壳材料的堆内行为,发现锆合金在反应堆内的蠕变现象会使锆管与燃料芯的接触区和非接触区之间的静水应力增加,改变应力分布的规律并增加氢化物析出的可能性,从而使锆合金材料的使用寿命降低。在失水事故等非正常运行情况下,锆合金包壳的蠕变性能对后续运行寿命和安全性更为重要,一方面长寿命要求包壳应具有尽可能低的蠕变速率,以减小反应堆运行过程中组件的宏观变形;另一方面,在失水事故过程中的迅速冷却等情况下,还需要包壳具有较大的蠕变速率,来缓解由于温度和压力的突然改变带来的局部应力,以免产生包壳的开裂等问题。因而,不同条件下蠕变的机制和规律的研究具有至关重要的作用。
1 研究方法
采用分子动力学方法对Zr多晶在不同条件下的辐照和蠕变过程进行模拟。首先采用原子建模软件ATOMSK[17]建立了含有约7 × 105万个Zr原子的纳米晶初始模型:借助Voronoi方法在初始模拟盒子内部的随机位置建立α-Zr的晶胞种子并使其按随机方向生长,直到这些晶胞之间相互接触或者晶胞生长到接触模拟盒子的边界。主要的计算模拟工作利用开源的分子动力学计算模拟软件LAMMPS[18]完成。在模拟蠕变过程中采用的势函数为嵌入原子势(embedded atom method,EAM)[19]。该势函数在描述hcp结构α-Zr的层错能和空位激活能等物理性质上与第一原理的计算结果较符合,在各类与α-Zr体系相关的分子动力学模拟研究中得到了较广泛的应用[20~22]。特别地,本工作在辐照模拟阶段,对原EAM势函数的近距离对势部分进行调整,使其能在级联碰撞的模拟中具有更高的准确性。在完成计算模拟工作后,使用OVITO软件[23]对模拟结果进行可视化处理,并利用其分析功能对模拟结果进行研究。
1.1 模型与参数变量
本工作中模拟蠕变过程的主要变量为纳米晶初始模型的晶粒平均尺寸(d)、模拟温度(T)和拉伸蠕变应力(σ),以及不同条件下的辐照等。模拟体系的初始尺寸在XYZ空间坐标系中的3个方向上均为25 nm,因而初始模型的体积为15625 nm3。将体系中的纳米晶粒近似地看作球体,根据不同模型内的晶粒数量(n)并结合球体的体积公式可以计算得到各模型中晶粒的平均尺寸。表1为5种初始纳米晶模型的参数。
表1 初始模型的晶粒数量及晶粒尺寸
Table 1
| Model name | n | d / nm |
|---|---|---|
| M1 | 10 | 14.39 |
| M2 | 20 | 11.43 |
| M3 | 30 | 9.98 |
| M4 | 40 | 9.07 |
| M5 | 50 | 8.42 |
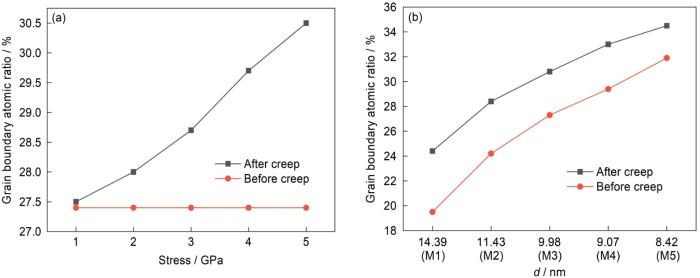
根据核用锆合金的使用温度(573~773 K),并考虑到实际工况下升降温过程的影响,以及某些非正常条件下的参数波动,本工作将蠕变过程的模拟温度设置为373、573及773 K。由于Zr的同素异构转变温度为1136 K,远高于本工作选择的模拟温度范围,因此拉伸蠕变模拟中不涉及α-Zr的同素异构转变现象。为确定合适的蠕变应力条件,对不同晶粒尺寸的纳米晶模型进行单向拉伸加载的预计算,结果如图1所示。根据上述计算,确定对模拟体系施加1~5 GPa的单向拉伸应力较为合理,以便获得比较理想的蠕变效果。另外,级联碰撞阶段的模拟温度设置为100 K,采用的初级碰撞原子(primary knock-on atom,PKA)动能为5 和10 keV,以探究级联过程PKA的能量对蠕变行为的影响。各体系的表示方式记为温度-晶粒尺寸-应力-PKA能量体系。
图1
1.2 计算模拟流程
首先将构造的纳米晶模型利用共轭梯度法(CG)进行能量最小化,然后在等温等容(NVT)系综下弛豫30 ps,以使体系达到均衡状态,最后在等温等压(NPT)系综下对单向拉伸蠕变过程进行模拟:在Z方向上施加恒定的拉应力,而在X和Y方向上不做应力控制。蠕变阶段的模拟持续300 ps,以获得良好的蠕变曲线。蠕变加载期间,每隔1 ps输出一次原子构型用于后续的分析工作。图2为模拟体系拉伸蠕变的示意图。在辐照对蠕变影响的模拟中,首先对经过弛豫的模拟体系进行微正则(NVE)系综下级联碰撞的模拟,并演化足够长的时间(本工作中设置为300 ps)以使体系内部完成一定的辐照积累及演化,之后再于NVT系综下弛豫回设定的温度,进行拉伸蠕变过程的模拟。
图2
图2
拉伸蠕变模拟示意图
Fig.2
Schematic of tensile creep simulation (Different colors represent different grains, F—tensile force)
1.3 EAM势函数的修正
在级联碰撞过程的模拟中,原EAM势函数的对势部分不能正确描述两原子之间距离较近时的相互作用。针对此种情况,对原势函数的近距离对势部分进行了修正,使其能更加合理地模拟级联碰撞阶段。根据EAM势函数的形式,总势能(
式中,
2 结果与讨论
2.1 蠕变曲线特征和影响因素
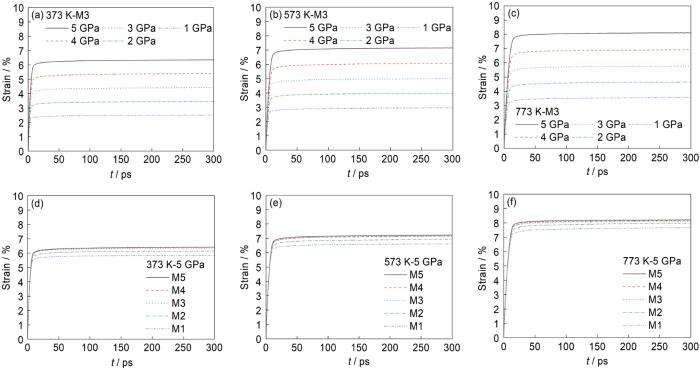
为探究温度、应力以及晶粒尺寸等对纳米晶α-Zr体系蠕变过程的影响,在不同温度下采用1~5 GPa的应力对弛豫后的M1~M5模型进行单轴拉伸蠕变过程的模拟,获得了模拟体系的应变随加载时间的变化曲线,如图3所示。由于在预计算后对应力范围做出了合理选择且模拟时间有限,本工作中的应变-时间曲线中只出现前2个蠕变阶段,即起始蠕变和稳态蠕变阶段,而第三阶段,即加速蠕变阶段并未出现。通过图中曲线斜率可以看出蠕变速率,在起始蠕变阶段中,体系在受到外加应力时产生初始应变响应,而后蠕变速率随着时间的延长不断降低,最终趋于平稳。而在稳态蠕变阶段,蠕变速率基本保持不变,模拟体系以较慢的速率发生塑性变形。本工作主要以纳米晶α-Zr体系的稳态蠕变阶段为研究对象。
图3
图3
不同温度-晶粒尺寸-应力模拟体系的应变-时间曲线
Fig.3
Strain-time curves for systems under different stresses and temperatures (a-c), and for systems with different grain sizes under different temperatures (d-f) (t—time)
2.2 蠕变过程中的微观结构演化
图4
图4
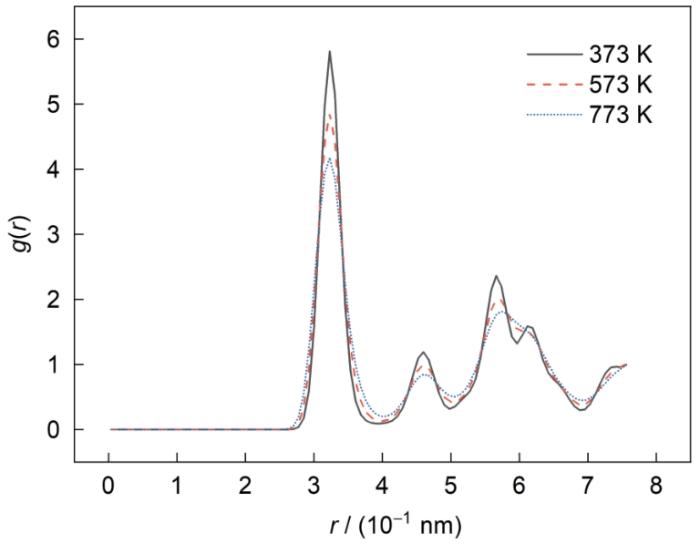
不同温度-M3-5 GPa模拟体系在蠕变终态时的径向分布函数
Fig.4
Radial distribution function (g(r)) curves of different temperature-M3-5 GPa systems at the final state of creep process (r—distarce between two atoms)
图5
图5
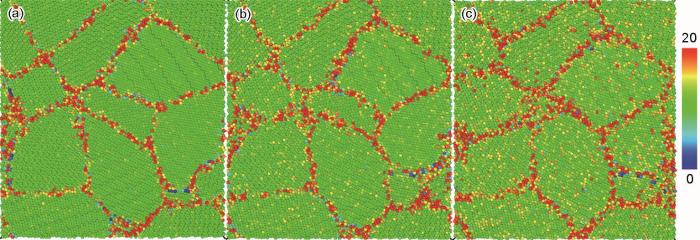
不同温度-M3-5 GPa模拟体系在蠕变终态(300 ps)时的原子快照
Fig.5
Atomic snapshots of different temperature-M3-5 GPa systems at the final state of creep process (300 ps) at 373 K (a), 573 K (b), and 773 K (c) (Colored by centrosymmetry parameter)
径向分布函数的物理意义是对体系中任意位置的粒子,其他粒子在此粒子附近的平均分布几率,因此可以利用RDF来评估原子排布的有序性。RDF曲线上的尖峰表示空间结构有序,展宽的圆形峰表示原子排列趋向无序,因此根据曲线上峰值的波形特征可以判断体系内原子结构有序性的变化。如图4所示,由于hcp结构中近邻及次近邻距离上分布的Zr原子较多,共同形成很高的第1峰,373和573 K时RDF曲线上的特征峰和曲线波动性相似,各主要峰值的高度也比较接近,这表明体系在此温度下蠕变后仍然保持着较为稳定的晶体结构,在蠕变的过程中模拟体系基本有序。而在较高温度下,773 K体系的RDF曲线形态变化较为明显,而且其后续的第2峰和第3峰形态明显变得更小而更宽。另外,随着温度的升高,曲线的第4峰高度降低并逐渐弱化,到773 K时已经近乎消失,这表明随着温度升高和应变的不断增大,体系有序度逐渐降低。
以中心对称参数(centrosymmetry parameter,CSP)的数值分布对各模拟体系的构型进行着色,如图5,以此表示体系内原子排布的有序性。图中绿色表示有序的hcp结构,而红色原子表示偏离有序的晶界区域,因此某区域内颜色越接近红色代表其局部区域原子排布的无序度越强。可以看出,温度为373 K的体系中晶界平直而且稳定,晶粒内部也基本保持着有序的hcp结构,晶体整体的有序结构受蠕变的影响较小。而在573 K时部分晶界出现了较小的变形和偏移,同时晶界粗化,说明蠕变对晶界产生一定影响。晶粒内部出现的少量黄色原子是由于温度升高促进原子振动而引起的偏离平衡位置,此时晶粒内在总体上仍然保持着较为有序的状态。而在图5c所示的773 K,已经发生了明显的晶界移动和晶粒变形,同时晶界粗化显著,晶粒内部也出现较多乱序原子,这表明晶格畸变程度随蠕变温度的升高而加剧。
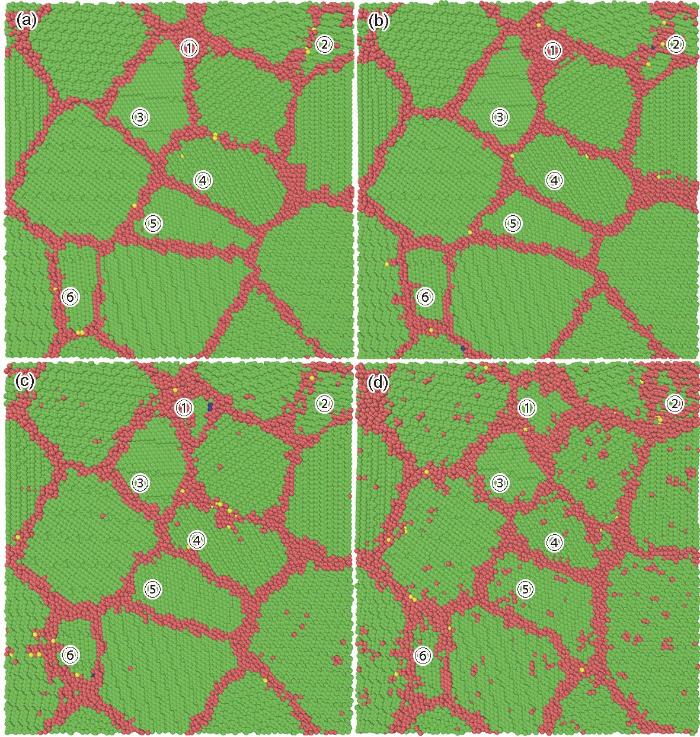
进一步对图5c中的组织变化进行公共近邻分析(common neighbor analysis,CNA),图6为稳态蠕变过程中不同时刻的微观结构演变,图中蓝色、黄色、绿色、红色原子分别代表着fcc、bcc、hcp结构和未知结构。从图6可以看到晶界处和晶粒内分布着一定数量的红色原子。在蠕变过程中,在晶内乱序原子基本不变的情况下,主要由晶界演化引起体系中的红色原子占比由27.4%提高到了30.5%。图6a所示的1、2、6号晶粒的尺寸逐渐长大,3、4号晶粒则逐渐缩小,而5号晶粒在长大的同时还发生了较为明显的变形。体系中一些较大尺寸的晶粒持续长大,而小晶粒则大多倾向于收缩。图6中对应的模型体系中共有13个晶粒的尺寸在稳态蠕变过程中明显增加,并且体系内晶界随蠕变过程的进行而逐渐粗化。
图6
图6
773 K-M3-5 GPa体系在蠕变过程中不同时刻的晶体结构
Fig.6
Microstructure evolution for 773 K-M3-5 GPa system during creep (Blue, yellow, green, and red atoms represent fcc, bcc, hcp structures, and unknown structures, respectively. The same in Figs.10, 11, and 16)
(a) 0 ps (b) 20 ps (c) 80 ps (d) 300 ps
增大应力和细化晶粒尺寸对纳米晶蠕变过程中微观结构的演化也有较大影响。图7所示为773 K时M3-不同应力体系及不同晶粒尺寸-5 GPa体系在蠕变前后体系中晶界原子比例的变化曲线。可以看出,体系内晶界原子的含量随着应力的增加而近似线性增加,且随晶粒尺寸的减小而不断增加,但相对于蠕变前体系的增加量呈现逐渐减小的趋势。可见,应力的增大和晶粒尺寸的减小加剧了蠕变过程。
图7
图7
773 K下,M3-不同应力体系及不同晶粒尺寸-5 GPa体系在蠕变前后的晶界原子含量变化
Fig.7
Grain boundary atom fraction evolution for systems under different conditions
(a) 773 K-M3-stress systems
(b) 773 K-grain size-5 GPa systems
综上所述,蠕变对纳米晶α-Zr体系的结构演化具有显著影响。体系内晶界原子的比例随蠕变应力的增加和晶粒尺寸的减小而明显增大,同时伴有较为明显的晶粒长大和晶界粗化现象发生。
2.3 纳米晶 α-Zr的稳态蠕变机制
图8
图8
不同温度-晶粒尺寸-应力模拟体系的位错密度变化曲线
Fig.8
Dislocation density curves for systems under different stresses and temperatures (a-c), and for systems with different grain sizes under different temperatures (d-f)
各体系中位错密度均出现波动变化,但整体呈现先快速下降,再缓慢振荡上升的趋势。通过对比图8a~c可以看出,对于相同体系在不同温度下,随着温度的升高位错密度逐渐降低。出现此现象的原因主要是由于温度升高时,晶界及附近的位错可动性提高,导致晶界上的位错或新位错在形核后很快运动到晶界或三晶交线处被晶界吸收,使总位错数量减少;二是由于高温的原子振动引发的晶界附近原子扩散的加强,导致由位错承担的部分应变降低,因而所需的位错数量相应减少;还有一种可能的原因是,高温使体系内的原子振动更加剧烈,使得界面处偏离平衡位置的原子更多,OVITO中位错识别DXA算法主要是对原子周围计算Burgers回路从而识别位错和判断类型,原子振动剧烈使得算法识别位错变得困难,因为剧烈振动的原子会让位错的Burgers矢量变得不容易估算,因此观察到温度升高而位错密度降低的现象。从图8a~c中不同载荷下位错密度的变化情况可以看出,随着载荷的加大,位错密度并没有加大,而是整体上呈现下降的趋势,特别是在温度最高的情况下。根据构型分析,这种反常趋势的原因之一,是由于在温度较高的情况下,晶界位错的可动性增强,其快速移动导致整体蠕变的发生,同时由于位错向三叉晶界等处的移动而导致位错的消失,但新的位错形核需要更大的应力和更长的时间,因而数量上无法补偿位错的消失,导致晶界位错的总体数目减少。这种趋势随着外应力的加大而增强,所以对于高应力的情况下,晶界上所剩的位错更少;特别是在高温体系中,由于扩散的增加,使位错形核的驱动力降低,导致图8a~c中高温位错密度逐渐降低。与此同时,在外加载荷下,位错之间的相互作用加快,有的单根位错进行分解,有的多根位错反应为单根位错,甚至有的正负位错相互作用而湮灭,因此位错密度在此过程中是波动变化,由于蠕变过程的不断进行,在整个过程中位错密度整体呈缓慢上升的趋势。
以573 K-M4-5 GPa模拟体系为例,分析稳态蠕变过程中纳米晶α-Zr体系内位错结构的演化。图9给出了此模拟体系在蠕变过程不同时刻的位错结构。可见,在蠕变过程中体系内位错结构的变化非常明显,如图9a和b所示,在变形初期体系内位错在外加载荷下运动并与晶界或三晶交线发生相互作用,部分消失在三晶交线中,使得位错密度下降,因此位错密度相比图9a显著减少,之后随着蠕变过程的进行而位错密度重新开始增加。从图9b~f可以看出,在蠕变过程中,位错基本分布于晶界处,而纳米晶内部没有发现位错结构,这一点与Zhu等[32]在纳米晶Ti的塑性变形研究中的结论类似。界面位错的结构和滑移行为涉及相邻2个晶粒及界面的取向,并与局部应力状态有关,相关的分析工作正在进行中。
图9
图9
573 K-M4-5 GPa体系在蠕变过程中不同时刻的位错结构
Fig.9
Dislocation structure evolutions of 573 K-M4-5 GPa system during creep process (Gray areas and colored lines represent grain boundaries and dislocation lines, respectively)
(a) 0 ps (b) 15 ps (c) 75 ps (d) 135 ps (e) 200 ps (f) 300 ps
在前面的部分结果中,晶粒的形态在稳态蠕变过程中发生了改变。Liu等[33]认为晶界对超细晶Ti的蠕变行为有着至关重要的影响,因此为明确本工作中纳米晶α-Zr体系的晶界结构变化对蠕变过程的影响,对模拟体系的微观结构变化作进一步分析,结果如图10和11所示。图10为773 K下M3在不同应力下蠕变始末时刻的原子快照。图10b中1 GPa蠕变后体系的微观结构变化较小,少数晶界发生较小幅度的移动,大部分晶粒的形态和相对位置与蠕变前基本相同,仅有1、3、5号晶粒的尺寸发生了大幅改变。而随着应力水平的增大,晶界迁移的作用显著增强,3 GPa蠕变体系的晶界结构比1 GPa体系的变化更加显著。而在5 GPa模拟中(图10d),几乎所有晶粒都已经发生了不同程度的变形,其中以1、3、5号晶粒的形貌变化最为显著,1、5晶粒明显长大,而晶粒3彻底消失。
图10
图10
773 K-M3-不同应力体系在蠕变始末状态时的原子快照
Fig.10
Atomic snapshots of 773 K-M3-different stress systems at the beginning and final states of creep process
(a) before creep (b) 1 GPa-300 ps (c) 3 GPa-300 ps (d) 5 GPa-300 ps
图11
图11
不同温度-M4-5 GPa体系在蠕变始末状态时的原子快照
Fig.11
Atomic snapshots of different temperature-M4-5 GPa systems at the beginning and final states of creep process
(a) before creep (b) 373 K-300 ps (c) 573 K-300 ps (d) 773 K-300 ps
图12
图12
573 K-M4-5 GPa体系在蠕变过程中的组织演化及晶界附近原子位移分析
Fig.12
Microstructure evolutions and atomic displacement analyses of 573 K-M4-5 GPa system during creep (The grey and red atoms show the original and crept grain boundary, respectively; yellow arrows in Figs.12f-h represent the displacements of the atoms) (a-d) crystal structures at 0 ps (a), 50 ps (b), 100 ps (c), and 150 ps (d), respectively (e, f) atomic displacement analyses at 30 ps (e) and 40 ps (f), respectively (g, h) partial enlarged views of the areas in Figs.12f
最后,以晶粒内的原子数量评估晶粒的体积增长情况,对不同温度和应力水平下M3模拟体系中的最大晶粒完成蠕变过程后的体积增长比例进行了统计分析,结果如图13所示。分析表明,应力会诱导纳米晶的晶粒长大,并且升高温度和应力使这种影响更加显著,Yang等[34]在纳米晶Ni剪切蠕变的研究中也有相似结论。在373 K的模拟体系中随应力水平的提高,最大晶粒的体积增长率由2.74%提高到6.03%,而在773 K的高温体系中则由14.2%提高至32.1%。本工作中当模拟蠕变条件为773 K-5 GPa时,M3体系中共有13个晶粒随蠕变过程的进行而逐渐长大,而另一些晶粒逐步缩小甚至消失。随着蠕变的进行,晶界迁移作用使微观组织发生了显著改变。
图13
图13
不同蠕变条件下M3模拟体系中最大尺寸晶粒的体积增长率
Fig.13
Growthes of the largest grains for M3 under different creep conditions
由前面分析可知,本工作模拟的蠕变过程主要受小尺寸的纳米晶粒影响:尺寸为10 nm左右的纳米晶粒严重限制了位错的活动,提高了位错在晶界形核的势垒,这一点与Yamakov等[35]在纳米晶Al的模拟研究中得到的结论一致。而Tjong和Chen[36]认为,当纳米晶粒的尺寸减小至10~20 nm的临界范围后,大部分原子会与晶界相关,因而高比例晶界的运动和变形在纳米晶材料的塑性变形中会发挥主导作用。这一理论在低温下也可以适用,并已经在许多研究中得到了印证[37,38]。而当温度进一步升高时,如反应堆在失水事故的条件下,堆芯所经历的瞬时温度可能显著高于本工作的温度范围,虽然晶界位错的可动性将有所提高,但由于原子的体扩散随温度的提升更快,使扩散在蠕变中有可能起到更大的作用,因而将会使晶界迁移及相关位错运动的贡献减弱,特别是在应力较低的情况下。
综上所述,对于本工作中的α-Zr纳米晶,较高比例的晶界作为界面位错的湮灭阱,严重影响了稳态蠕变过程中的位错运动的作用。而稳态蠕变过程中较大尺寸的纳米晶粒受拉应力作用,其体积逐渐增大,而小尺寸的晶粒则倾向于收缩,此作用随温度的提高和应力的增大而增强,并且晶界原子的比例也随之升高,这就导致纳米晶越来越偏离初始组织,使蠕变过程得以持续进行。因此应力诱导晶界迁移是本工作中α-Zr纳米晶在蠕变过程中的主要变形机制,特别是对于超细晶体系。
2.4 辐照损伤对蠕变行为的影响
对α-Zr纳米晶模型分别采用初始动能为5和10 keV的PKA进行级联碰撞的模拟,并将辐照弛豫后的稳定体系作为蠕变模拟的初始模型,图14为M4模型经不同的PKA级联碰撞前后的原子快照(已经完成弛豫并达到相对稳定状态)。
图14
图14
M4体系在受到不同能量的初级碰撞原子(PKA)级联碰撞后的原子快照
Fig.14
Atomic snapshots of M4 systems after irradiation with different PKA (colored by centrosymmetry parameter; PKA—primary knock-on atom)
(a) before irradiation (b) 5 keV irradiation (c) 10 keV irradiation (d) partial enlarged view of Fig.14c
与辐照前相比,级联后的无序度有一定增加。由图14c可见,10 keV级联后整体的无序度更大,部分晶粒的形态发生变化,并伴有一定的晶界粗化现象,表现为晶界及附近原子的中心对称参数增加。这是因为级联碰撞导致大量的点缺陷,其运动使晶界粗化并在一定程度上改变了晶粒的形态,也因此会对后续的蠕变过程产生影响。
前面几节中讨论的几种影响因素也同样适用于级联后的体系。不同温度、应力及晶粒尺寸条件下,辐照前后体系的部分应变-时间曲线如图15所示。可见其他条件相同时,辐照后体系的蠕变均高于未辐照体系,并且10 keV体系高于5 keV体系,即体系中的空位浓度和晶界原子含量随PKA动能的提高而增大,因而原子扩散和晶界运动对蠕变的贡献得到提升,因此整体上看来蠕变中更容易发生变形。与前面相比,辐照后的体系在蠕变过程中均产生了更大的应变量,且辐照PKA动能的提升使其蠕变进一步加快。
图15
图15
PKA能量对不同体系蠕变的影响
Fig.15
Strain-time curves for various irradiated systems under different temperatures (a) and different stresses (b), and for systems with different grain sizes (c)
图16
图16
不同温度-M4-5 GPa-PKA能量的级联体系在蠕变终态(300 ps)时的晶体结构
Fig.16
Crystal structures of the M4-5 GPa cascaded systems at the final state of creep process (300 ps)
(a) 373 K-5 keV (b) 573 K-5 keV (c) 773 K-5 keV
(d) 373 K-10 keV (e) 573 K-10 keV (f) 773 K-10 keV
图17
图17
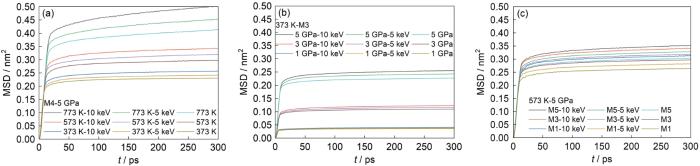
不同温度-晶粒尺寸-应力-PKA能量的级联体系的均方位移曲线
Fig.17
Mean square displacement (MSD) curves for various irradiated systems under different temperatures (a) and different stresses (b), and for systems with different grain sizes (c)
3 结论
(1) 温度、应力水平和晶粒尺寸是α-Zr蠕变行为的主要影响因素。升高温度、提高应力和细化晶粒会使材料的蠕变量加大。纳米晶的组织结构在蠕变过程中发生显著变化。随着变形程度提高,部分晶粒明显长大,另一些缩小甚至消失,一些晶粒内的晶格畸变加大,晶界区域部分无序原子的比例提高。
(2) 纳米晶中的高比例晶界对蠕变有重要贡献。晶界迁移及原子运动在高温下的细晶结构中更显著,2者均使界面位错的数量及运动减少,削弱位错对蠕变的作用。提高温度和增大应力会促进组织演变,同时使晶界宽化,有利于蠕变的进行。在本工作模拟条件下,晶界迁移是α-Zr纳米晶蠕变过程中的主要变形机制。
(3) 在原子间相互作用势的近距离修正的基础上进行辐照及蠕变模拟,辐照后的体系蠕变时产生更大的应变。分析表明,经级联碰撞后体系内产生大量缺陷,其扩散运动,以及在晶界处的汇集,进而提高晶界可动性,均对蠕变有促进作用。在蠕变过程中,10 keV级联体系的晶粒长大程度大于5 keV级联体系。
参考文献
Materials challenges in nuclear energy
[J].
Evolutionary developments of advanced PWR nuclear fuels and cladding materials
[J].
A review on neutron-irradiation-induced hardening of metallic components
[J].
Present limits and improvements of structural materials for fusion reactors—A review
[J].
Mechanism of creep deformation with evolution of microstructure and texture of Zr-2.5Nb alloy
[J].
Tensile creep and rupture behavior along with evolution of microstructure in a Zr-2.5Nb alloy
[J].
In situ monitored in-pile creep testing of zirconium alloys
[J].
Theory of the creep of zircaloy during neutron irradiation
[J].
Effect of irradiation creep on hydrogen-pick-up induced multi-field coupling behavior in zircaloy cladding tube
[J].
辐照蠕变对锆合金包壳管吸氢所致多场耦合行为的影响
[J].本文考虑辐照效应,改进了锆合金包壳管内部的氢原子扩散-氢化物析出-热-力耦合行为的微分控制方程。根据多物理场等效积分弱形式和所建立的耦合计算方法,在FEPG软件平台编制文件,生成多场耦合计算的有限元程序,并对程序进行了验证。计算分析了辐照蠕变对锆合金包壳管堆内吸氢所致多场耦合行为演化的影响,结果表明:辐照蠕变导致包壳管内产生应力松弛,促使Mises应力显著降低,同时导致静水应力由负值转变为正值,进而影响氢原子的扩散;与不考虑辐照蠕变的结果进行对比,发现辐照蠕变会增大燃料芯块与包壳管局部接触区域的负的静水应力的绝对值及向外的静水应力梯度,导致接触区域内的氢原子浓度减小,接触区域周围的氢原子浓度增大。
Dislocation slip or deformation twinning: Confining pressure makes a difference
[J].
Molecular dynamics investigation of deformation twinning in γ-TiAl sheared along the pseudo-twinning direction
[J].
The transformation of narrow dislocation dipoles in selected fcc metals and in γ-TiAl
[J].
Dynamic recrystallization initiated by direct grain reorientation at high-angle grain boundary in α-titanium
[J].Employing atomic-scale simulations, the response of a high-angle grain boundary (GB), the soft/hard GB, against external loading was systematically investigated. Under tensile loading close to the hard orientation, strain-induced dynamic recrystallization was observed to initiate through direct soft-to-hard grain reorientation, which was triggered by stress mismatch, inhibited by surface tension from the soft-hard GB, and proceeded by interface ledges. Such grain reorientation corresponds with expansion and contraction of the hard grain along and perpendicular to the loading direction, respectively, accompanied by local atomic shuffling, providing relatively large normal strain of 8.3% with activation energy of 0.04 eV per atom. Tensile strain and residual dislocations on the hard/soft GB facilitate the initiation of dynamic recrystallization by lowering the energy barrier and the critical stress for grain reorientation, respectively.
Atomsk: A tool for manipulating and converting atomic data files
[J].
LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales
[J].
Development of an interatomic potential for the simulation of phase transformations in zirconium
[J].
Molecular dynamics simulations of high-energy displacement cascades in hcp-Zr
[J].
Molecular dynamics study of self-diffusion in Zr
[J].
Molecular dynamics simulation of diffusion in supercooled Cu-Zr alloys
[J].
Visualization and analysis of atomistic simulation data with OVITO—The open visualization tool
[J].
Progress in research on creep behavior of ultrafine/nano-grained metallic materials
[J].
超细晶/纳米晶金属材料的蠕变行为研究进展
[J].
Grain size dependence of creep in nanocrystalline copper by molecular dynamics
[J].
Dislocation mechanics of creep
[J].
Fundamental problems of diffusional creep theory
[J].
扩散蠕变理论的基础问题研究
[J].
The high-temperature creep behaviour of an Fe-Al-Zr alloy strengthened by intermetallic precipitates
[J].
Creep behavior of ultra-fine grained commercial purity zirconium at room temperature
[D].
复合细化超细晶工业纯锆的室温蠕变行为研究
[D].
Influence of grain size on deformation mechanisms: An extension to nanocrystalline materials
[J].
Grain boundary-mediated plasticity in nanocrystalline nickel
[J].The plastic behavior of crystalline materials is mainly controlled by the nucleation and motion of lattice dislocations. We report in situ dynamic transmission electron microscope observations of nanocrystalline nickel films with an average grain size of about 10 nanometers, which show that grain boundary-mediated processes have become a prominent deformation mode. Additionally, trapped lattice dislocations are observed in individual grains following deformation. This change in the deformation mode arises from the grain size-dependent competition between the deformation controlled by nucleation and motion of dislocations and the deformation controlled by diffusion-assisted grain boundary processes.
Nanostructures in Ti processed by severe plastic deformation
[J].Metals and alloys processed by severe plastic deformation (SPD) can demonstrate superior mechanical properties, which are rendered by their unique defect structures. In this investigation, transmission electron microscopy and x-ray analysis were used to systematically study the defect structures, including grain and subgrain structures, dislocation cells, dislocation distributions, grain boundaries, and the hierarchy of these structural features, in nanostructured Ti produced by a two-step SPD procedure—warm equal channel angular pressing followed by cold rolling. The effects of these defect structures on the mechanical behaviors of nanostructured Ti are discussed.
Ambient-temperature nanoindentation creep in ultrafine-grained titanium processed by ECAP
[J].
Grain boundary migration in nanocrystalline Ni under constant shear strains and its mechanism
[J].
Length-scale effects in the nucleation of extended dislocations in nanocrystalline Al by molecular-dynamics simulation
[J].
Nanocrystalline materials and coatings
[J].
Stress-enhanced grain growth in a nanocrystalline material by molecular-dynamics simulation
[J].