最新录用 | 当期目录 | 过刊浏览 | 热点文章 | 虚拟专辑 | 阅读排行 | 下载排行 | 引用排行 | 期刊订阅

金属学报, 2024, 60(10): 1439-1450 DOI: 10.11900/0412.1961.2024.00143

研究论文

超快激光诱导Cu薄膜熔化的神经网络分子动力学研究

高天雨1,2, 曾启昱,1,2, 陈博1,2, 康冬冬1,2, 戴佳钰,1,2

1 国防科技大学 理学院 长沙 410072

2 国防科技大学 湖南省极端条件物理及应用重点实验室 长沙 410072

Neural Network Molecular Dynamics Study of Ultrafast Laser-Induced Melting of Copper Nanofilms

GAO Tianyu1,2, ZENG Qiyu,1,2, CHEN Bo1,2, KANG Dongdong1,2, DAI Jiayu,1,2

1 College of Science, National University of Defense Technology, Changsha 410072, China

2 Hunan Key Laboratory of Extreme Matter and Applications, National University of Defense Technology, Changsha 410072, China

通讯作者: 戴佳钰，jydai@nudt.edu.cn，主要从事极端条件下物质科学研究;曾启昱，zengqiyu@nudt.edu.cn，主要从事激光与物质相互作用的原子尺度模拟研究

收稿日期: 2024-05-07   修回日期: 2024-07-25  

基金资助: 国家自然科学基金项目(12104507)
湖南省科技创新领军人才项目(2021RC4026)
湖南省研究生科研创新项目(CX20220070)

Corresponding authors: DAI Jiayu, professor, Tel:(0731)87001006, E-mail:jydai@nudt.edu.cn;ZENG Qiyu, Tel: 18374847919, E-mail:zengqiyu@nudt.edu.cn

Received: 2024-05-07   Revised: 2024-07-25  

Fund supported: National Natural Science Foundation of China(12104507)
Science and Technology Innovation Program of Hunan Province(2021RC4026)
Postgraduate Technology Innovation Program of Hunan Province(CX20220070)

作者简介 About authors

高天雨，男，1995年生，博士生

摘要

在飞秒激光作用下，材料将经历从凝聚态到高温高压状态、甚至是理想等离子体的剧烈结构转变。在理解这一过程的微观图像上，分子动力学模拟扮演着重要角色，但是对激光作用带来的激发态等问题，传统分子动力学描述存在原理上的困难。本工作结合温度依赖的神经网络原子间势能面与双温模型分子动力学方法，在量子精度下实现激光加热Cu薄膜的大尺度模拟，深入探讨了不同激光通量作用下的热力学状态时空演化与相变动力学，揭示了随着激光通量的增加，激光诱导的熔化动力学从非均匀熔化机制到均匀熔化机制发生转变的物理图像，为深入理解激光-物质相互作用过程提供了原子尺度的微观参考。

关键词： 神经网络; 激光-物质相互作用; 熔化动力学; 双温模型

Abstract

Exploring ultrafast structural transitions in materials triggered by femtosecond laser pulses—from their condensed states to high-temperature, high-pressure conditions, and potentially to ideal plasmas—is a crucial scientific endeavor with profound implications for fields such as inertial confinement fusion, metal additive manufacturing, and laser processing. These extreme conditions, which are challenging to replicate and directly observe in experiments due to temporal and spatial resolution limitations, require theoretical models and simulations to decode the underlying microscopic mechanisms. Molecular dynamics (MD) simulations, especially when paired with advanced potential energy surfaces, are effective tools for addressing these challenges. However, maintaining a balance between computational efficiency and physical accuracy, particularly when simulating excited states induced by laser interactions, remains a formidable task. In this context, neural network potential energy surfaces (NNPES) have demonstrated exceptional capability for capturing the complex interactions and properties of materials under extreme conditions, providing vital links between quantum mechanics and macroscale phenomena. Using Cu as a prototypical example, the ability of NNPES to accurately depict lattice vibrations, thermophysical properties, and complex dynamics during laser-matter interactions has been demonstrated. By seamlessly integrating NNPES with a two-temperature MD model, this study directly simulates the atomic-scale dynamics of Cu thin films subjected to intense pulsed laser irradiation. This innovative approach, which combines quantum-level accuracy with large-scale thermodynamics and detailed microstructural evolution, provides unprecedented insights into the fundamental mechanisms of laser-induced melting. Our findings reveal two distinct melting behaviors in Cu, dependent on laser fluence. At fluences near the melting threshold, a heterogeneous melting process initiated at the film surface because of the lower free energy barrier was observed. The solid-liquid interface then moves inward at velocities of tens of meters per second, requiring hundreds of picoseconds for melting to complete. Conversely, at fluences well above the threshold, Cu films experience rapid and homogeneous melting, markedly different from conventional heating-induced melting. Here, the lattice temperature almost instantaneously exceeds the thermal stability limit, leading to uniform liquid nucleation and rapid growth throughout the film, culminating in complete melting within just tens of picoseconds. This study not only illuminates the atomic-scale dynamics of laser-induced melting but also underscores the transition from heterogeneous to homogeneous melting mechanisms as a function of laser fluence. This study serves as an invaluable research tool for enhancing our understanding of laser-matter interactions and their potential applications in optimizing laser-based manufacturing processes and predicting material behavior under extreme conditions. Moreover, the reliability and versatility of NNPES set the stage for extending the research to more complex systems, including alloys and amorphous materials. This expansion fosters robust connections between microscopic theories and macroscale applications, deepening our understanding of material responses to intense laser irradiation. Future studies employing this framework could explore complex physical phenomena such as explosive boiling and material disintegration during laser ablation, offering unique atomic-scale insights that could pave the way for groundbreaking discoveries and technological advancements.

Keywords： neural network; laser-matter interaction; melting dynamics; two-temperature model

PDF (1831KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

高天雨, 曾启昱, 陈博, 康冬冬, 戴佳钰. 超快激光诱导Cu薄膜熔化的神经网络分子动力学研究[J]. 金属学报, 2024, 60(10): 1439-1450 DOI:10.11900/0412.1961.2024.00143

GAO Tianyu, ZENG Qiyu, CHEN Bo, KANG Dongdong, DAI Jiayu. Neural Network Molecular Dynamics Study of Ultrafast Laser-Induced Melting of Copper Nanofilms[J]. Acta Metallurgica Sinica, 2024, 60(10): 1439-1450 DOI:10.11900/0412.1961.2024.00143

在超快激光(脉冲持续时间在亚皮秒量级)作用下，物质会达到由热电子与冷晶格构成的极端非平衡状态——电子温度远大于离子温度的双温状态。这是因为激光能量首先沉积在电子亚系统，在飞秒时间尺度内，电子亚系统通过电子-电子散射迅速达到热平衡，而晶格在此时间尺度内尚未升温(晶格平衡的时间尺度在皮秒量级)。在这种双温状态下，电子-晶格之间通过电声耦合进行能量交换，产生极高的晶格加热速率，并影响体系的动力学过程，使得激光-物质相互作用过程中的结构演化动力学显著区别于传统的热过程。由于超快激光-物质相互作用的普遍性和重要性，其在惯性约束聚变[1]、激光加工[2]、金属增材制造[3,4]等多个领域受到广泛关注。

在实验上，由于超快激光作用的瞬态特性，理解其动力学过程离不开超快时间分辨诊断技术。在过去的几十年里，人们陆续发展了光学泵浦探测实验[5,6]、超快电子衍射(ultrafast electron diffraction，UED)[7~10]、X射线近边吸收光谱(X-ray absorption near-edge spectra，XANES)[11,12]和时间分辨太赫兹电导率测量[13]等多种诊断方法来理解材料在超快激光作用下的电子、晶格结构响应。Cu、Au等贵金属化学性质稳定，且在工业上应用广泛，具有相对其他金属较弱的电声耦合系数，导致晶格加热的时间尺度更长，更有利于观察和研究激光激发产生的非平衡结构演化动力学[14~16]。研究者[12,17,18]通过测量X射线近边吸收谱的含时演化，观察到超高激光通量下Cu在皮秒乃至亚皮秒时间内就发生了晶格长程有序性的消失。Mo等[8]则通过时间分辨的超快电子衍射实验，观察到随激光通量增加Au薄膜熔化时间尺度表现出巨大的差异，跨越纳秒到皮秒量级。需要注意的是，时间分辨的XANES和UED实验提供的主要是电子结构或者长程统计的晶格结构，且空间分辨率有限，无法提供有效的微观结构信息，这使得激光诱导熔化动力学的微观机理依然不明确。

因此，从原子尺度出发的分子动力学(molecular dynamics，MD)模拟一直是理解激光-物质相互作用的重要研究手段。在这方面，人们将MD与双温模型(two-temperature model，TTM)耦合，将电子处理为连续介质，原子运动采用MD描述，可以有效研究金属在超快激光作用下的微观动力学。在具体实验和计算过程中，考虑到激发电子的弹道输运自由程通常在百纳米范围，通常采用厚度在几十纳米的金属薄膜作为实验和计算模拟的具体对象，以保证激光能量的均匀沉积，从而可以将整个研究体系当作温度均匀分布的体系处理，更利于实验观察和理论结果的解读与分析[16]。传统方法通常采用经典分子动力学方法，利用嵌入原子势(embedded-atom-method，EAM)考虑原子间相互作用，且通常忽略激发电子的贡献。例如，Lin和Zhigilei[19]使用基于EAM的TTM-MD方法，实现了20 nm厚Au薄膜的激光过程模拟，深入分析了均匀熔化和非均匀熔化2种熔化行为的微观机理。Molina和White[20]采用基于EAM的TTM-MD模拟还原了UED实验的衍射峰下降行为，分析了激光过程中可能的能量损失路径。这些工作有效弥补了实验分辨率的不足，为理解超快熔化动力学过程提供了基于原子尺度的微观图像。

但是，MD的准确性严重依赖于原子间相互作用势能面(potential energy surface，PES)。作为典型的非线性高维函数，PES难以直接被唯象模型所准确建模，尤其是激光过程涉及到从凝聚态到高温高压状态、甚至是理想等离子体的剧烈物态转变，且其中电子激发带来的影响至关重要。即使是对金属体系建模效果较好的EAM，也很难兼顾宽热力学区间且多相共存的准确描述[21~24]，特别是在绝大多数情况下，无法考虑随时间演化的电子激发的贡献。如近期Arefev等[25]采用高度优化的EAM，也无法通过任何具有物理意义的参数调整来复现UED实验所测量的Au薄膜熔化动力学。经验势的不足，意味着更完整精确的PES描述必须从其构建的基本原理，也就是量子力学出发。以密度泛函理论(density function theory，DFT)为代表的从头算分子动力学(ab initio molecular dynamics，AIMD)方法，通过求解Kohn-Sham (KS)方程可以获得高精度的原子间相互作用力。但由于第一性原理计算方法的计算复杂度与体系自由度的立方成正比，使其只能处理包含数百原子的小体系，无法满足直接模拟超快激光过程中结构演化、多相共存的规模需要。这种效率-精度两难的困境，制约了原子建模方法在理解激光-物质相互作用过程的应用，也很难为其提供更为深入的物理图像。

当前，随着深度学习技术广泛应用到原子建模领域，大量研究[26~35]证明了基于神经网络形式的势能面构建可以在有效保持第一性原理精度的同时保证线性的计算标度，这为建模宽热力学区间复杂高维的势能面提供了新的技术途径。近期Zeng等[36]发展了双温模型耦合深度势能分子动力学(two-temperature-model coupled deep potential molecular dynamics，TTM-DPMD)方法，将神经网络形式的PES与TTM-MD方法结合，实现了超快激光作用下热过程和非热过程的统一理论描述，为开展大尺度第一性原理精度超快激光驱动物质结构演化过程的直接模拟提供了有效手段。本工作以Cu为研究对象，验证了神经网络PES对激光与物质相互作用过程中产生的高温高压状态的描述能力，并结合所发展的TTM-DPMD方法，在量子精度下探讨了Cu薄膜在超快激光下的结构响应动力学。

1 研究方法

1.1 TTM-DPMD方法

与TTM-MD类似，在TTM-DPMD模型中用分子动力学描述原子运动，电子温度场则处理为连续介质，通过差分方法来求解[37~45]，不同的是原子间相互作用采用考虑了电子激发的温度依赖神经网络势能面。为了考虑电子-晶格系统之间的耦合，该方法在原子运动的动力学方程中引入Langevin项，以实现电子-晶格能量交换[41,42]，具体表达式为：

ce(Te)∂Te∂t=∇⋅(κe∇Te)-gei(Te)(Te-Ti)+S(r, t)
mid2ridt2=-∇iA(R, Te)-γiνi+F˜(t)

式中，ce为电子比热容，Te为电子温度，A(R, Te)表明势能面同时依赖于局域原子环境(R)和Te，κe为电子热导率，gei为电声耦合系数，Ti为晶格温度，mi为离子质量，vi为离子运动的速度，t为离子运动的时间，γi为Langevin动力学的摩擦系数，γi与gei存在如下关系[41,42]：

γi=TiMn3kBgei

式中，M为粒子质量，n为粒子数密度，kB为Boltzmann常数。

F˜(t)表示离子在虚拟电子海中受到的无规则碰撞而产生的涨落力，满足如下关系[41,42]：

<F˜(t)> =0
<F˜(t')⋅F˜(t)> =2kBTeγiδ(t'-t)

式中，t'为不同于t的离子运动时刻；δ表示Dirac函数，若t' = t，函数为0，若t' ≠ t，函数为无穷大。

S(r, t)表示激光源，在本工作中，激光垂直于薄膜平面(x-y平面)入射，其能量沉积沿着z方向根据光学穿透深度发生指数衰减。在时域上，激光是一个Gaussian分布，其表达式为[40]：

S(z, t)=Fabsσ2πLp(1-exp(-d / Lp))⋅
exp(-z / Lz)exp(-(t-t0)22σ2)

式中，Fabs为材料实际吸收的激光通量，σ为含时Gaussian分布的标准差，Lp为光学穿透深度，Lz 为z方向的光学穿透深度，d为样品厚度，t0为到达激光脉冲最大值的时间。

在上述基础上，本工作基于LAMMPS软件中修改过的EXTRA-FIX模块开展TTM-DPMD模拟[36]。在TTM-DPMD中，电声耦合系数选为0.9 × 1017 W/(m3·K)，激光为Gaussian形脉冲，激光脉冲脉宽为130 fs。为了描述温度梯度带来的热输运，κe采用Drude模型来描述：

κe(Te, Ti)=13νF2ce(Te)τe(Te, Ti)

式中，vF是Fermi速率，τe(Te, Ti)是由电子-电子散射和电子-声子散射时间定义的电子散射总时间，即：

1 / τe=1 / τe-e+1 / τe-ph=ATe2+BTe

式中，τe-e为电子散射时间，τe-ph为电子-声子散射时间。在模拟时， 式(8)中的参数A设置为1.28 × 107 s-1·K-2，参数B设置为1.23 × 1011 s-1·K-2， 式(7)中的vF为1.57 × 106 m/s[46]。为了实现对40 nm厚Cu薄膜体系的全尺度模拟，构建了20a0 × 20a0 × 11a0 (a0为晶格常数)的超胞，共包含176000个原子，为了描述薄膜自由表面的真实响应，模拟过程沿z方向自由表面前后各设置了40 nm厚的真空区域，x与y方向则设置为周期性边界条件。

1.2 深度势能(DP)模型构建

在TTM-DPMD方法中，可靠的深度势(DP势)是进行大尺度第一性原理精度超快激光驱动物质结构演化过程的直接模拟的保证。在深度势能(deep potential，DP)方法中，深度神经网络被用于建立描述子到单原子能量的高维映射关系，以描述从凝聚态到高温高压物质区间的复杂势能面。在有限温度密度泛函理论的框架下，在DP模型中额外引入了能量对电子温度的显式依赖，以包含电子熵对总能量的贡献，从而更好地建模金属体系。电子温度依赖的深度势能 (electron-temperature-dependent DP，ETD-DP)模型的数学表述如下[36]：

A(R, Te)=∑iNαi(Dαi(ri, {rj}j∈n(i)), Te)

式中，ri 表示第i个原子的坐标；Dαi为描述子，描述了原子i的局域环境信息；n(i) = {j|rji < rcut}表示原子i和j的距离(rji )小于rcut的原子近邻列表，{rj }表示近邻列表的原子位置rj 集合，rcut表示截断半径；Nαi表示通过神经网络建立第i个原子的描述子到其单原子能量之间的高维映射。在 式(9)的数学基础上，Cu的神经网络势能面通过DeePMD-kit软件包[37]和DP-Generator (DP-GEN)[38]软件生成。为了构建初始训练集，本工作以fcc结构和液相无序结构为初始构型(均包含32个原子)，采用等容等温系综(NVT，其中N代表粒子数，V代表系统体积，T代表系统温度)，分别在300、1000和3000 K下进行时长为4 ps的第一性原理分子动力学计算。时间步长设置为1 fs，每间隔10个时间步选取一个构型，获得800个fcc构型和400个液相构型。

为了有效地探索不同温度、压力下的fcc和液相结构，本工作进一步在初始训练集的基础上，构建4个初始随机数种子不同的DP模型，以模型偏差为判据，结合同步学习方案对激光过程涉及到的高温、高压区间进行构型采样。如表1所示，考虑到激光过程涉及到晶格的等容、等压加热过程和熔化动力学，本工作采用等温等压系综(NPT，其中P代表系统压强)和NVT对晶格温度为300~3000 K，压强为0~30 GPa的热力学空间进行充分探索，总共采样了3417个fcc构型和2160个液相构型。

表1   不同热力学条件下Cu深度势能(DP)模型的构型探索

Table 1  Details of the exploration strategy for the deep potential (DP) model of Cu system under different thermodynamics conditions

Iter.Lattice structureTime / psEnsemble typeTemperature / KPressure / GPaSampled configuration
0fcc0.5NPT30000
1fcc1NPT30000
2fcc2NPT30000
3fcc4NPT30000
4fcc8NPT30000
5fcc16NPT30005
6fcc4NVT200, 4007
7fcc16NVT200, 4001
8fcc2NVT50060
9fcc4NVT5005
10fcc16NVT50010
11fcc2NVT80013
12fcc4NVT8009
13fcc16NVT80060
14fcc2NVT1000, 1200, 150060
15fcc4NVT1000, 1200, 150060
16fcc16NVT1000, 1200, 150060
17fcc0.5NPT300021
18fcc1NPT300046
19fcc2NPT300060
20fcc4NPT300060
21fcc8NPT300060
22fcc16NVT30060
23fcc4NVT200, 40060
24fcc16NVT200, 40060
25fcc2NVT50060
26fcc4NVT50060
27fcc16NVT50060
28fcc2NVT80060
29fcc4NVT80060
30fcc16NVT80060
31fcc2NVT1000, 120060
32fcc4NVT1000, 120060
33fcc8NVT1000, 120060
34fcc, liquid2NVT1500, 2000, 250060, 60
35fcc, liquid4NVT1500, 2000, 250060, 60
36fcc, liquid8NVT1500, 2000, 250060, 60
37Liquid2NVT300060

(续表)

新窗口打开| 下载CSV


采样的构型通过第一性原理方法标定总能量、受力和Virial张量，自洽场迭代通过VASP软件实现[43]，交换关联泛函选取Perdew-Burke-Ernzerhof (PBE)近似[45]，赝势形式为投影缀加平面波(projector augmented wave，PAW)，包含11个价电子(电子构型为3d104s1)。为了保证能量精度收敛到1 eV/atom，倒空间Brillouin区采样密度为2.5 nm-1，动能截断为700 eV。势函数训练过程中，嵌入网格包含3层隐藏全连接层，每层神经元数目分别为25、50和100个，以端到端地提取局域原子环境的特征。拟合网络也包含3层隐藏层，每层用了240个神经元节点，同样为全连接网络。将能量、力和Virial项的训练权重初始时刻分别设置为0.2、1000和0.2，从而优先拟合受力，加快训练过程的收敛，在训练后期权重参数均设置为1，3者有着相同的权重，同时保证3者的精度。总共训练步数设置为100 × 104步，将神经网络模型的权值冻结后，就获得Cu在宽热力学区间的神经网络势函数。

  

IterLattice structureTime / psEnsemble typeTemperature / KPressure / GPaSampled configuration
38Liquid4NVT300060
39Liquid8NVT300060
40fcc2NPT

300, 500, 800,

1000, 1200, 1500

0, 1, 5, 10600
41fcc4NPT

300, 500, 800,

1000, 1200, 1500

0, 1, 5, 10600
42fcc8NPT

300, 500, 800,

1000, 1200, 1500

0, 1, 5, 10720
43Liquid2NPT1500, 2000, 2500, 30000, 1, 5, 10600
44Liquid4NPT1500, 2000, 2500, 30000, 1, 5, 10600
45Liquid8NPT1500, 2000, 2500, 30000, 1, 5, 10600

Note: The exploration of configuration is carried out along the melting curve of Cu for the thermodynamic space with lattice temperatures from 300 K to 3000 K and pressures from 0 to 30 GPa under isothermal and isobaric ensemble (NPT) and canonical ensemble (NVT)

新窗口打开| 下载CSV


2 研究结果与讨论

2.1 DP模型能量、力及Virial预测精度

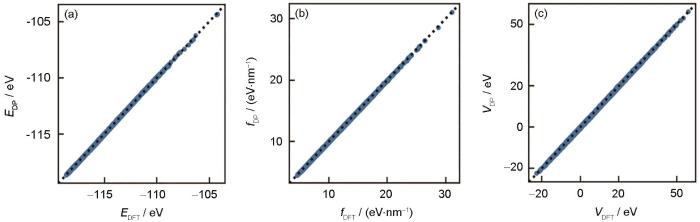
Cu的DP模型在数据集上的能量、受力、Virial预测精度如图1所示。其中，能量的均方根偏差(root mean square error，RMSE)为2.21 meV/atom，受力的RMSE为3.2 eV/nm，Virial张量的RMSE为0.27 eV。整体来看，与DFT计算相比，Cu的DP模型已经具有很高的精度。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   Cu的DP模型预测值和密度泛函理论(DFT)计算的能量、受力和Virial张量的对比

Fig.1   Comparisions of DP model predicted energy from DP model (EDP)，force (fDP), and virial tensor (VDP) of Cu with the energy (EDFT), force (fDFT), and virial tensor (VDFT) on the training set calculated by density functional theory (DFT)

(a) EDP-EDFT (b) fDP-fDFT (c) VDP-VDFT


2.2 Cu的基本热力学性质

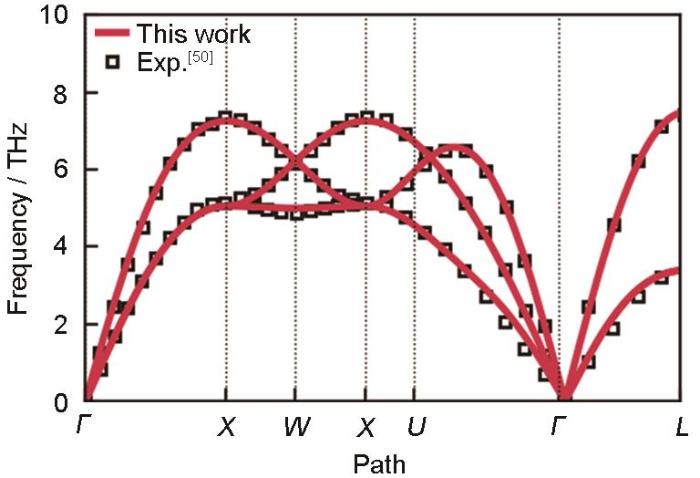
在完成DP模型在数据集上的精度验证后，需要对DP模型描述激光过程的可靠性开展更为细致的验证。超快激光诱导的熔化动力学研究，离不开对Cu热物理性质的准确评估。首先结合深度势能分子动力学(DPMD)，评估DP模型对Cu初态的描述能力，DPMD模拟均基于LAMMPS开源软件包[47]实现。本工作构建了包含4000个原子的fcc晶格，在NPT系综下(压力P = 105 Pa，温度T = 300 K)进行充分弛豫，获得其a0为0.3655 nm，与实验结果[48]相符合(见表2)，相对误差为1.12%。在平衡晶格常数的基础上，采用ALAMODE软件包[49]计算了声子谱，其与晶格的弹性常数、声速等密切相关。对2 × 2 × 2的fcc超胞计算原子间受力，通过有限位移法获得二阶力常数，其中施加的位移扰动为0.001 nm。计算得到的声子色散曲线如图2所示，与Nilsson和Rolandson[50]的实验测量结果对比，DP模型预测的声子谱在各个倒空间路径上均表现出良好的一致性，这说明DP模型可以准确描述Cu的晶格动力学。

表2   使用DP模型得到的Cu的晶格常数(a0)、熔点(Tm)、相变潜热(ΔHm)、熔化阈值(εm)及其与实验值[48,51,53~56]的对比

Table 2  Lattice constant (a0), melting point (Tm), latent heat of phase transition (ΔHm), and melting threshold (εm) of Cu obtained by using deep potential, and experimental results [48,51,53-56] for comparison

Itema0 / nmTm / KΔHm / (kJ·kg-1)εm / (kJ·kg-1)
Relative error / %1.120.390.520.40
DP result0.36551275 ± 25232.3 ± 11.2658.7 ± 49.1
Experiment result0.3615[48]1280[51]231.1[53]661.3[51,53-56]

新窗口打开| 下载CSV


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   温度为300 K时Cu声子谱的DP模型结果与实验结果[49]对比

Fig.2   Phonon spectrum of solid copper obtained using DP model, and the experimental result[50] for comparison (The horizontal axis shows the value of the in-plane wave vector, along the Γ-X-W-X-U-Γ-L paths in the frst Brillouin zone)


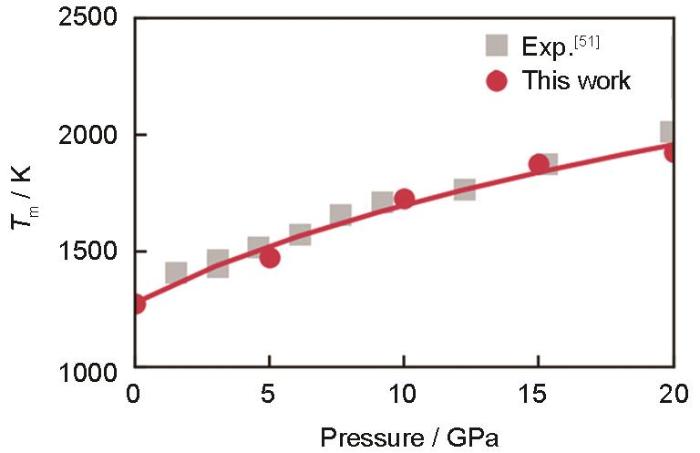
激光熔化过程离不开对熔点(Tm)、相变潜热(ΔHm)、焓变等热物理量的准确评估。在评估过程中构建了包含32000个原子的fcc晶格，通过两相法构建固/液界面以驱动熔化。在NPT下，两相法可以有效计算不同压强条件下的熔点，如图3所示，DPMD计算的熔化曲线与Japel等[51]的实验测量相符合。在常压下(P = 105 Pa)，Tm为(1275 ± 25) K，与实验值的偏差为0.39%，在误差范围内(表2)。随着压强增加到20 GPa，Cu的Tm单调上升为1894 K。采用Simon-Glatzel方程拟合Cu的熔化曲线[52]，具体表达式为Tm = T0(1 + P / a) b，得到拟合参数T0为1275 K，a为6.23 GPa，b为0.32。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不同压强条件下Cu熔点的DP模型结果与实验结果[51]对比

Fig.3   DP model results and experimental results of Cu melting point under different pressure conditions (The red dots are the melting points under different pressure conditions calculated using DP, the red curve is the melting curve fitted using Simon-Glatzel equation[52], and the silver squares are the experimental result[51])


ΔHm表示体系从固体转变到液相过程中所吸收的热量，是体系熔化过程中一个重要的热力学状态参量。通过计算常压Tm处固/液两相的焓(Hm)的差，即可得到ΔHm。Hm可以通过体系的总能量(Fm)及在Tm附近的能量对温度的梯度(ΔFm / ΔTm)计算得到：

Hm=Fm+TmΔFmΔTm

式中，Fm通过平衡后体系总能量求平均得到。通过 式(10)计算Cu的相变潜热为(232.3 ± 11.2) kJ/kg，与实验值[53]偏差为0.52% (表2)。

Cu在激光加热过程中由于电声耦合而升温，其升温过程的吸热与比热容密切相关，因此还需要进一步验证晶格比热容和电子比热容的准确性。考虑到样品存在自由表面，在加热过程中伴随着热膨胀，样品会经历等压过程，因此选择计算等压比热容(cp )。沿着P = 105 Pa的等压线开展DPMD，计算不同温度下的Hm，通过中心差分法计算得到cp。如图4a所示，晶格的等压比热容随着晶格温度升高而单调增加，且DPMD结果与Nizomov等[54]的实验测量符合较好。对于ce，由于涉及到电子熵的贡献，采用KS-DFT计算不同电子能量的内能，使用下式可以得到ce：

ce=Te∂Se∂Te

式中，Se为电子熵。使用 式(9)得到的ce如图4b所示。可以看到，ce随着电子温度升高而单调增加，在低温下(Te < 5000 K)与温度近似线性关系，说明满足自由电子气模型。随着电子温度进一步升高，ce显著偏离自由电子气模型，这与d壳层电子激发有关，该结果与Smirnov[55]的KS-DFT结果和XANES实验结果[56]符合较好。

图4

新窗口打开| 下载原图ZIP| 生成PPT

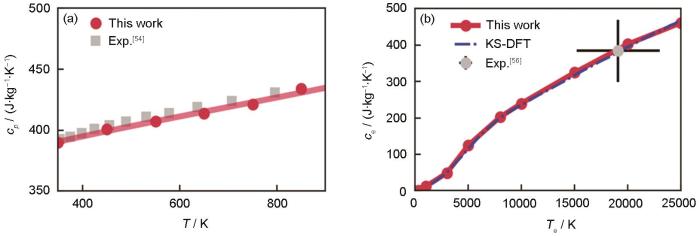
图4   Cu的晶格比热容(cp )和电子比热容(ce)

Fig.4   Lattice heat capacity (cp ) and electron heat capacity (ce) of Cu

(a) cp of Cu varied with ionic temperature (T) (The red dots are the result obtained using the DP potential, and the silver squares are the experimental result[54])

(b) ce of Cu varied with electron temperature (Te) (The red dots are the result of this work, the dashed blue lines are Smirnov's KS-DFT result[55] and the silver squares are the experimental result[56])


2.3 Cu熔化阈值

综合上述结果可见，本工作构造的DP模型可以有效描述Cu在激光加热到熔化过程中的热物理性质。在此基础上可以估算出激光熔化阈值(εm)，即给定厚度的Cu薄膜完成熔化所需要的激光能量。εm的表达式为：

εm=∫300Tmcl(T)dT+∫300Tmce(Te)dTe+ΔHm

式中，等式右侧第一项为晶格系统需要的能量，第二项为电子系统需要的能量。cl(T)为晶格热容，使用图4a中的结果，ce使用图4b中的结果，ΔHm和Tm采用表2中的结果，从而估计Cu的εm为(658.71 ± 49.11) kJ/kg (在40 nm厚的Cu薄膜中1 mJ/cm2 = 28.89 kJ/kg，因此εm也可以写为(22.8 ± 1.7) mJ/cm2)。其中，电子系统达到熔点所需能量为(8.2 ± 0.9) kJ/kg，晶格系统加热达到熔点所需能量为(419.4 ± 37.0) kJ/kg，熔化相变潜热所需能量为(232.3 ± 11.2) kJ/kg。与使用实验值计算得到的Cu的εm为661.3 kJ/kg[51,53~56]的误差仅为0.40% (表2)，其高度一致性为后续结合TTM-DPMD开展超快激光加热过程的熔化动力学研究提供了可靠保障。

2.4 低激光通量下的非均匀熔化动力学及其机理分析

首先探讨激光通量为18 mJ/cm2 (对应的能量密度为520 kJ/kg)作用下的Cu薄膜熔化动力学。在激光激发的亚皮秒时间尺度内，薄膜中的电子在超快激光激发后快速热化，由于Cu薄膜中激发态电子的平均自由程超过40 nm，弹道电子到达薄膜表面迅速反射，使得激光能量在40 nm厚的Cu薄膜内均匀沉积[14,55~57]，形成空间上均匀的双温状态，电子温度为6821 K，而晶格温度为300 K，如图5a所示，在接下来的10 ps内，电声耦合导致的非绝热能量交换使得冷晶格迅速升温，相应的加热速率高达113 K/ps。仅20 ps后，Cu薄膜达到电子-离子间的热平衡，平衡温度为1386 K，约是常压下Tm的1.1倍。由于这种极高的加热速率远大于热膨胀的时间尺度，在惯性约束下薄膜内部升温并积累热动压，体系沿着等容线演化，在t = 5 ps时，薄膜内部的压强为5.3 GPa，温度为865 K。随着压强从自由表面开始释放，薄膜发生膨胀的同时在内部逐步积累拉应力，在t = 10 ps时，形成5.2 GPa的负压。如图5b1~b4所示，这种应力波在薄膜内的传播与反射，伴随着压强、密度和温度的周期性震荡，并由于能量耗散[19]，震荡强度会逐渐衰减，表示能量逐步从晶格的集体运动传递给热动能。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   18 mJ/cm2激光通量下Cu薄膜的演化动力学过程

Fig.5   Evolutionary dynamics of Cu thin films at the laser flux of 18 mJ/cm2

(a) evolution of ion temperature (Ti) and (Te) over time

(b1-b4) evolutions of Te (b1), Ti (b2), density (ρ) (b3), and pressure (P) (b4) in different regions in the z direction of the Cu film with time

(c1-c6) atomic scale structural evolutions at time t = 0 ps (c1), 50 ps (c2), 100 ps (c3, c6), 150 ps (c4), and 200 ps (c5) (Fig.5c6 is the locally enlarged view of Fig.5c3, and polyhedral surface meshes (white interface) around fcc-type (brass) and liquid-type (gray) particles are constructed to highlight the heterogeneous phase transition)


从原子尺度出发，可观察到激光的结构演化表现出显著的各向异性。如图5c1~c6所示，在t = 50 ps时，晶格温度接近熔点(1300 K)，此时，薄膜表面由于自由能较低而先发生熔化，形成长程无序的液相结构；而薄膜内部虽然处于轻微的过热状态，但是尚不足以克服相变势垒，依然表现出热扰动的fcc晶格。这使得在薄膜表面区域形成了明显的固/液界面。固/液界面(熔化前沿)的形成显著降低了晶格发生固/液相变的势垒，从而促进内部区域吸收相变潜热并发生结构失稳，形成液相结构，在时空上表现为熔化前沿向内传播。该熔化前沿以50.6 m/s的速率向内传播，显著低于Cu的声速，驱动40 nm厚的薄膜完全熔化需要约400 ps，如此缓慢的熔化时间，与Lin和Zhigilei[19]的非均匀熔化图像相符合，也与Mo等[8]实验观察到的数百皮秒甚至纳秒时间尺度的熔化动力学相符。但在该激光通量(18 mJ/cm2)的TTM-DPMD模拟中，熔化前沿在200 ps左右已基本稳定，不再向内移动。其原因是该薄膜内超过熔点的热动能已完全转化为熔化潜热，薄膜温度下降到两相共存点，形成了固/液共存的不完全熔化状态。其本质是该激光通量的能量低于完全熔化阈值((22.8 ± 1.7) mJ/cm2)，还不足以使薄膜发生完全熔化，这与上一节的热物理性质计算相互印证。

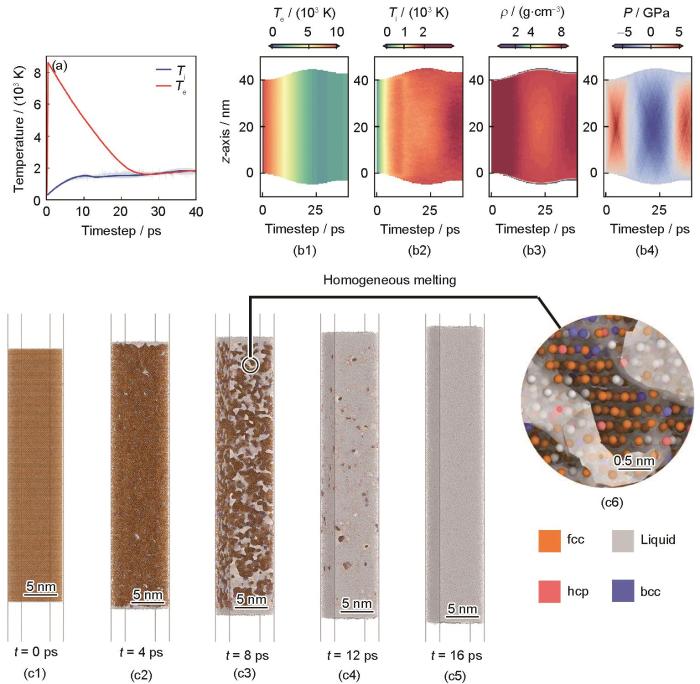
2.5 高激光通量下的均匀熔化动力学及其机理分析

进一步，将激光通量增加到30 mJ/cm2 (对应的能量密度为870 kJ/kg)，此时激光通量已经远高于熔化阈值。如图6a所示，在t = 1 ps时，激光能量的沉积产生了更加极端的双温状态，其中电子温度为8500 K，对应的电声耦合系统在28 ps后达到电子-离子之间的热平衡，加热速率约为154 K/ps，比低通量下的加热速率提高了36%。不同于低通量下的现象，由于高通量下更多的激光能量转换为薄膜内的热动能，晶格在t = 10 ps达到最高温度(1607 K，约1.25Tm)，已接近晶格热稳定性极限[46]，薄膜处于极端过热状态。但在接下来的2 ps内，离子温度显著下降约139 K，这表明薄膜内的热动能转换为相变潜热，意味着晶格在数个皮秒内就发生了熔化，这与低通量的结果截然不同。Cu薄膜的热力学状态时空演化进一步验证了这种超快熔化过程，如图6b1~b4所示，在12 ps以后，薄膜的温度、密度都发生了均匀而剧烈的下降，密度从8.64 g/cm3下降到7.52 g/cm3，对应了相变潜热的吸收与固/液转变带来的体积突变。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   30 mJ/cm2激光通量下Cu薄膜的演化动力学过程

Fig.6   Evolutionary dynamics of Cu thin films at the laser flux of 30 mJ/cm2

(a) evolutions of Ti and Te over time

(b1-b4) evolutions of Te (b1), Ti (b2), ρ (b3), and P (b4) in different regions in the z direction of the Cu film with time

(c1-c6) atomic scale structural evolutions at t = 0 ps (c1), 4 ps (c2), 8 ps (c3, c6), 12 ps (c4), and 16 ps (c5) (Fig.6c6 is the locally enlarged view of Fig.6c3, and polyhedral surface meshes (white interface) around fcc-type (brass) and liquid-type (gray) particles are constructed to highlight the homogeneous phase transition)


为了进一步探究高通量下的熔化机理，图6c1~c6展示了超快熔化过程中原子尺度演化微观图像。体系在惯性约束条件下等容加压，在t = 5 ps时内部应力高达6.8 GPa后，由于热动压只能沿着垂直于表面的方向上释放，这种单轴膨胀过程会导致晶格各向异性的畸变，从而降低晶格稳定性，加速体系的熔化[21,46]。在超快激光作用后t = 4 ps时，在薄膜中观察到液相部分成核位点的出现，主要集中于表面区域，这对应了部分晶格结构在热应力释放和高温下形成缺陷。随着晶格温度上升，液相成核位点大量出现，在t = 8 ps时在薄膜内均匀分布，并在接下来的4 ps内快速生长，驱动熔化的发生。在t = 16 ps时薄膜晶格结构已经完全消失，其熔化前沿传播的等效速率约为1000 m/s，是非均匀熔化速率的20倍，这是由于电声耦合带来的快速升温导致晶格温度迅速超过晶格热稳定性，同时由于激光能量的均匀沉积，使得薄膜体系内部发生了均匀的液相成核生长，产生了均匀熔化现象。该现象与Mo等[8]在Au上观察到的皮秒尺度熔化相符合，这也表明Jourdain等[12]基于XANES观察到的超快熔化机制很有可能来自均匀成核机制。

本研究为理解激光作用下的熔化动力学提供了原子尺度的微观图像，同时也为激光-物质相互作用提供了有效的研究手段。在本工作基础上，后续可以进一步研究材料在激光烧蚀中的爆炸沸腾、解体等复杂物理现象[58]，为强激光作用下的材料响应提供原子尺度的独特见解。同时，由于神经网络势能面的可靠性，研究对象可从金属单质拓展到合金、非晶等复杂体系，以建立从微观理论到宏观应用的桥梁。

3 结论

本工作以Cu为例，充分验证了神经网络PES在描述激光过程涉及到的晶格振动、热物理等性质上的准确性，并在此基础上，将神经网络模型与双温模型分子动力学结合，实现了Cu薄膜在脉冲激光作用下原子尺度动力学过程的直接模拟。结合量子精度、大尺度的热力学与微观结构演化，观察到在不同激光通量下，Cu的熔化动力学会表现出时间尺度截然不同的2种行为。激光通量接近熔化阈值时(18 mJ/cm2)，Cu薄膜发生非均匀熔化，固/液界面从表面出现，并以数十米/秒的速率向内传播，往往需要数百皮秒才能完成熔化过程；在激光通量远大于融化阈值时(30 mJ/cm2)，Cu薄膜会经历不同于传统加热过程的均匀熔化过程。由于晶格温度迅速超过热稳定性极限，薄膜内会出现均匀的液相成核并快速生长，完全熔化仅需十几皮秒。

参考文献

Abu-Shawareb H, Acree R, Adams P, et al.

Lawson criterion for ignition exceeded in an inertial fusion experiment

[J]. Phys. Rev. Lett., 2022, 129: 075001

[本文引用: 1]

Shugaev M V, Wu C P, Armbruster O, et al.

Fundamentals of ultrafast laser-material interaction

[J]. MRS Bull., 2016, 41: 960

[本文引用: 1]

Roy N K, Dibua O G, Jou W, et al.

A comprehensive study of the sintering of copper nanoparticles using femtosecond, nanosecond, and continuous wave lasers

[J]. J. Micro Nano-Manuf., 2018, 6: 010903

[本文引用: 1]

Cheng C W, Chang C L, Chen J K, et al.

Femtosecond laser melting of silver nanoparticles: Comparison of model simulations and experimental results

[J]. Appl. Phys., 2018, 124A: 371

[本文引用: 1]

Zhang H, Li C, Bevillon E, et al.

Ultrafast destructuring of laser-irradiated tungsten: Thermal or nonthermal process

[J]. Phys. Rev., 2016, 94B: 224103

[本文引用: 1]

Chen Z, Mo M, Soulard L, et al.

Interatomic potential in the nonequilibrium warm dense matter regime

[J]. Phys. Rev. Lett., 2018, 121: 075002

[本文引用: 1]

Ernstorfer R, Harb M, Hebeisen C T, et al.

The formation of warm dense matter: Experimental evidence for electronic bond hardening in gold

[J]. Science, 2009, 323: 1033

DOI      PMID      [本文引用: 1]

Under strong optical excitation conditions, it is possible to create highly nonequilibrium states of matter. The nuclear response is determined by the rate of energy transfer from the excited electrons to the nuclei and the instantaneous effect of change in electron distribution on the interatomic potential energy landscape. We used femtosecond electron diffraction to follow the structural evolution of strongly excited gold under these transient electronic conditions. Generally, materials become softer with excitation. In contrast, the rate of disordering of the gold lattice is found to be retarded at excitation levels up to 2.85 megajoules per kilogram with respect to the degree of lattice heating, which is indicative of increased lattice stability at high effective electronic temperatures, a predicted effect that illustrates the strong correlation between electronic structure and lattice bonding.

Mo M Z, Chen Z, Li R K, et al.

Heterogeneous to homogeneous melting transition visualized with ultrafast electron diffraction

[J]. Science, 2018, 360: 1451

DOI      PMID      [本文引用: 3]

The ultrafast laser excitation of matters leads to nonequilibrium states with complex solid-liquid phase-transition dynamics. We used electron diffraction at mega-electron volt energies to visualize the ultrafast melting of gold on the atomic scale length. For energy densities approaching the irreversible melting regime, we first observed heterogeneous melting on time scales of 100 to 1000 picoseconds, transitioning to homogeneous melting that occurs catastrophically within 10 to 20 picoseconds at higher energy densities. We showed evidence for the heterogeneous coexistence of solid and liquid. We determined the ion and electron temperature evolution and found superheated conditions. Our results constrain the electron-ion coupling rate, determine the Debye temperature, and reveal the melting sensitivity to nucleation seeds.Copyright © 2018 The Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science. No claim to original U.S. Government Works.

Mo M Z, Murphy S, Chen Z J, et al.

Visualization of ultrafast melting initiated from radiation-driven defects in solids

[J]. Sci. Adv., 2019, 5: eaaw0392

Wu J, Tang M X, Zhao L R, et al.

Ultrafast atomic view of laser-induced melting and breathing motion of metallic liquid clusters with MeV ultrafast electron diffraction

[J]. Proc. Natl. Acad. Sci. USA, 2022, 119: e2111949119

[本文引用: 1]

Mahieu B, Jourdain N, Ta Phuoc K, et al.

Probing warm dense matter using femtosecond X-ray absorption spectroscopy with a laser-produced betatron source

[J]. Nat. Commun., 2018, 9: 3276

DOI      PMID      [本文引用: 1]

Exploring and understanding ultrafast processes at the atomic level is a scientific challenge. Femtosecond X-ray absorption spectroscopy (XAS) arises as an essential experimental probing method, as it can simultaneously reveal both electronic and atomic structures, and thus potentially unravel their nonequilibrium dynamic interplay which is at the origin of most of the ultrafast mechanisms. However, despite considerable efforts, there is still no femtosecond X-ray source suitable for routine experiments. Here we show that betatron radiation from relativistic laser-plasma interaction combines ideal features for femtosecond XAS. It has been used to investigate the nonequilibrium dynamics of a copper sample brought at extreme conditions of temperature and pressure by a femtosecond laser pulse. We measured a rise-time of the electron temperature below 100 fs. This experiment demonstrates the great potential of the table-top betatron source which makes possible the investigation of unexplored ultrafast processes in manifold fields of research.

Jourdain N, Lecherbourg L, Recoules V, et al.

Ultrafast thermal melting in nonequilibrium warm dense copper

[J]. Phys. Rev. Lett., 2021, 126: 065001

[本文引用: 3]

Chen Z, Curry C B, Zhang R, et al.

Ultrafast multi-cycle terahertz measurements of the electrical conductivity in strongly excited solids

[J]. Nat. Commun., 2021, 12: 1638

DOI      PMID      [本文引用: 1]

Key insights in materials at extreme temperatures and pressures can be gained by accurate measurements that determine the electrical conductivity. Free-electron laser pulses can ionize and excite matter out of equilibrium on femtosecond time scales, modifying the electronic and ionic structures and enhancing electronic scattering properties. The transient evolution of the conductivity manifests the energy coupling from high temperature electrons to low temperature ions. Here we combine accelerator-based, high-brightness multi-cycle terahertz radiation with a single-shot electro-optic sampling technique to probe the evolution of DC electrical conductivity using terahertz transmission measurements on sub-picosecond time scales with a multi-undulator free electron laser. Our results allow the direct determination of the electron-electron and electron-ion scattering frequencies that are the major contributors of the electrical resistivity.

Hohlfeld J, Wellershoff S S, Güdde J, et al.

Electron and lattice dynamics following optical excitation of metals

[J]. Chem. Phys., 2000, 251: 237

[本文引用: 2]

Lin Z B, Zhigilei L V.

Thermal excitation of d band electrons in Au: Implications for laser-induced phase transformations

[A]. Proceedings of SPIE 6261, High-Power Laser Ablation VI [C]. Taos: SPIE, 2006: 62610U

Lin Z B, Zhigilei L V, Celli V.

Electron-phonon coupling and electron heat capacity of metals under conditions of strong electron-phonon nonequilibrium

[J]. Phys. Rev., 2008, 77B: 075133

[本文引用: 2]

Lee J W, Kim M, Kang G, et al.

Investigation of nonequilibrium electronic dynamics of warm dense copper with femtosecond X-ray absorption spectroscopy

[J]. Phys. Rev. Lett., 2021, 127: 175003

[本文引用: 1]

Grolleau A, Dorchies F, Jourdain N, et al.

Femtosecond resolution of the nonballistic electron energy transport in warm dense copper

[J]. Phys. Rev. Lett., 2021, 127: 275901

[本文引用: 1]

Lin Z B, Zhigilei L V.

Time-resolved diffraction profiles and atomic dynamics in short-pulse laser-induced structural transformations: Molecular dynamics study

[J]. Phys. Rev., 2006, 73B: 184113

[本文引用: 3]

Molina J M, White T G.

A molecular dynamics study of laser-excited gold

[J]. Matter Radiat. Extremes, 2022, 7: 036901

[本文引用: 1]

Ivanov D S, Zhigilei L V.

Effect of pressure relaxation on the mechanisms of short-pulse laser melting

[J]. Phys. Rev. Lett., 2003, 91: 105701

[本文引用: 2]

Daraszewicz S L, Giret Y, Naruse N, et al.

Structural dynamics of laser-irradiated gold nanofilms

[J]. Phys. Rev., 2013, 88B: 184101

Murphy S T, Daraszewicz S L, Giret Y, et al.

Dynamical simulations of an electronically induced solid-solid phase transformation in tungsten

[J]. Phys. Rev., 2015, 92B: 134110

Murphy S T, Giret Y, Daraszewicz S L, et al.

Contribution of electronic excitation to the structural evolution of ultrafast laser-irradiated tungsten nanofilms

[J]. Phys. Rev., 2016, 93B: 104105

[本文引用: 1]

Arefev M I, Shugaev M V, Zhigilei L V.

Kinetics of laser-induced melting of thin gold film: How slow can it get?

[J]. Sci. Adv., 2022, 8: eabo2621

[本文引用: 1]

Behler J, Parrinello M.

Generalized neural-network representation of high-dimensional potential-energy surfaces

[J]. Phys. Rev. Lett., 2007, 98: 146401

[本文引用: 1]

Zhang L F, Han J Q, Wang H, et al.

Deep potential molecular dynamics: A scalable model with the accuracy of quantum mechanics

[J]. Phys. Rev. Lett., 2018, 120: 143001

Zeng Q Y, Chen B, Yu X X, et al.

Towards large-scale and spatiotemporally resolved diagnosis of electronic density of states by deep learning

[J]. Phys. Rev., 2022, 105B: 174109

Zeng Q Y, Yu X X, Yao Y P, et al.

Ab initio validation on the connection between atomistic and hydrodynamic description to unravel the ion dynamics of warm dense matter

[J]. Phys. Rev. Res., 2021, 3: 033116

Yang F H, Zeng Q Y, Chen B, et al.

Lattice thermal conductivity of MgSiO3 perovskite and post-perovskite under lower mantle conditions calculated by deep potential molecular dynamics

[J]. Chin. Phys. Lett., 2022, 39: 116301

Niu H Y, Bonati L, Piaggi P M, et al.

Ab initio phase diagram and nucleation of gallium

[J]. Nat. Commun., 2020, 11: 2654

DOI      PMID     

Elemental gallium possesses several intriguing properties, such as a low melting point, a density anomaly and an electronic structure in which covalent and metallic features coexist. In order to simulate this complex system, we construct an ab initio quality interaction potential by training a neural network on a set of density functional theory calculations performed on configurations generated in multithermal-multibaric simulations. Here we show that the relative equilibrium between liquid gallium, α-Ga, β-Ga, and Ga-II is well described. The resulting phase diagram is in agreement with the experimental findings. The local structure of liquid gallium and its nucleation into α-Ga and β-Ga are studied. We find that the formation of metastable β-Ga is kinetically favored over the thermodinamically stable α-Ga. Finally, we provide insight into the experimental observations of extreme undercooling of liquid Ga.

Santos-Florez P A, Yanxon H, Kang B, et al.

Size-dependent nucleation in crystal phase transition from machine learning metadynamics

[J]. Phys. Rev. Lett., 2022, 129: 185701

Chen B, Zeng Q Y, Yu X X, et al.

Three-step formation of diamonds in shock-compressed hydrocarbons: Decomposition, species separation, and nucleation

[J]. arXiv: 2208. 01830, 2022

Chen B, Zeng Q Y, Wang H, et al.

Atomistic mechanism of phase transition in shock compressed gold revealed by deep potential

[J]. arXiv: 2006. 13136, 2021

Qiu R, Zeng Q Y, Wang H, et al.

Anomalous thermal transport across the superionic transition in ice

[J]. Chin. Phys. Lett., 2023, 40: 116301

[本文引用: 1]

Zeng Q Y, Chen B, Zhang S, et al.

Full-scale ab initio simulations of laser-driven atomistic dynamics

[J]. npj Comput. Mater., 2023, 9: 213

[本文引用: 3]

Wang H, Zhang L F, Han J Q, et al.

DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics

[J]. Comput. Phys. Commun., 2018, 228: 178

[本文引用: 2]

Zhang L F, Lin D Y, Wang H, et al.

Active learning of uniformly accurate interatomic potentials for materials simulation

[J]. Phys. Rev. Mater., 2019, 3: 023804

[本文引用: 1]

Zhang Y Z, Gao C, Liu Q R, et al.

Warm dense matter simulation via electron temperature dependent deep potential molecular dynamics

[J]. Phys. Plasmas, 2020, 27: 122704

Zeng Q Y, Dai J Y.

Structural transition dynamics of the formation of warm dense gold: From an atomic scale view

[J]. Sci. China Phys. Mech. Astron., 2020, 63: 263011

[本文引用: 1]

Dai J Y, Hou Y, Yuan J M.

Unified first principles description from warm dense matter to ideal ionized gas plasma: Electron-ion collisions induced friction

[J]. Phys. Rev. Lett., 2010, 104: 245001

[本文引用: 3]

Dai J Y, Kang D D, Zhao Z X, et al.

Dynamic ionic clusters with flowing electron bubbles from warm to hot dense iron along the hugoniot curve

[J]. Phys. Rev. Lett., 2012, 109: 175701

[本文引用: 3]

Kresse G, Furthmüller J.

Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set

[J]. Phys. Rev., 1996, 54B: 11169

[本文引用: 1]

Perdew J P, Burke K, Ernzerhof M.

Generalized gradient approximation made simple

[J]. Phys. Rev. Lett., 1996, 77: 3865

DOI      PMID     

Blöchl P E.

Projector augmented-wave method

[J]. Phys. Rev., 1994, 50B: 17953

[本文引用: 2]

Ivanov D S, Zhigilei L V.

Combined atomistic-continuum modeling of short-pulse laser melting and disintegration of metal films

[J]. Phys. Rev., 2003, 68B: 064114

[本文引用: 3]

Plimpton S.

Fast parallel algorithms for short-range molecular dynamics

[J]. J. Comput. Phys., 1995, 117: 1

[本文引用: 1]

Kittel C. Kittel's Introduction to Solid State Physic [M]. Beijing: Machine Press, 2020: 86

[本文引用: 4]

Tadano T, Gohda Y, Tsuneyuki S.

Anharmonic force constants extracted from first-principles molecular dynamics: Applications to heat transfer simulations

[J]. J. Phys.: Condens. Matter., 2014, 26: 225402

[本文引用: 2]

Nilsson G, Rolandson S.

Lattice dynamics of copper at 80 K

[J]. Phys. Rev., 1973, 7B: 2393

[本文引用: 2]

Japel S, Schwager B, Boehler R, et al.

Melting of copper and nickel at high pressure: The role of d electrons

[J]. Phys. Rev. Lett., 2005, 95: 167801

[本文引用: 8]

Simon F, Glatzel G.

Bemerkungen zur schmelzdruckkurve

[J]. Z. Anorg. Allg. Chem., 1929, 178: 309

[本文引用: 2]

Cagran C, Wilthan B, Pottlacher G.

Enthalpy heat of fusion and specific electrical resistivity of pure silver, pure copper and the binary Ag-28Cu alloy

[J]. Thermochim. Acta, 2006, 445: 104

[本文引用: 6]

Nizomov Z, Saidov R H, Gulov B N, et al.

Temperature dependence of the heat capacity of aluminium, copper, silicon, magnesium, zinc and comparison with Debye theory

[J]. Interconf, 2021, 55: 307

[本文引用: 2]

Smirnov N A.

Copper, gold, and platinum under femtosecond irradiation: Results of first-principles calculations

[J]. Phys. Rev., 2020, 101B: 094103

[本文引用: 3]

Cho B I, Ogitsu T, Engelhorn K, et al.

Measurement of electron-ion relaxation in warm dense copper

[J]. Sci. Rep., 2016, 6: 18843

DOI      PMID      [本文引用: 6]

Experimental investigation of electron-ion coupling and electron heat capacity of copper in warm and dense states are presented. From time-resolved x-ray absorption spectroscopy, the temporal evolution of electron temperature is obtained for non-equilibrium warm dense copper heated by an intense femtosecond laser pulse. Electron heat capacity and electron-ion coupling are inferred from the initial electron temperature and its decrease over 10 ps. Data are compared with various theoretical models.

Hohlfeld J, Müller J G, Wellershoff S S, et al.

Time-resolved thermoreflectivity of thin gold films and its dependence on film thickness

[J]. Appl. Phys., 1997, 64B: 387

[本文引用: 1]

Zhang Y W, Chen J K.

Ultrafast melting and resolidification of gold particle irradiated by pico- to femtosecond lasers

[J]. J. Appl. Phys., 2008, 104: 054910

[本文引用: 1]

/

〈 〉


版权所有 © 《金属学报》编辑部
地址: 沈阳市文化路72号, 中国科学院金属研究所(110016)
电话: +86- 024-23971286 　E-mail: jsxb@imr.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发 技术支持：support@magtech.com.cn