UN燃料具有密度高、导热系数高、熔点高、辐照稳定性好、裂变气体释放率低和具有较高的事故容错率等优点,是轻水反应堆、快堆的候选燃料。UN的U密度为13.55 g/cm3 [1 ] ,显著高于UO2 的U密度(9.75 g/cm3 )[2 ] ,采用燃料组件较小的UN燃料可以使得轻水反应堆的功率显著提高。室温下UN的导热系数为20.6 W/(m·K),显著高于UO2 的导热系数(3.5 W/(m·K)),采用高导热系数的UN燃料可以显著降低燃料温度,使得在过渡条件下拥有较大的安全裕度[3 ] 。然而,目前UN燃料芯块烧结制造工艺仍不成熟,其中一个重要原因是UN中的共价键比例高,烧结致密化较为困难[4 ] 。由于UN在高温下易分解,烧结温度提高和添加剂引入的限制,导致传统的烧结方法难以使芯块达到较高的致密度。此外,不同温度和燃耗的反应堆设计需要不同密度、孔隙率和几何形状的UN球团,孔隙率较低的高致密化UN颗粒可以强化燃料结构和延缓裂变气体释放[3 ] 。因此,研究UN球团烧结特性、微观组织对于指导UN烧结具有重要的意义。
近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3 ~9 ] 。实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面。尹邦跃和屈哲昊[4 ] 的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm。Muta等[6 ] 对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关。Malkki等[7 ] 采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6 ] 的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素。烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] 。烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化。表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输。然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理。因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义。
最近,Chen和Zhao[14 ] 总结了利用相场法设计材料以获得最佳性能的热力学基础和研究进展。Ishii等[15 ] 提出了一种新的数据同化方法来估算固相烧结材料的参数。陶瓷烧结过程的相场研究方面已经取得了一些成果[16 ~20 ] 。Ahmed等[16 ] 开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2 中晶粒长大动力学的影响。Kundin等[17 ] 提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响。Hötzer等[18 ] 提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2 O3 固态烧结过程。然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清。气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13 ,19 ] 。颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化。因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导。
本工作在表面扩散相场模型[16 ] 的基础上对扩散方程进行了修正,添加了含有平移旋转刚体运动的相互作用项,采用相场理论模拟了UN粉末在表面扩散与平移旋转刚体运动共同作用下颗粒间烧结颈的长大以及气孔的演化过程,研究了UN粉末烧结颈的形成过程、气孔收缩致密化的过程、形成稳定三叉晶界的过程以及多晶粒烧结过程,模拟结果与实验观察结果符合较好。
1 相场模型
1.1 相场变量
本模型通过引入与结构相关的一系列取向场变量η 1 ( r t ), η 2 ( r t ), …, ηp ( r t )和浓度场变量ρ ( r t )来表述不同取向的晶粒相和气孔相,它们是空间坐标( r t )的连续函数。其中,ηi (i = 1, 2, …, p )为非保守型相场变量,用来描述多晶中不同晶粒的取向,第i 个晶粒内部ηi 的取值为1,其余p - 1个取值为0;ρ ( r t )为保守型相场变量,在晶粒相取值为1,在气孔相取值为0。已有研究[20 ] 表明,当晶粒个数p > 32时,晶粒组织演变对p 取值的依赖性可以忽略。
1.2 自由能密度泛函数
本工作烧结相场模型的总自由能泛函数F 采用以下形式[21 ] :
F = ∫ V f ( ρ , η 1 , η 2 , ⋯ , η p ) + κ ρ 2 ∇ ρ 2 + κ η 2 ∑ i = 1 p ∇ η i 2 d V (1)
式中,第1项f 表示局部自由能密度函数;第2项和第3项为梯度自由能,分别表示气孔表面和晶界处的额外自由能;κρ 和κη 代表梯度能系数,取决于材料气孔表面和晶界处的能量和宽度,J/m;V 为空间体积。
$\begin{array}{l} f\left(\rho, \eta_{1}, \eta_{2}, \cdots, \eta_{p}\right)=A \rho^{2}(1-\rho)^{2}+B\left[\rho^{2}+\right. \\ \left.6(1-\rho) \sum_{i=1}^{p} \eta_{i}{ }^{2}-4(2-\rho) \sum_{i=1}^{p} \eta_{i}{ }^{3}+3\left(\sum_{i=1}^{p} \eta_{i}{ }^{2}\right)^{2}\right] \end{array}$(2)
式中,A 和B 为与材料气孔表面和晶界处能量和宽度有关的物理参数,J/m3 ;方程右侧第1项为双势阱函数,在晶粒内部与气孔内部取得平衡值;方程右侧方括号中为多势阱函数,在晶粒内部取得平衡值。本工作所采用的自由能泛函数能够保证在各个晶粒内部和气孔相的内部取得p + 1个极小值。
κ η = 3 γ g b δ 4 (3)
κ ρ = 3 δ 2 γ s - γ g b 4 (4)
A = 12 γ s - 7 γ g b δ (5)
B = γ g b δ (6)
式中,γ gb 和γ s 分别为材料的比晶界能和比表面能,J/m2 ;δ 为扩散界面的宽度,m。
1.3 动力学演化方程
假设烧结过程的质量是守恒的,为了描述烧结过程的气孔收缩和致密化,在演化动力学Cahn-Hilliard方程[21 ] 中引入平流通量项。因此,ρ 的演化方程为:
∂ ρ ∂ t = ∇ ⋅ M ∇ δ F δ ρ - ρ v a d v ( r ) = ∇ ⋅ M ∇ ∂ f ∂ ρ - κ ρ ∇ 2 ρ - ∇ ⋅ ρ v a d v ( r ) (7)
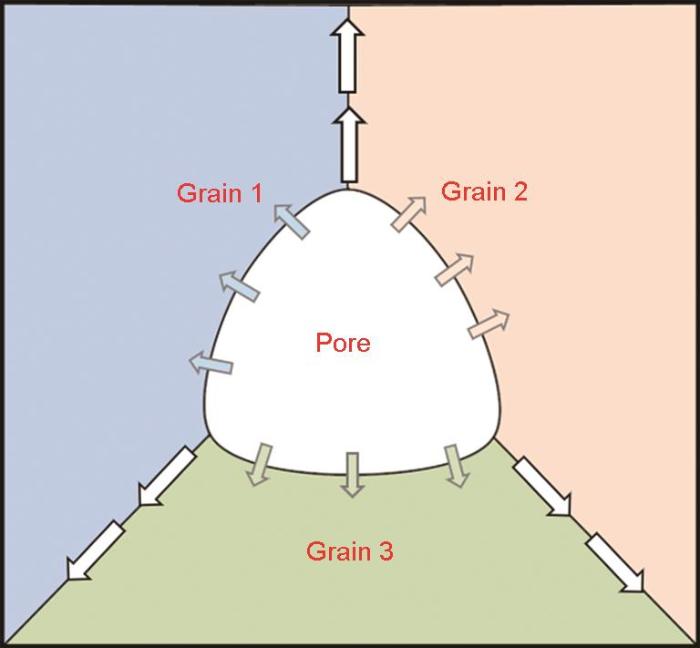
式中, v adv ( r v adv ( r 图1 为烧结模拟中空位扩散示意图,表示烧结过程中空位从凹面区域扩散到凸面区域。
图1
图1
烧结模拟中空位扩散示意图
Fig.1
Schematic of vacancy diffusion simulated in sintering simulation (Arrows show the paths of vacancy diffusion along free surfaces and grain boundaries)
M = v m D s R T (8)
D s = D s ρ 2 ( 1 - ρ 2 ) T s (9)
Τ s = I - n s ⊗ n s (10)
n s = ∇ ρ ∇ ρ (11)
式中,ν m 为摩尔体积;R 为气体常数;T 为温度; D s 为表面扩散系数张量;D s 为表面扩散率,取决于材料的性质; T s 为表面投影张量,保证表面扩散在晶粒与气孔接触的表面切线方向; I n s 为垂直于曲面的单位法向量。
ηi 的演化动力学方程由Allen-Cahn方程[21 ] 引入平流通量项后表示为:
∂ η i ∂ t = - L δ F δ η i - ∇ ⋅ η i v a d v i ( r ) = - L ∂ f ∂ η i - κ η ∇ 2 η i - ∇ ⋅ η i v a d v i ( r ) ( i = 1 , 2 , ⋯ , p ) (12)
式中, v adv i r r i 的平流速度;L 为表征晶界迁移率的系数,在各向同性假设下为常数,与材料的具体性质关系如下[24 ] :
L = γ g b M b κ η (13)
M b = v m D g b 10 R T δ (14)
式中,M b 为晶界迁移率;D gb 为晶界扩散率,取决于材料的性质。
根据 式(7)修正的Cahn-Hilliard方程与 式(12)修正的Allen-Cahn方程,可以求得相场变量随时间的演化过程。通过对相场变量的变化求解,可以计算出演化任意时刻的微观组织与空间分布。本工作采用的求解相场方程的数值方法为有限差分法。对于相互关联的非线性偏微分方程组,时间上采用显示Euler算法;空间上采用五点差分法求解Laplace项[25 ] 。
为了直观地表征烧结过程,本工作中可视化变量φ 为[20 ] :
φ = ∑ i η i 2 (15)
1.4 平流速度场 v adv (r )
烧结过程中粒子的刚体运动由平移和转动2部分组成, v adv ( r [22 ] :
v a d v ( r ) = ∑ i v a d v i ( r ) = ∑ i [ v t i ( r ) + v r i ( r ) ] (16)
式中, v t i r r i 的平移速度,表达式为[22 ] :
v t i ( r ) = m t η i ( r ) V i ∫ V κ F ∑ i ≠ j ρ - ρ 0 ⋅ f V η i , η j ∇ η i - ∇ η j d 3 r (17)
V i = ∫ V η i ( r ) d 3 r (18)
式中,m t 为平移迁移率,m2 /s;Vi 为晶粒i 的体积;积分项为作用在晶粒i 质心上的合力;κ F 为质量密度相对于在晶界平衡值变化的刚度系数,本工作取κ F = 100;常数ρ 0 为晶界质量密度的平衡值,本工作取ρ 0 = 0.98;r 为空间位置;函数fV 用来识别2颗粒晶界之间的区域,表达式为:
f V η i , η j = 1 ( η i η j ≥ c * ) 0 ( o t h e r w i s e ) (19)
式中,c * 为晶界阈值。 式(17)右侧的梯度运算在相邻粒子之间产生大小相等、方向相反的局域力。
v r i r r i 的旋转速度,表达式为[22 ] :
v r i ( r ) = m r V i T i × ( r - r c i ) η i ( r ) (20)
式中,m r 为转动迁移率,m2 /s; T i i 的扭矩,表达式为:
T i = ∫ V ( r - r c i ) × κ F ∑ i ≠ j ρ - ρ 0 f η i , η j ∇ η i - ∇ η j d 3 r (21)
r c i = 1 V i ∫ V r η i ( r ) d 3 r (22)
2 无量纲化处理
无量纲化后的动力学方程与量纲控制方程具有相同的形式,可以在不改变驱动力的情况下缩放模型参数,将模拟的数量级统一,减小计算误差。本工作相场模型的变量与参数采用无量纲形式进行描述。
根据 式(7),保守场演化方程含有量纲的量为t 、 M F 、∇、 v adv ( r l * 、参考时间t* 和参考能量密度ε * ,分别得到无量纲Hamilton算符∇ ˜ = l * ∇ τ = t / t* 和无量纲自由能F ˜ F / ε * 。因此, 式(7)变形得:
∂ ρ ∂ τ = ∇ ˜ ⋅ M ε * t * l * 2 ∇ ˜ δ F ˜ δ ρ - t * l * ρ v a d v ( r ) = ∇ ˜ ⋅ M ε * t * l * 2 ⋅ ∇ ˜ 1 ε * ∂ f ∂ ρ - κ ρ ε * l * 2 ∇ ˜ 2 ρ - ∇ ˜ ⋅ t * l * ρ v a d v ( r ) (23)
由此可得无量纲迁移率张量M ˜ M ε * t * / l *2 ;无量纲平移迁移率m ˜ t = m t t * / l * m ˜ r = m r t * / l *
根据 式(12),非保守场演化方程含有量纲的量为t 、L 、F 、∇和 v adv i r 式(12)变形得:
∂ η i ∂ τ = - L ε * t * δ F ˜ δ η i - ∇ ˜ ⋅ t * l * η i v a d v i ( r ) = - L ε * t * 1 ε * ∂ f ∂ η i - κ η ε * l * 2 ∇ 2 η i - ∇ ˜ ⋅ t * l * η i v a d v i ( r ) ( i = 1 , 2 , ⋯ , p ) (24)
本工作取t* = 1 / (Lε * ),ε * = B ;则L ˜ B = 1;l * 的取值与δ 有关,对应无量纲化之后一个单位长度占有的界面宽度,本工作中,l * = δ / m (其中,m 代表扩散界面在模拟中占据的格点数)。
根据所选取的参考物理量,无量纲迁移率张量M ˜ F ˜ A 、B 、κρ 、κη 等参数对应的无量纲形式分别为:
M ˜ = 15 D s m 2 2 D g b m ˜ t = m m t δ , m ˜ r = m m r δ A ˜ = A ε * = 12 γ s - 7 γ g b γ g b B ˜ = B ε * = 1 κ ˜ ρ = κ ρ ε * l * 2 = 3 4 2 γ s - γ g b γ g b m 2 κ ˜ η = κ η ε * l * 2 = 3 4 m 2 (25)
本工作利用相场模型对UN陶瓷粉末在1823 K温度下的烧结过程进行了数值模拟,模拟中用到的UN物理参数如表1 [26 ,27 ] 所示。
将UN的物理参数代入上述方程中,求得各无量纲参数的具体数值如表2 所示。
3 结果与讨论
3.1 2 个颗粒烧结
本工作采用相场模型,模拟了双晶粒结构中UN陶瓷粉末烧结过程,将该相场模型的模拟结果与未加平流通量相场模型的模拟结果进行对比分析。所选模拟区域差分网格尺寸为150 × 150,选取周期性边界条件。分析平流通量对UN陶瓷粉末烧结组织演变过程、烧结颈形成、平衡二面角和致密化的影响。
3.1.1 烧结颈的形成
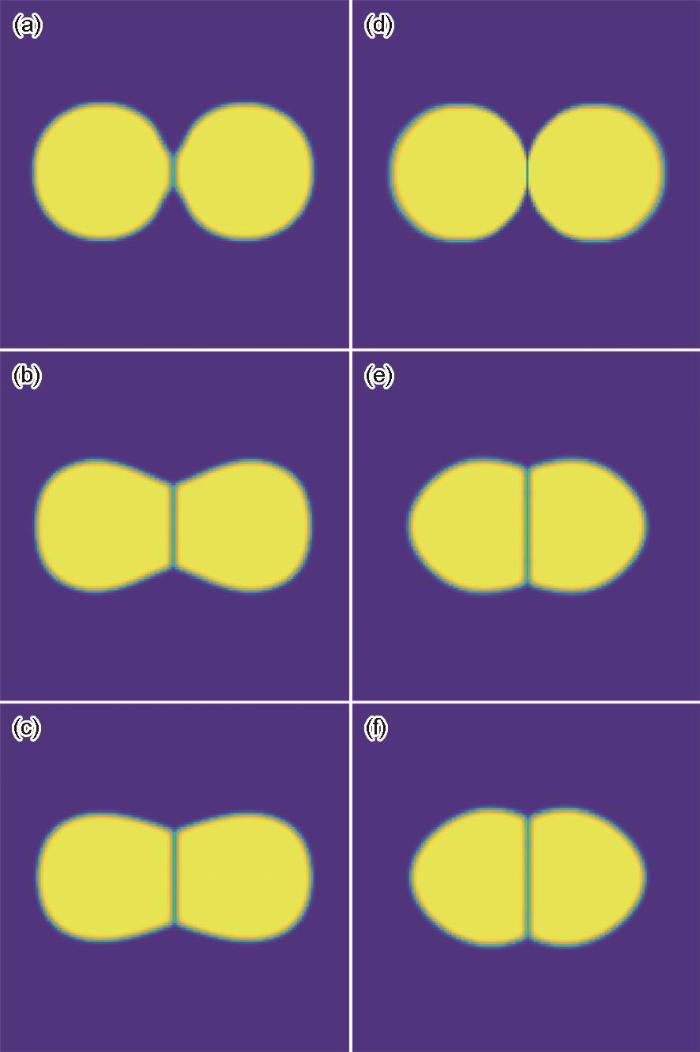
图2 为未引入平流通量和引入平流通量2个等尺寸的圆形颗粒在烧结过程中的组织演变。其中颗粒的半径R = 30,与平流通量模型模拟相关的参数m t = 30,c * = 0.05,κ F = 100,ρ 0 = 0.98。从图2a~c 与d~f 对比可以看出,未引入平流通量的模拟烧结颈形成较慢,颗粒位置无明显移动;含有平流通量的模拟烧结颈的形成明显更快,颗粒位置发生移动,且稳态时烧结颈的长度更长。这与文献[19 ]给出的致密化特征十分吻合。烧结致密化取决于颗粒-孔隙相互作用,表面扩散主导的未加平流通量模型对烧结过程孔隙收缩没有贡献,所以烧结颈形成较慢;引入平流通量模型含有颗粒刚体运动过程,空位可以被晶界吸收湮灭,所以不仅促进烧结颈增长,且随着烧结颈生长,颗粒彼此接近。
图2
图2
平流通量对2个晶粒烧结形貌演化的影响
Fig.2
Simulated effects of advection flux on morphologies of two grains with the boundary between them by the phase-field methods of without (a-c) and with (d-f) advection flux (a, d) 2 × 104 step (b, e) 50 × 104 step (c, f) 100 × 104 step
图3 为未引入平流通量与引入平流通量2种模拟数据的烧结颈对数增长曲线。可以看出,未引入平流通量模拟的烧结颈增长曲线近似为一条直线,斜率为0.21左右,满足烧结颈曲线增长规律[11 ] 。引入平流通量模拟的烧结颈曲线分为3个时期:烧结前期,烧结颈的增长较快,斜率为0.68左右,这是因为颗粒的致密化移动使得烧结颈更快增长,从A 点到B 点平流通量起主要作用导致晶界宽度变窄;烧结中期,从B 点到C 点平流通量作用减弱,晶界宽度恢复,导致烧结颈长度下降;烧结后期,烧结颈不再增长且相比于未引入平流通量模型提前达到稳态,斜率为0.06左右。引入平流通量模型对烧结颈的形成在烧结前期作用较强,后期作用不明显。
图3
图3
平流通量对2个颗粒烧结颈增长曲线的影响
Fig.3
Logarithmic growth curves of particle sintered neck methods for without and with advection flux (l —neck length, t' —time step)
3.1.2 平衡二面角
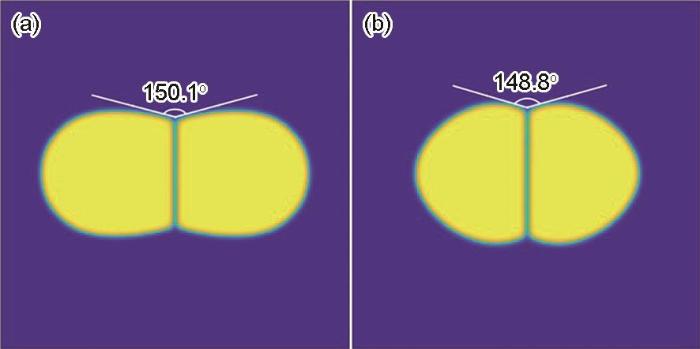
界面性质在烧结过程中的气孔收缩、致密化和粗化过程中起关键作用。相邻的2个粒子在相界处由于表面能和晶界能形成一个平衡二面角(Ψ ),在各向同性条件下,晶界处平衡二面角方程为[28 ] :
Ψ = 2 a r c c o s γ g b 2 γ s (26)
图4 分别为未引入平流通量与引入平流通量2种烧结模型的平衡二面角,演化的总时间为2 × 106 step。本工作UN烧结晶界能与界面能的比值为γ gb / γ s = 0.5,对应计算值为Ψ = 150°。从图4 可以看出,未引入平流通量模拟平衡二面角与理论计算值吻合较好,引入平流通量模拟最终平衡二面角与理论计算值有较小误差。证明了平流通量的引入会加快烧结颈的形成,但最终平衡二面角仍然不变,只由材料的特性所决定。这与只考虑表面扩散[29 ] 的结论一致,平衡二面角与晶界能和界面能的比值保持一致。
图4
图4
平流通量对平衡二面角的影响
Fig.4
Simulated equilibrium dihedral angles by two sintering models
(a) without advection flux (b) with advection flux
3.1.3 晶界处气孔的收缩
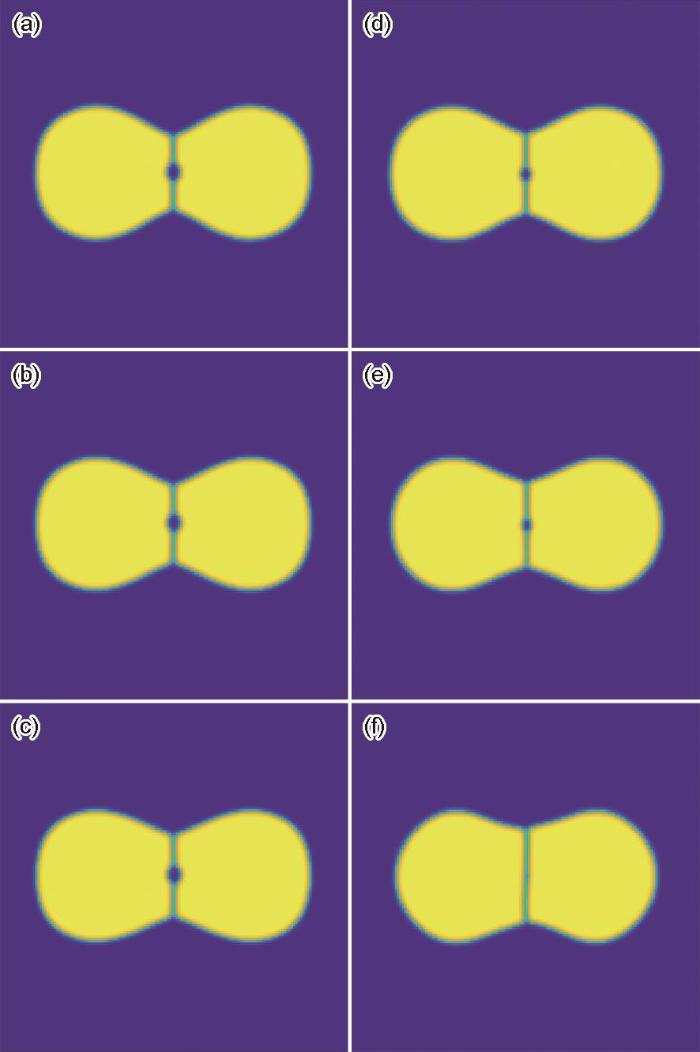
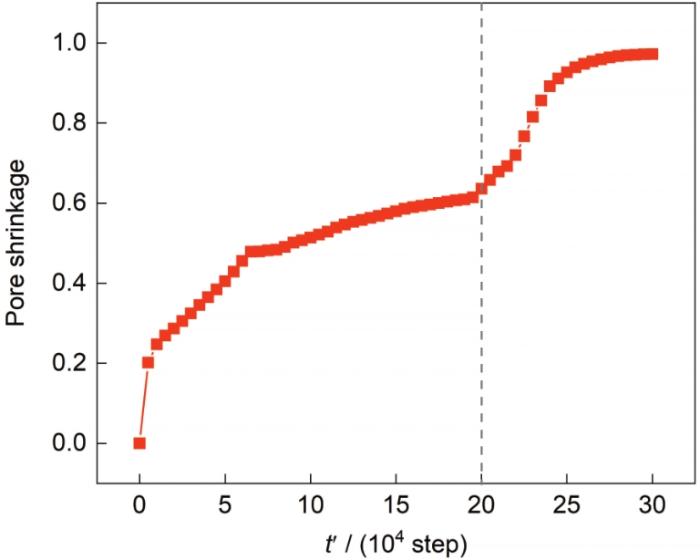
图5 为模拟双晶粒结构中晶界上含有气孔的致密化过程,将引入平流通量相场模型的模拟结果与未引入平流通量相场模型的模拟结果对比分析。从演化图像中可以看出,未引入平流通量模型晶界上的气孔稳定存在,引入平流通量模型晶界上的气孔逐渐收缩最终致密化。这与模型预期完全符合,表面扩散对致密化气孔收缩没有贡献。引入平流通量模型时2个颗粒晶界上气孔收缩随时间演化的曲线如图6 所示。从曲线可以看出,平流通量作用分为2个阶段,演化前期由表面扩散主导,平流通量致密化气孔收缩作用较小,气孔收缩较慢;演化后期平流通量致密化主导,致密化气孔收缩较快。
图5
图5
平流通量对2个颗粒烧结过程中晶界气孔演化的影响
Fig.5
Simulated evolutions of a pore in the grain boundary between two particles by the phase-field methods of without (a-c) and with (d-f) advection flux (a, d) 10 × 104 step (b, e) 20 × 104 step (c, f) 30 × 104 step
图6
图6
平流通量作用下2个颗粒烧结过程中晶界的气孔收缩率
Fig.6
Simulated pore shrinkage curve of grain boundary between two particles by the advection flux model
3.2 致密化烧结
3.2.1 三叉晶界处的气孔收缩
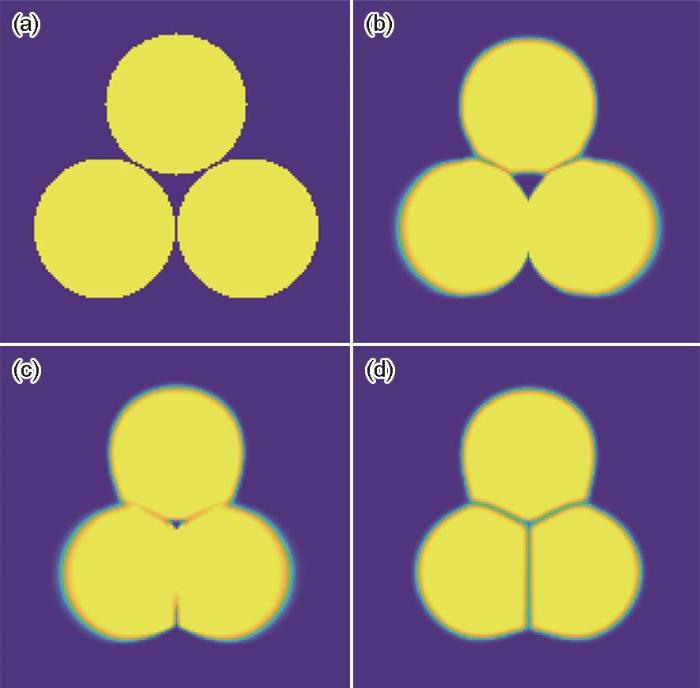
图7 为引入平流通量后,3个颗粒烧结的相场模拟结果。从图7b~d 可以看出,颗粒发生了平移,逐渐完成致密化收缩。为了更加清楚直观地理解平流通量的作用,图8 给出了与图7 对应的平流通量的空间分布和时间演变,其中蓝绿色的部分表示平流通量的作用,越接近蓝色表示平流通量的作用越强。从图8b~d 可以看出,平流通量作用于晶界与自由表面上,气孔收缩时平流通量逐渐增强,致密化完成后平流通量迅速减弱。
图7
图7
引入平流通量后3个颗粒烧结时的形貌演化过程
Fig.7
Simulated evolutions of three particles by the phase-field methods of advection flux
(a) 0 step (b) 2 × 104 step
(c) 4 × 104 step (d) 6 × 104 step
图8
图8
3个颗粒烧结时形貌演化过程所对应的平流通量
Fig.8
Simulated evolutions of advection flux on morphologies of three particles (The blue-green part shows the effect of the advective flux, and the closer to the blue, the stronger the effect of the advective flux)
(a) 0 step (b) 2 × 104 step
(c) 4 × 104 step (d) 6 × 104 step
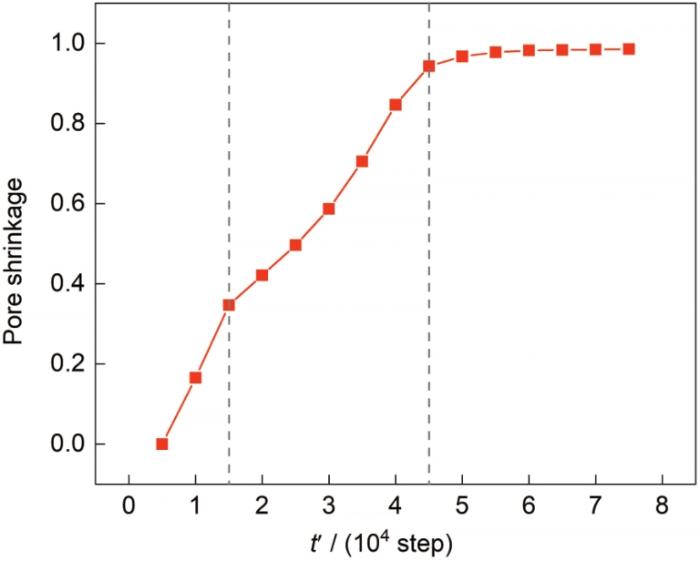
引入平流通量模型3个颗粒气孔收缩随时间演化的曲线如图9 所示。结合图8 平流通量的空间分布与时间演变,气孔收缩过程存在2个斜率的变化,可以将3个颗粒平流通量气孔收缩分为3个阶段:第1阶段,颗粒间形成颈缩;第2阶段,相邻颗粒通过平移运动导致粒子中心相互靠近;第3阶段,气孔完成收缩。在烧结过程中,涉及到2种机制:表面扩散机制和致密化平流通量机制。烧结初期,物质通过表面扩散主导传输,形成烧结颈;烧结中期烧结颈形成后,平流通量机制开始逐渐取代表面扩散主导,空位沿着晶界迁移,逐渐完成致密化过程;烧结后期最终致密化完成,达到稳态,平流通量迅速减弱。3个阶段斜率逐渐减小,表明随着烧结进行,烧结动力学逐渐减弱,平流通量随着烧结进行作用降低。
图9
图9
平流通量作用下3个颗粒烧结时晶界上封闭气孔的收缩率
Fig.9
Simulated pore shrinkage curve of grain boundary among three particles by the advection flux model
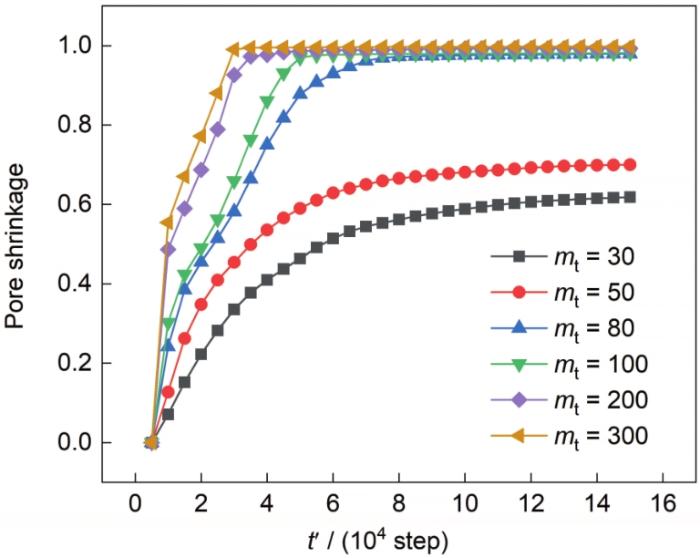
3.2.2 平流通量平移分量对气孔收缩的影响
为进一步探究颗粒平移和旋转对致密化气孔收缩的影响,图10 比较了不同平移迁移率下3个颗粒的气孔收缩。从图10 可以明显看出,颗粒平移对致密化气孔收缩具有显著促进作用,随着m t 的增大,致密化的速率增加,最终致密化的程度增加;当m t 超过80时,致密化程度相对不变,最终完成致密化;当m t 超过100时,致密化速率相对不变。与多相场(MPF)模型[30 ] 的结果对比发现,本工作模拟颗粒平移迁移率对致密化影响更加明显。
图10
图10
不同平移迁移率下的气孔收缩率
Fig.10
Pore shrinkage curves for different translation mobilities (m t )
3.3 稳定三叉晶界的形成
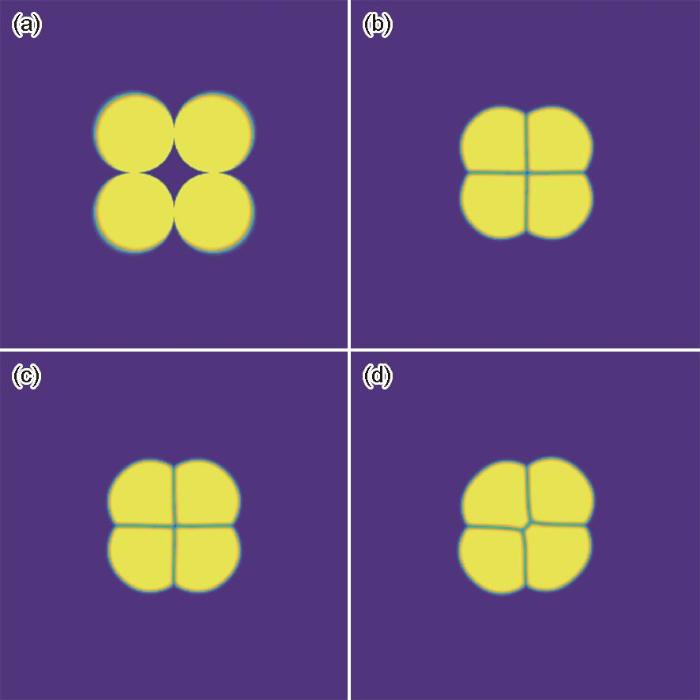
图11 为直径为60个格点的4个圆形颗粒形貌演变的相场模拟。可以看出,在演化初期,颗粒逐渐靠拢,气孔收缩完成致密化,形成角度为90°的四叉晶界;之后随着演化的进行,晶界发生变化,颗粒发生偏移,形成稳定的120°三叉晶界,这与大量的UN烧结实验[3 ~6 ,8 ,9 ] 结果相吻合。这是因为演化中期晶界为不稳定状态(相邻晶界间的夹角处于90°),当相邻晶界演化至夹角为120°时,三叉晶界形状保持稳定。结合图7 中3个颗粒烧结相场模拟结果,可以得出致密化气孔收缩完成趋向于形成稳定的120°三叉晶界。
图11
图11
引入平流通量后4个颗粒烧结时的形貌演化过程
Fig.11
Simulated evolutions of four particles by the phase-field methods of advection flux
(a) 1 × 104 step (b) 25 × 104 step
(c) 50 × 104 step (d) 100 × 104 step
3.4 多晶烧结过程
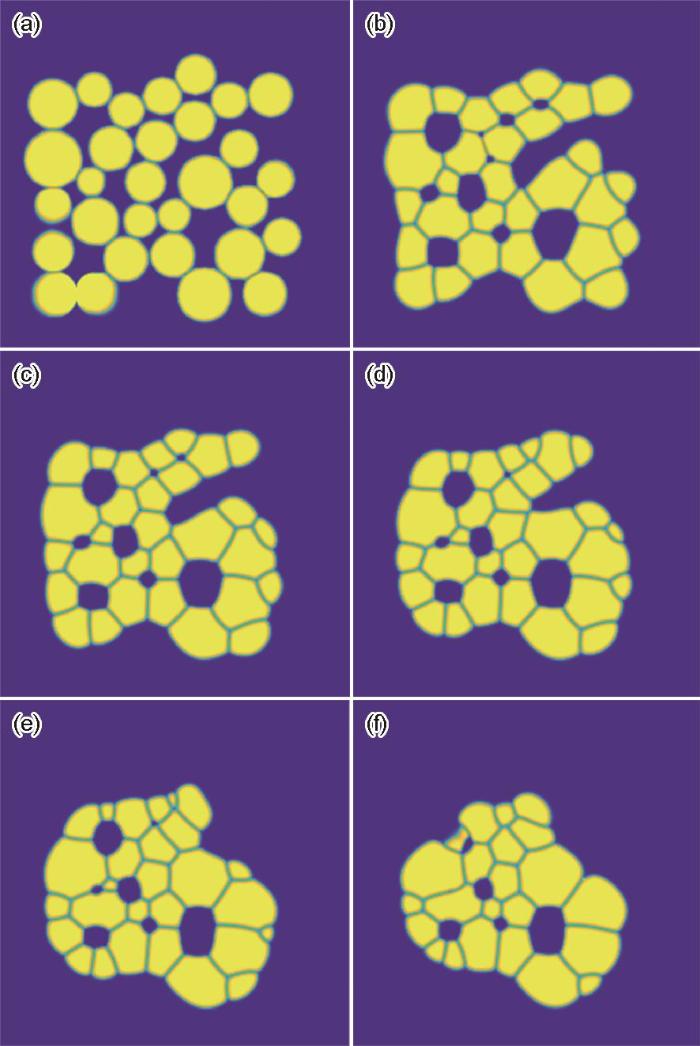
图12 为颗粒尺寸单峰分布的多晶烧结相场模拟,模拟所采用的组织为30个不同尺寸的颗粒(图12a )。为与实验条件一致,选择颗粒的平均半径为150 nm,整个模拟区域的网格尺寸为256 × 256,采用耦合平流通量的致密化模型进行相场模拟。从图12 可以看出,气孔对晶界移动起阻碍作用[31 ] ,气孔越大阻碍作用越强;相邻颗粒之间先形成烧结颈;颗粒之间形成气孔,气孔逐渐收缩,小气孔处晶界曲率较大、驱动力较强,优先完成致密化;致密化完成的部分逐渐形成稳定的120°三叉晶界。将本工作的演化模拟结果与真空热压烧结2 h的实验观察结果[4 ] 进行对比可得,UN烧结形貌演化形成三叉晶界、气孔收缩致密化的行为与实验结果趋势一致。
图12
图12
多晶烧结形貌演化的相场模拟
Fig.12
Simulated evolutions of multi-grain by the phase-field methods with unimodal particle size distribution
(a) 1 × 104 step (b) 40 × 104 step
(c) 80 × 104 step (d) 120 × 104 step
(e) 160 × 104 step (f) 200 × 104 step
4 结论
(1) 引入了描述粒子刚体运动的平流通量作用项,建立了固相烧结致密化过程的相场模型,动态再现了UN晶粒烧结过程中内部气孔完成收缩的全过程。研究发现:引入平流通量模型对烧结颈的形成,在烧结前期作用较强,后期作用不明显;平流通量刚体运动的加入会加快烧结颈的形成,但最终平衡二面角的取值仍然不变,只由晶界能和界面能的比值所决定。
(2) 烧结过程中气孔的收缩分为3个阶段:初始阶段由于表面扩散占主导地位,颗粒间形成颈缩;中间阶段,平流通量刚体运动引起的致密化逐渐占据主导地位,相邻晶粒通过平移运动导致粒子中心相互靠近;最终阶段,气孔完成收缩,即致密化完成阶段。随着烧结进行,烧结动力学逐渐减弱,平流通量刚体运动随着烧结进行作用降低。随着平移迁移率(m t )的增大,致密化速率逐渐增加,最终致密化程度增加;m t 超过100时致密化速率相对不变。
(3) 烧结相场模拟结果验证了相交120°的三叉晶界是能量上稳定的晶界,4个颗粒组成的晶界最终也演变成了稳定的三叉晶界;多晶UN颗粒烧结经历了烧结颈形成生长、气孔收缩致密化、稳定的三叉晶界形成等一系列微观过程;多晶烧结形成稳定的三叉晶界和气孔收缩致密化的现象与实验结果一致。
参考文献
View Option
[1]
Uno M Nishi T Takano M Thermodynamic and thermophysical properties of the actinide nitrides
[J]. Compr. Nucl. Mater. , 2012 , 2 : 61
[本文引用: 1]
[2]
Szpunar B Szpunar J A Thermal conductivity of uranium nitride and carbide
[J]. Int. J. Nucl. Energy , 2014 , 2014 : 178360
[本文引用: 1]
[3]
Yang K Kardoulaki E Zhao D et al Uranium nitride (UN) pellets with controllable microstructure and phase-fabrication by spark plasma sintering and their thermal-mechanical and oxidation properties
[J]. J. Nucl. Mater. , 2021 , 557 : 153272
DOI
URL
[本文引用: 4]
[4]
Yin B Y Qu Z H Property of uranium nitride ceramic pellet by hot press sintering
[J]. Atom. Energy Sci. Technol. , 2014 , 48 : 1850
[本文引用: 3]
尹邦跃 , 屈哲昊 热压烧结UN陶瓷芯块的性能
[J]. 原子能科学技术 , 2014 , 48 : 1850
DOI
[本文引用: 3]
UN燃料具有铀密度高、熔点高、热导率高、热膨胀系数低、辐照稳定性好等优点,是未来空间核电源、核火箭、快堆和ADS的重要候选燃料。本文采用金属铀粉与氮气在300~400℃直接发生化合反应,制得单相U<sub>2</sub>N<sub>3</sub>粉末。粒度为38.3 μm的U<sub>2</sub>N<sub>3</sub>粉末在1 600 ℃真空热压烧结,制得相对密度为93.5%、存在少量金属铀相的UN陶瓷;而18.1 μm的U<sub>2</sub>N<sub>3</sub>粉末在1 550 ℃真空热压烧结,制得相对密度为96.1%、不残留金属铀相的UN陶瓷,U与N的总质量分数为99.57%,每个金属杂质含量均低于50 μg/g,氧含量为1 048 μg/g,碳含量为502 μg/g。U<sub>2</sub>N<sub>3</sub>在1 027 ℃以上将会完全分解成UN,UN在1 627 ℃以上也会发生分解。
[5]
Mclaren J R Atkinson P W M The sintering of uranium mononitride
[J]. J. Nucl. Mater. , 1965 , 17 : 142
DOI
URL
[6]
Muta H Kurosaki K Uno M et al Thermal and mechanical properties of uranium nitride prepared by SPS technique
[J]. J. Mater. Sci. , 2008 , 43 : 6429
DOI
URL
[本文引用: 3]
[7]
Malkki P Jolkkonen M Hollmer T et al Manufacture of fully dense uranium nitride pellets using hydride derived powders with spark plasma sintering
[J]. J. Nucl. Mater. , 2014 , 452 : 548
DOI
URL
[本文引用: 1]
[8]
Johnson K D Wallenius J Jolkkonen M et al Spark plasma sintering and porosity studies of uranium nitride
[J]. J. Nucl. Mater. , 2016 , 473 : 13
DOI
URL
[本文引用: 1]
[9]
Johnson K D Lopes D A Grain growth in uranium nitride prepared by spark plasma sintering
[J]. J. Nucl. Mater. , 2018 , 503 : 75
DOI
URL
[本文引用: 2]
[10]
Mullins W W Two‐dimensional motion of idealized grain boundaries
[J]. J. Appl. Phys. , 1956 , 27 : 900
DOI
URL
[本文引用: 1]
To represent ideal grain boundary motion in two dimensions, a rule of motion of plane curves is considered whereby any given point of a curve moves toward its center of curvature with a speed that is proportional to the curvature. A general theorem is deduced concerning the change of area enclosed by such a curve. Three families of curves are found that obey the curvature rule of motion while undergoing the shape preserving transformations of uniform magnification, translation, and rotation respectively. Pieces of these curves represent the steady shapes of idealized grain boundaries under certain symmetrical conditions.
[11]
Rahaman M N Ceramic Processing and Sintering [M]. New York : Marcel Dekker , 1995 : 446
[本文引用: 1]
[12]
German R M Sintering Theory and Practice [M]. New York : Wiley-Interscience , 1996 : 130
[本文引用: 1]
[13]
Kazaryan A Wang Y Patton B R Generalized phase field approach for computer simulation of sintering: Incorporation of rigid-body motion
[J]. Scr. Mater. , 1999 , 41 : 487
DOI
URL
[本文引用: 2]
[14]
Chen L Q Zhao Y H From classical thermodynamics to phase-field method
[J]. Prog. Mater. Sci. , 2022 , 124 : 100868
DOI
URL
[本文引用: 1]
[15]
Ishii A Yamanaka A Miyoshi E et al Efficient estimation of material parameters using DMC-BO: Application to phase-field simulation of solid-state sintering
[J]. Mater. Today Commun. , 2022 , 30 : 103089
[本文引用: 1]
[16]
Ahmed K Pakarinen J Allen T et al Phase field simulation of grain growth in porous uranium dioxide
[J]. J. Nucl. Mater. , 2014 , 446 : 90
DOI
URL
[本文引用: 3]
[17]
Kundin J Sohaib H Schiedung R et al Phase-field modeling of pores and precipitates in polycrystalline systems
[J]. Modell. Simul. Mater. Sci. Eng. , 2018 , 26 : 065003
[本文引用: 1]
[18]
Hötzer J Seiz M Kellner M et al Phase-field simulation of solid state sintering
[J]. Acta Mater. , 2019 , 164 : 184
DOI
[本文引用: 1]
Manufacturing materials for high performance applications with tailored properties requires a deep knowledge about the sintering process and especially the underlying microstructure evolution. Due to the complex interplay of the material and process parameters as well as complex geometries it is challenging to predict the microstructure evolution during sintering with analytical models. A phase-field model based on the grand potential approach considering volume, surface and grain boundary diffusion is presented to describe the microstructural evolution during solid state sintering. To efficiently investigate realistic green bodies with multiple thousand particles in three dimensions, the model is implemented in a highly optimized manner in the massive parallel phase-field solver framework PACE3D. By comparing the neck growth rates and the particle approach in a two particle system for the different diffusion mechanisms a good agreement to analytic solutions is found. Based on a three dimensional green body of 24897 Al2O3-grains the densification is investigated with respect to the dominant diffusion mechanisms and compared with the analytic Coble model. Finally, the appearance of isolated pores in the microstructure is discussed. (C) 2018 Acta Materialia Inc. Published by Elsevier Ltd.
[19]
German R M Coarsening in sintering: grain shape distribution, grain size distribution, and grain growth kinetics in solid-pore systems
[J]. Crit. Rev. Solid State Mater. Sci. , 2010 , 35 : 263
DOI
URL
[本文引用: 2]
[20]
Fan D Chen L Q Computer simulation of grain growth using a continuum field model
[J]. Acta Mater. , 1997 , 45 : 611
DOI
URL
[本文引用: 3]
[21]
Cahn J W On spinodal decomposition
[J]. Acta Metall. , 1961 , 9 : 795
DOI
URL
[本文引用: 3]
[22]
Wang Y U Computer modeling and simulation of solid-state sintering: A phase field approach
[J]. Acta Mater. , 2006 , 54 : 953
DOI
URL
[本文引用: 4]
[23]
Ahmed K Yablinsky C A Schulte A et al Phase field modeling of the effect of porosity on grain growth kinetics in polycrystalline ceramics
[J]. Modell. Simul. Mater. Sci. Eng. , 2013 , 21 : 065005
[本文引用: 2]
[24]
Allen S M Cahn J W A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening
[J]. Acta Metall. , 1979 , 27 : 1085
DOI
URL
[本文引用: 1]
[25]
Biner S B Programming Phase-Field Modeling [M]. Switzerland : Springer International Publishing , 2017 : 18
[本文引用: 1]
[26]
Holt J B Almassy M Y Nitrogen diffusion in uranium nitride as measured by alpha particle activation of 15N
[J]. J. Am. Ceram. Soc. , 1969 , 52 : 631
DOI
URL
[本文引用: 4]
[27]
Bocharov D Gryaznov D Zhukovskii Y F et al Ab initio simulations of oxygen interaction with surfaces and interfaces in uranium mononitride
[J]. J. Nucl. Mater. , 2013 , 435 : 102
DOI
URL
[本文引用: 6]
[28]
Riedel H Svoboda J A theoretical study of grain growth in porous solids during sintering
[J]. Acta Metall. Mater. , 1993 , 41 : 1929
DOI
URL
[本文引用: 1]
[29]
Sun Z Y Yang C Liu W B Phase field simulations of the sintering process of UO2
[J]. Acta Metall. Sin. , 2020 , 56 : 1295
[本文引用: 1]
孙正阳 , 杨 超 , 柳文波 UO2 烧结过程的相场模拟
[J]. 金属学报 , 2020 , 56 : 1295
DOI
[本文引用: 1]
利用相场模型对UO<sub>2</sub>陶瓷粉末的烧结过程进行了模拟。在修正的相场模型中,不仅考虑了表面扩散、晶界扩散和晶格扩散3种各向异性的扩散机制对烧结组织形貌和烧结动力学的影响,而且考虑了不同陶瓷颗粒之间的界面能对烧结形貌的影响。基于实验条件和热力学物性参数,对UO<sub>2</sub>陶瓷粉末在2000 K的烧结过程进行了模拟。模拟结果显示:初始形貌为圆形的陶瓷粉末有利于烧结过程的进行;烧结过程中存在大晶粒吞噬小晶粒的现象;晶界扩散机制是UO<sub>2</sub>烧结过程中的主导机制;晶界能的改变导致晶界与相界之间的平衡二面角发生改变。在此基础上,模拟了多晶UO<sub>2</sub>陶瓷粉末的烧结过程,模拟结果与实验结果吻合较好。
[30]
Shi R P Wood M Heo T W et al Towards understanding particle rigid-body motion during solid-state sintering
[J]. J. Eur. Ceram. Soc. , 2021 , 41 : 211
DOI
URL
[本文引用: 1]
[31]
Sun Z Y Wang Y T Liu W B Phase-field simulation of the interaction between pore and grain boundary
[J]. Acta Metall. Sin. , 2020 , 56 : 1643
DOI
[本文引用: 1]
The grain boundary (GB) and average grain size considerably affect the properties of materials, such as the fracture strength, dielectric constant, and thermal conductivity. For instance, when subjected to irradiation at 1750 ℃, the swelling of the UO2 pellets and the release of fission gas from them decrease significantly with the increasing average grain size. However, several second-phase particles, such as pores, are inevitably introduced into a material during the solid-phase sintering or neutron radiation processes. Therefore, studying the interaction between the pores and GBs is considerably important. In this study, a phase-field model of the interaction between the pores and GBs is developed. Subsequently, the free-energy density function was modified, where the diffusion coefficient was incorporated in the tensor form. In addition, the selection of the phenomenological parameters, such as the coefficient in the free-energy density function of the phase-field model, was analyzed, and the influencing factors of interface energy and interface width were discussed. The phase-field model simulation results of the interaction between the pores and GBs show that the curvature of GB was the major driving force associated with the movement of GB and that pores resisted the movement of GB. Accordingly, the pores moved together with the GBs when the maximum pinning force exerted by the pores was larger than the driving force produced by the curvature of GB; however, the pores and GBs separated in the opposite case, during which the GB moved much faster than pores. The results of the phase-field simulation of the grain growth of the pore-containing UO2 show that the grain growth speed decreases with the increasing porosity. The average grain size of UO2 is a power function of time, the exponent of which increases with the increasing porosity.
孙正阳 , 王昱天 , 柳文波 气孔与晶界相互作用的相场模拟
[J]. 金属学报 , 2020 , 56 : 1643
DOI
[本文引用: 1]
对现有的气孔与晶界相互作用的相场模型进行改进,提出了新形式的自由能密度函数,并采用了张量形式的扩散系数。分析了相场模型中唯象参数的选择依据,并讨论了模型中界面能和界面宽度等物理参数的影响因素。气孔和晶界相互作用的相场模拟结果表明:晶界的曲率是晶界移动的动力,而气孔是晶界移动的阻力;当气孔施加的最大阻力大于等于晶界移动的动力时,气孔会随晶界一起运动;而当气孔施加的最大阻力小于晶界移动的动力时,气孔与晶界分离。若气孔与晶界未发生分离,体系的演化将由晶界主导转变为气孔主导,演化速率显著下降。含气孔UO<sub>2</sub>多晶体系的晶粒生长的相场模拟结果表明:气孔率越大,晶粒生长速率越慢;UO<sub>2</sub>平均晶粒直径与时间成幂函数关系,幂指数随气孔率的增大而增大。
Thermodynamic and thermophysical properties of the actinide nitrides
1
2012
... UN燃料具有密度高、导热系数高、熔点高、辐照稳定性好、裂变气体释放率低和具有较高的事故容错率等优点,是轻水反应堆、快堆的候选燃料.UN的U密度为13.55 g/cm3 [1 ] ,显著高于UO2 的U密度(9.75 g/cm3 )[2 ] ,采用燃料组件较小的UN燃料可以使得轻水反应堆的功率显著提高.室温下UN的导热系数为20.6 W/(m·K),显著高于UO2 的导热系数(3.5 W/(m·K)),采用高导热系数的UN燃料可以显著降低燃料温度,使得在过渡条件下拥有较大的安全裕度[3 ] .然而,目前UN燃料芯块烧结制造工艺仍不成熟,其中一个重要原因是UN中的共价键比例高,烧结致密化较为困难[4 ] .由于UN在高温下易分解,烧结温度提高和添加剂引入的限制,导致传统的烧结方法难以使芯块达到较高的致密度.此外,不同温度和燃耗的反应堆设计需要不同密度、孔隙率和几何形状的UN球团,孔隙率较低的高致密化UN颗粒可以强化燃料结构和延缓裂变气体释放[3 ] .因此,研究UN球团烧结特性、微观组织对于指导UN烧结具有重要的意义. ...
Thermal conductivity of uranium nitride and carbide
1
2014
... UN燃料具有密度高、导热系数高、熔点高、辐照稳定性好、裂变气体释放率低和具有较高的事故容错率等优点,是轻水反应堆、快堆的候选燃料.UN的U密度为13.55 g/cm3 [1 ] ,显著高于UO2 的U密度(9.75 g/cm3 )[2 ] ,采用燃料组件较小的UN燃料可以使得轻水反应堆的功率显著提高.室温下UN的导热系数为20.6 W/(m·K),显著高于UO2 的导热系数(3.5 W/(m·K)),采用高导热系数的UN燃料可以显著降低燃料温度,使得在过渡条件下拥有较大的安全裕度[3 ] .然而,目前UN燃料芯块烧结制造工艺仍不成熟,其中一个重要原因是UN中的共价键比例高,烧结致密化较为困难[4 ] .由于UN在高温下易分解,烧结温度提高和添加剂引入的限制,导致传统的烧结方法难以使芯块达到较高的致密度.此外,不同温度和燃耗的反应堆设计需要不同密度、孔隙率和几何形状的UN球团,孔隙率较低的高致密化UN颗粒可以强化燃料结构和延缓裂变气体释放[3 ] .因此,研究UN球团烧结特性、微观组织对于指导UN烧结具有重要的意义. ...
Uranium nitride (UN) pellets with controllable microstructure and phase-fabrication by spark plasma sintering and their thermal-mechanical and oxidation properties
4
2021
... UN燃料具有密度高、导热系数高、熔点高、辐照稳定性好、裂变气体释放率低和具有较高的事故容错率等优点,是轻水反应堆、快堆的候选燃料.UN的U密度为13.55 g/cm3 [1 ] ,显著高于UO2 的U密度(9.75 g/cm3 )[2 ] ,采用燃料组件较小的UN燃料可以使得轻水反应堆的功率显著提高.室温下UN的导热系数为20.6 W/(m·K),显著高于UO2 的导热系数(3.5 W/(m·K)),采用高导热系数的UN燃料可以显著降低燃料温度,使得在过渡条件下拥有较大的安全裕度[3 ] .然而,目前UN燃料芯块烧结制造工艺仍不成熟,其中一个重要原因是UN中的共价键比例高,烧结致密化较为困难[4 ] .由于UN在高温下易分解,烧结温度提高和添加剂引入的限制,导致传统的烧结方法难以使芯块达到较高的致密度.此外,不同温度和燃耗的反应堆设计需要不同密度、孔隙率和几何形状的UN球团,孔隙率较低的高致密化UN颗粒可以强化燃料结构和延缓裂变气体释放[3 ] .因此,研究UN球团烧结特性、微观组织对于指导UN烧结具有重要的意义. ...
... [3 ].因此,研究UN球团烧结特性、微观组织对于指导UN烧结具有重要的意义. ...
... 近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3 ~9 ] .实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面.尹邦跃和屈哲昊[4 ] 的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm.Muta等[6 ] 对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关.Malkki等[7 ] 采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6 ] 的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素.烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] .烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化.表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输.然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理.因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义. ...
... 图11 为直径为60个格点的4个圆形颗粒形貌演变的相场模拟.可以看出,在演化初期,颗粒逐渐靠拢,气孔收缩完成致密化,形成角度为90°的四叉晶界;之后随着演化的进行,晶界发生变化,颗粒发生偏移,形成稳定的120°三叉晶界,这与大量的UN烧结实验[3 ~6 ,8 ,9 ] 结果相吻合.这是因为演化中期晶界为不稳定状态(相邻晶界间的夹角处于90°),当相邻晶界演化至夹角为120°时,三叉晶界形状保持稳定.结合图7 中3个颗粒烧结相场模拟结果,可以得出致密化气孔收缩完成趋向于形成稳定的120°三叉晶界. ...
Property of uranium nitride ceramic pellet by hot press sintering
3
2014
... UN燃料具有密度高、导热系数高、熔点高、辐照稳定性好、裂变气体释放率低和具有较高的事故容错率等优点,是轻水反应堆、快堆的候选燃料.UN的U密度为13.55 g/cm3 [1 ] ,显著高于UO2 的U密度(9.75 g/cm3 )[2 ] ,采用燃料组件较小的UN燃料可以使得轻水反应堆的功率显著提高.室温下UN的导热系数为20.6 W/(m·K),显著高于UO2 的导热系数(3.5 W/(m·K)),采用高导热系数的UN燃料可以显著降低燃料温度,使得在过渡条件下拥有较大的安全裕度[3 ] .然而,目前UN燃料芯块烧结制造工艺仍不成熟,其中一个重要原因是UN中的共价键比例高,烧结致密化较为困难[4 ] .由于UN在高温下易分解,烧结温度提高和添加剂引入的限制,导致传统的烧结方法难以使芯块达到较高的致密度.此外,不同温度和燃耗的反应堆设计需要不同密度、孔隙率和几何形状的UN球团,孔隙率较低的高致密化UN颗粒可以强化燃料结构和延缓裂变气体释放[3 ] .因此,研究UN球团烧结特性、微观组织对于指导UN烧结具有重要的意义. ...
... 近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3 ~9 ] .实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面.尹邦跃和屈哲昊[4 ] 的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm.Muta等[6 ] 对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关.Malkki等[7 ] 采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6 ] 的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素.烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] .烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化.表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输.然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理.因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义. ...
... 图12 为颗粒尺寸单峰分布的多晶烧结相场模拟,模拟所采用的组织为30个不同尺寸的颗粒(图12a ).为与实验条件一致,选择颗粒的平均半径为150 nm,整个模拟区域的网格尺寸为256 × 256,采用耦合平流通量的致密化模型进行相场模拟.从图12 可以看出,气孔对晶界移动起阻碍作用[31 ] ,气孔越大阻碍作用越强;相邻颗粒之间先形成烧结颈;颗粒之间形成气孔,气孔逐渐收缩,小气孔处晶界曲率较大、驱动力较强,优先完成致密化;致密化完成的部分逐渐形成稳定的120°三叉晶界.将本工作的演化模拟结果与真空热压烧结2 h的实验观察结果[4 ] 进行对比可得,UN烧结形貌演化形成三叉晶界、气孔收缩致密化的行为与实验结果趋势一致. ...
热压烧结UN陶瓷芯块的性能
3
2014
... UN燃料具有密度高、导热系数高、熔点高、辐照稳定性好、裂变气体释放率低和具有较高的事故容错率等优点,是轻水反应堆、快堆的候选燃料.UN的U密度为13.55 g/cm3 [1 ] ,显著高于UO2 的U密度(9.75 g/cm3 )[2 ] ,采用燃料组件较小的UN燃料可以使得轻水反应堆的功率显著提高.室温下UN的导热系数为20.6 W/(m·K),显著高于UO2 的导热系数(3.5 W/(m·K)),采用高导热系数的UN燃料可以显著降低燃料温度,使得在过渡条件下拥有较大的安全裕度[3 ] .然而,目前UN燃料芯块烧结制造工艺仍不成熟,其中一个重要原因是UN中的共价键比例高,烧结致密化较为困难[4 ] .由于UN在高温下易分解,烧结温度提高和添加剂引入的限制,导致传统的烧结方法难以使芯块达到较高的致密度.此外,不同温度和燃耗的反应堆设计需要不同密度、孔隙率和几何形状的UN球团,孔隙率较低的高致密化UN颗粒可以强化燃料结构和延缓裂变气体释放[3 ] .因此,研究UN球团烧结特性、微观组织对于指导UN烧结具有重要的意义. ...
... 近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3 ~9 ] .实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面.尹邦跃和屈哲昊[4 ] 的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm.Muta等[6 ] 对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关.Malkki等[7 ] 采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6 ] 的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素.烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] .烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化.表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输.然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理.因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义. ...
... 图12 为颗粒尺寸单峰分布的多晶烧结相场模拟,模拟所采用的组织为30个不同尺寸的颗粒(图12a ).为与实验条件一致,选择颗粒的平均半径为150 nm,整个模拟区域的网格尺寸为256 × 256,采用耦合平流通量的致密化模型进行相场模拟.从图12 可以看出,气孔对晶界移动起阻碍作用[31 ] ,气孔越大阻碍作用越强;相邻颗粒之间先形成烧结颈;颗粒之间形成气孔,气孔逐渐收缩,小气孔处晶界曲率较大、驱动力较强,优先完成致密化;致密化完成的部分逐渐形成稳定的120°三叉晶界.将本工作的演化模拟结果与真空热压烧结2 h的实验观察结果[4 ] 进行对比可得,UN烧结形貌演化形成三叉晶界、气孔收缩致密化的行为与实验结果趋势一致. ...
The sintering of uranium mononitride
0
1965
Thermal and mechanical properties of uranium nitride prepared by SPS technique
3
2008
... 近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3 ~9 ] .实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面.尹邦跃和屈哲昊[4 ] 的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm.Muta等[6 ] 对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关.Malkki等[7 ] 采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6 ] 的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素.烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] .烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化.表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输.然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理.因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义. ...
... [6 ]的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素.烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] .烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化.表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输.然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理.因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义. ...
... 图11 为直径为60个格点的4个圆形颗粒形貌演变的相场模拟.可以看出,在演化初期,颗粒逐渐靠拢,气孔收缩完成致密化,形成角度为90°的四叉晶界;之后随着演化的进行,晶界发生变化,颗粒发生偏移,形成稳定的120°三叉晶界,这与大量的UN烧结实验[3 ~6 ,8 ,9 ] 结果相吻合.这是因为演化中期晶界为不稳定状态(相邻晶界间的夹角处于90°),当相邻晶界演化至夹角为120°时,三叉晶界形状保持稳定.结合图7 中3个颗粒烧结相场模拟结果,可以得出致密化气孔收缩完成趋向于形成稳定的120°三叉晶界. ...
Manufacture of fully dense uranium nitride pellets using hydride derived powders with spark plasma sintering
1
2014
... 近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3 ~9 ] .实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面.尹邦跃和屈哲昊[4 ] 的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm.Muta等[6 ] 对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关.Malkki等[7 ] 采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6 ] 的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素.烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] .烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化.表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输.然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理.因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义. ...
Spark plasma sintering and porosity studies of uranium nitride
1
2016
... 图11 为直径为60个格点的4个圆形颗粒形貌演变的相场模拟.可以看出,在演化初期,颗粒逐渐靠拢,气孔收缩完成致密化,形成角度为90°的四叉晶界;之后随着演化的进行,晶界发生变化,颗粒发生偏移,形成稳定的120°三叉晶界,这与大量的UN烧结实验[3 ~6 ,8 ,9 ] 结果相吻合.这是因为演化中期晶界为不稳定状态(相邻晶界间的夹角处于90°),当相邻晶界演化至夹角为120°时,三叉晶界形状保持稳定.结合图7 中3个颗粒烧结相场模拟结果,可以得出致密化气孔收缩完成趋向于形成稳定的120°三叉晶界. ...
Grain growth in uranium nitride prepared by spark plasma sintering
2
2018
... 近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3 ~9 ] .实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面.尹邦跃和屈哲昊[4 ] 的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm.Muta等[6 ] 对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关.Malkki等[7 ] 采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6 ] 的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素.烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] .烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化.表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输.然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理.因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义. ...
... 图11 为直径为60个格点的4个圆形颗粒形貌演变的相场模拟.可以看出,在演化初期,颗粒逐渐靠拢,气孔收缩完成致密化,形成角度为90°的四叉晶界;之后随着演化的进行,晶界发生变化,颗粒发生偏移,形成稳定的120°三叉晶界,这与大量的UN烧结实验[3 ~6 ,8 ,9 ] 结果相吻合.这是因为演化中期晶界为不稳定状态(相邻晶界间的夹角处于90°),当相邻晶界演化至夹角为120°时,三叉晶界形状保持稳定.结合图7 中3个颗粒烧结相场模拟结果,可以得出致密化气孔收缩完成趋向于形成稳定的120°三叉晶界. ...
Two‐dimensional motion of idealized grain boundaries
1
1956
... 近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3 ~9 ] .实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面.尹邦跃和屈哲昊[4 ] 的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm.Muta等[6 ] 对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关.Malkki等[7 ] 采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6 ] 的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素.烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] .烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化.表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输.然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理.因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义. ...
1
1995
... 图3 为未引入平流通量与引入平流通量2种模拟数据的烧结颈对数增长曲线.可以看出,未引入平流通量模拟的烧结颈增长曲线近似为一条直线,斜率为0.21左右,满足烧结颈曲线增长规律[11 ] .引入平流通量模拟的烧结颈曲线分为3个时期:烧结前期,烧结颈的增长较快,斜率为0.68左右,这是因为颗粒的致密化移动使得烧结颈更快增长,从A 点到B 点平流通量起主要作用导致晶界宽度变窄;烧结中期,从B 点到C 点平流通量作用减弱,晶界宽度恢复,导致烧结颈长度下降;烧结后期,烧结颈不再增长且相比于未引入平流通量模型提前达到稳态,斜率为0.06左右.引入平流通量模型对烧结颈的形成在烧结前期作用较强,后期作用不明显. ...
1
1996
... 近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3 ~9 ] .实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面.尹邦跃和屈哲昊[4 ] 的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm.Muta等[6 ] 对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关.Malkki等[7 ] 采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6 ] 的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素.烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] .烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化.表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输.然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理.因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义. ...
Generalized phase field approach for computer simulation of sintering: Incorporation of rigid-body motion
2
1999
... 近年来,国内外学者做了许多不同温度、不同时间、多种烧结方式下的UN烧结致密化实验[3 ~9 ] .实验结果主要集中在烧结后晶粒尺寸、致密化球团的孔隙率以及显微组织控制方面.尹邦跃和屈哲昊[4 ] 的热压烧结实验结果表明,1550℃烧结温度和2 h烧结时间下真空热压烧结UN芯块的致密度很高,晶粒细小均匀,平均尺寸≤ 10 μm.Muta等[6 ] 对比了传统热压烧结与放电等离子体烧结(SPS)制备的样品扫描电镜(SEM)像,结果表明,传统烧结方法制备的样品具有较大的孔隙率,大部分气孔存在于晶界;SPS方法制备的样品中仅观察到很小的晶内孔隙,较低的烧结温度抑制了晶粒和气孔的生长,气孔的尺寸和分布与烧结条件无关.Malkki等[7 ] 采用SPS方法在1650℃烧结温度和3 min烧结时间下得到孔隙率为0.17%的球团密度,并与Muta等[6 ] 的数据进行比较得出结论:在颗粒尺寸接近的条件下,烧结温度是决定最终密度的因素.烧结在实质上是颗粒表面自由能减少的固态扩散过程,其扩散机制主要分为表面扩散(空位和原子沿颗粒表面)、晶界扩散、体积扩散(晶格扩散)等,以及它们之间的耦合作用[10 ~12 ] .烧结过程的物质迁移包括表面迁移和颗粒平移旋转的刚体运动[13 ] ,2种迁移机制的区别在于能否完成烧结气孔致密化.表面迁移机制的物质迁移只存在于表面,主要表现为烧结颈的形成与生长,不涉及空位的传输;颗粒刚体运动的物质迁移存在于表面和晶界,主要表现为促进烧结颈增长,颗粒靠拢气孔致密化,涉及到空位的传输.然而,由于现有实验条件的局限性,难以对烧结微观组织致密化过程进行观测,这也间接导致了无法很好解释烧结致密化过程的机理.因此,采用计算机模拟UN烧结过程的孔隙演化与致密化过程具有十分重要的现实意义. ...
... 最近,Chen和Zhao[14 ] 总结了利用相场法设计材料以获得最佳性能的热力学基础和研究进展.Ishii等[15 ] 提出了一种新的数据同化方法来估算固相烧结材料的参数.陶瓷烧结过程的相场研究方面已经取得了一些成果[16 ~20 ] .Ahmed等[16 ] 开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2 中晶粒长大动力学的影响.Kundin等[17 ] 提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响.Hötzer等[18 ] 提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2 O3 固态烧结过程.然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清.气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13 ,19 ] .颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化.因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导. ...
From classical thermodynamics to phase-field method
1
2022
... 最近,Chen和Zhao[14 ] 总结了利用相场法设计材料以获得最佳性能的热力学基础和研究进展.Ishii等[15 ] 提出了一种新的数据同化方法来估算固相烧结材料的参数.陶瓷烧结过程的相场研究方面已经取得了一些成果[16 ~20 ] .Ahmed等[16 ] 开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2 中晶粒长大动力学的影响.Kundin等[17 ] 提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响.Hötzer等[18 ] 提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2 O3 固态烧结过程.然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清.气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13 ,19 ] .颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化.因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导. ...
Efficient estimation of material parameters using DMC-BO: Application to phase-field simulation of solid-state sintering
1
2022
... 最近,Chen和Zhao[14 ] 总结了利用相场法设计材料以获得最佳性能的热力学基础和研究进展.Ishii等[15 ] 提出了一种新的数据同化方法来估算固相烧结材料的参数.陶瓷烧结过程的相场研究方面已经取得了一些成果[16 ~20 ] .Ahmed等[16 ] 开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2 中晶粒长大动力学的影响.Kundin等[17 ] 提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响.Hötzer等[18 ] 提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2 O3 固态烧结过程.然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清.气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13 ,19 ] .颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化.因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导. ...
Phase field simulation of grain growth in porous uranium dioxide
3
2014
... 最近,Chen和Zhao[14 ] 总结了利用相场法设计材料以获得最佳性能的热力学基础和研究进展.Ishii等[15 ] 提出了一种新的数据同化方法来估算固相烧结材料的参数.陶瓷烧结过程的相场研究方面已经取得了一些成果[16 ~20 ] .Ahmed等[16 ] 开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2 中晶粒长大动力学的影响.Kundin等[17 ] 提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响.Hötzer等[18 ] 提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2 O3 固态烧结过程.然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清.气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13 ,19 ] .颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化.因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导. ...
... [16 ]开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2 中晶粒长大动力学的影响.Kundin等[17 ] 提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响.Hötzer等[18 ] 提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2 O3 固态烧结过程.然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清.气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13 ,19 ] .颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化.因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导. ...
... 本工作在表面扩散相场模型[16 ] 的基础上对扩散方程进行了修正,添加了含有平移旋转刚体运动的相互作用项,采用相场理论模拟了UN粉末在表面扩散与平移旋转刚体运动共同作用下颗粒间烧结颈的长大以及气孔的演化过程,研究了UN粉末烧结颈的形成过程、气孔收缩致密化的过程、形成稳定三叉晶界的过程以及多晶粒烧结过程,模拟结果与实验观察结果符合较好. ...
Phase-field modeling of pores and precipitates in polycrystalline systems
1
2018
... 最近,Chen和Zhao[14 ] 总结了利用相场法设计材料以获得最佳性能的热力学基础和研究进展.Ishii等[15 ] 提出了一种新的数据同化方法来估算固相烧结材料的参数.陶瓷烧结过程的相场研究方面已经取得了一些成果[16 ~20 ] .Ahmed等[16 ] 开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2 中晶粒长大动力学的影响.Kundin等[17 ] 提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响.Hötzer等[18 ] 提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2 O3 固态烧结过程.然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清.气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13 ,19 ] .颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化.因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导. ...
Phase-field simulation of solid state sintering
1
2019
... 最近,Chen和Zhao[14 ] 总结了利用相场法设计材料以获得最佳性能的热力学基础和研究进展.Ishii等[15 ] 提出了一种新的数据同化方法来估算固相烧结材料的参数.陶瓷烧结过程的相场研究方面已经取得了一些成果[16 ~20 ] .Ahmed等[16 ] 开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2 中晶粒长大动力学的影响.Kundin等[17 ] 提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响.Hötzer等[18 ] 提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2 O3 固态烧结过程.然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清.气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13 ,19 ] .颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化.因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导. ...
Coarsening in sintering: grain shape distribution, grain size distribution, and grain growth kinetics in solid-pore systems
2
2010
... 最近,Chen和Zhao[14 ] 总结了利用相场法设计材料以获得最佳性能的热力学基础和研究进展.Ishii等[15 ] 提出了一种新的数据同化方法来估算固相烧结材料的参数.陶瓷烧结过程的相场研究方面已经取得了一些成果[16 ~20 ] .Ahmed等[16 ] 开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2 中晶粒长大动力学的影响.Kundin等[17 ] 提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响.Hötzer等[18 ] 提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2 O3 固态烧结过程.然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清.气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13 ,19 ] .颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化.因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导. ...
... 图2 为未引入平流通量和引入平流通量2个等尺寸的圆形颗粒在烧结过程中的组织演变.其中颗粒的半径R = 30,与平流通量模型模拟相关的参数m t = 30,c * = 0.05,κ F = 100,ρ 0 = 0.98.从图2a~c 与d~f 对比可以看出,未引入平流通量的模拟烧结颈形成较慢,颗粒位置无明显移动;含有平流通量的模拟烧结颈的形成明显更快,颗粒位置发生移动,且稳态时烧结颈的长度更长.这与文献[19 ]给出的致密化特征十分吻合.烧结致密化取决于颗粒-孔隙相互作用,表面扩散主导的未加平流通量模型对烧结过程孔隙收缩没有贡献,所以烧结颈形成较慢;引入平流通量模型含有颗粒刚体运动过程,空位可以被晶界吸收湮灭,所以不仅促进烧结颈增长,且随着烧结颈生长,颗粒彼此接近. ...
Computer simulation of grain growth using a continuum field model
3
1997
... 最近,Chen和Zhao[14 ] 总结了利用相场法设计材料以获得最佳性能的热力学基础和研究进展.Ishii等[15 ] 提出了一种新的数据同化方法来估算固相烧结材料的参数.陶瓷烧结过程的相场研究方面已经取得了一些成果[16 ~20 ] .Ahmed等[16 ] 开发出一种考虑曲率驱动晶界运动和表面扩散引起孔隙迁移的新型相场模型,研究了孔隙度对UO2 中晶粒长大动力学的影响.Kundin等[17 ] 提出了2种类型的模型描述孔隙与晶界的相互作用,研究了孔隙动力学对陶瓷材料晶粒尺寸演化的影响.Hötzer等[18 ] 提出了一种考虑表面扩散和晶界扩散的相场模型描述Al2 O3 固态烧结过程.然而,表面扩散模型并不能模拟UN烧结后期的致密化过程,烧结致密化的机理有待进一步澄清.气孔致密化过程包含平移旋转刚体运动与晶界扩散,刚体运动的驱动力来源于晶界吸收作用,过饱和的空位被晶界吸收产生局部驱动力,将相邻颗粒通过平移旋转刚体运动相互靠拢[13 ,19 ] .颗粒的平移和旋转直接减小颗粒之间的距离,促进气孔完成致密化.因此,考虑颗粒之间的平移旋转刚体运动对晶界和致密化的影响,可以更好地了解烧结过程的物质传输机理,为烧结过程提供指导. ...
... 本模型通过引入与结构相关的一系列取向场变量η 1 ( r t ), η 2 ( r t ), …, ηp ( r t )和浓度场变量ρ ( r t )来表述不同取向的晶粒相和气孔相,它们是空间坐标( r t )的连续函数.其中,ηi (i = 1, 2, …, p )为非保守型相场变量,用来描述多晶中不同晶粒的取向,第i 个晶粒内部ηi 的取值为1,其余p - 1个取值为0;ρ ( r t )为保守型相场变量,在晶粒相取值为1,在气孔相取值为0.已有研究[20 ] 表明,当晶粒个数p > 32时,晶粒组织演变对p 取值的依赖性可以忽略. ...
... 为了直观地表征烧结过程,本工作中可视化变量φ 为[20 ] : ...
On spinodal decomposition
3
1961
... 本工作烧结相场模型的总自由能泛函数F 采用以下形式[21 ] : ...
... 假设烧结过程的质量是守恒的,为了描述烧结过程的气孔收缩和致密化,在演化动力学Cahn-Hilliard方程[21 ] 中引入平流通量项.因此,ρ 的演化方程为: ...
... ηi 的演化动力学方程由Allen-Cahn方程[21 ] 引入平流通量项后表示为: ...
Computer modeling and simulation of solid-state sintering: A phase field approach
4
2006
... 本工作采取的f 表达式如下[22 ] : ...
... 烧结过程中粒子的刚体运动由平移和转动2部分组成, v adv ( r [22 ] : ...
... 式中, v t i r r i 的平移速度,表达式为[22 ] : ...
... v r i r r i 的旋转速度,表达式为[22 ] : ...
Phase field modeling of the effect of porosity on grain growth kinetics in polycrystalline ceramics
2
2013
... F 中各常数与材料的物理参数之间的关系为[23 ] : ...
... M [23 ] : ...
A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening
1
1979
... 式中, v adv i r r i 的平流速度;L 为表征晶界迁移率的系数,在各向同性假设下为常数,与材料的具体性质关系如下[24 ] : ...
1
2017
... 根据 式(7) 修正的Cahn-Hilliard方程与 式(12) 修正的Allen-Cahn方程,可以求得相场变量随时间的演化过程.通过对相场变量的变化求解,可以计算出演化任意时刻的微观组织与空间分布.本工作采用的求解相场方程的数值方法为有限差分法.对于相互关联的非线性偏微分方程组,时间上采用显示Euler算法;空间上采用五点差分法求解Laplace项[25 ] . ...
Nitrogen diffusion in uranium nitride as measured by alpha particle activation of 15N
4
1969
... 本工作利用相场模型对UN陶瓷粉末在1823 K温度下的烧结过程进行了数值模拟,模拟中用到的UN物理参数如表1 [26 ,27 ] 所示. ...
... UN的物理参数[26 ,27 ] ...
... Physical parameters of UN at 1823 K[26 ,27 ] ...
... [
26 ]
D gb 0.01D s m2 ·s-1 γ s 1.6 J·m-2 [27 ] γ gb 0.8 J·m-2 [27 ] δ 6 nm [27 ] Note: D s —surface diffusivity, D gb —grain-boundary diffusivity, γ s —surface energy, γ gb —grain-boundary energy, δ —diffuse interface width ...
Ab initio simulations of oxygen interaction with surfaces and interfaces in uranium mononitride
6
2013
... 本工作利用相场模型对UN陶瓷粉末在1823 K温度下的烧结过程进行了数值模拟,模拟中用到的UN物理参数如表1 [26 ,27 ] 所示. ...
... UN的物理参数[26 ,27 ] ...
... Physical parameters of UN at 1823 K[26 ,27 ] ...
... [
27 ]
γ gb 0.8 J·m-2 [27 ] δ 6 nm [27 ] Note: D s —surface diffusivity, D gb —grain-boundary diffusivity, γ s —surface energy, γ gb —grain-boundary energy, δ —diffuse interface width ...
... [
27 ]
δ 6 nm [27 ] Note: D s —surface diffusivity, D gb —grain-boundary diffusivity, γ s —surface energy, γ gb —grain-boundary energy, δ —diffuse interface width ...
... [
27 ]
Note: D s —surface diffusivity, D gb —grain-boundary diffusivity, γ s —surface energy, γ gb —grain-boundary energy, δ —diffuse interface width ...
A theoretical study of grain growth in porous solids during sintering
1
1993
... 界面性质在烧结过程中的气孔收缩、致密化和粗化过程中起关键作用.相邻的2个粒子在相界处由于表面能和晶界能形成一个平衡二面角(Ψ ),在各向同性条件下,晶界处平衡二面角方程为[28 ] : ...
Phase field simulations of the sintering process of UO2
1
2020
... 图4 分别为未引入平流通量与引入平流通量2种烧结模型的平衡二面角,演化的总时间为2 × 106 step.本工作UN烧结晶界能与界面能的比值为γ gb / γ s = 0.5,对应计算值为Ψ = 150°.从图4 可以看出,未引入平流通量模拟平衡二面角与理论计算值吻合较好,引入平流通量模拟最终平衡二面角与理论计算值有较小误差.证明了平流通量的引入会加快烧结颈的形成,但最终平衡二面角仍然不变,只由材料的特性所决定.这与只考虑表面扩散[29 ] 的结论一致,平衡二面角与晶界能和界面能的比值保持一致. ...
UO2 烧结过程的相场模拟
1
2020
... 图4 分别为未引入平流通量与引入平流通量2种烧结模型的平衡二面角,演化的总时间为2 × 106 step.本工作UN烧结晶界能与界面能的比值为γ gb / γ s = 0.5,对应计算值为Ψ = 150°.从图4 可以看出,未引入平流通量模拟平衡二面角与理论计算值吻合较好,引入平流通量模拟最终平衡二面角与理论计算值有较小误差.证明了平流通量的引入会加快烧结颈的形成,但最终平衡二面角仍然不变,只由材料的特性所决定.这与只考虑表面扩散[29 ] 的结论一致,平衡二面角与晶界能和界面能的比值保持一致. ...
Towards understanding particle rigid-body motion during solid-state sintering
1
2021
... 为进一步探究颗粒平移和旋转对致密化气孔收缩的影响,图10 比较了不同平移迁移率下3个颗粒的气孔收缩.从图10 可以明显看出,颗粒平移对致密化气孔收缩具有显著促进作用,随着m t 的增大,致密化的速率增加,最终致密化的程度增加;当m t 超过80时,致密化程度相对不变,最终完成致密化;当m t 超过100时,致密化速率相对不变.与多相场(MPF)模型[30 ] 的结果对比发现,本工作模拟颗粒平移迁移率对致密化影响更加明显. ...
Phase-field simulation of the interaction between pore and grain boundary
1
2020
... 图12 为颗粒尺寸单峰分布的多晶烧结相场模拟,模拟所采用的组织为30个不同尺寸的颗粒(图12a ).为与实验条件一致,选择颗粒的平均半径为150 nm,整个模拟区域的网格尺寸为256 × 256,采用耦合平流通量的致密化模型进行相场模拟.从图12 可以看出,气孔对晶界移动起阻碍作用[31 ] ,气孔越大阻碍作用越强;相邻颗粒之间先形成烧结颈;颗粒之间形成气孔,气孔逐渐收缩,小气孔处晶界曲率较大、驱动力较强,优先完成致密化;致密化完成的部分逐渐形成稳定的120°三叉晶界.将本工作的演化模拟结果与真空热压烧结2 h的实验观察结果[4 ] 进行对比可得,UN烧结形貌演化形成三叉晶界、气孔收缩致密化的行为与实验结果趋势一致. ...
气孔与晶界相互作用的相场模拟
1
2020
... 图12 为颗粒尺寸单峰分布的多晶烧结相场模拟,模拟所采用的组织为30个不同尺寸的颗粒(图12a ).为与实验条件一致,选择颗粒的平均半径为150 nm,整个模拟区域的网格尺寸为256 × 256,采用耦合平流通量的致密化模型进行相场模拟.从图12 可以看出,气孔对晶界移动起阻碍作用[31 ] ,气孔越大阻碍作用越强;相邻颗粒之间先形成烧结颈;颗粒之间形成气孔,气孔逐渐收缩,小气孔处晶界曲率较大、驱动力较强,优先完成致密化;致密化完成的部分逐渐形成稳定的120°三叉晶界.将本工作的演化模拟结果与真空热压烧结2 h的实验观察结果[4 ] 进行对比可得,UN烧结形貌演化形成三叉晶界、气孔收缩致密化的行为与实验结果趋势一致. ...