Alloys-by-design: Application to nickel-based single crystal superalloys
1
2009
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
A statistical theory of solid solution hardening
1
1970
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
The theory of solution hardening
1
1977
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
Lattice distortion in a strong and ductile refractory high-entropy alloy
1
2018
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
Effect of Al content on stacking fault energy in austenitic Fe-Mn-Al-C alloys
1
2008
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes
2
2004
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
... [6 ~10 ].近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
A
1
2004
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures
1
2014
... CrCoNi作为FeCoNiCrMn高熵体系的衍生[8 ,31 ] ,其强韧性甚至超过了FeCoNiCrMn以及大多数的多相高熵合金,并具有突出的低温性能.第一性原理计算结果[19 ] 表明,CrCoNi中形成短程有序结构的趋势强烈,特别是Cr元素更倾向与Ni元素和Co元素成键.这与Zhang等[20 ] 基于X射线散射、中子散射和扩展X射线吸收精细结构分析的结果相一致.另外,Zhang等[22 ] 使用能量过滤透射电子显微镜(TEM)观察退火较长时间的CrCoNi中熵合金的显微结构时发现,高温时效会导致CrCoNi中形成明显的短程有序.他们通过纳米压痕实验对比研究了长时间时效后包含短程有序结构的CrCoNi和未进行时效处理的CrCoNi,发现时效后材料强度显著提升.这表明热处理工艺对高熵合金中的元素分布不均匀性有显著的调控作用,其结果会对材料力学性能产生重要影响.然而,在相关研究结果中还欠缺对于这种可能的短程有序结构的原子尺度结构分析.对于实际的短程有序结构和模拟计算中推测的短程有序结构是否一致这一问题还需更多的研究探索. ...
Exceptional damage-tolerance of a medium-entropy alloy CrCoNi at cryogenic temperatures
0
2016
Science and technology in high-entropy alloys
1
2018
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
A refractory Hf25 Nb25 Ti25 Zr25 high-entropy alloy with excellent structural stability and tensile properties
2
2014
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
... 与fcc高熵合金不同的是,bcc高熵合金中更倾向于形成局部的短程有序结构.除此之外,由短程有序结构所导致的元素分布不均匀性可以通过热处理、添加其他合金元素或改变合金中元素浓度等方式不断地扩大和加剧,导致bcc相中的局域短程有序结构会相互连接,最终形成多相结构,进而根本改变材料的变形机制及其力学性能.如图4 c[49 ] 所示,Maiti等[49 ] 通过长时间退火发现,HfNbTaZr中Hf和Zr原子会沿着垂直于<100>方向形成原子的聚集,并随着退火时间的增加,富含Hf和Zr短程有序结构相互连接形成六方相,最终导致HfNbTaZr合金形成两相交互结构.同时,与fcc高熵合金中的现象相似,bcc高熵合金中的元素分布不均匀性对微量元素的添加也十分敏感.例如,HfNbTaTiZr的衍生物TiZrHfNb合金[11 ] 本来只包含bcc单相.而Lei等[50 ] 通过在TiZrHfNb合金中添加2%的O元素观察到反常的强度和韧性的提高(如图4 d[50 ] ).传统认知认为,合金材料中含有O元素会形成陶瓷相使金属变脆,但Lei等[50 ] 研究表明当高熵合金中添加O元素时,在强度提升的同时,延展性也得到显著改善.通过高分辨扫描透射电子显微镜观察以及APT技术发现,O原子会以有序的方式占据Zr、Ti富集簇中的间隙位置,形成有序氧络合物.这种有序氧络合物的形成是由于高熵合金中所具有的化学短程有序所诱发和促进的.所形成的纳米级的有序区域迫使位错滑移由平面滑移转变为波浪滑移,改变了塑性变形方式.这种强化作用不同于传统的间隙原子强化,是一种由短程有序结构所导致的超常强化.与fcc高熵合金的研究相比,虽然目前对bcc高熵合金中元素分布的研究要少,但已有研究表明bcc高熵合金中元素分布的不均匀性相较于fcc高熵合金应该更为强烈.在常规材料制备,例如铸态合金中,往往会出现分相的现象.如Mo0.5 NbTa0.5 TiZr高熵合金[51 ] 在1500℃下为bcc单相.冷却后,该相分解成为2个成分不同的相(富Zr、Ti相和富Nb、Mo、Ta相),这2个相均具有bcc晶体结构和相似的晶格参数,但化学成分完全不同.又例如,添加了Al元素后,AlMo0.5 NbTa0.5 TiZr合金[52 ~54 ] 分相出不连续的无序bcc相和一个连续的B2相.就目前的研究结果来看,添加Al元素对bcc结构的元素分布具有重要影响,相关的结果还需更多的实验和理论探索. ...
Microstructure of a near-equimolar refractory high-entropy alloy
1
2014
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr[12 ,46 ] 和Co16.67 Fe36.67 Ni16.67 Ti30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等[41 ] 通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
Development and exploration of refractory high entropy alloys—A review
2
2018
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
... 尽管在设计之初,高熵合金得益于单相稳定这一概念,但实际上,大多数的高熵合金都是多相结构,Luan等[23 ] 使用振动理论模型对总计7085种高熵合金的稳定性进行了计算和预测.结果表明,高熵合金在多相结构下更容易保持稳定状态.同时,随着合金元素数量的增加,单相的高熵合金几乎不能稳定存在.这一结论在bcc体系高熵合金中得到了更好的体现.文献[39 ]表明,bcc结构的难熔高熵合金通常是一类具有多相结构的高熵合金.其中,常见的难熔高熵合金主要是HfNbTaTiZr、MoNbTaVW、AlMo0.5 NbTa0.5 TiZr、NbTiVZr及其衍生体系[13 ] . ...
Recent progress in high-entropy alloys
2
2006
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
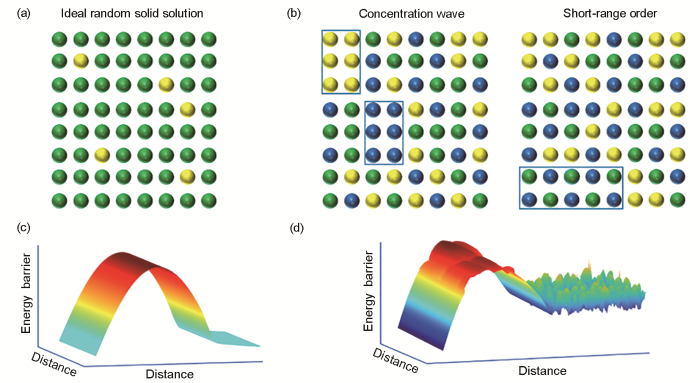
... 合金的性能首先取决于材料的组元,也可以说是材料的基因.在此基础上,显微结构的变化就如同后天的培养,在一定范围内能够有效地调控材料性能.高熵合金往往元素组成复杂,这是基因上的特点;而在成分一定的前提下,各种元素在晶格中如何分布就是结构的问题,也会对性能产生影响.而对于高熵合金中元素如何分布这个问题,一直以来还存在较大的争议.早期研究[14 ,17 ] 认为,多组元合金中各母元素的晶体结构虽然不同,但所获得的合金组织中不存在有害的金属间化合物、非晶或多相结构,这是由于多种元素近等原子比的混合会增加混合的构型熵,因此,能够形成稳定的单相固溶体.随后通过改变成分,科学家们又研发出大量双相高熵合金,利用强、韧相的混合来提升材料力学性能.这其中CuCoNiCrAlx [18 ] 是典型的双相高熵合金体系.通过增加Al元素的含量,能够形成稳定的双相固溶体结构.与传统合金中的理想固溶模型(如图1 a所示)相类似,高熵合金中的各组分原子在晶格中应该具有随机的占位,即形成各种元素均匀分布的完美固溶体.然而越来越多的研究[19 ~22 ] 表明,由于原子特性不同,例如半径、模量、电负性等,成分复杂合金体系中的原子排列可能不是理想的随机状态,即可能在原子尺度存在元素分布的不均匀性.特别是,当合金体系的组分中包含与其他组成元素的原子特性迥异的元素时,这种现象存在的机率极大.研究发现高熵合金中经常出现多相固溶体、非晶、金属间化合物等.在某些高熵体系中,单相固溶体不容易长期稳定存在[23 ] . ...
Multi-principal-element alloys with improved oxidation and wear resistance for thermal spray coating
1
2004
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
Phase transformations and mechanical properties of Fe-Mn-Si-Al TRIP-steels
1
1997
... 合金化是金属材料性能优化的重要手段,合金的制备和应用由来已久.随着冶炼技术的发展和钢铁时代的兴盛,合金化的相关理论[1 ] 在材料科学发展的过程中逐步建立.对于固溶体合金,经典的固溶强化理论[2 ,3 ] 已经可以解释相当一部分实际材料中的合金化效果问题.固溶强化理论认为,合金元素的添加在晶格中造成局域的应力场,该应力场与相遇的刃位错的应变场发生交互作用产生能量,使材料内能增加,产生强化[4 ] .近年来,随着材料制备工艺的显著进步,合金化的内容更加丰富和复杂.例如高锰钢[5 ] 、钛铝合金等具有优异力学性能的新型合金中往往有多种合金元素的添加.2004年,Yeh等[6 ] 和Cantor等[7 ] 分别提出高熵合金和等原子比多组元合金的概念.高熵合金最早定义为包含5种或5种以上元素(每个组元浓度在5%~35%之间,本文涉及分数均为原子分数)的合金材料.区别于传统合金基于1种或2种主元素的设计思路,这种新的合金设计理念极大丰富了合金种类,并且部分高熵合金被赋予了优异的力学性能,因此很快受到学术界的强烈关注[6 ~10 ] .近15年来,科研人员在开发不同体系、不同成分、不同结构的高熵合金及其性能优化上做了大量研究工作[11 ~13 ] ,提出高熵合金有4种突出效应[14 ,15 ] :①高熵效应;②晶格畸变效应;③迟滞扩散效应;④鸡尾酒效应.而实际上这4种效应应该广泛存在于多主元复杂合金中,例如高锰钢[16 ] ,理论上应该也是这4种效应的载体材料.因此,长期以来一个问题始终存疑:高熵合金与传统合金的本质区别到底是什么?是什么与众不同的特点赋予了材料特殊的性能? ...
Relative effects of enthalpy and entropy on the phase stability of equiatomic high-entropy alloys
3
2013
... 合金的性能首先取决于材料的组元,也可以说是材料的基因.在此基础上,显微结构的变化就如同后天的培养,在一定范围内能够有效地调控材料性能.高熵合金往往元素组成复杂,这是基因上的特点;而在成分一定的前提下,各种元素在晶格中如何分布就是结构的问题,也会对性能产生影响.而对于高熵合金中元素如何分布这个问题,一直以来还存在较大的争议.早期研究[14 ,17 ] 认为,多组元合金中各母元素的晶体结构虽然不同,但所获得的合金组织中不存在有害的金属间化合物、非晶或多相结构,这是由于多种元素近等原子比的混合会增加混合的构型熵,因此,能够形成稳定的单相固溶体.随后通过改变成分,科学家们又研发出大量双相高熵合金,利用强、韧相的混合来提升材料力学性能.这其中CuCoNiCrAlx [18 ] 是典型的双相高熵合金体系.通过增加Al元素的含量,能够形成稳定的双相固溶体结构.与传统合金中的理想固溶模型(如图1 a所示)相类似,高熵合金中的各组分原子在晶格中应该具有随机的占位,即形成各种元素均匀分布的完美固溶体.然而越来越多的研究[19 ~22 ] 表明,由于原子特性不同,例如半径、模量、电负性等,成分复杂合金体系中的原子排列可能不是理想的随机状态,即可能在原子尺度存在元素分布的不均匀性.特别是,当合金体系的组分中包含与其他组成元素的原子特性迥异的元素时,这种现象存在的机率极大.研究发现高熵合金中经常出现多相固溶体、非晶、金属间化合物等.在某些高熵体系中,单相固溶体不容易长期稳定存在[23 ] . ...
... 即使是在简单的单相固溶体中,也已有不少实验和模拟的研究提出[17 ,19 ,21 ,22 ] ,高熵合金中元素分布可能不均匀.而由于经典的固溶强化理论的建立基于一个重要的前提条件:溶质原子在溶剂中是随机、均匀分布的,这就引发了一个重要的科学问题,即经典的合金强化理论,例如固溶强化理论,在多元复杂合金体系中是否还适用?而对于不均匀性的理解大致可以分成2种:一种是合金中元素浓度的波动,被称为“浓度波”[24 ] .这种波动是指在固溶体中,原子尺度一定晶体方向上,各种元素的成分存在差异,偏离了合金设计中的化学配比.这种波动的波幅可能在百分之几到百分之几十之间,而波长往往在几个纳米.第2种不均匀性体现在短程有序结构[25 ] ,即在固溶体中,存在具有化学或拓扑组态的结构单元.如图1 b所示,这2种不均匀性均打破了高熵合金是理想固溶体的认知,对材料的力学性能产生重要影响.这2种不均匀性往往能够通过热处理、元素添加或改变元素配比来进行调控.如果其真实存在,势必对高熵合金中的位错滑移产生重要影响.同时,这也是高熵合金可以被利用的一种特性.通过调节这种元素分布的不均匀性,或许能有效改变合金材料的力学性能. ...
... Cantor合金[27 ] 是最早、研究最广泛的一种高熵合金.研究人员利用X射线衍射(XRD)、扫描电子显微镜(SEM)、背散射电子衍射(EBSD)及原子探针断层扫描(APT)等检测手段显示,Cantor合金中组成元素基本是均匀随机分布的[17 ,27 ~29 ] .在常规的热处理下,Cantor合金中元素分布的宏观尺度混合可以被维持,但由于晶格尺度的元素分布不均匀性难以被常规的检测方法所识别,在更小的尺度上,元素分布是否绝对均匀还有待探索[30 ] . ...
Formation of simple crystal structures in Cu-Co-Ni-Cr-Al-Fe-Ti-V alloys with multiprincipal metallic elements
1
2004
... 合金的性能首先取决于材料的组元,也可以说是材料的基因.在此基础上,显微结构的变化就如同后天的培养,在一定范围内能够有效地调控材料性能.高熵合金往往元素组成复杂,这是基因上的特点;而在成分一定的前提下,各种元素在晶格中如何分布就是结构的问题,也会对性能产生影响.而对于高熵合金中元素如何分布这个问题,一直以来还存在较大的争议.早期研究[14 ,17 ] 认为,多组元合金中各母元素的晶体结构虽然不同,但所获得的合金组织中不存在有害的金属间化合物、非晶或多相结构,这是由于多种元素近等原子比的混合会增加混合的构型熵,因此,能够形成稳定的单相固溶体.随后通过改变成分,科学家们又研发出大量双相高熵合金,利用强、韧相的混合来提升材料力学性能.这其中CuCoNiCrAlx [18 ] 是典型的双相高熵合金体系.通过增加Al元素的含量,能够形成稳定的双相固溶体结构.与传统合金中的理想固溶模型(如图1 a所示)相类似,高熵合金中的各组分原子在晶格中应该具有随机的占位,即形成各种元素均匀分布的完美固溶体.然而越来越多的研究[19 ~22 ] 表明,由于原子特性不同,例如半径、模量、电负性等,成分复杂合金体系中的原子排列可能不是理想的随机状态,即可能在原子尺度存在元素分布的不均匀性.特别是,当合金体系的组分中包含与其他组成元素的原子特性迥异的元素时,这种现象存在的机率极大.研究发现高熵合金中经常出现多相固溶体、非晶、金属间化合物等.在某些高熵体系中,单相固溶体不容易长期稳定存在[23 ] . ...
Tunable stacking fault energies by tailoring local chemical order in CrCoNi medium-entropy alloys
3
2018
... 合金的性能首先取决于材料的组元,也可以说是材料的基因.在此基础上,显微结构的变化就如同后天的培养,在一定范围内能够有效地调控材料性能.高熵合金往往元素组成复杂,这是基因上的特点;而在成分一定的前提下,各种元素在晶格中如何分布就是结构的问题,也会对性能产生影响.而对于高熵合金中元素如何分布这个问题,一直以来还存在较大的争议.早期研究[14 ,17 ] 认为,多组元合金中各母元素的晶体结构虽然不同,但所获得的合金组织中不存在有害的金属间化合物、非晶或多相结构,这是由于多种元素近等原子比的混合会增加混合的构型熵,因此,能够形成稳定的单相固溶体.随后通过改变成分,科学家们又研发出大量双相高熵合金,利用强、韧相的混合来提升材料力学性能.这其中CuCoNiCrAlx [18 ] 是典型的双相高熵合金体系.通过增加Al元素的含量,能够形成稳定的双相固溶体结构.与传统合金中的理想固溶模型(如图1 a所示)相类似,高熵合金中的各组分原子在晶格中应该具有随机的占位,即形成各种元素均匀分布的完美固溶体.然而越来越多的研究[19 ~22 ] 表明,由于原子特性不同,例如半径、模量、电负性等,成分复杂合金体系中的原子排列可能不是理想的随机状态,即可能在原子尺度存在元素分布的不均匀性.特别是,当合金体系的组分中包含与其他组成元素的原子特性迥异的元素时,这种现象存在的机率极大.研究发现高熵合金中经常出现多相固溶体、非晶、金属间化合物等.在某些高熵体系中,单相固溶体不容易长期稳定存在[23 ] . ...
... 即使是在简单的单相固溶体中,也已有不少实验和模拟的研究提出[17 ,19 ,21 ,22 ] ,高熵合金中元素分布可能不均匀.而由于经典的固溶强化理论的建立基于一个重要的前提条件:溶质原子在溶剂中是随机、均匀分布的,这就引发了一个重要的科学问题,即经典的合金强化理论,例如固溶强化理论,在多元复杂合金体系中是否还适用?而对于不均匀性的理解大致可以分成2种:一种是合金中元素浓度的波动,被称为“浓度波”[24 ] .这种波动是指在固溶体中,原子尺度一定晶体方向上,各种元素的成分存在差异,偏离了合金设计中的化学配比.这种波动的波幅可能在百分之几到百分之几十之间,而波长往往在几个纳米.第2种不均匀性体现在短程有序结构[25 ] ,即在固溶体中,存在具有化学或拓扑组态的结构单元.如图1 b所示,这2种不均匀性均打破了高熵合金是理想固溶体的认知,对材料的力学性能产生重要影响.这2种不均匀性往往能够通过热处理、元素添加或改变元素配比来进行调控.如果其真实存在,势必对高熵合金中的位错滑移产生重要影响.同时,这也是高熵合金可以被利用的一种特性.通过调节这种元素分布的不均匀性,或许能有效改变合金材料的力学性能. ...
... CrCoNi作为FeCoNiCrMn高熵体系的衍生[8 ,31 ] ,其强韧性甚至超过了FeCoNiCrMn以及大多数的多相高熵合金,并具有突出的低温性能.第一性原理计算结果[19 ] 表明,CrCoNi中形成短程有序结构的趋势强烈,特别是Cr元素更倾向与Ni元素和Co元素成键.这与Zhang等[20 ] 基于X射线散射、中子散射和扩展X射线吸收精细结构分析的结果相一致.另外,Zhang等[22 ] 使用能量过滤透射电子显微镜(TEM)观察退火较长时间的CrCoNi中熵合金的显微结构时发现,高温时效会导致CrCoNi中形成明显的短程有序.他们通过纳米压痕实验对比研究了长时间时效后包含短程有序结构的CrCoNi和未进行时效处理的CrCoNi,发现时效后材料强度显著提升.这表明热处理工艺对高熵合金中的元素分布不均匀性有显著的调控作用,其结果会对材料力学性能产生重要影响.然而,在相关研究结果中还欠缺对于这种可能的短程有序结构的原子尺度结构分析.对于实际的短程有序结构和模拟计算中推测的短程有序结构是否一致这一问题还需更多的研究探索. ...
Local structure and short-range order in a NiCoCr solid solution alloy
1
2017
... CrCoNi作为FeCoNiCrMn高熵体系的衍生[8 ,31 ] ,其强韧性甚至超过了FeCoNiCrMn以及大多数的多相高熵合金,并具有突出的低温性能.第一性原理计算结果[19 ] 表明,CrCoNi中形成短程有序结构的趋势强烈,特别是Cr元素更倾向与Ni元素和Co元素成键.这与Zhang等[20 ] 基于X射线散射、中子散射和扩展X射线吸收精细结构分析的结果相一致.另外,Zhang等[22 ] 使用能量过滤透射电子显微镜(TEM)观察退火较长时间的CrCoNi中熵合金的显微结构时发现,高温时效会导致CrCoNi中形成明显的短程有序.他们通过纳米压痕实验对比研究了长时间时效后包含短程有序结构的CrCoNi和未进行时效处理的CrCoNi,发现时效后材料强度显著提升.这表明热处理工艺对高熵合金中的元素分布不均匀性有显著的调控作用,其结果会对材料力学性能产生重要影响.然而,在相关研究结果中还欠缺对于这种可能的短程有序结构的原子尺度结构分析.对于实际的短程有序结构和模拟计算中推测的短程有序结构是否一致这一问题还需更多的研究探索. ...
Tuning element distribution, structure and properties by composition in high-entropy alloys
4
2019
... 即使是在简单的单相固溶体中,也已有不少实验和模拟的研究提出[17 ,19 ,21 ,22 ] ,高熵合金中元素分布可能不均匀.而由于经典的固溶强化理论的建立基于一个重要的前提条件:溶质原子在溶剂中是随机、均匀分布的,这就引发了一个重要的科学问题,即经典的合金强化理论,例如固溶强化理论,在多元复杂合金体系中是否还适用?而对于不均匀性的理解大致可以分成2种:一种是合金中元素浓度的波动,被称为“浓度波”[24 ] .这种波动是指在固溶体中,原子尺度一定晶体方向上,各种元素的成分存在差异,偏离了合金设计中的化学配比.这种波动的波幅可能在百分之几到百分之几十之间,而波长往往在几个纳米.第2种不均匀性体现在短程有序结构[25 ] ,即在固溶体中,存在具有化学或拓扑组态的结构单元.如图1 b所示,这2种不均匀性均打破了高熵合金是理想固溶体的认知,对材料的力学性能产生重要影响.这2种不均匀性往往能够通过热处理、元素添加或改变元素配比来进行调控.如果其真实存在,势必对高熵合金中的位错滑移产生重要影响.同时,这也是高熵合金可以被利用的一种特性.通过调节这种元素分布的不均匀性,或许能有效改变合金材料的力学性能. ...
... 2019年,Ding等[21 ] 利用原子尺度的能量色散X射线谱进行元素分布表征,揭示了Cantor合金中各元素在晶格尺度10%范围内的成分起伏.为实现复杂固溶体中原子分辨率的元素表征,研究人员通过特殊的实验设计和操作,如:①通过模拟计算得到了最佳信噪比所对应的样品厚度;②利用超低束流、超长扫描时间来获取更高的信噪比和降低对样品的损耗;③调控仪器硬件参数以实现超高样品杆稳定性等,克服了固溶体合金中元素分辨困难的问题[21 ] .研究发现这种浓度波的存在使得高熵合金中晶格尺度的滑移阻力连续变化、局部层错能起伏,同时影响晶格畸变进而导致内应力、应变场连续变化,从而影响位错滑移和材料力学性能.而这种浓度波的起伏大小与成分密切相关.如果将FeCoNiCrMn中的Mn替换成与合金组成元素相比具有较大原子半径和电负性差异的Pd原子,其组成元素浓度起伏可增大到最高60%.而这种浓度波动的波长为1~3 nm.FeCoNiCrPd合金中更大的浓度波动使得室温下材料主导塑性变形方式从平面滑移转变为大量均匀分布的交滑移,提高了材料的加工硬化.与Cantor合金相比,在保证相当水平的塑性变形能力的同时,强度显著提升[21 ] . ...
... [21 ].研究发现这种浓度波的存在使得高熵合金中晶格尺度的滑移阻力连续变化、局部层错能起伏,同时影响晶格畸变进而导致内应力、应变场连续变化,从而影响位错滑移和材料力学性能.而这种浓度波的起伏大小与成分密切相关.如果将FeCoNiCrMn中的Mn替换成与合金组成元素相比具有较大原子半径和电负性差异的Pd原子,其组成元素浓度起伏可增大到最高60%.而这种浓度波动的波长为1~3 nm.FeCoNiCrPd合金中更大的浓度波动使得室温下材料主导塑性变形方式从平面滑移转变为大量均匀分布的交滑移,提高了材料的加工硬化.与Cantor合金相比,在保证相当水平的塑性变形能力的同时,强度显著提升[21 ] . ...
... [21 ]. ...
Short-range order and its impact on the CrCoNi medium-entropy alloy
3
2020
... 合金的性能首先取决于材料的组元,也可以说是材料的基因.在此基础上,显微结构的变化就如同后天的培养,在一定范围内能够有效地调控材料性能.高熵合金往往元素组成复杂,这是基因上的特点;而在成分一定的前提下,各种元素在晶格中如何分布就是结构的问题,也会对性能产生影响.而对于高熵合金中元素如何分布这个问题,一直以来还存在较大的争议.早期研究[14 ,17 ] 认为,多组元合金中各母元素的晶体结构虽然不同,但所获得的合金组织中不存在有害的金属间化合物、非晶或多相结构,这是由于多种元素近等原子比的混合会增加混合的构型熵,因此,能够形成稳定的单相固溶体.随后通过改变成分,科学家们又研发出大量双相高熵合金,利用强、韧相的混合来提升材料力学性能.这其中CuCoNiCrAlx [18 ] 是典型的双相高熵合金体系.通过增加Al元素的含量,能够形成稳定的双相固溶体结构.与传统合金中的理想固溶模型(如图1 a所示)相类似,高熵合金中的各组分原子在晶格中应该具有随机的占位,即形成各种元素均匀分布的完美固溶体.然而越来越多的研究[19 ~22 ] 表明,由于原子特性不同,例如半径、模量、电负性等,成分复杂合金体系中的原子排列可能不是理想的随机状态,即可能在原子尺度存在元素分布的不均匀性.特别是,当合金体系的组分中包含与其他组成元素的原子特性迥异的元素时,这种现象存在的机率极大.研究发现高熵合金中经常出现多相固溶体、非晶、金属间化合物等.在某些高熵体系中,单相固溶体不容易长期稳定存在[23 ] . ...
... 即使是在简单的单相固溶体中,也已有不少实验和模拟的研究提出[17 ,19 ,21 ,22 ] ,高熵合金中元素分布可能不均匀.而由于经典的固溶强化理论的建立基于一个重要的前提条件:溶质原子在溶剂中是随机、均匀分布的,这就引发了一个重要的科学问题,即经典的合金强化理论,例如固溶强化理论,在多元复杂合金体系中是否还适用?而对于不均匀性的理解大致可以分成2种:一种是合金中元素浓度的波动,被称为“浓度波”[24 ] .这种波动是指在固溶体中,原子尺度一定晶体方向上,各种元素的成分存在差异,偏离了合金设计中的化学配比.这种波动的波幅可能在百分之几到百分之几十之间,而波长往往在几个纳米.第2种不均匀性体现在短程有序结构[25 ] ,即在固溶体中,存在具有化学或拓扑组态的结构单元.如图1 b所示,这2种不均匀性均打破了高熵合金是理想固溶体的认知,对材料的力学性能产生重要影响.这2种不均匀性往往能够通过热处理、元素添加或改变元素配比来进行调控.如果其真实存在,势必对高熵合金中的位错滑移产生重要影响.同时,这也是高熵合金可以被利用的一种特性.通过调节这种元素分布的不均匀性,或许能有效改变合金材料的力学性能. ...
... CrCoNi作为FeCoNiCrMn高熵体系的衍生[8 ,31 ] ,其强韧性甚至超过了FeCoNiCrMn以及大多数的多相高熵合金,并具有突出的低温性能.第一性原理计算结果[19 ] 表明,CrCoNi中形成短程有序结构的趋势强烈,特别是Cr元素更倾向与Ni元素和Co元素成键.这与Zhang等[20 ] 基于X射线散射、中子散射和扩展X射线吸收精细结构分析的结果相一致.另外,Zhang等[22 ] 使用能量过滤透射电子显微镜(TEM)观察退火较长时间的CrCoNi中熵合金的显微结构时发现,高温时效会导致CrCoNi中形成明显的短程有序.他们通过纳米压痕实验对比研究了长时间时效后包含短程有序结构的CrCoNi和未进行时效处理的CrCoNi,发现时效后材料强度显著提升.这表明热处理工艺对高熵合金中的元素分布不均匀性有显著的调控作用,其结果会对材料力学性能产生重要影响.然而,在相关研究结果中还欠缺对于这种可能的短程有序结构的原子尺度结构分析.对于实际的短程有序结构和模拟计算中推测的短程有序结构是否一致这一问题还需更多的研究探索. ...
Phase stabilities of high entropy alloys
2
2020
... 合金的性能首先取决于材料的组元,也可以说是材料的基因.在此基础上,显微结构的变化就如同后天的培养,在一定范围内能够有效地调控材料性能.高熵合金往往元素组成复杂,这是基因上的特点;而在成分一定的前提下,各种元素在晶格中如何分布就是结构的问题,也会对性能产生影响.而对于高熵合金中元素如何分布这个问题,一直以来还存在较大的争议.早期研究[14 ,17 ] 认为,多组元合金中各母元素的晶体结构虽然不同,但所获得的合金组织中不存在有害的金属间化合物、非晶或多相结构,这是由于多种元素近等原子比的混合会增加混合的构型熵,因此,能够形成稳定的单相固溶体.随后通过改变成分,科学家们又研发出大量双相高熵合金,利用强、韧相的混合来提升材料力学性能.这其中CuCoNiCrAlx [18 ] 是典型的双相高熵合金体系.通过增加Al元素的含量,能够形成稳定的双相固溶体结构.与传统合金中的理想固溶模型(如图1 a所示)相类似,高熵合金中的各组分原子在晶格中应该具有随机的占位,即形成各种元素均匀分布的完美固溶体.然而越来越多的研究[19 ~22 ] 表明,由于原子特性不同,例如半径、模量、电负性等,成分复杂合金体系中的原子排列可能不是理想的随机状态,即可能在原子尺度存在元素分布的不均匀性.特别是,当合金体系的组分中包含与其他组成元素的原子特性迥异的元素时,这种现象存在的机率极大.研究发现高熵合金中经常出现多相固溶体、非晶、金属间化合物等.在某些高熵体系中,单相固溶体不容易长期稳定存在[23 ] . ...
... 尽管在设计之初,高熵合金得益于单相稳定这一概念,但实际上,大多数的高熵合金都是多相结构,Luan等[23 ] 使用振动理论模型对总计7085种高熵合金的稳定性进行了计算和预测.结果表明,高熵合金在多相结构下更容易保持稳定状态.同时,随着合金元素数量的增加,单相的高熵合金几乎不能稳定存在.这一结论在bcc体系高熵合金中得到了更好的体现.文献[39 ]表明,bcc结构的难熔高熵合金通常是一类具有多相结构的高熵合金.其中,常见的难熔高熵合金主要是HfNbTaTiZr、MoNbTaVW、AlMo0.5 NbTa0.5 TiZr、NbTiVZr及其衍生体系[13 ] . ...
Concentration waves and Fermi surfaces in random metallic alloys
1
1983
... 即使是在简单的单相固溶体中,也已有不少实验和模拟的研究提出[17 ,19 ,21 ,22 ] ,高熵合金中元素分布可能不均匀.而由于经典的固溶强化理论的建立基于一个重要的前提条件:溶质原子在溶剂中是随机、均匀分布的,这就引发了一个重要的科学问题,即经典的合金强化理论,例如固溶强化理论,在多元复杂合金体系中是否还适用?而对于不均匀性的理解大致可以分成2种:一种是合金中元素浓度的波动,被称为“浓度波”[24 ] .这种波动是指在固溶体中,原子尺度一定晶体方向上,各种元素的成分存在差异,偏离了合金设计中的化学配比.这种波动的波幅可能在百分之几到百分之几十之间,而波长往往在几个纳米.第2种不均匀性体现在短程有序结构[25 ] ,即在固溶体中,存在具有化学或拓扑组态的结构单元.如图1 b所示,这2种不均匀性均打破了高熵合金是理想固溶体的认知,对材料的力学性能产生重要影响.这2种不均匀性往往能够通过热处理、元素添加或改变元素配比来进行调控.如果其真实存在,势必对高熵合金中的位错滑移产生重要影响.同时,这也是高熵合金可以被利用的一种特性.通过调节这种元素分布的不均匀性,或许能有效改变合金材料的力学性能. ...
Short-range ordering and its effects on mechanical properties of high-entropy alloys
2
2021
... 即使是在简单的单相固溶体中,也已有不少实验和模拟的研究提出[17 ,19 ,21 ,22 ] ,高熵合金中元素分布可能不均匀.而由于经典的固溶强化理论的建立基于一个重要的前提条件:溶质原子在溶剂中是随机、均匀分布的,这就引发了一个重要的科学问题,即经典的合金强化理论,例如固溶强化理论,在多元复杂合金体系中是否还适用?而对于不均匀性的理解大致可以分成2种:一种是合金中元素浓度的波动,被称为“浓度波”[24 ] .这种波动是指在固溶体中,原子尺度一定晶体方向上,各种元素的成分存在差异,偏离了合金设计中的化学配比.这种波动的波幅可能在百分之几到百分之几十之间,而波长往往在几个纳米.第2种不均匀性体现在短程有序结构[25 ] ,即在固溶体中,存在具有化学或拓扑组态的结构单元.如图1 b所示,这2种不均匀性均打破了高熵合金是理想固溶体的认知,对材料的力学性能产生重要影响.这2种不均匀性往往能够通过热处理、元素添加或改变元素配比来进行调控.如果其真实存在,势必对高熵合金中的位错滑移产生重要影响.同时,这也是高熵合金可以被利用的一种特性.通过调节这种元素分布的不均匀性,或许能有效改变合金材料的力学性能. ...
... 除上述FeCoNiCrMn合金和CrCoNi合金外,部分非等原子比高熵合金也可兼顾获得好的强度和延展性.改变高熵合金中各组元的原子比例或添加其他元素均可导致高熵合金中浓度波的变化,或产生短程有序的结构,甚至在某些条件下,形成纳米析出相等化学有序结构(详见章节4).例如Al[35 ,36 ] 、Mo[37 ] 、B[38 ] 、C元素的添加会导致高熵合金微观结构的显著变化,使得原子排布的非均匀性增加,更加偏离传统的随机固溶体模型.Al和Mo的原子半径大于Fe、Co、Ni、Cr和Mn的原子半径,而B、C元素作为间隙原子,可导致晶格畸变增大,从而提高局部应变能,使得局部区域形成有序结构的化学驱动力增大[25 ] .另一方面,由于晶界附近的高能量状态,B原子更容易聚集在晶界附近,但少量的可溶性B元素可以成为间隙原子固溶于非等原子高熵合金当中.Seol等[38 ] 发现,在低温77 K条件下变形时,非等原子比高熵合金Fe40 Mn40 Co10 Cr10 的晶粒内部的平面滑移带上会产生大量超细的短程有序域,在衍射斑点上显示出超晶格的斑点.这种特殊的现象被认为与母相中固溶B元素有关,是材料优异低温性能的主要来源.然而,由于缺乏原子尺度元素的分布信息,固溶体中B元素的固溶形式以及所起到的作用还无法得到准确的科学理解. ...
Reasons for the superior mechanical properties of medium-entropy CrCoNi compared to high-entropy CrMnFeCoNi
1
2017
... 目前fcc结构高熵合金中,研究最为广泛的主要是等原子比单相高熵合金FeCoNiCrMn,以及在此基础上衍生出的三元合金体系,如CrCoNi中熵合金;四元合金体系;六元合金体系等.作为最早被提出的一类高熵合金,此类合金具有单相稳定且无明显的宏观元素偏析的结构特点,使得这一体系合金成为研究高熵合金体系中元素不均匀性的模型及材料[26 ] . ...
Tensile properties of high- and medium-entropy alloys
2
2013
... Cantor合金[27 ] 是最早、研究最广泛的一种高熵合金.研究人员利用X射线衍射(XRD)、扫描电子显微镜(SEM)、背散射电子衍射(EBSD)及原子探针断层扫描(APT)等检测手段显示,Cantor合金中组成元素基本是均匀随机分布的[17 ,27 ~29 ] .在常规的热处理下,Cantor合金中元素分布的宏观尺度混合可以被维持,但由于晶格尺度的元素分布不均匀性难以被常规的检测方法所识别,在更小的尺度上,元素分布是否绝对均匀还有待探索[30 ] . ...
... ,27 ~29 ].在常规的热处理下,Cantor合金中元素分布的宏观尺度混合可以被维持,但由于晶格尺度的元素分布不均匀性难以被常规的检测方法所识别,在更小的尺度上,元素分布是否绝对均匀还有待探索[30 ] . ...
Insights into the phase diagram of the CrMnFeCoNi high entropy alloy
0
2015
Microstructural evolution after thermomechanical processing in an equiatomic, single-phase CoCrFeMnNi high-entropy alloy with special focus on twin boundaries
1
2014
... Cantor合金[27 ] 是最早、研究最广泛的一种高熵合金.研究人员利用X射线衍射(XRD)、扫描电子显微镜(SEM)、背散射电子衍射(EBSD)及原子探针断层扫描(APT)等检测手段显示,Cantor合金中组成元素基本是均匀随机分布的[17 ,27 ~29 ] .在常规的热处理下,Cantor合金中元素分布的宏观尺度混合可以被维持,但由于晶格尺度的元素分布不均匀性难以被常规的检测方法所识别,在更小的尺度上,元素分布是否绝对均匀还有待探索[30 ] . ...
Decomposition of the single-phase high-entropy alloy CrMnFeCoNi after prolonged anneals at intermediate temperatures
3
2016
... Cantor合金[27 ] 是最早、研究最广泛的一种高熵合金.研究人员利用X射线衍射(XRD)、扫描电子显微镜(SEM)、背散射电子衍射(EBSD)及原子探针断层扫描(APT)等检测手段显示,Cantor合金中组成元素基本是均匀随机分布的[17 ,27 ~29 ] .在常规的热处理下,Cantor合金中元素分布的宏观尺度混合可以被维持,但由于晶格尺度的元素分布不均匀性难以被常规的检测方法所识别,在更小的尺度上,元素分布是否绝对均匀还有待探索[30 ] . ...
... 同时,人们也尝试通过特殊的热处理过程来改变Cantor合金中的元素分布规律.例如,Otto等[30 ] 通过在低于800℃下的长时间退火(500 d)发现,原本单相稳定的FeCoNiCrMn合金会在晶界处分解出3种不同的相,包括bcc的富Cr相、L 10 的NiMn相以及B2的FeCo相.这也说明Cantor合金中,常温下合金元素的分布也处于一种亚稳态,在长时间退火条件下,元素的扩散使得元素分布趋向于更不均匀,甚至形成新相来达到热力学平衡.而当退火温度达到800℃以上时,Cantor合金中没有出现低温退火时的分相结构,但通过X射线能谱(EDS)表征,提出可能存在元素偏聚的情况.然而,根据他们表征的精度以及Cantor合金本身元素相近的特点,相关结果中的偏聚可能跟高温下特殊元素的选择性氧化有关.而在极低温度,例如液氮温度下,虽然并没有驱动力改变元素的分布,但是低温下各种元素的热震荡都大大减小,元素分布不均匀对于晶格阻力以及位错滑移的影响被更大程度地显现出来,其结果是在液氮温度下,Cantor合金中也会出现大量的交滑移[30 ] . ...
... [30 ]. ...
Dislocation mechanisms and 3D twin architectures generate exceptional strength-ductility-toughness combination in CrCoNi medium-entropy alloy
1
2017
... CrCoNi作为FeCoNiCrMn高熵体系的衍生[8 ,31 ] ,其强韧性甚至超过了FeCoNiCrMn以及大多数的多相高熵合金,并具有突出的低温性能.第一性原理计算结果[19 ] 表明,CrCoNi中形成短程有序结构的趋势强烈,特别是Cr元素更倾向与Ni元素和Co元素成键.这与Zhang等[20 ] 基于X射线散射、中子散射和扩展X射线吸收精细结构分析的结果相一致.另外,Zhang等[22 ] 使用能量过滤透射电子显微镜(TEM)观察退火较长时间的CrCoNi中熵合金的显微结构时发现,高温时效会导致CrCoNi中形成明显的短程有序.他们通过纳米压痕实验对比研究了长时间时效后包含短程有序结构的CrCoNi和未进行时效处理的CrCoNi,发现时效后材料强度显著提升.这表明热处理工艺对高熵合金中的元素分布不均匀性有显著的调控作用,其结果会对材料力学性能产生重要影响.然而,在相关研究结果中还欠缺对于这种可能的短程有序结构的原子尺度结构分析.对于实际的短程有序结构和模拟计算中推测的短程有序结构是否一致这一问题还需更多的研究探索. ...
Origin of strong solid solution strengthening in the CrCoNi-W medium entropy alloy
1
2021
... 除此之外,添加少量合金元素来改善材料的力学性能一直是合金设计的一种重要思路.其机制主要是由于溶质和溶剂原子相互作用产生的弹性能的局部增加从而对位错运动产生了阻碍作用.而最近的研究成果表明高熵合金体系对于微量元素的添加表现出更加强烈的反应,这种强化效果不能用传统的固溶强化理论完全解释,也明显区别于传统合金行为.例如,Chen等[32 ] 通过对比中熵合金CrCoNi和传统的纯Ni合金发现,在2种体系中添加等量3%W后,CrCoNi-3W合金的屈服强度提升至1 GPa,其相对于CrCoNi的屈服强度增量为500 MPa,而通过理论计算在相同条件下得到的强度增量应仅为150 MPa.与之对比,如果在纯Ni条件下添加3%W,Ni-3W合金体现出与相同条件下理论计算得到的强度增量相当,即约50 MPa.他们还通过原子级的元素分布以及内应力应变图进行表征.如图2 所示,少量W元素的添加在CrCoNi高熵体系中激发出了较大的浓度波起伏.CrCoNi合金中各元素的浓度起伏仅在10%浓度范围,而CrCoNi-3W中各主元素浓度起伏在15%~55%范围,晶格畸变也相应增加.相较而言,少量W元素的添加在纯Ni合金中仅引起微小的浓度起伏.浓度波的波幅大小对于位错在滑移过程中的形态以及滑移方式有着很大的影响.如图3 所示,在Ni-3W中,位错在滑移过程中显示出平直的滑移.同时,与CrCoNi合金中位错所呈现的较为均匀的分解不同,在CrCoNi-3W高熵合金中,由于浓度起伏以及较大的晶格畸变导致位错的滑移阻力连续变化,位错在滑移过程中显示出明显的纳米尺度分段钉扎的现象,并发生不均匀分解(如图3 c箭头所示).这种特殊的位错滑移行为与Ma等[33 ,34 ] 的模拟计算得到结果相一致.Ma等[33 ,34 ] 详细描述了这种nanoscale segment detrapping现象.不仅是位错的运动方式,浓度起伏也会对位错的交互作用产生影响,如图3 d所示,双相高熵合金Cr20 Mn10 Fe30 Co30 Ni10 位错锁的形成将在下文中详细说明. ...
Tailoring heterogeneities in high-entropy alloys to promote strength-ductility synergy
2
2019
... 除此之外,添加少量合金元素来改善材料的力学性能一直是合金设计的一种重要思路.其机制主要是由于溶质和溶剂原子相互作用产生的弹性能的局部增加从而对位错运动产生了阻碍作用.而最近的研究成果表明高熵合金体系对于微量元素的添加表现出更加强烈的反应,这种强化效果不能用传统的固溶强化理论完全解释,也明显区别于传统合金行为.例如,Chen等[32 ] 通过对比中熵合金CrCoNi和传统的纯Ni合金发现,在2种体系中添加等量3%W后,CrCoNi-3W合金的屈服强度提升至1 GPa,其相对于CrCoNi的屈服强度增量为500 MPa,而通过理论计算在相同条件下得到的强度增量应仅为150 MPa.与之对比,如果在纯Ni条件下添加3%W,Ni-3W合金体现出与相同条件下理论计算得到的强度增量相当,即约50 MPa.他们还通过原子级的元素分布以及内应力应变图进行表征.如图2 所示,少量W元素的添加在CrCoNi高熵体系中激发出了较大的浓度波起伏.CrCoNi合金中各元素的浓度起伏仅在10%浓度范围,而CrCoNi-3W中各主元素浓度起伏在15%~55%范围,晶格畸变也相应增加.相较而言,少量W元素的添加在纯Ni合金中仅引起微小的浓度起伏.浓度波的波幅大小对于位错在滑移过程中的形态以及滑移方式有着很大的影响.如图3 所示,在Ni-3W中,位错在滑移过程中显示出平直的滑移.同时,与CrCoNi合金中位错所呈现的较为均匀的分解不同,在CrCoNi-3W高熵合金中,由于浓度起伏以及较大的晶格畸变导致位错的滑移阻力连续变化,位错在滑移过程中显示出明显的纳米尺度分段钉扎的现象,并发生不均匀分解(如图3 c箭头所示).这种特殊的位错滑移行为与Ma等[33 ,34 ] 的模拟计算得到结果相一致.Ma等[33 ,34 ] 详细描述了这种nanoscale segment detrapping现象.不仅是位错的运动方式,浓度起伏也会对位错的交互作用产生影响,如图3 d所示,双相高熵合金Cr20 Mn10 Fe30 Co30 Ni10 位错锁的形成将在下文中详细说明. ...
... [33 ,34 ]详细描述了这种nanoscale segment detrapping现象.不仅是位错的运动方式,浓度起伏也会对位错的交互作用产生影响,如图3 d所示,双相高熵合金Cr20 Mn10 Fe30 Co30 Ni10 位错锁的形成将在下文中详细说明. ...
Unusual activated processes controlling dislocation motion in body-centered-cubic high-entropy alloys
4
2020
... 除此之外,添加少量合金元素来改善材料的力学性能一直是合金设计的一种重要思路.其机制主要是由于溶质和溶剂原子相互作用产生的弹性能的局部增加从而对位错运动产生了阻碍作用.而最近的研究成果表明高熵合金体系对于微量元素的添加表现出更加强烈的反应,这种强化效果不能用传统的固溶强化理论完全解释,也明显区别于传统合金行为.例如,Chen等[32 ] 通过对比中熵合金CrCoNi和传统的纯Ni合金发现,在2种体系中添加等量3%W后,CrCoNi-3W合金的屈服强度提升至1 GPa,其相对于CrCoNi的屈服强度增量为500 MPa,而通过理论计算在相同条件下得到的强度增量应仅为150 MPa.与之对比,如果在纯Ni条件下添加3%W,Ni-3W合金体现出与相同条件下理论计算得到的强度增量相当,即约50 MPa.他们还通过原子级的元素分布以及内应力应变图进行表征.如图2 所示,少量W元素的添加在CrCoNi高熵体系中激发出了较大的浓度波起伏.CrCoNi合金中各元素的浓度起伏仅在10%浓度范围,而CrCoNi-3W中各主元素浓度起伏在15%~55%范围,晶格畸变也相应增加.相较而言,少量W元素的添加在纯Ni合金中仅引起微小的浓度起伏.浓度波的波幅大小对于位错在滑移过程中的形态以及滑移方式有着很大的影响.如图3 所示,在Ni-3W中,位错在滑移过程中显示出平直的滑移.同时,与CrCoNi合金中位错所呈现的较为均匀的分解不同,在CrCoNi-3W高熵合金中,由于浓度起伏以及较大的晶格畸变导致位错的滑移阻力连续变化,位错在滑移过程中显示出明显的纳米尺度分段钉扎的现象,并发生不均匀分解(如图3 c箭头所示).这种特殊的位错滑移行为与Ma等[33 ,34 ] 的模拟计算得到结果相一致.Ma等[33 ,34 ] 详细描述了这种nanoscale segment detrapping现象.不仅是位错的运动方式,浓度起伏也会对位错的交互作用产生影响,如图3 d所示,双相高熵合金Cr20 Mn10 Fe30 Co30 Ni10 位错锁的形成将在下文中详细说明. ...
... ,34 ]详细描述了这种nanoscale segment detrapping现象.不仅是位错的运动方式,浓度起伏也会对位错的交互作用产生影响,如图3 d所示,双相高熵合金Cr20 Mn10 Fe30 Co30 Ni10 位错锁的形成将在下文中详细说明. ...
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr[12 ,46 ] 和Co16.67 Fe36.67 Ni16.67 Ti30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等[41 ] 通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
... [34 ],进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
Microstructure and wear behavior of Alx 1.5 CrFeNi1.5 Tiy
1
2011
... 除上述FeCoNiCrMn合金和CrCoNi合金外,部分非等原子比高熵合金也可兼顾获得好的强度和延展性.改变高熵合金中各组元的原子比例或添加其他元素均可导致高熵合金中浓度波的变化,或产生短程有序的结构,甚至在某些条件下,形成纳米析出相等化学有序结构(详见章节4).例如Al[35 ,36 ] 、Mo[37 ] 、B[38 ] 、C元素的添加会导致高熵合金微观结构的显著变化,使得原子排布的非均匀性增加,更加偏离传统的随机固溶体模型.Al和Mo的原子半径大于Fe、Co、Ni、Cr和Mn的原子半径,而B、C元素作为间隙原子,可导致晶格畸变增大,从而提高局部应变能,使得局部区域形成有序结构的化学驱动力增大[25 ] .另一方面,由于晶界附近的高能量状态,B原子更容易聚集在晶界附近,但少量的可溶性B元素可以成为间隙原子固溶于非等原子高熵合金当中.Seol等[38 ] 发现,在低温77 K条件下变形时,非等原子比高熵合金Fe40 Mn40 Co10 Cr10 的晶粒内部的平面滑移带上会产生大量超细的短程有序域,在衍射斑点上显示出超晶格的斑点.这种特殊的现象被认为与母相中固溶B元素有关,是材料优异低温性能的主要来源.然而,由于缺乏原子尺度元素的分布信息,固溶体中B元素的固溶形式以及所起到的作用还无法得到准确的科学理解. ...
Short-range chemical order and local lattice distortion in a compositionally complex alloy
1
2020
... 除上述FeCoNiCrMn合金和CrCoNi合金外,部分非等原子比高熵合金也可兼顾获得好的强度和延展性.改变高熵合金中各组元的原子比例或添加其他元素均可导致高熵合金中浓度波的变化,或产生短程有序的结构,甚至在某些条件下,形成纳米析出相等化学有序结构(详见章节4).例如Al[35 ,36 ] 、Mo[37 ] 、B[38 ] 、C元素的添加会导致高熵合金微观结构的显著变化,使得原子排布的非均匀性增加,更加偏离传统的随机固溶体模型.Al和Mo的原子半径大于Fe、Co、Ni、Cr和Mn的原子半径,而B、C元素作为间隙原子,可导致晶格畸变增大,从而提高局部应变能,使得局部区域形成有序结构的化学驱动力增大[25 ] .另一方面,由于晶界附近的高能量状态,B原子更容易聚集在晶界附近,但少量的可溶性B元素可以成为间隙原子固溶于非等原子高熵合金当中.Seol等[38 ] 发现,在低温77 K条件下变形时,非等原子比高熵合金Fe40 Mn40 Co10 Cr10 的晶粒内部的平面滑移带上会产生大量超细的短程有序域,在衍射斑点上显示出超晶格的斑点.这种特殊的现象被认为与母相中固溶B元素有关,是材料优异低温性能的主要来源.然而,由于缺乏原子尺度元素的分布信息,固溶体中B元素的固溶形式以及所起到的作用还无法得到准确的科学理解. ...
Segregation of Mo atoms into stacking faults in CrFeCoNiMo alloy
1
2019
... 除上述FeCoNiCrMn合金和CrCoNi合金外,部分非等原子比高熵合金也可兼顾获得好的强度和延展性.改变高熵合金中各组元的原子比例或添加其他元素均可导致高熵合金中浓度波的变化,或产生短程有序的结构,甚至在某些条件下,形成纳米析出相等化学有序结构(详见章节4).例如Al[35 ,36 ] 、Mo[37 ] 、B[38 ] 、C元素的添加会导致高熵合金微观结构的显著变化,使得原子排布的非均匀性增加,更加偏离传统的随机固溶体模型.Al和Mo的原子半径大于Fe、Co、Ni、Cr和Mn的原子半径,而B、C元素作为间隙原子,可导致晶格畸变增大,从而提高局部应变能,使得局部区域形成有序结构的化学驱动力增大[25 ] .另一方面,由于晶界附近的高能量状态,B原子更容易聚集在晶界附近,但少量的可溶性B元素可以成为间隙原子固溶于非等原子高熵合金当中.Seol等[38 ] 发现,在低温77 K条件下变形时,非等原子比高熵合金Fe40 Mn40 Co10 Cr10 的晶粒内部的平面滑移带上会产生大量超细的短程有序域,在衍射斑点上显示出超晶格的斑点.这种特殊的现象被认为与母相中固溶B元素有关,是材料优异低温性能的主要来源.然而,由于缺乏原子尺度元素的分布信息,固溶体中B元素的固溶形式以及所起到的作用还无法得到准确的科学理解. ...
Short-range order strengthening in boron-doped high-entropy alloys for cryogenic applications
2
2020
... 除上述FeCoNiCrMn合金和CrCoNi合金外,部分非等原子比高熵合金也可兼顾获得好的强度和延展性.改变高熵合金中各组元的原子比例或添加其他元素均可导致高熵合金中浓度波的变化,或产生短程有序的结构,甚至在某些条件下,形成纳米析出相等化学有序结构(详见章节4).例如Al[35 ,36 ] 、Mo[37 ] 、B[38 ] 、C元素的添加会导致高熵合金微观结构的显著变化,使得原子排布的非均匀性增加,更加偏离传统的随机固溶体模型.Al和Mo的原子半径大于Fe、Co、Ni、Cr和Mn的原子半径,而B、C元素作为间隙原子,可导致晶格畸变增大,从而提高局部应变能,使得局部区域形成有序结构的化学驱动力增大[25 ] .另一方面,由于晶界附近的高能量状态,B原子更容易聚集在晶界附近,但少量的可溶性B元素可以成为间隙原子固溶于非等原子高熵合金当中.Seol等[38 ] 发现,在低温77 K条件下变形时,非等原子比高熵合金Fe40 Mn40 Co10 Cr10 的晶粒内部的平面滑移带上会产生大量超细的短程有序域,在衍射斑点上显示出超晶格的斑点.这种特殊的现象被认为与母相中固溶B元素有关,是材料优异低温性能的主要来源.然而,由于缺乏原子尺度元素的分布信息,固溶体中B元素的固溶形式以及所起到的作用还无法得到准确的科学理解. ...
... [38 ]发现,在低温77 K条件下变形时,非等原子比高熵合金Fe40 Mn40 Co10 Cr10 的晶粒内部的平面滑移带上会产生大量超细的短程有序域,在衍射斑点上显示出超晶格的斑点.这种特殊的现象被认为与母相中固溶B元素有关,是材料优异低温性能的主要来源.然而,由于缺乏原子尺度元素的分布信息,固溶体中B元素的固溶形式以及所起到的作用还无法得到准确的科学理解. ...
Refractory high-entropy alloys
1
2010
... 尽管在设计之初,高熵合金得益于单相稳定这一概念,但实际上,大多数的高熵合金都是多相结构,Luan等[23 ] 使用振动理论模型对总计7085种高熵合金的稳定性进行了计算和预测.结果表明,高熵合金在多相结构下更容易保持稳定状态.同时,随着合金元素数量的增加,单相的高熵合金几乎不能稳定存在.这一结论在bcc体系高熵合金中得到了更好的体现.文献[39 ]表明,bcc结构的难熔高熵合金通常是一类具有多相结构的高熵合金.其中,常见的难熔高熵合金主要是HfNbTaTiZr、MoNbTaVW、AlMo0.5 NbTa0.5 TiZr、NbTiVZr及其衍生体系[13 ] . ...
Ab initio modeling of the energy landscape for screw dislocations in body-centered cubic high-entropy alloys
1
2020
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr[12 ,46 ] 和Co16.67 Fe36.67 Ni16.67 Ti30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等[41 ] 通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
Atomistic simulations of dislocations in a model BCC multicomponent concentrated solid solution alloy
2
2017
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr[12 ,46 ] 和Co16.67 Fe36.67 Ni16.67 Ti30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等[41 ] 通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
... [41 ]通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
Atomistic calculations of the generalized stacking fault energies in two refractory multi-principal element alloys
1
2020
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr[12 ,46 ] 和Co16.67 Fe36.67 Ni16.67 Ti30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等[41 ] 通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
Multiplicity of dislocation pathways in a refractory multiprincipal element alloy
1
2020
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr[12 ,46 ] 和Co16.67 Fe36.67 Ni16.67 Ti30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等[41 ] 通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
The effect of local chemical ordering on Frank-Read source activation in a refractory multi-principal element alloy
0
2020
Theory of screw dislocation strengthening in random BCC alloys from dilute to “High-Entropy” alloys
1
2020
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr[12 ,46 ] 和Co16.67 Fe36.67 Ni16.67 Ti30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等[41 ] 通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy
1
2011
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr[12 ,46 ] 和Co16.67 Fe36.67 Ni16.67 Ti30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等[41 ] 通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
Study of a bcc multi-principal element alloy: Tensile and simple shear properties and underlying deformation mechanisms
4
2018
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr[12 ,46 ] 和Co16.67 Fe36.67 Ni16.67 Ti30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等[41 ] 通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
... [47 ]),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
... [
47 ~
50 ]
(a) dislocation structures in HfNbTaTiZr HEAs[47 ] ...
... (a) dislocation structures in HfNbTaTiZr HEAs[47 ] ...
Natural-mixing guided design of refractory high-entropy alloys with as-cast tensile ductility
3
2020
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr[12 ,46 ] 和Co16.67 Fe36.67 Ni16.67 Ti30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等[41 ] 通过分子动力学模拟说明,Co16.67 Fe36.67 Ni16.67 Ti30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co16.67 Fe36.67 Ni16.67 Ti30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如图4 a[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如图4 b[48 ] 所示,Wei等[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
... [48 ]通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti38 V15 Nb23 Hf24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m2 之间).Wang等[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升. ...
... (b) dislocation structures in Ti38 V15 Nb23 Hf24 [48 ] ...
Structural-disorder and its effect on mechanical properties in single-phase TaNbHfZr high-entropy alloy
3
2016
... (c) short-range clustering structure in HfNbTaZr after annealing[49 ] ...
... 与fcc高熵合金不同的是,bcc高熵合金中更倾向于形成局部的短程有序结构.除此之外,由短程有序结构所导致的元素分布不均匀性可以通过热处理、添加其他合金元素或改变合金中元素浓度等方式不断地扩大和加剧,导致bcc相中的局域短程有序结构会相互连接,最终形成多相结构,进而根本改变材料的变形机制及其力学性能.如图4 c[49 ] 所示,Maiti等[49 ] 通过长时间退火发现,HfNbTaZr中Hf和Zr原子会沿着垂直于<100>方向形成原子的聚集,并随着退火时间的增加,富含Hf和Zr短程有序结构相互连接形成六方相,最终导致HfNbTaZr合金形成两相交互结构.同时,与fcc高熵合金中的现象相似,bcc高熵合金中的元素分布不均匀性对微量元素的添加也十分敏感.例如,HfNbTaTiZr的衍生物TiZrHfNb合金[11 ] 本来只包含bcc单相.而Lei等[50 ] 通过在TiZrHfNb合金中添加2%的O元素观察到反常的强度和韧性的提高(如图4 d[50 ] ).传统认知认为,合金材料中含有O元素会形成陶瓷相使金属变脆,但Lei等[50 ] 研究表明当高熵合金中添加O元素时,在强度提升的同时,延展性也得到显著改善.通过高分辨扫描透射电子显微镜观察以及APT技术发现,O原子会以有序的方式占据Zr、Ti富集簇中的间隙位置,形成有序氧络合物.这种有序氧络合物的形成是由于高熵合金中所具有的化学短程有序所诱发和促进的.所形成的纳米级的有序区域迫使位错滑移由平面滑移转变为波浪滑移,改变了塑性变形方式.这种强化作用不同于传统的间隙原子强化,是一种由短程有序结构所导致的超常强化.与fcc高熵合金的研究相比,虽然目前对bcc高熵合金中元素分布的研究要少,但已有研究表明bcc高熵合金中元素分布的不均匀性相较于fcc高熵合金应该更为强烈.在常规材料制备,例如铸态合金中,往往会出现分相的现象.如Mo0.5 NbTa0.5 TiZr高熵合金[51 ] 在1500℃下为bcc单相.冷却后,该相分解成为2个成分不同的相(富Zr、Ti相和富Nb、Mo、Ta相),这2个相均具有bcc晶体结构和相似的晶格参数,但化学成分完全不同.又例如,添加了Al元素后,AlMo0.5 NbTa0.5 TiZr合金[52 ~54 ] 分相出不连续的无序bcc相和一个连续的B2相.就目前的研究结果来看,添加Al元素对bcc结构的元素分布具有重要影响,相关的结果还需更多的实验和理论探索. ...
... [49 ]通过长时间退火发现,HfNbTaZr中Hf和Zr原子会沿着垂直于<100>方向形成原子的聚集,并随着退火时间的增加,富含Hf和Zr短程有序结构相互连接形成六方相,最终导致HfNbTaZr合金形成两相交互结构.同时,与fcc高熵合金中的现象相似,bcc高熵合金中的元素分布不均匀性对微量元素的添加也十分敏感.例如,HfNbTaTiZr的衍生物TiZrHfNb合金[11 ] 本来只包含bcc单相.而Lei等[50 ] 通过在TiZrHfNb合金中添加2%的O元素观察到反常的强度和韧性的提高(如图4 d[50 ] ).传统认知认为,合金材料中含有O元素会形成陶瓷相使金属变脆,但Lei等[50 ] 研究表明当高熵合金中添加O元素时,在强度提升的同时,延展性也得到显著改善.通过高分辨扫描透射电子显微镜观察以及APT技术发现,O原子会以有序的方式占据Zr、Ti富集簇中的间隙位置,形成有序氧络合物.这种有序氧络合物的形成是由于高熵合金中所具有的化学短程有序所诱发和促进的.所形成的纳米级的有序区域迫使位错滑移由平面滑移转变为波浪滑移,改变了塑性变形方式.这种强化作用不同于传统的间隙原子强化,是一种由短程有序结构所导致的超常强化.与fcc高熵合金的研究相比,虽然目前对bcc高熵合金中元素分布的研究要少,但已有研究表明bcc高熵合金中元素分布的不均匀性相较于fcc高熵合金应该更为强烈.在常规材料制备,例如铸态合金中,往往会出现分相的现象.如Mo0.5 NbTa0.5 TiZr高熵合金[51 ] 在1500℃下为bcc单相.冷却后,该相分解成为2个成分不同的相(富Zr、Ti相和富Nb、Mo、Ta相),这2个相均具有bcc晶体结构和相似的晶格参数,但化学成分完全不同.又例如,添加了Al元素后,AlMo0.5 NbTa0.5 TiZr合金[52 ~54 ] 分相出不连续的无序bcc相和一个连续的B2相.就目前的研究结果来看,添加Al元素对bcc结构的元素分布具有重要影响,相关的结果还需更多的实验和理论探索. ...
Enhanced strength and ductility in a high-entropy alloy via ordered oxygen complexes
5
2018
... 实际上,针对bcc结构的高熵合金中元素分布不均匀性的实验研究非常少,其可能原因在于人们更关注bcc结构高熵合金中的各相分布以及相结构的设计中,且所形成的相更多为化学有序的结构,这些结构往往具有较为确定的元素分布.但更多的理论计算研究
[40 ~45 ] 表明,单相bcc结构的高熵合金中存在着偏离随机固溶的结构.HfNbTaTiZr
[12 ,46 ] 和Co
16.67 Fe
36.67 Ni
16.67 Ti
30 [34 ,41 ] 是少数存在单相的bcc结构难熔高熵合金,Rao等
[41 ] 通过分子动力学模拟说明,Co
16.67 Fe
36.67 Ni
16.67 Ti
30 合金的螺位错核结构存在沿位错线的扩散现象.这可能是由于Co
16.67 Fe
36.67 Ni
16.67 Ti
30 中存在元素的浓度波动,使得不同的滑移路径上存在变化的层错能.位错滑移时需要克服不断变化的阻力
[34 ] ,进而使位错线发生扭折或弯曲,并在滑移过区域留下位错环等缺陷结构.Lilensten等
[47 ] 在HfNbTaTiZr合金中观察到与上述分子动力学模拟结果相类似的现象,通过离位实验表征塑性变形后的样品发现,位错滑移后,在滑移轨迹上存在位错环和位错偶极子等新的缺陷结构(如
图4 a
[47 ] ),这种现象可以说明基体中存在强的钉扎,这种钉扎被认为与固溶体中的元素波动相关.如
图4 b
[48 ] 所示,Wei等
[48 ] 通过组成元素的自然选择方法设计高熵合金,所制备出的稳定的Ti
38 V
15 Nb
23 Hf
24 相中存在广泛分布的纳米尺度的异质结构,这些结构在塑性变形前提供位错的启动阻力,位错启动后在局部钉扎位错,提供更好的强度.Xu等
[42 ] 通过分子静态模拟和密度泛函理论表明,在MoNbTi和NbTiZr高熵合金体系中,由于滑移面及其附近的局部化学元素偏离随机固溶模型,因此对于同一体系,平行的滑移面之间的局部层错能在很大范围内起伏(例如,在(111)面上起伏在-50~50 mJ/m
2 之间).Wang等
[43 ] 通过对MoNbTi材料的原子模拟计算表明,bcc合金中刃位错的主滑移面为{110},然而由于局部元素的分布,使得不同滑移面之间的滑移阻力差别减小,因此MoNbTi高熵合金中,刃位错具有最低滑移阻力的平面可能为{110}、{112}、{123}.这意味着多个滑移系可以同时启动,有利于材料塑性的提升.
图4 bcc类高熵合金中的元素分布均匀性及其位错行为<sup>[<xref ref-type="bibr" rid="R47">47</xref>~<xref ref-type="bibr" rid="R50">50</xref>]</sup> (a) dislocation structures in HfNbTaTiZr HEAs[47 ] ...
... (d) ordered oxygen complexes regions in TiZrHfNb with 2% oxygen[50 ] ...
... 与fcc高熵合金不同的是,bcc高熵合金中更倾向于形成局部的短程有序结构.除此之外,由短程有序结构所导致的元素分布不均匀性可以通过热处理、添加其他合金元素或改变合金中元素浓度等方式不断地扩大和加剧,导致bcc相中的局域短程有序结构会相互连接,最终形成多相结构,进而根本改变材料的变形机制及其力学性能.如图4 c[49 ] 所示,Maiti等[49 ] 通过长时间退火发现,HfNbTaZr中Hf和Zr原子会沿着垂直于<100>方向形成原子的聚集,并随着退火时间的增加,富含Hf和Zr短程有序结构相互连接形成六方相,最终导致HfNbTaZr合金形成两相交互结构.同时,与fcc高熵合金中的现象相似,bcc高熵合金中的元素分布不均匀性对微量元素的添加也十分敏感.例如,HfNbTaTiZr的衍生物TiZrHfNb合金[11 ] 本来只包含bcc单相.而Lei等[50 ] 通过在TiZrHfNb合金中添加2%的O元素观察到反常的强度和韧性的提高(如图4 d[50 ] ).传统认知认为,合金材料中含有O元素会形成陶瓷相使金属变脆,但Lei等[50 ] 研究表明当高熵合金中添加O元素时,在强度提升的同时,延展性也得到显著改善.通过高分辨扫描透射电子显微镜观察以及APT技术发现,O原子会以有序的方式占据Zr、Ti富集簇中的间隙位置,形成有序氧络合物.这种有序氧络合物的形成是由于高熵合金中所具有的化学短程有序所诱发和促进的.所形成的纳米级的有序区域迫使位错滑移由平面滑移转变为波浪滑移,改变了塑性变形方式.这种强化作用不同于传统的间隙原子强化,是一种由短程有序结构所导致的超常强化.与fcc高熵合金的研究相比,虽然目前对bcc高熵合金中元素分布的研究要少,但已有研究表明bcc高熵合金中元素分布的不均匀性相较于fcc高熵合金应该更为强烈.在常规材料制备,例如铸态合金中,往往会出现分相的现象.如Mo0.5 NbTa0.5 TiZr高熵合金[51 ] 在1500℃下为bcc单相.冷却后,该相分解成为2个成分不同的相(富Zr、Ti相和富Nb、Mo、Ta相),这2个相均具有bcc晶体结构和相似的晶格参数,但化学成分完全不同.又例如,添加了Al元素后,AlMo0.5 NbTa0.5 TiZr合金[52 ~54 ] 分相出不连续的无序bcc相和一个连续的B2相.就目前的研究结果来看,添加Al元素对bcc结构的元素分布具有重要影响,相关的结果还需更多的实验和理论探索. ...
... [50 ]).传统认知认为,合金材料中含有O元素会形成陶瓷相使金属变脆,但Lei等[50 ] 研究表明当高熵合金中添加O元素时,在强度提升的同时,延展性也得到显著改善.通过高分辨扫描透射电子显微镜观察以及APT技术发现,O原子会以有序的方式占据Zr、Ti富集簇中的间隙位置,形成有序氧络合物.这种有序氧络合物的形成是由于高熵合金中所具有的化学短程有序所诱发和促进的.所形成的纳米级的有序区域迫使位错滑移由平面滑移转变为波浪滑移,改变了塑性变形方式.这种强化作用不同于传统的间隙原子强化,是一种由短程有序结构所导致的超常强化.与fcc高熵合金的研究相比,虽然目前对bcc高熵合金中元素分布的研究要少,但已有研究表明bcc高熵合金中元素分布的不均匀性相较于fcc高熵合金应该更为强烈.在常规材料制备,例如铸态合金中,往往会出现分相的现象.如Mo0.5 NbTa0.5 TiZr高熵合金[51 ] 在1500℃下为bcc单相.冷却后,该相分解成为2个成分不同的相(富Zr、Ti相和富Nb、Mo、Ta相),这2个相均具有bcc晶体结构和相似的晶格参数,但化学成分完全不同.又例如,添加了Al元素后,AlMo0.5 NbTa0.5 TiZr合金[52 ~54 ] 分相出不连续的无序bcc相和一个连续的B2相.就目前的研究结果来看,添加Al元素对bcc结构的元素分布具有重要影响,相关的结果还需更多的实验和理论探索. ...
... [50 ]研究表明当高熵合金中添加O元素时,在强度提升的同时,延展性也得到显著改善.通过高分辨扫描透射电子显微镜观察以及APT技术发现,O原子会以有序的方式占据Zr、Ti富集簇中的间隙位置,形成有序氧络合物.这种有序氧络合物的形成是由于高熵合金中所具有的化学短程有序所诱发和促进的.所形成的纳米级的有序区域迫使位错滑移由平面滑移转变为波浪滑移,改变了塑性变形方式.这种强化作用不同于传统的间隙原子强化,是一种由短程有序结构所导致的超常强化.与fcc高熵合金的研究相比,虽然目前对bcc高熵合金中元素分布的研究要少,但已有研究表明bcc高熵合金中元素分布的不均匀性相较于fcc高熵合金应该更为强烈.在常规材料制备,例如铸态合金中,往往会出现分相的现象.如Mo0.5 NbTa0.5 TiZr高熵合金[51 ] 在1500℃下为bcc单相.冷却后,该相分解成为2个成分不同的相(富Zr、Ti相和富Nb、Mo、Ta相),这2个相均具有bcc晶体结构和相似的晶格参数,但化学成分完全不同.又例如,添加了Al元素后,AlMo0.5 NbTa0.5 TiZr合金[52 ~54 ] 分相出不连续的无序bcc相和一个连续的B2相.就目前的研究结果来看,添加Al元素对bcc结构的元素分布具有重要影响,相关的结果还需更多的实验和理论探索. ...
Observation of a refractory metal matrix containing Zr-Ti-rich precipitates in a Mo0.5 NbTa0.5 TiZr high entropy alloy
1
2020
... 与fcc高熵合金不同的是,bcc高熵合金中更倾向于形成局部的短程有序结构.除此之外,由短程有序结构所导致的元素分布不均匀性可以通过热处理、添加其他合金元素或改变合金中元素浓度等方式不断地扩大和加剧,导致bcc相中的局域短程有序结构会相互连接,最终形成多相结构,进而根本改变材料的变形机制及其力学性能.如图4 c[49 ] 所示,Maiti等[49 ] 通过长时间退火发现,HfNbTaZr中Hf和Zr原子会沿着垂直于<100>方向形成原子的聚集,并随着退火时间的增加,富含Hf和Zr短程有序结构相互连接形成六方相,最终导致HfNbTaZr合金形成两相交互结构.同时,与fcc高熵合金中的现象相似,bcc高熵合金中的元素分布不均匀性对微量元素的添加也十分敏感.例如,HfNbTaTiZr的衍生物TiZrHfNb合金[11 ] 本来只包含bcc单相.而Lei等[50 ] 通过在TiZrHfNb合金中添加2%的O元素观察到反常的强度和韧性的提高(如图4 d[50 ] ).传统认知认为,合金材料中含有O元素会形成陶瓷相使金属变脆,但Lei等[50 ] 研究表明当高熵合金中添加O元素时,在强度提升的同时,延展性也得到显著改善.通过高分辨扫描透射电子显微镜观察以及APT技术发现,O原子会以有序的方式占据Zr、Ti富集簇中的间隙位置,形成有序氧络合物.这种有序氧络合物的形成是由于高熵合金中所具有的化学短程有序所诱发和促进的.所形成的纳米级的有序区域迫使位错滑移由平面滑移转变为波浪滑移,改变了塑性变形方式.这种强化作用不同于传统的间隙原子强化,是一种由短程有序结构所导致的超常强化.与fcc高熵合金的研究相比,虽然目前对bcc高熵合金中元素分布的研究要少,但已有研究表明bcc高熵合金中元素分布的不均匀性相较于fcc高熵合金应该更为强烈.在常规材料制备,例如铸态合金中,往往会出现分相的现象.如Mo0.5 NbTa0.5 TiZr高熵合金[51 ] 在1500℃下为bcc单相.冷却后,该相分解成为2个成分不同的相(富Zr、Ti相和富Nb、Mo、Ta相),这2个相均具有bcc晶体结构和相似的晶格参数,但化学成分完全不同.又例如,添加了Al元素后,AlMo0.5 NbTa0.5 TiZr合金[52 ~54 ] 分相出不连续的无序bcc相和一个连续的B2相.就目前的研究结果来看,添加Al元素对bcc结构的元素分布具有重要影响,相关的结果还需更多的实验和理论探索. ...
Effect of aluminum on the microstructure and properties of two refractory high-entropy alloys
1
2014
... 与fcc高熵合金不同的是,bcc高熵合金中更倾向于形成局部的短程有序结构.除此之外,由短程有序结构所导致的元素分布不均匀性可以通过热处理、添加其他合金元素或改变合金中元素浓度等方式不断地扩大和加剧,导致bcc相中的局域短程有序结构会相互连接,最终形成多相结构,进而根本改变材料的变形机制及其力学性能.如图4 c[49 ] 所示,Maiti等[49 ] 通过长时间退火发现,HfNbTaZr中Hf和Zr原子会沿着垂直于<100>方向形成原子的聚集,并随着退火时间的增加,富含Hf和Zr短程有序结构相互连接形成六方相,最终导致HfNbTaZr合金形成两相交互结构.同时,与fcc高熵合金中的现象相似,bcc高熵合金中的元素分布不均匀性对微量元素的添加也十分敏感.例如,HfNbTaTiZr的衍生物TiZrHfNb合金[11 ] 本来只包含bcc单相.而Lei等[50 ] 通过在TiZrHfNb合金中添加2%的O元素观察到反常的强度和韧性的提高(如图4 d[50 ] ).传统认知认为,合金材料中含有O元素会形成陶瓷相使金属变脆,但Lei等[50 ] 研究表明当高熵合金中添加O元素时,在强度提升的同时,延展性也得到显著改善.通过高分辨扫描透射电子显微镜观察以及APT技术发现,O原子会以有序的方式占据Zr、Ti富集簇中的间隙位置,形成有序氧络合物.这种有序氧络合物的形成是由于高熵合金中所具有的化学短程有序所诱发和促进的.所形成的纳米级的有序区域迫使位错滑移由平面滑移转变为波浪滑移,改变了塑性变形方式.这种强化作用不同于传统的间隙原子强化,是一种由短程有序结构所导致的超常强化.与fcc高熵合金的研究相比,虽然目前对bcc高熵合金中元素分布的研究要少,但已有研究表明bcc高熵合金中元素分布的不均匀性相较于fcc高熵合金应该更为强烈.在常规材料制备,例如铸态合金中,往往会出现分相的现象.如Mo0.5 NbTa0.5 TiZr高熵合金[51 ] 在1500℃下为bcc单相.冷却后,该相分解成为2个成分不同的相(富Zr、Ti相和富Nb、Mo、Ta相),这2个相均具有bcc晶体结构和相似的晶格参数,但化学成分完全不同.又例如,添加了Al元素后,AlMo0.5 NbTa0.5 TiZr合金[52 ~54 ] 分相出不连续的无序bcc相和一个连续的B2相.就目前的研究结果来看,添加Al元素对bcc结构的元素分布具有重要影响,相关的结果还需更多的实验和理论探索. ...
Characterization of the microstructure of the compositionally complex alloy Al1 Mo0.5 Nb1 Ta0.5 Ti1 Zr1
0
2016
Compositional variation effects on the microstructure and properties of a refractory high-entropy superalloy AlMo0.5 NbTa0.5 TiZr
1
2018
... 与fcc高熵合金不同的是,bcc高熵合金中更倾向于形成局部的短程有序结构.除此之外,由短程有序结构所导致的元素分布不均匀性可以通过热处理、添加其他合金元素或改变合金中元素浓度等方式不断地扩大和加剧,导致bcc相中的局域短程有序结构会相互连接,最终形成多相结构,进而根本改变材料的变形机制及其力学性能.如图4 c[49 ] 所示,Maiti等[49 ] 通过长时间退火发现,HfNbTaZr中Hf和Zr原子会沿着垂直于<100>方向形成原子的聚集,并随着退火时间的增加,富含Hf和Zr短程有序结构相互连接形成六方相,最终导致HfNbTaZr合金形成两相交互结构.同时,与fcc高熵合金中的现象相似,bcc高熵合金中的元素分布不均匀性对微量元素的添加也十分敏感.例如,HfNbTaTiZr的衍生物TiZrHfNb合金[11 ] 本来只包含bcc单相.而Lei等[50 ] 通过在TiZrHfNb合金中添加2%的O元素观察到反常的强度和韧性的提高(如图4 d[50 ] ).传统认知认为,合金材料中含有O元素会形成陶瓷相使金属变脆,但Lei等[50 ] 研究表明当高熵合金中添加O元素时,在强度提升的同时,延展性也得到显著改善.通过高分辨扫描透射电子显微镜观察以及APT技术发现,O原子会以有序的方式占据Zr、Ti富集簇中的间隙位置,形成有序氧络合物.这种有序氧络合物的形成是由于高熵合金中所具有的化学短程有序所诱发和促进的.所形成的纳米级的有序区域迫使位错滑移由平面滑移转变为波浪滑移,改变了塑性变形方式.这种强化作用不同于传统的间隙原子强化,是一种由短程有序结构所导致的超常强化.与fcc高熵合金的研究相比,虽然目前对bcc高熵合金中元素分布的研究要少,但已有研究表明bcc高熵合金中元素分布的不均匀性相较于fcc高熵合金应该更为强烈.在常规材料制备,例如铸态合金中,往往会出现分相的现象.如Mo0.5 NbTa0.5 TiZr高熵合金[51 ] 在1500℃下为bcc单相.冷却后,该相分解成为2个成分不同的相(富Zr、Ti相和富Nb、Mo、Ta相),这2个相均具有bcc晶体结构和相似的晶格参数,但化学成分完全不同.又例如,添加了Al元素后,AlMo0.5 NbTa0.5 TiZr合金[52 ~54 ] 分相出不连续的无序bcc相和一个连续的B2相.就目前的研究结果来看,添加Al元素对bcc结构的元素分布具有重要影响,相关的结果还需更多的实验和理论探索. ...
Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off
2
2016
... 在单相高熵合金的研究基础上,为增强高熵合金的力学性能,人们引入了多相强化的机制[55 ,56 ] .然而,由于界面结构的存在以及多相结构本身原子结构的复杂性,认知具有复杂相结构的高熵合金中的元素分布规律更具挑战.Li等[55 ] 通过改变非等原子比的Fe80- x x 10 Cr10 中Mn的含量获得Fe50 Mn30 -Co10 Cr10 ,这是一种具有hcp和fcc相的双相高熵合金.变形初期以fcc→hcp的应力诱导相变为主要变形机制.通过EBSD和APT技术分析,认为所获得的hcp相和fcc相在成分上不存在差异,即固溶强化水平相同,在其三维重构结果中也没有观察到明显的元素偏析现象.然而,Chen等[57 ] 通过原子尺度的能量色散X射线谱证明,五元双相高熵合金Cr20 Mn6 Fe34 -Co34 Ni6 中存在明显的元素分布不均匀性,并且Ni与Mn具有更为显著的不均匀性,而Fe、Co、Cr的成分起伏比较小.值得注意的是,这种双相高熵合金与Cantor合金虽具有相同的组成元素,但由于不同的元素比例和不同的相结构,Cr20 Mn6 Fe34 Co34 Ni6 中元素分布的不均匀性比Cantor合金明显加大,使得材料内部产生更大的持续的滑移阻力,促使位错锁(Lomer-Cottrell locks)结构的形成,进而在变形过程中,受力诱导hcp相变.同样的结果还被发现在相变诱导塑性高熵合金材料中.如图3 d所示,在Cr20 Mn10 Fe30 Co30 Ni10 中也发现了相类似的Lomer-Cottrell locks (如图3 d箭头所示). ...
... [55 ]通过改变非等原子比的Fe80- x x 10 Cr10 中Mn的含量获得Fe50 Mn30 -Co10 Cr10 ,这是一种具有hcp和fcc相的双相高熵合金.变形初期以fcc→hcp的应力诱导相变为主要变形机制.通过EBSD和APT技术分析,认为所获得的hcp相和fcc相在成分上不存在差异,即固溶强化水平相同,在其三维重构结果中也没有观察到明显的元素偏析现象.然而,Chen等[57 ] 通过原子尺度的能量色散X射线谱证明,五元双相高熵合金Cr20 Mn6 Fe34 -Co34 Ni6 中存在明显的元素分布不均匀性,并且Ni与Mn具有更为显著的不均匀性,而Fe、Co、Cr的成分起伏比较小.值得注意的是,这种双相高熵合金与Cantor合金虽具有相同的组成元素,但由于不同的元素比例和不同的相结构,Cr20 Mn6 Fe34 Co34 Ni6 中元素分布的不均匀性比Cantor合金明显加大,使得材料内部产生更大的持续的滑移阻力,促使位错锁(Lomer-Cottrell locks)结构的形成,进而在变形过程中,受力诱导hcp相变.同样的结果还被发现在相变诱导塑性高熵合金材料中.如图3 d所示,在Cr20 Mn10 Fe30 Co30 Ni10 中也发现了相类似的Lomer-Cottrell locks (如图3 d箭头所示). ...
A TRIP-assisted dual-phase high-entropy alloy: Grain size and phase fraction effects on deformation behavior
1
2017
... 在单相高熵合金的研究基础上,为增强高熵合金的力学性能,人们引入了多相强化的机制[55 ,56 ] .然而,由于界面结构的存在以及多相结构本身原子结构的复杂性,认知具有复杂相结构的高熵合金中的元素分布规律更具挑战.Li等[55 ] 通过改变非等原子比的Fe80- x x 10 Cr10 中Mn的含量获得Fe50 Mn30 -Co10 Cr10 ,这是一种具有hcp和fcc相的双相高熵合金.变形初期以fcc→hcp的应力诱导相变为主要变形机制.通过EBSD和APT技术分析,认为所获得的hcp相和fcc相在成分上不存在差异,即固溶强化水平相同,在其三维重构结果中也没有观察到明显的元素偏析现象.然而,Chen等[57 ] 通过原子尺度的能量色散X射线谱证明,五元双相高熵合金Cr20 Mn6 Fe34 -Co34 Ni6 中存在明显的元素分布不均匀性,并且Ni与Mn具有更为显著的不均匀性,而Fe、Co、Cr的成分起伏比较小.值得注意的是,这种双相高熵合金与Cantor合金虽具有相同的组成元素,但由于不同的元素比例和不同的相结构,Cr20 Mn6 Fe34 Co34 Ni6 中元素分布的不均匀性比Cantor合金明显加大,使得材料内部产生更大的持续的滑移阻力,促使位错锁(Lomer-Cottrell locks)结构的形成,进而在变形过程中,受力诱导hcp相变.同样的结果还被发现在相变诱导塑性高熵合金材料中.如图3 d所示,在Cr20 Mn10 Fe30 Co30 Ni10 中也发现了相类似的Lomer-Cottrell locks (如图3 d箭头所示). ...
Real-time observations of TRIP-induced ultrahigh strain hardening in a dual-phase CrMnFeCoNi high-entropy alloy
1
2020
... 在单相高熵合金的研究基础上,为增强高熵合金的力学性能,人们引入了多相强化的机制[55 ,56 ] .然而,由于界面结构的存在以及多相结构本身原子结构的复杂性,认知具有复杂相结构的高熵合金中的元素分布规律更具挑战.Li等[55 ] 通过改变非等原子比的Fe80- x x 10 Cr10 中Mn的含量获得Fe50 Mn30 -Co10 Cr10 ,这是一种具有hcp和fcc相的双相高熵合金.变形初期以fcc→hcp的应力诱导相变为主要变形机制.通过EBSD和APT技术分析,认为所获得的hcp相和fcc相在成分上不存在差异,即固溶强化水平相同,在其三维重构结果中也没有观察到明显的元素偏析现象.然而,Chen等[57 ] 通过原子尺度的能量色散X射线谱证明,五元双相高熵合金Cr20 Mn6 Fe34 -Co34 Ni6 中存在明显的元素分布不均匀性,并且Ni与Mn具有更为显著的不均匀性,而Fe、Co、Cr的成分起伏比较小.值得注意的是,这种双相高熵合金与Cantor合金虽具有相同的组成元素,但由于不同的元素比例和不同的相结构,Cr20 Mn6 Fe34 Co34 Ni6 中元素分布的不均匀性比Cantor合金明显加大,使得材料内部产生更大的持续的滑移阻力,促使位错锁(Lomer-Cottrell locks)结构的形成,进而在变形过程中,受力诱导hcp相变.同样的结果还被发现在相变诱导塑性高熵合金材料中.如图3 d所示,在Cr20 Mn10 Fe30 Co30 Ni10 中也发现了相类似的Lomer-Cottrell locks (如图3 d箭头所示). ...
Multicomponent intermetallic nanoparticles and superb mechanical behaviors of complex alloys
2
2018
... 相变诱导马氏体的引入能够为材料带来更高的强度,这种双相合金通常存在两相在晶体结构上的差异,由于每个相中的元素分布存在不均匀性而两相元素分布比例相一致,所获得的强度提升仍然有限.而共格纳米析出相似乎可以为高熵合金带来更显著的强化.析出相与基体通常存在组成元素成分比例的不同,通过改变特定元素的含量以及制备方式可以细致调控析出相的结构、大小、分布以及析出相与基体之间的界面性质,进而影响材料的变形机制.最近,Yang等[58 ] 通过在fcc结构的FeCoNi基合金体系中引入高密度的共格纳米析出相,获得了具有高屈服强度(1.0 GPa)同时兼顾良好塑性(约50%)的(FeCoNi)86 -Al7 Ti7 合金.该合金具有fcc+L 12 双相结构,通过APT表征发现,该共格纳米析出相是一种具有元素组成为(Ni43.3 Co23.7 Fe8 )3 (Ti14.4 Al8.6 Fe2 )的L 12 化学有序相.其中,Ni占据A 3 B 中的A 位点,Ti、Al占据B 位点,Fe、Co可占据A 、B 位点.根据整体价电子浓度(OVEC)原理[58 ] ,添加Al元素能够降低材料的有序能量且提高材料的固有塑性,Ti元素的添加有利于降低由Al元素所造成的环境脆化.通过调控纳米析出相中的元素比例,使析出相与基体具有合适的低的晶格错配度,以保证析出相保持纳米尺度且均匀分布在基体中.这使得材料在变形过程中不会出现局部的应力集中,抑制了微裂纹的形成.同时,在均匀变形过程中所获得的(FeCoNi)86 -Al7 Ti7 合金具有多阶段的加工硬化.具体来说,变形初期(变形量< ~10%)材料的主要变形机制以位错的平面滑移为主.当变形量达到22%时,材料中出现细小的位错结构(HDDWs),激发位错交滑移.当变形量继续增加时,产生变形微带并继续发生均匀变形,进一步提供更大的应变强化.而所制备的(FeCoNi)86 -Al7 Ti7 合金虽具有相似的析出相结构,但在变形过程中并没有相似的变形微带结构和多阶段的加工硬化.也就是说,对于这类纳米析出相的系统调控,在某些情况下,甚至可以在不牺牲强度的条件下提高强度.然而精确调控析出物的组成及结构非常困难,例如同样添加Ti、Al在FeCoNiCr高熵合金中,就具有不同大小的析出相区域,使得材料的变形机制以及强化效果有所区别[59 ] . ...
... [58 ],添加Al元素能够降低材料的有序能量且提高材料的固有塑性,Ti元素的添加有利于降低由Al元素所造成的环境脆化.通过调控纳米析出相中的元素比例,使析出相与基体具有合适的低的晶格错配度,以保证析出相保持纳米尺度且均匀分布在基体中.这使得材料在变形过程中不会出现局部的应力集中,抑制了微裂纹的形成.同时,在均匀变形过程中所获得的(FeCoNi)86 -Al7 Ti7 合金具有多阶段的加工硬化.具体来说,变形初期(变形量< ~10%)材料的主要变形机制以位错的平面滑移为主.当变形量达到22%时,材料中出现细小的位错结构(HDDWs),激发位错交滑移.当变形量继续增加时,产生变形微带并继续发生均匀变形,进一步提供更大的应变强化.而所制备的(FeCoNi)86 -Al7 Ti7 合金虽具有相似的析出相结构,但在变形过程中并没有相似的变形微带结构和多阶段的加工硬化.也就是说,对于这类纳米析出相的系统调控,在某些情况下,甚至可以在不牺牲强度的条件下提高强度.然而精确调控析出物的组成及结构非常困难,例如同样添加Ti、Al在FeCoNiCr高熵合金中,就具有不同大小的析出相区域,使得材料的变形机制以及强化效果有所区别[59 ] . ...
A precipitation-hardened high-entropy alloy with outstanding tensile properties
1
2016
... 相变诱导马氏体的引入能够为材料带来更高的强度,这种双相合金通常存在两相在晶体结构上的差异,由于每个相中的元素分布存在不均匀性而两相元素分布比例相一致,所获得的强度提升仍然有限.而共格纳米析出相似乎可以为高熵合金带来更显著的强化.析出相与基体通常存在组成元素成分比例的不同,通过改变特定元素的含量以及制备方式可以细致调控析出相的结构、大小、分布以及析出相与基体之间的界面性质,进而影响材料的变形机制.最近,Yang等[58 ] 通过在fcc结构的FeCoNi基合金体系中引入高密度的共格纳米析出相,获得了具有高屈服强度(1.0 GPa)同时兼顾良好塑性(约50%)的(FeCoNi)86 -Al7 Ti7 合金.该合金具有fcc+L 12 双相结构,通过APT表征发现,该共格纳米析出相是一种具有元素组成为(Ni43.3 Co23.7 Fe8 )3 (Ti14.4 Al8.6 Fe2 )的L 12 化学有序相.其中,Ni占据A 3 B 中的A 位点,Ti、Al占据B 位点,Fe、Co可占据A 、B 位点.根据整体价电子浓度(OVEC)原理[58 ] ,添加Al元素能够降低材料的有序能量且提高材料的固有塑性,Ti元素的添加有利于降低由Al元素所造成的环境脆化.通过调控纳米析出相中的元素比例,使析出相与基体具有合适的低的晶格错配度,以保证析出相保持纳米尺度且均匀分布在基体中.这使得材料在变形过程中不会出现局部的应力集中,抑制了微裂纹的形成.同时,在均匀变形过程中所获得的(FeCoNi)86 -Al7 Ti7 合金具有多阶段的加工硬化.具体来说,变形初期(变形量< ~10%)材料的主要变形机制以位错的平面滑移为主.当变形量达到22%时,材料中出现细小的位错结构(HDDWs),激发位错交滑移.当变形量继续增加时,产生变形微带并继续发生均匀变形,进一步提供更大的应变强化.而所制备的(FeCoNi)86 -Al7 Ti7 合金虽具有相似的析出相结构,但在变形过程中并没有相似的变形微带结构和多阶段的加工硬化.也就是说,对于这类纳米析出相的系统调控,在某些情况下,甚至可以在不牺牲强度的条件下提高强度.然而精确调控析出物的组成及结构非常困难,例如同样添加Ti、Al在FeCoNiCr高熵合金中,就具有不同大小的析出相区域,使得材料的变形机制以及强化效果有所区别[59 ] . ...
Design of D 022 superlattice with superior strengthening effect in high entropy alloys
1
2019
... He等[60 ] 基于OVEC设计方法,开发出一种具有D 022 超晶格结构的共格析出相(称为γ'' 相)的Ni2 CoCrFeNb0.15 高熵合金.通过原子探针层析成像技术表征发现,γ'' 为富Nb、Ni、Co相,其具有高的反相边界能和高的晶格错配,从而能为材料提供有序相强化和共格强化.其他相关研究也证明了在高熵合金中引入不同元素,能形成复杂的化学有序相结构从而提高材料的力学性能.例如CoCrFeNiMox [61 ] 或在合金中形成碳化物相(如TiC、NbC、VC)等[62 ~65 ] .除了高熵合金中的纳米析出物以外,在高猛钢以及高铬钢中也通过引入这类纳米级析出相(如M 7 C3 、M 23 C6 ,其中M 表示可以形成碳化物的金属元素,包括但不限于Fe、Cr、Mo、V),显著增加强度. ...
Ductile CoCrFeNiMox
1
2016
... He等[60 ] 基于OVEC设计方法,开发出一种具有D 022 超晶格结构的共格析出相(称为γ'' 相)的Ni2 CoCrFeNb0.15 高熵合金.通过原子探针层析成像技术表征发现,γ'' 为富Nb、Ni、Co相,其具有高的反相边界能和高的晶格错配,从而能为材料提供有序相强化和共格强化.其他相关研究也证明了在高熵合金中引入不同元素,能形成复杂的化学有序相结构从而提高材料的力学性能.例如CoCrFeNiMox [61 ] 或在合金中形成碳化物相(如TiC、NbC、VC)等[62 ~65 ] .除了高熵合金中的纳米析出物以外,在高猛钢以及高铬钢中也通过引入这类纳米级析出相(如M 7 C3 、M 23 C6 ,其中M 表示可以形成碳化物的金属元素,包括但不限于Fe、Cr、Mo、V),显著增加强度. ...
Strengthening of a CrMnFeCoNi high-entropy alloy by carbide precipitation
1
2019
... He等[60 ] 基于OVEC设计方法,开发出一种具有D 022 超晶格结构的共格析出相(称为γ'' 相)的Ni2 CoCrFeNb0.15 高熵合金.通过原子探针层析成像技术表征发现,γ'' 为富Nb、Ni、Co相,其具有高的反相边界能和高的晶格错配,从而能为材料提供有序相强化和共格强化.其他相关研究也证明了在高熵合金中引入不同元素,能形成复杂的化学有序相结构从而提高材料的力学性能.例如CoCrFeNiMox [61 ] 或在合金中形成碳化物相(如TiC、NbC、VC)等[62 ~65 ] .除了高熵合金中的纳米析出物以外,在高猛钢以及高铬钢中也通过引入这类纳米级析出相(如M 7 C3 、M 23 C6 ,其中M 表示可以形成碳化物的金属元素,包括但不限于Fe、Cr、Mo、V),显著增加强度. ...
Controllable fabrication of a carbide-containing FeCoCrNiMn high-entropy alloy: Microstructure and mechanical properties
0
2017
Effect of carbon content and annealing on structure and hardness of the CoCrFeNiMn-based high entropy alloys
0
2016
The effect of interstitial carbon on the mechanical properties and dislocation substructure evolution in Fe40.4 Ni11.3 Mn34.8 Al7.5 Cr6 high entropy alloys
1
2016
... He等[60 ] 基于OVEC设计方法,开发出一种具有D 022 超晶格结构的共格析出相(称为γ'' 相)的Ni2 CoCrFeNb0.15 高熵合金.通过原子探针层析成像技术表征发现,γ'' 为富Nb、Ni、Co相,其具有高的反相边界能和高的晶格错配,从而能为材料提供有序相强化和共格强化.其他相关研究也证明了在高熵合金中引入不同元素,能形成复杂的化学有序相结构从而提高材料的力学性能.例如CoCrFeNiMox [61 ] 或在合金中形成碳化物相(如TiC、NbC、VC)等[62 ~65 ] .除了高熵合金中的纳米析出物以外,在高猛钢以及高铬钢中也通过引入这类纳米级析出相(如M 7 C3 、M 23 C6 ,其中M 表示可以形成碳化物的金属元素,包括但不限于Fe、Cr、Mo、V),显著增加强度. ...