应力和应变是研究物理、工程等科学问题的2个重要物理量,在连续介质尺度下的定义已经非常成熟。但在原子尺度下,应力和应变的定义至今尚无统一定论,这使得分子动力学的发展受到一定的限制。不少学者在原子尺度下的应力、应变定义与计算方面作了深入研究,并展开了激烈讨论。
柯西(Cauchy)应力是连续介质理论框架中的重要物理量,不少学者[1 ,2 ,3 ] 认为,在离散原子系统的virial应力等同于连续介质中的Cauchy应力,甚至不少分子动力学软件也输出virial应力作为原子尺度的应力计算结果。但是Zhou[4 ] 首次对此提出质疑,认为在原子尺度下,原子间内力的平均值才是应力,因此原子尺度的应力应当与原子速度无关,原子尺度的应力不等同于Cauchy应力。Zhou[4 ] 的观点引起了全球学者的大讨论。Liu等[5 ] 和Xu等[6 ] 支持Zhou[4 ] 提出的“原子尺度的应力应当与原子速度无关”这一结论,因为原子速度不是一个客观量,它会依赖观察者的人为选择,同时,进一步研究发现virial应力的势能部分也不完全等同于Cauchy应力,并举出多个反例证明了virial应力在某些情况下即使去掉包含速度的项后也不能正确预测Cauchy应力,提出了一个不包含原子速度项的Lagrange virial应力公式,如式(1)所示,并认为通过该式能得到正确的Cauchy应力:
式中,σ V 为计算体系的总体积,<r ij i 到原子j 的平均相对位置矢量,<f ij j 作用于原子i 上的平均力,⊗表示2个矢量的并矢运算。
Liu等[5 ] 和Xu等[6 ] 的研究是目前对原子应力研究的最新成果,虽有理有据,但仍未得到公认,也未被分子动力学软件(如Lammps、Material Studio等)采用。而对原子尺度应变的共识就更少了,至今尚没有一个分子动力学软件能输出原子尺度应变的计算结果。
研究原子尺度的应变对研究物理科学问题具有重要意义。Wang等[7 ] 认为,分析原子级应变分布和原子应力-应变曲线对研究锆基金属玻璃压痕的力学行为具有重要价值。Hirth等[8 ] 也提出,实现微观尺度下变形梯度张量和应变张量的计算将有利于识别和分析位错、晶界、复合微裂纹等微观缺陷的演化。Seol等[9 ] 研究发现,工程金属合金的动态应变时效(DSA)会引起材料相关性能的退化,因此有必要开展关于原子尺度应变的研究。
然而,一个困难的问题是,应变张量主要是通过连续体的局部变形定义的。应变并不是一个可直接测量的物理量,它是根据连续位移场的梯度计算的。而在微观尺度,很难用相邻离散时间间隔得到的各原子位置来定义局部变形,因此很难定义原子尺度的应变。近年来,不少学者开展了定义原子尺度应变的研究,并希望建立与连续介质尺度应变定义相统一的框架。
考虑到应变是一个连续量,学者们从连续位移场插值和梯度算子离散化2个角度提出了原子尺度应变的新定义和计算方法。Zimmerman等[10 ] 根据原子在不同时刻的位置关系定义了滑移矢量,成功地识别了晶格畸变和位错的形成,但是该方法不能在连续体框架中使用。Mott等[11 ] 提出了一种三维无序系统下局部原子尺度应变的计算方法,即首先运用Delaunay三角剖分方法,将所有原子视为节点,建立唯一的四面体单元网格,计算出相邻两原子的位移向量,然后定义局部原子变形梯度为相邻四面体的变形梯度的加权平均值,进而运用各原子的变形梯度计算原子尺度应变。Falk[12 ] 运用小应变定义得到了局部原子尺度应变张量,但这种定义方法不能反映刚体旋转时的虚拟剪切应变和有限应变。Kim等[13 ] 用原子分辨成像和先进的图像处理技术直接测量了InAs/GaSb II型应变层超晶格中的阴阳亚晶格应变,提出了一种原子尺度应变的测量方法。
Gullett等[14 ] 提出了通过离散变形梯度的定义求原子尺度应变的方法。与前面的方法相比,该方法具有如下优点:计算各原子变形梯度时无需先作几何分解;可直接根据变形梯度计算应变张量;对有限、多轴变形问题均适用。Gullett等[14 ] 指出,任一原子的变形梯度与其邻域原子均相关,而邻域各原子相对于原子的变形梯度均不同,故需计算每个原子周围所有领域原子对其共同作用的综合局部变形梯度。因此,Gullett等[14 ] 引入了一个系数固定的分段多项式递减权函数来反映邻域各原子对某原子的变形梯度的贡献度。该方法实现了原子尺度应变计算的重大突破。
本工作对Gullett等[14 ] 的方法作了进一步发展。研究表明,权函数的形式和系数对计算原子尺度应变具有重要影响,因此,针对不同的材料,计算其原子尺度应变时宜采用不同的优化权函数。基于此,本工作提出了基于离散变形梯度、邻域原子影响权函数的原子尺度应变定义方法,构造了计算原子综合局部变形梯度和应变张量的加权最小二乘法目标函数,建立了计算原子尺度应变张量的优化数学模型。
但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] 。因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] 。比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等。
本工作提出的优化算法综合了遗传算法与复形法的优点,改善了其缺点。遗传算法是一种智能化自适应优化算法,它遵循生物进化和遗传的基本规律与步骤,即通过繁殖、遗传、变异、竞争,实现优胜劣汰,进而一步一步地逼近问题的最优解。它在解决单峰值优化问题中具有全局搜索能力强、收敛性好、计算时间少、鲁棒性高等优点;但其缺点在于:优化前需要预先估计各参数的包含最优解的大致取值范围,且在解决多峰值优化问题时容易产生早熟现象,局部寻优能力较差。复形法是一种直接搜索法,其原理是构成一个包含若干顶点的复合形,通过比较各顶点的目标函数值,丢掉最坏点,寻求改进点,构成新的复合形,最终搜索到最优点。与遗传算法相比,该方法的优点在于:无需预先估计各参数包含最优解的大致取值范围;但该方法仍具有遗传算法的其它缺点。
本工作在遗传算法和复形法的基础上,提出了一种改进的自适应多层复形遗传算法,能显著提高参数识别的效率和精度[22 ] 。并以NiTi合金为研究对象,建立了NiTi合金变形与破坏的分子动力学演化模型并计算了各时刻的原子尺度应变云图,通过应变云图观察到了孪晶。经与NiTi合金三点弯曲冲击断裂试件裂纹尖端的微观观察实验作对照,验证了本工作建立的原子尺度应变定义方法的合理性及其在识别微观缺陷演化中的应用意义。
1 原子变形梯度与应变张量
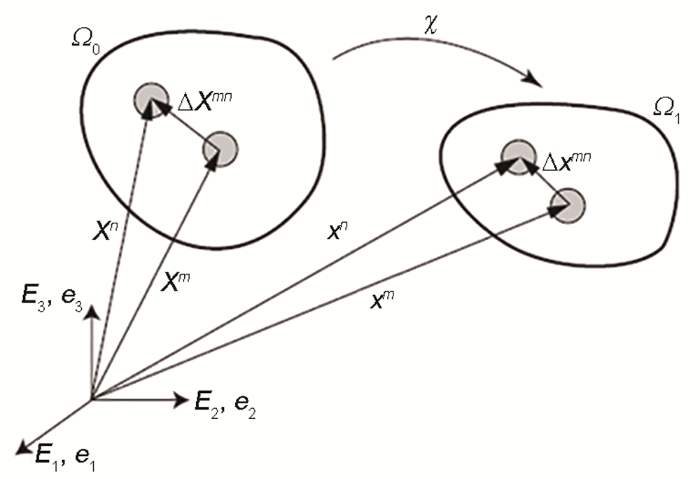
为描述在初始时刻t 0 和当前时刻t 1 时原子的位置,首先建立如图1 所示的直角坐标系。在图1 中,分别用X x Ω 0 (对应初始时刻t 0 )和即时构形Ω 1 (对应当前时刻t 1 )的坐标向量。
图1
图1
邻域内离散原子的运动示意图
Fig.1
General motion in the neighborhood of a discrete atomic particle (Ω 0 —reference configuration; Ω 1 —current configuration; E 1 , E 2 , E 3 —x , y , z coordinate vectors in Ω 0 , respectively; e 1 , e 2 , e 3 —x , y , z coordinate vectors in Ω 1 , respectively; X m X n m and atom n in Ω 0 at the initial time t 0 , respectively; x m x n m and atom n in Ω 1 at the current time t 1 , respectively; ΔX mn n relative to atom m in Ω 0 ; Δx mn n relative to atom m in Ω 1 ; χ —mapping from X x
设从X x χ ,χ 反映了原子在空间Ω 1 中坐标向量相对于其在空间Ω 0 中坐标向量的对应关系,它是关于位置与时间的函数,一般是非线性映射关系。则原子坐标向量的关系可表示为:
X = X i E i x = x i e i x = χ ( X ) (2)
式中,Xi 为第i 个原子在参考构形Ω 0 中的坐标,E i xi 为第i 个原子在即时构形Ω 1 中的坐标,e i
在连续尺度下,结构形变由原子团簇的位移场及其导数表示;而在微纳米尺度下,系统的状态仅由粒子的瞬时位置及其导数表示。因此,任一原子在参考构形X F
F ≡ ∂ x ∂ X (3)
在参考坐标系下将任一点处的微分dx
d x = χ ( X + d X ) - χ ( X ) = χ ( X ) + ∇ χ ( X ) ⋅ d X + ο ( d X ) - χ ( X ) ≈ ∇ χ ( X ) ⋅ d X ≈ F ⋅ d X (4)
式中,ο (dX X
根据式(4)计算得到的F 图1 中,任一原子m 的变形与其邻域原子的相对位置有关。设原子m 在空间Ω 0 、Ω 1 中的位置分别为X m x m n 的相对位置向量为:
Δ X m n = X n - X m Δ x m n = x n - x m Δ x m n = F m ⋅ Δ X m n (5)
式中,X n x n n 在空间Ω 0 、Ω 1 中的位置;ΔX mn x mn n 在空间Ω 0 、Ω 1 中相对于原子m 的位置;F m n 相对于原子m 的变形梯度。
根据式(5)可计算出F m m 的变形梯度与其邻域所有原子均相关,而邻域各原子相对于原子m 的变形梯度均不同,故不能仅用一个邻域原子n 来确定原子m 的变形梯度。因此,为确定原子m 的变形梯度,应考虑该原子邻域内所有原子的共同影响,求出原子m 综合局部变形梯度F ̂ m R cut ,仅统计以该原子为中心、以R cut 为半径的球内所有原子与它的相互作用。设原子m 周围的邻域原子数目为N ,则F ̂ m 式(6)所示的目标函数Wm 最小:
W m = ∑ n = 1 N ( Δ x m n - F ̂ m Δ X m n ) T ( Δ x m n - F ̂ m Δ X m n ) ω n (6)
式中,ωn 为权系数,它反映了邻域原子n 对F ̂ m
通过式(6)计算出F ̂ m m 的Lagrange应变张量E m
E m = 1 2 [ ( F ̂ m ) T F ̂ m - I ] (7)
E m E m J 2 定义原子m 的等效应变ε e f f m
ε e f f m = 3 J 2 = 3 ( E 11 E 12 E 21 E 22 + E 22 E 23 E 32 E 33 + E 11 E 13 E 31 E 33 ) (8)
式中,Eij (i , j =1, 2, 3)分别表示E m i 行第j 列的元素。
由式(6)可知,ωn 对F ̂ m ωn 的物理意义、表达形式进行分析。
1.1 权系数ωn
由于邻域各原子相对于原子m 的变形梯度共同决定了原子m 的变形梯度,但它们对原子m 变形梯度的贡献程度不同,因此权系数ωn 不应为一个常系数,而应为同时与原子间距Rmn 和R cut 有关的函数。为方便计算和讨论,定义无量纲量r 为:
r = R m n - R m i n R c u t (9)
式中,R min 表示原子m 的所有邻域原子中,距中心原子m 最近的原子间距。
则权系数ωn 可简化为关于r 的函数,以下改称为权函数。从权函数ωn 的物理意义可知,权函数ωn 应满足如下3个条件:(1) 距中心原子m 最近的原子对原子m 变形梯度的贡献度最大,即当r =0时,ωn =1;(2) 邻域原子距中心原子m 越远,对原子m 变形梯度的贡献度就越小,即ωn 随r 的增大而减小;(3) 当邻域原子距中心原子m 的距离超过R cut 时,它对原子m 变形梯度的贡献度就可忽略,即r ≥1时,ωn ≈0。
满足上述条件的权函数ωn 的形式很多,但不同的权函数形式和系数对计算原子变形梯度和应变的影响很大。为提高权函数拟合精度,将权函数离散为10条折线段,定义折线段的转折点为:
ω ( r = i 10 ) = 1 ( i = 0 ) ω i ( i = 1 , 2 , ⋯ , 9 ) 0 ( i = 10 ) (10)
由式(10)可知,权函数中包含ωi (i =1, 2, ⋯
ω n ( r ) = 1 ( r = 0 ) ω i + ( ω i + 1 - ω i ) ( 10 r - i ) ( i < 10 r < i + 1 , i = 1 , 2 , ⋯ , 9 ) 0 ( r ≥ 1.0 ) (11)
1.2 计算原子尺度应变张量的优化模型
将式(11)代入式(6)中可知,计算F ̂ m ωi (i =1, 2, ⋯ Wm (X
o b j : m i n W m ( X ) = ∑ n = 1 N ( Δ x m n - F ̂ m Δ X m n ) T ⋅ ( Δ x m n - F ̂ m Δ X m n ) ω n X = [ F ̂ 11 m , F ̂ 12 m , F ̂ 13 m , F ̂ 21 m , F ̂ 22 m , F ̂ 23 m , F ̂ 31 m , F ̂ 32 m , F ̂ 33 m , ω 1 , ω 2 , ω 3 , ω 4 , ω 5 , ω 6 , ω 7 , ω 8 , ω 9 ] T s . t . : X ˜ i m i n ≤ X i ≤ X ˜ i m a x (12)
式中,F ̂ i j m i , j =1, 2, 3)表示F ̂ m i 行第j 列的元素;X ˜ i m i n X ˜ i m a x i 个变量Xi 取值范围的上限和下限。
当Wm (X F ̂ i j m i , j =1, 2, 3)正好就是F ̂ m Wm (X F ̂ m ωi (i =1, 2, ⋯
需要说明的是,由于在不同时刻,各原子的坐标是不同的,其周围邻域原子的位置也是不同的,故式(12)的18个待定参数会随时刻的变化而变化。因此,为计算各原子在不同时刻的原子尺度应变,需要不断地对式(12)的18个待定参数进行优化识别。
为降低这18个参数的识别计算量,提高参数识别的效率和精度,本工作提出了一种将复形法与遗传算法相融合的改进遗传算法,该方法无需预设各参数包含最优解的取值范围,它能通过自适应调整和搜索,快速获得使Wm (X
1.3 改进的自适应多层复形遗传算法
改进的自适应多层复形遗传算法的基本步骤包括:形成初始复形、检验收敛条件、找到“最坏点” (使Wm (X X
首先对各变量x ¯ x ¯ ζ ¯ k x ¯ k
x ¯ k = a ¯ + ζ ¯ k ( b ¯ - a ¯ ) ( k = 1 , 2 , ⋯ , P ) (13)
式中,P 为各复形中顶点的个数,a ¯ b ¯
(2) 对复形各顶点的目标函数值进行排序,检验收敛条件。
采用冒泡法将各点的目标函数按从小到大的顺序排列。在构成当前复形的各顶点中,使Wm (X X x ¯ l Wm (X X x ¯ h x ¯ s h
设置迭代终止条件:第一层复形均以迭代次数作为停机准则,各个复形分别迭代5到10次则停止;第二层复形以式(14)作为终止迭代依据。若成立则终止迭代,反之进入“调优搜索”步进行再次迭代。
1 P ∑ k = 1 P ( W ( x ¯ k ) - W ( x ¯ o ) ) 2 < ε (14)
式中,ε 为预先设置的收敛精度,x ¯ o
x ¯ o = 1 P ∑ k = 1 P x ¯ k (15)
当第一层复形迭代完成后,则初始化第二层复形。这里有一个改进技巧:传统的多层复形法仅从各复形中取出最好与次好点组成第二层复形,但如果各复形顶点较多,则选点个数不仅仅局限于最好与次好点。适当增加选点个数可有效减少优化分析次数,而不会对精度造成影响。
记去掉最坏点x ¯ h x ¯ c x ¯ h x ¯ c
若x ¯ c x ¯ l x ¯ c x ¯ c
x ¯ α = x ¯ c + α ( x ¯ c - x ¯ h ) (16)
式中,x ¯ α α 为反射系数,一般取α ≥1。
检查x ¯ α α 减半,直到x ¯ α x ¯ α W ( x ¯ α )
① 若W ( x ¯ α ) W ( x ¯ l )
x ¯ β = x ¯ c + β ( x ¯ α - x ¯ c ) (17)
式中,x ¯ β β 为延伸系数,一般取β ≥1。
若x ¯ β W ( x ¯ β ) W ( x ¯ α ) x ¯ h x ¯ β x ¯ α
② 若W ( x ¯ α ) W ( x ¯ s h ) 式(16)的基础上继续将α 减半,不断求出并判断新的反射点是否有所改善,直至α 小于规定的数为止。若一直未能改善,则执行收缩操作:
x ¯ γ = x ¯ c + γ ( x ¯ h - x ¯ c ) (18)
式中,x ¯ γ γ 为收缩系数,一般取0<γ <1。
若W ( x ¯ β ) W ( x ¯ s h ) γ 减半后继续判断,直至γ 小于规定的数为止。若仍无改善,则以x ¯ l x ¯ l
③ 若W ( x ¯ α ) W ( x ¯ s h ) x ¯ α x ¯ h
完成调优搜索过程后,则返回第(3)步再次对新复形各顶点对应的目标函数排序和检验收敛条件。直到满足收敛条件式(14)时,复形迭代终止。
第(3)步完成后,设迭代获得的最优点对应的变量集为{X 1 * , X 2 * , ⋯ XN * },则设置各个变量的上下限边界条件为:
X i ∈ [ X i * - γ i , X i * + γ i ] ( i = 1 , 2 , … , N ) (19)
式中,N 为变量个数,γi 为变量Xi 附近的搜索邻域。
然后在调整后的范围内,对各变量运用遗传算法进行更精密的智能进化搜索,通过选择、交叉和变异运算,可获得精度更高的最优解。
2 实验结果
以NiTi合金为研究对象,对三点弯曲冲击断裂试件的裂纹尖端作微观观察实验,以证实NiTi合金变形与破坏的微观机理(如相变、孪晶、层错、位错等),为验证微观尺度的分子动力学模拟结果提供依据。而原子尺度应变的计算是基于分子动力学模拟获得的各时刻原子坐标进行的,因此,微观观察实验结果也能有效验证本工作建立的原子尺度应变定义方法的合理性及其在识别微观缺陷演化中的应用意义。
采用JSM-7500F/X-MAX50扫描电镜(SEM)观察NiTi合金三点弯曲冲击断裂试件的断口表面形貌,如图2 所示。由图2 可知,虽然该NiTi合金试样的断口有大量解理纹,但少数部位仍存在韧窝,因此可认为该NiTi合金试样主要为脆性断裂,局部有塑性变形特征。从NiTi合金的微观机理对宏观本构关系的影响理论[23 ,24 ,25 ] 可知,在室温条件下,应力诱发的马氏体相变一方面会使NiTi合金产生解理断裂,另一方面又会在裂纹面扩展的主方向上起到一定的韧化作用。
图2
图2
NiTi合金三点弯曲试样断口形貌的SEM像
Fig.2
Low (a) and high (b) magnified fracture surface SEM images of three point bending NiTi alloy specimens
为研究NiTi合金三点弯曲冲击断裂试件受动态冲击后裂纹扩展的微观变化机理,采用JEM-2100F透射电镜(TEM)观察NiTi合金裂纹尖端微观形貌,如图3 所示。图3 a中可见有明显的扭曲位错塞积,位错塞积的形成原因是在切应力作用下,由位错源产生的位错沿滑移面运动,因遇到障碍物被阻止前进,这些位错塞积之处将逐渐形成晶界、亚晶界等,并成为马氏体的优先形核部位。图3 b为NiTi合金裂纹表面的平行、弯曲位错。位错的形成能使马氏体更加稳定,这会使得NiTi形状记忆合金的记忆效应更为突出。但大量的位错塞积仍将成为NiTi合金材料宏观断裂失效的隐患。随着塞积的位错数目增多,位错对晶界、亚晶界的作用力也会增大,当这种作用力增大到一定程度时,就会在晶界间产生很大的应力集中,从而引发沿晶断裂,即造成材料的宏观破坏。这种因位错塞积而诱发的材料宏观破坏的原理与α -Ti钛合金是相似的。图3 c为两相区,中间有马氏体片条,马氏体内部有平行位错并交织成锁结构。NiTi合金在常温下为奥氏体相,马氏体片条的出现说明NiTi合金在冲击断裂的过程中发生了相变,即由奥氏体相变成了马氏体相。应力卸载后,马氏体会发生逆相变,转变为奥氏体相,但由于位错及残余应力的存在,部分马氏体会与奥氏体共存。这一现象与NiTi合金的理论分析结果吻合。图3 d显示层错带形貌。层错是一种晶格缺陷,它破坏了晶体的周期完整性并引起晶体内能升高。层错带的出现表明NiTi合金在冲击载荷的切应力作用下,晶面出现滑移,导致晶格畸变。图3 e显示了晶内的剪切变形,也进一步证明了在冲击载荷作用下NiTi合金三点弯曲试件裂尖附近存在切应力。图3 f所示为孪晶。孪晶的形成与层错密切相关,孪晶形成后会降低位错的平均自由程,起到硬化作用,降低材料的塑性,因此,孪晶的形成也是NiTi合金脆性断裂的原因之一。
图3
图3
NiTi合金裂纹表面的TEM像
Fig.3
TEM images of crack surface of NiTi alloy
(a) dislocation pile-up (b) parallel and bended dislocations (c) austenite-martensite phase region
(d) stacking fault bands (e) shear deformation in grains (f) twins
通过对NiTi合金的TEM观察,证实了在冲击断裂过程中,NiTi合金存在马氏体相变、位错、层错、孪晶等微观机理。
3 分析讨论
3.1 分子动力学模拟结果
采用LAMMPS软件建立带微观裂纹缺陷的NiTi合金分子动力学模型,模拟其在应力诱导下的相变过程。在等温等压(NPT)系综下,建立晶向为x -[1 1 ¯ 0 y -[110]、z -[001]的模型,系统温度保持450 K不变。对模型z 方向以3.5×1012 MPa/s的恒定加载速率施加压缩载荷,压缩应力从0增加到2.1 GPa,再卸载。对模型的3个方向施加周期性边界条件。
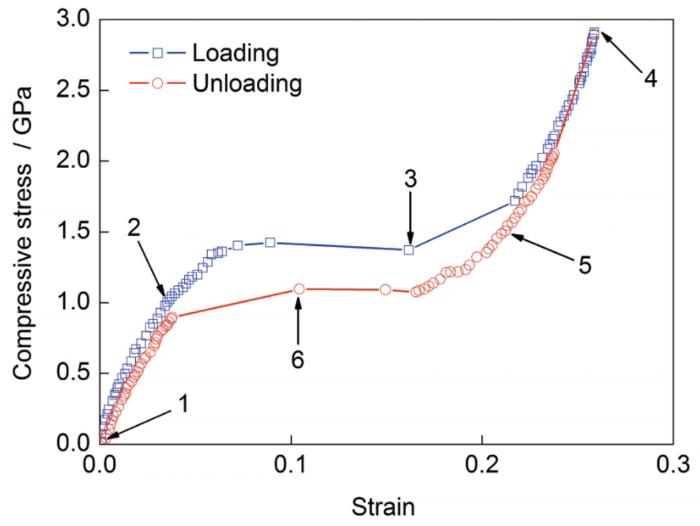
图4 给出了用分子动力学方法计算得到的450 K时NiTi合金的应力-应变曲线,图5 为曲线上关键转折点处所对应的原子构型图。由图4 可知,在加载初期,应力随应变的增大而增大,该阶段为马氏体相的弹性阶段。随后,由于发生从B2奥氏体相到B19'马氏体相的相变,应力-应变曲线中出现了一个平台。随着压缩载荷继续增加,马氏体相变结束,同时伴随出现另一个弹性阶段。在卸载过程中,B19'马氏体相会直接转变为B2奥氏体相。由图4 可见,经过一个完整的加载周期后,又会出现初始的B2奥氏体相,这表现了NiTi合金的超弹性行为,即NiTi合金可以产生很大的弹性应变。
图4
图4
NiTi合金应力-应变计算曲线
Fig.4
Calculated stress-strain curves of NiTi alloy
图5
图5
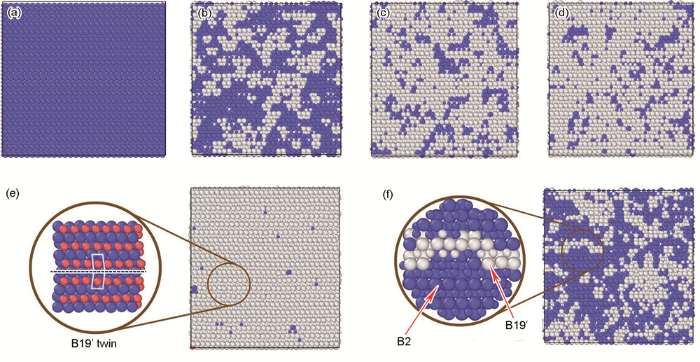
对应图4中关键点1~6的原子构型图
Fig.5
Atomic configurations of key points 1~6 in Fig.4, respectively
(a) initial state (b) loading process (c) stress flat during the loading process
(d) loading peak (e) unloading process (f) stress flat during the unloading process
根据图5 中的原子构型图并结合理论分析可知,在加载初期只有弹性压缩变形产生的弹性应变(约在0~5%的范围内),而没有马氏体相的变化,因此,此时的晶体结构与初始的B2奥氏体结构基本保持一致。但是,当应力水平达到1339 MPa时,原子发生了明显的重新排列,一些B2奥氏体晶格逐渐转变为B19'马氏体晶格。继续压缩加载,B19'马氏体结构的体积分数不断增加。由图5 e的放大图可知,在相变区域,单斜晶系的倾角约为97°,这与B2奥氏体的结构截然不同。此外,沿不同方向因相变新生成的B19'马氏体会形成多条镜像带(如图5 e放大图的水平虚线所示),即孪晶。该现象已从图3 所示的TEM像中得到了验证。
由图5 还可发现,NiTi合金在加载过程中的孪晶会一直持续到晶体完全转变为B19'马氏体相,此时应变约20%。随着加载继续进行,会导致孪晶马氏体出现弹性应变(约20%~26%)。当应变达到约26%时卸载,此时会同时经历弹性松弛和逆相转变(从B19'马氏体相转变为B2奥氏体相) 2个过程。由图5 e和f均可发现,B19'马氏体结构的体积分数在逐渐减少,接着会出现一个较低的应力平台,此时,含内部孪晶的B19'马氏体结构相对稳定。最终,当应力完全消除时,NiTi合金又会重新回到图4 中图5 a的状态,所有B19'马氏体相完全转变为B2奥氏体相。
3.2 原子尺度应变计算结果
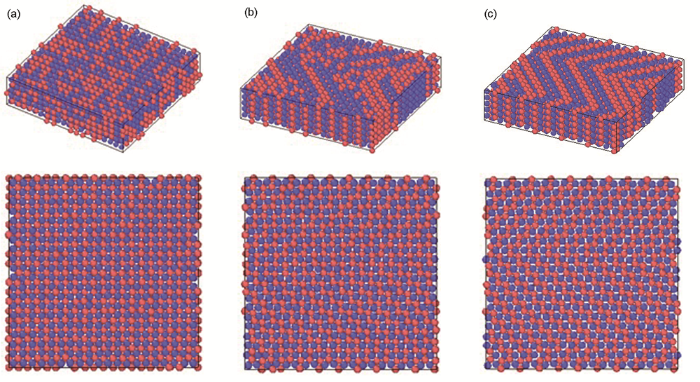
由图3 可知,相变和孪晶是NiTi合金在z 向压缩应力诱导下产生的重要微观特征。根据分子动力学方法模拟NiTi合金的计算结果,分别选取孪晶形成前(图6 a)、孪晶刚形成(图6 b)、孪晶完全形成(图6 c) 3个时刻的原子构型进行对比。
图6
图6
NiTi合金裂尖附近的分子动力学模拟结果
Fig.6
Molecular dynamics simulation results near crack tip of NiTi alloy (The top half is a three-dimensional view, and the bottom half is a top view)
(a) before twins formation (b) twins just formed (c) twins are fully formed
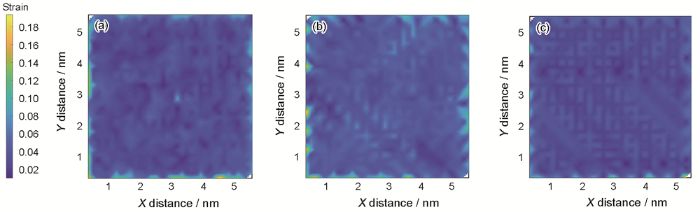
取t =0作为参考构形,选取图6 所示的孪晶形成前、孪晶刚形成、孪晶完全形成3个时刻的原子构型为即时构形。设置截断半径为1 nm,得到对应这3个时刻的原子尺度应变云图,如图7 所示。图7 a为孪晶形成前的原子尺度应变云图,原子尺度应变较小(最大应变为0.06),且各部分的原子尺度应变分布较均匀;图7 b为孪晶刚形成的原子尺度应变云图,原子尺度应变略有增大(最大应变为0.08),可看到孪晶形成的雏形;图7 c为孪晶完全形成的原子尺度应变云图,其平均原子尺度应变略有下降,且可看到规则分布的孪晶形态。这表明通过原子尺度应变图可观察到孪晶,这与分子动力学模拟结果(图4 )和TEM观察(图3 )吻合。由图7 c可以看到,当孪晶形成时,其原子尺度应变云图呈现出多条明显的“<”形折线,且各条折线相互平行,间距相差不大。因此,可初步推断,根据原子尺度应变云图局部呈现的某种具有显著代表特征的图形,有望用于快速识别材料变形过程中在微观尺度出现的孪晶、位错、层错等晶体缺陷。因此,本工作提出的原子尺度应变张量的定义和优化方法有望用于识别除NiTi合金以外的其它工程材料的微观缺陷演化。
图7
图7
与图6对应的原子尺度应变云图
Fig.7
Atomic strain nephograms corresponding to Fig.6
(a) before twins formation (b) twins just formed (c) twins are fully formed
计算各时刻各原子的应变本质上是求解使式(12)取得最小值时的参数识别问题。一般地,在不同时刻,当各原子所处的环境(如温度、压力等)变化时,即使是同种材料,权函数ωn 也将随之变化。因此,在每个时刻计算得到的权函数ωn 的值仅对该时刻有效。
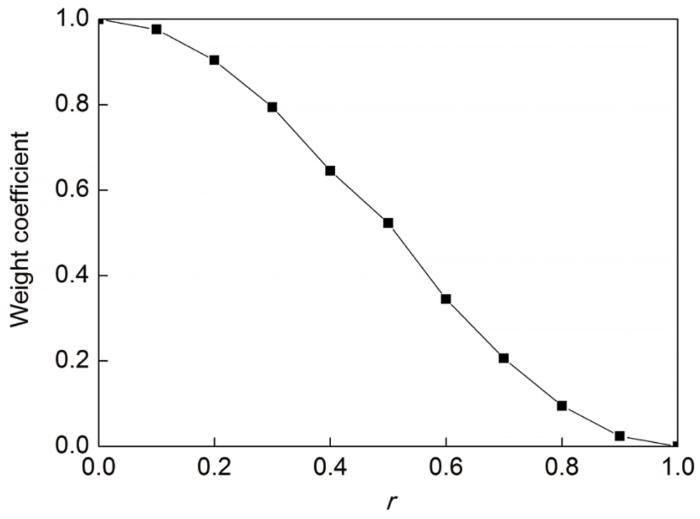
为得到权函数ωn 的性质和规律,研究截断半径对权函数ωn 取值的影响,本工作所采用的算例是在NPT系综下进行的。发现在不同时刻,权函数ωn 的9个参数值是比较接近的。计算得到适用于NiTi合金的权函数ωn (r ) (分段函数)各转折点的值分别为:ωn (0)=1、ωn (0.1)=0.976、ωn (0.2)=0.904、ωn (0.3)=0.794、ωn (0.4)=0.645、ωn (0.5)=0.523、ωn (0.6)=0.345、ωn (0.7)=0.206、ωn (0.8)=0.095、ωn (0.9)=0.024、ωn (1)=0。则权函数ωn (r )的函数图如图8 所示。
图8
图8
NiTi合金权函数ωn (r )的函数图
Fig.8
The function image of the weight function ωn (r ) of NiTi alloy (r —dimensionless quantity related to atom distance Rmn and cut-off radius R cut )
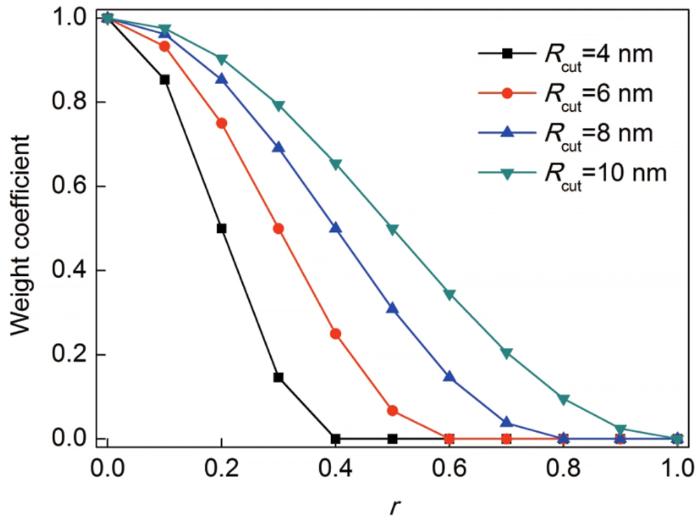
根据图8 与式(9),近似取R min ≈0,则可进一步得到不同R cut 时权函数ωn 相对于r (即Rmn /R cut )的函数图,如图9 所示。由图9 可知,当Rmn 不断增大时,ωn 的值从1.0逐渐衰减到0.0。当Rmn 趋近于R cut 时,ωn 趋近于0。当Rmn 超过R cut 时,ωn 均取0。因此,基于已确定的适用于NiTi合金的权函数ωn 的值,通过式(12)能非常方便地编程计算出式(12)的目标函数Wm (X n 对中心原子m 的应变的影响。
图9
图9
不同截断半径R cut 时NiTi合金权函数ω (r )的函数图
Fig.9
The function images of the weight function ω (r ) of NiTi alloy with different R cut
4 结论
(1) 提出了可同时适用于原子尺度和连续介质尺度的“变形”的计算方法(原子尺度下为离散变形梯度,连续介质尺度下为连续变形梯度)。在此基础上,引入邻域原子影响权函数ωn ,定义了多尺度下的应变张量,建立了计算任一中心原子m 的综合局部变形梯度和应变张量的加权最小二乘法目标函数(式(12)),将原子尺度应变的计算转化为解决目标函数的最小值优化问题。
(2) 提出的改进遗传算法能显著克服基本遗传算法与复形法的弊端,可高效地识别目标函数优化问题中的最优待定参数。
(3) 权函数的形式和系数对计算原子尺度应变具有重要影响,因此计算不同材料的原子尺度应变,宜通过优化法获得合理的权函数系数。
(4) 当无量纲量r 大于1时,截断半径外的邻域原子对中心原子的原子尺度应变的影响可忽略。建议截断半径的取值应与势函数的影响范围一致。
(5) 本工作提出的原子尺度应变张量的定义和优化方法有望用于识别除NiTi合金以外的其它工程材料的微观缺陷演化。
参考文献
View Option
[1]
Subramaniyan A K Sun C T Continuum interpretation of virial stress in molecular simulations
[J]. Int. J. Solids Struct. , 2008 , 45 : 4340
DOI
URL
[本文引用: 1]
[2]
Zimmerman J A Webb E B Hoyt J J et al . Calculation of stress in atomistic simulation
[J]. Modell. Simul. Mater. Sci. Eng. , 2004 , 12 : 319
[本文引用: 1]
[3]
Cormier J Rickman J M Delph T J Stress calculation in atomistic simulations of perfect and imperfect solids
[J]. J. Appl. Phys. , 2001 , 89 : 99
DOI
URL
[本文引用: 1]
[4]
Zhou M A new look at the atomic level virial stress: On continuum-molecular system equivalence
[J]. Proc. R. Soc. , 2003 , 459A : 2347
[本文引用: 3]
[5]
Liu B Qiu X M How to compute the atomic stress objectively?
[J]. J. Comput. Theor. Nanosci. , 2009 , 6 : 1081
DOI
URL
[本文引用: 2]
[6]
Xu R Liu B Investigation on applicability of various stress definitions in atomistic simulation
[J]. Acta Mech. Solida Sin. , 2009 , 22 : 644
DOI
URL
[本文引用: 2]
AbstractHow to correctly extract Cauchy stress from the atomistic simulations is a crucial issue in studying the mechanical behaviours of atomic systems, but is still in controversy. In this paper, three typical atomistic simulation examples are used to validate various existing stress definitions. It is found that the classical virial stress fails in predicting the stresses in these examples, because the velocity depends on the choice of the local average volume or the reference frame velocity and other factors. In contrast, the Lagrangian cross-section stress and Lagrangian virial stress are validated by these examples, and the instantaneous Lagrangian atomic stress definition is also proposed for dynamical problems.]]>
[7]
Wang Y C Wu C Y Chu J P et al . Indentation behavior of Zr-based metallic-glass films via molecular-dynamics simulations
[J]. Metall. Mater. Trans. , 2010 , 41A : 3010
[本文引用: 1]
[8]
Hirth J P Lothe J Theory of dislocations (2nd Ed.,)
[J]. J. Appl. Mech. , 1983 , 50 : 476
[本文引用: 1]
[9]
Seol J B Kim J G Na S H et al . Deformation rate controls atomic-scale dynamic strain aging and phase transformation in high Mn TRIP steels
[J]. Acta Mater. , 2017 , 131 : 187
DOI
URL
[本文引用: 1]
[10]
Zimmerman J A Bammann D J Gao H J Deformation gradients for continuum mechanical analysis of atomistic simulations
[J]. Int. J. Solids Struct. , 2009 , 46 : 238
DOI
URL
[本文引用: 1]
[11]
Mott P H Argon A S Suter U W The atomic strain tensor
[J]. J. Comput. Phys. , 1992 , 101 : 140
DOI
URL
[本文引用: 1]
[12]
Falk M L Molecular-dynamics study of ductile and brittle fracture in model noncrystalline solids
[J]. Phys. Rev. , 1999 , 60B : 7062
[本文引用: 1]
[13]
Kim H Meng Y F Rouviére J L et al . Peak separation method for sub-lattice strain analysis at atomic resolution: Application to InAs/GaSb superlattice
[J]. Micron , 2017 , 92 : 6
URL
PMID
[本文引用: 1]
[14]
Gullett P M Horstemeyer M F Baskes M I et al . A deformation gradient tensor and strain tensors for atomistic simulations
[J]. Modell. Simul. Mater. Sci. Eng. , 2008 , 16 : 015001
DOI
URL
[本文引用: 4]
[15]
Quyen T N T Variational method for multiple parameter identification in elliptic PDEs
[J]. J. Math. Anal. Appl. , 2018 , 461 : 676
DOI
URL
[本文引用: 1]
[16]
Sheng Y Zeng X G Chen H Y et al . Identification of target parameters and experimental verification for dislocation-mechanics-based constitutive relations of titanium alloy
[J]. J. Sichuan Univ. (Eng. Sci. Ed.) , 2015 , 47 (6 ): 69
[本文引用: 1]
(盛 鹰 , 曾祥国 , 陈华燕 等 . 基于位错机制钛合金本构关系的目标参数识别及实验验证
[J]. 四川大学学报(工程科学版) , 2015 , 47 (6 ): 69 )
[本文引用: 1]
[17]
Kramer O Genetic Algorithm Essentials [M]. Cham : Springer , 2017 : 1
[本文引用: 1]
[18]
Mei Y Sun Q L Yu L H et al . Grain size prediction of aluminum alloy dies castings based on GA-ELM
[J]. Acta Metall. Sin. , 2017 , 53 : 1125
DOI
URL
[本文引用: 1]
i.e. the output parameters. The GA-ELM model is trained and tested using these data. To verify the superiority of the GA-ELM model in grain size prediction, this study compares the prediction results of GA-ELM model with the GA-BP neural network model and the original ELM model, and eventually verifies the reliability of GA-ELM model prediction results through metallographic structure measurement experiment. The results show that the GA-ELM model has higher prediction accuracy than the GA-BP neural network model and the original ELM model. Besides, its prediction efficiency is higher than the GA-BP model, while is lower than the original ELM model. With fairly high prediction accuracy and efficiency, the GA-ELM model can meet the actual engineering requirements. Furthermore, its prediction reliability and excellent prediction effect are verified by the results of metallographic structure measurement experiment.]]>
(梅 益 , 孙全龙 , 喻丽华 等 . 基于GA-ELM的铝合金压铸件晶粒尺寸预测
[J]. 金属学报 , 2017 , 53 : 1125 )
DOI
URL
[本文引用: 1]
为提高铝合金压铸件晶粒尺寸预测的效率和准确率,应用遗传算法-极限学习机(GA-ELM)模型预测晶粒尺寸。ELM的输入层权值矩阵及隐含层阈值矩阵具有随机性,通过GA算法对ELM的输入层权值矩阵和隐含层阈值矩阵进行优化,建立GA-ELM模型。以晶粒尺寸作为输出参数,相关压铸工艺参数作为输入参数,通过压铸生产实验及金相测量获得相应数据,对GA-ELM模型进行实例分析,并与同样使用遗传算法优化的GA-BP神经网络模型和原始ELM模型预测结果进行对比。最后,通过金相组织测量实验验证GA-ELM模型预测结果的可靠性。结果表明,利用GA-ELM模型预测铝合金压铸件晶粒尺寸具有较高的预测精度及预测效率,与其它算法相比,具有一定的优越性。
[19]
Bradford E Schweidtmann A M Lapkin A Correction to: Efficient multiobjective optimization employing Gaussian processes, spectral sampling and a genetic algorithm
[J]. J. Global Optim. , 2018 , 71 : 407
DOI
URL
[本文引用: 1]
[20]
Yu B S Wang S L Yang T et al . BP neural netwok constitutive model based on optimization with genetic algorithm for SMA
[J]. Acta Metall. Sin. , 2017 , 53 : 248
DOI
URL
[本文引用: 1]
Systematic study was conducted on the variation regularity of stress-strain curve, feature point stress, dissipated energy and equivalent damping ratio of shape memory alloy (SMA) wires changed with wire diameter, strain amplitude, loading rate and loading cyclic number. By nonlinearly modeling experimental results for SMA using the neural network intelligent algorithm (a neural network algorithm with back-propagation training) and optimizing the initial weight and threshold value of neurons using genetic algorithm, a new BP neural network constitutive model for SMA optimized with genetic algorithm is established. This model successfully overcomes the shortcomings of other mathematical models such as the phenomenological Brinson, by which the various influence factors to mechanical properties in an experiment for SMA are hardly simulated exactly. In fact, the average error between experimental and simulated results is only 1.13% by using this model, much better than conventional BP neural network models. The results show that the BP neural networks constitutive model optimized with genetic algorithm can not only predict accurately the superelastic performance of SMA under cyclic loading, but also avoid the no convergence problem caused by concussion of BP network due to the improper initial weight and threshold value set up. Furthermore, this model would be a better model than others because of fully considering the dynamic influence of loading/unloading rate on SMA experiments.
(余滨杉 , 王社良 , 杨 涛 等 . 基于遗传算法优化的SMABP神经网络本构模型
[J]. 金属学报 , 2017 , 53 : 248 )
DOI
URL
[本文引用: 1]
系统研究了形状记忆合金丝(SMA)应力-应变曲线、特征点应力、耗能能力及等效阻尼比随材料直径、应变幅值、加载速率、加载循环次数的变化规律;由于SMA唯象Brinson等常见本构模型无法以数学模型方式精确描述SMA各影响因素对其力学性能的影响程度,基于SMA实验结果,本工作采用BP神经网络智能算法(一种利用误差反向传播训练的神经网络算法)对其进行非线性建模,同时利用遗传算法对神经元的初始权值和阈值进行优化,进而获得了一种基于遗传算法优化的SMA BP神经网络本构模型。利用该模型对SMA实验结果进行模拟,所得结果平均误差仅为1.13%,优于未优化的SMA BP神经网络模型。结果表明,基于遗传算法优化的SMA BP神经网络本构模型,能够精确地预测SMA在反复荷载作用下的超弹性性能,避免由于初始权/阈值取值不当引起的BP网络振荡而产生不收敛的问题,同时也充分考虑了加/卸载速率的动态影响,是一种良好的速率相关型动力本构模型。
[21]
Qian W W Chai J R Clustering genetic algorithm based on complex method
[J]. Comput. Eng. Appl. , 2017 , 53 (3 ): 87
[本文引用: 1]
(钱武文 , 柴军瑞 基于复合形法的聚类遗传算法
[J]. 计算机工程与应用 , 2017 , 53 (3 ): 87 )
[本文引用: 1]
[22]
Sheng Y Zeng X G Chen G P et al . Application of multilayer complex genetic algorithm in parameters identification of titanium alloy dynamic constitutive model
[J]. J. Chengdu Univ. (Nat. Sci.) , 2018 , 37 : 242
[本文引用: 1]
(盛 鹰 , 曾祥国 , 陈国平 等 . 自适应多层复形遗传算法在钛合金动态本构模型参数识别中的应用
[J]. 成都大学学报(自然科学版) , 2018 , 37 : 242 )
[本文引用: 1]
[23]
Luo J F Mao S C Han X D et al . High-cycle fatigue mechanisms of a NiTi shape memory alloy under different mean strains
[J]. Mater. Sci. Forum , 2009 , 610-613 : 1120
DOI
URL
[本文引用: 1]
[24]
Wei Z Z Ma X Zhang X P Topological modelling of the B2-B19' martensite transformation crystallography in NiTi alloy
[J]. Acta Metall. Sin. , 2018 , 54 : 1461
DOI
URL
[本文引用: 1]
' martensitic transformation in the alloy. Therefore, it is of great importance and interests to study the martensitic transformation crystallography in NiTi alloy. In this work, the martensitic transformation crystallography in an equiatomic NiTi alloy was investigated by using the topological model, as well as the optimum twist criterion developed lately. The optimum twist angle, ωo, in NiTi alloy was determined to be -0.969°, and the so-obtained transformation crystallography results, including the habit plane index and parent-martensite orientation relationship, agree well with the corresponding experimental data and theoretical calculations in the literature. Furthermore, the martensitic transformation strain of NiTi alloy was calculated based on the analysis of interfacial dislocation movement, and the total transformation strain can be resolved into an in-habit-plane shear strain and an axial strain perpendicular to the habit plane. In particular, the value of the axial strain that represents the volume change due to the B19' to B2 transformation was found to be negative, indicating that the NiTi alloy shrinks during the reverse martensitic phase transformation when heated, which might shed some light on the relationship between the NTE mechanism and martensitic transformation in NiTi alloy. The measured NTE strain is much smaller than the theoretical calculated phase transformation strain in NiTi alloy, due to the self-accommodation effect of martensite variants and the compensation of transformation strains in polycrystalline materials.]]>
(韦昭召 , 马 骁 , 张新平 NiTi合金B2-B19'马氏体相变晶体学的拓扑模拟研究
[J]. 金属学报 , 2018 , 54 : 1461 )
DOI
URL
[本文引用: 1]
'马氏体相变晶体学,根据最优扭转角(ωo)准则计算得到ωo=-0.969°,并获得了马氏体惯习面指数及母相-马氏体相界面位错结构特征,计算结果与实验测量值非常接近。NiTi合金马氏体相变所产生的相变应变包含一个平行于惯习面的剪切应变和一个垂直于惯习面的轴向应变,轴向应变量表示B2-B19'相变所引起的宏观体积变化为$ε_{33}^{HP}$=6.6879×10-3,表明NiTi合金的负热膨胀现象来源于合金中马氏体相变所产生的相变应变。]]>
[25]
Krishnan M Singh J B A novel B19' martensite in nickel titanium shape memory alloys
[J]. Acta Mater. , 2000 , 48 : 1325
DOI
URL
[本文引用: 1]
Continuum interpretation of virial stress in molecular simulations
1
2008
... 柯西(Cauchy)应力是连续介质理论框架中的重要物理量,不少学者[1 ,2 ,3 ] 认为,在离散原子系统的virial应力等同于连续介质中的Cauchy应力,甚至不少分子动力学软件也输出virial应力作为原子尺度的应力计算结果.但是Zhou[4 ] 首次对此提出质疑,认为在原子尺度下,原子间内力的平均值才是应力,因此原子尺度的应力应当与原子速度无关,原子尺度的应力不等同于Cauchy应力.Zhou[4 ] 的观点引起了全球学者的大讨论.Liu等[5 ] 和Xu等[6 ] 支持Zhou[4 ] 提出的“原子尺度的应力应当与原子速度无关”这一结论,因为原子速度不是一个客观量,它会依赖观察者的人为选择,同时,进一步研究发现virial应力的势能部分也不完全等同于Cauchy应力,并举出多个反例证明了virial应力在某些情况下即使去掉包含速度的项后也不能正确预测Cauchy应力,提出了一个不包含原子速度项的Lagrange virial应力公式,如式(1) 所示,并认为通过该式能得到正确的Cauchy应力: ...
Calculation of stress in atomistic simulation
1
2004
... 柯西(Cauchy)应力是连续介质理论框架中的重要物理量,不少学者[1 ,2 ,3 ] 认为,在离散原子系统的virial应力等同于连续介质中的Cauchy应力,甚至不少分子动力学软件也输出virial应力作为原子尺度的应力计算结果.但是Zhou[4 ] 首次对此提出质疑,认为在原子尺度下,原子间内力的平均值才是应力,因此原子尺度的应力应当与原子速度无关,原子尺度的应力不等同于Cauchy应力.Zhou[4 ] 的观点引起了全球学者的大讨论.Liu等[5 ] 和Xu等[6 ] 支持Zhou[4 ] 提出的“原子尺度的应力应当与原子速度无关”这一结论,因为原子速度不是一个客观量,它会依赖观察者的人为选择,同时,进一步研究发现virial应力的势能部分也不完全等同于Cauchy应力,并举出多个反例证明了virial应力在某些情况下即使去掉包含速度的项后也不能正确预测Cauchy应力,提出了一个不包含原子速度项的Lagrange virial应力公式,如式(1) 所示,并认为通过该式能得到正确的Cauchy应力: ...
Stress calculation in atomistic simulations of perfect and imperfect solids
1
2001
... 柯西(Cauchy)应力是连续介质理论框架中的重要物理量,不少学者[1 ,2 ,3 ] 认为,在离散原子系统的virial应力等同于连续介质中的Cauchy应力,甚至不少分子动力学软件也输出virial应力作为原子尺度的应力计算结果.但是Zhou[4 ] 首次对此提出质疑,认为在原子尺度下,原子间内力的平均值才是应力,因此原子尺度的应力应当与原子速度无关,原子尺度的应力不等同于Cauchy应力.Zhou[4 ] 的观点引起了全球学者的大讨论.Liu等[5 ] 和Xu等[6 ] 支持Zhou[4 ] 提出的“原子尺度的应力应当与原子速度无关”这一结论,因为原子速度不是一个客观量,它会依赖观察者的人为选择,同时,进一步研究发现virial应力的势能部分也不完全等同于Cauchy应力,并举出多个反例证明了virial应力在某些情况下即使去掉包含速度的项后也不能正确预测Cauchy应力,提出了一个不包含原子速度项的Lagrange virial应力公式,如式(1) 所示,并认为通过该式能得到正确的Cauchy应力: ...
A new look at the atomic level virial stress: On continuum-molecular system equivalence
3
2003
... 柯西(Cauchy)应力是连续介质理论框架中的重要物理量,不少学者[1 ,2 ,3 ] 认为,在离散原子系统的virial应力等同于连续介质中的Cauchy应力,甚至不少分子动力学软件也输出virial应力作为原子尺度的应力计算结果.但是Zhou[4 ] 首次对此提出质疑,认为在原子尺度下,原子间内力的平均值才是应力,因此原子尺度的应力应当与原子速度无关,原子尺度的应力不等同于Cauchy应力.Zhou[4 ] 的观点引起了全球学者的大讨论.Liu等[5 ] 和Xu等[6 ] 支持Zhou[4 ] 提出的“原子尺度的应力应当与原子速度无关”这一结论,因为原子速度不是一个客观量,它会依赖观察者的人为选择,同时,进一步研究发现virial应力的势能部分也不完全等同于Cauchy应力,并举出多个反例证明了virial应力在某些情况下即使去掉包含速度的项后也不能正确预测Cauchy应力,提出了一个不包含原子速度项的Lagrange virial应力公式,如式(1) 所示,并认为通过该式能得到正确的Cauchy应力: ...
... [4 ]的观点引起了全球学者的大讨论.Liu等[5 ] 和Xu等[6 ] 支持Zhou[4 ] 提出的“原子尺度的应力应当与原子速度无关”这一结论,因为原子速度不是一个客观量,它会依赖观察者的人为选择,同时,进一步研究发现virial应力的势能部分也不完全等同于Cauchy应力,并举出多个反例证明了virial应力在某些情况下即使去掉包含速度的项后也不能正确预测Cauchy应力,提出了一个不包含原子速度项的Lagrange virial应力公式,如式(1) 所示,并认为通过该式能得到正确的Cauchy应力: ...
... [4 ]提出的“原子尺度的应力应当与原子速度无关”这一结论,因为原子速度不是一个客观量,它会依赖观察者的人为选择,同时,进一步研究发现virial应力的势能部分也不完全等同于Cauchy应力,并举出多个反例证明了virial应力在某些情况下即使去掉包含速度的项后也不能正确预测Cauchy应力,提出了一个不包含原子速度项的Lagrange virial应力公式,如式(1) 所示,并认为通过该式能得到正确的Cauchy应力: ...
How to compute the atomic stress objectively?
2
2009
... 柯西(Cauchy)应力是连续介质理论框架中的重要物理量,不少学者[1 ,2 ,3 ] 认为,在离散原子系统的virial应力等同于连续介质中的Cauchy应力,甚至不少分子动力学软件也输出virial应力作为原子尺度的应力计算结果.但是Zhou[4 ] 首次对此提出质疑,认为在原子尺度下,原子间内力的平均值才是应力,因此原子尺度的应力应当与原子速度无关,原子尺度的应力不等同于Cauchy应力.Zhou[4 ] 的观点引起了全球学者的大讨论.Liu等[5 ] 和Xu等[6 ] 支持Zhou[4 ] 提出的“原子尺度的应力应当与原子速度无关”这一结论,因为原子速度不是一个客观量,它会依赖观察者的人为选择,同时,进一步研究发现virial应力的势能部分也不完全等同于Cauchy应力,并举出多个反例证明了virial应力在某些情况下即使去掉包含速度的项后也不能正确预测Cauchy应力,提出了一个不包含原子速度项的Lagrange virial应力公式,如式(1) 所示,并认为通过该式能得到正确的Cauchy应力: ...
... Liu等[5 ] 和Xu等[6 ] 的研究是目前对原子应力研究的最新成果,虽有理有据,但仍未得到公认,也未被分子动力学软件(如Lammps、Material Studio等)采用.而对原子尺度应变的共识就更少了,至今尚没有一个分子动力学软件能输出原子尺度应变的计算结果. ...
Investigation on applicability of various stress definitions in atomistic simulation
2
2009
... 柯西(Cauchy)应力是连续介质理论框架中的重要物理量,不少学者[1 ,2 ,3 ] 认为,在离散原子系统的virial应力等同于连续介质中的Cauchy应力,甚至不少分子动力学软件也输出virial应力作为原子尺度的应力计算结果.但是Zhou[4 ] 首次对此提出质疑,认为在原子尺度下,原子间内力的平均值才是应力,因此原子尺度的应力应当与原子速度无关,原子尺度的应力不等同于Cauchy应力.Zhou[4 ] 的观点引起了全球学者的大讨论.Liu等[5 ] 和Xu等[6 ] 支持Zhou[4 ] 提出的“原子尺度的应力应当与原子速度无关”这一结论,因为原子速度不是一个客观量,它会依赖观察者的人为选择,同时,进一步研究发现virial应力的势能部分也不完全等同于Cauchy应力,并举出多个反例证明了virial应力在某些情况下即使去掉包含速度的项后也不能正确预测Cauchy应力,提出了一个不包含原子速度项的Lagrange virial应力公式,如式(1) 所示,并认为通过该式能得到正确的Cauchy应力: ...
... Liu等[5 ] 和Xu等[6 ] 的研究是目前对原子应力研究的最新成果,虽有理有据,但仍未得到公认,也未被分子动力学软件(如Lammps、Material Studio等)采用.而对原子尺度应变的共识就更少了,至今尚没有一个分子动力学软件能输出原子尺度应变的计算结果. ...
Indentation behavior of Zr-based metallic-glass films via molecular-dynamics simulations
1
2010
... 研究原子尺度的应变对研究物理科学问题具有重要意义.Wang等[7 ] 认为,分析原子级应变分布和原子应力-应变曲线对研究锆基金属玻璃压痕的力学行为具有重要价值.Hirth等[8 ] 也提出,实现微观尺度下变形梯度张量和应变张量的计算将有利于识别和分析位错、晶界、复合微裂纹等微观缺陷的演化.Seol等[9 ] 研究发现,工程金属合金的动态应变时效(DSA)会引起材料相关性能的退化,因此有必要开展关于原子尺度应变的研究. ...
Theory of dislocations (2nd Ed.,)
1
1983
... 研究原子尺度的应变对研究物理科学问题具有重要意义.Wang等[7 ] 认为,分析原子级应变分布和原子应力-应变曲线对研究锆基金属玻璃压痕的力学行为具有重要价值.Hirth等[8 ] 也提出,实现微观尺度下变形梯度张量和应变张量的计算将有利于识别和分析位错、晶界、复合微裂纹等微观缺陷的演化.Seol等[9 ] 研究发现,工程金属合金的动态应变时效(DSA)会引起材料相关性能的退化,因此有必要开展关于原子尺度应变的研究. ...
Deformation rate controls atomic-scale dynamic strain aging and phase transformation in high Mn TRIP steels
1
2017
... 研究原子尺度的应变对研究物理科学问题具有重要意义.Wang等[7 ] 认为,分析原子级应变分布和原子应力-应变曲线对研究锆基金属玻璃压痕的力学行为具有重要价值.Hirth等[8 ] 也提出,实现微观尺度下变形梯度张量和应变张量的计算将有利于识别和分析位错、晶界、复合微裂纹等微观缺陷的演化.Seol等[9 ] 研究发现,工程金属合金的动态应变时效(DSA)会引起材料相关性能的退化,因此有必要开展关于原子尺度应变的研究. ...
Deformation gradients for continuum mechanical analysis of atomistic simulations
1
2009
... 考虑到应变是一个连续量,学者们从连续位移场插值和梯度算子离散化2个角度提出了原子尺度应变的新定义和计算方法.Zimmerman等[10 ] 根据原子在不同时刻的位置关系定义了滑移矢量,成功地识别了晶格畸变和位错的形成,但是该方法不能在连续体框架中使用.Mott等[11 ] 提出了一种三维无序系统下局部原子尺度应变的计算方法,即首先运用Delaunay三角剖分方法,将所有原子视为节点,建立唯一的四面体单元网格,计算出相邻两原子的位移向量,然后定义局部原子变形梯度为相邻四面体的变形梯度的加权平均值,进而运用各原子的变形梯度计算原子尺度应变.Falk[12 ] 运用小应变定义得到了局部原子尺度应变张量,但这种定义方法不能反映刚体旋转时的虚拟剪切应变和有限应变.Kim等[13 ] 用原子分辨成像和先进的图像处理技术直接测量了InAs/GaSb II型应变层超晶格中的阴阳亚晶格应变,提出了一种原子尺度应变的测量方法. ...
The atomic strain tensor
1
1992
... 考虑到应变是一个连续量,学者们从连续位移场插值和梯度算子离散化2个角度提出了原子尺度应变的新定义和计算方法.Zimmerman等[10 ] 根据原子在不同时刻的位置关系定义了滑移矢量,成功地识别了晶格畸变和位错的形成,但是该方法不能在连续体框架中使用.Mott等[11 ] 提出了一种三维无序系统下局部原子尺度应变的计算方法,即首先运用Delaunay三角剖分方法,将所有原子视为节点,建立唯一的四面体单元网格,计算出相邻两原子的位移向量,然后定义局部原子变形梯度为相邻四面体的变形梯度的加权平均值,进而运用各原子的变形梯度计算原子尺度应变.Falk[12 ] 运用小应变定义得到了局部原子尺度应变张量,但这种定义方法不能反映刚体旋转时的虚拟剪切应变和有限应变.Kim等[13 ] 用原子分辨成像和先进的图像处理技术直接测量了InAs/GaSb II型应变层超晶格中的阴阳亚晶格应变,提出了一种原子尺度应变的测量方法. ...
Molecular-dynamics study of ductile and brittle fracture in model noncrystalline solids
1
1999
... 考虑到应变是一个连续量,学者们从连续位移场插值和梯度算子离散化2个角度提出了原子尺度应变的新定义和计算方法.Zimmerman等[10 ] 根据原子在不同时刻的位置关系定义了滑移矢量,成功地识别了晶格畸变和位错的形成,但是该方法不能在连续体框架中使用.Mott等[11 ] 提出了一种三维无序系统下局部原子尺度应变的计算方法,即首先运用Delaunay三角剖分方法,将所有原子视为节点,建立唯一的四面体单元网格,计算出相邻两原子的位移向量,然后定义局部原子变形梯度为相邻四面体的变形梯度的加权平均值,进而运用各原子的变形梯度计算原子尺度应变.Falk[12 ] 运用小应变定义得到了局部原子尺度应变张量,但这种定义方法不能反映刚体旋转时的虚拟剪切应变和有限应变.Kim等[13 ] 用原子分辨成像和先进的图像处理技术直接测量了InAs/GaSb II型应变层超晶格中的阴阳亚晶格应变,提出了一种原子尺度应变的测量方法. ...
Peak separation method for sub-lattice strain analysis at atomic resolution: Application to InAs/GaSb superlattice
1
2017
... 考虑到应变是一个连续量,学者们从连续位移场插值和梯度算子离散化2个角度提出了原子尺度应变的新定义和计算方法.Zimmerman等[10 ] 根据原子在不同时刻的位置关系定义了滑移矢量,成功地识别了晶格畸变和位错的形成,但是该方法不能在连续体框架中使用.Mott等[11 ] 提出了一种三维无序系统下局部原子尺度应变的计算方法,即首先运用Delaunay三角剖分方法,将所有原子视为节点,建立唯一的四面体单元网格,计算出相邻两原子的位移向量,然后定义局部原子变形梯度为相邻四面体的变形梯度的加权平均值,进而运用各原子的变形梯度计算原子尺度应变.Falk[12 ] 运用小应变定义得到了局部原子尺度应变张量,但这种定义方法不能反映刚体旋转时的虚拟剪切应变和有限应变.Kim等[13 ] 用原子分辨成像和先进的图像处理技术直接测量了InAs/GaSb II型应变层超晶格中的阴阳亚晶格应变,提出了一种原子尺度应变的测量方法. ...
A deformation gradient tensor and strain tensors for atomistic simulations
4
2008
... Gullett等[14 ] 提出了通过离散变形梯度的定义求原子尺度应变的方法.与前面的方法相比,该方法具有如下优点:计算各原子变形梯度时无需先作几何分解;可直接根据变形梯度计算应变张量;对有限、多轴变形问题均适用.Gullett等[14 ] 指出,任一原子的变形梯度与其邻域原子均相关,而邻域各原子相对于原子的变形梯度均不同,故需计算每个原子周围所有领域原子对其共同作用的综合局部变形梯度.因此,Gullett等[14 ] 引入了一个系数固定的分段多项式递减权函数来反映邻域各原子对某原子的变形梯度的贡献度.该方法实现了原子尺度应变计算的重大突破. ...
... [14 ]指出,任一原子的变形梯度与其邻域原子均相关,而邻域各原子相对于原子的变形梯度均不同,故需计算每个原子周围所有领域原子对其共同作用的综合局部变形梯度.因此,Gullett等[14 ] 引入了一个系数固定的分段多项式递减权函数来反映邻域各原子对某原子的变形梯度的贡献度.该方法实现了原子尺度应变计算的重大突破. ...
... [14 ]引入了一个系数固定的分段多项式递减权函数来反映邻域各原子对某原子的变形梯度的贡献度.该方法实现了原子尺度应变计算的重大突破. ...
... 本工作对Gullett等[14 ] 的方法作了进一步发展.研究表明,权函数的形式和系数对计算原子尺度应变具有重要影响,因此,针对不同的材料,计算其原子尺度应变时宜采用不同的优化权函数.基于此,本工作提出了基于离散变形梯度、邻域原子影响权函数的原子尺度应变定义方法,构造了计算原子综合局部变形梯度和应变张量的加权最小二乘法目标函数,建立了计算原子尺度应变张量的优化数学模型. ...
Variational method for multiple parameter identification in elliptic PDEs
1
2018
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
基于位错机制钛合金本构关系的目标参数识别及实验验证
1
2015
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
基于位错机制钛合金本构关系的目标参数识别及实验验证
1
2015
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
1
2017
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
基于GA-ELM的铝合金压铸件晶粒尺寸预测
1
2017
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
基于GA-ELM的铝合金压铸件晶粒尺寸预测
1
2017
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
Correction to: Efficient multiobjective optimization employing Gaussian processes, spectral sampling and a genetic algorithm
1
2018
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
基于遗传算法优化的SMABP神经网络本构模型
1
2017
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
基于遗传算法优化的SMABP神经网络本构模型
1
2017
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
基于复合形法的聚类遗传算法
1
2017
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
基于复合形法的聚类遗传算法
1
2017
... 但本工作建立的计算原子尺度应变张量的优化数学模型共包含18个待定参数,若将每个参数在其取值范围内作密集离散,则对全部参数的识别计算工作量非常大[15 ] .因此,需要建立一种高效的优化算法,以降低参数识别的计算量,提高参数识别的效率和精度[16 ] .比较著名的优化算法有遗传算法[17 ,18 ,19 ] 、神经网络算法[20 ] 、复形法[21 ] 等等. ...
自适应多层复形遗传算法在钛合金动态本构模型参数识别中的应用
1
2018
... 本工作在遗传算法和复形法的基础上,提出了一种改进的自适应多层复形遗传算法,能显著提高参数识别的效率和精度[22 ] .并以NiTi合金为研究对象,建立了NiTi合金变形与破坏的分子动力学演化模型并计算了各时刻的原子尺度应变云图,通过应变云图观察到了孪晶.经与NiTi合金三点弯曲冲击断裂试件裂纹尖端的微观观察实验作对照,验证了本工作建立的原子尺度应变定义方法的合理性及其在识别微观缺陷演化中的应用意义. ...
自适应多层复形遗传算法在钛合金动态本构模型参数识别中的应用
1
2018
... 本工作在遗传算法和复形法的基础上,提出了一种改进的自适应多层复形遗传算法,能显著提高参数识别的效率和精度[22 ] .并以NiTi合金为研究对象,建立了NiTi合金变形与破坏的分子动力学演化模型并计算了各时刻的原子尺度应变云图,通过应变云图观察到了孪晶.经与NiTi合金三点弯曲冲击断裂试件裂纹尖端的微观观察实验作对照,验证了本工作建立的原子尺度应变定义方法的合理性及其在识别微观缺陷演化中的应用意义. ...
High-cycle fatigue mechanisms of a NiTi shape memory alloy under different mean strains
1
2009
... 采用JSM-7500F/X-MAX50扫描电镜(SEM)观察NiTi合金三点弯曲冲击断裂试件的断口表面形貌,如图2 所示.由图2 可知,虽然该NiTi合金试样的断口有大量解理纹,但少数部位仍存在韧窝,因此可认为该NiTi合金试样主要为脆性断裂,局部有塑性变形特征.从NiTi合金的微观机理对宏观本构关系的影响理论[23 ,24 ,25 ] 可知,在室温条件下,应力诱发的马氏体相变一方面会使NiTi合金产生解理断裂,另一方面又会在裂纹面扩展的主方向上起到一定的韧化作用. ...
NiTi合金B2-B19'马氏体相变晶体学的拓扑模拟研究
1
2018
... 采用JSM-7500F/X-MAX50扫描电镜(SEM)观察NiTi合金三点弯曲冲击断裂试件的断口表面形貌,如图2 所示.由图2 可知,虽然该NiTi合金试样的断口有大量解理纹,但少数部位仍存在韧窝,因此可认为该NiTi合金试样主要为脆性断裂,局部有塑性变形特征.从NiTi合金的微观机理对宏观本构关系的影响理论[23 ,24 ,25 ] 可知,在室温条件下,应力诱发的马氏体相变一方面会使NiTi合金产生解理断裂,另一方面又会在裂纹面扩展的主方向上起到一定的韧化作用. ...
NiTi合金B2-B19'马氏体相变晶体学的拓扑模拟研究
1
2018
... 采用JSM-7500F/X-MAX50扫描电镜(SEM)观察NiTi合金三点弯曲冲击断裂试件的断口表面形貌,如图2 所示.由图2 可知,虽然该NiTi合金试样的断口有大量解理纹,但少数部位仍存在韧窝,因此可认为该NiTi合金试样主要为脆性断裂,局部有塑性变形特征.从NiTi合金的微观机理对宏观本构关系的影响理论[23 ,24 ,25 ] 可知,在室温条件下,应力诱发的马氏体相变一方面会使NiTi合金产生解理断裂,另一方面又会在裂纹面扩展的主方向上起到一定的韧化作用. ...
A novel B19' martensite in nickel titanium shape memory alloys
1
2000
... 采用JSM-7500F/X-MAX50扫描电镜(SEM)观察NiTi合金三点弯曲冲击断裂试件的断口表面形貌,如图2 所示.由图2 可知,虽然该NiTi合金试样的断口有大量解理纹,但少数部位仍存在韧窝,因此可认为该NiTi合金试样主要为脆性断裂,局部有塑性变形特征.从NiTi合金的微观机理对宏观本构关系的影响理论[23 ,24 ,25 ] 可知,在室温条件下,应力诱发的马氏体相变一方面会使NiTi合金产生解理断裂,另一方面又会在裂纹面扩展的主方向上起到一定的韧化作用. ...