Ti based biomaterials, the ultimate choice for orthopaedic implants—A review
1
2009
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Variant selection during α precipitation in Ti-6Al-4V under the influence of local stress—A simulation study
1
2013
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Growth of (αTi) grain-boundary layers in Ti-Co alloys
1
2016
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Effect of the structure on the cutability of titanium alloys
1
2003
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Interaction of short cracks with the structure of metals
2
1990
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
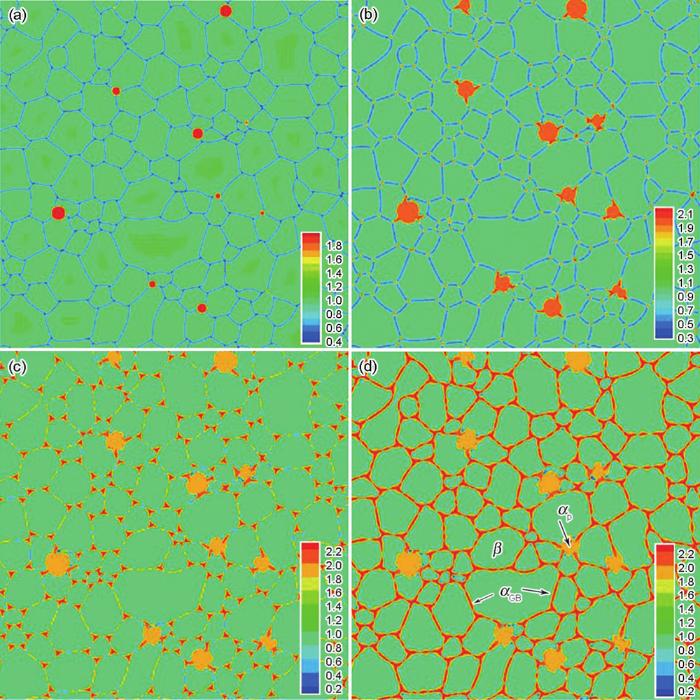
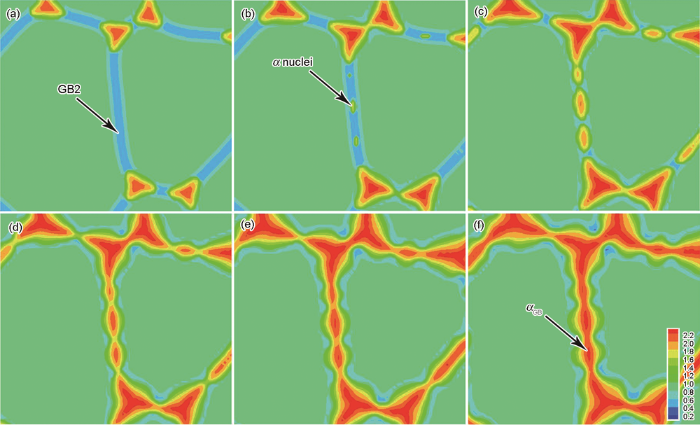
... 图1所示为1213 K下Ti-6Al-4V合金β→α相变组织演化的模拟结果,其中部分三岔点处预设α相核,长大后相当于前序热加工形成的少量初生α相(primary α,αP).模拟过冷度ΔT=55 K,噪声强度ξnoise=0.05,噪声时间tnoise=50 s.初始组织即为图1a所示的随机在β三岔晶界上放入12个不同尺寸的α相核,以作为先驱体激发部分界面反应生成[24].噪声项的存在降低了界面稳定性[5],不仅促进了α相在其它三岔点处的非均匀形核,也激发了晶界上αGB的形成,实现晶界被α相润湿,说明晶界不仅可被液相润湿,也可被第二相固相润湿[25].α会优先在β晶界析出,这是由于此类位置α相的形核激活能低.由图可知,位于三岔晶界的α核在约t=50 s时间步开始生长;在t=65 s,由于噪声的作用,αGB开始以连续的颗粒形状沿着β晶界析出,扩展后形成一薄层镶嵌在β晶界间;而且,此时只有很少的β/β晶界还未被αGB润湿.然后,当t≥50 s时,αGB同时在三岔晶界和β晶界处形核和生长.因此,出现了混合的α (αGB+αp)形貌,这种组织与他人实验中的结果[26,27]类似.如图1d所示,最终的组织为β基体、等轴αp相和αGB的共存体.整体上,沿β晶界在空间中形成了αGB网结构.当α相与β晶界接触时,在三岔晶界上的α核倾向于形成不规则带“触角”的圆形.这种形貌的形成主要是由于形核驱动力和β界面表面张力以及晶界扩散的作用所致.这种α相带触角的形貌类似于Nag等[28]的Ti-15Mo合金中α相在β三岔晶界析出的实验结果.总之,特殊构造的噪声项不仅可以促进三岔晶界上αGB的非均匀形核,而且可以激发在普通界面上αGB的晶界润湿相变,这与Kundin等[21]的Al-Cu-Ni合金中在能量有利点上噪声促进析出相的非均匀形核相似.也有研究[29]表明在最初的析出期间,αGB不仅在三岔晶界周围优先沉淀,也在β晶界的中间离散地形核,这与本工作的模拟结果相符.三岔晶界和β晶界由于结构的特殊性,显著降低了析出相形核的势垒,易在此类位置产生成分起伏以及富集杂质,均为形核的优先位置[30]. ...
Effect of particles of the insoluble phase Al9FeNi on the kinetics of fatigue crack propagation in alloy Ak4-1
1
1982
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Correlation between diagrams of isothermal and anisothermal transformations and phase composition diagram of hardened titanium alloys
1
2003
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Wetting of grain boundaries in Al by the solid Al3Mg2 phase
1
2010
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Titanium
2
2007
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
... 连续状αGB在近β和β钛合金中普遍存在,且损害合金的延展性[32,33,34].一般情况下,αGB通常会呈现连续的层状形貌,这是由于在β→α相变过程中α相优先在β晶界形核与长大.随着αGB的生成,α稳定元素(Al和O)从相邻区域扩散到αGB中,因而此处β相随后被稳定.这在一定程度上阻碍了具有细密强化作用的次生αs (secondary α)的生成,导致沿αGB形成较软的无析出相区(precipitate free zone,PFZ)[35,36].然后,在软化的PFZ和强化β基体间的高屈服应力差极易导致最初的裂纹形核[9,37].同时,由于PFZ为连续的且分布广泛,疲劳裂纹自然地沿连续的αGB开裂和增殖,继而导致沿晶断裂和低延展性[33,35].与之相反,如果αGB是不连续的,间断的αGB间细密的αs会阻碍沿晶界的裂纹扩展,因此导致穿晶断裂,进而提高延展性[36].因此,获得不连续的αGB组织对于提高钛合金的延展性能十分重要. ...
Computer experiments on point defect configurations and energies in Ti-M systems
1
1968
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Influence of processing on microstructure and mechanical properties of (α+β) titanium alloys
1
1998
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Perspectives on titanium science and technology
1
2013
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Crystallography and interfacial structure of proeutectoid α grain boundary allotriomorphs in a hypoeutectoid Ti-Cr alloy
2
1991
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
... 式中,为随机数;ξ0为涨落强度(无量纲量);R为气体常数;H=σ/(Wa1),σ为表面能,W为界面宽度,=.=,为发生β→α相变的自由能差,即相变驱动力,Gβ和Gα分别表示β和α相的化学自由能.式(5)的物理意义为:噪声项可在β/β界面处激发α相的涨落,强度与驱动力ΔGβ→α成正比,与表面能σ成反比.此式表明,噪声项取决于过冷和表面能,与形核理论相符[13].式(5)与i相的形核几率成比例,此式成立条件为二维条件下的形核能垒为. ...
Development of a pre-heat treatment for obtaining discontinuous grain boundary α in laser melting deposited Ti-5Al-5Mo-5V-1Cr-1Fe alloy
4
2014
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
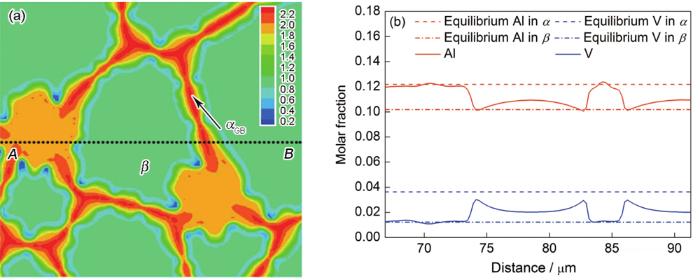
... 图3为αGB的模拟组织放大图及对应的Al和V的浓度分布.穿过一个三岔晶界α和2个αGB的直线AB上的Al和V浓度如图3b所示.由图可知,α相中的Al和V浓度大体上保持不变,且均与α和β相中平衡浓度接近.然而,当直线AB穿过β晶粒时,β与α相界上的Al浓度比β晶粒中心区域高,这使得β晶粒中的Al浓度形成类似“拱门”形状;与之相反,V浓度分布与Al的走势相反.伴随着αGB的形成,α稳定元素(Al和O)从β相的邻近区域扩散到α相中[14],使晶界附近的β相中Al浓度降低,而晶内的Al还来不及达到平衡浓度.此外,实验上固相中沿着晶界和自由表面的扩散比晶内扩散要快得多[31].这就解释了Al浓度“拱门”的现象.而且,β晶粒中的V浓度比平衡浓度略低,也是由于扩散不充分所致. ...
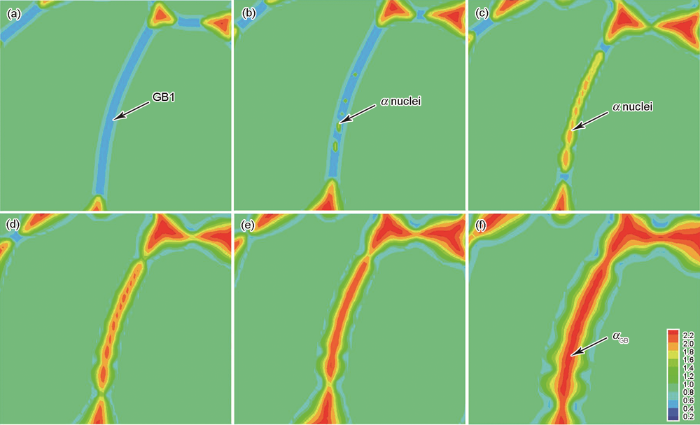
... 为探索不同形貌αGB的形成过程,选取局部位置放大进行分析.图4和5分别解析了连续αGB和不连续αGB的形成过程,模拟条件均为ξnoise=0.05、tnoise=50 s.由图4b可见,在晶界GB1上首先析出了一些α相小颗粒;随着时间的推进,析出的α相越来越多且距离适中;这些析出的α相继续长大直至相互连接为一体形成αGB,如图4c所示;随演化继续进行,成形的αGB逐渐粗化形成连续且稳定的、接近平滑形貌的αGB,如图4f所示.因此,连续αGB的形成是由于在αGB的形核初期生成了大量α核的原因,这与Liu等[14]的实验观测结果一致.而且,模拟组织与实验中的连续αGB形貌也是相似的,αGB均呈连续的波浪状. ...
... 由图5可见,在晶界GB2上首先析出了3颗距离较远的离散的α相核;随着时间的推进,这些析出的α相继续长大直至形成较为稳定的椭球状;演化继续进行,成形的αGB逐渐粗化且每个α颗粒头尾相连形成一串透镜状的αGB.因此,不连续形貌αGB的形成是由于在αGB的形核初期生成的α核量少的原因,这也与Liu等[14]的实验观测结果一致.而且,模拟组织与实验中的αGB形貌相似.图4和5的形成条件差别为初始α核的数量差异,而噪声条件均为ξnoise=0.05、tnoise=50 s.说明初始α析出相的数量可影响αGB的最终形貌为连续或不连续状态,实验上可通过改变形核条件如温度或变形来形成不同密度的αGB. ...
Grain boundary wetting by a second solid phase in Ti-Fe alloys
1
2018
... 钛合金具有优异的比强度和耐腐蚀等性能,在航空和生物医疗领域具有广泛应用[1].在钛合金中,由于α/β两相钛合金可通过热机械处理大范围调控组织和性能,此类钛合金的应用最为普遍[2].然而晶界上α层的形成强烈影响着合金的力学性能[3].由于钛合金通常要经过淬火和时效处理,这些α层的作用更为明显.许多研究表明,这种“镶边”会在本质上影响钛合金和铝合金的切削加工性能[4],且会促进疲劳等过程中的裂纹萌生[5,6].β晶界上的第二相αGB (grain boundary α)析出相即为此种镶边,因此对多晶钛合金的力学性能有很大的影响.αGB既可以通过体扩散[7]又可以通过晶界反应[8]形成.αGB对合金力学性能的影响还体现在对疲劳性能的作用上,即影响裂纹的扩展路径[9].一方面,αGB的生成通常会阻碍位错运动,强烈激发应力集中,进而作为裂纹形核的薄弱点[10].Lütjering[11]证明连续且相对较软的αGB相可以导致较低的断裂强度,并且影响裂纹的扩展路径.另一方面,Banerjee和Williams[12]报道离散的αGB可以导致不同魏氏体集束组织的形成,而不同集束组织之间的高密度界面将会缩短裂纹的有效扩展长度,导致裂纹扩展路径的弯曲,增加了屈服强度和疲劳强度.Furuhara和Aaronson[13]研究了亚共析Ti-Cr合金中αGB的晶体学和界面结构,结果表明αGB与相邻的一个β晶粒保持近Burgers取向关系,且通常与另一个β晶粒不具有特定的取向关系.在αGB的两侧界面上观测到了2种结构的台阶,一种是生长台阶,另一种是错配补偿台阶,这证明界面形核的αGB应该是与两侧的β基体都保持着部分共格.Liu等[14]采用预热处理工艺消除了Ti-5Al-5Mo-5V-1Cr-1Fe合金中连续的αGB,并将此工艺运用于近净成型钛合金部件.结果表明预热处理会促进离散且粗化αGB的生成,因此极大提升了该合金的疲劳性能.Gornakova等[15]研究了Ti-Fe合金的晶界润湿相变过程,发现完全湿润导致了连续的层状αGB的生成,而不完全润湿条件下,αGB的形貌为不连续的透镜状.然而,目前对于不同形貌的αGB形成规律的认识尚不清晰,因此使用模拟方法在介观上研究αGB形核与长大机理对于研究双相多晶钛合金的微观组织及性能调控意义重大. ...
Incorporating diffuse-interface nuclei in phase-field simulations
1
2010
... 相场中实现形核有2种方法,即Langevin噪声法和显式形核方法[16].微观上,体噪声来源于固相和液相中的热流中的涨落,而界面噪声来自于两相间原子的互换,例如界面上原子的附着和脱离[17].许多情况下,基体中的涨落(噪声)太过微弱,不足以在非平衡系统中影响结构演化[18].目前,使用相场模型实现界面处的非均匀形核有3种方式[19]:(1) 直接在固/液界面随机放入新相的核;(2) 加入随机噪声项,扰乱界面稳定性进而激发非均匀形核;(3) 第二相在三叉晶界的择优形核.本工作选择第2种方法,并通过改进Kim-Kim-Suzuki (KKS)[20]模型,在相场模型中添加噪声项,以实现β→α相变中α相在三叉晶界和普通β/β晶界处非均匀形核过程的相场模拟. ...
Phase-field model of dendritic sidebranching with thermal noise
1
1999
... 相场中实现形核有2种方法,即Langevin噪声法和显式形核方法[16].微观上,体噪声来源于固相和液相中的热流中的涨落,而界面噪声来自于两相间原子的互换,例如界面上原子的附着和脱离[17].许多情况下,基体中的涨落(噪声)太过微弱,不足以在非平衡系统中影响结构演化[18].目前,使用相场模型实现界面处的非均匀形核有3种方式[19]:(1) 直接在固/液界面随机放入新相的核;(2) 加入随机噪声项,扰乱界面稳定性进而激发非均匀形核;(3) 第二相在三叉晶界的择优形核.本工作选择第2种方法,并通过改进Kim-Kim-Suzuki (KKS)[20]模型,在相场模型中添加噪声项,以实现β→α相变中α相在三叉晶界和普通β/β晶界处非均匀形核过程的相场模拟. ...
Fluctuations in solidification
1
1993
... 相场中实现形核有2种方法,即Langevin噪声法和显式形核方法[16].微观上,体噪声来源于固相和液相中的热流中的涨落,而界面噪声来自于两相间原子的互换,例如界面上原子的附着和脱离[17].许多情况下,基体中的涨落(噪声)太过微弱,不足以在非平衡系统中影响结构演化[18].目前,使用相场模型实现界面处的非均匀形核有3种方式[19]:(1) 直接在固/液界面随机放入新相的核;(2) 加入随机噪声项,扰乱界面稳定性进而激发非均匀形核;(3) 第二相在三叉晶界的择优形核.本工作选择第2种方法,并通过改进Kim-Kim-Suzuki (KKS)[20]模型,在相场模型中添加噪声项,以实现β→α相变中α相在三叉晶界和普通β/β晶界处非均匀形核过程的相场模拟. ...
Effect of noise-induced nucleation on grain size distribution studied via the phase-field crystal method
1
2009
... 相场中实现形核有2种方法,即Langevin噪声法和显式形核方法[16].微观上,体噪声来源于固相和液相中的热流中的涨落,而界面噪声来自于两相间原子的互换,例如界面上原子的附着和脱离[17].许多情况下,基体中的涨落(噪声)太过微弱,不足以在非平衡系统中影响结构演化[18].目前,使用相场模型实现界面处的非均匀形核有3种方式[19]:(1) 直接在固/液界面随机放入新相的核;(2) 加入随机噪声项,扰乱界面稳定性进而激发非均匀形核;(3) 第二相在三叉晶界的择优形核.本工作选择第2种方法,并通过改进Kim-Kim-Suzuki (KKS)[20]模型,在相场模型中添加噪声项,以实现β→α相变中α相在三叉晶界和普通β/β晶界处非均匀形核过程的相场模拟. ...
Phase-field model for binary alloys
1
1999
... 相场中实现形核有2种方法,即Langevin噪声法和显式形核方法[16].微观上,体噪声来源于固相和液相中的热流中的涨落,而界面噪声来自于两相间原子的互换,例如界面上原子的附着和脱离[17].许多情况下,基体中的涨落(噪声)太过微弱,不足以在非平衡系统中影响结构演化[18].目前,使用相场模型实现界面处的非均匀形核有3种方式[19]:(1) 直接在固/液界面随机放入新相的核;(2) 加入随机噪声项,扰乱界面稳定性进而激发非均匀形核;(3) 第二相在三叉晶界的择优形核.本工作选择第2种方法,并通过改进Kim-Kim-Suzuki (KKS)[20]模型,在相场模型中添加噪声项,以实现β→α相变中α相在三叉晶界和普通β/β晶界处非均匀形核过程的相场模拟. ...
Phase-field modeling of the microstructure evolution and heterogeneous nucleation in solidifying ternary Al-Cu-Ni alloys
2
2015
... 噪声项的表达式为[21]: ...
... 图1所示为1213 K下Ti-6Al-4V合金β→α相变组织演化的模拟结果,其中部分三岔点处预设α相核,长大后相当于前序热加工形成的少量初生α相(primary α,αP).模拟过冷度ΔT=55 K,噪声强度ξnoise=0.05,噪声时间tnoise=50 s.初始组织即为图1a所示的随机在β三岔晶界上放入12个不同尺寸的α相核,以作为先驱体激发部分界面反应生成[24].噪声项的存在降低了界面稳定性[5],不仅促进了α相在其它三岔点处的非均匀形核,也激发了晶界上αGB的形成,实现晶界被α相润湿,说明晶界不仅可被液相润湿,也可被第二相固相润湿[25].α会优先在β晶界析出,这是由于此类位置α相的形核激活能低.由图可知,位于三岔晶界的α核在约t=50 s时间步开始生长;在t=65 s,由于噪声的作用,αGB开始以连续的颗粒形状沿着β晶界析出,扩展后形成一薄层镶嵌在β晶界间;而且,此时只有很少的β/β晶界还未被αGB润湿.然后,当t≥50 s时,αGB同时在三岔晶界和β晶界处形核和生长.因此,出现了混合的α (αGB+αp)形貌,这种组织与他人实验中的结果[26,27]类似.如图1d所示,最终的组织为β基体、等轴αp相和αGB的共存体.整体上,沿β晶界在空间中形成了αGB网结构.当α相与β晶界接触时,在三岔晶界上的α核倾向于形成不规则带“触角”的圆形.这种形貌的形成主要是由于形核驱动力和β界面表面张力以及晶界扩散的作用所致.这种α相带触角的形貌类似于Nag等[28]的Ti-15Mo合金中α相在β三岔晶界析出的实验结果.总之,特殊构造的噪声项不仅可以促进三岔晶界上αGB的非均匀形核,而且可以激发在普通界面上αGB的晶界润湿相变,这与Kundin等[21]的Al-Cu-Ni合金中在能量有利点上噪声促进析出相的非均匀形核相似.也有研究[29]表明在最初的析出期间,αGB不仅在三岔晶界周围优先沉淀,也在β晶界的中间离散地形核,这与本工作的模拟结果相符.三岔晶界和β晶界由于结构的特殊性,显著降低了析出相形核的势垒,易在此类位置产生成分起伏以及富集杂质,均为形核的优先位置[30]. ...
Deformation and diffusion modes in nanocrystalline materials
1
2005
... 在二维空间使用Euler法解方程(4)和(6),模拟体系尺寸为,对应实际边长114.48 μm.采用Euler算法和反周期性边界条件.相变温度T=1213 K,过冷度ΔT=55 K.合金组织中的三岔点为特殊位置[22],能量高,有利于非均匀形核过程的进行.因此,预先随机在三叉晶界上放入12个核作为反应先驱体以激发αGB的形核,进而实现α相在β/β界面上的晶界润湿相变,噪声可来源于实际中的各种涨落[23].模拟中参数设置如表1所示. ...
New coarse-grained derivation of a phase field model for precipitation
1
2008
... 在二维空间使用Euler法解方程(4)和(6),模拟体系尺寸为,对应实际边长114.48 μm.采用Euler算法和反周期性边界条件.相变温度T=1213 K,过冷度ΔT=55 K.合金组织中的三岔点为特殊位置[22],能量高,有利于非均匀形核过程的进行.因此,预先随机在三叉晶界上放入12个核作为反应先驱体以激发αGB的形核,进而实现α相在β/β界面上的晶界润湿相变,噪声可来源于实际中的各种涨落[23].模拟中参数设置如表1所示. ...
Modelling polycrystalline solidification using phase field theory
1
2004
... 图1所示为1213 K下Ti-6Al-4V合金β→α相变组织演化的模拟结果,其中部分三岔点处预设α相核,长大后相当于前序热加工形成的少量初生α相(primary α,αP).模拟过冷度ΔT=55 K,噪声强度ξnoise=0.05,噪声时间tnoise=50 s.初始组织即为图1a所示的随机在β三岔晶界上放入12个不同尺寸的α相核,以作为先驱体激发部分界面反应生成[24].噪声项的存在降低了界面稳定性[5],不仅促进了α相在其它三岔点处的非均匀形核,也激发了晶界上αGB的形成,实现晶界被α相润湿,说明晶界不仅可被液相润湿,也可被第二相固相润湿[25].α会优先在β晶界析出,这是由于此类位置α相的形核激活能低.由图可知,位于三岔晶界的α核在约t=50 s时间步开始生长;在t=65 s,由于噪声的作用,αGB开始以连续的颗粒形状沿着β晶界析出,扩展后形成一薄层镶嵌在β晶界间;而且,此时只有很少的β/β晶界还未被αGB润湿.然后,当t≥50 s时,αGB同时在三岔晶界和β晶界处形核和生长.因此,出现了混合的α (αGB+αp)形貌,这种组织与他人实验中的结果[26,27]类似.如图1d所示,最终的组织为β基体、等轴αp相和αGB的共存体.整体上,沿β晶界在空间中形成了αGB网结构.当α相与β晶界接触时,在三岔晶界上的α核倾向于形成不规则带“触角”的圆形.这种形貌的形成主要是由于形核驱动力和β界面表面张力以及晶界扩散的作用所致.这种α相带触角的形貌类似于Nag等[28]的Ti-15Mo合金中α相在β三岔晶界析出的实验结果.总之,特殊构造的噪声项不仅可以促进三岔晶界上αGB的非均匀形核,而且可以激发在普通界面上αGB的晶界润湿相变,这与Kundin等[21]的Al-Cu-Ni合金中在能量有利点上噪声促进析出相的非均匀形核相似.也有研究[29]表明在最初的析出期间,αGB不仅在三岔晶界周围优先沉淀,也在β晶界的中间离散地形核,这与本工作的模拟结果相符.三岔晶界和β晶界由于结构的特殊性,显著降低了析出相形核的势垒,易在此类位置产生成分起伏以及富集杂质,均为形核的优先位置[30]. ...
Solid-state wetting transitions at grain boundaries
1
2008
... 图1所示为1213 K下Ti-6Al-4V合金β→α相变组织演化的模拟结果,其中部分三岔点处预设α相核,长大后相当于前序热加工形成的少量初生α相(primary α,αP).模拟过冷度ΔT=55 K,噪声强度ξnoise=0.05,噪声时间tnoise=50 s.初始组织即为图1a所示的随机在β三岔晶界上放入12个不同尺寸的α相核,以作为先驱体激发部分界面反应生成[24].噪声项的存在降低了界面稳定性[5],不仅促进了α相在其它三岔点处的非均匀形核,也激发了晶界上αGB的形成,实现晶界被α相润湿,说明晶界不仅可被液相润湿,也可被第二相固相润湿[25].α会优先在β晶界析出,这是由于此类位置α相的形核激活能低.由图可知,位于三岔晶界的α核在约t=50 s时间步开始生长;在t=65 s,由于噪声的作用,αGB开始以连续的颗粒形状沿着β晶界析出,扩展后形成一薄层镶嵌在β晶界间;而且,此时只有很少的β/β晶界还未被αGB润湿.然后,当t≥50 s时,αGB同时在三岔晶界和β晶界处形核和生长.因此,出现了混合的α (αGB+αp)形貌,这种组织与他人实验中的结果[26,27]类似.如图1d所示,最终的组织为β基体、等轴αp相和αGB的共存体.整体上,沿β晶界在空间中形成了αGB网结构.当α相与β晶界接触时,在三岔晶界上的α核倾向于形成不规则带“触角”的圆形.这种形貌的形成主要是由于形核驱动力和β界面表面张力以及晶界扩散的作用所致.这种α相带触角的形貌类似于Nag等[28]的Ti-15Mo合金中α相在β三岔晶界析出的实验结果.总之,特殊构造的噪声项不仅可以促进三岔晶界上αGB的非均匀形核,而且可以激发在普通界面上αGB的晶界润湿相变,这与Kundin等[21]的Al-Cu-Ni合金中在能量有利点上噪声促进析出相的非均匀形核相似.也有研究[29]表明在最初的析出期间,αGB不仅在三岔晶界周围优先沉淀,也在β晶界的中间离散地形核,这与本工作的模拟结果相符.三岔晶界和β晶界由于结构的特殊性,显著降低了析出相形核的势垒,易在此类位置产生成分起伏以及富集杂质,均为形核的优先位置[30]. ...
Heat-treatment effects on the microstructure and tensile properties of powder metallurgy Ti-6Al-4V alloys modified with boron
1
2010
... 图1所示为1213 K下Ti-6Al-4V合金β→α相变组织演化的模拟结果,其中部分三岔点处预设α相核,长大后相当于前序热加工形成的少量初生α相(primary α,αP).模拟过冷度ΔT=55 K,噪声强度ξnoise=0.05,噪声时间tnoise=50 s.初始组织即为图1a所示的随机在β三岔晶界上放入12个不同尺寸的α相核,以作为先驱体激发部分界面反应生成[24].噪声项的存在降低了界面稳定性[5],不仅促进了α相在其它三岔点处的非均匀形核,也激发了晶界上αGB的形成,实现晶界被α相润湿,说明晶界不仅可被液相润湿,也可被第二相固相润湿[25].α会优先在β晶界析出,这是由于此类位置α相的形核激活能低.由图可知,位于三岔晶界的α核在约t=50 s时间步开始生长;在t=65 s,由于噪声的作用,αGB开始以连续的颗粒形状沿着β晶界析出,扩展后形成一薄层镶嵌在β晶界间;而且,此时只有很少的β/β晶界还未被αGB润湿.然后,当t≥50 s时,αGB同时在三岔晶界和β晶界处形核和生长.因此,出现了混合的α (αGB+αp)形貌,这种组织与他人实验中的结果[26,27]类似.如图1d所示,最终的组织为β基体、等轴αp相和αGB的共存体.整体上,沿β晶界在空间中形成了αGB网结构.当α相与β晶界接触时,在三岔晶界上的α核倾向于形成不规则带“触角”的圆形.这种形貌的形成主要是由于形核驱动力和β界面表面张力以及晶界扩散的作用所致.这种α相带触角的形貌类似于Nag等[28]的Ti-15Mo合金中α相在β三岔晶界析出的实验结果.总之,特殊构造的噪声项不仅可以促进三岔晶界上αGB的非均匀形核,而且可以激发在普通界面上αGB的晶界润湿相变,这与Kundin等[21]的Al-Cu-Ni合金中在能量有利点上噪声促进析出相的非均匀形核相似.也有研究[29]表明在最初的析出期间,αGB不仅在三岔晶界周围优先沉淀,也在β晶界的中间离散地形核,这与本工作的模拟结果相符.三岔晶界和β晶界由于结构的特殊性,显著降低了析出相形核的势垒,易在此类位置产生成分起伏以及富集杂质,均为形核的优先位置[30]. ...
Effect of aging heat treatment on microstructure and tensile properties of a new β high strength titanium alloy
1
2014
... 图1所示为1213 K下Ti-6Al-4V合金β→α相变组织演化的模拟结果,其中部分三岔点处预设α相核,长大后相当于前序热加工形成的少量初生α相(primary α,αP).模拟过冷度ΔT=55 K,噪声强度ξnoise=0.05,噪声时间tnoise=50 s.初始组织即为图1a所示的随机在β三岔晶界上放入12个不同尺寸的α相核,以作为先驱体激发部分界面反应生成[24].噪声项的存在降低了界面稳定性[5],不仅促进了α相在其它三岔点处的非均匀形核,也激发了晶界上αGB的形成,实现晶界被α相润湿,说明晶界不仅可被液相润湿,也可被第二相固相润湿[25].α会优先在β晶界析出,这是由于此类位置α相的形核激活能低.由图可知,位于三岔晶界的α核在约t=50 s时间步开始生长;在t=65 s,由于噪声的作用,αGB开始以连续的颗粒形状沿着β晶界析出,扩展后形成一薄层镶嵌在β晶界间;而且,此时只有很少的β/β晶界还未被αGB润湿.然后,当t≥50 s时,αGB同时在三岔晶界和β晶界处形核和生长.因此,出现了混合的α (αGB+αp)形貌,这种组织与他人实验中的结果[26,27]类似.如图1d所示,最终的组织为β基体、等轴αp相和αGB的共存体.整体上,沿β晶界在空间中形成了αGB网结构.当α相与β晶界接触时,在三岔晶界上的α核倾向于形成不规则带“触角”的圆形.这种形貌的形成主要是由于形核驱动力和β界面表面张力以及晶界扩散的作用所致.这种α相带触角的形貌类似于Nag等[28]的Ti-15Mo合金中α相在β三岔晶界析出的实验结果.总之,特殊构造的噪声项不仅可以促进三岔晶界上αGB的非均匀形核,而且可以激发在普通界面上αGB的晶界润湿相变,这与Kundin等[21]的Al-Cu-Ni合金中在能量有利点上噪声促进析出相的非均匀形核相似.也有研究[29]表明在最初的析出期间,αGB不仅在三岔晶界周围优先沉淀,也在β晶界的中间离散地形核,这与本工作的模拟结果相符.三岔晶界和β晶界由于结构的特殊性,显著降低了析出相形核的势垒,易在此类位置产生成分起伏以及富集杂质,均为形核的优先位置[30]. ...
Comparison of microstructural evolution in Ti-Mo-Zr-Fe and Ti-15Mo biocompatible alloys
1
2005
... 图1所示为1213 K下Ti-6Al-4V合金β→α相变组织演化的模拟结果,其中部分三岔点处预设α相核,长大后相当于前序热加工形成的少量初生α相(primary α,αP).模拟过冷度ΔT=55 K,噪声强度ξnoise=0.05,噪声时间tnoise=50 s.初始组织即为图1a所示的随机在β三岔晶界上放入12个不同尺寸的α相核,以作为先驱体激发部分界面反应生成[24].噪声项的存在降低了界面稳定性[5],不仅促进了α相在其它三岔点处的非均匀形核,也激发了晶界上αGB的形成,实现晶界被α相润湿,说明晶界不仅可被液相润湿,也可被第二相固相润湿[25].α会优先在β晶界析出,这是由于此类位置α相的形核激活能低.由图可知,位于三岔晶界的α核在约t=50 s时间步开始生长;在t=65 s,由于噪声的作用,αGB开始以连续的颗粒形状沿着β晶界析出,扩展后形成一薄层镶嵌在β晶界间;而且,此时只有很少的β/β晶界还未被αGB润湿.然后,当t≥50 s时,αGB同时在三岔晶界和β晶界处形核和生长.因此,出现了混合的α (αGB+αp)形貌,这种组织与他人实验中的结果[26,27]类似.如图1d所示,最终的组织为β基体、等轴αp相和αGB的共存体.整体上,沿β晶界在空间中形成了αGB网结构.当α相与β晶界接触时,在三岔晶界上的α核倾向于形成不规则带“触角”的圆形.这种形貌的形成主要是由于形核驱动力和β界面表面张力以及晶界扩散的作用所致.这种α相带触角的形貌类似于Nag等[28]的Ti-15Mo合金中α相在β三岔晶界析出的实验结果.总之,特殊构造的噪声项不仅可以促进三岔晶界上αGB的非均匀形核,而且可以激发在普通界面上αGB的晶界润湿相变,这与Kundin等[21]的Al-Cu-Ni合金中在能量有利点上噪声促进析出相的非均匀形核相似.也有研究[29]表明在最初的析出期间,αGB不仅在三岔晶界周围优先沉淀,也在β晶界的中间离散地形核,这与本工作的模拟结果相符.三岔晶界和β晶界由于结构的特殊性,显著降低了析出相形核的势垒,易在此类位置产生成分起伏以及富集杂质,均为形核的优先位置[30]. ...
A unified growth model of the secondary grain boundary α phase in TA15 Ti-alloy
1
2016
... 图1所示为1213 K下Ti-6Al-4V合金β→α相变组织演化的模拟结果,其中部分三岔点处预设α相核,长大后相当于前序热加工形成的少量初生α相(primary α,αP).模拟过冷度ΔT=55 K,噪声强度ξnoise=0.05,噪声时间tnoise=50 s.初始组织即为图1a所示的随机在β三岔晶界上放入12个不同尺寸的α相核,以作为先驱体激发部分界面反应生成[24].噪声项的存在降低了界面稳定性[5],不仅促进了α相在其它三岔点处的非均匀形核,也激发了晶界上αGB的形成,实现晶界被α相润湿,说明晶界不仅可被液相润湿,也可被第二相固相润湿[25].α会优先在β晶界析出,这是由于此类位置α相的形核激活能低.由图可知,位于三岔晶界的α核在约t=50 s时间步开始生长;在t=65 s,由于噪声的作用,αGB开始以连续的颗粒形状沿着β晶界析出,扩展后形成一薄层镶嵌在β晶界间;而且,此时只有很少的β/β晶界还未被αGB润湿.然后,当t≥50 s时,αGB同时在三岔晶界和β晶界处形核和生长.因此,出现了混合的α (αGB+αp)形貌,这种组织与他人实验中的结果[26,27]类似.如图1d所示,最终的组织为β基体、等轴αp相和αGB的共存体.整体上,沿β晶界在空间中形成了αGB网结构.当α相与β晶界接触时,在三岔晶界上的α核倾向于形成不规则带“触角”的圆形.这种形貌的形成主要是由于形核驱动力和β界面表面张力以及晶界扩散的作用所致.这种α相带触角的形貌类似于Nag等[28]的Ti-15Mo合金中α相在β三岔晶界析出的实验结果.总之,特殊构造的噪声项不仅可以促进三岔晶界上αGB的非均匀形核,而且可以激发在普通界面上αGB的晶界润湿相变,这与Kundin等[21]的Al-Cu-Ni合金中在能量有利点上噪声促进析出相的非均匀形核相似.也有研究[29]表明在最初的析出期间,αGB不仅在三岔晶界周围优先沉淀,也在β晶界的中间离散地形核,这与本工作的模拟结果相符.三岔晶界和β晶界由于结构的特殊性,显著降低了析出相形核的势垒,易在此类位置产生成分起伏以及富集杂质,均为形核的优先位置[30]. ...
An analytical study of the static state of multi-junctions in a multi-phase field model
1
2011
... 图1所示为1213 K下Ti-6Al-4V合金β→α相变组织演化的模拟结果,其中部分三岔点处预设α相核,长大后相当于前序热加工形成的少量初生α相(primary α,αP).模拟过冷度ΔT=55 K,噪声强度ξnoise=0.05,噪声时间tnoise=50 s.初始组织即为图1a所示的随机在β三岔晶界上放入12个不同尺寸的α相核,以作为先驱体激发部分界面反应生成[24].噪声项的存在降低了界面稳定性[5],不仅促进了α相在其它三岔点处的非均匀形核,也激发了晶界上αGB的形成,实现晶界被α相润湿,说明晶界不仅可被液相润湿,也可被第二相固相润湿[25].α会优先在β晶界析出,这是由于此类位置α相的形核激活能低.由图可知,位于三岔晶界的α核在约t=50 s时间步开始生长;在t=65 s,由于噪声的作用,αGB开始以连续的颗粒形状沿着β晶界析出,扩展后形成一薄层镶嵌在β晶界间;而且,此时只有很少的β/β晶界还未被αGB润湿.然后,当t≥50 s时,αGB同时在三岔晶界和β晶界处形核和生长.因此,出现了混合的α (αGB+αp)形貌,这种组织与他人实验中的结果[26,27]类似.如图1d所示,最终的组织为β基体、等轴αp相和αGB的共存体.整体上,沿β晶界在空间中形成了αGB网结构.当α相与β晶界接触时,在三岔晶界上的α核倾向于形成不规则带“触角”的圆形.这种形貌的形成主要是由于形核驱动力和β界面表面张力以及晶界扩散的作用所致.这种α相带触角的形貌类似于Nag等[28]的Ti-15Mo合金中α相在β三岔晶界析出的实验结果.总之,特殊构造的噪声项不仅可以促进三岔晶界上αGB的非均匀形核,而且可以激发在普通界面上αGB的晶界润湿相变,这与Kundin等[21]的Al-Cu-Ni合金中在能量有利点上噪声促进析出相的非均匀形核相似.也有研究[29]表明在最初的析出期间,αGB不仅在三岔晶界周围优先沉淀,也在β晶界的中间离散地形核,这与本工作的模拟结果相符.三岔晶界和β晶界由于结构的特殊性,显著降低了析出相形核的势垒,易在此类位置产生成分起伏以及富集杂质,均为形核的优先位置[30]. ...
Calculation of diffusion penetration curves for surface and grain boundary diffusion
1
1951
... 图3为αGB的模拟组织放大图及对应的Al和V的浓度分布.穿过一个三岔晶界α和2个αGB的直线AB上的Al和V浓度如图3b所示.由图可知,α相中的Al和V浓度大体上保持不变,且均与α和β相中平衡浓度接近.然而,当直线AB穿过β晶粒时,β与α相界上的Al浓度比β晶粒中心区域高,这使得β晶粒中的Al浓度形成类似“拱门”形状;与之相反,V浓度分布与Al的走势相反.伴随着αGB的形成,α稳定元素(Al和O)从β相的邻近区域扩散到α相中[14],使晶界附近的β相中Al浓度降低,而晶内的Al还来不及达到平衡浓度.此外,实验上固相中沿着晶界和自由表面的扩散比晶内扩散要快得多[31].这就解释了Al浓度“拱门”的现象.而且,β晶粒中的V浓度比平衡浓度略低,也是由于扩散不充分所致. ...
Influence of continuous grain boundary α on ductility of laser melting deposited titanium alloys
1
2016
... 连续状αGB在近β和β钛合金中普遍存在,且损害合金的延展性[32,33,34].一般情况下,αGB通常会呈现连续的层状形貌,这是由于在β→α相变过程中α相优先在β晶界形核与长大.随着αGB的生成,α稳定元素(Al和O)从相邻区域扩散到αGB中,因而此处β相随后被稳定.这在一定程度上阻碍了具有细密强化作用的次生αs (secondary α)的生成,导致沿αGB形成较软的无析出相区(precipitate free zone,PFZ)[35,36].然后,在软化的PFZ和强化β基体间的高屈服应力差极易导致最初的裂纹形核[9,37].同时,由于PFZ为连续的且分布广泛,疲劳裂纹自然地沿连续的αGB开裂和增殖,继而导致沿晶断裂和低延展性[33,35].与之相反,如果αGB是不连续的,间断的αGB间细密的αs会阻碍沿晶界的裂纹扩展,因此导致穿晶断裂,进而提高延展性[36].因此,获得不连续的αGB组织对于提高钛合金的延展性能十分重要. ...
Beta heat treatment of laser melting deposited high strength near β titanium alloy
2
2016
... 连续状αGB在近β和β钛合金中普遍存在,且损害合金的延展性[32,33,34].一般情况下,αGB通常会呈现连续的层状形貌,这是由于在β→α相变过程中α相优先在β晶界形核与长大.随着αGB的生成,α稳定元素(Al和O)从相邻区域扩散到αGB中,因而此处β相随后被稳定.这在一定程度上阻碍了具有细密强化作用的次生αs (secondary α)的生成,导致沿αGB形成较软的无析出相区(precipitate free zone,PFZ)[35,36].然后,在软化的PFZ和强化β基体间的高屈服应力差极易导致最初的裂纹形核[9,37].同时,由于PFZ为连续的且分布广泛,疲劳裂纹自然地沿连续的αGB开裂和增殖,继而导致沿晶断裂和低延展性[33,35].与之相反,如果αGB是不连续的,间断的αGB间细密的αs会阻碍沿晶界的裂纹扩展,因此导致穿晶断裂,进而提高延展性[36].因此,获得不连续的αGB组织对于提高钛合金的延展性能十分重要. ...
... [33,35].与之相反,如果αGB是不连续的,间断的αGB间细密的αs会阻碍沿晶界的裂纹扩展,因此导致穿晶断裂,进而提高延展性[36].因此,获得不连续的αGB组织对于提高钛合金的延展性能十分重要. ...
Formation of grain boundary α in β Ti alloys: Its role in deformation and fracture behavior of these alloys
1
2011
... 连续状αGB在近β和β钛合金中普遍存在,且损害合金的延展性[32,33,34].一般情况下,αGB通常会呈现连续的层状形貌,这是由于在β→α相变过程中α相优先在β晶界形核与长大.随着αGB的生成,α稳定元素(Al和O)从相邻区域扩散到αGB中,因而此处β相随后被稳定.这在一定程度上阻碍了具有细密强化作用的次生αs (secondary α)的生成,导致沿αGB形成较软的无析出相区(precipitate free zone,PFZ)[35,36].然后,在软化的PFZ和强化β基体间的高屈服应力差极易导致最初的裂纹形核[9,37].同时,由于PFZ为连续的且分布广泛,疲劳裂纹自然地沿连续的αGB开裂和增殖,继而导致沿晶断裂和低延展性[33,35].与之相反,如果αGB是不连续的,间断的αGB间细密的αs会阻碍沿晶界的裂纹扩展,因此导致穿晶断裂,进而提高延展性[36].因此,获得不连续的αGB组织对于提高钛合金的延展性能十分重要. ...
The influence of soft, precipitate-free zones at grain boundaries in Ti and Al alloys on their fatigue and fracture behavior
2
2007
... 连续状αGB在近β和β钛合金中普遍存在,且损害合金的延展性[32,33,34].一般情况下,αGB通常会呈现连续的层状形貌,这是由于在β→α相变过程中α相优先在β晶界形核与长大.随着αGB的生成,α稳定元素(Al和O)从相邻区域扩散到αGB中,因而此处β相随后被稳定.这在一定程度上阻碍了具有细密强化作用的次生αs (secondary α)的生成,导致沿αGB形成较软的无析出相区(precipitate free zone,PFZ)[35,36].然后,在软化的PFZ和强化β基体间的高屈服应力差极易导致最初的裂纹形核[9,37].同时,由于PFZ为连续的且分布广泛,疲劳裂纹自然地沿连续的αGB开裂和增殖,继而导致沿晶断裂和低延展性[33,35].与之相反,如果αGB是不连续的,间断的αGB间细密的αs会阻碍沿晶界的裂纹扩展,因此导致穿晶断裂,进而提高延展性[36].因此,获得不连续的αGB组织对于提高钛合金的延展性能十分重要. ...
... ,35].与之相反,如果αGB是不连续的,间断的αGB间细密的αs会阻碍沿晶界的裂纹扩展,因此导致穿晶断裂,进而提高延展性[36].因此,获得不连续的αGB组织对于提高钛合金的延展性能十分重要. ...
The significant effects of the alkali-metal cations on ZSM-5 zeolite synthesis: From mechanism to morphology
2
2014
... 连续状αGB在近β和β钛合金中普遍存在,且损害合金的延展性[32,33,34].一般情况下,αGB通常会呈现连续的层状形貌,这是由于在β→α相变过程中α相优先在β晶界形核与长大.随着αGB的生成,α稳定元素(Al和O)从相邻区域扩散到αGB中,因而此处β相随后被稳定.这在一定程度上阻碍了具有细密强化作用的次生αs (secondary α)的生成,导致沿αGB形成较软的无析出相区(precipitate free zone,PFZ)[35,36].然后,在软化的PFZ和强化β基体间的高屈服应力差极易导致最初的裂纹形核[9,37].同时,由于PFZ为连续的且分布广泛,疲劳裂纹自然地沿连续的αGB开裂和增殖,继而导致沿晶断裂和低延展性[33,35].与之相反,如果αGB是不连续的,间断的αGB间细密的αs会阻碍沿晶界的裂纹扩展,因此导致穿晶断裂,进而提高延展性[36].因此,获得不连续的αGB组织对于提高钛合金的延展性能十分重要. ...
... [36].因此,获得不连续的αGB组织对于提高钛合金的延展性能十分重要. ...
High-cycle fatigue crack initiation and propagation in laser melting deposited TC18 titanium alloy
1
2013
... 连续状αGB在近β和β钛合金中普遍存在,且损害合金的延展性[32,33,34].一般情况下,αGB通常会呈现连续的层状形貌,这是由于在β→α相变过程中α相优先在β晶界形核与长大.随着αGB的生成,α稳定元素(Al和O)从相邻区域扩散到αGB中,因而此处β相随后被稳定.这在一定程度上阻碍了具有细密强化作用的次生αs (secondary α)的生成,导致沿αGB形成较软的无析出相区(precipitate free zone,PFZ)[35,36].然后,在软化的PFZ和强化β基体间的高屈服应力差极易导致最初的裂纹形核[9,37].同时,由于PFZ为连续的且分布广泛,疲劳裂纹自然地沿连续的αGB开裂和增殖,继而导致沿晶断裂和低延展性[33,35].与之相反,如果αGB是不连续的,间断的αGB间细密的αs会阻碍沿晶界的裂纹扩展,因此导致穿晶断裂,进而提高延展性[36].因此,获得不连续的αGB组织对于提高钛合金的延展性能十分重要. ...
Grain boundary wetting transition in Al-Mg alloys
1
2017
... 晶界润湿相变有2种形式:当晶界与第二相的接触角为0°时,为完全润湿,此种情况下第二相可完全覆盖晶界;反之,当晶界与第二相的接触角不为0°时,为不完全润湿,此情况下晶界与第二相平衡共存[38].通过图4和5对αGB晶界润湿相变过程的再现,可推断第二相固相的晶界润湿由不完全润湿到完全润湿是一个过程,即在噪声的作用下,晶界上离散独立的第二相固相通过长大和粗化最终会相互连接,直至完全覆盖晶界,在此过程中并未发生其它相变.由图4b到c或图5c到d过程可知,在不完全润湿状态下,当第二相固相继续长大至首尾相连时,β晶界即完全被α相占据,达到完全润湿状态,如图6所示.这与Protasova等[39]得出的Al-Zn合金中由不连续润湿到连续润湿可由降低温度实现,而不需在基体中发生额外反应的结论是相似的. ...
Inversed solid-phase grain boundary wetting in the Al-Zn system
1
2011
... 晶界润湿相变有2种形式:当晶界与第二相的接触角为0°时,为完全润湿,此种情况下第二相可完全覆盖晶界;反之,当晶界与第二相的接触角不为0°时,为不完全润湿,此情况下晶界与第二相平衡共存[38].通过图4和5对αGB晶界润湿相变过程的再现,可推断第二相固相的晶界润湿由不完全润湿到完全润湿是一个过程,即在噪声的作用下,晶界上离散独立的第二相固相通过长大和粗化最终会相互连接,直至完全覆盖晶界,在此过程中并未发生其它相变.由图4b到c或图5c到d过程可知,在不完全润湿状态下,当第二相固相继续长大至首尾相连时,β晶界即完全被α相占据,达到完全润湿状态,如图6所示.这与Protasova等[39]得出的Al-Zn合金中由不连续润湿到连续润湿可由降低温度实现,而不需在基体中发生额外反应的结论是相似的. ...
Dependence of dendritic side-branches on parameters in phase-field simulations
1
2005
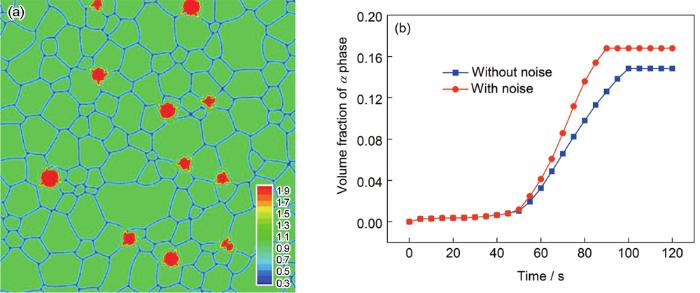
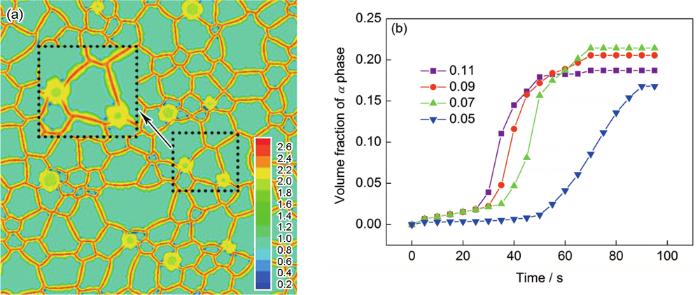
... 噪声的强度ξnoise如果设置得当,会对温度场产生明显影响[40],怎样选取噪声强度取决于实际应用条件.因此,选择ξnoise分别为0.05、0.07、0.09和0.11,以探究噪声强度对组织形成的作用.模拟表明,一定温度条件下,只有ξnoise≥0.05的噪声才能扰乱系统稳定性,产生α相的形核效果;然而,当ξnoise≥0.11时,平衡α相分数会低于理论值16%,这可能意味着大于0.11的噪声强度会抑制α相的生成.ξnoise=0.11的模拟组织如图7a所示.结果表明高噪声强度条件下,αGB倾向于形成连续平直层状结构.换句话说,高噪声强度会促进晶界润湿相变的进行,导致初始在β晶界上形核的α颗粒较多,即αGB会按照图4中所示的机制生长,因而导致了粗化的连续αGB形貌.如上所述,连续的αGB不利于合金延展性能.图7a与图3a中相同部位的局部放大图表明,不同的噪声强度也会产生不同形态的αGB.与高噪声强度的结果相比,当噪声强度较小的时候,αGB倾向于生长为凸透镜状,连续性较差,而且由于实际中的应力作用等外界因素,此种形貌的αGB较易被打断成不连续形态.图7b所示为不同噪声强度(0.05≤ξnoise≤0.11)对α相体积分数随时间演化的影响,结果表明ξnoise的提高加快了α相的生长速率,所以高噪声强度条件下的相变率先达到了平衡状态,减少了β→α相变的时间.值得注意的是,当ξnoise≥0.07时,α相平衡体积分数随噪声强度的升高而降低.噪声强度ξnoise从0.07升至0.11,α相平衡体积分数约从22%降低到17%.推测是由于较高的噪声强度系统率先达到平衡状态,当系统平衡时,生成相α基本保持原样不再生长,α相体积分数不再增加,因此高噪声强度导致了低α相的平衡体积分数.综上所述,想获得不连续的αGB,应在合理范围内尽量将噪声强度调低. ...
Modeling elasticity in crystal growth
1
2002
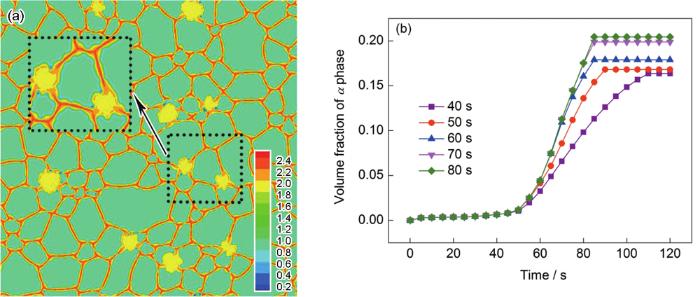
... 上述相场模拟结果表明,低噪声强度和短噪声时间均有利于不连续αGB的生成.即实际系统中的各种涨落在合理的范围内尽量小,以便可生成不连续αGB.有研究[41]认为噪声强度正比于温度的平方,即.也有报道[42]称温度可决定生成连续或是不连续形貌的αGB.因此,可理解为在符合工艺需求的情况下,尽量低的热处理温度或通过变形产生一些局部涨落,促进α相形核,会生成有利于延展性的不连续αGB. ...
Continuous and discontinuous grain-boundary wetting in ZnxAl1-x
1
2008
... 上述相场模拟结果表明,低噪声强度和短噪声时间均有利于不连续αGB的生成.即实际系统中的各种涨落在合理的范围内尽量小,以便可生成不连续αGB.有研究[41]认为噪声强度正比于温度的平方,即.也有报道[42]称温度可决定生成连续或是不连续形貌的αGB.因此,可理解为在符合工艺需求的情况下,尽量低的热处理温度或通过变形产生一些局部涨落,促进α相形核,会生成有利于延展性的不连续αGB. ...
Investigation of the heterogeneous nucleation in a peritectic AlNi alloy
1
2011
... 有报道[43]称差热扫描量热法(DSC)实验可以测量二元AlNi合金的形核速率和形核动力学,以优化相场模型中的参数,进而将噪声时间与反应时间联系起来,以指导实验中有利于疲劳性能的不连续αGB的生成.此外,由差热分析(DTA)实验数据和相场模型中得出的Al-Cu-Ni合金凝固过程的相分数吻合良好[44].因此,使用DSC和DTA曲线实验方法获得相变动力学信息,在此基础上进行有关相场中噪声强度与实验参数的拟合,并根据模拟获得的规律制定更合理的有利于析出不连续αGB的热处理制度,将具有重要探索价值. ...
Investigation of Al-Cu-Ni alloy solidification: Thermodynamics, experiments and phase-field modeling
1
2014
... 有报道[43]称差热扫描量热法(DSC)实验可以测量二元AlNi合金的形核速率和形核动力学,以优化相场模型中的参数,进而将噪声时间与反应时间联系起来,以指导实验中有利于疲劳性能的不连续αGB的生成.此外,由差热分析(DTA)实验数据和相场模型中得出的Al-Cu-Ni合金凝固过程的相分数吻合良好[44].因此,使用DSC和DTA曲线实验方法获得相变动力学信息,在此基础上进行有关相场中噪声强度与实验参数的拟合,并根据模拟获得的规律制定更合理的有利于析出不连续αGB的热处理制度,将具有重要探索价值. ...