随着现代科学技术的进步和发展,社会各领域对材料性能的要求不断提升,复合材料由于能够发挥组元材料各自的优势[1 ,2 ] ,表现出优异的内在和外在特性,因此被广泛应用到汽车、航空航天、医疗仪器、船舶、电力等领域[3 ] 。界面作为复合材料中普遍存在且非常重要的组成部分,也是复合材料实现其优异的综合性能的关键性因素[4 ,5 ] 。
界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] 。这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] 。除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律。
解析法作为科学实验中常用的一种方法,能够定量描述各物理量之间的函数关系,通过研究函数性质,使各物理量的变化规律更加清晰[16 ] 。同时,与实验法相比,解析法不受时间和空间条件的影响,能够节约大量的经济成本。在复合材料界面结合强度的解析计算过程中,主要是借助数学模型,通过层间的各向应力建立各物理量之间的联系,故界面强度解析的关键是建立合理的数学模型和应用适当的计算方法。目前,复合材料界面强度问题的解析思路大多是在断裂力学的基础上发展起来的,断裂力学主要从应力强度因子角度出发提出预测模型对界面强度进行评估,随着研究的深入,越来越多的学者在解析方法和数学模型上不断地进行改进。在最初的研究中,Dvorak等[17 ,18 ] 对弹性纤维复合材料的层间开裂进行了研究,基于断裂力学对复合材料在开裂过程中的开裂位移与外部载荷的关系以及应力应变情况进行了解析,并研究了这些物理量与界面结合强度的关系,虽然没有直接获得界面结合强度,但为接下来的工作做了铺垫。在此基础上,Reedy和Guess[19 ] 提出了基于广义应力强度因子的失效模型,讨论了对接界面角应力场的渐近形式。并通过与临界值作比较预测对接接头的结合强度,最后依据断裂准则推导出对接界面的拉伸强度与黏结厚度之间的函数关系。Adams[20 ] 对黏合剂黏接的复合材料进行强度评估,通过计算黏合剂层的应力应变并各自与临界值进行比较,从而评估复合材料的结合强度。这种方法对黏接复合材料的界面结合强度进行了成功的预测,但计算结果受材料几何参数的影响。为了解决这一问题,Dun等[21 ] 通过研究搭接接头界面缺口处的裂纹,同时考虑应力和能量平衡问题,成功地预测了界面结合强度,这种方法仅需要材料的强度和韧性,不受几何参数的限制。为了进一步提高计算精度,Maimí等[22 ,23 ] 针对层合板复合材料提出了一种连续体损伤模型,基于强度失效准则预测了层内失效机制,并通过建立断裂韧性、弹性模量和强度的函数关系式计算了层间破坏应力,最后通过实验验证了结论的准确性,该方法在建立损伤模型的基础上通过计算断裂韧性和层间破坏应力等参数来表征层合板界面强度。以上在解析过程中所建立的数学模型对研究复合材料界面层的损伤机制和裂纹扩展有着很大的帮助,但并未直接给出界面结合强度的计算方法,同时为了进一步提高计算精度,有必要对解析模型进行优化。
在复合材料界面结合强度的表征工作上,应用梁理论将复合梁模型融入到断裂力学的计算方法中,通过建立双悬臂梁模型,计算临界能量释放率和混合模式相角等参数,用于表征复合材料界面强度[24 ] ,许多学者在这方面做了大量的工作。Bennati等[25 ~27 ] 将纤维层合板视作弹脆性界面连接,提出了混合模式弯曲测试的力学模型,并分别在I型和II型断裂模式下,依据边界条件建立多组微分方程确定界面应力、内力和位移的表达式,评估复合材料层合板混合模式下的层间断裂韧性,以此表征界面结合强度。Hua等[28 ] 分别基于梁理论和断裂力学理论推导出不同纤维取向复合材料的层间断裂能,并与有限元和实验结果进行比较,结果表明,层间断裂韧性随加载速率的增加而增加,且在实验和数值仿真中呈现出相同的规律性,但随着裂纹的扩展,理论计算与实验之间的误差逐渐增大。现有的解析方法大多针对的是纤维复合材料或者黏合连接的复合材料,忽略了界面强度高于基体的情况,这些问题使得金属复合材料界面强度的求解存在改进空间。
本工作综合应用断裂力学理论和梁理论,在考虑界面塑性变形的基础上改进原有的界面模型,提出了一种更适用于双金属复合板界面断裂韧性评估的线性强化弹塑性界面模型。首先利用该模型对界面断裂能进行解析,然后以T2/A1050 Cu-Al复合板为研究对象,通过有限元仿真模型数值分析获得准确的界面结合强度。最后将界面结合强度和断裂能应用到渐进成形有限元模型中,对解析结果进行实验验证的同时讨论界面参数在成形精度中的应用。
1 双金属复合板层间断裂能的解析
在复合板界面参数的求解过程中,常借助双悬臂梁弹性-脆性界面模型对层间断裂韧性进行解析,该模型将复合板界面简化成不同方向的线弹性弹簧连接,可用于一些复合材料混合断裂模式下的层间断裂能[25 ~27 ] 的解析,而对于爆炸焊接或者轧制方式复合的双金属复合板,界面层为上下2层金属在外界高温或高压环境下相互作用而成,简单的线弹性不能准确描述其变形情况,无法进行界面参数的解析,为了获得此类材料的界面参数,本工作基于非对称双悬臂的弹性-脆性界面模型[27 ] 进行改进,考虑界面断裂前的塑性变形情况,提出弹塑性界面模型,通过力平衡方程构建界面应力与外部载荷的关系,并结合相关力学理论对层间断裂能进行解析。同时考虑到双金属复合材料各向异性参数获取比较困难,因此将其简化成各向同性问题进行处理。
1.1 界面层本构模型的优化
双悬臂梁实验可以用于评估复合材料界面断裂韧性,Bennati等[27 ] 在纤维复合材料混合断裂模式下的断裂韧性研究中基于此实验建立了非对称性双悬臂梁实验(asymmetric double cantilever beam)模型,并通过该模型的弹性-脆性界面推导出了界面应力、位移等参数的计算公式,本工作在此基础上进行界面层本构模型的优化,完成界面参数的解析。
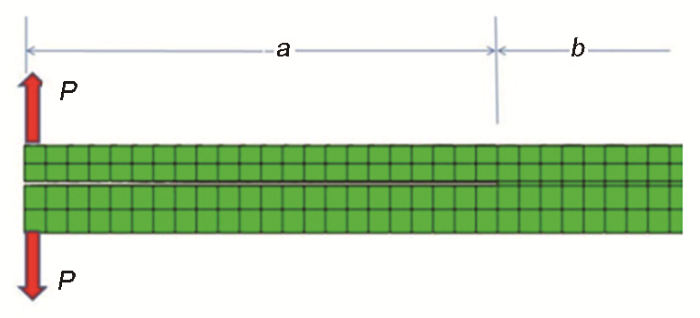
如文献[27 ]所示,该模型为长度为L 的层合板,在其一端有长度为a 的初始层间裂缝,b 为模型连接部分的长度。以界面层为分界,上下2种材料厚度分别为H 1 和H 2 ,模型的总厚度H =H 1 +H 2 (假设界面的厚度很小,可忽略不计)。模型的宽度为B ,2个方向相反的载荷P 施加在裂缝侧的末端。
在此模型中,子层合板由可变形的界面连接,该界面可视作线弹性弹簧的连续分布[27 ] 。通过线弹性弹簧特性对复合材料界面进行简化,能很好地评估一些界面结合强度不高的复合材料的结合性能,如纤维复合材料等。但由于双金属板界面为上下2层金属在外界高温或高压环境下相互作用而成,结合强度甚至有可能高于基体,界面变形情况也更为复杂,简单的线弹性不足以描述此类材料界面的变形情况。因此本工作在Bennati等[27 ] 工作的基础上,考虑界面的塑性变形情况,即将界面视作弹塑性弹簧的连续分布。
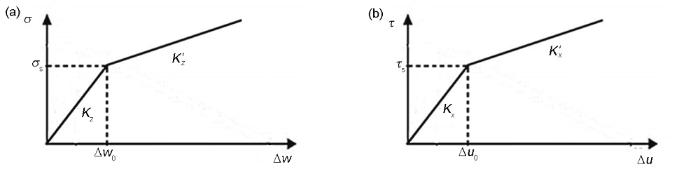
在裂纹扩展过程中,界面分别会发生拉伸变形和剪切变形。为了便于数学计算,将变形过程中的应力和位移关系简化成如图1 所示的线性弹塑性变化,其中K 和K' 分别为界面处在弹性变形阶段和塑性变形阶段的斜率,界面的断裂受混合模式裂纹扩展准则的控制,可由能量释放率表示[27 ] ,之后界面参数的公式推导过程将基于此界面模型展开。
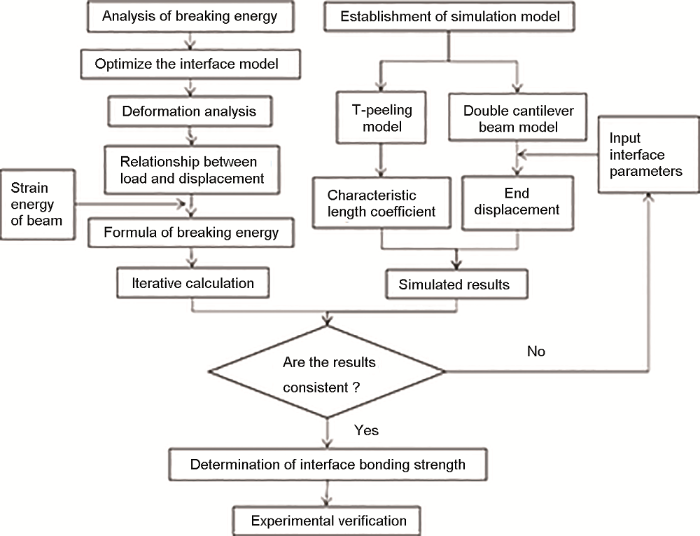
优化后的界面模型在外力作用下存在多种变形情况,且每种变形情况都对应着一种应力位移关系,在不同的应力位移状态下会求解出不同的界面断裂能解析式,为了确定准确的解析结果,需要借助仿真模型对每种情况进行判断。具体的研究思路图如图2 所示。
图1
图1
基于线性硬化假定的双线性弹塑性界面本构模型
Fig.1
Bilinear elastoplastic interface constitutive model based on linear hardening assumption in tensile direction (a) and shear direction (b) (σ —stress in the tensile direction of the interface, σ s —yield stress in the tensile direction of the interface, Δw 0 —deformation of the interface under the tensile yield state, Δw —deformation of the interface in the tensile direction, Kz —elastic stiffness coefficient in the tensile direction, K z ' τ —stress in the shear direction of the interface, τ s —yield stress in the shear direction of the interface, Δu 0 —deformation of the interface under the shear yield state, Δu —deformation of the interface in the shear direction, Kx —elastic stiffness coefficient in the shear direction, K x '
图2
图2
技术路线图
Fig.2
Technical roadmap
1.2 断裂能计算公式的推导
分析复合板界面连接部分的受力情况,可以得到层间力的平衡方程,该方程建立了外部载荷与层间内力的关系[27 ] :
d N α d s + n α = 0 , d Q α d s + q α = 0 , d M α d s + m α - Q α = 0 (1)
式中,Nα 为层间轴向内力,Qα 为层间切向内力,Mα 为层间弯矩,s 为界面裂纹扩展位移,nα 为模型宽度方向上的轴向载荷,qα 为模型宽度方向上的切向载荷,mα 为模型宽度方向上的弯矩。
根据界面模型,外力作用下,界面拉伸和剪切方向均可能发生弹性或塑性变形,因此存在多种变形情况。根据图1 ,可以整理出界面拉伸和剪切方向上的应力位移关系:
σ = K z × Δ w ( Δ w < w 0 ) σ = σ s + K z ' × Δ w - w 0 ( Δ w ≥ w 0 ) (2)
τ = K x × Δ u ( Δ u < u 0 ) τ = τ s + K x ' × Δ u - u 0 ( Δ u ≥ u 0 ) (3)
式中,σ 为界面拉伸应力,Δw 为界面拉伸位移,σ s 为界面拉伸状态下的屈服应力,w 0 为界面拉伸屈服状态下的位移,τ 为界面剪切应力,Δu 为界面剪切位移,τ s 为界面剪切状态下的屈服应力,u 0 为界面剪切屈服状态下的位移,Kz 为拉伸方向弹性刚度系数,K z ' Kx 为剪切方向下的弹性刚度系数,K x '
在外力作用下,考虑到2个方向上可能处于不同的变形阶段,一共存在4种变形情况,将不同变形情况下的界面应力位移关系带入到力平衡方程中可以建立界面应力与外界载荷的关系。再引入分层板的本构关系[27 ] :
N α = B A α ε α , Q α = B C α γ α , M α = B D α k α (4)
该本构方程中,B 为界面宽度,Aα 为子层合板拉伸刚度,εα 为子层合板轴向应变,Cα 为子层合板剪切刚度,γα 为子层合板剪切应变,Dα 为子层合板弯曲刚度,kα 为子层合板曲率。
通过该方程,依据界面应力推导出界面位移的表达式,再根据界面位移与载荷位移的关系推导出载荷位移表达式。所有变形情况下的载荷位移关系式如下:
δ = P B d 1 + d 2 a 3 3 + 1 K z ∑ i = 1 6 f i ( 1 - λ i a ) (5)
δ = P B d 1 + d 2 a 3 3 + 1 K z ∑ i = 1 6 f i 1 - λ i a +
2 ( τ s K x ' - u 0 ) H 1 (6-1)
δ = P B d 1 + d 2 a 3 3 + 1 K z ∑ i = 1 6 f i 1 - λ i a -
2 ( τ s K x ' - u 0 ) H 2 (6-2)
δ = P B d 1 + d 2 a 3 3 + 1 K z ∑ i = 1 6 f i 1 - λ i a ±
( σ s K z ' - w 0 ) (7)
δ = P B d 1 + d 2 a 3 3 + 1 K z ∑ i = 1 6 f i 1 - λ i a ±
( σ s K z ' - w 0 ) (8-1)
δ = P B d 1 + d 2 a 3 3 + 1 K z ∑ i = 1 6 f i 1 - λ i a +
2 ( τ s K x ' - u 0 ) H 1 ± ( σ s K z ' - w 0 ) (8-2)
δ = P B d 1 + d 2 a 3 3 + 1 K z ∑ i = 1 6 f i 1 - λ i a -
2 ( τ s K x ' - u 0 ) H 2 ± ( σ s K z ' - w 0 ) (8-3)
式中,δ 为端部位移;P 为端部载荷;d 1 =1/D 1 ,d 2 =1/D 2 ,D 1 和D 2 分别为上、下子层材料的刚度;H 1 和H 2 分别为上、下子层合板厚度;λi 为界面应力微分方程特征方程的根;fi =Fi B /P ,Fi 为界面应力微分方程求解过程中的积分常数;i =1~6,分别对应着界面应力微分方程的6个解。
为获得层间断裂能与双悬臂梁端部位移的关系式,需引入梁应变能的计算公式和层间断裂能与应变能的关系,分别如式(9)[28 ] 和式(10)[29 ] 所示:
U 1 = 1 2 ∫ l M 1 2 E 1 I 1 d x , U 2 = 1 2 ∫ l M 2 2 E 2 I 2 d x (9)
G = - 1 B ∂ U ∂ a = - 1 B [ ∂ U 1 ∂ a + ∂ U 2 ∂ a ] (10)
式中,U 1 为上梁应变能,U 2 为下梁应变能;G 为断裂能;E 1 为上梁弹性模量,E 2 为下梁弹性模量;I 1 为上梁截面惯性矩,I 2 为下梁截面惯性矩;M 1 为上梁弯矩,M 2 为下梁弯矩,由加载在梁端部载荷P 引起。
将式(9)带入到式(10)中,最终可以得到层间断裂能计算公式为:
G = 1 B 9 2 a 4 [ δ 1 2 E 1 I 1 + δ 2 2 E 2 I 2 ] (11)
将各种情况下的载荷位移表达式带入到式(11)即可计算出各种变形情况下的断裂能。
本节先建立双金属复合板界面的弹塑性模型,然后通过该模型解析双金属板界面断裂能。在断裂能的计算过程中,首先需要建立双悬臂梁模型,将模型的宽度和初始裂缝长度等几何参数作为已知量代入到解析式中,然后对界面结合强度取值范围做出假设,并以该值为标准,根据子层材料性能参数对界面屈服强度等参数进行估算。但由于界面结合强度值试取次数较多,且由载荷位移关系推导出了多个断裂能计算公式,计算量大,难以在计算过程中直接获得Kz (K z ' K x '
2 界面裂纹扩展的有限元模拟
根据前文中提到的界面应力位移曲线,当在双悬臂梁模型沿界面进行裂纹扩展时,界面在断裂前存在多种变形情况,需要借助有限元法对每种变形情况进行模拟以确定准确的应力位移关系。同时,对于双金属板,在表征双悬臂梁端部位移和载荷关系的解析式中,Kz 无法通过实验的方法直接获得。因此,本工作借助有限元法建立双悬臂梁模型和T型剥离模型,通过模拟复合板的界面裂纹扩展过程解决这2个问题。
2.1 双悬臂梁模型的建立
建立长度105 mm、宽度10 mm、厚度1.85 mm 的Cu-Al复合的双悬臂梁模型,其中铜层厚度为0.75 mm,铝层厚度为1 mm,中间界面层厚度为0.1 mm,该模型在结构上具有非对称性,模型的一端设有长度为11 mm的起始裂缝,并在此端的铜层和铝层边缘部位施加大小为100 N、方向相反的一对恒定载荷P ,如图3 所示。通过建立该模型模拟界面裂纹扩展过程,获得不同界面结合强度下的端部位移。
图3
图3
双悬臂梁仿真模型
Color online
Fig.3
Simulation model of double cantilever beam (a —length of initial layer crack, b —length of the connecting part of the model, P —end load of the model)
2.1.1 双金属板界面层属性
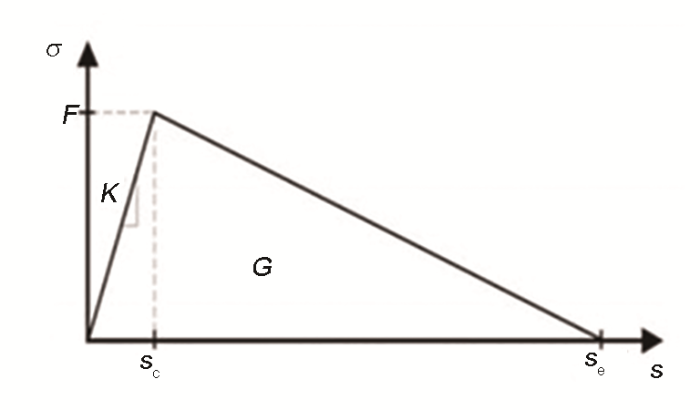
内聚力模型已经被广泛用于界面裂纹产生和扩展方面的数值模拟研究中,本工作内聚力模型采用双线性本构关系,如图4 所示。在外载荷的作用下,内聚力单元出现损伤前,内聚力单元裂纹张力随张开位移s 成线性增长,此时材料处于弹性状态。当位移继续增加到s c ,张力达到最大F 时,界面开始出现损伤。随着位移的继续增加,损伤出现扩展,材料出现刚度退化,界面张力也成线性下降,所能承受的外载荷也逐渐减小。当位移达到s e 时,材料刚度完全退化,界面裂纹完全拓展,材料失效。
图4
图4
内聚力单元的双线性本构关系
Fig.4
Bilinear traction-separation response of the cohesive element relation of F vs s (F —interface bonding strength, K —stiffness, G —breaking energy, s c —interface displacement at maximum crack tension, s e —interface displacement at material failure, s —displacement of interfacial crack propagation)
2.1.2 双金属板材料属性
本工作使用的双金属复合板为T2-A1050爆炸复合板,通过拉伸实验可以获得上下层金属物理性能参数,如表1 [30 ] 所示。
2.1.3 双悬臂梁模型精度及有效性验证
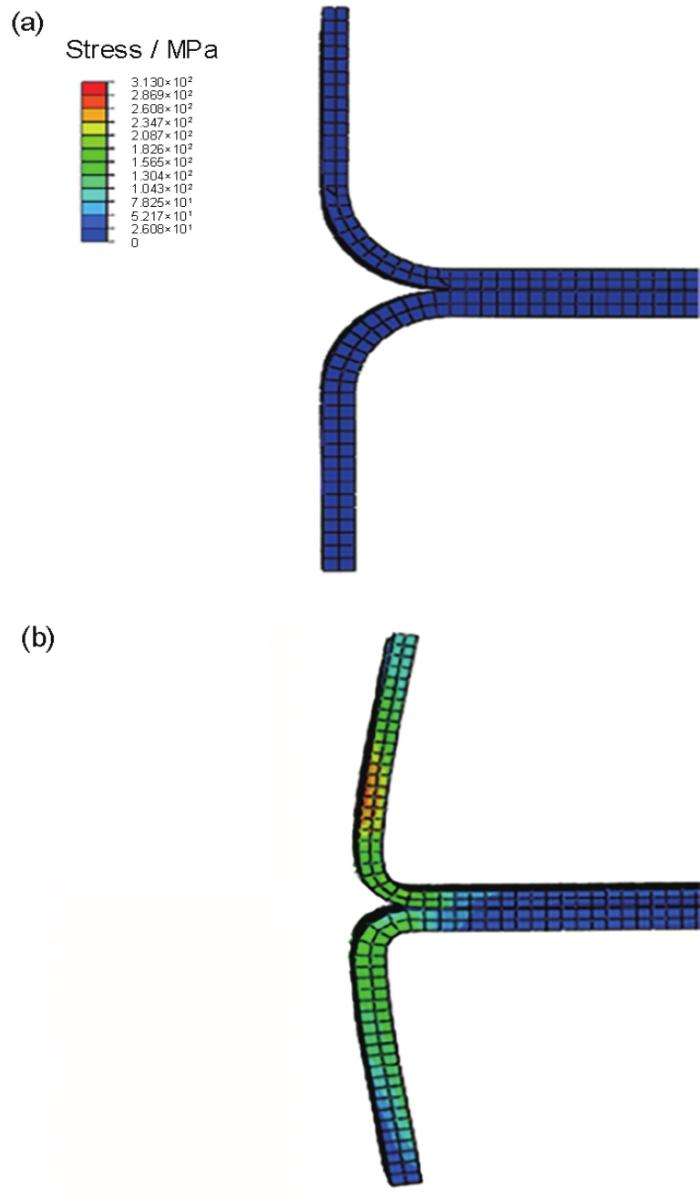
(1) 单元类型及单元尺寸对模型的影响。分别从单元类型和单元尺寸对双悬臂梁模型的精度和有效性进行验证。在同一外形尺寸(图3 )下,分别选取C3D8、C3D8R和C3D8I 3种网格单元进行建模,记录各单元类型上下梁端部位移δ 1 和δ 2 。结果表明,当单元类型选择C3D8时,双悬臂梁模型界面层不断开;在选取C3D8R单元时,δ 1 =1.08 mm,δ 2 =0.85 mm;选取C3D8I单元时,δ 1 =0.34 mm,δ 2 =0.21 mm。根据断裂能迭代运算程序结果:δ 1 在1.04 mm左右变化,δ 2 在0.75 mm左右变化,因此双悬臂梁模型可选取C3D8R类型单元进行模拟计算。
选取0.4、0.5、0.8和1.0 mm 4种单元尺寸,通过有限元模拟记录δ 1 和δ 2 的变化。结果表明,当单元尺寸取0.4和0.5 mm时,δ 1 分别为0.94和1.08 mm,δ 2 分别为0.82和0.85 mm,均与计算值(δ 1 =1.04 mm,δ 2 =0.75 mm)误差较小;当单元尺寸选取0.8和1.0 mm时,δ 1 分别为9.12和12.13 mm,δ 2 分别为6.69和9.13 mm,随着单元尺寸的增加,仿真结果与计算值的偏差越来越大,模拟精度也越来越差。但当单元尺寸过小时,模型网格数量过多,计算需要消耗大量时间,因此在保证模拟精度的前提下提高计算效率,选取单元尺寸0.5 mm进行仿真研究。
(2) 外形尺寸对模型的影响。为了研究双悬臂梁模型的外形尺寸是否对仿真结果产生影响,在图3 模型(记为模型1)尺寸的基础上另外设计2个仿真模型,分别记为模型2和模型3,模型2相对于模型1将宽度由原来的10 mm缩短到6 mm,模型3相对于模型1将宽度增长为14 mm,同时将总体厚度由原来的1.85 mm缩短为1.55 mm。结果发现,δ 1 、δ 2 与模型宽度之间存在着近似反比的关系,即模型2与模型1相比,宽度比为0.6∶1,δ 1 值比为0.58∶1,δ 2 值比为0.66∶1;模型1与模型3相比,宽度比为1∶1.4,δ 1 值比为1.38∶1,δ 2 值比为1.46∶1。该规律也符合本工作断裂能解析中的端部位移与模型宽度的关系,因此本工作建立的双悬臂梁仿真模型具有一定的模拟精度。
2.1.4 仿真模型结果
首先对界面结合强度取值范围做出假设,假设界面结合强度处于T2和A1050屈服强度之间并进行多次取值,在外力作用下,开口端的上下子层材料会在界面断裂前首先发生弯曲变形,当外力传递到界面连接部分时界面断裂,Cu-Al层发生相对位移,将该位移量记作端部位移。因此模型计算结束后,测量不同界面结合强度设定值下的端部位移并记录。部分仿真结果如表2 所示。
通过建立双悬臂梁仿真模型获得了不同界面参数下的端部位移,该结果将与下文中得到的断裂能迭代运算结果进行对比以确定准确的界面参数。
2.2 T 型剥离模型的建立
在断裂能的计算过程中,Kz 是建立拉伸变形方向下界面应力和位移关系的重要参数,为了确定该系数,首先通过实验直接获得材料的弹性模量E ,然后确定两参数比值t (特征长度系数,与材料厚度有关)的取值,由于无法通过实验方法直接获取双金属板的t 值,因此通过建立T型剥离模型确定t 值。
在本构模型的提出中,搭接弹簧变形中应力与应变关系的是刚度系数,而在拉伸(剪切)方向上,弹性刚度系数与弹性模量(切变模量)存在着线性关系[31 ] ,即[27 ] :
K z = E z t z , K x = G x t x (12)
式中,Ez 为界面拉伸方向弹性模量,tz 为拉伸方向上的特征长度系数,tx 为剪切方向上的特征长度系数,Gx 为界面剪切方向切变模量。
2.2.1 T型模型精度及有效性验证
(1) 单元类型及单元尺寸对模型的影响。为了对T型剥离模型精度及有效性进行验证,首先分别选取3种单元类型进行建模,记录模型界面中每个节点在剥离过程中的最大应力(σ max )以及界面层处于最大应力下的临界厚度与界面层原厚度的差值(ΔT ),通过比较2者的比值(即Kz )对模拟精度进行验证。结果表明,当采用C3D8单元时,模型网格产生了比较严重的扭曲,这会导致计算结果不精确;其余2种单元在计算结果上相差不大,Kz 比较接近,分别为3.28和3.29 kN/mm3 ,但C3D8I单元由于计算精度比较高,CPU运行的时间为45 h,约为C3D8R单元的2倍,考虑计算精度的同时兼顾计算效率,因此选取C3D8R单元进行建模。
选取0.4、0.5、0.8和1.0 mm 4种单元尺寸进行模拟,结果发现,当板坯单元尺寸为0.4和0.5 mm时,Kz 差距不大,约为3.30 kN/mm3 ;随着板坯单元尺寸的增加,弹性常数急剧减小,同时发现当单元尺寸为0.8 mm时,界面层临界厚度约为0.2 mm,比初始厚度大了一倍,随着单元尺寸增加,这个倍数还在扩大。因此当单元尺寸过大时计算精度较差。单元尺寸小使得计算效率低。综合考虑,选取板坯单元尺寸为0.5 mm。
(2) 外形尺寸对模型的影响。首先建立宽度10 mm、厚度1.85 mm、水平长度90 mm、T型头长度(垂直方向) 15 mm的模型(记为模型1),在此基础上另外设计2个仿真模型,记为模型2和模型3,模型2相比模型1的宽度少5 mm,其它尺寸不变,模型3相比模型1宽度增长为15 mm,同时将总体厚度由原来的1.85 mm缩短为1.55 mm。对这3种尺寸模型分别进行仿真模拟,结果表明,外形尺寸的确会对σ max 和ΔT 产生影响,但Kz 相差不大。本工作在T型剥离模型的建立上选取了模型1的尺寸数据。
2.2.2 仿真模型结果
建立T型剥离模型,在子层材料的端部施加大小相同、方向相反的位移,图5 所示为T型剥离模型界面结合强度为180 MPa时变形前后的仿真云图。并输出模型界面中每个节点应力随时间的变化曲线,记录模型在剥离过程中的最大应力,经统计为250 N/mm2 。建立长度系数与界面最大应力的解析关系(2个式子分别对应着有限元法和参数迭代法确定Kz 的2种思路)[27 ] :
图5
图5
T型剥离模型变形前后的仿真云图比较
Color online
Fig.5
Comparisons of simulation results of T-peeling model before (a) and after (b) deformation
K z = σ m a x ∆ T = E z t z , t z = H C (13)
式中,C 为比例系数。在该模型中,界面层的原厚度为0.1 mm,临界断裂厚度为0.176 mm,则ΔT =0.076 mm。因此,求出Ez 后,特征长度系数的求解问题也就解决了。
3 Cu-Al 双金属复合板界面结合强度的确定
3.1 迭代运算程序的建立
首先通过实验确定双金属板铜层和铝层的材料性能参数。前文已得到了多种变形情况下的断裂能计算公式(11),为了确定准确变形情况下的界面参数,采用基于MATLAB编写断裂能迭代计算程序,当输入不同的t 值时,界面结合强度在T2和A1050屈服强度之间以5 MPa为间隔进行取值,会输出不同的断裂能和端部位移。
在拉伸剪切方向均处于弹性阶段下,得到G =2.53 mJ/mm2 ,δ 1 =1.0974 mm,δ 2 =0.7600 mm,该计算结果为定值,不随t 值和界面结合强度变化,显然与实际情况不符。表3 列出了拉伸方向处于弹性阶段,剪切方向处于塑性阶段下断裂能和端部位移的计算结果。
其它变形情况也是类似的迭代计算方法,由于情况较多在此省略。
3.2 层间断裂能及界面结合强度的确定
前文已通过建立T型剥离模型获得了最大剥离应力,同时计算出ΔT =0.076 mm,文献[32 ]指出,Cu-Al复合板实际的界面厚度为微米级。因此结合有限元模型和特征长度系数与界面最大应力的解析关系可以推算出:当界面厚度为1 μm时,ΔT =0.00076 mm,C =3.4,当界面厚度为2 μm时,ΔT =0.00152 mm,C =6.8,…,以此类推,每一个C 对应一个t 。
根据迭代计算结果,当复合板界面拉伸方向处于弹性阶段,剪切方向处于塑性阶段,t =H /3.4,界面结合强度在T2和A1050屈服强度之间变化时,断裂能在1.7572 mJ/mm2 与2.3122 mJ/mm2 之间变化,δ 1 在1.04 mm左右变化,δ 2 在0.75 mm左右变化,根据表2 中有限元结果,当界面结合强度处于205 MPa与210 MPa之间时,仿真端部位移与迭代计算结果误差最小。
因此,通过有限元仿真与迭代计算,可以得到T2-A1050双金属复合板的界面结合强度为208 MPa,断裂能为2.31 mJ/mm2 。
3.3 界面参数的验证与应用
3.3.1 界面参数对最大成形深度的影响
在渐进成形过程中,板料不断受到拉应力出现减薄,当板料上局部区域出现严重的减薄就会产生破裂,界面损伤开裂,可见,界面参数对板料成形深度有着很大的影响。因此设置3组界面参数,借助渐进成形仿真实验,通过界面损伤情况研究界面参数对最大成形深度的影响,同时验证解析结果的准确性。
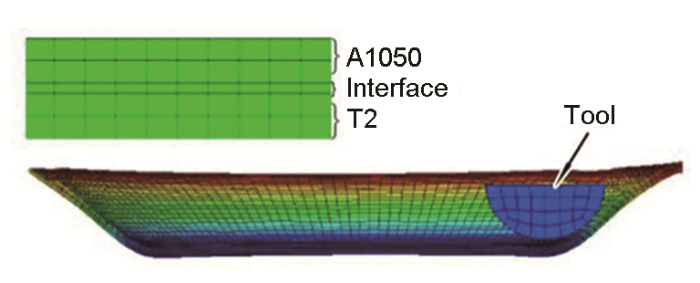
首先建立如图6 所示的仿真模型,A1050、Interface和T2分别对应复合板的铝层、界面层和铜层,Tool为单点渐进成形工具头。圆形复合板的直径为130 mm,厚度为2 mm,铜层和铝层厚度都为0.95 mm,界面层厚度为0.1 mm,工具头直径为10 mm。
图6
图6
单点渐进成形仿真模拟
Color online
Fig.6
The simulation of single point incremental forming (A1050—aluminum layer of bimetal plates, interface—interface layer of bimetal plates, T2—copper layer of bimetal plates, tool—tool head of the single point incremental forming)
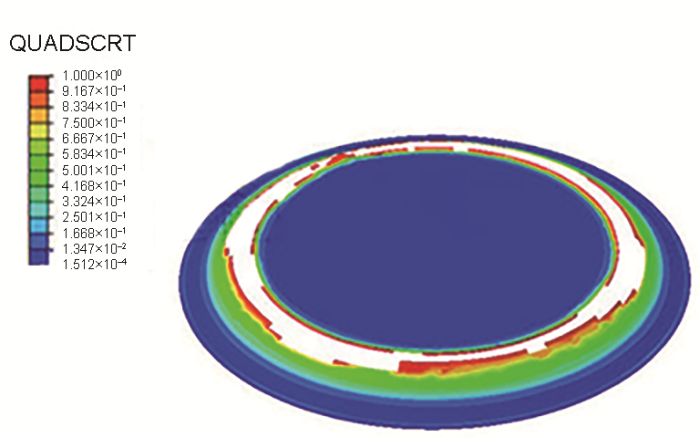
图7 为双金属Cu-Al复合板界面结合强度为150 MPa、断裂能为1.8 mJ/mm2 时界面内聚力单元损伤情况。QUADSCRT为二次应力判据,当其中达到1时,内聚力单元开始损伤。可以看出,双金属复合板渐进成形加工到10 mm,界面内聚力单元即出现了大面积的损伤裂纹。之后保持断裂能不变,将界面结合强度提高到180 MPa,发现当加工深度到达30 mm时,内聚力单元才出现损伤裂纹。
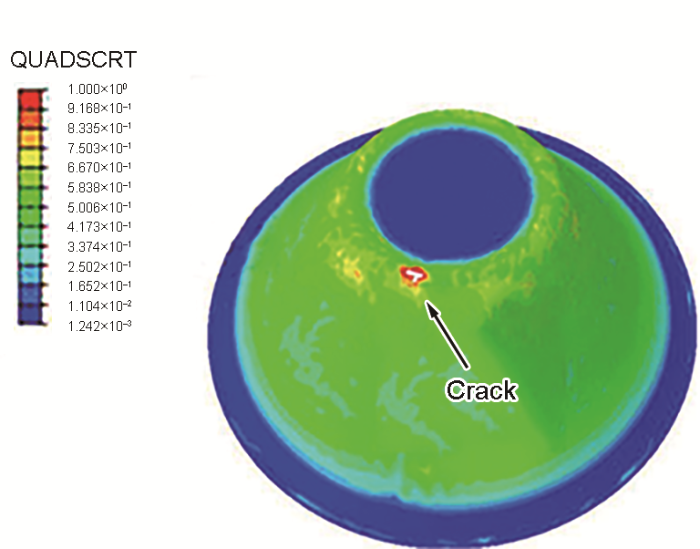
将本工作解析方法获得的界面参数带入到仿真模型中,发现当渐进成形深度达到31 mm时,内聚力单元在图8 中位置出现损伤裂纹,这与文献[30 ]实验中成形件加工开始出现裂纹的位置相同,且其裂纹出现的深度为32.59 mm。可见,本工作有限元模拟结果与实验[30 ] 相差5.3%。因此,利用解析法求得的Cu-Al复合板界面参数可以应用到渐进成形模型中。此外,当界面结合强度由150 MPa增加到208 MPa时,最大成形深度增加了210%。可以看出,增大界面结合强度有助于提高最大成形深度。
图7
图7
内聚力单元的损伤情况
Color online
Fig.7
The damage of the cohesive element (QUADSCRT represents secondary stress criterion)
图8
图8
复合板损伤模拟结果
Color online
Fig.8
Simulated result of the bimetal sheet damage
3.3.2 界面参数在渐进成形中的应用
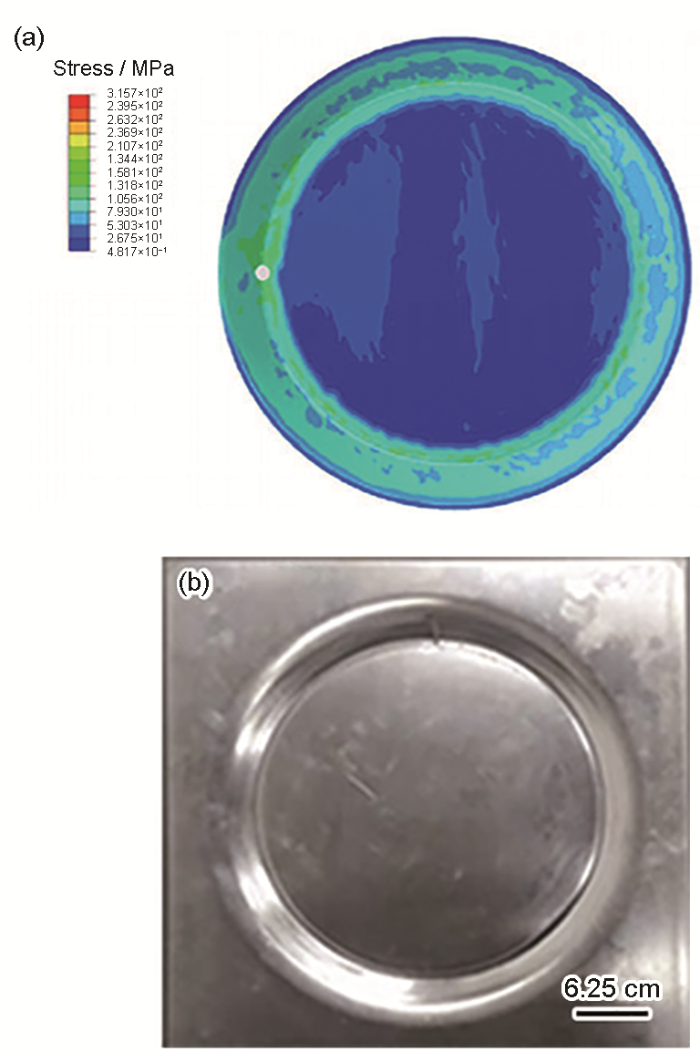
(1) 界面参数在渐进成形精度中的应用。建立双金属板渐进成形仿真模型,其中圆形复合板的直径为300 mm、厚度为2 mm,铜层厚度为0.25 mm,铝层厚度为1.65 mm,界面层厚度为0.1 mm,工具头直径为10 mm,每步压下量设为1 mm,仿真结果(应力云图)如图9 a所示。同时在HKT-1105B数控成形机床上进行板材加工,详细加工参数和压头路径按照仿真实验设置,圆形外部区域为夹具压边区域,为非成形区域。图9 b为成形件实物图。
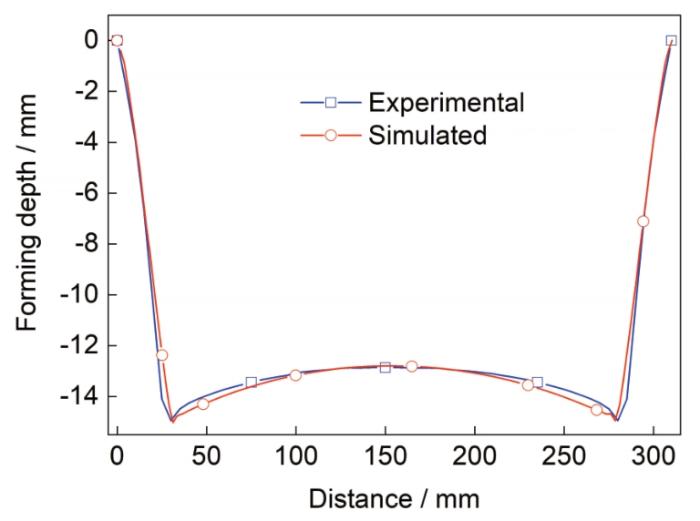
仿真计算结束后,提取成形件轮廓变化曲线,同时利用HandySCAN300三维激光扫描仪扫描成形件,并提取轮廓曲线,结果如图10 所示。从图10 可见,整体上实验曲线与仿真曲线拟合情况较好。在渐进成形过程中,当成形角度过小时,制件会出现一种严重的精度缺陷:底部鼓包。该缺陷产生的原因是成形件底部上下表面应力状态不同,上表面受拉,下表面受压,导致产生向上凸的鼓包。因此底部鼓包的大小可以反映成形件的加工精度。从图10 中可以看出,仿真结果与实验结果在底部鼓包高度上具有较好的一致性。
图9
图9
单点渐进成形仿真结果与实验结果的对比
Color online
(a) simulated result (b) experimental result
Fig.9
Comparisons between the result of single point incremental forming
图10
图10
单点渐进成形实验和仿真轮廓曲线
Fig.10
Experimental and simulated contour curves of single point incremental forming
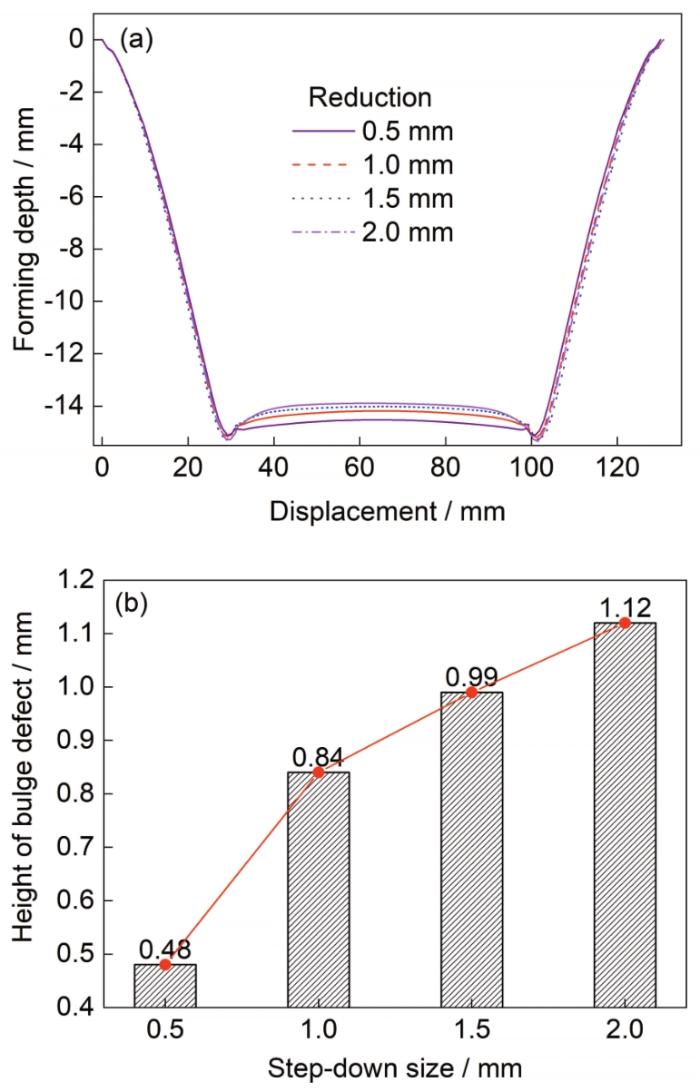
(2) 应用界面参数研究渐进成形底部鼓包问题。将解析获得的界面参数带入到仿真模型中,以图6 所示的直径为130 mm的复合板模型为研究对象,设置不同的压下量分别进行计算,测量不同压下量下成形件底部最大鼓包高度。图11 a为不同压下量下圆锥制件的截面轮廓,图11 b为不同压下量下的鼓包高度。可以看出,随着工具头压下量由2.0 mm变为0.5 mm,底部的鼓包高度由1.12 mm下降到0.48 mm,下降了57%。
图11
图11
不同压下量下圆锥制件的截面轮廓和底部鼓包高度
Fig.11
Sectional profiles of conical parts under different reductions (a) and the heights of bulge defect under different reductions (b)
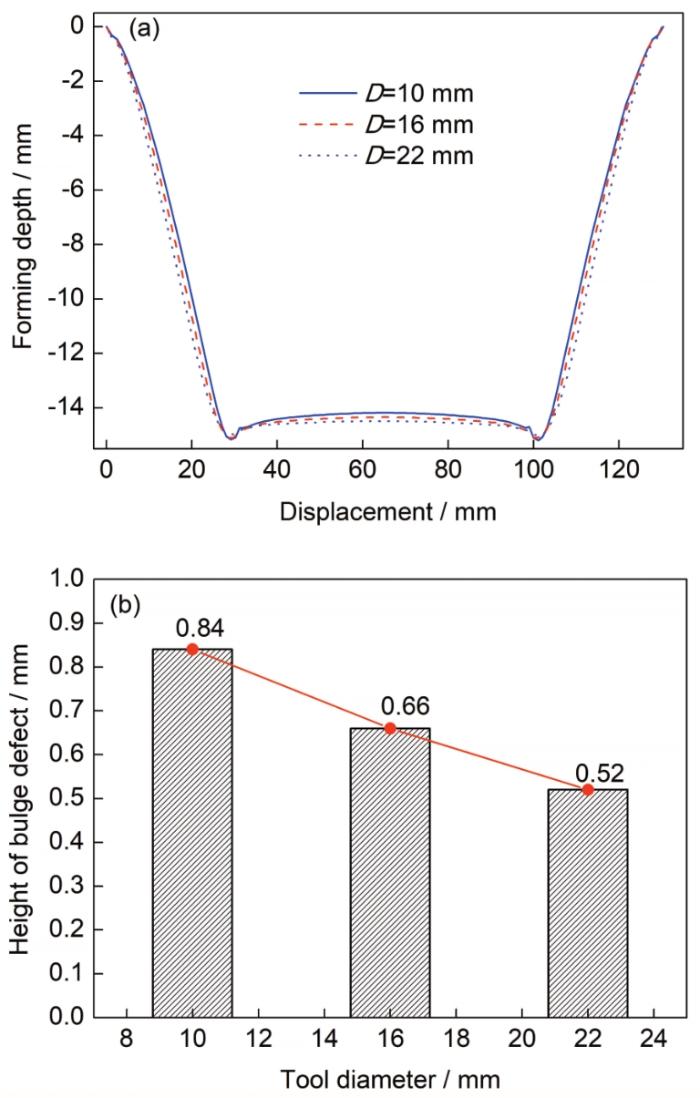
除了压下量,工具头直径也是影响渐进成形底部鼓包的因素,为了研究工具头直径对底部鼓包的影响,以圆锥台制件为例,选取工具头直径为10、16和22 mm时圆锥制件截面轮廓,并计算底部最大鼓包高度。图12 a为不同工具头直径下圆锥制件的截面轮廓,通过测量成形件底部最大鼓包高度可以发现,随着工具头直径由10 mm增加为22 mm,板料底部的鼓包高度有减小的趋势,如图12 b所示,在工具头直径为10、16和22 mm时,对应的底部鼓包高度分别为0.84、0.66和0.52 mm,底部鼓包高度和工具头直径的关系成负相关,随着工具头直径增加,鼓包高度下降了38%。
图12
图12
不同工具头直径下圆锥制件的截面轮廓和底部鼓包高度
Fig.12
Sectional profile curves of forming depth vs displacement of conical parts under different tool diameters (D ) (a) and histogram of height of bulge defect vs tool diameter (b)
根据上述分析,在实际的渐进成形加工中,各工艺参数的选取应综合考虑加工工艺参数的可操作性和对成形效率质量的影响。其中鼓包高度随着压下量的减小而减小,但如果一味减小每步压下量,会导致成形效率显著下降;鼓包高度随工具头直径增加而降低,增加工具头直径使得与板料接触面积增加,导致板料上下面应力差减小,从而抑制鼓包形成,但是随着工具头直径增加工具头对制件的影响加大,使能达到的加工精度降低。基于上述考虑,本工作提出一组较合理的参数组合为:压下量1.0 mm、工具头直径16 mm,经仿真计算得出鼓包高度为0.73 mm,比鼓包高度最大的参数组合(压下量2.0 mm、工具头直径10 mm、鼓包高度1.55 mm)下降了53%,成形效率提高了一倍,由于工具头直径减小,理论加工精度也更高。
通过以上研究可知,界面参数解析有助于建立考虑界面影响的双金属板模型,这样的模型在进行仿真实验时与实际情况更加相符,同时通过建立该模型可研究加工参数对渐进成形精度的影响,因此界面参数的解析能够推动渐进成形技术的仿真研究。
4 结论
(1) 基于目前普遍采用的非对称双悬臂梁模型,在充分考虑金属复合材料界面塑性变形行为的基础上,对模型进行优化,提出解析计算双金属板界面结合强度的改进方法。借助渐进成形实验验证了此方法的正确性,并应用该方法获得了爆炸复合的T2/A1050 Cu-Al双金属复合板界面结合强度为208 MPa。
(2) 通过模拟渐进成形加工过程研究了界面结合强度与最大成形深度的关系,发现最大成形深度与界面结合强度呈正相关,当界面结合强度从150 MPa增加到208 MPa时,最大成形深度增加了210%。
(3) 应用解析结果对渐进成形精度问题进行研究,发现压下量和工具头直径严重影响渐进成形鼓包高度,讨论了渐进成形底部鼓包在不同工艺参数下的变化规律,当压下量由2.0 mm降低至0.5 mm,鼓包高度可降低57%;工具头直径由22 mm下降至10 mm,鼓包高度下降38%。最后优选了一组较合理的参数组合为压下量1.0 mm、工具头直径16 mm,经仿真计算得出鼓包高度为0.73 mm,使双金属复合板鼓包高度下降53%。
参考文献
View Option
[1]
Zhang Y X Yang C H Recent developments in finite element analysis for laminated composite plates
[J]. Compos. Struct. , 2009 , 88 : 147
DOI
URL
[本文引用: 1]
AbstractA review of the recent development of the finite element analysis for laminated composite plates from 1990 is presented in this paper. The literature review is devoted to the recently developed finite elements based on the various laminated plate theories for the free vibration and dynamics, buckling and postbuckling analysis, geometric nonlinearity and large deformation analysis, and failure and damage analysis of composite laminated plates. The material nonlinearity effects and thermal effects on the buckling and postbuckling analysis, the first-ply failure analysis and the failure and damage analysis were emphasized specially. The future research is summarised finally.]]>
[2]
Chen X Z Review of laminar composite metal material manufacturing technique
[J]. Nonferrous Met. Mater. Eng. , 2017 , 38 : 63
[本文引用: 1]
(陈兴章 层状金属复合材料技术创新及发展趋势综述
[J]. 有色金属材料与工程 , 2017 , 38 : 63 )
[本文引用: 1]
[3]
Xiong J Ma L Pan S et al . Shear and bending performance of carbon fiber composite sandwich panels with pyramidal truss cores
[J]. Acta Mater. , 2012 , 60 : 1455
DOI
URL
[本文引用: 1]
Structural performance in direct (pure) shear and three-point bending was investigated for sandwich panels with a carbon fiber pyramidal truss core. Analytical estimates for sandwich panel strength for each loading condition were presented for possible competing failure modes. In the experimental part of the study, pyramidal truss cores were made using the hot press molding technique and then attached to flat carbon fiber composite face sheets to build all-composite sandwich panels. Panels with different configurations (e.g., core relative density and face sheet thickness) were tested to probe different failure modes and investigate the mechanical properties. In general, measured failure loads showed good agreement with the analytical predictions. Failure mechanism maps illustrate the controlling failure mechanisms in various regions of parameter space. (C) 2011 Acta Materialia Inc. Published by Elsevier Ltd.
[4]
Lü Z Y Research on interfacial bonding strength of asynchronous rolled copper/aluminum composite plate
[J]. J. Plast. Eng. , 2019 , 26 (4 ): 93
[本文引用: 1]
(吕震宇 异步轧制铜/铝复合板界面结合强度研究
[J]. 塑性工程学报 , 2019 , 26 (4 ): 93 )
[本文引用: 1]
[5]
Zhou J J Pang Y H Su X L et al . Development of manufacturing technology for layer-metal composite plate
[J]. Mater. Rev. , 2005 , 19 : 220
[本文引用: 1]
(周俊杰 , 庞玉华 , 苏晓莉 等 . 金属层状复合技术的研究现状与发展
[J]. 材料导报 , 2005 , 19 : 220 )
[本文引用: 1]
[6]
Qiu B Xing S M Dong Q Characterization of interfacial bonding strength of particles reinforced metal matrix composites: Theory model, finite element simulation and experimental test
[J]. Mater. Rev. , 2019 , 33 : 862
[本文引用: 2]
(邱 博 , 邢书明 , 董 琦 颗粒增强金属基复合材料界面结合强度的表征: 理论模型、有限元模拟和实验测试
[J]. 材料导报 , 2019 , 33 : 862 )
[本文引用: 2]
[7]
Muralidharan N Chockalingam K Dinaharan I et al . Microstructure and mechanical behavior of AA2024 aluminum matrix composites reinforced with in situ synthesized ZrB2 particles
[J]. J. Alloys Compd. , 2018 , 735 : 2167
[本文引用: 1]
[8]
Kim Y K Hong S I Influence of interface structure and stress distribution on fracture and mechanical performance of STS439/Al1050/STS304 clad composite
[J]. Mater. Sci. Eng. , 2019 , A749 : 35
[本文引用: 1]
[9]
Abbasi M Salehi M T Taheri A K An investigation on cold roll welding of copper to aluminum using electrical resistivity
[J]. Z. Metallkd. , 2001 , 92 : 423
[本文引用: 1]
[10]
Wang T H Sidhar H Mishra R S et al . Evaluation of intermetallic compound layer at aluminum/steel interface joined by friction stir scribe technology
[J]. Mater. Des. , 2019 , 174 : 107795
DOI
URL
[本文引用: 1]
[11]
Zhang Z L Theoretical and experimental study on the Iosipescu shear test method
[J]. J. Aeronaut. Mater. , 1996 , 16 (1 ): 55
[本文引用: 1]
(张子龙 复合材料面内剪切Iosipescue方法分析及试验研究
[J]. 航空材料学报 , 1996 , 16 (1 ): 55 )
URL
[本文引用: 1]
讨论了采用双V形开槽试样的Iosipescu剪切试验方法的应用,分析了影响试验的因素,对T300/5222复合材料单向板及π/4多向铺层层合板进行了试验研究.试验结果表明,此方法可以很好地用于复合材料剪切试验.
[12]
You J H Lutz W Gerger H et al . Fiber push-out study of a copper matrix composite with an engineered interface: Experiments and cohesive element simulation
[J]. Int. J. Solids Struct. , 2009 , 46 : 4277
DOI
URL
[本文引用: 1]
[13]
Nishikawa M Okabe T Takeda N Determination of interface properties from experiments on the fragmentation process in single-fiber composites
[J]. Mater. Sci. Eng. , 2008 , A480 : 549
[14]
Nishikawa M Okabe T Hemmi K et al . Micromechanical modeling of the microbond test to quantify the interfacial properties of fiber-reinforced composites
[J]. Int. J. Solids Struct. , 2008 , 45 : 4098
DOI
URL
[本文引用: 1]
[15]
Ni L H Interface and performance analysis of explosively welded Cu-Al bimetallic composite
[D]. Zhenjiang : Jiangsu University of Science and Technology , 2015
[本文引用: 1]
(倪梁华 铜铝爆炸复合材料界面及性能分析
[D]. 镇江 : 江苏科技大学 , 2015 )
[本文引用: 1]
[16]
Qu H P Study on semi-analytical solution for thermoelastic composite laminated plate
[D]. Tianjin : Civil Aviation University of China , 2018
[本文引用: 1]
(屈鹤鹏 复合材料层合板热弹性问题半解析法研究
[D]. 天津 : 中国民航大学 , 2018 )
[本文引用: 1]
[17]
Dvorak G J Laws N Analysis of progressive matrix cracking in composite laminates II. First ply failure
[J]. J. Compos. Mater. , 1987 , 21 : 309
DOI
URL
[本文引用: 1]
[18]
Dvorak G J Laws N Hejazi M Analysis of progressive matrix cracking in composite laminates I. Tthermoelastic properties of a ply with cracks
[J]. J. Compos. Mater. , 1985 , 19 : 216
DOI
URL
[本文引用: 1]
[19]
Reedy E D Guess T R Butt joint tensile strength: Interface corner stress intensity factor prediction
[J]. J. Adhes. Sci. Technol. , 1995 , 9 : 237
DOI
URL
[本文引用: 1]
[20]
Adams R Structural Adhesive Joints in Engineering [M]. Netherlands : Springer , 1984 : 1
[本文引用: 1]
[21]
Dunn M L Suwito W Cunningham S Fracture initiation at sharp notches: Correlation using critical stress intensities
[J]. Int. J. Solids Struct. , 1997 , 34 : 3873
DOI
URL
[本文引用: 1]
[22]
Maimí P Camanho P P Mayugo J A et al . A continuum damage model for composite laminates: Part I—Constitutive model
[J]. Mech. Mater. , 2007 , 39 : 897
DOI
URL
[本文引用: 1]
AbstractA continuum damage model for the prediction of the onset and evolution of intralaminar failure mechanisms and the collapse of structures manufactured in fiber-reinforced plastic laminates is proposed. The failure mechanisms occurring in the longitudinal and transverse directions of a ply are represented by a set of scalar damage variables. Crack closure effects under load reversal are taken into account by using damage variables that are established as a function of the sign of the components of the stress tensor. Damage activation functions based on the LaRC04 failure criteria are used to predict the different failure mechanisms occurring at the ply level.]]>
[23]
Maimí P Camanho P P Mayugo J A et al . A continuum damage model for composite laminates: Part II—Computational implementation and validation
[J]. Mech. Mater. , 2007 , 39 : 909
DOI
URL
[本文引用: 1]
AbstractThis papers describes the computational implementation of a new damage model for laminated composites proposed in a previous paper. The objectivity of the numerical solution is assured by regularizing the energy dissipated at a material point by each failure mechanism. A viscous model is proposed to mitigate the convergence difficulties associated with strain softening constitutive models. To verify the accuracy of the approach, analyses of coupon specimens were performed, and the numerical predictions were compared with experimental data.]]>
[24]
Xiao F Hui C Y Kramer E J Analysis of a mixed mode fracture specimen: The asymmetric double cantilever beam
[J]. J. Mater. Sci. , 1993 , 28 : 5620
DOI
URL
[本文引用: 1]
[25]
Bennati S Fisicaro P Valvo P S An enhanced beam-theory model of the mixed-mode bending (MMB) test—Part I: Literature review and mechanical model
[J]. Meccanica , 2013 , 48 : 443
DOI
URL
[本文引用: 2]
[26]
Bennati S Fisicaro P Valvo P S An enhanced beam-theory model of the mixed-mode bending (MMB) test—Part II: Applications and results
[J]. Meccanica , 2013 , 48 : 465
DOI
URL
The paper presents an enhanced beam-theory (EBT) model of the mixed-mode bending (MMB) test, whereby the specimen is considered as an assemblage of two sublaminates partly connected by an elastic-brittle interface. Analytical expressions for the compliance, energy release rate, and mode mixity are deduced. A compliance calibration strategy enabling numerical or experimental evaluation of the interface elastic constants is also presented. Furthermore, analytical expressions for the crack length correction parameters-analogous to those given by the corrected beam-theory (CBT) model for unidirectional laminated specimens-are furnished for multidirectional laminated specimens, as well. Lastly, an example application to experimental data reduction is presented.
[27]
Bennati S Colleluori M Corigliano D et al . An enhanced beam-theory model of the asymmetric double cantilever beam (ADCB) test for composite laminates
[J]. Compos. Sci. Technol. , 2009 , 69 : 1735
DOI
URL
[本文引用: 12]
[28]
Hua X G Li H G Lu Y et al . Interlaminar fracture toughness of GLARE laminates based on asymmetric double cantilever beam (ADCB)
[J]. Composites , 2019 , 163B : 175
[本文引用: 2]
[29]
Williams J G Fracture mechanics of anisotropic materials
[J]. Compos. Mater. Ser. , 1989 , 6 : 3
[本文引用: 1]
[30]
Honarpisheh M Jobedar M M Alinaghian I Multi-response optimization on single-point incremental forming of hyperbolic shape Al-1050/Cu bimetal using response surface methodology
[J]. Int. J. Adv. Manuf. Technol. , 2018 , 96 : 3069
DOI
URL
[本文引用: 5]
[31]
Bennati S Valvo P S Delamination growth in composite plates under compressive fatigue loads
[J]. Compos. Sci. Technol. , 2006 , 66 : 248
DOI
URL
[本文引用: 1]
[32]
Li X Q Diffusion thickness and heat transfer performance of Cu-Al composite pate under service condions
[D]. Shenyang : Shenyang University of Technology , 2019
[本文引用: 1]
(李雪琪 服役条件下铜铝复合板的扩散层厚度及传热性能
[D]. 沈阳 : 沈阳工业大学 , 2019 )
[本文引用: 1]
Recent developments in finite element analysis for laminated composite plates
1
2009
... 随着现代科学技术的进步和发展,社会各领域对材料性能的要求不断提升,复合材料由于能够发挥组元材料各自的优势[1 ,2 ] ,表现出优异的内在和外在特性,因此被广泛应用到汽车、航空航天、医疗仪器、船舶、电力等领域[3 ] .界面作为复合材料中普遍存在且非常重要的组成部分,也是复合材料实现其优异的综合性能的关键性因素[4 ,5 ] . ...
层状金属复合材料技术创新及发展趋势综述
1
2017
... 随着现代科学技术的进步和发展,社会各领域对材料性能的要求不断提升,复合材料由于能够发挥组元材料各自的优势[1 ,2 ] ,表现出优异的内在和外在特性,因此被广泛应用到汽车、航空航天、医疗仪器、船舶、电力等领域[3 ] .界面作为复合材料中普遍存在且非常重要的组成部分,也是复合材料实现其优异的综合性能的关键性因素[4 ,5 ] . ...
层状金属复合材料技术创新及发展趋势综述
1
2017
... 随着现代科学技术的进步和发展,社会各领域对材料性能的要求不断提升,复合材料由于能够发挥组元材料各自的优势[1 ,2 ] ,表现出优异的内在和外在特性,因此被广泛应用到汽车、航空航天、医疗仪器、船舶、电力等领域[3 ] .界面作为复合材料中普遍存在且非常重要的组成部分,也是复合材料实现其优异的综合性能的关键性因素[4 ,5 ] . ...
Shear and bending performance of carbon fiber composite sandwich panels with pyramidal truss cores
1
2012
... 随着现代科学技术的进步和发展,社会各领域对材料性能的要求不断提升,复合材料由于能够发挥组元材料各自的优势[1 ,2 ] ,表现出优异的内在和外在特性,因此被广泛应用到汽车、航空航天、医疗仪器、船舶、电力等领域[3 ] .界面作为复合材料中普遍存在且非常重要的组成部分,也是复合材料实现其优异的综合性能的关键性因素[4 ,5 ] . ...
异步轧制铜/铝复合板界面结合强度研究
1
2019
... 随着现代科学技术的进步和发展,社会各领域对材料性能的要求不断提升,复合材料由于能够发挥组元材料各自的优势[1 ,2 ] ,表现出优异的内在和外在特性,因此被广泛应用到汽车、航空航天、医疗仪器、船舶、电力等领域[3 ] .界面作为复合材料中普遍存在且非常重要的组成部分,也是复合材料实现其优异的综合性能的关键性因素[4 ,5 ] . ...
异步轧制铜/铝复合板界面结合强度研究
1
2019
... 随着现代科学技术的进步和发展,社会各领域对材料性能的要求不断提升,复合材料由于能够发挥组元材料各自的优势[1 ,2 ] ,表现出优异的内在和外在特性,因此被广泛应用到汽车、航空航天、医疗仪器、船舶、电力等领域[3 ] .界面作为复合材料中普遍存在且非常重要的组成部分,也是复合材料实现其优异的综合性能的关键性因素[4 ,5 ] . ...
金属层状复合技术的研究现状与发展
1
2005
... 随着现代科学技术的进步和发展,社会各领域对材料性能的要求不断提升,复合材料由于能够发挥组元材料各自的优势[1 ,2 ] ,表现出优异的内在和外在特性,因此被广泛应用到汽车、航空航天、医疗仪器、船舶、电力等领域[3 ] .界面作为复合材料中普遍存在且非常重要的组成部分,也是复合材料实现其优异的综合性能的关键性因素[4 ,5 ] . ...
金属层状复合技术的研究现状与发展
1
2005
... 随着现代科学技术的进步和发展,社会各领域对材料性能的要求不断提升,复合材料由于能够发挥组元材料各自的优势[1 ,2 ] ,表现出优异的内在和外在特性,因此被广泛应用到汽车、航空航天、医疗仪器、船舶、电力等领域[3 ] .界面作为复合材料中普遍存在且非常重要的组成部分,也是复合材料实现其优异的综合性能的关键性因素[4 ,5 ] . ...
颗粒增强金属基复合材料界面结合强度的表征: 理论模型、有限元模拟和实验测试
2
2019
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
... [6 ],因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
颗粒增强金属基复合材料界面结合强度的表征: 理论模型、有限元模拟和实验测试
2
2019
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
... [6 ],因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
Microstructure and mechanical behavior of AA2024 aluminum matrix composites reinforced with in situ synthesized ZrB2 particles
1
2018
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
Influence of interface structure and stress distribution on fracture and mechanical performance of STS439/Al1050/STS304 clad composite
1
2019
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
An investigation on cold roll welding of copper to aluminum using electrical resistivity
1
2001
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
Evaluation of intermetallic compound layer at aluminum/steel interface joined by friction stir scribe technology
1
2019
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
复合材料面内剪切Iosipescue方法分析及试验研究
1
1996
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
复合材料面内剪切Iosipescue方法分析及试验研究
1
1996
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
Fiber push-out study of a copper matrix composite with an engineered interface: Experiments and cohesive element simulation
1
2009
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
Determination of interface properties from experiments on the fragmentation process in single-fiber composites
2008
Micromechanical modeling of the microbond test to quantify the interfacial properties of fiber-reinforced composites
1
2008
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
铜铝爆炸复合材料界面及性能分析
1
2015
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
铜铝爆炸复合材料界面及性能分析
1
2015
... 界面结合强度作为复合材料界面结合性能的重要指标[6 ] ,一直以来是广大学者研究的重点和难点[7 ] ,常用的获取金属复合材料界面结合强度的方法主要包含实验法和解析法2大类,传统的实验方法包括以复合材料宏观性能来评价界面应力状态的一些宏观实验方法,例如横向弯曲实验[8 ] 、横向拉伸实验[9 ] 、导槽剪切实验[10 ] 和Iosipescu剪切实验[11 ] 等,以及早期采用的对单纤维模型与基体所构成的复合材料进行测试的微观力学实验方法[12 ~14 ] .这些实验方法在黏合剂黏接复合材料和纤维复合材料界面结合强度的测量中仍在广泛应用,但是对于爆炸焊接、轧制等工艺复合而成的金属复合材料,由于界面结合强度大于基体强度,在实验过程中发现了基材率先出现破坏或者断裂现象而导致无法确定其界面强度的情况[15 ] .除此之外,实验法费时费力,耗费大量的经济成本,而且由于研究材料、试样准备方法以及实验程序的差异,即便采用同一种方法和材料进行测试,结果也往往相差甚远[6 ] ,因此有必要利用解析方法研究复合材料的界面结合强度的变化机理或规律. ...
复合材料层合板热弹性问题半解析法研究
1
2018
... 解析法作为科学实验中常用的一种方法,能够定量描述各物理量之间的函数关系,通过研究函数性质,使各物理量的变化规律更加清晰[16 ] .同时,与实验法相比,解析法不受时间和空间条件的影响,能够节约大量的经济成本.在复合材料界面结合强度的解析计算过程中,主要是借助数学模型,通过层间的各向应力建立各物理量之间的联系,故界面强度解析的关键是建立合理的数学模型和应用适当的计算方法.目前,复合材料界面强度问题的解析思路大多是在断裂力学的基础上发展起来的,断裂力学主要从应力强度因子角度出发提出预测模型对界面强度进行评估,随着研究的深入,越来越多的学者在解析方法和数学模型上不断地进行改进.在最初的研究中,Dvorak等[17 ,18 ] 对弹性纤维复合材料的层间开裂进行了研究,基于断裂力学对复合材料在开裂过程中的开裂位移与外部载荷的关系以及应力应变情况进行了解析,并研究了这些物理量与界面结合强度的关系,虽然没有直接获得界面结合强度,但为接下来的工作做了铺垫.在此基础上,Reedy和Guess[19 ] 提出了基于广义应力强度因子的失效模型,讨论了对接界面角应力场的渐近形式.并通过与临界值作比较预测对接接头的结合强度,最后依据断裂准则推导出对接界面的拉伸强度与黏结厚度之间的函数关系.Adams[20 ] 对黏合剂黏接的复合材料进行强度评估,通过计算黏合剂层的应力应变并各自与临界值进行比较,从而评估复合材料的结合强度.这种方法对黏接复合材料的界面结合强度进行了成功的预测,但计算结果受材料几何参数的影响.为了解决这一问题,Dun等[21 ] 通过研究搭接接头界面缺口处的裂纹,同时考虑应力和能量平衡问题,成功地预测了界面结合强度,这种方法仅需要材料的强度和韧性,不受几何参数的限制.为了进一步提高计算精度,Maimí等[22 ,23 ] 针对层合板复合材料提出了一种连续体损伤模型,基于强度失效准则预测了层内失效机制,并通过建立断裂韧性、弹性模量和强度的函数关系式计算了层间破坏应力,最后通过实验验证了结论的准确性,该方法在建立损伤模型的基础上通过计算断裂韧性和层间破坏应力等参数来表征层合板界面强度.以上在解析过程中所建立的数学模型对研究复合材料界面层的损伤机制和裂纹扩展有着很大的帮助,但并未直接给出界面结合强度的计算方法,同时为了进一步提高计算精度,有必要对解析模型进行优化. ...
复合材料层合板热弹性问题半解析法研究
1
2018
... 解析法作为科学实验中常用的一种方法,能够定量描述各物理量之间的函数关系,通过研究函数性质,使各物理量的变化规律更加清晰[16 ] .同时,与实验法相比,解析法不受时间和空间条件的影响,能够节约大量的经济成本.在复合材料界面结合强度的解析计算过程中,主要是借助数学模型,通过层间的各向应力建立各物理量之间的联系,故界面强度解析的关键是建立合理的数学模型和应用适当的计算方法.目前,复合材料界面强度问题的解析思路大多是在断裂力学的基础上发展起来的,断裂力学主要从应力强度因子角度出发提出预测模型对界面强度进行评估,随着研究的深入,越来越多的学者在解析方法和数学模型上不断地进行改进.在最初的研究中,Dvorak等[17 ,18 ] 对弹性纤维复合材料的层间开裂进行了研究,基于断裂力学对复合材料在开裂过程中的开裂位移与外部载荷的关系以及应力应变情况进行了解析,并研究了这些物理量与界面结合强度的关系,虽然没有直接获得界面结合强度,但为接下来的工作做了铺垫.在此基础上,Reedy和Guess[19 ] 提出了基于广义应力强度因子的失效模型,讨论了对接界面角应力场的渐近形式.并通过与临界值作比较预测对接接头的结合强度,最后依据断裂准则推导出对接界面的拉伸强度与黏结厚度之间的函数关系.Adams[20 ] 对黏合剂黏接的复合材料进行强度评估,通过计算黏合剂层的应力应变并各自与临界值进行比较,从而评估复合材料的结合强度.这种方法对黏接复合材料的界面结合强度进行了成功的预测,但计算结果受材料几何参数的影响.为了解决这一问题,Dun等[21 ] 通过研究搭接接头界面缺口处的裂纹,同时考虑应力和能量平衡问题,成功地预测了界面结合强度,这种方法仅需要材料的强度和韧性,不受几何参数的限制.为了进一步提高计算精度,Maimí等[22 ,23 ] 针对层合板复合材料提出了一种连续体损伤模型,基于强度失效准则预测了层内失效机制,并通过建立断裂韧性、弹性模量和强度的函数关系式计算了层间破坏应力,最后通过实验验证了结论的准确性,该方法在建立损伤模型的基础上通过计算断裂韧性和层间破坏应力等参数来表征层合板界面强度.以上在解析过程中所建立的数学模型对研究复合材料界面层的损伤机制和裂纹扩展有着很大的帮助,但并未直接给出界面结合强度的计算方法,同时为了进一步提高计算精度,有必要对解析模型进行优化. ...
Analysis of progressive matrix cracking in composite laminates II. First ply failure
1
1987
... 解析法作为科学实验中常用的一种方法,能够定量描述各物理量之间的函数关系,通过研究函数性质,使各物理量的变化规律更加清晰[16 ] .同时,与实验法相比,解析法不受时间和空间条件的影响,能够节约大量的经济成本.在复合材料界面结合强度的解析计算过程中,主要是借助数学模型,通过层间的各向应力建立各物理量之间的联系,故界面强度解析的关键是建立合理的数学模型和应用适当的计算方法.目前,复合材料界面强度问题的解析思路大多是在断裂力学的基础上发展起来的,断裂力学主要从应力强度因子角度出发提出预测模型对界面强度进行评估,随着研究的深入,越来越多的学者在解析方法和数学模型上不断地进行改进.在最初的研究中,Dvorak等[17 ,18 ] 对弹性纤维复合材料的层间开裂进行了研究,基于断裂力学对复合材料在开裂过程中的开裂位移与外部载荷的关系以及应力应变情况进行了解析,并研究了这些物理量与界面结合强度的关系,虽然没有直接获得界面结合强度,但为接下来的工作做了铺垫.在此基础上,Reedy和Guess[19 ] 提出了基于广义应力强度因子的失效模型,讨论了对接界面角应力场的渐近形式.并通过与临界值作比较预测对接接头的结合强度,最后依据断裂准则推导出对接界面的拉伸强度与黏结厚度之间的函数关系.Adams[20 ] 对黏合剂黏接的复合材料进行强度评估,通过计算黏合剂层的应力应变并各自与临界值进行比较,从而评估复合材料的结合强度.这种方法对黏接复合材料的界面结合强度进行了成功的预测,但计算结果受材料几何参数的影响.为了解决这一问题,Dun等[21 ] 通过研究搭接接头界面缺口处的裂纹,同时考虑应力和能量平衡问题,成功地预测了界面结合强度,这种方法仅需要材料的强度和韧性,不受几何参数的限制.为了进一步提高计算精度,Maimí等[22 ,23 ] 针对层合板复合材料提出了一种连续体损伤模型,基于强度失效准则预测了层内失效机制,并通过建立断裂韧性、弹性模量和强度的函数关系式计算了层间破坏应力,最后通过实验验证了结论的准确性,该方法在建立损伤模型的基础上通过计算断裂韧性和层间破坏应力等参数来表征层合板界面强度.以上在解析过程中所建立的数学模型对研究复合材料界面层的损伤机制和裂纹扩展有着很大的帮助,但并未直接给出界面结合强度的计算方法,同时为了进一步提高计算精度,有必要对解析模型进行优化. ...
Analysis of progressive matrix cracking in composite laminates I. Tthermoelastic properties of a ply with cracks
1
1985
... 解析法作为科学实验中常用的一种方法,能够定量描述各物理量之间的函数关系,通过研究函数性质,使各物理量的变化规律更加清晰[16 ] .同时,与实验法相比,解析法不受时间和空间条件的影响,能够节约大量的经济成本.在复合材料界面结合强度的解析计算过程中,主要是借助数学模型,通过层间的各向应力建立各物理量之间的联系,故界面强度解析的关键是建立合理的数学模型和应用适当的计算方法.目前,复合材料界面强度问题的解析思路大多是在断裂力学的基础上发展起来的,断裂力学主要从应力强度因子角度出发提出预测模型对界面强度进行评估,随着研究的深入,越来越多的学者在解析方法和数学模型上不断地进行改进.在最初的研究中,Dvorak等[17 ,18 ] 对弹性纤维复合材料的层间开裂进行了研究,基于断裂力学对复合材料在开裂过程中的开裂位移与外部载荷的关系以及应力应变情况进行了解析,并研究了这些物理量与界面结合强度的关系,虽然没有直接获得界面结合强度,但为接下来的工作做了铺垫.在此基础上,Reedy和Guess[19 ] 提出了基于广义应力强度因子的失效模型,讨论了对接界面角应力场的渐近形式.并通过与临界值作比较预测对接接头的结合强度,最后依据断裂准则推导出对接界面的拉伸强度与黏结厚度之间的函数关系.Adams[20 ] 对黏合剂黏接的复合材料进行强度评估,通过计算黏合剂层的应力应变并各自与临界值进行比较,从而评估复合材料的结合强度.这种方法对黏接复合材料的界面结合强度进行了成功的预测,但计算结果受材料几何参数的影响.为了解决这一问题,Dun等[21 ] 通过研究搭接接头界面缺口处的裂纹,同时考虑应力和能量平衡问题,成功地预测了界面结合强度,这种方法仅需要材料的强度和韧性,不受几何参数的限制.为了进一步提高计算精度,Maimí等[22 ,23 ] 针对层合板复合材料提出了一种连续体损伤模型,基于强度失效准则预测了层内失效机制,并通过建立断裂韧性、弹性模量和强度的函数关系式计算了层间破坏应力,最后通过实验验证了结论的准确性,该方法在建立损伤模型的基础上通过计算断裂韧性和层间破坏应力等参数来表征层合板界面强度.以上在解析过程中所建立的数学模型对研究复合材料界面层的损伤机制和裂纹扩展有着很大的帮助,但并未直接给出界面结合强度的计算方法,同时为了进一步提高计算精度,有必要对解析模型进行优化. ...
Butt joint tensile strength: Interface corner stress intensity factor prediction
1
1995
... 解析法作为科学实验中常用的一种方法,能够定量描述各物理量之间的函数关系,通过研究函数性质,使各物理量的变化规律更加清晰[16 ] .同时,与实验法相比,解析法不受时间和空间条件的影响,能够节约大量的经济成本.在复合材料界面结合强度的解析计算过程中,主要是借助数学模型,通过层间的各向应力建立各物理量之间的联系,故界面强度解析的关键是建立合理的数学模型和应用适当的计算方法.目前,复合材料界面强度问题的解析思路大多是在断裂力学的基础上发展起来的,断裂力学主要从应力强度因子角度出发提出预测模型对界面强度进行评估,随着研究的深入,越来越多的学者在解析方法和数学模型上不断地进行改进.在最初的研究中,Dvorak等[17 ,18 ] 对弹性纤维复合材料的层间开裂进行了研究,基于断裂力学对复合材料在开裂过程中的开裂位移与外部载荷的关系以及应力应变情况进行了解析,并研究了这些物理量与界面结合强度的关系,虽然没有直接获得界面结合强度,但为接下来的工作做了铺垫.在此基础上,Reedy和Guess[19 ] 提出了基于广义应力强度因子的失效模型,讨论了对接界面角应力场的渐近形式.并通过与临界值作比较预测对接接头的结合强度,最后依据断裂准则推导出对接界面的拉伸强度与黏结厚度之间的函数关系.Adams[20 ] 对黏合剂黏接的复合材料进行强度评估,通过计算黏合剂层的应力应变并各自与临界值进行比较,从而评估复合材料的结合强度.这种方法对黏接复合材料的界面结合强度进行了成功的预测,但计算结果受材料几何参数的影响.为了解决这一问题,Dun等[21 ] 通过研究搭接接头界面缺口处的裂纹,同时考虑应力和能量平衡问题,成功地预测了界面结合强度,这种方法仅需要材料的强度和韧性,不受几何参数的限制.为了进一步提高计算精度,Maimí等[22 ,23 ] 针对层合板复合材料提出了一种连续体损伤模型,基于强度失效准则预测了层内失效机制,并通过建立断裂韧性、弹性模量和强度的函数关系式计算了层间破坏应力,最后通过实验验证了结论的准确性,该方法在建立损伤模型的基础上通过计算断裂韧性和层间破坏应力等参数来表征层合板界面强度.以上在解析过程中所建立的数学模型对研究复合材料界面层的损伤机制和裂纹扩展有着很大的帮助,但并未直接给出界面结合强度的计算方法,同时为了进一步提高计算精度,有必要对解析模型进行优化. ...
1
1984
... 解析法作为科学实验中常用的一种方法,能够定量描述各物理量之间的函数关系,通过研究函数性质,使各物理量的变化规律更加清晰[16 ] .同时,与实验法相比,解析法不受时间和空间条件的影响,能够节约大量的经济成本.在复合材料界面结合强度的解析计算过程中,主要是借助数学模型,通过层间的各向应力建立各物理量之间的联系,故界面强度解析的关键是建立合理的数学模型和应用适当的计算方法.目前,复合材料界面强度问题的解析思路大多是在断裂力学的基础上发展起来的,断裂力学主要从应力强度因子角度出发提出预测模型对界面强度进行评估,随着研究的深入,越来越多的学者在解析方法和数学模型上不断地进行改进.在最初的研究中,Dvorak等[17 ,18 ] 对弹性纤维复合材料的层间开裂进行了研究,基于断裂力学对复合材料在开裂过程中的开裂位移与外部载荷的关系以及应力应变情况进行了解析,并研究了这些物理量与界面结合强度的关系,虽然没有直接获得界面结合强度,但为接下来的工作做了铺垫.在此基础上,Reedy和Guess[19 ] 提出了基于广义应力强度因子的失效模型,讨论了对接界面角应力场的渐近形式.并通过与临界值作比较预测对接接头的结合强度,最后依据断裂准则推导出对接界面的拉伸强度与黏结厚度之间的函数关系.Adams[20 ] 对黏合剂黏接的复合材料进行强度评估,通过计算黏合剂层的应力应变并各自与临界值进行比较,从而评估复合材料的结合强度.这种方法对黏接复合材料的界面结合强度进行了成功的预测,但计算结果受材料几何参数的影响.为了解决这一问题,Dun等[21 ] 通过研究搭接接头界面缺口处的裂纹,同时考虑应力和能量平衡问题,成功地预测了界面结合强度,这种方法仅需要材料的强度和韧性,不受几何参数的限制.为了进一步提高计算精度,Maimí等[22 ,23 ] 针对层合板复合材料提出了一种连续体损伤模型,基于强度失效准则预测了层内失效机制,并通过建立断裂韧性、弹性模量和强度的函数关系式计算了层间破坏应力,最后通过实验验证了结论的准确性,该方法在建立损伤模型的基础上通过计算断裂韧性和层间破坏应力等参数来表征层合板界面强度.以上在解析过程中所建立的数学模型对研究复合材料界面层的损伤机制和裂纹扩展有着很大的帮助,但并未直接给出界面结合强度的计算方法,同时为了进一步提高计算精度,有必要对解析模型进行优化. ...
Fracture initiation at sharp notches: Correlation using critical stress intensities
1
1997
... 解析法作为科学实验中常用的一种方法,能够定量描述各物理量之间的函数关系,通过研究函数性质,使各物理量的变化规律更加清晰[16 ] .同时,与实验法相比,解析法不受时间和空间条件的影响,能够节约大量的经济成本.在复合材料界面结合强度的解析计算过程中,主要是借助数学模型,通过层间的各向应力建立各物理量之间的联系,故界面强度解析的关键是建立合理的数学模型和应用适当的计算方法.目前,复合材料界面强度问题的解析思路大多是在断裂力学的基础上发展起来的,断裂力学主要从应力强度因子角度出发提出预测模型对界面强度进行评估,随着研究的深入,越来越多的学者在解析方法和数学模型上不断地进行改进.在最初的研究中,Dvorak等[17 ,18 ] 对弹性纤维复合材料的层间开裂进行了研究,基于断裂力学对复合材料在开裂过程中的开裂位移与外部载荷的关系以及应力应变情况进行了解析,并研究了这些物理量与界面结合强度的关系,虽然没有直接获得界面结合强度,但为接下来的工作做了铺垫.在此基础上,Reedy和Guess[19 ] 提出了基于广义应力强度因子的失效模型,讨论了对接界面角应力场的渐近形式.并通过与临界值作比较预测对接接头的结合强度,最后依据断裂准则推导出对接界面的拉伸强度与黏结厚度之间的函数关系.Adams[20 ] 对黏合剂黏接的复合材料进行强度评估,通过计算黏合剂层的应力应变并各自与临界值进行比较,从而评估复合材料的结合强度.这种方法对黏接复合材料的界面结合强度进行了成功的预测,但计算结果受材料几何参数的影响.为了解决这一问题,Dun等[21 ] 通过研究搭接接头界面缺口处的裂纹,同时考虑应力和能量平衡问题,成功地预测了界面结合强度,这种方法仅需要材料的强度和韧性,不受几何参数的限制.为了进一步提高计算精度,Maimí等[22 ,23 ] 针对层合板复合材料提出了一种连续体损伤模型,基于强度失效准则预测了层内失效机制,并通过建立断裂韧性、弹性模量和强度的函数关系式计算了层间破坏应力,最后通过实验验证了结论的准确性,该方法在建立损伤模型的基础上通过计算断裂韧性和层间破坏应力等参数来表征层合板界面强度.以上在解析过程中所建立的数学模型对研究复合材料界面层的损伤机制和裂纹扩展有着很大的帮助,但并未直接给出界面结合强度的计算方法,同时为了进一步提高计算精度,有必要对解析模型进行优化. ...
A continuum damage model for composite laminates: Part I—Constitutive model
1
2007
... 解析法作为科学实验中常用的一种方法,能够定量描述各物理量之间的函数关系,通过研究函数性质,使各物理量的变化规律更加清晰[16 ] .同时,与实验法相比,解析法不受时间和空间条件的影响,能够节约大量的经济成本.在复合材料界面结合强度的解析计算过程中,主要是借助数学模型,通过层间的各向应力建立各物理量之间的联系,故界面强度解析的关键是建立合理的数学模型和应用适当的计算方法.目前,复合材料界面强度问题的解析思路大多是在断裂力学的基础上发展起来的,断裂力学主要从应力强度因子角度出发提出预测模型对界面强度进行评估,随着研究的深入,越来越多的学者在解析方法和数学模型上不断地进行改进.在最初的研究中,Dvorak等[17 ,18 ] 对弹性纤维复合材料的层间开裂进行了研究,基于断裂力学对复合材料在开裂过程中的开裂位移与外部载荷的关系以及应力应变情况进行了解析,并研究了这些物理量与界面结合强度的关系,虽然没有直接获得界面结合强度,但为接下来的工作做了铺垫.在此基础上,Reedy和Guess[19 ] 提出了基于广义应力强度因子的失效模型,讨论了对接界面角应力场的渐近形式.并通过与临界值作比较预测对接接头的结合强度,最后依据断裂准则推导出对接界面的拉伸强度与黏结厚度之间的函数关系.Adams[20 ] 对黏合剂黏接的复合材料进行强度评估,通过计算黏合剂层的应力应变并各自与临界值进行比较,从而评估复合材料的结合强度.这种方法对黏接复合材料的界面结合强度进行了成功的预测,但计算结果受材料几何参数的影响.为了解决这一问题,Dun等[21 ] 通过研究搭接接头界面缺口处的裂纹,同时考虑应力和能量平衡问题,成功地预测了界面结合强度,这种方法仅需要材料的强度和韧性,不受几何参数的限制.为了进一步提高计算精度,Maimí等[22 ,23 ] 针对层合板复合材料提出了一种连续体损伤模型,基于强度失效准则预测了层内失效机制,并通过建立断裂韧性、弹性模量和强度的函数关系式计算了层间破坏应力,最后通过实验验证了结论的准确性,该方法在建立损伤模型的基础上通过计算断裂韧性和层间破坏应力等参数来表征层合板界面强度.以上在解析过程中所建立的数学模型对研究复合材料界面层的损伤机制和裂纹扩展有着很大的帮助,但并未直接给出界面结合强度的计算方法,同时为了进一步提高计算精度,有必要对解析模型进行优化. ...
A continuum damage model for composite laminates: Part II—Computational implementation and validation
1
2007
... 解析法作为科学实验中常用的一种方法,能够定量描述各物理量之间的函数关系,通过研究函数性质,使各物理量的变化规律更加清晰[16 ] .同时,与实验法相比,解析法不受时间和空间条件的影响,能够节约大量的经济成本.在复合材料界面结合强度的解析计算过程中,主要是借助数学模型,通过层间的各向应力建立各物理量之间的联系,故界面强度解析的关键是建立合理的数学模型和应用适当的计算方法.目前,复合材料界面强度问题的解析思路大多是在断裂力学的基础上发展起来的,断裂力学主要从应力强度因子角度出发提出预测模型对界面强度进行评估,随着研究的深入,越来越多的学者在解析方法和数学模型上不断地进行改进.在最初的研究中,Dvorak等[17 ,18 ] 对弹性纤维复合材料的层间开裂进行了研究,基于断裂力学对复合材料在开裂过程中的开裂位移与外部载荷的关系以及应力应变情况进行了解析,并研究了这些物理量与界面结合强度的关系,虽然没有直接获得界面结合强度,但为接下来的工作做了铺垫.在此基础上,Reedy和Guess[19 ] 提出了基于广义应力强度因子的失效模型,讨论了对接界面角应力场的渐近形式.并通过与临界值作比较预测对接接头的结合强度,最后依据断裂准则推导出对接界面的拉伸强度与黏结厚度之间的函数关系.Adams[20 ] 对黏合剂黏接的复合材料进行强度评估,通过计算黏合剂层的应力应变并各自与临界值进行比较,从而评估复合材料的结合强度.这种方法对黏接复合材料的界面结合强度进行了成功的预测,但计算结果受材料几何参数的影响.为了解决这一问题,Dun等[21 ] 通过研究搭接接头界面缺口处的裂纹,同时考虑应力和能量平衡问题,成功地预测了界面结合强度,这种方法仅需要材料的强度和韧性,不受几何参数的限制.为了进一步提高计算精度,Maimí等[22 ,23 ] 针对层合板复合材料提出了一种连续体损伤模型,基于强度失效准则预测了层内失效机制,并通过建立断裂韧性、弹性模量和强度的函数关系式计算了层间破坏应力,最后通过实验验证了结论的准确性,该方法在建立损伤模型的基础上通过计算断裂韧性和层间破坏应力等参数来表征层合板界面强度.以上在解析过程中所建立的数学模型对研究复合材料界面层的损伤机制和裂纹扩展有着很大的帮助,但并未直接给出界面结合强度的计算方法,同时为了进一步提高计算精度,有必要对解析模型进行优化. ...
Analysis of a mixed mode fracture specimen: The asymmetric double cantilever beam
1
1993
... 在复合材料界面结合强度的表征工作上,应用梁理论将复合梁模型融入到断裂力学的计算方法中,通过建立双悬臂梁模型,计算临界能量释放率和混合模式相角等参数,用于表征复合材料界面强度[24 ] ,许多学者在这方面做了大量的工作.Bennati等[25 ~27 ] 将纤维层合板视作弹脆性界面连接,提出了混合模式弯曲测试的力学模型,并分别在I型和II型断裂模式下,依据边界条件建立多组微分方程确定界面应力、内力和位移的表达式,评估复合材料层合板混合模式下的层间断裂韧性,以此表征界面结合强度.Hua等[28 ] 分别基于梁理论和断裂力学理论推导出不同纤维取向复合材料的层间断裂能,并与有限元和实验结果进行比较,结果表明,层间断裂韧性随加载速率的增加而增加,且在实验和数值仿真中呈现出相同的规律性,但随着裂纹的扩展,理论计算与实验之间的误差逐渐增大.现有的解析方法大多针对的是纤维复合材料或者黏合连接的复合材料,忽略了界面强度高于基体的情况,这些问题使得金属复合材料界面强度的求解存在改进空间. ...
An enhanced beam-theory model of the mixed-mode bending (MMB) test—Part I: Literature review and mechanical model
2
2013
... 在复合材料界面结合强度的表征工作上,应用梁理论将复合梁模型融入到断裂力学的计算方法中,通过建立双悬臂梁模型,计算临界能量释放率和混合模式相角等参数,用于表征复合材料界面强度[24 ] ,许多学者在这方面做了大量的工作.Bennati等[25 ~27 ] 将纤维层合板视作弹脆性界面连接,提出了混合模式弯曲测试的力学模型,并分别在I型和II型断裂模式下,依据边界条件建立多组微分方程确定界面应力、内力和位移的表达式,评估复合材料层合板混合模式下的层间断裂韧性,以此表征界面结合强度.Hua等[28 ] 分别基于梁理论和断裂力学理论推导出不同纤维取向复合材料的层间断裂能,并与有限元和实验结果进行比较,结果表明,层间断裂韧性随加载速率的增加而增加,且在实验和数值仿真中呈现出相同的规律性,但随着裂纹的扩展,理论计算与实验之间的误差逐渐增大.现有的解析方法大多针对的是纤维复合材料或者黏合连接的复合材料,忽略了界面强度高于基体的情况,这些问题使得金属复合材料界面强度的求解存在改进空间. ...
... 在复合板界面参数的求解过程中,常借助双悬臂梁弹性-脆性界面模型对层间断裂韧性进行解析,该模型将复合板界面简化成不同方向的线弹性弹簧连接,可用于一些复合材料混合断裂模式下的层间断裂能[25 ~27 ] 的解析,而对于爆炸焊接或者轧制方式复合的双金属复合板,界面层为上下2层金属在外界高温或高压环境下相互作用而成,简单的线弹性不能准确描述其变形情况,无法进行界面参数的解析,为了获得此类材料的界面参数,本工作基于非对称双悬臂的弹性-脆性界面模型[27 ] 进行改进,考虑界面断裂前的塑性变形情况,提出弹塑性界面模型,通过力平衡方程构建界面应力与外部载荷的关系,并结合相关力学理论对层间断裂能进行解析.同时考虑到双金属复合材料各向异性参数获取比较困难,因此将其简化成各向同性问题进行处理. ...
An enhanced beam-theory model of the mixed-mode bending (MMB) test—Part II: Applications and results
2013
An enhanced beam-theory model of the asymmetric double cantilever beam (ADCB) test for composite laminates
12
2009
... 在复合材料界面结合强度的表征工作上,应用梁理论将复合梁模型融入到断裂力学的计算方法中,通过建立双悬臂梁模型,计算临界能量释放率和混合模式相角等参数,用于表征复合材料界面强度[24 ] ,许多学者在这方面做了大量的工作.Bennati等[25 ~27 ] 将纤维层合板视作弹脆性界面连接,提出了混合模式弯曲测试的力学模型,并分别在I型和II型断裂模式下,依据边界条件建立多组微分方程确定界面应力、内力和位移的表达式,评估复合材料层合板混合模式下的层间断裂韧性,以此表征界面结合强度.Hua等[28 ] 分别基于梁理论和断裂力学理论推导出不同纤维取向复合材料的层间断裂能,并与有限元和实验结果进行比较,结果表明,层间断裂韧性随加载速率的增加而增加,且在实验和数值仿真中呈现出相同的规律性,但随着裂纹的扩展,理论计算与实验之间的误差逐渐增大.现有的解析方法大多针对的是纤维复合材料或者黏合连接的复合材料,忽略了界面强度高于基体的情况,这些问题使得金属复合材料界面强度的求解存在改进空间. ...
... 在复合板界面参数的求解过程中,常借助双悬臂梁弹性-脆性界面模型对层间断裂韧性进行解析,该模型将复合板界面简化成不同方向的线弹性弹簧连接,可用于一些复合材料混合断裂模式下的层间断裂能[25 ~27 ] 的解析,而对于爆炸焊接或者轧制方式复合的双金属复合板,界面层为上下2层金属在外界高温或高压环境下相互作用而成,简单的线弹性不能准确描述其变形情况,无法进行界面参数的解析,为了获得此类材料的界面参数,本工作基于非对称双悬臂的弹性-脆性界面模型[27 ] 进行改进,考虑界面断裂前的塑性变形情况,提出弹塑性界面模型,通过力平衡方程构建界面应力与外部载荷的关系,并结合相关力学理论对层间断裂能进行解析.同时考虑到双金属复合材料各向异性参数获取比较困难,因此将其简化成各向同性问题进行处理. ...
... [27 ]进行改进,考虑界面断裂前的塑性变形情况,提出弹塑性界面模型,通过力平衡方程构建界面应力与外部载荷的关系,并结合相关力学理论对层间断裂能进行解析.同时考虑到双金属复合材料各向异性参数获取比较困难,因此将其简化成各向同性问题进行处理. ...
... 双悬臂梁实验可以用于评估复合材料界面断裂韧性,Bennati等[27 ] 在纤维复合材料混合断裂模式下的断裂韧性研究中基于此实验建立了非对称性双悬臂梁实验(asymmetric double cantilever beam)模型,并通过该模型的弹性-脆性界面推导出了界面应力、位移等参数的计算公式,本工作在此基础上进行界面层本构模型的优化,完成界面参数的解析. ...
... 如文献[27 ]所示,该模型为长度为L 的层合板,在其一端有长度为a 的初始层间裂缝,b 为模型连接部分的长度.以界面层为分界,上下2种材料厚度分别为H 1 和H 2 ,模型的总厚度H =H 1 +H 2 (假设界面的厚度很小,可忽略不计).模型的宽度为B ,2个方向相反的载荷P 施加在裂缝侧的末端. ...
... 在此模型中,子层合板由可变形的界面连接,该界面可视作线弹性弹簧的连续分布[27 ] .通过线弹性弹簧特性对复合材料界面进行简化,能很好地评估一些界面结合强度不高的复合材料的结合性能,如纤维复合材料等.但由于双金属板界面为上下2层金属在外界高温或高压环境下相互作用而成,结合强度甚至有可能高于基体,界面变形情况也更为复杂,简单的线弹性不足以描述此类材料界面的变形情况.因此本工作在Bennati等[27 ] 工作的基础上,考虑界面的塑性变形情况,即将界面视作弹塑性弹簧的连续分布. ...
... [27 ]工作的基础上,考虑界面的塑性变形情况,即将界面视作弹塑性弹簧的连续分布. ...
... 在裂纹扩展过程中,界面分别会发生拉伸变形和剪切变形.为了便于数学计算,将变形过程中的应力和位移关系简化成如图1 所示的线性弹塑性变化,其中K 和K' 分别为界面处在弹性变形阶段和塑性变形阶段的斜率,界面的断裂受混合模式裂纹扩展准则的控制,可由能量释放率表示[27 ] ,之后界面参数的公式推导过程将基于此界面模型展开. ...
... 分析复合板界面连接部分的受力情况,可以得到层间力的平衡方程,该方程建立了外部载荷与层间内力的关系[27 ] : ...
... 在外力作用下,考虑到2个方向上可能处于不同的变形阶段,一共存在4种变形情况,将不同变形情况下的界面应力位移关系带入到力平衡方程中可以建立界面应力与外界载荷的关系.再引入分层板的本构关系[27 ] : ...
... 在本构模型的提出中,搭接弹簧变形中应力与应变关系的是刚度系数,而在拉伸(剪切)方向上,弹性刚度系数与弹性模量(切变模量)存在着线性关系[31 ] ,即[27 ] : ...
... 建立T型剥离模型,在子层材料的端部施加大小相同、方向相反的位移,图5 所示为T型剥离模型界面结合强度为180 MPa时变形前后的仿真云图.并输出模型界面中每个节点应力随时间的变化曲线,记录模型在剥离过程中的最大应力,经统计为250 N/mm2 .建立长度系数与界面最大应力的解析关系(2个式子分别对应着有限元法和参数迭代法确定Kz 的2种思路)[27 ] : ...
Interlaminar fracture toughness of GLARE laminates based on asymmetric double cantilever beam (ADCB)
2
2019
... 在复合材料界面结合强度的表征工作上,应用梁理论将复合梁模型融入到断裂力学的计算方法中,通过建立双悬臂梁模型,计算临界能量释放率和混合模式相角等参数,用于表征复合材料界面强度[24 ] ,许多学者在这方面做了大量的工作.Bennati等[25 ~27 ] 将纤维层合板视作弹脆性界面连接,提出了混合模式弯曲测试的力学模型,并分别在I型和II型断裂模式下,依据边界条件建立多组微分方程确定界面应力、内力和位移的表达式,评估复合材料层合板混合模式下的层间断裂韧性,以此表征界面结合强度.Hua等[28 ] 分别基于梁理论和断裂力学理论推导出不同纤维取向复合材料的层间断裂能,并与有限元和实验结果进行比较,结果表明,层间断裂韧性随加载速率的增加而增加,且在实验和数值仿真中呈现出相同的规律性,但随着裂纹的扩展,理论计算与实验之间的误差逐渐增大.现有的解析方法大多针对的是纤维复合材料或者黏合连接的复合材料,忽略了界面强度高于基体的情况,这些问题使得金属复合材料界面强度的求解存在改进空间. ...
... 为获得层间断裂能与双悬臂梁端部位移的关系式,需引入梁应变能的计算公式和层间断裂能与应变能的关系,分别如式(9) [28 ] 和式(10) [29 ] 所示: ...
Fracture mechanics of anisotropic materials
1
1989
... 为获得层间断裂能与双悬臂梁端部位移的关系式,需引入梁应变能的计算公式和层间断裂能与应变能的关系,分别如式(9) [28 ] 和式(10) [29 ] 所示: ...
Multi-response optimization on single-point incremental forming of hyperbolic shape Al-1050/Cu bimetal using response surface methodology
5
2018
... 本工作使用的双金属复合板为T2-A1050爆炸复合板,通过拉伸实验可以获得上下层金属物理性能参数,如表1 [30 ] 所示. ...
... Cu-Al 双金属板物理性能参数[30 ] ...
... Physical property parameters of Cu-Al bimetal plates of A1050 and T2[30 ] ...
... 将本工作解析方法获得的界面参数带入到仿真模型中,发现当渐进成形深度达到31 mm时,内聚力单元在图8 中位置出现损伤裂纹,这与文献[30 ]实验中成形件加工开始出现裂纹的位置相同,且其裂纹出现的深度为32.59 mm.可见,本工作有限元模拟结果与实验[30 ] 相差5.3%.因此,利用解析法求得的Cu-Al复合板界面参数可以应用到渐进成形模型中.此外,当界面结合强度由150 MPa增加到208 MPa时,最大成形深度增加了210%.可以看出,增大界面结合强度有助于提高最大成形深度. ...
... [30 ]相差5.3%.因此,利用解析法求得的Cu-Al复合板界面参数可以应用到渐进成形模型中.此外,当界面结合强度由150 MPa增加到208 MPa时,最大成形深度增加了210%.可以看出,增大界面结合强度有助于提高最大成形深度. ...
Delamination growth in composite plates under compressive fatigue loads
1
2006
... 在本构模型的提出中,搭接弹簧变形中应力与应变关系的是刚度系数,而在拉伸(剪切)方向上,弹性刚度系数与弹性模量(切变模量)存在着线性关系[31 ] ,即[27 ] : ...
服役条件下铜铝复合板的扩散层厚度及传热性能
1
2019
... 前文已通过建立T型剥离模型获得了最大剥离应力,同时计算出ΔT =0.076 mm,文献[32 ]指出,Cu-Al复合板实际的界面厚度为微米级.因此结合有限元模型和特征长度系数与界面最大应力的解析关系可以推算出:当界面厚度为1 μm时,ΔT =0.00076 mm,C =3.4,当界面厚度为2 μm时,ΔT =0.00152 mm,C =6.8,…,以此类推,每一个C 对应一个t . ...
服役条件下铜铝复合板的扩散层厚度及传热性能
1
2019
... 前文已通过建立T型剥离模型获得了最大剥离应力,同时计算出ΔT =0.076 mm,文献[32 ]指出,Cu-Al复合板实际的界面厚度为微米级.因此结合有限元模型和特征长度系数与界面最大应力的解析关系可以推算出:当界面厚度为1 μm时,ΔT =0.00076 mm,C =3.4,当界面厚度为2 μm时,ΔT =0.00152 mm,C =6.8,…,以此类推,每一个C 对应一个t . ...