超洁净轴承钢中夹杂物与滚动接触疲劳寿命的关系

doi:10.11900/0412.1961.2019.00337

超洁净轴承钢中夹杂物与滚动接触疲劳寿命的关系

孙飞龙¹, 耿克², 俞峰³, 罗海文^,¹

1.北京科技大学冶金与生态工程学院北京 100083

2.江阴兴澄特钢有限公司江阴 214400

3.钢铁研究总院北京 100081

Relationship of Inclusions and Rolling Contact Fatigue Life for Ultra-Clean Bearing Steel

SUN Feilong¹, GENG Ke², YU Feng³, LUO Haiwen^,¹

1.Metallurgical Department of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China

2.Jiangyin Xingcheng Special Steel Works Co. Ltd. , Jiangyin 214400, China

3.Central Iron and Steel Research Institute，Beijing 100081, China

通讯作者: 罗海文，luohaiwen@ustb.edu.cn，主要从事先进钢铁材料及制造的研究

收稿日期: 2019-10-10 修回日期: 2019-11-15 网络出版日期: 2020-04-23

基金资助:

国家重点研发计划项目.  2016YFB0300102
国家国际科技合作专项项目.  2015DFG51950
中央高校基本科研业务费专项资金项目.  FRF-TP-18-002C2

Corresponding authors: LUO Haiwen, professor, Tel:(010)62332911, E-mail:luohaiwen@ustb.edu.cn

Received: 2019-10-10 Revised: 2019-11-15 Online: 2020-04-23

作者简介 About authors

孙飞龙，男，1993年生，硕士生

摘要

以3种不同工艺工业生产的总O含量均≤6×10^-6的超洁净GCr15轴承钢为研究对象，通过推力片实验测试这3种钢的滚动接触疲劳寿命并获得额定寿命(L₁₀)和中值寿命(L₅₀)，通过ASPEX扫描电镜获得各工艺下的夹杂物样本数据并进行统计分析，使用极值法(SEV)和广义Pareto分布法(GPD)估算出样品中最大夹杂物特征尺(CSMI)，然后将其与实测L₁₀和L₅₀进行对比和分析。结果表明，SEV法仅检测每个样品的最大夹杂物，无法通过其获得的CSMI来合理解释3种钢L₁₀和L₅₀的变化，2者之间相关性较差；而GPD法分析夹杂物时，需要对阈值尺寸以上的所有夹杂物进行表征和统计分析，可以获得夹杂物的数量密度以及不同类型夹杂物的CSMI，GPD法所预测出的最危险类型TiN夹杂物的CSMI可以合理解释L₁₀的变化，2者之间有较好相关性，但无法据此解释L₅₀的变化；但将总的夹杂物数量密度与TiN夹杂物最大特征尺寸相结合，能合理解释3种钢的L₅₀差异，这是因为当更多样品失效时，裂纹萌生位置将不再仅仅局限于最危险类型夹杂物。因此，最危险类型夹杂物的CSMI与超纯净轴承钢中的早期疲劳失效的L₁₀相关性最强，而夹杂物的数量密度对高概率的中值疲劳寿命L₅₀也有重要影响。

关键词： 轴承钢 ; 夹杂物 ; 滚动接触疲劳寿命 ; 统计极值法 ; 广义Pareto分布法

Abstract

The cleanliness of bearing steels produced in China has been greatly improved due to the significant progress in the steelmaking technologies in the past decade, leading to their total oxygen (T.O.) contents lowered to no more than 6×10^-6. Under such a high cleanliness, it is then expected that the influence of non-metallic inclusions on fatigue property should be different from the previous knowledge, because both the size and quantity of inclusions are reduced greatly. Therefore, both inclusions and fatigue properties for three ultra-clean GCr15 (100Cr6) bearing steels containing T.O. around 6×10^-6, which were manufactured via different industrial production processes, were studied for this purpose. First, inclusions were characterized by ASPEX SEM and then statically analyzed by the statistics of extreme values (SEV) and the generalized Pareto distribution (GPD). Next, their rolling contact fatigue lives (RCF) L₁₀ and L₅₀ were measured by flat washer tests. Only the largest inclusion in each sample is required for predicting the characteristic sizes of maximum inclusion (CSMI) for the three steels using the SEV method. The calculated CSMIs, however, are not consistent with the variation of either L₁₀ or L₅₀, indicating they are not relevant. In contrast, the types of inclusions above threshold (u) size can be classified and their number density of inclusions quantified when the GPD method is employed. In particularly, the CSMIs of different types of inclusions can be determined. In this case, it has been found that the CSMI of TiN inclusion, which is the most dangerous for initiating cracking, is in a good agreement with the low probability rolling fatigue life (L₁₀), suggesting that they are very correlated. This, however, cannot explain the variation of high-probability fatigue life (L₅₀). Instead, the density of total inclusions also played an important role on the L₅₀ of ultra-clean bearing steels in addition to the CSMI of TiN inclusions. This is reasonable because cracking shall be initiated at not only the most dangerous TiN inclusion during the early failure but also some other highly dense inclusions particularly during the late failure. Therefore, it is then concluded that the L₁₀ is much more related to the CSMI of most dangerous TiN inclusion; whilst the L₅₀ is strongly affected by the number density of total inclusions.

Keywords： bearing steel ; inclusion ; rolling contact fatigue life ; statistics of extreme values method ; generalized Pareto distribution method

PDF (2358KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孙飞龙, 耿克, 俞峰, 罗海文. 超洁净轴承钢中夹杂物与滚动接触疲劳寿命的关系. 金属学报[J], 2020, 56(5): 693-703 DOI:10.11900/0412.1961.2019.00337

SUN Feilong, GENG Ke, YU Feng, LUO Haiwen. Relationship of Inclusions and Rolling Contact Fatigue Life for Ultra-Clean Bearing Steel. Acta Metallurgica Sinica[J], 2020, 56(5): 693-703 DOI:10.11900/0412.1961.2019.00337

目前我国钢铁行业在冶炼装备和生产技术方面取得了长足的进步，先进的特钢企业已经可以将轴承钢总O含量控制在6×10^-6左右，同时也能够将N、S、Ti含量控制在较低的水平。在这样的高洁净度条件下，轴承钢中非金属夹杂物的数量、类型、尺寸与分布等均发生了很大的变化，因此，需要更多研究对滚动接触疲劳寿命的影响程度与具体机制进行澄清。轴承的破坏通常出现在大尺寸非金属夹杂物或碳化物聚集处^[1]，因此预测轴承的接触疲劳寿命需要对轴承钢中夹杂物进行检测与评价。目前，全球钢铁行业广泛使用ISO 4967标准在金相显微镜下对A、B、C、D、Ds等类型夹杂物按照尺寸进行评级，而在高洁净度条件下(如总O含量≤6×10^-6，S含量≤3×10^-5)，由于夹杂物数量大幅减少、尺寸显著降低，导致该标准难以区分轴承钢的冶金质量^[2]，这就迫切需要一个新的夹杂物评价方法。为此，除了发展夹杂物自动检测等新实验技术以在高洁净度条件下获得更多夹杂物统计样本^[3]，还需要通过概率理论，发展出预测大体积钢中夹杂物最大尺寸的科学方法。目前，在此领域Murakami^[4]提出了统计极值(SEV)法，Shi等^[5]提出了广义Pareto分布(GPD)法。SEV法发展较早，被广泛应用于材料研究领域的许多方面，包括估算材料表面腐蚀坑的深度^[6]、合金显微结构杂质最大偏析程度、估计应力腐蚀引起的使用寿命的变化^[7]等，在夹杂物方面，部分国际领先的轴承制造商也已采用该法对高洁净轴承钢的夹杂物进行评级，并已列入美国ASTM E2283标准^[8]；GPD法虽然更符合实际过程^[9]，但由于起步较晚，尚未被广泛应用。这2种方法都是先通过显微检测获得样品中夹杂物的尺寸数据，再通过概率模型来估计大体积钢中最大夹杂物的特征尺寸，避免了小体积样品中夹杂物检测结果波动大、再次检测重现性差的问题，与轴承滚动接触疲劳寿命更相关。若通过某概率模型计算出的结果与疲劳寿命呈现强相关性，则该概率模型可用于轴承钢夹杂物的分级评价。

因此，本工作对不同工艺生产的超洁净轴承钢的夹杂物进行了检测、表征与统计分析，并分别通过SEV法和GPD法预测出大体积钢中的最大夹杂物尺寸，将其与实测接触疲劳寿命结果对比，分析这2种概率模型的有效性。

1 实验方法和夹杂物评价模型

1.1 实验材料

以国内某企业生产的3组不同生产工艺的GCr15轴承钢为研究对象，记作No.1、No.2、No.3。化学成分如表1所示，其总O含量≤6×10^-6，S含量<3×10^-5，Ti含量≤1.2×10^-5，已达到超洁净度水平，另外No.1和No.3钢为转炉、钢包(LF)精炼和真空循环脱气(RH)精炼工艺生产，其中No.3钢热轧粗轧压下比要大于No.1钢；而No.2钢为电炉、LF精炼和真空脱气(VD)精炼工艺生产，N含量较高。因此，不同工艺生产的夹杂物类型和尺寸分布均不同，尽管其总O含量相近。前期工作^[10]已经对这3种钢在热处理过程中碳化物的析出与演变行为进行了详细研究，发现其最终碳化物颗粒分布均匀且尺寸均在0~1 μm，3者之间并无明显区别，也未发现碳偏析带，因此碳化物并不会对这3种轴承钢的疲劳寿命有显著影响。

表1 GCr15轴承钢的化学成分 (mass fraction / %)

Table 1 Chemical compositions of GCr15 bearing steel

No.	C	Si	Mn	Cr	Ni	Mo	Cu	Al_t	Al_s	P	S	Ca	Mg	Ti	N	O	Fe
1	0.95	0.27	0.41	1.55	0.02	0.01	0.02	0.017	0.015	0.013	0.0021	0.0005	0.0007	0.0012	0.0022	0.0006	Bal.
2	0.99	0.26	0.36	1.48	0.06	0.02	0.08	0.015	0.012	0.012	0.0028	0.0005	0.0009	0.0012	0.0047	0.0005	Bal.
3	0.95	0.24	0.36	1.44	0.02	0.01	0.02	0.017	0.016	0.004	0.0014	0.0005	0.0008	0.0008	0.0022	0.0006	Bal.

Note: Al_t—total aluminum, Al_s—acid soluble aluminum

新窗口打开| 下载CSV

1.2 极值(statistics of extreme values，SEV)法

SEV法采用Gumbel分布^[11]，分布函数为：

G (x) = e x p (- e x p (- (x - λ) / α))

(1)

式中， $G (x)$ 表示夹杂物的尺寸不超过x的概率，x为夹杂物的尺寸， $α$ 为尺寸参数， $λ$ 为位置参数。

由式(1)可得：

x = α [- l n (- l n G (x))] + λ

(2)

令：

y = - l n (- l n G (x))

(3)

重复N个标准检验区S₀ (S₀为面积，mm²)，每个S₀中最大夹杂物的尺寸(x_i)从小到大排列x₁≤x₂≤ $\dots$ ≤x_i≤ $\dots$ ≤x_N (其中，1 $\leq$ i $\leq$ N)，夹杂物尺寸不大于x_i的累计频率G(x_i)为：

G (x_{i}) = i / (N + 1)

(4)

做 $x_{i}$ - $y_{i}$ 关系图，其中 $y_{i} = - l n (- l n G (x_{i}))$ ，根据拟合直线获得参数 $α$ 和 $λ$ 。

设T为返回周期，推导获得体积 $V$ 中最大夹杂物的特征尺寸(characteristic size of the maximum inclusion，CSMI) $x_{v}$ 的表达式为^[12]：

x_{v} = α [- l n (- l n ((T - 1) / T))] + λ

(5)

实验表明，由极大似然法估计出的参数 $α$ 和 $λ$ 值最为有效^[13]，误差最小，似然函数( $L$ )为：

L = \overset{N}{\prod_{i = 1}} \frac{1}{α} e x p \{- (\frac{x_{i} - λ}{α} + e x p (\frac{- (x_{i} - λ)}{α}))\}

(6)

1.3 广义Pareto分布(generalized Pareto distribution，GPD)法

GPD法假设钢中超过阈值u的夹杂物的尺寸x符合GPD分布^[14]，即：

F (x) = 1 - {(1 + ξ (x - u) / σ)}^{- 1 / ξ}

(7)

式中， $F (x)$ 表示夹杂物尺寸不大于x的条件概率， $σ$ 为尺寸参数， $ξ$ 为形状参数。

推导获得体积V中 $x_{v}$ 的表达式为^[15]：

x_{v} = u - \frac{σ}{ξ} \{1 - {(N_{v} (u) V)}^{ξ}\}

(8)

式中， $N_{v} (u)$ 为单位体积中预期超过阈值u的夹杂物的数量。

当V很大，且参数 $ξ < 0$ 时，式(8)中 ${(N_{v} (u) V)}^{ξ} ≪ 1$ ，则有夹杂物的尺寸上限( $x_{l i m}$ )：

x_{l i m} = u - \frac{σ}{ξ}

(9)

以一系列的阈值u与超额均值 $\frac{1}{n} \overset{n}{\sum_{k = 1}} (x_{k} - u)$ (其中， $x_{k}$ 和n分别为大于阈值u的夹杂物的尺寸和数量)做散点图，取线性部分，获得临界阈值，通常以临界阈值作为阈值u的估计值^[16]。采用极大似然法精确估计参数 $σ$ 与 $ξ$ 的值，似然函数 $L$ 为^[17]：

L = \overset{n}{\prod_{k = 1}} \frac{1}{σ} {\{1 + \frac{ξ (x_{k} - u)}{σ}\}}^{- (1 / ξ) - 1}

(10)

2种方法主要区别为：(1) SEV法预测出的最大夹杂物尺寸与钢的体积呈线性关系^[18]，偏离实际情况。而GPD估算方法存在一个最大夹杂物尺寸的预测上限，与实际情况吻合。尺寸上限的存在也使得GPD法成为抗疲劳部件设计的有力工具^[19]。(2) SEV法仅仅考虑所观察视场中最大尺寸的夹杂物，而GPD法在夹杂物统计过程中，则考虑了次大夹杂物和夹杂物类型对疲劳寿命的影响，后者明显更合理。

1.4 夹杂物检测与接触疲劳寿命测试方法

ASTM E2283标准规定，采用SEV法分析时样品数量为24个，因此在直径为60 mm的No.1~No.3 GCr15轴承钢热轧棒材的1/2半径处，采用线切割各切取24个金相试样，观察面为棒材的横截面，标准检验区面积(S₀)为30 mm²。为提高夹杂物尺寸和成分的检测精度，采用ASPEX自动扫描电镜(SEM)对样品中的夹杂物形貌、尺寸和成分进行检测，ASPEX对夹杂物尺寸的确定方法为：通过软件分析计算夹杂物的质心后，从质心引出16条大约以11°间隔分布的弦来计算检测到的夹杂物尺寸，获得夹杂物尺寸的最大值(D_max)、最小值(D_min)和平均值(D_ave)^[20]。前期通过电解萃取法检测这3种钢中的夹杂物的三维形貌，发现对疲劳寿命危害性大的立方状TiN和球状氧化物夹杂在三维空间上均接近对称形状^[21]，这种情况下，按照常规的检验实践，用随机截取获得的二维平面上夹杂物D_ave代表夹杂物的尺寸。

采用SEV法分析时，对每组的24个试样中大于5 μm的夹杂物进行ASPEX检测，扫描面积S₀=30 mm²，确定出每个样品上最大夹杂物的尺寸x_i，并按照x_i (i=1, 2, …, 24)的大小顺序进行样品排列编号；采用GPD法分析时，对大于1 μm的夹杂物进行ASPEX检测。由于此时所检测到的夹杂物数量大幅度增加，检测时间成倍增加，为确保每组样品扫描总面积均大于100 mm²并同时提高实验效率，随机选取24个金相样品中的4个进行检测，每个试样扫描面积大于25 mm²。

为了研究GCr15轴承钢的疲劳寿命，将3种钢的样品在相同的实验参数下进行滚动接触疲劳(RCF)寿命测试。RCF样品为直径60 mm的轴承钢棒材上切下的环状圆片，外径52 mm，内孔直径30 mm，高度10 mm，每种钢测试的样品数量为20个，实验过程中样品滚动接触表面也为棒材的横截面，与夹杂物观察面相同。为保证RCF样品的组织均匀性和机械加工性能，GCr15轴承钢经过热处理和精加工后制成符合粗糙度要求的RCF样品。实验在JP－52推力型接触疲劳试验机上于室温下进行，转速为1500 r/min，使用32号机油润滑，设定最大接触应力为4.5 GPa。RCF样品表面出现剥落凹坑即判定为疲劳失效，或者样品RCF寿命达到10⁸ cyc时，视为样品符合要求，停止测试。

2 实验结果

2.1 SEV法分析结果

经过ASPEX扫描电镜检测，测得每组的24个样品中最大夹杂物的尺寸和形貌如表2所示。可见，No.1~No.3轴承钢样品的最大夹杂物尺寸x_i (i=1, 2, …, 24)分布区间分别位于5.32~29.10、4.95~15.68和5.79~20.98 μm。每组的24个样品中每个样品的最大夹杂物的类型多数是TiN，其次为球状氧化物。在本课题组^[21]前期的电解萃取法实验中，也发现了球状氧化物等大尺寸夹杂物，两者结果基本吻合。

表2 ASPEX检测出的最大夹杂物尺寸和形貌

Table 2 Diameters and morphologies of the maximum inclusions in 24 specimens examined by ASPEX

i	No.1			No.2			No.3
	x_i / μm	Type	Figure	x_i / μm	Type	Figure	x_i / μm	Type	Figure
1	5.32	Glo.-O		4.95	Glo.-O		5.79	TiN
2	5.85	TiN		5.26	Al₂O₃		6.57	TiN
3	6.65	TiN		5.90	TiN		6.97	TiN
4	6.92	Glo.-O		6.08	TiN		7.02	TiN
5	6.93	TiN		6.10	Al₂O₃		7.14	MnS
6	7.15	Al₂O₃		6.99	TiN		7.79	TiN
7	7.16	Sul.-O		7.89	Sul.-O		7.99	Glo.-O
8	7.19	Al₂O₃		7.90	Al₂O₃		8.24	TiN
9	7.69	TiN		7.93	TiN		9.01	TiN
10	7.99	TiN		8.19	Al₂O₃		9.37	TiN
11	8.94	TiN		8.61	TiN		9.40	TiN
12	9.48	Glo.-O		8.75	TiN		9.44	TiN
13	10.77	Glo.-O		8.98	MnS		10.10	TiN
14	10.96	Glo.-O		8.99	Al₂O₃		10.63	MnS
15	11.35	TiN		9.03	Glo.-O		11.47	TiN
16	11.82	TiN		9.08	Glo.-O		11.53	TiN
17	12.43	Glo.-O		9.13	Sul.-O		11.83	TiN
18	12.85	Glo.-O		9.32	TiN		11.88	TiN
19	14.21	Sul.-O		10.58	Glo.-O		12.37	TiN
20	14.80	TiN		10.62	Glo.-O		12.49	TiN
21	18.42	MnS		10.75	TiN		13.87	Sul.-O
22	21.59	Sul.-O		11.53	Glo.-O		14.44	Glo.-O
23	21.83	TiN		12.07	TiN		17.10	TiN
24	29.10	MnS		15.68	Glo.-O		20.98	Glo.-O

Note: Sul.-O—sulfide-oxide, Glo.-O—globular oxide

新窗口打开| 下载CSV

根据检测结果采用SEV法进行分析，如图1所示。通过拟合直线得到No.1~No.3钢所对应SEV法中参数 $α$ 和 $λ$ 的值，当返回周期T=1000时，对应的最大夹杂物的尺寸不超过x的概率G(x)=99.9%，此时 $y = 6.91$ ，估算出样品中最大夹杂物的特征尺寸x_v，结果如表3所示。由此可知，No.2钢最大夹杂物特征尺寸最小；而No.1钢最大夹杂物特征尺寸最大。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 统计极值(SEV)法估算的最大夹杂物特征尺寸结果

Fig.1 Estimating the characteristic sizes of maximum inclusions by the statistics of extreme values (SEV) method (x—inclusion size;S₀—standard inspection area; G—Gumbel function; x_v—characteristic size of the maximum inclusion (CSMI))

(a~c) linear fittings with 95% confidence intervals of No.1, No.2 and No.3 steels

(d) comparison of three SEV linear fittings

表3 SEV法最大夹杂物估算结果

Table 3 The derived results on the inclusions of three steels using the SEV method

No.	$α$	$λ$	Linear fit	x_v / μm
1	5.55	8.62	x=5.55y+8.62	46.96
2	2.22	7.59	x=2.22y+7.59	22.92
3	3.26	8.83	x=3.26y+8.83	31.35

Note: $α$ —scale parameter, $λ$ —location parameter

新窗口打开| 下载CSV

2.2 GPD法分析结果

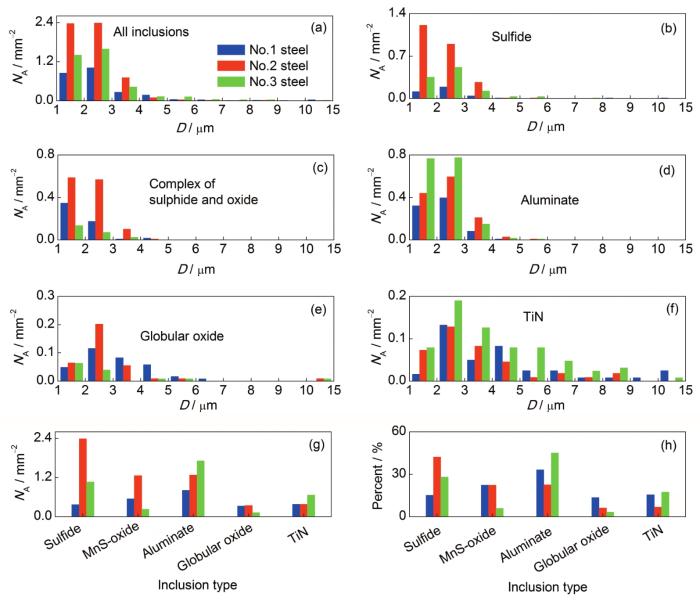
GPD实验中No.1~No.3轴承钢样品检测总面积分别为120.86、109.23和126.42 mm²，夹杂物统计分析结果如图2所示。由图2a可知，No.2钢中总夹杂物数量密度最大，夹杂物数量最多，No.1钢中总夹杂物数量密度最小，夹杂物数量最少，No.3钢居中。由图2b~f，3种钢中硫化物、硫化物氧化物复合夹杂物、Al₂O₃、球状氧化物的尺寸主要分布在1~7 μm之间，大于7 μm的夹杂物主要为TiN夹杂；No.1钢中还含有少量的大于7 μm的硫化物夹杂。由图2g和h可见，No.2钢中硫化物数量密度为2.39 mm^-2，数量最多，占夹杂物总数量的42%，No.1和No.3钢中数量最多的为Al₂O₃，比例分别为33%和45%。夹杂物构成类型的不同与No.2钢为电炉工艺冶炼且S含量相对较高，而No.1和No.3钢为转炉工艺冶炼相关。由于这3种钢中的Ti含量在8×10^-6~12×10^-6，而N含量在2.2×10^-5~4.7×10^-5范围而处于过剩状态，因此所形成TiN夹杂的数量主要由Ti含量决定，虽然No.2钢的N含量是No.1和No.3钢的2倍，但并不能导致其生成最多的TiN。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 ASPEX检测出的No.1~No.3钢中1 μm以上夹杂物的统计分析结果

Fig.2 Experimentals results on the inclusions greater 1 μm in the three steels, examined by ASPEX (D—diameter; N_A—number density)

Color online

(a~f) number density and size distribution of all or different inclusions

(g) number density of each type of inclusions

(h) number percentage of each type of inclusions

3种钢中1 μm以上夹杂物的典型分布如图3所示。可见No.1钢夹杂物数量密度最低，其大尺寸夹杂物主要为TiN和硫化物；No.2钢夹杂物数量密度最高，大尺寸夹杂物主要是TiN，其中硫化物和硫化物氧化物的复合夹杂数量最多且分布密集，夹杂物之间距离明显最短；No.3钢中大尺寸夹杂物主要为TiN，夹杂物密度略高于No.1，但也明显小于No.2。图3中的大夹杂物类型与表2中的最大夹杂物检测结果一致。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 No.1~No.3钢中不同类型和尺寸的夹杂物典型分布

Fig.3 Distributions of the inclusions of different types and sizes in No.1 (a), No.2 (b) and No.3 (c) steels (X_ABS and Y_ABS—the abscissa and ordinate of inclusion measured on the sample surface, respectively)

Color online

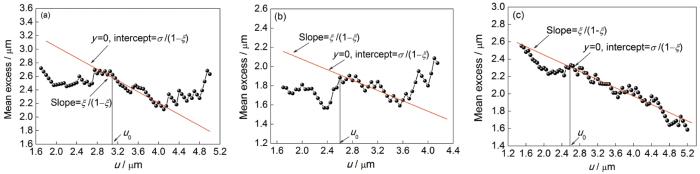
根据检测结果，可以采用GPD法对不同类型的夹杂物进行分析。由于不同类型夹杂物作为疲劳裂纹萌生核心的能力不同，通常认为不易变形、尺寸较大的、具有尖锐棱角的TiN最容易启裂，有实验结果^[22,23]表明，7 μm的TiN与25 μm的氧化物夹杂对疲劳寿命的危害程度相当；其次是点状氧化物、氧硫化夹杂物，最后是易变形的硫化物夹杂，且夹杂物越大产生裂纹的可能性越大^[24]。而表2和图2的夹杂物检测结果均显示，最大尺寸夹杂物多为TiN。因此超洁净轴承钢在TiN处萌生裂纹的可能性最大，故本工作着重对TiN夹杂物进行GPD分析，其超额均值图如图4所示。以临界阈值u₀为阈值u的最终估计值，得到No.1~No.3钢TiN夹杂物的阈值u分别为3.1、2.6和2.6 μm，然后通过本团队所开发的计算机软件^[25]，计算出最大夹杂物的特征尺寸x_v和尺寸上限x_lim，其它类型的夹杂物也按照同样的方法进行分析计算，结果列于表4，表中x_max表示实际检测到的最大夹杂物的尺寸。其中，No.1钢的硫化物夹杂和No.2、No.3钢的球状氧化物夹杂进行GPD分析时，由于形状参数 $ξ$ >0而无法进行预测，推测是因为它们之中存在偶然性大尺寸夹杂物，导致夹杂物尺寸分布不符合预期的规律所致^[26]。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 广义Pareto分布(GPD)法阈值u的确定

Fig.4 The mean excess plots for estimating u in the generalized Pareto distribution (GPD) method (u—threshold, u₀—critical threshold, $σ$ —scale parameter, $ξ$ —shape parameter)

(a) No.1 steel (b) No.2 steel (c) No.3 steel

表4 GPD法估计最大夹杂物的结果

Table 4 Estimating the characteristic sizes of maximum inclusions using the GPD method

Type	No.	u	$ξ$	$σ$	x_max / μm	x_v / μm	x_lim / μm
Sulfide	1	-	-	-	10.14	-	-
	2	2.60	-0.17	0.71	5.25	6.30	6.80
	3	3.80	-0.13	1.30	7.76	11.34	13.96
Sul.-O	1	2.00	-0.13	0.76	4.54	6.63	7.87
	2	2.60	-0.30	0.82	4.64	5.24	5.31
	3	1.90	-0.37	0.92	3.84	4.33	4.36
Al₂O₃	1	1.80	-0.32	0.93	4.32	4.70	4.75
	2	2.40	-0.31	0.99	5.00	5.52	5.58
	3	2.00	-0.05	0.62	5.35	8.06	13.99
Glo.-O	1	2.90	-0.29	1.37	6.28	7.41	7.56
	2	-	-	-	11.53	-	-
	3	-	-	-	14.44	-	-
TiN	1	3.10	-0.29	3.87	11.82	16.01	16.51
	2	2.60	-0.14	2.16	8.75	14.86	17.79
	3	2.60	-0.23	2.84	11.83	14.40	15.12

Note:x_max—measured maximum inclusion size, x_lim—upper limit of inclusion size as predicted using GPD

新窗口打开| 下载CSV

需要指出的是，GPD法计算得到的x_v不仅仅与实际检测到的最大值相关，也与夹杂物尺寸分布有关，其分布越离散，预测出的最大特征尺寸和尺寸上限也越趋于保守，即预测值越高，但所包含误差也越大。由图2f知，No.3钢在每个尺寸范围内均有数量较多的TiN，尺寸分布集中，离散程度最低，而No.2钢TiN尺寸分布离散程度最高，尤其是尺寸大于4 μm后，出现夹杂物数量反复增减的情况，No.1钢TiN尺寸分布离散程度居中，当尺寸大于4 μm后，夹杂物逐渐减少，符合夹杂物尺寸越大数量越少的规律。因此，通过GPD法预测得到的No.2钢的x_v和x_lim均显著高于实检的最大TiN尺寸，且No.2钢的x_lim还超过了含有较大实检尺寸TiN的No.1和No.3钢，这充分说明了GPD法的预测结果是严格根据实际夹杂物的数据，通过科学的概率理论分析而得到的。

注意到表2列出的SEV法检测出的No.1~No.3钢中最大TiN尺寸分别约22、12和17 μm，GPD法所预测No.1钢中TiN的x_v和x_lim分别为16和16.5 μm，均显著小于720 mm²面积下检出的最大TiN尺寸(22 μm)。这说明GPD法预测存在误差，尤其是当样本数据较少且数据离散度较高时，未来需要量化GPD法预测值的误差范围；而要减小误差，只有增加统计样本数，即获得更多夹杂物数据才能达到目的。

2.3 接触疲劳寿命实验结果

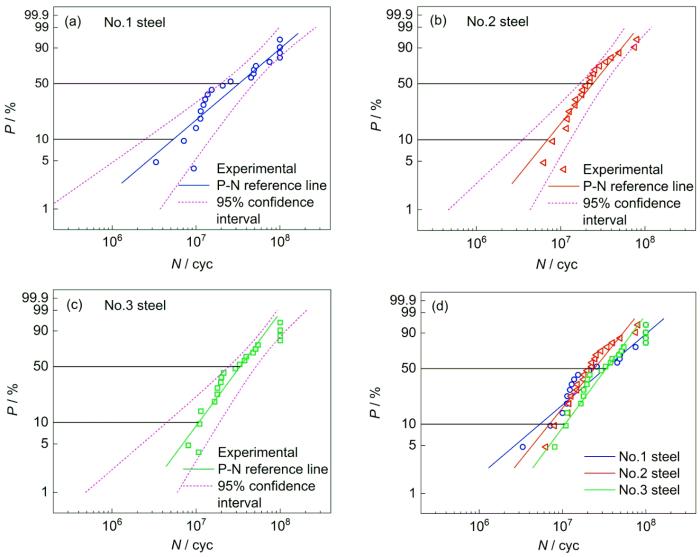
由于检测出的滚动接触疲劳寿命分散度较高，因此对所研究的这3种钢每种钢进行20次推力片实验获得20个疲劳寿命，将所有测试结果绘制于图5的失效概率(P)与疲劳寿命(N)的关系曲线上，并按Weibull概率分布确定疲劳寿命特征值L₁₀ (额定寿命：10%的样品出现疲劳失效)和L₅₀ (中值寿命：50%的样品出现疲劳失效)并进行区间估计。3组样品的L₁₀和L₅₀的95%置信度区间有所重叠，即这3组样品中某些样品的疲劳寿命可能是接近的(图5d)，但以10%样品发生失效作为判据，No.3钢疲劳寿命最长而No.1钢疲劳寿命最短的可能性最大，3种钢的L₁₀依次增大；即使考虑95%置信度区间，No.3钢的L₁₀上下限也明显高于其它钢。如果以50%的样品发生失效作为判据，No.2钢接触疲劳寿命最短的可能性最大，因为No.2钢的L₅₀明显较小，其95%置信度区间也最窄。为建立SEV法和GPD法分析结果与轴承钢疲劳寿命的联系，将这2种方法的分析结果与3种钢中夹杂物总数量密度N_At和接触疲劳实验结果均列于表5。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 3种钢的滚动接触疲劳寿命与Weibull曲线及95%置信区间

Fig.5 Measured rolling contact fatigue (RCF) lives and Weibull fittings with 95% confidence interval for the three steels (P—failure probability, N—RCF life)

(a~c) No.1~No.3 steels (d) the comparison of RCF lives and Weibull fittings in the three steels

表5 3组钢滚动接触疲劳寿命与夹杂物数量密度及SEV和GPD法预测的最大夹杂物特征尺寸对比

Table 5 The measured density of inclusion and CSMIs predicted by both SEV and GPD in comparison with L₁₀ and L₅₀ values of RCF lives for the three steels

No.	L₁₀ / 10⁷ cyc	L₅₀ / 10⁷ cyc	N_At	x_v	x_v (GPD) / μm
	(95% confidence	(95% confidence	mm^-2	(SEV)	Sul	Sul.-O	Al₂O₃	Glo.-O	TiN
	intervals)	intervals)		μm
1	0.54	3.26	2.44	46.96	~	6.63	4.70	7.41	16.01
	(0.25, 1.48)	(1.98, 4.90)
2	0.70	2.41	5.67	22.92	6.30	5.24	5.52	~	14.86
	(0.35, 1.30)	(1.68, 3.34)
3	1.07	3.34	3.81	31.35	11.34	4.33	8.06	~	14.40
	(0.45, 1.90)	(2.45, 5.15)

Note: Sul—sulfide, ~—failed in estimation, N_At—number density of all inclusions

新窗口打开| 下载CSV

3 分析讨论

SEV法计算出的3种钢CSMI相差明显，No.1钢最大、No.2钢最小而No.3钢居中；而以额定寿命L₁₀而言，No.1钢最差，No.3钢最好。普遍认为钢中夹杂物尺寸越小，对应疲劳性能应越好，SEV法预测出No.1钢的x_v最大，与No.1钢最差的L₁₀相吻合；但无法解释为何No.2钢的CSMI明显小于No.3钢，但No.3钢的L₁₀更好而No.2钢的L₅₀却最差。原因是轴承钢在滚动接触疲劳失效时，通常是在位于亚表面的高剪切应力区、超过一定临界尺寸的脆性夹杂物上启裂^[27,28]，但这些启裂位置并不一定总是最大尺寸夹杂物，因为不同类型的夹杂物其裂纹倾向性是不同的，如7 μm大的TiN对疲劳寿命的危害程度就与25 μm的氧化物夹杂相当^[22,23]，而且当相当多夹杂物聚集时其裂纹倾向性也很大^[22]，因此简单依据所有夹杂物中的最大夹杂物来判断轴承钢接触疲劳寿命并不可靠。

GPD法需要对钢中所有类型阈值尺寸以上的夹杂物进行检测与统计，从而获得比SEV法更为详细的数据信息，包括各种类型夹杂物的尺寸分布与数量密度。研究发现，GPD法预测的No.1、No.2和No.3钢中最大TiN夹杂物特征尺寸CSMI依次减小，而L₁₀相对应依次增大(表5)，可见2者有很好的相关度，而且其它类型的夹杂物最大特征尺寸无此相关性。这也能解释为何No.2钢比No.3钢的L₅₀更小，但无法解释为何No.1钢与No.3钢的L₅₀相近，这意味除了最大TiN夹杂物外，还应该有别的因素影响L₅₀寿命。

L₁₀对应的是10%样品刚出现疲劳失效的寿命，这种早期失效最可能发生在那些高剪切应力区含有尺寸大、不易变形的危险夹杂物的样品中。SEV和GPD法均揭示出No.1钢的最大夹杂物特征尺寸最高，这与其最低L₁₀相吻合；但是SEV法无法解释为何No.3钢最大夹杂物特征尺寸大于No.2钢而L₁₀也更高的原因；而基于最危险TiN夹杂物的GPD法则预测出No.3钢TiN夹杂物的CSMI比No.2钢更小，因此与L₁₀结果是一致的。

而当疲劳实验继续进行到50%样品都发生疲劳失效时，处于亚表面高剪切应力区的为数不多的TiN等危险夹杂物等都已经发生启裂，因此对于那些在高剪切应力区不存在TiN等危险夹杂物的样品，在继续的疲劳测试中，将不得不在其它类型夹杂物上启裂；这时那些数量多、分布聚集的夹杂物启裂的倾向性显著增强。图2说明No.2钢由于S含量最高其夹杂物数量密度显著高于No.1和No.3钢，图3说明No.2钢中夹杂物分布也最密集，同时该钢中GPD法预测出的TiN的CSMI位于居中水平，即也可通过TiN导致足够的早期断裂失效，综合以上因素，No.2钢更容易实现50%样品的失效，即L₅₀最小；而No.1钢夹杂物数量密度略低于No.3钢，但TiN特征尺寸略高于No.3钢，导致2者的L₅₀相差较小。

因此，数量众多、密集分布的硫化物和氧硫化物复合夹杂物可能会恶化L₅₀，这与硫化物由于是可变形夹杂物而裂纹敏感性低的传统印象不符。但已有研究^[29]指出，在超洁净轴承钢氧化物夹杂大幅减少的情况下，若硫化物数量众多且密集分布时，也可能危害超洁净轴承钢疲劳性能。超洁净钢中长条状可变形的MnS夹杂尖端就曾发现过微裂纹^[30]；而且，如果硫化物含有Ca时将会变成不变形点状夹杂物，裂纹敏感性显著增强^[31]；另外，链状分布的硫化物与接触压应力垂直时其危害也甚大，如Neishi等^[32]宣称可变形硫化物比球状硫化物造成更严重的失效破坏，因为长条状硫化物可以通过与基体界面解离的方式帮助裂纹的扩展。因此，在超洁净钢中，通过二次精炼深脱S以限制S含量，对L₅₀应该有重要影响^[29]。

综上所述，SEV法预测出的CSMI与疲劳寿命相关性差；GPD法将各类型夹杂物的CSMI进行分类预测后，获得最危险夹杂物TiN的CSMI与早期疲劳失效寿命L₁₀相关性很好，并结合GPD法获得的夹杂物数量密度，也可解释轴承钢中的L₅₀的变化。

4 结论

(1) 电炉工艺冶炼的No.2钢中S含量较高，其夹杂物主要为硫化物和硫化物氧化物复合夹杂，而采用转炉工艺生产的No.1和No.3样品中数量最多的为Al₂O₃；3种钢的最大夹杂物均以TiN居多；No.1钢中夹杂物总数最少，No.2钢因为S含量最高而夹杂物总数最多。推力片实验结果表明，这3种钢的额定滚动接触疲劳寿命L₁₀值No.3钢最高，No.1钢最低；而中值疲劳寿命L₅₀值No.2钢最低，No.3钢最高。

(2) SEV法预测出的最大夹杂物特征尺寸(CSMI)无法合理解释这3种钢L₁₀和L₅₀值的变化，2者相关性较差；而GPD法获得的最危险夹杂物TiN的CSMI与早期疲劳失效寿命L₁₀两者相关性好，可预测其变化趋势；与通过该方法获得的夹杂物数量密度和夹杂物聚集状态相结合，也可解释中期疲劳寿命L₅₀的变化，因此该方法具有更大的应用潜力。

(3) 应用GPD法对超洁净轴承钢中夹杂物进行分析并与滚动接触疲劳寿命的测试结果对比，揭示出早期疲劳失效寿命L₁₀与超纯净轴承钢中的残余Ti含量相关；而且在保持低Ti含量同时，进一步降低S含量、减少夹杂物总数量，可提高中期疲劳寿命L₅₀。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Tomita

Improved fracture toughness of ultrahigh strength steel through control of non-metallic inclusions

[J]. J. Mater. Sci., 1993, 28: 853