中图分类号: TG166.3
通讯作者:
收稿日期: 2013-08-5
修回日期: 2013-12-11
网络出版日期: --
版权声明: 2014 《金属学报》编辑部 版权所有 2014, 金属学报编辑部。使用时,请务必标明出处。
基金资助:
作者简介:
王小娜, 女, 1990年生, 硕士
展开
摘要
利用等转变量方法和恒速升温时效过程中的电阻实验研究了NZ30K镁合金的析出动力学, 获得了动力学模型的激活能
关键词:
Abstract
Age-hardening effect is considerably strong in magnesium alloys containing Nd, making it possible to develop magnesium alloys with low cost and high strength. Although there have been massive researches about the precipitation product sequence and strengthening models in magnesium, aluminum and other light alloys during their ageing processes, those of NZ30K-Mg alloy, a newly-developed magnesium alloy, has not been carefully investigated. The present work mainly focuses on the model of precipitation kinetics and strengthening of NZ30K-Mg alloy. The precipitation kinetics has been investigated using electrical resistivity testing during continuous heating with different heating rates and formulated based on the isoconversional method. Two related model parameters, modified pre-exponential factor
Keywords:
镁合金因其轻质高强的特点而广泛应用于车辆、航空和电子产品等领域[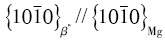 , β′相与基体呈半共格关系[
, β′相与基体呈半共格关系[
针对时效强化合金的强度预测, Esmaeili等[
根据电阻率的基本理论[
根据现有的动力学理论可知, 某一转变过程的转变速率可以用温度T, 相对转变量
尽管已有文献报道了镁合金时效过程中的沉淀析出序列及强化模型, 但迄今为止, 有关NZ30K镁合金的析出动力学及其强度预测模型研究仍少有报道. 本工作在电阻率分析的基础上结合等转变量法得到NZ30K镁合金析出动力学参数, 并利用不同等温时效条件下实验测试获得的屈服强度拟合相关参数, 完善NZ30K镁合金析出强化模型, 以期为该材料的力学性能预测提供理论依据.
实验合金以纯Mg, 纯Zn, 中间合金Mg-Nd和Mg-Zr为原料, 在有SF6/CO2气体保护的井式电阻坩埚炉中熔炼, 并以铸铁模浇铸. 合金铸件在空气电阻炉中进行固溶处理, 固溶处理工艺为540 ℃保温4~10 h, 固溶后空气冷却. 合金化学成分(质量分数, %)为Nd 3.02, Zn 0.26, Zr 0.41, Mg余量.
采用电阻实验法研究了合金时效过程的沉淀析出动力学. 实验在高纯N2气保护的电阻炉中进行, 并采用四点探针法测量时效过程中试样的电阻. 试样尺寸为30 mm×8 mm×2 mm, 在实验前先用砂纸去除试样表面氧化层. 实验参数包括: 恒定输入电流1.5 A, 数据采集步长1.7 s. 分别采用0.10, 0.17, 0.55, 1.08, 2.30, 5.90 和7.25 ℃/min 7个不同加热速度, 测定连续升温过程中电阻的变化.
为研究该镁合金的时效强化模型, 同时进行了不同温度和时效时间处理后镁合金试样的强度测试. 时效温度分别为180, 200和250 ℃, 时效时间为0~200 h. 时效在电阻炉中进行, 空气冷却. 对等温时效材料使用线切割制备获得图1所示拉伸试样, 每组时效条件分别制备3个试样. 室温拉伸实验在Zwick/Roell-20KN材料试验机上进行, 拉伸速率为0.5 mm/min.
经固溶处理的NZ30K镁合金试样在不同加热速率下连续升温过程中的电阻率变化曲线如图2a所示. 随着温度升高, 电阻率曲线出现了2个拐点, 分别对应β″相和β′相的析出[
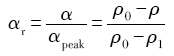 (1)
(1)
式中,α代表时效过程中任一时刻第二相的析出量, αpeak代表峰时效时第二相的析出量. ρ0, ρ1和ρ分别是固溶状态、时效过程中和完全析出后试样的电阻率.
等转变量方法[
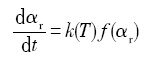 (2)
(2)
式中, k(T)为转变速率常数, 与温度T有关, 表示转变速率
转变速率常数k(T)一般符合Arrhenius方程:
 (3)
(3)
式中,
将式(2)与式(3)合并可以得到:
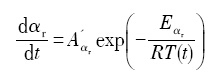 (4)
(4)
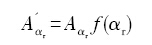 (5)
(5)
式中,
利用等转变量方法确定析出转变动力学时, 通常可用Friedman微分等转变量法[
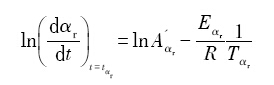 (6)
(6)
式中
对于加热速率恒定为Φ的连续升温过程, 上式可表示为:
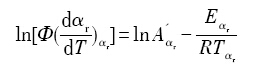 (7)
(7)
显然, 上述处理中无需给出析出转变模型
利用上述确定的2个动力学参数不仅可以获得任意等速加热条件下NZ30K镁合金中析出相的相对析出体积分数曲线, 还可通过下式计算得到在不同温度T等温的时效析出动力学:
 (8)
(8)
式中, T0为等温温度,
图4为计算获得的在170~250 ℃等温时效时NZ30K镁合金的析出动力学曲线.
对NZ30K镁合金分别在180, 200和250 ℃进行不同时间的等温时效处理, 其力学性能如表1所示. 显然, NZ30K镁合金屈服强度随着等温时效温度的升高和等温时间的延长而增大, 直至达到峰时效. 同时, 合金在180, 200和250 ℃ 3个温度下的峰时效屈服强度很接近, 均为150 MPa左右.
对于镁合金而言, 屈服强度
σy =σ0 +σss +σppt (9)
其中, 纯Mg自身的强度σ0为55 MPa[
合金中固溶原子体积分数随时效过程中强化相的沉淀析出而减小, 固溶强化作用逐渐减小. 假设时效过程中第二相析出体积分数与合金发生完全时效时 (此时第二相充分析出, 基体过饱和度接近为0), 第二相析出体积分数之比为相对析出体积分数σr, 则固溶强化对合金屈服强度的贡献可定量表示为[
σss = σ0ss(1-αr)2/3 (10)
其中, σ0ss为未经时效处理的合金中固溶原子对合金屈服强度的贡献. 本研究中实验测得单相固溶态NZ30K镁合金的屈服强度为85 MPa, 与文献[7]数据完全吻合, 由此可知,σ0ss为30 MPa.
析出相的强化作用σppt源于其与位错的相互作用, 与析出相粒子间的平均距离成反比, 可用下式表示[
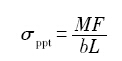 (11)
(11)
其中, M为Taylor因子, b为Burgers矢量模, F代表位错与析出相之间的相互作用力, L表示阻碍位错运动的析出相粒子间的平均距离. F和L均为受时效温度和时间影响的微观组织特征变量.
在欠时效和峰时效阶段, 位错与析出相之间的相互作用力随着析出相尺寸增大而增大, 可表示为:
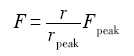 (12)
(12)
其中,r代表时效过程中任一时刻析出相的截面等效半径,
基体晶体结构为hcp的NZ30K镁合金中析出相β″相和β′相均为板条状, 它们的惯习面为
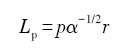 (13)
(13)
式中, p为与基体晶体结构相关的常数. 此处惯习面的析出相粒子平均距离可视为式(11)中阻碍位错运动的析出相粒子间的平均距离.
表1 NZ30K镁合金等温时效处理后试样的相对析出体积分数和屈服强度
Table 1 The relative precipitation volume fraction and yield strength of NZ30K-Mg alloy isothermally aged with different conditions ( σy —yield strength)
| Specimen No. | T / ℃ | t / h | ||
|---|---|---|---|---|
| 1 | 180 | 1 | 0.111 | 109.71 |
| 2 | 180 | 2 | 0.174 | 111.43 |
| 3 | 180 | 5 | 0.269 | 122.25 |
| 4 | 180 | 10 | 0.332 | 125.68 |
| 5 | 180 | 20 | 0.397 | 131.29 |
| 6 | 180 | 50 | 0.513 | 133.39 |
| 7 | 180 | 100 | 0.684 | 141.19 |
| 8 | 180 | 200 | 0.897 | 148.88 |
| 9 | 200 | 1 | 0.197 | 127.43 |
| 10 | 200 | 2 | 0.282 | 135.24 |
| 11 | 200 | 5 | 0.397 | 138.00 |
| 12 | 200 | 10 | 0.504 | 144.44 |
| 13 | 200 | 20 | 0.697 | 148.50 |
| 14 | 200 | 50 | 0.941 | 151.53 |
| 15 | 250 | 0.25 | 0.304 | 138.28 |
| 16 | 250 | 0.5 | 0.548 | 148.89 |
| 17 | 250 | 0.75 | 0.717 | 149.60 |
| 18 | 250 | 1 | 0.850 | 152.59 |
将式(12)和(13)代入式(11), 即可得到NZ30K镁合金的析出强化模型:
 (14)
(14)
式中, C为表示时效强化的参数. 由上式可知, C决定于不同温度时效时的
假设镁合金峰时效时析出相已经充分析出, 即相对体积分数
将上述模型应用于实际时效过程屈服强度的预测, 必须要确定参数C. 一方面, 根据图4的等温时效析出动力学曲线可得到不同温度和时间进行等温时效时的相对体积分数
 (15)
(15)
式中, j代表所有测试力学性能试样对应的时效条件,
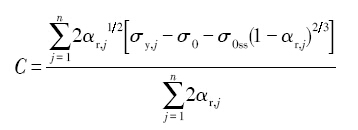 (16)
(16)
将实验数据以及已知的
(1) 利用NZ30K镁合金在连续升温过程中的电阻率变化曲线和等转变量方法研究了该材料时效过程析出动力学, 确定了模型参数激活能
(2) 推导了适用于NZ30K镁合金欠时效阶段和峰时效的强化模型, 此时, 镁合金中析出强化作用在一定温度范围内只与强化相的相对体积分数
(3) 利用实验测试数据和最小二乘法确定了180~250 ℃范围内时效时析出强化模型中的参数C值为93 MPa. 该模型能够较为准确地表征NZ30K镁合金时效过程中的强化效应, 可用于欠时效和峰时效条件下屈服强度的预测.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|

/
| 〈 |
|
〉 |