Metal matrix composites—From science to technological significance
1
2005
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
Manufacturing of light metal matrix composites by combined thermal spray and semisolid forming process—Summary of the current state of technology
0
2010
Damage accumulation during high temperature fatigue of Ti/SiCf metal matrix composites under different stress amplitudes
1
2021
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
Overview of research and development for aluminum matrix composites driven by aerospace equipment demand
1
2023
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
航天装备牵引下的铝基复合材料研究进展与展望
1
2023
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
Elastoplastic modeling of circular fiber-reinforced ductile matrix composites considering a finite RVE
1
2010
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
Micromechanical analysis of strain rate-dependent deformation and failure in composite microstructures under dynamic loading conditions
2
2012
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
... 织物增强复合材料中纱线材料是主要的承载结构,本工作通过建立纱线的代表性单胞有限元模型计算并预测其在高温下的横向和轴向力学性能参数.铝基复合材料中,纱线本质上是浸润填充基体铝合金的碳纤维束,可将其等效为单向纤维增强铝基复合材料.从图3d可见,纱线内部纤维分布均匀且基体中不存在微观空洞和裂纹缺陷.采用Image-Pro Plus软件对图3d中的纤维和基体区域进行色差识别,通过计算纤维与基体面积之比可知,纱线的纤维体积分数为70%.对于纤维分布均匀的单向复合材料,通常假设纤维具有hcp分布特征(图7a),从而最大程度反映其宏观性能的横观各向同性[6].根据纤维直径(6 μm)和纤维体积分数(70%),计算得到纱线的微观尺度RVE模型尺寸,如图7b所示.采用ABAQUS软件中的8节点六面体单元(C3D8R)进行基体和纤维材料的有限元网格划分(图7c),同时在2者之间插入零厚度的内聚力单元(COH3D8)建立界面模型.微观尺度RVE模型网格划分共产生14850个单元,由于其相互平行的表面上节点的面内坐标保持严格对应关系,对该模型直接施加 式(1)所示的周期性边界条件. ...
Effect of fiber cross section geometry on cyclic plastic behavior of continuous fiber reinforced aluminum matrix composites
1
2017
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
Micromechanical modeling on cyclic plastic behavior of unidirectional fiber reinforced aluminum matrix composites
1
2016
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
Micromechanical analysis of interfacial debonding in metal matrix composites subjected to off-axis loading
1
2013
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
Modeling & simulation of interface stability in metal matrix composites subjected to off-axis loading using cohesive zone model under elevated temperature: A review
1
2018
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
The transverse creep and tensile behaviour of SCS-6/Ti-6Al-4V metal matrix composites at 482 oC
1
1994
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
Mechanical behavior of unidirectional SiC/Ti composites subjected to off-axis loading at elevated temperatures
2
2017
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
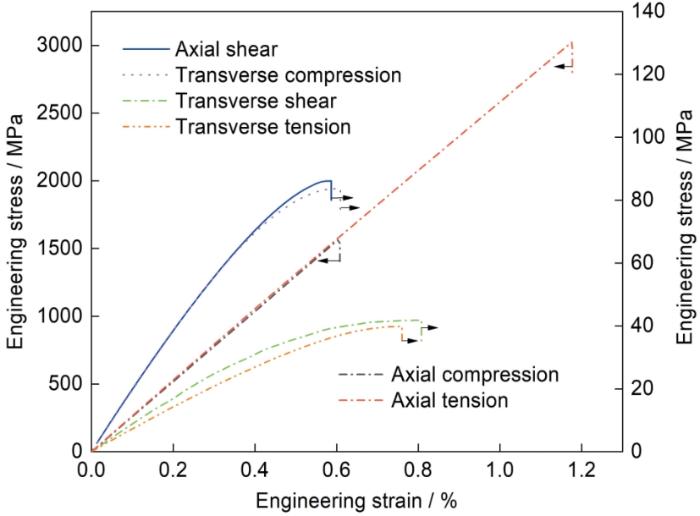
... 利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
Damage initiation and collapse behavior of unidirectional metal matrix composites at elevated temperatures
2
2013
... 相比于传统金属材料和树脂基复合材料,连续纤维增强金属基复合材料具有轻质、高比模量、高比强度、耐热老化以及良好的高温性能,在航空发动机、超音速武器的耐热结构中有着广阔的应用前景[1~3].为了推动连续纤维增强金属基复合材料在航空航天结构中的应用,有必要开展关于其在高温环境下的力学特性与失效行为机理研究[4].近20年来,国内外研究者对连续纤维增强金属基复合材料的断裂力学行为进行了大量研究.在室温力学行为研究方面,Kim和Lee[5]提出了基于有限代表性体积单元(RVE)的弹塑性细观力学损伤模型,用于预测圆截面纤维增强韧性基体复合材料的整体弹塑性损伤行为,进而采用该细观力学模型计算了单向B纤维/Al复合材料和单向SiC/Ti复合材料的横向拉伸力学行为,通过与已有文献报道的实验结果的对比,验证并评估了所提出的细观力学损伤模型的预测能力.Chen和Ghosh[6]研究了加载特性对SiC纤维/Al7075复合材料力学响应和应力波传播的影响.结果表明,体积分数为15%~20%的六角形纤维的排列方式使得复合材料具有较好的能量耗散性能,破坏模式和能量耗散性能与载荷类型、纤维体积分数及分布形态有较强的相关性,但与应变速率的相关性较低.Giugliano等[7,8]对具有不同纤维体积分数的连续纤维增强铝基复合材料的循环塑性行为进行细观力学有限元仿真,发现当纤维体积分数大于40%时,复合材料的承载能力有较大提高.Zhu等[9]基于广义单元法(GMC)和常柔界面(CCI)模型建立了纤维增强金属基复合材料的细观力学模型,研究了界面脱黏和纤维体积分数对复合材料偏轴力学性能的影响,发现纤维体积分数的增加有利于提高复合材料的刚度.近年来,Behera等[10]对连续纤维增强金属基合材料的高温力学行为展开了初步探索.针对连续SiCf (SCS-6)/Ti复合材料,Eggleston和Krempl[11]采用细观力学有限元法分析了其在482 ℃下的横向拉伸蠕变行为,结果表明弱界面结合模型能够较好地预测其横向拉伸力学行为,界面脱黏是造成横向拉伸强度低的主要原因.Aghdam等[12,13]采用基于内聚力模型(CZM)的细观力学有限元模型,研究了SiCf/Ti复合材料在高温偏轴加载过程中的损伤和非线性力学行为,揭示了不同加载角度下复合材料的高温承载破坏机制. ...
... 式中,DInt为界面损伤因子,为界面等效分离位移,和分别为界面初始损伤和界面失效时对应的临界分离位移.根据碳纤维增强铝基复合材料的实验和数值分析结果[36], 式(5)和(6)中的界面性能参数如下: = 16.0 MPa, = = 9.5 MPa, = 0.08 × 10-6 m, = 0.72 × 10-6 m.目前的实验测试手段难以获得界面的高温性能参数,有限元模型中假设室温至400 ℃范围内界面结合性能参数不随温度而发生变化,这在连续纤维增强钛基复合材料高温拉伸力学行为的力学建模与分析中被证明是可行的[13,38]. ...
Continuous fibre reinforced titanium and aluminium composites: A comparison
1
1999
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Microstructure and mechanical properties of z-pinned carbon fiber reinforced aluminum alloy composites
1
2015
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Microstructure and mechanical properties of 2D woven Grf/Al composite
1
2006
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Effect of specific pressure on fabrication of 2D-Cf/Al composite by vacuum and pressure infiltration
1
2013
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Investigation on compressive failure mechanism of 2D cross-ply Cf/Al composites by extrusion directly following vacuum pressure infiltration process
1
2014
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
真空吸渗挤压二维正交铺层复合材料压缩失效机制
1
2014
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Development of textile-reinforced carbon fibre aluminium composites manufactured with gas pressure infiltration methods
1
2009
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Fabrication and mechanical properties of Cu-coated woven carbon fibers reinforced aluminum alloy composite
1
2014
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Bending mechanical property and failure mechanisms of woven carbon fiber-reinforced aluminum alloy composite
1
2016
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Fabrication of woven carbon fibers reinforced Al-Mg (95-5wt%) matrix composites by an electromagnetic casting process
1
2015
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Semisolid-rolling and annealing process of woven carbon fibers reinforced Al-matrix composites
1
2017
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Effect of fiber geometry on the elastic constants of the plain woven fabric reinforced aluminum matrix composites
1
2003
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
Multi scale modeling and characterization of inelastic deformation mechanisms in continuous fiber and 2D woven fabric reinforced metal matrix composites
3
2014
... 大量研究[14,15]表明,单向纤维增强金属基复合材料沿纤维方向的力学性能优异,然而其较差的横向或偏轴性能限制了其构件设计与应用.为了克服单向金属基复合材料的性能短板,近年来国内外研究者提出并开发了各类纤维织物增强金属基复合材料.Zhang等[16]以叠层碳纤维布为增强体制备了纤维分布均匀的铝基复合材料,平行于纤维方向的面内拉伸强度和模量分别为366.2 MPa和110.7 GPa,断口呈现界面脱黏和纤维拔出形貌.Ma等[17]和周计明等[18]采用叠层的正交碳布为增强体,通过真空吸渗挤压法制备了铝基复合材料,其平均拉伸强度为254 MPa (面内0°/90°方向),面内压缩失效形式为界面脱黏和开裂.Hufenbach等[19]实现了镀镍碳纤维布叠层增强镁基和铝基复合材料平板的精密成形,并指出开发三维织物增强金属基复合材料是提高层间性能和可设计性的关键.Yang等[20,21]制备的镀铜碳纤维布叠层增强ZL205铝基复合材料的弯曲强度为357 MPa,其良好的性能归结于高比强度纤维和有效的应力传递.Zhang等[22,23]采用电磁辅助浸渗法制备了叠层碳布增强铝基复合材料,通过半固态轧制强化基体合金并减少浸渗缺陷,显著提高了其面内弯曲强度.研究人员通过构建叠层碳纤维布增强铝基复合材料的细观结构有限元模型,研究织物增强铝基复合材料的断裂力学行为机理.Lee等[24]预测了平纹编织物增强铝基复合材料宏观变形时的弹性力学性能,并通过超声共振光谱测量结果验证了理论预测的有效性.针对叠层Al2O3纤维布增强Al-2Cu复合材料,McWilliams等[25]建立了基于多尺度力学框架的有限元模型,并结合实验分析了其室温拉伸力学行为和渐进破坏过程.结果表明,纱线的横向开裂和界面脱黏是导致其拉伸破坏的主要机制,复合材料的面内抗拉强度在280~353 MPa范围内.现有研究主要集中在纤维织物增强铝基复合材料制备与室温性能的实验分析方面,有关宏/细观力学行为和失效模式的研究十分有限,尚未发现关于其在高温环境下的力学行为特性与失效机理的报道. ...
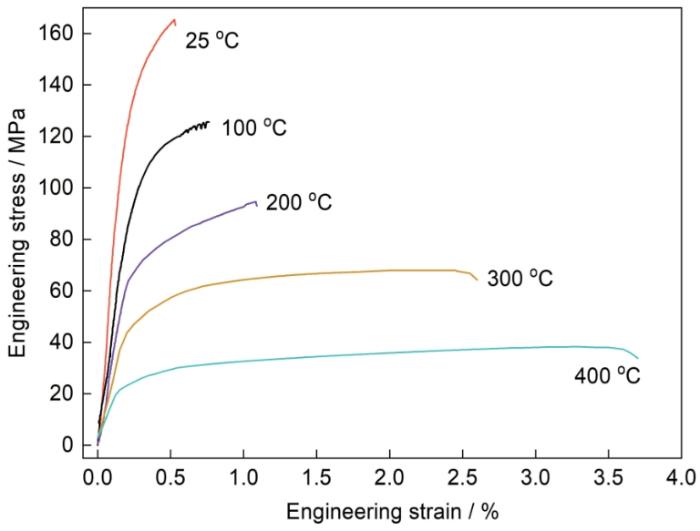
... 铝基复合材料中碳纤维起主要的承载作用,基体铝合金填充固结纤维并发挥载荷转移和传递的作用.研究[25]表明,有限元建模时可将铝基复合材料中的基体合金视为各向同性的弹塑性材料,并采用同类型铝合金的力学性能测试结果确定其性能参数.采用准静态拉伸实验测试与复合材料同炉制备的基体铝合金在不同温度下的拉伸变形力学行为,结果如图6所示.可以看出,基体铝合金在室温下的延伸率较低,原因可能在于随炉冷却较低的冷却时速率导致铝合金晶粒组织粗大,而且未对其进行固溶和时效处理.随着拉伸温度提高,基体铝合金的延伸率有所增大.根据拉伸应力-应变曲线计算得到基体铝合金与温度相关的弹性和塑性力学性能参数,如表1所示.假设其Possion比不随温度变化(始终为0.3),而与温度相关的热膨胀系数[34]也列于表1中.采用von-Mises准则判断基体合金的各向同性屈服行为,利用简化的Johnson-Cook (J-C)本构模型[35]定义基体合金屈服后的塑性流动力学行为: ...
... 对于连续纤维增强金属基复合材料,一般采用延性损伤准则描述其基体合金的损伤演化行为[25,36].基于等效塑性应变相关的线性软化法则,定义铝基复合材料中基体合金的损伤演化因子(DMat)如下[36]: ...
Quasi-static tensile behavior and failure mechanism of laminated puncture CF/Al composites
3
2021
... 本课题组前期采用真空辅助压力浸渗法制备了斜纹碳布缝合织物结构增强铝基复合材料,探索了其室温拉伸、弯曲和压缩性能[26~28],但尚缺乏对其高温拉伸力学性能和失效机理的深入研究.为此,本工作采用数值模拟与实验相结合的方法研究了其在400 ℃高温下的拉伸断裂力学行为,根据复合材料内部纱线的微观组织和分布特征,分别建立纱线和复合材料的微观和细观尺度单胞有限元模型,计算并分析复合材料在高温拉伸载荷下的宏观力学响应、组元结构损伤演化与断裂行为,结合高温拉伸力学实验与断口形貌特征,阐明了细观结构损伤对宏观力学响应及失效模式的影响机制,以期为该复合材料的高温结构设计与制备提供理论依据. ...
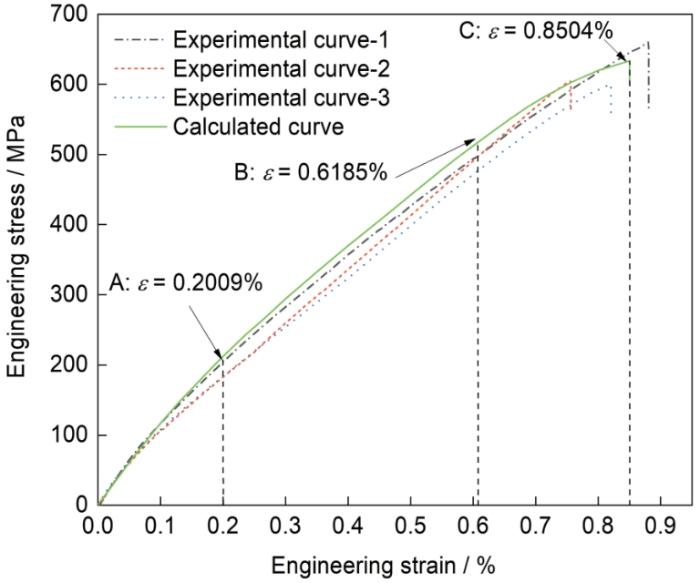
... 在拉伸变形初始阶段,拉伸应力随应变的增大而呈现线性增长趋势,具有类似线弹性的力学响应特征.当拉伸应变超过0.15%后,拉伸应力继续增大但其增长速率有所降低,复合材料表现出非线性力学行为.在最后变形阶段,复合材料发生破坏时出现应力急剧下降的现象.值得注意的是,虽然3条高温拉伸实验曲线具有相似的变化趋势,但并不能完全重合,其原因在于缝合织物编织和缝合都会对碳纤维造成损伤,导致所制备的复合材料内部纱线难以保证很好的分布均匀性和一致性[26~28].此外,高温拉伸弹性模量和断裂应变的预测值均略高于实验平均值.主要原因可能在于纱线内纤维的不均匀分布导致铝基复合材料中存在少量的浸渗空洞或裂纹等缺陷[29],这些缺陷引起的应力集中使得局部纤维过早发生断裂,而细观尺度单胞模型中无法考虑这些微观缺陷对铝基复合材料宏观和细观力学性能的影响. ...
... 图15e为高温拉伸后复合材料中经纱断口的SEM像.可见,大量纤维具有断裂拔出现象且拔出方向基本保持一致,进一步表明复合材料中的经纱发生了轴向拉伸破坏.如前所述,纱线的轴向力学性能远高于其横向性能(表3),复合材料中的纬纱和缝合纱因垂直于拉伸载荷方向而易于发生早期的横向开裂,处于轴向拉应力状态的经纱则起到了主要承载作用.经纱的轴向断裂是引起复合材料最终发生整体失效的主要机制,这与数值模拟分析结果是一致的.应该指出的是,本工作结合数值模拟和拉伸断口分析了复合材料内部组元结构的渐进损伤和失效行为,但难以捕捉铝基复合材料试样表面纱线交织区的破坏过程,未来可采用数字图像相关技术(DIC)测量并分析拉伸试样表面的应变和裂纹扩展行为.此外,相比于该铝基复合材料室温拉伸后的经纱断口[26],高温拉伸后的经纱拉伸断口还出现较为明显的基体合金撕裂痕迹以及不规则条带状基体合金.主要原因可能在于高温环境会导致基体合金拉伸强度下降,但会改善其塑性变形能力,纤维断裂以及界面脱黏和滑移导致了基体合金发生剪切撕裂,并伴随纤维拔出,进而在断口表面形成条带状基体材料. ...
叠层穿刺CF/Al复合材料准静态拉伸力学行为与失效机制
3
2021
... 本课题组前期采用真空辅助压力浸渗法制备了斜纹碳布缝合织物结构增强铝基复合材料,探索了其室温拉伸、弯曲和压缩性能[26~28],但尚缺乏对其高温拉伸力学性能和失效机理的深入研究.为此,本工作采用数值模拟与实验相结合的方法研究了其在400 ℃高温下的拉伸断裂力学行为,根据复合材料内部纱线的微观组织和分布特征,分别建立纱线和复合材料的微观和细观尺度单胞有限元模型,计算并分析复合材料在高温拉伸载荷下的宏观力学响应、组元结构损伤演化与断裂行为,结合高温拉伸力学实验与断口形貌特征,阐明了细观结构损伤对宏观力学响应及失效模式的影响机制,以期为该复合材料的高温结构设计与制备提供理论依据. ...
... 在拉伸变形初始阶段,拉伸应力随应变的增大而呈现线性增长趋势,具有类似线弹性的力学响应特征.当拉伸应变超过0.15%后,拉伸应力继续增大但其增长速率有所降低,复合材料表现出非线性力学行为.在最后变形阶段,复合材料发生破坏时出现应力急剧下降的现象.值得注意的是,虽然3条高温拉伸实验曲线具有相似的变化趋势,但并不能完全重合,其原因在于缝合织物编织和缝合都会对碳纤维造成损伤,导致所制备的复合材料内部纱线难以保证很好的分布均匀性和一致性[26~28].此外,高温拉伸弹性模量和断裂应变的预测值均略高于实验平均值.主要原因可能在于纱线内纤维的不均匀分布导致铝基复合材料中存在少量的浸渗空洞或裂纹等缺陷[29],这些缺陷引起的应力集中使得局部纤维过早发生断裂,而细观尺度单胞模型中无法考虑这些微观缺陷对铝基复合材料宏观和细观力学性能的影响. ...
... 图15e为高温拉伸后复合材料中经纱断口的SEM像.可见,大量纤维具有断裂拔出现象且拔出方向基本保持一致,进一步表明复合材料中的经纱发生了轴向拉伸破坏.如前所述,纱线的轴向力学性能远高于其横向性能(表3),复合材料中的纬纱和缝合纱因垂直于拉伸载荷方向而易于发生早期的横向开裂,处于轴向拉应力状态的经纱则起到了主要承载作用.经纱的轴向断裂是引起复合材料最终发生整体失效的主要机制,这与数值模拟分析结果是一致的.应该指出的是,本工作结合数值模拟和拉伸断口分析了复合材料内部组元结构的渐进损伤和失效行为,但难以捕捉铝基复合材料试样表面纱线交织区的破坏过程,未来可采用数字图像相关技术(DIC)测量并分析拉伸试样表面的应变和裂纹扩展行为.此外,相比于该铝基复合材料室温拉伸后的经纱断口[26],高温拉伸后的经纱拉伸断口还出现较为明显的基体合金撕裂痕迹以及不规则条带状基体合金.主要原因可能在于高温环境会导致基体合金拉伸强度下降,但会改善其塑性变形能力,纤维断裂以及界面脱黏和滑移导致了基体合金发生剪切撕裂,并伴随纤维拔出,进而在断口表面形成条带状基体材料. ...
Bending properties and failure analysis of laminated puncture structural Cf/Al composites
0
2020
叠层穿刺结构Cf/Al复合材料的弯曲性能及失效分析
0
2020
Residual compression mechanical properties after low-speed impact for laminated stitched carbon fiber reinforced aluminum matrix composite
2
2022
... 本课题组前期采用真空辅助压力浸渗法制备了斜纹碳布缝合织物结构增强铝基复合材料,探索了其室温拉伸、弯曲和压缩性能[26~28],但尚缺乏对其高温拉伸力学性能和失效机理的深入研究.为此,本工作采用数值模拟与实验相结合的方法研究了其在400 ℃高温下的拉伸断裂力学行为,根据复合材料内部纱线的微观组织和分布特征,分别建立纱线和复合材料的微观和细观尺度单胞有限元模型,计算并分析复合材料在高温拉伸载荷下的宏观力学响应、组元结构损伤演化与断裂行为,结合高温拉伸力学实验与断口形貌特征,阐明了细观结构损伤对宏观力学响应及失效模式的影响机制,以期为该复合材料的高温结构设计与制备提供理论依据. ...
... 在拉伸变形初始阶段,拉伸应力随应变的增大而呈现线性增长趋势,具有类似线弹性的力学响应特征.当拉伸应变超过0.15%后,拉伸应力继续增大但其增长速率有所降低,复合材料表现出非线性力学行为.在最后变形阶段,复合材料发生破坏时出现应力急剧下降的现象.值得注意的是,虽然3条高温拉伸实验曲线具有相似的变化趋势,但并不能完全重合,其原因在于缝合织物编织和缝合都会对碳纤维造成损伤,导致所制备的复合材料内部纱线难以保证很好的分布均匀性和一致性[26~28].此外,高温拉伸弹性模量和断裂应变的预测值均略高于实验平均值.主要原因可能在于纱线内纤维的不均匀分布导致铝基复合材料中存在少量的浸渗空洞或裂纹等缺陷[29],这些缺陷引起的应力集中使得局部纤维过早发生断裂,而细观尺度单胞模型中无法考虑这些微观缺陷对铝基复合材料宏观和细观力学性能的影响. ...
叠层缝合碳纤维增强铝基复合材料低速冲击及冲击后剩余压缩力学性能
2
2022
... 本课题组前期采用真空辅助压力浸渗法制备了斜纹碳布缝合织物结构增强铝基复合材料,探索了其室温拉伸、弯曲和压缩性能[26~28],但尚缺乏对其高温拉伸力学性能和失效机理的深入研究.为此,本工作采用数值模拟与实验相结合的方法研究了其在400 ℃高温下的拉伸断裂力学行为,根据复合材料内部纱线的微观组织和分布特征,分别建立纱线和复合材料的微观和细观尺度单胞有限元模型,计算并分析复合材料在高温拉伸载荷下的宏观力学响应、组元结构损伤演化与断裂行为,结合高温拉伸力学实验与断口形貌特征,阐明了细观结构损伤对宏观力学响应及失效模式的影响机制,以期为该复合材料的高温结构设计与制备提供理论依据. ...
... 在拉伸变形初始阶段,拉伸应力随应变的增大而呈现线性增长趋势,具有类似线弹性的力学响应特征.当拉伸应变超过0.15%后,拉伸应力继续增大但其增长速率有所降低,复合材料表现出非线性力学行为.在最后变形阶段,复合材料发生破坏时出现应力急剧下降的现象.值得注意的是,虽然3条高温拉伸实验曲线具有相似的变化趋势,但并不能完全重合,其原因在于缝合织物编织和缝合都会对碳纤维造成损伤,导致所制备的复合材料内部纱线难以保证很好的分布均匀性和一致性[26~28].此外,高温拉伸弹性模量和断裂应变的预测值均略高于实验平均值.主要原因可能在于纱线内纤维的不均匀分布导致铝基复合材料中存在少量的浸渗空洞或裂纹等缺陷[29],这些缺陷引起的应力集中使得局部纤维过早发生断裂,而细观尺度单胞模型中无法考虑这些微观缺陷对铝基复合材料宏观和细观力学性能的影响. ...
Micro-defects of 3D-Cf/Al composites by vacuum pressure infiltration
2
2018
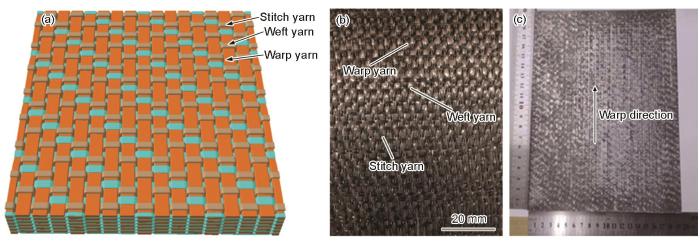
... 选择铸造ZL301铝合金作为基体材料,其化学成分(质量分数,%)为:Mg 9.5~11.0,Si 0.3,Cu 0.1,Mn 0.15,Ti 0.15,Al余量.增强纤维选用M40JB-6K高模量碳纤维,其密度为1.77 g/cm3,纱线细度225 tex,弹性模量380 GPa,极限强度4400 MPa,延伸率1.2%.作为增强体的斜纹碳布缝合织物结构如图1a所示.采用三上一下的编织法制备斜纹碳布,其中经纱和纬纱的细度分别为450和225 tex,经纱和纬纱的编织密度均为3 yarn/10 mm;将斜纹碳布叠层至设定厚度后沿碳布纬纱方向进行缝合,缝合针距为3 mm,最终获得纤维体积分数为48%的斜纹碳布缝合织物增强体,如图1b所示.采用真空辅助气压浸渗法制备铝基复合材料,工艺原理及流程见文献[29].主要制备参数如下:预制体温度500 ℃,铝熔体温度720 ℃,浸渗压力7 MPa.斜纹碳布缝合织物结构增强铝基复合材料板材的表面形貌如图1c所示. ...
... 在拉伸变形初始阶段,拉伸应力随应变的增大而呈现线性增长趋势,具有类似线弹性的力学响应特征.当拉伸应变超过0.15%后,拉伸应力继续增大但其增长速率有所降低,复合材料表现出非线性力学行为.在最后变形阶段,复合材料发生破坏时出现应力急剧下降的现象.值得注意的是,虽然3条高温拉伸实验曲线具有相似的变化趋势,但并不能完全重合,其原因在于缝合织物编织和缝合都会对碳纤维造成损伤,导致所制备的复合材料内部纱线难以保证很好的分布均匀性和一致性[26~28].此外,高温拉伸弹性模量和断裂应变的预测值均略高于实验平均值.主要原因可能在于纱线内纤维的不均匀分布导致铝基复合材料中存在少量的浸渗空洞或裂纹等缺陷[29],这些缺陷引起的应力集中使得局部纤维过早发生断裂,而细观尺度单胞模型中无法考虑这些微观缺陷对铝基复合材料宏观和细观力学性能的影响. ...
真空气压浸渗3D-Cf/Al复合材料微观缺陷分析
2
2018
... 选择铸造ZL301铝合金作为基体材料,其化学成分(质量分数,%)为:Mg 9.5~11.0,Si 0.3,Cu 0.1,Mn 0.15,Ti 0.15,Al余量.增强纤维选用M40JB-6K高模量碳纤维,其密度为1.77 g/cm3,纱线细度225 tex,弹性模量380 GPa,极限强度4400 MPa,延伸率1.2%.作为增强体的斜纹碳布缝合织物结构如图1a所示.采用三上一下的编织法制备斜纹碳布,其中经纱和纬纱的细度分别为450和225 tex,经纱和纬纱的编织密度均为3 yarn/10 mm;将斜纹碳布叠层至设定厚度后沿碳布纬纱方向进行缝合,缝合针距为3 mm,最终获得纤维体积分数为48%的斜纹碳布缝合织物增强体,如图1b所示.采用真空辅助气压浸渗法制备铝基复合材料,工艺原理及流程见文献[29].主要制备参数如下:预制体温度500 ℃,铝熔体温度720 ℃,浸渗压力7 MPa.斜纹碳布缝合织物结构增强铝基复合材料板材的表面形貌如图1c所示. ...
... 在拉伸变形初始阶段,拉伸应力随应变的增大而呈现线性增长趋势,具有类似线弹性的力学响应特征.当拉伸应变超过0.15%后,拉伸应力继续增大但其增长速率有所降低,复合材料表现出非线性力学行为.在最后变形阶段,复合材料发生破坏时出现应力急剧下降的现象.值得注意的是,虽然3条高温拉伸实验曲线具有相似的变化趋势,但并不能完全重合,其原因在于缝合织物编织和缝合都会对碳纤维造成损伤,导致所制备的复合材料内部纱线难以保证很好的分布均匀性和一致性[26~28].此外,高温拉伸弹性模量和断裂应变的预测值均略高于实验平均值.主要原因可能在于纱线内纤维的不均匀分布导致铝基复合材料中存在少量的浸渗空洞或裂纹等缺陷[29],这些缺陷引起的应力集中使得局部纤维过早发生断裂,而细观尺度单胞模型中无法考虑这些微观缺陷对铝基复合材料宏观和细观力学性能的影响. ...
Progressive failure analysis of 2D woven composites at the meso-micro scale
1
2017
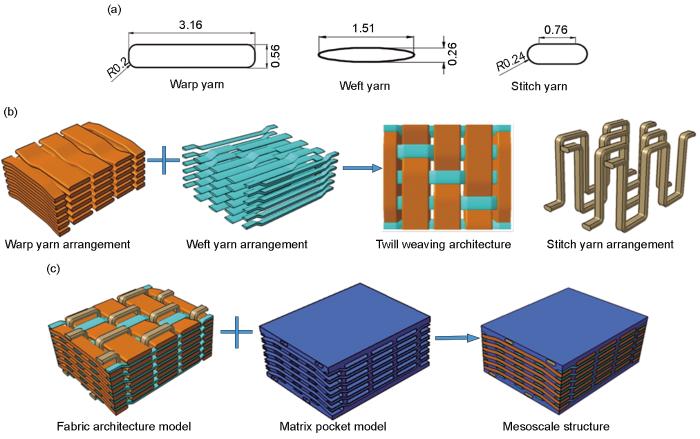
... 织物复合材料中纱线的空间分布形态对复合材料宏观力学性能有重要影响,构建能够反映纱线空间分布结构的代表性体积单元模型是开展复合材料宏/细观力学分析的基础.一般来说,复合材料中织物的纱线形态和构造会导致局部畸变[30].本工作结合织物编织结构参数和复合材料组织观测结果建立细观尺度的纱线结构模型.采用OM观察铝基复合材料内部纱线的截面形状及分布状态,采用SEM观察纱线内部的微观组织和纤维分布形态,结果如图3所示.其中图3a~c分别为经纱、纬纱和缝合纱的横截面形态,图3d为纱线内部的微观组织形貌.从图3a和b可以看出,大多数经纱的横截面表出类似矩形的形状特征,而纬纱横截面则呈现出双面凸透镜的特征,这是由于制备过程中在缝合纱的压紧作用下细度大的经纱对纬纱产生挤压所致. ...
Boundary conditions for unit cells from periodic microstructures and their implications
1
2008
... 根据细观力学有限元理论,应在代表复合材料周期性结构的RVE模型边界上施加周期性边界条件,以满足相邻单胞之间边界上的应力连续性和位移协调性[31].如果RVE模型中相互平行的2个表面上节点的面内坐标是严格相等的,则2个平行面上具有相同面内坐标的一对节点的位移关系需满足如下条件[32]: ...
A unified periodical boundary conditions for representative volume elements of composites and applications
1
2003
... 根据细观力学有限元理论,应在代表复合材料周期性结构的RVE模型边界上施加周期性边界条件,以满足相邻单胞之间边界上的应力连续性和位移协调性[31].如果RVE模型中相互平行的2个表面上节点的面内坐标是严格相等的,则2个平行面上具有相同面内坐标的一对节点的位移关系需满足如下条件[32]: ...
Tensile behavior and failure mechanism of 3D woven fabric reinforced aluminum composites
10
2023
... 将细观尺度RVE模型采用四面体单元进行有限元网格划分后,其2个平行表面上节点的面内坐标无法保持完全一致,无法直接施加 式(1)所示的一般周期性边界条件.为此,本工作采用前期研究[33]中基于Python开发的一种改进的周期性边界条件,实现细观尺度RVE模型上周期性边界条件的施加,如图5c所示. ...
... 式中,为初始损伤时的等效塑性应变,为损伤完成(即失效)时的等效塑性应变.表1中给出了根据图6中拉伸应力-应变曲线测得的不同温度下的和.在损伤演化过程中,采用材料刚度下降法处理基体材料损伤后的力学本构关系[33],即: ...
... 由于高模量碳纤维具有良好的耐高温力学性能,本工作将纤维视为与温度无关的线弹性材料,M40J-6K碳纤维的弹性常数、极限强度和热膨胀系数等性能参数如表2[33,39~41]所示.在微观尺度单胞有限元模型中通过定义横观各向同性的弹性常数描述其弹性变形力学行为.采用最大主应力准则作为纤维断裂失效的判据,即当纤维的轴向或横向上任一应力分量达到该方向上的极限强度时,纤维处于失效状态.纤维失效前满足横观各向同性的线弹性力学本构关系,利用刚度折减法处理纤维失效后的力学本构关系. ...
... 纤维材料的弹性常数、极限强度及热膨胀系数[33,39~41] ...
... Elastic constants, ultimate strengths, and thermal expansion coefficients of fiber[33,39-41] ...
... [
33]
| Axial shear strength | | 340 | MPa | [33] |
| Axial elastic modulus | | 377 | GPa | [41] |
| Axial shear modulus | | 8.9 | GPa | [39] |
| Axial Poisson's ratio | | 0.26 | | [33] |
| Axial thermal expansion coefficient | | -0.83 | 10-6 K-1 | [39] |
| Transverse tensile strength | | 175 | MPa | [40] |
| Transverse compressive strength | | 590 | MPa | [40] |
| Transverse shear strength | | 240 | MPa | [40] |
| Transverse elastic modulus | | 19 | GPa | [39] |
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... [
33]
| Axial elastic modulus | | 377 | GPa | [41] |
| Axial shear modulus | | 8.9 | GPa | [39] |
| Axial Poisson's ratio | | 0.26 | | [33] |
| Axial thermal expansion coefficient | | -0.83 | 10-6 K-1 | [39] |
| Transverse tensile strength | | 175 | MPa | [40] |
| Transverse compressive strength | | 590 | MPa | [40] |
| Transverse shear strength | | 240 | MPa | [40] |
| Transverse elastic modulus | | 19 | GPa | [39] |
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... [
33]
| Axial thermal expansion coefficient | | -0.83 | 10-6 K-1 | [39] |
| Transverse tensile strength | | 175 | MPa | [40] |
| Transverse compressive strength | | 590 | MPa | [40] |
| Transverse shear strength | | 240 | MPa | [40] |
| Transverse elastic modulus | | 19 | GPa | [39] |
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... [
33]
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... 为了分析高温状态下铝基复合材料内部的热应力分布状态,需在细观尺度单胞有限元模型中定义纱线随温度变化的热膨胀和弹性性能参数.本工作将纱线等效为纤维体积分数为70%的单向复合材料,通过解析法计算其在不同温度下的热膨胀和弹性力学性能.研究[43]表明,可以采用Schapery公式[44]和ChamBerlain公式[45]预测单向复合材料的轴向和横向线性热膨胀系数.根据基体合金和纤维材料的热膨胀系数(表1和2[33,39~41]),采用Schapery和ChamBerlain公式计算得到的纱线轴向和横向线性热膨胀系数如表4所示.基于基体和纤维的弹性力学性能参数,采用Hopkins和Chamis[46]提出的细观力学理论公式计算不同温度下纱线在轴向和横向2个方向的弹性力学性能常数,结果见表4. ...
Thermal expansion of aluminum and various important aluminum alloys
5
1925
... 铝基复合材料中碳纤维起主要的承载作用,基体铝合金填充固结纤维并发挥载荷转移和传递的作用.研究[25]表明,有限元建模时可将铝基复合材料中的基体合金视为各向同性的弹塑性材料,并采用同类型铝合金的力学性能测试结果确定其性能参数.采用准静态拉伸实验测试与复合材料同炉制备的基体铝合金在不同温度下的拉伸变形力学行为,结果如图6所示.可以看出,基体铝合金在室温下的延伸率较低,原因可能在于随炉冷却较低的冷却时速率导致铝合金晶粒组织粗大,而且未对其进行固溶和时效处理.随着拉伸温度提高,基体铝合金的延伸率有所增大.根据拉伸应力-应变曲线计算得到基体铝合金与温度相关的弹性和塑性力学性能参数,如表1所示.假设其Possion比不随温度变化(始终为0.3),而与温度相关的热膨胀系数[34]也列于表1中.采用von-Mises准则判断基体合金的各向同性屈服行为,利用简化的Johnson-Cook (J-C)本构模型[35]定义基体合金屈服后的塑性流动力学行为: ...
... 基体铝合金的弹-塑性力学性能参数和热膨胀系数[34] ...
... Elastic-plastic mechanical property parameters and thermal expansion coefficients[34] of the matrix aluminum alloy ...
... [
34]
| 25 | 70.48 | 0.27 | 1.2 | 22.7 |
| 100 | 45.65 | 0.43 | 1.5 | 25.4 |
| 200 | 33.14 | 0.74 | 2.0 | 26.5 |
| 300 | 24.22 | 2.20 | 3.2 | 27.8 |
| 400 | 12.89 | 3.20 | 4.5 | 29.9 |
Note:Em—elastic modulus of the matrix, —equivalent plastic strain at damage initiation, —equivalent plastic strain at fracture, α—coefficient of thermal expansion ...
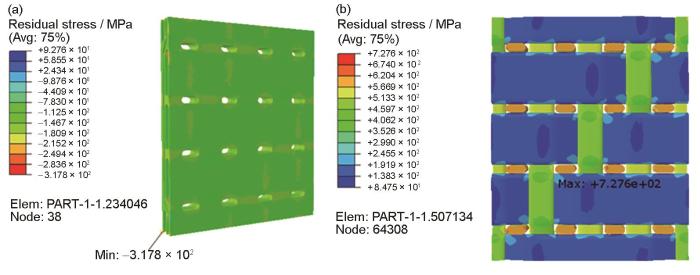
... 一般来说,Cf/Al复合材料中存在制备残余应力.研究[47]表明,退火处理后Cf/Al复合材料基体中的位错数量极少,这意味着制备残余应力得以消除.本工作假设经过退火处理后的复合材料试样中基体和纱线均处于自由应力状态.基于细观尺度单胞有限元分析模型,计算并预测了铝基复合材料升温至高温(400 ℃)后内部的热应力分布状态,如图10所示.可以看出,复合材料中基体合金处于压应力状态且应力分布较均匀,而3类纱线则在整体上处于不同程度的拉应力状态.这是由于纱线的轴向和横向热膨胀系数(表4)均远低于基体合金(表1[34]),升温过程中纱线的轴向和横向热膨胀均小于基体合金,纱线结构对基体合金的热膨胀变形具有抑制作用.特别是经纱和纬纱之间的基体合金热膨胀变形受到2者的共同约束作用,从而使得经/纬纱交错搭接间隙内的基体合金处于局部的高应力水平(最大应力317.8 MPa),如图10a所示.从纱线结构的热应力分布(图10b)来看,经纱和纬纱的拉应力水平均低于缝合纱线,原因在于经纱和纬纱均处于局部屈曲形态,基体合金热膨胀变形对其牵引作用不明显,特别是经纱与纬纱交错处的应力水平较低.处于平直分布状态的缝合纱的轴向热膨胀远远低于其附近的基体合金,基体较大的热膨胀变形对缝合纱产生显著的轴向拉伸作用,导致高温(400 ℃)状态下复合材料内部缝合纱的热应力水平较高(最大应力727.6 MPa). ...
2
2012
... 铝基复合材料中碳纤维起主要的承载作用,基体铝合金填充固结纤维并发挥载荷转移和传递的作用.研究[25]表明,有限元建模时可将铝基复合材料中的基体合金视为各向同性的弹塑性材料,并采用同类型铝合金的力学性能测试结果确定其性能参数.采用准静态拉伸实验测试与复合材料同炉制备的基体铝合金在不同温度下的拉伸变形力学行为,结果如图6所示.可以看出,基体铝合金在室温下的延伸率较低,原因可能在于随炉冷却较低的冷却时速率导致铝合金晶粒组织粗大,而且未对其进行固溶和时效处理.随着拉伸温度提高,基体铝合金的延伸率有所增大.根据拉伸应力-应变曲线计算得到基体铝合金与温度相关的弹性和塑性力学性能参数,如表1所示.假设其Possion比不随温度变化(始终为0.3),而与温度相关的热膨胀系数[34]也列于表1中.采用von-Mises准则判断基体合金的各向同性屈服行为,利用简化的Johnson-Cook (J-C)本构模型[35]定义基体合金屈服后的塑性流动力学行为: ...
... 采用二次名义应力准则[35]作为微观尺度单胞有限元模型中基体与纤维之间界面的初始损伤判据: ...
Micromechanics analysis on the microscopic damage mechanism and mechanical behavior of graphite fiber-reinforced aluminum composites under transverse tension loading
3
2020
... 对于连续纤维增强金属基复合材料,一般采用延性损伤准则描述其基体合金的损伤演化行为[25,36].基于等效塑性应变相关的线性软化法则,定义铝基复合材料中基体合金的损伤演化因子(DMat)如下[36]: ...
... [36]: ...
... 式中,DInt为界面损伤因子,为界面等效分离位移,和分别为界面初始损伤和界面失效时对应的临界分离位移.根据碳纤维增强铝基复合材料的实验和数值分析结果[36], 式(5)和(6)中的界面性能参数如下: = 16.0 MPa, = = 9.5 MPa, = 0.08 × 10-6 m, = 0.72 × 10-6 m.目前的实验测试手段难以获得界面的高温性能参数,有限元模型中假设室温至400 ℃范围内界面结合性能参数不随温度而发生变化,这在连续纤维增强钛基复合材料高温拉伸力学行为的力学建模与分析中被证明是可行的[13,38]. ...
Irreversible deformation of metal matrix composites: A study via the mechanism-based cohesive zone model
3
2015
... 式中,tn、ts、tt分别为界面法向、切向和环向的应力分量,t、t、t分别为界面法向、切向和环向的强度极限,< >为Macaulay运算符.界面应力状态满足 式(5)时,该处的界面损伤开始累积,通过定义依赖于界面等效位移的损伤因子来表征界面的损伤程度[37]: ...
... 利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
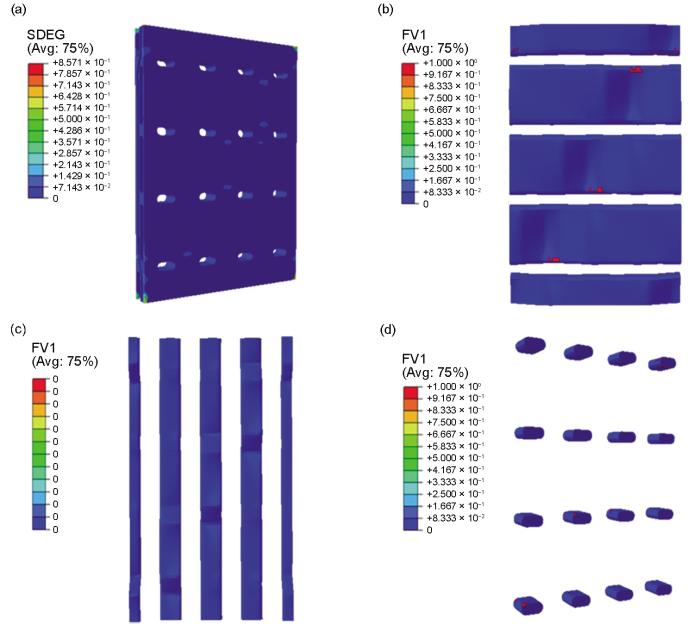
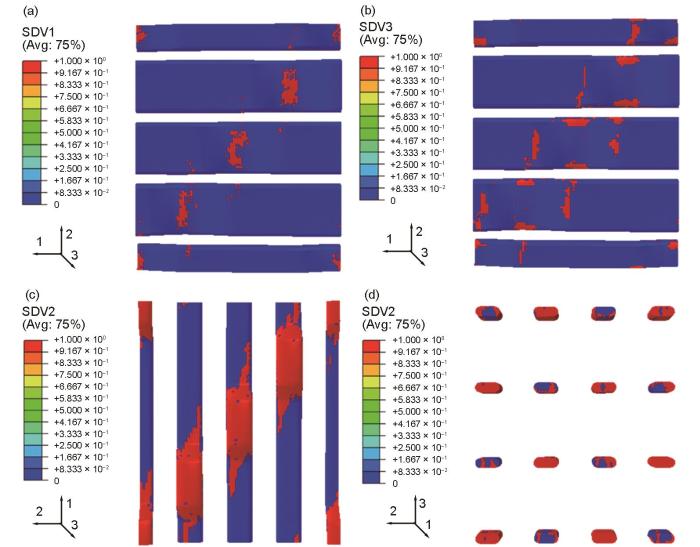
... 图15为铝基复合材料高温拉伸试样的断口形貌.由图15a~c可以看出,大多数断裂后的经纱长短不一并呈现出取向不齐的形貌,而复合材料中纬纱和缝合纱的断裂面则相对较为平整.图16给出了高温拉伸断裂时经纱、纬纱和缝合纱的失效状态模拟结果,其中SDV1为表示纱线轴向失效状态的场变量,SDV2和SDV3分别表示纱线沿宽度和厚度方向失效状态的场变量.从图16a可以看出,经纱的弯曲部位发生了显著的破坏,且以轴向失效模式为主.轴向断裂后经纱中存在大量的纤维拔出现象,且拔出长度参差不齐,如图15d所示.由于经/纬纱交织处纱线之间的相互约束作用,该部位的经纱还出现了沿其厚度方向的失效(图16b),这导致复合材料断口处发生轴向断裂的经纱的取向并不完全一致(图15a~c).由图16c和d可见,纬纱和缝合纱的主要失效模式均为沿其宽度方向的横向开裂,原因是纱线的横向力学性能主要取决于其内部基体和界面的性能[37],承受横向拉伸载荷的纬纱和缝合纱易于发生大面积的界面脱黏而开裂,裂纹在纬纱或缝合纱与基体的界面处沿着碳纤维长轴方向扩展,从而形成如图15a~c所示的较为平坦的断裂面形貌. ...
The analysis on transverse tensile behavior of SiC/Ti-6Al-4V composites by finite element method
1
2010
... 式中,DInt为界面损伤因子,为界面等效分离位移,和分别为界面初始损伤和界面失效时对应的临界分离位移.根据碳纤维增强铝基复合材料的实验和数值分析结果[36], 式(5)和(6)中的界面性能参数如下: = 16.0 MPa, = = 9.5 MPa, = 0.08 × 10-6 m, = 0.72 × 10-6 m.目前的实验测试手段难以获得界面的高温性能参数,有限元模型中假设室温至400 ℃范围内界面结合性能参数不随温度而发生变化,这在连续纤维增强钛基复合材料高温拉伸力学行为的力学建模与分析中被证明是可行的[13,38]. ...
An evaluation of the elastic properties and thermal expansion coefficients of medium and high modulus graphite fibers
8
2005
... 由于高模量碳纤维具有良好的耐高温力学性能,本工作将纤维视为与温度无关的线弹性材料,M40J-6K碳纤维的弹性常数、极限强度和热膨胀系数等性能参数如表2[33,39~41]所示.在微观尺度单胞有限元模型中通过定义横观各向同性的弹性常数描述其弹性变形力学行为.采用最大主应力准则作为纤维断裂失效的判据,即当纤维的轴向或横向上任一应力分量达到该方向上的极限强度时,纤维处于失效状态.纤维失效前满足横观各向同性的线弹性力学本构关系,利用刚度折减法处理纤维失效后的力学本构关系. ...
... 纤维材料的弹性常数、极限强度及热膨胀系数[33,39~41] ...
... Elastic constants, ultimate strengths, and thermal expansion coefficients of fiber[33,39-41] ...
... [
39]
| Axial Poisson's ratio | | 0.26 | | [33] |
| Axial thermal expansion coefficient | | -0.83 | 10-6 K-1 | [39] |
| Transverse tensile strength | | 175 | MPa | [40] |
| Transverse compressive strength | | 590 | MPa | [40] |
| Transverse shear strength | | 240 | MPa | [40] |
| Transverse elastic modulus | | 19 | GPa | [39] |
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... [
39]
| Transverse tensile strength | | 175 | MPa | [40] |
| Transverse compressive strength | | 590 | MPa | [40] |
| Transverse shear strength | | 240 | MPa | [40] |
| Transverse elastic modulus | | 19 | GPa | [39] |
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... [
39]
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... [
39]
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... 为了分析高温状态下铝基复合材料内部的热应力分布状态,需在细观尺度单胞有限元模型中定义纱线随温度变化的热膨胀和弹性性能参数.本工作将纱线等效为纤维体积分数为70%的单向复合材料,通过解析法计算其在不同温度下的热膨胀和弹性力学性能.研究[43]表明,可以采用Schapery公式[44]和ChamBerlain公式[45]预测单向复合材料的轴向和横向线性热膨胀系数.根据基体合金和纤维材料的热膨胀系数(表1和2[33,39~41]),采用Schapery和ChamBerlain公式计算得到的纱线轴向和横向线性热膨胀系数如表4所示.基于基体和纤维的弹性力学性能参数,采用Hopkins和Chamis[46]提出的细观力学理论公式计算不同温度下纱线在轴向和横向2个方向的弹性力学性能常数,结果见表4. ...
Measurement of the transverse mechanical properties of high performance fibres
4
1990
... Elastic constants, ultimate strengths, and thermal expansion coefficients of fiber
[33,39-41]Table 2| Parameter | Symbol | Value | Unit | Ref. |
|---|
| Axial tensile strength | | 4400 | MPa | [41] |
| Axial compressive strength | | 2250 | MPa | [33] |
| Axial shear strength | | 340 | MPa | [33] |
| Axial elastic modulus | | 377 | GPa | [41] |
| Axial shear modulus | | 8.9 | GPa | [39] |
| Axial Poisson's ratio | | 0.26 | | [33] |
| Axial thermal expansion coefficient | | -0.83 | 10-6 K-1 | [39] |
| Transverse tensile strength | | 175 | MPa | [40] |
| Transverse compressive strength | | 590 | MPa | [40] |
| Transverse shear strength | | 240 | MPa | [40] |
| Transverse elastic modulus | | 19 | GPa | [39] |
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... [
40]
| Transverse shear strength | | 240 | MPa | [40] |
| Transverse elastic modulus | | 19 | GPa | [39] |
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... [
40]
| Transverse elastic modulus | | 19 | GPa | [39] |
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... [
40]
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
Tensile mechanical behavior of T300 and M40J fiber bundles at different strain rate
6
2001
... 由于高模量碳纤维具有良好的耐高温力学性能,本工作将纤维视为与温度无关的线弹性材料,M40J-6K碳纤维的弹性常数、极限强度和热膨胀系数等性能参数如表2[33,39~41]所示.在微观尺度单胞有限元模型中通过定义横观各向同性的弹性常数描述其弹性变形力学行为.采用最大主应力准则作为纤维断裂失效的判据,即当纤维的轴向或横向上任一应力分量达到该方向上的极限强度时,纤维处于失效状态.纤维失效前满足横观各向同性的线弹性力学本构关系,利用刚度折减法处理纤维失效后的力学本构关系. ...
... 纤维材料的弹性常数、极限强度及热膨胀系数[33,39~41] ...
... Elastic constants, ultimate strengths, and thermal expansion coefficients of fiber[33,39-41] ...
... [
41]
| Axial compressive strength | | 2250 | MPa | [33] |
| Axial shear strength | | 340 | MPa | [33] |
| Axial elastic modulus | | 377 | GPa | [41] |
| Axial shear modulus | | 8.9 | GPa | [39] |
| Axial Poisson's ratio | | 0.26 | | [33] |
| Axial thermal expansion coefficient | | -0.83 | 10-6 K-1 | [39] |
| Transverse tensile strength | | 175 | MPa | [40] |
| Transverse compressive strength | | 590 | MPa | [40] |
| Transverse shear strength | | 240 | MPa | [40] |
| Transverse elastic modulus | | 19 | GPa | [39] |
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... [
41]
| Axial shear modulus | | 8.9 | GPa | [39] |
| Axial Poisson's ratio | | 0.26 | | [33] |
| Axial thermal expansion coefficient | | -0.83 | 10-6 K-1 | [39] |
| Transverse tensile strength | | 175 | MPa | [40] |
| Transverse compressive strength | | 590 | MPa | [40] |
| Transverse shear strength | | 240 | MPa | [40] |
| Transverse elastic modulus | | 19 | GPa | [39] |
| Transverse shear modulus | | 7.3 | GPa | [40] |
| Transverse Poisson's ratio | | 0.3 | | [33] |
| Transverse thermal expansion coefficient | | 8.0 | 10-6 K-1 | [39] |
利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
... 为了分析高温状态下铝基复合材料内部的热应力分布状态,需在细观尺度单胞有限元模型中定义纱线随温度变化的热膨胀和弹性性能参数.本工作将纱线等效为纤维体积分数为70%的单向复合材料,通过解析法计算其在不同温度下的热膨胀和弹性力学性能.研究[43]表明,可以采用Schapery公式[44]和ChamBerlain公式[45]预测单向复合材料的轴向和横向线性热膨胀系数.根据基体合金和纤维材料的热膨胀系数(表1和2[33,39~41]),采用Schapery和ChamBerlain公式计算得到的纱线轴向和横向线性热膨胀系数如表4所示.基于基体和纤维的弹性力学性能参数,采用Hopkins和Chamis[46]提出的细观力学理论公式计算不同温度下纱线在轴向和横向2个方向的弹性力学性能常数,结果见表4. ...
Maturity of 3D failure criteria for fiber-reinforced composites: Comparison between theories and experiments: Part B of WWFE-II
1
2013
... 利用微观尺度RVE有限元模型分析了纱线在400 ℃高温下的轴向和横向拉伸、压缩和剪切力学行为,通过均匀化计算得到的工程应力-应变曲线如图8所示.可以看出,纱线具有相近的轴向拉伸和压缩弹性模量,但拉伸强度远高于压缩强度,原因在于轴向受载时纤维是主要承载组元,而纤维的轴向压缩强度低于其拉伸强度.由于在横向载荷作用下,纱线的力学性能主要受基体和界面性能支配[12,37],因此其横向拉伸和压缩力学性能显著低于其轴向力学性能.此外,在剪切载荷作用下界面易于脱黏而丧失基体与纤维之间的应力传递能力,因此纱线表现出较差的纵向和横向剪切力学性能.根据不同载荷条件下纱线的高温力学响应曲线(图8),计算得到纱线的高温弹性常数与强度性能参数,见表3.在铝基复合材料细观尺度单胞有限元模型中将纱线作为各向异性材料,根据表3中纱线的轴向、横向强度和剪切强度,采用Tsai-Wu强度准则[42]作为纱线的失效判据: ...
Micro-mechanical model of thermal expansion/contraction for damaged fiber reinforced composites
1
2014
... 为了分析高温状态下铝基复合材料内部的热应力分布状态,需在细观尺度单胞有限元模型中定义纱线随温度变化的热膨胀和弹性性能参数.本工作将纱线等效为纤维体积分数为70%的单向复合材料,通过解析法计算其在不同温度下的热膨胀和弹性力学性能.研究[43]表明,可以采用Schapery公式[44]和ChamBerlain公式[45]预测单向复合材料的轴向和横向线性热膨胀系数.根据基体合金和纤维材料的热膨胀系数(表1和2[33,39~41]),采用Schapery和ChamBerlain公式计算得到的纱线轴向和横向线性热膨胀系数如表4所示.基于基体和纤维的弹性力学性能参数,采用Hopkins和Chamis[46]提出的细观力学理论公式计算不同温度下纱线在轴向和横向2个方向的弹性力学性能常数,结果见表4. ...
纤维增强复合材料考虑损伤的温度胀缩细观力学模型
1
2014
... 为了分析高温状态下铝基复合材料内部的热应力分布状态,需在细观尺度单胞有限元模型中定义纱线随温度变化的热膨胀和弹性性能参数.本工作将纱线等效为纤维体积分数为70%的单向复合材料,通过解析法计算其在不同温度下的热膨胀和弹性力学性能.研究[43]表明,可以采用Schapery公式[44]和ChamBerlain公式[45]预测单向复合材料的轴向和横向线性热膨胀系数.根据基体合金和纤维材料的热膨胀系数(表1和2[33,39~41]),采用Schapery和ChamBerlain公式计算得到的纱线轴向和横向线性热膨胀系数如表4所示.基于基体和纤维的弹性力学性能参数,采用Hopkins和Chamis[46]提出的细观力学理论公式计算不同温度下纱线在轴向和横向2个方向的弹性力学性能常数,结果见表4. ...
Thermal expansion coefficients of composite materials based on energy principles
1
1968
... 为了分析高温状态下铝基复合材料内部的热应力分布状态,需在细观尺度单胞有限元模型中定义纱线随温度变化的热膨胀和弹性性能参数.本工作将纱线等效为纤维体积分数为70%的单向复合材料,通过解析法计算其在不同温度下的热膨胀和弹性力学性能.研究[43]表明,可以采用Schapery公式[44]和ChamBerlain公式[45]预测单向复合材料的轴向和横向线性热膨胀系数.根据基体合金和纤维材料的热膨胀系数(表1和2[33,39~41]),采用Schapery和ChamBerlain公式计算得到的纱线轴向和横向线性热膨胀系数如表4所示.基于基体和纤维的弹性力学性能参数,采用Hopkins和Chamis[46]提出的细观力学理论公式计算不同温度下纱线在轴向和横向2个方向的弹性力学性能常数,结果见表4. ...
The thermal expansion of carbon fibre reinforced plastics: Part 3 The influence of resin type
1
1978
... 为了分析高温状态下铝基复合材料内部的热应力分布状态,需在细观尺度单胞有限元模型中定义纱线随温度变化的热膨胀和弹性性能参数.本工作将纱线等效为纤维体积分数为70%的单向复合材料,通过解析法计算其在不同温度下的热膨胀和弹性力学性能.研究[43]表明,可以采用Schapery公式[44]和ChamBerlain公式[45]预测单向复合材料的轴向和横向线性热膨胀系数.根据基体合金和纤维材料的热膨胀系数(表1和2[33,39~41]),采用Schapery和ChamBerlain公式计算得到的纱线轴向和横向线性热膨胀系数如表4所示.基于基体和纤维的弹性力学性能参数,采用Hopkins和Chamis[46]提出的细观力学理论公式计算不同温度下纱线在轴向和横向2个方向的弹性力学性能常数,结果见表4. ...
A unique set of micromechanics equations for high-temperature metal matrix composites
1
1985
... 为了分析高温状态下铝基复合材料内部的热应力分布状态,需在细观尺度单胞有限元模型中定义纱线随温度变化的热膨胀和弹性性能参数.本工作将纱线等效为纤维体积分数为70%的单向复合材料,通过解析法计算其在不同温度下的热膨胀和弹性力学性能.研究[43]表明,可以采用Schapery公式[44]和ChamBerlain公式[45]预测单向复合材料的轴向和横向线性热膨胀系数.根据基体合金和纤维材料的热膨胀系数(表1和2[33,39~41]),采用Schapery和ChamBerlain公式计算得到的纱线轴向和横向线性热膨胀系数如表4所示.基于基体和纤维的弹性力学性能参数,采用Hopkins和Chamis[46]提出的细观力学理论公式计算不同温度下纱线在轴向和横向2个方向的弹性力学性能常数,结果见表4. ...
Effect of thermal cycling on the mechanical properties of Cf/Al composites
1
2013
... 一般来说,Cf/Al复合材料中存在制备残余应力.研究[47]表明,退火处理后Cf/Al复合材料基体中的位错数量极少,这意味着制备残余应力得以消除.本工作假设经过退火处理后的复合材料试样中基体和纱线均处于自由应力状态.基于细观尺度单胞有限元分析模型,计算并预测了铝基复合材料升温至高温(400 ℃)后内部的热应力分布状态,如图10所示.可以看出,复合材料中基体合金处于压应力状态且应力分布较均匀,而3类纱线则在整体上处于不同程度的拉应力状态.这是由于纱线的轴向和横向热膨胀系数(表4)均远低于基体合金(表1[34]),升温过程中纱线的轴向和横向热膨胀均小于基体合金,纱线结构对基体合金的热膨胀变形具有抑制作用.特别是经纱和纬纱之间的基体合金热膨胀变形受到2者的共同约束作用,从而使得经/纬纱交错搭接间隙内的基体合金处于局部的高应力水平(最大应力317.8 MPa),如图10a所示.从纱线结构的热应力分布(图10b)来看,经纱和纬纱的拉应力水平均低于缝合纱线,原因在于经纱和纬纱均处于局部屈曲形态,基体合金热膨胀变形对其牵引作用不明显,特别是经纱与纬纱交错处的应力水平较低.处于平直分布状态的缝合纱的轴向热膨胀远远低于其附近的基体合金,基体较大的热膨胀变形对缝合纱产生显著的轴向拉伸作用,导致高温(400 ℃)状态下复合材料内部缝合纱的热应力水平较高(最大应力727.6 MPa). ...
Multi-scale study on the fracture behavior of hot compression B4C/6061Al composite
1
2019
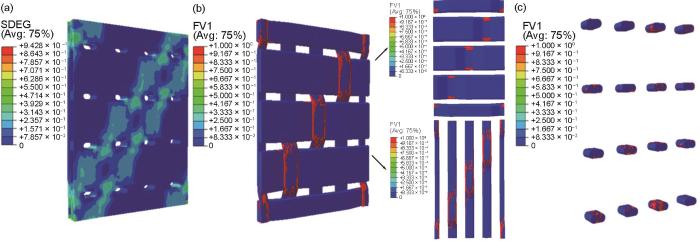
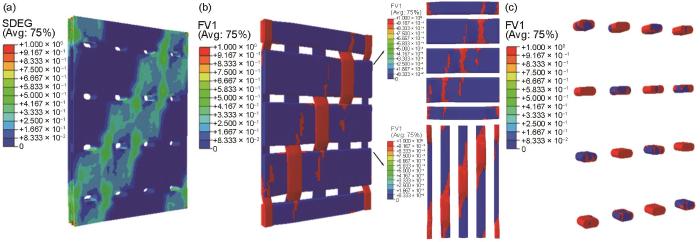
... 图14为复合材料拉伸断裂前(应变0.8504%)内部结构损伤与失效状态的数值模拟结果.可以看出,基体损伤带的位置未发生明显变化,即仍沿着织物的斜纹方向分布,但基体的损伤程度随应变增加而显著加重,在纱线交织区间隙内的Al基体材料出现了局部失效现象(SDEG = 1),见图14a.与之相对应的是该斜纹方向上也出现了经纱和纬纱的失效区,如图14b所示.由此表明拉伸过程中基体的损伤演化与纱线的渐进失效之间有显著的相互作用,纱线交织处基体合金薄弱且由于受纱线的挤压作用而发生严重损伤,损伤程度的加剧使得基体合金的力学性能和载荷传递能力减弱[48],从而导致纱线交织处产生应力集中并先后诱发纬纱和经纱的局部失效.由于拉伸的最后阶段变形量的增大,使得大多数缝合纱出现了整体失效的现象,如图14c所示.值得注意的是,拉伸末期的经纱和纬纱上均出现了完全贯穿其横截面的失效单元,这表明2者此时已发生完全的断裂,特别是作为主要承载结构体的经纱完全断裂,使得复合材料失去了拉伸载荷的承载能力,这表现为图11中应力增长速率在C点的急剧下降. ...
B4C/6061Al复合材料热压缩断裂行为的多尺度研究
1
2019
... 图14为复合材料拉伸断裂前(应变0.8504%)内部结构损伤与失效状态的数值模拟结果.可以看出,基体损伤带的位置未发生明显变化,即仍沿着织物的斜纹方向分布,但基体的损伤程度随应变增加而显著加重,在纱线交织区间隙内的Al基体材料出现了局部失效现象(SDEG = 1),见图14a.与之相对应的是该斜纹方向上也出现了经纱和纬纱的失效区,如图14b所示.由此表明拉伸过程中基体的损伤演化与纱线的渐进失效之间有显著的相互作用,纱线交织处基体合金薄弱且由于受纱线的挤压作用而发生严重损伤,损伤程度的加剧使得基体合金的力学性能和载荷传递能力减弱[48],从而导致纱线交织处产生应力集中并先后诱发纬纱和经纱的局部失效.由于拉伸的最后阶段变形量的增大,使得大多数缝合纱出现了整体失效的现象,如图14c所示.值得注意的是,拉伸末期的经纱和纬纱上均出现了完全贯穿其横截面的失效单元,这表明2者此时已发生完全的断裂,特别是作为主要承载结构体的经纱完全断裂,使得复合材料失去了拉伸载荷的承载能力,这表现为图11中应力增长速率在C点的急剧下降. ...