最新录用 | 当期目录 | 过刊浏览 | 热点文章 | 虚拟专辑 | 阅读排行 | 下载排行 | 引用排行 | 期刊订阅

金属学报, 2025, 61(5): 797-808 DOI: 10.11900/0412.1961.2024.00096

研究论文

钽合金表面渗碳层中碳化物析出及其性能的第一性原理研究

孟祥龙1, 刘瑞良,1, Li D. Y.,2

1 哈尔滨工程大学 材料科学与化学工程学院 超轻材料与表面技术教育部重点实验室 哈尔滨 150001

2 Department of Chemical and Materials Engineering, University of Alberta, Edmonton, AB, Canada T6G 1H9

First Principles Study on the Precipitation and Properties of Carbides in the Surface Carburized Layer of Tantalum Alloys

MENG Xianglong1, LIU Ruiliang,1, Li D. Y.,2

1 Key Laboratory of Superlight Material and Surface Technology of Ministry of Education, College of Materials Science and Chemical Engineering, Harbin Engineering University, Harbin 150001, China

2 Department of Chemical and Materials Engineering, University of Alberta, Edmonton, AB, Canada T6G 1H9

通讯作者: 刘瑞良，liuruiliang@hrbeu.edu.cn，主要从事金属材料强韧化及其表面改性研究；D. Y. Li，dongyang.li@ualberta.ca，主要从事材料表/界面以及计算材料学研究

责任编辑: 李海兰

收稿日期: 2024-03-27   修回日期: 2024-04-29  

基金资助: 国家自然科学基金项目(52371060)
黑龙江省自然科学基金项目(LH2023E060)
中央高校基本科研业务费项目(3072023WD010)

Corresponding authors: LIU Ruiliang, professor, Tel:(0451)82518731, E-mail:liuruiliang@hrbeu.edu.cn;D. Y. Li, Tel:(0451)82518731, E-mail:dongyang.li@ualberta.ca

Received: 2024-03-27   Revised: 2024-04-29  

Fund supported: National Natural Science Foundation of China(52371060)
Natural Science Foundation of Heilongjiang Province(LH2023E060)
Fundamental Research Funds for the Central Universities(3072023WD010)

作者简介 About authors

孟祥龙，男，1999年生，硕士

摘要

Ta及其合金具有熔点高和耐磨性好等特点，采用渗碳等表面改性技术可在Ta及其合金表面获得含碳化钽的改性层，显著提高其表面性能，但是不同钽合金表面析出碳化钽的结构和性能尚不清楚。本工作以Ta-Mo和Ta-W钽合金为研究对象，构建了含不同种类及含量合金元素的fcc和hcp结构复合碳化钽(Ta, M)C (M = Mo、W)模型，利用基于密度泛函理论的第一性原理方法对不同复合碳化钽结构的能量和力学性质进行计算，探索复合碳化钽的强韧化机制。计算结果表明，当Mo和W含量低于50%时，易于形成fcc结构的复合碳化钽，且Mo、W原子浓度越高，具有fcc结构的复合碳化钽的模量和硬度越低，韧性越好；当Mo和W含量高于50%时，易于形成hcp结构的Ta的碳化物，随着Mo、W原子浓度的提高，具有hcp结构的复合碳化钽的模量和硬度增加，韧性降低。

关键词： 钽合金; 复合碳化钽; 第一性原理计算; 晶体结构; 稳定性; 力学性能

Abstract

Tantalum and its alloys have high melting points and good wear resistance, which are primarily used in fields such as the aerospace and nuclear energy industry. Surface modification techniques such as carburization can be used to obtain a modified layer containing tantalum carbide on the surface of tantalum and its alloys, thereby significantly improving their surface properties. However, the structure and properties of tantalum carbide precipitated on the surface of different tantalum alloys remain unclear. This study focuses on Ta-Mo and Ta-W alloys, and constructs fcc and hcp complex tantalum carbide (Ta, M)C (M = Mo, W) models with different alloying elements and their contents. The energy and mechanical properties of different complex tantalum carbide structures were calculated using the first principles method based on the density functional theory to explore the strengthening and toughening mechanisms of complex tantalum carbides. Calculation results indicate that when the content of Mo and W is less than 50%, fcc structured complex tantalum carbide can be easily formed, and the higher the concentration of Mo and W atoms, the lower the modulus and hardness of the complex tantalum carbide with an fcc structure, and the better the toughness. When the content of Mo and W exceeds 50%, tantalum carbides with an hcp structure are easy to form. As the concentration of Mo and W atoms increases, the modulus and hardness of complex tantalum carbides with an hcp structure increase, whereas the toughness decreases.

Keywords： tantalum alloy; complex tantalum carbide; first-principles calculation; crystal structure; stability; mechanical property

PDF (1843KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

孟祥龙, 刘瑞良, Li D. Y.. 钽合金表面渗碳层中碳化物析出及其性能的第一性原理研究[J]. 金属学报, 2025, 61(5): 797-808 DOI:10.11900/0412.1961.2024.00096

MENG Xianglong, LIU Ruiliang, Li D. Y.. First Principles Study on the Precipitation and Properties of Carbides in the Surface Carburized Layer of Tantalum Alloys[J]. Acta Metallurgica Sinica, 2025, 61(5): 797-808 DOI:10.11900/0412.1961.2024.00096

金属Ta具有熔点高、加工性能好、高温稳定性强、耐化学腐蚀性优异等优点，是一种重要的基础材料和战略资源，在电子通讯、机械制造、航空航天、医疗卫生、核能工业等重要领域发挥着不可替代的关键作用[1,2]。随着尖端科学技术的不断发展，对钽制装置和设备在严苛环境下服役寿命的要求越来越高。利用表面处理技术对钽制品表面进行增强，通过引入新的元素在Ta基体材料表面形成新的涂层，制备出性能更加优异的复合材料，显著提升钽制部件的高温稳定性及耐磨损、抗腐蚀等重要性能，促进钽制设备整体性能的显著提升，有效降低Ta及其合金材料失效，具有重要的理论研究意义和社会经济价值[3,4]。

Ta的碳化物相比于纯Ta具有更高的强度、硬度、优良的抗烧蚀性能和耐磨性能，工业上一般采用渗碳、化学沉积、等离子喷涂等方式在钽材料表面获得碳化钽层[5~9]。其中渗碳是一种常见的表面热处理工艺，通过渗碳处理可以在Ta及其合金表面形成一层碳化物，能够有效提高材料的使用性能。唐全红等[7]利用真空碳管炉和真空感应炉进行Ta金属渗碳工艺优化，通过调控炉压、渗载比、渗碳时间，成功制备了可耐受2000 ℃高温的短时抗氧化和抗烧蚀渗层。郑欣[8]利用等离子渗碳技术增强钽材料电阻、耐磨和耐腐蚀性能，通过调节渗碳参数能够改变渗层中TaC和 Ta2C的比例，当渗层中TaC为主要成分时，渗层的腐蚀速率较纯Ta可降低100倍以上。周寰林等[9,10]利用离子渗碳在Ta金属表面制备出6 μm的渗碳层，随着渗碳过程的进行，Ta材表面的缺陷逐渐减少，表面层变得更加平整，渗碳后表层硬度提高至原始Ta材的6倍以上，且抗氧化能力显著提升。李佳等[11]利用真空渗碳的方法对金属Ta及Ta-W合金进行渗碳处理，通过对渗碳温度和渗碳时间的优化调控，在Ta基体表面生成含碳化钽的渗层厚度可达40 μm，该工艺能够有效提升Ta基体材料的强度、硬度及抗烧蚀能力，但该工作未对Ta-W合金表面渗碳层进行精细表征。惠鹏飞[12]利用间隙原子渗碳原理对Ta基体进行表面增强处理，在金属Ta表面制备了致密的碳化钽硬质保护层，碳化钽层的显微硬度达到1900 HV，较原始基体提高了13.8倍，有效提升了Ta表面的硬度及耐磨性能。研究者[13,14]对Ta-Mo-C体系和Ta-W-C体系在fcc和hcp之间变化的相图进行了理论研究，分析了Ta-Mo-C、Ta-W-C、Ta-C-N和W-C-N三元体系的相平衡、溶解度和液相线变化。以上研究表明：Ta-Mo和Ta-W合金以及Ta-Mo-C和Ta-W-C体系受到越来越多的关注，而Ta-Mo和Ta-W合金表面渗碳层中的物相组成，特别是Ta的碳化物结构对渗碳层的性能有重要影响，但是利用实验的方法研究Ta的碳化物析出行为及其性能工作量大，时间和经济成本较高。

基于密度泛函理论的第一性原理计算是微观尺度计算中的重要方法之一[15]。一方面，可采用第一性原理从原子尺度对Ta中碳化物的析出行为进行研究，将0 K、0 Pa下的形成能作为判断析出物热力学稳定性的依据，分析析出物的析出顺序[16]；另一方面，通过第一性原理计算，可以对体系的晶体结构、键合作用、扩散过程和相变过程等进行量化描述。已有研究[17,18]表明，第一性原理计算结果与相关实验结果吻合较好。

综上原因，本工作以钽合金为研究对象，构建了含不同合金元素和含量的复合碳化钽(Ta, M)C (M = Mo、W)模型结构，计算了复合碳化钽结构在不同原子组分占比下的能量及其模量、硬度和延展性等力学性能，预测Ta-Mo及Ta-W合金表面复合碳化钽的析出顺序及其性能，通过电子结构分析，探讨复合碳化钽的强化和韧化机制。相关结果可为阐明钽合金表面渗碳层中析出相的析出及形成机制、揭示渗碳层的强韧化机理提供理论指导。

1 计算方法与建立模型

1.1 第一性原理理论计算方法

第一性原理计算是基于密度泛函理论以VASP程序包和投影平面缀加波(PAW)进行的[19,20]。交换关联泛函采用广义梯度近似的Perdew-Burke-Ernzerhof (PBE)方法来描述[21]。晶体结构的弛豫通过共轭梯度方案进行。以Gamma点方案在5 × 5 × 5网格的Brillouin区进行K点采样[22]。平面波截断能取500 eV，能量的收敛阈值为10-6 eV，力的收敛标准为0.1 eV/ nm。

1.2 能量与力学性质计算方法

复合碳化钽(Ta, M)C (M = W、Mo)的内聚能(Ec)[23]和形成能(Ef)[24]使用以下表达式进行计算：

Ec=(ETotal-∑NiEatomi) / ∑Ni   (i= W, Mo, C)
Ef=(ETotal-∑NiEsolidi) / ∑Ni   (i= W, Mo, C)

式中，ETotal是总能量，Ni 为每种元素的原子个数，Eatomi为不同原子的能量，Esolidi为每种原子形成稳定单质的能量。

弹性性质是固体材料重要的物理参数，可以通过弹性常数来判断材料的弹性及脆韧性。立方结构有3个独立弹性常数(C¯11、C¯12、C¯44)。复合碳化钽中由于晶格畸变使立方结构在不同方向的晶格参数发生变化。本工作中，立方结构的3个独立弹性常数(C¯11、C¯12、C¯44)可用以下计算公式处理得到：

C¯11=(C11+C22+C33) / 3
C¯12=(C12+C13+C23) / 3
C¯44=(C44+C55+C66) / 3

式中，Cij 为弹性常数，多晶结构的弹性模量具有更加普遍的应用性，因此本工作中只进行多晶结构模量的计算。

立方结构的弹性模量公式为[25,26]：

BV=BR=(C¯11+2C¯12) / 3
GV=(3C¯44+C¯11-C¯12) / 5
GR=5C¯11-C¯12C¯44 / [4C44+3C¯11-C¯12]

六方结构的弹性模量公式为[27,28]：

BV=1/9[2C11+C12+4C13+C33]
GV=(1/30) / (P+12C44+12C66)
BR=C2 / P
GR=5/2C2C44C66 / [3BVC44C66+C2(C44+C66)]
P=C11+C12+2C33-4C13
C2=C11+C12C33-2C132

式中，BV表示Voigt体积模量计算方法，GV表示Voigt剪切模量计算方法，BR表示Reuss体积模量计算方法，GR表示Reuss剪切模量计算方法，P和C分别代表一种多项式。

体积模量(B)、剪切模量(G)、Young's模量(E)和Poisson比(ν)由Voigt-Reuss-Hill (VRH)法[29]计算得到：

B=(BV+BR) / 2
G=(GV+GR) / 2
E=9GB / (G+3B)
ν=(3B-E) / 6B

硬度被定义为抗压痕和抗划痕的能力。通过半经验模型，有微观和宏观2种方法来获得硬度。其中，陈氏方法[30]给出的微观模型将硬度(HV)表示为普氏模量比(k)和剪切模量(G)的函数。k是G和B的函数，k = G / B，该模型与实验值非常一致[30]：

HV=2k2G0.585-3

1.3 结构模型

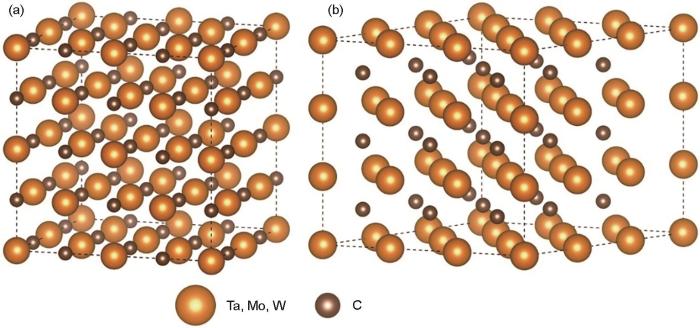
通过特殊准随机结构(SQS)建模方法，使用合金理论自动化工具包中的mcsqs代码对复合碳化钽分别构建2种晶体结构的超级晶胞[31,32]。其中阴离子位点被C原子占据，阳离子位点按照一定比例的过渡金属原子随机分布。本工作将(Ta, M)C (M = W、Mo)构建为2种晶体结构，如图1a为fcc结构(空间群为Fm3¯m)，图1b为六方WC结构 (空间群为P6¯m2[33])。Yu等[34]通过从头算研究不同晶体结构的碳化钽，Ta2C (P3¯m1)是不同结构中能量最低的构型之一。因此，本工作对Ta2C构建空间群为P3¯m1的六方晶体结构。在构建的超级晶胞中，fcc结构的复合碳化钽含有64个原子(2 × 2 × 2超胞)，六方结构的复合碳化钽含有54个原子(3 × 3 × 3超胞)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   不同结构复合碳化钽的特殊准随机结构(SQS)超胞模型

Fig.1   Super structural models of the special quasi-random structure (SQS) of complex tantalum carbides

(a) fcc (b) hcp


2 计算结果与讨论

2.1 结构稳定性分析

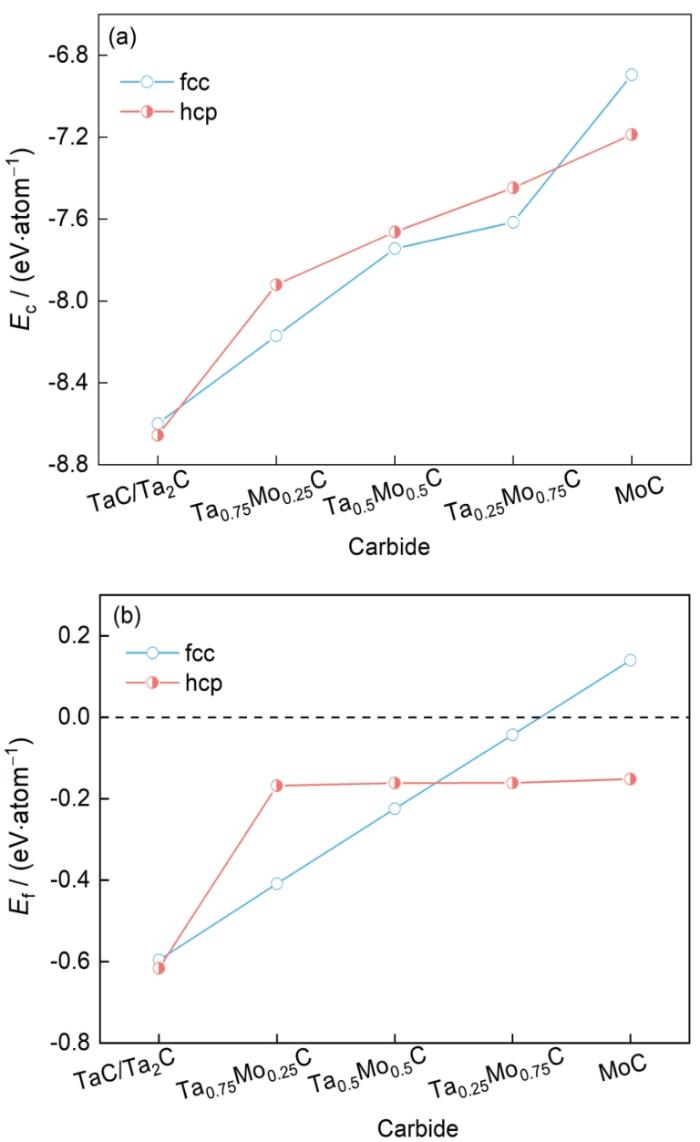
内聚能是指原子停留在晶体或分子中时所具有的能量，内聚能越低，说明结构越稳定[35]。形成能是指化合物或晶体形成过程中发生的能量变化，反映了形成最终产物的能力[36,37]。

表1为含Mo复合碳化钽结构的晶体参数、内聚能和形成能的具体数据。图2为含Mo复合碳化钽分别在fcc和hcp晶体结构下，不同Mo原子浓度时的内聚能和形成能变化趋势。图2中，hcp晶体结构曲线中的碳化钽为Ta2C，在横坐标中不以Ta2C符号表示，以TaC的符号简略表示(下文所有图中的hcp晶体结构曲线，横坐标碳化钽都以TaC符号简略表示)。由表1可知，fcc相的Ec随着体系中Mo原子浓度的增加而逐渐增大，这意味着具有fcc相结构的含Mo复合碳化钽的稳定性随着Mo浓度的增加而逐渐降低。随着体系中Mo原子浓度的增加，含Mo复合碳化钽的Ef逐渐增大，这表明Mo不利于具有fcc结构的含Mo复合碳化钽的形成。在体系中的Ta被Mo完全取代之前，Ef为负，这表明形成过程在热力学上是有利的。当体系中的Ta完全被Mo取代后，MoC的Ef为正，表明形成过程中存在能量障碍。从表1可以看出，随着体系中Mo原子浓度的增加，hcp相的Ec和Ef逐渐增大，这表明具有hcp结构的含Mo复合碳化钽的稳定性和材料形成能力随着Mo原子浓度的增加而逐渐降低。

表1   含Mo复合碳化钽结构的晶体参数、形成能(Ef)和内聚能(Ec)

Table 1  Crystallographic parameters, formation energy (Ef), and cohesive energy (Ec) of complex tantalum carbide with Mo

Crystal structureCarbide

Lattice constant

nm

Angle

(°)

Volume

nm3

Ef

eV·atom-1

Ec

eV·atom-1

fccTaC, this worka¯ = 0.44781α = β = γ = 90.000.71839-0.5962-8.5998
TaC[34]a = 0.447-0.59
Ta0.75Mo0.25Ca¯ = 0.44554α = 90.04, β = γ = 90.000.70753-0.4089-8.1705
Ta0.5Mo0.5Ca¯ = 0.44320α = β =89.78, γ = 90.220.69645-0.2246-7.7442
Ta0.25Mo0.75Ca¯ = 0.44061α = 89.79, β = γ = 90.000.68428-0.0432-7.6155
MoCa¯ = 0.43699α = β = γ = 90.000.667560.1400-6.8956
hcpTa2C

a = b = 0.31249,

c = 0.49593

α = β = 90.00,

γ = 120.00

0.33551-0.6163-8.6566
(P3¯m1, this work)
Ta2C (P3¯m1)[34]

a = b = 0.311,

c = 0.495

γ = 120.00-0.60
Ta0.75Mo0.25C

a = 0.45271,

b = 0.45256,

c = 0.43049

α = 90.05,

β = 89.96,

γ = 120.01

0.68590-0.1681-7.9208
Ta0.5Mo0.5C

a = 0.44703,

b = 0.44702,

c = 0.42883

α = 90.07,

β = 89.98,

γ = 120.01

0.59361-0.1616-7.6633
Ta0.25Mo0.75C

a = 0.44261,

b = 0.44227,

c = 0.42681

α = 89.99,

β = 90.01,

γ = 120.02

0.57870-0.1610-7.4476
MoC

a = b = 0.43761,

c = 0.42422

α = β = 90.00,

γ = 120.00

0.56283-0.1519-7.1876

Note:a¯ = (a + b + c) / 3

新窗口打开| 下载CSV


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   不同结构含Mo复合碳化钽的Ec和Ef

Fig.2   Ec (a) and Ef (b) of complex tantalum carbide containing Mo with different structures


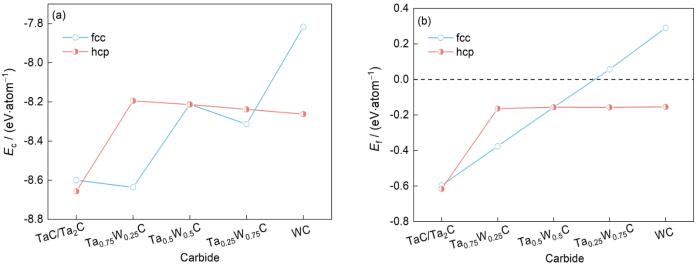
由图2a可以看出，当Mo的原子浓度不超过75%时，fcc体系的Ec (-7.6155 eV/atom)低于hcp体系(-7.4476 eV/atom)。这说明具有fcc晶体结构的含Mo复合碳化钽更为稳定。当Mo原子浓度超过75%时，fcc体系的Ec大于hcp体系，表明具有hcp晶体结构的含Mo复合碳化钽更稳定。从图2b可以看出，当Mo原子的原子浓度不高于50%时，fcc体系的Ef低于hcp体系，表明在该成分组成下容易形成fcc晶体结构。当Mo原子浓度超过50%时，fcc体系的Ef大于hcp体系，表明此时的成分组成偏向于形成hcp晶体结构。

表2为含W复合碳化钽结构的晶体参数、内聚能和形成能。图3给出了fcc和hcp结构含W复合碳化钽内聚能与形成能的关系。从表2可以看出，在TaC中添加25%的W原子会降低系统的Ec。这表明，少量W原子取代了Ta的位置，从而提高了材料的稳定性。W原子浓度的进一步增加会降低体系的Ec，这表明较高浓度的W原子不利于具有fcc相结构的含W复合碳化钽的稳定性。随着体系中W浓度的增加，含W复合碳化钽的Ef也逐渐增加，这表明W不利于形成具有fcc相结构的含W复合碳化钽。W原子浓度在75%及以上时，Ef为正，这意味着形成过程存在能量障碍。从表2可以看出，随着体系中W原子浓度的增加，具有hcp相结构的含W复合碳化钽的Ec先减小后增大，这说明少量的W原子会破坏体系的稳定性，而高浓度的W原子则有利于体系的稳定。随着W原子浓度的增加，体系的Ef逐渐增大，表明形成含W复合碳化钽的能力下降。

表2   含W复合碳化钽结构的晶体参数、Ef和Ec

Table 2  Lattice parameters, Ef, and Ec of complex tantalum carbide with W

Crystal structureCarbide

Lattice constant

nm

Angle

(°)

Volume

nm3

Ef

eV·atom-1

Ec

eV·atom-1

fccTaC, this worka¯ =0.44781α = β = γ = 90.000.71839-0.5962-8.5998
TaC[34]a = 0.447-0.59
Ta0.75W0.25Ca¯ = 0.44543

α = 90.00,

β = 89.99,

γ = 90.00

0.70699-0.3759-8.6364
Ta0.5W0.5Ca¯ = 0.44339

α = 89.79,

β = 90.19,

γ = 90.06

0.69731-0.1566-8.2123
Ta0.25W0.75Ca¯ = 0.44096

α = β = 90.00,

γ = 90.06

0.685900.0565-8.3138
WCa¯ = 0.43821α = β = γ = 90.000.673200.2909-7.8169
hcpTa2C

a = b = 0.31249,

c = 0.49593

α = β = 90.00,

γ = 120.00

0.33551-0.6163-8.6566
(P3¯m1, this work)
Ta2C (P3¯m1)[34]

a = b = 0.311,

c = 0.495

γ = 120-0.60
Ta0.75W0.25C

a = 0.45263,

b = 0.45262,

c = 0.43127

α = 89.94,

β =90.08,

γ = 120.00

0.61212-0.1640-8.1946
Ta0.5W0.5C

a = 0.44731,

b = 0.44718,

c = 0.43034

α = 89.93,

β = 89.98,

γ = 120.00

0.59638-0.1561-8.2137
Ta0.25W0.75C

a = 0.44306,

b = 0.44305,

c = 0.42889

α = 90.00,

β = 89.99,

γ = 119.99

0.58335-0.1573-8.2381
WC

a = b =0.43868,

c = 0.42730

α = β = 90.00,

γ = 120.00

0.56968-0.1543-8.2621

新窗口打开| 下载CSV


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不同结构含W复合碳化钽的Ec和Ef

Fig.3   Energy of complex tantalum carbides containing W with different structures

(a) Ec (b) Ef


由图3a可以看出，当W原子浓度分别为25%和75%时，fcc体系的Ec明显低于hcp体系，这意味着具有fcc晶体结构的含W复合碳化钽更为稳定。当W原子浓度为50%时，fcc体系的Ec (-8.2123 eV/atom)略高于hcp体系(-8.2137 eV/atom)，这表明具有hcp晶体结构的复合碳化钽体系在此成分下更为稳定。从图3b可以看出，当W原子浓度不高于50%时，fcc体系的Ef值低于hcp体系，表明这种成分组合容易形成fcc晶体结构。当W原子浓度高于50%时，fcc体系的Ef值高于hcp体系，这意味着含W复合碳化钽偏向于形成hcp晶体结构。

以上结果表明，当取代Ta原子的Mo原子和W原子的浓度不超过75%时，具有fcc晶体结构的复合碳化钽更稳定；具有hcp晶体结构的复合碳化钽在Mo/W原子浓度超过75%时更为稳定。其次，当分别取代Ta原子的Mo原子和W原子的浓度不超过50%时，复合碳化钽倾向于形成fcc晶体结构。当浓度超过50%时，复合碳化钽更有可能形成hcp晶体结构。

2.2 力学性能

材料的力学性能与其在工业中的应用密切相关。对六方晶体都有5个独立的弹性常数C11、C12、C13、C33和C44[27]，其机械稳定性标准为C44 > 0, C11 > |C12|，(C11 + 2C12)C33 > 2C13  2。对立方晶体都有3个独立的弹性常数C11、C12和C44[25]，机械稳定性准则为C11 > 0，C44 > 0，C11 > |C12|，(C11 + 2C12) > 0。表3~5列出了不同晶体结构复合碳化钽的力学性质。

表3   fcc结构复合碳化钽的弹性常数和力学性质

Table 3  Elastic constants and mechanical properties of complex tantalum carbides with fcc structure

Carbide (fcc)

C11 (C¯11)

GPa

C12 (C¯12)

GPa

C44 (C¯44)

GPa

G

GPa

B

GPa

E

GPa

HV

GPa

G / Bν
TaC, this work72013415420033050021.80.6070.25
TaC[34]737141175216.90339.6724.53
Ta0.75Mo0.25C66813815216730242320.90.6050.25
Ta0.5Mo0.5C57616514615131038917.00.5540.27
Ta0.25Mo0.75C58117412312233932713.20.4860.29
MoC684166702003314997.00.3600.34
Ta0.75W0.25C71513915617931045021.50.6030.25
Ta0.5W0.5C63015014715634140718.80.5770.26
Ta0.25W0.75C61120713212937034612.40.4580.30
WC769170672003305007.00.3480.34

Note:C11, C¯11, C12, C¯12, C44, and C¯44 are elastic constants of carbide with fcc structure; G is shear modulus; B is bulk modulus; E is Young's modulus; HV is Vickers hardness; G / B is Pugh' ratio; ν is Poisson' ratio

新窗口打开| 下载CSV


表4   hcp结构复合碳化钽的弹性常数 (GPa)

Table 4  Elastic constants of complex tantalum carbides with hcp structure

Carbide (hcp)C11C12C13C33C44
Ta2C (P3¯m1, this work)480143138498120
Ta2C (P3¯m1)[34]479164149504133
Ta0.75Mo0.25C511194138764120
Ta0.5Mo0.5C532203151783157
Ta0.25Mo0.75C568206159811203
MoC618213159854263
Ta0.75W0.25C537197138787130
Ta0.5W0.5C581209154823181
Ta0.25W0.75C621224164878235
WC699232167953302

新窗口打开| 下载CSV


表5   hcp结构复合碳化钽的力学性质

Table 5  Mechanical properties of complex tantalum carbides with hcp structure

Carbide

(hcp)

G

GPa

B

GPa

E

GPa

Hv

GPa

G / B

GPa

ν
Ta2C (P3¯m1, this work)14925537416.90.5830.26
Ta2C (P3¯m1)[34]148.08264.6615.87
Ta0.75Mo0.25C16030040715.60.5320.27
Ta0.5Mo0.5C18031545418.80.5730.26
Ta0.25Mo0.75C20933051723.60.6320.24
MoC24634859730.30.7060.21
Ta0.75W0.25C17131043317.20.5520.27
Ta0.5W0.5C20333350722.10.6090.25
Ta0.25W0.75C23435657626.80.6580.23
WC28238568134.70.7320.21

新窗口打开| 下载CSV


由表3和4可知，计算得到的弹性常数都满足力学稳定性准则，这意味着每种复合碳化钽都具有力学稳定性。不同晶体结构中Mo原子取代Ta原子后的力学性质图4所示。从图4a和b可以看出，当含Mo复合碳化钽中Mo原子浓度小于50%时，fcc晶体结构的含Mo复合碳化钽具有较高的G、B、E和HV。当含Mo复合碳化钽中的Mo原子浓度不低于50%时，具有hcp晶体结构的含Mo复合碳化钽具有更高的G、B、E和HV。

图4

新窗口打开| 下载原图ZIP| 生成PPT

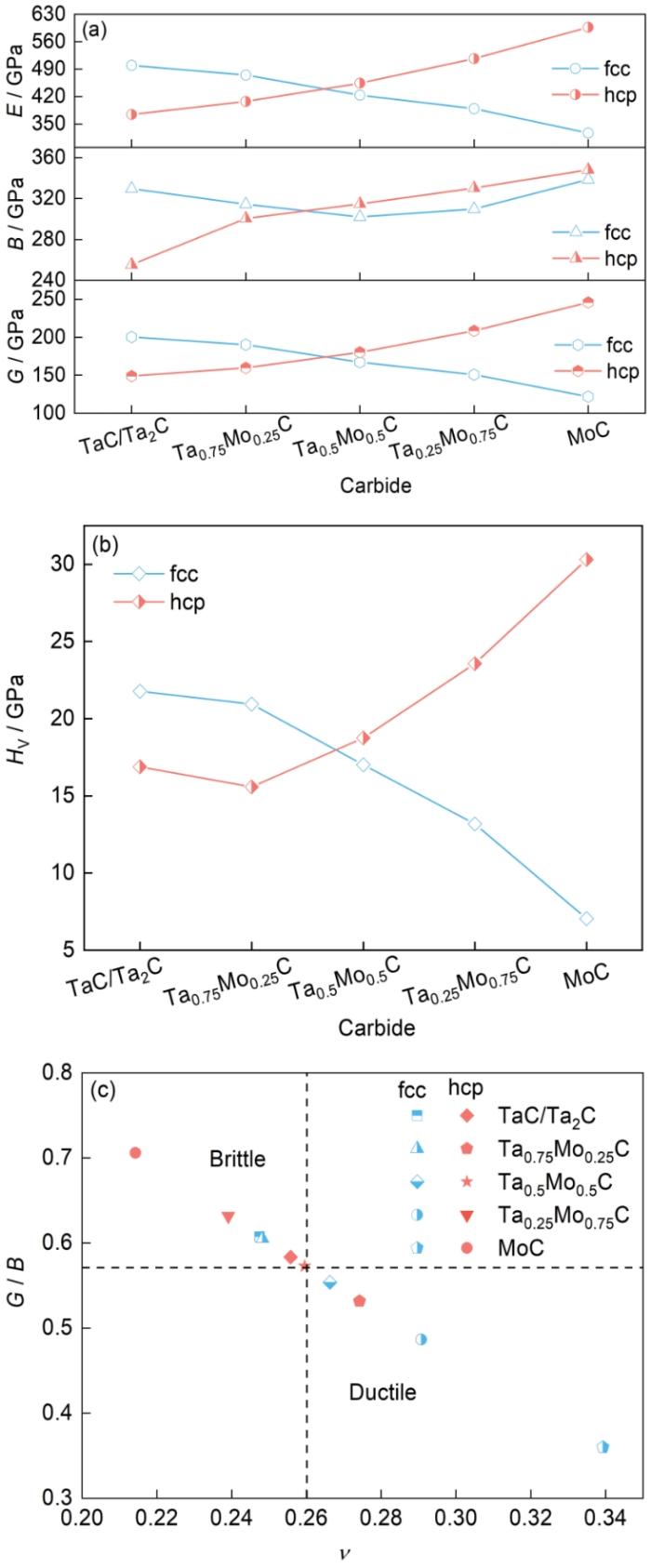
图4   不同结构含Mo复合碳化钽的力学性质

Fig.4   Mechanical properties of complex tantalum carbide containing Mo with different structures

(a) modulus

(b) Vickers hardness

(c) G / Bvs Poisson's ratio


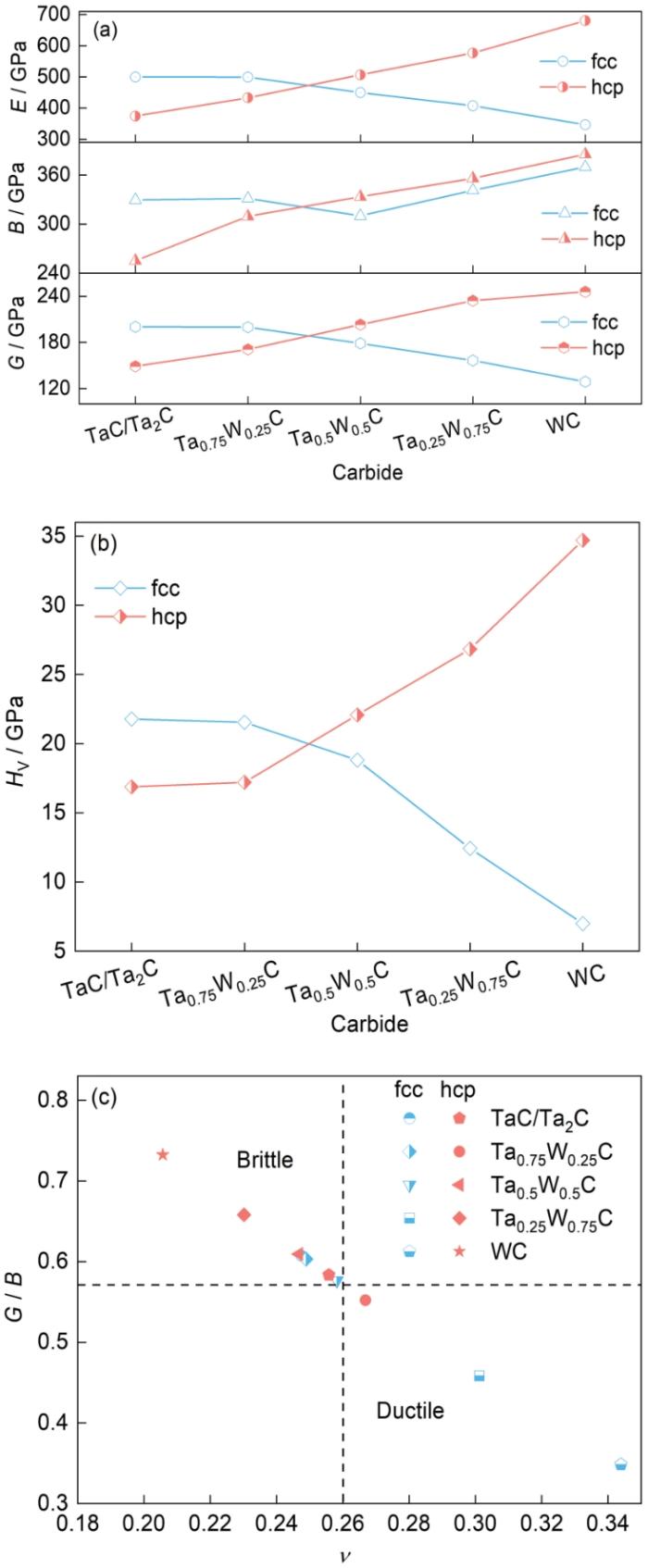
碳化钽的脆性限制了材料的广泛应用。本工作使用G / B和临界Possion比对复合碳化钽的韧性材料和脆性材料进行分类[38]。G / B < 0.571表示材料脆性较大，G / B ≥ 0.571表示材料的延展性较好；ν< 0.26表示材料为脆性，ν≥ 0.26表示材料为韧性。如图4c所示，图中的点越靠近左上方，其G / B越大、ν越小，表明材料的脆性较大；图中的点越靠近右下方，其G / B越小、ν越大，表明材料的延展性越好。由图4c可知，对于fcc晶体结构的含Mo复合碳化钽，随着Mo原子浓度的增加，代表相应原子组合的点处于图中的右下方，即含Mo复合碳化钽的延展性提高，这表明Mo原子浓度增加，含Mo复合碳化钽的延展性增大。对于具有hcp晶体结构的含Mo复合碳化钽，随着Mo原子浓度的增加，代表相应原子组合的点先靠近图中的右下方，然后靠近图中的左上方，即含Mo复合碳化钽的延展性先增加后降低。这表明，低浓度的Mo原子使含Mo复合碳化钽更具韧性，而高浓度的Mo原子则使含Mo复合碳化钽更具脆性。

类似地，图5给出了含W复合碳化钽中W原子取代部分Ta原子后的力学性质如图5a和b所示，当W原子浓度小于50%时，fcc晶体结构的含W复合碳化钽具有更高的G、B、E和HV。相反，当W原子浓度不低于50%时，具有hcp晶体结构的含W复合碳化钽具有更高的G、B、E和HV。如图5c所示，对于fcc结构的含W复合碳化钽，W原子浓度的增加会导致含W复合碳化钽的延展性增加。对于具有hcp结构的含W复合碳化钽，低浓度的W原子会增加含W复合碳化钽的延展性，而高浓度的W原子则会降低含W复合碳化钽的延展性。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同结构含W复合碳化钽的力学性质

Fig.5   Mechanical properties of complex tantalum carbide containing W with different structures

(a) modulus

(b) Vickers hardness

(c) G / Bvs Poisson's ratio


综合图4和5的分析结果，不同浓度的Mo原子和W原子会影响复合碳化钽的力学性能。对组成成分相同但晶体结构不同的复合碳化钽也有不同的影响。Mo和W原子的浓度对具有不同晶体结构的复合碳化钽的力学性能具有不同的影响。当体系中Mo原子浓度和W原子浓度小于50%时，具有fcc晶体结构的复合碳化钽具有更高的G、B、E和HV。当Mo和W原子浓度不低于50%时，具有hcp晶体结构的复合碳化钽具有更高的G、B、E和HV。对于具有fcc晶体结构的复合碳化钽，从表3和5、图4c和5c可以看出，随Mo、W的原子浓度增大，ν增加且G / B降低，即延展性提高。这表明Mo原子和W原子占取代Ta原子，有利于提高复合碳化钽的延展性。对于hcp晶体结构的复合碳化钽，少量的Mo原子和W原子取代Ta原子有利于提高延展性，而大量的Mo原子和W原子取代Ta原子则会增加其脆性。

2.3 电子结构分析

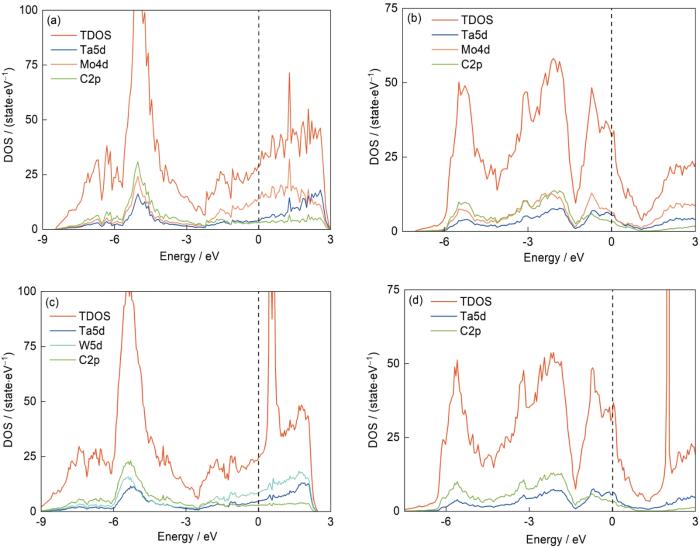
为了深入了解复合碳化钽的键合性质，计算了典型复合碳化钽的总态密度(TDOS)和投影态密度(DOS) (图6)。通过研究原子的轨道杂化度，可以有效地表征化学键的离域程度和各原子的轨道杂化性质，有利于分析原子间的成键特征。如图6所示，Fermi能级附近的成键峰主要由Ta5d、Mo4d、W5d和C2p态占据，表明它们对复合碳化钽体系的化学成键有贡献，每种复合碳化钽的总态密度都跨越了Fermi能级，这意味着复合碳化钽能够表现出某些金属特性。在Fermi能级左侧，存在来自金属Ta、Mo或W的d轨道和C的2p轨道之间的杂化重叠，表明Ta、Mo或W金属原子和Cd原子之间存在共价键。在fcc结构中，相比于Mo原子取代，采用W原子取代时，金属和C原子之间的交互作用更强，共价键更强。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   不同结构复合碳化钽的总态密度和投影态密度

Fig.6   Total and projected density of states (DOS) of the same component in multi-component carbides in different crystal structures (The dashed lines indicate the Fermi energy levels; TDOS—total density of states)

(a) Ta0.5Mo0.5C (fcc) (b) Ta0.5Mo0.5C (hcp) (c) Ta0.5W0.5C (fcc) (d) Ta0.5W0.5C (hcp)


一般来说，体系在Fermi能级上的DOS值越高，该体系的金属键就越强[28]，通常用金属丰度(fm)来描述某结构体系的金属键强度，fm可以由 式(20)计算[39]：

fm=nm / ne=kBTDf / ne=0.026Df / ne

式中，nm和ne分别为超胞的热激发电子和价电子密度，kB为Boltzmann常数，T是温度，Df是Fermi能级的DOS值。ne = N / Vcell，N是价电子总数，Vcell是晶胞体积。

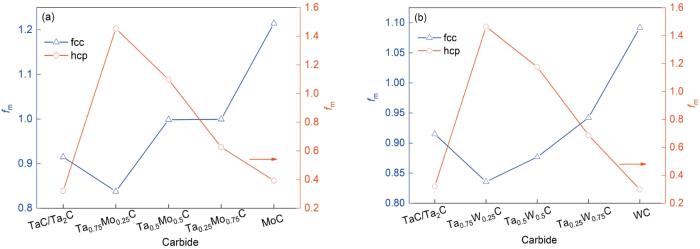
图7为不同结构复合碳化钽fm的变化情况。由图可知，Mo、W原子浓度低于25%时金属键强度降低，Mo、W原子浓度高于25%时金属键强度提高。对比图4c和7a，对于fcc结构的复合碳化钽，fm先减小后增大，复合碳化钽的延展性呈先减小后增大的趋势；对于hcp结构的复合碳化钽，fm先增大后减小，复合碳化钽的延展性呈先增大后减小的趋势。比较图5c和7b，fcc结构的复合碳化钽的fm先减小后增大，延展性同样呈先减小后增大的趋势；具有hcp结构的复合碳化钽的fm先增大后减小，其延展性的变化也是先增大后减小。对上述数据的分析表明，用于描述复合碳化钽金属结合性能的fm与延展性之间存在很强的相关性，复合碳化钽的延展性随着fm的增大而增大。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   不同结构复合碳化钽的金属丰度(fm)

Fig.7   fm values of complex tantalum carbide containing Mo (a) and W (b) with different structures (fm is an indicator of metal bonding strength)


Mo和W原子的加入有可能改善复合碳化钽的本征脆性。然而，增加Mo和W原子的比例可能会使复合碳化钽结构形成hcp结构。结果表明，Mo和W原子在不同浓度下取代Ta位点时，形成了不同的稳定晶体结构。对于fcc结构的复合碳化钽，Mo和W原子浓度越高，其延展性越好。对于hcp结构的复合碳化钽，少量的Mo和W原子取代Ta位提高了延展性。

表6所示的Bader电荷计算进一步证明了电荷从金属原子转移到C原子，揭示了离子键的作用。表6表明，随着Mo、W原子浓度在复合碳化钽中的增加，离子键强度逐渐降低。由图7和表3可知，Mo、W原子浓度低于25%时金属键强度降低，Mo、W原子浓度高于25%时金属键强度提高；随着Mo、W原子浓度在复合碳化钽中的提高，Poisson比从TaC的0.25逐渐提高到MoC的0.34和WC的0.34，表明复合碳化钽的延展性增强。因此，当Mo、W原子浓度低于25%时，复合碳化钽的离子键强度降低，金属键强度降低，复合碳化钽的延展性不变；当Mo、W原子浓度高于25%时，复合碳化钽的离子键强度降低，金属键强度增强，复合碳化钽的延展性提高。

表6   不同结构复合碳化钽中各原子的平均Bader电荷

Table 6  Average Bader charge of each atom in complex tantalum carbide with different structures

Crystal structureCarbideCTaMoW
fccTaC1.7981-1.7982
Ta0.75Mo0.25C1.6594-1.8032-1.2279
Ta0.5Mo0.5C1.5107-1.7975-1.2240
Ta0.25Mo0.75C1.4359-1.8233-1.3068
MoC1.3520-1.3520
Ta0.75W0.25C1.6932-1.7852-1.4175
Ta0.5W0.5C1.5430-1.5437
Ta0.25W0.75C1.5538-1.8413-1.4579
WC1.5449-1.5449
hcpTa2C1.8033-0.9016
Ta0.75Mo0.25C1.4781-1.6082-1.1061
Ta0.5Mo0.5C1.3812-1.6431-1.1380
Ta0.25Mo0.75C1.3137-1.6530-1.1950
MoC1.1998-1.1998
Ta0.75W0.25C1.5063-1.6027-1.2308
Ta0.5W0.5C1.4430-1.6329-1.2666
Ta0.25W0.75C1.4100-1.6492-1.3263
WC1.3852-1.3852

新窗口打开| 下载CSV


3 结论

(1) 以Ta-W和Ta-Mo合金为研究对象，构建了含不同合金元素和含量的复合碳化钽(Ta, M)C (M = Mo、W)模型结构。当Mo原子和W原子的浓度不超过75%时，具有fcc结构的复合碳化钽最为稳定。当Mo原子和W原子的浓度超过75%时，六方结构的复合碳化钽最为稳定。当Mo原子和W原子的浓度不超过50%时，复合碳化钽偏向于形成fcc结构。当Mo原子和W原子的浓度超过50%时，复合碳化钽倾向于形成六方结构。

(2) Mo、W原子的加入能够改善复合碳化钽的本征脆性。对于具有fcc结构的复合碳化钽，Mo、W原子浓度的越高，延展性越好；对于具有hcp结构的复合碳化钽，少量Mo、W原子取代Ta原子，有利于提高复合碳化钽的韧性。高浓度Mo、W原子取代Ta原子使复合碳化钽的模量和硬度提高。

(3) 复合碳化钽的成键模式为金属键、共价键和离子键3种键合类型共存，复合碳化钽的延展性变化归因于键合强度的变化，随着金属键强度的增加，(Ta, M)C (M = Mo、W)的延展性增加，离子键强度降低且金属键强度提高是延展性提高的原因。

参考文献

Taberna P L, Simon P, Fauvarque J F.

Electrochemical characteristics and impedance spectroscopy studies of carbon-carbon supercapacitors

[J]. J. Electrochem. Soc., 2003, 150: A292

[本文引用: 1]

Mani G, Porter D, Grove K, et al.

A comprehensive review of biological and materials properties of tantalum and its alloys

[J]. J. Biomed. Mater. Res., 2022, 110A: 1291

[本文引用: 1]

Massot L, Chamelot P, Taxil P.

Preparation of tantalum carbide films by reaction of electrolytic carbon coating with the tantalum substrate

[J]. J. Alloys Compd., 2006, 424: 199

[本文引用: 1]

Wang Z H.

Advances on surface treatment process of tantalum

[J]. Heat Treat. Met., 2024, 49: 259

[本文引用: 1]

王哲昊.

金属钽表面处理工艺进展

[J]. 金属热处理, 2024, 49: 259

[本文引用: 1]

Carette L, Jacquet P, Cotton D, et al.

(TaC/Ta2C) bilayer formed on carburized and annealed tantalum; development of a numerical growth model

[J]. Appl. Surf. Sci., 2019, 467-468: 84

[本文引用: 1]

Zhao Z Y, Cao L, Liang F, et al.

A new strategy for preparing carbide coatings on easily oxidized tantalum by non-vacuum carburizing: Fe-coating-mediated carburization

[J]. Vacuum, 2024, 221: 112951

Tang Q H, Zhuang X L, Fang J F, et al.

Surface carburising of tantalum and its alloys

[J]. Rare. Met., 1991, (2): 116

[本文引用: 1]

唐全红, 庄祥麟, 方金法 等.

钽及其合金的表面渗碳强化

[J]. 稀有金属, 1991, (2): 116

[本文引用: 1]

Zheng X.

Surface treatment to improve the corrosion resistance of tantalum

[J]. Rare. Met. Lett., 2002, (4): 21

[本文引用: 1]

郑 欣.

提高钽耐蚀性的表面处理法

[J]. 稀有金属快报, 2002, (4): 21

[本文引用: 1]

Zhou H L, Hu Y, Zhu K W, et al.

Surface modification of tantalum sheets by methane plasma carburizing

[J]. Chin. J. Vac. Sci. Technol., 2018, 38A: 48

[本文引用: 2]

周寰林, 胡 殷, 朱康伟 等.

钽表面的甲烷等离子渗碳改性技术研究

[J]. 真空科学与技术学报, 2018, 38: 48

[本文引用: 2]

Zhou H L.

Study of ionic carburisation modification of tantalum surfaces

[D]. Mianyang: China Academy of Engineering Physics, 2017

[本文引用: 1]

周寰林.

钽表面离子渗碳改性研究

[D]. 绵阳: 中国工程物理研究院, 2017

[本文引用: 1]

Li J, Yan X D, Yang Y, et al.

Vacuum carburization process of Ta and Ta-W alloys

[J]. Chin. J. Rare Met., 2018, 42: 925

[本文引用: 1]

李 佳, 闫晓东, 杨 银 等.

Ta及Ta-W合金真空渗碳工艺研究

[J]. 稀有金属, 2018, 42: 925

[本文引用: 1]

Hui P F.

Microstructure and properties of carbide coatings on metal (Ta, Mo, Ti6Al4V) surface prepared by interstitial carburization

[D]. Xi'an: Xi'an University of Technology, 2019

[本文引用: 1]

惠鹏飞.

间隙原子渗碳法制备金属(Ta、Mo、Ti6Al4V)表面碳化层的组织和性能研究

[D]. 西安: 西安理工大学, 2019

[本文引用: 1]

Zhang C, Yin H Q, Du Y, et al.

Thermodynamic modeling of the Ta-Mo-C ternary system

[J]. Calphad, 2017, 59: 99

[本文引用: 1]

Frisk K.

A thermodynamic analysis of the Ta-W-C and the Ta-W-C-N systems

[J]. Int. J. Mater. Res., 1999, 90: 704

[本文引用: 1]

Junquera J, Ghosez P.

Critical thickness for ferroelectricity in perovskite ultrathin films

[J]. Nature, 2003, 422: 506

[本文引用: 1]

Khazaei M, Arai M, Sasaki T, et al.

Novel electronic and magnetic properties of two-dimensional transition metal carbides and nitrides

[J]. Adv. Funct. Mater., 2013, 23: 2185

[本文引用: 1]

Sarker P, Harrington T, Toher C, et al.

High-entropy high-hardness metal carbides discovered by entropy descriptors

[J]. Nat. Commun., 2018, 9: 4980

DOI      PMID      [本文引用: 1]

High-entropy materials have attracted considerable interest due to the combination of useful properties and promising applications. Predicting their formation remains the major hindrance to the discovery of new systems. Here we propose a descriptor-entropy forming ability-for addressing synthesizability from first principles. The formalism, based on the energy distribution spectrum of randomized calculations, captures the accessibility of equally-sampled states near the ground state and quantifies configurational disorder capable of stabilizing high-entropy homogeneous phases. The methodology is applied to disordered refractory 5-metal carbides-promising candidates for high-hardness applications. The descriptor correctly predicts the ease with which compositions can be experimentally synthesized as rock-salt high-entropy homogeneous phases, validating the ansatz, and in some cases, going beyond intuition. Several of these materials exhibit hardness up to 50% higher than rule of mixtures estimations. The entropy descriptor method has the potential to accelerate the search for high-entropy systems by rationally combining first principles with experimental synthesis and characterization.

Liu R L, Li D Y.

Electron work function as an indicator for tuning the bulk modulus of MC carbide by metal-substitution: A first-principles computational study

[J]. Scr. Mater., 2021, 204: 114148

[本文引用: 1]

Kresse G, Furthmüller J.

Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set

[J]. Phys. Rev., 1996, 54B: 11169

[本文引用: 1]

Kresse G, Joubert D.

From ultrasoft pseudopotentials to the projector augmented-wave method

[J]. Phys. Rev., 1999, 59B: 1758

[本文引用: 1]

Perdew J P, Burke K, Ernzerhof M.

Generalized gradient approximation made simple

[J]. Phys. Rev. Lett., 1996, 77: 3865

DOI      PMID      [本文引用: 1]

Monkhorst H J, Pack J D.

Special points for Brillouin-zone integrations

[J]. Phys. Rev., 1976, 13B: 5188

[本文引用: 1]

Liu Z T Y, Gall D, Khare S V.

Electronic and bonding analysis of hardness in pyrite-type transition-metal pernitrides

[J]. Phys. Rev., 2014, 90B: 134102

[本文引用: 1]

Yang Y, Wang W, Gan G Y, et al.

Structural, mechanical and electronic properties of (TaNbHfTiZr)C high entropy carbide under pressure: Ab initio investigation

[J]. Phys. Rev., 2018, 550B: 163

[本文引用: 1]

Tasnádi F, Odén M, Abrikosov I A.

Ab initio elastic tensor of cubic Ti0.5Al0.5N alloys: Dependence of elastic constants on size and shape of the supercell model and their convergence

[J]. Phys. Rev., 2012, 85B: 144112

[本文引用: 2]

Hossain M D, Borman T, Kumar A, et al.

Carbon stoichiometry and mechanical properties of high entropy carbides

[J]. Acta Mater., 2021, 215: 117051

[本文引用: 1]

Wu Z J, Zhao E J, Xiang H P, et al.

Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles

[J]. Phys. Rev., 2007, 76B: 054115

[本文引用: 2]

Shi Y J, Du Y L, Chen G.

First-principles study on the elastic and electronic properties of hexagonal ε-Fe3N

[J]. Comput. Mater. Sci., 2013, 67: 341

[本文引用: 2]

Hill R.

The elastic behaviour of a crystalline aggregate

[J]. Proc. Phys. Soc., 1952, 65A: 349

[本文引用: 1]

Chen X Q, Niu H Y, Li D Z, et al.

Modeling hardness of polycrystalline materials and bulk metallic glasses

[J]. Intermetallics, 2011, 19: 1275

[本文引用: 2]

Van De Walle A, Asta M, Ceder G.

The alloy theoretic automated toolkit: A user guide

[J]. Calphad, 2002, 26: 539

[本文引用: 1]

Zunger A, Wei S H, Ferreira L G, et al.

Special quasirandom structures

[J]. Phys. Rev. Lett., 1990, 65: 353

PMID      [本文引用: 1]

Mattheiss L F, Hamann D R.

Bulk and surface electronic structure of hexagonal WC

[J]. Phys. Rev., 1984, 30B: 1731

[本文引用: 1]

Yu X X, Weinberger C R, Thompson G B.

Ab initio investigations of the phase stability in tantalum carbides

[J]. Acta Mater., 2014, 80: 341

[本文引用: 8]

Liu R L, Zhang D, Tang Y Q, et al.

(W1 - x, Mx ) C carbides with desired combinations of compatible density and properties—A first-principles study

[J]. J. Am. Ceram. Soc., 2021, 104: 4239

[本文引用: 1]

Edström D, Sangiovanni D G, Hultman L, et al.

Elastic properties and plastic deformation of TiC- and VC-based pseudobinary alloys

[J]. Acta Mater., 2018, 144: 376

[本文引用: 1]

Zhao S J.

Defect energetics and stacking fault formation in high-entropy carbide ceramics

[J]. J. Eur. Ceram. Soc., 2022, 42: 5290

[本文引用: 1]

Shao L, Jiang H H, Xu C R, et al.

The lattice distortion, mechanical and thermodynamic properties of A(Zr0.2Sn0.2Ti0.2Hf0.2Nb0.2)O3 (A = Sr, Ba) high-entropy perovskite with B-site disorder: First principles prediction

[J]. Mater. Des., 2022, 224: 111308

[本文引用: 1]

Blakemore J S. Solid State Physics [M]. Cambridge: Cambridge University Press, 1985: 1

[本文引用: 1]

/

〈 〉


版权所有 © 《金属学报》编辑部
地址: 沈阳市文化路72号, 中国科学院金属研究所(110016)
电话: +86- 024-23971286 　E-mail: jsxb@imr.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发 技术支持：support@magtech.com.cn