3
2003
... 极端条件下材料的动态力学行为(如塑性变形、冲击相变、动态断裂)是冲击动力学、固体力学、材料科学等学科研究的重要内容,也是高速撞击、内爆压缩等动高压工程领域关注的科学问题.当冲击波在金属自由面或金属/气体界面反射时,金属在入射稀疏波与自由面反射稀疏波的拉伸作用下会发生动态断裂,也称为层裂[1].该现象广泛存在于航空航天、国防及民用领域,因此自发现以来就受到了极大关注.经过一个世纪的实验与理论研究,人们对固态金属动态断裂行为已获得了深入的认识,发展了多种损伤理论模型以描述损伤成核至最终断裂的过程[1~3]. ...
... [1~3]. ...
... MD模拟结果(见2.1节)表明基体材料熔化后He泡增长是导致材料拉伸断裂的主导物理机制,传统的孔洞成核、增长机制被显著抑制,与基体材料为固态时一致[51].因此,在建立损伤模型时本工作忽略孔洞成核、增长项,仅考虑He泡增长项.模型以孔洞增长模型[1~3]为基本框架,考虑He泡内压的影响,具体表达式如 式(3)所示,包括外加应力、He泡内压、惯性、黏性及表面张力对He泡增长的作用. ...
Dynamic failure of solids
0
1987
Dynamic fracture and spallation in ductile solids
2
1981
... 极端条件下材料的动态力学行为(如塑性变形、冲击相变、动态断裂)是冲击动力学、固体力学、材料科学等学科研究的重要内容,也是高速撞击、内爆压缩等动高压工程领域关注的科学问题.当冲击波在金属自由面或金属/气体界面反射时,金属在入射稀疏波与自由面反射稀疏波的拉伸作用下会发生动态断裂,也称为层裂[1].该现象广泛存在于航空航天、国防及民用领域,因此自发现以来就受到了极大关注.经过一个世纪的实验与理论研究,人们对固态金属动态断裂行为已获得了深入的认识,发展了多种损伤理论模型以描述损伤成核至最终断裂的过程[1~3]. ...
... MD模拟结果(见2.1节)表明基体材料熔化后He泡增长是导致材料拉伸断裂的主导物理机制,传统的孔洞成核、增长机制被显著抑制,与基体材料为固态时一致[51].因此,在建立损伤模型时本工作忽略孔洞成核、增长项,仅考虑He泡增长项.模型以孔洞增长模型[1~3]为基本框架,考虑He泡内压的影响,具体表达式如 式(3)所示,包括外加应力、He泡内压、惯性、黏性及表面张力对He泡增长的作用. ...
Influence of melting on shocked free surface behavior using Doppler laser interferometry and X ray densitometry
1
1984
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Shock-induced spall in solid and liquid Cu at extreme strain rates
2
2009
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
... [5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Hydrodynamic instability experiments with three-dimensional modulations at the national ignition facility
1
2015
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Spallation as a dominant source of pusher-fuel and hot-spot mix in inertial confinement fusion capsules
0
2016
Ultrashort laser ablation of bulk copper targets: Dynamics and size distribution of the generated nanoparticles
0
2014
Modification of cu surface with picosecond laser pulses
0
2014
Generation of nanocrystalline surface layer in short pulse laser processing of metal targets under conditions of spatial confinement by solid or liquid overlayer
1
2017
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Dynamic strength of tin and lead melts
1
2015
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Dynamic fragmentation of laser shock-melted tin: Experiment and modelling
0
2010
Experimental investigation of liquid spall in laser shock-loaded tin
0
2007
Investigation of fragments size resulting from dynamic fragmentation in melted state of laser shock-loaded tin
0
2010
An improved Asay window technique for investigating the micro-spall of an explosively-driven tin
0
2017
Piezoelectric characterization of ejecta from shocked tin surfaces
1
2005
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Experimental determination of the dynamic tensile strength of liquid Sn, Pb, and Zn
2
2016
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
... [17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Response of copper to shock-wave loading at temperatures up to the melting point
0
2013
Elastic-plastic deformation and fracture of shock-compressed single-crystal and polycrystalline copper near melting
0
2013
Spall fracture properties of aluminum and magnesium at high temperatures
1
1996
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Influence of impurities on the resistance to spall fracture of aluminum near the melting temperature
0
2016
Dynamic yield and tensile strength of aluminum single crystals at temperatures up to the melting point
2
2001
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
... ~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Molecular dynamics simulations of micro-spallation of single crystal lead
1
2013
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Spall strength of aluminium single crystals under high strain rates: molecular dynamics study
1
2013
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
Strain rate dependence of spall strength for solid and molten lead and tin
4
2020
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
... [25~27]. ...
... 大量的实验与理论研究已表明,金属的拉伸强度会随着应变率的升高而增加[25,59~62],而应变率对拉伸强度的影响机制与不同应变率下的损伤成核机制有关[25,62].对于完美晶体,高/低应变率下的损伤都是均匀成核的,所需的成核应力较高.因此,层裂强度也较高,且层裂强度随应变率的降低而缓慢下降,如图7中的金属纯Al.对于含缺陷金属,应变率较低时,损伤是非均匀成核的,以缺陷处的成核增长为主,所需的成核应力较低;应变率较高时,非均匀成核不足以将应力弛豫,均匀成核也会被激发.因此,含缺陷金属的层裂强度会随着应变率的降低而显著降低,且低于完美晶体,如图7中的含He泡金属.对应变率为3.0 × 1010 s-1时含He泡铝的微结构分析证明,高应变率下除了He泡增长,还出现了新的孔洞成核、增长(如图8所示),这与更低应变率下的损伤仅由He泡增长控制有所不同. ...
... [25,62].对于完美晶体,高/低应变率下的损伤都是均匀成核的,所需的成核应力较高.因此,层裂强度也较高,且层裂强度随应变率的降低而缓慢下降,如图7中的金属纯Al.对于含缺陷金属,应变率较低时,损伤是非均匀成核的,以缺陷处的成核增长为主,所需的成核应力较低;应变率较高时,非均匀成核不足以将应力弛豫,均匀成核也会被激发.因此,含缺陷金属的层裂强度会随着应变率的降低而显著降低,且低于完美晶体,如图7中的含He泡金属.对应变率为3.0 × 1010 s-1时含He泡铝的微结构分析证明,高应变率下除了He泡增长,还出现了新的孔洞成核、增长(如图8所示),这与更低应变率下的损伤仅由He泡增长控制有所不同. ...
Evolution of pore ensemble in solid and molten aluminum under dynamic tensile fracture: Molecular dynamics simulations and mechanical models
2
2019
... 基体材料的状态方程采用二阶多项式表示[26]: ...
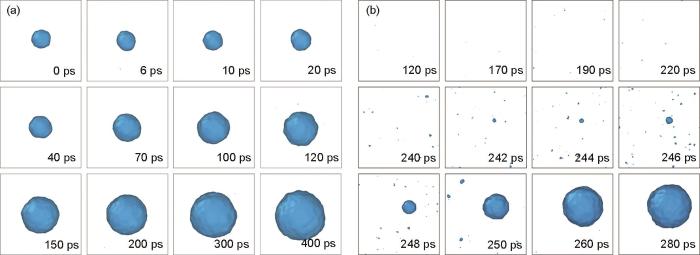
... 相同应变率下液态纯Al中孔洞的演化过程如图2b所示.与含He泡铝不同,纯Al的动态拉伸断裂机制为孔洞成核、增长.由OVITO软件确定的孔洞成核最早发生在约120 ps,但由孔洞的演化过程可知,早期形成的孔洞是随机分布的且不能稳定存在,这可能是由于热涨落而形成的一些点缺陷.直到拉伸应力增大到3.061 GPa ( t = 242 ps),孔洞的成核点才逐渐稳定下来并开始长大(如图2b中最大的孔洞),其余孔洞在表面张力的作用下逐渐塌缩.最终,在模拟样品中仅有一个孔洞长大,这与Mayer等[26,27]的研究结果一致. ...
Evolution of foamed aluminum melt at high rate tension: A mechanical model based on atomistic simulations
2
2018
... 近年来,对液态金属动态断裂的研究逐渐得到关注.在较强的冲击载荷下,金属会发生卸载熔化或冲击熔化,导致动态断裂发生在液态[4,5].在现代工业装置(如面向未来聚变能源的惯性约束聚变装置)和激光驱动的表面微加工中,也观察到熔化后金属的动态断裂现象[6~10].对低熔点金属(如Pb和Sn)的层裂实验发现,与固态金属不同,液态金属的自由面速率曲线没有明显的回跳信号,且表面会形成大量的物质喷射[11~16].对高熔点金属,科研人员通过对样品加热再施加冲击载荷,研究了液态金属Cu、Al等的层裂行为[17~22].Zaretsky[17]发现Sn和Zn在温度仅低于熔点10 K的情况下仍然具有较高的层裂强度,但是当金属完全熔化后其强度比固态低了一个量级,而液态金属Pb的层裂强度只比固态低3倍.对金属Al的层裂实验则发现高温下的层裂强度仍然与金属的微结构密切相关,商用铝合金AD1的层裂强度在初始温度接近熔点时降低至接近零,但高纯度的多晶铝A999和单晶Al在熔化后的层裂强度仍然很高[20~22].分子动力学(MD)模拟表明,固态和液态金属的层裂机制都是孔洞成核、增长、贯通,2者的主要差异表现在孔洞数量、体积分布、损伤深度以及层裂强度上[5,23,24].Mayer等[25]采用MD模拟研究了动态拉伸下金属Pb和Sn的断裂行为,发现纯金属的层裂强度显著高于实验结果,但当考虑金属中存在杂质时,该差异被消除.他们结合MD模拟与连续介质力学理论计算,发展了液态金属的损伤理论模型[25~27]. ...
... 相同应变率下液态纯Al中孔洞的演化过程如图2b所示.与含He泡铝不同,纯Al的动态拉伸断裂机制为孔洞成核、增长.由OVITO软件确定的孔洞成核最早发生在约120 ps,但由孔洞的演化过程可知,早期形成的孔洞是随机分布的且不能稳定存在,这可能是由于热涨落而形成的一些点缺陷.直到拉伸应力增大到3.061 GPa ( t = 242 ps),孔洞的成核点才逐渐稳定下来并开始长大(如图2b中最大的孔洞),其余孔洞在表面张力的作用下逐渐塌缩.最终,在模拟样品中仅有一个孔洞长大,这与Mayer等[26,27]的研究结果一致. ...
Radiation damage in metallic materials
2
1997
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
... [28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Helium accumulation in metals during irradiation—Where do we stand?
3
2003
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
... ,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
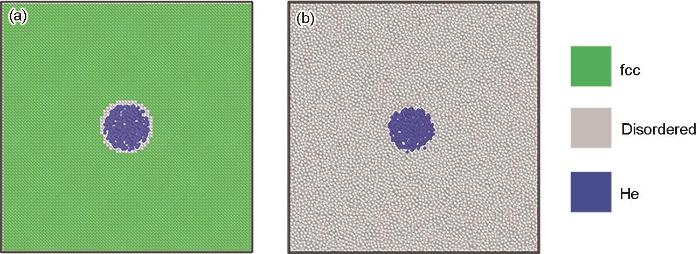
... 含He泡液态金属铝(下文简称含He泡铝)样品的初始结构如图1a所示,在[100]、[010]、[001] 3个方向各有40个晶体单胞.Al单胞为fcc结构,晶格常数为0.405 nm,故样品在3个方向的尺寸均为16.2 nm.为了在样品中构建He泡,首先通过删除金属原子在样品中心构建了一个半径R0 = 1.5 nm的球形孔洞,再往孔洞里添加He原子.He原子的数量由He原子/金属原子空位的数量比(δ)确定,本工作设置为δ = 0.5.根据He原子与金属原子的数量,计算出He原子的浓度为0.188%.根据He泡体积与样品尺寸,计算出He泡的初始体积分数D0 = 0.33%.He泡的初始状态如R0、δ和D0均基于已有研究结果[29,32]. ...
A neutron irradiation-induced displacement damage of indium vacancies in α-In2Se3 nanoflakes
0
2020
A new loop-punching mechanism for helium bubble growth in tungsten
0
2017
Characterization and modelling of helium bubbles in self-irradiated plutonium alloys
4
2005
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
... ,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
... ,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
... 含He泡液态金属铝(下文简称含He泡铝)样品的初始结构如图1a所示,在[100]、[010]、[001] 3个方向各有40个晶体单胞.Al单胞为fcc结构,晶格常数为0.405 nm,故样品在3个方向的尺寸均为16.2 nm.为了在样品中构建He泡,首先通过删除金属原子在样品中心构建了一个半径R0 = 1.5 nm的球形孔洞,再往孔洞里添加He原子.He原子的数量由He原子/金属原子空位的数量比(δ)确定,本工作设置为δ = 0.5.根据He原子与金属原子的数量,计算出He原子的浓度为0.188%.根据He泡体积与样品尺寸,计算出He泡的初始体积分数D0 = 0.33%.He泡的初始状态如R0、δ和D0均基于已有研究结果[29,32]. ...
Helium solubility and bubble formation in a nanostructured ferritic alloy
1
2014
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Evolving density and static mechanical properties in plutonium from self-irradiation
1
2009
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Effect of helium on irradiation-induced hardening of iron: A simulation point of view
0
2007
Atomic-scale mechanisms of helium bubble hardening in iron
0
2015
Nanobubble fragmentation and bubble-free-channel shear localization in helium-irradiated submicron-sized copper
1
2016
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Radiation-induced helium nanobubbles enhance ductility in submicron-sized single-crystalline copper
1
2016
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Helium bubbles enhance strength and ductility in small-volume Al-4Cu alloys
1
2019
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Dynamic fracture and spall in aluminum with helium bubbles
2
2010
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
... [40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Shock compression and spall formation in aluminum containing helium bubbles at room temperature and near the melting temperature: Experiments and simulations
3
2014
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
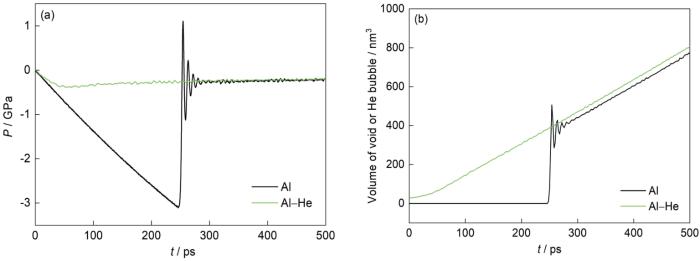
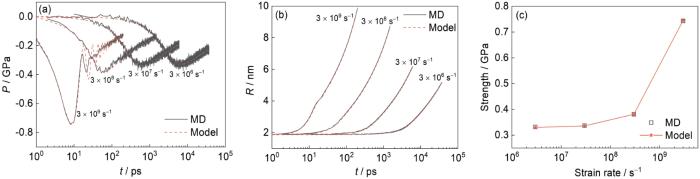
... 样品的动态拉伸强度随着应变率的升高而增大,尤其是当应变率高于3.0 × 108 s-1时呈现出明显的应变率强化效应,如图7所示.当应变率为3.0 × 106、3.0 × 107、3.0 × 108和3.0 × 109 s-1时,含He泡铝样品的动态拉伸强度分别为0.332、0.337、0.381和0.743 GPa,显著低于纯Al的强度(2.774、2.920、3.111和3.533 GPa),表明金属熔化后He泡仍然会降低金属的强度,这与Glam等[41]开展的加热层裂实验结果一致.初始温度为600 ℃的纯Al和含He泡铝平板撞击实验结果表明,He泡显著降低了金属的层裂强度(1.37 GPa vs 0.4 GPa)[41].前期对冲击载荷下含He泡铝层裂的MD模拟发现,熔化后He泡对层裂强度的影响很小[49,50],这与本工作的研究结果不同,其主要原因是应变率不同.在冲击层裂模拟中,样品所经历的应变率接近1011 s-1,高于本工作动态拉伸模拟的应变率.为此,本工作补充了应变率为3.0 × 1010 s-1的动态拉伸模拟,得到含He泡铝和纯Al样品的强度分别为3.355和4.63 GPa.这表明随着应变率进一步增加,含He泡铝的强度显著增加,使得He泡对动态拉伸强度的影响有所减弱,趋向于冲击层裂的MD模拟结果.对于纯Al,飞秒激光实验结果得到的温度为2500 K时的层裂强度高达2.5 GPa[58],比本工作在1100 K的计算结果略低. ...
... [41].前期对冲击载荷下含He泡铝层裂的MD模拟发现,熔化后He泡对层裂强度的影响很小[49,50],这与本工作的研究结果不同,其主要原因是应变率不同.在冲击层裂模拟中,样品所经历的应变率接近1011 s-1,高于本工作动态拉伸模拟的应变率.为此,本工作补充了应变率为3.0 × 1010 s-1的动态拉伸模拟,得到含He泡铝和纯Al样品的强度分别为3.355和4.63 GPa.这表明随着应变率进一步增加,含He泡铝的强度显著增加,使得He泡对动态拉伸强度的影响有所减弱,趋向于冲击层裂的MD模拟结果.对于纯Al,飞秒激光实验结果得到的温度为2500 K时的层裂强度高达2.5 GPa[58],比本工作在1100 K的计算结果略低. ...
Experimental investigation of spall damage in pure aluminum with helium bubbles
1
2021
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
氦泡铝的层裂特性实验研究
1
2021
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Spall in aluminium with helium bubbles under laser shock loading
1
2017
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Dynamic analysis of helium bubble growth in the pure al under high strain-rate loading
1
2007
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
高应变率拉伸下纯铝中氦泡长大的动力学研究
1
2007
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Numerical analysis of spall response in aluminum with helium bubbles
1
2017
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
含氦泡金属铝层裂响应的数值分析
1
2017
... 在辐照环境中,金属材料内部会产生大量的缺陷,如空位、He原子、位错等[28~32].He原子因其在金属中的低溶解性会聚集成大量纳米尺度的He泡,并具有很高的内压[29,32,33].大量实验和理论研究[28,29,32,34~37]表明,He泡会对金属的力学性能产生显著影响,包括局部硬化、延展性降低、高裂纹率及低断裂时间等.最近的拉伸实验结果发现,He泡能够同时增强百纳米直径的单晶Cu和单晶Al-Cu合金的强度和延展性[38,39].此外,近年来He泡对金属冲击压缩与动态拉伸断裂等动态力学性能的影响开始得到关注.对含He泡掺B铝层裂行为的平板撞击实验结果发现,He泡会降低金属的层裂强度[40~42],并且通过样品回收观察到He泡的长大与汇合现象[40,41].高能激光实验结果发现,He泡和B均会降低金属的层裂强度,且B对层裂强度的影响比He泡更加明显[43].在理论模型方面,祁美兰等[44]在孔洞增长模型基础上建立了恒定拉应力下He泡的生长方程,讨论了He泡内压、黏性、惯性及温度对He泡生长的影响.张凤国等[45]基于耦合材料初始损伤、孔洞尺寸及惯性效应的损伤模型,将He泡内压作为外力,研究了含He泡金属铝的层裂行为. ...
Dynamic strength of metals in shock deformation
1
2006
... 由于He泡涉及微观尺度,当前的实验手段难以获得对He泡动态演化的直接观测,而通过回收检测受冲击样品也很难获得对其演化过程和微观机理的认识.此外,实验样品中存在的其他缺陷使得确定He泡单一因素的影响非常困难.另一方面,已有的理论模型只是将He泡内压作为外力耦合进描述纯金属的损伤模型中,它们能否正确描述纳米级He泡的动态演化规律和损伤发展还有待考察.MD模拟为研究动载荷下含He泡金属的动态力学行为提供了另一种可行路径,可为He泡动态演化规律及其对金属动态响应的影响提供原子层面的重要信息.Kubota等[46]采用MD方法研究了含He泡金属铝在冲击作用下的动力学响应,获得了Hugoniot曲线和临界剪切强度.Wang等[47]对比研究了冲击载荷下含He泡或孔洞金属铝的塑性变形,发现He泡会更加显著地促进周围位错环的发射.Shao等[48]研究了衰减冲击波加载下He泡对金属铝层裂破坏的影响,结果表明,当冲击压力较低时He泡显著降低了金属的层裂强度.本课题组研究发现,He泡增长、汇合是导致延性金属断裂的主要机制,He泡会显著抑制孔洞的成核、增长[49,50];采用动态拉伸MD模拟,获得了宽应变率范围内含He泡固态金属铝的损伤演化规律,并结合连续介质力学理论计算发展了能描述固态金属中He泡增长的损伤模型[51]. ...
Atomistic modelling of the plastic deformation of helium bubbles and voids in aluminium under shock compression
4
2014
... 由于He泡涉及微观尺度,当前的实验手段难以获得对He泡动态演化的直接观测,而通过回收检测受冲击样品也很难获得对其演化过程和微观机理的认识.此外,实验样品中存在的其他缺陷使得确定He泡单一因素的影响非常困难.另一方面,已有的理论模型只是将He泡内压作为外力耦合进描述纯金属的损伤模型中,它们能否正确描述纳米级He泡的动态演化规律和损伤发展还有待考察.MD模拟为研究动载荷下含He泡金属的动态力学行为提供了另一种可行路径,可为He泡动态演化规律及其对金属动态响应的影响提供原子层面的重要信息.Kubota等[46]采用MD方法研究了含He泡金属铝在冲击作用下的动力学响应,获得了Hugoniot曲线和临界剪切强度.Wang等[47]对比研究了冲击载荷下含He泡或孔洞金属铝的塑性变形,发现He泡会更加显著地促进周围位错环的发射.Shao等[48]研究了衰减冲击波加载下He泡对金属铝层裂破坏的影响,结果表明,当冲击压力较低时He泡显著降低了金属的层裂强度.本课题组研究发现,He泡增长、汇合是导致延性金属断裂的主要机制,He泡会显著抑制孔洞的成核、增长[49,50];采用动态拉伸MD模拟,获得了宽应变率范围内含He泡固态金属铝的损伤演化规律,并结合连续介质力学理论计算发展了能描述固态金属中He泡增长的损伤模型[51]. ...
... MD模拟的核心是描述原子间相互作用的势函数.本工作采用Zope和Mishin[52]发展的嵌入原子方法(embedded atom method,EAM)势函数来描述金属Al原子间的相互作用.He原子间、Al-He原子间相互作用分别采用 式(1)[53]和 式(2)[47]的对势来描述,势函数参数来自文献[47].相关势函数已广泛用于金属Al和Al-He体系力学性质的研究[47~51]. ...
... 的对势来描述,势函数参数来自文献[47].相关势函数已广泛用于金属Al和Al-He体系力学性质的研究[47~51]. ...
... [47~51]. ...
Influence of voids or He bubbles on the spall damage in single crystal Al
1
2014
... 由于He泡涉及微观尺度,当前的实验手段难以获得对He泡动态演化的直接观测,而通过回收检测受冲击样品也很难获得对其演化过程和微观机理的认识.此外,实验样品中存在的其他缺陷使得确定He泡单一因素的影响非常困难.另一方面,已有的理论模型只是将He泡内压作为外力耦合进描述纯金属的损伤模型中,它们能否正确描述纳米级He泡的动态演化规律和损伤发展还有待考察.MD模拟为研究动载荷下含He泡金属的动态力学行为提供了另一种可行路径,可为He泡动态演化规律及其对金属动态响应的影响提供原子层面的重要信息.Kubota等[46]采用MD方法研究了含He泡金属铝在冲击作用下的动力学响应,获得了Hugoniot曲线和临界剪切强度.Wang等[47]对比研究了冲击载荷下含He泡或孔洞金属铝的塑性变形,发现He泡会更加显著地促进周围位错环的发射.Shao等[48]研究了衰减冲击波加载下He泡对金属铝层裂破坏的影响,结果表明,当冲击压力较低时He泡显著降低了金属的层裂强度.本课题组研究发现,He泡增长、汇合是导致延性金属断裂的主要机制,He泡会显著抑制孔洞的成核、增长[49,50];采用动态拉伸MD模拟,获得了宽应变率范围内含He泡固态金属铝的损伤演化规律,并结合连续介质力学理论计算发展了能描述固态金属中He泡增长的损伤模型[51]. ...
Spall damage in single crystal Al with helium bubbles under decaying shock loading via molecular dynamics study
2
2019
... 由于He泡涉及微观尺度,当前的实验手段难以获得对He泡动态演化的直接观测,而通过回收检测受冲击样品也很难获得对其演化过程和微观机理的认识.此外,实验样品中存在的其他缺陷使得确定He泡单一因素的影响非常困难.另一方面,已有的理论模型只是将He泡内压作为外力耦合进描述纯金属的损伤模型中,它们能否正确描述纳米级He泡的动态演化规律和损伤发展还有待考察.MD模拟为研究动载荷下含He泡金属的动态力学行为提供了另一种可行路径,可为He泡动态演化规律及其对金属动态响应的影响提供原子层面的重要信息.Kubota等[46]采用MD方法研究了含He泡金属铝在冲击作用下的动力学响应,获得了Hugoniot曲线和临界剪切强度.Wang等[47]对比研究了冲击载荷下含He泡或孔洞金属铝的塑性变形,发现He泡会更加显著地促进周围位错环的发射.Shao等[48]研究了衰减冲击波加载下He泡对金属铝层裂破坏的影响,结果表明,当冲击压力较低时He泡显著降低了金属的层裂强度.本课题组研究发现,He泡增长、汇合是导致延性金属断裂的主要机制,He泡会显著抑制孔洞的成核、增长[49,50];采用动态拉伸MD模拟,获得了宽应变率范围内含He泡固态金属铝的损伤演化规律,并结合连续介质力学理论计算发展了能描述固态金属中He泡增长的损伤模型[51]. ...
... 样品的动态拉伸强度随着应变率的升高而增大,尤其是当应变率高于3.0 × 108 s-1时呈现出明显的应变率强化效应,如图7所示.当应变率为3.0 × 106、3.0 × 107、3.0 × 108和3.0 × 109 s-1时,含He泡铝样品的动态拉伸强度分别为0.332、0.337、0.381和0.743 GPa,显著低于纯Al的强度(2.774、2.920、3.111和3.533 GPa),表明金属熔化后He泡仍然会降低金属的强度,这与Glam等[41]开展的加热层裂实验结果一致.初始温度为600 ℃的纯Al和含He泡铝平板撞击实验结果表明,He泡显著降低了金属的层裂强度(1.37 GPa vs 0.4 GPa)[41].前期对冲击载荷下含He泡铝层裂的MD模拟发现,熔化后He泡对层裂强度的影响很小[49,50],这与本工作的研究结果不同,其主要原因是应变率不同.在冲击层裂模拟中,样品所经历的应变率接近1011 s-1,高于本工作动态拉伸模拟的应变率.为此,本工作补充了应变率为3.0 × 1010 s-1的动态拉伸模拟,得到含He泡铝和纯Al样品的强度分别为3.355和4.63 GPa.这表明随着应变率进一步增加,含He泡铝的强度显著增加,使得He泡对动态拉伸强度的影响有所减弱,趋向于冲击层裂的MD模拟结果.对于纯Al,飞秒激光实验结果得到的温度为2500 K时的层裂强度高达2.5 GPa[58],比本工作在1100 K的计算结果略低. ...
Dynamic evolution of He bubble and its effects on void nucleation-growth and thermomechanical properties in the spallation of aluminum
2
2020
... 由于He泡涉及微观尺度,当前的实验手段难以获得对He泡动态演化的直接观测,而通过回收检测受冲击样品也很难获得对其演化过程和微观机理的认识.此外,实验样品中存在的其他缺陷使得确定He泡单一因素的影响非常困难.另一方面,已有的理论模型只是将He泡内压作为外力耦合进描述纯金属的损伤模型中,它们能否正确描述纳米级He泡的动态演化规律和损伤发展还有待考察.MD模拟为研究动载荷下含He泡金属的动态力学行为提供了另一种可行路径,可为He泡动态演化规律及其对金属动态响应的影响提供原子层面的重要信息.Kubota等[46]采用MD方法研究了含He泡金属铝在冲击作用下的动力学响应,获得了Hugoniot曲线和临界剪切强度.Wang等[47]对比研究了冲击载荷下含He泡或孔洞金属铝的塑性变形,发现He泡会更加显著地促进周围位错环的发射.Shao等[48]研究了衰减冲击波加载下He泡对金属铝层裂破坏的影响,结果表明,当冲击压力较低时He泡显著降低了金属的层裂强度.本课题组研究发现,He泡增长、汇合是导致延性金属断裂的主要机制,He泡会显著抑制孔洞的成核、增长[49,50];采用动态拉伸MD模拟,获得了宽应变率范围内含He泡固态金属铝的损伤演化规律,并结合连续介质力学理论计算发展了能描述固态金属中He泡增长的损伤模型[51]. ...
... 样品的动态拉伸强度随着应变率的升高而增大,尤其是当应变率高于3.0 × 108 s-1时呈现出明显的应变率强化效应,如图7所示.当应变率为3.0 × 106、3.0 × 107、3.0 × 108和3.0 × 109 s-1时,含He泡铝样品的动态拉伸强度分别为0.332、0.337、0.381和0.743 GPa,显著低于纯Al的强度(2.774、2.920、3.111和3.533 GPa),表明金属熔化后He泡仍然会降低金属的强度,这与Glam等[41]开展的加热层裂实验结果一致.初始温度为600 ℃的纯Al和含He泡铝平板撞击实验结果表明,He泡显著降低了金属的层裂强度(1.37 GPa vs 0.4 GPa)[41].前期对冲击载荷下含He泡铝层裂的MD模拟发现,熔化后He泡对层裂强度的影响很小[49,50],这与本工作的研究结果不同,其主要原因是应变率不同.在冲击层裂模拟中,样品所经历的应变率接近1011 s-1,高于本工作动态拉伸模拟的应变率.为此,本工作补充了应变率为3.0 × 1010 s-1的动态拉伸模拟,得到含He泡铝和纯Al样品的强度分别为3.355和4.63 GPa.这表明随着应变率进一步增加,含He泡铝的强度显著增加,使得He泡对动态拉伸强度的影响有所减弱,趋向于冲击层裂的MD模拟结果.对于纯Al,飞秒激光实验结果得到的温度为2500 K时的层裂强度高达2.5 GPa[58],比本工作在1100 K的计算结果略低. ...
Atomistic simulation and continuum modeling of the dynamic tensile fracture and damage evolution of solid single crystalline al with He bubble
9
2022
... 由于He泡涉及微观尺度,当前的实验手段难以获得对He泡动态演化的直接观测,而通过回收检测受冲击样品也很难获得对其演化过程和微观机理的认识.此外,实验样品中存在的其他缺陷使得确定He泡单一因素的影响非常困难.另一方面,已有的理论模型只是将He泡内压作为外力耦合进描述纯金属的损伤模型中,它们能否正确描述纳米级He泡的动态演化规律和损伤发展还有待考察.MD模拟为研究动载荷下含He泡金属的动态力学行为提供了另一种可行路径,可为He泡动态演化规律及其对金属动态响应的影响提供原子层面的重要信息.Kubota等[46]采用MD方法研究了含He泡金属铝在冲击作用下的动力学响应,获得了Hugoniot曲线和临界剪切强度.Wang等[47]对比研究了冲击载荷下含He泡或孔洞金属铝的塑性变形,发现He泡会更加显著地促进周围位错环的发射.Shao等[48]研究了衰减冲击波加载下He泡对金属铝层裂破坏的影响,结果表明,当冲击压力较低时He泡显著降低了金属的层裂强度.本课题组研究发现,He泡增长、汇合是导致延性金属断裂的主要机制,He泡会显著抑制孔洞的成核、增长[49,50];采用动态拉伸MD模拟,获得了宽应变率范围内含He泡固态金属铝的损伤演化规律,并结合连续介质力学理论计算发展了能描述固态金属中He泡增长的损伤模型[51]. ...
... MD模拟的核心是描述原子间相互作用的势函数.本工作采用Zope和Mishin[52]发展的嵌入原子方法(embedded atom method,EAM)势函数来描述金属Al原子间的相互作用.He原子间、Al-He原子间相互作用分别采用 式(1)[53]和 式(2)[47]的对势来描述,势函数参数来自文献[47].相关势函数已广泛用于金属Al和Al-He体系力学性质的研究[47~51]. ...
... 以优化后的结构作为施加动态拉伸载荷的初始结构,采用恒定应变率的三轴拉伸,拉伸过程中样品内原子坐标变化通过LAMMPS自带的“deform”命令来实现.动态拉伸过程采用等温等容(canonical,NVT)系综,温度保持在目标温度1100 K.拉伸的体积应变率(,下文的应变率均指体积应变率)范围为3.0 × 106~3.0 × 1010 s-1,以研究宽应变率范围内样品的动态拉伸断裂行为.MD模拟中采用三维周期性边界条件,时间步长为1 fs.动态拉伸过程中He泡与孔洞等微结构的演化通过Open Visualization Tool (OVITO)软件中的“Construct surface mesh”方法[55]进行可视化分析.在该方法中,当孔洞半径大于最近邻原子半径时被识别为孔洞.孔洞体积采用本课题组最近发展的统计方法和程序来计算[51].具体做法为:将样品在三维空间划分为若干个立方体单元,单元尺寸与金属的晶格常数相当,将样品内所有原子根据其坐标划分到这些立方体中;若在3个方向连续2个单元内均没有原子,则识别为孔洞;将相互连接的多个空单元合并为一个孔洞,该孔洞的体积为这些空单元的体积之和.与“Construct surface mesh”方法相比,该孔洞统计方法能有效排除点缺陷.He泡作为一种含气孔洞,其统计方法与孔洞相同,只需先删除He原子. ...
... MD模拟结果(见2.1节)表明基体材料熔化后He泡增长是导致材料拉伸断裂的主导物理机制,传统的孔洞成核、增长机制被显著抑制,与基体材料为固态时一致[51].因此,在建立损伤模型时本工作忽略孔洞成核、增长项,仅考虑He泡增长项.模型以孔洞增长模型[1~3]为基本框架,考虑He泡内压的影响,具体表达式如 式(3)所示,包括外加应力、He泡内压、惯性、黏性及表面张力对He泡增长的作用. ...
... 式中,左边第一项P为外界施加的拉伸应力;左边第二项为He泡内压[56],R指He泡半径,R0和均指He泡初始参数(即初始半径和初始内压),n表示He泡气压随半径的衰减系数;右边第一项为惯性,ρs为基体材料的密度;表示R随时间(t)的一阶导数,即He泡半径变化的速度,表示R随t的二阶导数,即He泡半径变化的加速度;右边第二项为材料黏性,η为黏性系数;右边第三项为表面张力,γ为表面能.MD模拟可给出He泡内压随He泡半径的变化规律,从而可以确定He泡内压项的指数n (见补充材料图S1).He泡的表面能可由MD模拟给出的He泡初始半径和初始内压依据Laplace-Young方程( = 2γ / R0)[57]确定.方程(3)中仅有一个待定参数η.与固态的损伤模型不同[51],在描述液相的损伤发展时,本工作不再考虑基体材料的强度. ...
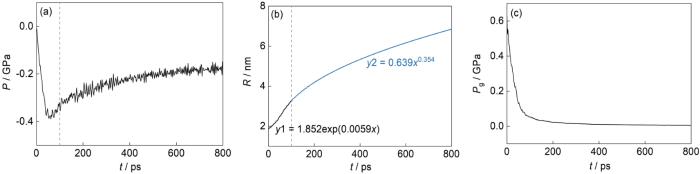
... 以应变率为3.0 × 108 s-1为例对动态拉伸过程进行详细讨论.图2a是该应变率下含He泡铝样品中He泡的微结构演化过程,拉伸应力、He泡半径以及He泡内压随时间的变化见图3.由图2a可以看出,在拉伸应力作用下,He泡很快发生膨胀,说明基体材料熔化后,He泡增长的临界应力很低(约为0.068 GPa),显著低于固态.固态时,He泡膨胀需要克服材料的屈服强度,当基体材料发生塑性变形后He泡才会发生明显增长,因此临界应力较高[51].在膨胀过程中,液态时He泡基本保持为球形,而固态时为八面体结构[51].此外,在整个拉伸过程中,没有观察到孔洞成核、增长,表明He泡增长是导致液态金属拉伸断裂的主导物理机制,这与固态时的断裂机制[51]相同. ...
... [51].此外,在整个拉伸过程中,没有观察到孔洞成核、增长,表明He泡增长是导致液态金属拉伸断裂的主导物理机制,这与固态时的断裂机制[51]相同. ...
... [51]相同. ...
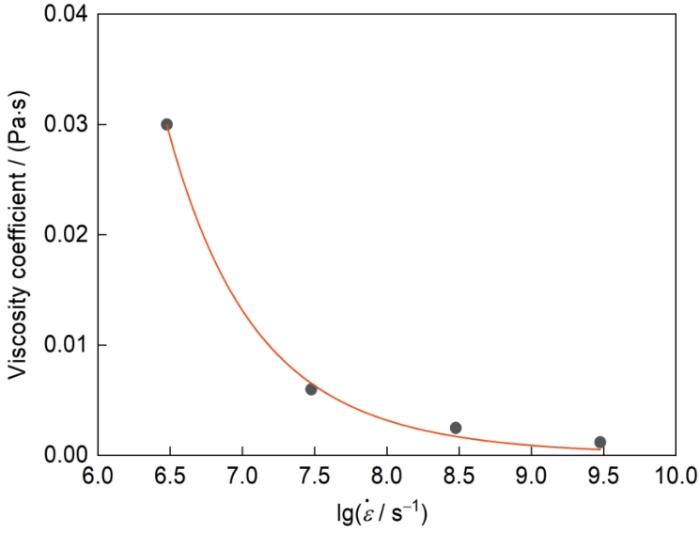
... 损伤模型中唯一的待定参数η通过拟合MD模拟得到的拉伸应力与He泡半径随时间的变化确定,其随应变率的变化如图10所示.黏性系数随着温度的升高会显著降低,因此液体的黏性系数会明显低于固体材料[51].此外,黏性系数随着应变率的升高而降低,这与已有研究结果[63,64]一致.将黏性系数随应变率的变化按照 式(7)进行拟合,得到拟合系数c1 = 1.208 × 107,c2 =10.606. ...
Interatomic potentials for atomistic simulations of the Ti-Al system
1
2003
... MD模拟的核心是描述原子间相互作用的势函数.本工作采用Zope和Mishin[52]发展的嵌入原子方法(embedded atom method,EAM)势函数来描述金属Al原子间的相互作用.He原子间、Al-He原子间相互作用分别采用 式(1)[53]和 式(2)[47]的对势来描述,势函数参数来自文献[47].相关势函数已广泛用于金属Al和Al-He体系力学性质的研究[47~51]. ...
Equation of state and melting curve of helium to very high pressure
1
1981
... MD模拟的核心是描述原子间相互作用的势函数.本工作采用Zope和Mishin[52]发展的嵌入原子方法(embedded atom method,EAM)势函数来描述金属Al原子间的相互作用.He原子间、Al-He原子间相互作用分别采用 式(1)[53]和 式(2)[47]的对势来描述,势函数参数来自文献[47].相关势函数已广泛用于金属Al和Al-He体系力学性质的研究[47~51]. ...
Fast parallel algorithms for short-range molecular dynamics
1
1995
... 式中,ϕ为原子间相互作用的势能;r为原子之间的距离;a、α和β为拟合系数,a = 13.1,α = 0.024 eV;β = 7.046;ε / k = 12.4,为拟合系数(其中,ε为原子间相互作用势能的最低值,k为Boltzmann常数);r* = 0.325 nm,为He原子间相互作用的截断半径(cut-off radius);ra = 0.567 nm,为Al-He原子间相互作用的截断半径.MD模拟采用国际开源程序Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)[54].首先采用共轭梯度法对样品进行能量最小化,再采用等温等压(NPT)系综在300 K和零压下对样品进行20 ps的结构优化.随后将样品升温至熔化后的目标温度(T = 1100 K),再采用NPT系综进行该温度和零压下的结构优化,优化时间为50 ps以确保样品完全熔化.优化后的样品结构如图1b所示,样品密度为2.372 g/cm3,He泡初始半径R0 = 1.868 nm,He泡初始内压 = 0.632 GPa. ...
Visualization and analysis of atomistic simulation data with OVITO—The open visualization tool
1
2010
... 以优化后的结构作为施加动态拉伸载荷的初始结构,采用恒定应变率的三轴拉伸,拉伸过程中样品内原子坐标变化通过LAMMPS自带的“deform”命令来实现.动态拉伸过程采用等温等容(canonical,NVT)系综,温度保持在目标温度1100 K.拉伸的体积应变率(,下文的应变率均指体积应变率)范围为3.0 × 106~3.0 × 1010 s-1,以研究宽应变率范围内样品的动态拉伸断裂行为.MD模拟中采用三维周期性边界条件,时间步长为1 fs.动态拉伸过程中He泡与孔洞等微结构的演化通过Open Visualization Tool (OVITO)软件中的“Construct surface mesh”方法[55]进行可视化分析.在该方法中,当孔洞半径大于最近邻原子半径时被识别为孔洞.孔洞体积采用本课题组最近发展的统计方法和程序来计算[51].具体做法为:将样品在三维空间划分为若干个立方体单元,单元尺寸与金属的晶格常数相当,将样品内所有原子根据其坐标划分到这些立方体中;若在3个方向连续2个单元内均没有原子,则识别为孔洞;将相互连接的多个空单元合并为一个孔洞,该孔洞的体积为这些空单元的体积之和.与“Construct surface mesh”方法相比,该孔洞统计方法能有效排除点缺陷.He泡作为一种含气孔洞,其统计方法与孔洞相同,只需先删除He原子. ...
1
1965
... 式中,左边第一项P为外界施加的拉伸应力;左边第二项为He泡内压[56],R指He泡半径,R0和均指He泡初始参数(即初始半径和初始内压),n表示He泡气压随半径的衰减系数;右边第一项为惯性,ρs为基体材料的密度;表示R随时间(t)的一阶导数,即He泡半径变化的速度,表示R随t的二阶导数,即He泡半径变化的加速度;右边第二项为材料黏性,η为黏性系数;右边第三项为表面张力,γ为表面能.MD模拟可给出He泡内压随He泡半径的变化规律,从而可以确定He泡内压项的指数n (见补充材料图S1).He泡的表面能可由MD模拟给出的He泡初始半径和初始内压依据Laplace-Young方程( = 2γ / R0)[57]确定.方程(3)中仅有一个待定参数η.与固态的损伤模型不同[51],在描述液相的损伤发展时,本工作不再考虑基体材料的强度. ...
1
2006
... 式中,左边第一项P为外界施加的拉伸应力;左边第二项为He泡内压[56],R指He泡半径,R0和均指He泡初始参数(即初始半径和初始内压),n表示He泡气压随半径的衰减系数;右边第一项为惯性,ρs为基体材料的密度;表示R随时间(t)的一阶导数,即He泡半径变化的速度,表示R随t的二阶导数,即He泡半径变化的加速度;右边第二项为材料黏性,η为黏性系数;右边第三项为表面张力,γ为表面能.MD模拟可给出He泡内压随He泡半径的变化规律,从而可以确定He泡内压项的指数n (见补充材料图S1).He泡的表面能可由MD模拟给出的He泡初始半径和初始内压依据Laplace-Young方程( = 2γ / R0)[57]确定.方程(3)中仅有一个待定参数η.与固态的损伤模型不同[51],在描述液相的损伤发展时,本工作不再考虑基体材料的强度. ...
Strength properties of an aluminum melt at extremely high tension rates under the action of femtosecond laser pulses
1
2010
... 样品的动态拉伸强度随着应变率的升高而增大,尤其是当应变率高于3.0 × 108 s-1时呈现出明显的应变率强化效应,如图7所示.当应变率为3.0 × 106、3.0 × 107、3.0 × 108和3.0 × 109 s-1时,含He泡铝样品的动态拉伸强度分别为0.332、0.337、0.381和0.743 GPa,显著低于纯Al的强度(2.774、2.920、3.111和3.533 GPa),表明金属熔化后He泡仍然会降低金属的强度,这与Glam等[41]开展的加热层裂实验结果一致.初始温度为600 ℃的纯Al和含He泡铝平板撞击实验结果表明,He泡显著降低了金属的层裂强度(1.37 GPa vs 0.4 GPa)[41].前期对冲击载荷下含He泡铝层裂的MD模拟发现,熔化后He泡对层裂强度的影响很小[49,50],这与本工作的研究结果不同,其主要原因是应变率不同.在冲击层裂模拟中,样品所经历的应变率接近1011 s-1,高于本工作动态拉伸模拟的应变率.为此,本工作补充了应变率为3.0 × 1010 s-1的动态拉伸模拟,得到含He泡铝和纯Al样品的强度分别为3.355和4.63 GPa.这表明随着应变率进一步增加,含He泡铝的强度显著增加,使得He泡对动态拉伸强度的影响有所减弱,趋向于冲击层裂的MD模拟结果.对于纯Al,飞秒激光实验结果得到的温度为2500 K时的层裂强度高达2.5 GPa[58],比本工作在1100 K的计算结果略低. ...
Dynamic fracture kinetics, influence of temperature and microstructure in the atomistic model of aluminum
1
2010
... 大量的实验与理论研究已表明,金属的拉伸强度会随着应变率的升高而增加[25,59~62],而应变率对拉伸强度的影响机制与不同应变率下的损伤成核机制有关[25,62].对于完美晶体,高/低应变率下的损伤都是均匀成核的,所需的成核应力较高.因此,层裂强度也较高,且层裂强度随应变率的降低而缓慢下降,如图7中的金属纯Al.对于含缺陷金属,应变率较低时,损伤是非均匀成核的,以缺陷处的成核增长为主,所需的成核应力较低;应变率较高时,非均匀成核不足以将应力弛豫,均匀成核也会被激发.因此,含缺陷金属的层裂强度会随着应变率的降低而显著降低,且低于完美晶体,如图7中的含He泡金属.对应变率为3.0 × 1010 s-1时含He泡铝的微结构分析证明,高应变率下除了He泡增长,还出现了新的孔洞成核、增长(如图8所示),这与更低应变率下的损伤仅由He泡增长控制有所不同. ...
Behavior of aluminum near an ultimate theoretical strength in experiments with femtosecond laser pulses
0
2010
Strength of liquid tin at extremely high strain rates under a femtosecond laser action
0
2016
Spall fracture: Methodological aspects, mechanisms and governing factors
2
2010
... 大量的实验与理论研究已表明,金属的拉伸强度会随着应变率的升高而增加[25,59~62],而应变率对拉伸强度的影响机制与不同应变率下的损伤成核机制有关[25,62].对于完美晶体,高/低应变率下的损伤都是均匀成核的,所需的成核应力较高.因此,层裂强度也较高,且层裂强度随应变率的降低而缓慢下降,如图7中的金属纯Al.对于含缺陷金属,应变率较低时,损伤是非均匀成核的,以缺陷处的成核增长为主,所需的成核应力较低;应变率较高时,非均匀成核不足以将应力弛豫,均匀成核也会被激发.因此,含缺陷金属的层裂强度会随着应变率的降低而显著降低,且低于完美晶体,如图7中的含He泡金属.对应变率为3.0 × 1010 s-1时含He泡铝的微结构分析证明,高应变率下除了He泡增长,还出现了新的孔洞成核、增长(如图8所示),这与更低应变率下的损伤仅由He泡增长控制有所不同. ...
... ,62].对于完美晶体,高/低应变率下的损伤都是均匀成核的,所需的成核应力较高.因此,层裂强度也较高,且层裂强度随应变率的降低而缓慢下降,如图7中的金属纯Al.对于含缺陷金属,应变率较低时,损伤是非均匀成核的,以缺陷处的成核增长为主,所需的成核应力较低;应变率较高时,非均匀成核不足以将应力弛豫,均匀成核也会被激发.因此,含缺陷金属的层裂强度会随着应变率的降低而显著降低,且低于完美晶体,如图7中的含He泡金属.对应变率为3.0 × 1010 s-1时含He泡铝的微结构分析证明,高应变率下除了He泡增长,还出现了新的孔洞成核、增长(如图8所示),这与更低应变率下的损伤仅由He泡增长控制有所不同. ...
Strain-rate dependence of the effective viscosity under steady-wave shock compression
1
1981
... 损伤模型中唯一的待定参数η通过拟合MD模拟得到的拉伸应力与He泡半径随时间的变化确定,其随应变率的变化如图10所示.黏性系数随着温度的升高会显著降低,因此液体的黏性系数会明显低于固体材料[51].此外,黏性系数随着应变率的升高而降低,这与已有研究结果[63,64]一致.将黏性系数随应变率的变化按照 式(7)进行拟合,得到拟合系数c1 = 1.208 × 107,c2 =10.606. ...
Dependence of bulk viscosity of polypropylene on strain, strain rate, and melt temperature
1
2017
... 损伤模型中唯一的待定参数η通过拟合MD模拟得到的拉伸应力与He泡半径随时间的变化确定,其随应变率的变化如图10所示.黏性系数随着温度的升高会显著降低,因此液体的黏性系数会明显低于固体材料[51].此外,黏性系数随着应变率的升高而降低,这与已有研究结果[63,64]一致.将黏性系数随应变率的变化按照 式(7)进行拟合,得到拟合系数c1 = 1.208 × 107,c2 =10.606. ...