现有数值模拟研究主要集中于液-固相变或固-固相变等单一相变过程,尚未建立起能够完全耦合凝固与固态相变的一体化模拟[9]。这主要是因为凝固过程中典型组织(如枝晶等)的尺寸通常为数十到数百微米,而固态相变的典型组织(如析出相)则在纳米尺度,2者在尺寸上存在数量级的差距,实现跨尺度的数据耦合是凝固-固态相变一体化模拟的难点之一。目前,主要的研究方法是将凝固模拟结果作为初始条件输入到固态相变模拟。Meng等[10]通过2个不同网格尺寸的元胞自动机模型,模拟了Fe-C-Mn-S合金凝固过程中的枝晶生长及后续MnS相的析出,但其模拟过程仅在含有MnS杂质的元胞中进行后续固态相变模拟,未能将初始凝固组织信息完整嵌入固态相变研究中,导致析出相尺寸与实际情况存在较大偏差。Shi等[11]针对TC4合金的激光熔覆过程,提出了包含基于元胞自动机方法的凝固微观组织模拟及基于相场模型的固态相变模拟一体化框架,但仅构建了理论框架,并未展示完整的实例研究。Liu等[12]通过耦合宏观温度场有限元模拟和凝固及固态相变微观组织的相场法模拟,建立了适用于TC4合金增材制造过程的一体化模型,但其固态相变组织的初始浓度仍采用均匀的名义成分分布,未能将凝固形成的溶质偏析与固态相变过程有效耦合。张琪等[13]采用晶体相场模型模拟了二元合金多晶凝固及后续调幅分解全过程,结果表明该模型可完整再现包括形核、生长、粗化、晶界形成等多晶生长过程,以及从凝固到调幅分解的多相变过程,但由于晶体相场模型与实际材料特性难以准确耦合,限制了其在实际合金凝固-固态相变微观组织演变一体化模拟中的应用。可见,尽管凝固-固态相变一体化微观组织模拟已取得了相关进展,但在统一模型构建及跨尺度信息传递(如晶粒取向、溶质场分布等)等方面仍需进一步完善。迫切需要建立可靠的多尺度模拟策略,实现从晶粒尺度、枝晶尺度到析出相尺度的微观组织演化连续模拟。
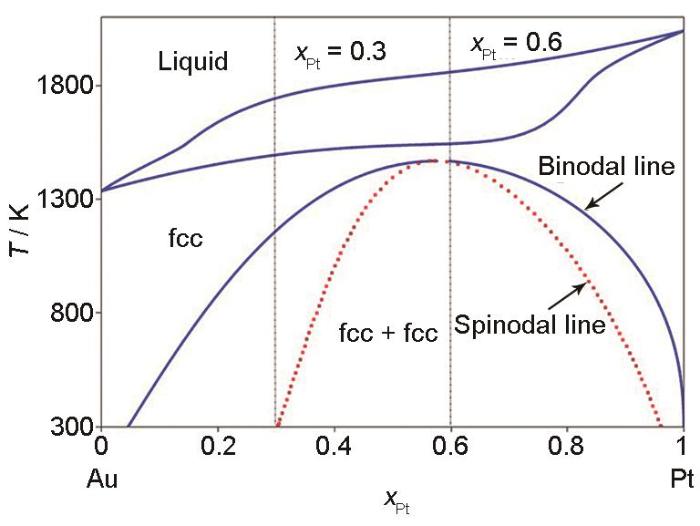
通过对抗磁性Au和顺磁性Pt混合比例的调控,可得到近零磁化率的Au-Pt合金,这种合金是空间引力波探测中“检验质量”立方体的理想材料,欧洲空间引力波探测器的“检验质量”即采用了Au-25%Pt (原子分数)合金[14~18],但制备该设备需要得到成分均匀、磁化率极低的千克级Au-Pt合金块体材料,而在合金熔炼、成形及后处理过程中容易出现相分离、成分不均匀及引入磁性杂质等问题。因此,深入理解Au-Pt合金的凝固及固态相变微观组织演化规律,是开发高纯度、高均匀性千克级“检验质量”制备技术的前提和关键。此外,从Au-Pt合金相图可以看出,合金的最终微观组织是由初始的凝固和后期的固态相变共同决定的,因此Au-Pt合金也是研究凝固-固态相变微观组织演化一体化模拟的理想对象。
综上问题,本工作以Au-Pt合金为例,首先给出可传递溶质偏析及晶粒取向信息的凝固及固态相变微观组织演化一体化模型构建策略,然后通过将模拟获得的凝固组织作为固态相变的初始条件,研究凝固微观偏析和晶界对后续固态相变过程的影响。
1 模型与方法
1.1 多相场模型
式中,Vm为摩尔体积;T为温度;c为体系中溶质元素的浓度;V为计算域空间体积;εij 为第
式中,h(ϕl) = ϕ
根据Ginzburg-Landau方程可得到
式中,Mϕ 为表征界面迁移率的相场动力学系数。
而溶质场的演化满足Cahn-Hilliard方程,其表达形式为:
式中,c = h(ϕ1)cα +[1 - h(ϕ1)]cβ 为混合浓度,cα 和cβ 分别为溶质在α相和β相中的浓度,Dα 和Dβ 分别为溶质在α相和β相中的扩散系数。
1.2 凝固-固态相变一体化模拟策略
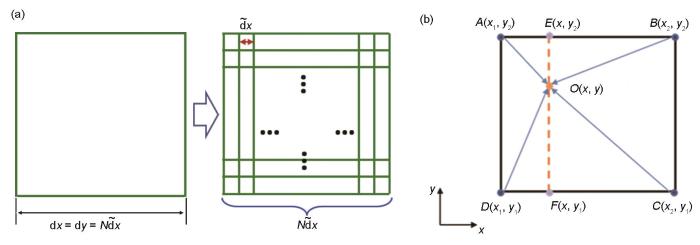
如何实现2个不同尺度间的数据传递是研究凝固-固态相变微观组织演化一体化模拟的难点,本工作通过双线性插值方法将二维凝固模拟获得的浓度场和取向场信息传递到后续固态相变模拟中(三维模拟中需要三线性插值)。如图1a所示,不同尺度间的信息传递时,需要将较大尺度计算域中网格(网格尺寸较大)的信息传递到较小尺度的计算域(网格尺寸较小)上,此时需要采用插值方法,获得细网格中每个网格节点的值。双线性插值是有2个变量的插值函数的线性插值扩展,其核心思想是分别从2个坐标方向分别对变量进行一次线性插值,线性插值的结果与插值顺序无关。如图1b所示,对尺寸较大的网格,如果已知4个端点A、B、C、D处的坐标和数据,就可通过双线性插值算法得到其内部任意坐标处的数值,从而将信息从尺寸较大的网格传递到尺寸较小的网格上。具体过程如下:首先基于A、B和C、D分别进行线性插值得到点E、F的数值,然后再基于E、F 2点进行插值得到待求点O的数值,如
式中,I为某个坐标点的浓度场值或相场值。
图1
图1
不同尺度间插值的示意图
Fig.1
Schematics of interpolation between different scales (dx and dy are grid sizes for a large spatial scale used for modeling of solidification microstructure evolution, while
(a) coarse and fine grids at different scales (b) bilinear interpolation algorithm
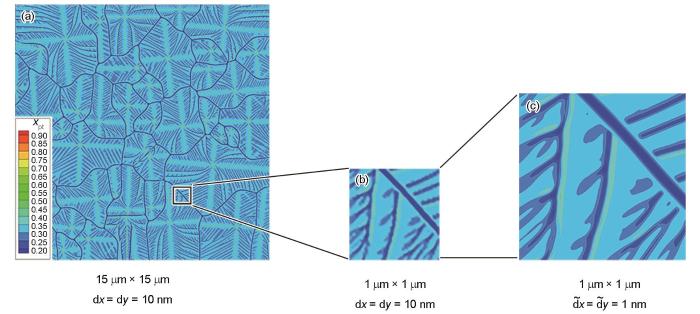
图2给出了凝固-固态相变微观组织演化一体化模拟中溶质场插值过程及结果。图2a为采用相场法模拟所得的初始凝固组织,此时模拟的空间步长为dx = dy = 10 nm,模拟区域尺寸为15 μm × 15 μm;图2b是为进行后续固态相变过程模拟而选取的代表性初始凝固组织区域,区域尺寸为1 μm × 1 μm,此时网格尺寸仍为dx = dy = 10 nm;图2c为经过双线性插值计算后得到的溶质场,此时模拟的空间步长为
图2
图2
溶质场插值过程示意图
Fig.2
Schematics of interpolation process of solute field
(a) simulated solidification microstructure with a domain of 15 μm × 15 μm and a coarse grid size (dx = dy = 10 nm; xPt—mole fraction of Pt)
(b) microstructure extracted from Fig.2a with a small domain (1 μm × 1 μm) and a coarse grid size (dx = dy = 10 nm)
(c) microstructure interpolated from Fig.2b with a much finer grid size (
1.3 模拟条件设置
图3
表1 Au-Pt合金的热物性参数及模拟参数
Table1
| Parameter | Variable | Unit | Value |
|---|---|---|---|
| Liquid phase solute diffusivity | DL | m2·s-1 | 3.5 × 10-9 [23] |
| Solid phase solute diffusivity | DS | m2·s-1 | 0.5 × 10-12[23] |
| Solid-liquid interface energy | σSL | J·m-2 | 0.5 |
| Solid-solid interface energy | σSS | J·m-2 | 1 |
| Mole volume | Vm | m3·mol-1 | 9.8 × 10-6 |
| Thickness of solid-liquid interface | λLS | μm | 5dx |
| Thickness of solid-solid interface | λSS | μm | 5dx |
| Anisotropy coefficient of interface energy | γ4 | - | 0.02 |
| Mean radius of initial nucleus | r | μm | 10dx |
2 结果与分析
2.1 Au-Pt合金凝固微观组织演化模拟
图4所示为初始温度1600 K、冷却速率
图4
图4
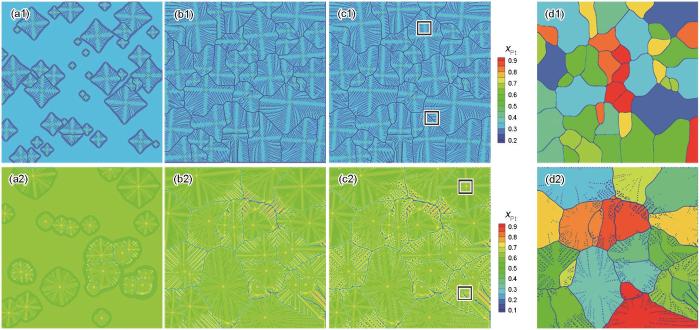
不同初始成分条件下Au-Pt合金多晶组织的成分场演化及凝固末期的晶粒取向分布情况
Fig.4
Evolutions of the concentration field during solification at t = 2 × 103Δt (a1, a2), 1 × 104Δt (b1, b2), and 5 × 104Δt (c1, c2); and the orientation fields at the late stage (d1, d2) of Au-Pt alloys with different initial compositions (Each color in Figs.4d1 and d2 represents grains with the same orientation; t—time, Δt—time step)
(a1-d1) xPt = 0.3 (a2-d2) xPt = 0.6
2.2 Au-Pt合金固态相变微观组织演化模拟
图5
图5
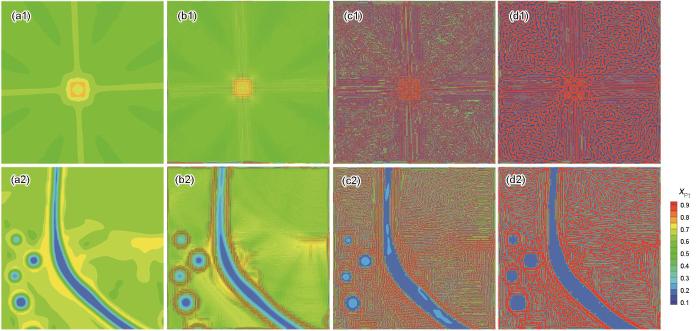
xPt = 0.3时图4c1中红框所示区域凝固组织的后续脱溶析出及调幅分解组织演化情况
Fig.5
Microstructure evolutions during subsequnet solid-state phase transformation at t = 0 (a1, a2), 1.2 × 103Δt (b1, b2), 8 × 103Δt (c1, c2), and 4 × 104Δt (d1, d2) when xPt = 0.3 with different initial microstructures as shown in the rectangle areas in Fig.4c1
(a1-d1) domain in grains (a2-d2) domain near grain boundaries
图6
图6
xPt = 0.6时图4c2中红框所示区域凝固组织的后续固态相变组织演化情况
Fig.6
Microstructure evolutions during subsequnet solid state phase transformation at t = 0 (a1, a2), 1.2 × 103Δt (b1, b2), 8 × 103Δt (c1, c2), and 4 × 104Δt (d1, d2) when xPt = 0.6 with different initial microstructures as shown in the rectangle areas in Fig.4c2
(a1-d1) domain in grains (a2-d2) domain near grain boundaries
图5展示了xPt = 0.3时,图4c1中方框区域内的凝固组织在后续脱溶析出及调幅分解过程中的演化情况。由图5a1~d1可以看出,初始凝固组织为枝晶结构,其中枝晶干区域的溶质含量较高,根据相图可知,溶质含量高易达到发生调幅分解的条件,而枝晶二次臂间的区域为最后凝固的区域,溶质含量较低,未达到调幅分解的临界成分范围。因此,在后续固态相变过程中,枝晶干区域发生了调幅分解,而二次枝晶臂区域则发生了脱溶析出。前者无需形核,直接在已有组织中进行相分离,后者则需要形核并逐渐长大。模拟结果完美反映了这2种相变过程:调幅分解形成条状或粒状组织,具体形态取决于空间分布,而脱溶析出的相则在形核后长成粒状结构。随着时间的推移,2种结构均出现了粗化长大现象。图5a2~d2所示的区域中包含晶界,模拟结果表明此区域内的成分均低于调幅分解所需的临界值。由于晶界区域是最后凝固的部分,溶质含量最低(Au-Pt合金的溶质再分配系数大于1),甚至低于脱溶转变的临界成分。因此,在这种初始成分分布下,晶界及其周围低溶质含量的区域没有发生脱溶析出或调幅分解。而在其他高于脱溶转变临界成分的区域,脱溶析出过程得以进行。随着时间的推移,由于界面能的作用,析出相逐渐发生Ostwald熟化,导致相结构的粗化和长大。通过这些模拟结果,可以清晰地看到不同微观区域内成分分布的差异对固态相变过程的影响,尤其是晶界与枝晶间的成分差异,导致了不同区域内调幅分解和脱溶析出的先后顺序,这为理解Au-Pt合金的凝固组织在后续热处理过程中的微观演化提供了重要的理论依据。
图6展示了xPt = 0.6时,图4c2中方框区域内凝固组织的后续脱溶析出和调幅分解的演化过程。由于此时初始溶质含量较高,凝固后微观组织中大部分区域的成分都位于调幅分解区,因此无论是在晶粒内部还是在晶界附近,都发生了调幅分解。然而,晶界及最后凝固的液滴区域溶质含量较低,未发生后续的固态相变,如图6a2~d2所示。从图6a1~d1可以看出,调幅分解的相分离首先发生在溶质含量较高的区域(如先凝固的枝晶干),随着相分离的进行,晶界附近的区域也开始相分离,只要该区域的成分处于调幅分解线范围之内。相分离随后逐渐扩散至整个枝晶区域,直至所有成分点都发生相分离现象。通过对模拟结果的观察可以看出,当晶界处的成分位于调幅分解线内时,相较于晶粒内部,晶界边缘会率先发生调幅分解,并逐渐向晶内扩散和长大。同时,晶粒内部的调幅分解通常从枝晶中心的高成分区域开始,逐步向周围低成分区域扩展。晶界处析出相的形态与晶界微观结构密切相关,已有研究[26~28]表明,调幅分解往往从晶界开始,并沿着垂直于晶界的方向延伸到整个晶粒。通常将这种与晶界具有特定取向关系(如平行于晶界或垂直于晶界)的相分离过程称为晶界调制的调幅分解。发生晶界调制的调幅分解主要原因在于晶界原子的迁移率较高,使得晶界处的成分偏聚速率更快,成分波动更大。成分波会在梯度能的驱动下由平行于晶界转变为垂直于晶界,从而降低晶界前原子富集程度,造成晶界处调幅分解组织的垂直界面方向性,进而呈现出由晶界向晶粒内部扩展的特征。
综上所述,本工作提出的凝固-固态相变一体化模拟策略能够准确反映出具有不同微观偏析程度的凝固组织对后续脱溶析出和调幅分解的影响,揭示了晶界与晶粒内部不同区域调幅分解的先后顺序。这种模拟策略不仅揭示了凝固组织中不同成分对固态相变的影响,还为进一步研究微观组织的演化规律提供了可靠依据。
3 结论
(1) 构建了Au-Pt二元合金体系凝固-固态相变组织一体化相场模拟策略,通过双线性插值算法可有效地将凝固组织信息传递到后续固态相变模拟中,实现了Au-Pt合金体系凝固及固态相变组织耦合的微观组织演化模拟。
(2) 凝固微观偏析程度显著影响后续固态相变的动力学进程。以Au-Pt二元合金调幅分解为例,对于具有不同凝固微观偏析程度的枝晶组织,合金的调幅分解过程总是从溶质含量更高的枝晶中心开始发生,随后从枝晶中心及枝晶主干区域逐渐向低浓度区域扩散。
(3) 凝固过程中形成的晶界也会显著影响后续调幅分解过程。当凝固组织中包含晶界时,调幅分解的相分离先于晶界处发生,且靠近晶界的组织呈现出由晶界向晶粒内部延伸的特征。
参考文献
Progress in modelling solidification microstructures in metals and alloys: dendrites and cells from 1700 to 2000
[J].
Progress in modelling solidification microstructures in metals and alloys. Part II: Dendrites from 2001 to 2018
[J].
Progress and prospect of solidification research for metallic materials
[J].
金属材料凝固过程研究现状与未来展望
[J].
Unified analysis of non-equilibrium solidification and solid-state phase transformations
[J].Considering both phase transition and material hot-working or material design, unified analysis of non-equilibrium solidification and solid-state phase transformations has profound significance of science and great prospect of engineering application. Here, non-equilibrium solidification and solid state transformation behavior, correlated with peritectic reaction, massive transformation, metastable-stable transformation, precipitation, recrystallization and grain growth, for single phase solid solution alloy, eutectic alloy, peritectic alloy, multi-component super alloy and aluminum alloy, have been systematically reviewed. Regarding further the influence of non-equilibrium solidification on subsequent solid-state transformations, the new transformation mechanism induced by non-equilibrium solidification and the integrated microstructure regulation, the physical correlation between non-equilibrium solidification and subsequent solid-state transformations were discussed, and eventually, the microstructure control under the joint action of non-equilibrium solidification and solid phase transformations was realized. This review is expected to provide theoretical support for quantitative characterization of non-equilibrium solidification effect and microstructure prediction under the joint action of non-equilibrium solidification and solid-state transformations.
非平衡凝固与固态相变的一体化研究
[J].
Modeling of hierarchical solidification microstructures in metal additive manufacturing: challenges and opportunities
[J].
Progress and application of microstructure simulation of alloy solidification
[J].Solidification structures are the interaction links between the alloy components and their mechanical properties. Scientifically comprehending about the formation mechanisms, dominant factors and control methods in alloy solidification has a significant effect on the structure control and optimization. Dendritic structure is the most frequently observed solidification microstructure of alloys and controlled by heat, solute, melt flow, capillary and many other factors. Modelling and simulating can accurately quantify various phenomena and evolution rules in the process of solidification, thus play an increasingly important role in the design, preparation, processing and performance optimization of alloy materials. Over the past two decades, remarkable progress has been made and various models have been proposed in microstructure simulation during alloy solidification process, such as deterministic method, phase field (PF), Monte Carlo (MC) and cellular automaton (CA). With the advantages of clear physical meaning, easily programming and high calculation efficiency, CA method has been widely applied in the study of solidification structure simulation and exhibits great advantages. Considering the current development level of computer hardware, numerical model and calculation method, microstructure simulation of large components mainly adopts macro-microscopic coupling calculation method, such as CA-FD/FE model. The heat transfer and other multi-physical fields are calculated at the level of coarse mesh, where as nucleation and dendritic growth are simulated at a much finer grid level. This paper reviews the main models and development of CA method used for nucleation simulation. The key aspects in the simulation of dendritic growth including mean solid-interface interface curvature, growth kinetics and the algorithm for eliminating “pseudo anisotropy” are discussed. Based on this, the development and application status of macro-micro coupling model during casting, directional solidification and other manufacturing fields are summarized. Finally, the existing problems and future tendency for simulation of solidification structures are analyzed.
合金凝固组织微观模拟研究进展与应用
[J].凝固组织是连接合金成分与性能的桥梁,准确认识和把握合金凝固微观组织的形成机理、主导因素与控制途径,对凝固组织与性能的优化具有重要意义。近年来凝固过程数值模拟取得了显著进展,元胞自动机(cellular automaton,CA)在合金凝固组织模拟研究方面展现出极大潜力。本文阐述了凝固组织计算中常见的形核模型与特点,对CA法枝晶生长模拟中的关键环节进行了分析和探讨,在此基础上,简要概括了铸造、定向凝固等相关领域凝固组织宏观-微观耦合模型的开发和应用现状,并对凝固组织模拟的发展趋势进行了展望。
Recent progresses in competitive grain growth during directional solidification
[J].Competitive growth between different structures including phases, dendrites and grains is a common phenomenon existing in various microstructure evolution processes. The overgrowth outcome of competitive growth has a paramount influence on final solidification microstructures and mechanical behaviors of materials. The competitive grain growth during directional solidification is a key factor for microstructures controlling, especially for the preparation of single crystal turbine blades. In recent years, the competitive grain growth during directional solidification becomes a hot spot due to an increasing demand for the single crystal preparation and inconsistent experimental results with the classical Walton-Chalmers model. In this paper, the mechanism of competitive grain growth based on the classical Walton-Chalmers model and its challenges were firstly discussed, and then some recent research progresses in converging growth and diverging growth in two dimensional spaces, and non-uniplanar growth in three dimensional spaces were reviewed. Furthermore, the recent works of our group on competitive grain growth during directional solidification by using the phase field method were introduced. Finally, the outlooks of future studies on competitive grain growth during directional solidification are presented.
定向凝固晶粒竞争生长的研究进展
[J].竞争生长是材料微观组织演化过程中普遍存在的现象,不同组织间(包括相、枝晶、晶粒等)均可能存在竞争生长,这些竞争作用对最终微观组织的形成及力学性能具有重要影响。不同取向晶粒间的竞争生长控制是材料微观组织调控的重要环节,尤其是对定向单晶叶片的制备,不同取向晶粒间的竞争生长是决定能否成功获得完整单晶结构的关键因素。近年来,一方面单晶材料制备要求的不断提高,迫切需要有关晶粒竞争生长机制及规律方面的理论性指导,另一方面经典晶粒竞争生长理论预测结果与实验观测并不相符,有时甚至可能完全相反,这使得定向凝固过程中不同取向晶粒间的竞争生长问题日益成为一个热门的研究课题。本文首先回顾了Walton-Chalmers模型的晶粒竞争生长机制及其所受到的严重挑战,然后分别对定向凝固二维条件下汇聚生长和发散生长及三维条件下晶粒竞争生长的研究现状进行了述评,并介绍了本课题组近年来基于相场法数值模拟在定向凝固晶粒竞争生长研究方面的工作进展,最后对定向凝固过程中不同取向晶粒之间的竞争生长研究进行了总结与展望。
Advances in multi-scale modeling of solidification and casting processes
[J].
Coupled modelling of solidification and solution heat treatment of advanced single crystal nickel base superalloy
[J].
Cross-scale modeling of MnS precipitation for steel solidification
[J].
Integrated simulation framework for additively manufactured Ti-6Al-4V: Melt pool dynamics, microstructure, solid-state phase transformation, and microelastic response
[J].
Integration of phase-field model and crystal plasticity for the prediction of process-structure-property relation of additively manufactured metallic materials
[J].
Simulation of multi-grain solidification and subsequent spinodal decomposition by using phase field crystal model
[J].
多晶凝固及后续调幅分解过程的晶体相场法模拟
[J].
Preparation of an Au-Pt alloy free from artifacts in magnetic resonance imaging
[J].When magnetic resonance imaging (MRI) is performed on patients carrying metallic implants, artifacts can disturb the images around the implants, often making it difficult to interpret them appropriately. However, metallic materials are and will be indispensable as raw materials for medical devices because of their electric conductivity, visibility under X-ray fluoroscopy, and other favorable features. What is now desired is to develop a metallic material which causes no artifacts during MRI.In the present study, we prepared a single-phase and homogeneous Au-Pt alloys (Au; diamagnetic metal, and Pt; paramagnetic metal) by the processing of thermal treatment. Volume magnetic susceptibility was measured with a SQUID Flux Meter and MRI artifact was evaluated using a 1.5-T scanner.After final thermal treatment, an entirely recrystallized homogeneous organization was noted. The Au-35Pt alloy was shown to have a volume magnetic susceptibility of -8.8ppm, causing almost free from artifacts during MRI.We thus prepared an Au-35Pt alloy which had a magnetic susceptibility very close to that of living tissue and caused much fewer artifacts during MRI. It is promising as a material for spinal cages, intracranial electrodes, cerebral aneurysm embolization coils, markers for MRI and so on.Copyright © 2017 Elsevier Inc. All rights reserved.
Volume magnetic susceptibility of gold-platinum alloys: Possible materials to make mass standards for the watt balance experiment
[J].
Phase decomposition in nanoporous Au-Pt
[J].
A simulation study on the orientational phase transformation behavior of Au-Pt alloy for different concentration of Pt
[J].
The LISA DFACS: Model Predictive Control design for the test mass release phase
[J].
A phase-field model with antitrapping current for multicomponent alloys with arbitrary thermodynamic properties
[J].
A generalized field method for multiphase transformations using interface fields
[J].
Experimental study of the miscibility gap and calculation of the spinodal curves of the Au-Pt system
[J].
Experimental study of Au-Pt-Sn phase equilibria and thermodynamic assessment of the Au-Pt and Au-Pt-Sn systems
[J].
Phase boundary migration, Kirkendall marker shift and atomic mobilities in fcc Au-Pt alloys
[J].
Probabilistic modelling of microstructure formation in solidification processes
[J].
Electrochemical deposition of Au-Pt alloy particles with cauliflower-like microstructures for electrocatalytic methanol oxidation
[J].
Spinodal decomposition in polycrystalline alloys
[J].
Segregation-driven grain boundary spinodal decomposition as a pathway for phase nucleation in a high-entropy alloy
[J].