Ti及钛合金具有重量轻、耐腐蚀性好、强度高、生物相容性好等优点,被广泛应用于航空航天、海洋工程、生物医学等领域[1,2]。纳米结构可以有效地提高金属合金强度而备受关注[3,4]。纳米晶化金属表现出与粗粒化金属不同的力学性能。与块体多晶材料相比,纳米晶材料的强度、硬度和韧性增加,但弹性模量降低[5]。Hajizadeh等[6]通过对商业纯Ti (CP-Ti)等通道转角挤压(ECAP)加工后显示出高拉伸强度和高断裂伸长率。晶界塑性支配着纳米晶材料的力学行为。研究[7]发现具有低迁移率的晶界通过晶体孪生动态调整其构型和局部变形几何形状,从而改变晶界动力学并增强晶界迁移率。Liu等[8]发现晶粒尺寸对多晶板材的塑性有显著影响。剪切应力集中和附加硬化发生在软硬取向晶粒的晶界处。高温下硬化参数和热软化因子降低,多晶板材的屈服应力也大大降低。变形金属退火通常会导致强度降低。然而对于纳米晶材料,在低温退火后则观察到相反的效果。Sotniczuk等[9]研究发现,可动位错湮灭和晶界弛豫是出现这种效果的原因。位错密度和晶界特性也会影响其耐腐蚀性。因此,低温退火是进一步提高纳米Ti力学和腐蚀性能的快速、简单、廉价的方法,是植入材料的关键。
间隙O原子对Ti的力学性能和塑性变形机制有显著影响。本课题组前期研究[10]发现,随着多晶α-Ti中O含量增加,变形孪晶和柱面滑移发生的频率降低,取而代之的是锥面<a>和<c+a>滑移。塑性变形机制从多晶Ti-O (0.1%,质量分数)中的单滑移转变为多晶Ti-O (0.3%,质量分数)中的双滑移或多滑移。在低O含量的多晶Ti-O (0.1%,质量分数)中更易观察到变形孪晶{10
本工作通过分子动力学模拟,深入分析O含量(0.1%~1.0%,原子分数,下同)对纳米多晶Ti力学性能及变形机制的影响。同时计算了温度(300、500和700 K)和应变速率(1 × 108、5 × 108和1 × 109 s-1)对含0.3%O多晶Ti-O (Ti-0.3O)的力学性能及变形机制的影响,为制备优良力学性能的纳米尺度含O多晶Ti材料提供参考。
1 计算方法
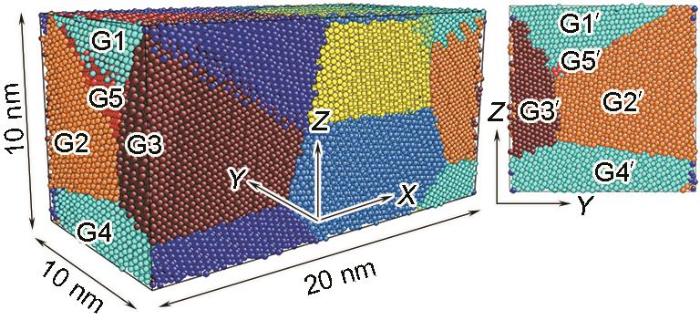
采用高效、稳定、准确的Voronoi算法[14]构建了尺寸为20 nm × 10 nm × 10 nm、O含量为(0.1%~1.0%)的多晶Ti模型。多晶Ti为hcp结构,表示为α-Ti,间隙O出现在hcp晶胞正八面体位置。模型中共有8个晶粒,平均晶粒尺寸为7.8 nm,包含113492~114570个原子。模型示意图如图1所示,其中右图为右侧端原子视图,图中晶粒相互对应,如G1-G1′等。采用Lee等[15]开发的第二近邻修正嵌入式原子势(second nearest-neighbor modified embedded-atom method,2NNMEAM)描述Ti和O原子之间的相互作用势,该势很好地拟合了O含量从0~50%的一系列Ti-O结构的基本性能。具体参数见表1和2[15]。本工作使用Ti-Ti、O-O和Ti-O势的形式包括2个项:非静电和静电相互作用项。因此,包含N个原子的系统总能量ETotal表示为:
图1
图1
计算模型示意图
Fig.1
Schematic diagram of calculation model (The left side grains G1-G5 correspond to the right side grains G1′-G5′, respectively)
| Parameter | hcp Ti | Dimer O | Unit |
|---|---|---|---|
| Ec | 4.87 | 2.56 | eV |
| Re | 0.292 | 0.121 | nm |
| α | 4.7195 | 6.8800 | - |
| A | 0.66 | 1.44 | - |
| t(1) | 6.80 | 0.10 | - |
| t(2) | -2.00 | 0.11 | - |
| t(3) | -12.00 | 0.00 | - |
| β(0) | 2.70 | 5.47 | - |
| β(1) | 1.00 | 5.30 | - |
| β(2) | 3.00 | 5.18 | - |
| β(3) | 1.00 | 5.57 | - |
| Cmin | 1.00 | 2.00 | - |
| Cmax | 1.44 | 2.80 | - |
| χ0 | -1.192 | 10.11 | eV·e-1 |
| J0 | 8.436 | 20.5 | eV·e-2 |
| ΔE(2) | 7.97 | 5.63 | eV |
| ΔE(3) | 105 a | 105 a | eV |
| ζ | 8.3 | 23.9 | nm-1 |
| Z | 1.408 | 0.00 | e |
| Parameter | Ti-O | Unit |
|---|---|---|
| ΔEc | 1.5280 | eV |
| Re | 0.20649 | nm |
| α | 7.4455 | - |
| d | 0.01 | - |
| Cmin(i j i) | 1.00 | - |
| Cmin(j i j) | 0.97 | - |
| Cmin(i i j) | 1.46 | - |
| Cmin(i j j) | 1.46 | - |
| Cmax(i j i) | 2.80 | - |
| Cmax(j i j) | 2.51 | - |
| Cmax(i i j) | 2.80 | - |
| Cmax(i j j) | 2.80 | - |
| ρ0(O) / ρ0(Ti) | 12.0 | - |
式中,EMEAM和EES分别为非静电和静电能量,X = {X1,X2,…,XN }和q = {q1,q2,…,qN }分别是原子位置和电荷的可变集合。非静电项和静电项相互独立。Rose通用状态方程(EOS)[16]很好地描述了金属和共价固体中总能量和原子间距离之间的普遍关系。因此系统总能量使用基于Rose状态方程的2NNMEAM项(
式中,Fi 是嵌入函数,
静电能用原子能
2 计算结果
2.1 力学性能
图2
图2
不同条件下纳米多晶α-Ti拉伸应力-应变曲线
Fig.2
Tensile stress-strain curves of polycrystalline α-Ti with O content at 300 K and 5.0 × 108 s-1 (a) and of Ti-0.3O with temperature at 5.0 × 108 s-1 (b) and strain rate at 300 K (c)
选择力学性能相对优异的多晶Ti-0.3O研究温度对多晶α-Ti力学性能和变形机制的影响。图2b为300、500和700 K下多晶Ti-0.3O的拉伸应力-应变曲线。随着温度升高,含O多晶α-Ti中原子的平均动能增大,原子之间更容易发生相对移动进而造成原子间相互作用力降低,导致宏观性能下降。同时,温度升高会减弱间隙O原子对位错的钉扎阻碍作用,使含O纳米多晶α-Ti的屈服应力降低。
2.2 间隙O对变形机制的影响
图3所示为图2a应力-应变曲线中AB部分的原子截图。本文图3、6~9和12中红色原子代表hcp结构,绿色原子代表fcc结构,蓝色原子代表bcc结构,白色原子代表晶界原子以及OVITO无法识别的紊乱原子,用OTHER表示。应变为0.064时,间隙O所在位置出现位错缠结,如图3d黑色虚线圆圈所示,位错缠结导致位错运动受阻,因此造成加工硬化,这种缠结效果并不能激活新的位错。可见α-Ti中添加间隙O原子可以增加其硬度,然而同时也容易导致材料变脆。而在复合材料中,α-Ti中引入层状石墨烯后力学性能显著提高[25]。在Ti层较薄时,应变诱发位错的传播受到显著限制,从而导致更多的位错诱发滑移,产生独特的塑性变形。图3c中黑色箭头所指的原子半径小的白色原子为O原子。删除理想排列的原子后可以看到晶粒中的位错缠结和堆垛层错。
图3
图3
多晶Ti-0.1O拉伸后位错缠结引起的加工硬化
Fig.3
Work hardening caused by dislocation tangle after tensile of polycrystalline Ti-0.1O (The red atom represents the hcp structure, the green atom the fcc structure, the blue atom the bcc structure, and the white atom the grain boundary atom and the disordered atom being not able to be recognized by OVITO, which are represented by OTHER. Same as in Figs.6-9 and 12) (a, c) atomic diagrams at strains ε = 0 (a) and 0.064 (c), respectively (b) diagram with only fcc atoms and dislocation lines at ε = 0.062 (d) dislocation tangle diagram with only fcc atoms and dislocation lines at ε = 0.064
图4
图4
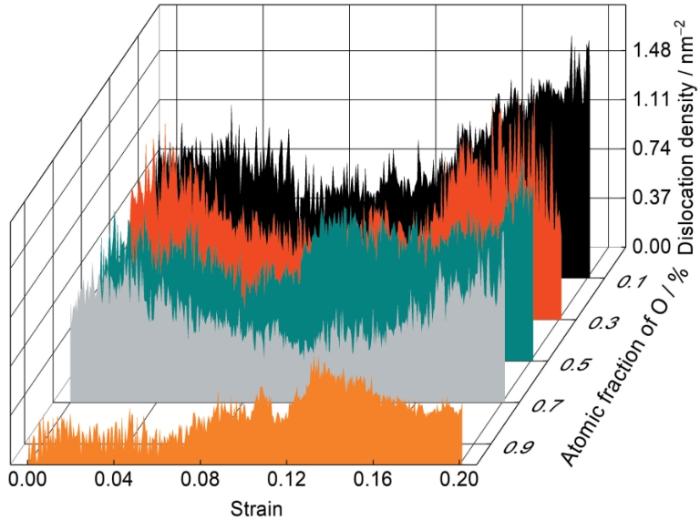
不同O含量多晶α-Ti总位错密度随应变变化曲线
Fig.4
Total dislocation density with various O contents and strains
图5
图5
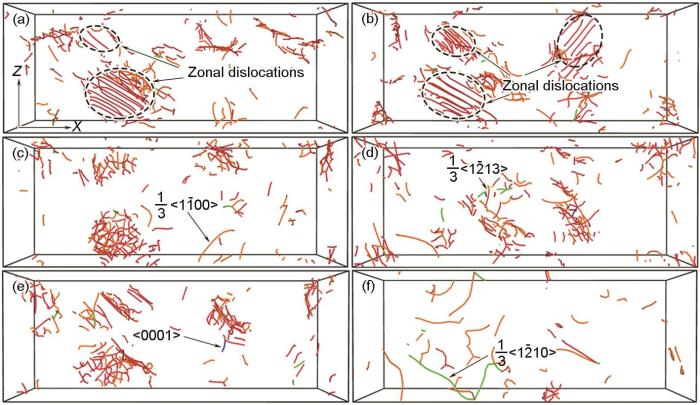
不同O含量多晶α-Ti拉伸产生的位错类型
(a) Ti (b) Ti-0.1O (c) Ti-0.3O (d) Ti-0.5O (e) Ti-0.7O (f) Ti-1.0O
Fig.5
Activated dislocation types in polycrystalline α-Ti under tensile loading at different O contents
图6
图6
{10
Fig.6
Atomic structure of twin{10
图7
图7
300 K下多晶Ti-0.1O拉伸过程中层错的形成
Fig.7
Formation of stacking faults during tensile of polycrystalline Ti-0.1O at 300 K and ε = 0.191
图8
图8
300 K时多晶Ti-0.3O的Tihcp→Tibcc→Tihcp转变过程
Fig.8
Snapshots of transformation process of Tihcp→Tibcc→Tihcp of polycrystalline Ti-0.3O at 300 K (a-c) Tihcp→Tibcc (d-f) Tibcc→Tihcp (g) oxygen atom pinning grain boundary
图9
图9
不同温度下多晶Ti-0.3O拉伸过程中晶界的运动
Fig.9
Grain boundary movement of polycrystalline Ti-0.3O at 300 K (a-c), 500 K (d-f), and 700 K (g-i) with ε = 0 (a, d, g), ε = 0.086 (b, e, h), and ε = 0.166 (c, f, i) (Black dotted circles in Figs.9b, c, e, f, h, and i represent the disordered atoms caused by lattice distortion after adding interstitial O atoms, and dotted yellow circles represent the disordered atoms produced during the strain at different temperatures)
图10
图10
不同应变速率下多晶Ti-0.3O中各类原子含量随应变的变化
Fig.10
Atomic fraction curves of bcc (a), hcp (b), fcc (c), and OTHER (d) atoms at different strain rates
图11
图11
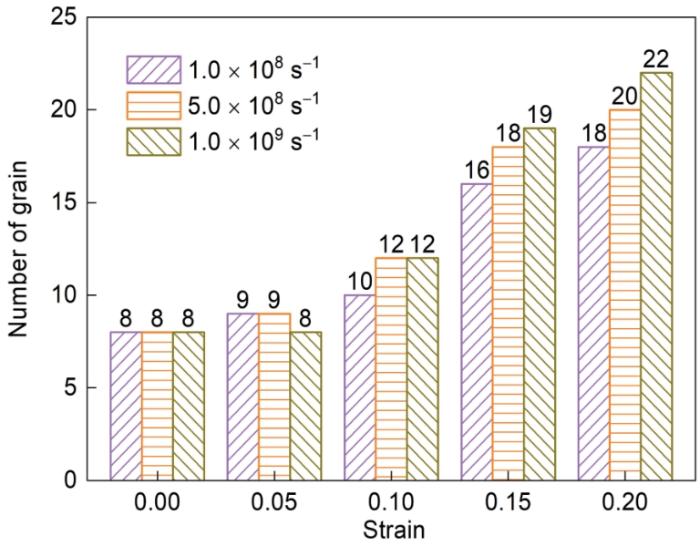
不同应变速率下多晶Ti-0.3O拉伸过程中晶粒的数量
Fig.11
Number of grains in polycrystalline Ti-0.3O under tensile loading at different strain rates
图12
图12
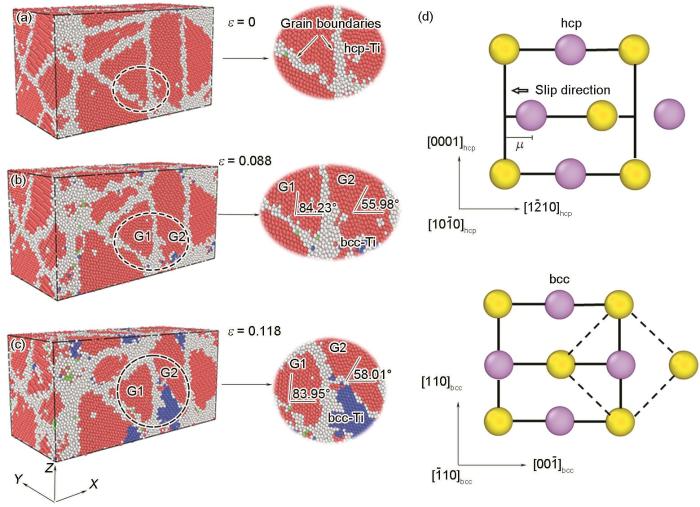
多晶Ti-0.3O拉伸过程中不稳定相变的产生以及相变机理结构示意图
Fig.12
Unstable phase transition during tenison of polycrystalline Ti-0.3O (a-c), and schematic of Tihcp→Tibcc phase transition mechanism (d) (μ—a parameter describing relative slip distance)
不同O含量下多晶α-Ti拉伸时总位错密度随应变的变化如图4所示。总位错密度随O含量的增高而降低。300 K下拉伸不同O含量的多晶α-Ti,在零应变时,所有的纳米晶样品中都存在不同数量的弛豫位错(集中在晶界区域)。这种晶界位错较短而且不稳定,在外加载荷下会被晶界吸收而湮灭,对应图4中总位错密度在应变开始时有降低趋势。随着应变增加,位错源被激活,产生大量位错,位错密度升高。在位错增殖和湮灭的共同作用下,位错密度也呈现出高低起伏的趋势。变形过程中位错类型主要为全位错
低O含量多晶α-Ti在拉伸加载时,通常首先激活柱面<a>滑移和变形孪晶。随着应变增加,<a>位错会发生分解反应,生成不全位错。图5为不同O含量多晶α-Ti在拉伸应变为0.2时产生的位错与孪晶。图5a和b中观察到平直且平行的红色位错(黑色虚线圆圈所示)定义为“孪晶位错”[26],这种“孪晶位错”通常称之为“带状位错”(zonal dislocation),协调孪晶长大。将图5a中下方黑色虚线圆圈部分的原子图放大如图6所示。图6b为孪晶面和孪晶面上的“孪晶位错”的原子截图。图中红色线条为“孪晶位错”,整齐排列一层的白色原子组成的面是孪晶边界。晶体学分析显示该孪晶类型为{10
体系内孪晶的数量随着O含量的增加而减小[10],含量增加到0.3%及以上时,几乎没有“孪晶位错”的出现,如图5c~f所示,位错类型受晶粒尺寸限制,主要以排列无序的刃型位错为主。透射电子显微镜研究[28]表明,对于在室温下拉伸变形的CP-Ti,垂直和平行于柱面的位错主要是螺型位错。增加O含量到0.3%产生的主要是刃型位错,位错几乎没有对齐的趋势[29]。当O含量超过0.3%时,在多晶α-Ti中观察到了锥面<c+a>位错
2.3 温度对变形机制的影响
在纳米多晶Ti-0.3O塑性变形过程中fcc结构原子以层错的形式存在,观察到300 K下堆垛层错比较宽,700 K下层错明显减少或变小。同时观察到具有bcc结构的原子,图8给出了300 K时多晶Ti-0.3O应变过程中bcc相从出现到消失的全过程。首先在结构较混乱的晶界区域出现bcc结构原子,即在晶界处优先形成新相晶核如图8b所示,形成了一个hcp结构和bcc结构共存的新晶粒。从图8a~c中可以看出,随着应变的增加,Tihcp→Tibcc转变增多,相变不仅伴随晶粒旋转还伴随着晶界的运动。应变大于0.125后bcc结构逐渐变小直至消失,如图8d~f所示。在整个Tihcp→Tibcc→Tihcp转变过程中,生成新晶粒G2。可见新晶粒的生成与晶粒旋转有密切的关系。Li等[31]用实验展示了单个晶粒旋转和相邻晶粒旋转/生长的完整过程。揭示了诱导晶粒旋转和生长是纳米多晶材料的塑性变形机制之一。
纳米晶的变形机制主要是基于晶界的晶界滑动、晶界旋转[32]等机制。图9是多晶Ti-0.3O分别在300、500和700 K温度下沿X轴拉伸晶界运动的原子截图。比较图9应变为0.086 (图9b、e和h)和应变为0.166 (图9c、f和i)时晶界(黑色虚线标记)运动后的位置,700 K时相同应变下晶界运动明显快于500和300 K时。研究[33]发现当温度升高或晶粒尺寸减小时,晶界滑动成为主要机制,并能有效地协调塑性变形。另外标记晶粒G1和晶粒G2中的紊乱原子如图9中的虚线圆圈所示,其中黑色虚线圆圈是加入间隙O原子后引起晶格畸变造成的紊乱原子,黄色虚线圆圈为不同温度下应变过程中产生的紊乱原子。这些紊乱原子中的一部分来自于晶界,随着拉伸进行晶界原子向晶粒内迁移,使得晶界变薄。同样比较图9b、e、h和图9c、f、i中晶粒G1和晶粒G2中的黄色虚线圆圈看出,随着温度升高,晶界周围紊乱原子增多,这是因为温度升高,原子的活性大幅度增加,打破了原子间结合力,使得原子扩散到周围的区域。
2.4 应变速率对变形机制的影响
图10为不同应变速率时多晶Ti-0.3O拉伸过程中bcc、hcp、fcc、OTHER原子含量占比随应变的变化曲线。观察图10b和d,不同应变速率下hcp和OTHER原子均在屈服点0.07左右出现大幅度转变,转变速率随着应变速率的增加而增加。应变速率越高,hcp和OTHER转换的原子数越多。观察图10a中3个应变速率下bcc原子占比曲线,在应变为0.10~0.15之间bcc原子占比出现先增大后减小的浮动,说明晶体内部出现Tihcp→Tibcc→Tihcp转变,这种原子转变伴随着新晶粒的形成。图11统计了1.0 × 108、5.0 × 108和1.0 × 109 s-1下多晶Ti-0.3O不同应变下的晶粒数量。多晶Ti-0.3O的初始晶粒有8个,随着应变的进行生成不同数量的新晶粒。统计发现生成新晶粒的数量与应变速率存在一定的线性关系,即含O多晶α-Ti应变速率越高生成新晶粒的数量越多。不同应变速率下含O多晶α-Ti在应变区间0.10~0.15时生成新晶粒的数量最多,这与图10a中bcc原子数量占比的起伏相对应,说明生成新晶粒的过程中确实伴随着不稳定的相变。
3 分析讨论
在低温下,纯Ti和大多数Ti合金为hcp结构,当温度高于(882 ± 2)℃时转变为稳定的bcc结构,发生同素异构转变。然而在300 K纳米多晶Ti-0.3O拉伸时观察到了不稳定的bcc结构,如图12a~c中蓝色原子所示。晶界上的Ti原子受到拉伸载荷作用,平面内晶粒取向改变,2个晶粒之间相对旋转导致出现不稳定的bcc晶体结构。比较图12b和c发现,当应变从0.088增加到0.118时G1相对旋转了1.72°,G2相对旋转了2.03°。图12d显示了Tihcp→Tibcc相变机理的结构示意图。黄色和粉色的原子球分别表示在[00
图13
图13
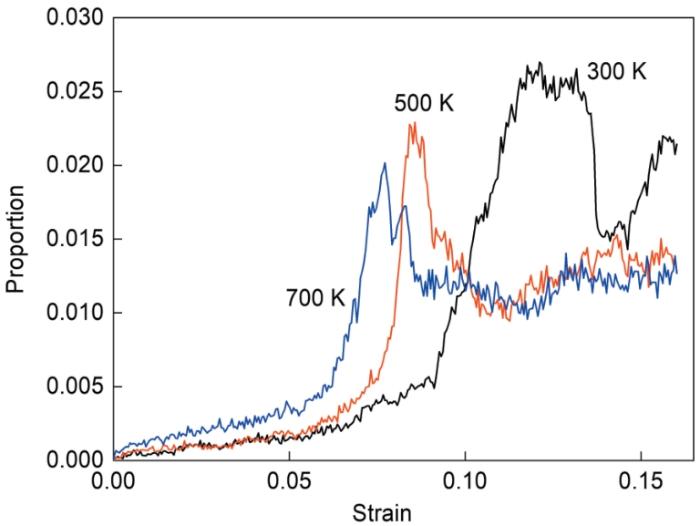
不同温度下多晶Ti-0.3O拉伸过程bcc原子占比与应变关系
Fig.13
Relationship between proportion of bcc atoms and strain during tension of polycrystalline Ti-0.3O at different temperatures
模拟单晶Ti[34]和多晶Ti[35]在压缩载荷下的塑性变形过程中都发现Tihcp→Tibcc不稳定相变。为了定量评估纯Ti的不同晶体结构的能量和晶格转变势垒,了解纳米多晶Ti变形过程中不稳定相变的原因,Zope和Mishin[36]计算了Tihcp和Tibcc的平衡晶格能,计算结果显示Tihcp在平衡晶格参数(0.295 nm)处具有最低能量(-4.85 eV/atom)。该能量比Tibcc低30 meV/atom。Mehl和Papaconstantopoulos[37]使用密度泛函理论(DFT)计算晶体结构的晶格能量得出Tihcp的能量最低,Tibcc的能量最高,Tihcp和Tibcc之间的能量差为67 meV/atom。动态Tihcp→Tibcc转换的能垒通过原子模拟计算出约为38 meV/atom[34]。结合原子计算结果和DFT计算结果,可见2种密排结构的Tibcc和Tihcp之间的能量非常接近。因此,不稳定相变是由外部应变触发的。
4 结论
(1) 通过分子动力学计算了拉伸载荷下不同O含量纳米多晶α-Ti以及多晶Ti-0.3O在不同温度、速率下的力学性能和变形机制。结果表明,含O纳米多晶α-Ti的变形机制主要为位错滑移、晶粒旋转、晶界滑移和晶界迁移。
(2) 间隙O原子造成晶格畸变阻碍位错运动,使含O多晶α-Ti的屈服应力随O含量的增加而增大,位错密度随O含量的增加而减小。O含量小于0.3%时,观察到变形孪晶{10
(3) 多晶Ti-0.3O在不同温度下的拉伸实验表明,随着温度的升高,屈服应力、位错密度降低。拉伸过程中由于晶粒旋转造成Tihcp→Tibcc→Tihcp的不稳定相变,进而产生新晶粒,且高温载荷下更利于此现象产生。高温下晶界运动速率明显加快,晶界上O原子的钉扎作用阻碍钉扎部位及附近晶界迁移,使其明显慢于同一晶界其他部位的迁移。
(4) 多晶Ti-0.3O在拉伸载荷下生成新晶粒的个数随应变速率的升高而增加,新晶粒的产生伴随不稳定相变并且使晶界原子数增多,因此hcp与OTHER原子之间的转换随着应变速率的增大而增多。
参考文献
Mechanical properties of near alpha titanium alloys for high-temperature applications—A review
[J].
Deformation behavior and microstructure evolution of titanium alloys with lamellar microstructure in hot working process: A review
[J].Titanium alloys have been widely used in many industrial clusters such as automotive, aerospace and biomedical industries due to their excellent comprehensive properties. In order to obtain fine microstructures and favorable properties, a well-designed multi-step thermomechanical processing (TMP) is critically needed in manufacturing of titanium components. In making of titanium components, subtransus processing is a critical step to breakdown lamellar microstructure to fine-structure in hot working process and thus plays a key role in tailoring the final microstructure and properties. To realize this goal, huge efforts have been made to investigate the mechanisms of microstructure evolution and flow behavior during the subtransus processing. This paper reviews the recent experimental and modelling progresses, which aim to provide some guidelines for the process design and microstructure tailoring for titanium alloy research community. The characteristics of the initial lamellar microstructure are presented, followed by the discussion on microstructure evolution during subtransus processing. The globularization of lamellar α is analyzed in detail from three aspects, i.e., globularization mechanism, heterogeneity and kinetics. The typical features of flow behaviors and the explanations of significant flow softening are then summarized. The recent advances in modelling of microstructure evolution and flow behaviors in the subtransus processing are also articulated. The current tantalized issues and challenges in understanding of the microstructure evolution and flow behaviors of the titanium alloys with lamellar microstructure are presented and specified in future exploration of them.
Onset criterion for flash sintering
[J].
Molecular dynamics simulation of nanometer scale mechanical properties of hexagonal Mg-Li alloy
[J].
Structure and properties of nanocrystalline materials
[J].
Stored energy and recrystallization kinetics of ultrafine grained titanium processed by severe plastic deformation
[J].
Twinning-assisted dynamic adjustment of grain boundary mobility
[J].Grain boundary (GB) plasticity dominates the mechanical behaviours of nanocrystalline materials. Under mechanical loading, GB configuration and its local deformation geometry change dynamically with the deformation; the dynamic variation of GB deformability, however, remains largely elusive, especially regarding its relation with the frequently-observed GB-associated deformation twins in nanocrystalline materials. Attention here is focused on the GB dynamics in metallic nanocrystals, by means of well-designed in situ nanomechanical testing integrated with molecular dynamics simulations. GBs with low mobility are found to dynamically adjust their configurations and local deformation geometries via crystallographic twinning, which instantly changes the GB dynamics and enhances the GB mobility. This self-adjust twin-assisted GB dynamics is found common in a wide range of face-centred cubic nanocrystalline metals under different deformation conditions. These findings enrich our understanding of GB-mediated plasticity, especially the dynamic behaviour of GBs, and bear practical implication for developing high performance nanocrystalline materials through interface engineering.© 2021. The Author(s).
Multiscale modeling of crystal plastic deformation of polycrystalline titanium at high temperatures
[J].
Enhancement of the corrosion resistance and mechanical properties of nanocrystalline titanium by low-temperature annealing
[J].Annealing deformed metals usually leads to reduced strength. In the case of nanocrystalline materials, the opposite effect was observed after low-temperature annealing. The annihilation of mobile dislocations and a relaxation of grain boundaries are probable reasons for the observed phenomenon. Dislocation density and grain boundaries character affect also on the corrosion resistance. Hence, in this work the effect of low-temperature annealing on both the hardness and corrosion resistance of nanotitanium was investigated. The results indicated that low-temperature annealing is a fast, simple and inexpensive way to further enhance nanotitanium's mechanical and corrosion properties, which are crucial for implantable materials.
Effect of oxygen content on active deformation systems in pure titanium polycrystals
[J].
Dislocation structure and the strength of titanium
[A].
Orientation dependent slip in polycrystalline titanium
[J].
Origin of dramatic oxygen solute strengthening effect in titanium
[J].\n The motion of dislocations or defects in a metal influences its strength and toughness. If these defects can be “pinned” by adding alloying elements, it should be possible to create a stronger alloy. It was thought that there shouldn't be much of an interaction between screw dislocations and any alloying elements. However, Yu\n et al.\n show that for α-Ti, the profound hardening effect of oxygen is due to the strong interactions with the core of the dislocations. First-principles calculations reveal that distortion of the interstitial sites at the dislocation core creates a very strong but short-range repulsion for oxygen atoms.\n
Nouvelles applications des paramètres continus à théorie des formes quadratiques. Deuxième Mémoire. Recherches sur les paralléloèdres primitifs
[J].
A modified embedded-atom method interatomic potential for ionic systems: 2NNMEAM + Qeq
[J].
Universal features of the equation of state of metals
[J].
Fast parallel algorithms for short-range molecular dynamics
[J].
Atomsk: A tool for manipulating and converting atomic data files
[J].
Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool
[J].
AtomEye: An efficient atomistic configuration viewer
[J].
Solute drag on perfect and extended dislocations
[J].
Automated identification and indexing of dislocations in crystal interfaces
[J].
Strain rate induced amorphization in metallic nanowires
[J].
Molecular dynamics study of the mechanical behavior of nickel nanowire: Strain rate effects
[J].
Mechanical properties and enhancement mechanisms of titanium-graphene nanocomposites
[J].
Zonal dislocations mediating $\{10\bar{1}1\}$ $<10\bar{1}\bar{2}>$ twinning in magnesium
[J].
Atomistic simulation of tension-compression asymmetry and its mechanism in titanium single-crystal nanopillars oriented along the $[11\bar{2}0]$ direction
[J].
Plastic deformation of Ti-Al single crystals in prismatic slip
[J].
Effect of interstitial solutes on the strength and ductility of titanium
[J].
Deformation-induced grain rotation and growth in nanocrystalline Ni
[J].
Deformation nanomechanics and dislocation quantification at the atomic scale in nanocrystalline magnesium
[J].
Molecular dynamics simulation study of the effect of temperature and grain size on the deformation behavior of polycrystalline cementite
[J].
Transitory phase transformations during $\{10\bar{1}2\}$ twinning in titanium
[J].
An atomistic simulation on the tensile and compressive deformation mechanisms of nano-polycrystalline Ti
[J].
Interatomic potentials for atomistic simulations of the Ti-Al system
[J].