316L不锈钢因具有耐高温、耐腐蚀和高韧性等优点,被广泛应用于航空航天、海洋船舶、医疗器械、轨道交通、电子通讯等制造领域。部分316L不锈钢构件兼具轻量化、复杂难加工、高性能等特征,多服务于极端严苛环境中,因而对构件的材料、结构、工艺和性能等提出极大挑战[1 ] 。激光增材制造技术通过逐点累积成面,逐面累积成体的离散制造模式,不受形状、结构复杂程度及尺寸的限制,可以实现复杂构件的材料-结构-性能一体化制造[2 ] 。激光定向能量沉积是将激光熔覆和同步送粉相结合的一种激光增材制造技术,在沉积速率和成形质量方面具有特殊优势[3 ] ,可用于制造构型复杂、性能可控的316L不锈钢零件。
激光束空域形态是指聚焦激光束在横截面上的功率密度分布形态。3种典型的激光束空域形态分别是Gaussian形态(Gaussian profile,GP)、超Gaussian形态(super-Gaussian profile,SGP)、完全平顶形态(flat-topped profile,FTP)。因为聚焦激光束的空域形态决定着熔池表面的能量密度分布形态及其大小,所以影响着熔池的热输运行为。为了探究激光束空域形态对激光材料加工中热输运行为的影响,国内外有关学者开展了一系列研究。Roehling等[4 ] 发现在粉床熔化沉积增材制造中,圆形Gaussian和椭圆Gaussian光束形态创建的熔池热场和流场是有明显差异的。Tumkur等[5 ] 研究了Bessel光束和Gaussian光束对粉床熔化沉积增材制造过程中熔池热输运的影响,发现Bessel光束能够降低熔池的温度梯度和延长熔池的凝固时间。Kubiak等[6 ] 数值模拟了GP与SGP下激光加热过程中的热输运特征,发现温度场有较大差别。Sundqvist等[7 ] 认为不同激光束空域形态下的激光点焊温度场是明显不同的。上述研究表明,激光束空域形态展示出其对激光粉床熔化沉积、激光热处理、激光焊接等激光加工过程中热输运行为的调控潜力。但是,目前有关激光束空域形态在同步送粉式激光定向能量沉积中的应用和研究较少,开展这方面的研究有助于拓宽激光束空域形态的应用范围,指导定制或优化激光束空域形态,提升对热输运的调控能力和水平。
目前,工艺实验和数值模拟是研究激光定向能量沉积熔池热输运行为的2种主要手段。常规的工艺实验方法难以明晰深层的物理机制,且时间成本和经济成本高,因此,基于物理过程的数值模拟成为了探明熔池热输运行为的最有效手段。在熔池热输运的数值模拟方面,Ya等[8 ] 基于能量和质量守恒创建了激光熔覆热传导模型,预测了熔覆道的生长和传热。Song等[9 ] 提出了一种基于有限元的三维热-结构耦合模型,研究了激光熔覆过程中铝合金的温度场和应力场。Gao等[10 ] 建立了送粉式激光熔覆热传导模型,进而研究熔池的温度分布以及预测组织凝固。但是这些热传导模型忽略了流体流动的影响。对于某些特定工况,熔池内的流体流动微弱,对热输运的影响小,这意味着忽略流体流动的影响不仅不会明显降低模型预测精度,而且能显著改进模型的计算效率和收敛性。但在流体流动较强的情况下,热传导模型的预测精度会显著降低,例如,Manvatkar等[11 ] 发现忽略流体的影响会导致预测的冷却速率提高2倍。为了解决这一问题,Li等[12 ] 开发了基于质量、动量和能量守恒定律的多场耦合三维有限元数值模型,研究激光功率对温度场和流场的影响规律。Wang等[13 ] 同样考虑熔池的流体输运建立了三维有限元模型,研究熔池的热输运和微观组织演化。但这些模型没有考虑激光和粉末的相互作用对模型热输入的影响。He等[14 ] 和Qi等[15 ] 在建立的模型中考虑了激光和粉末的相互作用,但是为了简化光-粉耦合模型,忽略了热对流和热辐射的影响。
本工作以316L不锈钢粉末为沉积材料,考虑激光束、粉束流和熔池的耦合作用、热流耦合作用、固液相变和多重传热等,基于质量守恒、动量守恒和能量守恒三大守恒定律,建立激光定向能量沉积的三维热输运模型,并通过实验验证模型的可靠性。最后,分析了4种典型激光束空域形态对熔池传热和流体流动特征的影响。
1 热输运建模与求解
1.1 数值模型
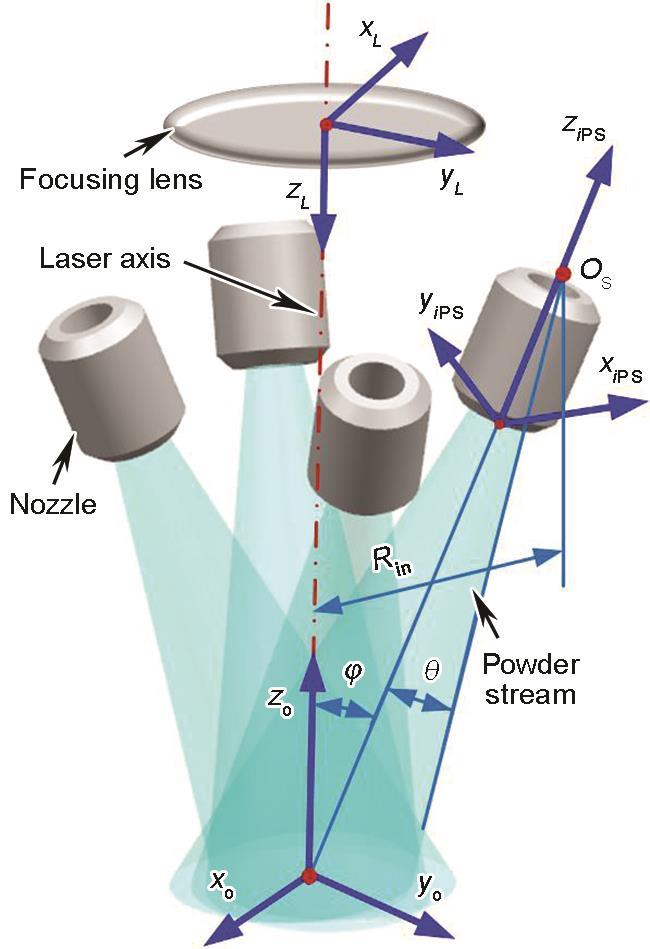
图1 绘制了沿沉积道纵向中心面处截断的激光定向能量沉积示意图。在沉积过程中,来自激光器的激光束经送粉头的准直透镜和聚焦透镜后照射到基板上,在基板上形成熔池,与此同时来自四喷嘴同轴送粉头的粉末被输送进熔池,并通过激光加热熔化,然后随着激光束与同轴送粉头的同步移动,熔池中的液态材料快速凝固形成沉积道。
图1
图1
激光定向能量沉积原理的示意图
Fig.1
Principle schematic of laser directed energy deposition
为了兼顾激光定向能量沉积热输运模型的求解效率和计算精度,需要做以下假设:
(1) 假设熔池中的流体不可压缩,流动模式为层流[16 ] ;
(4) 粉末颗粒做恒速直线运动,落入熔池后即刻熔化[17 ] 。
1.1.1 基本控制方程
在激光定向能量沉积过程中,熔池区的热输运与流体流动形成耦合效应,彼此相互影响,因此沉积区的热输运过程由质量、动量和能量三大守恒定律控制,其基本控制方程分别为[18 ] :
ρ ∇ ⋅ u = 0 (1)
ρ ∂ u ∂ t + ρ u ⋅ ∇ u = ∇ μ ( ∇ u + ( ∇ u ) T ) -
p I - 2 μ 3 ∇ ⋅ u I - K 0 1 - s l i q 2 s l i q 3 + D u (2)
ρ c p ∂ T ∂ t + ρ c p u ⋅ ∇ T =
∇ ⋅ k ∇ T - ∂ Δ H ∂ t - ρ u ⋅ ∇ Δ H (3)
s l i q = 1 ( T > T l i q ) T - T s o l T l i q - T s o l ( T s o l ≤ T ≤ T l i q ) 0 ( T < T s o l ) (4)
式中,u ρ t μ T p I K 0 D s l i q c p k Δ H Δ H = L s l i q L T s o l T l i q
1.1.2 固/液相变
固/液相变发生在固相和液相混合的糊状区(固/液界面),因此相变过程中的热物性参数可由表观热熔法表示[19 ,20 ] ,即:
c p h a s e = f s o l c s o l + f l i q c l i q + L ∂ α m ∂ T (5)
α m = 1 2 s l i q ρ l i q - ( 1 - s l i q ) ρ s o l ρ p h a s e (6)
ρ p h a s e = s l i q ρ l i q + 1 - s l i q ρ s o l (7)
k p h a s e = s l i q k l i q + 1 - s l i q k s o l (8)
f l i q = s l i q ρ l i q ρ p h a s e (9)
f s o l = 1 - s l i q ρ s o l ρ p h a s e (10)
式中,c phase 、ρ phase 和k phase 分别表示糊状区的比热容、密度和热导率,c liq 、ρ liq 和k liq 分别表示液相的比热容、密度和热导率,c sol 、ρ sol 和k sol 分别表示固相的比热容、密度和热导率,f sol 和f liq 分别表示固相和液相的质量分数(满足f sol + f liq = 1),α m 是相变潜热分布函数。
1.1.3 激光束和粉束流
实验使用的聚焦光纤激光束为超Gaussian光束,其横截面上的功率密度Q 服从超Gaussian分布,其数学表达式为[6 ] :
Q x L , y L , z L = 2 1 / K K P π r b 2 Γ 1 / K e x p - 2 x L 2 + y L 2 r b 2 K (11)
式中,P 表示激光功率;Γ 表示Gamma函数;r b xL 、yL 、zL 表示激光束坐标系{ L K 为空域形态因子,当K = 1时,激光束的空域形态为GP,当K > 1时,激光束的空域形态演变为SGP,当K 无限大时,则演变为全平顶形态[21 ,22 ] 。
对于K > 1的情况,激光束空域形态的顶部有平整区域,而且平整区域随K K 。激光束的平顶率设置为0、0.33、0.66和1,对应的K 1 × 10 3 图2 所示。需要指出的是,当平顶率为1时,激光束为全平顶形态,记为FTP,其理论上的K 值为无穷大数。当K = 1 × 103 时,激光束的平顶率约为0.998,接近1,故将K = 1 × 103 代替无穷大数。K = 4.2和K = 9.8的空域形态为SGP,分别记为SGP1和SGP2。
图2
图2
不同空域形态因子(K )下的激光束空间密度分布示意图
Fig.2
Schematics of the spatial density distributions of GP (a), SGP1 (b), SGP2 (c), and FTP (d) respectively when the laser power P = 700 W and the beam radius r b = 1.2 mm (GP—Gaussian profile, SGP—super-Gaussian profile, FTP—flat-topped profile)
每一个送粉头喷嘴的粉束流在横截面上的粉末质量浓度(Ci PS )服从Gaussian分布,其表达式为[23 ] :
C i P S x i P S , y i P S , z i P S = 2 m n π R i P S 2 v p e x p - 2 x i P S 2 + y i P S 2 R i P S 2 (12)
式中,m 为送粉质量流率;n 为同轴多路送粉头的喷嘴数量;Ri PS 是第i 个粉束流元截面的等效半径,定义为截面上某点的质量浓度降为中心质量浓度的1/e2 时的径向距离;v p 为粉末粒子速率,由实验测量得到;xi PS 、yi PS 、zi PS 表示粉束流元坐标系{i PS }的坐标,如图3 所示。图中φ 为粉束流元的喷射角,表示粉束流元轴线zi PS 与激光轴z L 的夹角;θ 为粉束流元发散角,定义为粉束流元的轮廓边界与轴线zi PS 的夹角。沉积坐标系{ O L i PS }不重合,因此利用齐次变换理论进行坐标变换[24 ] 。
图3
图3
同轴粉末束的坐标系示意图
Fig.3
Schematic of the coordinate systems { O L i PS } of the coaxial powder stream (The injection angle φ refers to the angle between the axis zi PS of the powder stream component and the laser axis z L ; the divergence angle θ is the angle between the axis zi PS and boundary of the powder stream component; R in is the distance from the intersection point O S of the extended powder stream component to the laser axis z L )
通过对4个粉束流元的粉末质量浓度进行求和,得到同轴粉束流的质量浓度(C CPS )为[23 ,24 ] :
C C P S x , y , z = ∑ i = 1 4 C i P S x , y , z (13)
1.1.4 光-粉耦合模型
激光能量衰减和粉末加热是激光束和粉束流相互作用过程中的2个关键热物理量。激光能量衰减归因于粉末的吸收和散射作用,粉末加热则因为激光的照射。根据Lambert-Beer定律,激光束通过任意体积元后的剩余强度(Ii , j , k [25 ] :
I i , j , k = I i , j , k - 1 e x p - π r p 2 Q e x t N C M S k Δ z (14)
N C M S k = 3 4 π r p 3 ρ p C C P S x i , y j , z k (15)
式中,Ii , j , k - 1 表示(xi , yj , zk - 1 )处的激光功率密度,Q ext 是粉末材料的消光系数,r p 为粉末半径,ρ p 为粉末密度,N C M S k
通过 式(14)的迭代计算,可得到激光束穿过粉束衰减后的功率密度。
依据集总参数法,利用能量守恒定律可以得到单个粉末的热输运模型为[24 ] :
m p c p d T p d t = 1 4 ξ I S p A I i , j , k - h p S p ( T p - T r e f ) -
ε σ S p ( T p 4 - T r e f 4 ) - ξ m L d m m d t (16)
d m m d t = - 4 π ρ p r s o l / l i q 2 d r s o l / l i q d t (17)
ξ I = 0 ( O t h e r ) 1 ( C o u p l i n g z o n e ) , ξ m = 0 ( T p ≠ T m ) 1 ( T p = T m ) (18)
式中,m p S p S p = 4 π r p 2 ) ,A 表示粉末对激光的吸收效率,h p 表示粉末表面的对流换热系数,T p 和T ref 分别表示粉末到达熔池表面的温度和初始环境温度,T m 为粉末的熔点,ε 表示粉末颗粒表面辐射率,σ 表示Boltzmann常数,m m 是单颗粉末熔化的质量(表示为m m = m p - 4 π r p r s o l / l i q 3 / 3 ) ,r s o l / l i q
1.1.5 边界条件
q c l a d x , y = η q r + q p - h c o n T - T r e f - ε σ T 4 - T r e f 4 (19)
式中,η 表示激光能量吸收率;h c o n q r q p q p
q p = η c v p C C P S H p 1 - H p 0 (20)
H p 0 = ∫ T r e f T s o l c s o l d T + L + ∫ T r e f T p o o l c l i q d T (21)
H p 1 = ∫ T r e f T s o l c s o l d T + L + ∫ T r e f T p c l i q d T (22)
式中,η c 表示熔池的集粉效率,其值取0.9[26 ] ;H p 0 T p o o l H p 1
F L / G = σ T κ ⋅ n L / G - γ T ∇ s T (23)
式中,F L / G n L / G κ 表示熔池气/液界面的曲率;σ T 和γ T 分别表示表示表面张力系数和热毛细系数,其计算公式参见本课题组前期工作结果[25 ] ;∇ s T
在任意Lagrange-Euler法(ALE)动网格框架下,熔池气/液界面的法向移动速度V L / G [28 ] :
V L / G = u ⋅ n L / G + η c v p C C P S ρ p e z ⋅ n L / G (24)
1.2 数值求解
以COMSOL多物理场仿真软件作为求解平台,利用软件中的流体传热模块和层流模块分别求解热输运方程和流体输运方程;利用多物理场模块中的Marangoni效应子模块求解自由界面的Marangoni剪切力,非等温流动子模块求解温度梯度引起的浮力流;利用变形几何模块求解最终气/液界面。
单道单层沉积道沿纵向中心面对称(见图1 ),因此选择纵向中心面一侧的沉积道作为建模对象,如图4 所示,计算域尺寸为10 mm × 4 mm × 3 mm。为了兼顾计算效率、求解精度和收敛性,将计算域划分为流体域a和固相域b。流体域a有热-流耦合作用,设置较细小的三棱柱网格以保证求解精度和收敛性,最大和最小单元尺寸分别为128和14 μm;固相域b只有热输运作用,设置较粗大的自由四面体网格以提高计算效率,同时保证求解精度,最大和最小单元尺寸分别为1140和242 μm。瞬态求解器的最大时间步长设置为1 ms,相对容差设定为0.01。
图4
图4
数值模型的网格划分
Fig.4
Meshing of 3D deposition model (unit: mm)
仿真用的参数列于表1 中。根据实际沉积工艺,数值计算的初始值设置如表2 所示。
2 实验设计
2.1 实验设备及材料
为了验证模型的有效性,本工作借助自主搭建的大功率激光复合加工平台开展单道单层的激光定向能量沉积实验。实验平台如图5 所示。激光器为YLS-10000型光纤激光器,最大输出功率10 kW,波长1.07 μm。送粉器为ECPF2-2 LC型盘式送粉器,其送粉误差低于1%。送粉头为ECA312KW型同轴四喷嘴送粉头,其准直透镜和聚焦透镜的焦距分别为100和300 mm,由激光定向能量沉积实验的执行机构六轴机器人(ABB)搭载并控制。保护气体和运粉气体均选用纯度为99%的高纯Ar气,并设计Ar气保护仓以减少沉积过程中的氧化现象,提高沉积质量。
图5
图5
定向能量沉积实验平台
Fig.5
Single-track single-layer deposition experiment
沉积粉末为气雾化制备的球形316L不锈钢粉末,粒径范围53~105 μm,其化学成分(质量分数,%)为:Cr 16.98,Ni 10.82,Mn 1.47,Mo 2.44,Si 0.58,C 0.021,O 0.038,S 0.02,Fe余量。采用MIRA LMS型扫描电镜(SEM)观察粉末粒子的微观形貌,如图5 所示。基板为尺寸120 mm × 120 mm × 10 mm的热轧316L不锈钢钢板。
2.2 实验方法
实验前,将粉末放在120℃真空干燥箱里面干燥30 min,用砂纸磨去基板表面的氧化层。
实验中的光束调节为SGP1,激光定向能量沉积工艺参数见表3 。
完成沉积实验后,采用线切割将沉积试件横向切割,对切面用400~3000号砂纸逐级打磨,再用金刚石悬浮液抛光处理,然后用王水腐蚀样件。采用XD30M型光学显微镜(OM)拍摄沉积道的横向截面图。最后利用图像测量软件Image Pro Plus测量沉积高度和熔透深度。为了提高精度,降低随机误差,每隔10 mm在同一个沉积道上取3个样。
3 结果与分析
3.1 模型验证
图6 为SGP1作用下不同功率时沉积道形貌的实验结果与熔池热输运动力学模型预测的结果,相应的熔池形貌特征参数(包括:沉积道宽度、沉积深度和沉积高度)如表4 所示。可见,实验结果和模型预测结果的最大相对误差为10.95%,平均相对误差低于6.20%。表明预测的沉积道形貌与实验得到的沉积道形貌吻合良好。
图6
图6
超Gaussian形态(SGP1,K = 4.2)作用下不同功率时沉积道形貌的数值模拟结果与实验结果
Fig.6
Experimental and simulated results at laser powers of 600 W (a), 700 W (b), and 800 W(c) under the action of SGP1
3.2 熔池热输运特征
图7 显示了GP、SGP1、SGP2和FTP 4种激光束空域形态在相同工艺参数(激光扫描速率v = 600 mm/min,P = 700 W,m = 10.2 g/min,r b = 1.2 mm)下600 ms时刻的温度场,其中红线为固/液界线,白线为等温线。由Rosenthal热传导解析解[33 ] 可知,在激光扫描方向上,4种激光束空域形态下熔池前端的等温线被压缩,所以等温线分布密集;而熔池后端的等温线被拉伸,导致等温线分布稀疏。在GP、SGP1、SGP2和FTP作用下,熔池的峰值温度分别为2825、2681、2574和2470 K,表明熔池内的峰值温度随着K 的增大而减小。主要原因可能是,随着K 的增大,激光束的平顶面积逐渐增大,而光束中心的峰值功率密度逐渐减小,如图2 所示,使得光束中心处的材料吸收更少的激光能量。
图7
图7
4种激光束空域形态下熔池的温度场
Fig.7
Temperature (T ) fields of molten pool under actions of GP (a), SGP1 (b), SGP2 (c), and FTP (d)
为了定量分析GP、SGP1、SGP2和FTP 4种激光束空域形态对熔池温度的影响,图8 绘制了600 ms时刻相同工艺参数(P = 700 W,v = 600 mm/min,m = 10.2 g/min,r b = 1.2 mm)下4种光束作用下轨迹1 (图4 trajectory 1)的温度分布。对比分析可得:在4种激光束空域形态下,固相区的温度曲线近似一致,而液相区的温度曲线有明显差异,特别是在光束中心(x = 6 mm)附近,经计算,SGP1、SGP2和FTP作用下的峰值温度分别较GP作用下分别小5.1%、8.9%和12.6%。这是因为在激光束的中心区域,GP的功率密度比SGP1、SGP2和FTP的高。
图8
图8
4种激光束空域形态下图4中轨迹1的温度分布
Fig.8
Temperature distributions of trajectory 1 in Fig.4 under the four spatial laser beam profiles
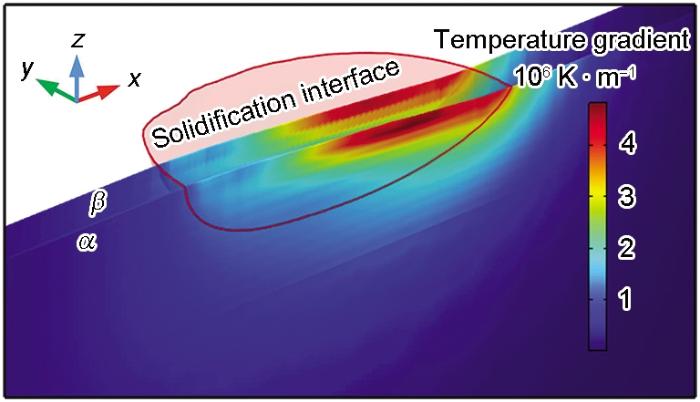
凝固界面(固/液界面或凝固前沿)上的温度梯度是影响凝固组织的关键因素之一。为了定量探究激光束空域形态对熔池凝固界面上的温度梯度的影响,选取y = 0和y = 0.3时的纵向切面为分析对象,分别记为α 和β ,如图9 所示。
图9
图9
Gaussian形态(GP)下熔池纵向切片的温度梯度
Fig.9
Temperature gradient of longitudinal slice of molten pool under GP
针对α 和β 2个纵向切面,选取GP、SGP1、SGP2和FTP 4种光束形态下熔池凝固界线上A 、B 、C 、D 、E 、F 共6个点作为分析对象,如图10 所示,其中A 点位于切面上熔池凝固界线上的最顶部,F 点位于切面上熔池凝固界线上的底部,A 、B 、C 、D 、E 在高度方向上等距选取,α 和β 2个纵向切面凝固界线上的点分别记为A 1 ~F 1 和A 2 ~F 2 。
图10
图10
GP下2个纵向切面上的温度梯度分布
Fig.10
Temperature gradient distributions on two longitudinal sections α (a) and β (b) under GP
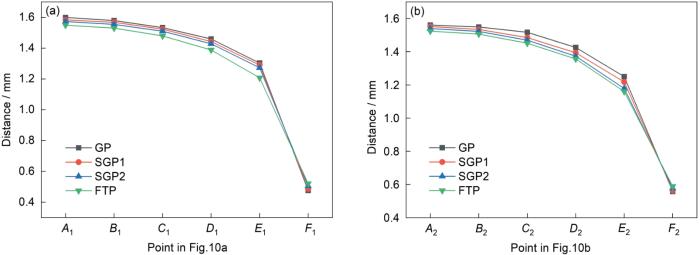
图11 绘制了在GP、SGP1、SGP2和FTP 4种激光束空域形态下,α 和β 切面的熔池凝固界线上的考察位置(A 1 ~F 1 和A 2 ~F 2 )的温度梯度。本工作从2个方面解释从位置A 到位置F 的温度梯度的演变机制:其一,根据Rosenthal热传导解析解[33 ] 可知,在材料和激光加工参数相同的条件下,材料上任意位置的温度与其到熔池表面的光束中心的距离呈负指数关系,即,在远离熔池表面的光束中心区域,其温度变化越平稳,温度梯度越小,反之温度变化越剧烈,温度梯度越大;其二,热流沿等温线或凝固界线的法方向向外传输,这意味着如果凝固界线的法向越偏离激光扫描方向,则激光扫描速率对等温线的拉伸效应越弱,温度梯度越大。由图12 和13 可知,位置A 1 ~F 1 和位置A 2 ~F 2 到熔池表面的光束中心的距离逐渐减小,而其法向与激光扫描方向的夹角逐渐增大,所以图11 中位置A 1 ~F 1 和位置A 2 ~F 2 的温度梯度是逐渐增大的。在GP、SGP1、SGP2和FTP作用下,α 和β 2个切面中靠近熔池后部的相同位置A ~D 处的温度梯度依次增大,这是因为4种空域形态下相同位置A ~D 到光束中心的距离依次减小,而法向与激光扫描方向的夹角逐渐增大。由于位置F 位于凝固界线的最底部,其法向与激光扫描方向的夹角都是90°,所以该位置的温度梯度主要依赖于其到光束中心的距离。从图11 可以看出,GP、SGP1、SGP2和FTP作用下位置F 到光束中心的距离依次增大,因此温度梯度依次减小。
图11
图11
4种激光束空域形态作用下2个切面凝固界线上考察点的温度梯度
Fig.11
Temperature gradients at the observation points on the solidification boundary of the α -plane (a) and β -plane (b) under the four spatial laser beam profiles
图12
图12
4种激光束空域形态作用下切面凝固界线上考察点到熔池表面光束中心的距离
Fig.12
Distances from the observation points on the solidification boundary of α -plane (a) and β -plane (b) to the beam center of the molten pool surface under the four spatial laser beam profiles
图13
图13
4种激光束空域形态作用下激光扫描方向与切面凝固界线上考察点处法线方向的夹角
Fig.13
Angles between the laser scanning direction and the normal direction at the observation points on the solidification boundary of α -plane (a) and β -plane (b) under the four spatial laser beam profiles
根据柱状晶到等轴晶的转变机理,高的温度梯度有利于柱状晶的形成[34 ] 。因此,在GP、SGP1、SGP2和FTP 4种光束中,FTP光束最有利于在熔池的后部形成柱状晶,GP光束最有利于在熔池的底部形成柱状晶。
3.3 熔池流体流动特征
图14 绘制了600 ms时4种空域形态下的熔池速度场。在GP、SGP1、SGP2和FTP 4种空域形态作用下,光束中心附近区域的316L不锈钢熔池温度(图7 )均超过热毛细系数γ T [25 ] ,即热毛细系数从正数过渡到负数,所以在Marangoni剪切力(γ T ∇ s T ) 作用下,熔池具有由内向外的环形流动模式,而且熔池的峰值流速发生在靠近熔池边缘的附近。
图14
图14
4种激光束空域形态下熔池的速度场
Fig.14
Velocity fields of molten pool under actions of GP (a), SGP1 (b), SGP2 (c), and FTP (d)
图15 绘制了600 ms时刻4种激光束空域形态下沿轨迹线1 (图4 )的流速分布。可以看出,流速曲线呈现“M”双峰分布,与前期研究[25 ] 得到的结果类同,主要原因有2个:其一,由于Marangoni剪切应力的作用方向相反,“M”双峰分界处的流速近似为零;其二,在分界处,2个涡流的流速大小近似相等且方向相反,导致分界处的流体合成速度近似为零。比较图15 中的数据可以发现3个差异:其一,SGP1、SGP2和FTP下的左侧峰(熔池后端)较右侧峰(熔池前端)高,但是GP下的左侧峰(熔池后端)较右侧峰(熔池前端)低;其二,相较于GP,SGP1、SGP2和FTP下的左侧峰明显更高,但是右侧峰(熔池前端)却更低;其三,GP,SGP1、SGP2和FTP下的平均流速是逐渐减小的,分别为0.0200、0.0196、0.0173和0.0141 m/s。由此可见,通过改变激光束的空域形态可以对熔池的流动特征进行调控。
图15
图15
4种激光束空域形态下图4中轨迹1的流速分布
Fig.15
Velocity distributions of trajectory 1 in Fig.4 under the four spatial laser beam profiles
Marangoni数(M a ) 定义为熔池表面的剪切应力与流体内部的黏滞力之比,用来研究Marangoni剪切应力对流体流动的影响程度,从而判断熔池流体流动的驱动机制[35 ] 。当M a > 1 [35 ] 。Marangoni数的表达式为:
M a = - γ T ⋅ L e Δ T m a x μ α (25)
式中,L e Δ T m a x α 是热扩散系数。
经计算,4种激光束空域形态作用下熔池的M a
为了分析流体流动在熔池传热中的贡献作用,这里引入了Peclet数(Pe T )作为评价指标,当Pe T < 5时,熔池中热传导起主要作用;当Pe T > 100时,熔池中Marangoni对流传热起主要作用[18 ] 。Peclet数的计算式为:
P e T = u m a x L e α (26)
GP、SGP1、SGP2和FTP下的熔池最大流速分别为0.18、0.20、0.19和0.18 m/s,如图14 所示。由 式(26)计算得到GP、SGP1、SGP2和FTP 4种空域形态下熔池的Peclet数分别为7.69、8.45、8.01和7.41,均大于5,但小于100,说明熔池的传热均由Marangoni对流传热和热传导共同主导。
4 结论
(1) 考虑激光束、粉束流和熔池的耦合作用、热流耦合作用、固液相变和多重传热等重要物理量,建立了激光定向能量沉积三维传热模型,模型的预测结果与实验测量结果吻合良好。
(2) 在GP、SGP1、SGP2和FTP 4种激光束空域形态下,熔池的峰值温度依次降低,SGP1、SGP2和FTP下的峰值温度分别较GP的峰值温度分别小5.1%、8.9%和12.6%。
(3) 凝固界面的温度梯度随其到熔池表面光束中心的距离增大而减小,随法向与激光扫描方向的夹角增大而增大。GP、SGP1、SGP2和FTP下熔池凝固界面上的温度梯度从熔池最顶部到熔池最底部逐渐增大;在GP、SGP1、SGP2和FTP下,靠近熔池后部的相同凝固界面处的温度梯度依次增大,但熔池底部相同位置的温度梯度依次减小。
(4) 在GP、SGP1、SGP2和FTP作用下,熔池具有由内向外的环形流动模式,峰值流速发生在靠近熔池边缘的附近;GP、SGP1、SGP2和FTP作用下熔池中的平均流速依次减小。Marangoni剪切应力是驱动流体流动的主导因素,Marangoni对流传热和热传导共同主导熔池传热。
参考文献
View Option
[1]
Gu D D Zhang H M Chen H Y et al . Laser additive manufacturing of high-performance metallic aerospace components
[J]. Chin. J. Lasers , 2020 , 47 : 0500002
[本文引用: 1]
顾冬冬 , 张红梅 , 陈洪宇 等 . 航空航天高性能金属材料构件激光增材制造
[J]. 中国激光 , 2020 , 47 : 0500002
[本文引用: 1]
[2]
Li D C He J K Tian X Y et al . Additive manufacturing: Integrated fabrication of macro/microstructures
[J]. J. Mech. Eng. , 2013 , 49 (6 ): 129
[本文引用: 1]
李涤尘 , 贺健康 , 田小永 等 . 增材制造: 实现宏微结构一体化制造
[J]. 机械工程学报 , 2013 , 49 (6 ): 129
[本文引用: 1]
增材制造技术是基于分层制造原理发展而来的先进制造技术,是信息技术、新材料技术与制造技术多学科融合发展的产物,是当今世界各制造强国竞相发展的热点技术。基于增材制造材料逐点累积的成形过程,提出宏微结构一体化制造的学术观点。该方法在金属、陶瓷与复合材料的成形制造中有着其他制造方法难以替代的优势,可以实现制造短流程化,并推动大批量制造模式向个性化制造模式发展。列举近年在金属零件定向晶组织制造、光子晶体制造、生物组织器官支架制造方面的研究成果,论述宏微结构一体化增材制造技术的实现方法与工程应用,解决了传统制造技术难以解决的宏微结构一体化制造难题,给制造技术展示出全新的发展前景,为相关学科和产业发展提供有力的制造技术支撑。
[3]
Gong G H Ye J J Chi Y M et al . Research status of laser additive manufacturing for metal: A review
[J]. J. Mater. Res. Technol. , 2021 , 15 : 855
[本文引用: 1]
[4]
Roehling T T Wu S S Q Khairallah S A et al . Modulating laser intensity profile ellipticity for microstructural control during metal additive manufacturing
[J]. Acta Mater. , 2017 , 128 : 197
[本文引用: 1]
[5]
Tumkur T U Voisin T Shi R P et al . Nondiffractive beam shaping for enhanced optothermal control in metal additive manufacturing
[J]. Sci. Adv. , 2021 , 7 : eabg9358
[本文引用: 1]
[6]
Kubiak M Piekarska W Stano S Modelling of laser beam heat source based on experimental research of Yb:YAG laser power distribution
[J]. Int. J. Heat Mass Transfer , 2015 , 83 : 679
[本文引用: 2]
[7]
Sundqvist J Kaplan A F H Shachaf L et al . Analytical heat conduction modelling for shaped laser beams
[J]. J. Mater. Process. Technol. , 2017 , 247 : 48
[本文引用: 1]
[8]
Ya W Pathiraj B Liu S J 2D modelling of clad geometry and resulting thermal cycles during laser cladding
[J]. J. Mater. Process. Technol. , 2016 , 230 : 217
[本文引用: 1]
[9]
Song M J Wu L S Liu J M et al . Effects of laser cladding on crack resistance improvement for aluminum alloy used in aircraft skin
[J]. Opt. Laser Technol. , 2021 , 133 : 106531
[本文引用: 1]
[10]
Gao W Y Zhao S S Wang Y B et al . Numerical simulation of thermal field and Fe-based coating doped Ti
[J]. Int. J. Heat Mass Transfer , 2016 , 92 : 83
[本文引用: 1]
[11]
Manvatkar V De A DebRoy T Heat transfer and material flow during laser assisted multi-layer additive manufacturing
[J]. J. Appl. Phys. , 2014 , 116 : 124905
[本文引用: 1]
[12]
Li C Zhang D C Gao X et al . Numerical simulation method of the multi-field coupling mechanism for laser cladding 316L powder
[J]. Weld. World , 2022 , 66 : 423
[本文引用: 1]
[13]
Wang L P Zhang D C Chen C Z et al . Multi-physics field coupling and microstructure numerical simulation of laser cladding for engine crankshaft based on CA-FE method and experimental study
[J]. Surf. Coat. Technol. , 2022 , 438 : 128396
[本文引用: 1]
[14]
He X Mazumder J Transport phenomena during direct metal deposition
[J]. J. Appl. Phys. , 2007 , 101 : 053113
[本文引用: 1]
[15]
Qi H Mazumder J Ki H Numerical simulation of heat transfer and fluid flow in coaxial laser cladding process for direct metal deposition
[J]. J. Appl. Phys. , 2006 , 100 : 024903
[本文引用: 1]
[16]
Wirth F Wegener K A physical modeling and predictive simulation of the laser cladding process
[J]. Addit. Manuf. , 2018 , 22 : 307
[本文引用: 1]
[17]
Li C Yu Z B Gao J X et al . Numerical simulation and experimental study of cladding Fe60 on an ASTM 1045 substrate by laser cladding
[J]. Surf. Coat. Technol. , 2019 , 357 : 965
[本文引用: 1]
[18]
Gan Z T Yu G He X L et al . Numerical simulation of thermal behavior and multicomponent mass transfer in direct laser deposition of Co-base alloy on steel
[J]. Int. J. Heat Mass Transfer , 2017 , 104 : 28
[本文引用: 2]
[19]
Zhang T Li H Liu S et al . Evolution of molten pool during selective laser melting of Ti-6Al-4V
[J]. J. Phys. , 2019 , 52D : 055302
[本文引用: 1]
[20]
Han L Phatak K M Liou F W Modeling of laser cladding with powder injection
[J]. Metall. Mater. Trans. , 2004 , 35B : 11390
[本文引用: 1]
[21]
Tovar A A Propagation of flat-topped multi-Gaussian laser beams
[J]. J. Opt. Soc. Am. , 2001 , 18A : 18974
[本文引用: 1]
[22]
Kaplan A F H Analysis and modeling of a high-power Yb:fiber laser beam profile
[J]. Opt. Eng. , 2011 , 50 : 054201
[本文引用: 1]
[23]
Wu J Z Zhao P H Wei H Y et al . Development of powder distribution model of discontinuous coaxial powder stream in laser direct metal deposition
[J]. Powder Technol. , 2018 , 340 : 449
[本文引用: 2]
[24]
Wu J Z Liu T W Chen H Y et al . Simulation of laser attenuation and heat transport during direct metal deposition considering beam profile
[J]. J. Mater. Process. Technol. , 2019 , 270 : 92
[本文引用: 3]
[25]
Wu J Z Ren S Zhang Y et al . Influence of spatial laser beam profiles on thermal-fluid transport during laser-based directed energy deposition
[J]. Virtual Phys. Prototy. , 2021 , 16 : 444
[本文引用: 4]
[26]
Gan Z T Yu G He X L et al . Surface-active element transport and its effect on liquid metal flow in laser-assisted additive manufacturing
[J]. Int. Commun. Heat Mass Transfer , 2017 , 86 : 206
[本文引用: 2]
[27]
He X L Song L J Yu G et al . Solute transport and composition profile during direct metal deposition with coaxial powder injection
[J]. Appl. Surf. Sci. , 2011 , 258 : 898
[本文引用: 1]
[28]
Morville S Carin M Peyre P et al . 2D longitudinal modeling of heat transfer and fluid flow during multilayered direct laser metal deposition process
[J]. J. Laser Appl. , 2012 , 24 : 032008
[本文引用: 1]
[29]
Wen S Y Shin Y C Modeling of transport phenomena during the coaxial laser direct deposition process
[J]. J. Appl. Phys. , 2010 , 108 : 044908
[本文引用: 1]
[30]
Ai Y W Jiang P Shao X Y et al . A three-dimensional numerical simulation model for weld characteristics analysis in fiber laser keyhole welding
[J]. Int. J. Heat Mass Transfer , 2017 , 108 : 614
[本文引用: 1]
[31]
Knapp G L Mukherjee T Zuback J S et al . Building blocks for a digital twin of additive manufacturing
[J]. Acta Mater. , 2017 , 135 : 390
[本文引用: 1]
[32]
Wu J Z Zheng X Q Zhang Y et al . Modeling of whole-phase heat transport in laser-based directed energy deposition with multichannel coaxial powder feeding
[J]. Addit. Manuf. , 2022 , 59 : 103161
[本文引用: 1]
[33]
Promoppatum P Yao S C Pistorius P C et al . A comprehensive comparison of the analytical and numerical prediction of the thermal history and solidification microstructure of Inconel 718 products made by laser powder-bed fusion
[J]. Engineering , 2017 , 3 : 685
[本文引用: 2]
[34]
Wei H L Mukherjee T Zhang W et al . Mechanistic models for additive manufacturing of metallic components
[J]. Prog. Mater. Sci. , 2021 , 116 : 100703
[本文引用: 1]
[35]
Debroy T Wei H L Zuback J S et al . Additive manufacturing of metallic components—Process, structure and properties
[J]. Prog. Mater. Sci. , 2018 , 92 : 112
[本文引用: 2]
Laser additive manufacturing of high-performance metallic aerospace components
1
2020
... 316L不锈钢因具有耐高温、耐腐蚀和高韧性等优点,被广泛应用于航空航天、海洋船舶、医疗器械、轨道交通、电子通讯等制造领域.部分316L不锈钢构件兼具轻量化、复杂难加工、高性能等特征,多服务于极端严苛环境中,因而对构件的材料、结构、工艺和性能等提出极大挑战[1 ] .激光增材制造技术通过逐点累积成面,逐面累积成体的离散制造模式,不受形状、结构复杂程度及尺寸的限制,可以实现复杂构件的材料-结构-性能一体化制造[2 ] .激光定向能量沉积是将激光熔覆和同步送粉相结合的一种激光增材制造技术,在沉积速率和成形质量方面具有特殊优势[3 ] ,可用于制造构型复杂、性能可控的316L不锈钢零件. ...
航空航天高性能金属材料构件激光增材制造
1
2020
... 316L不锈钢因具有耐高温、耐腐蚀和高韧性等优点,被广泛应用于航空航天、海洋船舶、医疗器械、轨道交通、电子通讯等制造领域.部分316L不锈钢构件兼具轻量化、复杂难加工、高性能等特征,多服务于极端严苛环境中,因而对构件的材料、结构、工艺和性能等提出极大挑战[1 ] .激光增材制造技术通过逐点累积成面,逐面累积成体的离散制造模式,不受形状、结构复杂程度及尺寸的限制,可以实现复杂构件的材料-结构-性能一体化制造[2 ] .激光定向能量沉积是将激光熔覆和同步送粉相结合的一种激光增材制造技术,在沉积速率和成形质量方面具有特殊优势[3 ] ,可用于制造构型复杂、性能可控的316L不锈钢零件. ...
Additive manufacturing: Integrated fabrication of macro/microstructures
1
2013
... 316L不锈钢因具有耐高温、耐腐蚀和高韧性等优点,被广泛应用于航空航天、海洋船舶、医疗器械、轨道交通、电子通讯等制造领域.部分316L不锈钢构件兼具轻量化、复杂难加工、高性能等特征,多服务于极端严苛环境中,因而对构件的材料、结构、工艺和性能等提出极大挑战[1 ] .激光增材制造技术通过逐点累积成面,逐面累积成体的离散制造模式,不受形状、结构复杂程度及尺寸的限制,可以实现复杂构件的材料-结构-性能一体化制造[2 ] .激光定向能量沉积是将激光熔覆和同步送粉相结合的一种激光增材制造技术,在沉积速率和成形质量方面具有特殊优势[3 ] ,可用于制造构型复杂、性能可控的316L不锈钢零件. ...
增材制造: 实现宏微结构一体化制造
1
2013
... 316L不锈钢因具有耐高温、耐腐蚀和高韧性等优点,被广泛应用于航空航天、海洋船舶、医疗器械、轨道交通、电子通讯等制造领域.部分316L不锈钢构件兼具轻量化、复杂难加工、高性能等特征,多服务于极端严苛环境中,因而对构件的材料、结构、工艺和性能等提出极大挑战[1 ] .激光增材制造技术通过逐点累积成面,逐面累积成体的离散制造模式,不受形状、结构复杂程度及尺寸的限制,可以实现复杂构件的材料-结构-性能一体化制造[2 ] .激光定向能量沉积是将激光熔覆和同步送粉相结合的一种激光增材制造技术,在沉积速率和成形质量方面具有特殊优势[3 ] ,可用于制造构型复杂、性能可控的316L不锈钢零件. ...
Research status of laser additive manufacturing for metal: A review
1
2021
... 316L不锈钢因具有耐高温、耐腐蚀和高韧性等优点,被广泛应用于航空航天、海洋船舶、医疗器械、轨道交通、电子通讯等制造领域.部分316L不锈钢构件兼具轻量化、复杂难加工、高性能等特征,多服务于极端严苛环境中,因而对构件的材料、结构、工艺和性能等提出极大挑战[1 ] .激光增材制造技术通过逐点累积成面,逐面累积成体的离散制造模式,不受形状、结构复杂程度及尺寸的限制,可以实现复杂构件的材料-结构-性能一体化制造[2 ] .激光定向能量沉积是将激光熔覆和同步送粉相结合的一种激光增材制造技术,在沉积速率和成形质量方面具有特殊优势[3 ] ,可用于制造构型复杂、性能可控的316L不锈钢零件. ...
Modulating laser intensity profile ellipticity for microstructural control during metal additive manufacturing
1
2017
... 激光束空域形态是指聚焦激光束在横截面上的功率密度分布形态.3种典型的激光束空域形态分别是Gaussian形态(Gaussian profile,GP)、超Gaussian形态(super-Gaussian profile,SGP)、完全平顶形态(flat-topped profile,FTP).因为聚焦激光束的空域形态决定着熔池表面的能量密度分布形态及其大小,所以影响着熔池的热输运行为.为了探究激光束空域形态对激光材料加工中热输运行为的影响,国内外有关学者开展了一系列研究.Roehling等[4 ] 发现在粉床熔化沉积增材制造中,圆形Gaussian和椭圆Gaussian光束形态创建的熔池热场和流场是有明显差异的.Tumkur等[5 ] 研究了Bessel光束和Gaussian光束对粉床熔化沉积增材制造过程中熔池热输运的影响,发现Bessel光束能够降低熔池的温度梯度和延长熔池的凝固时间.Kubiak等[6 ] 数值模拟了GP与SGP下激光加热过程中的热输运特征,发现温度场有较大差别.Sundqvist等[7 ] 认为不同激光束空域形态下的激光点焊温度场是明显不同的.上述研究表明,激光束空域形态展示出其对激光粉床熔化沉积、激光热处理、激光焊接等激光加工过程中热输运行为的调控潜力.但是,目前有关激光束空域形态在同步送粉式激光定向能量沉积中的应用和研究较少,开展这方面的研究有助于拓宽激光束空域形态的应用范围,指导定制或优化激光束空域形态,提升对热输运的调控能力和水平. ...
Nondiffractive beam shaping for enhanced optothermal control in metal additive manufacturing
1
2021
... 激光束空域形态是指聚焦激光束在横截面上的功率密度分布形态.3种典型的激光束空域形态分别是Gaussian形态(Gaussian profile,GP)、超Gaussian形态(super-Gaussian profile,SGP)、完全平顶形态(flat-topped profile,FTP).因为聚焦激光束的空域形态决定着熔池表面的能量密度分布形态及其大小,所以影响着熔池的热输运行为.为了探究激光束空域形态对激光材料加工中热输运行为的影响,国内外有关学者开展了一系列研究.Roehling等[4 ] 发现在粉床熔化沉积增材制造中,圆形Gaussian和椭圆Gaussian光束形态创建的熔池热场和流场是有明显差异的.Tumkur等[5 ] 研究了Bessel光束和Gaussian光束对粉床熔化沉积增材制造过程中熔池热输运的影响,发现Bessel光束能够降低熔池的温度梯度和延长熔池的凝固时间.Kubiak等[6 ] 数值模拟了GP与SGP下激光加热过程中的热输运特征,发现温度场有较大差别.Sundqvist等[7 ] 认为不同激光束空域形态下的激光点焊温度场是明显不同的.上述研究表明,激光束空域形态展示出其对激光粉床熔化沉积、激光热处理、激光焊接等激光加工过程中热输运行为的调控潜力.但是,目前有关激光束空域形态在同步送粉式激光定向能量沉积中的应用和研究较少,开展这方面的研究有助于拓宽激光束空域形态的应用范围,指导定制或优化激光束空域形态,提升对热输运的调控能力和水平. ...
Modelling of laser beam heat source based on experimental research of Yb:YAG laser power distribution
2
2015
... 激光束空域形态是指聚焦激光束在横截面上的功率密度分布形态.3种典型的激光束空域形态分别是Gaussian形态(Gaussian profile,GP)、超Gaussian形态(super-Gaussian profile,SGP)、完全平顶形态(flat-topped profile,FTP).因为聚焦激光束的空域形态决定着熔池表面的能量密度分布形态及其大小,所以影响着熔池的热输运行为.为了探究激光束空域形态对激光材料加工中热输运行为的影响,国内外有关学者开展了一系列研究.Roehling等[4 ] 发现在粉床熔化沉积增材制造中,圆形Gaussian和椭圆Gaussian光束形态创建的熔池热场和流场是有明显差异的.Tumkur等[5 ] 研究了Bessel光束和Gaussian光束对粉床熔化沉积增材制造过程中熔池热输运的影响,发现Bessel光束能够降低熔池的温度梯度和延长熔池的凝固时间.Kubiak等[6 ] 数值模拟了GP与SGP下激光加热过程中的热输运特征,发现温度场有较大差别.Sundqvist等[7 ] 认为不同激光束空域形态下的激光点焊温度场是明显不同的.上述研究表明,激光束空域形态展示出其对激光粉床熔化沉积、激光热处理、激光焊接等激光加工过程中热输运行为的调控潜力.但是,目前有关激光束空域形态在同步送粉式激光定向能量沉积中的应用和研究较少,开展这方面的研究有助于拓宽激光束空域形态的应用范围,指导定制或优化激光束空域形态,提升对热输运的调控能力和水平. ...
... 实验使用的聚焦光纤激光束为超Gaussian光束,其横截面上的功率密度Q 服从超Gaussian分布,其数学表达式为[6 ] : ...
Analytical heat conduction modelling for shaped laser beams
1
2017
... 激光束空域形态是指聚焦激光束在横截面上的功率密度分布形态.3种典型的激光束空域形态分别是Gaussian形态(Gaussian profile,GP)、超Gaussian形态(super-Gaussian profile,SGP)、完全平顶形态(flat-topped profile,FTP).因为聚焦激光束的空域形态决定着熔池表面的能量密度分布形态及其大小,所以影响着熔池的热输运行为.为了探究激光束空域形态对激光材料加工中热输运行为的影响,国内外有关学者开展了一系列研究.Roehling等[4 ] 发现在粉床熔化沉积增材制造中,圆形Gaussian和椭圆Gaussian光束形态创建的熔池热场和流场是有明显差异的.Tumkur等[5 ] 研究了Bessel光束和Gaussian光束对粉床熔化沉积增材制造过程中熔池热输运的影响,发现Bessel光束能够降低熔池的温度梯度和延长熔池的凝固时间.Kubiak等[6 ] 数值模拟了GP与SGP下激光加热过程中的热输运特征,发现温度场有较大差别.Sundqvist等[7 ] 认为不同激光束空域形态下的激光点焊温度场是明显不同的.上述研究表明,激光束空域形态展示出其对激光粉床熔化沉积、激光热处理、激光焊接等激光加工过程中热输运行为的调控潜力.但是,目前有关激光束空域形态在同步送粉式激光定向能量沉积中的应用和研究较少,开展这方面的研究有助于拓宽激光束空域形态的应用范围,指导定制或优化激光束空域形态,提升对热输运的调控能力和水平. ...
2D modelling of clad geometry and resulting thermal cycles during laser cladding
1
2016
... 目前,工艺实验和数值模拟是研究激光定向能量沉积熔池热输运行为的2种主要手段.常规的工艺实验方法难以明晰深层的物理机制,且时间成本和经济成本高,因此,基于物理过程的数值模拟成为了探明熔池热输运行为的最有效手段.在熔池热输运的数值模拟方面,Ya等[8 ] 基于能量和质量守恒创建了激光熔覆热传导模型,预测了熔覆道的生长和传热.Song等[9 ] 提出了一种基于有限元的三维热-结构耦合模型,研究了激光熔覆过程中铝合金的温度场和应力场.Gao等[10 ] 建立了送粉式激光熔覆热传导模型,进而研究熔池的温度分布以及预测组织凝固.但是这些热传导模型忽略了流体流动的影响.对于某些特定工况,熔池内的流体流动微弱,对热输运的影响小,这意味着忽略流体流动的影响不仅不会明显降低模型预测精度,而且能显著改进模型的计算效率和收敛性.但在流体流动较强的情况下,热传导模型的预测精度会显著降低,例如,Manvatkar等[11 ] 发现忽略流体的影响会导致预测的冷却速率提高2倍.为了解决这一问题,Li等[12 ] 开发了基于质量、动量和能量守恒定律的多场耦合三维有限元数值模型,研究激光功率对温度场和流场的影响规律.Wang等[13 ] 同样考虑熔池的流体输运建立了三维有限元模型,研究熔池的热输运和微观组织演化.但这些模型没有考虑激光和粉末的相互作用对模型热输入的影响.He等[14 ] 和Qi等[15 ] 在建立的模型中考虑了激光和粉末的相互作用,但是为了简化光-粉耦合模型,忽略了热对流和热辐射的影响. ...
Effects of laser cladding on crack resistance improvement for aluminum alloy used in aircraft skin
1
2021
... 目前,工艺实验和数值模拟是研究激光定向能量沉积熔池热输运行为的2种主要手段.常规的工艺实验方法难以明晰深层的物理机制,且时间成本和经济成本高,因此,基于物理过程的数值模拟成为了探明熔池热输运行为的最有效手段.在熔池热输运的数值模拟方面,Ya等[8 ] 基于能量和质量守恒创建了激光熔覆热传导模型,预测了熔覆道的生长和传热.Song等[9 ] 提出了一种基于有限元的三维热-结构耦合模型,研究了激光熔覆过程中铝合金的温度场和应力场.Gao等[10 ] 建立了送粉式激光熔覆热传导模型,进而研究熔池的温度分布以及预测组织凝固.但是这些热传导模型忽略了流体流动的影响.对于某些特定工况,熔池内的流体流动微弱,对热输运的影响小,这意味着忽略流体流动的影响不仅不会明显降低模型预测精度,而且能显著改进模型的计算效率和收敛性.但在流体流动较强的情况下,热传导模型的预测精度会显著降低,例如,Manvatkar等[11 ] 发现忽略流体的影响会导致预测的冷却速率提高2倍.为了解决这一问题,Li等[12 ] 开发了基于质量、动量和能量守恒定律的多场耦合三维有限元数值模型,研究激光功率对温度场和流场的影响规律.Wang等[13 ] 同样考虑熔池的流体输运建立了三维有限元模型,研究熔池的热输运和微观组织演化.但这些模型没有考虑激光和粉末的相互作用对模型热输入的影响.He等[14 ] 和Qi等[15 ] 在建立的模型中考虑了激光和粉末的相互作用,但是为了简化光-粉耦合模型,忽略了热对流和热辐射的影响. ...
Numerical simulation of thermal field and Fe-based coating doped Ti
1
2016
... 目前,工艺实验和数值模拟是研究激光定向能量沉积熔池热输运行为的2种主要手段.常规的工艺实验方法难以明晰深层的物理机制,且时间成本和经济成本高,因此,基于物理过程的数值模拟成为了探明熔池热输运行为的最有效手段.在熔池热输运的数值模拟方面,Ya等[8 ] 基于能量和质量守恒创建了激光熔覆热传导模型,预测了熔覆道的生长和传热.Song等[9 ] 提出了一种基于有限元的三维热-结构耦合模型,研究了激光熔覆过程中铝合金的温度场和应力场.Gao等[10 ] 建立了送粉式激光熔覆热传导模型,进而研究熔池的温度分布以及预测组织凝固.但是这些热传导模型忽略了流体流动的影响.对于某些特定工况,熔池内的流体流动微弱,对热输运的影响小,这意味着忽略流体流动的影响不仅不会明显降低模型预测精度,而且能显著改进模型的计算效率和收敛性.但在流体流动较强的情况下,热传导模型的预测精度会显著降低,例如,Manvatkar等[11 ] 发现忽略流体的影响会导致预测的冷却速率提高2倍.为了解决这一问题,Li等[12 ] 开发了基于质量、动量和能量守恒定律的多场耦合三维有限元数值模型,研究激光功率对温度场和流场的影响规律.Wang等[13 ] 同样考虑熔池的流体输运建立了三维有限元模型,研究熔池的热输运和微观组织演化.但这些模型没有考虑激光和粉末的相互作用对模型热输入的影响.He等[14 ] 和Qi等[15 ] 在建立的模型中考虑了激光和粉末的相互作用,但是为了简化光-粉耦合模型,忽略了热对流和热辐射的影响. ...
Heat transfer and material flow during laser assisted multi-layer additive manufacturing
1
2014
... 目前,工艺实验和数值模拟是研究激光定向能量沉积熔池热输运行为的2种主要手段.常规的工艺实验方法难以明晰深层的物理机制,且时间成本和经济成本高,因此,基于物理过程的数值模拟成为了探明熔池热输运行为的最有效手段.在熔池热输运的数值模拟方面,Ya等[8 ] 基于能量和质量守恒创建了激光熔覆热传导模型,预测了熔覆道的生长和传热.Song等[9 ] 提出了一种基于有限元的三维热-结构耦合模型,研究了激光熔覆过程中铝合金的温度场和应力场.Gao等[10 ] 建立了送粉式激光熔覆热传导模型,进而研究熔池的温度分布以及预测组织凝固.但是这些热传导模型忽略了流体流动的影响.对于某些特定工况,熔池内的流体流动微弱,对热输运的影响小,这意味着忽略流体流动的影响不仅不会明显降低模型预测精度,而且能显著改进模型的计算效率和收敛性.但在流体流动较强的情况下,热传导模型的预测精度会显著降低,例如,Manvatkar等[11 ] 发现忽略流体的影响会导致预测的冷却速率提高2倍.为了解决这一问题,Li等[12 ] 开发了基于质量、动量和能量守恒定律的多场耦合三维有限元数值模型,研究激光功率对温度场和流场的影响规律.Wang等[13 ] 同样考虑熔池的流体输运建立了三维有限元模型,研究熔池的热输运和微观组织演化.但这些模型没有考虑激光和粉末的相互作用对模型热输入的影响.He等[14 ] 和Qi等[15 ] 在建立的模型中考虑了激光和粉末的相互作用,但是为了简化光-粉耦合模型,忽略了热对流和热辐射的影响. ...
Numerical simulation method of the multi-field coupling mechanism for laser cladding 316L powder
1
2022
... 目前,工艺实验和数值模拟是研究激光定向能量沉积熔池热输运行为的2种主要手段.常规的工艺实验方法难以明晰深层的物理机制,且时间成本和经济成本高,因此,基于物理过程的数值模拟成为了探明熔池热输运行为的最有效手段.在熔池热输运的数值模拟方面,Ya等[8 ] 基于能量和质量守恒创建了激光熔覆热传导模型,预测了熔覆道的生长和传热.Song等[9 ] 提出了一种基于有限元的三维热-结构耦合模型,研究了激光熔覆过程中铝合金的温度场和应力场.Gao等[10 ] 建立了送粉式激光熔覆热传导模型,进而研究熔池的温度分布以及预测组织凝固.但是这些热传导模型忽略了流体流动的影响.对于某些特定工况,熔池内的流体流动微弱,对热输运的影响小,这意味着忽略流体流动的影响不仅不会明显降低模型预测精度,而且能显著改进模型的计算效率和收敛性.但在流体流动较强的情况下,热传导模型的预测精度会显著降低,例如,Manvatkar等[11 ] 发现忽略流体的影响会导致预测的冷却速率提高2倍.为了解决这一问题,Li等[12 ] 开发了基于质量、动量和能量守恒定律的多场耦合三维有限元数值模型,研究激光功率对温度场和流场的影响规律.Wang等[13 ] 同样考虑熔池的流体输运建立了三维有限元模型,研究熔池的热输运和微观组织演化.但这些模型没有考虑激光和粉末的相互作用对模型热输入的影响.He等[14 ] 和Qi等[15 ] 在建立的模型中考虑了激光和粉末的相互作用,但是为了简化光-粉耦合模型,忽略了热对流和热辐射的影响. ...
Multi-physics field coupling and microstructure numerical simulation of laser cladding for engine crankshaft based on CA-FE method and experimental study
1
2022
... 目前,工艺实验和数值模拟是研究激光定向能量沉积熔池热输运行为的2种主要手段.常规的工艺实验方法难以明晰深层的物理机制,且时间成本和经济成本高,因此,基于物理过程的数值模拟成为了探明熔池热输运行为的最有效手段.在熔池热输运的数值模拟方面,Ya等[8 ] 基于能量和质量守恒创建了激光熔覆热传导模型,预测了熔覆道的生长和传热.Song等[9 ] 提出了一种基于有限元的三维热-结构耦合模型,研究了激光熔覆过程中铝合金的温度场和应力场.Gao等[10 ] 建立了送粉式激光熔覆热传导模型,进而研究熔池的温度分布以及预测组织凝固.但是这些热传导模型忽略了流体流动的影响.对于某些特定工况,熔池内的流体流动微弱,对热输运的影响小,这意味着忽略流体流动的影响不仅不会明显降低模型预测精度,而且能显著改进模型的计算效率和收敛性.但在流体流动较强的情况下,热传导模型的预测精度会显著降低,例如,Manvatkar等[11 ] 发现忽略流体的影响会导致预测的冷却速率提高2倍.为了解决这一问题,Li等[12 ] 开发了基于质量、动量和能量守恒定律的多场耦合三维有限元数值模型,研究激光功率对温度场和流场的影响规律.Wang等[13 ] 同样考虑熔池的流体输运建立了三维有限元模型,研究熔池的热输运和微观组织演化.但这些模型没有考虑激光和粉末的相互作用对模型热输入的影响.He等[14 ] 和Qi等[15 ] 在建立的模型中考虑了激光和粉末的相互作用,但是为了简化光-粉耦合模型,忽略了热对流和热辐射的影响. ...
Transport phenomena during direct metal deposition
1
2007
... 目前,工艺实验和数值模拟是研究激光定向能量沉积熔池热输运行为的2种主要手段.常规的工艺实验方法难以明晰深层的物理机制,且时间成本和经济成本高,因此,基于物理过程的数值模拟成为了探明熔池热输运行为的最有效手段.在熔池热输运的数值模拟方面,Ya等[8 ] 基于能量和质量守恒创建了激光熔覆热传导模型,预测了熔覆道的生长和传热.Song等[9 ] 提出了一种基于有限元的三维热-结构耦合模型,研究了激光熔覆过程中铝合金的温度场和应力场.Gao等[10 ] 建立了送粉式激光熔覆热传导模型,进而研究熔池的温度分布以及预测组织凝固.但是这些热传导模型忽略了流体流动的影响.对于某些特定工况,熔池内的流体流动微弱,对热输运的影响小,这意味着忽略流体流动的影响不仅不会明显降低模型预测精度,而且能显著改进模型的计算效率和收敛性.但在流体流动较强的情况下,热传导模型的预测精度会显著降低,例如,Manvatkar等[11 ] 发现忽略流体的影响会导致预测的冷却速率提高2倍.为了解决这一问题,Li等[12 ] 开发了基于质量、动量和能量守恒定律的多场耦合三维有限元数值模型,研究激光功率对温度场和流场的影响规律.Wang等[13 ] 同样考虑熔池的流体输运建立了三维有限元模型,研究熔池的热输运和微观组织演化.但这些模型没有考虑激光和粉末的相互作用对模型热输入的影响.He等[14 ] 和Qi等[15 ] 在建立的模型中考虑了激光和粉末的相互作用,但是为了简化光-粉耦合模型,忽略了热对流和热辐射的影响. ...
Numerical simulation of heat transfer and fluid flow in coaxial laser cladding process for direct metal deposition
1
2006
... 目前,工艺实验和数值模拟是研究激光定向能量沉积熔池热输运行为的2种主要手段.常规的工艺实验方法难以明晰深层的物理机制,且时间成本和经济成本高,因此,基于物理过程的数值模拟成为了探明熔池热输运行为的最有效手段.在熔池热输运的数值模拟方面,Ya等[8 ] 基于能量和质量守恒创建了激光熔覆热传导模型,预测了熔覆道的生长和传热.Song等[9 ] 提出了一种基于有限元的三维热-结构耦合模型,研究了激光熔覆过程中铝合金的温度场和应力场.Gao等[10 ] 建立了送粉式激光熔覆热传导模型,进而研究熔池的温度分布以及预测组织凝固.但是这些热传导模型忽略了流体流动的影响.对于某些特定工况,熔池内的流体流动微弱,对热输运的影响小,这意味着忽略流体流动的影响不仅不会明显降低模型预测精度,而且能显著改进模型的计算效率和收敛性.但在流体流动较强的情况下,热传导模型的预测精度会显著降低,例如,Manvatkar等[11 ] 发现忽略流体的影响会导致预测的冷却速率提高2倍.为了解决这一问题,Li等[12 ] 开发了基于质量、动量和能量守恒定律的多场耦合三维有限元数值模型,研究激光功率对温度场和流场的影响规律.Wang等[13 ] 同样考虑熔池的流体输运建立了三维有限元模型,研究熔池的热输运和微观组织演化.但这些模型没有考虑激光和粉末的相互作用对模型热输入的影响.He等[14 ] 和Qi等[15 ] 在建立的模型中考虑了激光和粉末的相互作用,但是为了简化光-粉耦合模型,忽略了热对流和热辐射的影响. ...
A physical modeling and predictive simulation of the laser cladding process
1
2018
... (1) 假设熔池中的流体不可压缩,流动模式为层流[16 ] ; ...
Numerical simulation and experimental study of cladding Fe60 on an ASTM 1045 substrate by laser cladding
1
2019
... (4) 粉末颗粒做恒速直线运动,落入熔池后即刻熔化[17 ] . ...
Numerical simulation of thermal behavior and multicomponent mass transfer in direct laser deposition of Co-base alloy on steel
2
2017
... 在激光定向能量沉积过程中,熔池区的热输运与流体流动形成耦合效应,彼此相互影响,因此沉积区的热输运过程由质量、动量和能量三大守恒定律控制,其基本控制方程分别为[18 ] : ...
... 为了分析流体流动在熔池传热中的贡献作用,这里引入了Peclet数(Pe T )作为评价指标,当Pe T < 5时,熔池中热传导起主要作用;当Pe T > 100时,熔池中Marangoni对流传热起主要作用[18 ] .Peclet数的计算式为: ...
Evolution of molten pool during selective laser melting of Ti-6Al-4V
1
2019
... 固/液相变发生在固相和液相混合的糊状区(固/液界面),因此相变过程中的热物性参数可由表观热熔法表示[19 ,20 ] ,即: ...
Modeling of laser cladding with powder injection
1
2004
... 固/液相变发生在固相和液相混合的糊状区(固/液界面),因此相变过程中的热物性参数可由表观热熔法表示[19 ,20 ] ,即: ...
Propagation of flat-topped multi-Gaussian laser beams
1
2001
... 式中,P 表示激光功率;Γ 表示Gamma函数;r b xL 、yL 、zL 表示激光束坐标系{ L K 为空域形态因子,当K = 1时,激光束的空域形态为GP,当K > 1时,激光束的空域形态演变为SGP,当K 无限大时,则演变为全平顶形态[21 ,22 ] . ...
Analysis and modeling of a high-power Yb:fiber laser beam profile
1
2011
... 式中,P 表示激光功率;Γ 表示Gamma函数;r b xL 、yL 、zL 表示激光束坐标系{ L K 为空域形态因子,当K = 1时,激光束的空域形态为GP,当K > 1时,激光束的空域形态演变为SGP,当K 无限大时,则演变为全平顶形态[21 ,22 ] . ...
Development of powder distribution model of discontinuous coaxial powder stream in laser direct metal deposition
2
2018
... 每一个送粉头喷嘴的粉束流在横截面上的粉末质量浓度(Ci PS )服从Gaussian分布,其表达式为[23 ] : ...
... 通过对4个粉束流元的粉末质量浓度进行求和,得到同轴粉束流的质量浓度(C CPS )为[23 ,24 ] : ...
Simulation of laser attenuation and heat transport during direct metal deposition considering beam profile
3
2019
... 式中,m 为送粉质量流率;n 为同轴多路送粉头的喷嘴数量;Ri PS 是第i 个粉束流元截面的等效半径,定义为截面上某点的质量浓度降为中心质量浓度的1/e2 时的径向距离;v p 为粉末粒子速率,由实验测量得到;xi PS 、yi PS 、zi PS 表示粉束流元坐标系{i PS }的坐标,如图3 所示.图中φ 为粉束流元的喷射角,表示粉束流元轴线zi PS 与激光轴z L 的夹角;θ 为粉束流元发散角,定义为粉束流元的轮廓边界与轴线zi PS 的夹角.沉积坐标系{ O L i PS }不重合,因此利用齐次变换理论进行坐标变换[24 ] . ...
... 通过对4个粉束流元的粉末质量浓度进行求和,得到同轴粉束流的质量浓度(C CPS )为[23 ,24 ] : ...
... 依据集总参数法,利用能量守恒定律可以得到单个粉末的热输运模型为[24 ] : ...
Influence of spatial laser beam profiles on thermal-fluid transport during laser-based directed energy deposition
4
2021
... 激光能量衰减和粉末加热是激光束和粉束流相互作用过程中的2个关键热物理量.激光能量衰减归因于粉末的吸收和散射作用,粉末加热则因为激光的照射.根据Lambert-Beer定律,激光束通过任意体积元后的剩余强度(Ii , j , k [25 ] : ...
... 式中,F L / G n L / G κ 表示熔池气/液界面的曲率;σ T 和γ T 分别表示表示表面张力系数和热毛细系数,其计算公式参见本课题组前期工作结果[25 ] ;∇ s T
... 图14 绘制了600 ms时4种空域形态下的熔池速度场.在GP、SGP1、SGP2和FTP 4种空域形态作用下,光束中心附近区域的316L不锈钢熔池温度(图7 )均超过热毛细系数γ T [25 ] ,即热毛细系数从正数过渡到负数,所以在Marangoni剪切力(γ T ∇ s T ) 作用下,熔池具有由内向外的环形流动模式,而且熔池的峰值流速发生在靠近熔池边缘的附近. ...
... 图15 绘制了600 ms时刻4种激光束空域形态下沿轨迹线1 (图4 )的流速分布.可以看出,流速曲线呈现“M”双峰分布,与前期研究[25 ] 得到的结果类同,主要原因有2个:其一,由于Marangoni剪切应力的作用方向相反,“M”双峰分界处的流速近似为零;其二,在分界处,2个涡流的流速大小近似相等且方向相反,导致分界处的流体合成速度近似为零.比较图15 中的数据可以发现3个差异:其一,SGP1、SGP2和FTP下的左侧峰(熔池后端)较右侧峰(熔池前端)高,但是GP下的左侧峰(熔池后端)较右侧峰(熔池前端)低;其二,相较于GP,SGP1、SGP2和FTP下的左侧峰明显更高,但是右侧峰(熔池前端)却更低;其三,GP,SGP1、SGP2和FTP下的平均流速是逐渐减小的,分别为0.0200、0.0196、0.0173和0.0141 m/s.由此可见,通过改变激光束的空域形态可以对熔池的流动特征进行调控. ...
Surface-active element transport and its effect on liquid metal flow in laser-assisted additive manufacturing
2
2017
... 式中,η c 表示熔池的集粉效率,其值取0.9[26 ] ;H p 0 T p o o l H p 1
... Parameter values of the thermal transfer model
Table 1 Physical parameter Value Unit Ref. Solidus temperature T sol 1648 K Liquidus temperature T liq 1673 K Solid specific heat c sol 604 J·kg-1 ·K-1 Liquid specific heat c liq 824 J·kg-1 ·K-1 Solid thermal conductivity k sol 25 W·m-1 ·K-1 Liquid thermal conductivity k liq 36 W·m-1 ·K-1 Room temperature T ref 293.15 K Solid density ρ sol 8000 kg·m-3 Liquid density ρ liq 6893 kg·m-3 Emissivity ε 0.7 [26 ] Laser absorptivity η 0.38 Latent heat of fusion L 2.5 × 105 J·kg-1 [29 ] Convective heat transfer coefficient h con 80 W·m-2 ·K-1 [30 ] Thermal expansion coefficients α exp 5.85 × 10-5 K-1 [31 ] Dynamic viscosity μ 6 × 10-3 kg·m-1 ·s-1 [32 ] Permittivity of vacuum σ' 5.67 × 10-8 W·m-2 ·K-4
表2 模拟中的初始值 ...
Solute transport and composition profile during direct metal deposition with coaxial powder injection
1
2011
... 气/液界面动量方程的边界条件为[27 ] : ...
2D longitudinal modeling of heat transfer and fluid flow during multilayered direct laser metal deposition process
1
2012
... 在任意Lagrange-Euler法(ALE)动网格框架下,熔池气/液界面的法向移动速度V L / G [28 ] : ...
Modeling of transport phenomena during the coaxial laser direct deposition process
1
2010
... Parameter values of the thermal transfer model
Table 1 Physical parameter Value Unit Ref. Solidus temperature T sol 1648 K Liquidus temperature T liq 1673 K Solid specific heat c sol 604 J·kg-1 ·K-1 Liquid specific heat c liq 824 J·kg-1 ·K-1 Solid thermal conductivity k sol 25 W·m-1 ·K-1 Liquid thermal conductivity k liq 36 W·m-1 ·K-1 Room temperature T ref 293.15 K Solid density ρ sol 8000 kg·m-3 Liquid density ρ liq 6893 kg·m-3 Emissivity ε 0.7 [26 ] Laser absorptivity η 0.38 Latent heat of fusion L 2.5 × 105 J·kg-1 [29 ] Convective heat transfer coefficient h con 80 W·m-2 ·K-1 [30 ] Thermal expansion coefficients α exp 5.85 × 10-5 K-1 [31 ] Dynamic viscosity μ 6 × 10-3 kg·m-1 ·s-1 [32 ] Permittivity of vacuum σ' 5.67 × 10-8 W·m-2 ·K-4
表2 模拟中的初始值 ...
A three-dimensional numerical simulation model for weld characteristics analysis in fiber laser keyhole welding
1
2017
... Parameter values of the thermal transfer model
Table 1 Physical parameter Value Unit Ref. Solidus temperature T sol 1648 K Liquidus temperature T liq 1673 K Solid specific heat c sol 604 J·kg-1 ·K-1 Liquid specific heat c liq 824 J·kg-1 ·K-1 Solid thermal conductivity k sol 25 W·m-1 ·K-1 Liquid thermal conductivity k liq 36 W·m-1 ·K-1 Room temperature T ref 293.15 K Solid density ρ sol 8000 kg·m-3 Liquid density ρ liq 6893 kg·m-3 Emissivity ε 0.7 [26 ] Laser absorptivity η 0.38 Latent heat of fusion L 2.5 × 105 J·kg-1 [29 ] Convective heat transfer coefficient h con 80 W·m-2 ·K-1 [30 ] Thermal expansion coefficients α exp 5.85 × 10-5 K-1 [31 ] Dynamic viscosity μ 6 × 10-3 kg·m-1 ·s-1 [32 ] Permittivity of vacuum σ' 5.67 × 10-8 W·m-2 ·K-4
表2 模拟中的初始值 ...
Building blocks for a digital twin of additive manufacturing
1
2017
... Parameter values of the thermal transfer model
Table 1 Physical parameter Value Unit Ref. Solidus temperature T sol 1648 K Liquidus temperature T liq 1673 K Solid specific heat c sol 604 J·kg-1 ·K-1 Liquid specific heat c liq 824 J·kg-1 ·K-1 Solid thermal conductivity k sol 25 W·m-1 ·K-1 Liquid thermal conductivity k liq 36 W·m-1 ·K-1 Room temperature T ref 293.15 K Solid density ρ sol 8000 kg·m-3 Liquid density ρ liq 6893 kg·m-3 Emissivity ε 0.7 [26 ] Laser absorptivity η 0.38 Latent heat of fusion L 2.5 × 105 J·kg-1 [29 ] Convective heat transfer coefficient h con 80 W·m-2 ·K-1 [30 ] Thermal expansion coefficients α exp 5.85 × 10-5 K-1 [31 ] Dynamic viscosity μ 6 × 10-3 kg·m-1 ·s-1 [32 ] Permittivity of vacuum σ' 5.67 × 10-8 W·m-2 ·K-4
表2 模拟中的初始值 ...
Modeling of whole-phase heat transport in laser-based directed energy deposition with multichannel coaxial powder feeding
1
2022
... Parameter values of the thermal transfer model
Table 1 Physical parameter Value Unit Ref. Solidus temperature T sol 1648 K Liquidus temperature T liq 1673 K Solid specific heat c sol 604 J·kg-1 ·K-1 Liquid specific heat c liq 824 J·kg-1 ·K-1 Solid thermal conductivity k sol 25 W·m-1 ·K-1 Liquid thermal conductivity k liq 36 W·m-1 ·K-1 Room temperature T ref 293.15 K Solid density ρ sol 8000 kg·m-3 Liquid density ρ liq 6893 kg·m-3 Emissivity ε 0.7 [26 ] Laser absorptivity η 0.38 Latent heat of fusion L 2.5 × 105 J·kg-1 [29 ] Convective heat transfer coefficient h con 80 W·m-2 ·K-1 [30 ] Thermal expansion coefficients α exp 5.85 × 10-5 K-1 [31 ] Dynamic viscosity μ 6 × 10-3 kg·m-1 ·s-1 [32 ] Permittivity of vacuum σ' 5.67 × 10-8 W·m-2 ·K-4
表2 模拟中的初始值 ...
A comprehensive comparison of the analytical and numerical prediction of the thermal history and solidification microstructure of Inconel 718 products made by laser powder-bed fusion
2
2017
... 图7 显示了GP、SGP1、SGP2和FTP 4种激光束空域形态在相同工艺参数(激光扫描速率v = 600 mm/min,P = 700 W,m = 10.2 g/min,r b = 1.2 mm)下600 ms时刻的温度场,其中红线为固/液界线,白线为等温线.由Rosenthal热传导解析解[33 ] 可知,在激光扫描方向上,4种激光束空域形态下熔池前端的等温线被压缩,所以等温线分布密集;而熔池后端的等温线被拉伸,导致等温线分布稀疏.在GP、SGP1、SGP2和FTP作用下,熔池的峰值温度分别为2825、2681、2574和2470 K,表明熔池内的峰值温度随着K 的增大而减小.主要原因可能是,随着K 的增大,激光束的平顶面积逐渐增大,而光束中心的峰值功率密度逐渐减小,如图2 所示,使得光束中心处的材料吸收更少的激光能量. ...
... 图11 绘制了在GP、SGP1、SGP2和FTP 4种激光束空域形态下,α 和β 切面的熔池凝固界线上的考察位置(A 1 ~F 1 和A 2 ~F 2 )的温度梯度.本工作从2个方面解释从位置A 到位置F 的温度梯度的演变机制:其一,根据Rosenthal热传导解析解[33 ] 可知,在材料和激光加工参数相同的条件下,材料上任意位置的温度与其到熔池表面的光束中心的距离呈负指数关系,即,在远离熔池表面的光束中心区域,其温度变化越平稳,温度梯度越小,反之温度变化越剧烈,温度梯度越大;其二,热流沿等温线或凝固界线的法方向向外传输,这意味着如果凝固界线的法向越偏离激光扫描方向,则激光扫描速率对等温线的拉伸效应越弱,温度梯度越大.由图12 和13 可知,位置A 1 ~F 1 和位置A 2 ~F 2 到熔池表面的光束中心的距离逐渐减小,而其法向与激光扫描方向的夹角逐渐增大,所以图11 中位置A 1 ~F 1 和位置A 2 ~F 2 的温度梯度是逐渐增大的.在GP、SGP1、SGP2和FTP作用下,α 和β 2个切面中靠近熔池后部的相同位置A ~D 处的温度梯度依次增大,这是因为4种空域形态下相同位置A ~D 到光束中心的距离依次减小,而法向与激光扫描方向的夹角逐渐增大.由于位置F 位于凝固界线的最底部,其法向与激光扫描方向的夹角都是90°,所以该位置的温度梯度主要依赖于其到光束中心的距离.从图11 可以看出,GP、SGP1、SGP2和FTP作用下位置F 到光束中心的距离依次增大,因此温度梯度依次减小. ...
Mechanistic models for additive manufacturing of metallic components
1
2021
... 根据柱状晶到等轴晶的转变机理,高的温度梯度有利于柱状晶的形成[34 ] .因此,在GP、SGP1、SGP2和FTP 4种光束中,FTP光束最有利于在熔池的后部形成柱状晶,GP光束最有利于在熔池的底部形成柱状晶. ...
Additive manufacturing of metallic components—Process, structure and properties
2
2018
... Marangoni数(M a ) 定义为熔池表面的剪切应力与流体内部的黏滞力之比,用来研究Marangoni剪切应力对流体流动的影响程度,从而判断熔池流体流动的驱动机制[35 ] .当M a > 1 [35 ] .Marangoni数的表达式为: ...
... [35 ].Marangoni数的表达式为: ...