基于机器学习的中厚板变形抗力模型建模与应用

doi:10.11900/0412.1961.2021.00283

基于机器学习的中厚板变形抗力模型建模与应用

冀秀梅¹^,², 侯美伶², 王龙^,¹, 刘玠¹, 高克伟²

1 上海大学材料科学与工程学院上海 200444

2 江阴兴澄特种钢铁有限公司江阴 214400

Modeling and Application of Deformation Resistance Model for Medium and Heavy Plate Based on Machine Learning

JI Xiumei¹^,², HOU Meiling², WANG Long^,¹, LIU Jie¹, GAO Kewei²

1 School of Materials Science and Engineering, Shanghai University, Shanghai 200444, China

2 Jiangyin Xingcheng Special Steel Co. Ltd., Jiangyin 214400, China

通讯作者: 王龙，longwang@shu.edu.cn，主要从事基于新一代人工智能技术的流程型工业智能制造创新性应用研究

责任编辑: 肖素红

收稿日期: 2021-07-12 修回日期: 2021-11-09

Corresponding authors: WANG Long, senior engineer, Tel: 18616377700, E-mail:longwang@shu.edu.cn

Received: 2021-07-12 Revised: 2021-11-09

作者简介 About authors

冀秀梅，女，1986年生，硕士生

摘要

为提高变形抗力预测精度，以兴澄特钢中厚板轧机实际生产数据为基础，针对性提出2种利用机器学习对变形抗力进行预测的方法：一种是极限学习机(ELM)与传统数学模型结合的多钢种变形抗力模型及建模方法，另一种是基于TensorFlow深度学习框架的变形抗力模型及建模方法。方法一参考周纪华-管克智变形抗力模型，改进原变形抗力模型结构形式，计算出低合金钢、合金钢及高合金钢代表钢种的基准变形抗力；通过非线性回归计算出与钢种无关的变形参数影响系数，引进ELM神经网络算法，采用灰色关联分析及交叉验证优选神经网络参数，通过线性插值对预测结果进行平滑处理，减小ELM预测残差，最后与传统数学模型相结合得到变形抗力。方法二基于深度学习技术，结合机理，构建2种不同结构的深度神经网络，采用小批量(mini-batch)和均方根传播(RMSprop)优化算法寻优，结合批标准化(BN)和早停(early stopping)正则化策略提高模型泛化能力与稳定性，最后综合工艺特性，分别对粗轧机(RM)、精轧机(FM)建立变形抗力预测模型，提高模型精度。研究结果表明，利用深度学习预测变形抗力具有较高的预测精度，经离线分析，平均绝对百分误差(MAPE)由原模型的9.27%降至平均2.59%；在线应用后，轧制力预测精度相对误差10%以内比例由72.31%提高到平均90.24%，提高了现场生产的工艺水平。

关键词： 机器学习; 变形抗力预测; ELM神经网络; 深度学习; 基准变形抗力; 灰色关联分析

Abstract

Based on the actual production data of the plate mill of Xingcheng Special Steel, two machine learning methods for predicting deformation resistance are proposed to improve prediction accuracy. The first is a multi-steel deformation resistance model and modeling method that is combined with an extreme learning machine (ELM) and a traditional mathematical model, and the second is a deformation resistance model and modeling method that is based on the TensorFlow deep learning framework. Method one: The structural form of the original deformation resistance model was improved by referring to the Zhou Jihua-Guan Kezhi deformation resistance model, and the reference deformation resistances of representative steel grades of low alloy steel, alloy steel, and high alloy steel were calculated. The influence coefficient of deformation parameters independent of steel grade was calculated using nonlinear regression. The ELM neural network algorithm was presented, and neural network parameters were optimized using grey correlation analysis and cross-validation. To reduce the residual error of ELM prediction, the prediction results were smoothed using linear interpolation and then combined with the traditional mathematical model to obtain the deformation resistance. Method two: Based on deep learning technology, two types of deep neural networks with different structures were built and combined with the mechanism. To improve the generalizability and stability of the model, the mini-batch and RMSprop optimization algorithms were used in conjunction with batch normalization (BN) and early stopping regularization strategies. Finally, deformation resistance prediction models for roughing mill (RM) and finishing mill (FM) were developed respectively in conjunction with the process characteristics to improve model accuracy. The results showed that the deformation resistance prediction using deep learning has high prediction accuracy. Offline analysis indicated that the mean absolute percentage error decreased from 9.27% of the original model to an average of 2.59%. The online application demonstrated that the ratio of rolling force prediction accuracy within 10% relative error increased from 72.31% to an average of 90.24%, raising the technological level of onsite production.

Keywords： machine learning; prediction of deformation resistance; ELM neural network; deep learning; reference deformation resistance; grey relational analysis

PDF (2306KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

冀秀梅, 侯美伶, 王龙, 刘玠, 高克伟. 基于机器学习的中厚板变形抗力模型建模与应用[J]. 金属学报, 2023, 59(3): 435-446 DOI:10.11900/0412.1961.2021.00283

JI Xiumei, HOU Meiling, WANG Long, LIU Jie, GAO Kewei. Modeling and Application of Deformation Resistance Model for Medium and Heavy Plate Based on Machine Learning[J]. Acta Metallurgica Sinica, 2023, 59(3): 435-446 DOI:10.11900/0412.1961.2021.00283

过程控制模型是中厚板轧制过程中的关键技术，精确预测轧制压力是过程控制模型的重要目标之一，既关系到最终产品的质量，也关系到生产设备的安全运行。变形抗力是轧制压力计算的核心，提高各种金属材料、各种工艺条件下的变形抗力预测精度对科学地制定轧制规程、提高生产效率非常必要^[1,2]。目前，国内很多钢铁生产企业的轧制过程控制模型从国外引进，因此有必要在理解引进模型的基础上，逐步掌握核心技术，研发适合自身生产工艺要求的过程控制新模型。

李英等^[3]提出，计算变形抗力主要有2种方法：一是传统数学公式建模，大量研究^[4~8]基于不同的结构式，通过对实验数据拟合获得回归系数，其中周纪华-管克智公式^[4]应用较多，它改进了应变速率指数与变形温度的关系，用非线性函数修正了应变的影响，但由于实验条件与实际生产存在一定差异，在实际轧制应用时基于实验数据得到的模型需进行优化和调整，故部分研究^[9~11]采用现场轧制过程的实测数据，通过轧制压力计算公式进行逆运算，得到材料的实测变形抗力近似值，再利用回归分析建立不同钢种的变形抗力模型。另一种是利用人工神经网络建模，宿彦京等^[12]提出应用机器学习、人工智能等技术，实现数据分析、模型建立，探索新材料、新性能。目前，大多研究者针对特定钢种的实验数据开展研究。王涛等^[13]利用反向传播(BP)神经元网络技术对GH4720Li合金热变形过程中的流变力学行为进行预测。李淼泉等^[14]利用热模拟压缩实验数据，基于模糊神经网络，把变形温度、应变速率和应变作为输入变量，进行GH4169镍基高温合金高温变形时的流变应力模型预测。Phaniraj和Lahiri^[15]利用人工神经网络方法进行建模，网络输入变量为：C当量、变形温度、应变、应变速率。

上述模型算法都有各自的特点，大大提高了预测精度，但实际应用中也存在一定的局限性。传统回归公式建模大多只适用特定的钢种，有的公式虽从形式上考虑了部分化学元素对变形抗力的影响，但通常是针对某钢种成分的标准值进行计算，不能充分反映同一钢种化学成分波动时变形抗力的变化。周纪华等^[16]基于9个钢号的碳钢，通过回归得到C、Si、Mn、Cu元素含量对流动应力的影响。赵嫚嫚等^[17]研究了Al、Ni加入量对1Cr9Al(1~3)Ni(1~7)WVNbB (质量分数，%)钢热变形行为、峰值应力及热变形激活能的影响。神经网络建模大都基于实验数据，在理论研究方面取得许多成果，部分已应用于在线生产。为充分利用现场二级数据中所蕴含的信息，建立基于实际生产过程实测数据的变形抗力模型，更为符合轧线实际轧制情况。不仅精度更高，且对现场生产有更直接的参考价值和指导意义^[5]。

本工作针对兴澄特钢中厚板品种多、合金化程度高的产品特点及极限规格、特殊钢种及换钢种规格后第一块板控制精度低的难点，改进了由国外某公司提供的依靠经验数据回归建模的传统变形抗力模型(以下简称“原模型”)。以现场实际生产数据为基础，引入2种神经网络算法，一种是单隐层神经网络极限学习机(ELM)与传统回归模型结合，得到一个精度较高的多钢种变形抗力模型，不仅考虑变形温度、应变速率和应变等主要因素，还充分考虑化学成分波动的影响；另一种是基于TensorFlow机器学习框架的深度学习模型，采用早停(early stopping)正则化策略提高模型泛化能力，采用小批量(mini-batch)和均方根传播(RMSprop)结合的优化算法避免模型训练过程陷入局部最小点，最后根据工艺特性，分别对粗轧机(RM)、精轧机(FM)变形抗力建模进行预测，进一步提高模型精度。最终在保持现有轧制力模型不变的前提下，将原有变形抗力模型替换为基于TensorFlow的RM、FM单独建模的深度学习神经网络预测模型。

1 模型理论

1.1 轧制力与变形抗力数学模型

轧制力模型采用Sims公式，模型基本形式为^[18]：

P = K B \sqrt[]{R' Δ h} Q_{p}

(1)

式中，P为轧制力，kN；K为金属变形抗力，取决于金属材料化学成分及变形条件，K = 1.15σ，MPa (σ为金属单应力状态下的变形抗力，MPa)；B为轧件宽度，mm；R'为工作辊压扁半径，mm；Δh为道次压下量，mm；Q_p为应力状态影响系数。

变形抗力数学模型采用的是同钢种使用相同变形抗力参数曲线，没有考虑化学成分波动对变形抗力的影响，基本形式为^[18]：

σ = σ_{0} k_{t} k_{ε} k_{\dot{ε}}

(2)

式中，σ₀指在变形温度t = 1200℃、应变ε = 0.1、应变速率 $\dot{ε}$ = 10 s^-1时的基准变形抗力；k_t = A₁exp(a₁(t - t_REF))、k_ε = A₂ε $^{a_{2}}$ 和 $k_{\dot{ε}}$ = $A_{3} {\dot{ε}}^{a_{3}}$ 分别为变形温度、应变和应变速率对变形抗力的影响系数，t_REF为基准变形温度1200℃，A₁~A₃和a₁~a₃为与钢种相关的回归系数。

实测变形抗力(K_act)通过实测轧制力反算近似得到，计算公式为^[9]：

K_{a c t} = \frac{P}{B \sqrt[]{R' Δ h} Q_{p}}

(3)

1.2 改进现有变形抗力模型回归公式

实际生产过程中，因特定钢种在特定温度下对应的应变、应变速率数据非连续，故从在线生产数据库中随机选取化学成分差异较大的3个钢种X70 (简称A)、12Cr2Mo1R (简称B)和1.2311 (简称C) (见表1)对应的热模拟实验数据^[18]制图，如图1所示。变形温度升高，所有钢种变形抗力都不同程度下降；应变速率对变形抗力的影响，不仅与钢种有关，且与变形温度有关；应变与变形抗力并非简单的幂函数关系，随着变形温度、应变速率的变化出现上升或者下降趋势。

表1 试样化学成分 (mass fraction / %)

Table 1 Chemical composition of samples

Steel	C	Si	Mn	P	S	Cu	Ni	Cr
A	0.03-0.06	0.2-0.3	1.5-1.6	≤ 0.012	≤ 0.002	≤ 0.15	0.12-0.16	0.1-0.2
B	0.14-0.15	≤ 0.1	0.5-0.6	≤ 0.006	≤ 0.002	≤ 0.15	0.14-0.18	2.3-2.5
C	0.38-0.42	0.2-0.4	1.4-1.6	≤ 0.015	≤ 0.005	≤ 0.25	≤ 0.3	1.8-2.0
Steel	V	Al	Ti	Mo	N	Nb	B	Fe
A	≤ 0.01	0.025-0.045	0.01-0.02	0.12-0.15	≤ 0.005	0.042-0.05	≤ 0.0005	Bal.
B	≤ 0.03	0.02-0.045	0.01-0.02	0.95-1.1	≤ 0.0002	0.015-0.2	≤ 0.001	Bal.
C	0	0.02-0.04	0	0.18-0.25	0	0	0	Bal.

新窗口打开| 下载CSV

图1

新窗口打开| 下载原图ZIP| 生成PPT

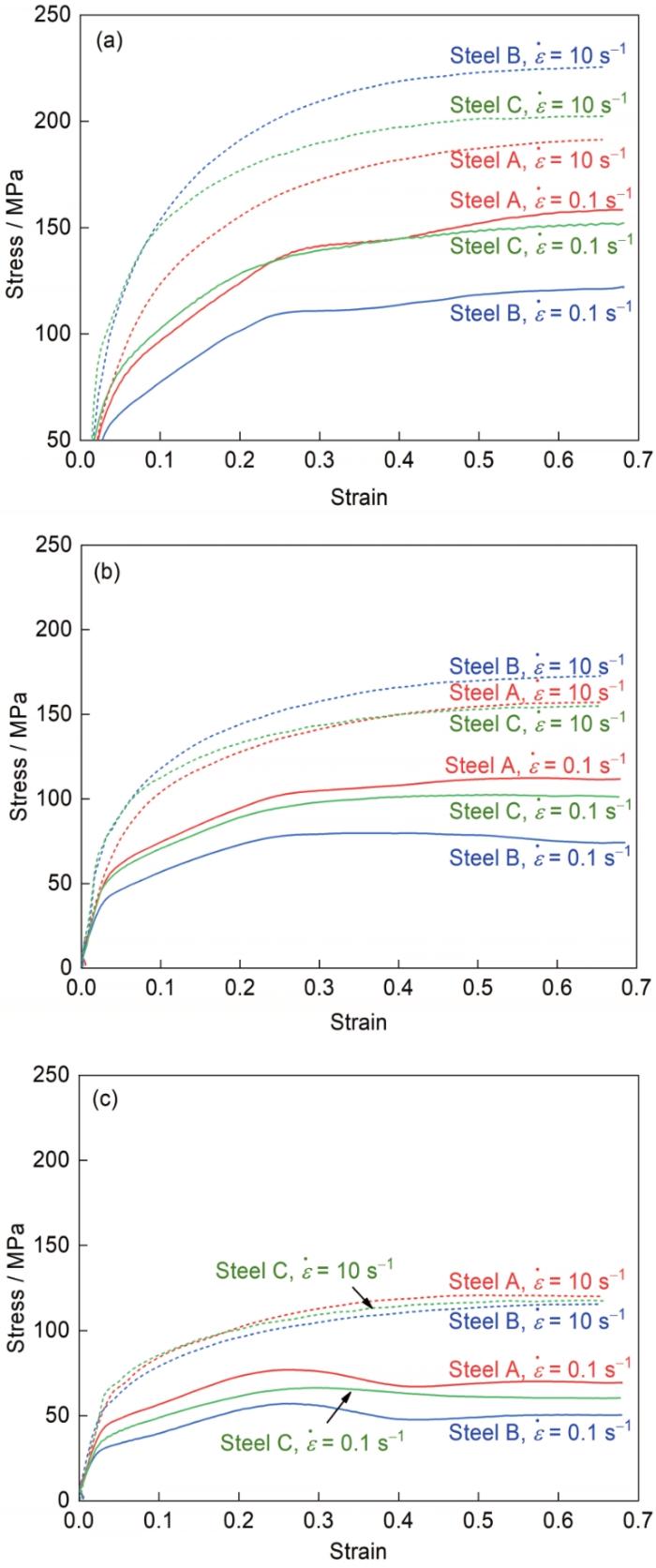
图1 试样在不同变形温度(t)和不同应变速率( $\dot{ε}$ )下的应力-应变曲线

Fig.1 Stress-strain curves of samples under deformation temperatures of t = 900^oC (a), t = 1000^oC (b), and t = 1100^oC (c) and strain rates of $\dot{ε}$ = 0.1 s^-1 and $\dot{ε}$ = 10 s^-1

需要说明的是，式(2)中应变、应变速率与变形抗力只是简单的幂函数关系，且应变速率没有考虑变形温度的影响。为进一步验证式(2)的适用性，收集钢种A、B和C现场生产数据，基于原变形抗力参数库，由式(2)和(3)分别得到计算变形抗力、反算的实测变形抗力，绘制其与变形温度、应变速率、应变关系图，如图2所示。计算变形抗力随变形温度的升高而升高，与轧制工艺规律不符；应变速率和应变对计算变形抗力的影响规律也与实际不符。因此，无论从实验研究还是现场实测数据分析，现有变形抗力模型公式都无法较好地反映各因素影响，故需进行改进。

图2

新窗口打开| 下载原图ZIP| 生成PPT

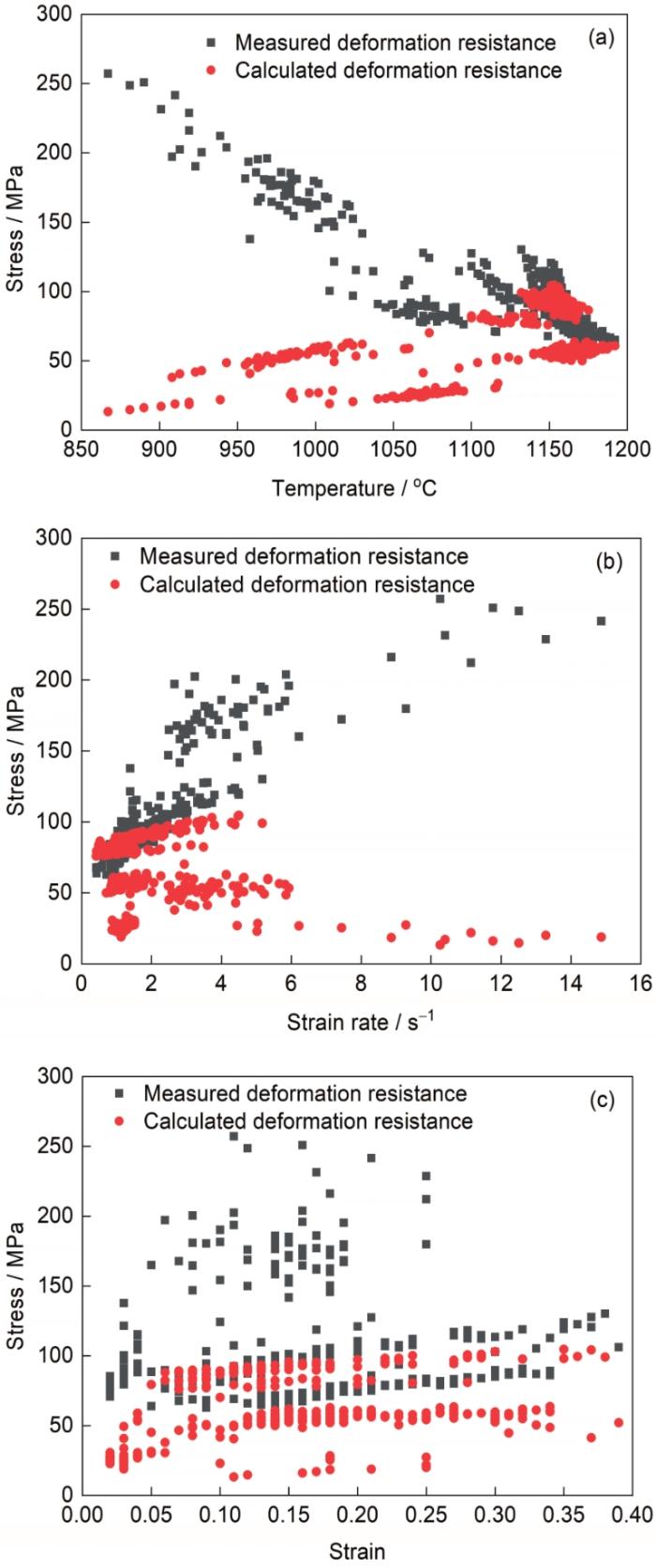
图2 变形抗力与变形温度、应变速率和应变的关系

Fig.2 Relationship between deformation resistance and deformation temperature (a), strain rate (b), and strain (c)

参考常用的周纪华-管克智公式^[4]结构，其用非线性函数表示变形条件之间对变形抗力的交互影响，形式如下：

σ = σ_{0}^{'} e x p (a_{1} T + a_{2}) {(\frac{\dot{ε}}{10})}^{(a_{3} T + a_{4})} \cdot

[a_{6} {(\frac{ε}{0.4})}^{a_{5}} - (a_{6} - 1) \frac{ε}{0.4}]

(4)

式中， $T = \frac{t + 273}{1000}$ ，K； $σ_{0}^{'}$ 为基准变形抗力，即t = 1000℃、ε = 0.4和 $\dot{ε}$ = 10 s^-1时的变形抗力；a₁~a₆为与钢种有关的回归系数。

基准变形抗力的选取并不唯一，周纪华-管克智模型是实验研究测定102个钢和合金的高温高速下的塑形变形抗力，变形条件为： $t$ 为850~1150℃， $\dot{ε}$ 为5~80 s^-1，ε为0.05~0.69，其取t = 1000℃、ε = 0.4和 $\dot{ε}$ = 10 s^-1为基准变形条件。通过实际生产数据分析，满足基准条件ε = 0.4和 $\dot{ε}$ = 10 s^-1的样本数仅分别占总样本的0.42%和9.7%，故本工作根据现场实际生产条件，分别选取 $t$ 为751~1195℃、 $\dot{ε}$ 为0.03~28.55 s^-1、 $ε$ 为0.01~0.47的近似平均值，即t = 1000℃、ε = 0.24和 $\dot{ε}$ = 5 s^-1作为基准变形条件，并采用如下变形抗力模型公式：

σ = σ_{0}^{″} K_{t}^{} K_{ε}^{} K_{\dot{ε}}^{}

(5)

式中， $σ_{0}^{″}$ 为t = 1000℃、ε = 0.24和 $\dot{ε}$ = 5 s^-1时的基准变形抗力； $K_{t}^{}$ = $e x p (b_{1} (t - 1000))$ 、 $K_{ε}^{}$ = $b_{5} {(\frac{ε}{0.24})}^{b_{4}} - (b_{5} - 1) \frac{ε}{0.24}$ 和 $K_{\dot{ε}}^{}$ = ${(\frac{\dot{ε}}{5})}^{b_{2} t + b_{3}}$ 分别表示温度、应变和应变速率对变形抗力的影响系数，b₁~b₅为回归系数。

选取钢种A、B和C现场生产数据各300条，分别用式(2)和(5)进行回归，另取同钢种不同时间段的生产数据各50条分别进行回归模型验证，模型预测能力用均方根误差(RMSE)和相关系数(r)进行评价：

R M S E = \sqrt[]{\frac{1}{N} \sum_{i = 1}^{N} (P_{i} - M_{i})^{2}}

(6)

式中，M_i 表示实测值，P_i 表示计算值，N表示样本数。RMSE越小，回归模型预测精度越高。r绝对值越接近1，回归模型预测精度越高。可知，式(2)和(5)计算出的变形抗力的RMSE平均值分别为23.15和12.32 MPa，r平均值分别为0.967和0.981，故改进的式(5)可以较好地预测相应的单个钢种的变形抗力。

1.3 ELM神经网络

ELM是一种单隐含层前馈神经网络，其特点是网络输入层与隐含层间的连接权值和隐含层神经元的阈值可随机生成，且整个训练过程无需调整。研究表明，与传统的BP、径向基函数(RBF)等基于梯度思想的神经网络算法相比，ELM具有待定参数少、学习速度快^[19]、预测精度高及泛化性能好等优点^[20~22]，具体算法如下。

给定任意N个不同样本(x_i, y_i )，其中x_i ∈Rⁿ 、y_i ∈R^m 分别为n维和m维实数向量空间，则具有L个隐层节点个数(L ≤ N)和激活函数g(x)的模型可表示为：

y_{j} = \sum_{i = 1}^{L} g (a_{i} x_{j} + b_{i}) \cdot β_{i} (j = 1, 2, \dots, n)

(7)

式中，y_j 为样本输出，a_i 为输入层到第i个隐含层的输入权值，x_j 为样本输入，b_i 为第i个隐层节点阈值，β_i 为第i个隐层神经元与输出层权值，g(a_ix_j + b_i )为第i个隐层神经元的输出。

由以上可知，ELM算法步骤为：给定训练样本(x_i, y_i )；确定隐层神经元个数L，随机生成输入权重a和隐层阈值b；选择激活函数，计算隐层输出矩阵；通过求广义逆得到输出权重β。

1.4 基于TensorFlow的深度学习网络

深度学习为解决复杂非线性问题提供了新的途径^[23]，TensorFlow是端到端的开源机器学习平台。Keras是用于构建和训练深度学习模型的TensorFlow高阶应用程序接口(API)，具有易使用、兼容性大和灵活性高的特点，可实现快速原型设计。

深度学习通过一系列的数据变换层来实现输入数据到目标结果的映射。在深度学习中，每层的变换由一组权重来实现，利用损失函数衡量网络输出结果的质量，再将损失值作为反馈信号进行权重调节。深度学习的工作原理：首先对神经网络的权重随机赋值，然后根据预测值和真实目标值的差(损失值)，利用反向传播算法微调神经网络每层的参数，从而降低损失值；根据调整的参数继续计算损失值；不断重复，直到整个网络的损失值达到最小，即算法收敛。

2 基于实测数据的神经网络变形抗力预测模型建模

2.1 样本数据获取

收集现场一段时间内连续生产的175个钢种的176835条生产数据，首先对检测异常数据进行清洗^[24]，得到99422条训练样本数据，另取训练样本以外的58944条测试样本数据。为降低变量差异对模型的影响，建模前对数据进行z-score标准化处理^[25]：

x^{*} = \frac{x - \bar{x}}{s}

(8)

式中，x^*为标准化后的样本数据， $\bar{x}$ 和s分别为样本数据的均值和标准差。

2.2 神经网络输入变量分析

结合生产工艺，采用灰色关联分析方法^[26]，将变形抗力与其影响因素进行灰色关联分析，分析结果如表2所示，选择关联度大于0.85的参数作为模型自变量，包括ε、t、 $\dot{ε}$ 及Al、C、Cu、Mn、P、Si、B、S、Nb、Ti、Ni、V、Mo、Cr等化学成分，N、Sn、W等化学成分灰色关联度较低，即对变形抗力影响较小，这与实际工艺过程基本吻合。

表2 变形抗力影响因素的灰色关联度

Table 2 Grey correlation degrees of influencing factors of deformation resistance

Process parameter/composition	Relational degree	Process parameter/composition	Relational degree
Al	0.9437	Ti	0.9033
C	0.9435	Ni	0.9017
Cu	0.9428	V	0.8589
Mn	0.9345	Mo	0.8544
P	0.9328	Cr	0.8517
Si	0.9324	N	0.8171
$ε$	0.9309	Sn	0.7974
t	0.9291	W	0.7832
$\dot{ε}$	0.9288	As	0.6871
B	0.9133	Bi	0.6453
S	0.9084	Sn	0.6098
Nb	0.9059	Ca	0.5074

Note:ε—strain

新窗口打开| 下载CSV

2.3 神经网络变形抗力模型建模

用相同的训练样本和测试样本，进行如下4个变形抗力建模实验。

2.3.1 基于ELM的变形抗力模型建模(方案1)

选用3层神经网络(即1个输入层、1个隐含层和1个输出层)进行建模，其中输入层共17个输入变量：化学元素Al、B、C、Si、Mn、Cu、Cr、Ni、Mo、Nb、Ti、V、P、S含量；t、ε、 $\dot{ε}$ 。隐含层单元数为180；输出变量为σ。激活函数采用Sigmoid函数，表达式为^[13]：

f (x) = \frac{1}{1 + e x p (- x)}

(9)

2.3.2 ELM与传统回归数学模型相结合(方案2)

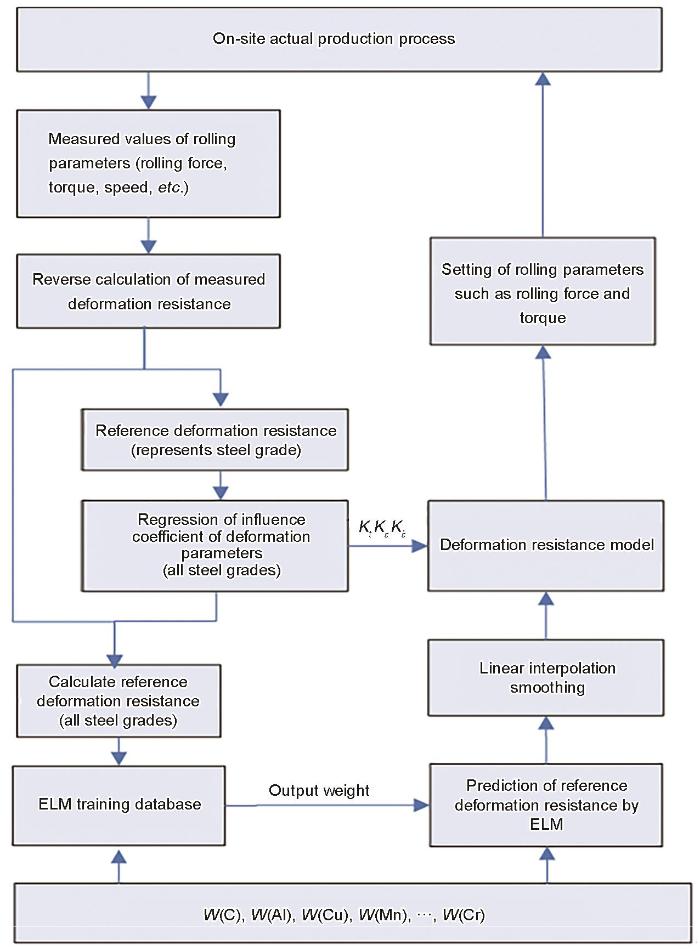
收集现场生产的175个钢种，包括：低合金钢(DH36、X70等149个钢种)、合金钢(12Cr2Mo1R、NM500等18个钢种)、高合金钢(1.2311、06Ni9DR等8个钢种)，参照王健等^[9]的方法，得到每个钢种的基准变形抗力，结合每个钢种反算的K_act，根据式(5)，将175个钢种回归式联立可求出一组变形参数b₁~b₅，即可得 $K_{t}^{} K_{ε}^{} K_{\dot{ε}}^{}$ 。

为建立多钢种变形抗力预测模型，引入ELM神经网络预测基准变形抗力，将其与数学模型回归的变形参数影响系数相乘。对现场任一钢种，根据K_act及 $K_{t}^{} K_{ε}^{} K_{\dot{ε}}^{}$ ，则可得出只与化学成分相关的基准变形抗力σ_0,chem = K_act / ( $K_{t}^{} K_{ε}^{} K_{\dot{ε}}^{}$ )，计算框图如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 极限学习机(ELM)神经网络与数学模型结合计算框图

Fig.3 Calculation diagram of extreme learning machine (ELM) neural network and mathematical model (W(C), W(Al), $\dots$ , W(Cr)—mass fractions of C, Al, …, and Cr, respectively; $K_{t}^{} K_{ε}^{} K_{\dot{ε}}^{}$ —product of the influence coefficients of temperature, strain, and strain rate on deformation resistance)

选用3层神经网络进行建模：将灰度分析的14个化学成分(Al、B、C、Si、Mn、Cu、Cr、Ni、Mo、Nb、Ti、V、P、S)作为神经网络输入变量；采用10折10次交叉验证^[18]确定网络隐含层节点数为180；σ_{0, chem}作为神经网络输出变量，训练后得到输出权重。网络结构图如图4所示，激活函数采用Sigmoid函数。

图4

新窗口打开| 下载原图ZIP| 生成PPT

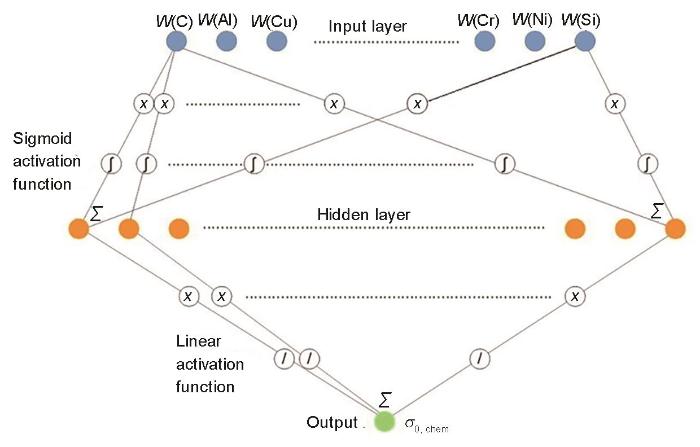
图4 基准变形抗力模型网络结构图

Fig.4 Network structure of reference deformation resistance model (σ_{0, chem}—reference deformation resistance relative to chemical composition)

实际轧制过程中，根据坯料化学成分及网络训练得到的输出权重，即可得到基准变形抗力，再与 $K_{t}^{} K_{ε}^{} K_{\dot{ε}}^{}$ 相乘，可得变形抗力。

2.3.3 基于TensorFlow的深度神经网络变形抗力模型建模

首先，选择深度神经网络的结构参数，包括：网络输入变量、网络层数、神经元数，其中输入变量为根据灰色关联分析得出的17个变量，隐含层数设置为1~5层，神经元数设置为30~300个，以10个为步长，分别进行实验，按照训练时间与精确度相对最优的条件，确定神经网络隐含层数与隐含层单元数。

其次，进行激活函数选择及超参数设置，传统神经网络多用Sigmoid与Tanh函数作为激活函数，但容易产生梯度消失或梯度爆炸问题，目前深度神经网络中多使用Relu函数，其特点是可以更好地使网络稀疏，提高学习精度，降低过拟合，表达式为：f(x) = max(0, x)。

选取深度神经网络常用的优化算法Adam算法^[27]。与传统的随机梯度下降不同，Adam算法结合了Momentum和RMSprop梯度下降法，通过计算梯度的一阶矩估计和二阶矩估计，为不同的参数设计独立的自适应性学习率，适用于多种结构的神经网络。

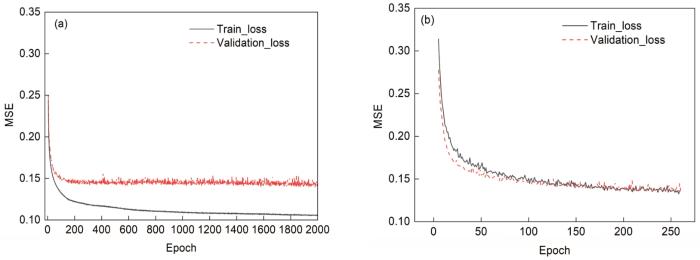
由于深度神经网络中模型参数较多，为防止模型过拟合，选取常用的早停法和批标准化(BN)策略。早停法主要思想是：在训练中计算模型在验证集上的表现，当模型在验证集上的表现开始下降的时候，停止训练，这样就能避免继续训练导致过拟合。BN主要思想是：通过规范化，把每层神经网络任意神经元输入值的分布拉到均值为0、方差为1的标准正态分布，让梯度变大，避免梯度消失问题产生，加快学习收敛速度。将无正则化和使用早停法、BN策略进行训练对比，损失函数变化曲线如图5所示。以均方误差(MSE)作为损失函数，从图5可以看出，无正则化时，模型训练速度慢，且测试集损失与训练集损失差距大，存在过拟合问题。使用BN和早停法后，网络收敛快，测试集损失更接近训练集损失，模型预测精度较高，且在模型训练过程中截取保存了结果最优的参数，防止过拟合。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同策略下损失函数变化曲线

(a) no regularization (b) early stopping and batch normalization

Fig.5 Change curves of loss function under different strategies (MSE—mean square error)

(1) RM、FM合并建模(方案3)

将RM、FM数据不加区分地全部用于训练同一个深度神经网络模型^[27] (记为Deep_All)，经测试，选择5层网络进行建模，其中输入层共17个输入变量：化学元素Al、B、C、Si、Mn、Cu、Cr、Ni、Mo、Nb、Ti、V、P、S含量；t、ε、 $\dot{ε}$ 。隐含层为3层，隐含层单元数分别为150、150和150；输出变量为σ；激活函数选用Relu函数。

(2) RM、FM分开建模(方案4)

基于现场双机架轧制的工艺特点，分析RM和FM变形抗力及其影响因素的平均值、标准差、最小值及最大值，如表3所示。RM、FM数据分布相差较大，因此将RM、FM数据分开训练，建立不同的深度神经网络模型(分别记为Deep_RM和Deep_FM)，经测试，均选用5层网络进行建模，输入层均为17个输入变量：化学元素Al、B、C、Si、Mn、Cu、Cr、Ni、Mo、Nb、Ti、V、P、S含量；t、ε、 $\dot{ε}$ 。隐含层都为3层，RM、FM隐含层单元数分别为180、180、180和200、200、200；输出变量为σ；激活函数选用Relu函数。

表3 变形抗力及其影响因素数据分布

Table 3 Data distributions of deformation resistance and its influencing factors

Index	Strain		Strain rate / s^-1		Temperature / ^oC		Deformation resistance / MPa
Index	RM	FM	RM	FM	RM	FM	RM	FM
Mean	0.16	0.14	1.97	5.99	1130.00	895	90.57	217.35
std	0.08	0.07	1.44	5.22	25.70	76	19.13	56.88
Min.	0.01	0.01	0.25	0.30	950.00	726	44.00	45.00
Max.	0.46	0.46	8.19	29.76	1187.00	1166	181.00	486.00

Note: std—standard deviation, RM—roughing mill, FM—finishing mill

新窗口打开| 下载CSV

2.4 模型评估

模型预测能力用RMSE、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)及相对误差(E_r)小于5%的样本占总样本的百分数进行评价，其表达式分别为^[25]：

M A E = \frac{1}{N} \sum_{i = 1}^{N} |P_{i} - M_{i}|

(10)

M A P E = \frac{1}{N} \sum_{i = 1}^{N} |\frac{P_{i} - M_{i}}{M_{i}}| \times 100 %

(11)

E_{r} = \frac{P_{i} - M_{i}}{M_{i}} \times 100 %

(12)

3 实验结果

3.1 离线训练与结果分析

4组建模方案的预测精度如表4和图6所示。表4从RMSE、MAE、MAPE等多角度反映了各模型预测精度。从图6散点图可以明显看出不同实验方案对应的模型预测值和真实值的散列程度。图7和8分别示出2种深度神经网络模型Deep_RM与Deep_All及Deep_FM与Deep_All的预测值与真实值的偏差绝对值分布。

表4 原模型及4组方案预测精度

Table 4 Prediction accuracies of the original model and four groups of schemes

Item	RMSE / MPa	MAE / MPa	MAPE / %	δ / %
Original model	21.35	13.84	9.27	42.05
Scheme 1	16.44	10.93	6.56	49.10
Scheme 2	10.29	7.11	4.35	68.25
Scheme 3	7.39	5.25	3.36	76.89
Scheme 4 (RM)	3.12	2.41	2.72	86.38
Scheme 4 (FM)	6.97	5.21	2.45	88.05

Note: RMSE—root mean square error; MAE—mean absolute error; MAPE—mean absolute percentage error; δ—the percentage of samples with a relative error (E_r) less than 5% of the total samples; Scheme 1—ELM model; Scheme 2—integrated neural network model based on ELM and mathematical model; Scheme 3—deep neural network model; Scheme 4 (RM)—deep neural network model based on RM; Scheme 4 (FM)—deep neural network model based on FM

新窗口打开| 下载CSV

图6

新窗口打开| 下载原图ZIP| 生成PPT

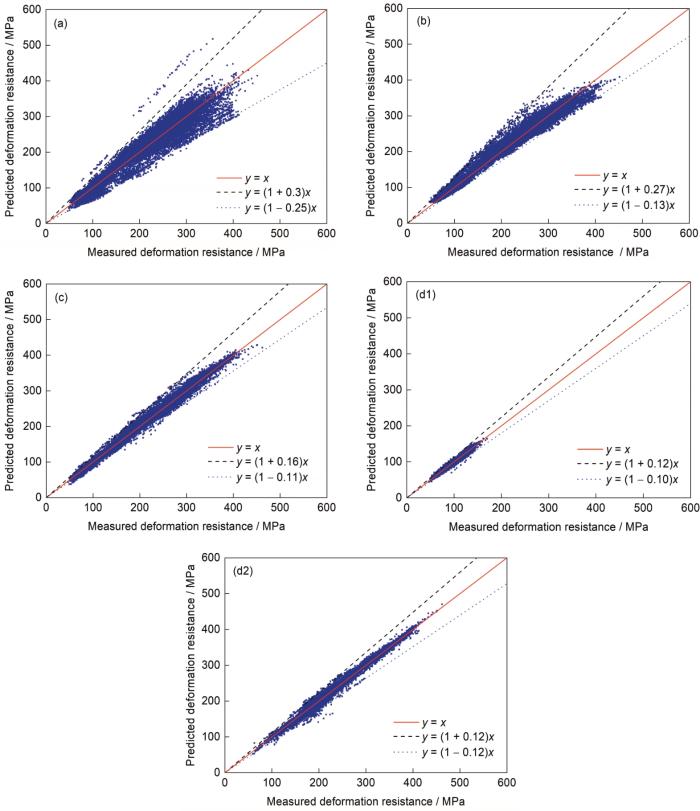
图6 变形抗力预测值和实测值比较

Fig.6 Comparisons of the measured value and the predicted value of deformation resistance for scheme 1 (a), scheme 2 (b), scheme 3 (c), scheme 4 (RM) (d1), and scheme 4 (FM) (d2)

图7

新窗口打开| 下载原图ZIP| 生成PPT

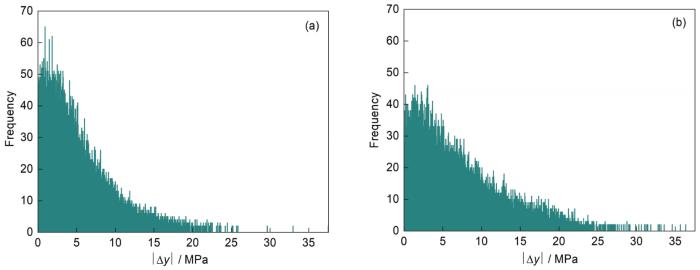
图7 Deep_RM和Deep_All预测值分别与RM真实值的偏差绝对值分布对比

Fig.7 Comparisons of the distribution of the absolute value of the deviation between the true value of RM deformation resistance and the predicted value obtained by Deep_RM (a) and Deep_All (b) ( $|Δ y|$ —absolute value of the deviation between the true value and predicted value)

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 Deep_FM和Deep_All预测值分别与FM真实值的偏差绝对值分布对比

Fig.8 Comparisons of the distribution of the absolute value of the deviation between the true value of FM deformation resistance and the predicted value obtained by Deep_FM (a) and Deep_All (b)

由表4可知，在相同样本条件下，4个方案预测精度均比原模型预测精度高，其中方案1单独使用ELM神经网络预测精度最低；方案2基于ELM神经网络，利用化学成分计算基准变形抗力，再与传统模型相结合，比方案1单一神经网络模型精度高；方案3 Deep_All比方案1、方案2单隐含层神经网络模型精度高；方案4 Deep_RM、Deep_FM比方案3的Deep_All更进一步提高了预测精度。由图6可知，方案4模型预测值和实际值散列程度最小，说明方案4的预测精度最高，与表4的分析结果相一致。如图7所示，Deep_RM预测的RM变形抗力与RM真实变形抗力的绝对偏差分布更集中，偏差绝对值都在15 MPa以内，而Deep_ALL相对应的偏差绝对值都在20 MPa以，说明Deep_RM预测精度更高。同理，如图8所示，Deep_FM预测的FM变形抗力与FM真实变形抗力的绝对偏差分布更集中，偏差绝对值都在30 MPa以内，而Deep_ALL相对应的偏差绝对值都在35 MPa以内，说明Deep_FM预测精度更高。

通过计算，以MAPE为例，方案1~3分别为6.56%、4.35%和3.36%，方案4平均为2.59% (RM单独建模为2.72%，FM单独建模为2.45%)，与原模型的9.27%相比，分别降低了2.71%、4.92%、5.91%和6.68%；以相对误差小于5%的样本占总样本的百分比为例，方案4平均为87.22% (RM单独建模为86.38%，FM单独建模为 88.05%)，比方案3、方案2、方案1和原模型分别高10.33%、18.97%、38.12%和45.17%。图7a和b标准差分别为1.97和2.72 MPa，图8a和b标准差分别为4.63和6.05 MPa，也进一步说明方案4精度最高。

3.2 在线应用效果

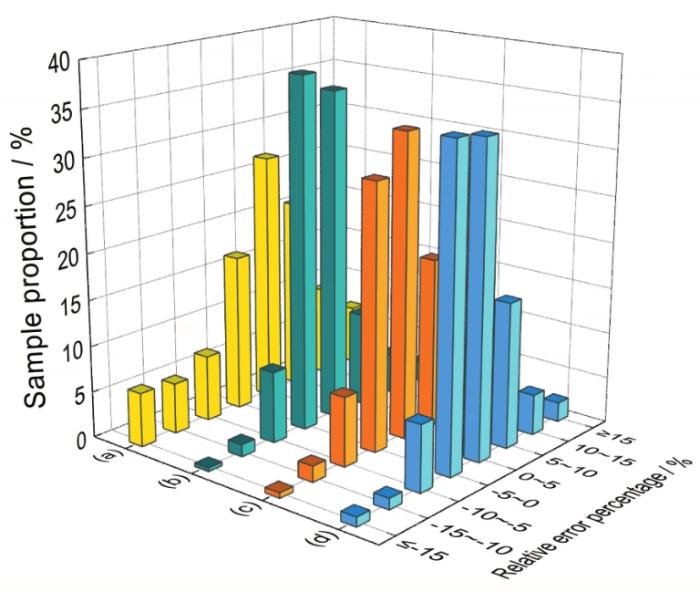
为了证明新模型的泛化能力，连续跟踪现场3个月共153个钢种的实际生产情况进行验证，轧制力预测相对误差分布如图9所示。图9展示了模型改造前、后的轧制力预测误差数据，证明了新模型不仅能有效提高模型预测精度，而且有较强的泛化能力，对不同生产月份的数据都有较好的预测效果。轧制力预测精度由改造前的72.31%提高到改造后平均90.24% (|E_r| < 10%占比)，提高了17.93%；而|E_r| ≥ 15%占比，由改造前的12.35%降至改造后平均3.06%，降低了9.29%，满足实际生产的要求。掌握核心技术，自主研发过程控制模型是钢铁生产企业不断优化生产工艺、持续提升产品质量、研发高附加值钢材品种的技术保障，对企业降低生产成本、提高经济效益具有重要意义。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 模型改造前、后轧制力预测相对误差分布

Fig.9 Relative error distributions of rolling force prediction

(a) before model modification

(b) the first month after model modification

(d) the third month after model modification

4 结论

(1) 提出了基于ELM单隐层神经网络和TensorFlow深度神经网络2种机器学习变形抗力预测方法。选取最优变形抗力模型结构及参数，提高模型预测精度：根据灰色关联分析，结合生产实际，全面考虑对变形抗力影响较大的神经网络输入变量；基于10折10次交叉验证，选取合适的隐层节点数。采用mini-batch和RMSprop优化算法寻优，结合BN和早停正则化策略提高模型泛化能力与稳定性，综合轧制工艺特性，分别进行RM、FM深度神经网络变形抗力模型建模，进一步提高模型预测精度，MAPE由原模型的9.27%降至平均2.59%。

(2) 基于现场生产数据建立的新变形抗力模型，可从根本上提高轧制力初始预算精度，改变传统的过分依赖自适应方法，提高控制精度，对实际生产及在线控制具有更为准确的指导意义。在线生产表明，不改变现有轧制力计算模型，采用RM、FM分别建模的深度神经网络模型计算变形抗力，轧制力预测精度平均达90.24% (相对误差10%以内比例)，比改造前提高17.93%，满足现场在线控制精度要求。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Zhang

D H

, Peng

, Sun

, et al.

Key intelligent technologies of steel strip rolling process

[J]. J. Iron Steel Res., 2019, 31: 174

[本文引用: 1]

张殿华, 彭文, 孙杰等.

板带轧制过程中的智能化关键技术

[J]. 钢铁研究学报, 2019, 31: 174

[本文引用: 1]

[2]

Liu

X H

, Wang

G D

Development of advanced technology in hot strip rolling

[J]. Res. Iron Steel, 2000, (5): 1

[本文引用: 1]

刘相华, 王国栋.

热轧带钢新技术的发展

[J]. 钢铁研究, 2000, (5): 1

[本文引用: 1]

[3]

, Liu

J X

, Ke

X T

Development and research of deformation resistance model in hot rolling process

[J]. Res. Iron Steel, 2009, 37(6): 59

[本文引用: 1]

李英, 刘建雄, 柯晓涛.

轧制变形抗力数学模型的发展与研究动态

[J]. 钢铁研究, 2009, 37(6): 59

[本文引用: 1]

[4]

Zhou

J H

, Guan

K Z

. Plastic Deformation Resistance of Metal [M]. Beijing: Machinery Industry Press, 1989: 212

[本文引用: 3]

周纪华, 管克智. 金属塑性变形阻力 [M]. 北京: 机械工业出版社, 1989: 212

[本文引用: 3]

[5]

Wang

, Wang

X G

, Yang

H T

, et al.

A new mathematical model for predicting flow stress of X70HD under hot deformation

[J]. J. Cent. South Univ., 2015, 22: 2052

DOI URL [本文引用: 1]

[6]

Feng

Y L

, Li

, Ai

L Q

, et al.

Deformation resistance of Fe-Mn-V-N alloy under different deformation processes

[J]. Rare Met., 2017, 36: 833

DOI URL

[7]

Kingkam

, Zhao

C Z

, Li

, et al.

Hot deformation and corrosion resistance of high-strength low-alloy steel

[J]. Acta Metall. Sin. (Engl. Lett.), 2019, 32: 495

DOI URL

[8]

Wei

L X

, Zhang

, Sun

, et al.

Online cold rolling prediction based on improved OS-ELM

[J]. Acta Metrol. Sin., 2019, 40: 111

[本文引用: 1]

魏立新, 张宇, 孙浩等.

基于改进OS-ELM的冷连轧在线轧制力预报

[J]. 计量学报, 2019, 40: 111

[本文引用: 1]

[9]

Wang

, Wang

, Xie

H B

, et al.

Deformation resistance model based on measured data of hot rolling

[J]. J. Plast. Eng., 2015, 22(1): 55

[本文引用: 3]

王健, 王宇, 谢红飙等.

基于热连轧实测数据的金属材料变形抗力模型

[J]. 塑性工程学报, 2015, 22(1): 55

[本文引用: 3]

[10]

W G

, Liu

, Zhao

Y T

, et al.

Modeling deformation resistance for hot rolling based on generalized additive model

[J]. J. Iron Steel Res. Int., 2017, 24: 1177

DOI URL

[11]

Xie

X Q

, Li

W G

, Fu

W P

, et al.

Deformation resistance model for hot-rolled strip based on measured data

[J]. Metall. Ind. Autom., 2019, 43(2): 29

[本文引用: 1]

谢向群, 李维刚, 付文鹏等.

基于实测数据的热轧带钢变形抗力模型

[J]. 冶金自动化, 2019, 43(2): 29

[本文引用: 1]

[12]

Y J

, Fu

H D

, Bai

, et al.

Progress in materials genome engineering in China

[J]. Acta Metall. Sin., 2020, 56: 1313

[本文引用: 1]

宿彦京, 付华栋, 白洋等.

中国材料基因工程研究进展

[J]. 金属学报, 2020, 56: 1313

[本文引用: 1]

[13]

Wang

, Wan

Z P

, Sun

, et al.

Dynamic softening behavior and microstructure evolution of nickel base superalloy

[J]. Acta Metall. Sin., 2018, 54: 83

DOI [本文引用: 2]

Ni-based supperalloys are widely applied in manufacturing of compressor and turbine discs and polycrystal turbine blades in the hot section of aero-engines, since they possessed excellent mechanical strength and creep resistance at high temperatures. Generally, hot working is an effective way for shaping metals and alloys. Lots of typical metallurgical behaviors occurred, which were related to the hot working parameters, including deformation temperature, strain rate and strain. And BP-ANN (artificial neural network based on the error-back propagation) as well as Arrhenius types models were the two of most acknowledged constitutive models to determine the relationship between the flow behavior and hot deformation parameters of various metals and alloys, at present. In order to investigate the relationship between deformation parameters and flow stress behavior, and precisely simulate the flow behavior during hot deformation processes of GH4720Li alloy, the hot compressive tests of GH4720Li alloy were conducted at the deformation temperature range of 1060~1140 ℃ and strain rate range of 0.001~1 s-1 on Gleeble 3500D thermal simulation testing machine in this work. The relationship between microstructure and hot deformation conditions was identified. The influence of hot processing parameters on flow stress behavior was analyzed. The temperature sensitivity of the flow stress decreased with increasing temperature at a strain rate of 0.1 s-1. The peak stress increased 23 MPa when the deformation temperature decreased from 1100 ℃ to 1080 ℃, only increased 7 MPa when decreased from 1140 ℃ to 1120 ℃. In addition, the Arrhenius model as well as BP artificial neural network model was established according to the true stress-strain curves. It shows that the established BP artificial neural network model can well exhibit the flow stress behavior of GH4720Li alloy compared with the Arrhenius model during hot deformation. The correlation coefficient between experimental findings and predicted flow stress determined by ANN model and Arrhenius model is 0.998 and 0.949, respectively. In addition, the dynamic recrystallization mechanism of the studied alloy was identified according to the deformed microstructure. Microstructure observation of the samples deformed at 1140 ℃ indicated that the discontinuous dynamic recrystallization was the main nucleation mechanism and newly grain nuclei distributed along the deformed grain boundaries. The dynamic recrystallization grain size of GH4720Li alloy decreases with the increase of strain rate when the samples deformed at 1140 ℃ and a strain of 0.8.

王涛, 万志鹏, 孙宇等.

镍基变形高温合金动态软化行为与组织演变规律研究

[J]. 金属学报, 2018, 54: 83

[本文引用: 2]

[14]

M Q

, Yao

X Y

, Luo

, et al.

Modeling for flow stress of the nickel-based GH4169 superalloy at high temperature deformation

[J]. Acta Metall. Sin., 2007, 43: 937

[本文引用: 1]

Isothermal compression has been carried out at a Thermecmaster-Z simulator. According the analysis of experimental results, the peak and steady stress significantly decreases with the increasing of the deformation temperature and the decreasing of the strain rate, and the deformation temperature would also affect the critical value of strain to reach the steady flow at the high temperature deformation of the nickel-based GH4169 superalloy. Meanwhile, a model for flow stress of the nickel-based GH4169 superalloy at high temperature deformation has been established in terms of the fuzzy artificial neural network. The maximum difference between the calculated and the experimental results is 10.18%, the average difference is 2.11%. The calculated precision is better than those through the regression method.

李淼泉, 姚晓燕, 罗皎等.

镍基高温合金GH4169高温变形流动应力模型研究

[J]. 金属学报, 2007, 43: 937

[本文引用: 1]

镍基高温合金GH4169热模拟压缩实验结果表明:变形温度的升高和应变速率的减小使该合金高温变形时的峰值应力和稳态应力显著降低,变形温度会影响其进入稳态变形时变形程度的大小. 基于高温合金GH4169高温变形时的流动应力特征, 运用模糊神经网络理论建立了该合金高温变形时的流动应力模型. 计算与实验的流动应力的最大误差为10.18%,平均误差为2.11%,该模型的计算精度明显高于由回归法建立的高温合金GH4169高温变形时的流动应力模型.

[15]

Phaniraj

M P

, Lahiri

A K

The applicability of neural network model to predict flow stress for carbon steels

[J]. J. Mater. Process. Technol., 2003, 141: 219

DOI URL [本文引用: 1]

[16]

Zhou

J H

, Guan

K Z

, Liu

, et al.

An mathematical model of flow stress for hot strip mill

[J]. J. Univ. Sci. Technol. Beijing, 1991, 13: 20

[本文引用: 1]

周纪华, 管克智, 刘玠等.

热轧碳钢流动应力的数学模型

[J]. 北京科技大学学报, 1991, 13: 20

[本文引用: 1]

[17]

Zhao

M M

, Qin

, Feng

, et al.

Effect of Al and Ni on hot deformation behavior of 1Cr9Al(1~3)Ni(1~7)WVNbB steel

[J]. Acta Metall. Sin., 2020, 56: 960

DOI [本文引用: 1]

The addition of Al and Ni to ferritic heat resistant steel can improve its high temperature strength and high temperature oxidation resistance. Al and Ni in steel have some effects on the thermal deformation behavior of steel. But there is less research on it. In this work, a new type of 1Cr9Al(1~3)Ni(1~ 7)WVNbB high aluminum ferrite heat-resistant steel was prepared by adding Al element to T92 steel and adjusting Ni content properly. Gleeble-3800 thermal simulation test machine was used to conduct isothermal and constant speed thermal compression experiment with 60% deformation at 950~1150 ℃ and 0.1~10 s-1 strain rates, respectively. The effects of Al and Ni additions on the hot deformation behavior, peak stress and activation energy of hot deformation of the steel were studied. The rheological stress expression containing Zener-Hollomon parameters were obtained by fitting, and the constitutive equation of the test steel was established. The results show that the addition of Al and the increase of Al content significantly reduces rheological stress and peak stress under thermal compression, which greatly reduces the difficulty of test steel processing. Compared with T92 steel, the thermal deformation activation energies of four sample groups increase by 38.136%, 19.188%, 28.003%, and 11.915%, respectively. The peak stress calculated by the constitutive equation is in good agreement with the experimental data. The results show that the constitutive equation has high accuracy. The relationship between peak flow stress, deformation temperature and strain rate can be expressed well.

赵嫚嫚, 秦森, 冯捷等.

Al、Ni对1Cr9Al(1~3)Ni(1~7)WVNbB钢热变形行为的影响

[J]. 金属学报, 2020, 56: 960

DOI [本文引用: 1]

在T92钢的成分基础上添加了Al元素并对Ni含量进行适当调整后制备出新型1Cr9Al(1~3)Ni(1~ 7)WVNbB高铝铁素体耐热钢。利用Gleeble-3800热模拟试验机，对1Cr9Al(1~3)Ni(1~7)WVNbB高铝钢进行了950~1150 ℃、0.1~10 s<sup>-1</sup>应变速率下60%变形量的等温恒速热压缩实验，研究了Al、Ni加入量对钢热变形行为、峰值应力及热变形激活能的影响，并通过拟合得到了含有Zener-Hollomon参数的流变应力表达式，建立了该耐热钢的本构方程。结果表明，Al的添加及Al含量的增大明显降低了热压缩下的流变应力与峰值应力，即明显降低了钢的加工难度；与T92钢相比，4组试样的热变形激活能分别提高了38.136%、19.188%、28.003%和11.915%。

[18]

X M

, Wang

, Gao

K W

, et al.

Application of ELM to predict plate rolling force

[J]. J. Iron Steel Res., 2020, 32: 393

[本文引用: 4]

冀秀梅, 王龙, 高克伟等.

极限学习机在中厚板轧制力预报中的应用

[J]. 钢铁研究学报, 2020, 32: 393

[本文引用: 4]

[19]

Mei

, Sun

Q L

, Yu

L H

, et al.

Grain size prediction of aluminum alloy dies castings based on GA-ELM

[J]. Acta Metall. Sin., 2017, 53: 1125

[本文引用: 1]

梅益, 孙全龙, 喻丽华等.

基于GA-ELM的铝合金压铸件晶粒尺寸预测

[J]. 金属学报, 2017, 53: 1125

[本文引用: 1]

[20]

Huang

G B

, Zhu

Q Y

, Siew

C K

Extreme learning machine: Theory and applications

[J]. Neurocomputing, 2006, 70: 489

DOI URL [本文引用: 1]

[21]

Deng

C W

, Huang

G B

, Xu

, et al.

Extreme learning machines: New trends and applications

[J]. Sci. China Inform. Sci., 2015, 58: 1

[22]

Huang

G B

, Zhou

H M

, Ding

X J

, et al.

Extreme learning machine for regression and multiclass classification

[J]. IEEE Trans. Syst. Man Cybern., 2012, 42B: 513

[本文引用: 1]

[23]

Poudel

, Bae

S H

, Jang

Comparison of different deep learning optimizers for modeling photovoltaic power

[J]. J. Chosun Nat. Sci., 2018, 11: 204

[本文引用: 1]

[24]

W G

, Yang

, Zhao

Y T

, et al.

Modeling hot strip rolling process under framework of generalized additive model

[J]. J. Cent. South Univ., 2019, 26: 2379

DOI URL [本文引用: 1]

[25]

, Li

W G

, Zhao

Y T

, et al.

Prediction of hot-rolled roll force based on deep learning

[J]. J. Iron Steel Res., 2019, 31: 805

[本文引用: 2]

马威, 李维刚, 赵云涛等.

基于深度学习的热连轧轧制力预测

[J]. 钢铁研究学报, 2019, 31: 805

[本文引用: 2]

[26]

Liu

D H

, Li

J H

, Peng

, et al.

Comprehensive evaluation of sintering basic characteristics of iron ore based on grey relational analysis

[J]. J. Iron Steel Res. Int., 2019, 26: 691

DOI URL [本文引用: 1]

[27]

Zhang

, Zhang

Z H

, Tian

, et al.

Research and application of deep learning method for plate ultra fast cooling

[J]. J. Northeastern Univ. (Nat. Sci.), 2019, 40: 635

[本文引用: 2]

张田, 张子豪, 田勇等.

深度学习在中厚板轧后超快速冷却系统中的研究与应用

[J]. 东北大学学报(自然科学版), 2019, 40: 635

[本文引用: 2]

板带轧制过程中的智能化关键技术

2019

... 过程控制模型是中厚板轧制过程中的关键技术，精确预测轧制压力是过程控制模型的重要目标之一，既关系到最终产品的质量，也关系到生产设备的安全运行.变形抗力是轧制压力计算的核心，提高各种金属材料、各种工艺条件下的变形抗力预测精度对科学地制定轧制规程、提高生产效率非常必要^[1,2].目前，国内很多钢铁生产企业的轧制过程控制模型从国外引进，因此有必要在理解引进模型的基础上，逐步掌握核心技术，研发适合自身生产工艺要求的过程控制新模型. ...

板带轧制过程中的智能化关键技术

2019

热轧带钢新技术的发展

2000

热轧带钢新技术的发展

2000

轧制变形抗力数学模型的发展与研究动态

2009

... 李英等^[3]提出，计算变形抗力主要有2种方法：一是传统数学公式建模，大量研究^[4~8]基于不同的结构式，通过对实验数据拟合获得回归系数，其中周纪华-管克智公式^[4]应用较多，它改进了应变速率指数与变形温度的关系，用非线性函数修正了应变的影响，但由于实验条件与实际生产存在一定差异，在实际轧制应用时基于实验数据得到的模型需进行优化和调整，故部分研究^[9~11]采用现场轧制过程的实测数据，通过轧制压力计算公式进行逆运算，得到材料的实测变形抗力近似值，再利用回归分析建立不同钢种的变形抗力模型.另一种是利用人工神经网络建模，宿彦京等^[12]提出应用机器学习、人工智能等技术，实现数据分析、模型建立，探索新材料、新性能.目前，大多研究者针对特定钢种的实验数据开展研究.王涛等^[13]利用反向传播(BP)神经元网络技术对GH4720Li合金热变形过程中的流变力学行为进行预测.李淼泉等^[14]利用热模拟压缩实验数据，基于模糊神经网络，把变形温度、应变速率和应变作为输入变量，进行GH4169镍基高温合金高温变形时的流变应力模型预测.Phaniraj和Lahiri^[15]利用人工神经网络方法进行建模，网络输入变量为：C当量、变形温度、应变、应变速率. ...

轧制变形抗力数学模型的发展与研究动态

2009

1989

... [4]应用较多，它改进了应变速率指数与变形温度的关系，用非线性函数修正了应变的影响，但由于实验条件与实际生产存在一定差异，在实际轧制应用时基于实验数据得到的模型需进行优化和调整，故部分研究^[9~11]采用现场轧制过程的实测数据，通过轧制压力计算公式进行逆运算，得到材料的实测变形抗力近似值，再利用回归分析建立不同钢种的变形抗力模型.另一种是利用人工神经网络建模，宿彦京等^[12]提出应用机器学习、人工智能等技术，实现数据分析、模型建立，探索新材料、新性能.目前，大多研究者针对特定钢种的实验数据开展研究.王涛等^[13]利用反向传播(BP)神经元网络技术对GH4720Li合金热变形过程中的流变力学行为进行预测.李淼泉等^[14]利用热模拟压缩实验数据，基于模糊神经网络，把变形温度、应变速率和应变作为输入变量，进行GH4169镍基高温合金高温变形时的流变应力模型预测.Phaniraj和Lahiri^[15]利用人工神经网络方法进行建模，网络输入变量为：C当量、变形温度、应变、应变速率. ...

... 参考常用的周纪华-管克智公式^[4]结构，其用非线性函数表示变形条件之间对变形抗力的交互影响，形式如下： ...

1989

... 参考常用的周纪华-管克智公式^[4]结构，其用非线性函数表示变形条件之间对变形抗力的交互影响，形式如下： ...

A new mathematical model for predicting flow stress of X70HD under hot deformation

2015

... 上述模型算法都有各自的特点，大大提高了预测精度，但实际应用中也存在一定的局限性.传统回归公式建模大多只适用特定的钢种，有的公式虽从形式上考虑了部分化学元素对变形抗力的影响，但通常是针对某钢种成分的标准值进行计算，不能充分反映同一钢种化学成分波动时变形抗力的变化.周纪华等^[16]基于9个钢号的碳钢，通过回归得到C、Si、Mn、Cu元素含量对流动应力的影响.赵嫚嫚等^[17]研究了Al、Ni加入量对1Cr9Al(1~3)Ni(1~7)WVNbB (质量分数，%)钢热变形行为、峰值应力及热变形激活能的影响.神经网络建模大都基于实验数据，在理论研究方面取得许多成果，部分已应用于在线生产.为充分利用现场二级数据中所蕴含的信息，建立基于实际生产过程实测数据的变形抗力模型，更为符合轧线实际轧制情况.不仅精度更高，且对现场生产有更直接的参考价值和指导意义^[5]. ...

Deformation resistance of Fe-Mn-V-N alloy under different deformation processes

2017

Hot deformation and corrosion resistance of high-strength low-alloy steel

2019

基于改进OS-ELM的冷连轧在线轧制力预报

2019

基于改进OS-ELM的冷连轧在线轧制力预报

2019

基于热连轧实测数据的金属材料变形抗力模型

2015

... 实测变形抗力(K_act)通过实测轧制力反算近似得到，计算公式为^[9]： ...

... 收集现场生产的175个钢种，包括：低合金钢(DH36、X70等149个钢种)、合金钢(12Cr2Mo1R、NM500等18个钢种)、高合金钢(1.2311、06Ni9DR等8个钢种)，参照王健等^[9]的方法，得到每个钢种的基准变形抗力，结合每个钢种反算的K_act，根据式(5)，将175个钢种回归式联立可求出一组变形参数b₁~b₅，即可得

K_{t}^{} K_{ε}^{} K_{\dot{ε}}^{}

. ...

基于热连轧实测数据的金属材料变形抗力模型

2015

... 实测变形抗力(K_act)通过实测轧制力反算近似得到，计算公式为^[9]： ...

K_{t}^{} K_{ε}^{} K_{\dot{ε}}^{}

. ...

Modeling deformation resistance for hot rolling based on generalized additive model

2017

基于实测数据的热轧带钢变形抗力模型

2019

基于实测数据的热轧带钢变形抗力模型

2019

中国材料基因工程研究进展

2020

中国材料基因工程研究进展

2020

镍基变形高温合金动态软化行为与组织演变规律研究

2018

... 选用3层神经网络(即1个输入层、1个隐含层和1个输出层)进行建模，其中输入层共17个输入变量：化学元素Al、B、C、Si、Mn、Cu、Cr、Ni、Mo、Nb、Ti、V、P、S含量；t、ε、

\dot{ε}

.隐含层单元数为180；输出变量为σ.激活函数采用Sigmoid函数，表达式为^[13]： ...

镍基变形高温合金动态软化行为与组织演变规律研究

2018

\dot{ε}

.隐含层单元数为180；输出变量为σ.激活函数采用Sigmoid函数，表达式为^[13]： ...

镍基高温合金GH4169高温变形流动应力模型研究

2007

镍基高温合金GH4169高温变形流动应力模型研究

2007

The applicability of neural network model to predict flow stress for carbon steels

2003

热轧碳钢流动应力的数学模型

1991

热轧碳钢流动应力的数学模型

1991

Al、Ni对1Cr9Al(1~3)Ni(1~7)WVNbB钢热变形行为的影响

2020

Al、Ni对1Cr9Al(1~3)Ni(1~7)WVNbB钢热变形行为的影响

2020

极限学习机在中厚板轧制力预报中的应用

2020

... 轧制力模型采用Sims公式，模型基本形式为^[18]： ...

... 变形抗力数学模型采用的是同钢种使用相同变形抗力参数曲线，没有考虑化学成分波动对变形抗力的影响，基本形式为^[18]： ...

... 实际生产过程中，因特定钢种在特定温度下对应的应变、应变速率数据非连续，故从在线生产数据库中随机选取化学成分差异较大的3个钢种X70 (简称A)、12Cr2Mo1R (简称B)和1.2311 (简称C) (见表1)对应的热模拟实验数据^[18]制图，如图1所示.变形温度升高，所有钢种变形抗力都不同程度下降；应变速率对变形抗力的影响，不仅与钢种有关，且与变形温度有关；应变与变形抗力并非简单的幂函数关系，随着变形温度、应变速率的变化出现上升或者下降趋势. ...

... 选用3层神经网络进行建模：将灰度分析的14个化学成分(Al、B、C、Si、Mn、Cu、Cr、Ni、Mo、Nb、Ti、V、P、S)作为神经网络输入变量；采用10折10次交叉验证^[18]确定网络隐含层节点数为180；σ_{0, chem}作为神经网络输出变量，训练后得到输出权重.网络结构图如图4所示，激活函数采用Sigmoid函数. ...

极限学习机在中厚板轧制力预报中的应用

2020

... 轧制力模型采用Sims公式，模型基本形式为^[18]： ...

... 变形抗力数学模型采用的是同钢种使用相同变形抗力参数曲线，没有考虑化学成分波动对变形抗力的影响，基本形式为^[18]： ...

基于GA-ELM的铝合金压铸件晶粒尺寸预测

2017

... ELM是一种单隐含层前馈神经网络，其特点是网络输入层与隐含层间的连接权值和隐含层神经元的阈值可随机生成，且整个训练过程无需调整.研究表明，与传统的BP、径向基函数(RBF)等基于梯度思想的神经网络算法相比，ELM具有待定参数少、学习速度快^[19]、预测精度高及泛化性能好等优点^[20~22]，具体算法如下. ...

基于GA-ELM的铝合金压铸件晶粒尺寸预测

2017

Extreme learning machine: Theory and applications

2006

Extreme learning machines: New trends and applications

2015

Extreme learning machine for regression and multiclass classification

2012

Comparison of different deep learning optimizers for modeling photovoltaic power

2018

... 深度学习为解决复杂非线性问题提供了新的途径^[23]，TensorFlow是端到端的开源机器学习平台.Keras是用于构建和训练深度学习模型的TensorFlow高阶应用程序接口(API)，具有易使用、兼容性大和灵活性高的特点，可实现快速原型设计. ...

Modeling hot strip rolling process under framework of generalized additive model

2019

... 收集现场一段时间内连续生产的175个钢种的176835条生产数据，首先对检测异常数据进行清洗^[24]，得到99422条训练样本数据，另取训练样本以外的58944条测试样本数据.为降低变量差异对模型的影响，建模前对数据进行z-score标准化处理^[25]： ...

基于深度学习的热连轧轧制力预测

2019

... 模型预测能力用RMSE、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)及相对误差(E_r)小于5%的样本占总样本的百分数进行评价，其表达式分别为^[25]： ...

基于深度学习的热连轧轧制力预测

2019

... 模型预测能力用RMSE、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)及相对误差(E_r)小于5%的样本占总样本的百分数进行评价，其表达式分别为^[25]： ...

Comprehensive evaluation of sintering basic characteristics of iron ore based on grey relational analysis

2019

... 结合生产工艺，采用灰色关联分析方法^[26]，将变形抗力与其影响因素进行灰色关联分析，分析结果如表2所示，选择关联度大于0.85的参数作为模型自变量，包括ε、t、

\dot{ε}

及Al、C、Cu、Mn、P、Si、B、S、Nb、Ti、Ni、V、Mo、Cr等化学成分，N、Sn、W等化学成分灰色关联度较低，即对变形抗力影响较小，这与实际工艺过程基本吻合. ...

深度学习在中厚板轧后超快速冷却系统中的研究与应用

2019

... 选取深度神经网络常用的优化算法Adam算法^[27].与传统的随机梯度下降不同，Adam算法结合了Momentum和RMSprop梯度下降法，通过计算梯度的一阶矩估计和二阶矩估计，为不同的参数设计独立的自适应性学习率，适用于多种结构的神经网络. ...

... 将RM、FM数据不加区分地全部用于训练同一个深度神经网络模型^[27] (记为Deep_All)，经测试，选择5层网络进行建模，其中输入层共17个输入变量：化学元素Al、B、C、Si、Mn、Cu、Cr、Ni、Mo、Nb、Ti、V、P、S含量；t、ε、

\dot{ε}

.隐含层为3层，隐含层单元数分别为150、150和150；输出变量为σ；激活函数选用Relu函数. ...

深度学习在中厚板轧后超快速冷却系统中的研究与应用

2019

\dot{ε}

.隐含层为3层，隐含层单元数分别为150、150和150；输出变量为σ；激活函数选用Relu函数. ...

〈

〉