目前针对冶金器多相流的研究主要集中在冶金器中底吹作用下的渣眼行为[6]、气体流量、流场[7,8]、钢液混匀时间[9]、卷渣状况[10,11]和夹杂物去除[12,13]等方面,对气泡上升过程穿过渣-金界面夹带钢液进入渣层并与渣层作用的现象研究相对较少。Han和Holappa[14]利用热态实验研究气泡在渣-金界面产生夹带的临界直径大约为9 mm,此时对应的渣-金界面张力为1.4 N/m。如果渣-金界面张力为1.8 N/m时,对应的气泡临界直径大约为12.5 mm[15]。同时发现,气泡夹带量(夹带钢液进入渣层的体积量)与气泡尺寸成正比,与界面张力和黏度成反比[16]。Ekengård等[17]对钢包过程中不同阶段渣中钢液滴的分布进行研究发现,渣中钢液滴的数量在脱气操作之前较多,并且电极的使用会影响渣中钢液滴的数量。另外,也有学者[18,19]研究了其他金属和高温盐等熔池中气泡的夹带作用。由于气泡在相界面的夹带现象也广泛存在于机械、石油工程、生物医学和化工等工艺中,因此,相关研究人员对不同工艺下的气泡在相界面的夹带现象进行了大量研究。Reiter和Schwerdtfeger[20]用高速摄影技术研究了气泡通过液/液界面时的夹带现象。研究发现,随着气泡尺寸的增大,被带入上层相的下层相数量也随之增加,并且很大程度上取决于液/液体系的物理性质。Greene等[21]通过物理模拟研究了由气泡上升引起的夹带问题,根据实验总结出气泡夹带的临界公式,表明气泡夹带量与渣-金密度比和界面张力有很强的关联性。Zhao等[22]使用空气-水-油物理实验研究了不同气量产生的多气泡通过不同黏度油层的界面时发生的界面现象,发现低气量时油层黏度对夹带影响明显,夹带液柱高度和夹带量在大气量时均有较大变化。此外,Singh等[23]和Natsui等[24]基于不同数值模拟方法建模,对单个气泡通过液/液之间界面现象进行模拟,研究了界面张力、密度、黏度等对气泡夹带过程的影响。
综上所述,前期的相关研究内容主要针对冷态或水-油体系,与冶金过程中钢-渣体系物性差别较大,而且未对冶金中关注的钢液夹带量和夹带过程中渣-金界面面积变化等重要现象进行过多关注。本工作以冶金工艺过程中气泡穿过渣-金界面行为作为研究对象,建立物理模型对气泡通过渣-金界面时产生夹带现象的影响因素进行研究,并通过数学模型研究钢-渣-气三相体系气泡夹带行为。考察气泡尺寸、渣层黏度、渣层密度、渣-金界面张力等因素对气泡夹带行为的影响规律,为进一步研究气-渣-金界面传质和传热行为提供理论依据和参考。
1 物理模型
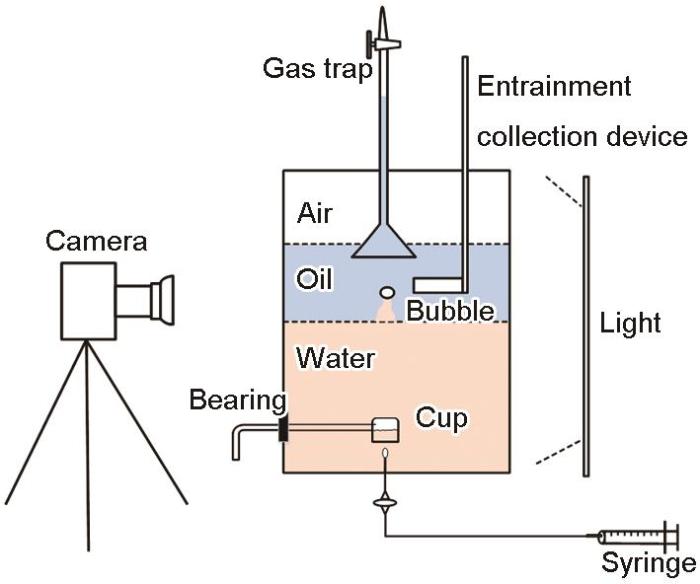
通过物理实验中对单个气泡通过油-水界面夹带行为进行研究,考察气泡尺寸和具有不同物性的油对夹带量的影响,实验装置如图1所示。不同油的物性及其与水的界面张力参数如表1所示。实验装置主体为长方体有机玻璃容器,顶部敞口,内尺寸为300 mm × 200 mm × 60 mm,水面高度200 mm,油层高度100 mm,托杯位置(气泡释放位置)距离两相界面100 mm。通过注射器向托杯内注入一定量气体,旋转轴承释放气泡。气泡在水中上升通过两相界面并夹带水进入上部油层中。此时利用图中装置对夹带进入油层中的水进行收集并测量。气泡在油层中继续上升进入倒扣的滴定管中,根据滴定管上部液面变化测得气泡体积,根据体积计算气泡当量直径,每组实验重复3次,求平均值。实验过程中保持水和油层高度不变,主要研究使用不同油模拟渣层时气泡直径对夹带量的影响。
图1
表1 物理实验流体物性参数
Table 1
| Material | Density / (kg·m-3) | Viscosity / (Pa·s) | Surface tension / (N·m-1) | Interfacial tension / (N·m-1) |
|---|---|---|---|---|
| Water | 1000 | 1 × 10-4 | 0.0728 | - |
| Bubble | 1.17 | 2.125 × 10-5 | - | - |
| Silicone oil (10 mm·s-1) | 940 | 9.4 × 10-3 | 0.019 | 0.0108 |
| Silicone oil (100 mm·s-1) | 964 | 9.64 × 10-2 | 0.0209 | 0.0311 |
| Paraffin | 760.5 | 2.8 × 10-3 | 0.029 | 0.05 |
2 数学模拟
利用数值模拟方法对气泡夹带现象进行建模,首先模拟物理实验中现象对数模进行验证,再用数值模型研究钢-渣界面的气泡夹带现象。本工作重点研究气泡和渣等物性对夹带量的影响规律,假设熔池流体在气泡释放前静止,在气泡运动过程中为层流,未考虑实际气泡上升过程中气泡间相互影响及渣-金相互运动等因素。
2.1 模型假设
本工作针对水-油和钢-渣体系的建模均基于如下假设:(1) 气泡释放前计算域流体速度为零;(2) 假设每一相均为不可压缩流体,密度、黏度及各相间界面张力为常数;(3) 计算过程不考虑温度对体系的影响;(4) 假设气泡竖直上升,在上升过程中无水平移动;(5) 气泡由静止释放,气泡初始速度为0,初始状态为球形;(6) 各相与壁面接触角均为90°;(7) 本研究中忽略实际钢液中的夹杂物可能对气泡夹带现象产生的影响。
2.2 控制方程
式中,ρ为密度, u 为流体速度,t为时间,p为压力,μ为流体黏度, g 为重力加速度, Fst和F分别为相界面张力和界面自由能。
式中,
式中,Mconst为常数,本工作取1 × 10-4 m3/s;ε为界面的特征尺寸;CT、Ci 和Cj 为与界面张力相关的系数,计算方式如下:
其中,方程(6)中等号右边为三相体系中,气-钢液、气-渣和渣-钢液两相之间的界面张力。动量方程(1)中的 Fst和F通过以下方程计算:
对于动量守恒方程中多相流界面控制体中流体的ρ和μ通过如下方程进行计算:
2.3 边界条件和网格
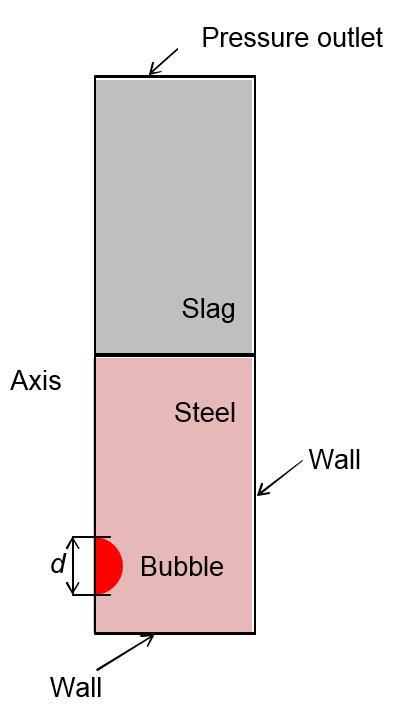
数值模拟首先利用物理模型中的油-水体系实验结果进行验证,随后模拟钢-渣体系。数值模拟采用二维轴对称模型进行计算。忽略壁面对流体的影响,上部出口为压力边界,计算域及模型初始状态和边界条件如图2所示。
图2
图2
计算域及边界条件示意图
Fig.2
Schematic of the computational domain and boundary conditions (d—diameter)
考虑到气泡的运动过程中形状随时间变化,及气泡与液-液界面相互作用过程中,气泡、界面和钢液滴等几何形变较大,模型采用三角形非结构网格。计算域初始网格最大单元尺寸0.4 mm,最小0.016 mm,最大单元增长率设为1.13。在计算过程中,使用自动加密网格方法,对相界面区域进行自动加密,网格加密最大层数为3层,最小尺寸0.05 mm,计算域气泡附近局部网格划分如图3所示。
图3
2.4 模拟参数与方案
为验证数学模型的可靠性,首先建立数学模型对物理模拟中的参数进行计算并对比。再利用类似模型对钢-渣-气体系中的气泡夹带现象进行研究。主要考察气泡直径、渣黏度、密度和渣-金界面张力对气泡夹带进入渣层钢液量的影响。由于较小气泡在穿过渣层时不产生夹带或夹带量较小,较大气泡在上升过程中形变较大,甚至破碎,本工作只考虑气泡形变不大并能产生夹带的直径范围。冶金过程中不同工艺使用渣系不同,成分变化复杂且范围较大,多数渣平均密度在2500~4500 kg/m3 [27],本工作密度研究范围设定为2000~5000 kg/m3。同样,由于不同冶炼工艺中渣成分和熔池温度变化范围较大,渣层黏度、表面张力和钢渣界面张力选取较有代表性的数据范围,详细参数如表2[27]所示。
| Parameter | Value | Unit |
|---|---|---|
| Molten steel density | 6080 | kg·m-3 |
| Molten steel viscosity | 0.0062 | Pa·s |
| Molten steel density surface tension | 1.7 | N·m-1 |
| Bubble density | 1.62 | kg·m-3 |
| Bubble viscosity | 2.125 × 10-5 | Pa·s |
| Bubble diameter | 10, 12, 14, 16 | mm |
| Slag density | 2000, 3000, 4000, 5000 | kg·m-3 |
| Slag viscosity | 0.05, 0.5, 1, 2 | Pa·s |
| Slag-metal interfacial tension | 0.65, 0.8, 0.95, 1.1 | N·m-1 |
数值模拟对气泡夹带进入渣层的钢液量进行统计,分析气泡上升不同时刻渣中钢液夹带量的变化。在瞬态计算完成后,对渣中的钢液量体积进行积分,得到渣中不同时刻钢液量体积变化。渣-金间的接触面使用类似的积分方法,通过对渣-金两相界面进行积分获得不同时刻渣-金界面面积变化。
3 结果与分析
3.1 物理模拟结果与讨论
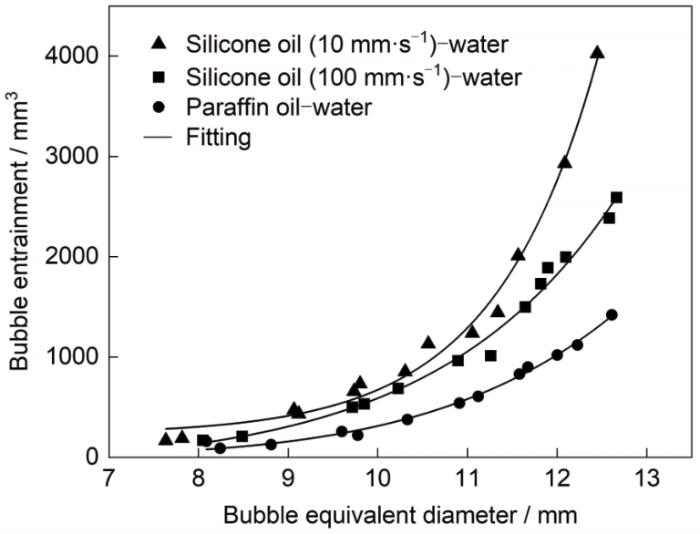
图4为不同油-水体系气泡夹带量和气泡尺寸的关系。实验中,气泡小于7 mm时不产生夹带,气泡大于13 mm时在上升过程中形状变化较大甚至破碎。因此,图中为尺寸在7~13 mm范围内气泡的夹带量结果。可以看出,气泡直径越大,夹带量越大。气泡从7.3 mm增大到12.5 mm左右,使用10 mm/s硅油时,气泡夹带量由167 mm3增大至4205 mm3,增大了约24倍;使用100 mm/s硅油时,气泡夹带量由170 mm3增大至2590 mm3,增大了约14倍。气泡夹带量均随气泡直径增大而增大,并且夹带量与气泡直径呈非线性关系,气泡直径为7.3~11 mm时,夹带量较小,当气泡直径大于11 mm时,夹带量增大明显。大尺寸气泡在穿过渣-金界面时具有更大的速度和界面接触面积,这有助于气泡夹带更多的钢液进入渣层。例如钢包精炼过程中,底吹气泡较小时,可能更多的作用是去除夹杂物,对于活跃渣-金界面作用有限,增大底吹强度时,大量大尺寸气泡上升,穿过渣-金界面时夹带大量钢液进入渣层,增大了渣-金作用面积和时间,使渣-金界面作用效率大大增强。
图4
图4
不同油-水体系气泡夹带量变化
Fig.4
Variations of bubble entrainment in different oil-water systems
对比使用100和10 mm/s硅油可以看出,油层黏度和界面张力增大,夹带量减小。当气泡直径小于11 mm时,2者相差不大;当气泡直径大于11 mm时,随着夹带量增大,2者相差明显。渣层黏度和界面张力增大时,气泡穿过渣-金界面夹带钢液阻力增大,因此夹带量下降,实际冶炼过程中,渣层黏度增加,渣-金界面相互作用强度下降,进而影响渣-金作用效率。
石蜡油的密度和黏度均小于10 mm/s硅油,界面张力也不同,气泡在石蜡油层中的水夹带量比使用硅油时少,且随着气泡直径增大,夹带量上升量较少。
从以上分析可以看出,物理模拟可以较为直观地研究气泡尺寸和夹带量的关系,得出一些量化的结论。但是,对于渣层密度、黏度和界面张力等性质和气泡夹带量的单参数定量关系的研究较为困难。原因是模拟渣层的不同流体,黏度、密度和界面张力等性质均不同,得出的实验结果不能明确地分析出起主要作用的因素,也较难分析出不同因素对夹带量的影响。因此,本研究利用数值模型对渣层物理性质和气泡夹带量的关系进行量化研究,讨论渣层黏度、密度和界面张力等性质与气泡夹带量的关系。
3.2 数值模拟研究结果与讨论
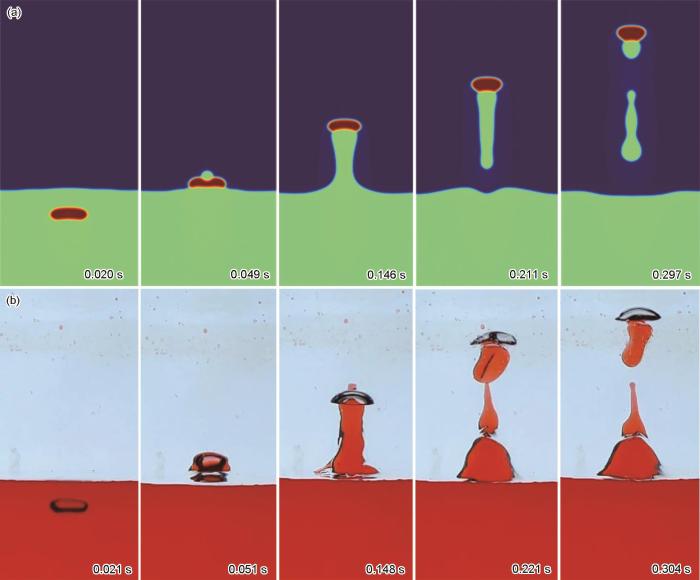
首先建立数值模型对石蜡油-水体系中气泡夹带进行模拟并验证。石蜡油-水液液体系实验相关参数如表1所示,气泡直径取10 mm。气泡上升过程的数值模拟和物理模拟对比如图5所示。气泡释放后在上升过程中产生变形,随后以一定速度到达相界面,穿过界面时,由于尾流的作用,一部分水随气泡上升在气泡下部形成水柱,气泡到达一定高度后,夹带的水柱脱离界面,随后断裂,一部分水随着气泡继续上升,另一部分开始下降,最终穿过相界面,返回到下部。与物理模拟对比发现,数值模拟与物理模拟在气泡上升和夹带过程中均比较类似。由于容器中其他因素的干扰,物理模拟中气泡在上升过程中表现出一定的非对称性行为,这也是数值模拟和物理模拟结果不一致的重要因素。
图5
图5
气泡上升过程的数值模拟和物理模拟结果对比
Fig.5
Comparisons between the mathematical (a) and experimental (b) results of bubble rising process
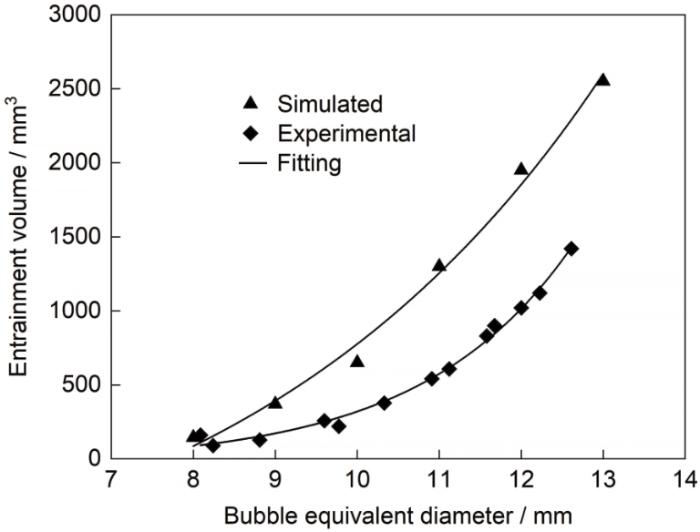
为了定量验证数值模拟结果,对数值模拟不同气泡尺寸夹带量进行统计并与实验结果进行对比,如图6所示。从图中可以看出,当气泡尺寸较小时,没有夹带产生,气泡超过8 mm左右时产生夹带,气泡夹带量随气泡尺寸的增大而增大。气泡较小时夹带量较小且夹带量随气泡尺寸增大增长缓慢,随着气泡尺寸的增大,气泡夹带量开始迅速增大,数值模拟和物理模拟变化趋势一致。但同时也发现,相同气泡尺寸时,气泡夹带量数值模拟结果与实验结果存在偏差,数值模拟结果偏大。气泡尺寸较小时,偏差约10%,气泡尺寸较大时,偏差可达90%左右。其中一个重要原因是,数值模拟统计值为两相界面以上的夹带总量,包括未脱离界面的部分,而物理模拟对于这部分未脱离界面的夹带收集困难,并未统计,导致量上的差异。造成数值模拟和物理模拟结果偏差的其他主要原因分析如下:(1) 实验中上升气泡在介质中的运动空间为三维,同时释放的气泡形状很难保持稳定统一,体积和形状存在一定波动,实验中气泡释放装置人为控制,存在一定的扰动和误差;(2) 数值模拟为二维中心轴对称模型,初始状态和气泡上升过程均无外部扰动源,严格意义上说这个与物理模拟不同,只能近似。
图6
图6
气泡夹带数值模拟结果和实验结果对比
Fig.6
Comparison between the mathmatical and experimental results of bubble entrainment
虽然物理模拟在实验上数据存在一定波动,但其得出的模拟结果和趋势与物理模拟结果具有较高的一致性。因此,利用建立的数学模型可以对实际炼钢过程中的渣-金界面处气泡的夹带和运动行为进行研究。另外,数值模拟对于体系内尤其是物理实验较难测量的参数的动态监测有着绝对的优势,为研究提供了新的视野。
实际渣系在改变成分时,其密度、黏度、表面张力以及渣-金界面张力等都可能随之改变,不易分析单变量对气泡夹带的影响。本工作为了研究单一参数对体系的影响,只改变渣的其中某一个参数,其他参数保持不变,因此本工作中的渣性质不特定针对某一渣系,只研究渣的性质对气泡夹带的影响。
3.2.1 气泡夹带量分析
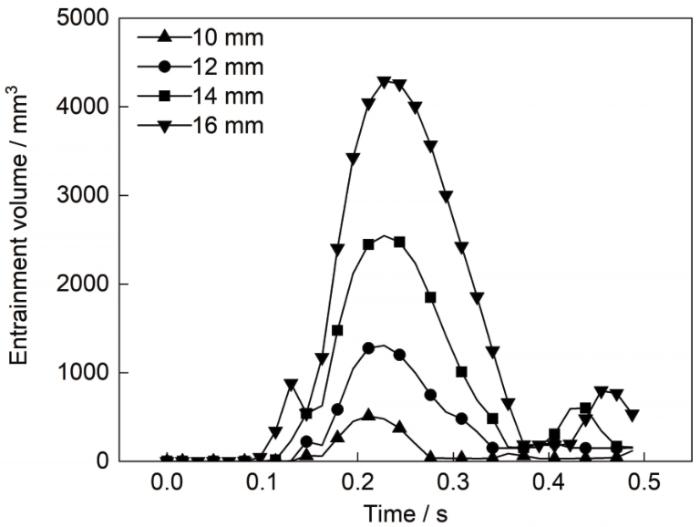
图7为不同直径气泡穿过渣-金界面时渣中钢液夹带量随时间的变化关系。图中夹带量统计量为渣-金界面以上的钢液量,钢液在渣中的变化过程与图5类似。从图中可以看出,气泡在钢液中上升,未到达渣-金界面时夹带量为零。气泡在穿过界面时产生夹带,渣中钢液量开始增加,随着气泡的上升,渣中钢液量达到峰值,随后由于钢液柱断裂、回落,渣中钢液量减少,最终全部返回下部熔池。对比不同尺寸气泡的夹带量发现,较大气泡夹带量较大,这是由于较大气泡在上升过程中能带动更多钢液随气泡运动而上升,使更多的钢液进入到渣层当中,且向上运动距离较长,使夹带钢液在渣中停留更长时间,表明大尺寸气泡能使更多钢液与渣层混合,更有利于促进渣-金界面反应。
图7
图7
渣层中钢液体积随时间的变化
Fig.7
Variations of entrainment volume of molten steel as a function of time
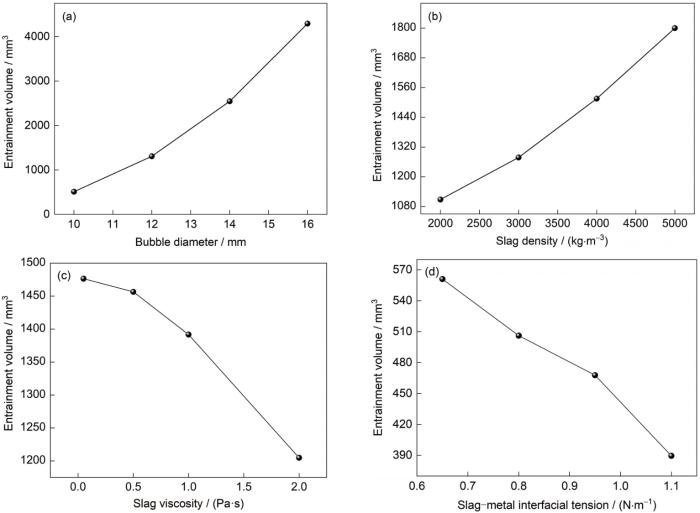
图8
图8
不同因素对气泡夹带量的影响
Fig.8
Influences of bubble diameter (a), slag density (b), slag viscosity (c), and slag-metal interfacial tension (d) on the entrainment volume of molten steel
实际生产过程中,不同冶炼工艺中渣层成分和含量不同,从而导致渣层密度产生变化。图8b为渣层密度变化时气泡对钢液夹带量的影响。从图中可以看出,渣层密度由2000 kg/m3增大到5000 kg/m3,气泡夹带量由1110 mm3增大到1800 mm3,气泡夹带量增大了62.2%。由于渣层密度增大时,渣-金密度差降低,使钢液更易进入渣中并停留较长时间。可见,渣层密度增加时可以使得更多钢液夹带进入渣中。
图8c为渣层黏度对夹带量的影响。可见,渣层黏度范围在0.05~2.00 Pa·s时,气泡夹带量由1480 mm3减小到1200 mm3,气泡夹带量减小了18.4%。说明渣层的黏度增大对气泡夹带有抑制作用,气泡夹带量随渣层黏度增大而减小。这是由于渣黏度的增大会增大气泡上升阻力,降低气泡进入渣层后的速度,进而影响气泡尾流携带钢液量。因此,实际冶炼过程中,渣层黏度较大时,渣-金界面作用效率会因此而下降。
渣层成分、含量和冶炼温度均会影响渣-金界面张力。图8d为渣-金界面张力从0.65 N/m增大到1.1 N/m时气泡夹带量的变化。可以看出,气泡夹带量由560 mm3减小到390 mm3,减小了30.6%,说明渣-金界面张力对气泡夹带量有显著影响,渣-金界面张力越大,气泡夹带钢液量越小。这是由于气泡在到达渣-金界面时需要克服渣-金界面作用力而穿过,渣-金界面增大时阻力增加,因此,夹带钢液量降低。
3.2.2 渣-金界面面积
气泡通过渣-金界面夹带钢液进入渣层中,由于夹带量及夹带钢液滴在渣中的形状变化,影响了渣-金界面面积的变化,进而影响了渣-金界面作用效率。图9为数值模拟气泡上升通过渣-金界面产生夹带时渣-金界面面积变化。从图中可以看出,渣-金界面面积变化规律与体积变化规律类似。当气泡在钢液中上升未到达渣-金界面时,渣-金界面面积保持不变,当气泡上升到达渣-金界面时,钢液在气泡作用下进入渣中,渣-金界面面积开始增大,随着气泡继续上升将钢液夹带到渣层中,渣-金界面面积持续增大,渣中夹带钢液在界面张力和重力的作用下形状产生变化,渣-金界面面积持续变化,当形变稳定后,渣-金界面面积趋于稳定。
图9
图9
渣-金界面面积变化
Fig.9
Variations of slag-metal interfacial area as a fun-ction of time
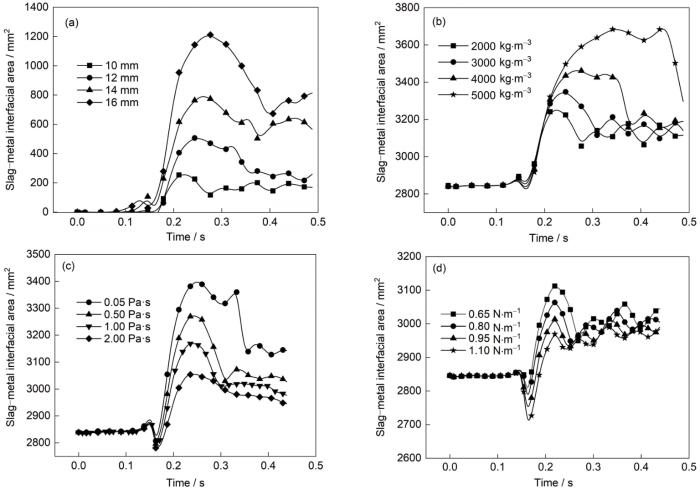
图10a为不同气泡初始直径对渣-金界面面积的影响。从图中可以看出,当气泡直径为10 mm时,渣-金界面面积增长仅为200 mm2左右,且整个过程中变化不大。气泡越大,渣-金界面面积增长越大。对比整个夹带过程中界面面积峰值,气泡直径从10 mm增加20%、40%和60% (12、14和16 mm)时,渣-金界面面积最大值分别增加了95.2%、208.0%和367.0%。可见,渣-金界面面积随着气泡增加而迅速增大,且呈非线性增长关系。实际冶炼过程中,在某一供气区间增加供气强度,产生较大气泡,将使更大量的钢液带入渣中,增加渣-金相互作用面积。
图10
图10
物性参数对渣-金界面面积的影响
Fig.10
Influences of bubble size (a), slag density (b), slag viscosity (c), and slag-metal interfacial tension (d) on the interfacial area
图10b为渣层密度对气泡夹带过程中渣-金界面面积的影响。渣层密度从2000 kg/m3增加到3000、4000和5000 kg/m3时,渣-金界面面积最大值分别增加了2.8%、6.4%和13.1%。可见,渣层密度的增加对于促进渣-金界面相互作用有积极作用,但是作用小于气泡直径增加的作用。
从以上分析可以看出,气泡尺寸,渣层黏度、渣层密度和渣-金界面张力对气泡夹带量均产生影响。其中,气泡尺寸对夹带量影响最大,当气泡小于一定尺寸时,不产生夹带,随着气泡尺寸增加,夹带量急剧上升。其次是渣层密度对夹带量的影响,渣层黏度和渣-金界面张力的影响较小。需要指出的是:除本研究所述的因素外,气泡速度、钢液特性、渣层厚度和渣-金界面相互运动等也可能对气泡在渣-金界面的夹带行为产生影响,其影响规律有待进一步研究。
4 结论
(1) 物理模拟实验中,气泡尺寸达到一定值时开始产生夹带并且夹带量均随气泡直径增大而增大。气泡尺寸增大时,夹带量迅速上升,与气泡尺寸增长呈非线性关系;夹带量随油层黏度增大而减小,随油层密度增大而增大,气泡直径较小时油层黏度和密度对夹带的影响不明显,气泡直径较大时影响显著。
(2) 数值模拟结果表明,气泡尺寸是影响钢液夹带量的最主要因素,气泡初始直径由10 mm增大到16 mm时,气泡夹带量增大了7.41倍;其次是渣层密度,渣层密度由2000 kg/m3增大到5000 kg/m3,气泡夹带量增大了62.34%;渣层黏度和界面张力在本研究数值范围内影响较小,渣层黏度由0.05 Pa·s增加到 2 Pa·s时,气泡夹带量减小了18.4%,渣-金界面张力从0.65 N/m增大到1.1 N/m,气泡夹带量减小了30.6%。
(3) 对渣-金界面面积变化的研究发现与夹带量类似的现象,气泡尺寸是影响渣-金界面面积变化的最主要因素。气泡初始直径为12、14和16 mm较气泡初始直径为10 mm时渣-金界面面积增量最大值分别增加了95.2%、208.0%和367.0%。渣层密度5000 kg/m3较渣层密度为2000 kg/m3时渣-金界面面积最大值增加了13.1%;渣-金界面张力和渣层黏度对气泡夹带有抑制作用,渣-金界面张力从0.65 N/m调高至1.10 N/m时,渣-金界面面积最大值减小6.4%,渣层黏度从0.05 Pa·s升高到2.0 Pa·s时渣-金界面面积最大值减小10.2%。
参考文献
Application of desulphurization technique by magnesium injection in molten iron
[J].
铁水喷镁脱硫技术的应用
[J].
Research on the effect of bottom blowing on bath stirring in a 250 t converter
[J].
250吨转炉底吹对熔池搅拌的影响研究
[J].采用物理模拟和数值模拟,研究了某钢厂250 t转炉底吹对熔池混匀时间、气液两相区速度、熔池低速区体积、炉底剪切力和气体能量利用率的影响。结果表明,熔池混匀时间随底吹气量增大而减少,随底吹孔数增加而减少。底吹孔数为12个时,底吹气量由15 L/min增至50 L/min,熔池混匀时间降低54.8%。底吹气量不变(50 L/min),底吹孔数由12个减至3个时,混匀时间增加52.9%。底吹枪数量减少,搅拌区域减小,熔池中“死区”和“低速区”体积比分别增加4.89%和28.9%。底吹枪减至3个时,单个底枪气量增大,气液两相区最大速度由0.34 m/s增至0.64 m/s,底吹孔处炉底所受剪切力增大52%,对炉底耐材寿命不利。从数值模拟结果也可发现,底吹工况的变化影响气体在熔池中的利用效率。底吹总气量增大时,熔池动能增加,但气体能量利用率降低。底吹气量较小时,底吹孔数的变化对气体能量利用率影响较小。底吹气量较大(50 L/min)时,相比于12个底吹孔,6个和3个底吹孔的气体能量利用率分别下降18.4%和23.3%。
Modeling and optimisation of gas stirred ladle systems
[J].
Mixing time and fluid flow phenomena in liquids of varying kinematic viscosities agitated by bottom gas injection
[J].
Effect of submerged entry nozzle argon blowing on slab quality
[J].
连铸板坯浸入式水口吹氩工艺研究
[J].
Modeling of three-phase flows and behavior of slag/steel interface in an argon gas stirred ladle
[J].
Study on the impact characteristics of coherent supersonic jet and conventional supersonic jet in EAF steelmaking process
[J].
Numerical simulation of multiphase flow in converter top blowing process
[J].
转炉顶吹过程多相流数值模拟
[J].
Optimization of the mixing time using asymmetrical arrays in both gas flow and injection positions in a dual-plug ladle
[J].
Review of mold flux entrainment mechanisms and model investigation of entrainment by shear-layer instability
[A].
The interfacial behavior of molten steel and liquid slag in slab continuous casting mold with electromagnetic brake and argon gas injection
[J].
板坯结晶器电磁制动和吹氩过程的钢/渣界面行为
[J].利用数值模拟方法研究了板坯结晶器电磁制动和吹氩耦合作用下吹氩量、拉速和线圈电流强度等不同工艺参数对钢/渣界面行为的影响规律, 分析了结晶器内液面波动指数F与液面波动间的关系.研究表明, 在一定拉速和电磁制动条件下, 吹氩量增加会加剧钢/渣界面的局部波动, F值随吹氩量增加而增大, 弯月面处的液渣厚度与F值呈线性递增关系; 在一定吹氩量和电磁制动条件下, 拉速增加并没有恶化水口附近的钢/渣界面波动, 而使F值增大, 弯月面处的液渣厚度与$F$值呈线性递减关系; 在一定拉速和吹氩量条件下, 增加线圈电流强度会加剧水口附近的钢/渣界面波动.
Removal behavior of inclusions in molten steel by bubble wake flow based on water model experiment
[J].
Numerical simulation for the influence of EMS position on fluid flow and inclusion removal in a slab continuous casting mold
[J].
Formation of metal droplets from gas bubbles bursting on iron melt
[J].
Bubble bursting phenomenon in gas/metal/slag systems
[J].
Characteristics of iron entrainment into slag due to rising gas bubbles
[J].
Distribution of metal droplets in top slags during ladle treatment
[J].
Influence of the interfacial tension on the droplet formation by bubble rupture in Sn(Te) and salt system
[J].
Influence of bottom bubbling rate on formation of metal emulsion in Al-Cu alloy and molten salt system
[J].
Observations of physical phenomena occurring during passage of bubbles through liquid/liquid interfaces
[J].
Onset of entrainment between immiscible liquid layers due to rising gas bubbles
[J].
Bubble motion and interfacial phenomena during bubbles crossing liquid-liquid interfaces
[J].In metallurgical and chemical engineering processes, the gas–liquid–liquid multiphase flow phenomenon is often encountered. The movement of bubbles in the liquid, and the influence of bubbles on the liquid–liquid interface, have been the focus of extensive research. In the present work, an air–water–oil system was used to explore the movement of bubbles and the phenomenon that occurs when bubbles pass through an interface with various oil viscosities at various gas flow rates. The results show that bubble movement is greatly influenced by the viscosity of the oil at low gas flow rates. The type of phase entrainment and the jet height was changed when increasing the gas flow rate. The stability of the water–oil interface was enhanced with increasing viscosity of the oil phase.
CFD Simulation of the phenomenon of passage of a bubble through the interface between two initially quiescent liquids
[J].
Multiphase particle simulation of gas bubble passing through liquid/liquid interfaces
[J].
Study of a three component Cahn-Hilliard flow model
[J].
Cahn-Hilliard/Navier-Stokes model for the simulation of three-phase flows
[J].