多晶体材料由大量结构相同但空间取向各异的结构基元——晶粒构成。相邻晶粒取向各不相同,由此不同的晶粒之间形成几何必需界面,称之为晶界(grain boundary,GB)。由于晶界两侧晶粒的原子排列存在一定差异,二者都力图使晶界上的原子排列符合于自己的取向,导致晶界上的原子排列不规则而造成结构疏松,使得晶界往往具有较高的能量,并由此导致晶界具有一些不同于晶粒的特性,从而影响着材料制备、加工和服役的方方面面。因此,深入理解晶界的塑性变形动力学机制是实现晶界工程的理论基础。当前,关于晶界及晶界变形的研究进展大致为:(1) 通过理论或实验表征提出几何模型来描述晶界及晶界缺陷的微观结构;(2) 在此基础上,结合实验和计算模拟探究晶界缺陷运动协调晶界塑性变形的动力学机制;(3) 晶界塑性变形对宏观材料形变、损伤的影响。针对不同的问题,学术界常采用双晶体系或多晶体系来分析晶界塑性的典型特征。对双晶体系,研究人员大多关注单个晶界的定量行为及其微观变形机制;对多晶体系,学术界侧重于分析多个晶粒的宏观统计性行为及其协调机制,如晶粒长大等。尽管学术界对晶界的塑性变形开展了大量研究,但其原子尺度的微观动力学机制长期缺失,导致不同晶界变形机制之间难以建立有效的关联,系统的晶界塑性变形理论尚未建立。本文将系统梳理晶界塑性变形机制的实验研究进展,在此基础上总结晶界塑性变形所涵盖的内容及其原子尺度机制,为晶界塑性变形理论的发展提供参考。
1 晶界及其结构
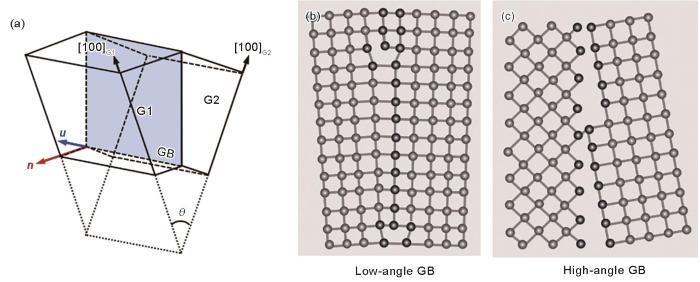
图1
图1
晶界的宏观几何自由度示意图
Fig.1
Schematics of macroscopic geometric freedoms of grain boundaries
(a) three-dimensional schematic of grain boundary geometry ( u —rotation axis; n —normal direction of grain boundary plane; θ—rotation angle; GB—grain boundary; G1, G2—neighboring grains)
(b) low-angle grain boundary (LAGB)(c) high-angle grain boundary (HAGB)
基于晶界的几何特征,学术界对晶界的结构模型开展了大量研究,并提出了若干构型。1934年,Taylor[1,2]率先提出了晶界的位错模型,将晶界简化为由晶格中刃位错规则排列形成的位错墙;1956年,Hirsch等[3]首次在透射电子显微镜(TEM)下观察到了变形态Al中的位错型界面。随后,Frank[4]和Bilby等[5]从晶界处的晶格相容性出发,提出了经典的Frank-Bilby公式( B = ( S
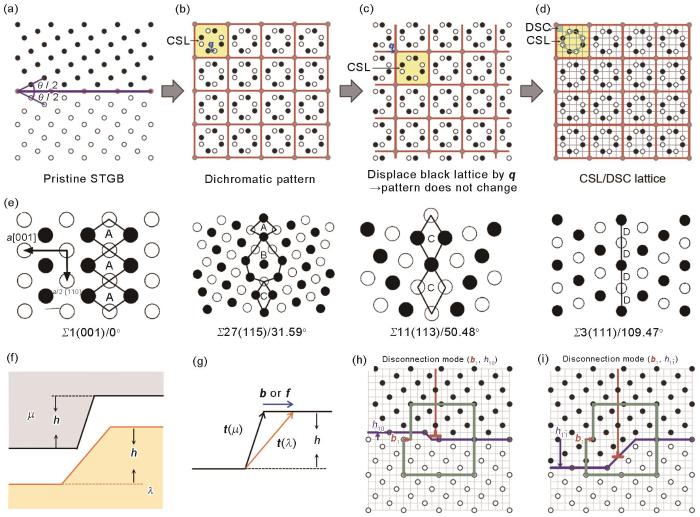
图2
Fig.2
Schematics of grain boundary model and disconnection geometry
(a-d) double crystal lattice with a Σ5 [100] symmetric tilt grain boundary and its CSL lattice[7] (The Burgers vectors of DSC dislocations are indicated by the blue arrows in Figs.2b and c, and CSL-based DSC lattice model is shown in Fig.2d. STGB—symmetric tilt grain boundary;
(e) structure units of different <110> symmetric tilt grain boundaries in Cu[11] (Σ1(001) grain boundary (single crystal) only contains A structure units; Σ11(113) grain boundary is composed of C structure units; Σ27(115) grain boundary, across which the tilt angle is between the above two grain boundaries, is comprised of A, B, and C structure units; Σ3(111) grain boundary, namely coherent twin boundary, is constructed by sequential D structure units; a—lattice constant) (f, g) geometric structures of grain boundary disconnections[15] (μ, λ—neighboring grain; h—step height; b —Burgers vector; f —Frank vector; t —translation vector) (h, i) different configurations on the same grain boundary[7] ( b1—Burgers vector of the disconnection; there are multiple possible step heights corresponding to a disconnection with b1, and the step height can be h1j = (1 + 5j)az, where j is integer and az is the size of the DSC unit cell; h10—step height with az;
为更好描述界面的结构特征及动态行为,研究人员[12~14]考察了大量界面(包括晶界、相界、孪晶界)的微观结构,首次提出了一种阶错(disconnection)的界面缺陷结构,如图2f和g[15]所示。阶错是一种同时具有特定长程应力场(用Burgers矢量 b 表示)和高度(h)组合的界面缺陷,其普遍存在于材料内的各类界面中,并影响着界面形变、相变、再结晶等过程[16,17]。若h较小,其长程应力场与位错趋于一致,如fcc金属中Σ3共格孪晶界上的孪晶位错等价于一个 b = 1/6<112>、h = 1d111 (其中d111为{111}晶面间距)的单层阶错;若h较大,则还需考虑阶错引起的界面切向旋转位移(即向错,disclination)。通常,同一晶界可包含多种不同的阶错构型(图2h和i[7]),阶错类型受晶界结构、晶界曲率、受力状态、温度等多方面因素影响。晶界阶错的形核、运动和交互作用深刻影响着晶界的塑性变形。分切应力作用下,晶界阶错沿晶界平面进行迁移,伴随发生晶界阶错前端的晶界原子发生局部重新排列,导致晶界迁移[7];不同的阶错组合( b, h)决定着宏观的晶界迁移耦合因子,即β[7]。在实际变形过程中,阶错的形核模式、构型以及交互作用等主导着晶界变形的表现形式。
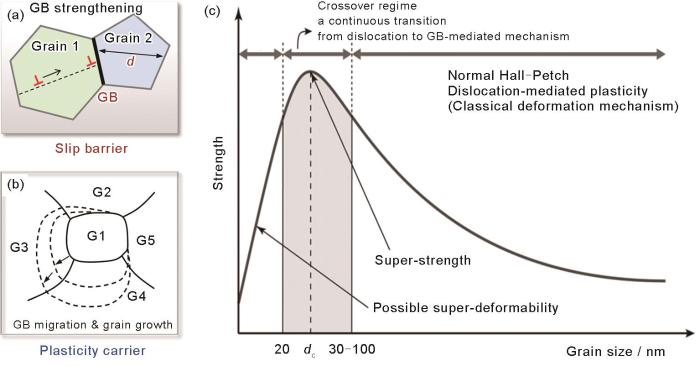
晶界的独特结构特征导致其呈现出有别于理想晶格的物理和化学特性。首先,晶界作为多晶材料中普遍存在的面缺陷,既可作为缺陷形核源又会对缺陷运动产生阻碍,从而对金属材料的塑性变形和强化有着重要影响(图3a)。该原理也是细晶强化的微观机理,在一定晶粒尺寸的范围内可同时提高材料的强度和塑性。其次,晶界结构尤其是其动力学行为控制着晶界塑性变形、晶粒生长等过程,从而对材料的力学性能、结构稳定性等产生重要影响。随着晶粒尺寸减小至纳米级,晶内的Frank-Read位错源被显著抑制,而晶界密度以及晶界原子比例的急剧增加又会激发晶界作为塑性变形的重要载体参与变形(图3b)。在纳米晶材料中,晶粒内的有限空间难以容纳大量晶格位错的运动与塞积;与此同时,晶界塑性变形的大量激活又会逐步释放应变能,从而抑制晶内位错塑性的发生。晶界迁移(grain boundary migration)、晶界滑动(grain boundary sliding)、晶粒转动(grain rotation)和晶粒粗化(grain coalescence,常伴随晶粒转动发生)等[18]诸多晶界变形机制的大量激活,使得晶界对纳米晶材料塑性变形的贡献愈发显著。晶界塑性的激发为金属纳米晶材料提供了额外的塑性变形能力,但也会诱发材料发生快速软化,产生反Hall-Petch效应,如图3c[19]所示。此外,晶界相对疏松的结构与较高的界面能也会导致合金元素和杂质原子的晶界聚集,改变晶界的局部化学成分、界面结构、相结构、错配度等,从而显著影响材料的物理性能(如电导率、扩散)和力学性能(如晶界脆性)。近年来,学术界基于晶界的结构特征和变形动力学行为提出了“晶界工程”的概念,通过晶界结构的调控、优化改善了高熔点金属、金属间化合物等材料的沿晶脆性[20]。
图3
图3
晶界变形与金属材料性能之间的关系[19]
Fig.3
Relationships between grain boundary deformation and properties of metallic materials
(a) strengthening of metallic materials due to the impediment of dislocation motion at grain boundaries (d—grain size)
(b) grain boundary deformation mediated plastic deformation of metallic materials (G1-G5—different grains in grain boundary networks; dotted lines—sequential grain boundary positions during grain growth)
(c) change law of the strength of polycrystalline metal materials with the grain size[19] (dc—critical grain size between Hall-Petch relation and “inverse” Hall-Petch relation)
2 晶界塑性变形机制研究进展
晶界塑性变形的研究手段一般包括实验观察和理论模拟。这里分别从实验和模拟的角度简要概述晶界塑性变形行为的研究进展。
2.1 晶界变形的实验观测
晶界塑性变形机制的实验观察主要在光学显微镜(OM)、X射线衍射仪(XRD)、扫描电镜(SEM)、TEM等分析设备中开展。随着测试方法和观测精度的不断提升,研究人员可以更加深入系统地研究晶界变形的微观机制,并且结合原位力学测试和跨尺度实验等方法,从不同层面精准解析晶界演化的动态过程。Okada等[21]利用SEM的背散射电子衍射(EBSD)成像系统,以Σ3 n 晶界为对象,研究了Al和Cu多晶材料中三叉晶界对晶界滑动的抑制与调节作用,并发现在蠕变过程中褶皱形成的难易程度会影响晶界开裂。Winning和Rollett[22]基于XRD,自行设计了一套块体双晶加载测试平台,并通过参考点标记法研究了fcc金属双晶晶界的运动激活焓。结果[22,23]表明,晶界的运动激活焓和晶界可动性在小角晶界和大角晶界之间存在一个明显的转变,而在两侧的区间内随晶界取向差无明显变化。Molodov等[24,25]利用类似方法分析了Al双晶中不同晶界的迁移行为,计算了<100>倾转小角晶界的剪切耦合因子,还定量揭示了不同倾转轴Σ7大角晶界的迁移速率与其温度敏感性。
相较于OM和SEM,TEM具有更高的空间分辨率,可获得更加全面、详细的微观结构演化信息。目前,晶界塑性变形的原位电镜研究主要利用多晶/纳米晶薄膜或纳米双晶体实现。对薄膜样品,可将试样固定至特殊设计的拉伸基片并施加轴向载荷实现拉伸[26],或在双倾原位加热样品杆中利用热膨胀系数各异的双金属片实现热-力转换[27]。薄膜试样制样相对简单,但难以精确调整晶界结构,使得分辨率受到一定限制。本团队[28]也利用原位电子探针样品杆发展了纳米双晶原位制备-力学加载的耦合实验方法,可获得含不同晶界的高质量纳米双晶体,并可施加稳定的拉伸、压缩、剪切、循环变形等载荷,有助于原位高分辨观察,但适用的材料相对有限。也有研究人员[29]利用纳米压痕的方法,将晶界变形与载荷变化相关联来研究晶界的塑性变形行为及其强化效应,但该方法的分辨率相对较低。
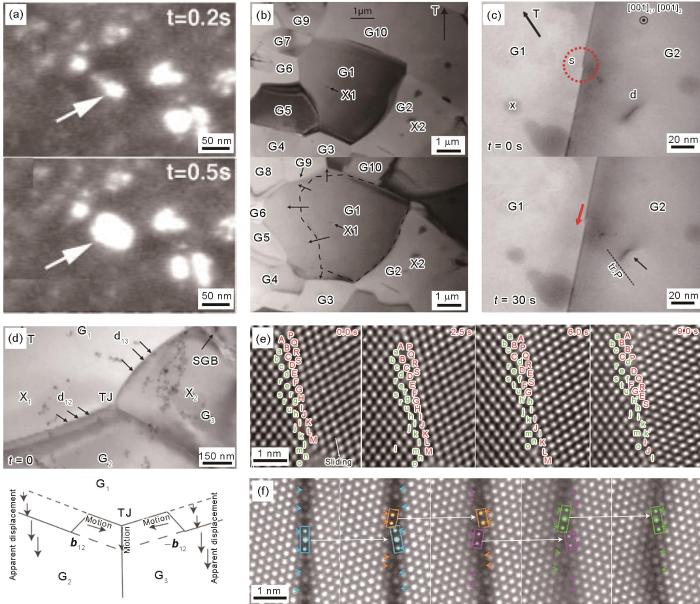
基于这些原位纳米力学测试方法,学术界对晶界的塑性变形行为开展了系统的实验研究,揭示了一系列典型的晶界变形机制,包括晶界迁移的台阶机制、位错机制和晶界-缺陷交互机制等[26,30~32],为阐明金属材料的晶界动力学行为提供了有力的证据。Bobcock和Balluffi[33]于20世纪80年代研究了热应力下Au、Al薄膜中的晶界行为。结果表明,Au中的Σ5晶界和混合晶界可通过晶界位错的滑移-攀移协调运动诱发晶界迁移行为[33];而Al中的大角晶界迁移则主要通过晶界台阶处的原子协调迁移与局部重构(shuffling)进行[34]。Jin等[35]对超细晶Al进行原位纳米压痕测试,观察到了晶界迁移、晶粒旋转协调作用下的晶粒长大行为。Shan等[36]对Ni纳米晶薄膜开展原位拉伸测试,并结合TEM暗场像观察,首次揭示了纳米晶Ni (晶粒尺寸约为10 nm)在塑性变形过程中的晶粒转动以及由此诱发的晶粒团聚行为,并系统阐明了金属纳米晶材料中晶界主导的塑性变形机制(图4a[36])。此后,Legros等[26]和Rupert等[37]发现,Al纳米晶薄膜的裂纹尖端会产生明显的晶界迁移现象,诱发纳米晶晶粒发生快速长大。Mompiou等[30]和Caillard等[38]借助原位高温力学样品杆对超细晶Al开展原位热-力耦合加载,观察到了多晶体中经典的晶界剪切耦合迁移过程及其导致的晶粒长大(图4b[30])。这一过程中,晶界运动通过晶界阶错的扩展进行,阶错扩展不涉及原子的长程扩散,但需通过近邻原子的局部重构与剪切载荷的共同作用进行。Rajabzadeh等[31,32]进一步研究了纯Al双晶体的大角晶界迁移行为(图4c[31])。研究发现,晶粒内部位错 b = 1/2<110>可扩展进入晶界,并在晶界发生分解产生晶界阶错,最终诱发连续的剪切耦合晶界迁移。在Al多晶薄膜中,晶界台阶可沿晶界面运动并最终湮灭在晶界三叉点处,导致晶界与三叉点的协调迁移(图4d[31])。也有学者借助原位纳米压痕测试分析了晶界对材料强化的贡献。Imrich等[29]发现,相较于单晶体,含大角晶界的Cu双晶微米柱往往具有更高的压缩强度、较强的加工硬化和较小的载荷突降,这种行为主要来源于位错-界面交互作用。在Al、Cu、Ni、Ta、Sn等亚微米试样中,单一晶界对强度和塑性的影响呈现出类似的特征,且随试样尺寸的减小同样表现出“越小越强”的尺寸效应[39~43]。需要指出,块体纳米晶材料随晶粒尺寸减小常常发生强度的反Hall-Petch效应,即当晶粒尺寸减小至某一临界值后会发生软化;晶粒尺寸与试样尺寸相耦合则会进一步加剧纳米晶材料的软化行为。例如,随试样尺寸减小,晶粒尺寸12 nm的Pt纳米柱[44]和晶粒尺寸60 nm的Ni-W纳米晶[45]均表现出“越小越弱”的反Hall-Petch关系。这种转变主要源于尺寸效应诱发的晶界塑性变形与晶粒内部位错运动之间的动态竞争。这些基于电子显微镜的原位纳米力学测试,将晶界的动态演变与材料的塑性变形直接关联了起来,丰富了学术界对晶界塑性变形行为的认识,促进了晶界塑性变形理论的完善与发展。
图4
图4
晶界变形行为的实验研究[30,31,36,54,55]
Fig.4
Experimental investigations on grain boundary deformation behaviors
(a) deformation-induced grain rotation and grain agglomeration in nanocrystalline Ni[36] (t—time; the arrows indicate the growing grain)
(b) shear-coupled grain boundary migration[30] (G1-G10—different grains in grain boundary networks; X1, X2—pre-existing precipitates acting as fiducial markers; T—tension direction)
(c) movement of steps (s) on the 76.4°<001> grain boundary in Al bicrystals at 400oC[31] (s—2 nm height step; d—a lattice dislocation; x—a fixed point;
(d) dislocations move along the grain boundary and annihilate at the triple junction of the grain boundaries[31] (TJ—triple junction; d12, d13—moving grain boundary dislocations during grain boundary migration; arrows in the bottom schematic indicate the directions of grain boundary step motion, grain boundary migration and triple junction motion; SGB—subgrain boundary; b12—Burgers vector of grain boundary dislocation)
(e) atomically resolved sliding at an asymmetric <110>-tilt 20.1° GB[54] (Atom-columns on the face of left grain are marked by green lowercase letters, and atom-columns on the face of right grain by red uppercase letters)
(f) local atomic displacement during the motion of Σ7(2
受时间和空间分辨率的制约,上述原位研究难以解析晶界塑性变形的原子尺度动力学机制。近年来,球差校正电子显微技术和原位纳米力学技术的不断进步逐渐将晶界动态行为的研究推进至原子尺度。Merkle等[46~50]早在21世纪初就利用原位加热研究了Al和Au薄膜试样中不同类型晶界的演化行为。他们发现,晶界迁移主要通过界面滑动、台阶迁移、界面原子的协调迁移3种机制进行,其驱动力主要来自于晶界曲率和界面能。晶界迁移具体通过哪种机制进行主要取决于晶界结构。多数大角晶界(如普通大角晶界)通常以晶界原子的协调运动发生迁移;能量较低的大角晶界,如(113)对称倾转晶界,主要通过台阶机制进行,晶界台阶侧向滑动导致晶界迁移[46,51];伴随晶界迁移往往会发生晶界原子的协调运动,以协调局部的晶格结构,导致近邻晶粒发生长大[46]。电子显微镜空间分辨率和图像获取速度的不断提升进一步推动着晶界变形机制的研究。晶界迁移机制方面,Radetic等[52]发现Au薄膜的晶界迁移动力学行为受晶界阶错形核和扩展的影响;Bowers等[53]利用高分辨扫描透射显微镜(STEM)和图像快速获取-叠加处理方法分析了Au双晶中90°<110>晶界的迁移行为,发现晶界阶错通过晶界原子的协调运动发生合并,随后诱发晶界迁移,该过程伴随发生层错从晶界的形核;本课题组[28]则系统研究了Σ11(113)对称倾转晶界的剪切耦合迁移行为,揭示了晶界迁移过程中的阶错形核、合并、分解等动态交互过程,发现不同类型阶错的相互转变有助于克服阶错的滑移阻力。最近,Wang等[54]利用高分辨球差校正透射电镜研究了Pt双晶中普通非对称晶界的晶界滑动行为,发现此过程中除了晶界面之间的相对滑动外,还会伴随发生晶界阶错运动主导的晶界面附近的原子转移行为(图4e[54])。非金属材料体系(如α-Al2O3)中的晶界阶错同样会发生局部原子重排,导致晶界构型在不同低能亚稳态之间发生转变(图4f[55]),最终诱发晶界迁移[55]。这些研究表明,晶界的剪切耦合迁移与阶错动力学行为密切相关。
2.2 晶界迁移的模拟计算研究
原子尺度模拟在验证实验结论的同时,能够给出实验中难以分辨的晶界原子尺度演化过程,因此也获得了大量关注。研究人员[56~61]利用分子动力学(molecular dynamics,MD)模拟深入分析了阶错的动力学行为及其诱发晶界剪切耦合迁移的微观机制,揭示了Σ11(113)晶界在切应力作用下的阶错运动与晶界迁移耦合的动态过程,如图5a[61]所示。一般而言,晶界迁移通过晶界阶错的形核、扩展进行;阶错形核可分为均匀形核和非均匀形核2种机制,其受晶界结构、微区应力、剪切方向等因素的影响[58~60];晶界迁移过程中,存在多种阶错类型之间的耦合与竞争[56]。Wan和Wang[62,63]突破了电镜二维图像的局限性,利用计算模拟分析了fcc金属中Σ11和Σ9晶界上的三维阶错构型,并揭示了剪切加载下阶错在晶界平面上形核与扩展的组态。图5b和c[62]分别为Σ11(113)晶界上阶错沿晶界法向的俯视图与三维透视图。该结果表明,晶界面上的阶错具有准三维结构,且存在与位错类似的扭折结构[64]。在复杂晶界网络中,晶界三叉点在阶错形核、晶界运动中扮演着重要角色[57],学术界基于此现象发展了晶界-三叉点耦合迁移理论和基于阶错机制的微观结构演化连续模型[65,66]。这些跨尺度的计算和模拟在一定程度上验证了晶界塑性变形行为的实验结果,丰富了人们对晶界塑性变形动力学的认识。
图5
图5
fcc金属双晶中Σ11(113)晶界迁移的阶错机制[61,62]
Fig.5
Disconnection mechanism of Σ11(113) grain boundary migration in fcc metallic bicrystals
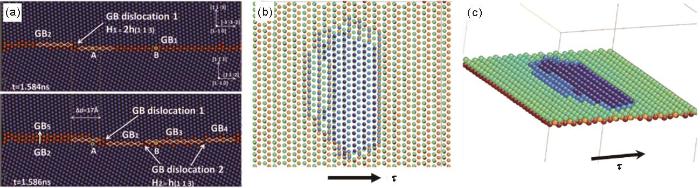
(a) front view of GB disconnection from <110> orientation[61] (GB1-GB4—different GB segments divided by GB disconnections; H1, H2—single- and double-layer GB disconnections)
(b) top and (c) perspective views of a GB disconnection from <113> orientation[62] ( τ —shear direction)
3 晶界缺陷与晶界塑性变形动力学机制
多晶体材料的晶界结构复杂多样,其晶界主导的塑性变形也表现出多样化的行为。在诸多晶界塑性变形机制中,晶界迁移是一种较为本征的晶界塑性变形模式,晶界滑动、晶粒转动、晶粒粗化等过程均会伴随发生晶界迁移。第2小节从晶界的微观结构和晶界本征缺陷出发,初步介绍了晶界迁移机制的研究进展。然而,尽管目前已有大量关于晶界迁移的理论、实验和模拟研究,学术界对于晶界变形物理本质的认识仍存在较大的局限性,主要原因在于晶界塑性变形原子尺度机理的缺失,这使得系统构建晶界结构-动力学关系面临极大的挑战。本小节将从晶界阶错的动力学行为出发,深入分析晶界的迁移机制并初步构建晶界塑性变形的理论体系。
3.1 晶界本征缺陷与晶界迁移模型
实验和理论模拟均表明,晶界迁移通常伴随晶界的剪切而发生,因此常被称为剪切耦合的晶界迁移(shear-coupled GB migration)。其耦合因子(β)由晶界迁移量(m)与剪切量(s)的比值定义,即β = s / m。随着研究的逐步深入,学术界从简单到复杂提出了多种模型来描述晶界的剪切耦合迁移行为。基于Read和Shockley[6]提出的小角晶界位错模型,Cahn等[67]认为某些大角晶界也可用位错构型进行描述(图6a[67]),他们分析了fcc金属中的<001>倾转晶界,成功预测了不同取向差下的晶界剪切耦合迁移行为,并验证了晶界迁移的β随取向差和温度的变化行为[67,68]。Babcock和Balluffi[34]则认为,晶界迁移可通过晶界台阶附近的原子重排(shuffling)进行(图6b[34])。Rae和Smith[69]以及Guillope和Poirier[70]针对CSL晶界(以及近CSL晶界)的迁移,提出了一种完全离散剪切位错模型(discrete shear complete dislocation model)。该模型认为,完全离散剪切位错具有台阶状的结构特征,这种位错可沿晶界面发生运动,并伴随发生晶界原子的重新排布(图6c[70]);若取向偏离CSL晶界时,晶界上会形成一个二次完全离散剪切位错以消除失配应力,其运动方向理论上与晶界面垂直[71]。Caillard等[38]则将剪切耦合的晶界迁移理论进一步推广至多晶材料中普遍存在的非CSL晶界结构,提出了一种剪切迁移几何模型(shear migration geometrical model, SMIG) (图6d[38])。Hirth和Pond等[12~14]在总结上述模型的基础上,结合对晶界、孪晶界、相界的大量研究,认为上述模型中的晶界缺陷均可归结为晶界阶错,一种同时具有特定长程应力场( b )和高度(h)组合的晶界缺陷结构,如图2f和g[15]所示。通常,特定晶界可拥有多种不同( b, h)组合的阶错结构,其决定着宏观晶界迁移的耦合因子,即β = s / m[7]。晶界迁移一般由形核能较低的阶错主导;当温度较高或应力较大时,更高能量的( b, h)也可被激活,导致宏观耦合因子β的改变[72]。
图6
Fig.6
Theoretical model of tilt grain boundary migration
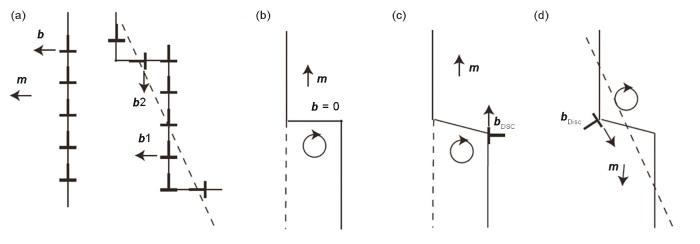
(a) Cahn model of symmetric and asymmetric grain boundary migration[67] ( m —the motion direction of grain boundary defects; the latter case involves the cooperative gliding of two sets of dislocation families of Burgers vectors b 1 and b 2)
(b) pure shuffling model[34] (circles—atomic rearrangement)
(c) discrete shear complete dislocation model[70] ( bDSC—Burgers vector of secondary discrete shear complete edge dislocation)
(d) shear complete dislocation model (SMIG) model[38] ( bDisc—Burgers vector of GB dislocation step, i.e. disconnection)
3.2 晶界阶错的原子尺度动力学行为
晶界阶错的原子尺度动力学行为决定着剪切耦合的晶界迁移。平直晶界的动力学行为主要由晶界阶错的形核、扩展、湮灭和交互作用等主导,其中阶错形核动力学是晶界迁移速率的决定因素。根据阶错的形核位置,可将阶错形核机制划分为均匀形核和非均匀形核,前者主要通过晶界自身分解形成阶错对,后者主要包括自由表面形核和晶界三叉点形核。Zhu等[28]结合具有高空间分辨率的球差校正透射电子显微镜和稳定的原位力学实验方法对fcc金属Au中常见的低能Σ11(113)倾转晶界开展了系统测试,揭示了阶错主导的晶界迁移原子尺度机制。Au纳米晶体在剪切加载下,其自由表面与Σ11(113)晶界的交互点处容易产生应力集中,表面处几何约束的缺失容易诱发局部剪切,促进阶错的形核(图7a[28])。而在纳米晶和多晶材料中,表面形核机制被大幅抑制,取而代之的是晶界网络中大量三叉点处的阶错形核(图7b[28])。需要强调的是,晶界三叉点处的阶错形核通常伴随着多个晶界之间的协同结构演化以及晶界三叉点的迁移。晶界均匀形核在分子动力学模拟中被大量观察到,阶错通常以偶极子的方式通过局部原子位置的波动产生(图7c[7])。然而,相比于阶错的表面和三叉点形核,实验中尚未直接证实这种晶界内部的均匀形核机制。这是由于,一方面均匀形核的能垒较高(一般为表面形核的2倍以上),另一方面实际材料中存在大量缺陷和应力集中位点,极大压缩了晶界均匀形核的空间。
图7
Fig.7
Atomic-scale dynamics of grain boundary disconnections
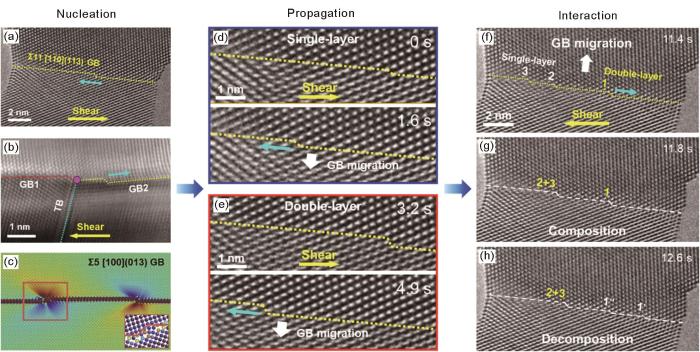
(a-c) nucleation mechanism of grain boundary disconnections: (a) free surface nucleation of Σ11(113) grain boundary disconnections in Au bicrystals[28]; (b) triple junction nucleation in Au nanocrystalline metals[28] (TB—twin boundary); (c) homogeneous nucleation of disconnections in Σ5(013) grain boundary in Cu bicrystals[7] (Inset shows the atomic structure of the disconnection in the region marked out by the rectangle) (d, e) propagation of single-layer (d) and double-layer (e) disconnections and coupled grain boundary migration under shear loading[28] (f-h) dynamic coalescence and decomposition of grain boundary disconnections[28]
原子尺度的阶错动态分析还表明,同一形核位置可产生多个不同类型的晶界阶错,多种阶错同时参与晶界迁移过程。例如表面形核机制可在Σ11(113)晶界上同时产生单原子层( b = 1/22<471>)和双原子层( b = 1/22<332>) 2种阶错。在水平方向的剪切作用下,单层和双层阶错均沿晶界平面侧向滑移(图7d和e[28]);由于本征高度不同,阶错在滑移的过程中引发后侧晶界相应地沿[113]方向迁移1或2个原子层(如白色箭头所示)。最终,沿(113)晶界平面运动的阶错在纳米双晶的表面湮灭,导致晶界整体向下移动1或2个原子层;而连续的阶错运动可诱发Σ11(113)晶界的大范围迁移。与晶内位错类似,阶错运动过程中还会发生阶错之间的交互作用。例如,Σ11(113)晶界的迁移过程中,多个单层或双层阶错经常在晶界上共存并频繁地发生动态交互作用。当不同类型阶错沿晶界同向运动时,可发生2个单层阶错的合并或1个双层阶错的分解,如图7f~h[28]所示。相应的动态交互作用与不同阶错间的长程相互作用及能量转换密切相关。当阶错沿晶界相向运动时,则会发生阶错相消或湮灭。大量实验表明,阶错间的动态交互作用与转换过程在晶界迁移过程中十分普遍,这表明阶错主导的晶界迁移过程不仅包含阶错的依次形核与滑移,还经常通过阶错间的动态交互作用来不断调节晶界的迁移速率。需要指出,近期的MD模拟[73]报道了孪晶界在面外扭转作用下转化为由大量几何必需位错缠结构成的扭转晶界,在不需要进行孪晶界迁移的前提下即可实现退孪生,这与面内载荷导致的晶界迁移模式是不同的。
多尺度下的晶界变形行为研究进一步验证了阶错主导的晶界动力学机制的普适性及其对材料力学性能的影响[74]。针对块体多晶材料开展的(> 1 μm)原位力学测试也观察到了类似的台阶主导的晶界迁移行为[31,75,76],然而晶界运动的微观机制受分辨率限制仍不清楚。上述晶界阶错的原子尺度动力学机制可以很好地解释晶界通过台阶侧向运动发生晶界宏观变形的现象,进一步说明了晶界微观动力学机制对实际多晶材料的重要意义。研究表明,阶错主导的晶界迁移在金属纳米晶薄膜的塑性变形和损伤断裂中发挥着重要作用。Liebig等[75]通过原位力学实验,报道了拥有良好变形能力的Au块体薄膜样品,其在保持高强度的同时,可容纳≥ 10%的塑性变形,这种异常高的延展性主要来源于晶界滑动和阶错主导的晶界迁移。类似地,低倍TEM下同样可观察到由层层台阶的形核、侧向运动及交互作用实现较大幅度的孪晶界迁移[76]。此外,相较于低温下多数晶界通过特定类型的阶错实现大幅剪切变形,高温加载下的晶界阶错活动更加丰富,多个不同构型的阶错可同时启动、交互作用,触发晶界滑动或非剪切耦合的晶界迁移[65,77,78];也有研究[21,79,80]报道了块体材料中由晶界迁移与晶界滑动耦合的晶界协调变形(尤其在三叉晶界处的晶界变形),其中的晶界阶错运动可在一定程度上提高材料的变形能力。需要指出的是,晶界阶错(台阶)在不同金属材料体系或不同加载环境下的表现形式不尽相同。例如,阶错在fcc金属中的微观表现形式通常为单层及双层阶错的运动以及交互作用(包括合并与分解)[28,81,82]。相对地,在hcp金属体系中晶界阶错通常表现出更大的台阶高度,例如对于其孪晶界,七层高度的晶界阶错能量最低,因而最为常见[15,17];这种高度的台阶运动在低倍TEM下相对于fcc中的台阶运动更易于捕捉,并且其通常具有向错应力场,在运动的过程中可通过发射缺陷的形式得到缓解[15,17]。由此可见,阶错主导的晶界变形对提高实际金属多晶材料延展性有一定贡献,可抑制或延缓材料的缩颈及断裂失效[75]。此外,阶错运动造成的晶界滑动,尤其是其在三叉晶界处的协调变形,可能会对多晶材料在高温下的晶界蠕变或应力松弛产生重要影响。
3.3 缺陷交互作用对晶界塑性变形的影响
晶体中通常存在大量晶格缺陷,这些晶格缺陷在塑性变形过程中不可避免地会与晶界发生交互作用,从而影响甚至改变晶界的变形机制。位错与晶界的交互作用通常包括位错在晶界处发生塞积(pile-up)、晶界吸收位错(absorption)、位错滑移穿越晶界(transmission)或在晶界处发生反射(reflection)。大量研究表明,位错能否穿越晶界主要取决于晶界两侧滑移系的连续性、分切应力和晶界残余位错的Burgers矢量大小,这种行为可由经典的Lee-Robertson-Birnbaum (LRB)准则[83]和m'因子(m' = cos(ψ)cos(κ),其中,κ和ψ分别为滑移矢量和滑移面法向与载荷轴向的夹角)[84]进行理论描述。Kacher和Robertson[85]通过观察304不锈钢中不全位错与晶界的交互作用,发现位错滑移穿越晶界由其滑移穿越后留下的晶界残余阶错的Burgers矢量控制,从而验证了位错穿越晶界准则。温度升高并不影响位错穿越晶界的基本机制,但会降低晶界吸收和重新发射位错的能垒,导致多种机制之间存在一定竞争。Zhu等[86]则进一步研究了晶格缺陷的交互作用下的晶界迁移行为,通过分析Au双晶中单一的Σ11(113)晶界与位错、层错、孪晶等晶格缺陷交互作用机制及其对后续晶界迁移行为的影响,更深层次地阐释了晶格缺陷交互作用下的晶界变形行为(图8a~g[86])。原子尺度动态分析表明,全位错核心被Σ11(113)晶界吸收后会改变晶界局部的应力场,促使晶界向相邻晶粒内部发射层错,并在晶界上留下一个可动的残余晶界阶错(图8a和b[86])。这个可动残余阶错既可沿晶界运动,参与晶界变形,也可与晶界上的其他阶错发生湮灭或合并,保证晶界的连续迁移能力(图8c~e[86])。某些情况下,晶界与位错的交互作用也会产生不可动阶错;不可动阶错会诱发局部应力集中,导致其两侧晶界发生非协同迁移。Σ11(113)晶界与层错、孪晶等面缺陷发生交互作用时,晶界-孪晶界的交互点可作为晶界阶错的有效形核位点,通过交点处的耦合结构演化实现其协调变形,包括晶界迁移和孪晶的同步长大或缩小(图8f和g[86])。其中,全位错和层错在与晶界发生交互作用时表现出强烈的滑移几何依赖性,例如当晶界两侧的滑移连续性较差时位错难以穿越晶界,这与经典LRB几何准则[83]相对应。Rajabzadeh等[32]同样发现,Al双晶体中的晶内位错在进入Σ41 [001](540)大角晶界后会分解出可动晶界位错与不同类型的晶界阶错(其Burgers矢量通常包含平行于晶界的滑移分量和垂直于晶界的攀移分量),从而参与晶界变形。由于缺陷与晶界的交互作用会产生新的可动晶界阶错,其可作为额外的晶界阶错非均匀形核源[28,32],因此对多晶材料的晶界塑性变形具有普遍意义。Kondo等[87]进一步分析了SrTiO3中的Σ5大角晶界和小角晶界对位错运动的阻碍作用,认为晶界对位错运动的阻碍作用不仅仅取决于几何因素,同时受晶界核心附近的局部结构稳定性的影响,并且这种影响对小角晶界来说更为明显(图8h[87])。位错-孪晶界交互作用也会对孪晶界的迁移造成影响[88~91]。根据位错滑移系与孪晶界面的几何关系,位错与孪晶界的交互作用可分为3种模式[92]:(1) 位错滑移面与滑移方向均平行于孪晶界(软模式I),其中当位错滑移面沿孪晶界时则可诱发孪晶界迁移和退孪生;(2) 位错滑移方向平行于孪晶界,但位错滑移面倾斜于孪晶界(硬模式I);(3) 位错滑移面与滑移方向均不平行于孪晶界(硬模式II)。硬模式I和II中,位错-孪晶界交互作用后会在孪晶界上残留滑移面沿孪晶界的部分位错,诱发孪晶界迁移和退孪生。多晶材料中,位错也会在晶界与孪晶界交割点附近形核(孪晶界位错),随后沿着孪晶界扩展,导致退孪生和材料软化[93]。
图8
Fig.8
Interactions between grain boundary and lattice defects
(a, b) full dislocations interact with Σ11(113) grain boundary in Au bicrystals with the emission of stacking faults from the grain boundary[86] (S and D—the pre-existing single- and double-layer GB disconnections, respectively; 1-4—full dislocations; the triangles indicate crystal planes in two neighboring grains) (c-e) atomistic mechanism of dislocation core decomposition at grain boundaries[86] (The yellow and white rhombus delineate the C type structure units on the flat GB and at the disconnection core, respectively; the purple and red irregular rhombus indicate the distorted atom columns induced by the long-range stress field and the core of the incoming dislocation, respectively) (f, g) interaction and coordinated deformation between Σ11(113) grain boundary and nanotwins in Au[86] (The purple arrows indicate the moving direction of a disconnection D; the cyan arrow delineates the rotation of the twin-GB intersection facets; the numbers in each snapshot indicate the distance (in the context of d113) of the right GB segment from the reference point) (h) dislocation transmission across LAGB in SrTiO3 (STO)[87] (The green and red arrows indicate the grain boundary position and the dislocation that impeded on the grain boundary plane, respectively)
需要指出,晶内位错的运动会对材料的塑性变形产生重要影响。 这一过程中,晶内缺陷必然与晶界的本征塑性变形发生竞争,从而影响晶界变形行为。Wang等[27,94,95]通过大量研究发现:Pt纳米晶内可存储密度高达6.4 × 1016 m-2的大量位错,位错在晶内发生交互作用、形成Lomer位错或相互湮灭;这些位错交互作用会在一定程度上导致晶粒的结构松弛并抑制晶界变形;伴随晶粒尺寸减小,纳米晶的变形机制由较大晶粒中(d > 6 nm)的晶内位错滑移逐渐转变至较小晶粒中(d < 6 nm)的晶粒旋转。Mompiou等[96]和Colla等[97]的研究结果也证实了位错湮灭是导致纳米晶材料发生结构松弛的主要原因,相比之下,晶界对纳米晶材料的蠕变变形并未产生明显影响。鉴于原位测试中较小的试样厚度,晶粒之间的约束效应相对较弱,晶界变形和晶内位错运动之间的竞争有待进一步考察。
在块体多晶材料中,由于大量位错源的启动,晶界-位错的交互作用更为频繁,对晶界变形及材料力学性能产生巨大影响。例如,多晶材料的疲劳断裂往往与晶界变形及晶界-位错交互作用密切相关。循环应力下,晶粒内运动的晶格位错在受到晶界的阻碍作用后会在晶界处塞积并发生应力集中,经长期动态作用可诱发晶界开裂[98~110]。张哲峰团队[98~104,109,111~113]基于SEM结合EBSD及电子通道衬度(ECC)等技术,系统研究了循环加载下晶界与裂纹的耦合行为,阐明了决定晶界、孪晶界是否开裂的控制因素。块体多晶材料中,疲劳裂纹是否在晶界处形核、扩展取决于晶界结构与密度、晶界与驻留滑移带的交互作用、加载轴与晶界面的相对取向、晶界能量等多种因素。晶界结构对晶界疲劳开裂的影响大致为:小角晶界和非共格孪晶界的疲劳开裂抗力强于大角晶界,而共格孪晶界的疲劳裂纹抗力介于以上2者之间(图9[98,99])。类似于晶界-位错的原子尺度交互机制(图8[86,87]),晶界两侧的滑移连续性从根本上决定了位错/滑移带穿过晶界的难易程度,这也是影响晶界疲劳开裂行为的关键因素[98]。小角晶界和非共格晶界两侧滑移连续性较好,晶内位错/滑移带较容易穿过晶界,不易引发晶界附近明显的应力集中,因此疲劳开裂抗力较好(图9a和c[98]);因晶格位错穿过晶界分解出的晶界缺陷(如晶界位错或阶错)的运动可引发小角晶界和非共格孪晶界的迁移,消耗疲劳加载所做的部分功,进一步提高材料的晶间疲劳开裂抗力[98]。而对于两侧滑移连续性较差的大角晶界,晶格位错难以穿越,很难发生分解并塞积在晶界附近,不能为后续晶界变形提供足够的缺陷源(如全位错与晶界反应分解得到的二次阶错源),最终位错塞积导致的应力集中诱发晶界处微裂纹的萌生[98,101](图9b[98])。共格孪晶界作为一种具有特殊对称性的大角晶界,其本征的疲劳断裂行为与小角和大角晶界有所差异,表现出强烈的加载方向依赖性(图9d[99]):当共格孪晶界与加载方向平行或垂直时,表现出较好的疲劳断裂抗力,可用于调控材料的疲劳性能[99,102~104]。此外,通过适当的合金化,降低金属层错能与晶界能量,也可在一定程度上改善晶界的疲劳开裂抗力[99,104]。相比传统晶粒尺寸的材料,纳米晶材料拥有更高的疲劳断裂抗力,但对于疲劳裂纹扩展的阻碍作用通常较弱[18,114];裂纹一旦形核,微裂纹可沿晶界发生快速贯穿[115]。
图9
Fig.9
Fatigue cracking modes for different GBs in bulk metals
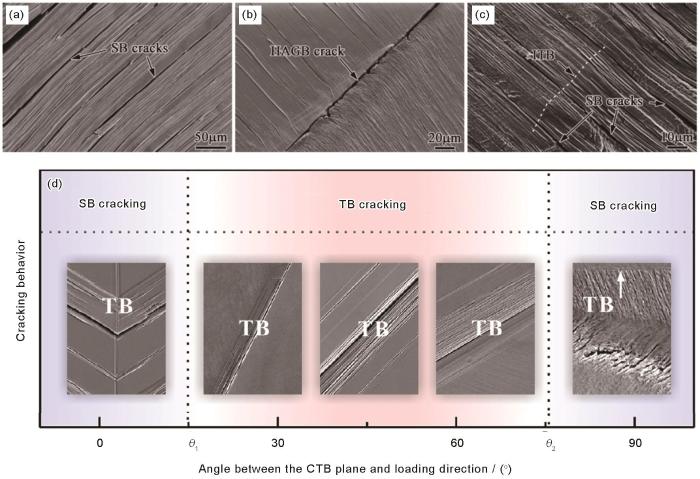
(a-c) fatigue cracking morphologies of the samples with a LAGB (a), a HAGB (b), and an incoherent twin boundary (ITB) (c)[98] (SB—slip band)
(d) orientation-dependent cracking mode for TB[99] (CTB—coherent twin boundary; θ1, θ2—critical angle values between different cracking modes for TB)
3.4 晶界结构与晶界网络的影响
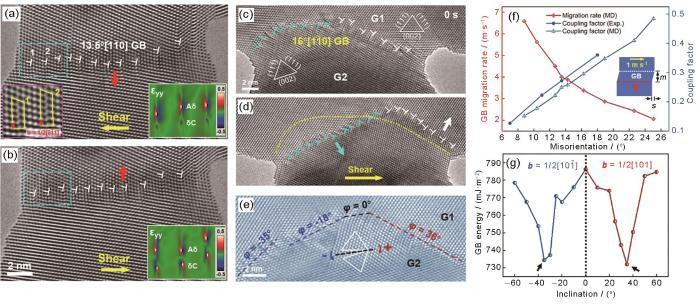
室温下fcc金属中大角晶界的迁移行为由阶错主导,具体表现为晶界阶错在应力作用下通过不同方式发生形核、沿晶界面侧向滑移并伴随发生阶错核心处的局部原子位移,最终诱发晶界迁移。相比大角晶界受限于阶错形核的塑性变形机制,由规则排列的几何必需位错构成的小角晶界(一般认为两侧晶粒取向差小于15°)在外加载荷的作用下可通过晶界位错沿相邻晶粒内的滑移面协调运动,直接诱发晶界的整体迁移。考虑到位错与阶错的结构特征,晶界迁移的位错机制与阶错机制应具有内在的相似性,但表现出不同的动力学行为。在同样的剪切载荷下,fcc金属小角晶界上的晶界位错可快速分解,形成一个由2个部分位错构成的位错偶极子[116]。2个部分位错的滑移系分别位于2个晶粒内,且其中间夹着一个层错,由此保证了位错滑移的连续性(图10a和b[116])。循环载荷下,分解的小角晶界可发生良好的可逆滑移,实现稳定的循环变形[116]。调控晶界结构和几何尺寸可在一定程度上调节晶界往复迁移的速率和幅度(图10f[116]),实现不同加载条件下金属纳米结构的可控循环变形[116]。此外,材料中的晶界通常并非理想的平直界面,而晶界曲率可为弯曲晶界迁移提供额外的驱动力[117]。以Au中的位错型晶界为例,晶界曲率会导致弯曲晶界在单向剪切加载下发生非均匀迁移行为(图10c和d[118]),并从晶体学角度阐明了晶界曲率对晶界塑性变形的影响。本质上,弯曲晶界由具有不同倾角(φ)的晶界段组成(图9e[118]),因此Δφ即为晶界曲率的晶体学表述。随倾角的变化,晶界表现出不同的原子结构和相应的界面能(图10g[118])。对于弯曲的位错型晶界,当曲率较小时(Δφ ≤ 35°),晶界由单一种类的位错构成,因此通常表现出单向的迁移行为,最终趋于形成平直的结构以降低系统能量;当曲率较大时(Δφ > 35°),晶界由2种晶界位错构成,因而在外力作用下会发生不同的应力响应,导致晶界的非均匀迁移。该理论模型可进一步解释外力加载下多晶材料中的晶粒异常长大现象[119]。对大角晶界,晶界曲率的改变也会进一步加剧晶界塑性和晶内塑性的竞争,从而影响晶界的本征变形行为。由此可见,晶界的迁移机制的具体表现形式受晶界结构和晶界曲率的影响。
图10
图10
晶界结构和曲率对晶界塑性变形的影响[116,118]
Fig.10
Influence of grain boundary structure and curvature on grain boundary plastic deformation
(a, b) cyclic migration of 13.5°[1
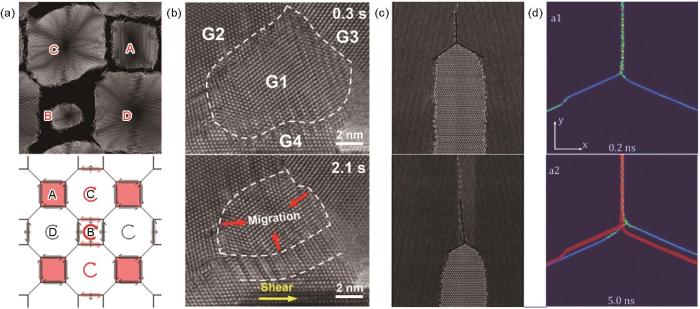
需要指出,实际材料中由于晶界结构和服役环境的复杂性,晶界在迁移过程中往往伴随其他晶界变形机制的发生,如晶界滑动、晶粒转动、晶界扩散等。这些机制对纳米晶材料的塑性变形也具有重要意义。一般地,晶界滑动通过晶界阶错等缺陷的产生及其在晶界面上的运动进行[120],其阶错动力学与3.2节中描述的阶错行为类似。普通倾转晶界和混合晶界的迁移运动也主要通过晶界阶错的形核、扩展、交互作用进行[120]。孪晶界也可通过孪晶位错(即孪晶界阶错)沿孪晶界的滑动来诱发孪晶滑移,实现大幅度的剪切变形[121~123]。高温条件下,晶界滑动的趋势愈加显著,其往往通过多种模式阶错的同时启动与交互作用进行[15]。晶粒转动通常是由晶界迁移或晶界滑动耦合作用诱发的一种晶界变形行为,可导致纳米晶粒的长大(或湮灭)和合并[124~126]。一般认为,晶粒转动的诱导机制为晶界位错的攀移[125,127,128]或晶界上向错偶极子的产生[7,129];然而,三维构型的晶界阶错网络的运动亦可诱发晶粒之间发生相对转动,相关机制有待深入研究。
另外,相较于双晶体中单一晶界表面处较弱的几何约束(图6[34,38,67,70]、7[7,28]、8[86,87]、10[116,118]),多晶材料的晶界变形往往会受到周围晶界网络(特别是相邻晶界)的物理限制,诱发一些不同于双晶体的晶界变形行为。晶界网络中,包围某一晶粒的若干条晶界通常具有不同的原子结构和剪切耦合因子;而剪切诱导的晶界迁移会不可避免地引发相邻晶粒晶格的转动。因此,某一晶粒或晶界的变形会改变其周边晶界的构型(如取向差)与变形行为,必须通过相互协调来实现。Thomas等[130]通过大量MD模拟发现,晶粒长大与剪切耦合晶界迁移是相互耦合的,其中晶界迁移会伴随晶粒转动,促进相邻晶界间的协调变形(图11a[130])。Chen等[125]在原位剪切循环加载测试中发现,Au纳米晶粒的持续收缩可通过包围晶粒的各个晶界向晶粒中心协同迁移实现;当构成纳米晶粒的某个晶界构型发生改变时,相邻晶界的变形会同步发生一定的调整(图11b[125])。除晶界迁移与晶粒转动耦合造成的晶界变形协调效应之外,相邻晶界之间的三叉点在相邻晶界的协调变形中起着至关重要的作用。Upmanyu等[131]针对不同几何形状的三叉晶界开展了大量模拟计算发现,晶界三叉点对相邻晶界的拖拽阻碍作用在小尺寸、低Σ晶界或低温时表现得更为明显;这种拖拽阻碍作用会影响三叉晶界的二面角大小,反过来进一步影响三叉晶界的迁移(图11c[131])。Thomas等[65]提出了以阶错模型为基础的三叉晶界运动模型(图11d[65])。晶界之间的协调变形可以通过不同相邻晶界之间的阶错转换进行,三叉晶界在其中扮演着阶错转换和协调变形的作用。Chen等[132]以Au纳米多晶中晶界-孪晶界交割结构为例,通过大量的原位纳米力学测试揭示了孪晶界协调作用下的晶界迁移行为:由阶错主导的晶界迁移在受到阻碍时可通过发射孪晶的形式导致晶界分解,而后新产生的晶界可继续通过阶错运动的形式动态调整晶界平面,最终导致多重孪晶结构的形核和长大。进一步地,Chen等[133]揭示了五重孪晶的本征变形。类似于多晶材料中的晶界三叉点,五重孪晶核心的存在使得五重孪晶各个孪晶界的变形密切相关。通过五重孪晶各个孪晶界之间的协调迁移和滑动,五重孪晶核心发生重构,产生一个五边形的区域。孪晶界的这种协调变形与三叉节点处的晶界协调变形类似。这些研究验证了晶界协调变形在多晶材料中的普遍性。尽管晶界协调运动对多晶材料的晶界网络演化、晶粒长大、再结晶、蠕变等过程具有不可言喻的重要意义,晶界网络的复杂性和多自由度大大增加了分析的难度,目前晶界协调变形的机制(尤其是原子尺度上的实验研究)还有待进一步的探索。
图11
Fig.11
Mechanism of coordinated grain boundary deformation
(a) shear-coupled grain boundary migration accompanied by grain rotation[130]
(b) coordinated grain boundary deformation governed grain shrinkage[125]
(c) drag effect of triple junction on neighboring grain boundaries[131]
(d) disconnection description of triple junction motion[65]
多界面协调变形在金属多晶材料的再结晶、蠕变、断裂等行为中扮演着重要角色。考虑到很多晶界的迁移和滑动均可由晶界阶错、位错描述(见3.3节),晶界缺陷运动主导的晶界变形在以上这些材料微结构演化现象及性能转变中应有不可忽视的地位。Yu等[134~137]和Shuai等[138]基于冷轧态层状多晶Al或Ni的退火结构演化,系统阐释了Y型三叉晶界运动主导的晶界协调变形对形变金属再结晶的影响。退火过程中,层状多晶Al或Ni通过Y型晶界三叉点主导的晶界协调变形进行。相邻的层间晶界及连接亚晶界会在一定程度上拖拽三叉点运动,这种阻碍效应随三叉点两侧晶界的取向差增大而增大,由此引发三叉点“停停走走”的迁移模式,从而减缓再结晶的进程[135,137,138]。加入微量合金元素后,合金元素的晶界偏析可大幅降低组成Y型三叉晶界的层间大角晶界的晶界能,进一步阻碍三叉点和相连晶界的迁移、减缓再结晶的速率[136,138]。晶界协调变形对多晶金属(尤其是超细晶、纳米晶金属)的蠕变和超塑性变形也有重要贡献,常通过晶界协同滑动主导的协调变形进行[7,139,140]。该过程中,晶界网络的结构也会随之演化,不可避免会涉及其他一些晶界变形机制(如晶界迁移、晶粒转动、晶界位错滑移或三叉晶界附近位错发射等)的辅助启动,以协调多个晶界耦合滑动导致的局部应力状态[80,140~144]。此外,由于三叉点的存在,晶界滑动会受到阻碍,此时晶界滑动相关的晶界缺陷(如滑动的晶界位错或阶错)可在三叉点处分解并滑移至相邻晶界,进而促进相邻晶界运动[142,145]。可见,这些晶界变形机制会互相影响,发生交互作用,对于纳米金属多晶材料的蠕变和超塑性变形行为至关重要[80,140~143]。例如,晶界滑动-迁移协同机制(grain boundary sliding and migration,GBSM)被认为是晶界网络及三叉晶界演化的主要机制之一,其在能量角度上比“纯”晶界滑动更容易发生[80,142,145]。另一方面,晶界滑动可致使在三叉点附近产生一对向错偶极子,其应力场会促进裂纹萌生[80,143,145],此效应在低塑性的纳米晶材料中尤为显著。此外,三叉晶界处缺陷塞积产生的应力集中除了可通过相邻晶界的协调变形释放之外,也可通过在三叉点处(或附近)发射缺陷(如位错、层错、孪晶等)至相邻晶粒内得到缓解[141,144,145],从而抑制裂纹在三叉点处形核。最近,有研究[79,80,146~149]指出纳米多晶材料裂纹尖端处发生的晶界协调变形(包括相邻晶界的迁移、滑动以及晶粒转动等机制的同时启动)可促进裂纹尖端钝化,抑制裂纹长大,从而提高材料的断裂韧性。
4 总结与展望
晶界塑性变形深刻影响着金属多晶材料的结构演化与形变损伤。微观上,深刻认知晶界变形与晶界缺陷的本征关系、构建晶界结构-动力学关系是系统建立晶界塑性变形理论的关键所在;宏观上,基于晶界变形动力学机制开展材料的晶界工程调控是实现多晶材料的性能优化和损伤容限设计的重要手段。本文从晶界及其微观结构出发,详细总结了近年来晶界变形的微观机制及其实验、理论研究进展;在此基础上,围绕晶界缺陷动力学行为,深入探讨晶界迁移的原子尺度行为及其在不同因素下的表现形式,以期为晶界塑性变形理论的发展和先进金属材料的设计提供普适性的基本理论依据。借由飞速发展的显微表征手段及原位纳米力学测试技术,科研人员能够在原子尺度开展精细的结构表征、调控乃至设计晶界微观结构,进而实现对于金属材料宏观性能的人为干预与升级。然而,全面构建晶界动力学与材料性能的关联尚存在诸多问题与挑战,需要进一步开展更加深入和广泛的研究。
(1) 晶界的不同运动模式均与晶界阶错存在一定关联。当前,晶界及其缺陷二维结构的研究并不能完全反映实际复杂多变的晶界变形行为;进一步考虑晶界阶错在三维网络中的复杂构型及其动力学行为,有望建立基于晶界阶错动力学的相对统一的晶界塑性变形理论。
(2) 除晶界本征结构的影响外,晶界相对疏松的结构及较高的界面能也会诱发元素的晶界偏析[150],导致晶界处的局部化学成分、界面结构、相结构、错配度等发生改变。结合先进电子显微学与原位纳米力学测试来解析偏析晶界的塑性变形动力学,应具有广泛的科学意义和工程价值。如何同步实现原子尺度的成分分析、稳定的力学加载以及快速的动态成像是当前所面临的关键技术难题,相关方法正在发展中。
(3) 块体多晶材料中,晶界之间的协调、约束在材料结构演化中扮演着关键角色。当前界面协调变形微观机制的理论和实验研究主要集中在结构相对简单的<001>大角倾转晶界。未来,结合多尺度、多场耦合测试和应变定量分析技术,将单一晶界的原子尺度迁移机制拓展至多个晶界耦合的协调变形理论,建立界面微观演化机制与材料宏观组织演化、损伤行为的关联关系,有望为多晶、多相材料的组织调控和损伤控制提供理论支撑和技术指导,最终实现高性能金属材料的优化设计。
总之,从界面的本征结构特征出发,深入研究界面结构转变和协同演化的动态机制,有机关联界面动力学与缺陷动力学,发展基于微结构演变的材料本构关系,构建系统的界面塑性变形理论体系,对工程材料的结构调控、性能优化和损伤控制具有重要意义。
参考文献
The mechanism of plastic deformation of crystals. Part I.—Theoretical
[J].
The mechanism of plastic deformation of crystals. Part II.—Comparison with observations
[J].
Direct observations of the arrangement and motion of dislocations in aluminum
[J].
Crystal dislocations—Elementrary concepts and definitions
[J].
Continuous distributions of dislocations: A new application of the methods of non-Riemannian geometry
[J].
Dislocation models of crystal grain boundaries
[J].
Grain-boundary kinetics: A unified approach
[J].
The symmetry and interfacial structure of bicrystals
[J].
On the structure of tilt grain boundaries in cubic metals II. Asymmetrical tilt boundaries
[J].
On the structure of tilt grain boundaries in cubic metals I. Symmetrical tilt boundaries
[J].
<110> symmetric tilt grain-boundary structures in fcc metals with low stacking-fault energies
[J].
Steps, dislocations and disconnections as interface defects relating to structure and phase transformations
[J].
The disconnection mechanism of coupled migration and shear at grain boundaries
[J].
Defects at surfaces and interfaces
[J].
Disclinations and disconnections in minerals and metals
[J].
The role of disconnections in phase transformations
[J].
Disconnections and other defects associated with twin interfaces
[J].
Mechanical properties of nanocrystalline materials
[J].
Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect
[J].
The control of brittleness and development of desirable mechanical properties in polycrystalline systems by grain boundary engineering
[J].
Grain-boundary sliding and its accommodation at triple junctions in aluminum and copper tricrystals
[J].
Transition between low and high angle grain boundaries
[J].
Stress induced grain boundary motion
[J].
Low angle tilt boundary migration coupled to shear deformation
[J].
Migration of the Σ7 tilt grain boundary in Al under an applied external stress
[J].
In situ TEM observations of fast grain-boundary motion in stressed nanocrystalline aluminum films
[J].
Grain rotation mediated by grain boundary dislocations in nanocrystalline platinum
[J].
In situ atomistic observation of disconnection-mediated grain boundary migration
[J].Shear-coupled grain boundary (GB) migration is of general significance in the deformation of nanocrystalline and polycrystalline materials, but comprehensive understanding of the migration mechanism at the atomic scale remains largely lacking. Here, we systematically investigate the atomistic migration of Σ11(113) coherent GBs in gold bicrystals using a state-of-art in situ shear testing technique combined with molecular dynamic simulations. We show that shear-coupled GB migration can be realised by the lateral motion of layer-by-layer nucleated GB disconnections, where both single-layer and double-layer disconnections have important contributions to the GB migration through their frequent composition and decomposition. We further demonstrate that the disconnection-mediated GB migration is fully reversible in shear loading cycles. Such disconnection-mediated GB migration should represent a general deformation phenomenon in GBs with different structures in polycrystalline and nanocrystalline materials, where the triple junctions can act as effective nucleation sites of GB disconnections.
Differences in deformation behavior of bicrystalline Cu micropillars containing a twin boundary or a large-angle grain boundary
[J].
Grain boundary shear-migration coupling—I. In situ TEM straining experiments in Al polycrystals
[J].
Evidence of grain boundary dislocation step motion associated to shear-coupled grain boundary migration
[J].
The role of disconnections in deformation-coupled grain boundary migration
[J].
Grain boundary kinetics—I. In situ observations of coupled grain boundary dislocation motion, crystal translation and boundary displacement
[J].
Grain boundary kinetics—II. In situ observations of the role of grain boundary dislocations in high-angle boundary migration
[J].
Direct observation of deformation-induced grain growth during the nanoindentation of ultrafine-grained Al at room temperature
[J].
Grain boundary-mediated plasticity in nanocrystalline nickel
[J].
Experimental observations of stress-driven grain boundary migration
[J].In crystalline materials, plastic deformation occurs by the motion of dislocations, and the regions between individual crystallites, called grain boundaries, act as obstacles to dislocation motion. Grain boundaries are widely envisaged to be mechanically static structures, but this report outlines an experimental investigation of stress-driven grain boundary migration manifested as grain growth in nanocrystalline aluminum thin films. Specimens fabricated with specially designed stress and strain concentrators are used to uncover the relative importance of these parameters on grain growth. In contrast to traditional descriptions of grain boundaries as stationary obstacles to dislocation-based plasticity, the results of this study indicate that shear stresses drive grain boundaries to move in a manner consistent with recent molecular dynamics simulations and theoretical predictions of coupled grain boundary migration.
Grain-boundary shear-migration coupling. II. Geometrical model for general boundaries
[J].
An insight into the role of the grain boundary in plastic deformation by means of a bicrystalline pillar compression test and atomistic simulation
[J].
Grain boundary orientation effects on deformation of Ta bicrystal nanopillars under high strain-rate compression
[J].
Effect of a high angle grain boundary on deformation behavior of Al nanopillars
[J].
Stepwise work hardening induced by individual grain boundary in Cu bicrystal micropillars
[J].Vast experiments have demonstrated that the external specimen size makes a large difference in the deformation behavior of crystalline materials. However, as one important kind of internal planar defects, the role of grain boundary (GB) in small scales needs to be clarified in light of the scarce and inconsistent experimental results at present. Through compression of Cu bicrystal and its counterpart monocrystal micropillars, it is found that, in contrast to the monocrystals, the bicrystals are characterized by work hardening with discrete strain bursts. Interestingly, the stress rise between two adjacent strain bursts of the bicrystals increases with the decrease of specimen size. The results suggest that GBs play a critical role in the work hardening of materials in small scales, which may provide important implications to further understand the general work hardening behaviors of materials in the future.
Microscale deformation behavior of bicrystal boundaries in pure tin (Sn) using micropillar compression
[J].
Size-dependent deformation of nanocrystalline Pt nanopillars
[J].
Size-induced weakening and grain boundary-assisted deformation in 60 nm grained Ni nanopillars
[J].
Atomic-scale observation of grain boundary motion
[J].
High-resolution electron microscopy at a (113) symmetric Thermally activated step motion observed by tilt grain-boundary in aluminium
[J].
Collective effects in grain boundary migration
[J].
Dynamics of grain boundary motion at the atomic level
[J].
In-situ HREM studies of grain boundary migration
[J].
High-resolution electron microscopy at a (113) symmetric Thermally activated step motion observed by tilt grain-boundary in aluminium
[J].
Mechanism and dynamics of shrinking island grains in mazed bicrystal thin films of Au
[J].
Step coalescence by collective motion at an incommensurate grain boundary
[J].
Tracking the sliding of grain boundaries at the atomic scale
[J].
Direct imaging of atomistic grain boundary migration
[J].
A Continuum Multi-Disconnection-Mode model for grain boundary migration
[J]. J.
Equation of motion for a grain boundary
[J].
Heterogeneous disconnection nucleation mechanisms during grain boundary migration
[J].
Shear-coupled grain-boundary migration dependence on normal strain/stress
[J].
Effects of a disconnection dipole on the shear-coupled grain boundary migration
[J].
The shear response of copper bicrystals with Σ11 symmetric and asymmetric tilt grain boundaries by molecular dynamics simulation
[J].
Shear response of the Σ11, <110>{131} symmetric tilt grain boundary studied by molecular dynamics
[J].
Shear response of the Σ9<110>{221} symmetric tilt grain boundary in fcc metals studied by atomistic simulation methods
[J].
Disconnections kinks and competing modes in shear-coupled grain boundary migration
[J].
Disconnection description of triple-junction motion
[J].
Grain boundary triple junction dynamics: A continuum disconnection model
[J].
Coupling grain boundary motion to shear deformation
[J].
Duality of dislocation content of grain boundaries
[J].
On the mechanisms of grain boundary migration
[J].
A model for stress-induced migration of tilt grain boundaries in crystals of NaCl structure
[J].
Sliding behavior of coincidence grain boundaries deviating from ideal symmetric tilt relationship
[J].
Equation of motion for a grain boundary
[J].
Torsional detwinning domino in nanotwinned one-dimensional nanostructures
[J].
Characterization of the terrace-defect interfaces using in situ straining techniques
[J].
Grain boundary mediated plasticity: A blessing for the ductility of metallic thin films?
[J].
Superplasticity and cooperative grain boundary sliding in nanocrystalline Ni3Al
[J].
High-temperature grain boundary sliding behavior and grain boundary energy in cubic zirconia bicrystals
[J].
In-situ observation of cooperative grain boundary sliding and migration in the nano-twinned nanocrystalline-Au thin-films
[J].
Review on superior strength and enhanced ductility of metallic nanomaterials
[J].
Migration kinetics of twinning disconnections in nanotwinned Cu: An in situ HRTEM deformation study
[J].
In situ observation of twin boundary migration in copper with nanoscale twins during tensile deformation
[J].
TEM in situ deformation study of the interaction of lattice dislocations with grain boundaries in metals
[J].
Compatibility of deformation in two-phase Ti-Al alloys: Dependence on microstructure and orientation relationships
[J].
Quasi-four-dimensional analysis of dislocation interactions with grain boundaries in 304 stainless steel
[J].
In situ atomistic observation of grain boundary migration subjected to defect interaction
[J].
Direct observation of individual dislocation interaction processes with grain boundaries
[J].
Deformation mechanisms, length scales and optimizing the mechanical properties of nanotwinned metals
[J].
Dislocation interactions with grain boundaries
[J].
In situ studies of irradiation-induced twin boundary migration in nanotwinned Ag
[J].
In-situ high-resolution transmission electron microscopy investigation of grain boundary dislocation activities in a nanocrystalline CrMnFeCoNi high-entropy alloy
[J]. J.
Plastic deformation mechanism in nanotwinned metals: An insight from molecular dynamics and mechanistic modeling
[J].
Ideal maximum strengths and defect-induced softening in nanocrystalline-nanotwinned metals
[J].
In situ observation of dislocation behavior in nanometer grains
[J].
Transmission electron microscopy observations of dislocation annihilation and storage in nanograins
[J].
In situ TEM observations of reverse dislocation motion upon unloading in tensile-deformed UFG aluminium
[J].
Dislocation-mediated relaxation in nanograined columnar palladium films revealed by on-chip time-resolved HRTEM testing
[J].Colla, M. -S.; Idrissi, H.; Pardoen, T. Catholic Univ Louvain, Inst Mech Mat & Civil Engn, B-1348 Louvain La Neuve, Belgium. Amin-Ahmadi, B.; Idrissi, H.; Schryvers, D. Univ Antwerp, Dept Phys, Elect Microscopy Mat Sci EMAT, B-2020 Antwerp, Belgium. Malet, L.; Godet, S. Univ Libre Bruxelles, 4MAT Mat Engn Characterizat Synth & Recycling, B-1050 Brussels, Belgium. Raskin, J. -P. Catholic Univ Louvain, ICTEAM, B-1348 Louvain La Neuve, Belgium.
Distinct fatigue cracking modes of grain boundaries with coplanar slip systems
[J].
Twin boundary: Controllable interface to fatigue cracking
[J].
Dependence of intergranular fatigue cracking on the interactions of persistent slip bands with grain boundaries
[J].
Grain boundary effects on cyclic deformation and fatigue damage
[J].
Strain localization and fatigue cracking behaviors of Cu bicrystal with an inclined twin boundary
[J].
Controllable fatigue cracking mechanisms of copper bicrystals with a coherent twin boundary
[J].High-angle grain boundaries are always the preferential fatigue cracking sites, while the intrinsic fatigue cracking mechanism of coherent twin boundary remains elusive. Here we systematically investigate the fatigue cracking behaviours of copper bicrystals with a coherent twin boundary as their sole internal boundary. It is found with direct experimental evidence for the first time that, unlike the random grain boundaries, the cracking behaviour of the twin boundary strongly depends on its orientation with respect to the loading direction. When the twin boundary is parallel or perpendicular to the loading direction, the fatigue cracks nucleate along the slip bands preferentially; when it is inclined at an angle to the loading direction, the fatigue crack is especially apt to nucleate along the twin boundary first. The controllable fatigue cracking mechanisms of the twin boundary may provide new and important implications for the optimized interfacial design of the high-performance materials.
Fatigue cracking at twin boundaries: Effects of crystallographic orientation and stacking fault energy
[J].
Intrinsically higher fatigue cracking resistance of the penetrable and movable incoherent twin boundary
[J].Incoherent twin boundaries (ITBs) are widespread and play a crucial role in unidirectional deformation behavior of materials, however, the intrinsic role of individual ITB under cyclic loading remains elusive. Here we show the fatigue cracking behavior of Cu bicrystal with an ITB as its sole interface for the first time. The slip bands (SBs) could transfer through the ITB; meanwhile, the ITB could migrate with the motion of partial dislocations. Both the penetrability and mobility contribute to the higher fatigue cracking resistance of the ITB and hence the fatigue crack nucleates along the SBs preferentially. These new findings not only shed light on the fatigue cracking mechanisms of a penetrable boundary with direct evidence but also could provide important implications for future interfacial optimization of metallic materials.
Twin boundary: Stronger or weaker interface to resist fatigue cracking?
[J].
Fatigue cracking at twin boundary: Effect of dislocation reactions
[J].
Higher fatigue cracking resistance of twin boundaries than grain boundaries in Cu bicrystals
[J].
Effects of grain boundaries on cyclic deformation behavior of copper bicrystals and columnar crystals
[J].
Effect of grain size on fatigue cracking at twin boundaries in a CoCrFeMnNi high-entropy alloy
[J].The fatigue cracking behavior at twin boundaries (TBs) in a CoCrFeMnNi high-entropy alloy with three different grain sizes was systematically investigated under low-cycle fatigue. Irrespective of grain size, the change from slip band cracking to TB cracking occurred with increasing the difference in the Schmid factors (DSF) between matrix and twin. However, the required critical DSF for the transition of the dominant cracking mode decreases with decreasing grain size due to the reduced slip band spacing that increases the impingement sites on the TBs and facilitates the coalescence of defects and voids to initiate TB cracks.
Difference in fatigue cracking behaviors of Cu bicrystals with the same component grains but different twin boundaries
[J].
Shear fatigue cracking of twin boundary and grain boundary without dislocation impingement
[J].
Deformation behaviors of Cu bicrystals with an inclined twin boundary at multiple scales
[J].
Grain size effects on the fatigue response of nanocrystalline metals
[J].
Atomistic simulations of crack nucleation and intergranular fracture in bulk nanocrystalline nickel
[J].
Metallic nanocrystals with low angle grain boundary for controllable plastic reversibility
[J].Advanced nanodevices require reliable nanocomponents where mechanically-induced irreversible structural damage should be largely prevented. However, a practical methodology to improve the plastic reversibility of nanosized metals remains challenging. Here, we propose a grain boundary (GB) engineering protocol to realize controllable plastic reversibility in metallic nanocrystals. Both in situ nanomechanical testing and atomistic simulations demonstrate that custom-designed low-angle GBs with controlled misorientation can endow metallic bicrystals with endurable cyclic deformability via GB migration. Such fully reversible plasticity is predominantly governed by the conservative motion of Shockley partial dislocation pairs, which fundamentally suppress damage accumulation and preserve the structural stability. This reversible deformation is retained in a broad class of face-centred cubic metals with low stacking fault energies when tuning the GB structure, external geometry and loading conditions over a wide range. These findings shed light on practical advances in promoting cyclic deformability of metallic nanomaterials.
On the effect of purity and orientation on grain boundary motion
[J].
Inclination-governed deformation of dislocation-type grain boundaries
[J].
Dynamic abnormal grain growth: A new method to produce single crystals
[J].
Atomistic dynamics of disconnection-mediated grain boundary plasticity: A case study of gold nanocrystals
[J].
Sliding of coherent twin boundaries
[J].
Twin boundary sliding in single crystalline Cu and Al nanowires
[J].
Revealing extreme twin-boundary shear deformability in metallic nanocrystals
[J].
Simultaneous grain boundary migration and grain rotation
[J].
Coordinated grain boundary deformation governed nanograin annihilation in shear cycling
[J].
Simultaneous grain boundary motion, grain rotation, and sliding in a tricrystal
[J].
Grain rotation mediated by grain boundary dislocations in nanocrystalline platinum
[J].
On nanograin rotation by dislocation climb in nanocrystalline materials
[J].
Atomic-level observation of disclination dipoles in mechanically milled, nanocrystalline Fe
[J].Plastic deformation of materials occurs by the motion of defects known as dislocations and disclinations. High-resolution transmission electron microscopy was used to directly reveal the individual dislocations that constitute partial disclination dipoles in nanocrystalline, body-centered cubic iron that had undergone severe plastic deformation by mechanical milling. The mechanisms by which the formation and migration of such partial disclination dipoles during deformation allow crystalline solids to fragment and rotate at the nanometer level are described. Such rearrangements are important basic phenomena that occur during material deformation, and hence, they may be critical in the formation of nanocrystalline metals by mechanical milling and other deformation processes.
Reconciling grain growth and shear-coupled grain boundary migration
[J].
Molecular dynamics simulation of triple junction migration
[J].
A geometrical model for grain boundary migration mediated formation of multifold twins
[J].
Penta-twin destruction by coordinated twin boundary deformation
[J].
Recovery by triple junction motion in aluminium deformed to ultrahigh strains
[J].
Linking recovery and recrystallization through triple junction motion in aluminum cold rolled to a large strain
[J].
Strong pinning of triple junction migration for robust high strain nanostructures
[J].
In situ observation of triple junction motion during recovery of heavily deformed aluminum
[J].
Segregation and precipitation stabilizing an ultrafine lamellar-structured Al-0.3%Cu alloy
[J].
Grain-boundary sliding and its accommodation during creep and superplasticity
[J].
Superplasticity resulting from cooperative grain boundary sliding
[J].
Grain-boundary sliding in nanocrystalline fcc metals
[J].
Cooperative grain boundary sliding and migration process in nanocrystalline solids
[J].
Grain boundary sliding, triple junction disclinations and strain hardening in ultrafine-grained and nanocrystalline metals
[J].
Cooperative processes during plastic deformation in nanocrystalline fcc metals: A molecular dynamics simulation
[J].
Synergy of grain boundary sliding and shear-coupled migration process in nanocrystalline materials
[J].
Effect of cooperative grain boundary sliding and migration on crack growth in nanocrystalline solids
[J].
Effect of cooperative grain boundary sliding and migration on dislocation emitting from a semi-elliptical blunt crack tip in nanocrystalline solids
[J].
Effect of cooperative grain boundary sliding and migration on emission of dislocations from a crack tip in nanocrystalline materials
[J].
Effect of cooperative nanograin boundary sliding and migration on dislocation emission from a blunt nanocrack tip in nanocrystalline materials
[J].