团簇动力学模型是模拟材料中析出^[1~5]、点缺陷^[6~10]或气泡^[11,12]等形成的一个有力工具。与其他析出动力学模型相比，它计算量小，而且有几个显著的优点。首先，它能通过同一组速率方程将整个析出演化描述为一个连续和竞争的过程，而不需要区分孕育期、形核期、长大期和粗化期的不同本质。其次，它同时追踪了从单分子、不稳定晶胚、稳定晶核到粗化颗粒的所有团簇尺寸，其计算结果容易与具有不同分辨率极限的各种实验测量结果比较，即使对小于稳定晶核的团簇尺寸但能在实验中探测到的结果也如此。最后，模型中所有变量都有其物理含义，不需要额外引入拟合参数或显式定律。例如，在MLS^[13]、KWN^[14]和Matcalc^[15]等析出模型中常用的Becker-Döring成核理论^[16]，也隐含在团簇动力学模型中。

然而，初始的团簇动力学模型建立在团簇分子数简单线性增加的基础上，当团簇尺寸持续长大时，计算会遇到不少困难。因此，粒径分组法被经常引入。该方法的基本思想是将整个析出尺寸范围分割成连续的粒径组，最终评估每个粒径组内总的团簇密度变化，而不再追踪各单一尺寸的团簇。为了简化，经常需要预先假定各组内的团簇密度分布。例如，以前的研究工作中经常采用均匀^[6,7]或线性^[8,9]分布的假设。尽管已经建立的这些分组法使得大尺度析出模拟成为了可能，但是多数模拟结果往往用于与实验测量值相比较，而与未分组模型的直接验证还较少，因此其准确性还并没有得到很好的证实。

近来，国内也有部分学者利用团簇动力学模型进行了相关研究。张立峰等^[17]采用团簇动力学模型研究了钢水中夹杂物的形核、长大、运动、去除和捕捉，该研究条件下夹杂物形成主要依赖于碰撞机理，组内团簇密度均匀分布的假设可能已经满足其精度要求。Li等^[18]和高超^[19]还利用团簇动力学模型分别模拟了He在中子辐照钨中的积累与扩散^[18]以及Fe-Cu合金在电子辐射下的缺陷演化^[19]。由于这些研究考虑了自间隙原子、空位、缺陷原子以及可能形成的复合体等多种微观结构，对于该类复杂问题目前只能采用均匀分布进行分组简化。目前，对于固相中自扩散引起的析出现象，国内采用团簇动力学模型进行的研究工作还很少。本工作的目的是建立一种基于组内团簇密度对数线性分布的新分组方法，通过比较未分组模型和已有分组法的数值解来严格验证新分组法的准确性。最后，利用未分组和分组团簇动力学模型模拟了300℃时Al₃Sc在Al-0.18%Sc (原子分数)合金中的等温析出行为，并与文献中的实验测量数据进行了比较。

在团簇动力学模型中，所有团簇被假设为正圆球形，而第二相析出的总体积相对于基体材料可以忽略。对于固相中扩散导致的析出，假设所有团簇的生长和收缩都仅由析出相的单分子运动引起。对于团簇i (包含有i个第二相析出分子的分子团)，其单位体积内的数量n_i被定义为“数量密度”，其演化满足以下速率方程^[1,3,4]：

式中，t是时间，J_i是从团簇i到团簇i + 1的传输质量流，定义为：

式中，β_i和α_{i + 1}分别是团簇i的捕获速率和团簇i+1的释放速率。该方程表明了团簇i的消耗主要源于其自身的长大和收缩，但补充则源于团簇i - 1捕获1个分子或者团簇i + 1释放1个分子。

析出相单分子的密度演化遵循如下规律：

式中，δ_{i, j}是Kronecker记号，当i = j，δ_{i, j}= 1；当i ≠ j，δ_{i, j}= 0；i_M是计算中最大团簇包含的分子数量。方程(3)指出了单分子的消耗主要源于团簇长大，但补充则源于团簇收缩。如果模拟中选择的i_M足够大，密度无限小，∑i=1iMi∂ni(t)/∂t=-(iM+1)JiM≈0，因此以上速率方程组能保证所有团簇中包含的析出相总分子数量始终守恒。

对于捕获速率，一般可以从团簇i表面的浓度梯度得出^[1~4]：

式中，r_i是团簇i的半径；D是析出速率。如果析出相不是单元素的，认为析出速率由扩散最慢的元素的扩散系数决定。

释放速率可以从反应前后的Gibbs自由能变化得出。当团簇i分解为团簇i - 1和单分子时，体积相关的相变自由能不变，而表面积相关的界面能增加，释放速率可表述为^[1~4]：

式中，n1eq是溶解的析出相单分子在曲率半径无限大的水平界面处的平衡态浓度；γ_i是团簇i和基体间的界面能；k_B是Boltzmann常数；T是热力学温度。方程组(1)~(5)构成了未分组团簇动力学模型的精确解。

上面介绍的团簇动力学模型从物理上看起来非常完美。通过适当的数值方法积分给定的偏微分方程组和初始条件就可以得到所有团簇随时间演化的完整图谱。然而，由于未分组团簇动力学模型中团簇尺寸的分子数是简单线性增加的，当团簇尺寸在模拟中生长到足够大以后，计算将变得很困难甚至无法实现。为解决该问题，往往需要引入粒径分组法，通过将整个析出尺寸范围分割成几十到几百个分别覆盖了某一特定尺寸范围的团簇组，只追踪每个组内总团簇密度的变化，从而减少待求解变量和偏微分方程数量。在分组法中，组内和组间的质量传输必须准确量化以满足质量守恒以及相关的动力学规律。

根据组宽∆x_j= x_j- x_{j - 1}对团簇进行分组，其中下标j是团簇组的序号。团簇组j覆盖了含有分子数从i = x_{j - 1} + 1到x_j的所有团簇，其总团簇数量密度(N_j)被定义为：

团簇组j包含的平均分子数xj为：

一个比较常用的粒径分组方法为：

这里λ是一个可选择分数，函数ceil(x)给出不小于实数x的整数。该分组方法始于x₁ = 1，并确保x_j为不小于其组序号j的正整数。当λ足够小时，对于序号小的团簇组Δx_j = 1，然后Δx_j随序号的增大而增加。这时整个团簇尺寸范围被分为2个连续的部分，第1个从单分子开始的离散区域内团簇分子数保持简单线性增加，而紧随的第2个组合区域内团簇被集合成团簇组。

关于组内的团簇密度分布情况，本工作研究了3种假设情况。

最简单的假设无疑是均匀分布。这个方法最早由Kiritani^[6]提出，然后被Koirwa^[7]、Golubov等^[8]和Ovcharenko等^[9]验证了其在点缺陷团簇演化中的准确性。在组宽很大时，未分组团簇动力学模型的离散形式(1)和(2)可由Taylor展开变换为类似Fokker-Planck方程的连续性格式，然后在团簇组尺度上重新离散化为^[6,7]：

团簇组j内任一尺寸团簇的平均密度满足n¯j = N_j / Δx_j。与未分组模型相比，方程(9)采用了组间步长(Δx_j + Δx_{j + 1}) / 2来计算团簇组j和j + 1之间的团簇长大和收缩。为满足质量守恒，单分子团簇演化遵循：

这里G_M是最大的团簇组序号，可由模拟所需的最大分子数i_M和采用的分组方法确定。假定组内所有团簇具有相同的捕获和释放速率，取其为在团簇组中心处的值：

方程(9)~(11)构成了Kiritani分组方法的解。

均匀分布往往过于简单而不能匹配实际情况。为了提高准确性，Golubov等^[8]和Ovcharenko等^[9]建议改用线性分布，并且被Golubov等^[12]用于模拟两相氦-空位的团簇演化。在这些工作中，假定团簇组j内的团簇密度分布为：

式中，L0j和L1j分别为线性分布的截距和斜率。将上述分布从i = x_{j - 1} + 1到x_j叠加，则总团簇密度的演化遵循如下方程：

这表明团簇组j内的总团簇密度变化仅由其两侧组边界处的质量流Jxj-1和Jxj造成。把方程(1)和(12)乘以i并在组内叠加，团簇组j内总的析出相分子数(S_j)变化满足：

令未分组和分组模型中的N_j和S_j相等，给出线性分布参数L0j和L1j的演化方程为：

其中，J_j^*是团簇组j内的平均传输质量流，其定义和近似的计算方法为：

对于单分子团簇，由于∆x₁ = 1，L11 = 0，其密度演化遵循：

需要注意的是，当∆x_j = 1时，L1j = 0，J_j^* = 0，因此上述分组法完全可用于描述未分组情形。方程(12)、(16)~(19)构成了G-O (Golubov-Ovcharenko)分组方法的解。

为进一步提高准确性，特别是确保所有团簇密度在计算过程中始终非负，一个相对简单的方法是假设其在组内对数线性分布。基于作者之前的思路^[20]，假设团簇组j内的团簇密度分布为：

式中，q_j是对数线性(即等比数列)分布的公比。将该分布带入方程(6)和(14)，得出：

联立方程(21)和(22)消去nxj-1+1，q_j可以由下式决定：

根据上式，采用折半查找直到方程(23)左边的绝对误差小于设定的容许误差ε_tol = 10^-4。计算从j = 1开始，当∆x_j = 1时nxj-1+1=nxj=Nj。当∆x_j> 1时，先根据方程(23)求解出q_j后，组内左右两侧边界的团簇密度nxj-1+1和nxj可由方程(20)和(21)得出。

方程(13)、(14)、(18)、(20)~(23)构成了假设团簇密度对数线性分布的新分组方法的解。

在计算中，设置最大团簇i_M或团簇组G_M为密度恒为零的边界。为保证i_M或G_M足够大而满足质量守恒，要求第2大团簇i_M - 1或团簇组G_M - 1的密度必须足够小。如方程(1)和(2)所示，团簇i的密度依赖于其自身的大小。因此，对于条件稳定的显式积分格式，如果时间步长过大，团簇i的消耗在该步长内就可能被过高估计，造成数值失稳从而使得团簇密度变负。该问题可通过采用无条件稳定的隐式积分格式或者可变时间步长的显式积分格式解决。在显式格式的时间步k时，采用初始步长Δtk积分后，评估密度相对变化值(ξk)：

当nik-1=0时令ξik=0。如果miniM≥i≥1nik < 0，则ξk < -1，这意味着某些团簇密度小于零，因此需要更小的时间步长重新进行积分。由于团簇密度变化与时间步长线性相关，因此建议新的积分时间步长Δtknew为：

另外，析出相的总质量守恒决定了所有的团簇密度不可能同时增加或减小。如果miniM≥i≥1nik≥0，则0>ξk≥-1，这时所有的团簇密度均非负，计算能安全转移到下一个时间步k + 1。为提高计算效率，建议下一个时间步的积分步长为：

对于分组团簇动力学模型，数值积分时需要类似的考虑。另外，团簇动力学模型能追踪的最小团簇尺寸为单个分子级别，而这是几乎所有实验技术能达到的分辨率极限。因此，在将团簇动力学模型的计算结果与实验比较时，需要设定一个最小截断半径r_tr (对应于团簇分子数i_tr或团簇组数G_tr)，模型中定义实验中可测量到的析出颗粒总密度N_P和平均半径rP为：

通过类似计算，就可以合理地比较团簇动力学模型中得出的结果与相同实验条件下，具有不同分辨率极限的不同实验技术的测量数据。

以上建立的团簇动力学模型是基于均质析出的，而多数现实情况下发生的是在位错、晶界和其他第二相粒子表面等晶体缺陷处的异质析出。已证实Al-Sc合金中Al₃Sc析出时数量很少，而且在尺寸较小的情况下会以近球形和共格形式均质析出，因此在最近几十年里被广泛研究和用于验证各种析出动力学模型的可靠性^[3,4,21~28]。在实验中，纯Sc或高纯Al-Sc合金被加入到超纯Al熔体中，在惰性气氛下搅拌，以得到所需Sc含量的混合物，然后，混合物被浇注和冷轧成几百个微米厚度的薄带。对这些样品在低于熔点的某固溶温度均匀化处理数小时，以完全溶解其中存在的Al₃Sc析出，然后被快速冷却到析出温度并保温。当所需的析出产生后，再次快速冷却样品到室温进行测量。

Al₃Sc的晶体结构为L1₂，即8个Sc原子在立方体顶点和6个Al原子在面中心的fcc结构^[21]。它在室温的晶格常数为a = 0.4105 nm^[22]，仅比Al基体大1.3%，摩尔体积VmP = N_Aa³ = 4.166 × 10^-5 m³/mol，团簇i的半径r_i = (3V_i / 4π)^1/3 = (3i / 4π)^1/3a。其中，N_A为Avogadro常数，V_i为团簇i的体积。在Al-Sc相图靠近Al的一侧，Sc的平衡态摩尔体积浓度CSceq (%) = exp2.25exp(-7766 / T)^[23]，扩散系数D_Sc (m²/s) = 5.31 × 10^-4exp(-173000 / (R_gT))^[24]，其中，R_g为理想气体常数。假定界面能γ与团簇尺寸无关，模拟结果中与实验测量吻合较好的值为γ = 0.12 J/m²，这与其他工作中报导的数值很接近^[3,25,26]。

由于本工作的目的主要是验证分组法的有效性，因此选择对较低温度(300℃)时Al-Sc合金中的小尺寸析出进行模拟。对于未分组模型，取i_M= 16000，对应riM = 6.42 nm，模型计算到当niM-1 > 1 m^-3时终止，由此对应的实际析出时间约为1 × 10⁷ s。根据方程(8)，如选择λ = 0.05，最小需要G_M = 147个团簇组。对于所有模拟，初始和最小的积分时间步长都设置为1 s，而模拟中也证实了进一步减小该步长并不能提高计算精度或改善数值稳定性。为了提高计算精度，采用可变时间步长的4阶Runge-Kutta显式格式对微分方程组积分。

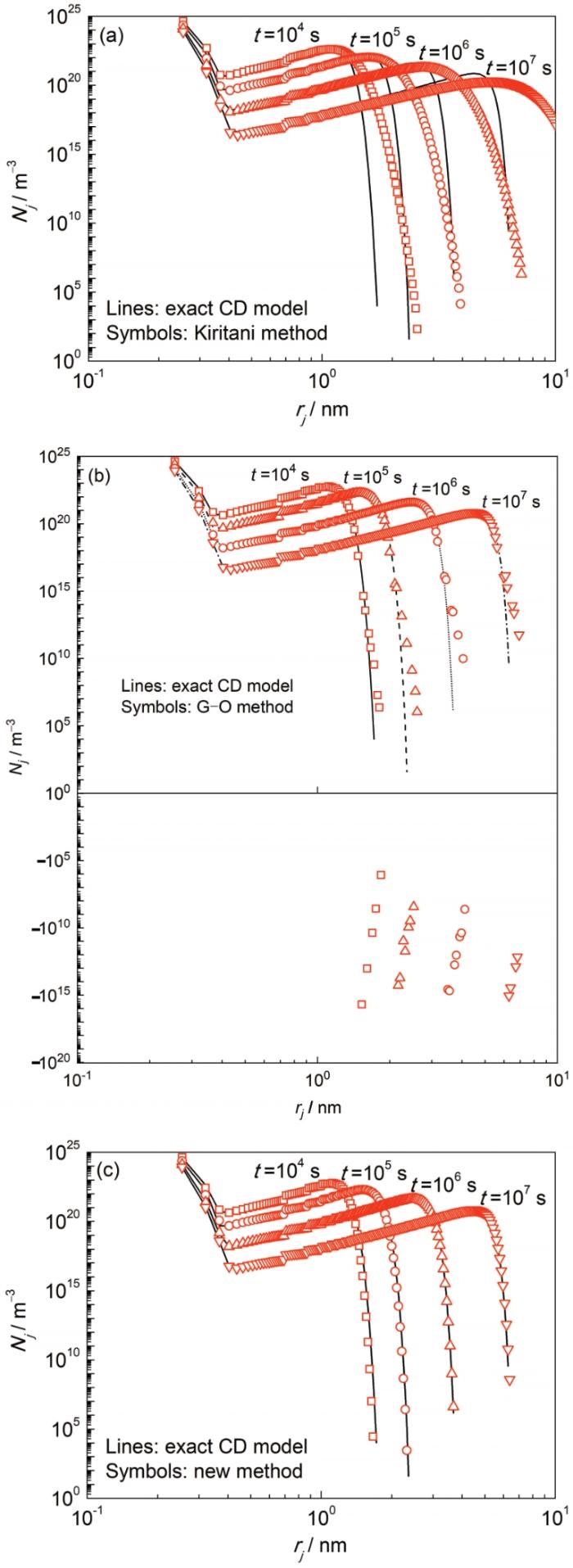
为了直观比较，本工作给出了未分组和分组团簇动力学模型计算出的团簇组密度在不同析出时间的分布曲线，如图1所示，图中的x轴代表各团簇组的平均半径，即对应于不同团簇组平均分子数<x>_j的团簇半径。未分组模型的团簇组密度需要经后处理，从单一尺寸团簇密度在每个团簇组范围内简单叠加得出。从图1可以看出，这些曲线在有些位置并不光滑，这主要是因为在这些位置组宽发生了变化。例如，在j = 20或r_j = 0.7 nm附近，组宽从∆x_j = 1变化到了∆x_{j + 1} = 2，造成该尺寸附近团簇组密度的一个小跳跃，而同样的行为在组宽被改变的其他位置也可能发生。

由图1a可见，假设的均匀分布造成了团簇密度在每个组内右侧边界处被过高估计，特别是在该组内团簇刚开始形成的时候。因此，这导致了Kiritani方法的计算结果比实际扩散更快，得到的析出尺寸分布偏大。在图1b中，基于线性分布的G-O方法给出了与未分组模型更好的匹配，但是有部分团簇组密度为负。值得指出的是，进一步的计算证实了这些负密度的出现可能来自于线性分布假设本身，不能通过进一步减小时间步长或提高Jj*估算值的准确性来避免。在图1c中，新的对数线性分布假设给出了与未分组模型非常接近的结果，而且有效避免了负团簇组密度的出现。

为了阐明分组法的效率，未分组和分组团簇动力学模型的计算空间和时间结果被汇总在表1内。所有的计算均用Matlab 语言在Intel I7 6700K中央处理器和32 GB内存的个人计算机上实现。与未分组模型相比，分组法显示出其在计算上的显著优越性。如果要模拟更大尺寸的Al₃Sc析出，比如说在550℃时析出1 h 后Al₃Sc的最大尺寸即能达到67 nm^[27]，这对应于约1.82 × 10⁷个分子。同时，伴随温度和尺寸的增加，Al₃Sc析出还会发生共格向半共格以及均质向异质析出的转变^[26,27]。这是进一步扩大团簇动力学模型适用范围的重点发展方向，而在一般计算机上这些模拟仅能由分组模型来实现。另外还可以看出，尽管G-O方法的线性密度分布假设比新分组法更简单，但由于其产生了负团簇组密度，因此后期计算中只能一直使用最小时间步长进行积分，这明显影响了其计算效率，计算时间反而明显长于Kiritani方法，甚至也长于新的分组法。

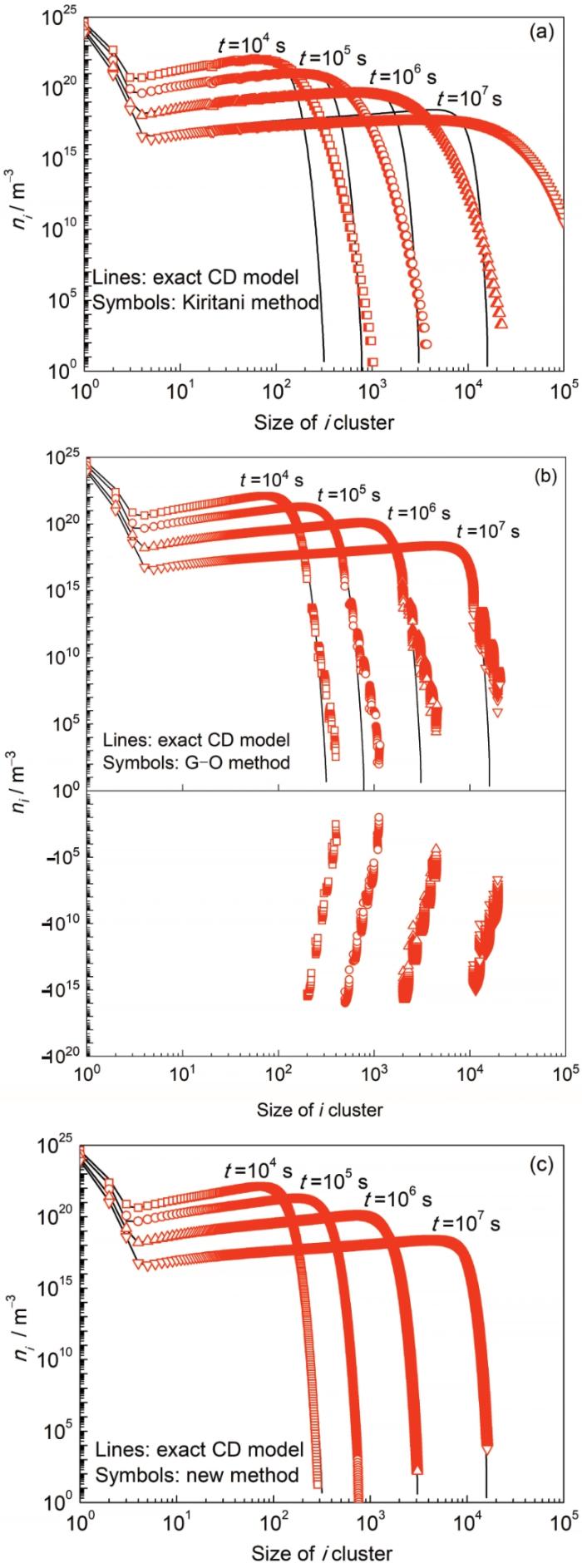
基于团簇组内的团簇数量密度分布假设和总团簇数量密度，可以得出分子数简单线性增加尺度上的单一团簇尺寸密度分布。图2比较了未分组和3种分组法的团簇密度的演化。图中的竖直线分别对应团簇组边界x_j + 1/2，而分组法结果中的每个符号均对应了包含整数分子数的各单一尺寸团簇密度。通过对比，证实了新分组法即使在分子尺度上，与未分组团簇动力学模型结果匹配也非常好，同时也有效避免了负团簇密度的产生。

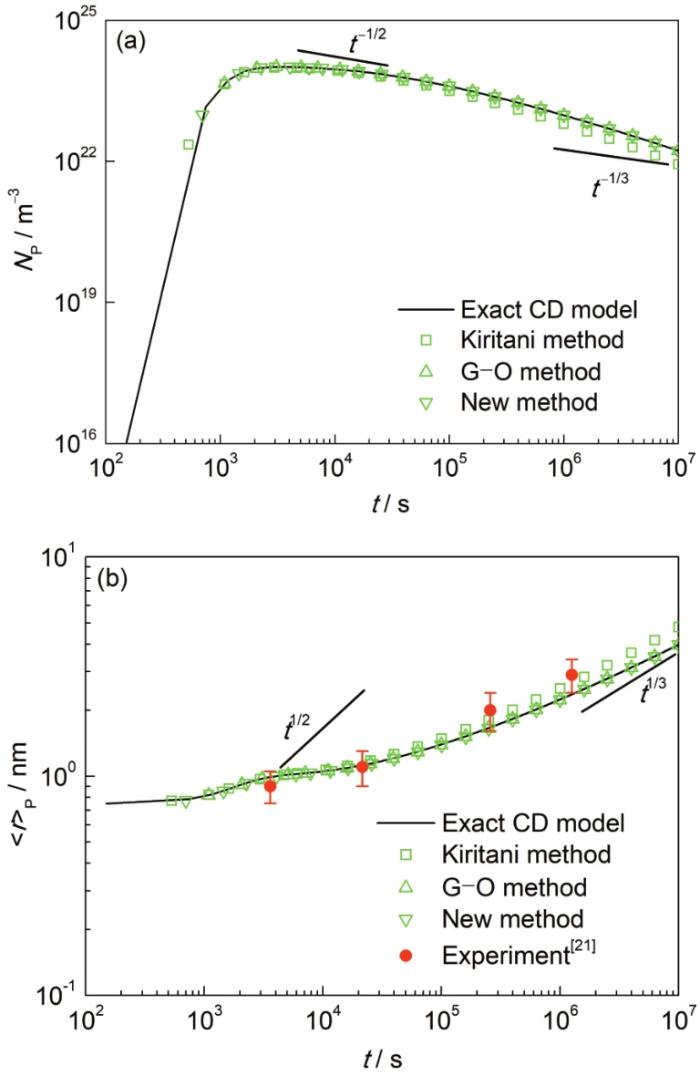
未分组和分组团簇动力学模型计算的在300℃等温析出时Al₃Sc颗粒的平均半径和总颗粒密度随时间的变化如图3所示。为了匹配透射电子显微镜测量结果，截断半径近似取为电镜图像中能观测到的最小粒子尺寸r_tr = 0.745 nm (对应i_tr = 25或G_tr = 23)。由于基于均匀分布假设的Kiritani方法使得团簇密度分布向更大尺寸方向偏移，因此随析出时间增加，得出的析出平均半径逐渐偏大，而总密度逐渐偏小。而线性和对数线性的分布均给出了与未分组模型更好的匹配结果，这也部分证实了Golubov等^[8]关于线性分布假设下负团簇组密度的出现并不显著影响析出总体性质的结论。在长大阶段，总密度近似满足Zener^[29]理论推导的关系NP∝t-1/2，但平均半径远小于rP∝t1/2的斜率。而在粗化阶段，模拟曲线近似满足LSW (Lifshiz-slyozov-Wanger)理论推导的NP∝t-1/3和rP∝t1/3关系^[30]。造成不匹配的原因很可能是实验中析出的形核、长大和粗化是同时发生和相互竞争的机制所致，故难以满足Zener生长理论的严苛条件。同时，LSW粗化理论仅适用于极稀溶体的最终析出阶段，然而在实验结束时可能仍无法严格满足该要求。最后，通过与实验的对比，所有模拟结果与测量析出半径都比较吻合，这也证实了团簇动力学模型的有效性。

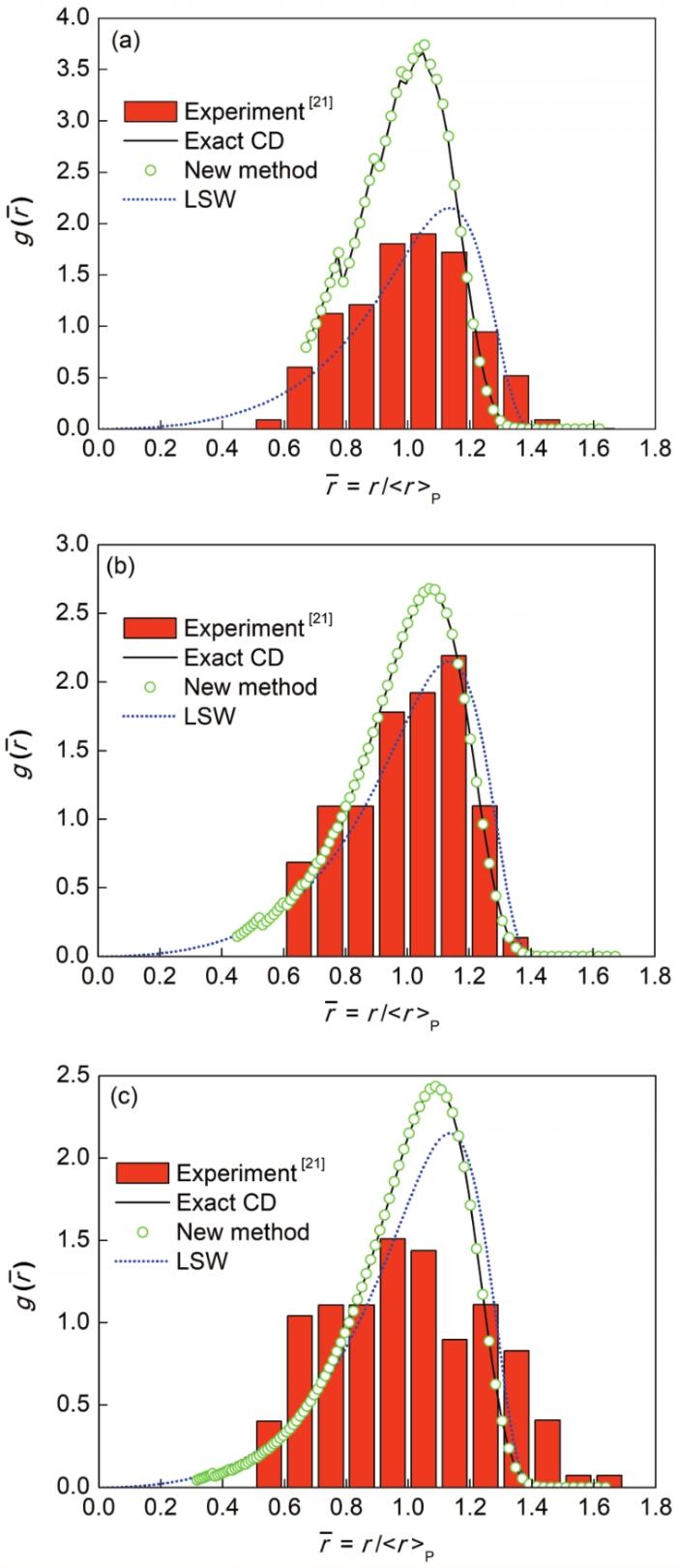
图4比较了由未分组和新分组团簇动力学模型计算出的不同时间归一化析出尺寸分布、实验测量以及LSW理论分布。图中，x轴是归一化半径r¯=r/rP，y轴是组内归一化密度与归一化半径间隔的比值，即g(r¯)=ΔN/NP/Δr/rP，其中ΔN和Δr分别是每个团簇组内的团簇总数量密度与最大团簇和最小团簇的半径差值。从对比结果可以看出，在析出6 h后，不管是未分组还是新分组法团簇动力学模型，得到的密度分布与Marquis的测量值^[21]和LSW分布匹配都比较差，这很可能是因为这时还远离粗化阶段，而且计算中采用的主要用于拟合粗化阶段测量值的界面能0.12 J/m²与匹配形核阶段测量值的界面能(0.094 ± 0.023) J/m^{2 [30]}相差也较大。但随时间的增加，计算结果不光逐渐趋近于实验测量分布，而且与其渐近极限LSW分布也更吻合。另外，新分组和未分组团簇动力学模型的完美匹配再次证明了新分组法的准确性。

(1) 通过采用3种不同粒径分组方法的团簇动力学模型模拟了Al₃Sc在Al-Sc合金的析出行为，并与未分组模型的精确解进行了比较。可以看出，假设组内团簇数量密度线性分布的Kiritani方法通常只能预测更大的析出平均尺寸和更宽的析出尺寸分布，密度线性分布的G-O方法与未分组模型结果吻合更好，但会造成某些团簇组密度为负，而本工作提出的密度对数线性分布假设是一种能够给出与未分组模型整体和局部性质都匹配较好的分组方法。

(2) 各模型的计算结果与300℃时Al-0.18%Sc中Al₃Sc等温析出的实验结果进行了比较。除了Kiritani方法预测的析出平均半径偏大和总密度偏小外，G-O方法和新分组法均给出了与测量值更吻合的平均半径。还用未分组和新分组法团簇动力学模型计算了析出尺寸分布，证实与不同析出时间的测量分布也比较接近。随时间延长，计算结果逐渐趋向于经典的粗化LSW分布函数。

(3) 与未分组团簇动力学模型相比，新的分组法在对准确性影响不大的同时显著降低了计算空间和时间要求。与已有的基于假设组内团簇数量密度均匀或线性分布的方法相比，新分组法给出了与未分组模型更加匹配的结果，证实了在不太增加计算成本的情况下完成大尺度析出模拟的可能性和良好的应用前景。