晶界能(γ)作为晶界的重要性质之一，可定量表征单位面积晶界因原子错排而具有的附加能量^[1]。深入了解晶界能有助于探明晶界对多晶材料与晶界相关行为和性能(例如再结晶、塑性变形和裂纹扩展)的影响本质，同时也为基于晶界工程定向调控材料性能提供重要的理论依据^[2~5]。例如，Liu和Kirchheim^[2]发现溶质原子在晶界偏析会显著降低纳米材料的晶界能，有效减弱晶粒粗化所需热动力学驱动力，最终提升纳米材料的结构稳定性；Hu等^[3]基于Ni-Mo超细晶纳米材料的相关研究进一步发现，材料强化不仅可通过调控晶粒尺寸这一传统方法实现，降低晶界能量、提升晶界稳定性也是行之有效的方法；大量有关Fe、Cu和Al等金属的再结晶研究表明，再结晶晶粒并非在基体组织内随机形核或均匀形核，而是呈现明显形核位置择优的特征，具有较高晶界能的大角度晶界正是主要择优形核位置之一^[4]。晶界能主要受温度、晶界的晶体学取向以及诸如原子结合能和晶格类型等材料本质属性的影响^[6]。温度和材料属性等因素对晶界能的影响规律已获得较为全面的认识，但是有关晶界取向的影响及机理的认识仍不够充分，同时也是晶界能持续研究的热点^[6~8]。这可能主要与晶界取向需要多个参数确定有关。完整描述晶界的晶体学取向需要5个参数，3个描述相邻晶粒的取向差(常以取向差轴( O )和取向差角(θ)的形式表示)，另2个描述晶界面取向( n )^[9]。

有关晶界能与取向差角的相关性，目前比较认可的是通过Read-Shockley公式^[1]描述2者的关系。根据该公式，当θ超过一定值时(一般为15°)晶界的能量将保持不变，然而实际材料的γ(θ)曲线常在大角度范围内存在显著的能量低谷^[10,11]。晶界能的实验测定和模拟计算主要集中在<100>、<110>、<111>和<210>等少数几组低Miller指数和高对称性的取向差轴^[10~17]，相关晶界能数据明显不足，从而导致无法针对γ- O 相关性进行有效的统计性分析。针对γ- n 的相关性开展了相对较为广泛的研究，但尚未形成统一的认识。例如，Wolf^[15,18]认为晶界面越密排时晶界能越低，Merkle^[19]提出晶界面取向的Miller指数越小时晶界能越低，Rohrer^[6]认为晶界面对应的表面能较低时晶界能随之较低。显然，要想较为全面了解晶界能与晶界取向的相关性，构建涵盖充分晶界取向多样性的晶界能数据库具有重要意义。

近年来，研究者不断通过分子动力学模拟构建数量可观的晶界能数据库，并统计性分析晶界能的相关性质^[8,20~23]。针对fcc金属，只有Olmsted等^[8]和Yang等^[20]开展了相关研究。其中，Olmsted等^[8]分别为金属Ni和Al构建了涵盖388组晶界的数据库，然而并未发现晶界能与取向参数间存在明显可见的关联。此数据库只选取了重位因子(Σ)较小的重位点阵(CSL)晶界，且对应的取向差轴和晶界面取向均为低Miller指数，由于晶界取向多样性不足从而很难揭示晶界能与各取向参数的相关性。近期Yang等^[20]针对金属Al构建了涵盖CSL晶界和非CSL晶界、倾斜晶界和扭转晶界、163个取向差轴、0°~180°取向差角的数据库，在晶界能与晶界取向的相关性方面揭示了大量新的规律和特征，较全面了解了2者的相关性和相应机理。例如，当 O 从取向投影三角形的中间区域向边部再向顶点变化时，倾斜晶界的能量逐渐降低，扭转晶界则在投影三角形<111>轴附近存在一个显著低能量区；在θ、 O 和 n 共3类参数中，θ对晶界能的影响程度最大，其次为 n。针对bcc金属，虽然也已构建了2组晶界数量可观的数据库^[21~23]，但所揭示的影响规律却十分有限。Kim等^[21]模拟计算了68705组Fe晶界的能量，但是所用晶界能计算模型存在明显缺陷^[24,25]，导致计算结果的准确性无法得到保证，从而尚未用于统计性分析。Ratanaphan等^[22,23]采用了与文献[8]相同的晶界选取方法，为金属Fe、Mo和W构建了涵盖408组晶界的数据库，由于晶界取向参数多样性不充分，主要揭示了晶界面对晶界能的影响要强于取向差、具有(110)晶界面的晶界具有相对更低能量。综上可知，bcc金属中晶界能与晶界取向参数的相关性研究仍存在明显不足，有待基于新的晶界能数据库进一步分析。

本工作采用截断球状双晶分子动力学模型，计算bcc结构Fe中共1568组倾斜晶界的能量，统计分析晶界能与晶界取向参数间可能存在的关联并揭示潜在机理。与其他模型相比，截断球状双晶模型可计算任意晶界的能量，从而所构建晶界能数据库不再局限于重位因子较小、取向差轴和晶界面取向Miller指数较小的CSL晶界，可充分考虑晶界取向参数的多样性，并且还可考虑较少被研究的非CSL晶界。本工作所构建晶界能数据库还可用于插值法拟合任意晶界的能量，以及为与晶界能相关的晶粒长大、再结晶和裂纹扩展等热力学行为模拟提供数据库。

目前主要有块状双晶^[8,17]和球状双晶^[24,25] 2种分子动力学模型计算晶界能，这2种模型的计算原理相似。但是，前者由于采用周期性边界条件，只适用于CSL晶界，且一般只用于Σ较小的CSL晶界。后者采用自由表面，可计算任意晶界的能量，但是原始球状模型^[24]在计算晶界能时只考虑一种初始晶界结构，且自由表面和晶界间相互作用会显著影响晶界能。近期本课题组^[25]对原始球状模型进行了改进，提出了截断球状模型。该模型引入了原子删除操作以删除晶界处相距过近的原子，并可以考虑更多初始晶界结构，同时在球状模型尺寸(半径R)的基础上引入截断半径(R_c)以排除自由表面和晶界间相互作用的影响，从而显著提升晶界能的计算精度。

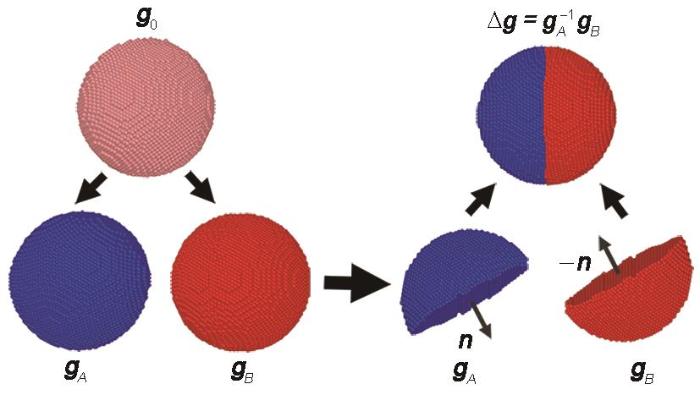
图1给出了截断球状模型构建包含特定晶界双晶体系的主要步骤。首先，在0 K时将取向为 g₀的球状单晶按一定要求转动，分别获得取向为 g_A 和 g_B 的A和B晶粒，沿给定 n 将2个晶粒分别分割成2个同等大小的半球，随后将晶粒A和B的2个半球刚性对接成晶粒取向满足取向差Δg=gA-1gB的双晶。当双晶构建完成后，删除晶界处间距小于临界间距d₀的两相邻原子中的任意一个，d₀以一定增量d_s在最小间距d_min和最大间距d_max间取值，以获得不同的初始晶界结构，最终选定所有初始晶界结构中对应能量最低者为晶界的结构。随后，基于共轭梯度法对双晶进行能量最小化弛豫，统计双晶内距球心间距不超过R_c的原子总数N_c和对应总能量Ec，用Ec减去单晶内N_c个无畸变原子对应的能量Nce0 (其中，e₀为与材料相关的单个原子的结合能)，并除以截断双晶中晶界的面积(SGBc=πRc2)，可得到对应晶界能γ，即：

本工作选定bcc结构Fe为研究对象，同时选取倾斜晶界(tilt GB，TIGB)构建晶界能数据库，以分析晶界能与晶界取向的相关性。已有研究^[26,27]表明，TIGB在材料微观组织内常被观察到，且其比例高于扭转晶界。这类晶界由于自身结构对称性的特点，只需相邻晶粒间取向差( O, θ) 3个自由度即可完整描述其晶体学取向。以下为TIGB的抽样选取方法，具体为：(1) 在 O 空间内，选取<hkl>位于0到5之间的所有取向差轴，具有等同晶体学取向的轴只选取1次；如此，共选定40个 O，即从[100]、[110]、[111]开始到最后的[553]和[554]轴。(2) 对于每个选定 O，获取该轴下Ʃ < 3000所有CSL晶界对应的取向差角{θ}，再从{θ}集合中筛选出不小于且又最接近于θ_i = 5i (i = 1, 2, 3, …, 36)的角的集合{θ'}；若{θ}中第1个角大于θ_i，则以上筛选从θ_{i + 1}开始。(3) 若{θ'}集合中第1个角θ1' (也即最小角)大于10°时，则在该集合较小θ'一侧从5°开始以5°等间距添加小于θ1'且对应晶界为非CSL晶界的取向差角，以获得取向差角集合{θ''}；该操作是为保证每个 O 下都可选取充分数量的小角度晶界；至此，40个取向差轴下共选定了1441个晶界。(4) 为保证每组 O 下具有较低Ʃ的晶界同时被选取到，{θ''}集合将额外再补充Ʃ ≤ 29的CSL晶界对应的取向差角，最终共抽样选取了1568个晶界。

对于所选取的各晶界，在利用截断球状双晶模型计算各晶界的能量前，需先根据晶体学理论基于抽样选取的取向差推导构建双晶模型所需2个晶粒的取向。在构建数据库时，通过参考之前的相关研究^[25]，并经过模拟测试发现当模型半径和截断半径分别设定为5和4.42 nm时，既可以保证晶界能计算结果不受尺寸效应的影响，还可以确保较高的计算效率。对于其他模拟设定，原子删除参数dmin=dnn/3，dmax=0.85dnn，d_s = 0.005 nm (其中，dnn=a0/3，表示bcc纯Fe内的最小原子间距，a₀为点阵常数)。选用文献[28]提出的2NN-MEAM原子势函数来描述原子的能量和相互作用力，该势函数对应的a₀ = 0.285 nm和e₀ = -4.2899996 eV。本工作所有分子动力学模拟均利用Lammps^[29]软件完成。

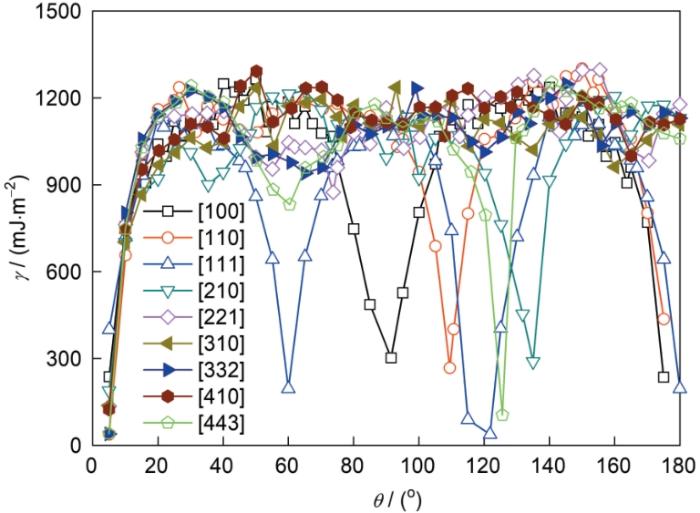
图2所示是晶界能数据库中部分取向差轴下晶界的能量随θ的变化。由图可知，在较小θ范围(例如θ < 20°)内，晶界能随θ变化趋势整体保持一致，也即整体上都随θ增大而升高；当θ进一步增大时，各晶界能量的变化趋势将呈现显著差异，有些晶界的能量近似保持稳定而有些则存在明显波动。例如，在大角度范围内，<100>、<110>和<111>晶界的能量分别在90°、110°、60°和120°附近存在明显的能量低谷，而<310>、<332>和<410>等晶界的能量则在最大值附近小范围内波动。这些结果表明，当晶界对应的取向差轴不同时，其晶界能(尤其在大角度范围内)可能显著不同，诸如Read-Shockley公式^[1]此类仅考虑部分晶界取向参数影响的晶界能计算公式或模型在准确预测晶界能方面存在明显缺陷，要想准确获取晶界能必须完整考虑各取向参数的影响。

图3为不区分取向差轴下所有晶界的能量随θ的变化。由图3a可知，对于具有相同θ的不同晶界，对应的晶界能并不相同，而是会在较大范围内波动。这主要是由于晶界能还受到晶界面取向和取向差轴等其他取向参数的影响。当θ较小时(如θ < 15°)，晶界能整体随θ增大而提高；当θ进一步增大时，晶界能整体保持平稳，但在θ = 60°和120°附近存在2个呈现较大散布的能量低谷。整体来看，这些变化趋势与图2中<310>和<410>等晶界的趋势相近。在已有实验和模拟研究^{[10,13~15,25]}中也常观察到以上晶界能随θ的整体变化趋势以及能量低谷，但几乎都只限于具有较低Miller指数(如<100>、<110>和<111>)的晶界。与非CSL晶界相比，CSL晶界对应相邻晶粒点阵会在晶界产生重叠，因而长期以来CSL晶界被认为具有更低的结构畸变度(也即更低的能量)^[6,30]。然而，由图3a中θ = 5°和10°非CSL晶界的能量可知，非CSL晶界的能量可高于也可低于CSL 晶界，晶界能的相对高低与晶界附近的点阵是否存在重叠并无关联；当θ较小时，非 CSL晶界的能量随θ的变化趋势与CSL晶界相同。在此前针对金属Al的晶界能统计性分析^[20]中也观察到这些特征。

为更好呈现晶界能随θ的整体变化趋势，图3b给出了图3a中晶界能经最小二乘拟合所得γ(θ)曲线，同时还添加Read-Shockley模型所得γ(θ)曲线以进一步检验此模型预测晶界能的准确性。对于Read-Shockley模型，不同θ的γ为^[1]：

式中，γ_m和θ_m分别表示拟合γ(θ)曲线上的最大晶界能和对应的取向差角。由图3b可知，在θ <30°范围内，拟合所得与模型所得结果一致，晶界能都随θ增大而迅速提高。当θ进一步增大时，虽然拟合所得晶界能要低于Read-Shockley模型(尤其在θ = 60°和120°波谷位置)，但2种方法所得晶界能仍可认为相符较好。综合图2和3b可知，若从严格的统计性角度来看，小角度晶界的能量要低于高角度晶界，Read-Shockley模型在θ较小时可获取较为准确的γ(θ)曲线。

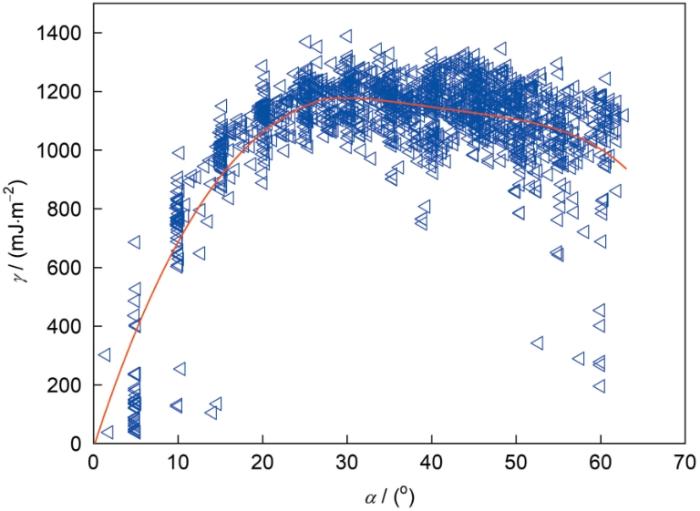
需要说明的是，图2和3中所探究γ-θ相关性中的θ是在给定晶界类型(即TIGB)条件下晶界对应的角度，θ取值范围为0°~180°。然而，在实际有关晶界能的预测和模拟时，很难获取晶粒类型和晶界对应取向差轴，因而为了问题简化常采用晶界对应偏转角(disorientation angle，α)来计算晶界能^[1,31,32]。考虑晶体对称性条件下，在所有表征两晶粒取向差的轴角对( O，θ)中，最小θ角被定义为偏转角α，取值范围为0°~62.8°。为探究γ-α相关性，图4给出了晶界能库中所有晶界的能量随α的变化。由图可知，具有相同α角晶界的能量会在一定范围内波动，具有更大α的晶界并不一定具有更高的能量。这些特征类似于图3所示晶界能随θ变化的特征。同时，最小二乘拟合所得γ(α)曲线的整体变化趋势也与图3b拟合和Read-Shockley模型所得γ(θ)曲线类似，但稍有不同的是γ(α)曲线在后期呈现持续下降的趋势。这说明晶界能-晶界角度的数据与所选取的晶界角度类型(θ或α)有关，实际应用时应谨慎选取。在Ratanaphan等^[22]有关金属Fe和Mo的研究中，晶界能随α的变化趋势与当前研究整体一致，但在α = 60°附近未观察到晶界能整体下降的趋势，在α = 40°附近却存在一个晶界能低谷。这2点差异主要与 Ratanaphan等^[22]所研究的晶界有关，也即绝大部分晶界都是具有高对称性取向差轴和低指数晶界面取向的CSL晶界。

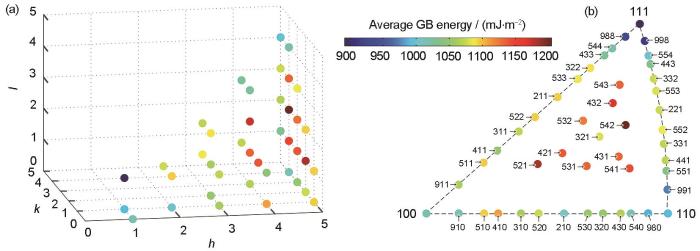
为探究晶界能与取向差轴的相关性，图5分别给出了在三维晶体取向空间和标准球面投影三角形内晶界能随取向差轴的变化。显然，在常规三维取向差轴空间内，晶界能分布比较杂乱，晶界能与取向差轴的相关性很难观察到一定的规律(图5a)。相对而言，在投影三角形内，则能观察到明显可见的规律(图5b)。为了使相关规律更为明显，补充计算了<910>、<911>、<980>、<988>、<991>和<998>共6个较高Miller指数取向差轴下晶界的能量。从图5b可观察到以下3个主要特征：(1) O 位于三角形边部晶界的能量要明显低于 O 位于三角形内部晶界的能量，即γedge<γcenter；(2) 在 O 位于三角形边部的所有晶界中，<100>、<110>和<111> 3个顶点附近的晶界具有明显更低的能量(也即γcorner<γedge)，且边部晶界的能量整体呈现渐变的特征；(3) 在3个顶点能量低谷处，又以<111>轴附近的晶界能整体最低，其次为<110>和<100>，即γ<100>>γ<110>>γ<111>。

以上特征呈现的总体晶界能顺序为γcorner<γedge<γcenter，此顺序大致可认为是晶界结构的对称性随 O 改变而逐渐降低所导致的。当TIGB对应的 O 位于三角形内部时， O 的各Miller指数互不相同且不为0，双晶模型中2个晶界面法向是非等同取向(θ = 180°时除外)，此时TIGB实质上是非对称倾斜晶界(ATGB)，而 O 位于三角形边部的晶界实质上是具有相对更高结构对称性的对称倾斜晶界(STGB)，位于顶点附近的晶界又由于 O 的高对称性特征而具有比其他边部晶界更高的结构对称性。以上结果表明，从统计性角度来看STGB的能量要低于ATGB。在Olmsted等^[8]和Ratanaphan等^[22,23]分别构建的388组fcc和408组bcc晶界数据库中，都只针对几个常见低指数轴的晶界，因而未能观察到图5b所揭示的相关特征。其他有关晶界能的实验和模拟研究^[10~19]，由于考虑的晶界数量更少，从而更加无法观察到以上特征。在近期Yang等^[20]有关Al 的TIGB晶界能统计性分析中，也观察到了γcorner<γedge<γcenter，但顶点附近的晶界能顺序则是γ<110><γ<111>≈γ<100>。显然，在本工作和文献[20]中γcorner<γedge<γcenter的特征都是受晶界结构对称性的影响，而顶点附近能量顺序的差异则主要是由晶格类型不同所导致。

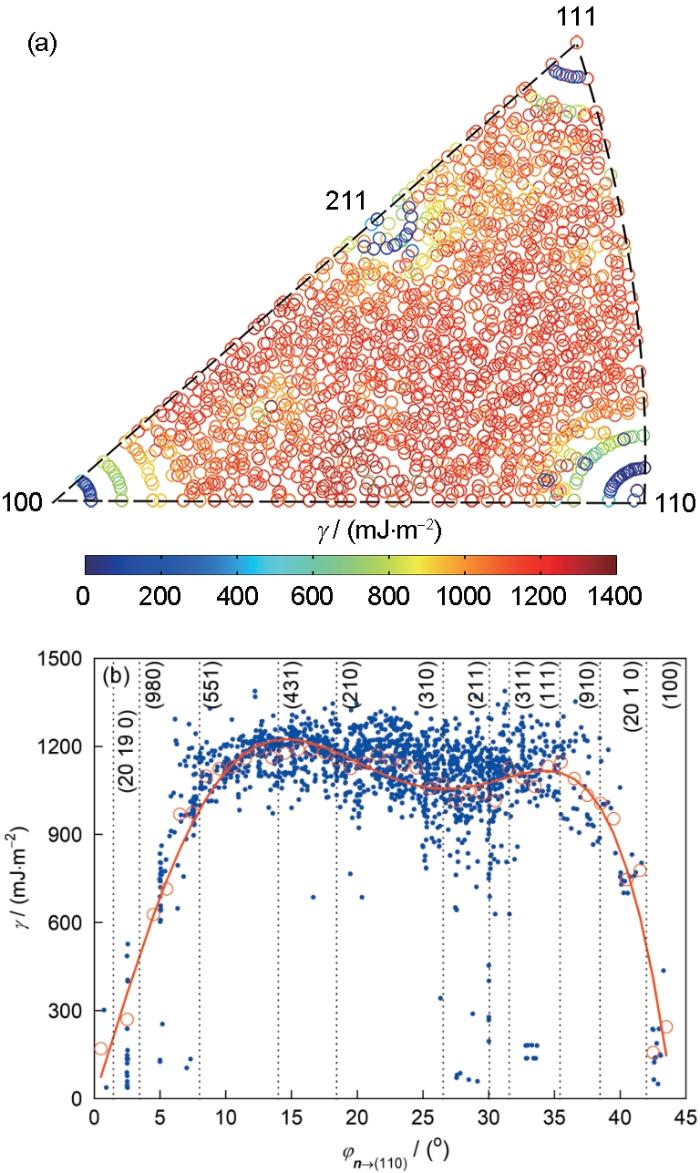
有关 n 对晶界能的影响，研究者认为当晶界面具有低取向指数、高面原子密度或靠近(111)面等特征时fcc晶界的能量将相对较低^[6,15,18,19]，而当晶界面为高密排面或取向为(110)时bcc晶界的能量将相对更低^[22,33]。为进一步探究bcc金属中γ与 n 的相关性，图6a给出了数据库中所有晶界能在晶界面取向标准球面投影三角形内的分布。由图可知， n 位于三角形内部的晶界具有明显整体更高的能量，在3个边角附近的晶界能要整体更低。然而，由于边角附近所考虑的晶界数量不足，无法定量统计这些位置晶界能的相对高低。整体来看，具有高密排晶界面的晶界似乎具有相对较低的能量，此规律与Wolf^[33]在分析金属Fe和Mo晶界能时所揭示的规律类似。需要注意的是，在(111)附近同时还存在一些明显更高能量的晶界，而在(211)附近的晶界能也可能整体更低。对于具有bcc晶格类型的金属，晶面密排程度的顺序为：(110) > (100) > (211) > (310) > (111) > (321) > (411) > (210)。

为验证已有研究关于晶界能与晶界面密排程度相关性的认识，图6b给出了晶界能随 n 偏离(110)面(即bcc金属中最密排面)角度φn→(110)的变化情况。为计算简便和意义明确，将各晶面取向的等同取向(uvw)用于计算φn→(110)，该等同取向的特征是u ≥ v ≥ w ≥ 0。由离散数据可看出，在 n 固定时，晶界的能量将在一定范围内波动，晶界能与φn→(110)整体上并不存在简单的正或负相关性。然而，由拟合γ-φn→(110)曲线可知，当φn→(110)靠近最小和最大值时，即随 n 靠近最密排面(110)和次密排面(100)时，晶界能整体上都急剧降低；当φn→(110)位于中间取值时，晶界能整体上保持较高水平。Ratanaphan等^[22]对408组Fe和Mo晶界能统计性分析时，只发现具有(110)晶界面的晶界具有相对更低的能量，但未观察到其他特征。图6b的结果还表明，Wolf^[33]提出的由高密排晶界面构成的晶界具有较低能量的观点，只针对部分晶界面取向且只有在统计性角度才成立。例如，对于由(20 1 0)、(980)和(20 19 0)等高指数、低密排面构成的晶界，其能量却明显低于(111)和(210)等低指数、高密排面晶界对应的晶界能。这些结果同时也否定了Merkle^[19]提出的由低指数晶界面构成的晶界会具有低能量的观点。

从晶界形成的断键(broken-bond)模型来看，晶界能可认为是形成晶界两侧相邻晶粒对应表面的能量与2个表面结合时所需能量的差^[34]。因此，根据此模型的定义，晶界能与晶界面的相关性值得从晶界面对应表面能的角度进一步探究。然而，本工作数据库中TIGB对应的晶界面取向总数过多，且包含取向指数极大的晶面以及取向难以Miller指数化的晶面(见图6a)，因而很难甚至无法基于分子动力学逐一计算每组晶界面的表面能。在此情况下，可先计算部分特殊表面(或晶界面)对应的表面能，然后基于已计算结果利用线性插值法得到数据库中各晶界面的表面能。

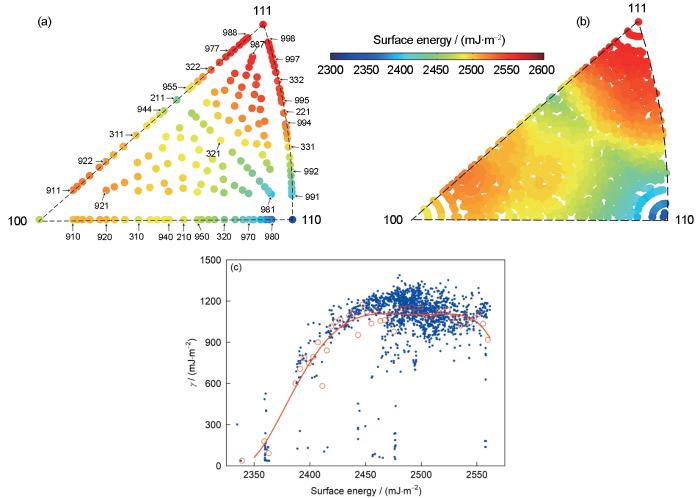
图7a给出了模拟计算所得bcc结构 Fe中从(100)、(110)、(111)到(997)和(998)共163个自由表面对应的表面能。表面能计算方法为，将含有特定表面的周期性块状晶体的能量减去同等原子数量且无结构缺陷体晶的能量，再除以表面的面积。由图可知，所选取自由表面的取向较为均匀地分布在取向空间内，且对应的表面能呈现平滑渐变的特征。这2个特征可确保后续线性插值所得表面能具有较高的准确性。在投影三角形的(110)和(111)取向附近分别存在一个面积较大的显著低能量区和高能量区，三角形内部和边部的表面能整体上并无明显差异。基于图7a中表面能，利用线性插值法拟合所得晶界能数据库中各晶界面对应的表面能分布如图7b所示。对比分析2个图可知，拟合所得表面能的分布特征(图7b)与计算所得结果(图7a)保持一致，即拟合所得表面能表现出了预期的准确性和可靠性，可用于后续有关晶界能和表面能相关性的分析。图7c进一步提供了数据库中各晶界能随晶界面对应表面能的变化。从离散数据点来看，在表面能固定时，晶界能分散较大，晶界能随表面能的整体变化趋势不明确。从拟合能量曲线可明显看出，当表面能相对较小时，晶界能随表面能增大而升高。当表面能继续增大时，晶界能则保持较高水平。从断键模型^[33]角度来看，对于晶界能在此水平状态的晶界而言，形成晶界时所需结合能对晶界能的贡献等同于表面能的贡献，从而晶界能整体保持不变。在Yang等^[20]有关Al晶界能与表面能的统计性分析中也观察到了与图7b中相同的趋势，而在Wolf针对Cu^[15]和Fe^[33]以及Wo^[33]的研究中晶界能整体随表面能持续增大。该差异主要是由于Wolf^[15,33]所研究的晶界都是具有相对高对称性取向差轴和较低能量的晶界。

点阵重位因子Σ表示CSL晶界两侧相邻晶粒的点阵在晶界处的重合程度，Σ越小时相邻点阵的重合度就越高，因而长期以来都有研究者^[30,35,36]认为低Σ晶界具有相对更低的能量，在部分研究^[10,17]中也都观察到了此规律。为进一步探究γ-Σ的相关性，图8给出了不区分取向差轴和区分取向差轴下晶界能随重位因子的变化。由图8a所示数据可知，晶界能与Σ整体上不会呈现任何可见的相关性，具有相同Σ晶界的能量会在较大范围内波动。这表明低Σ晶界具有相对较低能量的观点显然是不正确的，例如对于具有最小Σ的Σ3晶界，能量波动范围可达到约1000 mJ/m²，其能量并不一定低于其他高Σ晶界。这一结论实质上在图3a中也已得到了体现，即CSL晶界的能量并不一定低于非CSL晶界(对应Σ趋近于无限大)。以上观察与Yang等^[20]和Olmsted等^[8]统计性分析fcc以及Ratanaphan等^[22]分析bcc金属内晶界能与Σ相关性的结果一致，尽管文献[20]和当前研究中最大Σ高达2997，而文献[8,22]分别只有385和323。本工作将已有晶界能分析扩展到高Σ晶界和非CSL晶界时发现，这2种晶界往往可能具有极低的能量。进一步分析发现，这些晶界实质上是Read-Shockley模型中所描述的“小角度晶界”，即晶界结构可基于位错模型表征的晶界。显然，该结果再次强调了取向差对晶界能的显著影响以及仅基于Σ预测晶界能相对高低的不可靠性。

尽管整体上晶界能与Σ无可见相关性，但若将2者相关性的讨论只限定在相同 O 下的同类型晶界时，则会获得一些其他认识。图8b~d以<100>、<211>和<541>为例给出了数据库中部分固定 O 下Σ < 30晶界的能量在γ-θ曲线上的分布特征。由图可发现，曲线上的能量低谷一般都位于具有局部极小Σ晶界处(图中蓝色空心圆)，也即当某晶界的Σ比左右相邻晶界都小很多时，该晶界会具有局部极小能量。与相邻晶界相比，这类晶界对应的晶粒点阵在晶界处的重合度会更高，相应的晶界结构畸变度更低，从而晶界能较低。需说明的是，该解释只限于具有相同取向差轴的同类型晶界，并不能用于整个晶界取向空间内分析Σ对晶界能的影响。由此可见，低Σ可认为是晶界具有较低能量的必要但不充分条件。此外，进一步统计后发现，对于位于较小Σ处的能量低谷，其相对大小和宽度并不会随Σ的升高而增大或减小。综合以上分析可知，Σ用于预测晶界能的可靠性非常有限，仅能判断具有相同晶界类型和相同取向差轴下局部晶界能量的相对高低。

(1) 对于金属Fe内倾斜晶界，虽然不同 O 下晶界能随θ变化趋势在大角度范围内存在显著差异，但是从统计性角度来看，晶界能在较小取向差角和偏转角时都随角度的增大而提高，然后整体保持平稳。该趋势与Read-Shockley模型预测结果整体上较为一致。非CSL晶界的能量并不高于CSL晶界，且在较小θ范围随θ的变化趋势与CSL晶界相同。

(2) 晶界的能量与对应取向差轴存在密切的相关性，当 O 从取向投影三角形的内部区域向边部再向顶点变化时，随着倾斜晶界结构的对称性整体上逐渐升高，晶界的能量逐渐降低，且在<111>轴附近存在一个明显的低能量区。

(3) 已有关于具有低Miller指数、高密排晶界面的晶界具有较低能量的观点并不正确，晶界能与晶界面取向的相关性最适合在断键模型下从晶界面对应表面能的角度进行解释。晶界的能量整体上都随晶界面对应表面能的增大而升高，直至整体保持平稳。

(4) 晶界能与Σ整体上不存在可见相关性，但固定 O 下晶界能-取向差角曲线上的能量低谷一般都位于具有极小Σ的晶界，能量低谷对应晶界能的相对大小和低谷宽度与Σ无关。bcc金属内晶界能与晶界取向的相关性及规律和已探明的fcc金属对应结果存在大量相似或相同之处。