长期以来,材料的力学性能一直是材料科学研究的重点。Fe是应用最为广泛的金属,并且作为一种模型材料,对其力学性能已经开展过不少研究。例如Dever [1]研究了单晶Fe的弹性常数,表明温度是通过影响自旋序列影响弹性常数。Benito等[2]对室温下多晶纯Fe在拉伸变形时的弹性模量进行了实验研究,发现弹性模量的高低与位错密度有关。分子动力学等数值模拟研究工作表明,Fe在应力条件下会发生相变而导致微观结构更加复杂[3,4],塑性变形机制也会随应力不同而发生改变[5]。Dutta[6]对Fe纳米柱的压缩过程进行了原子模拟研究,指出温度对位错活动有明显的影响,进而对材料的整体塑性产生影响。近年来,Rawat和Chaturvedi[7]研究了温度对单晶Fe三轴拉伸过程中孔洞等微观缺陷演化的影响,Zhang等[8]及Wu等[9]则研究了Fe纳米线和其他纳米材料中五重孪晶的强化作用。众所周知,宏观力学性能与微观结构变化密切相关,尽管之前已经报道了不少相关的研究工作,但是对于bcc单晶Fe变形过程的研究仍然不够充分,尤其是不同拉伸取向、不同温度等条件下的局域结构和位错演化过程仍值得深入研究。
目前分子动力学模拟等原子模拟方法已经成为研究材料变形机理的重要手段,尽管存在着变形速率过高和描述对象的尺寸过小等问题,但在分析材料性能与微观结构的关系时仍能提供很多可参考的信息。用分子动力学模拟得到的金属单晶塑性变形过程的应力-应变曲线,一般都出会出现1个或多个最高点,通常把第1个最高点的位置对应于屈服强度和屈服应变。从Zolnikov等[10]所作的模拟工作中可直观看出,Fe微晶中塑性的开始与位错或孪晶成核的关系,而位错或孪晶的出现则是局部结构转变的结果。金属的塑性变形机理与位错运动密切相关,而以往的相关模拟研究工作则较少把位错作为变形热动力学的标准。变形与相变一样都可视为热力学驱动下的动力学行为[11],近年来本课题组[12~16]提出了热-动力学相关性的概念,即热力学协同或“互斥”,并基于这一概念发展了新的材料力学性能优化设计思想,即相变和变形广义稳定性准则[17,18]。实际上变形和相变的热-动力学遵循共同的协同机制,即驱动力的提高总是伴随动力学能垒降低,反之亦然。对于材料变形过程,理解其热-动力学相关性的关键在于掌握位错运动和演变的规律,了解位错运动的驱动力和能垒的变化关系。本工作采用分子动力学方法,对单晶α-Fe沿不同晶向进行单轴拉伸模拟,通过考察其在变形中的局域结构变化和位错演变过程,研究单晶α-Fe变形的热动力学行为。
1 模拟方法
选取[010]、[111]、[
表1 单晶α-Fe拉伸模拟模型的尺寸
Table 1
| Crystal orientation | Model size / nm | Atomic number | ||||
|---|---|---|---|---|---|---|
| X | Y | Z | LX | LY | LZ | |
| 19.987 | 59.961 | 19.987 | 2058000 | |||
| 19.583 | 59.841 | 19.786 | 1992144 | |||
| 19.782 | 59.763 | 19.583 | 1989120 | |||
| 19.786 | 59.449 | 19.782 | 1999200 | |||
2 结果与讨论
2.1 应力-应变与能量变化曲线
在温度10 K、应变速率109 s-1的条件下模拟了α-Fe沿不同晶向([010]、[111]、[
图1
图1
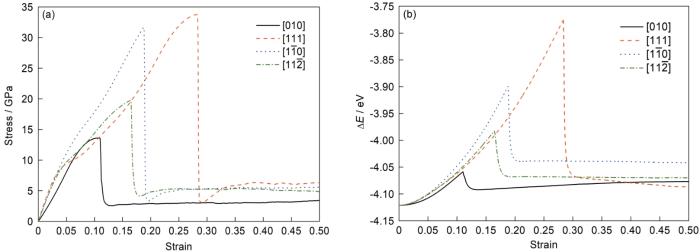
α-Fe在10 K温度下沿不同晶向拉伸过程的应力-应变曲线和势能变化曲线
Fig.1
Stress-strain curves (a) and potential energy (ΔE) curves (b) of α-Fe along different orientations at 10 K
2.2 结构变化
单晶Fe拉伸过程中的结构与位错变化导致了宏观力学行为的差异,而结构与位错的变化则取决于过程的热-动力学条件。通过对模拟结果的分析,在拉伸中的弹性阶段,晶体保持完整有序的结构,没有明显的缺陷形成,当外部持续加载使得应力达到一定程度时,原子局部晶格结构失稳,发生了较大的局域结构变化,位错也开始萌生和运动,材料试样发生屈服,因而可知图1a中应力-应变曲线中应力的最高点即为屈服应力,此时对应的应变为屈服应变。之后进入均匀塑性变形阶段,应力基本不随应变增加而发生变化。
拉伸模拟过程中观察到的局域原子结构变化主要发生在屈服点附近,在此后的塑性变形阶段则没有明显的结构变化。通过CNA获取了沿不同晶向拉伸时屈服点处的原子局域结构分布图,10 K温度下的结果如图2所示。由图2a可见,沿[010]晶向拉伸时,单晶Fe在屈服时已经存在fcc结构,此时的fcc结构为一种特殊的中间态,后期fcc局域结构占比降低而bcc结构占比回升,且fcc结构多聚集在与拉伸轴垂直或者呈45°夹角的位置。类似的bcc/fcc结构转变现象在Sandoval和Urbassek[29]对单晶Fe纳米线拉伸过程的模拟研究中也有报道,其结果表明,大量局域bcc结构随拉伸进行转变为密排结构,之后密排结构消失,bcc结构占比回升。闻鹏等[30]对单晶Fe及Fe-C合金拉伸过程的模拟中也发现了同样现象。这种结构变化的发生,可能是由于不同相结构中的平面之间存在特殊的平行关系[31, 32],因而沿Bain路径发生bcc/fcc结构转变。在黄丹等[33]对bcc和fcc纳米丝的研究中,fcc结构的破坏也比bcc结构更快。本工作中沿其他晶向([111]、[
图2
图2
10 K下不同晶向α-Fe屈服时的局域原子结构分布
Fig.2
Local atomic structure distributions of α-Fe along different orientations at yield points (10 K, ε—strain)
(a) [010] (ε = 0.106) (b) [111] (ε = 0.284)
(c) $[1\bar{1}0]$(ε = 0.188) (d) $[11\bar{2}]$ (ε = 0.165)
2.3 位错萌生及演化
由模拟结果发现,在α-Fe的拉伸过程中除伴随着局域结构的变化外还有大量的位错产生,利用DXA分析得到的10 K温度下拉伸时的位错密度变化曲线如图3所示。由图3可见,拉伸过程初期(弹性形变阶段)虽部分晶向已发生局域结构的变化,但均未有位错出现;拉伸至屈服点附近时,伴随着晶格畸变和原子的偏离,开始产生位错。对照应力-应变曲线可知,此时发生屈服现象,由于初始模型中不含位错,屈服只受位错形核控制,对应的应力相当高。屈服后伴随着位错滑移和晶格重新定向,位错数量快速增多,应力迅速降低,且系统势能也降低(图1b)。模拟结果显示,沿不同晶向拉伸时位错萌生的难度不同,塑性变形出现时间不同,屈服强度也有较大差异,位错萌生越早,屈服强度越低。
图3
图3
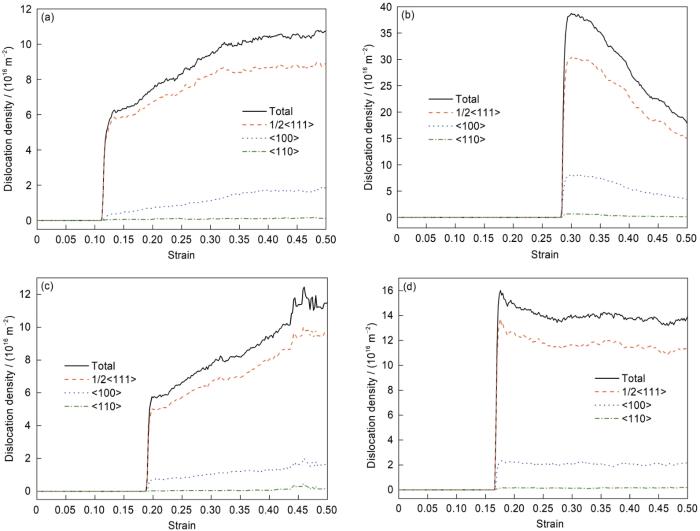
10 K下α-Fe沿不同晶向的位错密度曲线
Fig.3
Dislocation density curves of α-Fe along different orientations at 10 K
(a) [010] (b) [111] (c) [$1 \bar{1}0$] (d) [$11\bar{2}$]
沿着[010]晶向拉伸时,首先出现的是1/2<111>螺位错(图3a)。而应变达到0.114时,位错数目开始快速增多,并且出现了<100>位错。之后位错数目进一步增多,位错主要类型仍然为1/2<111>位错,而<100>位错的数目也继续增多,同时出现<110>位错,并且已经可以比较明显地观察到位错变化。且沿此晶向拉伸,在局域结构发生变化后才有位错萌生。
沿着[111]晶向拉伸时的位错密度变化过程如图3b所示。位错萌生初期<100>位错最多,经进一步分析发现,此时<100>位错的形态多为环状。经过位错环的扩张,位错开始增殖或反应,1/2<111>位错线数量迅速占优。而沿着[010]、
沿[
以上模拟结果表明,同一温度下沿不同晶向拉伸时具有不同的力学行为,各个晶向屈服应力的差异主要源于位错演变过程不同。
2.4 温度的影响
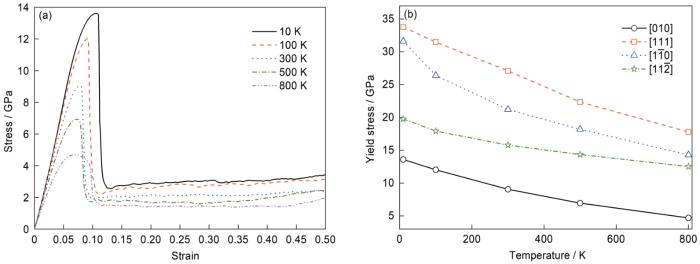
在本工作中,模拟了α-Fe在不同温度(10、100、300、500和800 K)下沿各晶向以109 s-1的应变速率拉伸的过程。沿[010]晶向拉伸时在不同温度下的应力-应变曲线及各晶向在不同温度下的屈服应力如图4所示。由图4a可见,单晶Fe塑性变形对温度的变化具有较高的敏感性,且不同温度下应力-应变曲线的变化趋势基本相同。随着温度的上升,拉伸应力-应变曲线的弹性阶段斜率变小。这是由于温度提高使得热振动加剧,原子间距离增大,导致弹性模量降低。由图4b可见,沿4个晶向拉伸时的屈服强度均随温度升高呈下降趋势,在Wu等[34]对纳米线拉伸过程的模拟研究中也有类似发现。这是因为温度升高会使原子在晶格附近的运动速度加快,增加了位错热激活的概率,金属发生软化,同时临界分切应力随温度的升高而降低,进而导致屈服强度降低。
图4
图4
α-Fe沿[010]晶向在不同温度下的应力-应变曲线及不同晶向在不同温度下的屈服应力
Fig.4
Stress-strain curves along [010] orientation (a) and yield stress along different orientations (b) of α-Fe at different temperatures
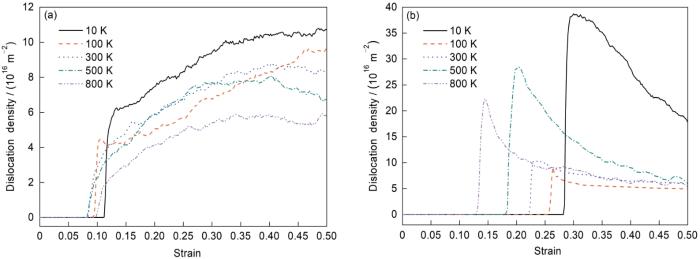
为探讨温度对单晶Fe位错演化的影响,获取了不同晶向在不同温度下拉伸时的位错密度曲线。结果表明,沿不同晶向拉伸时,温度对位错密度产生不同的影响。以[010]和[111]晶向为例,如图5所示,沿着[010]晶向拉伸时,位错密度逐渐升高,而沿着[111]晶向拉伸时,位错密度在发生突然增加后又逐步降低。图5还显示,总体上随着温度升高位错萌生越来越容易,屈服强度也随着位错萌生时间提前而降低。但是沿[010]晶向拉伸时,800 K时位错萌生时间却比500 K时更晚,而屈服强度也相对较低。经过分析发现,沿[010]晶向拉伸时,在位错萌生之前即发生bcc结构向其他局域结构的转变,且随着温度升高,结构转变发生的时间越来越早。温度较低时,主要发生bcc向fcc结构的转变(图2),但800 K温度下在弛豫后即有非bcc结构出现,且拉伸时出现了大量的bcc结构向其他非密排局域结构转变的情况,这些局域结构变化行为可能是其位错萌生时间虽晚但屈服强度却也有所降低的原因。综上所述,温度的升高会改变局域结构的演变过程,也会造成位错萌生及演化的差异,进而导致材料屈服行为发生变化。
图5
图5
α-Fe在不同温度下沿[010]和[111]晶向拉伸时的位错密度曲线
Fig.5
Dislocation density curves of α-Fe along different orientations at different temperatures
(a) [010] (b) [111]
2.5 位错演化过程的热-动力学分析
基于前述热-动力学平衡关系,本课题组[18]进一步提出了广义稳定性(generalized stability,GS)准则,将控制微观组织演化的热稳定性和力学稳定性进行扩展和统一,评估力作用下的热-动力学过程。以下将通过驱动力(ΔG)、能垒(Q)及广义稳定性(Δ)来探讨单晶Fe塑性变形过程的热-动力学。
变形过程的ΔG为施加的应力(ΔGσ )与位错相互作用产生的滑动阻力(ΔGτ )之差,即[18]:
式中,σb为流变应力,G为剪切模量,b为Burgers矢量模,ρ为位错密度,α与C为几何因子,M为Taylor因子。
而屈服点处的驱动力(ΔGy)为:
式中,σy为屈服应力。
材料应变速率(
式中,R为摩尔气体常数,T为热力学温度,ρm为可动位错密度,
Δ定义为:
式中,参考状态取为屈服点(用下标y表示),即在参考状态下Q = Qy,ΔG = ΔGy,Δ = 0。
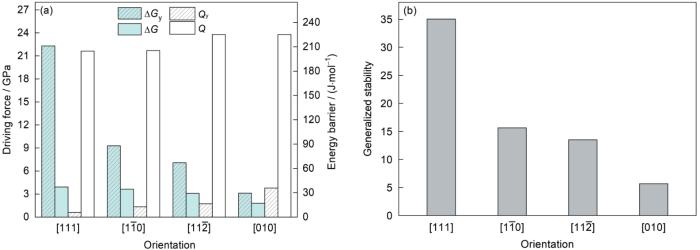
为探讨分子动力学模拟的单晶Fe变形过程中的热-动力学关联,计算了不同晶向在拉伸应变为0.5时的热力学驱动力、动力学能垒及广义稳定性,如图6所示。由图6a可见,对于单一变形过程,模拟计算的结果为ΔG < ΔGy,Q > Qy,即随着应变增加ΔG减小,而Q则增大,变形过程的热力学驱动力与动力学能垒具有互斥性。而在真实实验中,从屈服到均匀塑性变形的过程表现为ΔG增大而Q减小[18]。模拟与实验之间的差异原因主要在于位错机制的不同,由于本模型中不存在初始位错,屈服与位错的形核相关,这导致晶格的突然应变诱导重定向,并伴随着屈服后应力的降低及驱动力、能垒、广义稳定性的变化,这种现象在其他模拟中也有报道[35]。此外,沿不同晶向拉伸过程中的热-动力学关系也有不同。由图6a可见,[111]晶向的ΔG最高而Q最低。这是由于拉伸时位错萌生时间越晚,则热力学稳定性越高,即需要更大的热力学驱动力,从而表现出更高的屈服强度,屈服后的塑性变形中结构演变也通常会加快,这表现为位错密度快速升至最高,对应于更低的动力学能垒。
图6
图6
α-Fe在10 K下沿不同晶向变形中的驱动力、动力学能垒和广义稳定性
Fig.6
Thermodynamic driving force and energy barrier (a) and generalized stability (b) for plasticity deformation of α-Fe along different orientations at 10 K (ΔG—driving force at 0.5 strain, ΔGy—driving force at reference state (yield point), Q—energy barrier at 0.5 strain, Qy—energy barrier at yield point)
通过对变形中的广义稳定性研究发现(图6b),在单一变形模拟过程中,屈服时的Δ为0,屈服后Δ (正值)随应变增加而升高。对应的实验过程则是,从屈服到颈缩的变形过程中,Δ (负值)不断减小,而Δ较小 (即绝对值较大)意味着位错演化更加可持续。对不同晶向下的变形过程模拟而言,由图6b可见,在给定应变条件下,[111]晶向的ΔG 最高(即强度最高),且Δ最高,即塑性提升空间降低,塑性最差;[010]晶向的ΔG最低(即强度最低),且Δ最低,即塑性最好。这一模拟结果虽然与实验中Δ的变化趋势相反,但反映的力学行为其实是一致的。因而,可以用Δ的绝对值来表达广义稳定性,即Δ的绝对值越小,均匀塑性变形越慢(即塑性变形越持久),从而保持瞬时状态的能力越大,则塑性越好。
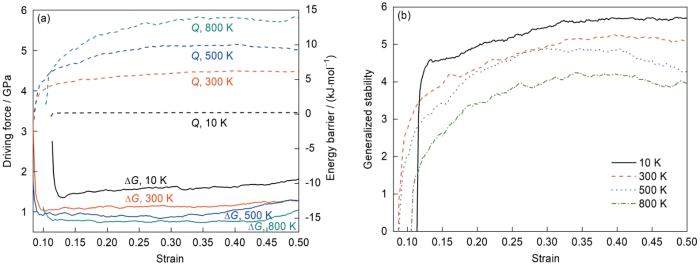
图7
图7
α-Fe沿[010]晶向在不同温度下塑性变形时的驱动力、能垒及广义稳定性曲线
Fig.7
Driving force and energy barriers curves (a) and generalized stability curves (b) of α-Fe for plasticity deformation along [010] orientation at different temperatures
3 结论
(1) 单晶Fe在10 K下沿着不同晶向([010]、[111]、[
(2) 温度对单晶Fe的力学行为有着重要影响。随温度升高,沿不同晶向拉伸的弹性模量和屈服强度均降低。温度可以通过影响局域结构的变化来影响位错萌生进而影响屈服行为,总体上温度升高使得位错萌生时间提前(即热力学稳定性降低)。在不同温度下的拉伸变形过程符合热-动力学互斥相关性,且在屈服后的同一应变条件下,随温度升高,沿不同晶向拉伸时的驱动力均呈降低趋势,而广义稳定性也降低,即塑性提高。
参考文献
Temperature dependence of the elastic constants in α-iron single crystals: Relationship to spin order and diffusion an-omalies
[J].
Change of Young's modulus of cold-deformed pure iron in a tensile test
[J].
Interactions of plasticity and phase transformation under shock in iron bicrystals
[J].
Formation mechanism of face-centered cubic phase in impact process of single crystal iron along [101] direction
[J].
单晶铁沿[101]晶向冲击过程中面心立方相的形成机制
[J].
Deformation behaviour of body centered cubic iron nanopillars containing coherent twin boundaries
[J].
Compressive deformation of Fe nanopillar at high strain rate: Modalities of dislocation dynamics
[J].
Effect of temperature on the evolution dynamics of voids in dynamic fracture of single crystal iron: A molecular dynamics study
[J].
Simultaneous stiffening and strengthening of nanodiamond by fivefold twins
[J].
Role of five-fold twin boundary on the enhanced mechanical properties of fcc Fe nanowires
[J].The role of 5-fold twin boundary on the structural and mechanical properties of fcc Fe nanowire under tension is explored by classical molecular dynamics. Twin-stabilized fcc nanowire with various diameters (6-24 nm) are examined by tension tests at several temperatures ranging from 0.01 to 1100 K. Significant increase in the Young's modulus of the smaller nanowires is revealed to originate from the central area of quinquefoliolate-like stress-distribution over the 5-fold twin, rather than from the surface tension that is often considered as the main source of such size-effects found in nanostructures. Because of the excess compressive stress caused by crossing twin-boundaries, the atoms in the center behave stiffer than those in bulk and even expand laterally under axial tension, providing locally negative Poisson's ratio. The yield strength of nanowire is also enhanced by the twin boundary that suppresses dislocation nucleation within a fcc twin-domain; therefore, the plasticity of nanowire is initiated by strain-induced fcc→bcc phase transformation that destroys the twin structure. After the yield, the nucleated bcc phase immediately spreads to the entire area, and forms a multigrain structure to realize ductile deformation followed by necking. As temperature elevated close to the critical temperature between bcc and fcc phases, the increased stability of fcc phase competes with the phase transformation under tension, and hence dislocation nucleations in fcc phase are observed exclusively at the highest temperature in our study.
Anisotropy of plasticity and structural transformations under uniaxial tension of iron crystallites
[J].
Competitions correlated with nucleation and growth in non-equilibrium solidification and solid-state transformation
[J].
非平衡凝固与固态相变中有关形核和长大的竞争研究
[J].
A thermo-kinetic correlation for grain growth in nanocrystalline alloys
[J].
Precipitation modeling via the synergy of thermo-dynamics and kinetics
[J].
基于热力学和动力学协同的析出相模拟
[J].
A thermokinetic description of nanoscale grain growth: Analysis of the activation energy effect
[J].
A strategy for designing stable nanocrystalline alloys by thermo-kinetic synergy
[J].Aiming to design stable nanocrystalline (NC) materials, so far, it has been proposed to construct nanostructure stability maps in terms of thermodynamic parameters, while kinetic stabilization has seldom been considered, despite the synergy of thermodynamics and kinetics. Consequently, the thermodynamically stabilized NC materials may be easily subjected to grain growth at high temperatures due to the weakly kinetic stabilization. Starting from the thermo-kinetic synergy, a stabilization criterion is proposed as a function of intrinsic solute parameters (e.g. the activation energy for bulk diffusion and the segregation enthalpy), intrinsic solvent parameters (e.g. the intrinsic activation energy for GB migration and the GB energy) and processing parameters (e.g. the grain size, the temperature and the solute concentration). Using first-principles calculations for a series of combinations between fifty-one substitutional alloying atoms as solute atoms and Fe atom as fixed solvent atom, it is shown that the thermal stability neither simply increases with increasing the segregation enthalpy as expected by thermodynamic stabilization, nor monotonically increases with increasing the activation energy for bulk diffusion as described by kinetic stabilization. By combination of thermodynamic and kinetic contributions, the current stabilization criterion evaluates quantitatively the thermal stability, thus permitting convenient comparisons among NC materials involved by various combinations of the solute atoms, the solvent atoms, or the processing conditions. Validity of this thermo-kinetic stabilization criterion has been tested by current experiment results of Fe-Y alloy and previously published data of Fe-Ni, Fe-Cr, Fe-Zr and Fe-Ag alloys, etc., which opens a new window for designing NC materials with sufficiently high thermal stability and sufficiently small grain size.
Generalized stability criterion for exploiting optimized mechanical properties by a general correlation between phase transformations and plastic deformations
[J].
Thermo-kinetic connectivity by integrating thermo-kinetic correlation and generalized stability
[J].Designing structured materials with optimized mechanical properties generally focuses on engineering microstructures, which are closely determined by the processing routes, such as phase transformations (PTs) and plastic deformations (PDs). Both PTs and PDs follow inherent trade-off relation between thermodynamic driving force ΔG and kinetic energy barrier Q, i.e., so-called thermo-kinetic correlation. By analyzing nucleation and growth and proposing a conception of negative driving force integrating strain energy, interface energy and any kind of energy that equivalently inhibits the PT itself, ΔGS, unified expressions for the thermo-kinetic correlation and generalized stability (GS) were derived for three kinds of PTs, i.e., diffusive PTs with simultaneously decreased ΔG and increased Q, diffusive PTs with simultaneously increased ΔG and decreased Q, and displacive PTs with simultaneously increased ΔG and decreased Q. This leads to so-called thermo-kinetic connectivity by integrating the thermo-kinetic correlation and the GS, where, by application in typical PTs, it was clearly shown, a criterion of high ΔG-high GS can be predicted by modulating chemical driving force, negative driving force and kinetic energy barrier for diffusion or nucleation. Following thermo-kinetic connectivity, analogous procedure for dislocation evolution upon PDs was performed, and materials design in terms of the high ΔG-high GS criterion was discussed and prospected.
Atomsk: A tool for manipulating and converting atomic data files
[J].
Fast parallel algorithms for short-range molecular dynamics
[J].
Development of new interatomic potentials appropriate for crystalline and liquid iron
[J].
Molecular dynamics simulation study of the effect of grain size on the deformation behavior of nanocrystalline body-centered cubic iron
[J].
Atomistic simulation study of tensile deformation in bulk nanocrystalline bcc iron
[J].
Deformation mechanisms and slip-twin interactions in nanotwinned body-centered cubic iron by molecular dynamics simulations
[J].
Visualization and analysis of atomistic simulation data with OVITO—The open visualization tool
[J].
Automated identification and indexing of dislocations in crystal interfaces
[J].
Structure identification methods for atomistic simulations of crystalline materials
[J].
Effect of crystal orientation on tensile mechanical properties of single-crystal tungsten nanowire
[J].
Transformation pathways in the solid-solid phase transitions of iron nanowires
[J].
Molecular dynamics simulation on the uniaxial tension property of metal Fe interacting with C
[J]
C原子对Fe-C合金拉伸性能影响的分子动力学分析
[J].
Finite-size effects in Fe-nanowire solid-solid phase transitions: A molecular dynamics approach
[J].By means of classical molecular-dynamics simulations, we investigate solid-solid phase transitions in cylindrical iron nanowires. The interatomic potential employed has been shown to be capable of describing the martensite-austenite phase transition in iron. We investigate the dependence of the transition temperature on the wire diameter, the heating/cooling rate, and a tensile stress applied in axial direction. We observe that the phase transition temperature is inversely proportional to the wire diameter during heating and depends linearly on an applied axial tensile stress. The transition temperature becomes independent of the heating/cooling rate for the smallest rates investigated. The time the wire needs for completing the structural change is found to be independent of the diameter, the tensile loading, and the heating/cooling rate for the range of parameters considered. Finally, we find that there exists a maximum tensile stress above which the nanowire can no longer recover its initial structure after cooling.
Solid-solid phase transitions in Fe nanowires induced by axial strain
[J].
Molecular dynamics simulation for axial tension process of α-Fe and Ni nano wires
[J].
α-Fe和Ni纳米丝单向拉伸过程的分子动力学模拟
[J].
Molecular dynamics simulations of the effect of temperature and strain rate on the plastic deformation of body-centered cubic iron nanowires
[J].
Probing the limits of metal plasticity with molecular dynamics simulations
[J],