熔模铸造工艺是制造高温合金热端零部件(如航空发动机涡轮机匣)的主要技术,其特点是产品精度高、形状复杂和具有严格的几何公差。熔模铸造工艺流程长、工序多、成型难度大,存在尺寸超差问题,高温合金复杂铸件铸造系统中,蜡模的收缩和变形、型壳不可逆相变及退让性、金属凝固收缩变形,都是造成尺寸偏差和变形的重要因素,导致航空发动机高温合金复杂铸件批量制造的重大难题[1]。
尺寸偏差变化规律的研究通常通过实验过程建立或改进数学模型,并且利用计算机数值模拟预测变形和计算尺寸偏差[2~5]。熔模铸造数值模拟在软件中各工序分开计算,各软件离散单元尺寸和量纲不一致,空间物理场的准确继承和传递难以实现,因此工艺之间没有关联。依赖于传感器技术的高速发展,三维扫描技术在工业中已经广泛应用[6~8],利用扫描点云文件节点坐标构建铸件变形位移场是实现工艺关联的有效手段,在简单的几何中测量误差已经在0.01 mm以下,在复杂铸件中的测量误差也在0.05 mm以内[9],在点云匹配算法的不断改进下测量误差在不断减小[6],尺寸偏差传递精度也得到进一步提高。例如,赵代银等[10]分别对蜡模、模壳、铸件进行蓝光扫描获得汽轮机叶片不同位置的变形,并根据与标准模型比对指导模具收缩率设置。铸件模具的反变形设计是控制关键尺寸偏差的有效方法,Galles等[11,12]根据材料的本构方程,在变形加载过程中进行有限元反变形分析;Dong等[13]和Zhang等[14]则根据实验或模拟的位移结果直接进行几何反变形放缩设计,该设计方法提高了叶片的尺寸精度,在模拟仿真中面向尺寸偏差,利用STL文件所有节点坐标也同样可以实现位移场的建立。但是关于尺寸在多工序下如何传递的报道较少,而且已有报道[13~17]也未提出变形网格和未变形之间节点是如何正确匹配的,因此难以统计所有节点的位移向量准确传递。
数字孪生是以数字化方式创建物理实体的虚拟模型,借助数据模拟物理实体在现实环境中的行为,通过虚实交互反馈、数据融合分析、决策迭代优化等手段,为物理实体增加或扩展新的能力,数字孪生技术已经在智能制造领域得到了广泛的应用和发展[18]。铸造工艺较为固定且各个流程工艺不易实时反馈和调节,铸造领域的数字孪生应用较少,而数据建模也多应用于工艺优化和几何设计[19]。Ebrahimi等[20]将数字孪生方法用于压铸过程,对整个过程工艺链进行分析,假设所考虑的部件在铸造后进行固溶处理,然后进行淬火和沉淀硬化,可能会导致类似于凝固和冷却的变形,因此在压铸流程引入非均匀冷却,以抵消残余应力和在上述过程产生的变形,进而预测和控制部件变形。高精度测量仪器和传感器的发展可以获得实际铸件的点云,为位移场的传递提供方法,为数字孪生建模提供数据基础。模型是数字孪生的核心,基于机理模型的数值模拟需要耗费较多的时间,目前机理和数据混合建模的方法已经成为各个研究领域的核心,Chen等[21]提出了一种新的迭代虚拟和物理融合算法,通过将测量的温度数据融合到“移动热源”分析中,来计算搅拌摩擦焊接过程中的三维温度场。Zhang等[22]设计了一种新的基于物理模型和数据模型的模具温度预测混合建模方法,根据模具表面温度不均调整工艺,有效减少热压成型件的尺寸偏差。而对于熔模铸造过程,构建输入工艺参数和输出结果之间的回归数据模型是尺寸数字孪生建模的关键。
本工作主要针对熔模铸造铸件的尺寸构建数字孪生模型,其关键技术之一是建立铸件在多流程之间位移场传递的计算方法,使得尺寸偏差的传递可以在模拟过程和实际生产过程相互传递。关键技术之二是基于位移场的传递方法,以数值模拟及其降阶的数据模型开展多流程下数据驱动的成型工艺优化。在上述2个关键技术的基础之上,结合数字孪生的概念进一步构建工序间工艺参数过程控制和铸件模具几何设计的2个应用的数字孪生模型,使得数字孪生在设计和生产阶段具有真正的应用,以提高熔模精密铸件的尺寸精度。本工作阐述了熔模铸造尺寸控制数字孪生框架,提出了铸件变形的位移场数据传递与基于数值模拟的降阶数据模型建模方法;以环套环特征铸件为案例,对多工序间尺寸偏差控制方法给出应用示例,并计算出反变形设计后的几何外形,实现闭环控制;以涡轮叶片铸件为案例,展示了全节点位移场在实际铸件生产过程中的传递过程,为熔模铸造过程的尺寸精确控形提供新的思路。
1 研究方法
1.1 熔模铸造尺寸控制数字孪生框架
图1
图1
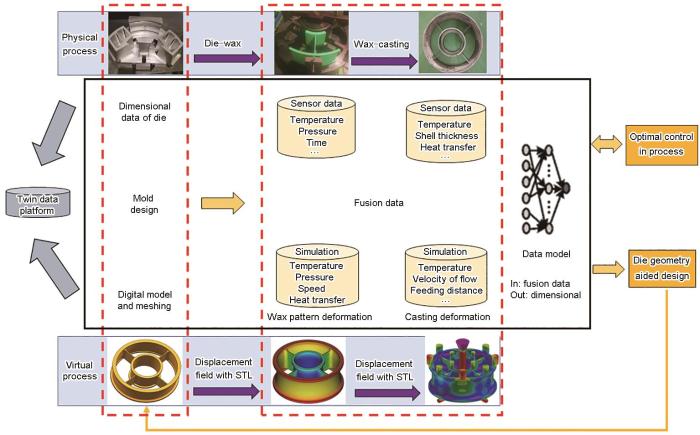
铸件尺寸控制数字孪生建模仿真基本框架
Fig.1
Digital twin modeling and simulation framework for casting dimensions
物理实体是数字孪生的构成基础,为简化计算,仅研究对尺寸偏差影响较大的2个单元级设备:注蜡机和浇注系统,2者组成一个较简单的系统。虚拟实体包括所设计的三维几何模型,与物理实体具有时空一致性。物理实体映射下的模拟仿真模型以及工艺参数和尺寸之间的数据模型,注蜡过程用Moldflow数值模拟软件进行计算,浇注过程用ProCAST软件进行计算。服务和应用则对整个数字孪生过程运行所需数据、算法、模型、仿真进行封装,最后面向尺寸控制形成2个应用:(1) 利用数据模型的快速响应在生产工序之间进行工艺参数的优化调整;(2) 利用尺寸传递迭代反变形方法进行模具几何的优化设计。孪生数据包括物理实体数据、虚拟实体数据、服务数据、知识数据,应用所关注的虚拟实体数据主要为多流程下的工艺参数,能反映位移场的STL文件,仿真模型和数据模型及其结果。
数据模型是数字孪生的核心,如图1所示,将所有工艺参数融合可以构建“全流程工艺参数-铸件尺寸”数据模型,也可单独构建蜡模注射成型工艺-尺寸数据模型[24]、凝固变形过程中工艺参数-尺寸数据模型[25]。数据模型的建立可以基于数值模拟数据,或实验数据,或2者的融合数据。数值模拟的数据准确性取决于构建准确的数学模型和边界条件,这在各种软件的模拟仿真过程中通常存在不可预测的偏差。而在实际的生产过程中可以利用多种传感器采集注蜡型腔压力、浇注温度、型壳温度等构建真实的数据模型,其准确性更多取决于工艺的波动和数据的测量精度。本工作中数字孪生框架中涉及的融合数据主要以模拟数据代替,利用数据模型在蜡模与预计几何模型出现偏差下确定最优化浇注工艺,使铸件成型的几何模型与设计几何一致。
1.2 铸件变形的尺寸控制方法
数字孪生框架为铸件尺寸控制提供方法。以环套环典型铸件为研究对象,利用多种商业软件进行集成实现工艺的连续,以节点的位移作为尺寸偏差数据进行传递,预测铸件的变形情况;基于节点尺寸偏差数据,开展集成多个流程成型工艺-尺寸关系研究,构建数据模型,结合基于拉丁超立方技术的实验设计和粒子群优化算法寻找多流程下的最优参数[26];分别构建各流程下的工艺-尺寸数据模型,在蜡模注射成型尺寸偏差已经确定的情况下,基于浇注过程工艺-尺寸数据模型寻找最优浇注工艺参数,使得铸件变形后的几何模型与铸件计算机辅助设计(CAD)模型之间的尺寸偏差最小,实现生产工序之间的过程控制;基于位移场进行反变形迭代计算,获得理论上较为精确的铸件模具内腔几何模型。
1.2.1 铸件变形的位移场数据传递与逆向设计
位移场的数据传递是数字主线中最为关键的部分,其具有连接设计阶段与制造阶段、虚拟模型和物理模型之间的功能,解决数据孤岛问题。利用UG软件建立特征铸件三维几何模型,将模型导入Moldflow软件中,通过数值模拟预测蜡模注射成型过程的变形,并且以STL文件格式输出蜡模变形后的几何模型,将STL文件导入MATLAB软件进行各节点的位移偏差计算。利用UG软件建立浇注系统装配后的三维CAD模型并且导入ProCAST 软件中划分网格,将上述计算的位移偏差插值代入划分后的网格,进行凝固和冷却过程的变形模拟,再输出变形后的STL文件并导入MATLAB计算铸件与初始几何尺寸偏差。实际铸件则以点云文件与上述各对应环节的STL文件进行匹配和对比分析。
图2
图2
节点位移偏差计算示意图
Fig.2
Calculation diagram of node displacement deviation (Surface 1 is original geometry, surface 2 is wax pattern deformation, and surface 3 is casting deformation; d is the node displacement of wax mold, and d1 is the node displacement of casting)
(1) 位移数据正向传递
以节点A为例,找到表面2上的最近点B,计算点A的法向量AC,AC长度d为AB在AC方向上的投影。将点C作为点A在表面2上虚拟的对应点,并且以AC作为位移向量,长度记为d,同理向量CC1为铸件变形,长度记为d1,AC1的长度即为原始几何到铸件的总变形量,由此可以计算出点A处的误差传递。并依次计算表面1上的所有节点,即为全节点的位移。
(2) 节点逆向补偿迭代设计
对于点A,铸件变形表面3到表面1的距离的法向变形为AC1,定义逆向补偿系数k (本工作计算过程k值直接取为1),计算点A反向位移点坐标A(1):
式中,x、y和z为点A(n)的坐标,n为迭代次数。
以逆向补偿后的几何模型进行全流程数值模拟或者实验,迭代计算AC1,依次记为AC1(1),AC1(2),…,AC1(n),计算达到精度后,即确定点A迭代修正后的坐标位置。由此计算整个几何迭代优化后的几何模型。点A的逆向补偿向量为AA(n)。
图3
1.2.2 基于数值模拟的降阶数据模型
复杂铸件的数值模拟过程通常需要较长的时间,难以快速响应实际的生产过程,而建立数据模型可以在秒级进行快速响应,以确保虚拟的孪生模型和实际生产过程数据能快速交互。确立注射成型关键工艺参数为:保压压力X1 (MPa)、注射速率X2 (cm3/s)、注射温度X3 (℃)。确立浇注过程的关键工艺参数为:合金浇注温度X4 (℃),型壳预热温度X5 (℃),边界换热系数X6 (W/(m2·℃));因此在实验设计中,设计变量记为:X = [X1, X2, X3, X4, X5, X6],它们的变量范围如表1所示。因变量记为Y = [Y1, Y2],其中Y1和Y2分别为直径平均偏差和直径最大偏差。采用优化的拉丁超立方采样方法布置设计变量在设计空间的分布,并通过自动化数值模拟获得对应的32组仿真结果数据。
表1 设计变量及其区间
Table 1
| Boundary | X1 MPa | X2 cm3·s-1 | X3 oC | X4 oC | X5 oC | X6 W·m-2·oC-1 |
|---|---|---|---|---|---|---|
| Upper | 0.5 | 30 | 62 | 1450 | 900 | 50 |
| Lower | 5 | 300 | 70 | 1600 | 1100 | 200 |
此外,借助数据模型可以用易于求解的模型来描述设计变量与响应之间的潜在关系,并且该模型也可以用来预测未知点的响应,从而以较少的仿真消耗建立响应空间,再加上多目标优化算法,这种数据模型协同多目标优化策略有助于加速寻优过程,大大降低局部最优解的可能[28]。该过程包括:多参数实验设计→数据模型构建→全局优化→响应输出,实现了软件平台仿真数据的自动传递和共享,该数据驱动控制方法是实现数字孪生的重要部分。在虚实交互方面,以实际蜡模的扫描点云文件作为计算目标函数的数据,利用粒子群优化算法计算获得铸造过程的优化工艺。
2 环套环铸件尺寸控制数字孪生建模示例与讨论
2.1 位移场数据传递
图4
图4
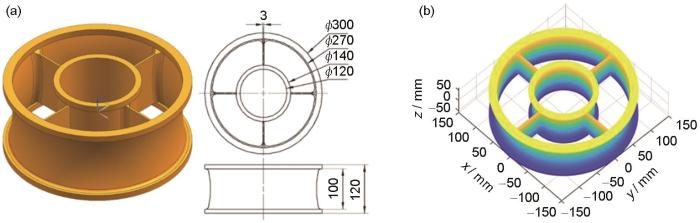
铸件几何模型
Fig.4
Casting geometric model
(a) schematic view of a typical casting (unit: mm) (b) model of STL format
图5
图5
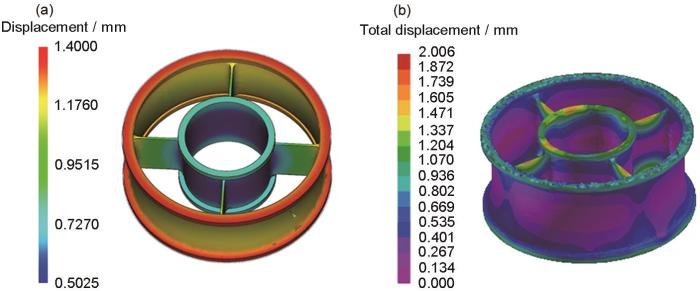
蜡模变形和铸件变形模拟结果
Fig.5
Deformation simulation results of wax pattern (a) and casting (b)
图6
图6
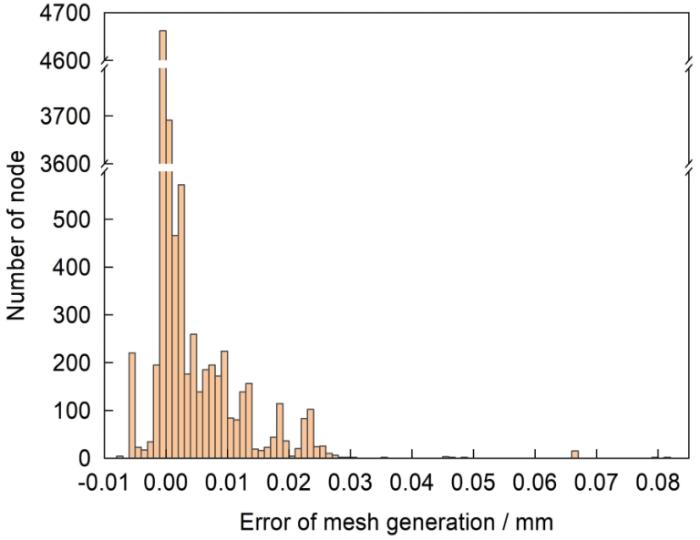
位移场和统计分布直方图表示位移的传递过程
Fig.6
Displacement fields (a1-c1) and statistics histograms (a2-c2) of wax pattern (a1, a2), casting (b1, b2), and total deformation between CAD and casting (c1, c2) showing displacement transfer process
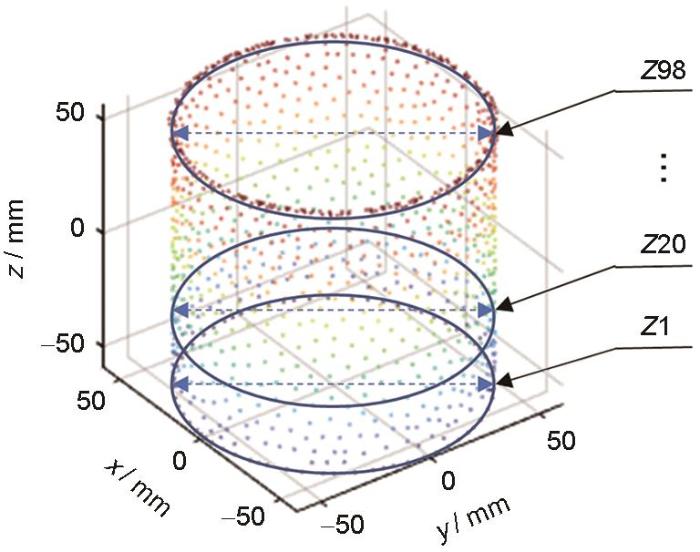
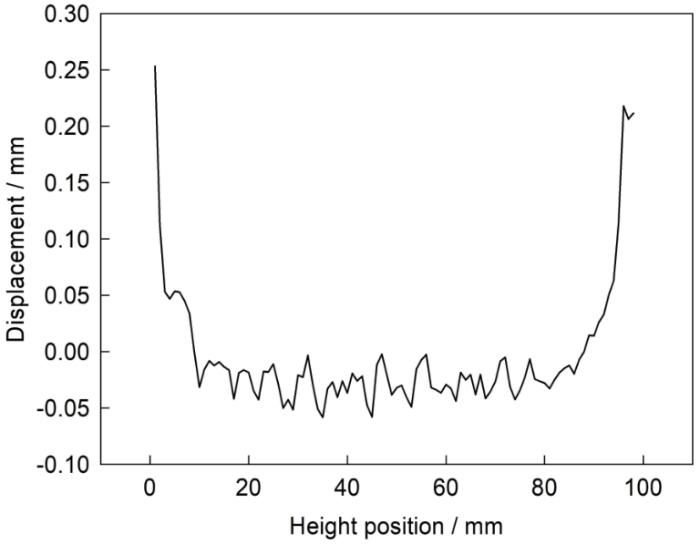
根据全节点位移数据的传递结果,计算内环的尺寸。提取出内环所有节点如图7所示,计算铸件每2 mm内所有节点的平均位移偏差,且以每1 mm递增分段,记为随高度变化的内径 Z1,Z2,Z3,…,Z98。
图7
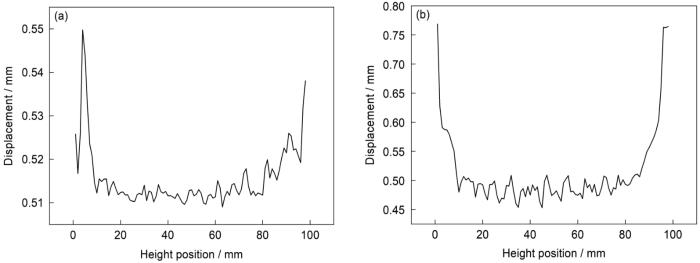
与初始CAD几何对比,蜡模和铸件内环不同高度沿径向收缩的尺寸偏差如图8所示。从图8a可见,蜡模尺寸偏差在0.50~0.55 mm之间较为均匀。从图8b可见,铸件两端尺寸偏差较中间大约0.3 mm,考虑到内环的尺寸对装配的重要性以及对位移偏差有定性的评价,选取铸件内环Y = [Y1, Y2]作为尺寸偏差的评价,其中Y1为内环直径在所有高度的均值,计算可得内环直径平均偏差为0.513 mm,最大偏差为0.769 mm。凝固模型未考虑浇注的充型流动过程,直接从冷却开始计算,因此上下端面呈现一致的尺寸误差变化趋势,在中间部分尺寸波动在0.1 mm以内。在实际铸件中采用均匀放缩难以实现整体尺寸控制,可以按图8b给定随高度变化的放缩值。
图8
图8
蜡模和铸件不同高度的尺寸偏差
Fig.8
Dimensional deviations of wax pattern (a) and casting (b) at different heights
2.2 几何迭代反变形设计
在实际生产之前,利用数值模拟和位移传递的方法开展模具的虚拟设计,该方法恰好符合数字孪生中充分利用物理模型、运行历史数据,集成多学科、多物理量,在虚拟空间中完成映射等一系列定义。如图1所示框架,反变形的设计可以利用融合实际生产和模拟数据,并且在实际生产过程中采集传感器数据,不断更新模拟过程,以及建立新的数据模型。本工作主要基于模拟数据,进行反变形的迭代设计。
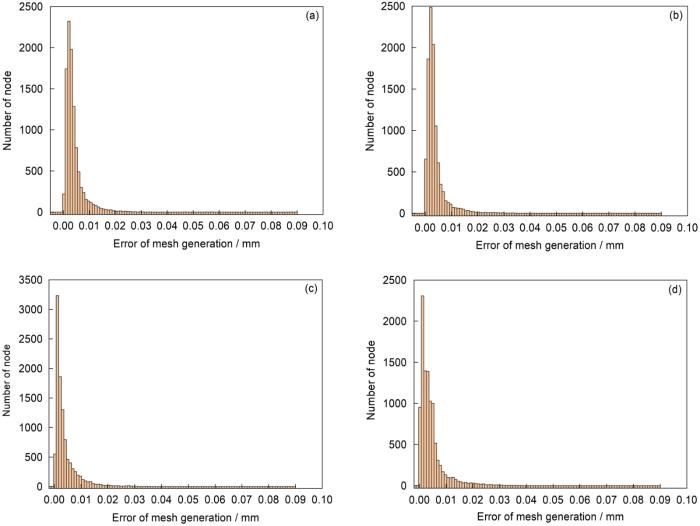
根据蜡模和铸件在模拟过程中位移场的传递进行反变形计算可以对所有节点位置进行精确设计。模拟可得铸件与初始几何的最大尺寸偏差在2 mm以上,将铸件变形几何的位移场反向叠加到初始几何,并按照上述位移场的传递计算方法,再次计算蜡模变形和铸件凝固变形,最后计算出总的位移场,以此反复迭代。如图9所示,经过4次迭代计算,铸件几何形状与标准三维模型所有节点的位移差值达到最大值,在0.04 mm。在工业实际生产上利用三维扫描代替模拟获得铸件真实的位移数据,也可以利用同样的方法对实际铸件的初始几何形状进行反变形设计。
图9
图9
基于几何迭代反变形设计的铸件总位移分布
Fig.9
Node displacements of casting after iterative design of initial geometric
(a) first iteration (b) second iteration (c) third iteration (d) fourth iteration
2.3 工艺参数-尺寸偏差数据建模及多工艺参数优化
降阶的数据模型是实现数字孪生系统快速响应和优化控制的核心,本节构建全流程工艺参数-尺寸和浇注工艺参数-尺寸的数据模型,并且提出多工序之间利用数字孪生模型进行工艺参数优化的策略,即在蜡模偏差确定的情况下寻找最优的浇注工艺。在多流程中尺寸传递规律复杂,需要集成考虑多流程因素的交互影响,明确工艺参数对铸件尺寸的影响,建立多工艺参数回归方程。利用数值模拟结果建立数据模型可以快速获得工艺参数的响应,将数据模型作为目标函数结合全局优化算法以便在设计空间寻优。采用优化拉丁超立方实验设计(DOE)得到32组工艺参数的组合,不同工艺参数模拟结果表明,Y1的最大值在0.500~0.516 mm之间,Y2的值在0.752~0.787 mm之间,下文为对优化控制方法的示例。
数据模型有多项式响应面模型(response surface model,RSM)、克里金(Kriging)模型和径向基函数(radial basis function,RBF)等[29],利用MATLAB统计学习工具箱构建纯二次响应面,对多工艺参数回归方程进行分析研究,利用x2fx函数对工艺参数X1~X6进行纯二次展开,根据工艺参数得出的铸件平均直径和最大直径的回归方程如下:
式中,x2fx为纯二次展开的符号;β1和β2是所用展开项的系数:β1 = [4.69, 5.61 × 10-3, 2.85 × 10-5, -7.15 × 10-3, -3.24 × 10-3, -1.27 × 10-3, -1.14 × 10-5, -1.86 × 10-3, -4.43 × 10-8, 3.76 × 10-5, 1.05 × 10-6, 6.52 × 10-7, 2.42 × 10-7],β2 = [1.55 × 101, 8.30 × 10-4, 5.63 × 10-5, 3.67 × 10-3, -1.63 × 10-3, 2.04 × 10-4, -3.01 × 10-7, -4.55 × 10-4, -1.61 × 10-7, -3.46 × 10-5, 5.38 × 10-7, -1.01 × 10-7, -3.26 × 10-8]。
拟合优度R2衡量预测值对于真值的拟合好坏程度,本工作构建的响应面模型的R2为0.98,说明其拟合程度较高。利用粒子群算法对该数据模型寻找最优点使得Y2的值最小,得到X1 = 5 MPa、X2 = 119.2 cm3/s、X3 = 70℃、X4 = 1558.3℃、X5 = 981.5℃、X6 = 50 W/(m2·℃),对应Y2为0.747 mm。
在实际生产过程中,由于材料成分、工艺等波动,蜡模尺寸可能出现偏差,可以利用3D扫描仪扫描蜡模尺寸获得三维点云数据,选择最优化的后续工艺则可以提高铸件的合格率。下文以模拟结果作为蜡模实际检测结果进行浇注工艺参数寻优示例。
以集成注蜡注射和浇注凝固的数值模拟为例,利用 RBF神经网络建立浇注工艺-尺寸偏差的数据模型。设计变量记为:X = [X4, X5, X6],变量范围如表1所示,因变量为蜡模与铸件内径不同高度平均直径偏差,记为DZ = [Z1, Z2, Z3, …, Z98],该数据模型输入参数为浇注工艺,输出为98个元素的向量,代表不同高度的直径偏差。选取DOE模拟实验中的第25组蜡模偏差数据作为实际偏差,目标几何选取第2组实验的铸件几何,即根据尺寸传递方法,选择最优工艺使得最终铸件成型的几何模型与第2组铸件的几何模型一致。铸件与蜡模各高度直径偏差D如图10所示,最优化的浇注工艺应满足D减去DZ 最小。目标函数为最小化所有尺寸的和(Sum(D - DZ)),利用粒子群算法,计算最优化结果为X = [1561.3℃, 900.0℃, 59.7 W/(m2·℃)],D与DZ 之间直径的最大偏差为0.011 mm。
图10
图10
铸件与蜡模之间不同高度的尺寸偏差
Fig.10
Dimensional deviations of different heights between casting and wax pattern
3 涡轮叶片实际铸件尺寸传递
在数字孪生系统中,建立数据模型主要依据的是数值模拟得到仿真数据。然而,由于数值模拟的准确性高度依赖于机理模型和边界条件,为了保证数字孪生系统的精度,还必须融入实际蜡模和铸件尺寸的测量数据,这就需要解决测量数据和软件系统之间的传递问题。
图11
图11
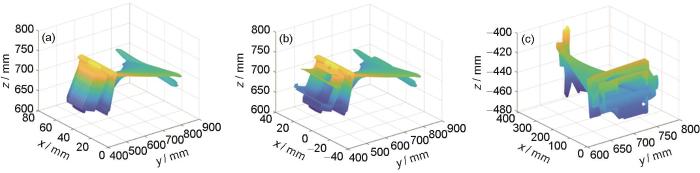
CAD模型、蜡模和铸件的点云
Fig.11
Point clouds of CAD model (a), wax pattern (b), and casting (c)
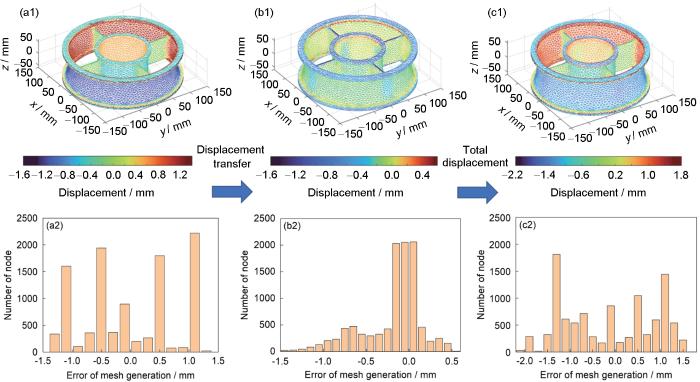
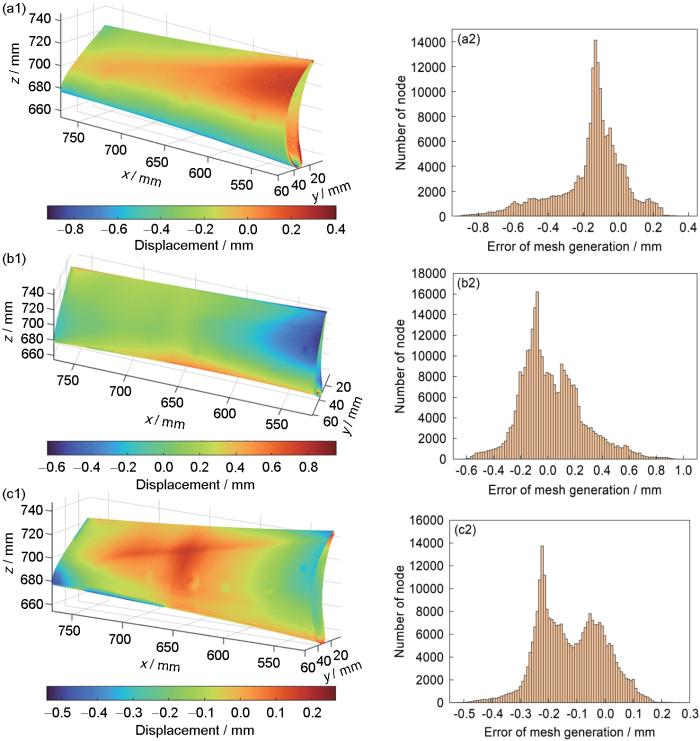
对蜡模、铸件与CAD模型分别进行一次粗匹配和精确匹配,粗匹配提取出叶片气道面,将蜡模、铸件提取部分与CAD提取部分进行第2次点云匹配 ,计算出点云之间的变换矩阵,再将所有坐标点进行变换。在点云匹配完成后利用尺寸传递的方法得到所有节点的位移,如图12所示。图12a1和a2为蜡模与CAD几何之间的节点位移场云图和统计分布直方图。可以看出,蜡模存在正方向和负方向的位移,最大负位移在0.8 mm以上,蜡模整体为收缩,但是在中间部分位置,由于应力产生向外的正向位移。图12b1和b2为蜡模与铸件几何之间节点位移场云图和统计分布直方图。可见,最大负位移为0.6 mm,正位移接近1 mm。图12c1和c2为铸件与CAD几何之间节点位移场云图和统计分布直方图。大部分节点位移为负值,最大负位移为-0.5 mm,偏差值大部分位置集中在负位移0.15~0.3 mm之间,整体的叶片存在一定的收缩,但叶背中间有所凸起。统一给定放缩率的设计难以平衡不同位置的变形,依据图12c1和c2的节点位移,可以直接给出反变形后的几何模型。
图12
图12
不同几何模型之间节点位移场云图和统计分布直方图
Fig.12
Displacement fields (a1-c1) and statistical histograms (a2-c2) between different geometric models
(a1, a2) wax pattern point cloud with CAD model
(b1, b2) wax pattern point cloud with casting point cloud
(c1, c2) casting point cloud with CAD model
图13
图13
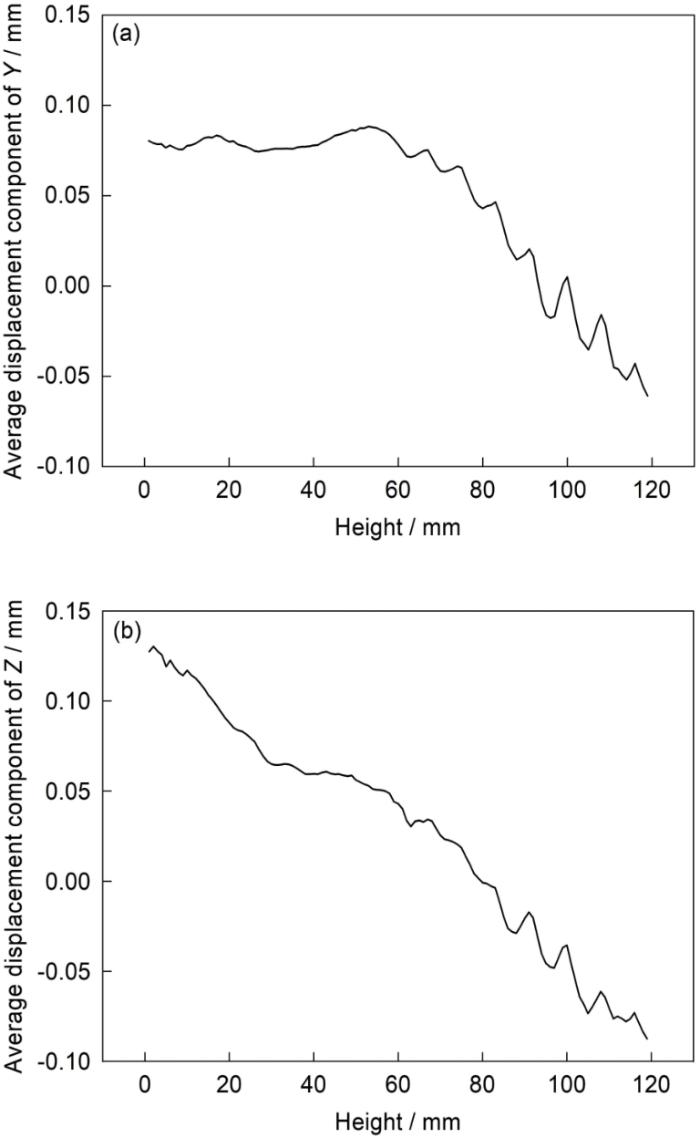
Y方向和Z方向平均位移向量分量随叶片截面高度的变化曲线
Fig.13
Curves of average displacement vector component with blade height
(a) Y direction (b) Z direction
4 结论
(1) 提出铸件在多流程之间全节点位移传递的计算方法,构建了数字孪生建模过程的尺寸数字主线,实现了尺寸数据在不同流程的传递,解决了数据孤岛问题。
(2) 以环套环特征铸件的数字孪生模型为案例,反变形设计出模具内腔的三维几何模型,铸件模拟节点位移偏差在0.04 mm以下。建立工艺与尺寸的数据模型,并提出结合尺寸偏差数据在多工序之间的优化调控方法。
(3) 将位移传递的方法应用于实际叶片铸件,计算出实际铸件所有节点的位移,确定了尺寸偏差的传递和分布规律,为分析蜡模收缩和合金凝固收缩规律提供方法。
参考文献
Simulation of distortions and pattern allowances for a production steel casting
[A].
Development of a device for dynamical measurement of the load on casting and the contraction of the casting in a sand mold during cooling
[J].
In situ measurement and prediction of stresses and strains during casting of steel
[J].
Wax patterns for integrally cast rotors/stators of aeroengine gas turbines
[J].
Improving the performance of 3D shape measurement of moving objects by fringe projection and data fusion
[J].
Development of structured light 3D-scanner with high spatial resolution and its applications for additive manufacturing quality assurance
[J].
Redesign of car body by reverse engineering technique using steinbichler 3D scanner and projet 3D printer
[J].
Accurate calibration method for blade 3D shape metrology system integrated by fringe projection profilometry and conoscopic holography
[J].
Dimension control of X-type heavy duty gas turbine solid blade in investment casting process
[J].
某型重型燃机实心动叶片的精密铸造过程尺寸控制
[J].在某型重型燃机叶片的开发过程中,采用3D打印光敏树脂叶片进行铸造工艺试验,获得铸造收缩率,结合蜡料收缩率参数,开发了蜡模模具;通过MoldFlow模拟发现,采用冷蜡芯可以有效地减小蜡模的非均匀收缩并将蜡模尺寸控制在公差允许范围之内。通过对解剖后的叶片型壳进行蓝光扫描,获得了烧结状态型壳的尺寸。结果表明,模具的收缩率设置合理,采用冷蜡芯工艺和胎具定形工艺有助于最终铸件尺寸的保证。
Determination of pattern allowances for a steel casting using an inverse elastoplastic deformation analysis
[J].
Determination of pattern allowances for steel castings using the finite element inverse deformation analysis
[J].
Geometric parameter-based optimization of the die profile for the investment casting of aerofoil-shaped turbine blades
[J].
Cavity optimization for investment casting die of turbine blade based on reverse engineering
[J].
Method of virtual mold-repair for hollow turbine blades
[J].
精铸空心涡轮叶片模具虚拟修模方法
[J].
Research development on shrinkage fraction distribution of investment castings
[J].
精铸件收缩率分布规律研究进展
[J].
Displacement transfer with the mesh deformation method in multidisciplinary optimization of turbine blades
[J].
基于网格变形技术的涡轮叶片变形传递
[J].
Digital twin data: Methods and key technologies
[J].
Engineering computing and data-driven for gating system design in investment casting
[J].
A digital twin approach to predict and compensate distortion in a high pressure die casting (HPDC) process chain
[J].
Digital twin modeling for temperature field during friction stir welding
[J].
A physical model and data-driven hybrid prediction method towards quality assurance for composite components
[J].
Five-dimension digital twin model and its ten applications
[J].As an enabling technology for implementing smart manufacturing,industrial 4.0,industrial internet and smart city,digital twin has received great attention from both academics and industry,especially its industrial applications.Model is the foundation and core of digital twin theories and technologies,but the traditional three-dimension digital twin model can no longer meet the new application requirements and technology development trends.To promote the application of digital twin in more fields,a five-dimension digital twin model was put forward in authors' previous research to digital twin shop-floor.In view of the new demands on digital twin and based on the previous research,a more systematic five-dimension digital twin model was presented.Furthermore,its applications in ten fields were discussed,including satellite/space communication network,ships,vehicles,power plant,aircraft,complex equipment,stereoscopic warehouse,medical,shop-floor and smart city,which could provide theoretical and methodological references for the application of digital twin in the future.
数字孪生五维模型及十大领域应用
[J].
The propagation and accumulation of dimensional shrinkage for ring-to-ring structure in investment casting
[J].
Process parameter effects on solidification behavior of the superalloy during investment casting
[J].
Data-driven design of cast nickel-based superalloy and precision forming of complex castings
[J].The development of material genomics engineering and intelligent material-processing technology provides new ideas for researching, developing, and manufacturing key thermal superalloy components of aeroengines. Based on the demand for superalloy materials and casting processing, a high-throughput dynamic simulation software system was developed. Combined with the screening criteria of nickel-based casting superalloy, a new nickel-based casting superalloy was selected and developed from more than 5.2 million-component combinations. High-temperature durability at 815oC and 400 MPa is better than foreign Inconel 939 superalloy. For the precision molding of complex superalloy casting, the data-driven process of the casting deformation is integrated, which reveals the correlation between the process parameters and size precision during solidification deformation. Thus, a data-driven process parameter optimization method is proposed herein. A data-driven casting outlet design method based on the model and algorithm, combined with the test design and multi-target genetic algorithm, which optimized the casting process parameters, was established, and the production rate of the casting process increased by 13.39% after the test verification. The combination of data-driven component design and data model-based process design will accelerate the development and application of aviation materials and components.
数据驱动镍基铸造高温合金设计及复杂铸件精确成形
[J].材料基因组工程与材料智能制备加工技术的发展为航空发动机高温合金关键热端部件的研发与制造提供了新的思路。针对航空发动机涡轮机匣类结构件高温合金材料与铸造成型的需求,开发了高通量并发式的热动力学模拟软件系统,结合镍基铸造高温合金的筛选判据,从520万余种成分组合中筛选并研制了一种新型镍基铸造高温合金,815℃、400 MPa下高温持久性能优于国外Inconel 939高温合金。针对高温合金复杂铸件的精密成型,开展了数据驱动铸件变形全流程集成计算,揭示蜡模注射工艺参数与尺寸映射关系以及凝固变形过程中工艺参数与尺寸精度关联关系,提出了一种基于数据驱动的工艺参数优化方法。建立了基于“模型+算法”的数据驱动的铸造冒口设计方法,结合试验设计和多目标遗传算法,优化了铸造工艺参数,试验验证后铸件工艺出品率提高13.39%。基于数据驱动的成分设计与基于数据模型的工艺设计结合,将加速航空材料与构件的研发与应用。
Evaluation of partially overlapping 3D point cloud's registration by using ICP variant and CloudCompare
[J].
A multi-objective optimization method based on the approximate model manaement
[J].
一种基于近似模型管理的多目标优化方法
[J].