最新录用 | 当期目录 | 过刊浏览 | 热点文章 | 虚拟专辑 | 阅读排行 | 下载排行 | 引用排行 | 期刊订阅

金属学报, 2024, 60(4): 522-536 DOI: 10.11900/0412.1961.2022.00523

研究论文

锂离子电池用微米厚度超薄集流体Cu箔和Al箔疲劳强度及损伤行为

程福来1,2, 罗雪梅,1, 胡炳利1,2, 张滨3, 张广平,1

1 中国科学院金属研究所 沈阳材料科学国家研究中心 沈阳 110016

2 中国科学技术大学 材料科学与工程学院 沈阳 110016

3 东北大学 材料科学与工程学院 材料各向异性与织构教育部重点实验室 沈阳 110819

Fatigue Strength and Damage Behavior of Micron-Thick Ultrathin Current Collector Cu Foil and Al Foil for Lithium-Ion Battery

CHENG Fulai1,2, LUO Xuemei,1, HU Bingli1,2, ZHANG Bin3, ZHANG Guangping,1

1 Shenyang National Laboratory for Materials Science, Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China

2 School of Materials Science and Engineering, University of Science and Technology of China, Shenyang 110016, China

3 Key Laboratory for Anisotropy and Texture of Materials, Ministry of Education, School of Materials Science and Engineering, Northeastern University, Shenyang 110819, China

通讯作者: 张广平，gpzhang@imr.ac.cn，主要从事金属材料疲劳与断裂研究;罗雪梅，xmluo@imr.ac.cn，主要从事金属材料疲劳与断裂研究

责任编辑: 毕淑娟

收稿日期: 2022-10-14   修回日期: 2023-02-14  

基金资助: 国家自然科学基金项目(52071319)

Corresponding authors: ZHANG Guangping, professor, Tel:(024)23971938, E-mail:gpzhang@imr.ac.cn;LUO Xuemei, associate professor, Tel:(024)83978029, E-mail:xmluo@imr.ac.cn

Received: 2022-10-14   Revised: 2023-02-14  

Fund supported: National Natural Science Foundation of China(52071319)

作者简介 About authors

程福来，男，1997年生，博士生

摘要

随着高性能、高能量密度锂离子电池的飞速发展，锂离子电池用集流体金属箔轻薄化已成为行业技术升级的一个重要方向，随着集流体厚度的减小，其疲劳失效问题变得日益突出。本工作通过拉-拉疲劳实验和EBSD技术研究了循环载荷作用下锂离子电池用集流体Cu箔和Al箔的高周疲劳强度及失效行为。结果表明，Cu箔疲劳裂纹主要萌生于较大晶粒内部的滑移带处，并沿滑移带扩展。基于对损伤晶粒微观结构的观察和统计分析，获得了Cu箔疲劳裂纹萌生和材料微观结构(晶粒尺寸及其变异系数、晶粒取向、Schmid因子(Ω))的统计关系图。Al箔由于表面含有轧制缺陷，其疲劳裂纹优先在表面加工缺陷处萌生。通过极值统计法成功预测了Al箔样品中可能的缺陷分布以及存在的最大缺陷尺寸，并基于Kitagawa-Takahashi图建立了缺陷尺寸与疲劳极限之间的关系。

关键词： 高周疲劳; 裂纹萌生; 超薄箔; Kitagawa-Takahashi图; 集流体; 锂离子电池

Abstract

With the rapid development of high-performance and high-energy-density lithium-ion batteries, lightweight current collector metal foils for lithium-ion batteries have become a crucial direction of industrial technological advancements. As the thickness of the current collector decreases, the fatigue failure problem becomes increasingly prominent. Once the fatigue failure of the current collector occurs, it will have a catastrophic impact on the electrochemical and safety performances of lithium-ion batteries. Here, to further clarify the fatigue damage mechanism of current collector foils, the high cycle fatigue strength and fatigue failure behavior of current collector Cu and Al foils for lithium-ion batteries under cyclic loading were experimentally investigated using tensile-tensile fatigue test and the EBSD technique. Results show that the fatigue cracks of the Cu foils mainly originate from the slip bands with larger grain sizes and propagate along the slip bands. Based on the microstructure observation and analysis of damaged grains, a statistical relationship between fatigue crack initiation and microstructure (grain size and its coefficient of variation, grain orientation, and Schmid factor (Ω)) of the Cu foils was obtained. Due to the presence of rolled defects on the surface of Al foils, the fatigue cracks are preferentially initiated at the surface defects. Extreme value statistics accurately predicted the possible defect population and the largest defect size in the Al foils, and the relationship between the defect size and fatigue limit was established using the Kitagawa-Takahashi diagram.

Keywords： high cycle fatigue; crack initiation; ultrathin foil; Kitagawa-Takahashi diagram; current collector; lithium-ion battery

PDF (3694KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

程福来, 罗雪梅, 胡炳利, 张滨, 张广平. 锂离子电池用微米厚度超薄集流体Cu箔和Al箔疲劳强度及损伤行为[J]. 金属学报, 2024, 60(4): 522-536 DOI:10.11900/0412.1961.2022.00523

CHENG Fulai, LUO Xuemei, HU Bingli, ZHANG Bin, ZHANG Guangping. Fatigue Strength and Damage Behavior of Micron-Thick Ultrathin Current Collector Cu Foil and Al Foil for Lithium-Ion Battery[J]. Acta Metallurgica Sinica, 2024, 60(4): 522-536 DOI:10.11900/0412.1961.2022.00523

近年来，随着高性能、高能量密度锂离子电池的飞速发展，锂离子电池用集流体金属箔轻薄化已成为行业技术升级的一个重要方向。随着集流体厚度的减小，对集流体在服役条件下可靠性的要求愈来愈高。锂离子电池在充放电过程中，锂离子的扩散会导致其在活性材料内部产生浓度梯度，而不同位置的不均匀锂浓度会造成活性材料的不均匀变形，从而产生扩散应力[1,2]。由于活性材料被涂覆在集流体表面，集流体将抑制其变形，导致集流体面内承受较大应力[1~3]。随着充放电循环的进行，集流体面内将承受循环载荷作用，即使在该循环载荷远低于材料强度极限的情况下，集流体也会发生失效，这种失效方式称为疲劳失效[4]。一旦集流体发生疲劳失效，将会严重影响锂离子电池的电化学性能和使用寿命，甚至引起严重的安全事故。随着集流体厚度的减小，集流体疲劳失效问题日益突出。因此，针对集流体材料进行疲劳损伤行为的研究，对其在锂离子电池中的服役可靠性具有十分重要的意义。

20世纪50年代起，人们对工程材料的疲劳损伤行为进行了大量研究[5~10]。结果表明，材料的疲劳损伤行为同时受表面和内部状态(缺陷)、微观结构(晶粒尺寸、取向、孪晶)以及样品几何尺度(厚度)的影响。样品表面和内部状态，如增材制造产生的气孔、疏松和未熔合缺陷[10~12]以及铸造产生的孔洞缺陷[13~15]，均对材料的疲劳损伤行为产生显著影响。由于表面和内部缺陷可认为是短裂纹，其在服役条件下将会引起更大的应力集中。虽然这些缺陷的存在对静态加载下的影响较小，材料往往能满足拉伸性能的要求，但是在循环加载下，缺陷会成为典型的应力集中源，诱导疲劳裂纹形核，不仅大幅降低材料的疲劳强度和寿命，还会导致疲劳寿命呈现出极大的离散性[16,17]。因此对于含缺陷的材料而言，缺陷特征(位置、尺寸和形态)成为影响其疲劳损伤行为的主导因素[18]。目前，针对含缺陷材料，主要采用经典的Murakami模型[19,20]以及Kitagawa-Takahashi (KT)图[21,22]来评价缺陷对疲劳强度的影响，并根据缺陷的几何特征对含缺陷材料的疲劳强度和寿命进行合理预测。

对于表面和内部无明显缺陷的光滑样品，在循环载荷的作用下，块体粗晶材料中疲劳裂纹往往萌生于伴随有挤出/侵入的驻留滑移带(persistent slip band，PSB)，以及PSB和大角晶界交界处[4]。微观上，晶粒内部位错会形成低能位错结构，在疲劳过程中，微观位错结构会按如下顺序发生变化：含脉络结构的基体相→PSB位错梯墙结构和迷宫结构→胞结构[23]。随着晶粒尺寸细化到超细晶/纳米晶尺度，由于晶粒内容纳位错的能力有限，难以形成类似粗晶材料典型的位错结构，疲劳裂纹往往萌生于剪切带处[24~27]。此外，大量研究[28~30]发现，晶粒取向也会影响材料的疲劳损伤行为，疲劳裂纹更倾向于在面外取向靠近<100>的晶粒中萌生，而<111>面外取向的晶粒由于具有高的位错滑移所需要的临界分切应力，不利于晶粒内位错开动以及塑性应变的累积，从而延缓了<111>面外取向晶粒疲劳裂纹的萌生[29]。孪晶界作为一种特殊的晶界同样会影响材料的疲劳损伤行为。研究[31~33]表明，当基体和孪晶具有高的Schmid因子(Ω)、高的模量差或共格孪晶界的长度至少是平均晶粒尺寸的2倍时，孪晶界也会成为有利于疲劳裂纹萌生的位点。

目前，对于金属箔的疲劳损伤研究主要集中在20~500 μm厚度范围内。大量研究[8,34~38]表明，尽管厚度在20~500 μm范围内的金属箔疲劳后仍能观察到类似块体粗晶的挤出/侵入损伤形貌以及典型的疲劳位错结构，但是金属箔的疲劳性能明显不同于块体材料，表现出明显的样品尺寸效应。Lavenstein等[39]发现，虽然13 μm厚单晶Ni箔样品的表面同样存在与块体材料相似的挤出/侵入形貌，并且材料内部也形成了PSB位错墙结构，但与块体材料(102~104 cyc)相比，挤出/侵入以及PSB的形核，需要相对更大的循环次数(> 106 cyc)。

集流体箔(厚度在6~13 μm)作为锂离子电池结构材料的一种，目前对其疲劳研究还主要以理论计算的方式为主。Song等[2]和Xu等[40]分别分析了集流体的应力分布，并通过低周疲劳Coffin-Manson公式建立了集流体厚度与疲劳寿命之间的关系，但这些研究并没有过多关注其疲劳损伤行为。目前尚缺少对微米厚度集流体箔疲劳损伤行为的研究，其疲劳损伤微观机制亟待进一步澄清。因此，本工作选用商业锂离子电池用微米厚度集流体Cu箔和Al箔为研究对象，系统研究了集流体金属箔的高周疲劳强度及损伤行为。基于对Cu箔中损伤晶粒微观结构的大量观察和统计分析，获得了Cu箔疲劳裂纹萌生和材料微观结构(晶粒尺寸及其变异系数、晶粒取向、Ω)的统计关系图。通过极值统计法成功预测了Al箔样品中可能的缺陷分布以及存在的最大缺陷尺寸，并基于Kitagawa-Takahashi图建立了集流体Al箔中缺陷尺寸与疲劳极限之间的关系。

1 实验方法

锂离子电池集流体主要包括负极集流体和正极集流体，考虑到制造成本、工艺、导电性和电极电位等因素，商业上通常以Cu箔为负极集流体，Al箔为正极集流体。为了研究集流体材料的疲劳强度和疲劳损伤行为，实验使用的材料是商用锂离子电池正负极集流体箔，包括6和8 μm厚Cu箔以及10和13 μm厚Al箔，其中Cu箔采用电沉积的方式制备，Al箔采用轧制的方式制备。样品原始态表面形貌以及疲劳后表面损伤形貌采用Supra 35场发射扫描电子显微镜(SEM)表征。样品表面的微观晶粒结构以及疲劳后样品采用Tecnai 20透射电子显微镜(TEM)表征，TEM样品采用Gatan Model 695精密离子减薄仪制备，减薄温度设置在-160℃。疲劳后样品的损伤区域采用HKL Channel 5电子背散射衍射(EBSD)探头表征，其中Cu箔的扫描步长为0.13 μm，Al箔的扫描步长为0.07 μm。

拉伸及疲劳样品采用VMSP0202-GL-25绿光飞秒激光切割机(CCD)加工，其中拉伸样品加工成狗骨头棒型，样品标距宽度为12.5 mm，标距段长度为50 mm。疲劳样品加工成漏斗形状，样品的最窄宽度为6 mm，样品总长度为40 mm。拉伸实验所用应变速率为2 × 10-4 s-1，拉伸应变采用非接触数字图像相关法(DIC)测量。为了确保拉伸性能的准确性，至少测试3个样品。考虑到样品厚度十分薄(6~13 μm)，拉-压疲劳(主要适用于样品厚度在毫米尺度的大尺寸样品)是无法实现的，而拉-拉疲劳是薄箔材料最常用的疲劳加载方法之一。综合考虑到薄箔疲劳加载的最大应力和最小应力，同时应力比尽可能小等原因，本工作疲劳实验采用应力控制下的拉-拉加载方式，应力比为0.2，加载频率为50 Hz，加载波形为正弦波，所用设备为MMT-101NV-10微力测试系统。样品的疲劳极限采用升降法获得，进行升降法实验时，选取Cu箔和Al箔的应力增量为4 MPa。如果样品在某一应力幅下达到107 cyc之前发生破坏，则随后的实验就降低一个应力增量进行实验，反之则提高一个应力增量进行实验。然后根据升降图，将相邻应力水平在107 cyc之前发生破坏/未破坏所对应的数据点进行配对，最后对包含至少3对配对样品所对应的应力幅求平均值，从而获得样品的疲劳极限。

样品表面粗糙度(Rz)以及表面缺陷尺寸采用OLS4000激光共聚焦3D显微镜(LSCM)测量，其二维分辨率为120 nm，Z方向分辨率为10 nm。首先将每种样品切成10 mm × 10 mm的小样品，每个小样品测量一个区域。其中表面粗糙度测量3个小样品，单个测量区域大小为259 μm × 259 μm。表面缺陷尺寸测量12个小样品，单个测量区域大小为129 μm × 129 μm，每个区域测量35个缺陷尺寸。

2 实验结果

2.1 Cu箔实验结果

2.1.1 Cu箔表面形貌及微观结构

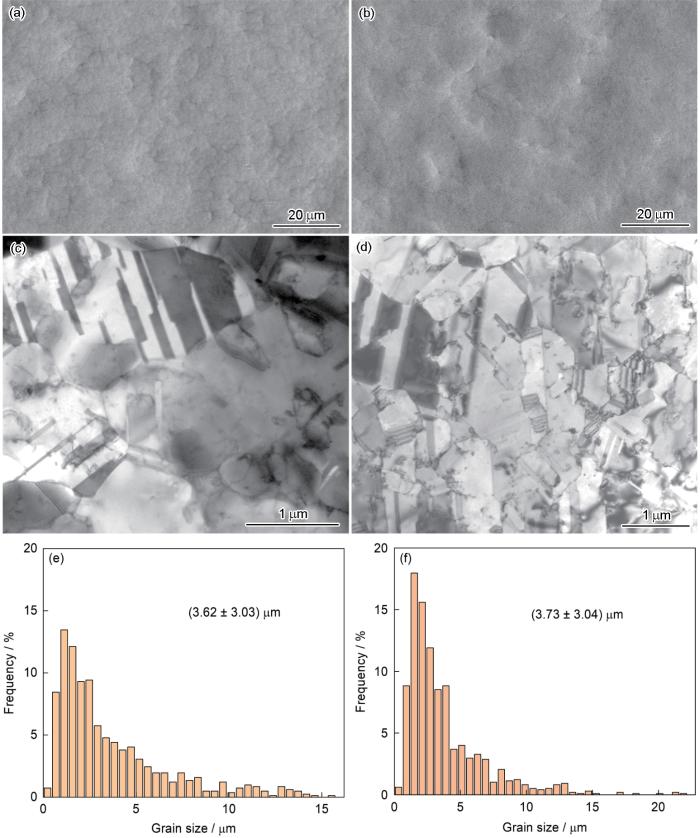
图1为6和8 μm厚Cu箔表面形貌SEM像、微观结构TEM像以及晶粒尺寸统计分布(每种厚度的Cu箔统计了约500个晶粒)。从图1a和b中可以看出，不同厚度Cu箔的表面形貌相似，表面略有凹凸不平的起伏，无明显表面裂纹和其他缺陷，6和8 μm厚Cu箔的表面粗糙度分别为(1.08 ± 0.11)和(1.19 ± 0.17) µm。图1c和d微观结构观察表明，6和8 μm厚Cu箔的晶粒内部均包含高密度的生长孪晶，孪晶片层宽度分别为(137 ± 109)和(122 ± 89) nm，孪晶面积分数分别为30%和29%。晶粒尺寸统计分布结果(图1e和f)表明，6和8 μm厚Cu箔的平均晶粒尺寸相近，分别为(3.62 ± 3.03)和(3.73 ± 3.04) μm。从晶粒尺寸统计分布图可以看出，2种厚度的Cu箔均拖带着很长的尾巴，这也从一定程度上反应出Cu箔样品晶粒尺寸的不均匀性。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   6和8 μm厚度Cu箔表面SEM像、微观结构TEM像及晶粒尺寸分布图

Fig.1   SEM images of surface morphologies (a, b), TEM images of microstructures (c, d), and grain size distributions (e, f) of Cu foils with thicknesses of 6 μm (a, c, e) and 8 μm (b, d, f)


2.1.2 Cu箔拉伸及疲劳性能

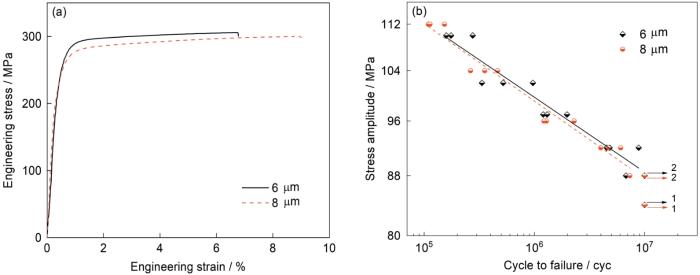
图2a和b为不同厚度Cu箔的拉伸应力-应变曲线以及应力幅-疲劳寿命曲线。从图2a可以看出，6和8 μm厚Cu箔的强度相差不大，但塑性存在明显差别。其中6和8 μm厚Cu箔的抗拉强度分别为(303 ± 3)和(301 ± 1) MPa，屈服强度分别为(263 ± 8)和(252 ± 4) MPa，总断裂延伸率分别为(6.14 ± 0.57)%和(8.67 ± 0.50)%。从图2b可以看出，6和8 μm厚Cu箔的疲劳性能无明显差别，通过升降法，可得2种厚度Cu箔的高周疲劳极限均为88.67 MPa。早期的研究[41,42]表明，材料的高周疲劳性能与材料强度有很大关系，材料的强度越高，高周疲劳性能越好。6和8 μm厚Cu箔的抗拉强度分别为303和301 MPa，由于2种厚度Cu箔的抗拉强度相差不大，因此其疲劳性能无明显差别。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   不同厚度Cu箔的工程应力-应变曲线以及应力幅-疲劳寿命曲线

Fig.2   Engineering stress-strain (a) and stress amplitude-fatigue life (b) curves of Cu foils with different thicknesses (The arrows indicate that the specimen is not failure under this stress amplitude and cycle)


2.1.3 Cu箔疲劳裂纹萌生

考虑到2种厚度Cu箔表面形貌以及微观结构的相似性，本工作仅以8 μm厚Cu箔为例，来阐述Cu箔在循环载荷下的疲劳损伤机制。图3给出了8 μm厚Cu箔高周疲劳试样在应力幅92 MPa、总寿命为4 × 106 cyc下的损伤萌生位点微观结构以及损伤特征。由图3a~c可以看出，疲劳裂纹萌生于较大晶粒内部的滑移带处(如图中黑色单箭头所示)，并沿着滑移带扩展。该损伤晶粒尺寸约为10 μm，约为平均晶粒尺寸的3倍。另外该损伤晶粒还具有很高的最大 Schmid因子(Ωmax = 0.499)。同时，通过总结多个损伤晶粒的情况发现，疲劳损伤均倾向于在具有高的Ω的大晶粒内部滑移带处萌生。根据Hall-Petch关系[43]，具有较大晶粒尺寸的软取向晶粒由于屈服应力较低，更有利于局部塑性滑移和损伤在这些晶粒内的累积。因此，可以认为，大的晶粒尺寸和软取向应该是Cu箔塑性滑移局部化和疲劳裂纹萌生的主要原因。一般而言，对于含孪晶界的材料，孪晶界也会成为疲劳裂纹萌生位点，尤其当位错在孪晶界面两侧发生平行滑移时[31,32]，但是本工作中并未观察到明显的沿孪晶界开裂的情况。根据EBSD获得的晶体取向计算了图3b中基体和孪晶12个滑移系的Ω，如表1所示，其中粗体代表Ωmax，其对应的滑移系为最先激活的滑移系。可以看出，基体和孪晶中开动的滑移系并不平行，即位错在孪晶界面两侧并未发生平行滑移，这可能是未导致孪晶界开裂的原因。从TEM微观结构观察(图3d)可知，疲劳后Cu箔样品晶粒内部并没有典型的PSB位错结构形成，大量的位错主要塞积在孪晶界处。为进一步探究损伤晶粒的特点，随机选取了30个发生疲劳损伤的晶粒，并将孪晶和基体中平行于面外方向(ND)及加载方向(LD)的晶体取向和Ωmax分别绘制在图3e和f中。从图中可以总结出损伤晶粒还具有以下2个特点：一是从ND看损伤晶粒的基体和孪晶其中一个取向靠近<100>，而从LD看基体和孪晶的取向则是随机分布的；二是基体和孪晶中至少其中一个的Ωmax因子不低于0.44。Cu箔疲劳损伤更倾向于在<100>ND的晶粒中形成，这与文献[28~30]报道的循环载荷作用下的Cu薄膜和Ag薄膜的损伤特征一致。主要原因可以归因于：一方面，从实验结果可以看出，<100>ND的晶粒具有高的Ωmax(≥ 0.44)；另外文献[29,33]也报道了相比其他取向晶粒，<100>ND的晶粒具有低的弹性模量，即<100>ND的晶粒为软取向晶粒，位错滑移所需要的临界分切应力也相对较小[29]。在相同的总应变幅下，<100>ND的晶粒更有利于位错滑移的开动，导致晶粒内累积更高的塑性应变。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   8 μm厚Cu箔高周疲劳试样在应力幅92 MPa、总寿命为4 × 106 cyc下的损伤萌生位点微观结构以及损伤特征

Fig.3   Microstructures and damage features of fatigue damage initiation sites in 8 μm-thick Cu foils under a stress amplitude of 92 MPa and fatigue life of 4 × 106 cyc (The arrows in Figs.4a-c represent fatigue damage sites. Black and white lines in Figs.4b and c are grain boundaries and twin boundaries, respectively)

(a) SEM image (LD—loading direction) (b) EBSD grain orientation map (ND—normal direction)

(c) Schmid factor map (d) post-fatigue TEM image

(e, f) inverse pole figures depicting the orientations of parent and twin grains associated with the fatigue damage in the surface ND (e) and LD (f), respectively


表1   根据图3b中基体和孪晶的12个滑移系计算的Schmid因子(Ω)

Table 1  Schmid factors (Ω) for the 12 slip systems of a pair of parent and twin in Fig.3b (Bold values indicate maximum Schmid factors (Ωmax))

Slip

system

(1¯11)(111)(111¯)(1¯11¯)
[011¯][1¯01¯][110][011¯][1¯01][1¯10][011][1¯01¯][1¯10][110][1¯01][011]
Parent0.4970.200.300.220.060.280.230.110.340.320.160.48
Twin0.190.040.150.350.150.200.300.150.450.4970.260.24

新窗口打开| 下载CSV


2.2 Al箔实验结果

2.2.1 Al箔表面形貌及微观结构

图4为10和13 μm厚Al箔表面形貌SEM像、微观结构TEM像以及晶粒尺寸统计分布图(每种厚度的Al箔统计了约500个晶粒)。从图4a和b可以看出，不同厚度Al箔的表面形貌相似，表面均存在明显的平行于轧制方向的轧制痕迹以及几乎垂直于轧制方向的微米尺寸裂纹。10和13 μm厚Al箔的表面粗糙度分别为(1.80 ± 0.43)和(1.47 ± 0.42) µm。图4c和d微观结构观察表明，不同厚度Al箔晶粒内部均存在由于轧制过程产生的位错。晶粒尺寸统计分布结果(图4e和f)表明，10和13 μm厚Al箔的平均晶粒尺寸分别为(0.76 ± 0.41)和(1.19 ± 0.66) μm。

图4

新窗口打开| 下载原图ZIP| 生成PPT

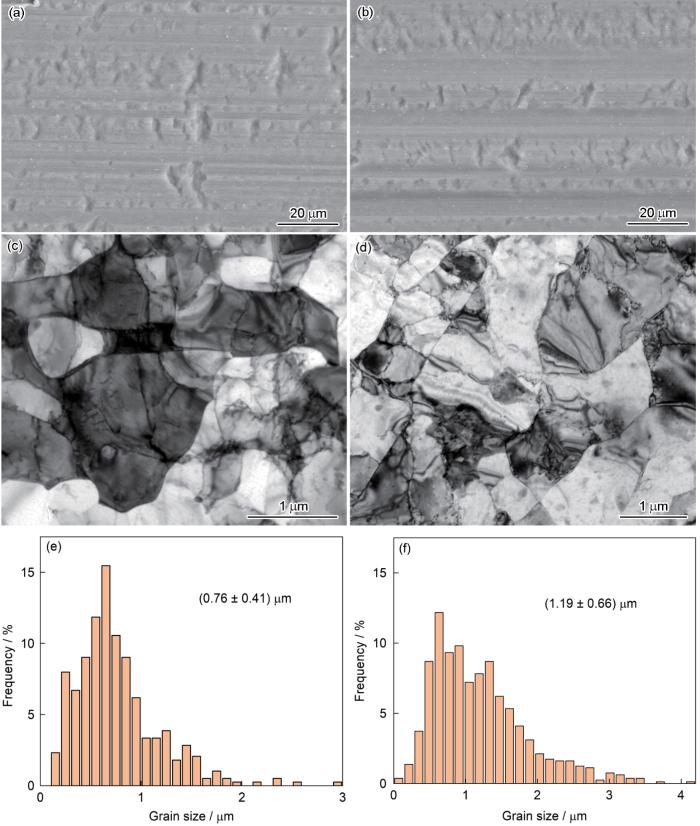
图4   10和13 μm厚度Al箔表面SEM像、微观结构TEM像及晶粒尺寸分布图

Fig.4   SEM images of surface morphologies (a, b), TEM images of microstructures (c, d), and grain size distributions (e, f) of Al foils with thicknesses of 10 μm (a, c, e) and 13 μm (b, d, f)


2.2.2 Al箔拉伸及疲劳性能

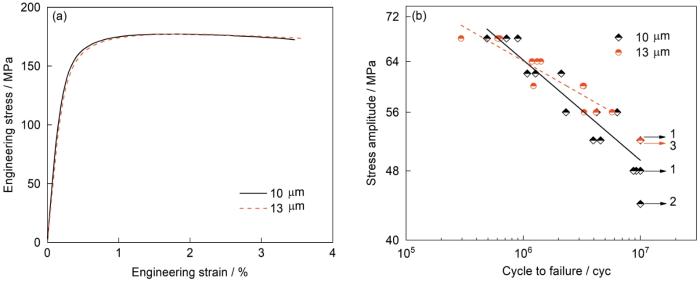
图5a和b为不同厚度Al箔的拉伸应力-应变曲线以及应力幅-疲劳寿命曲线。从图5a可以看出，10和13 μm厚Al箔的强度和塑性比较接近，其抗拉强度分别为(178 ± 1)和(177 ± 1) MPa，屈服强度分别为(162 ± 2)和(161 ± 3) MPa，均匀延伸率分别为(1.83 ± 0.08)%和(1.72 ± 0.08)%，总断裂延伸率分别为(3.42 ± 0.17)%和(3.45 ± 0.17)%。不同于Cu箔，10和13 μm厚Al箔的疲劳性能表现出很大差别，更厚的Al箔具有更高的疲劳极限，10和13 μm厚Al箔的高周疲劳极限分别为49和54 MPa (图5b)。对于10和13 μm厚Al箔，其抗拉强度分别为178和177 MPa，虽然相差不大，但疲劳性能却存在明显区别，而且疲劳寿命相比于电沉积Cu箔表现出更大的离散性，这可能与表面存在的轧制缺陷有关，将在下文进行详细讨论。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同厚度Al箔的工程应力-应变曲线以及应力幅-疲劳寿命曲线

Fig.5   Engineering stress-strain (a) and stress amplitude-fatigue life (b) curves of Al foils with different thicknesses (The arrows indicate that the specimen is not failure under this stress amplitude and cycle)


2.2.3 Al箔表面缺陷

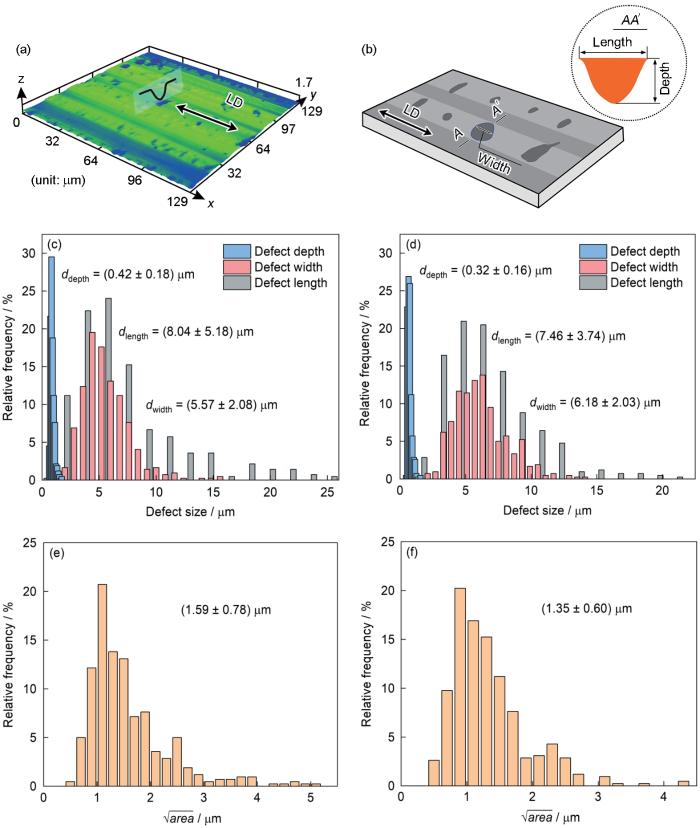
图6a给出了激光共聚焦显微镜测量的Al箔表面的三维形貌图，图中黑色实线为相应横截面的轮廓曲线。测量的表面缺陷深度、长度及宽度几何示意图如图6b所示。每种厚度的Al箔统计了420个缺陷，其缺陷深度、长度及宽度统计分布如图6c和d所示。统计结果表明，10 μm厚Al箔的表面缺陷深度、长度及宽度分别为(0.42 ± 0.18)、(8.04 ± 5.18)和(5.57 ± 2.08) μm (图6c)。13 μm厚Al箔的表面缺陷深度、长度及宽度分别为(0.32 ± 0.16)、(7.46 ± 3.74)和(6.18 ± 2.03) μm (图6d)。可以看出，随着Al箔轧制厚度的降低，将会在样品表面产生更大的缺陷深度和长度。考虑到Al箔表面缺陷具有不规则的形状，因此借助Murakami参数(area)，即三维缺陷在垂直于加载方向上的投影面积(如图6b右侧部分阴影面积)的平方根值，来作为缺陷尺寸参数，并用该参数来表征缺陷尺寸与材料疲劳性能的关系[44]。由于该阴影区域可以近似为椭圆，因此该参数可通过计算椭圆面积来获得，即通过测量的缺陷长度(dlength)和缺陷深度(ddepth)获得：

area=π·dlength·ddepth / 4

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   Al箔表面三维形貌图、表面缺陷示意图以及不同厚度Al箔缺陷尺寸和缺陷参数(area)分布

Fig.6   3D topography, schematic of surface defect, and distributions of defect size and defect parameter (area) for Al foils with different thicknesses

(a) 3D laser confocal image

(b) schematic of surface defect and the cross-sectional morphology along the AA' line

(c-f) distributions of defect size (c, d) and defect parameter (area) (e, f) of 10 μm (c, e) and 13 μm (d, f) Al, respectively (ddepth—defect depth, dlength—defect length, dwidth—defect width)


一般来讲，该值越大，其缺陷危险等级越高，越有可能诱发疲劳裂纹萌生。对于10和13 μm厚Al箔，其平均缺陷参数area分别为(1.59 ± 0.78)和(1.35 ± 0.60) μm，如图6e和f所示，可以看出，更薄的Al箔具有更高的缺陷尺寸。因此，更薄的Al箔诱发疲劳裂纹萌生的可能性越大，这与更薄的Al箔疲劳极限更低(图5b)一致。

2.2.4 Al箔疲劳裂纹萌生

考虑到不同厚度Al箔表面形貌以及微观结构的相似性，本工作仅以13 μm厚Al箔为例，来阐述Al箔在循环载荷下的疲劳损伤机制。图7给出了13 μm厚Al箔高周疲劳试样在应力幅64 MPa、总寿命为1.4 × 106 cyc的表面损伤形貌SEM像、裂纹的高倍SEM像以及裂纹附近的EBSD像。从图7a和b中可以看出，Al箔疲劳表面并没有明显的滑移带痕迹。由于表面轧制缺陷的深度、长度及宽度约为0.32、7.46和6.18 μm，因此表面缺陷可以看成为短裂纹，在循环载荷的作用下，缺陷处将产生更高的应力集中，这些应力集中点往往会成为裂纹萌生源，因此可以合理地认为Al箔疲劳裂纹的萌生与表面缺陷的存在有十分密切的关系。为了进一步表征疲劳裂纹如何扩展，对裂纹附近区域进行了EBSD表征，如图7c所示，其中黑色线为高角度晶界(> 10°)，灰色线为低角度晶界(2°~10°)。从图中可以看出，其疲劳裂纹扩展路径(红色线)主要沿着高角度晶界扩展。因此可以认为，Al箔的疲劳裂纹优先萌生于表面缺陷处，并可能沿着高角度晶界扩展。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   13 μm厚Al箔高周疲劳试样在应力幅64 MPa、总寿命为1.4 × 106 cyc的表面损伤形貌SEM像、裂纹的高倍SEM像以及裂纹附近的EBSD像

Fig.7   Surface damage morphology (a) and high magnified (b) SEM images, and EBSD characterization (c) of 13 μm-thick Al foils under a stress amplitude of 64 MPa and fatigue life of 1.4 × 106 cyc (Black line, gray line, and red line in Fig.7c represent high angle grain boundaries (> 10°), low angle grain boundaries (2°~10°), and crack propagation path, respectively)


3 分析讨论

Cu箔和Al箔的表面状态以及疲劳损伤行为明显不同。Cu箔表面相对比较平整，没有明显的裂纹(图1a和b)，其疲劳裂纹主要萌生于表面滑移带处(图3a)，而且损伤晶粒与晶粒取向以及Ωmax等微观结构参数息息相关。然而Al箔表面存在大量的微米尺寸的裂纹(图4a和b)，其疲劳裂纹主要萌生于表面缺陷处(图7a)。因此接下来将从微观结构和表面缺陷等角度分别对Cu箔和Al箔进行分析讨论。

3.1 Cu箔疲劳裂纹萌生机制

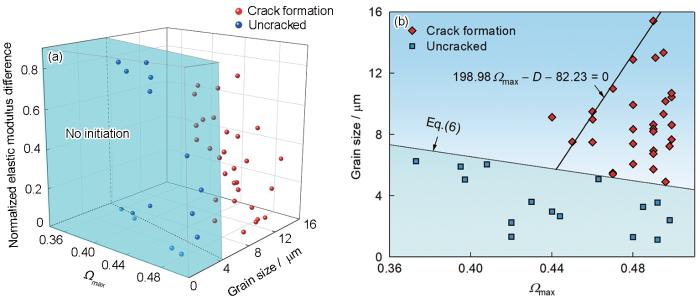
考虑到Cu箔疲劳裂纹主要萌生于较大晶粒内部的滑移带处，且疲劳裂纹的萌生与晶粒取向及Ωmax等微观结构参数息息相关。除了取向和Ωmax外，Cu箔的疲劳裂纹萌生还可能受其他微观结构参数(如晶粒尺寸及弹性模量)的影响。为了进一步澄清Cu箔疲劳裂纹萌生的微观结构特征，统计了30个损伤晶粒和15个未损伤晶粒的晶粒尺寸、Ωmax以及归一化的弹性模量差(基体与孪晶模量差的绝对值与其平均值之比)，如图8a所示。这里需要说明的是，损伤晶粒均具有近<100>ND。从图中可以看出，30个损伤晶粒中最小的晶粒尺寸约为5 μm，Ωmax的最小值为0.44。当晶粒尺寸低于5 μm或者Ωmax低于0.44时，即使基体和孪晶之间具有高的弹性模量差，疲劳裂纹也不易萌生。而在同时满足晶粒尺寸和Ωmax的条件下，不仅高弹性模量差的晶粒会萌生裂纹，低弹性模量差的晶粒同样萌生裂纹。因此可以认为界面两侧弹性模量差并不是Cu箔疲劳裂纹萌生的必要条件。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   有利于Cu箔疲劳裂纹萌生的晶粒特点

Fig.8   Grain configurations favoring fatigue crack initiation for Cu foils

(a) grain size, maximum Schmid factor (Ωmax), and normalized elastic modulus difference of the twin and parent grain pairs which present crack initiation and no crack initiation

(b) grain size (D) and Ωmax of the twin and parent grain pairs which present crack initiation and no crack initiation


图8b为损伤晶粒和未损伤晶粒的晶粒尺寸以及Ωmax的分布特征。可以看出，萌生裂纹和未萌生裂纹的数据点存在一个分界线。对于二维分类问题，可以采用机器学习中的支持向量机[45,46]来获得分界线方程。支持向量机分类的思想是找到给定数据集合边缘上的若干数据点(支持向量)，用这些点找出超平面的参数( w, b)，使得支持向量到该平面的距离最大。规定训练样本集S = {( x1, y1), ( x2, y2), …, ( xm, ym)}，其中 xi = (Ωmax,i, Di)，yi ∈ {-1, +1} (其中，-1代表无裂纹萌生类别，+1代表存在裂纹萌生类别)。支持向量分类(SVC)的目标函数优化问题可以表达为[47]：

minw,b,εi12w2+C∑i=1mεis.t.DiwTxi+b≥1-εiεi≥0, i=1, 2, ⋯, m

式中，s.t.代表目标函数的约束条件公式； w 是法向量，决定了超平面的方向；上角标T代表矩阵转置， wT是转置后的法向量；b为位移项，决定了超平面与原点之间的距离；C为引入的惩罚系数，即对宽容行为的惩罚力度；ε为松弛变量，表征该样本不满足约束的程度；D为晶粒尺寸；下角标i代表不同的样本点；m代表样本点的总个数。根据Karush-Kuhn-Tucker (KKT)条件将 式(2)转化为对偶问题，其表达式为[47]：

maxα∑i=1mαi-12∑i=1m∑j=1mαiαjyiyjxiTxjs.t.∑i=1mαiyi=00≤αi≤C, i=1, 2, ⋯, m

式中，α为Lagrange乘子，下角标j代表不同的样本点。其中本次分类问题取为硬间隔，即按照C为无穷大进行计算，通过 式(3)可解出αi，然后代入 式(4)：

w=∑i=1mαiyixib=1-wTxs

式中， xs = (Ωmax,s,Ds)为支持向量，将解出的 w= (w1, w2)和b代入超平面所对应的模型中，即 式(5)：

wTx+b=0

最终可得分界线方程为：

19.58Ωmax+D-14.39=0

分界线的上半部分区域对应着裂纹萌生区，下半部分区域则没有裂纹形成。在裂纹萌生区域，对损伤晶粒的边界数据点进行线性拟合，从而获得疲劳裂纹萌生所需满足的晶粒尺寸和Ωmax的边界线。从图8b中可以看出，具有较大的晶粒尺寸(≥ 5 μm)，低的Ωmax (< 0.44)的晶粒不利于裂纹萌生；而高的Ωmax(≥ 0.48)，小的晶粒尺寸(< 5 μm)也不利于萌生裂纹。因此可以认为，Cu箔疲劳裂纹萌生除需要满足晶粒取向具有近<100>ND外，还需同时满足大的晶粒尺寸以及高的Ωmax。

通过以上分析，可以总结出同时具有近<100>ND、大的晶粒尺寸以及高的Ωmax等特点的晶粒更有利于疲劳裂纹萌生。然而，在同时满足晶粒取向靠近<100>ND、Ωmax ≥ 0.44以及晶粒尺寸≥ 5 μm条件的晶粒中选取26个晶粒进行实验观察，结果表明并不是所有满足以上条件的晶粒都会萌生疲劳裂纹，这意味着疲劳裂纹萌生同时受其他参数影响。对损伤晶粒及其周围晶粒进行晶粒尺寸统计时，发现损伤晶粒与周围的晶粒尺寸并不是十分均匀，如图9a所示。为了定量描述晶粒尺寸的不均匀性，这里引入概率论和统计学中的变异系数(γ)来描述损伤晶粒及其周围晶粒尺寸的不均匀性程度[48,49]：

γ=σμ

图9

新窗口打开| 下载原图ZIP| 生成PPT

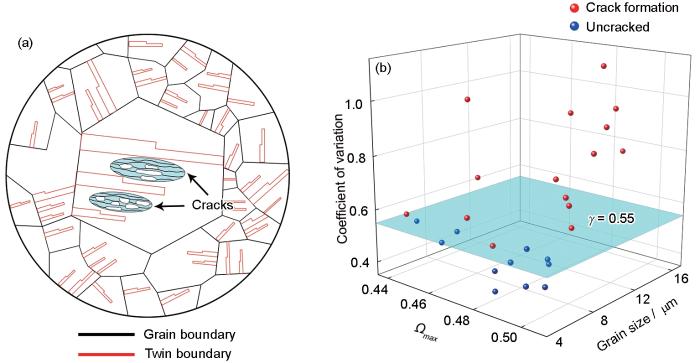
图9   损伤晶粒及周围晶粒不均匀性示意图以及有利于裂纹萌生的晶粒不均匀性特点

Fig.9   Schematic of damage grain and surrounding grain inhomogeneity (a) and characteristics of grain inhomogeneity favorable to crack initiation (b) (All grains presenting crack initiation and no crack initiation have a high Ωmax (≥ 0.44), large grain size (≥ 5 μm), and grain orientation close to <100>ND. γ—coefficient of variation)


式中，σ为一组测量数据的标准差，μ为该组数据的均值。γ越大，表明晶粒尺寸分布越不均匀。普遍认为当晶粒尺寸服从正态分布时，其晶粒尺寸分布是均匀的。对晶粒尺寸满足正态分布的Cu、Au、Ti箔而言，其γ在0.09~0.37范围内变化[28,50,51]。

图9b总结了同时满足晶粒取向靠近<100>ND、Ωmax ≥ 0.44以及晶粒尺寸≥ 5 μm条件的晶粒及其周围晶粒尺寸的γ值。从图中可知，存在临界的γ值，当γ ≥ 0.55时，由于晶粒不均匀性导致的变形不协调，加剧了大晶粒内部的应变局部化程度，最终导致大晶粒内部萌生疲劳裂纹。而当γ < 0.55时，虽然满足萌生裂纹所需要的条件(晶粒取向、晶粒尺寸及Ωmax)，但由于周围晶粒的协调变形，可以减缓大晶粒内部的应变局部化程度，减缓了裂纹萌生的趋势。

通过以上分析，可以认为微观结构参数(晶粒尺寸及其变异系数、晶粒取向、Ωmax)在主导Cu箔的疲劳裂纹萌生的过程。电沉积态Cu箔疲劳裂纹萌生需要同时满足以下条件：(i) 晶粒尺寸不低于5 μm (30个损伤晶粒的最小晶粒尺寸)；(ii) 大晶粒周围的晶粒不均匀性系数不低于0.55；(iii) 一对基体和孪晶中，其中一个取向靠近<100>ND；(iv) Ωmax不低于0.44。

3.2 Al箔疲劳极限预测

3.2.1 表面缺陷极值统计

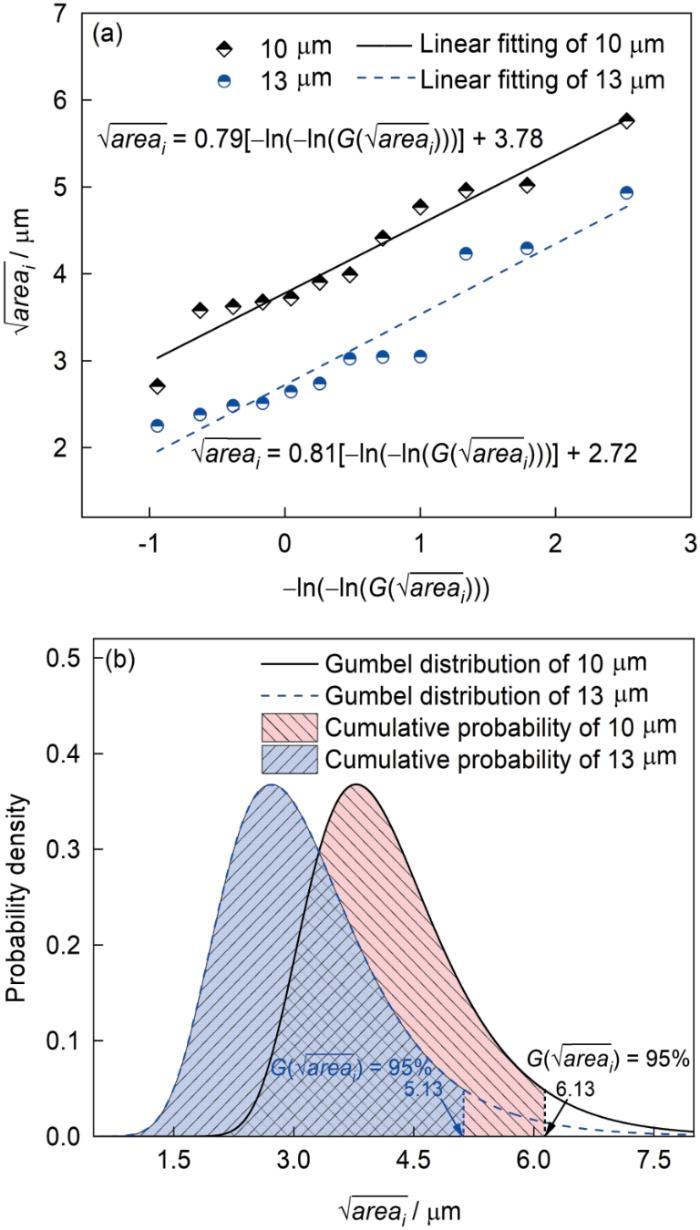
考虑到Al箔疲劳裂纹优先萌生于表面缺陷处，而对于含缺陷材料而言，缺陷的存在会减小材料的有效承载面积，成为典型的应力集中源，因此疲劳裂纹倾向于在缺陷处萌生，尤其是最大缺陷处。为了获得轧制Al箔表面可能存在的最大缺陷尺寸，采用极值统计方法中的分区取值法(block method，BM)，进行最大缺陷尺寸预测。该方法是将样品划分为若干个等效样本，然后在每个样本中选取最大值，每个样本的最大缺陷分布满足Gumbel分布[52]：

G(z)=exp[-exp(-(z-λ) / β)]

式中，G(z)为尺寸小于或等于最大缺陷特征尺寸z的概率，β为尺寸参数，λ为位置参数。

采用BM预测最大缺陷尺寸时，需要重复测量n个样本，若第i个样本的最大缺陷特征尺寸表示为areai，并对其值进行升序排列，则areai的累积概率(G(areai))可表示为：

Gareai=i / (n+1)=
exp-exp-areai-λ / β

通过 式(9)，可得第i个样本的最大缺陷特征尺寸满足：

areai=β[-ln(-ln(G(areai)))]+λ

将计算所得-ln(-ln(G(areai)))与相应测量样本的areai进行线性拟合，可得Gumbel分布函数参数β和λ的值，从而获得总体缺陷尺寸的分布特征，并根据分布特征来预测样品中可能存在的最大缺陷尺寸。

基于以上理论，对随机选取的12个互不重叠且面积均为129 μm × 129 μm的样本进行最大缺陷尺寸统计，数据拟合结果如图10a所示。其中10 μm厚Al箔的β = 0.79，λ = 3.78；13 μm厚Al箔的β = 0.81，λ = 2.72。从图中可知2种厚度Al箔的每个样本中的最大缺陷尺寸areai与相应-ln(-ln(G(areai)))各点分布均显示出良好的直线关系，说明各个样本最大缺陷尺寸能较好地符合Gumbel分布。图10b为2种不同厚度Al箔缺陷的Gumbel分布曲线以及累积概率，令G(areai)=95% (即5%的可能性样本中缺陷尺寸大于此值)，从而可获得10和13 μm厚Al箔表面最大缺陷尺寸分别为6.13和5.13 μm。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   极值统计法预测最大缺陷尺寸

Fig.10   Extreme value statistics predicting maximum defect size

(a) linear fitting for parameters of Gumbel function for Al foils with different thicknesses (areai—Murakami defect size parameter, G(areai)—cumulative probability of defect size)

(b) prediction of the maximum defect size under 95% probability


3.2.2 疲劳极限预测

Al箔表面存在的缺陷可以看作是短裂纹，其等效尺寸为垂直于加载方向的投影面积的平方根值，缺陷对疲劳极限的影响可以通过改进的Kitagawa-Takahashi (KT)图进行预测，即El-Haddad模型，该模型在标准KT图的基础上考虑了短裂纹，引入本征缺陷尺寸area0对原始缺陷尺寸area进行修正，该模型可描述如下[16,53]：

ΔK=FwΔσπarea
area0=1πΔKthFwΔσw02
Δσw=Δσw0area0area0+area

式中，ΔK为循环应力强度因子；Fw为Murakami几何因子，对于表面缺陷Fw = 0.65；Δσ为应力范围；ΔKth为长裂纹扩展门槛值，其值受D、疲劳比(R)、材料强度等因素的影响[21,54]：

ΔKth=3.28σycD(1-R)

式中，σyc为循环屈服强度，其值可近似为材料屈服强度。Al箔屈服强度为162 MPa，计算可得ΔKth = 0.37 MPa·m1/2。Δσw为预测的含缺陷材料的疲劳极限范围；Δσw0为无缺陷材料的疲劳极限范围，该值为对理想材料的纯理论估计，可通过下面的经验模型进行预估[55]：

σw'=Aσb-P·σb2

式中，σw'为R = -1时的疲劳极限，A为理想线性疲劳强度系数，σb为抗拉强度，P为疲劳缺陷敏感系数。对于Al箔，A = 0.55可通过文献[56]对数据进行抛物线拟合获得，P = 0表示没有缺陷的影响。因此可计算出R = -1时无缺陷Al箔的疲劳极限为98 MPa，然后根据Gerber准则[4]，可得R = 0.2时无缺陷Al箔的疲劳极限为80 MPa。

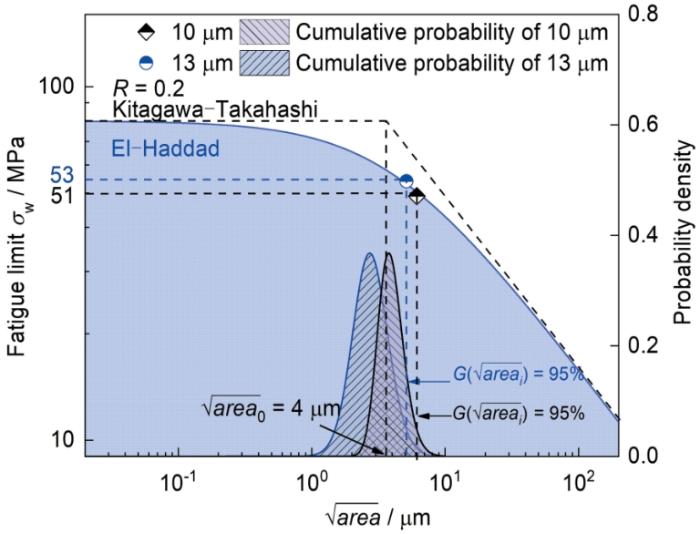
图11为基于El-Haddad方程改进的KT图。为了获得一个保守的估计，假设样品包含最大的缺陷，因此10和13 μm厚Al箔预测的疲劳极限分别是51和53 MPa，而实验测得为49和54 MPa (如图中圆形和菱形符号所示)，预测结果与实验结果误差在5%范围之内(表2)。因此采用KT图并根据最大缺陷尺寸可以很好地预测含缺陷Al箔的疲劳极限，这对集流体缺陷控制具有十分重要的意义。从图11中还可以获得本征缺陷尺寸area0= 4 μm。通过以上分析，可以认为表面缺陷(尤其最大缺陷)主导Al箔的疲劳裂纹萌生的过程。当样品中最大缺陷尺寸低于本征缺陷尺寸时，表面缺陷对疲劳性能的影响可以被忽略。而当最大缺陷尺寸大于此值时，可以认为最大缺陷是决定疲劳极限的重要因素，并且疲劳强度随缺陷尺寸的增大而降低。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   不同厚度Al箔的Kitagawa-Takahashi图

Fig.11   Kitagawa-Takahashi diagram of the Al foils with different thicknesses described by the El-Haddad formulation considering the expected defect distribution (Data points of the black rhombus and blue circle are the experimental fatigue limit (from Fig.5b), and shaded areas of black and blue lines are the cumulative probability of defect size (from Fig.10b) for Al foils with thicknesses of 10 and 13 μm, respectively; R—fatigue stress ratio; area0—intrinsic defect size)


表2   10和13 μm厚Al箔的疲劳极限预测值与实验值

Table 2  Fatigue limit predictions (from Fig.11) and experimental results (from Fig.5b) of Al foils with thicknesses of 10 and 13 μm

ThicknessPredictedExperimental
μm

G(area)

%

areamax
μm

σw

MPa

σw

MPa

Deviation

%

10956.135149+4.1
13955.135354-1.9

Note:areamax—maximum defect size, σw—fatigue limit under stress ratio R = 0.2

新窗口打开| 下载CSV


3.3 Cu箔与Al箔损伤行为对比

通过对Cu箔和Al箔疲劳损伤行为研究发现，Cu箔疲劳损伤主要萌生于表面滑移带处，而Al箔疲劳损伤主要萌生于表面缺陷处。这2种材料表现出不同的疲劳损伤行为，主要归因于2种材料的制备方法不同(Cu箔采用电沉积工艺，Al箔采用轧制工艺)，从而导致2种材料的表面状态不同。电沉积态Cu箔表面相对光滑，无明显表面裂纹和缺陷，疲劳过程中不易在裂纹和缺陷处产生应力集中。此外，微米尺度晶粒内部可以容纳足够多的位错滑移，随着循环应变的不断累积，最终在滑移带处产生应力集中并萌生裂纹。另外，萌生滑移带损伤的晶粒与其微观结构参数(晶粒尺寸及其变异系数、晶粒取向、Ωmax)息息相关，因此可以认为微观结构在主导Cu箔的疲劳损伤萌生的过程。而对于轧制态Al箔，其表面存在明显的几乎垂直于轧制方向的微米尺寸缺陷。这些缺陷的存在可以看成短裂纹，在循环载荷的作用下，缺陷处产生更高的应力集中，这些应力集中点往往会成为疲劳裂纹萌生源，因此可以认为表面缺陷主导Al箔的疲劳损伤萌生。

通过对电沉积态Cu箔的疲劳损伤研究发现，具有大的晶粒尺寸且与周围晶粒具有高的变异系数、<100>ND取向以及高的Ωmax等特点的晶粒，在疲劳过程中更倾向于疲劳裂纹萌生。因此想要提高Cu箔的疲劳性能，可以通过细化晶粒尺寸到5 μm以下并提高其均匀性以及弱化<100>ND织构等方式。研究[57,58]表明，提高电流密度，不仅可以起到细化晶粒的作用，还可以起到弱化<100>ND织构的作用。此外，晶粒细化剂的加入，在起到细化晶粒的同时还有利于提高晶粒均匀性[59]。因此在满足要求的情况下，尽量使用高的电流密度，并通过加入晶粒细化剂来提高Cu箔的疲劳性能。

通过对轧制态Al箔的疲劳损伤研究发现，当缺陷尺寸低于本征缺陷尺寸(4 μm)时，缺陷对疲劳性能的影响并不显著，而高于此值时，材料的疲劳性能随缺陷尺寸的增加而降低。因此，想要提高Al箔的疲劳性能，应减少表面轧制缺陷的存在，并严格控制缺陷尺寸低于本征缺陷尺寸。由于Al箔是Al锭通过多次轧制形成的，当Al锭存在氧化膜、气孔、非金属夹杂、偏析等缺陷时，轧制加工时易沿此缺陷而产生表面微裂纹，因此应严格控制Al锭的质量[60,61]。此外，当样品表面存在金属或非金属屑异物时，轧制过程中由于压下量大，会擦伤轧辊。当存在异物的轧辊通过金属变形区时将导致变形不均匀而引起该处撕裂，从而在样品表面留下微裂纹。因此需要优化轧制工艺，严格控制轧辊的凸度和表面粗糙度，并改善工作环境，从而减少样品表面微裂纹的数量和尺寸，来提高Al箔的疲劳性能。

4 结论

(1) 电沉积态微米晶Cu箔疲劳裂纹主要萌生于较大晶粒内部的滑移带处并沿着滑移带扩展。

(2) 有利于电沉积态微米晶Cu箔疲劳裂纹萌生的晶粒需要同时满足以下条件：(i) 晶粒尺寸不低于5 μm；(ii) 大晶粒周围的晶粒不均匀性系数不低于0.55；(iii) 一对基体和孪晶中，其中一个取向靠近<100>ND；(iv) Ωmax不低于0.44。

(3) 轧制态超细晶Al箔疲劳裂纹优先萌生于表面缺陷处。基于Kitagawa-Takahashi图，建立了轧制态超细晶Al箔缺陷特征尺寸与疲劳极限之间的关系。并采用极值统计法，预测了样品中可能存在的最大缺陷尺寸，基于最大缺陷尺寸，对轧制态超细晶Al箔的疲劳极限进行了评价，预测结果与实验结果误差在5%以内。

参考文献

Zhang J Q, Lu B, Song Y C, et al.

Diffusion induced stress in layered Li-ion battery electrode plates

[J]. J. Power Sources, 2012, 209: 220

DOI      URL     [本文引用: 2]

Song Y C, Li Z Z, Zhang J Q.

Reducing diffusion induced stress in planar electrodes by plastic shakedown and cyclic plasticity of current collector

[J]. J. Power Sources, 2014, 263: 22

DOI      URL     [本文引用: 2]

He Y L, Hu H J, Song Y C, et al.

Effects of concentration-dependent elastic modulus on the diffusion of lithium ions and diffusion induced stress in layered battery electrodes

[J]. J. Power Sources, 2014, 248: 517

DOI      URL     [本文引用: 1]

Suresh S. Fatigue of Materials[M]. 2nd Ed., Cambridge: Cambridge University Press, 1998: 95

[本文引用: 3]

Thompson N, Wadsworth N, Louat N.

The origin of fatigue fracture in copper

[J]. Philos. Mag., 1956, 1: 113

DOI      URL     [本文引用: 1]

Grosskreutz J C, Waldow P.

Substructure and fatigue fracture in aluminum

[J]. Acta Metall., 1963, 11: 717

DOI      URL    

Boettner R C, McEvily A J, Liu Y C.

On the formation of fatigue cracks at twin boundaries

[J]. Philos. Mag., 1964, 10: 95

Dai C Y, Zhang B, Xu J, et al.

On size effects on fatigue properties of metal foils at micrometer scales

[J]. Mater. Sci. Eng., 2013, A575: 217

[本文引用: 1]

Wan H Y, Chen G F, Li C P, et al.

Data-driven evaluation of fatigue performance of additive manufactured parts using miniature specimens

[J]. J. Mater. Sci. Technol., 2019, 35: 1137

DOI     

This overview firstly introduces the state-of-the-art research progress in length scale-related fatigue performance of conventionally-fabricated metals evaluated by miniature specimens. Some key factors for size effects sensitive to microstructures including the specimen thickness, grain size and a ratio between them are highlighted to summarize some general rules for size effects. Then, ongoing research progress and new challenges in evaluating the fatigue performance of additive manufactured parts controlled by location-specific defects, microstructure heterogeneities as well as mechanical anisotropy using miniature specimen testing technique are discussed and addressed. Finally, a potential roadmap to establish a data-driven evaluation platform based on a large number of miniature specimen-based experiment data, theoretical computations and the ‘big data’ analysis with machine learning is proposed. It is expected that this overview would provide a novel strategy for the realistic evaluation and fast qualification of fatigue properties of additive manufactured parts we have been facing to.

Sanaei N, Fatemi A.

Defects in additive manufactured metals and their effect on fatigue performance: A state-of-the-art review

[J]. Prog. Mater. Sci., 2021, 117: 100724

DOI      URL     [本文引用: 2]

Tang M, Pistorius P C.

Fatigue life prediction for AlSi10Mg components produced by selective laser melting

[J]. Int. J. Fatigue, 2019, 125: 479

DOI      URL    

Wu Z K, Wu S C, Bao J G, et al.

The effect of defect population on the anisotropic fatigue resistance of AlSi10Mg alloy fabricated by laser powder bed fusion

[J]. Int. J. Fatigue, 2021, 151: 106317

DOI      URL     [本文引用: 1]

Atxaga G, Pelayo A, Irisarri A M.

Effect of microstructure on fatigue behaviour of cast Al-7Si-Mg alloy

[J]. Mater. Sci. Technol., 2001, 17: 446

DOI      URL     [本文引用: 1]

Jiang H, Bowen P, Knott J F.

Fatigue performance of a cast aluminium alloy Al-7Si-Mg with surface defects

[J]. J. Mater. Sci., 1999, 34: 719

DOI      URL    

El Khoukhi D, Morel F, Saintier N, et al.

Probabilistic modeling of the size effect and scatter in high cycle fatigue using a Monte-Carlo approach: Role of the defect population in cast aluminum alloys

[J]. Int. J. Fatigue, 2021, 147: 106177

DOI      URL     [本文引用: 1]

Beretta S, Romano S.

A comparison of fatigue strength sensitivity to defects for materials manufactured by AM or traditional processes

[J]. Int. J. Fatigue, 2017, 94: 178

DOI      URL     [本文引用: 2]

Gong H J, Rafi K, Gu H F, et al.

Influence of defects on mechanical properties of Ti-6Al-4V components produced by selective laser melting and electron beam melting

[J]. Mater. Des., 2015, 86: 545

DOI      URL     [本文引用: 1]

Dezecot S, Maurel V, Buffiere J Y, et al.

3D characterization and modeling of low cycle fatigue damage mechanisms at high temperature in a cast aluminum alloy

[J]. Acta Mater., 2017, 123: 24

DOI      URL     [本文引用: 1]

Murakami Y.

Material defects as the basis of fatigue design

[J]. Int. J. Fatigue, 2012, 41: 2

DOI      URL     [本文引用: 1]

Murakami Y, Usuki H.

Quantitative evaluation of effects of non-metallic inclusions on fatigue strength of high strength steels. II: Fatigue limit evaluation based on statistics for extreme values of inclusion size

[J]. Int. J. Fatigue, 1989, 11: 299

DOI      URL     [本文引用: 1]

Wu S C, Song Z, Kang G Z, et al.

The Kitagawa-Takahashi fatigue diagram to hybrid welded AA7050 joints via synchrotron X-ray tomography

[J]. Int. J. Fatigue, 2019, 125: 210

DOI      URL     [本文引用: 2]

Zerbst U, Bruno G, Buffière J Y, et al.

Damage tolerant design of additively manufactured metallic components subjected to cyclic loading: State of the art and challenges

[J]. Prog. Mater. Sci., 2021, 121: 100786

DOI      URL     [本文引用: 1]

Li P. Investigation on the cyclic deformation behaviors of face-centered cubic crystals[D]. Shenyang: Institute of Metal Research, Chinese Academy of Sciences, 2009

[本文引用: 1]

李 鹏. 面心立方晶体循环形变行为研究[D]. 沈阳: 中国科学院金属研究所, 2009

[本文引用: 1]

An X H, Wu S D, Wang Z G, et al.

Enhanced cyclic deformation responses of ultrafine-grained Cu and nanocrystalline Cu-Al alloys

[J]. Acta Mater., 2014, 74: 200

DOI      URL     [本文引用: 1]

Wong M, Kao W, Lui J, et al.

Cyclic deformation of ultrafine-grained aluminum

[J]. Acta Mater., 2007, 55: 715

DOI      URL    

Zhang Z J, Zhang P, Zhang Z F.

Cyclic softening behaviors of ultra-fine grained Cu-Zn alloys

[J]. Acta Mater., 2016, 121: 331

DOI      URL    

An X H, Lin Q Y, Wu S D, et al.

Improved fatigue strengths of nanocrystalline Cu and Cu Al alloys

[J]. Mater. Res. Lett., 2015, 3: 135

DOI      URL     [本文引用: 1]

Glushko O, Kiener D.

Initiation of fatigue damage in ultrafine grained metal films

[J]. Acta Mater., 2021, 206: 116599

DOI      URL     [本文引用: 3]

Mönig R. Thermal fatigue of Cu thin films[D]. Stuttgart: Universität Stuttgart, 2005

[本文引用: 3]

Schwaiger R, Kraft O.

Size effects in the fatigue behavior of thin Ag films

[J]. Acta Mater., 2003, 51: 195

DOI      URL     [本文引用: 2]

Stinville J C, Vanderesse N, Bridier F, et al.

High resolution mapping of strain localization near twin boundaries in a nickel-based superalloy

[J]. Acta Mater., 2015, 98: 29

DOI      URL     [本文引用: 2]

Stinville J C, Lenthe W C, Miao J, et al.

A combined grain scale elastic-plastic criterion for identification of fatigue crack initiation sites in a twin containing polycrystalline nickel-base superalloy

[J]. Acta Mater., 2016, 103: 461

DOI      URL     [本文引用: 1]

Stinville J C, Lenthe W C, Echlin M P, et al.

Microstructural statistics for fatigue crack initiation in polycrystalline nickel-base superalloys

[J]. Int. J. Fract., 2017, 208: 221

DOI      [本文引用: 2]

Dai C Y, Zhang G P, Yan C.

Size effects on tensile and fatigue behaviour of polycrystalline metal foils at the micrometer scale

[J]. Philos. Mag., 2011, 91: 932

DOI      URL     [本文引用: 1]

Judelewicz M.

Cyclic deformation of 100 μm thin polycrystalline copper foils

[J]. Scr. Metall. Mater., 1993, 29: 1463

DOI      URL    

Judelewicz M, Künzi H U, Merk N, et al.

Microstructural development during fatigue of copper foils 20-100 μm thick

[J]. Mater. Sci. Eng., 1994, A186: 135

Hong S, Weil R.

Low cycle fatigue of thin copper foils

[J]. Thin Solid Films, 1996, 283: 175

DOI      URL    

Kammuri K, Kitamura M, Fujii T, et al.

Effects of thickness and crystallographic orientation on fatigue life of single-crystalline copper foils

[J]. Mater. Trans., 2015, 56: 200

DOI      URL     [本文引用: 1]

Lavenstein S, Gu Y J, Madisetti D, et al.

The heterogeneity of persistent slip band nucleation and evolution in metals at the micrometer scale

[J]. Science, 2020, 370: eabb2690

DOI      URL     [本文引用: 1]

\n Metal fatigues when repeatedly loaded, ultimately failing when cracks form and propagate through the material. Lavenstein\n et al.\n studied the origins of this process in nickel. Using high-resolution observations, they tracked how dislocations evolved into microstructural features called persistent slip bands that preceded crack formation. The evolution of tangles of dislocations to a more regularly spaced pattern form the basis for the persistent slip bands and provide a road map for understanding fatigue cracking in metals.\n

Xu K N, Song Y C, Lu B, et al.

Design of ultrathin current collectors via cyclically plastic yield for fabrication of high capacity lithium ion batteries

[J]. J. Electrochem. Soc., 2020, 167: 110557

DOI      URL     [本文引用: 1]

Mughrabi H, Höppel H W.

Cyclic deformation and fatigue properties of very fine-grained metals and alloys

[J]. Int. J. Fatigue, 2010, 32: 1413

DOI      URL     [本文引用: 1]

Saitova L R, Höppel H W, Göken M, et al.

Cyclic deformation behavior and fatigue lives of ultrafine-grained Ti-6AL-4V ELI alloy for medical use

[J]. Int. J. Fatigue, 2009, 31: 322

DOI      URL     [本文引用: 1]

Hall E O.

Variation of hardness of metals with grain size

[J]. Nature, 1954, 173: 948

[本文引用: 1]

Murakami Y, Endo M.

Effects of defects, inclusions and inhomogeneities on fatigue strength

[J]. Int. J. Fatigue, 1994, 16: 163

DOI      URL     [本文引用: 1]

Cortes C, Vapnik V.

Support-vector networks

[J]. Mach. Learn., 1995, 20: 273

[本文引用: 1]

Ding S F, An Y X, Zhang X K, et al.

Wavelet twin support vector machines based on glowworm swarm optimization

[J]. Neurocomputing, 2017, 225: 157

DOI      URL     [本文引用: 1]

Zhou Z H. Machine Learning[M]. Beijing: Tsinghua University Press, 2016: 122

[本文引用: 2]

周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 122

[本文引用: 2]

Calzada M E, Scariano S M.

A synthetic control chart for the coefficient of variation

[J]. J. Stat. Comput. Sim., 2013, 83: 853

DOI      URL     [本文引用: 1]

Krishnamoorthy K, Lee M.

Improved tests for the equality of normal coefficients of variation

[J]. Computation. Stat., 2014, 29: 215

[本文引用: 1]

Chen H L, Luo X M, Wang D, et al.

Achieving very high cycle fatigue performance of Au thin films for flexible electronic applications

[J]. J. Mater. Sci. Technol., 2021, 89: 107

DOI      URL     [本文引用: 1]

Zhao P, Chen B, Kelleher J, et al.

High-cycle-fatigue induced continuous grain growth in ultrafine-grained titanium

[J]. Acta Mater., 2019, 174: 29

DOI      [本文引用: 1]

The cyclic deformation behaviour and microstructural stability of severe plastic deformation processed bulk nanostructured (ultrafine-grained, UFG) commercially pure cp-Ti were investigated by using in situ neutron diffraction combined with R = -1 high-cycle-fatigue (HCF) loading at room and cryogenic temperatures. The UFG microstructure was created by equal channel angular pressing (ECAP) and multi-direction forging (MDF). A considerable continuous grain growth was revealed by neutron diffraction for MDF cp-Ti fatigued at 25 degrees C, as opposed to that at -200 degrees C. The same HCF fatigue loading at 25 degrees C only caused very limited grain growth for ECAP cp-Ti. Transmission electron microscopy confirmed the grain growth. Further confirmation of the room-temperature HCF fatigue-induced grain growth was obtained by transmission Kikuchi diffraction based analysis. Novel insights into fatigue induced grain growth mechanism in UFG cp-Ti are thus provided: (i) the thermally activated process plays an important role in grain growth during the room-temperature HCF fatigue; (ii) Continuous dynamic recrystallisation is responsible for the grain growth and dislocation slip or twinning is not essential to trigger such a grain growth; (iii) the anisotropic grain growth behaviour in {0002} grain family can be reconciled by accepting that these grains accumulated highly stored energy during initial severe plastic deformation and the subsequent recrystallisation nucleation occurred at these highly deformed regions. (C) 2019 Acta Materialia Inc. Published by Elsevier Ltd.

Beretta S, Murakami Y.

Statistical analysis of defects for fatigue strength prediction and quality control of materials

[J]. Fatigue Fract. Eng. Mater. Struct., 1998, 21: 1049

DOI      URL     [本文引用: 1]

A wide range of studies and experimental evidence have shown that the lower bound of fatigue properties can be correctly predicted by considering the maximum occurring defect size. The estimate of this dimension can be done by analysing the defect sizes using the statistics of extremes.

El Haddad M H, Topper T H, Smith K N.

Prediction of non propagating cracks

[J]. Eng. Fract. Mech., 1979, 11: 573

DOI      URL     [本文引用: 1]

Herold H, Streitenberger M, Zinke M, et al.

An experimental and theoretical approach for an estimation of ΔKth

[J]. Fatigue Fract. Eng. Mater. Struct., 2000, 23: 805

DOI      URL     [本文引用: 1]

The existence of a fatigue threshold value may affect the design process when a damage‐tolerant design is considered that uses non‐destructive techniques for evaluating the shape and dimensions of the defects inside materials. Obviously it should be possible to estimate the stress field surrounding these defects and this is not generally a problem with modern numerical methods.

Pang J C, Li S X, Wang Z G, et al.

General relation between tensile strength and fatigue strength of metallic materials

[J]. Mater. Sci. Eng., 2013, A564: 331

[本文引用: 1]

Wang B B, Wu L H, Xue P, et al.

Improved high cycle fatigue property of ultrafine grained pure aluminum

[J]. Mater. Lett., 2020, 277: 128289

DOI      URL     [本文引用: 1]

Lee Y K, O'Keefe T J.

Evaluating and monitoring nucleation and growth in copper foil

[J]. JOM, 2002, 54(4): 37

[本文引用: 1]

Kondo K, Murakami H.

Crystal growth of electrolytic Cu foil

[J]. J. Electrochem. Soc., 2004, 151: C514

DOI      URL     [本文引用: 1]

Lin Y M, Yen S C.

Effects of additives and chelating agents on electroless copper plating

[J]. Appl. Surf. Sci., 2001, 178: 116

DOI      URL     [本文引用: 1]

Liao Z Y, Yang S T.

Analysis and discussion on effect factors of aluminum foil rolling process

[J]. Nonferrous Met. Process., 2014, 43(1): 21

[本文引用: 1]

廖志宇, 杨松涛.

铝箔轧制工艺影响因素的分析与探讨

[J]. 有色金属加工, 2014, 43(1): 21

[本文引用: 1]

Niu M, Zhao G H.

Effect of aluminium stock quality on aluminium foil rolling and aluminium foil quality

[J]. Light Alloy Fabr. Technol., 2003, 31(12): 20

[本文引用: 1]

牛 猛, 赵光辉.

铝箔毛料质量对铝箔轧制生产的影响

[J]. 轻合金加工技术, 2003, 31(12): 20

[本文引用: 1]

/

〈 〉


版权所有 © 《金属学报》编辑部
地址: 沈阳市文化路72号, 中国科学院金属研究所(110016)
电话: +86- 024-23971286 　E-mail: jsxb@imr.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发 技术支持：support@magtech.com.cn