随着温度的降低,水凝结成冰,这一司空见惯的现象正是自然界中最普遍的材料凝固过程。形核是材料凝固的起点,其对后续材料的组织形貌以及最终材料的服役性能具有决定性的影响。从水结冰到金属材料加工,从锂离子电池到药物制备,深入理解材料的凝固形核过程并对其进行调控是材料科学、物理、生物和地球科学等诸多自然科学领域最重要和最基础的研究课题之一。
受限于空间和时间分辨率,现有的实验手段难以从原子尺度对材料的凝固形核过程进行原位表征和分析。以分子动力学(molecular dynamics,MD)为代表的计算材料学方法在材料凝固形核研究领域发挥了举足轻重的作用。该方法基于经典力学和统计力学基本原理数值求解原子运动轨迹,可为研究材料的形核过程提供足够的时空分辨率。采用分子动力学进行材料凝固研究可追溯到20世纪中叶通用计算机发展的早期阶段。例如,1957年Alder和Wainwright[1~3]在UNIVAC计算机上使用分子动力学研究了硬球体系的凝固过程及相变热力学。随着计算机性能的不断提升和相关数值模拟算法的发展,分子动力学已被广泛应用于研究各种复杂体系的凝固行为。势函数在分子动力学中扮演着至关重要的角色,它描述了所模拟的系统中所有原子或分子间的相互作用,因此又常称为“力场”。传统的势函数一般是基于材料物理性质的实验数据,对经典或量子力学的简化模型进行参数拟合而得到的。这类势函数也常常被称为经验势函数。一般来说,经验势函数虽然计算效率较高,但缺乏足够的精度来描述凝固形核过程中的结构演化。1985年,Car和Parrinello[4]提出了计算第一性原理分子动力学的CPMD (Car-Parrinello Molecular Dynamics)方法。然而,CPMD等基于第一性原理的计算方法虽然精度较高,但高昂的计算成本使其无法进行大规模和长时间的模拟,因此无法广泛地应用于凝固形核研究。
机器学习(machine learning,ML)技术的迅猛发展为突破传统分子动力学模拟精度与效率的两难困境带来了新的希望,尤其是深度学习技术在科学领域的应用。基于神经网络(neural network,NN)的机器学习技术具有卓越的高维空间非线性建模能力和基于有限先验信息的强泛化能力,而这正契合当前分子动力学研究领域的需求。1995年Blank等[5]首次使用前馈神经网络拟合系统的势能面。之后各种类型的ML势函数蓬勃发展,2007年由Behler和Parrinello[6]提出的BPNN (Behler-Parrinello neural network)是其中最具代表性与影响力的方法。该方法将系统总能量分解为各个原子的能量之和,各原子的能量通过神经网络描述。Zeng等[7]和Wang等[8]在BPNN方法的基础上提出了DPNN (deep potential neutral network)方法,并开发了用于深度神经网络势函数(DP)分子动力学模拟的开源软件包DeePMD-kit。DP势的构建采用拟合第一性原理计算数据的方式,使其在计算构型能量与受力时精度能够达到第一性原理级别。近年来,DeePMD-kit在多种复杂体系中实现了高精度的建模与预测,已成功应用于如水[9,10]、金属材料[11,12]、陶瓷材料[13]电池材料[14]、溶液反应[15,16]等多个领域。
材料的凝固形核源于体系中自发结构起伏的累积效应,多数材料的形核现象从统计力学上可被视为一种“稀有事件”。因此,材料形核模拟研究的另一个挑战是如何实现超高维度构型空间中的跨时间尺度采样。为了突破稀有事件带来的采样难题,学者基于统计力学系综理论和Landau自由能理论,逐步发展了一系列增强采样(enhanced sampling)方法。增强采样方法通过调控系统各微观态的概率来提高分子模拟的采样效率,从而能够更准确地预测系统的宏观行为,使科研人员能够在可承受的计算成本内研究复杂系统的统计性特征。例如,增强采样方法的一个重要应用是在机器学习势函数的构建过程中,使用增强采样方法提高训练集的完备性,从而提高机器学习势函数对全局势能面的描述精度。近年来,国内外许多学者在设计增强采样方法时融合机器学习技术,一定程度上改善了稀有事件模拟所面临的精度与效率、时间尺度与空间尺度相互制约的困境,在材料相变、材料催化等领域得到了广泛应用。
本文首先回顾了形核理论、机器学习势函数、增强采样方法、形核序参量设计等领域的理论基础,然后综述了机器学习分子动力学在材料凝固形核研究中的最新应用案例,最后对该领域的未来发展进行了展望。
1 理论基础
1.1 形核理论
在凝固形核研究领域,经典形核理论(classical nucleation theory,CNT)是最基础、使用最广泛的理论。经典形核理论起源于对过冷条件下大气中过饱和水蒸气凝结过程的研究,经历Volmer等[17]、Farkas[18]、Becker等[19]、Zeldovich[20]等多位科学家的发展和完善,该理论已成为解释材料科学中各种凝固形核现象的基础理论框架。经典形核理论的基本假设是:形核过程的驱动力源于系统体自由能的减少,阻力为新相形成导致的界面能增加。若液相形核过程中自由能变为
式中,系数
式中,
式中,
式中,
值得说明的是,
经典形核理论的另一个不完善之处是完全忽略了液相动力学因素的影响。在预测形核率时经典形核理论假定形核是以原子为单元的Markov过程(Markov process)。然而,真实的形核过程往往十分复杂,而在非平衡如大过冷度的条件下液相动力学的重要性将更加凸显。例如,大过冷度条件下形核率较高,液相将出现大量小的晶胚,出现大晶核吞噬小晶胚现象的概率将大幅度增加,而这与经典形核理论的基本假设相违背。此外,大过冷度条件下的液相扩散被抑制,液相变得不再均匀,部分体系甚至会发生“条幅分解” (spinodal decomposition)[26]的现象,也即从均匀的单相状态自发分解成不混溶的多相。这些因素的综合作用致使晶核在不同方向上的生长展现出更加显著的差异性与随机性。这些现象已超过了经典形核理论框架所能涵盖的范畴,也彰显了对不同条件下凝固形核微观机制进行系统研究的必要性。
1.2 机器学习势函数
分子动力学的计算效率与模拟结果的精度直接依赖于选用的势函数,势函数的更新迭代贯穿分子动力学的发展历史。从最简单的硬球势[3,27],到描述非极性体系Pauli斥力与London力的Lennard-Jones (LJ)势[28,29],再到许多至今仍广泛使用的力场,如修正嵌入原子法(MEAM)[30,31]、Tersoff[32]、ReaxFF[33]等,这些采用经典的或量子的简化模型,基于实验数据拟合模型参数的势函数统称为经验势函数。一般来说,经验势函数计算效率高但精度较低。1965年,Kohn-Sham方程[34]的提出使基于密度泛函理论求解系统基态能量成为可能。密度泛函理论也随之得到广泛应用,2种基于密度泛函理论的第一性原理分子动力学(AIMD)方法先后被提出。1978年,Hiberty和Leforestier[35]提出的基于Born-Oppenheimer近似的分子动力学(BOMD)方法,通过自洽求解体系基态能量并计算原子受力。1985年,Car和Parrinello[4]提出CPMD方法。该方法在BOMD方法的基础上,将电子波函数视作独立的自由度,通过引入Lagrange乘子约束各电子波函数互相正交,从而避免了电子密度自洽计算。第一性原理分子动力学虽然计算精度高,但效率较低,难以满足长时间、大尺度凝固形核模拟研究的需求。
随着计算机科学的发展,人们提出使用机器学习势函数(machine learning potentials)来描述原子间的相互作用。机器学习方法能够精准拟合高维输入数据与输出数据间的高度非线性关系,通过拟合大量第一性原理计算数据,其精度能够达到或接近第一性原理级别,同时其计算成本显著低于自洽迭代计算。尽管机器学习势函数是受益于近年来计算机算力、人工智能技术的迅猛发展才取得重大进步并得到广泛应用的,其基本思想及方法却可以追溯到20世纪末。例如,1994年Ercolessi和Adams[36]通过拟合大量第一性原理计算数据来优化经典力场中的参数,获得了“与第一性原理计算精度相当的经验势函数”。1995年,Blank等[5]首次使用神经网络替代解析函数对势能面进行拟合。早期的神经网络势函数定制化地针对特定体系和自由度进行训练,尚未形成一套通用的训练流程。
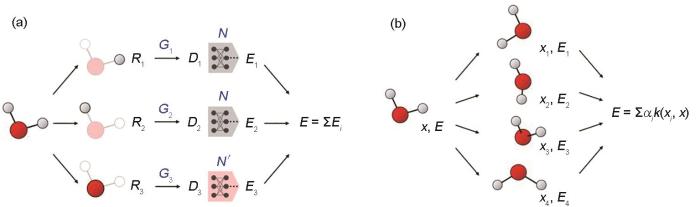
2007年,Behler和Parrinello[6]提出BPNN方法,其原理如图1a所示。BPNN采用了具有旋转不变性的中心原子对称函数,描述各原子与其近邻环境内原子的两体或多体相互作用,并作为神经网络的输入计算每个原子的能量,然后将体系内各个原子的能量进行加和得到体系总能量,原子的受力通过神经网络的反向求导获得。BPNN的架构使其天然满足平移、旋转、置换不变性,并具有一定的迁移能力与可扩展性。2018年,Zhang等[37]对BPNN方法进行了改进,提出了DPNN方法。该方法直接将描述各原子近邻环境的“描述符”(descriptor)作为神经网络的输入计算各原子的能量。同年,用于DPNN势函数构建的开源软件包DeePMD-kit发布。该软件包提供了一套完整的神经网络势函数通用训练框架以及工具集,包括数据集转化,模型的训练、验证、压缩等功能,同时可以与主流分子动力学软件如LAMMPS、GROMACS等联用并通过图形处理器(GPU)加速模型推导。2020年,该团队成功进行了上亿个Cu原子体系和H2O分子体系的分子动力学模拟,并获得了同年的戈登-贝尔奖(Gordon Bell Prize)[38]。2022年,该团队进一步提出了考虑长程静电相互作用的机器学习势函数模型[39]。该方法使用第一性原理计算得到的最大局域化Wannier函数(maximally localized Wannier function)信息,构建神经网络模型预测Wannier核的位置,从而获得分子偶极矩,再通过Ewald求和计算长程的的Coulomb相互作用。系统的总能量为短程项(由原始的神经网络势函数计算)与长程项之和。
图1
图1
机器学习势函数原理示意图
Fig.1
Principles of machine learning potential
(a) Behler-Parrinello neural network (BPNN) (The subscript
(b) machine learning potential based on the kernel method (x is the environmental matrix; xi and Ei are the i-th reference configuration in the training set and the corresponding energy, respectively; αi is the i-th fitting coefficient; k
另一类广泛应用的机器学习势函数基于核方法(kernel method),其原理如图1b所示。与BPNN类似,这种方法同样针对每个原子的近邻环境构建具有对称性的描述符,但不直接将描述符输入神经网络进行训练,而是借助描述符构建核函数评估各原子局域环境与训练集中结构的相似程度,进而通过插值方法计算每个原子的能量,再对所有原子求和得到体系总能量。相较于神经网络势函数的训练,核方法超参数数量较少,实现较简单,模型的可解释性更强。但是,核方法模型推理的时间复杂度随训练集增大而增加,这一特点限制了训练集的规模,使其无法发挥大规模数据的优势。著名的商业第一性原理计算软件VASP (Vienna ab initio simulation package)在其AIMD模块中,集成了基于SOAP (smooth overlap atomic positions)[40]的核方法,旨在显著提升AIMD计算效率[41~43]。模拟过程中,使用Bayes回归分析[44]的方法评估模型预测误差,并动态地调整模型的训练集。
在任何机器学习技术的相关应用中,训练集无疑都扮演着至关重要的角色,是确保模型准确性和泛化能力的核心要素。机器学习势函数依赖于训练集,训练集自身的精度以及构型的完备性决定了机器学习势函数的质量。在构建机器学习势函数时,一般使用已知的热力学稳定或亚稳相以及高精度的第一性原理分子动力学采样数据作为训练集。然而,包括凝固形核在内的相变过程往往是热力学上的稀有事件,基于这种方法获得的训练集难以覆盖相变路径上各种高能的中间态的结构特征,如液固共存结构等,因此难以精准地描述整个分子动力学模拟过程。为了解决这一问题,常用的策略是基于主动学习(active learning)的基本思想,对训练集和势函数进行迭代优化。例如,在神经网络势函数并行训练框架DP-Gen[45]中就使用了“委员会质询” (Query by Committee)的方法。其原理可概述为:使用相同训练集训练多个势函数,使用其中一个进行分子动力学模拟,所有势函数同时对模拟过程中采样获得的构型进行能量预测,筛选出不确定度在一定范围内的构型(不确定度过大的构型往往是不合理构型),作为当前势函数预测较差的候选构型加入训练集,最后使用新的训练集训练下一代势函数。此外,在主动学习过程中可结合“增强采样”方法,基于第一性原理计算或已有的势函数,通过提高模拟过程中高能中间态的出现概率加速探索相空间,获得更完备的训练集并训练新一代神经网络势函数。然后,按类似的步骤迭代优化训练集,直至训练获得的势函数满足精度要求。增强采样方法相关内容将在下一节中介绍。
1.3 增强采样方法
由于Boltzmann因子具有自然指数的形式,材料凝固形核的能垒每线性提高一个
目前常用的采样方法大致可分为3类。第一类方法基于Landau自由能理论,通过对系统额外施加依赖于集合变量(collective variable,CV)的偏势(bias),使系统各态的出现概率服从预设的目标分布[46]。偏势可通过下式表达:
式中,
式中,
第二类方法通过构造“扩展系综”进行增强采样。扩展系综包含多个常规的子系综,各子系综具有不同的热力学参量。扩展系综微观态的概率分布等于各子系综对应微观态概率分布之和。由于不同条件下系统的微观态服从不同的概率分布,扩展系综在不损失子系综热力学信息的情况下,将各微观态出现的概率进行叠加与归一化。该类方法的代表有副本交换法 (replica exchange molecular dynamics,REMD)[49]、温度积分采样法 (integrated tempering sampling,ITS)[39]等。副本交换法对同一个系统创建多个副本,然后并行地在不同条件下对这些副本进行模拟。每隔一定步数,各副本之间通过一定准则交换各自的微观态信息。交换准则需要满足细致平衡原理,例如,Metropolis-Hastings准则是最常用的准则之一。副本交换法中每个副本显式地对应一个子系综,所有副本共同构成扩展系综。2008年,Gao[50]提出的温度积分采样法在扩展系综的构建思路上则有所不同。温度积分采样法通过对系统施加依赖于系统能量的偏势,直接使系统的微观态概率分布满足扩展系综概率分布。这意味着通过一次模拟即可获得多个不同条件下系统的热力学信息。值得说明的是,基于扩展系综的加速采样方法也可视为将体系微观态的势能等视作“集合变量”构造偏势。势能是系统中所有相互作用的综合反映,基于势能的偏势将对系统的全部自由度进行增强。2018年,Yang等[51]提出了MetaITS方法,该方法综合了第一类与第二类方法的优势,在构建扩展系综时对各子系综使用Metadynamics方法进行增强采样,从而实现了同时对特定集合变量与全局自由度的加速采样。
第三类方法通过构造反应路径系综(transition path ensemble)实现针对特定反应过程的充分采样。反应路径系综是大量连结反应物与产物的完整反应轨迹的集合。该类方法虽然依赖于一个给定的集合变量(该方法中常称反应坐标),用以鉴别反应物与产物并衡量反应进程,但不施加任何基于集合变量的偏势。1998年Dellago等[52]提出的过渡路径采样(transition path sampling,TPS)和2006年Allan等[53,54]提出的正向通量采样(forward flux sampling,FFS)是该类方法的代表。这2种方法的区别在于反应路径系综的构造方式:过渡路径采样方法通过Monte Carlo算法反复对当前轨迹上的微观态进行微调以获得新轨迹;正向通量采样方法将整个反应分为多个阶段,然后构建连结各阶段的大量模拟轨迹。与前2类方法不同,基于反应路径系综的方法集合变量仅用作区分结构的标识,因此不会歪曲相变过程中微观结构的本征演化行为。由于系统本身的动力学特征得以保留,在路径系综的采样过程中可基于过渡态理论(transition state theory,TST)直接计算反应速率(如形核率)。
受近年来飞速发展的机器学习技术的启发,在增强采样方法中融合机器学习算法成为该领域发展的主要方向之一。机器学习算法旨在通过有限的数据集构建全局预测模型,而相变模拟研究中采样的核心目标之一是基于有限的采样数据获得相变全局构型空间的热力学信息,这2者之间具有一定的相似性。2014年,Valsson和Parrinello[59]提出的变分增强采样方法(variational enhanced sampling,VES)利用KL散度(Kullback-Leibler divergence)评估施加偏势后采样获得的数据分布与预设目标分布之间的差异,并将该散度作为损失函数关于偏势的泛函从而对偏势进行迭代优化。这种自主迭代优化的策略体现了机器学习中强化学习的基本思想。但是,在优化过程中,KL散度对于未采样区域可能出现非对称和梯度爆炸等问题,这导致了在部分情况下该方法稳定性较差。2019年,Zhang等[60]在变分增强采样方法的基础上提出了TALOS (targeted adversarial learning optimized sampling)方法。该方法使用推土机距离(earth mover's distance,EMD)作为分布差异的量度,引入生成对抗神经网络(generative adversarial network,GAN),将施加偏势的分子动力学模拟视作产生“假”数据的生成器,并以对抗的形式迭代优化鉴别器(discriminator)和偏势,当偏势使系统满足目标分布时2者优化过程的对抗达到纳什均衡(Nash equilibrium)。TALOS方法所采用的推土机距离相比KL散度拥有更好的连续性和鲁棒性,算法的收敛能力因此得到显著提升。
1.4 形核序参量
材料的凝固形核过程伴随着原子构型的重构,这一过程系统的自由度数量显然是巨大的。如何将与形核过程无关的大量自由度剔除,进而解析出真实的形核路径,是从微观尺度研究并理解材料凝固形核过程的关键之一。在原子模拟领域,常使用特定“序参量”作为研究对象。序参量是高维构型空间在低维流形上的投影,是为规避相变过程中高维问题的复杂性而采用的数学简化手段。这里需要额外说明的是,虽然“序参量”这一概念在相变理论中具有更加明确的物理意义,而“集合变量”仅仅是数学上的概念,在许多文献中常常把“序参量”和“集合变量”2个定义混用,也即任何集合变量都可以当作序参量使用。
在实际模拟研究中,解析或构建体系的形核序参量主要起到以下3方面的作用:(1) 对体系进行降维,简化信息,挖掘隐藏在高维构型空间背后的本质物理特征;(2) 对凝固相变前后及相变过程中原子的结构类型进行判定;(3) 在增强采样方法中作为一种导向因子引导体系的相变。换句话说,序参量(或集合变量)既是相结构特征的反映,也可作为“反应坐标”衡量形核进度。在以Metadynamics及伞型采样(umbrella sampling)为代表的增强采样方法中,其成功的核心在于选取一个能正确描述反应路径的序参量。良好的序参量可以提高采样效率,促使模拟更好地遍历相空间。但若选择了不合适的序参量,可能获得与客观事实不符的相变轨迹,甚至误导对相变机理的分析。在对研究体系先验信息受限的情况下,探索并设计出能正确反映原子重构过程的序参量一直是凝固形核模拟领域的研究热点。
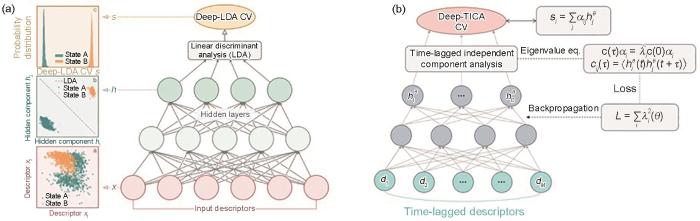
在对凝固过程微观机理了解受限的情况下,想要设计出合适的形核序参量绝非易事。上述经典的序参量虽然具有清晰的物理意义,但可能无法捕捉一些较为复杂的相变行为,且非常依赖于研究人员的物理直觉和研究体系的具体特征。近年来,一些学者借助机器学习技术基于有限先验信息的泛化能力,结合已知的凝固行为特征,通过机器学习算法将常用的序参量进行组合并获得新的序参量。例如,2018年,Mendels等[74]提出,基于相变已知的初态和末态结构信息,使用监督学习线性判别分析(linear discriminant analysis,LDA)算法,将多种常用序参量进行线性组合,可获得可良好区分相变初态与末态的新序参量。在该方法的基础上,2020年,Bonati等[75]提出了Deep-LDA算法,利用深度神经网络实现多种常用序参量的非线性组合。如图2a[75]所示,Deep-LDA以多种序参量作为输入经过神经网络映射后执行LDA分析,然后根据Fisher准则对神经网络进行优化。
图2
Fig.2
Machine learning to aid design of nucleation order parameters[75] (
LDA方法构造序参量的过程中未考虑任何中间体和过渡态信息,因此也无法保证能准确描述凝固过程。从热力学角度来看,最优的形核序参量应具有最大的涨落和发生凝固相变最小的代价。基于这一思想,2011年,Naritomi和Fuchigami[76]提出可使用时滞独立成分分析(time-lagged independent component analysis,TICA)算法,获得已知相变轨迹中自时间关联最强的集合变量线性组合。2021年,Bonati等[77]基于TICA算法与深度神经网络实现了非线性的Deep-TICA算法(图2b[77])。在实际应用中,使用Deep-LDA方法构建的形核序参量在区分凝固的初态和末态方面表现出色,但对中间态的识别存在较大的不稳定性,而使用Deep-TICA方法构建的形核序参量常常能呈线性相关地描述整个凝固过程。
2 典型应用
本节选取几个具有代表性的体系,介绍近期机器学习分子动力学在凝固形核研究方面取得的重要进展。
2.1 硒化镉(CdSe)结晶机制研究
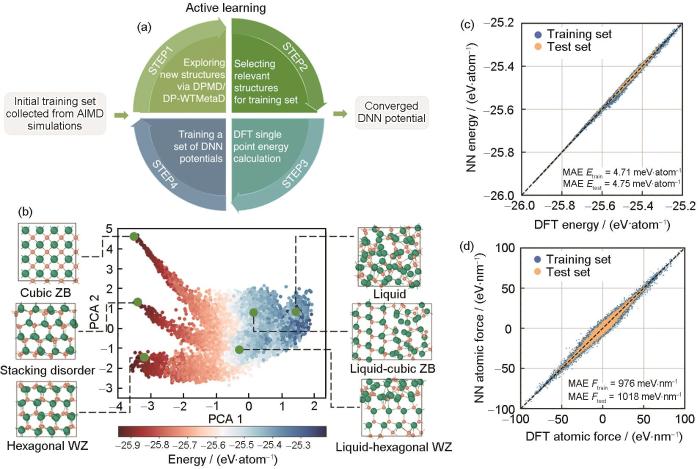
CdSe的化学键同时具有离子性和共价性特征,相互作用力复杂。为进行高精度的分子动力学形核模拟,Zhang等[69]融合增强采样方法和主动学习策略,构建了具有第一性原理精度的深度神经网络势函数(如图3a[69])。首先,使用第一性原理分子动力学获取初始训练集,构建初代神经网络势函数。然后,基于该势函数进行增强采样分子动力学模拟,获得大量液/固相变路径上的重要中间态构型。将上述获得的构型进行主成分分析(principal component analysis,PCA,图3b[69]),筛选具有代表性的结构加入训练集,并训练获得下一代势函数。按照相似的策略迭代优化训练集,使训练集逐步涵盖CdSe液/固相变过程中系统的所有结构特征。对于每一代势函数,以第一性原理计算结果作为参考评估其计算体系能量与受力信息的均方根误差,最终获得的CdSe深度神经网络势函数的精度如图3c和d[69]所示。作者基于构建的深度神经网络势函数对CdSe的结晶过程进行了分子动力学模拟。通过对形核轨迹的分析,揭示了CdSe的结晶过程中六方纤锌矿与立方闪锌矿之间存在竞争关系,这种竞争关系受温度的影响。随着温度接近熔点,结晶倾向于形成六方纤锌矿结构。进一步分析发现,Cd原子与Se原子在凝固过程中的动力学行为存在显著差异,Se原子的中程有序性在CdSe的结晶过程起着主导作用。Se原子因其迁移能力较低,在凝固过程中先行形成稳定的四面体结构,随后Cd原子逐步填充这些四面体的中心,直至Se原子的第三配位层原子占据合适的晶格位点,最终实现凝固结晶。
图3
图3
CdSe结晶机制的研究[69]
Fig.3
Research on the nucleation mechanism of CdSe[69]
(a) flowchart of the active learning procedure to train the deep neural network (DNN) potential (AIMD—ab initio molecular dynamics, DPMD/DP-WTMetaD—DNN-based molecular dynamics (DPMD) simulations and their variants accelerated by WTMetaD (DP-WTMetaD), DFT—density functional theory)
(b) distribution of training set configurations in the two-dimensional space mapped with the principal component analysis (PCA) (Typical structures are marked in the plot. Green and brown spheres are Se and Cd, respectively. ZB—zinc blende, WZ—wurtzite)
(c, d) error of the DNN potential relative to the DFT calculation. The values of mean absolute error (MAE) correspond to the potential energy (E) (c) and the force (F) (d) are stamped in the plot[69] (NN—neural network)
2.2 Si的凝固形核过程模拟研究
Si作为一种极其重要的材料,在半导体等许多领域中发挥着重要作用。由于Si在固体状态下具有半导体性质,在液体状态下具有金属性质[83],传统的经验力场难以精确描述Si的奇特性质,这使得其凝固形核过程的模拟长期以来面临困难。
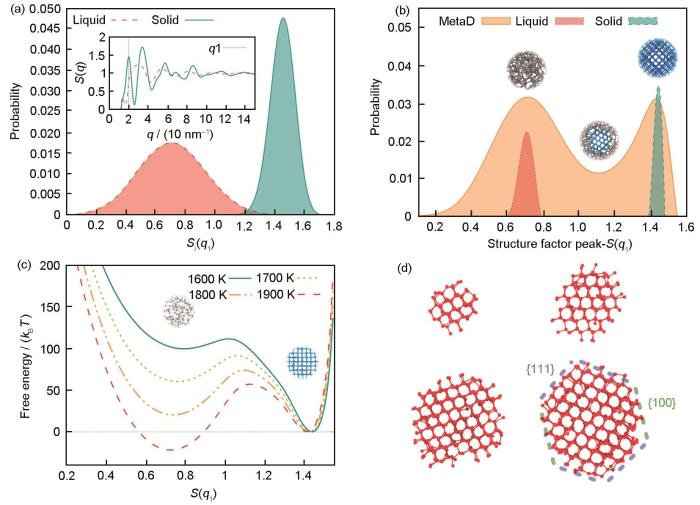
近期,Bonati和Parrinello[66]基于机器学习方法,构建了能够以第一性原理精度同时描述Si的固相、液相和液/固界面结构的神经网络势函数。由于Si的形核能垒较高,作者采用Niu等[62]提出的X射线衍射(XRD)强度作为形核序参量,并结合Well-Tempered Metadynamics方法进行增强采样模拟。如图4a[66]所示,该形核序参量能够很好地分辨模拟体系中液相和固相Si原子。作者首先对小体系的Si进行了增强采样模拟以获取轨迹中的固/液共存构型并将其加入训练集,以完备训练集并获得高精度的神经网络势函数。图4b[66]对比了纯固相模拟、纯液相模拟以及增强采样模拟中采样获得的序参量分布图,由图可见增强采样模拟中已充分采集到了液/固相变过程的中间态构型。此外,作者通过增强采样方法计算了熔点附近多个温度下的液/固相变自由能面,其结果如图4c[66]所示。图4d[66]中展示了增强采样模拟中获得的Si晶核形貌。
图4
图4
Si的凝固形核过程模拟研究[66]
Fig.4
Research on the nucleation process of Si[66]
(a) distributions of the order parameters using local structure factor Si (q1) in the liquid and solid phase (Inset shows the structure factor patterns and the position of the module of the wave number
(b) distributions of the configurations as a function of the structure factor at the first peak in well-tempered sampling, liquid phase, and solid phase, respectively (Insets present the typical configuration, whose structure factor peak corresponds to the position of abscissa. Disordered configurations are colored in grey, and ordered ones, i.e., ice-like structures, are colored in blue. The same applies to Fig.4c)
(c) free energy surface of the solidification at different temperatures (kB—Boltzmann constant, T—temperature)
(d) snapshots of Si nuclei
2.3 水结冰过程的原子尺度计算模拟实现及机制研究
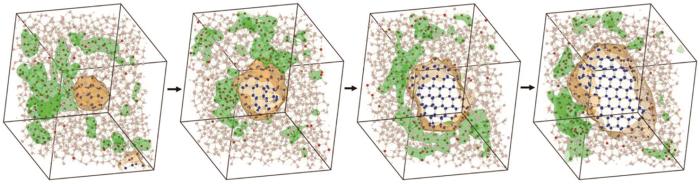
水结冰的现象在地球上随处可见,该过程与材料学、凝聚态物理、航空航天、气象学和生物学等诸多领域息息相关[84]。然而,由于水中H键网络的复杂性及液/固相变的高能垒,如何实现原子尺度下水结冰过程的计算模拟被认为是水科学研究领域的重要难题。水科学及计算科学领域的Matsumoto等[85]、Tanaka[86]、Bullock等[87]、Moore等[88]、Fitzner等[89]、Niu等[70]和Haji-Akbari等[90]在研究工作中对水结冰的微观图景形成了一定共识:冰于水中较为有序的区域中产生,这种“较为有序的区域”具有长寿命H键、高四面体度和低流动性的特征。然而,这一图景没有从根本上解答水的H键网络如何重构成有序的冰这一关键科学问题。而且,长久以来人们采用的经验水模型对复杂的分子内和分子间相互作用有所简化,难以准确描述水的结构和动力学特性。近期,Chen等[91]使用深度神经网络水模型,采用正向通量采样方法实现了具有第一性原理精度的水凝固形核过程分子动力学模拟,经过对所获得的大量凝固轨迹的统计性分析,发现高流动性和低流动性H2O分子存在显著的聚集性特征,也即过冷水的动力学特征表现出空间分布上的异质性。过冷水中低流动性区域H键网络结构稳定,这阻碍了水的液/固相变过程。反之,高流动性区域H键网络剧烈重构,这既可以使冰形核生长,又可以使已形成的冰核消融。进一步分析发现,过冷水中的动力学异质性源于其结构异质性。依据H键配位情况,H2O分子可分为完美配位(perfectly coordinated,PC)和非完美配位(imperfectly coordinated,IC) 2类。非完美配位H2O分子因其近邻环境不稳定,活性较高,因此主导了高流动性区域的形成。与之对应,低流动性区域则以完美配位H2O分子为主。为理解非完美配位H2O分子重构H键网络的微观机制,对所获得晶核的所有六元环形成过程进行了追踪分析,发现非完美配位H2O分子在其形成、转移和湮灭过程中促使无序的液态H2O重构为有序的冰(如图5[91]所示),也就是非完美的H2O分子造就了完美的冰。
图5
图5
第一性原理精度的水均质形核过程分子动力学模拟[91]
Fig.5
Molecular dynamics simulation of the homogeneous ice nucleation with ab-initio accuracy[91] (The areas wrapped in orange are the ice nuclei. The areas wrapped in green are high-mobile regions. Solid-like, liquid-like, and imperfect coordinated water molecules are colored in blue, pink, and red, respectively)
通过上述分析可发现,与传统水结冰微观图景不同,水并不是在低流动性的“较为有序的区域”孕育形核,而是在低流动性和高流动性区域共同作用下形核长大。其中,H2O的结构异质性是决定其凝固行为的关键因素。完美配位和非完美配位H2O分子都扮演着“双面性”的角色:高活性的非完美配位H2O分子主导了H键网络的重构,既可以促进晶核生长,又能使晶核融化;完美配位H2O分子较稳定,既能保护已经形成的晶核,又阻碍了晶核的继续长大。2种H2O分子的共同作用下造就了冰晶核尺寸和形貌在长大过程中存在大幅动态波动的奇异凝固特性。
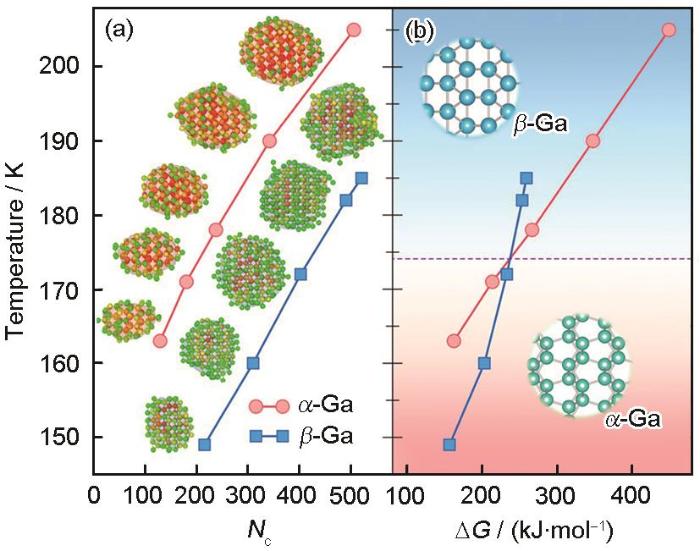
2.4 金属Ga凝固形核的竞争机制
图6
2.5 碳酸钙球霰石相的晶体结构解析
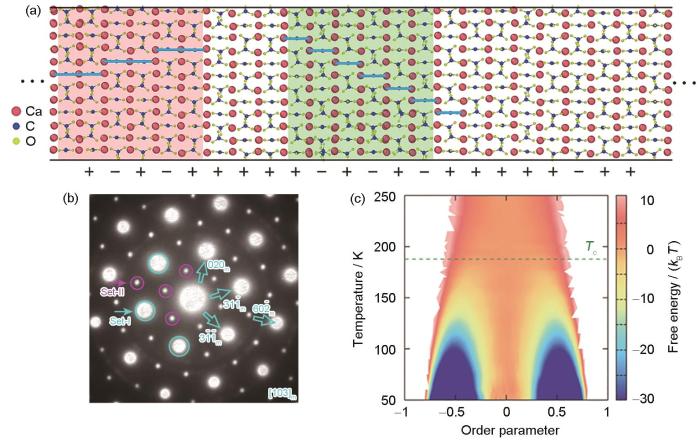
碳酸钙(CaCO3)是生物矿物系统中储量最为丰富的天然物质之一。球霰石(vaterite)是碳酸钙的3种同质异形体之一,在自然界中常作为CaCO3的无定形相向稳定相转变过程中的过渡相,或以生物体组织的形式出现。然而,实验观测显示球霰石相中可能存在堆垛无序结构,这为解析该相的晶体结构带来了困难。研究人员对球霰石的晶体结构已争论了将近一个世纪仍未达成共识。
图7
图7
碳酸钙球霰石相的晶体结构解析[102]
Fig.7
Research on crystal structure of vaterite CaCO3[102]
(a) theoretically grown vaterite with an intergrowth of different polytypic structures (The symbols “+” and “-” inserted indicate the stacking sequences of carbonate layers)
(b) selected area electron diffraction (SAED) pattern of vaterite along [103]m,where the subscript letter “m” denotes the monolithic crystal system
(c) two-dimensional free energy surface of vaterite as a function of order parameter and temperature
3 总结与展望
近十年来,机器学习与材料凝固形核模拟研究实现了多角度、多方位的深度融合。首先是机器学习势函数的出现与相关软件工具的发展,为解决传统分子动力学模拟所面临的精度与效率的两难问题带来了希望。与此同时,基于增强采样方法的先进分子动力学方法与机器学习技术相结合,一方面有力推动了机器学习势函数训练集的精细化构建,另一方面凝固形核过程的先验规律和知识经由数据驱动融入增强采样的核心流程,从而显著提升了机器学习势函数与增强采样方法在各类应用情形下的准确性和可靠性。“机器学习+分子动力学+增强采样”已成为目前典型的材料形核模拟研究范式之一。
当下,各种新兴机器学习技术仍在蓬勃发展,凝固形核及相变模拟研究领域也在不断吸收着新鲜的血液。例如,通过将注意力机制(attention)引入机器学习势函数,显著提高了势函数对多组元复杂体系的描述能力。不仅如此,机器学习领域的预训练模型与大模型等理念也开始影响分子动力学领域,其代表性工作如DPA-2原子大模型[103]。在硬件方面,如FPGA (field programmable gate array)[104]等加速机器学习模型推理的新型硬件架构的出现,将允许更长时间、更大尺度的计算模拟。此外,针对不同体系的各类高质量数据库也在紧锣密鼓地筹备当中[105]。2023年,DeepModeling社区发布“大原子模型计划(OpenLAM)”,以“征服元素周期表”为目标,旨在建立全球材料科研人员共享的大型微观模型开放生态系统[106]。软件、硬件、数据、社区多方面齐头推进,共同致力于完善AI for Science (AI4S)的基础设施建设。
但是,受限于当前的认知水平,机器学习势函数可靠性的证明以及误差的严格评估仍存在一定困难。将严谨的物理模型融入机器学习势函数,以提升模型的可靠性与可解释性,正是当前领域发展的热门方向之一。另外,目前机器学习势函数训练数据全部基于第一性原理计算获得,而泛函本身的误差可能导致第一性原理计算自身的结果与真实情况存在差异。近期,已有学者考虑在机器学习势函数的构建过程中拟合宏观统计量,但在实际操作时要达到令人满意的拟合效果尚需进一步深入研究。
再者,虽然目前机器学习技术已经广泛应用于增强采样中偏势的构造和序参量的设计,但在可靠性方面仍面临诸多棘手的挑战。基于机器学习方法构建的序参量虽然在区分凝固相变过程的始态和终态已达到了良好的效果,但是无法保证其能同样良好地识别过渡态结构。值得注意的是,神经网络的引入导致序参量的表示形式变得复杂,通过偏势所额外引入的力的影响也将更加不可控,甚至扭曲系统原有的动力学特征。另一方面,在使用机器学习构造偏势时,高度依赖于对原有自由能面的评估。然而,由于采样数据数量有限,以小样本评估全局分布极为困难。对于这些问题,当前备受关注的小样本学习和零样本学习领域相关前沿技术,可能为解决机器学习技术在材料凝固模拟中数据稀缺性和泛化能力的难题提供新的思路和方法。
除了本文重点讨论的典型凝固形核问题和实际应用体系以外,在材料科学、凝聚态物理领域依然存在诸多其他重要问题亟待深入研究。这些问题包括但不限于:多元复杂体系的形核现象;杂质或掺杂原子、多物理场(如电场、磁场、声场)耦合以及溶液-表界面相互作用等条件对形核过程的影响;原子尺度上的凝固形核与介观尺度上材料组织形成之间的内在关联等。这些问题所涉及的采样空间更为复杂,时空尺度壁垒难题更加突出。然而,随着从微观至宏观层面机器学习物理模型的日趋成熟,以及新型先进采样技术的持续发展,克服这些多尺度难题正逐渐成为可能。
总体来说,在将机器学习应用于材料凝固形核模拟研究的过程中,尽管已经取得了显著进展,但相较于传统的根植于物理原理的方法,其内在的物理机制诠释尚存在一定的不足,这意味着机器学习构建的力场模型在预测系统的热动力学性质时,并不能确保其绝对优于依赖实验观测数据所建立的经验力场模型。这一局限性构成了当前学术界部分研究者针对机器学习方法在分子动力学模拟领域应用的关键争议焦点。但毋庸置疑的是,机器学习以及增强采样方法为应对相空间的高维复杂性、跨越时空尺度壁垒以及挖掘潜在物理规律方面提供了一套普适性的解决方案。其展现出的潜力正不断激励着科研人员去探索更先进的算法框架,以进一步扩宽现有分子动力学方法的应用范畴。因此,深化机器学习算法在物理机制层面上的理解与融合,进而弥合理论认知与实践应用之间的鸿沟,已成为该领域内学者们集中攻克并亟待突破的关键课题之一。相关研究将对推动实现更高精度、更高效率的材料仿真模拟,以及引导凝固工艺、材料设计等领域迈向智能化的新时代,具有深远的现实意义。
参考文献
Studies in molecular dynamics. III. A mixture of hard spheres
[J].
Studies in molecular dynamics. I. General method
[J].
Phase transition for a hard sphere system
[J].
Unified approach for molecular dynamics and density-functional theory
[J].
Neural network models of potential energy surfaces
[J].
Generalized neural-network representation of high-dimensional potential-energy surfaces
[J].
DeePMD-kit v2: A software package for deep potential models
[J].
DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics
[J].
Phase diagram of a deep potential water model
[J].
Anomalous thermal transport across the superionic transition in ice
[J].
Electronically driven 1D cooperative diffusion in a simple cubic crystal
[J].
Data-driven prediction of complex crystal structures of dense lithium
[J].Lithium (Li) is a prototypical simple metal at ambient conditions, but exhibits remarkable changes in structural and electronic properties under compression. There has been intense debate about the structure of dense Li, and recent experiments offered fresh evidence for yet undetermined crystalline phases near the enigmatic melting minimum region in the pressure-temperature phase diagram of Li. Here, we report on an extensive exploration of the energy landscape of Li using an advanced crystal structure search method combined with a machine-learning approach, which greatly expands the scale of structure search, leading to the prediction of four complex Li crystal structures containing up to 192 atoms in the unit cell that are energetically competitive with known Li structures. These findings provide a viable solution to the observed yet unidentified crystalline phases of Li, and showcase the predictive power of the global structure search method for discovering complex crystal structures in conjunction with accurate machine learning potentials.© 2023. The Author(s).
Microstructure evolution under thermo-mechanical operating of rocksalt-structure TiN via neural network potential
[J].
Impact of the local environment on Li ion transport in inorganic components of solid electrolyte interphases
[J].The spontaneously formed passivation layer, the solid electrolyte interphase (SEI) between the electrode and electrolyte, is crucial to the performance and durability of Li ion batteries. However, the Li ion transport mechanism in the major inorganic components of the SEI (LiCO and LiF) is still unclear. Particularly, whether introducing an amorphous environment is beneficial for improving the Li ion diffusivity is under debate. Here, we investigate the Li ion diffusion mechanism in amorphous LiF and LiCO via machine-learning-potential-assisted molecular dynamics simulations. Our results show that the Li ion diffusivity in LiF at room temperature cannot be accurately captured by the Arrhenius extrapolation from the high temperature (>600 K) diffusivities (difference of ∼2 orders of magnitude). We reveal that the spontaneous formation of Li-F regular tetrahedrons at low temperatures (<500 K) leads to an extremely low Li ion diffusivity, suggesting that designing an amorphous bulk LiF-based SEI cannot help with the Li ion transport. We further show the critical role of LiCO in suppressing the Li-F regular tetrahedron formation when these two components of SEIs are mixed. Overall, our work provides atomic insights into the impact of the local environment on Li ion diffusion in the major SEI components and suggests that suppressing the formation of large-sized bulk-phase LiF might be critical to improve battery performance.
Development of range-corrected deep learning potentials for fast, accurate quantum mechanical/molecular mechanical simulations of chemical reactions in solution
[J].We develop a new deep potential-range correction (DPRc) machine learning potential for combined quantum mechanical/molecular mechanical (QM/MM) simulations of chemical reactions in the condensed phase. The new range correction enables short-ranged QM/MM interactions to be tuned for higher accuracy, and the correction smoothly vanishes within a specified cutoff. We further develop an active learning procedure for robust neural network training. We test the DPRc model and training procedure against a series of six nonenzymatic phosphoryl transfer reactions in solution that are important in mechanistic studies of RNA-cleaving enzymes. Specifically, we apply DPRc corrections to a base QM model and test its ability to reproduce free-energy profiles generated from a target QM model. We perform these comparisons using the MNDO/d and DFTB2 semiempirical models because they differ in the way they treat orbital orthogonalization and electrostatics and produce free-energy profiles which differ significantly from each other, thereby providing us a rigorous stress test for the DPRc model and training procedure. The comparisons show that accurate reproduction of the free-energy profiles requires correction of the QM/MM interactions out to 6 Å. We further find that the model's initial training benefits from generating data from temperature replica exchange simulations and including high-temperature configurations into the fitting procedure, so the resulting models are trained to properly avoid high-energy regions. A single DPRc model was trained to reproduce four different reactions and yielded good agreement with the free-energy profiles made from the target QM/MM simulations. The DPRc model was further demonstrated to be transferable to 2D free-energy surfaces and 1D free-energy profiles that were not explicitly considered in the training. Examination of the computational performance of the DPRc model showed that it was fairly slow when run on CPUs but was sped up almost 100-fold when using NVIDIA V100 GPUs, resulting in almost negligible overhead. The new DPRc model and training procedure provide a potentially powerful new tool for the creation of next-generation QM/MM potentials for a wide spectrum of free-energy applications ranging from drug discovery to enzyme design.
Accelerated computation of free energy profile at ab initio quantum mechanical/molecular mechanics accuracy via a semi-empirical reference potential. I. Weighted thermodynamics perturbation
[J].Free energy profile (FE Profile) is an essential quantity for the estimation of reaction rate and the validation of reaction mechanism. For chemical reactions in condensed phase or enzymatic reactions, the computation of FE profile at the ab initio (ai) quantum mechanical/molecular mechanics (QM/MM) level is still far too expensive. Although semiempirical (SE) method can be hundreds or thousands of times faster than the ai methods, the accuracy of SE methods is often unsatisfactory due to the approximations that have been adopted in these methods. In this work, we propose a new method termed MBAR+wTP in which the ai QM/MM free energy profile is computed by a weighted thermodynamic perturbation (TP) correction to the SE profile generated by the multistate Bennett acceptance ratio (MBAR) analysis of the trajectories from umbrella samplings (US). The weight factors used in the TP calculations are a byproduct of the MBAR analysis in the postprocessing of the US trajectories, which are often discarded after the free energy calculations. The raw ai QM/MM free energy profile is then smoothed using Gaussian process regression in which the noise of each datum is set to be inversely proportional to the exponential of the reweighting entropy. The results show that this approach can enhance the efficiency of ai FE profile calculations by several orders of magnitude with only a slight loss of accuracy. This method can significantly enhance the applicability of ai QM/MM methods in the studies of chemical reactions in condensed phase and enzymatic reactions.
Kinetic theory for nucleation of supersaturated structures
[J].
Keimbildungsgeschwindigkeit in übersättigten Dämpfen
[J].
Kinetische behandlung der keimbildung in übersättigten dämpfen
[J].
On the theory of new phase formation: Cavitation
[J].
Microphysics of clouds and precipitation
[J].
Recent progresses in modeling of nucleation during solidification on the atomic scale
[J].Nucleation, the starting point of first-order discontinuous phase transformations, has long been an important issue in condensed matter physics and materials science. It plays a key role in determining the microstructures and mechanical properties of crystalline materials. As nucleation occurs at the atomic length scale and the diffusional time scale and is a typical stochastic event, investigating such kind of multiple scale issues will be taken up an enormous challenge. Because of the limitations of present experimental methods, it is still very hard to observe the nucleation process in situ. With the development of computational materials science, a deeper understanding of nucleation process has been obtained with the numerical modeling of nucleation process on the atomic scale. In this paper, some recent developments in modeling and simulation of nucleation process during solidification on the atomic scale are reviewed. Firstly, the development of classical nucleation theory and the step nucleation theory are reviewed. Then the developments in modeling of nucleation process by using the phase field method, Monte-Carlo method, Molecular dynamics method and the phase field crystal model are discussed. After that, some recent progresses in modeling of nucleation process during solidification in our research group by using the phase field crystal model are demonstrated. Finally, the outlooks of the future study on the nucleation during solidification are also presented.
原子尺度下凝固形核计算模拟研究的进展
[J].形核是一级不连续相变的起点,对后续材料组织的形成及最终产品的性能具有重要影响。形核过程、机制及其控制一直是材料科学和凝聚态物理等领域中最为活跃的研究课题之一。形核过程发生在原子空间尺度及扩散时间尺度,同时还具有随机性,因此充分认识形核过程将面临极大的挑战。受实验条件的限制,目前难以通过实验方法直接观测金属凝固中晶核的形成过程。近年来,随着计算材料科学的兴起,借助于数值模拟方法,凝固形核问题研究取得了很大的进展。本文首先回顾了形核理论的发展历程,然后对当前凝固形核模拟的研究进展进行述评,并介绍本课题组近年来基于晶体相场模型在形核研究方面的工作进展,最后对形核研究进行了展望。
Crystal nucleation in liquids: Open questions and future challenges in molecular dynamics simulations
[J].The nucleation of crystals in liquids is one of nature's most ubiquitous phenomena, playing an important role in areas such as climate change and the production of drugs. As the early stages of nucleation involve exceedingly small time and length scales, atomistic computer simulations can provide unique insights into the microscopic aspects of crystallization. In this review, we take stock of the numerous molecular dynamics simulations that, in the past few decades, have unraveled crucial aspects of crystal nucleation in liquids. We put into context the theoretical framework of classical nucleation theory and the state-of-the-art computational methods by reviewing simulations of such processes as ice nucleation and the crystallization of molecules in solutions. We shall see that molecular dynamics simulations have provided key insights into diverse nucleation scenarios, ranging from colloidal particles to natural gas hydrates, and that, as a result, the general applicability of classical nucleation theory has been repeatedly called into question. We have attempted to identify the most pressing open questions in the field. We believe that, by improving (i) existing interatomic potentials and (ii) currently available enhanced sampling methods, the community can move toward accurate investigations of realistic systems of practical interest, thus bringing simulations a step closer to experiments.
Thermodynamics and kinetics of prenucleation clusters, classical and non-classical nucleation
[J].Recent observations of prenucleation species and multi-stage crystal nucleation processes challenge the long-established view on the thermodynamics of crystal formation. Here, we review and generalize extensions to classical nucleation theory. Going beyond the conventional implementation as has been used for more than a century now, nucleation inhibitors, precursor clusters and non-classical nucleation processes are rationalized as well by analogous concepts based on competing interface and bulk energy terms. This is illustrated by recent examples of species formed prior to/instead of crystal nucleation and multi-step nucleation processes. Much of the discussed insights were obtained from molecular simulation using advanced sampling techniques, briefly summarized herein for both nucleation-controlled and diffusion-controlled aggregate formation. © 2015 The Authors. Published by Wiley-VCH Verlag GmbH & Co. KGaA. This is an open access article under the terms of the Creative Commons Attribution Non-Commercial NoDerivs License, which permits use and distribution in any medium, provided the original work is properly cited, the use is non-commercial and no modifications or adaptations are made.
Pre-nucleation clusters as solute precursors in crystallisation
[J].Crystallisation is at the heart of various scientific disciplines, but still the understanding of the molecular mechanisms underlying phase separation and the formation of the first solid particles in aqueous solution is rather limited. In this review, classical nucleation theory, as well as established concepts of spinodal decomposition and liquid-liquid demixing, is introduced together with a description of the recently proposed pre-nucleation cluster pathway. The features of pre-nucleation clusters are presented and discussed in relation to recent modifications of the classical and established models for phase separation, together with a review of experimental work and computer simulations on the characteristics of pre-nucleation clusters of calcium phosphate, calcium carbonate, iron(oxy)(hydr)oxide, silica, and also amino acids as an example of small organic molecules. The role of pre-nucleation clusters as solute precursors in the emergence of a new phase is summarized, and the link between the chemical speciation of homogeneous solutions and the process of phase separation via pre-nucleation clusters is highlighted.
Further results on Monte Carlo equations of state
[J].
On the determination of molecular fields. —II. From the equation of state of a gas
[J].
On the determination of molecular fields. —I. From the variation of the viscosity of a gas with temperature
[J].
Application of the embedded-atom method to covalent materials: A semiempirical potential for silicon
[J].
Semiempirical modified embedded-atom potentials for silicon and germanium
[J].
New empirical approach for the structure and energy of covalent systems
[J].
ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation
[J].
Self-consistent equations including exchange and correlation effects
[J].
Expansion of molecular orbital wave functions into valence bond wave functions. A simplified procedure
[J].
Interatomic potentials from first-principles calculations: The force-matching method
[J].
Deep potential molecular dynamics: A scalable model with the accuracy of quantum mechanics
[J].
Pushing the limit of molecular dynamics with ab initio accuracy to 100 million atoms with machine learning
[A].
A deep potential model with long-range electrostatic interactions
[J].
On representing chemical environments
[J].
Descriptors representing two- and three-body atomic distributions and their effects on the accuracy of machine-learned inter-atomic potentials
[J].
On-the-fly machine learning force field generation: Application to melting points
[J].
Phase transitions of hybrid perovskites simulated by machine-learning force fields trained on the fly with Bayesian inference
[J].
DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models
[J].
Unified approach to enhanced sampling
[J].
Escaping free-energy minima
[J].We introduce a powerful method for exploring the properties of the multidimensional free energy surfaces (FESs) of complex many-body systems by means of coarse-grained non-Markovian dynamics in the space defined by a few collective coordinates. A characteristic feature of these dynamics is the presence of a history-dependent potential term that, in time, fills the minima in the FES, allowing the efficient exploration and accurate determination of the FES as a function of the collective coordinates. We demonstrate the usefulness of this approach in the case of the dissociation of a NaCl molecule in water and in the study of the conformational changes of a dialanine in solution.
Well-tempered metadynamics: A smoothly converging and tunable free-energy method
[J].
Replica Monte Carlo simulation of spin-glasses
[J].
An integrate-over-temperature approach for enhanced sampling
[J].
Combining metadynamics and integrated tempering sampling
[J].The simulation of rare events is one of the key problems in atomistic simulations. Toward its solution, a plethora of methods have been proposed. Here we combine two such methods: metadynamics and integrated tempering sampling. In metadynamics, the fluctuations of a carefully chosen collective variable are amplified, while in integrated tempering sampling the system is pushed to visit an approximately uniform interval of energies and allows exploring a range of temperatures in a single run. We describe our approach and apply it to the two prototypical systems a S2 chemical reaction and to the freezing of silica. The combination of metadynamics and integrated tempering sampling leads to a powerful method. In particular in the case of silica we have measured more than 1 order of magnitude acceleration.
Transition path sampling and the calculation of rate constants
[J].
Simulating rare events in equilibrium or nonequilibrium stochastic systems
[J].
Forward flux sampling-type schemes for simulating rare events: Efficiency analysis
[J].
Efficient and direct generation of multidimensional free energy surfaces via adiabatic dynamics without coordinate transformations
[J].
Order-parameter-aided temperature-accelerated sampling for the exploration of crystal polymorphism and solid-liquid phase transitions
[J].
Numerical computation of rare events via large deviation theory
[J].
Variational approach to rare event simulation using least-squares regression
[J].
Variational approach to enhanced sampling and free energy calculations
[J].
Targeted adversarial learning optimized sampling
[J].Boosting transitions of rare events is critical to simulations of chemical and biophysical dynamic systems in order to close the time scale gaps between theoretical modeling and experiments. We present a novel approach, called targeted adversarial learning optimized sampling (TALOS), to modify the potential energy surface in order to drive the system to a user-defined target distribution where the free-energy barrier is lowered. Combining statistical mechanics and generative learning, TALOS formulates a competing game between a sampling engine and a virtual discriminator, enables unsupervised construction of bias potentials, and seeks for an optimal transport plan that transforms the system into a target. Through multiple experiments, we show that on-the-fly training of TALOS benefits from the state-of-art optimization techniques in deep learning and thus is efficient, robust, and interpretable. TALOS is also closely connected to the actor-critic reinforcement learning and hence leads to a new way of flexibly manipulating the many-body Hamiltonian systems.
On the root mean square quantitative chirality and quantitative symmetry measures
[J].
Molecular dynamics simulations of liquid silica crystallization
[J].Silica is one of the most abundant minerals on Earth and is widely used in many fields. Investigating the crystallization of liquid silica by atomic simulations is of great importance to understand the crystallization mechanism; however, the high crystallization barrier and the tendency of silica to form glasses make such simulations very challenging. Here we have studied liquid silica crystallization to β-cristobalite with metadynamics, using X-ray diffraction (XRD) peak intensities as collective variables. The frequent transitions between solid and liquid of the biased runs demonstrate the highly successful use of the XRD peak intensities as collective variables, which leads to the convergence of the free-energy surface. By calculating the difference in free energy, we have estimated the melting temperature of β-cristobalite, which is in good agreement with the literature. The nucleation mechanism during the crystallization of liquid silica can be described by classical nucleation theory.Copyright © 2018 the Author(s). Published by PNAS.
Ultrafast X-ray probing of water structure below the homogeneous ice nucleation temperature
[J].
Time-resolved diffraction profiles and atomic dynamics in short-pulse laser-induced structural transformations: Molecular dynamics study
[J].
Silicon liquid structure and crystal nucleation from ab initio deep metadynamics
[J].
Improving collective variables: The case of crystallization
[J].
Liquid-liquid critical point in phosphorus
[J].
Unveiling the crystallization mechanism of cadmium selenide via molecular dynamics simulation with machine-learning-based deep potential
[J].Cadmium selenide (CdSe) is an inorganic semiconductor with unique optical and electronic properties that make it useful in various applications, including solar cells, light-emitting diodes, and biofluorescent tagging. In order to synthesize high-quality crystals and subsequently integrate them into devices, it is crucial to understand the atomic scale crystallization mechanism of CdSe. Unfortunately, such studies are still absent in the literature. To overcome this limitation, we employed an enhanced sampling-accelerated active learning approach to construct a deep neural potential with <em>ab initio</em> accuracy for studying the crystallization of CdSe. Our brute-force molecular dynamics simulations revealed that a spherical-like nucleus formed spontaneously and stochastically, resulting in a stacking disordered structure where the competition between hexagonal wurtzite and cubic zinc blende polymorphs is temperature-dependent. We found that pure hexagonal crystal can only be obtained approximately above 1430 K, which is 35 K below its melting temperature. Furthermore, we observed that the solidification dynamics of Cd and Se atoms were distinct due to their different diffusion coefficients. The solidification process was initiated by lower mobile Se atoms forming tetrahedral frameworks, followed by Cd atoms occupying these tetrahedral centers and settling down until the third-shell neighbor of Se atoms sited on their lattice positions. Therefore, the medium-range ordering of Se atoms governs the crystallization process of CdSe. Our findings indicate that understanding the complex dynamical process is the key to comprehending the crystallization mechanism of compounds like CdSe, and can shed lights in the synthesis of high-quality crystals.
Temperature dependence of homogeneous nucleation in ice
[J].
Phase transition between crystalline variants of ordinary ice
[J].Water is one of the most abundant molecules on Earth. However, this common and "simple" material has more than 18 different phases, which poses a great challenge to theoretically study the nature of water and ice. We designed two reaction coordinates that can distinguish between water and various ice states and used them to efficiently sample all possible states of the system in all-atom molecular dynamics simulation at ambient temperature and pressure. Various structural and thermodynamics properties, including the water-ice phase diagrams, can thus be calculated. We also present a simple model that successfully explains the thermodynamic stability of different ice states. Our work provides effective methods and data for theoretical studies of different phases of water and ice.
Melting of MgSiO3 determined by machine learning potentials
[J].
A combined molecular dynamics and experimental study of two-step process enabling low-temperature formation of phase-pure α-FAPbI3
[J].
Collective variables from local fluctuations
[J].We introduce a method to obtain one-dimensional collective variables for studying rarely occurring transitions between two metastable states separated by a high free energy barrier. No previous information, not even approximated, on the path followed during the transition is needed. The only requirement is to know the fluctuations of the system while in the two metastable states. With this information in hand, we build the collective variable using a modified version of Fisher's linear discriminant analysis. The usefulness of this approach is tested on the metadynamics simulation of two representative systems. The first is the freezing of silver iodide into the superionic α-phase, and the second is the study of a classical Diels-Alder reaction. The collective variable works very well in these two diverse cases.
Data-driven collective variables for enhanced sampling
[J].Designing an appropriate set of collective variables is crucial to the success of several enhanced sampling methods. Here we focus on how to obtain such variables from information limited to the metastable states. We characterize these states by a large set of descriptors and employ neural networks to compress this information in a lower-dimensional space, using Fisher's linear discriminant as an objective function to maximize the discriminative power of the network. We test this method on alanine dipeptide, using the nonlinearly separable data set composed by atomic distances. We then study an intermolecular aldol reaction characterized by a concerted mechanism. The resulting variables are able to promote sampling by drawing nonlinear paths in the physical space connecting the fluctuations between metastable basins. Lastly, we interpret the behavior of the neural network by studying its relation to the physical variables. Through the identification of its most relevant features, we are able to gain chemical insight into the process.
Slow dynamics in protein fluctuations revealed by time-structure based independent component analysis: The case of domain motions
[J].
Deep learning the slow modes for rare events sampling
[J].
CdSe optical parametric oscillator operating at 12.07 µm with 170 mW output
[J].
Tunable 10- to 11-μm CdSe optical parametric oscillator pumped by a 2.1-μm Ho: YAG laser
[J].
Optical properties of cubic and hexagonal CdSe
[J].
Nonlinear optical properties of CdSe quantum dots
[J].
Growth of CdSe single crystals by temperature gradient solution zoning in excess Se
[J].
Structural bonding, dynamical, and electronic properties of liquid silicon: An ab initio molecular-dynamics study
[J].
Ten things we need to know about ice and snow
[J].
Molecular dynamics simulation of the ice nucleation and growth process leading to water freezing
[J].
Bond orientational order in liquids: Towards a unified description of water-like anomalies, liquid-liquid transition, glass transition, and crystallization: Bond orientational order in liquids
[J].
Low-density liquid water is the mother of ice: On the relation between mesostructure, thermodynamics and ice crystallization in solutions
[J].Predicting the temperature and extent of ice freezing in aqueous solutions is crucial for areas as diverse as cryobiology and materials design. It has long been recognized that the thermodynamics of liquid water controls the temperature and kinetics of ice crystallization. Parameterizations of the freezing temperatures in terms of the water activity of the solution have been successfully established, but the fundamental origin of the thermodynamic control of the non-equilibrium crystallization of ice has remained elusive. Here we use large-scale molecular simulations to elucidate the relationship between the structure, thermodynamics, and ice crystallization temperatures for solutions of mW water and a strongly hydrophilic solute that mimics LiCI ions. Fast cooling of solutions with up to 20 mol% ions results in the formation of nanosegregated glasses with domains of low-density amorphous ice and an ion-rich vitrified solution. Slow cooling of the mixtures results in nucleation and growth of ice within the domains of four-coordinated liquid water. The temperature of crystallization Tx coincides with the temperature of appearance of nanoscopic domains of four-coordinated liquid water in the mixture, T(L). We use the insight provided by the simulations to derive a thermodynamic expression for the crystallization temperature as a function of the water activity, T(X)(a(W)), analogous to the dependence of the melting temperature, T(m)(a(W)). The simple expression derived in this work provides a good account of the experimental freezing temperatures of water and the well-known steepest dependence of Tx on solute concentration compared to that of T(m).
Structural transformation in supercooled water controls the crystallization rate of ice
[J].
Ice is born in low-mobility regions of supercooled liquid water
[J].When an ice crystal is born from liquid water, two key changes occur: () The molecules order and () the mobility of the molecules drops as they adopt their lattice positions. Most research on ice nucleation (and crystallization in general) has focused on understanding the former with less attention paid to the latter. However, supercooled water exhibits fascinating and complex dynamical behavior, most notably dynamical heterogeneity (DH), a phenomenon where spatially separated domains of relatively mobile and immobile particles coexist. Strikingly, the microscopic connection between the DH of water and the nucleation of ice has yet to be unraveled directly at the molecular level. Here we tackle this issue via computer simulations which reveal that () ice nucleation occurs in low-mobility regions of the liquid, () there is a dynamical incubation period in which the mobility of the molecules drops before any ice-like ordering, and () ice-like clusters cause arrested dynamics in surrounding water molecules. With this we establish a clear connection between dynamics and nucleation. We anticipate that our findings will pave the way for the examination of the role of dynamical heterogeneities in heterogeneous and solution-based nucleation.Copyright © 2019 the Author(s). Published by PNAS.
Direct calculation of ice homogeneous nucleation rate for a molecular model of water
[J].Ice formation is ubiquitous in nature, with important consequences in a variety of environments, including biological cells, soil, aircraft, transportation infrastructure, and atmospheric clouds. However, its intrinsic kinetics and microscopic mechanism are difficult to discern with current experiments. Molecular simulations of ice nucleation are also challenging, and direct rate calculations have only been performed for coarse-grained models of water. For molecular models, only indirect estimates have been obtained, e.g., by assuming the validity of classical nucleation theory. We use a path sampling approach to perform, to our knowledge, the first direct rate calculation of homogeneous nucleation of ice in a molecular model of water. We use TIP4P/Ice, the most accurate among existing molecular models for studying ice polymorphs. By using a novel topological approach to distinguish different polymorphs, we are able to identify a freezing mechanism that involves a competition between cubic and hexagonal ice in the early stages of nucleation. In this competition, the cubic polymorph takes over because the addition of new topological structural motifs consistent with cubic ice leads to the formation of more compact crystallites. This is not true for topological hexagonal motifs, which give rise to elongated crystallites that are not able to grow. This leads to transition states that are rich in cubic ice, and not the thermodynamically stable hexagonal polymorph. This mechanism provides a molecular explanation for the earlier experimental and computational observations of the preference for cubic ice in the literature.
Imperfectly coordinated water molecules pave the way for homogeneous ice nucleation
[DB/OL].
Homogeneous ice nucleation in an ab initio machine-learning model of water
[J].
Homogeneous ice nucleation rates for mW and TIP4P/ICE models through Lattice Mold calculations
[J].
α-gallium: A metallic molecular crystal
[J].
Liquid gallium: Comparison of x-ray and neutron-diffraction data
[J].
Liquid metals: Fundamentals and applications in chemistry
[J].Post-transition elements, together with zinc-group metals and their alloys belong to an emerging class of materials with fascinating characteristics originating from their simultaneous metallic and liquid natures. These metals and alloys are characterised by having low melting points (i.e. between room temperature and 300 °C), making their liquid state accessible to practical applications in various fields of physical chemistry and synthesis. These materials can offer extraordinary capabilities in the synthesis of new materials, catalysis and can also enable novel applications including microfluidics, flexible electronics and drug delivery. However, surprisingly liquid metals have been somewhat neglected by the wider research community. In this review, we provide a comprehensive overview of the fundamentals underlying liquid metal research, including liquid metal synthesis, surface functionalisation and liquid metal enabled chemistry. Furthermore, we discuss phenomena that warrant further investigations in relevant fields and outline how liquid metals can contribute to exciting future applications.
Ab initio phase diagram and nucleation of gallium
[J].Elemental gallium possesses several intriguing properties, such as a low melting point, a density anomaly and an electronic structure in which covalent and metallic features coexist. In order to simulate this complex system, we construct an ab initio quality interaction potential by training a neural network on a set of density functional theory calculations performed on configurations generated in multithermal-multibaric simulations. Here we show that the relative equilibrium between liquid gallium, α-Ga, β-Ga, and Ga-II is well described. The resulting phase diagram is in agreement with the experimental findings. The local structure of liquid gallium and its nucleation into α-Ga and β-Ga are studied. We find that the formation of metastable β-Ga is kinetically favored over the thermodinamically stable α-Ga. Finally, we provide insight into the experimental observations of extreme undercooling of liquid Ga.
Multithermal-multibaric molecular simulations from a variational principle
[J].
Seeding approach to crystal nucleation
[J].
Unlocking the mysterious polytypic features within vaterite CaCO3
[J].Calcium carbonate (CaCO), the most abundant biogenic mineral on earth, plays a crucial role in various fields such as hydrosphere, biosphere, and climate regulation. Of the four polymorphs, calcite, aragonite, vaterite, and amorphous CaCO, vaterite is the most enigmatic one due to an ongoing debate regarding its structure that has persisted for nearly a century. In this work, based on systematic transmission electron microscopy characterizations, crystallographic analysis and machine learning aided molecular dynamics simulations with ab initio accuracy, we reveal that vaterite can be regarded as a polytypic structure. The basic phase has a monoclinic lattice possessing pseudohexagonal symmetry. Direct imaging and atomic-scale simulations provide evidence that a single grain of vaterite can contain three orientation variants. Additionally, we find that vaterite undergoes a second-order phase transition with a critical point of ~190 K. These atomic scale insights provide a comprehensive understanding of the structure of vaterite and offer advanced perspectives on the biomineralization process of calcium carbonate.© 2023. The Author(s).
DPA-2: Towards a universal large atomic model for molecular and material simulation
[DB/OL].
Accurate and efficient molecular dynamics based on machine learning and non von Neumann architecture
[J].
Progress in materials genome engineering in China
[J].Materials genome engineering (MGE) is a frontier technology in the field of material science and engineering, which is well capable to revolutionize the research and development (R&D) mode of new materials, greatly improve the R&D efficiency, shorten the R&D time, and reduce the cost. This paper reviews the progress of MGE in China from the aspects of the fundamental theory and methods, key technology and equipment, the R&D of new materials and related engineering application, talents training, formation and promotion of new concept of material genetic engineering. The paper also looks forward to the future development of MGE in China.
中国材料基因工程研究进展
[J].材料基因工程是材料领域的颠覆性前沿技术,将对材料研发模式产生革命性的变革,全面加速材料从设计到工程化应用的进程,大幅度提升新材料的研发效率,缩短研发周期,降低研发成本,促进工程化应用。本文从基础理论与方法、关键技术与装备、新材料研发与工程化应用、人才培养以及材料基因工程新理念的形成和推广等方面,综述了中国材料基因工程的研究进展,并提出了未来发展方向建议。