原子模拟在材料科学中的作用日益重要,正在改变以实验为主导的研究方式[1]。材料模拟中,原子模拟需要使用某种形式的势能面来描述原子间的相互作用,从而确定原子的受力。最准确获得势能面的方法是在Born-Oppenheimer近似[2]下,求解基于电子结构量子力学的Schrodinger方程[3]。然而,在广泛应用的电子结构方法密度泛函理论(DFT)[4]中,计算量与原子数的三次方成正比。这种正比关系使得DFT在应用于大型材料体系(超过1000个原子)和长模拟时间(纳秒量级)时代价很大。对于这一效率问题,一种通用的解决方法是开发传统经验原子间势函数[5~10],这些势函数通常是基于物理和化学的认知,通过假定一个解析函数来描述原子位置与系统能量之间的关系。利用经验原子间势函数可以进行大规模、长时间的原子模拟,但其准确性往往受限于经验描述中的固有假设。在这种情况下,就产生了一个矛盾,即量子力学方法的准确性较高,但效率极低;而经验原子间势函数效率高,但通常准确性有限。
目前,提出了许多方法来平衡原子模拟中准确性与效率之间的矛盾。在克服DFT效率低下方面,一种广泛应用的方法是开发ONETEP程序[11]。该程序通过在并行计算机上的中央处理器(CPU)进行平面波DFT计算,使得计算成本与原子数呈线性关系。此外,DFT计算也同样在图形处理器(GPU)上实现[12~15],其计算速率相较于CPU机器快超过20倍[15]。在解决经验原子间势函数准确性方面,普遍方法是开发包含许多附加参数的解析函数来解释额外的物理认知。一个典型的例子是修正嵌入原子势(MEAM)[10],它通过考虑电子密度分布的角度特性扩展了嵌入原子势(EAM)[9]。然而,与简单的EAM相比,这种改变导致MEAM的计算速率下降,且角度项也比简单的势函数更难以加速。尽管这2种方法受到了广泛的认可和应用,然而随着研究的材料体系愈加庞大和复杂,对可预测性的要求也越来越高,这些方法已无法满足需要。如何更好地平衡原子模拟的准确性和效率成为一项紧迫且具有挑战性的问题,解决这一问题需要根本的革新而非对现有技术的微调,而近年来机器学习(ML)领域的进展可能为此带来新的思路。ML以其在模式识别等领域的应用而受到广泛关注,已开发了许多不同的ML方法[16~18]。ML势函数可以用灵活的分析形式参数化势能面,以更全面的方式描述分子的性质和行为。与经验原子间势相比,ML势函数提高了准确度;与DFT相比,ML方法显著提高了效率。因此,开发能够兼具DFT的高准确性和经验原子间势的高效率的ML势是未来的研究挑战。
自从Blank等[19]首次引入用于描述势能面的ML神经网络方法以来,研究者已经开发出了各种ML势。Behler和Parrinello[20]发布了ML神经网络势函数(NNP),其中径向和角对称函数被用作原子环境描述符,NNP在块状Si、C、TiO2和许多其他材料中得到了应用。Schütt等[21,22]基于神经网络框架开发了用于模拟分子材料化学性质和势能面的SchNet和SchNetPack包。此外还有许多适用于不同材料体系的NNPs[23~26]。除NNP和SchNet外,还有几种其他类型的ML势:Gaussian近似势(GAP)、矩张量势(MTP)、谱邻域分析势(SNAP)、梯度域ML等。Zuo等[27]对目前主要ML势的准确性和效率进行了全面的比较。
深度势能(DP)[28~30]作为NNP的一种,于2017年首次发布,已被广泛用于不同的材料体系。DP方法的基础理论也在不断发展和完善,有望实现准确性和效率的完美组合。最近,DP已在最先进的超级计算机上以第一性原理的精度应用于超过1亿个原子的分子动力学(MD)模拟[31],这是将物理建模、机器学习和高性能计算完美结合的一个典型实例。DPA-1引入了基于注意力机制的描述符,进一步提高了模型预测的准确性并可同时覆盖多种元素[32]。最近提出的DPA-2更是采用大型原子模型架构,可以接受各种数据集的预训练,涵盖合金、半导体、电池材料和药物分子等多领域体系,可同时包含73种元素,具有极强的泛化能力[33]。本文主要介绍了DP方法在材料科学中的应用,并对DP方法的发展前景进行了展望。
1 DP方法简介
本节总结了开发DP模型的主要步骤:准备训练数据集、模型训练和模型验证,并介绍了如何在原子模拟中应用DP模型。
1.1 数据集构建
DP数据集的构建分为2个部分:(1) 提供原子构型信息(即原子坐标和晶胞的形状张量);(2) 标记(即计算构型的能量、原子力和Virial张量)。首先获得由原子坐标描述的许多不同系统构型的总能量、原子力和Virial张量,并将其作为训练标签用于训练ML势。DP的核心思想是将系统的总能量分解为各个原子的能量之和,其中每个原子的能量依赖于其局域原子构型,即原子坐标和局部环境。DP模型包含2组神经网络:第一组是嵌入网络,第二组是拟合网络。在嵌入网络中,为了实现物质系统总能量在平移、旋转和置换等对称操作下的不变性,需要引入原子环境的描述符。这些描述符需具备足够的分辨率,以便区分不同性质的局部原子环境。目前,DP模型主要使用2类描述符来描述原子环境:非光滑描述符[29,30]和光滑描述符[34]。非光滑描述符的理论是为每个原子及其截断半径内的相邻原子建立一个局部坐标系,并根据到中心原子的距离对相邻原子进行排序。这种方法能够确保原子环境在平移、旋转和置换下保持对称。然而,由于近邻原子的选择存在不确定性,会导致描述符本身也变得非光滑。尽管如此,非光滑描述符的优点在于能够保留所有近邻原子的信息。光滑描述符的构建涉及3个主要步骤:构建局部环境矩阵、构建嵌入矩阵和构建描述子。嵌入矩阵分为两体嵌入和三体嵌入矩阵。两体嵌入矩阵依赖于相邻原子之间的径向距离或坐标,而三体嵌入则考虑相邻原子之间的夹角,从而提供更高的精度和分辨率。在实践中,训练具有高分辨率的描述符较为困难,通常会混合使用不同类型的描述符,形成混合描述符。例如,可以使用截断半径较小的描述符来描述近邻构型,同时使用截断半径较大的描述符来捕捉远离原子的环境信息,这样的混合策略能够有效提高描述符的综合性能和模型的预测能力。
计算过程是通过DFT计算实现的,常用的DFT软件包包括VASP (Vienna ab initio simulation package),QE (quantum ESPRESSO)和ABACUS (atomic-orbital based ab-initio computation at UStc)。由于DP是在DFT计算数据集上进行的训练,故DP的精度不会超过其DFT计算的精度。DFT计算中的误差主要有2个来源:首先是由于交换-关联泛函的近似形式引入的误差,这可以通过攀升更为精确的交换-关联泛函(更高的计算成本)的Jacob梯子[35]来减小,此外也可以使用高阶的post-Hartree Fork方法,如Møller-Plesset微扰理论、耦合簇方法和构型相互作用来进行标记[36];另一个误差来源是数值误差,即波函数在实空间和k空间中的数值离散化和收敛所引入的误差,这可以使用更完整的基组(增加平面波近似中的能量截断)、减小k空间网络间距以及使用更严格的自洽场迭代收敛标准,从而系统性地控制此类误差。总体来说,提高标记的准确度会产生更大的计算代价,因此需要在计算的准确度和成本之间谋求平衡。
构建DP数据集的2个主要问题是:完备性和紧凑性。数据的完备性意味着训练数据需在相关构型空间中尽可能完整地采样,以涵盖各种可能的情况和变化,提高训练数据的多样性以确保训练后的模型具有较好的泛化能力;数据集的紧凑性意味着训练数据应为从采样构型中提取出的最小子集,通过该子集训练出的模型在采样构型上具有统一的精度,从而减少DFT计算时间。对构型空间进行采样的常用方法有:MD、遗传算法、增强采样法、主动学习以及并行学习方案。其中,深度势能生成器(DP-GEN)的并行学习方案能有效地生成兼具完备性和紧凑性的训练数据集。
1.2 模型训练
使用DeePMD-kit软件包[30]来训练DP,同时使用名为dpdata的Python软件包,把DFT软件中得到的标签转换为DeePMD-kit软件可接受的数据形式。
在训练过程中有以下3个关键问题。首先,训练DP要避免过拟合和欠拟合。欠拟合是训练过程中常见的问题,意味着DP在训练和验证数据集上表现不佳,这可以通过增加拟合参数的数量(更宽或更深的深度神经网络(DNN))或调整ML算法来避免;过拟合意味着DP在复现数据方面表现良好,但在预测方面表现不佳,这可以通过扩大训练数据集,减少拟合参数数量,或者使用力和Virial张量作为标签来解决。过拟合更难以识别,因此需要进行全面的测试。第二,训练过程中可能会涉及能量、力和Virial张量等标签,但并非所有标签都是必要的。本文强烈推荐使用力标签,这是因为力能提供更多的信息,其与能量标签相比为3N比1;而且使用梯度信息训练有助于避免过拟合。第三,DeePMD-kit的训练过程中有许多可调的超参数,包括神经网络尺寸、学习率、损失函数的前置因子。实践中观察到DP模型的质量对这些超参数不是非常敏感, DeePMD-kit中的默认设置通常能够满足计算的精度要求,而某些情况可能需要使用更大的能量前置因子进行“微调”,以实现更高的精度。
1.3 模型评估
训练完成后,建议对所得DP模型进行验证,以判断在原子模拟之前是否需要额外的训练数据集。评估DP性能有以下2种主要方法:(1) 构建一个与训练数据无关的小数据集,用DP预测该数据集的总能量、原子力和Virial张量,并将结果与相同原子构型的DFT结果进行比较,经验表明,若能量和力的均方根误差(RMSE)分别小于约10 meV/atom和1000 meV/nm,说明DP预测结果良好,而通常情况下误差大约为1 meV/atom和小于500 meV/nm;(2) 用DP计算材料的相关性质,将测试结果与同一体系的DFT或实验结果进行比较。例如,弹性常数作为力学性能的重要指标,可由DFT、DP和MD计算得到并进行对比分析。为进一步评估DP模型的准确性,Li等[37]推出了开源APEX软件包。APEX为DP提供了更为高效、便捷和高兼容性的合金性质计算测试工作流,APEX支持DFT和MD计算,能够得到能量与体积的关系曲线(EOS)、弹性常数、表面能、点缺陷形成能、层错能和声子等性质,为DP模型评估提供了一个系统且自动化的方法。
1.4 模型推理
模型推理(ML社区常用术语)是向ML模型提供实时数据以获得预测结果的过程。在势能面ML模型中,推理指的是将构型(原子坐标和晶胞张量)作为输入,计算能量、力和Virial张量的过程,通过DeePMD-kit包提供的接口,可以轻松地在Python或C++编程环境中对DP进行推理。若将DeePMD-kit与分子模拟软件包进行连接,如大规模原子/分子并行模拟器(LAMMPS)、原子模拟环境(ASE)、i-PI和GROMACS等,能将DP应用于各种原子模拟任务,如MD、Monte Carlo、结构优化等。
1.5 大原子模型的开发与应用
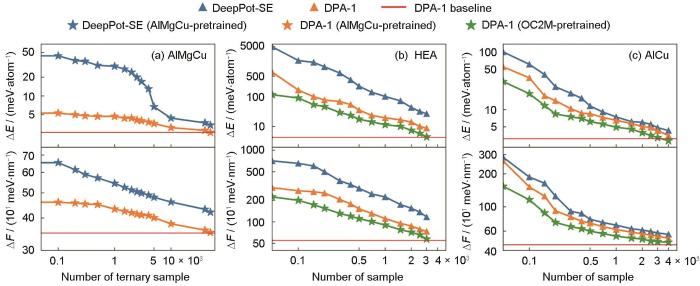
大原子模型针对大型原子系统的特殊性和复杂性,需要处理大量原子及其复杂的相互作用,因此在数据集构建、模型训练和应用过程中需要更多的考量和优化。大原子模型在不同构型之间进行转换的迁移能力是其性能的重要评估标准,在DPA-1模型的迁移实验中,Zhang等[32]将元素种类不同的训练集划分为多个子集,子集之间的组分、构型有明显差异,在其中一些子集上训练,而在另一些子集上进行测试,以得到模型在极端条件下的迁移能力。如图1[32]所示,样品数量相同时,DPA-1模型(橘黄色线)的误差比DeepPot-SE模型(蓝色线)要小很多,这说明DPA-1模型比DeepPot-SE模型具有更高的数据效率。绿色线是在OC2M数据集上进行预训练的DPA-1模型,它的误差比橘黄色线低,说明模型有一定程度的提升,其精度可与图形神经网络(GNN)模型DimeNet++[38]相媲美。实验结果说明DPA-1在实际应用中能学习到数据间隐藏的原子交互信息,具有强大的迁移能力[32]。为评估DPA-1模型的可解释性,研究者[32]将模型学习到的元素编码进行了主成分分析(PCA)降维和可视化,结果表明:元素在隐空间中螺旋分布,元素分布规律与其在元素周期表中的位置相对应,证明了DPA-1模型优异的可解释性。通过多方面测评,DPA-1的预测精度和训练效率也表现出色,证明了“预训练+少量数据微调”的可行性。
图1
图1
DeepPot-SE 和 DPA-1 在不同设置和不同体系上的能量和力的学习曲线[32]
Fig.1
Learning curves of both energy (ΔE) and force (ΔF) with DeepPot-SE and DPA-1, under different setups and on different systems[32]
(a) learning curves on the AlMgCu ternary subset, with DeepPot-SE and DPA-1 models pretrained on single-element and binary subsets
(b, c) learning curves on high-entropy alloy (HEA) (b) and AlCu (c), with DeepPot-SE (from scratch) and DPA-1 (both from scratch and pretrained on OC2M)
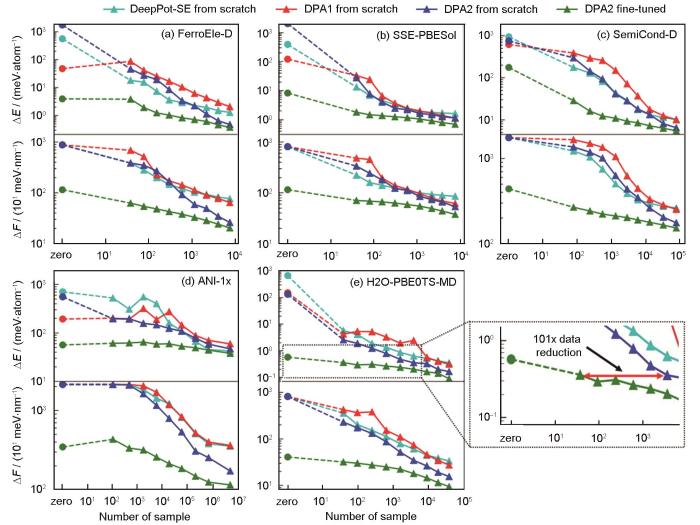
DPA-2模型在DPA-1之后对DP模型进行了又一次改进升级,提出了多任务预训练(multi-task pretraining)框架,可以共享大部分网络参数,对不同数据集使用不同的head,从而能够在多种任意来源的数据集上同时进行多任务训练[33]。与单一来源数据训练的模型相比,多任务预训练极大地扩展了其泛化能力和应用范围。预训练完成后,需要对下游数据进行微调,Zhang等[33]在不同的下游数据集上,对 DPA-2预训练之后的模型进行了迁移能力的测试,结果如图2[33]所示。可以看到,在多任务预训练结束后,DPA-2模型的能量和受力的收敛误差要远远低于从头训练,说明DPA-2达到同等精度水平所需的数据量大大减少[33]。平均来看,多任务预训练获得的DPA-2模型能节省90%以上的数据。预训练方案强大的泛化能力使得模型通常存在计算效率低下的问题,导致DPA-2应用受限。为了解决这个问题,DPA-2采用了模型蒸馏的方式:将下游体系上微调结束后的模型称为Teacher模型,用Teacher模型去训练更简单的Student模型(如DPA-1、DeepPot-SE等),使其在特定的下游体系上具有接近Teacher模型的精度,且效率提升近2个量级,从而可用于大规模高效率的应用模拟[33]。图3[33]展示了蒸馏后模型在水上的径向分布函数、固态电解质上的扩散系数和钙钛矿铁电固溶体上晶格常数随温度的变化及其与DP-PBE LiSnPS模型和从头算分子动力学(AIMD)模拟以及实验结果的对比。使用预训练后微调、蒸馏的模型,在3个体系上分别仅使用了原来数据的0.25%、1.01%和7.86%,证明了整套流程的可靠性。研究者还将DPA-2模型和其他大原子模型,如Gemnet-OC (GNO)、Equiformer-V2 (EFV2)、Nequip、Allegro进行了对比,证明了DPA-2在各个数据集上计算的精度更为稳定。
图2
图3
图3
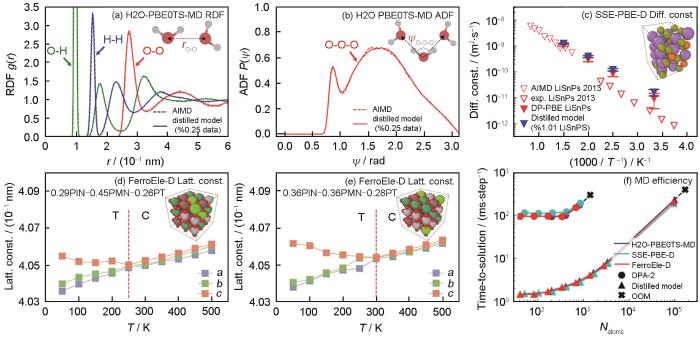
DPA-2蒸馏后的模型在下游体系中的应用测试[33]
Fig.3
Evaluations of the distilled model across various downstream applications[33]
(a, b) comparisons of the radial distribution function (RDF) (a) and angular distribution function (ADF) (b) for the H2O-PBE0TS-MD dataset between the reference ab initio molecular dynamics (AIMD) results[35] and the distilled mode (rO-O—radial distribution function for O-O, ψO-O-O—angular distribution function for O-O-O)
(c) comparisons of diffusion constants for the solid-state electrolyte Li10SnP2S12 (T—temperature)
(d, e) temperature-dependent lattice constants (a, b, and c) for the ternary solid solution ferroelectric perovskite oxides Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 (PIN-PMN-PT) (T—tetragonal, C—cubic)
(f) computational efficiency assessment for the aforementioned three systems (Natoms—number of atoms)
2 DP效率的优化
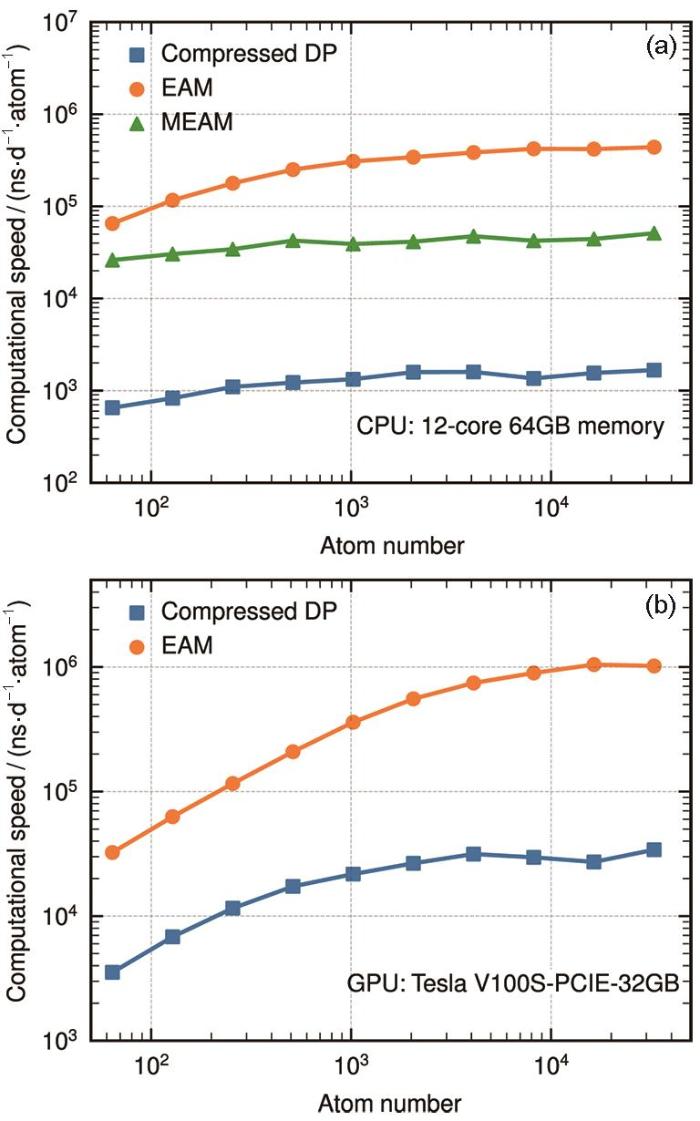
使用DP方法的过程中,最花费计算时间的步骤是嵌入网络的计算和描述符的组装[40]。DP压缩模型的目的是减少与嵌入网络相关的计算和内存开销,并保证压缩后模型的精度。DP的评估涉及从一个标量到一个M维向量的映射,该向量的每一个维度都可以用一个分段的五阶插值多项式来近似。嵌入网络的范围被离散化为节点x1, x2,…, xl, xl + 1,并假设区间的长度(表格步长)相同。在每个区间(例如[xl, xl + 1]),通过将嵌入网络在节点xl 和xl + 1处的值和导数与多项式的值、一阶导数和二阶导数相对应,来唯一确定第五阶多项式的6个拟合参数。这种近似称为表格化,因为多项式的参数存储在表中,当计算嵌入网络时只需在表中查找多项式。表格的精度由表格步长控制,步长为0.01时,能量和力的误差分别小于10-7 eV/atom和10-5 eV/nm。表格化后,嵌入矩阵与环境矩阵之间的乘法成为难题。嵌入矩阵计算后存储在内存中,然后从内存加载到寄存器中进行矩阵乘法,这需要与内存进行大量的输入/输出操作。通过将矩阵乘法与表格化步骤合并,可以消除这种情况,即,一旦通过表格化计算出嵌入网络的一个分量,它立即与寄存器中预加载的环境矩阵相乘,并累积到结果中。通过这种优化,可以避免嵌入网络与环境矩阵中冗余的零元素之间的乘法。
DP压缩模型已经在Cu、H2O和Al-Cu-Mg三元合金的DP上进行了测试[40]。在CPU上,模型推理的速率分别提高了9.7、4.3和18.0倍,在英伟达V100 GPU上,分别提高了9.7、3.7和16.2倍。同时,单个GPU处理的最大原子数也分别从12 × 103、49 × 103和5 × 103增加到了129 × 103、246 × 103和61 × 103。
图4
3 DP在材料科学中的应用
在过去3年中,DP方法已被应用到了各种不同的材料体系中,包括单质体系、多元体系、水体系、分子体系和团簇以及表面和低维体系。本文从单质体系、多元体系和水体系中选择几个例子,简要讨论DP方法在相应体系中的应用。
3.1 单质体系
迄今为止,DP方法已广泛应用于单质体系,包括Al、Mg、Cu、Ni、Ti、W、Ga、C、Si。Al是首个应用DP和开发出通用DP的金属体系[45],该通用DP能精确复现晶格参数、弹性常数、空位和间隙形成能、表面能、晶界能(孪晶)、层错能、熔点、熔化焓和扩散系数。其他金属元素的通用DP也能精确预测以上性质。对于训练数据集中未包含的性质,DP在声子色散关系、状态方程和液态径向分布函数方面比MEAM[10]更接近DFT[45]计算结果。在此基础上,Wang等[46]将ZBL (Ziegler-Biersack-Littmark)筛选的核斥力势与DP平滑插值,得到了用于辐照损伤模拟的DP-ZBL模型,超越了广泛采用的ZBL MEAM或EAM。随后,研究者开发了Al DP来模拟流体动力学极限附近的离子动力学、结构和动力学性质以及电子和离子导热系数,还开发了用于计算剪切速率的高温高压液态Al DP。
位错性质在大多数结构材料(包括Ti和W等)的塑性响应中起着重要作用。专门优化的Ti DP准确地描述了不同平面上的的层错能曲线γ-line,预测了Prism和Pyramidal I平面之间的<a>方向螺位错核心能量排序。此外,Prism和Pyramidal I平面上<a>方向螺位错的核心结构也与DFT结果惊人的一致[47]。由于位错核心结构无法直接包含在DFT训练数据集中,Ti DP的例子表明,可以使用替代性质来优化DP,以获得复杂hcp相的位错性质。虽然bcc W的位错核心结构不像hcp Ti那样复杂,但bcc W的Peierls势垒很难用其他经验势复现。只具有两体嵌入描述符的DP-SE2模型对Peierls势垒的预测结果非常差,但混合了两体和三体嵌入描述符的DP-HYB模型非常准确地复现了这一特性[48]。Ti和W的例子表明,DP可以准确地描述bcc和hcp金属的位错核心结构和Peierls势垒。
在元素周期表中,Ni、Co、Fe、Cr、Mn具有独特的磁性特征,这种磁矩显著影响着元素的各种性质,如力学性能。然而,开发准确的磁性体系ML势函数一直是一个挑战,因为训练过程中往往需要特定的磁性描述符,这显著增加了训练的复杂度和计算成本。最近,Gong等[49]从自旋极化密度泛函理论计算得出的训练数据集出发,开发了一种Ni的“磁隐藏”DP模型,该方法无需明确描述磁性自由度,能够高精度地预测fcc和hcp相的各种非磁性性质,如弹性常数、点缺陷、表面能、堆垛层错、位错核、晶界、理想强度和声子谱等。同时,该Ni DP模型在有限温度下也表现出色,能够准确描述晶格常数和弹性常数与温度的关系。还对比了其他经典和机器学习势函数,发现Ni DP模型在各方面性质上都显著优于其他势函数。这种磁性Ni DP模型有助于对复杂的力学行为进行精确的大规模原子模拟,并可作为开发镍基高温合金和其他多组分合金原子间势函数的基础。
DP方法也已应用于Ag和Au (催化应用)。Saidi团队[50]和王涵团队[51]开发了Ag和Au的DP,该DP能够精确预测晶格参数、弹性常数、表面形成能、间隙和空位形成能。Andolina等[50]计算了吸附原子在{100}、{110}和{111}面上的吸附能和扩散势垒,其结果与DFT结果一致。Wang等[51]使用DP对Au{111}表面重构进行了全面研究,其结果与DFT结果非常吻合。另外,Chen等[52]使用DP MD模拟研究了Au的动态压缩过程,所开发的DP能准确复现实验确定的相边界,并提出了通过短程和中程有序来降低受冲击结构的Gibbs自由能。上述Ag和Au的例子表明DP方法在催化和冲击压缩领域应用的可行性和有效性。
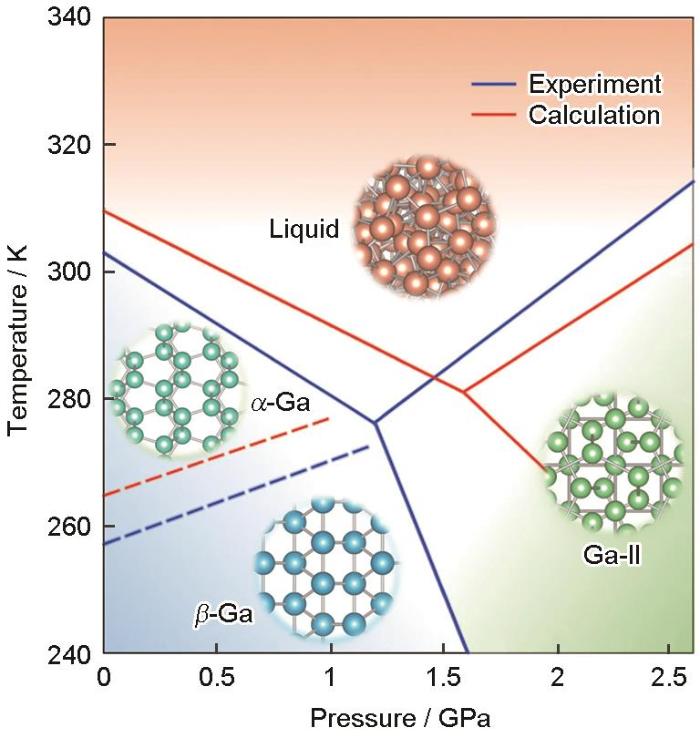
此外,DP方法还被应用于其他单质体系,以下仅列举了部分示例。Li是电池中的重要元素,Jiao等[53]开发了DP方法来揭示大型Li金属系统中的自愈合机制。Niu等[54]采集了MD模拟Ga凝固过程的有效结构信息作为训练集,并采用DFT训练集的相关性质,利用DP构建了能同时描述液态Ga和3种固态结构(α-Ga、β-Ga和Ga-II)的势函数以及液态Ga、α-Ga、β-Ga和Ga-Ⅱ的相图,如图5[54]所示,与实验结果吻合良好。在研究Ga的凝固机制中发现当温度高于174 K时,β相的形核能垒更低,成功解释了过冷液态Ga容易形成亚稳态β相而不是稳态α相的实验难题。此外,还研究了液态Ga的局部结构以及α-Ga、β-Ga的成核过程[54]并计算了凝固速率。在150 K以上,两相的凝固形核势垒极大且凝固速率极低,与Ga的深过冷特性相吻合。从理论上解释了金属Ga的深过冷特性以及α相和β相在凝固过程中的竞争规律,并为构建复杂体系的高精度势函数和温度-压力相图及凝固形核机理提供了系统性的研究方法。Wang等[55]模拟了12种不同的块体和低维C原子结构的结构特性。对于同时具有共价键和金属键特征的Si,Bonati和Parrinello[56]利用DP研究了Si在结晶和液固相变过程中的自由能表面,发现临界点附近的许多热力学性质与实验数据接近。Li等[57]用晶态、液态和非晶态Si的DFT数据训练DP,结果精确复现了热导率。最后,Yang等[58]利用DP研究了P中的液-液相变,建立了液相图的主要特征。
图5
单质体系是DP方法在材料科学中应用的首次尝试。DP方法在不同晶体结构和各种性质(力学、催化、辐照、相变、导热等)方面的成功应用,促使其扩展到了多元体系和更为复杂的现象中。
3.2 多元体系
Al-Mg是第一个开发出精确DP的合金体系[45],该DP用于描述Materials Project (MP)数据库中28种Al-Mg合金的晶体结构[59],包括准确预测形成能、平衡体积、弹性常数、空位和间隙形成能以及非弛豫表面能。Wang等[60]将该Al-Mg DP应用于晶体结构预测,并通过DP + CALYPSO验证了其可靠性。这项工作将DeePMD-kit包和晶体结构预测软件相结合。Andolina等[61]基于原始DP开发了Al-Mg DP来研究各向异性表面偏聚。在此基础上,Jiang等[62]开发了整个成分空间的Al-Cu-Mg三元DP。在DP-GEN中共探索了27.3亿种合金构型,得到的DP与MEAM相比,对58种晶体结构的能量、力学和缺陷性质的预测结果更为准确。对于高熵合金,由于可用的经验势十分有限,多组分DP方法应用更为广泛,Cao等[63]利用DP MD模拟了GaFeMnNiCu高熵合金的冷却过程,验证了液态金属对实现高熵合金原子级精准制造的重要作用。液态金属如Ga具有较负的混合焓,能够作为原子之间的“黏结剂”,在温和条件下实现高熵合金的多组元原子混溶,将GaFeMnNiCu DP模型的预测结果与DFT结果进行比较,验证了DP模型的准确性,之后对降温过程中样品的结构进行了MD模拟,发现bcc相的体积分数随着模拟步骤的增加而增大,与实验观察到的样品的晶化行为保持一致,证明了该策略的合理性。
王才壮团队[67~70]对一系列铝基合金进行了DP MD模拟,Al-Cr准晶体[69]是DP与实验研究相结合的示例。通过脉冲激光沉积法,在Al13Cr2近似相(由Al90Cr10薄膜形成)中观察到了亚稳准晶的枝晶生长,其结构类似于Al13Cr2基体的准晶。采用Al-Cr DP模拟了Al90Cr10合金在1011 K/s速率下由2200 K降至700 K的淬火过程。在Al13Cr2近似相中存在3种13个原子的二十面体和1个二十面体的Al-Cr准晶体,这4个二十面体的结构非常相似,但Cr—Al键长度略有不同。这4个二十面体结构均以Cr为中心,准晶和近似相中都有二十面体结构,这说明激光照射后仍保留了13个原子的二十面体,DP MD模拟与实验相符。基于DP的模拟能够准确复现液体结构,是DP方法成功应用的范例。
DP的另一类成功应用是锂和/或钠基电池材料,本文以Li10GeP2S12型超离子导体[73]为例介绍。用DP-GEN方案生成3种固态电解质材料(Li10GeP2S12、Li10SiP2S12和Li10SnP2S12)的DP,将其用于约1000 个原子在宽温度范围内的扩散模拟。预测的扩散系数略高于实验值,但在可接受的误差范围内。这些基于DP的模拟为固态电解质材料的大尺度和长时间MD研究提供了一个新途径。
DPA-1和DPA-2的发布使DP方法在多元体系的应用迈入新阶段。Zhang等[32]将DPA-1应用于AlMgCu三元合金和TaNbWMoVAl高熵合金以测试模型的迁移能力和对不同力学性能的预测精度,结果表明,对于AlMgCu系统,当仅在单元素和二元元素样品上进行训练时,DPA-1在三元样品上的RMSE (6.99meV/atom)比DeepPot-SE的RMSE (65.1 meV/atom)小了1个数量级。这表明DPA-1模型能从二元Al-Mg、Al-Cu、Mg-Cu和单元素相互作用中学习到三元Al-Mg-Cu相互作用。在力学性能的预测方面,DPA-1预测的弹性常数、结合能、扩散系数等都获得了与DFT和实验结果令人满意的一致性。DPA-2目标是做到材料领域无监督训练大模型,使用更丰富的、大量无DFT标注的数据来训练模型,从而扩展到材料性质预测等应用场景[33]。DPA-2在预测LiSnPS固态电解质和铁电钙钛矿氧化物等多元体系上的结果均与DFT和实验一致,且效率大大提升[33]。
DP方法也同样应用于其他多元体系,包括金属氧化物、金属硫化物、热电SnSe材料、金属硼化物和金属碳化物体系。
3.3 水体系
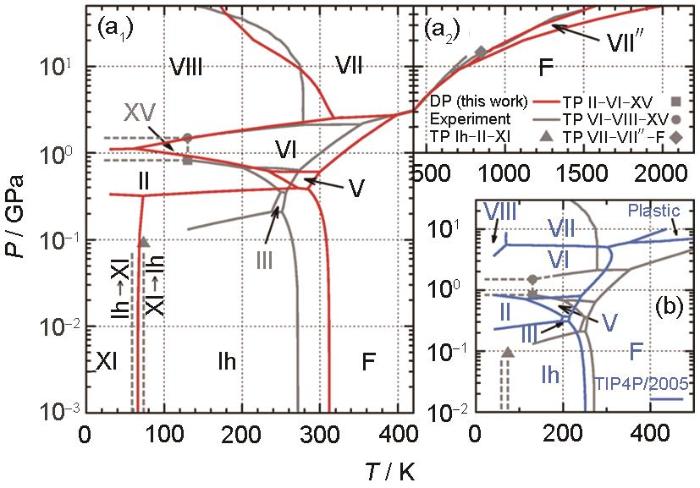
Sommers等[78]训练了能以从头算精度预测液态H2O极化率的DP,以便在长时间尺度上计算Roman光谱。Gartner等[79]训练了能检验H2O中是否存在液-液过渡问题的DP。Andreani等[80]结合中子散射实验和DP MD研究了超临界H2O中的氢动力学,在DP MD中观察到的振动态密度显示了分子内振动、分子间振动和旋转运动的耦合。Piaggi等[81]利用DP研究了H2O、六边形冰和立方冰中的冰成核现象,DP结果与实验达到了定量一致(优于最先进的半经验势)。而通过构建低温、低压到约2400 K和约50 GPa的DP相图,能够更完整地描述H2O不同相之间的相平衡[82]。如图6[82]所示,DP和经验势函数TIP4P/2005[83]在低、中压范围内均表现良好,DP在高压时与实验结果更为接近,特别是在冰VIII、VII和VI的相边界处。与实验不同,TIP4P/2005预测了一种从冰VII到塑性相的一级相转变,而DP的预测与实验相符。考虑到H2O的重要性、H2O相图中温度和压强的变化范围以及表示自由能所需的高精度,H2O相图的研究对DP而言是一个里程碑。
图6
牛海洋团队[88]利用DNN水模型和MD模拟探测了均匀冰成核的微观机制。经验水模型在均匀成核条件下计算的成核速率通常与实验值不符,需要利用DNN水模型捕捉H2O分子复杂的分子内和分子间相互作用,通过添加液体、晶体的相空间,特别是两相共存的成核区的特征结构来扩展DNN模型的训练集。在过冷条件下,对一个由2880个H2O分子组成的系统进行了MD模拟,得到了均匀条件下从头算精度的DNN水模型MD模拟的冰成核轨迹,发现具有高迁移率的不完全配位(IC) H2O分子为H键网络重排铺平了道路,导致冰核的生长或收缩;由完美配位(PC) H2O分子形成的H键网络保护了现有的冰核,使其不会生长或融化,因此,冰是通过IC和PC分子之间的竞争和合作而产生的。牛海洋团队对冰成核微观机制的描述为H2O和其他相关材料的性质研究提供了新的见解。
DP方法同样被广泛应用于H2O相关体系。Xu等[89]开发了一种用于液态H2O中Zn2+ MD模拟的DP。DP MD模拟很好地复现了实验观测到的Zn-H2O径向分布函数以及X射线吸收近边结构光谱。最近,Limmer团队[90,91]利用DP研究了液-气界面,发现通过引入缓慢变化的长程相互作用的显式模型,并只对短程部分进行神经网络训练,能够获得准确的界面特性。此外,训练了能够重现H2O和N2O5势能面的DP模型,并采用DP MD和重要性采样来研究水性气溶胶对N2O5的吸收[91]。与以往的气凝胶吸收过程主要发生在凝胶内部的观点不同,认为由于液-气界面溶液进行水解和竞争性的再蒸发,水性气溶胶对N2O5活性吸收过程不是水相介导,而主要在液-气界面上完成。这项工作不仅为一个长期存在的问题带来了新的见解,还将DP方法的应用扩展到了液-气界面。DP方法在水体系中的其他应用实例还包括TiO2-H2O界面、冰Ih/XI转变以及高压冰VII的动力学状态。
4 总结与展望
随着对更高精度、更大尺寸、更长时间尺度和更高计算效率原子模拟需求的增加,ML势函数广泛应用于材料科学领域,尤其是性质微妙和复杂的材料体系。本文综述了DP 方法(ML势函数的一种),总结了基本方法、如何开发DP,并讨论了DP方法的精度和效率,最后回顾了一些DP方法的应用范例。经过多年的发展,DP方法现已相对成熟,而且在开源社区框架下其准确性和效率仍在不断提高。预计DP方法会在未来几年持续发展,可用数据库也会继续扩大。
DP方法大致会在以下5个方向继续发展。首先是开发有更好预测能力、更智能的描述子。从W[45]的例子中看到,Peierls势垒(位错滑动的势垒)只能通过扩展DP描述符至包含三体嵌入才能准确复现。随着DP方法广泛应用于不同的材料体系,此类问题会越来越多。智能描述符的出现会改进DP的训练过程,例如,对于目前的混合描述符,即同时包含两体和三体嵌入的描述符,需要考量此类描述符中三体嵌入所占的权重,而目前的策略主要是基于经验,未来有机会将这一过程转变为机器驱动。
第二个方向是使DP训练和“专门优化”更加自动。在DeePMD-kit和DP-GEN软件中,不同的设置有时会影响训练后DP的表现。DP-GEN中信任等级的自动选择已处于测试阶段,“专门优化”步骤也会更加自动化以减少人为干预:(1) 需要什么类型的专门化数据集?(2) 与DP-GEN数据集结合需要多少个专门化数据集?(3) 何时添加专门化数据集以及如何修改DeePMD-kit和DP-GEN设置?更加自动化的训练和“专门化”方案将加速DP的发展,扩大其应用空间。
第三个方向是进一步优化DP方法的计算速率。目前,许多经验势的速率比DP更快 (至少10倍),这导致用户在精度要求不高时更倾向于使用经验势。DP中有大量参数,原则上不会比经验势快,但减少使用DP方法时计算效率的损失可以改变效率-精度平衡,实现更有效的材料模拟。如上所述,DP与大多数经验势相比具有巨大的精度优势,能够应用于经验势无法正确描述的现象。
第四个方向是开发领域通用的大原子模型。目前,DPA-2方法能同时包含73种元素信息,得到第一性原理精度的能量、力等信息,模型具有很强的泛化能力。近期的主要目标为开发领域通用的大原子模型,并使得该通用大模型得到广泛应用。例如在合金领域,近期本团队致力于开发对50种以上金属元素均适用的大原子模型,该模型不仅可准确描述这些元素的能量、力等信息,还可以准确描述单质、金属间化合物、随机固溶体的晶格常数、弹性常数、点缺陷形成能、广义堆垛层错能等性质。在准确描述上述性质的基础上,该大模型可广泛应用于合金体系的分子动力学模拟中,来研究包括相转变、位错运动、晶界动力学等相关问题。同时,该模型可作为一个准确、理想的出发点,用于开发、优化得到能更准确描述特定问题的势函数模型。
第五个方向是继续改进开源的AIS Square (DP数据库,包括训练数据集、训练方案、DP模型和测试结果)。增加所包含的模型数量和训练数据,目标覆盖元素周期表。这将是一项长久的工作,需要领域内全体研究人员的努力。此外,需提高AIS Square的灵活度,以方便用户使用。
DP方法(以及相关的ML势函数、大原子模型)的开发是材料原子模拟领域的一个重要里程碑,它依赖于ML技术和原子环境描述符的进步。DP相较于经验势具有更高的精度(接近DFT)和合理的计算效率,其准确度和效率为原子模拟打开了全新的应用领域。
参考文献
Quantum mechanics of many-electron systems
[J].
Self-consistent equations including exchange and correlation effects
[J].
Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules
[J].
High-temperature equation of state by a perturbation method. I. Nonpolar gases
[J].
Modeling solid-state chemistry: Interatomic potentials for multicomponent systems
[J].
Fitting the Stillinger-Weber potential to amorphous silicon
[J]. J.
Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals
[J].
Modified embedded-atom potentials for cubic materials and impurities
[J].
The ONETEP linear-scaling density functional theory program
[J].
Accelerating VASP electronic structure calculations using graphic processing units
[J].We present a way to improve the performance of the electronic structure Vienna Ab initio Simulation Package (VASP) program. We show that high-performance computers equipped with graphics processing units (GPUs) as accelerators may reduce drastically the computation time when offloading these sections to the graphic chips. The procedure consists of (i) profiling the performance of the code to isolate the time-consuming parts, (ii) rewriting these so that the algorithms become better-suited for the chosen graphic accelerator, and (iii) optimizing memory traffic between the host computer and the GPU accelerator. We chose to accelerate VASP with NVIDIA GPU using CUDA. We compare the GPU and original versions of VASP by evaluating the Davidson and RMM-DIIS algorithms on chemical systems of up to 1100 atoms. In these tests, the total time is reduced by a factor between 3 and 8 when running on n (CPU core + GPU) compared to n CPU cores only, without any accuracy loss.Copyright © 2012 Wiley Periodicals, Inc.
VASP on a GPU: Application to exact-exchange calculations of the stability of elemental boron
[J].
The analysis of a plane wave pseudopotential density functional theory code on a GPU machine
[J].
Fast plane wave density functional theory molecular dynamics calculations on multi-GPU machines
[J].
Machine learning: Trends, perspectives, and prospects
[J].Machine learning addresses the question of how to build computers that improve automatically through experience. It is one of today's most rapidly growing technical fields, lying at the intersection of computer science and statistics, and at the core of artificial intelligence and data science. Recent progress in machine learning has been driven both by the development of new learning algorithms and theory and by the ongoing explosion in the availability of online data and low-cost computation. The adoption of data-intensive machine-learning methods can be found throughout science, technology and commerce, leading to more evidence-based decision-making across many walks of life, including health care, manufacturing, education, financial modeling, policing, and marketing. Copyright © 2015, American Association for the Advancement of Science.
Neural network models of potential energy surfaces
[J].
Generalized neural-network representation of high-dimensional potential-energy surfaces
[J].
SchNet—A deep learning architecture for molecules and materials
[J].
SchNetPack: A deep learning toolbox for atomistic systems
[J].SchNetPack is a toolbox for the development and application of deep neural networks that predict potential energy surfaces and other quantum-chemical properties of molecules and materials. It contains basic building blocks of atomistic neural networks, manages their training, and provides simple access to common benchmark datasets. This allows for an easy implementation and evaluation of new models. For now, SchNetPack includes implementations of (weighted) atom-centered symmetry functions and the deep tensor neural network SchNet, as well as ready-to-use scripts that allow one to train these models on molecule and material datasets. Based on the PyTorch deep learning framework, SchNetPack allows one to efficiently apply the neural networks to large datasets with millions of reference calculations, as well as parallelize the model across multiple GPUs. Finally, SchNetPack provides an interface to the Atomic Simulation Environment in order to make trained models easily accessible to researchers that are not yet familiar with neural networks.
Interatomic potentials for ionic systems with density functional accuracy based on charge densities obtained by a neural network
[J].
Predicting molecular properties with covariant compositional networks
[J].
PhysNet: A neural network for predicting energies, forces, dipole moments, and partial charges
[J].In recent years, machine learning (ML) methods have become increasingly popular in computational chemistry. After being trained on appropriate ab initio reference data, these methods allow for accurately predicting the properties of chemical systems, circumventing the need for explicitly solving the electronic Schrödinger equation. Because of their computational efficiency and scalability to large data sets, deep neural networks (DNNs) are a particularly promising ML algorithm for chemical applications. This work introduces PhysNet, a DNN architecture designed for predicting energies, forces, and dipole moments of chemical systems. PhysNet achieves state-of-the-art performance on the QM9, MD17, and ISO17 benchmarks. Further, two new data sets are generated in order to probe the performance of ML models for describing chemical reactions, long-range interactions, and condensed phase systems. It is shown that explicitly including electrostatics in energy predictions is crucial for a qualitatively correct description of the asymptotic regions of a potential energy surface (PES). PhysNet models trained on a systematically constructed set of small peptide fragments (at most eight heavy atoms) are able to generalize to considerably larger proteins like deca-alanine (Ala): The optimized geometry of helical Ala predicted by PhysNet is virtually identical to ab initio results (RMSD = 0.21 Å). By running unbiased molecular dynamics (MD) simulations of Ala on the PhysNet-PES in gas phase, it is found that instead of a helical structure, Ala folds into a "wreath-shaped" configuration, which is more stable than the helical form by 0.46 kcal mol according to the reference ab initio calculations.
Physically informed artificial neural networks for atomistic modeling of materials
[J].
Performance and cost assessment of machine learning interatomic potentials
[J].
Deep potential: A general representation of a many-body potential energy surface
[J].
Deep potential molecular dynamics: A scalable model with the accuracy of quantum mechanics
[J].
DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics
[J].
Pushing the limit of molecular dynamics with ab initio accuracy to 100 million atoms with machine learning
[A].
Pretraining of attention-based deep learning potential model for molecular simulation
[J].
DPA-2: Towards a universal large atomic model for molecular and materials simulation
[DB/OL].
End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems
[A].
Jacob's ladder of density functional approximations for the exchange-correlation energy
[J].
The individual and collective effects of exact exchange and dispersion interactions on the ab initio structure of liquid water
[J].
An extendable cloud-native alloy property explorer
[DB/OL].
GemNet-OC: Developing graph neural networks for large and diverse molecular simulation datasets
[J].
86 PFLOPS deep potential molecular dynamics simulation of 100 million atoms with ab initio accuracy
[J].
DP compress: A model compression scheme for generating efficient deep potential models
[J].Machine-learning-based interatomic potential energy surface (PES) models are revolutionizing the field of molecular modeling. However, although much faster than electronic structure schemes, these models suffer from costly computations via deep neural networks to predict the energy and atomic forces, resulting in lower running efficiency as compared to the typical empirical force fields. Herein, we report a model compression scheme for boosting the performance of the Deep Potential (DP) model, a deep learning-based PES model. This scheme, we call DP Compress, is an efficient postprocessing step after the training of DP models (DP Train). DP Compress combines several DP-specific compression techniques, which typically speed up DP-based molecular dynamics simulations by an order of magnitude faster and consume an order of magnitude less memory. We demonstrate that DP Compress is sufficiently accurate by testing a variety of physical properties of Cu, HO, and Al-Cu-Mg systems. DP Compress applies to both CPU and GPU machines and is publicly available online.
Specialising neural network potentials for accurate properties and application to the mechanical response of titanium
[J].
Development of an interatomic potential for the simulation of defects, plasticity, and phase transformations in titanium
[J].
Classical potential describes martensitic phase transformations between the α, β, and ω titanium phases
[J].
Deep potentials for materials science
[J].
Active learning of uniformly accurate interatomic potentials for materials simulation
[J].
Deep learning inter-atomic potential model for accurate irradiation damage simulations
[J].
Dislocation locking versus easy glide in titanium and zirconium
[J].Clouet, Emmanuel; Chaari, Nermine CEA, DEN, Serv Rech Met Phys, F-91191 Gif Sur Yvette, France. Caillard, Daniel CNRS, CEMES, F-31055 Toulouse, France. Onimus, Fabien CEA, DEN, Serv Rech Met Appl, F-91191 Gif Sur Yvette, France. Rodney, David Univ Lyon 1, CNRS, UMR 5306, Inst Lumiere Mat, F-69622 Villeurbanne, France.
A tungsten deep neural-network potential for simulating mechanical property degradation under fusion service environment
[J].
An accurate and transferable machine learning interatomic potential for nickel
[J].
Robust, multi-length-scale, machine learning potential for Ag-Au bimetallic alloys from clusters to bulk materials
[J].
A generalizable machine learning potential of Ag-Au nanoalloys and its application to surface reconstruction, segregation and diffusion
[J].
Atomistic mechanism of phase transition in shock compressed gold revealed by deep potential
[DB/OL].
Self-healing mechanism of lithium in lithium metal
[J].
Ab initio phase diagram and nucleation of gallium
[J].Elemental gallium possesses several intriguing properties, such as a low melting point, a density anomaly and an electronic structure in which covalent and metallic features coexist. In order to simulate this complex system, we construct an ab initio quality interaction potential by training a neural network on a set of density functional theory calculations performed on configurations generated in multithermal-multibaric simulations. Here we show that the relative equilibrium between liquid gallium, α-Ga, β-Ga, and Ga-II is well described. The resulting phase diagram is in agreement with the experimental findings. The local structure of liquid gallium and its nucleation into α-Ga and β-Ga are studied. We find that the formation of metastable β-Ga is kinetically favored over the thermodinamically stable α-Ga. Finally, we provide insight into the experimental observations of extreme undercooling of liquid Ga.
A deep learning interatomic potential developed for atomistic simulation of carbon materials
[J].
Silicon liquid structure and crystal nucleation from ab initio deep metadynamics
[J].
A unified deep neural network potential capable of predicting thermal conductivity of silicon in different phases
[J].
Liquid-liquid critical point in phosphorus
[J].
Commentary: The materials project: A materials genome approach to accelerating materials innovation
[J].
Crystal structure prediction of binary alloys via deep potential
[J].
Improved Al-Mg alloy surface segregation predictions with a machine learning atomistic potential
[J].
Accurate deep potential model for the Al-Cu-Mg alloy in the full concentration space
[J].
Liquid metal for high-entropy alloy nanoparticles synthesis
[J].
Transforming solid-state precipitates via excess vacancies
[J].Many phase transformations associated with solid-state precipitation look structurally simple, yet, inexplicably, take place with great difficulty. A classic case of difficult phase transformations is the nucleation of strengthening precipitates in high-strength lightweight aluminium alloys. Here, using a combination of atomic-scale imaging, simulations and classical nucleation theory calculations, we investigate the nucleation of the strengthening phase θ' onto a template structure in the aluminium-copper alloy system. We show that this transformation can be promoted in samples exhibiting at least one nanoscale dimension, with extremely high nucleation rates for the strengthening phase as well as for an unexpected phase. This template-directed solid-state nucleation pathway is enabled by the large influx of surface vacancies that results from heating a nanoscale solid. Template-directed nucleation is replicated in a bulk alloy as well as under electron irradiation, implying that this difficult transformation can be facilitated under the general condition of sustained excess vacancy concentrations.
Co-segregation of Mg and Zn atoms at the planar η1-precipitate/Al matrix interface in an aged Al-Zn-Mg alloy
[J].
Development of a deep machine learning interatomic potential for metalloid-containing Pd-Si compounds
[J].
Development of interatomic potential for Al-Tb alloys using a deep neural network learning method
[J].An interatomic potential for the Al-Tb alloy around the composition of AlTb is developed using the deep neural network (DNN) learning method. The atomic configurations and the corresponding total potential energies and forces on each atom obtained from ab initio molecular dynamics (AIMD) simulations are collected to train a DNN model to construct the interatomic potential for the Al-Tb alloy. We show that the obtained DNN model can well reproduce the energies and forces calculated by AIMD simulations. Molecular dynamics (MD) simulations using the DNN interatomic potential also accurately describe the structural properties of the AlTb liquid, such as partial pair correlation functions (PPCFs) and bond angle distributions, in comparison with the results from AIMD simulations. Furthermore, the developed DNN interatomic potential predicts the formation energies of the crystalline phases of the Al-Tb system with an accuracy comparable to ab initio calculations. The structure factors of the AlTb metallic liquid and glass obtained by MD simulations using the developed DNN interatomic potential are also in good agreement with the experimental X-ray diffraction data. The development of short-range order (SRO) in the AlTb liquid and the undercooled liquid is also analyzed and three dominant SROs, i.e., Al-centered distorted icosahedron (DISICO) and Tb-centered '3661' and '15551' clusters, respectively, are identified.
Short- and medium-range orders in Al90Tb10 glass and their relation to the structures of competing crystalline phases
[J].
Dynamic observation of dendritic quasicrystal growth upon laser-induced solid-state transformation
[J].
Molecular dynamics simulation of metallic Al-Ce liquids using a neural network machine learning interatomic potential
[J].
Deep machine learning interatomic potential for liquid silica
[J].
Thermoelastic properties of bridgmanite using deep-potential molecular dynamics
[J].
Deep potential generation scheme and simulation protocol for the Li10GeP2S12-type superionic conductors
[J].
Isotope effects in liquid water via deep potential molecular dynamics
[J].
Isotope effects in x-ray absorption spectra of liquid water
[J].
Isotope effects in molecular structures and electronic properties of liquid water via deep potential molecular dynamics based on the SCAN functional
[J].
Resolving the structural debate for the hydrated excess proton in water
[J].It has long been proposed that the hydrated excess proton in water (aka the solvated "hydronium" cation) likely has two limiting forms, that of the Eigen cation (HO) and that of the Zundel cation (HO). There has been debate over which of these two is the more dominant species and/or whether intermediate (or "distorted") structures between these two limits are the more realistic representation. Spectroscopy experiments have recently provided further results regarding the excess proton. These experiments show that the hydrated proton has an anisotropy reorientation time scale on the order of 1-2 ps. This time scale has been suggested to possibly contradict the picture of the more rapid "special pair dance" phenomenon for the hydrated excess proton, which is a signature of a distorted Eigen cation. The special pair dance was predicted from prior computational studies in which the hydrated central core hydronium structure continually switches (O-H···O)* special pair hydrogen-bond partners with the closest three water molecules, yielding on average a distorted Eigen cation with three equivalent and dynamically exchanging distortions. Through state-of-art simulations it is shown here that anisotropy reorientation time scales of the same magnitude are obtained that also include structural reorientations associated with the special pair dance, leading to a reinterpretation of the experimental results. These results and additional analyses point to a distorted and dynamic Eigen cation as the most prevalent hydrated proton species in aqueous acid solutions of dilute to moderate concentration, as opposed to a stabilized or a distorted (but not "dancing") Zundel cation.
Raman spectrum and polarizability of liquid water from deep neural networks
[J].We introduce a scheme based on machine learning and deep neural networks to model the environmental dependence of the electronic polarizability in insulating materials. Application to liquid water shows that training the network with a relatively small number of molecular configurations is sufficient to predict the polarizability of arbitrary liquid configurations in close agreement with ab initio density functional theory calculations. In combination with a neural network representation of the interatomic potential energy surface, the scheme allows us to calculate the Raman spectra along 2-nanosecond classical trajectories at different temperatures for HO and DO. The vast gains in efficiency provided by the machine learning approach enable longer trajectories and larger system sizes relative to ab initio methods, reducing the statistical error and improving the resolution of the low-frequency Raman spectra. Decomposing the spectra into intramolecular and intermolecular contributions elucidates the mechanisms behind the temperature dependence of the low-frequency and stretch modes.
Signatures of a liquid-liquid transition in an ab initio deep neural network model for water
[J].The possible existence of a metastable liquid-liquid transition (LLT) and a corresponding liquid-liquid critical point (LLCP) in supercooled liquid water remains a topic of much debate. An LLT has been rigorously proved in three empirically parametrized molecular models of water, and evidence consistent with an LLT has been reported for several other such models. In contrast, experimental proof of this phenomenon has been elusive due to rapid ice nucleation under deeply supercooled conditions. In this work, we combined density functional theory (DFT), machine learning, and molecular simulations to shed additional light on the possible existence of an LLT in water. We trained a deep neural network (DNN) model to represent the ab initio potential energy surface of water from DFT calculations using the Strongly Constrained and Appropriately Normed (SCAN) functional. We then used advanced sampling simulations in the multithermal-multibaric ensemble to efficiently explore the thermophysical properties of the DNN model. The simulation results are consistent with the existence of an LLCP, although they do not constitute a rigorous proof thereof. We fit the simulation data to a two-state equation of state to provide an estimate of the LLCP's location. These combined results-obtained from a purely first-principles approach with no empirical parameters-are strongly suggestive of the existence of an LLT, bolstering the hypothesis that water can separate into two distinct liquid forms.
Hydrogen dynamics in supercritical water probed by neutron scattering and computer simulations
[J].In this work, an investigation of supercritical water is presented combining inelastic and deep inelastic neutron scattering experiments and molecular dynamics simulations based on a machine-learned potential of quality. The local hydrogen dynamics is investigated at 250 bar and in the temperature range of 553-823 K, covering the evolution from subcritical liquid to supercritical gas-like water. The evolution of libration, bending, and stretching motions in the vibrational density of states is studied, analyzing the spectral features by a mode decomposition. Moreover, the hydrogen nuclear momentum distribution is measured, and its anisotropy is probed experimentally. It is shown that hydrogen bonds survive up to the higher temperatures investigated, and we discuss our results in the framework of the coupling between intramolecular modes and intermolecular librations. Results show that the local potential affecting hydrogen becomes less anisotropic within the molecular plane in the supercritical phase, and we attribute this result to the presence of more distorted hydrogen bonds.
Phase equilibrium of water with hexagonal and cubic ice using the SCAN functional
[J].Machine learning models are rapidly becoming widely used to simulate complex physicochemical phenomena with accuracy. Here, we use one such model as well as direct density functional theory (DFT) calculations to investigate the phase equilibrium of water, hexagonal ice (Ih), and cubic ice (Ic), with an eye toward studying ice nucleation. The machine learning model is based on deep neural networks and has been trained on DFT data obtained using the SCAN exchange and correlation functional. We use this model to drive enhanced sampling simulations aimed at calculating a number of complex properties that are out of reach of DFT-driven simulations and then employ an appropriate reweighting procedure to compute the corresponding properties for the SCAN functional. This approach allows us to calculate the melting temperature of both ice polymorphs, the driving force for nucleation, the heat of fusion, the densities at the melting temperature, the relative stability of ices Ih and Ic, and other properties. We find a correct qualitative prediction of all properties of interest. In some cases, quantitative agreement with experiment is better than for state-of-the-art semiempirical potentials for water. Our results also show that SCAN correctly predicts that ice Ih is more stable than ice Ic.
Phase diagram of a deep potential water model
[J].
The phase diagram of water at high pressures as obtained by computer simulations of the TIP4P/2005 model: The appearance of a plastic crystal phase
[J].In this work the high pressure region of the phase diagram of water has been studied by computer simulation by using the TIP4P/2005 model of water. Free energy calculations were performed for ices VII and VIII and for the fluid phase to determine the melting curve of these ices. In addition, molecular dynamics simulations were performed at high temperatures (440 K) observing the spontaneous freezing of the liquid into a solid phase at pressures of about 80,000 bar. The analysis of the structure obtained lead to the conclusion that a plastic crystal phase was formed. In the plastic crystal phase the oxygen atoms were arranged forming a body center cubic structure, as in ice VII, but the water molecules were able to rotate almost freely. Free energy calculations were performed for this new phase, and it was found that for TIP4P/2005 this plastic crystal phase is thermodynamically stable with respect to ices VII and VIII for temperatures higher than about 400 K, although the precise value depends on the pressure. By using Gibbs-Duhem simulations, all coexistence lines were determined, and the phase diagram of the TIP4P/2005 model was obtained, including ices VIII and VII and the new plastic crystal phase. The TIP4P/2005 model is able to describe qualitatively the phase diagram of water. It would be of interest to study if such a plastic crystal phase does indeed exist for real water. The nearly spherical shape of water makes possible the formation of a plastic crystal phase at high temperatures. The formation of a plastic crystal phase at high temperatures (with a bcc arrangements of oxygen atoms) is fast from a kinetic point of view occurring in about 2 ns. This is in contrast to the nucleation of ice Ih which requires simulations of the order of hundreds of ns.
Heat transport in liquid water from first-principles and deep neural network simulations
[J].
Modeling liquid water by climbing up Jacob's ladder in density functional theory facilitated by using deep neural network potentials
[J].
Using neural network force fields to ascertain the quality of ab initio simulations of liquid water
[J].
Condensed phase water molecular multipole moments from deep neural network models trained on ab initio simulation data
[J].Ionic solvation phenomena in liquids involve intense interactions in the inner solvation shell. For interactions beyond the first shell, the ion-solvent interaction energies result from the sum of many smaller-magnitude contributions that can still include polarization effects. Deep neural network (DNN) methods have recently found wide application in developing efficient molecular models that maintain near-quantum accuracy. Here we extend the DeePMD-kit code to produce accurate molecular multipole moments in the bulk and near interfaces. The new method is validated by comparing the DNN moments with those generated by simulations. The moments are used to compute the electrostatic potential at the center of a molecular-sized hydrophobic cavity in water. The results show that the fields produced by the DNN models are in quantitative agreement with the AIMD-derived values. These efficient methods will open the door to more accurate solvation models for large solutes such as proteins.
Imperfectly coordinated water molecules pave the way for homogeneous ice nucleation
[DB/OL].
Molecular dynamics simulation of zinc ion in water with an ab initio based neural network potential
[J].
Learning intermolecular forces at liquid-vapor interfaces
[J].
Reactive uptake of N2O5 by atmospheric aerosol is dominated by interfacial processes
[J].