合金熔体中组分间的活度相互作用系数除了可以通过实验测定外,还可以采用理论模型进行计算。在理论计算方面,Alcock和Richardson[13,14]首先通过拟化学模型[15]解释了铁基熔体中O和S的热力学相互作用行为,开启了理论计算合金中组分间活度相互作用系数的序幕。Lupis和Elliott[16]进一步采用拟化学模型及扩展的拟化学模型建立了计算任意基体中组分间活度相互作用系数的模型,并计算了部分合金体系中组分间的一阶和二阶活度相互作用系数,得到的结果与实验值具有很好的一致性。但是,该方法中所需的关键参数需从实验数据中获取,因此,该模型难以推广。此后,研究者们提出了许多计算方法。例如,Tanaka等[17]采用自由体积模型计算了Fe-N-X合金系中组分间的活度相互作用系数
20世纪90年代初,丁学勇等[23~26]首次采用Toop模型(Toop-Kohler模型)[32]耦合Miedema模型[27~29]建立了计算任意基体中组分间的活度相互作用系数的模型,并利用该模型大量计算了铁基合金中组元间的一阶活度相互作用系数,计算值与实验值吻合很好。然而,Toop-Kohler模型[32]属于非对称模型,在计算之前需确定非对称组元,并且当非对称组元为溶剂组分时,Toop-Kohler模型[32]耦合的Miedema模型[27~29]无法导出正确的活度相互作用系数的计算式。针对此种情况,丁学勇等[33]采用Hillert模型(Toop-Colinet模型)[34]给出了计算此种条件下的活度相互作用系数的计算式。此外,丁学勇等[33]还研究了非对称组分的选择对活度相互作用系数的计算值的影响,以及在同一非对称组分下(溶质组分为非对称组分的情况),对比了Toop-Kohler模型[32]和Hillert模型[34]计算的活度相互作用系数与实验值的吻合程度。结果表明,对于大多数合金来说,选择不同的非对称组分的计算结果差别较大;在同一个非对称组分条件下,Toop-Kohler模型[32]的计算结果与实验值的吻合度总体上要好于Hillert模型[34]的计算结果与实验值的吻合度。这说明,不同的合金体系需要采用不同的外推模型进行处理。Chartrand和Pelton[35]也指出,不同的外推模型具有其自身适用的合金体系。Dogan和Arslan[36]在对比不同外推模型的预测效果时也得到与此相一致的结论。因此,在采用外推模型耦合Miedema模型[27~29]来计算活度相互作用系数时,理论上可以根据不同合金系的性质选择适用的外推模型。然而,已报道的大量外推模型[30,32,34,35,37~43]均没有给出他们分别适用于何种性质的体系,这就导致了在实际操作中的困难。
为了开发一个理论自洽、适应体系范围更广的通用模型,范鹏等[44,45]和Zhang等[46]都采用了Chou模型[39]耦合Miedema模型[27~29]来构建活度相互作用系数的计算模型。Chou模型[39]通过引入组分间的相似系数,打破了传统外推模型的对称和非对称界限。并且,随着被处理体系性质的变化,Chou模型[39]可以还原到大多数的传统外推模型。即,Chou模型[39]可以利用组分间的相似系数概念对大多数传统外推模型给出的二元项的摩尔组成点的选择提供依据。但是,Chou模型[39]中的相似系数概念并不能清楚解释Kohler模型[42]给出的二元项的摩尔组成点[47]。这意味着由Chou模型[39]导出的活度相互作用系数模型对适用于Kohler模型[42]/Toop-Kohler模型[32]的体系依然缺乏说服力。
在前期工作中[47],作者考虑到任意两两组分间的性质差别存在差异,从外推模型的通用数学表达式[30]出发,认为对多元系的摩尔性质产生贡献的子二元项的摩尔组成受系统中余下组分的影响,但二元项的相互作用规律不受其影响。即,系统中余下每一组分根据其与选定二元项中的组分在性质上的差别大小,对选定二元项中各组分的摩尔量有贡献,以此构成该二元项在多元系中产生效应的摩尔组成,从而导出了一个在数学上可以覆盖所有传统外推模型的新模型——统一外推模型(unified extrapolation model,EM)。随后,将UEM[47]与Miedema模型[27~29]耦合建立了一个在数学上可以还原到任意传统外推模型耦合Miedema模型构建的计算稀合金溶液中溶质间活度相互作用系数的模型[48]。但是,前期工作[48]给出的模型并未考虑过剩熵项的影响。因此,本工作将进一步介绍该模型的特点及应用,并给出在考虑过剩熵条件下的活度相互作用系数模型的计算表达式。
1 活度相互作用系数的计算模型
式中,Tm, i 、Tm, j 分别为组分i、j的熔点,单位K。
因此,根据混合焓、过剩熵、过剩Gibbs自由能3者之间的关系,当温度为T时,二元系的摩尔过剩Gibbs自由能(
结合文献[48]对活度相互作用系数模型的推导,当考虑过剩熵时,基体k中组分j对i的活度相互作用系数
其中,
式中,R为通用气体常数,其值为8.314 J/(mol·K);Vi 、
式中,Dk-i 和Dk-j 分别表示组分k与组分i以及组分k与组分j在性质上的差值。
2 模型特点及应用
表1 本模型中贡献系数值与常见外推模型导出的活度相互作用系数模型之间的对应关系
Table 1
| Extrapolation model + Miedema model | Asymmetric component | ||||
|---|---|---|---|---|---|
| 1/2 | 1/2 | 1/2 | 1/2 | Muggianu model[43] + Miedema model[27-29] | - |
| 0 | 1 | 0 | 0 | Toop-Kohler model[32] + Miedema model[27-29] | i |
| 1 | 0 | 0 | 0 | Toop-Kohler model[32] + Miedema model[27-29] | j |
| 1/2 | 1/2 | 1 | 1 | Toop-Muggianu model[34] + Miedema model[27-29] | k |
| 0 | 1 | 0 | 1/2 | Toop-Muggianu model[34] + Miedema model[27-29] | i |
| 1 | 0 | 1/2 | 0 | Toop-Muggianu model[34] + Miedema model[27-29] | j |
| Similarity coefficient of Chou's model方正汇总行[39] | Chou's model[39] + Miedema model[27-29] | ||||
此外,从
根据贡献系数与组分间的性质差的大小对应关系(
(1) k、i、j两两之间的性质差均较大(Dk-i 、Dk-j 、Dj-i 3者的值均较大)。此种情况下,
(2) i与j之间存在较大性质差,但他们中的某一组分与k之间的性质差较小。以i与k之间的性质差较小,而k与j之间的性质差较大的情况为例(i与j之间存在较大的性质差,而k与i之间的性质差较小,则必然有k与j之间的性质差较大),此时
(3) i与j的性质差较小。此时,
为了说明这几种情况,以铁基熔体中Fe-C-Pb、Fe-C-Mn、Fe-Mn-Cr和Fe-Si-Al 4个合金系为例。其中,Fe-C-Pb属于两两组分间的性质差均较大的情况;Fe-C-Mn属于溶质组分间的性质差较大,但其中一组分与基体元素(Fe)之间的性质差较小的情况;Fe-Mn-Cr和Fe-Si-Al合金系属于溶质组分间的性质差较小的情况。这是因为,C属于非金属元素,而Pb和Mn属于金属元素,Mn与Cr属于相邻的过渡族金属元素,Al、Si属于相邻的主族元素。Fe和Pb虽然同属于金属元素,但Fe属于过渡族金属元素,而Pb属于主族金属元素,且它们在元素周期表中的位置也相离较远。因此,可以认为Fe与Pb之间同样存在较大性质差。
表2为在人为指定贡献系数值的条件下运用
表2
1873 K铁液中活度相互作用系数
Table 2
| k-i-j | ||||||
|---|---|---|---|---|---|---|
| Fe-C-Pb | 1 | 0 | 0 | 0 | 4.15 | 5.73 |
| 0 | 1 | 0 | 0 | 1.32 | ||
| 0 | 1 | 1 | 1 | -7.56 | ||
| 1 | 0 | 1 | 1 | -4.73 | ||
| 1 | 0 | 0 | 1 | -1.34 | ||
| 1 | 0 | 1 | 0 | 0.76 | ||
| 0 | 1 | 0 | 1 | -4.17 | ||
| 0 | 1 | 1 | 0 | -2.07 | ||
| Fe-C-Mn | 1 | 0 | 0 | 0 | -8.96 | -1.88 |
| 0 | 1 | 0 | 0 | -1.62 | ||
| 0 | 1 | 1 | 1 | -5.01 | ||
| 1 | 0 | 1 | 1 | -12.35 | ||
| 1 | 0 | 0 | 1 | -8.96 | ||
| 1 | 0 | 1 | 0 | -12.35 | ||
| 0 | 1 | 0 | 1 | -1.62 | ||
| 0 | 1 | 1 | 0 | -5.01 | ||
| Fe-Mn-Cr | 1 | 0 | 0 | 0 | 0.74 | 0.90 |
| 0 | 1 | 0 | 0 | 0.74 | ||
| 0 | 1 | 1 | 1 | 0.73 | ||
| 1 | 0 | 1 | 1 | 0.74 | ||
| 1 | 0 | 0 | 1 | 0.74 | ||
| 1 | 0 | 1 | 0 | 0.74 | ||
| 0 | 1 | 0 | 1 | 0.73 | ||
| 0 | 1 | 1 | 0 | 0.74 | ||
| Fe-Al-Si | 1 | 0 | 0 | 0 | 6.03 | 6.97 |
| 0 | 1 | 0 | 0 | 6.01 | ||
| 0 | 1 | 1 | 1 | 6.80 | ||
| 1 | 0 | 1 | 1 | 6.82 | ||
| 1 | 0 | 0 | 1 | 6.51 | ||
| 1 | 0 | 1 | 0 | 6.34 | ||
| 0 | 1 | 0 | 1 | 6.49 | ||
| 0 | 1 | 1 | 0 | 6.32 |
3 组分间性质差的计算
在文献[48]中,采用A、B组分分别与C组分相互作用时表现出的性质差异来表征A、B两组分间的性质差,在不考虑过剩熵的条件下同样取得了计算值与实验值相一致的结果。但是,在后来的研究[54]中发现,文献[48]中采用的组分间的性质差的计算式是不充分的。之所以在文献[48]中依然能取得计算值与实验值相一致的结果,其原因是对于大多数的合金系,组元间的活度相互作用系数大小主要取决于溶剂k对溶质i和j的贡献系数的相对大小,即
式中,
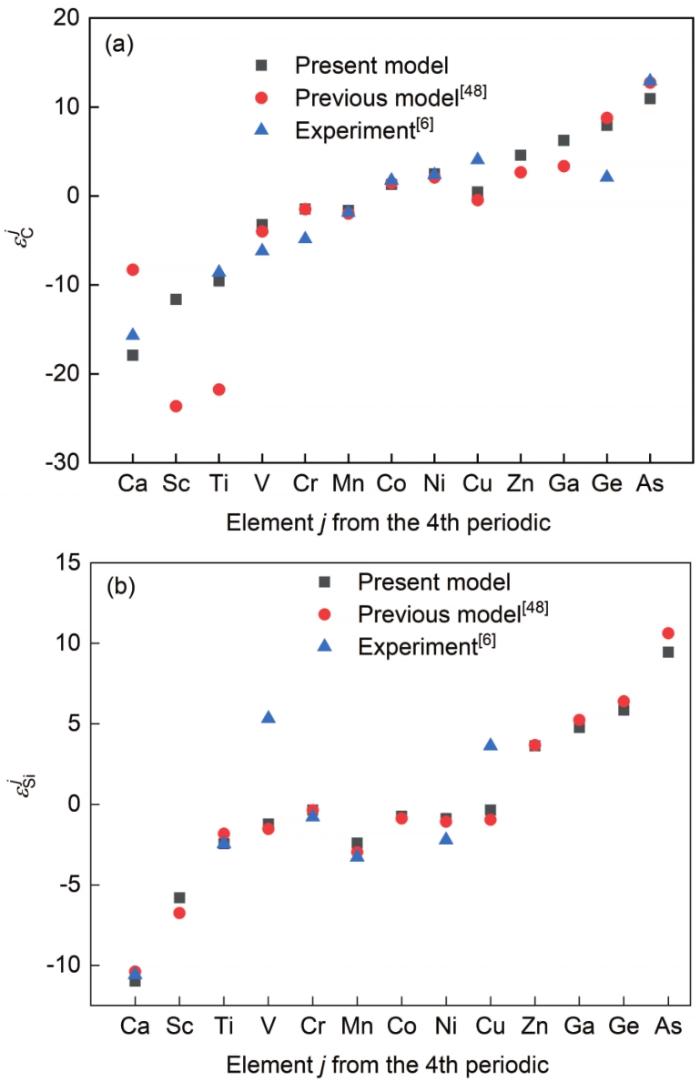
图1
4 结论
(1) 本工作给出了利用UEM结合Miedema模型、Tanaka过剩熵关系式导出的计算任意基体中溶质间活度相互作用系数的模型。该模型在数学上不仅可以覆盖其他传统外推模型耦合Miedema模型导出的活度相互作用系数模型,还可以利用组分间的性质差大小定性解释传统外推模型给出的活度相互作用系数模型的预测特点及适用体系。
(2) 通过实例分析表明,准确表征两组分间的性质差大小对本模型的预测可靠性具有至关重要的影响。本工作中,将两组分间的性质差表示成这两组分彼此被对方完全包围时所表现出的性质差异,该模型表现出了较先前模型计算结果与实验值更一致的结果。
参考文献
The thermodynamics of dilute liquid copper alloys
[J].
The thermodynamics of liquid dilute iron alloys
[J].
The thermodynamics of dilute liquid cobalt alloys
[J].
The thermodynamics of dilute liquid nickel alloys
[J].
On the interaction of calcium and oxygen in liquid iron
[J].
Measurement of interaction parameter between Cu and Al in molten high Al steel
[J].
Calculation of interaction coefficient
镍基高温合金中钛对氮相互作用系数
Effect of silicon on tin formation in liquid iron
[J].
Determination of interaction parameters between elements in molten iron by evaporation and chemical equilibration techniques
[J].
蒸気圧法ならびに化学平衡法による溶鉄中元素間の相互作用パラメータの測定
[J].
Thermodynamics of copper-rich liquid Cu-Fe-Bi alloys determined by vapour pressure measurements
[J].
Dilute solutions in molten metals and alloys
[J].
Dilute solutions in alloys
[J].
Generalized interaction coefficients
[J].
Thermodynamic relationship between the enthalpy interaction parameter and entropy interaction parameter in liquid iron-nitrogen based ternary alloys
[J].
Prediction expressions of component activity coefficients in Si-based melts
[J].
Prediction of thermodynamic properties of solute elements in Si solutions using first-principles calculations
[J].
Estimation of activity coefficients and interaction parameters of solutes in silicon melts
[J].
Theoretical treatment of interaction parameters in multicomponent metallic solutions
[J].
Interaction parameters in metallic solutions estimated from liquid structure and the heat of solution at infinite dilution
[J].
Thermodynamic calculation of Fe-P-j system melt
[J].
Fe-P-j三元系熔体的热力学计算
[J].利用导出的热力学模型,计算了1873K下Fe液中合金元素对P的活度相互作用系数ε_P,结果表明,计算值和实验值正负号一致率达94.7%,并基本处于同一数量级.
Models of activity and activity interaction parameter in ternary metallic melt
[J].

The calculating models for activity and activity interaction parameter in ternary metallic melts were established.1nγof any element,ε,εand,ρ,ρ,ρbetween any element in any metallic melt could be calculated rapidly and accurately except for O,S,Se and Te.The models could be used in both solid and liquid metallic solutions.The factors to affect 1nγ were the electron density,nWS,electronegativity,Φ,and molar volume,V of solute i and solvent k.The values of 1nγ by calculation were well accordant with those by experiments.The fraction of same sign between calculating values and experiment data for Fe-base alloys reached 95.7%.The factors to affectεandεwere nWS,Φ,V of solute i,j and solvent k.The data by calculation and experiments were basically same.The fraction of same sign was above 80%.The more reliable the experiments,the more the ratio of the same sign.
三元系金属熔体中的活度和活度相互作用系数模型
[J].

提出计算金属液中活度和活度相互作用系数的模型.据此可以快速、准确地计算出任何三元系金属熔体中除O,S,Se,Te外任何组元的1nγ和任何组元间的一级活度相互作用系数ε,ε以及二级活度相互作用系数ρ,ρ,ρ.影响1nγ的因素是i(溶质)和k(溶剂)的nWS(电子密度)、Φ(电负性)以及i的V(摩尔体积)值。由模型计算出的1nγ值与实验值吻合较好,对铁基合金正负号一致率达95.7%;影响活度相互作用系数的因素是溶质i和j以及溶剂k的nWS,Φ和V,ε,ε的计算值和实验值基本一致,对液态铁合金正负号一致率达80%以上.
Thermodynamic model calculation in copper liquid
[J].
铜液中的热力学模型计算
[J].
Thermodynamic calculation for alloy systems
[J].
Cohesion in alloys—Fundamentals of a semi-empirical model
[J].
On the heat of formation of solid alloys. II
[J]. J.
A study of ternary geometrical models
[J].
Generalized interaction coefficients: Part I: Definitions
[J].
Predicting ternary activities using binary data
[J].
Empirical methods of predicting and representing thermodynamic properties of ternary solution phases
[J].
On the choice of “geometric” thermodynamic models
[J].
Comparative thermodynamic prediction of integral properties of six component, quaternary, and ternary systems
[J].
A new solution model for predicting ternary thermodynamic properties
[J].
“Equidistant method” to estimate thermodynamic properties of multicomponent solutions by using data on binary boundary systems
[J].
A new generation solution model for predicting thermodynamic properties of a multicomponent system from binaries
[J].
A general “geometric” thermodynamic model for multicomponent solutions
[J].
The estimation of the thermodynamic properties of ternary alloys from binary data using the shortest distance composition path
[J].
Estimation of the thermodynamic data for a ternary system from the corresponding binary systems
[J].
Enthalpies de formation des alliages liquides bismuth-étain-gallium à 723 k. Choix d'une représentation analytique des grandeurs d'excès intégrales et partielles de mélange
[J].
A model for predicting thermodynamic properties of metallic solutions from fundmental physical quantities of constituent elements
[J].
由组元的物性参数预测金属熔体的热力学性质
[J].
A self-consistent model for predicting interaction parameters in multicomponent alloys
[J].
Modeling activity and interaction coefficients of components of multicomponent alloy melts: An example of iron melt
[J].As a popular thermodynamic calculation method for binary alloys, Miedema's model has been applied in many fields. Chou's Model, a new generation of geometric model for ternary and multicomponent alloy systems, overcomes the intrinsic theoretical defects (including symmetric and asymmetric) existing in some original geometric models. Here, by means of combining Miedema's model and Chou's model as well as including the consideration of the excess entropy we attempted to build the new thermodynamic model to evaluate thermodynamic properties of ternary and multicomponent alloying systems in terms of the physical parameters (molar volume, electronegativity, electronic density and melting point) of constituents. Moreover, the activity and interaction coefficients of a wide of components in iron melt have been discussed in details.
A new perspective on geometric thermodynamic models
[J].To estimate the thermodynamic properties of a multi-component system using traditional geometric models, lack of a physical meaning generates many puzzles during choosing a concrete method. In this paper, we introduced a perspective in terms of the molar quantity of the components in the sub-binary of a ternary system affected by the third component and deduced a new model to unify all other traditional geometric models (e.g. Kohler, Muggianu, Toop-Kohler, etc.) into one model. The effects could be represented by so-called contribution coefficients, whose values only depend on the degree of identity between the thermodynamic properties of the third component and those of the selected components in the sub-binary, and which gives the physical meaning for the present model.
A general model for solutes activity interaction parameters in dilute metallic solutions
[J].
Relationship between enthalpy of mixing and excess entropy in liquid binary alloys
[J].
Thermodynamic relationship between enthalpy of mixing and excess entropy in liquid binary alloys
[J].
Thermodynamic relationship between enthalpy of mixing and excess entropy in solid solutions of binary alloys
[J].
Enthalpy of formation of binary solid and liquid Mg alloys—Comparison of Miedema-model calculations with data reported in literature
[J].
On the definition of the components' difference in properties in the unified extrapolation model
[J].