Dislocation density within lath martensite in Fe-C and Fe-Ni alloys
2
2003
... 板条马氏体钢具有超高的强度和较高塑性,因而具有广泛的工业应用.板条马氏体组织中的精细板条结构和高密度位错(> 1015 m-2)是马氏体钢具有超高强度的主要原因[1~3].20世纪70年代以来,研究者们致力于板条马氏体钢微观组织结构与强塑性能之间关系的研究.板条马氏体结构可具体划分为板条、板条块、子板条块、板条束和原奥氏体晶粒[4,5].一个原奥氏体晶粒内可形成若干个马氏体板条束,板条束又进一步划分为板条块,板条块由板条组成;板条束内的板条具有相同的惯习面,板条块内的板条具有相同的取向;板条块两两成对形成具有10°取向差晶界的子板条块[4,5].这些精细结构就构成了马氏体“有效晶粒”组织单元.板条束的尺寸影响了板条马氏体钢的强度[6]和塑性[7],而板条块则是决定强度的主要组织单元[8,9]. ...
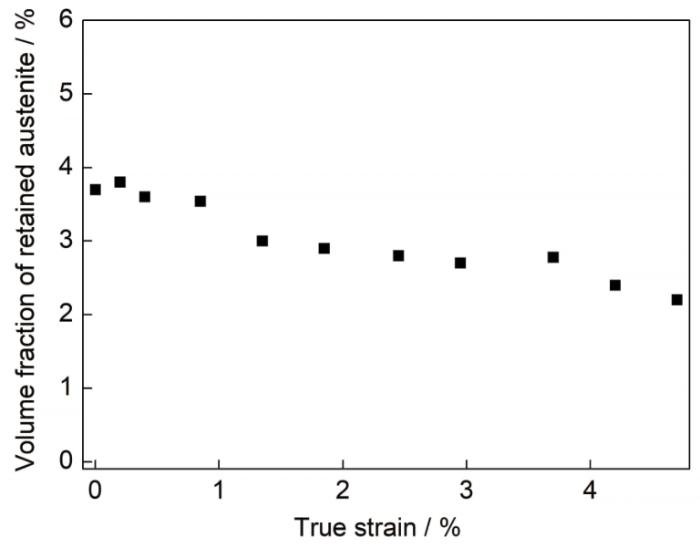
... 22SiMn2TiB钢淬火回火后的SEM和EBSD像如图2所示.由图2a可见,22SiMn2TiB钢淬火回火组织为典型的板条马氏体组织.图2b的EBSD像给出了马氏体板条的取向分布,图中采用黑色实线绘制板条束和板条块之间的大角度晶界.由图2b可以看出,一个板条束内通常包含3个完全不同取向(颜色)的板条块.经测试,其硬度为45.8 HRC,马氏体板条束和板条块的平均尺寸分别为15.8和3.90 μm.22SiMn2TiB钢形变前的STEM-BF和ADF像如图3所示.由图3的ADF像可清楚地观察到马氏体板条内的位错,其显示了22SiMn2TiB钢内的高密度位错结构.经测试,22SiMn2TiB钢内的位错密度在8.79 × 1014~1.48 × 1015 m-2之间,平均位错密度为1.17 × 1015 m-2,与Morito等[1,8]对Fe-0.2C-2Mn马氏体钢的位错密度测量结果接近.对22SiMn2TiB钢进行CMWP拟合得出:q = 1.9,表明22SiMn2TiB钢板条马氏体内的位错为刃、螺型位错的混合位错;M = 2.0,表明位错的分布呈随机分布特征[2].初始组织中残余奥氏体含量为3.7%. ...
Study of tempering behavior of lath martensite using in situ neutron diffraction
1
2015
... 22SiMn2TiB钢淬火回火后的SEM和EBSD像如图2所示.由图2a可见,22SiMn2TiB钢淬火回火组织为典型的板条马氏体组织.图2b的EBSD像给出了马氏体板条的取向分布,图中采用黑色实线绘制板条束和板条块之间的大角度晶界.由图2b可以看出,一个板条束内通常包含3个完全不同取向(颜色)的板条块.经测试,其硬度为45.8 HRC,马氏体板条束和板条块的平均尺寸分别为15.8和3.90 μm.22SiMn2TiB钢形变前的STEM-BF和ADF像如图3所示.由图3的ADF像可清楚地观察到马氏体板条内的位错,其显示了22SiMn2TiB钢内的高密度位错结构.经测试,22SiMn2TiB钢内的位错密度在8.79 × 1014~1.48 × 1015 m-2之间,平均位错密度为1.17 × 1015 m-2,与Morito等[1,8]对Fe-0.2C-2Mn马氏体钢的位错密度测量结果接近.对22SiMn2TiB钢进行CMWP拟合得出:q = 1.9,表明22SiMn2TiB钢板条马氏体内的位错为刃、螺型位错的混合位错;M = 2.0,表明位错的分布呈随机分布特征[2].初始组织中残余奥氏体含量为3.7%. ...
A
1
1999
... 板条马氏体钢具有超高的强度和较高塑性,因而具有广泛的工业应用.板条马氏体组织中的精细板条结构和高密度位错(> 1015 m-2)是马氏体钢具有超高强度的主要原因[1~3].20世纪70年代以来,研究者们致力于板条马氏体钢微观组织结构与强塑性能之间关系的研究.板条马氏体结构可具体划分为板条、板条块、子板条块、板条束和原奥氏体晶粒[4,5].一个原奥氏体晶粒内可形成若干个马氏体板条束,板条束又进一步划分为板条块,板条块由板条组成;板条束内的板条具有相同的惯习面,板条块内的板条具有相同的取向;板条块两两成对形成具有10°取向差晶界的子板条块[4,5].这些精细结构就构成了马氏体“有效晶粒”组织单元.板条束的尺寸影响了板条马氏体钢的强度[6]和塑性[7],而板条块则是决定强度的主要组织单元[8,9]. ...
The morphology and crystallography of lath martensite in Fe-C alloys
4
2003
... 板条马氏体钢具有超高的强度和较高塑性,因而具有广泛的工业应用.板条马氏体组织中的精细板条结构和高密度位错(> 1015 m-2)是马氏体钢具有超高强度的主要原因[1~3].20世纪70年代以来,研究者们致力于板条马氏体钢微观组织结构与强塑性能之间关系的研究.板条马氏体结构可具体划分为板条、板条块、子板条块、板条束和原奥氏体晶粒[4,5].一个原奥氏体晶粒内可形成若干个马氏体板条束,板条束又进一步划分为板条块,板条块由板条组成;板条束内的板条具有相同的惯习面,板条块内的板条具有相同的取向;板条块两两成对形成具有10°取向差晶界的子板条块[4,5].这些精细结构就构成了马氏体“有效晶粒”组织单元.板条束的尺寸影响了板条马氏体钢的强度[6]和塑性[7],而板条块则是决定强度的主要组织单元[8,9]. ...
... [4,5].这些精细结构就构成了马氏体“有效晶粒”组织单元.板条束的尺寸影响了板条马氏体钢的强度[6]和塑性[7],而板条块则是决定强度的主要组织单元[8,9]. ...
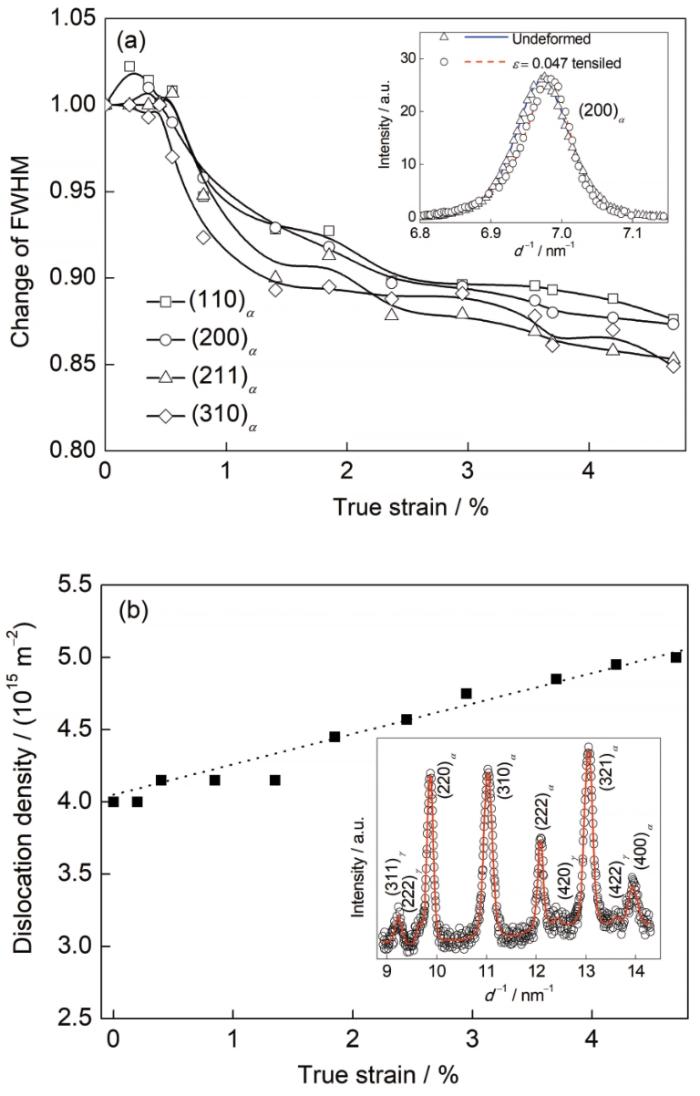
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
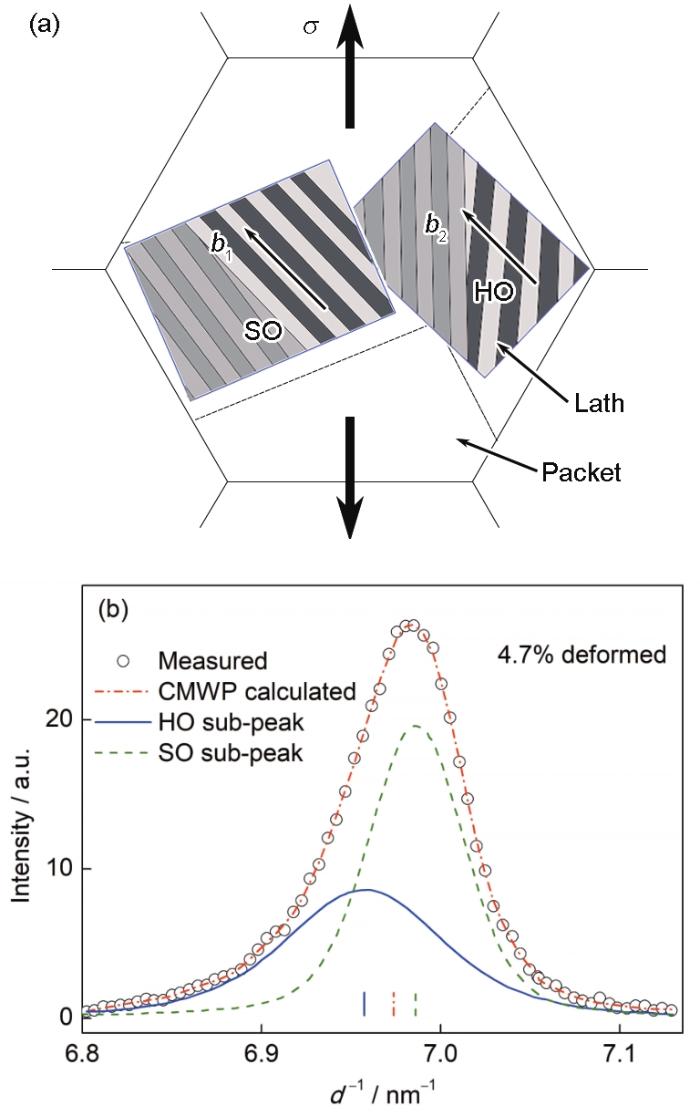
... 马氏体板条束内的板条具有相同的(110)惯习面,一个板条束内的板条又形成了具有不同取向分布的板条块;板条块内的板条可能具有另外的(110)或者(200)等晶面[4,5].板条马氏体组织的微尺寸塑性变形实验研究[41,42]表明,马氏体的微尺寸试样如果只包含一个板条块时,其拉伸塑性变形过程没有加工硬化现象;微尺寸试样内包含2个及以上板条块时,试样在拉伸塑性变形过程中才会出现明显的加工硬化.这说明,板条马氏体塑性变形过程中应力在板条束内进行再分配,板条的塑性应变和板条取向有关.由此,应力作用下的板条束可划分为2种类型[33]:滑移系(Burgers矢量)位于板条平面内、板条取向利于位错滑移的板条束定义为软取向(SO)板条束,滑移系不在板条平面内、板条取向不利于位错滑移的板条束定义为硬取向(HO)板条束,如图9a所示.塑性变形过程中软取向板条束内的滑移系在较低的剪切应力作用下即可产生滑移,位错密度降低,出现加工软化特征;硬取向板条束内的滑移系需要更高的剪切应力作用,位错密度升高,出现加工硬化特征.采用CMWP方法对衍射峰进行拟合计算,结果如图9b所示.马氏体的衍射峰可拆分为硬取向和软取向2个子峰,具有较高强度、较低FWHM的子峰对应软取向板条束;强度低、FWHM宽的子峰对应硬取向板条束.通过拟合计算得到2个子峰的体积分数(fHO、fSO)和位错密度(ρHO、ρSO),进行加权平均计算得到马氏体的平均位错密度(ρAV): ...
The morphology and crystallography of lath martensite in alloy steels
4
2006
... 板条马氏体钢具有超高的强度和较高塑性,因而具有广泛的工业应用.板条马氏体组织中的精细板条结构和高密度位错(> 1015 m-2)是马氏体钢具有超高强度的主要原因[1~3].20世纪70年代以来,研究者们致力于板条马氏体钢微观组织结构与强塑性能之间关系的研究.板条马氏体结构可具体划分为板条、板条块、子板条块、板条束和原奥氏体晶粒[4,5].一个原奥氏体晶粒内可形成若干个马氏体板条束,板条束又进一步划分为板条块,板条块由板条组成;板条束内的板条具有相同的惯习面,板条块内的板条具有相同的取向;板条块两两成对形成具有10°取向差晶界的子板条块[4,5].这些精细结构就构成了马氏体“有效晶粒”组织单元.板条束的尺寸影响了板条马氏体钢的强度[6]和塑性[7],而板条块则是决定强度的主要组织单元[8,9]. ...
... ,5].这些精细结构就构成了马氏体“有效晶粒”组织单元.板条束的尺寸影响了板条马氏体钢的强度[6]和塑性[7],而板条块则是决定强度的主要组织单元[8,9]. ...
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
... 马氏体板条束内的板条具有相同的(110)惯习面,一个板条束内的板条又形成了具有不同取向分布的板条块;板条块内的板条可能具有另外的(110)或者(200)等晶面[4,5].板条马氏体组织的微尺寸塑性变形实验研究[41,42]表明,马氏体的微尺寸试样如果只包含一个板条块时,其拉伸塑性变形过程没有加工硬化现象;微尺寸试样内包含2个及以上板条块时,试样在拉伸塑性变形过程中才会出现明显的加工硬化.这说明,板条马氏体塑性变形过程中应力在板条束内进行再分配,板条的塑性应变和板条取向有关.由此,应力作用下的板条束可划分为2种类型[33]:滑移系(Burgers矢量)位于板条平面内、板条取向利于位错滑移的板条束定义为软取向(SO)板条束,滑移系不在板条平面内、板条取向不利于位错滑移的板条束定义为硬取向(HO)板条束,如图9a所示.塑性变形过程中软取向板条束内的滑移系在较低的剪切应力作用下即可产生滑移,位错密度降低,出现加工软化特征;硬取向板条束内的滑移系需要更高的剪切应力作用,位错密度升高,出现加工硬化特征.采用CMWP方法对衍射峰进行拟合计算,结果如图9b所示.马氏体的衍射峰可拆分为硬取向和软取向2个子峰,具有较高强度、较低FWHM的子峰对应软取向板条束;强度低、FWHM宽的子峰对应硬取向板条束.通过拟合计算得到2个子峰的体积分数(fHO、fSO)和位错密度(ρHO、ρSO),进行加权平均计算得到马氏体的平均位错密度(ρAV): ...
Steels: Heat Treatment and Processing Principles
1
1990
... 板条马氏体钢具有超高的强度和较高塑性,因而具有广泛的工业应用.板条马氏体组织中的精细板条结构和高密度位错(> 1015 m-2)是马氏体钢具有超高强度的主要原因[1~3].20世纪70年代以来,研究者们致力于板条马氏体钢微观组织结构与强塑性能之间关系的研究.板条马氏体结构可具体划分为板条、板条块、子板条块、板条束和原奥氏体晶粒[4,5].一个原奥氏体晶粒内可形成若干个马氏体板条束,板条束又进一步划分为板条块,板条块由板条组成;板条束内的板条具有相同的惯习面,板条块内的板条具有相同的取向;板条块两两成对形成具有10°取向差晶界的子板条块[4,5].这些精细结构就构成了马氏体“有效晶粒”组织单元.板条束的尺寸影响了板条马氏体钢的强度[6]和塑性[7],而板条块则是决定强度的主要组织单元[8,9]. ...
Effect of microstructural refinement on the toughness of low carbon martensitic steel
2
2008
... 板条马氏体钢具有超高的强度和较高塑性,因而具有广泛的工业应用.板条马氏体组织中的精细板条结构和高密度位错(> 1015 m-2)是马氏体钢具有超高强度的主要原因[1~3].20世纪70年代以来,研究者们致力于板条马氏体钢微观组织结构与强塑性能之间关系的研究.板条马氏体结构可具体划分为板条、板条块、子板条块、板条束和原奥氏体晶粒[4,5].一个原奥氏体晶粒内可形成若干个马氏体板条束,板条束又进一步划分为板条块,板条块由板条组成;板条束内的板条具有相同的惯习面,板条块内的板条具有相同的取向;板条块两两成对形成具有10°取向差晶界的子板条块[4,5].这些精细结构就构成了马氏体“有效晶粒”组织单元.板条束的尺寸影响了板条马氏体钢的强度[6]和塑性[7],而板条块则是决定强度的主要组织单元[8,9]. ...
... 马氏体组织在拉伸形变过程中通常没有明显的屈服现象,具有较高的屈服强度和抗拉强度.这表明马氏体组织在屈服后发生塑性变形初期会产生明显的加工硬化现象.马氏体在塑性变形过程中的主要方式是位错沿着滑移面的滑移过程,随着变形度的增加,马氏体中的位错密度逐渐增加,板条束或板条块之间的大角度晶界会阻碍位错的滑移形成表面浮凸[7,10].C原子等在刃型位错上偏析形成“Cottrell气团”也可阻碍位错的运动,从而提高强度[11].Morooka等[12]研究了冷轧Fe-18Ni合金的板条马氏体拉伸形变过程中的位错密度变化规律,他们基于经典的Williamson-Hall (W-H)曲线斜率的降低得出了高位错密度的马氏体组织塑性变形过程中位错密度下降的结论.马氏体板条之间通常有薄膜状或片状的残余奥氏体,形变过程中残余奥氏体会吸收位错(DARA),导致残余奥氏体内的位错密度随应变量的增加而增加;因而残余奥氏体表现出较高的加工硬化率,而形变马氏体则处于“软化态”或“未加工硬化态”[13,14].由此可见,板条马氏体组织形变过程中的加工硬化与其组织结构单元、位错密度之间的依赖关系仍然不够清晰. ...
A
3
2006
... 板条马氏体钢具有超高的强度和较高塑性,因而具有广泛的工业应用.板条马氏体组织中的精细板条结构和高密度位错(> 1015 m-2)是马氏体钢具有超高强度的主要原因[1~3].20世纪70年代以来,研究者们致力于板条马氏体钢微观组织结构与强塑性能之间关系的研究.板条马氏体结构可具体划分为板条、板条块、子板条块、板条束和原奥氏体晶粒[4,5].一个原奥氏体晶粒内可形成若干个马氏体板条束,板条束又进一步划分为板条块,板条块由板条组成;板条束内的板条具有相同的惯习面,板条块内的板条具有相同的取向;板条块两两成对形成具有10°取向差晶界的子板条块[4,5].这些精细结构就构成了马氏体“有效晶粒”组织单元.板条束的尺寸影响了板条马氏体钢的强度[6]和塑性[7],而板条块则是决定强度的主要组织单元[8,9]. ...
... 22SiMn2TiB钢淬火回火后的SEM和EBSD像如图2所示.由图2a可见,22SiMn2TiB钢淬火回火组织为典型的板条马氏体组织.图2b的EBSD像给出了马氏体板条的取向分布,图中采用黑色实线绘制板条束和板条块之间的大角度晶界.由图2b可以看出,一个板条束内通常包含3个完全不同取向(颜色)的板条块.经测试,其硬度为45.8 HRC,马氏体板条束和板条块的平均尺寸分别为15.8和3.90 μm.22SiMn2TiB钢形变前的STEM-BF和ADF像如图3所示.由图3的ADF像可清楚地观察到马氏体板条内的位错,其显示了22SiMn2TiB钢内的高密度位错结构.经测试,22SiMn2TiB钢内的位错密度在8.79 × 1014~1.48 × 1015 m-2之间,平均位错密度为1.17 × 1015 m-2,与Morito等[1,8]对Fe-0.2C-2Mn马氏体钢的位错密度测量结果接近.对22SiMn2TiB钢进行CMWP拟合得出:q = 1.9,表明22SiMn2TiB钢板条马氏体内的位错为刃、螺型位错的混合位错;M = 2.0,表明位错的分布呈随机分布特征[2].初始组织中残余奥氏体含量为3.7%. ...
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
Effect of tensile deformation of austenite on the morphology and strength of lath martensite
1
2012
... 板条马氏体钢具有超高的强度和较高塑性,因而具有广泛的工业应用.板条马氏体组织中的精细板条结构和高密度位错(> 1015 m-2)是马氏体钢具有超高强度的主要原因[1~3].20世纪70年代以来,研究者们致力于板条马氏体钢微观组织结构与强塑性能之间关系的研究.板条马氏体结构可具体划分为板条、板条块、子板条块、板条束和原奥氏体晶粒[4,5].一个原奥氏体晶粒内可形成若干个马氏体板条束,板条束又进一步划分为板条块,板条块由板条组成;板条束内的板条具有相同的惯习面,板条块内的板条具有相同的取向;板条块两两成对形成具有10°取向差晶界的子板条块[4,5].这些精细结构就构成了马氏体“有效晶粒”组织单元.板条束的尺寸影响了板条马氏体钢的强度[6]和塑性[7],而板条块则是决定强度的主要组织单元[8,9]. ...
板条马氏体钢变形与断裂过程的原位观察
1
2012
... 马氏体组织在拉伸形变过程中通常没有明显的屈服现象,具有较高的屈服强度和抗拉强度.这表明马氏体组织在屈服后发生塑性变形初期会产生明显的加工硬化现象.马氏体在塑性变形过程中的主要方式是位错沿着滑移面的滑移过程,随着变形度的增加,马氏体中的位错密度逐渐增加,板条束或板条块之间的大角度晶界会阻碍位错的滑移形成表面浮凸[7,10].C原子等在刃型位错上偏析形成“Cottrell气团”也可阻碍位错的运动,从而提高强度[11].Morooka等[12]研究了冷轧Fe-18Ni合金的板条马氏体拉伸形变过程中的位错密度变化规律,他们基于经典的Williamson-Hall (W-H)曲线斜率的降低得出了高位错密度的马氏体组织塑性变形过程中位错密度下降的结论.马氏体板条之间通常有薄膜状或片状的残余奥氏体,形变过程中残余奥氏体会吸收位错(DARA),导致残余奥氏体内的位错密度随应变量的增加而增加;因而残余奥氏体表现出较高的加工硬化率,而形变马氏体则处于“软化态”或“未加工硬化态”[13,14].由此可见,板条马氏体组织形变过程中的加工硬化与其组织结构单元、位错密度之间的依赖关系仍然不够清晰. ...
板条马氏体钢变形与断裂过程的原位观察
1
2012
... 马氏体组织在拉伸形变过程中通常没有明显的屈服现象,具有较高的屈服强度和抗拉强度.这表明马氏体组织在屈服后发生塑性变形初期会产生明显的加工硬化现象.马氏体在塑性变形过程中的主要方式是位错沿着滑移面的滑移过程,随着变形度的增加,马氏体中的位错密度逐渐增加,板条束或板条块之间的大角度晶界会阻碍位错的滑移形成表面浮凸[7,10].C原子等在刃型位错上偏析形成“Cottrell气团”也可阻碍位错的运动,从而提高强度[11].Morooka等[12]研究了冷轧Fe-18Ni合金的板条马氏体拉伸形变过程中的位错密度变化规律,他们基于经典的Williamson-Hall (W-H)曲线斜率的降低得出了高位错密度的马氏体组织塑性变形过程中位错密度下降的结论.马氏体板条之间通常有薄膜状或片状的残余奥氏体,形变过程中残余奥氏体会吸收位错(DARA),导致残余奥氏体内的位错密度随应变量的增加而增加;因而残余奥氏体表现出较高的加工硬化率,而形变马氏体则处于“软化态”或“未加工硬化态”[13,14].由此可见,板条马氏体组织形变过程中的加工硬化与其组织结构单元、位错密度之间的依赖关系仍然不够清晰. ...
Yield strength enhancement by carbon trapping in ferrite of the quenching and partitioning steel
1
2018
... 马氏体组织在拉伸形变过程中通常没有明显的屈服现象,具有较高的屈服强度和抗拉强度.这表明马氏体组织在屈服后发生塑性变形初期会产生明显的加工硬化现象.马氏体在塑性变形过程中的主要方式是位错沿着滑移面的滑移过程,随着变形度的增加,马氏体中的位错密度逐渐增加,板条束或板条块之间的大角度晶界会阻碍位错的滑移形成表面浮凸[7,10].C原子等在刃型位错上偏析形成“Cottrell气团”也可阻碍位错的运动,从而提高强度[11].Morooka等[12]研究了冷轧Fe-18Ni合金的板条马氏体拉伸形变过程中的位错密度变化规律,他们基于经典的Williamson-Hall (W-H)曲线斜率的降低得出了高位错密度的马氏体组织塑性变形过程中位错密度下降的结论.马氏体板条之间通常有薄膜状或片状的残余奥氏体,形变过程中残余奥氏体会吸收位错(DARA),导致残余奥氏体内的位错密度随应变量的增加而增加;因而残余奥氏体表现出较高的加工硬化率,而形变马氏体则处于“软化态”或“未加工硬化态”[13,14].由此可见,板条马氏体组织形变过程中的加工硬化与其组织结构单元、位错密度之间的依赖关系仍然不够清晰. ...
Heterogeneous deformation behavior studied by in situ neutron diffraction during tensile deformation for ferrite, martensite and pearlite steels
5
2008
... 马氏体组织在拉伸形变过程中通常没有明显的屈服现象,具有较高的屈服强度和抗拉强度.这表明马氏体组织在屈服后发生塑性变形初期会产生明显的加工硬化现象.马氏体在塑性变形过程中的主要方式是位错沿着滑移面的滑移过程,随着变形度的增加,马氏体中的位错密度逐渐增加,板条束或板条块之间的大角度晶界会阻碍位错的滑移形成表面浮凸[7,10].C原子等在刃型位错上偏析形成“Cottrell气团”也可阻碍位错的运动,从而提高强度[11].Morooka等[12]研究了冷轧Fe-18Ni合金的板条马氏体拉伸形变过程中的位错密度变化规律,他们基于经典的Williamson-Hall (W-H)曲线斜率的降低得出了高位错密度的马氏体组织塑性变形过程中位错密度下降的结论.马氏体板条之间通常有薄膜状或片状的残余奥氏体,形变过程中残余奥氏体会吸收位错(DARA),导致残余奥氏体内的位错密度随应变量的增加而增加;因而残余奥氏体表现出较高的加工硬化率,而形变马氏体则处于“软化态”或“未加工硬化态”[13,14].由此可见,板条马氏体组织形变过程中的加工硬化与其组织结构单元、位错密度之间的依赖关系仍然不够清晰. ...
... 在钢铁热处理与控轧控冷工艺(TMCP)研究中,原位中子衍射技术被证明是强有力的研究工具[12,15~19].原位中子衍射技术利用中子强有力的穿透作用原位采集试样大面积范围的数据,较其他测试方法具有更高的统计性和可靠性.因此,本工作采用原位中子衍射技术来测试超高强度马氏体22SiMn2TiB钢的拉伸塑性变形行为,进一步揭示板条马氏体组织的塑性变形行为. ...
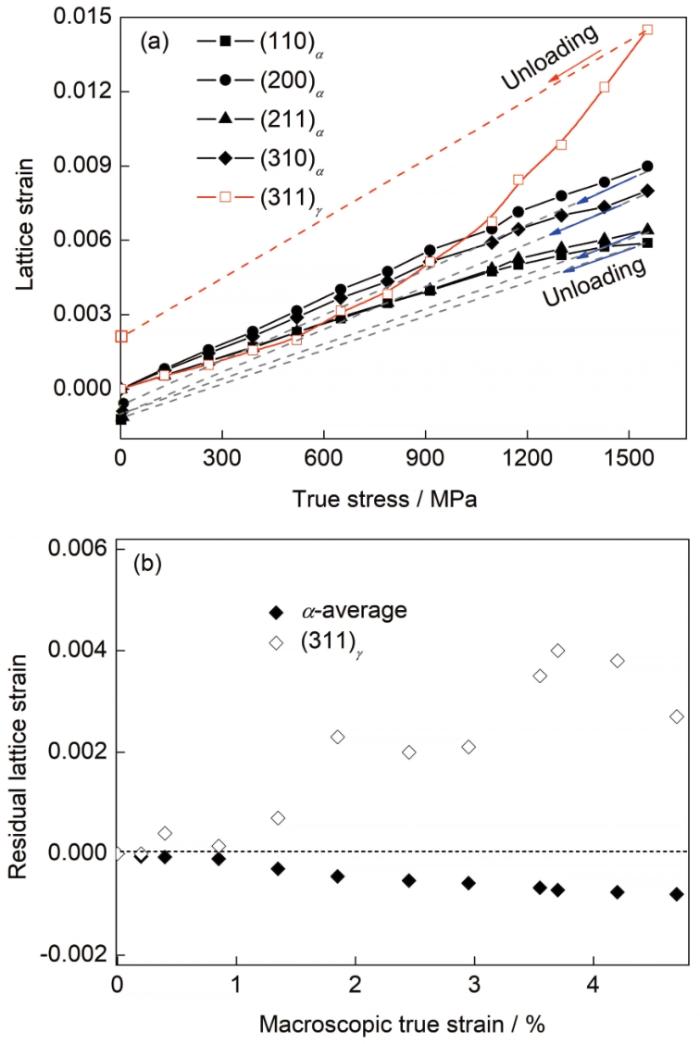
... 式中,和分别指的是变形过程中(hkl)的晶面间距和无应力状态下的晶面间距,本工作中试样形变前的晶面间距确定为.图8a给出了拉伸实验过程中马氏体(110)、(200)、(211)、(310)和奥氏体(311)的晶格应变ε110、ε200、ε211、ε310和ε311随外加载荷的变化规律.图8b给出了拉伸塑性变形卸载后晶格内的残余应变.基于Daymond等[34]和Harjo等[25]的研究结果,奥氏体基体的应变可以采用(311)的晶格应变来表征.由图8a可见,加载过程中马氏体的晶格应变随外加应力几乎为线性增长规律;奥氏体(311)的晶格应变与外加应力不呈线性关系,在较高外加应力作用下,奥氏体(311)的晶格应变量明显增加.从图中曲线斜率可以计算得到马氏体各晶面的Young's模量Ehkl.经计算,E200为164 GPa,E110和E211为223 GPa,E310为180 GPa,这些结果与目前已有的研究结果[12,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
... [12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
... [12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
残余奥氏体增强低碳Q-P-T钢塑性的新效应
2
2012
... 马氏体组织在拉伸形变过程中通常没有明显的屈服现象,具有较高的屈服强度和抗拉强度.这表明马氏体组织在屈服后发生塑性变形初期会产生明显的加工硬化现象.马氏体在塑性变形过程中的主要方式是位错沿着滑移面的滑移过程,随着变形度的增加,马氏体中的位错密度逐渐增加,板条束或板条块之间的大角度晶界会阻碍位错的滑移形成表面浮凸[7,10].C原子等在刃型位错上偏析形成“Cottrell气团”也可阻碍位错的运动,从而提高强度[11].Morooka等[12]研究了冷轧Fe-18Ni合金的板条马氏体拉伸形变过程中的位错密度变化规律,他们基于经典的Williamson-Hall (W-H)曲线斜率的降低得出了高位错密度的马氏体组织塑性变形过程中位错密度下降的结论.马氏体板条之间通常有薄膜状或片状的残余奥氏体,形变过程中残余奥氏体会吸收位错(DARA),导致残余奥氏体内的位错密度随应变量的增加而增加;因而残余奥氏体表现出较高的加工硬化率,而形变马氏体则处于“软化态”或“未加工硬化态”[13,14].由此可见,板条马氏体组织形变过程中的加工硬化与其组织结构单元、位错密度之间的依赖关系仍然不够清晰. ...
... 式中,和分别指的是变形过程中(hkl)的晶面间距和无应力状态下的晶面间距,本工作中试样形变前的晶面间距确定为.图8a给出了拉伸实验过程中马氏体(110)、(200)、(211)、(310)和奥氏体(311)的晶格应变ε110、ε200、ε211、ε310和ε311随外加载荷的变化规律.图8b给出了拉伸塑性变形卸载后晶格内的残余应变.基于Daymond等[34]和Harjo等[25]的研究结果,奥氏体基体的应变可以采用(311)的晶格应变来表征.由图8a可见,加载过程中马氏体的晶格应变随外加应力几乎为线性增长规律;奥氏体(311)的晶格应变与外加应力不呈线性关系,在较高外加应力作用下,奥氏体(311)的晶格应变量明显增加.从图中曲线斜率可以计算得到马氏体各晶面的Young's模量Ehkl.经计算,E200为164 GPa,E110和E211为223 GPa,E310为180 GPa,这些结果与目前已有的研究结果[12,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
残余奥氏体增强低碳Q-P-T钢塑性的新效应
2
2012
... 马氏体组织在拉伸形变过程中通常没有明显的屈服现象,具有较高的屈服强度和抗拉强度.这表明马氏体组织在屈服后发生塑性变形初期会产生明显的加工硬化现象.马氏体在塑性变形过程中的主要方式是位错沿着滑移面的滑移过程,随着变形度的增加,马氏体中的位错密度逐渐增加,板条束或板条块之间的大角度晶界会阻碍位错的滑移形成表面浮凸[7,10].C原子等在刃型位错上偏析形成“Cottrell气团”也可阻碍位错的运动,从而提高强度[11].Morooka等[12]研究了冷轧Fe-18Ni合金的板条马氏体拉伸形变过程中的位错密度变化规律,他们基于经典的Williamson-Hall (W-H)曲线斜率的降低得出了高位错密度的马氏体组织塑性变形过程中位错密度下降的结论.马氏体板条之间通常有薄膜状或片状的残余奥氏体,形变过程中残余奥氏体会吸收位错(DARA),导致残余奥氏体内的位错密度随应变量的增加而增加;因而残余奥氏体表现出较高的加工硬化率,而形变马氏体则处于“软化态”或“未加工硬化态”[13,14].由此可见,板条马氏体组织形变过程中的加工硬化与其组织结构单元、位错密度之间的依赖关系仍然不够清晰. ...
... 式中,和分别指的是变形过程中(hkl)的晶面间距和无应力状态下的晶面间距,本工作中试样形变前的晶面间距确定为.图8a给出了拉伸实验过程中马氏体(110)、(200)、(211)、(310)和奥氏体(311)的晶格应变ε110、ε200、ε211、ε310和ε311随外加载荷的变化规律.图8b给出了拉伸塑性变形卸载后晶格内的残余应变.基于Daymond等[34]和Harjo等[25]的研究结果,奥氏体基体的应变可以采用(311)的晶格应变来表征.由图8a可见,加载过程中马氏体的晶格应变随外加应力几乎为线性增长规律;奥氏体(311)的晶格应变与外加应力不呈线性关系,在较高外加应力作用下,奥氏体(311)的晶格应变量明显增加.从图中曲线斜率可以计算得到马氏体各晶面的Young's模量Ehkl.经计算,E200为164 GPa,E110和E211为223 GPa,E310为180 GPa,这些结果与目前已有的研究结果[12,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
High strength-ductility Nb-microalloyed low martensitic carbon steel: Novel process and mechanism
1
28
... 马氏体组织在拉伸形变过程中通常没有明显的屈服现象,具有较高的屈服强度和抗拉强度.这表明马氏体组织在屈服后发生塑性变形初期会产生明显的加工硬化现象.马氏体在塑性变形过程中的主要方式是位错沿着滑移面的滑移过程,随着变形度的增加,马氏体中的位错密度逐渐增加,板条束或板条块之间的大角度晶界会阻碍位错的滑移形成表面浮凸[7,10].C原子等在刃型位错上偏析形成“Cottrell气团”也可阻碍位错的运动,从而提高强度[11].Morooka等[12]研究了冷轧Fe-18Ni合金的板条马氏体拉伸形变过程中的位错密度变化规律,他们基于经典的Williamson-Hall (W-H)曲线斜率的降低得出了高位错密度的马氏体组织塑性变形过程中位错密度下降的结论.马氏体板条之间通常有薄膜状或片状的残余奥氏体,形变过程中残余奥氏体会吸收位错(DARA),导致残余奥氏体内的位错密度随应变量的增加而增加;因而残余奥氏体表现出较高的加工硬化率,而形变马氏体则处于“软化态”或“未加工硬化态”[13,14].由此可见,板条马氏体组织形变过程中的加工硬化与其组织结构单元、位错密度之间的依赖关系仍然不够清晰. ...
In situ neutron diffraction during tensile deformation of a ferrite-cementite steel
3
2003
... 在钢铁热处理与控轧控冷工艺(TMCP)研究中,原位中子衍射技术被证明是强有力的研究工具[12,15~19].原位中子衍射技术利用中子强有力的穿透作用原位采集试样大面积范围的数据,较其他测试方法具有更高的统计性和可靠性.因此,本工作采用原位中子衍射技术来测试超高强度马氏体22SiMn2TiB钢的拉伸塑性变形行为,进一步揭示板条马氏体组织的塑性变形行为. ...
... 式中,和分别指的是变形过程中(hkl)的晶面间距和无应力状态下的晶面间距,本工作中试样形变前的晶面间距确定为.图8a给出了拉伸实验过程中马氏体(110)、(200)、(211)、(310)和奥氏体(311)的晶格应变ε110、ε200、ε211、ε310和ε311随外加载荷的变化规律.图8b给出了拉伸塑性变形卸载后晶格内的残余应变.基于Daymond等[34]和Harjo等[25]的研究结果,奥氏体基体的应变可以采用(311)的晶格应变来表征.由图8a可见,加载过程中马氏体的晶格应变随外加应力几乎为线性增长规律;奥氏体(311)的晶格应变与外加应力不呈线性关系,在较高外加应力作用下,奥氏体(311)的晶格应变量明显增加.从图中曲线斜率可以计算得到马氏体各晶面的Young's模量Ehkl.经计算,E200为164 GPa,E110和E211为223 GPa,E310为180 GPa,这些结果与目前已有的研究结果[12,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
... 式中,为奥氏体[311]方向的Poisson比,取值0.32[34];为奥氏体(311)晶面沿拉伸载荷方向的晶格应变,和为奥氏体(311)晶面分别沿x2和x3轴的晶格应变.单轴拉伸状态下所测得的和要远小于,且 = ,因此其影响在计算中可以忽略不计.同时,采用式(4)和马氏体(110)的衍射数据计算确定马氏体上的分应力(),取值0.3[15].试样塑性变形期间,马氏体和残余奥氏体上的分应力符合Mughrabi混合加权计算法则[39,40],即: ...
Neutrons and Electrons Scattering
0
2010
In situ neutron diffraction study on ferrite and pearlite transformations for a 1.5Mn-1.5Si-0.2C steel
0
2018
In-situ X-ray diffraction evidence of dynamic transformation of austenite to ferrite during hot compression test in the single austenite phase field
1
2020
... 在钢铁热处理与控轧控冷工艺(TMCP)研究中,原位中子衍射技术被证明是强有力的研究工具[12,15~19].原位中子衍射技术利用中子强有力的穿透作用原位采集试样大面积范围的数据,较其他测试方法具有更高的统计性和可靠性.因此,本工作采用原位中子衍射技术来测试超高强度马氏体22SiMn2TiB钢的拉伸塑性变形行为,进一步揭示板条马氏体组织的塑性变形行为. ...
Crystallite size distribution and dislocation structure determined by diffraction profile analysis: Principles and practical application to cubic and hexagonal crystals
3
2001
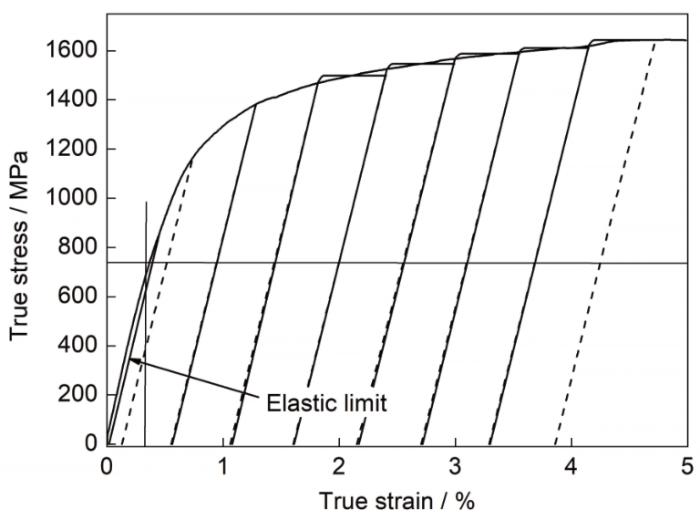
... 试样布置及入射中子束、衍射束的位置关系如图1所示,试样坐标轴的x1轴沿试样的纵轴,为拉伸载荷方向,x2和x3轴为试样横截面坐标轴.弹性阶段拉伸载荷为步进式加载方式;塑性阶段试样的应变速率为10-5 s-1,采用应变控制方法控制试样的塑性变形,塑性变形过程采用步进式应变、连续加载方式.采用Z-Rietveld软件解析衍射数据获得晶格应变(ε)、晶格常数和相体积分数等数据,采用卷积多重全曲线拟合(CMWP)方法[20,21]拟合分析位错密度、位错分布及类型等特征.CMWP方法的计算参数q表征位错类型——螺型位错或刃型位错.衍射谱的各向异性应变宽化现象通常由晶体弹性的各向异性引起,与衍射面指数相关,因此应变各向异性采用各滑移系不同(hkl)指数下的位错衬度因子(C)来修正;对于无织构的立方晶系多晶材料,通常假定位错均匀分布于各滑移系,则需要用平均衬度因子(),其为q的单参数函数,即 = (其中,H2 = (h2k2 + k2l2 +l2h2) / (h2 + k2 + l2)2)[22].依据对bcc晶格<111>{110}滑移系的拟合计算,q = 0.2对应刃型位错,q = 2.5对应螺型位错[22],在这个区间q值越大表示混合位错中螺型位错的数量就越多.参数 (其中,Re为位错有效外截止半径,ρ为位错密度),表征位错的分布特征[20,22];Re是由Wilkens[23]定义用于计算位错弹性能的物理量,他提出位错“有限随机分布”概念,Re则表示位错晶体内相等数量的异号严格平行螺型位错随机分布区域的等效半径.M > 1表示位错偶极子和位移场屏蔽效应弱,位错的分布为随机分布特征;M ≤ 1则表示位错偶极子和位移场屏蔽效应强,位错的分布特征为沿小角度晶界分布[20].Z-Rietveld分析全部衍射数据,CMWP拟合采用卸载后无应力状态下的衍射数据.残余奥氏体的体积分数()通过比较法计算得出: ...
... [20,22];Re是由Wilkens[23]定义用于计算位错弹性能的物理量,他提出位错“有限随机分布”概念,Re则表示位错晶体内相等数量的异号严格平行螺型位错随机分布区域的等效半径.M > 1表示位错偶极子和位移场屏蔽效应弱,位错的分布为随机分布特征;M ≤ 1则表示位错偶极子和位移场屏蔽效应强,位错的分布特征为沿小角度晶界分布[20].Z-Rietveld分析全部衍射数据,CMWP拟合采用卸载后无应力状态下的衍射数据.残余奥氏体的体积分数()通过比较法计算得出: ...
... [20].Z-Rietveld分析全部衍射数据,CMWP拟合采用卸载后无应力状态下的衍射数据.残余奥氏体的体积分数()通过比较法计算得出: ...
A
1
2004
... 试样布置及入射中子束、衍射束的位置关系如图1所示,试样坐标轴的x1轴沿试样的纵轴,为拉伸载荷方向,x2和x3轴为试样横截面坐标轴.弹性阶段拉伸载荷为步进式加载方式;塑性阶段试样的应变速率为10-5 s-1,采用应变控制方法控制试样的塑性变形,塑性变形过程采用步进式应变、连续加载方式.采用Z-Rietveld软件解析衍射数据获得晶格应变(ε)、晶格常数和相体积分数等数据,采用卷积多重全曲线拟合(CMWP)方法[20,21]拟合分析位错密度、位错分布及类型等特征.CMWP方法的计算参数q表征位错类型——螺型位错或刃型位错.衍射谱的各向异性应变宽化现象通常由晶体弹性的各向异性引起,与衍射面指数相关,因此应变各向异性采用各滑移系不同(hkl)指数下的位错衬度因子(C)来修正;对于无织构的立方晶系多晶材料,通常假定位错均匀分布于各滑移系,则需要用平均衬度因子(),其为q的单参数函数,即 = (其中,H2 = (h2k2 + k2l2 +l2h2) / (h2 + k2 + l2)2)[22].依据对bcc晶格<111>{110}滑移系的拟合计算,q = 0.2对应刃型位错,q = 2.5对应螺型位错[22],在这个区间q值越大表示混合位错中螺型位错的数量就越多.参数 (其中,Re为位错有效外截止半径,ρ为位错密度),表征位错的分布特征[20,22];Re是由Wilkens[23]定义用于计算位错弹性能的物理量,他提出位错“有限随机分布”概念,Re则表示位错晶体内相等数量的异号严格平行螺型位错随机分布区域的等效半径.M > 1表示位错偶极子和位移场屏蔽效应弱,位错的分布为随机分布特征;M ≤ 1则表示位错偶极子和位移场屏蔽效应强,位错的分布特征为沿小角度晶界分布[20].Z-Rietveld分析全部衍射数据,CMWP拟合采用卸载后无应力状态下的衍射数据.残余奥氏体的体积分数()通过比较法计算得出: ...
The contrast factors of dislocations in cubic crystals: The dislocation model of strain anisotropy in practice
3
1999
... 试样布置及入射中子束、衍射束的位置关系如图1所示,试样坐标轴的x1轴沿试样的纵轴,为拉伸载荷方向,x2和x3轴为试样横截面坐标轴.弹性阶段拉伸载荷为步进式加载方式;塑性阶段试样的应变速率为10-5 s-1,采用应变控制方法控制试样的塑性变形,塑性变形过程采用步进式应变、连续加载方式.采用Z-Rietveld软件解析衍射数据获得晶格应变(ε)、晶格常数和相体积分数等数据,采用卷积多重全曲线拟合(CMWP)方法[20,21]拟合分析位错密度、位错分布及类型等特征.CMWP方法的计算参数q表征位错类型——螺型位错或刃型位错.衍射谱的各向异性应变宽化现象通常由晶体弹性的各向异性引起,与衍射面指数相关,因此应变各向异性采用各滑移系不同(hkl)指数下的位错衬度因子(C)来修正;对于无织构的立方晶系多晶材料,通常假定位错均匀分布于各滑移系,则需要用平均衬度因子(),其为q的单参数函数,即 = (其中,H2 = (h2k2 + k2l2 +l2h2) / (h2 + k2 + l2)2)[22].依据对bcc晶格<111>{110}滑移系的拟合计算,q = 0.2对应刃型位错,q = 2.5对应螺型位错[22],在这个区间q值越大表示混合位错中螺型位错的数量就越多.参数 (其中,Re为位错有效外截止半径,ρ为位错密度),表征位错的分布特征[20,22];Re是由Wilkens[23]定义用于计算位错弹性能的物理量,他提出位错“有限随机分布”概念,Re则表示位错晶体内相等数量的异号严格平行螺型位错随机分布区域的等效半径.M > 1表示位错偶极子和位移场屏蔽效应弱,位错的分布为随机分布特征;M ≤ 1则表示位错偶极子和位移场屏蔽效应强,位错的分布特征为沿小角度晶界分布[20].Z-Rietveld分析全部衍射数据,CMWP拟合采用卸载后无应力状态下的衍射数据.残余奥氏体的体积分数()通过比较法计算得出: ...
... [22],在这个区间q值越大表示混合位错中螺型位错的数量就越多.参数 (其中,Re为位错有效外截止半径,ρ为位错密度),表征位错的分布特征[20,22];Re是由Wilkens[23]定义用于计算位错弹性能的物理量,他提出位错“有限随机分布”概念,Re则表示位错晶体内相等数量的异号严格平行螺型位错随机分布区域的等效半径.M > 1表示位错偶极子和位移场屏蔽效应弱,位错的分布为随机分布特征;M ≤ 1则表示位错偶极子和位移场屏蔽效应强,位错的分布特征为沿小角度晶界分布[20].Z-Rietveld分析全部衍射数据,CMWP拟合采用卸载后无应力状态下的衍射数据.残余奥氏体的体积分数()通过比较法计算得出: ...
... ,22];Re是由Wilkens[23]定义用于计算位错弹性能的物理量,他提出位错“有限随机分布”概念,Re则表示位错晶体内相等数量的异号严格平行螺型位错随机分布区域的等效半径.M > 1表示位错偶极子和位移场屏蔽效应弱,位错的分布为随机分布特征;M ≤ 1则表示位错偶极子和位移场屏蔽效应强,位错的分布特征为沿小角度晶界分布[20].Z-Rietveld分析全部衍射数据,CMWP拟合采用卸载后无应力状态下的衍射数据.残余奥氏体的体积分数()通过比较法计算得出: ...
The determination of density and distribution of dislocations in deformed single crystals from broadened X-Ray diffraction profiles
1
1970
... 试样布置及入射中子束、衍射束的位置关系如图1所示,试样坐标轴的x1轴沿试样的纵轴,为拉伸载荷方向,x2和x3轴为试样横截面坐标轴.弹性阶段拉伸载荷为步进式加载方式;塑性阶段试样的应变速率为10-5 s-1,采用应变控制方法控制试样的塑性变形,塑性变形过程采用步进式应变、连续加载方式.采用Z-Rietveld软件解析衍射数据获得晶格应变(ε)、晶格常数和相体积分数等数据,采用卷积多重全曲线拟合(CMWP)方法[20,21]拟合分析位错密度、位错分布及类型等特征.CMWP方法的计算参数q表征位错类型——螺型位错或刃型位错.衍射谱的各向异性应变宽化现象通常由晶体弹性的各向异性引起,与衍射面指数相关,因此应变各向异性采用各滑移系不同(hkl)指数下的位错衬度因子(C)来修正;对于无织构的立方晶系多晶材料,通常假定位错均匀分布于各滑移系,则需要用平均衬度因子(),其为q的单参数函数,即 = (其中,H2 = (h2k2 + k2l2 +l2h2) / (h2 + k2 + l2)2)[22].依据对bcc晶格<111>{110}滑移系的拟合计算,q = 0.2对应刃型位错,q = 2.5对应螺型位错[22],在这个区间q值越大表示混合位错中螺型位错的数量就越多.参数 (其中,Re为位错有效外截止半径,ρ为位错密度),表征位错的分布特征[20,22];Re是由Wilkens[23]定义用于计算位错弹性能的物理量,他提出位错“有限随机分布”概念,Re则表示位错晶体内相等数量的异号严格平行螺型位错随机分布区域的等效半径.M > 1表示位错偶极子和位移场屏蔽效应弱,位错的分布为随机分布特征;M ≤ 1则表示位错偶极子和位移场屏蔽效应强,位错的分布特征为沿小角度晶界分布[20].Z-Rietveld分析全部衍射数据,CMWP拟合采用卸载后无应力状态下的衍射数据.残余奥氏体的体积分数()通过比较法计算得出: ...
High-resolution electron microscopy of detonation nanodiamond
1
2008
... 马氏体板条束和板条块形貌分别利用Quanta 200扫描电镜(SEM)和Quanta 650FEG热场发射扫描电镜所附带的Oxford Nordlys F+ 电子背散射衍射系统(EBSD)进行观察.板条束、板条块的宽度皆采用直线截取的方法,分别取200和120个数据的平均值.马氏体的板条形貌观察采用Tecnai G2 F20扫描透射电子显微镜(STEM),利用明场(BF)像和环形暗场(ADF)像2种模式.STEM测试区域的薄膜厚度(t)采用电子能量损失谱的方法[24]确定,板条内的位错密度采用Harjo等[25]的方法:利用5张ADF像,其中3张ADF像的入射电子束沿<111>方向,2张ADF像的入射电子束沿<001>方向(电子束沿此方向入射可显示所有a / 3 <111>型位错).在ADF像位错密集处做网络交线(水平和垂直直线网络),分别统计其与位错的交点数,按照Hirsch等[26]提出的截线法计算位错密度: ...
Work hardening, dislocation structure, and load partitioning in lath martensite determined by in situ neutron diffraction line profile analysis
6
2017
... 马氏体板条束和板条块形貌分别利用Quanta 200扫描电镜(SEM)和Quanta 650FEG热场发射扫描电镜所附带的Oxford Nordlys F+ 电子背散射衍射系统(EBSD)进行观察.板条束、板条块的宽度皆采用直线截取的方法,分别取200和120个数据的平均值.马氏体的板条形貌观察采用Tecnai G2 F20扫描透射电子显微镜(STEM),利用明场(BF)像和环形暗场(ADF)像2种模式.STEM测试区域的薄膜厚度(t)采用电子能量损失谱的方法[24]确定,板条内的位错密度采用Harjo等[25]的方法:利用5张ADF像,其中3张ADF像的入射电子束沿<111>方向,2张ADF像的入射电子束沿<001>方向(电子束沿此方向入射可显示所有a / 3 <111>型位错).在ADF像位错密集处做网络交线(水平和垂直直线网络),分别统计其与位错的交点数,按照Hirsch等[26]提出的截线法计算位错密度: ...
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
... 式中,和分别指的是变形过程中(hkl)的晶面间距和无应力状态下的晶面间距,本工作中试样形变前的晶面间距确定为.图8a给出了拉伸实验过程中马氏体(110)、(200)、(211)、(310)和奥氏体(311)的晶格应变ε110、ε200、ε211、ε310和ε311随外加载荷的变化规律.图8b给出了拉伸塑性变形卸载后晶格内的残余应变.基于Daymond等[34]和Harjo等[25]的研究结果,奥氏体基体的应变可以采用(311)的晶格应变来表征.由图8a可见,加载过程中马氏体的晶格应变随外加应力几乎为线性增长规律;奥氏体(311)的晶格应变与外加应力不呈线性关系,在较高外加应力作用下,奥氏体(311)的晶格应变量明显增加.从图中曲线斜率可以计算得到马氏体各晶面的Young's模量Ehkl.经计算,E200为164 GPa,E110和E211为223 GPa,E310为180 GPa,这些结果与目前已有的研究结果[12,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
... ,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
... ,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
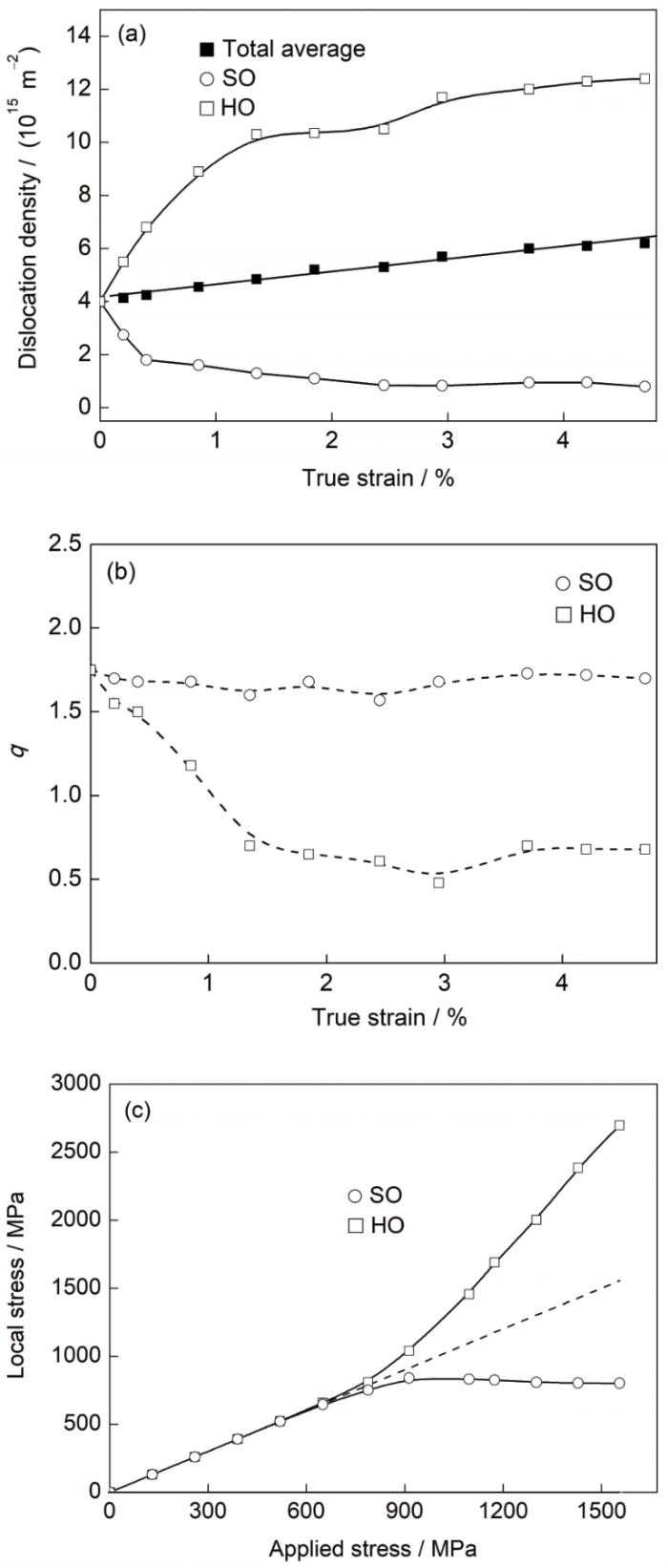
... 其中,σ0、G、MT和b分别取值350 MPa、77.3 GPa、2.8和0.248 nm;αHO和αSO分别为硬取向和软取向板条束的比例系数,初始值分别取0.4和0.18,但由于α值与位错结构、位错分布有关,会随试样上的应力应变而改变,因此通过CMWP拟合计算进行修正[25,33].由此分别计算出硬取向和软取向板条束上的分应力,如图10c所示.可见,塑性阶段硬取向板条束上分配的分应力高于软取向板条束上的分应力,2类板条束上的分应力差值随外加载荷和塑性变形量的加大而增加.卸载后,硬取向板条束和软取向板条束间形成残余内应力: ...
1
1965
... 马氏体板条束和板条块形貌分别利用Quanta 200扫描电镜(SEM)和Quanta 650FEG热场发射扫描电镜所附带的Oxford Nordlys F+ 电子背散射衍射系统(EBSD)进行观察.板条束、板条块的宽度皆采用直线截取的方法,分别取200和120个数据的平均值.马氏体的板条形貌观察采用Tecnai G2 F20扫描透射电子显微镜(STEM),利用明场(BF)像和环形暗场(ADF)像2种模式.STEM测试区域的薄膜厚度(t)采用电子能量损失谱的方法[24]确定,板条内的位错密度采用Harjo等[25]的方法:利用5张ADF像,其中3张ADF像的入射电子束沿<111>方向,2张ADF像的入射电子束沿<001>方向(电子束沿此方向入射可显示所有a / 3 <111>型位错).在ADF像位错密集处做网络交线(水平和垂直直线网络),分别统计其与位错的交点数,按照Hirsch等[26]提出的截线法计算位错密度: ...
Ultra?ne structure and high strength in cold-rolled martensite
4
2012
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
... [27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
... [27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
... [27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
Ultrahigh strength-ductility steel treated by a novel quenching- partitioning- tempering process
1
2014
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
Investigation on the morphology of martensite in carbon steels
1
1996
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
Formation and subdivision of deformation structures during plastic deformation
1
2006
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
基于中子衍射和同步辐射X射线衍射的TWIP钢位错密度计算方法
1
2020
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
基于中子衍射和同步辐射X射线衍射的TWIP钢位错密度计算方法
1
2020
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
Asymmetric X-ray line broadening of plastically deformed crystals. II. Evaluation procedure and application to [001]-Cu crystals
1
1989
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
Composite behavior of lath martensite steels induced by plastic strain, a new paradigm for the elastic-plastic response of martensitic steels
4
2017
... 拉伸过程中马氏体组织内的位错密度分别采用Z-Rietveld和CMWP 2种方法进行解析,同时采用TEM对拉伸后组织内的位错密度进行对比分析.TEM测试所得拉伸形变后马氏体板条内的位错密度在9.05 × 1014~1.45 × 1015 m-2之间,平均位错密度为1.18 × 1015 m-2.与形变前相比,板条马氏体内的位错密度几乎没有变化.Z-Rietveld解析后的衍射谱采用Gauss单峰拟合的方法,得出衍射峰半峰宽(FWHM)的变化规律.马氏体4个衍射峰(110)、(200)、(211)、(310)的FWHM随应力的变化关系曲线如图6a所示.衍射峰的FWHM通常决定于晶粒尺寸和位错密度,本工作中塑性变形量只有4.7%,可以认为晶粒尺寸不受塑性变形的影响,因此FWHM的变化是由位错密度变化产生的微应变引起.从图6a可以看出,马氏体4个衍射峰的FWHM随真应变的变化规律一致,小应变状态下(对应的真应力小于Rp0.2),FWHM几乎没有变化;在应变量较大(即真应力高于Rp0.2)时,FWHM呈现出较为明显的下降趋势,随后随真应变的增大缓慢降低,即试样内的位错密度因为塑性变形作用下降.对比FWHM测得的位错密度变化规律和TEM位错密度数据可知,2种方法测得的数据规律不同.因而进一步采用CMWP方法对衍射数据进行拟合分析,所得的位错密度随真应变的变化关系如图6b所示.从图6b可以看出,随着真应变(外加应力)的增加,钢内的位错密度增大.CMWP拟合所得的位错密度(如钢内初始位错密度4.0 × 1015 m-2)远高于TEM测试的数据.TEM测试的位错密度低于中子衍射方法测试的位错密度,可能存在多种原因.在本工作中,则是因为TEM测试只计算了板条内的位错,而CMWP方法考虑了位错类型的影响,同时还计算了亚晶界上的位错.Huang等 [27]认为板条马氏体组织的总位错密度是板条内、板条界和子板条块界上的位错密度之和,三部分区域的位错密度分别可达到3 × 1014、3 × 1014和2 × 1014 m-2.板条和子板条块之间的晶界为小角度晶界,其取向差分别在5°以下和10°左右[4,5,8].由Huang等[27]的研究可以断定,位错在小角度晶界上聚集呈现了较高的分布密度.这些晶界又被称为“位错晶界”,其位错密度是板条内位错密度的2倍左右.本工作用22SiMn2TiB钢的C含量(0.21%)高于Huang等[27]研究用钢的C含量(0.0026%),通常马氏体板条、板条块和板条束尺寸随C含量的升高而降低[28,29],由此22SiMn2TiB钢的位错晶界数量高于Huang等[27]所报道的数量,粗略判定22SiMn2TiB钢中的总位错密度是板条内位错密度的3倍,因而CMWP拟合所得的位错密度要高于TEM测试的位错密度结果.塑性变形中,马氏体组织由于存在各种复杂组态的显微位错结构,其衍射峰形并不是对称结构[30].采用Williamson-Hall方法计算以及FWHM表征的板条马氏体内位错密度随应变量下降的结果是因为没有考虑衍射峰的不对称问题.李亦庄和黄明欣[31]亦认为修正Williamson-Hall法不适合于马氏体钢,马氏体组织的钢种由于变形过程中位错组态会发生改变,而这些信息仅体现在衍射峰的“尾部”[32],修正Williamson-Hall法所利用的半高宽则忽略了衍射峰尾部的额外信息.而CMWP方法对衍射峰进行全曲线的拟合,所以测得的位错密度数据准确度更高.由以上分析可知,拉伸塑性变形导致马氏体衍射峰为不对称结构,单峰拟合FWHM所表征的位错密度变化规律并不准确;马氏体的位错密度随拉伸塑性变形作用而增大.CMWP的位错类型参数(q)随真应变的增大而降低,说明随真应变量的增加,刃型位错在总位错中的占比升高[25,33].这些结果表明,板条马氏体在拉伸作用下存在位错的湮灭和增殖过程,位错增殖过程大于其湮灭过程;螺型位错在滑移过程中相互交割形成刃型位错,导致刃型位错比例增加. ...
... 式中,和分别指的是变形过程中(hkl)的晶面间距和无应力状态下的晶面间距,本工作中试样形变前的晶面间距确定为.图8a给出了拉伸实验过程中马氏体(110)、(200)、(211)、(310)和奥氏体(311)的晶格应变ε110、ε200、ε211、ε310和ε311随外加载荷的变化规律.图8b给出了拉伸塑性变形卸载后晶格内的残余应变.基于Daymond等[34]和Harjo等[25]的研究结果,奥氏体基体的应变可以采用(311)的晶格应变来表征.由图8a可见,加载过程中马氏体的晶格应变随外加应力几乎为线性增长规律;奥氏体(311)的晶格应变与外加应力不呈线性关系,在较高外加应力作用下,奥氏体(311)的晶格应变量明显增加.从图中曲线斜率可以计算得到马氏体各晶面的Young's模量Ehkl.经计算,E200为164 GPa,E110和E211为223 GPa,E310为180 GPa,这些结果与目前已有的研究结果[12,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
... 马氏体板条束内的板条具有相同的(110)惯习面,一个板条束内的板条又形成了具有不同取向分布的板条块;板条块内的板条可能具有另外的(110)或者(200)等晶面[4,5].板条马氏体组织的微尺寸塑性变形实验研究[41,42]表明,马氏体的微尺寸试样如果只包含一个板条块时,其拉伸塑性变形过程没有加工硬化现象;微尺寸试样内包含2个及以上板条块时,试样在拉伸塑性变形过程中才会出现明显的加工硬化.这说明,板条马氏体塑性变形过程中应力在板条束内进行再分配,板条的塑性应变和板条取向有关.由此,应力作用下的板条束可划分为2种类型[33]:滑移系(Burgers矢量)位于板条平面内、板条取向利于位错滑移的板条束定义为软取向(SO)板条束,滑移系不在板条平面内、板条取向不利于位错滑移的板条束定义为硬取向(HO)板条束,如图9a所示.塑性变形过程中软取向板条束内的滑移系在较低的剪切应力作用下即可产生滑移,位错密度降低,出现加工软化特征;硬取向板条束内的滑移系需要更高的剪切应力作用,位错密度升高,出现加工硬化特征.采用CMWP方法对衍射峰进行拟合计算,结果如图9b所示.马氏体的衍射峰可拆分为硬取向和软取向2个子峰,具有较高强度、较低FWHM的子峰对应软取向板条束;强度低、FWHM宽的子峰对应硬取向板条束.通过拟合计算得到2个子峰的体积分数(fHO、fSO)和位错密度(ρHO、ρSO),进行加权平均计算得到马氏体的平均位错密度(ρAV): ...
... 其中,σ0、G、MT和b分别取值350 MPa、77.3 GPa、2.8和0.248 nm;αHO和αSO分别为硬取向和软取向板条束的比例系数,初始值分别取0.4和0.18,但由于α值与位错结构、位错分布有关,会随试样上的应力应变而改变,因此通过CMWP拟合计算进行修正[25,33].由此分别计算出硬取向和软取向板条束上的分应力,如图10c所示.可见,塑性阶段硬取向板条束上分配的分应力高于软取向板条束上的分应力,2类板条束上的分应力差值随外加载荷和塑性变形量的加大而增加.卸载后,硬取向板条束和软取向板条束间形成残余内应力: ...
Measured and predicted intergranular strains in textured austenitic steel
3
2000
... 式中,和分别指的是变形过程中(hkl)的晶面间距和无应力状态下的晶面间距,本工作中试样形变前的晶面间距确定为.图8a给出了拉伸实验过程中马氏体(110)、(200)、(211)、(310)和奥氏体(311)的晶格应变ε110、ε200、ε211、ε310和ε311随外加载荷的变化规律.图8b给出了拉伸塑性变形卸载后晶格内的残余应变.基于Daymond等[34]和Harjo等[25]的研究结果,奥氏体基体的应变可以采用(311)的晶格应变来表征.由图8a可见,加载过程中马氏体的晶格应变随外加应力几乎为线性增长规律;奥氏体(311)的晶格应变与外加应力不呈线性关系,在较高外加应力作用下,奥氏体(311)的晶格应变量明显增加.从图中曲线斜率可以计算得到马氏体各晶面的Young's模量Ehkl.经计算,E200为164 GPa,E110和E211为223 GPa,E310为180 GPa,这些结果与目前已有的研究结果[12,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
... [34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
... 式中,为奥氏体[311]方向的Poisson比,取值0.32[34];为奥氏体(311)晶面沿拉伸载荷方向的晶格应变,和为奥氏体(311)晶面分别沿x2和x3轴的晶格应变.单轴拉伸状态下所测得的和要远小于,且 = ,因此其影响在计算中可以忽略不计.同时,采用式(4)和马氏体(110)的衍射数据计算确定马氏体上的分应力(),取值0.3[15].试样塑性变形期间,马氏体和残余奥氏体上的分应力符合Mughrabi混合加权计算法则[39,40],即: ...
Interphase and intergranular stress generation in carbon steels
1
2004
... 式中,和分别指的是变形过程中(hkl)的晶面间距和无应力状态下的晶面间距,本工作中试样形变前的晶面间距确定为.图8a给出了拉伸实验过程中马氏体(110)、(200)、(211)、(310)和奥氏体(311)的晶格应变ε110、ε200、ε211、ε310和ε311随外加载荷的变化规律.图8b给出了拉伸塑性变形卸载后晶格内的残余应变.基于Daymond等[34]和Harjo等[25]的研究结果,奥氏体基体的应变可以采用(311)的晶格应变来表征.由图8a可见,加载过程中马氏体的晶格应变随外加应力几乎为线性增长规律;奥氏体(311)的晶格应变与外加应力不呈线性关系,在较高外加应力作用下,奥氏体(311)的晶格应变量明显增加.从图中曲线斜率可以计算得到马氏体各晶面的Young's模量Ehkl.经计算,E200为164 GPa,E110和E211为223 GPa,E310为180 GPa,这些结果与目前已有的研究结果[12,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
In situ neutron diffraction investigation of the collaborative deformation -transformation mechanism in TRIP-assisted steels at room and elevated temperatures
1
2008
... 式中,和分别指的是变形过程中(hkl)的晶面间距和无应力状态下的晶面间距,本工作中试样形变前的晶面间距确定为.图8a给出了拉伸实验过程中马氏体(110)、(200)、(211)、(310)和奥氏体(311)的晶格应变ε110、ε200、ε211、ε310和ε311随外加载荷的变化规律.图8b给出了拉伸塑性变形卸载后晶格内的残余应变.基于Daymond等[34]和Harjo等[25]的研究结果,奥氏体基体的应变可以采用(311)的晶格应变来表征.由图8a可见,加载过程中马氏体的晶格应变随外加应力几乎为线性增长规律;奥氏体(311)的晶格应变与外加应力不呈线性关系,在较高外加应力作用下,奥氏体(311)的晶格应变量明显增加.从图中曲线斜率可以计算得到马氏体各晶面的Young's模量Ehkl.经计算,E200为164 GPa,E110和E211为223 GPa,E310为180 GPa,这些结果与目前已有的研究结果[12,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
The enhancement of ductility in high-strength steels
1
1967
... 式中,和分别指的是变形过程中(hkl)的晶面间距和无应力状态下的晶面间距,本工作中试样形变前的晶面间距确定为.图8a给出了拉伸实验过程中马氏体(110)、(200)、(211)、(310)和奥氏体(311)的晶格应变ε110、ε200、ε211、ε310和ε311随外加载荷的变化规律.图8b给出了拉伸塑性变形卸载后晶格内的残余应变.基于Daymond等[34]和Harjo等[25]的研究结果,奥氏体基体的应变可以采用(311)的晶格应变来表征.由图8a可见,加载过程中马氏体的晶格应变随外加应力几乎为线性增长规律;奥氏体(311)的晶格应变与外加应力不呈线性关系,在较高外加应力作用下,奥氏体(311)的晶格应变量明显增加.从图中曲线斜率可以计算得到马氏体各晶面的Young's模量Ehkl.经计算,E200为164 GPa,E110和E211为223 GPa,E310为180 GPa,这些结果与目前已有的研究结果[12,25,33,35]接近.外加载荷较低时(< 500 MPa),奥氏体(311)的E311为238 GPa,与Daymond等[34]的结果接近;随后E311随外加应力的增大而降低,在外加载荷高于Rp0.2以上时降低至66 GPa.这说明板条间的残余奥氏体在马氏体板条的作用下表现出较高的应变抗力,在拉伸形变过程中,尤其是在高应力作用下,承载了较高的应力.由图8a还可以得出,不同取向的马氏体晶粒具有不同的塑性变形行为:[110]和[211]取向的晶粒属于软取向晶粒,更容易发生塑性变形;[200]取向的晶粒属于硬取向晶粒,不易发生塑性变形[12,15].可见,塑性变形过程中外加应力将会在马氏体不同取向的晶粒上产生再分配.卸载后晶格内仍存在残余应变,奥氏体晶格的残余应变为拉伸应变,马氏体晶格的残余应变为压缩应变,这个结论与已有的研究结论[12,25]一致.不同取向的马氏体板条残余变形量亦不同,[200]取向晶粒的晶格残余压缩应变量最低(图8a).且马氏体和奥氏体的晶格残余应变随试样真应变量的增大而增大(图8b).Muránsky等[36]的研究结果表明,相变诱导塑性(TRIP)钢在拉伸塑性变形过程中,残余奥氏体表现为硬相,他们把这个现象归结为残余奥氏体因具有较高的C含量而导致的强度增强现象.显然本实验结果并不能从残余奥氏体的C含量来解释.王颖等[13]的研究结果表明,随真应变增大到7%,残余奥氏体内的平均位错密度从初始的11.0 × 1014 m-2增加到了41.0 × 1014 m-2,且远高于马氏体内的平均位错密度(由初始7.26 × 1014 m-2降至6.23 × 1014 m-2).塑性变形过程中残余奥氏体具有较大的晶格应变,且有一部分残余奥氏体在形变过程中发生马氏体相变,对板条马氏体的塑性变形行为还会产生TRIP效应[37]. ...
Tensile behavior of TRIP-aided multi-phase steels studied by in situ neutron diffraction
1
2004
... 根据图8a所测得的E311数据,利用Hooke定律计算塑性拉伸过程中残余奥氏体上的分应力()[38]: ...
Dislocation wall and cell structures and long-range internal stresses in deformed metal crystals
2
1983
... 式中,为奥氏体[311]方向的Poisson比,取值0.32[34];为奥氏体(311)晶面沿拉伸载荷方向的晶格应变,和为奥氏体(311)晶面分别沿x2和x3轴的晶格应变.单轴拉伸状态下所测得的和要远小于,且 = ,因此其影响在计算中可以忽略不计.同时,采用式(4)和马氏体(110)的衍射数据计算确定马氏体上的分应力(),取值0.3[15].试样塑性变形期间,马氏体和残余奥氏体上的分应力符合Mughrabi混合加权计算法则[39,40],即: ...
... 硬取向和软取向板条束上的剪切应力同样采用Mughrabi混合加权计算方法[39,40],即马氏体组织所受到的剪切力为硬取向板条和软取向板条上的分切应力之和: ...
X-ray line-broadening study of the dislocation cell structure in deformed [001]-orientated copper single crystals
2
1984
... 式中,为奥氏体[311]方向的Poisson比,取值0.32[34];为奥氏体(311)晶面沿拉伸载荷方向的晶格应变,和为奥氏体(311)晶面分别沿x2和x3轴的晶格应变.单轴拉伸状态下所测得的和要远小于,且 = ,因此其影响在计算中可以忽略不计.同时,采用式(4)和马氏体(110)的衍射数据计算确定马氏体上的分应力(),取值0.3[15].试样塑性变形期间,马氏体和残余奥氏体上的分应力符合Mughrabi混合加权计算法则[39,40],即: ...
... 硬取向和软取向板条束上的剪切应力同样采用Mughrabi混合加权计算方法[39,40],即马氏体组织所受到的剪切力为硬取向板条和软取向板条上的分切应力之和: ...
Micro-tension behaviour of lath martensite structures of carbon steel
2
2013
... 马氏体板条束内的板条具有相同的(110)惯习面,一个板条束内的板条又形成了具有不同取向分布的板条块;板条块内的板条可能具有另外的(110)或者(200)等晶面[4,5].板条马氏体组织的微尺寸塑性变形实验研究[41,42]表明,马氏体的微尺寸试样如果只包含一个板条块时,其拉伸塑性变形过程没有加工硬化现象;微尺寸试样内包含2个及以上板条块时,试样在拉伸塑性变形过程中才会出现明显的加工硬化.这说明,板条马氏体塑性变形过程中应力在板条束内进行再分配,板条的塑性应变和板条取向有关.由此,应力作用下的板条束可划分为2种类型[33]:滑移系(Burgers矢量)位于板条平面内、板条取向利于位错滑移的板条束定义为软取向(SO)板条束,滑移系不在板条平面内、板条取向不利于位错滑移的板条束定义为硬取向(HO)板条束,如图9a所示.塑性变形过程中软取向板条束内的滑移系在较低的剪切应力作用下即可产生滑移,位错密度降低,出现加工软化特征;硬取向板条束内的滑移系需要更高的剪切应力作用,位错密度升高,出现加工硬化特征.采用CMWP方法对衍射峰进行拟合计算,结果如图9b所示.马氏体的衍射峰可拆分为硬取向和软取向2个子峰,具有较高强度、较低FWHM的子峰对应软取向板条束;强度低、FWHM宽的子峰对应硬取向板条束.通过拟合计算得到2个子峰的体积分数(fHO、fSO)和位错密度(ρHO、ρSO),进行加权平均计算得到马氏体的平均位错密度(ρAV): ...
... 对于非均匀微观组织的塑性变形的混合模型中,ΔτHO和ΔτSO即是存在于硬取向板条束和软取向板条束上的“长程内应力”[41,42]. ...
Microscale-calibrated modeling of the deformation response of low-carbon martensite
2
2013
... 马氏体板条束内的板条具有相同的(110)惯习面,一个板条束内的板条又形成了具有不同取向分布的板条块;板条块内的板条可能具有另外的(110)或者(200)等晶面[4,5].板条马氏体组织的微尺寸塑性变形实验研究[41,42]表明,马氏体的微尺寸试样如果只包含一个板条块时,其拉伸塑性变形过程没有加工硬化现象;微尺寸试样内包含2个及以上板条块时,试样在拉伸塑性变形过程中才会出现明显的加工硬化.这说明,板条马氏体塑性变形过程中应力在板条束内进行再分配,板条的塑性应变和板条取向有关.由此,应力作用下的板条束可划分为2种类型[33]:滑移系(Burgers矢量)位于板条平面内、板条取向利于位错滑移的板条束定义为软取向(SO)板条束,滑移系不在板条平面内、板条取向不利于位错滑移的板条束定义为硬取向(HO)板条束,如图9a所示.塑性变形过程中软取向板条束内的滑移系在较低的剪切应力作用下即可产生滑移,位错密度降低,出现加工软化特征;硬取向板条束内的滑移系需要更高的剪切应力作用,位错密度升高,出现加工硬化特征.采用CMWP方法对衍射峰进行拟合计算,结果如图9b所示.马氏体的衍射峰可拆分为硬取向和软取向2个子峰,具有较高强度、较低FWHM的子峰对应软取向板条束;强度低、FWHM宽的子峰对应硬取向板条束.通过拟合计算得到2个子峰的体积分数(fHO、fSO)和位错密度(ρHO、ρSO),进行加权平均计算得到马氏体的平均位错密度(ρAV): ...
... 对于非均匀微观组织的塑性变形的混合模型中,ΔτHO和ΔτSO即是存在于硬取向板条束和软取向板条束上的“长程内应力”[41,42]. ...
Annihilation of dislocations during tensile and cyclic deformation and limits of dislocation densities
1
1979
... 其中,fHO + fSO = 1.所得结果绘制于图10a.CMWP拟合所得2类板条束内的q绘于图10b.可见,硬取向板条束内的位错密度随着应变量的增加而增大,其数值高达1016 m-2;软取向板条束内的位错密度在形变开始时急速降至1014 m-2,随后保持在一个较为稳定的数值.图10a中的平均位错密度要略高于图6b中的数据,可见马氏体组织的加工硬化主要是通过硬取向板条束的位错增殖来实现.由图10b可见,硬取向板条束的q随应变量的增加而降低,软取向板条束的q几乎不随应变量变化.这些结果说明,塑性变形过程中硬取向板条束内产生应力集中,位错由螺型位错转变为刃型位错并实现位错增殖;软取向板条束内的位错组成基本没有变化.螺型位错可以向任何方向移动,因而较容易湮灭,而刃形位错只能在短距离范围内滑移或者攀移来实现湮灭或增殖[43]. ...
The mechanism of plastic deformation of crystals: Part I. -Theoretical
1
1934
... 根据Taylor公式[44]计算2种类型板条束上分配的拉伸应力: ...
Direct determination of elastic strains and dislocation densities in individual subgrains in deformation structures
1
2007
... 其中,σ为与位错密度相关、作用于板条束上的拉伸应力,σ0为材料摩擦应力,α为比例系数,G为切变模量,MT为Taylor因子,b为Burgers矢量模.试样上的拉伸应力与剪切应力(τ)之间存在以下关系[45]: ...