高熵合金(high-entropy alloy)设计是2004年Yeh等[1]提出的一种新的合金设计范式[1~4]。从成分上讲,高熵合金是指含有5种或者以上金属元素以等原子比混合的合金;从结构上讲,最初的高熵合金主要指的是具有简单晶体结构的金属固溶体,例如面心立方(fcc)、体心立方(bcc)或者六方密堆(hcp)结构;从概念上讲,相对应于传统合金而言(比如钛合金、铝合金),高熵合金的化学成分中缺乏单一主导元素,因此被认为具有较高的化学无序度和构型熵[4~6]。通过过去十几年的研究,高熵合金领域得到了飞速的发展。随着新合金以及合金体系的发现和开发,人们逐渐意识到高熵合金具有一些传统合金所不具备的独特的结构和功能性能,比如打破强度与塑性不可兼得的“魔咒”[7,8]、极高的断裂韧性[9]、高硬度[10]、良好的耐磨性能与抗腐蚀性能等[11~13]。在高熵合金研究初期,人们把高熵合金中独特的结构和性能来源归结为4种基本要素的协同作用[14],即:高熵效应(high-entropy effect)、迟滞扩散(sluggish diffusion)、晶格畸变(lattice distortion)以及“鸡尾酒”效应(“cocktail” effect)。虽然高熵合金的优越性能得到了广泛的认可,然而,人们对以上4种基本要素如何在高熵合金中起到相应的作用还存在异议[15~17]。因此,还需要更多的研究进一步理解高熵合金优越性能的物理起源。
在以上高熵合金的4大核心效应中,晶格畸变效应与高熵合金的结构和力学性能紧密相关。正确理解高熵合金中的晶格畸变效应对于揭示高熵合金中独特的强韧化行为具有重要意义[18~21]。当多种合金元素以近等原子比进行混合而形成单相固溶体结构时,由于各成分原子之间的原子半径存在差异和弹性模量等物理性能之间的不匹配,高熵合金的晶格结构不可避免地出现畸变。根据Hume-Rothery提出的经验准则[22],在传统二元合金中单相固溶体的形成要求溶质与溶剂原子半径差异应小于15%。同样,在高熵合金中,当不同组成原子的半径差异过大,就可能造成晶格畸变。过高的晶格畸变会使得单相固溶体结构失稳,从而导致第二相析出甚至非晶化[19]。另一方面,晶格畸变还会对位错的运动产生阻碍,从而提供独特的材料强化机制。然而,关于高熵合金中晶格畸变的直接观测与定量表征仍是一大挑战[18,23,24]。在近十几年的高熵合金的发展过程中,晶格畸变一直是高熵合金中的一大研究热点。由于高熵合金中独特的结构特征,难以区分溶质和溶剂原子,这一特点使得传统的基于固溶体的理论模型难以直接应用到高熵合金体系中。为此,研究人员建立了一系列的理论模型定量描述高熵合金中的晶格畸变效应[19,20,25,26]。结合理论模型,第一性原理模拟计算也被广泛应用于研究合金中的晶格畸变效应[27]。然而实验上定量观测高熵合金的晶格畸变仍然有一定的难度,研究人员也进行了有益的尝试[28,29]。理想晶体的结构均可用晶体学单胞和基矢通过空间的平移和对称操作来进行确定[30,31]。Bravais晶格(Bravais lattices)按照晶体的宏观对称性可以分属为7个晶系,理想晶格的单胞可以按照晶系来进行确定[30,31]。然而在高熵合金中,不同成分原子之间的相互作用往往使得原子的排列偏离严格的周期对称性。因此,畸变晶格中局域的单胞结构会随着空间位置的不同而变化。其偏离理想单胞的程度反映了局域晶格的畸变大小。然而,实验中得到的晶格类型和晶格常数信息往往反映的是晶体空间群的整体平均效应,不足以揭示局域畸变信息。采用类似的思想,在模拟分析中,可以通过Voronoi分形方法将空间分割成以各个原子为中心的Voronoi多面体[32]。Voronoi多面体反映了以每个原子为中心的局域结构,通过不同指数的Voronoi多面体的分布,可以定量表征偏离理想晶格的畸变程度。本文对最近关于高熵合金晶格畸变的研究做一个简要综述。根据最近的研究成果,集中讨论高熵合金中晶格畸变产生的物理来源,以及晶格畸变对无序固溶体的相稳定性和性能的影响。
1 理论模型
1.1 “畸变晶格”与“理想晶格”
在多组元高熵合金中,由于各成分元素原子分数相近,难以区分溶质与溶剂原子,这就导致传统的固溶体理论不足以描述高熵合金中晶体结构的结构缺陷,比如晶格畸变。2008年,Zhang等[25]提出原子尺寸差异(atomic size difference)参数δ来量化高熵合金中的平均原子尺寸差异效应:δ =
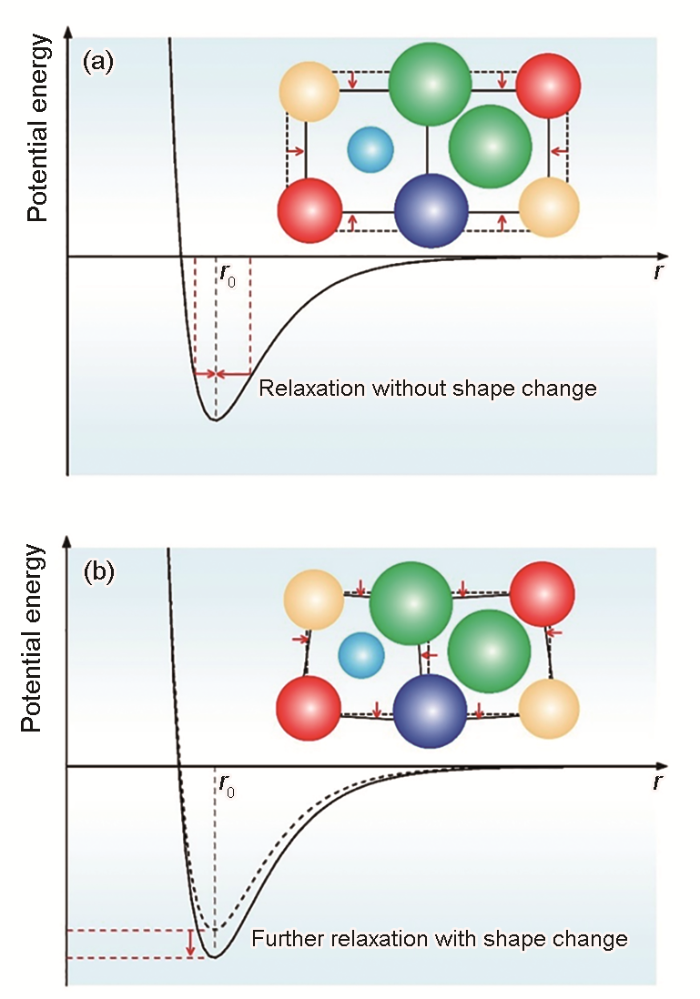
为解决这一问题,Ye等[20]结合密度泛函理论和第一性原理计算,于2018年探讨了“理想晶格”的选取方式。首先构造了无序固溶体结构模型,通过第一性原理计算分2步进行结构驰豫。在第1阶段,限制晶胞结构的形状改变,只允许结构膨胀或收缩。如图1a所示,通过不断驰豫得到体系的势能随体积变化的关系,然后通过拟合得到体系达到平衡状态所对应的晶格常数。由于在这一阶段不涉及剪切应变(但包含体应变),所以将驰豫后的结构作为参考态——即不包含剪切应变的“理想晶格”。在第2阶段,允许晶胞在第一阶段的基础上改变形状,即:通过第1阶段得到的“理想晶格”在不施加任何限制的条件下被进一步驰豫以释放体系能量,如图1b所示。经过第2阶段驰豫,由于各成分原子半径差异以及性能的不匹配,各原子偏离“理想晶格”的点阵结构,形成了“畸变晶格”。值得注意的是,体系的晶格常数在第2阶段的驰豫过程中并没有明显的变化[20],因此第2阶段的驰豫主要是由于晶胞形状的改变。如图1b所示,“畸变晶格”的势能相对于“理想晶格”更低,通过晶胞形状的改变,“理想晶格”中由于成分原子之间原子半径和模量不匹配所造成的弹性畸变能被进一步释放。因此,“畸变晶格”相对于“理想晶格”是一种更为稳定的结构形式。通过这种方式,各原子相对于“理想晶格”点阵的位置变化与内禀残余应变场可被精确定义与描述。
图1
图1
高熵合金中体系的势能随平均原子间距的变化
(a) structural relaxation without shear displacements, leading to an ideal lattice (r is the interatomic distance, r0 is the first nearest neighbor interatomic distance)(b) further structural relaxation by allowing atoms undergo both shear and normal displacements
Fig.1
The potential energy variation with the average inter-atomic distance in high-entropy alloys
1.2 晶格畸变与内禀残余应变场
当不同尺寸原子混合形成单相固溶体结构时,各个成分原子之间的相互作用造成不同尺寸的原子不可避免地产生“挤压”或“拉伸”,在晶格内部形成残余应变场。在传统合金中,残余应变场的形成可以视作溶质原子“镶嵌”在一个由溶剂原子所形成的弹性介质中,该问题可以通过Eshelby[35]的平均场理论得到很好的描述。然而在高熵合金中,由于成分原子种类较多并且含量接近,无法区分“溶质”和“溶剂”原子,这就使得在高熵合金中直接应用Eshelby[35]的平均场产生困难。为描述高熵合金中的残余应变场,Ye等[19]提出了一个自洽的几何模型。该模型假设晶格结构保持不变,各成分原子通过原子半径的改变相互适应以占据“完美晶格”的点阵结构,达到一个平衡的晶体致密度。原子半径的改变带来了残余体应变场,然而由于原子尺度的局域环境不同,残余应变在不同的点阵位置也不尽相同。根据Ye等[19]的几何模型,当体系总体残余应变的平均值接近于零时,对于多组元合金中第i元素的残余体应变
式中,ωij为j原子相对于中心原子i所占据的空间角,Cj为在中心原子最近邻位置发现j原子的概率,ck为k元素的原子分数,
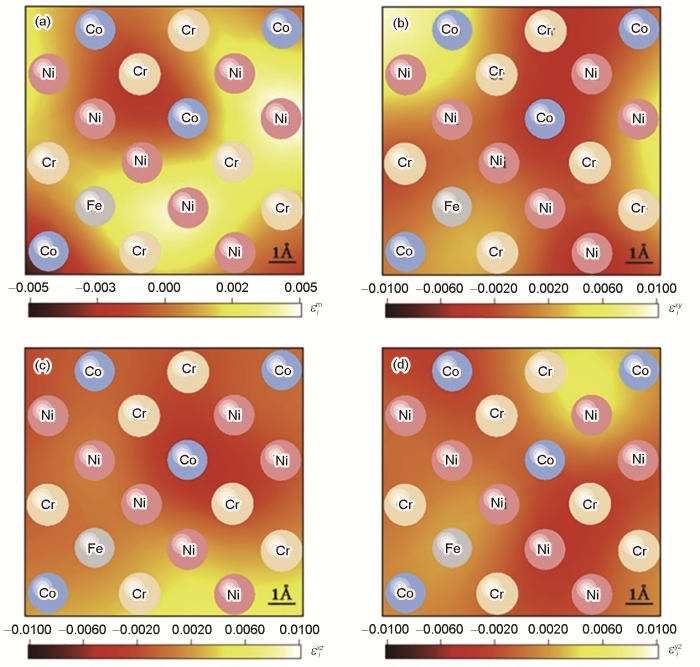
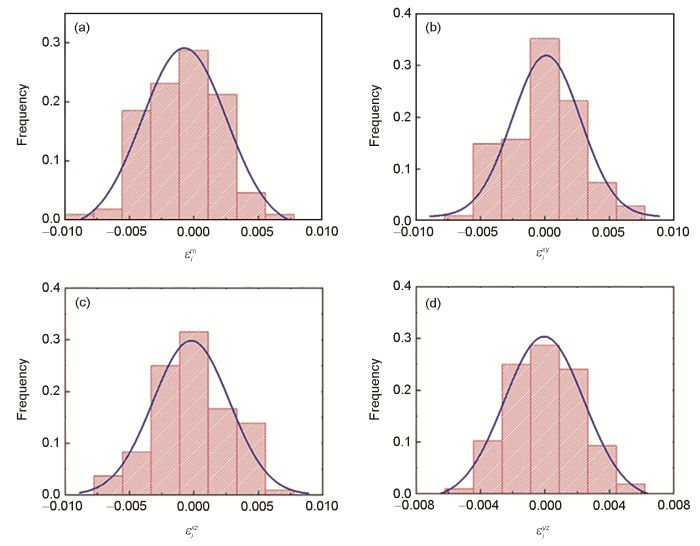
理论上,“畸变晶格”所造成的残余应变场不仅包含体应变分量,也包括切应变分量。然而上述几何模型仅仅针对“理想晶格”考虑了体应变变化,还不足以全面描述“畸变晶格”的残余应变场。为此,Ye等[20]结合密度泛函理论和第一性原理计算,引入切应变用以描述畸变晶格所引起的残余应变场。在该工作中,Ye等[20]首先采用图1a中所示的方式构建了“理想晶格”,然后在“理想晶格”的基础上进一步驰豫,得到“畸变晶格”。因此,以“理想晶格”为参照,“畸变晶格”的各个残余应变分量可以得到精确的描述。图2[20]所示为一典型fcc结构FeCoNiCr合金的各残余应变分量的分布,图3[20]为对应的应变分量分布的直方图。可以看出,各个应变分量的平均值都接近于零,但是其分布却较为弥散,意味着晶格内部不同位置的残余应变存在不同程度的波动。为描述这种“畸变晶格”中波动的残余应变场,Ye等[20]提出了等效切应变
图2
图2
fcc结构FeCoNiCr合金中的残余应变场各个应变分量沿(001)晶面的等高线分布图[20]
(a) the local atomic volumetric strain ε
(c) the shear strain in xz plane ε
Fig.2
The contour plots of the local atomic strain components derived from the fcc FeCoNiCr alloy in the (001) plane[20]
图3
式中,C11、C12和C44为弹性常数;
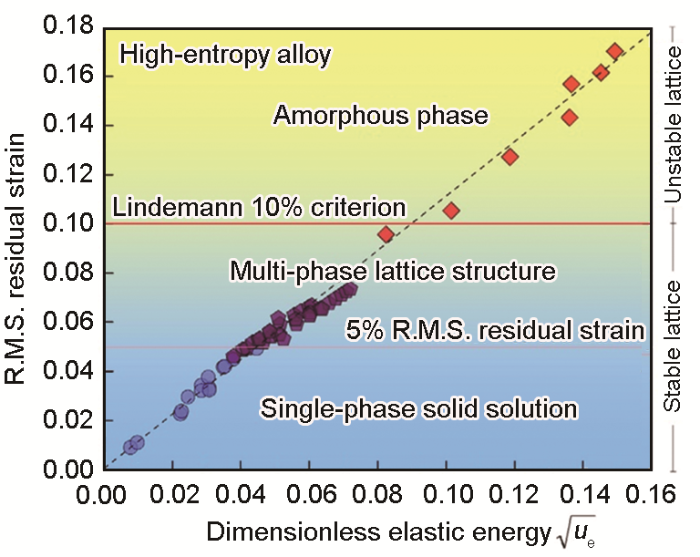
残余体应变和切应变的存在都会对体系的弹性畸变能产生影响,如果仅考虑只存在体应变分量的“理想晶格”,其弹性畸变能可表示为E1,同样,对于同时存在体积和形状变化的“畸变晶格”,其弹性畸变能可表示为E2。因此,从能量角度考虑,晶格形状的改变仅仅在满足“畸变晶格”与“理想晶格”弹性畸变能差异ΔE = E2 - E1 < 0的情况下才能够自发进行。根据Ye等[20]的理论模型,ΔE可表示为体系的残余应变分量与弹性常数的函数,因此满足上述能量的条件可表示为如下形式:
式中,
1.3 晶格畸变与相稳定性
图4
2 实验验证
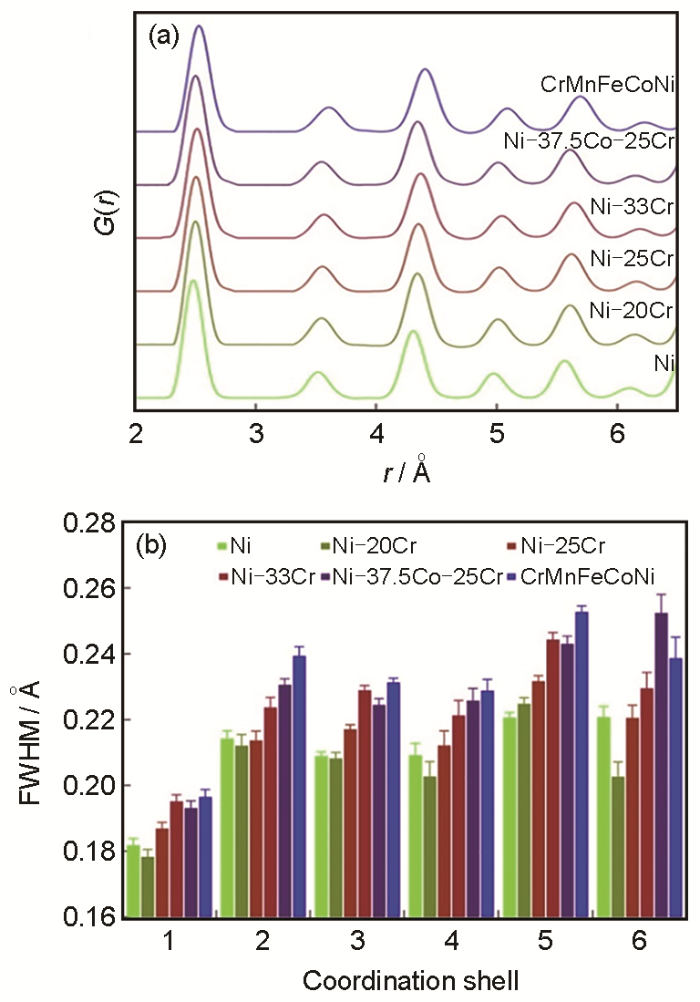
晶格畸变发生在原子尺度,而且在实验上往往与很多其他因素相互耦合,因此通过实验直接观测晶格畸变还存在很大的挑战。2004年,Yeh等[36,37]首次尝试通过X射线衍射方法来表征高熵合金中的晶格畸变。Yeh等[36,37]认为高熵合金中过大的晶格畸变增加X射线散射的程度,因此使得X射线衍射峰的强度降低,增加衍射峰的峰宽。但是由于X射线衍射与晶粒微观结构和织构等结构因素密切相关,这就使得通过X射线衍射峰的强度降低来表征晶格畸变存在疑惑。为解决这一问题,Owen等[28]于2017年通过中子衍射(neutron diffraction)的方式,试图给出高熵合金中晶格畸变的直接实验证据。为了揭示高熵合金中多组元成分的效应,Owen等[28]系统性地选取了6种单相fcc固溶体结构的合金:Ni、Ni80Cr20、Ni75Cr25、Ni67Cr33、Ni37.5Co37.5Cr25和FeCoNiMnCr。在该种方法中,由于中子衍射具有较强的穿透性,较高的分辨率和信噪比,相对于普通的X射线衍射实验更能精确地确定材料内部的精细晶体结构。如图5[28]所示,通过分析一系列固溶体合金中的约化双体关联函数G(r)的前6个近邻壳层的半高宽发现,相对于单质Ni、两组元和三元合金,高熵合金FeCoNiMnCr虽然拥有较强的局域晶格应变,但整体平均晶格应变并没有“显著”增加。Zhang等[38]利用高能X射线衍射法(high energy X-ray diffraction)和扩展X射线吸收精细结构谱(extended X-ray absorption fine structure),详细研究了在FeCoNiCr fcc固溶体结构中添加大原子Pd所造成的晶格畸变。研究[38]发现,四元合金FeCoNiCr体系中的晶格畸变几乎可以忽略,然而,随着Pd原子含量的增加,晶格畸变效应逐渐显著。图6[29]显示,在最近的一项预发布研究工作中,Shao等[29]选取Al0.1CoCrFeNi高熵合金体系作为研究对象,通过能量过滤透射电子显微镜(energy filter transmission electron microscope),利用扫描电子纳米束衍射方式(scanning electron nanodiffraction),直接观测到了高熵合金体系的晶格畸变效应。图6a和b[29]展示了Al0.1CoCrFeNi高熵合金中晶格残余应变的分布图。从线分布图6c和d[29]中可以看出残余应变在晶格中的不同位置不尽相同。图6e[29]的频率分布直方图显示,晶格残余应变的整体平均值接近于零,但其分布存在一个较大的波动,该实验观测得到的晶格残余应变与之前的理论模型具有很好的吻合性[20]。
图5
图6
图6
Al0.1CoCrFeNi高熵合金中的局域晶格残余应变和残余应变的波动[29]
Fig.6
Lattice strain and strain fluctuations in Al0.1CoCr- FeNi high-entropy alloy[29](a) contour map of residual strain in (220) plane(b) contour map of residual strain in (
3 总结与展望
本文简要综述了关于高熵合金中晶格畸变的理论模型与已有的实验结果。当把原子半径不同的元素混合形成单相固溶体结构时,固溶体的晶格结构不可避免地会发生畸变。完整描述畸变晶格的残余应变场需要综合考虑残余体应变和切应变分量。关于高熵合金中的晶格畸变效应目前学术界仍未取得一致看法,其原因在于直接的实验观测具有挑战性。尽管目前已存在一些实验证据,人们仍然需要更多的实验观测以厘清高熵合金中的晶格畸变的程度。
经过十几年的发展,高熵合金吸引了越来越多的研究兴趣,已成为一大研究热点。越来越多的高性能高熵合金被成功开发出来。然而,关于高熵合金中的一系列基础问题仍然存有争议,有待揭示。晶格畸变作为高熵合金中的独特的结构特征仍需要更多的研究。几个重要问题仍有待研究:(1) 如何定量的观测高熵合金中的晶格畸变程度;(2) 晶格畸变与成分原子的原子半径、性质如何关联;(3) 晶格畸变对材料力学与物理性能的影响;(4) 新的实验手段仍有待开发以应用于晶格畸变的定量观测。
参考文献
Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes
[J].
Microstructural development in equiatomic multicomponent alloys
[J].A
High-entropy alloy: Challenges and prospects
[J].
Microstructures and properties of high-entropy alloys
[J].
Science and technology in high-entropy alloys
[J].
Design of high-entropy alloy: A perspective from nonideal mixing
[J].
Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off
[J].
Enhanced strength and ductility in a high-entropy alloy via ordered oxygen complexes
[J].
A fracture-resistant high-entropy alloy for cryogenic applications
[J].
Mechanical properties, microstructure and thermal stability of a nanocrystalline CoCrFeMnNi high-entropy alloy after severe plastic deformation
[J].
Microstructure and wear behavior of AlxCo1.5CrFeNi1.5Tiy high-entropy alloys
[J].
Intrinsic surface hardening and precipitation kinetics of Al0.3CrFe1.5MnNi0.5 multi-component alloy
[J].
Corrosion resistant nanostructured eutectic high entropy alloy
[J].
Alloy design strategies and future trends in high-entropy alloys
[J].
High-entropy alloys: A critical assessment of their founding principles and future prospects
[J].
A critical review of high entropy alloys and related concepts
[J].
Chemical short range order strengthening in a model FCC high entropy alloy
[J].
On lattice distortion in high entropy alloys
[J].
A geometric model for intrinsic residual strain and phase stability in high entropy alloys
[J].
Atomic-scale distorted lattice in chemically disordered equimolar complex alloys
[J].
Lattice distortion in a strong and ductile refractory high-entropy alloy
[J].
Hume-Rothery Rules for Structurally Complex Alloy Phases
[M].
Local lattice distortion in high-entropy alloys
[J].
Lattice distortions in high-entropy alloys
[J].
Solid-solution phase formation rules for multi-component alloys
[J].
Atomic-size effect and solid solubility of multicomponent alloys
[J].
A review of ab initio calculation on lattice distortion in high-entropy alloys
[J].
An assessment of the lattice strain in the CrMnFeCoNi high-entropy alloy
[J].
The paracrystalline nature of lattice distortion in a high entropy alloy
[Z].
Random packings and the structure of simple liquids. I. The geometry of random close packing
[J].
Prediction of high-entropy stabilized solid-solution in multi-component alloys
[J].
Quantitative size-factors for metallic solid solutions
[J].
Formation of simple crystal structures in Cu-Co-Ni-Cr-Al-Fe-Ti-V alloys with multiprincipal metallic elements
[J].
Anomalous decrease in X-ray diffraction intensities of Cu-Ni-Al-Co-Cr-Fe-Si alloy systems with multi-principal elements
[J].
Lattice distortion and phase stability of Pd-doped NiCoFeCr solid-solution alloys
[J].