金属热导率(λ)的传统表征方法主要是通过计算密度、比热容和热扩散系数的乘积,即采用公式λ=αρcp (其中,α为热扩散系数,ρ为材料密度,cp为比热容)。为利用该公式首先需要知道材料的密度,再采用差热分析仪测试比热容,然后通过闪光法导热测试仪等设备测量热扩散系数,最终3者乘积得到材料的热导率。这种方法虽然能够直观地获得材料的导热性能,但是效率低下,且成本较高,因此急需开发出高效快速的材料性能评估方法。
近几年来,随着计算机技术与理论物理学的发展,计算材料学作为一门新的学科逐渐兴起,应用第一性原理计算材料的力学、光学、磁学、腐蚀与热力学性质的方法也逐渐被更多的科研工作者所接受,并不断发展完善[4,5]。刘金[6]采用第一性原理与虚晶近似方法对纯金属Cu、Fe、Al及其合金的电子热导率进行了研究,总结了电子热导率随温度变化的微观机理。温斌和冯幸[7]应用第一性原理的方法,结合Debye模型、形变势模型和Drude自由电子气模型,分别对Al的电子热导率与声子热导率进行了研究。Tong和Bao[8]应用第一性原理详细分析了金属间化合物NiAl和Ni3Al中电子-电子、电子-声子、声子-声子之间的散射作用,准确计算出各种散射机制共存时材料的电子与声子热导率。Ma等[9]应用第一性原理与Slack模型计算了300、500与700 K温度下AgIn5Te8的电子热导率与声子热导率,并对材料的热电特性进行了评估。总体而言,虽然国内外学者提出了虚晶近似等较多的热导率计算方法,但是普遍存在适用范围小、耗时较长、效率较低等缺点。例如应用第一性原理方法求解电子弛豫时间时,需要耗费大量机时,不仅提高了研发成本,而且也延长了新材料的研发周期。
本工作通过引入常弛豫时间近似方法[10],在保证计算结果准确性的基础上有效提高了计算效率,并且在应用Slack方程计算材料声子热导率的过程中,创新性地将Birch-Murnaghan能量体积状态方程与Debye模型结合,推导出Grüneisen参量的表达式,提出了快速准确计算声子热导率的新方法。并采用上述计算方法分别对Al、Mg、Zn纯金属的电子和声子热导率进行了研究,在此基础上深入讨论了金属材料导热的微观机制。
1 实验方法
其中,
1.1 电子热导率计算
根据Drude自由电子理论,金属中的价电子不受原子的束缚,可以自由地在金属中运动。电子的分布状态满足Fermi-Dirac分布规律[13]:
式中,
根据Boltzmann方程,在外加电场(
其中,s表示电导率;S是Seebeck系数;K表示与热导率相关的某一数值,满足关系κe = K - S2σT;e表示元电荷;
本工作使用正则赝势计算电子的波函数、能带结构以及基态总能量,使用的交换关联势为Perdew-Burke-Ernzerhof (PBE),属于广义梯度近似方法。涉及的金属材料的电子弛豫时间均采用常弛豫时间近似。Den[10]在研究中指出,对于金属材料而言,在各种散射机制同时存在的情况下,电子的弛豫时间可近似为1.0 × 10-14 s,并且近似处理后的计算结果与实验测试结果吻合。Madsen等[14]与Motta等[15]的研究也分别证明了常弛豫时间近似方法的可行性。为此,本工作基于密度泛函理论(DFT)和最大局域化Wannier函数(MLWFs),采用Quantum-Espresso软件计算电子的能带结构,并结合wannier90程序包计算出电子速率,最后通过式(
MLWFs方法通过引入最大局域化的概念,使得Wannier函数在具有局域化特点的基础上,实现了唯一性,因此MLWFs方法能够用来简化计算材料的电子能带结构和电子速率[16]。构造Wannier函数时,需要仔细调节总能带数(需要总能带数能够覆盖所需研究的能带(特别是Fermi面附近的能带)以及覆盖投影子具有投影成分的能带)、投影子(调节后确保轨道更加局域)以及解纠缠能量窗口(确保投影子在能量空间之内,若能量过大容易造成轨道不够局域),确保由Wannier函数计算得到的电子能带在Fermi面附近与DFT计算的电子能带相互匹配。
1.2 声子热导率计算
式中,
分析
Debye理论指出,晶格振动时声子频率总会存在一个极限值,这个有限的声子频率被称为Debye频率。根据Debye理论,可以将Grüneisen参量改写为如下形式:
由Debye模型分析可知,
式中,
根据大量实验结果分析可知,一般金属材料的
式中,
1.3 计算效率评估
表1对比了采用本工作的计算方法与其他方法在计算热导率时的耗时情况。结果显示,相比于Quantum-Espresso与VASP,本工作提出的新方法在计算效率方面呈现明显的优势,如在计算纯Mg的电子热导率时,耗时仅为Quantum-Espresso办法的1/5,VASP的1/3,而且在材料结构更为复杂的Mg2Si和Mg2Ca体系中,计算效率更加显著。这是由于传统的Quantum-Espresso与VASP软件在计算电子弛豫时间时需要耗费大量的时间,因此本工作中应用的常弛豫时间近似方法能够明显提高材料的电子热导率计算效率。
表1 电子热导率与声子热导率常用计算方法的用时比较
Table 1
| Material | ||||||
|---|---|---|---|---|---|---|
| C.R.T | Quantum-Espresso | VASP | Slack | Phonon-Boltzmann | ||
| Mg | 1 | 5 | 3 | 1 | 14 | |
| Mg2Si | 2 | 14 | 9 | 1 | 28 | |
| Mg2Ca | 2 | 13 | 8 | 1 | 24 | |
2 实验结果
2.1 几何优化与能带结构
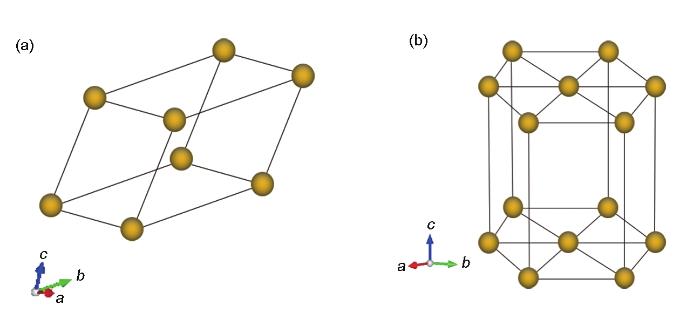
图1
图1
Al、Mg和Zn的原子结构示意图
Fig.1
Schematics of atomic structures of Al (a), Mg and Zn (b)
表2 Al、Mg和Zn的晶体结构与点阵常数
Table 2
图2
图2
基于DFT与MLWFs的Al、Mg和Zn的电子能带结构比较
Fig.2
Comparisons of the electronic band structures based on density functional theory (DFT) and maximally localized Wannier functions (MLWFs) of Al (a), Mg (b), and Zn (c) (The open circles are the band structures calculated based on DFT, and the solid lines represent the band structures calculated by MLWFs)
2.2 电子输运性质
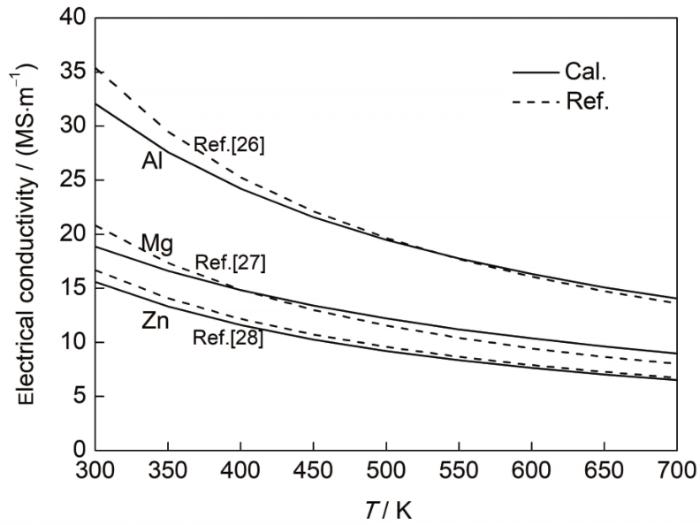
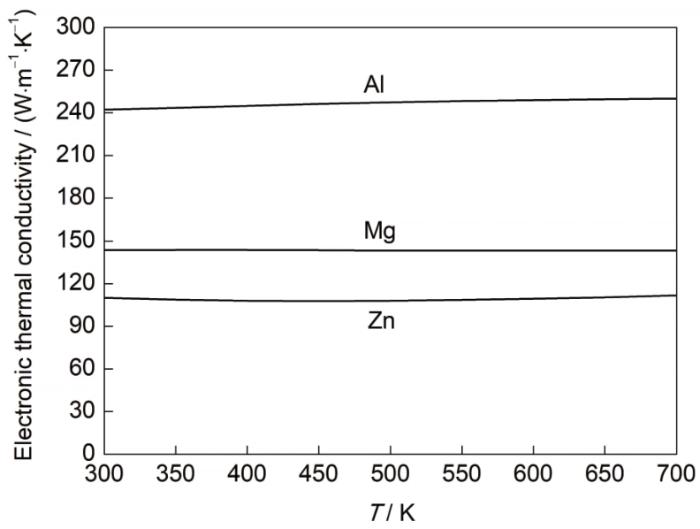
表3统计了3种金属在300、500与700 K温度下的电导率和电子热导率,并将电导率与实验测量值[26~28]进行了比较。结果显示,Al、Mg、Zn这3种金属在300 K下的电导率分别为32.07、18.87和15.58 MS/m,与实测的电导率数值[26~28]较为接近,计算结果与实测值的偏差均在10%以内,证明了计算方法的准确性。而且,随着温度的升高,电导率的计算值变化趋势与实测值保持一致,均呈现下降的趋势。计算结果表明,在300 K温度下Al、Mg、Zn的电子热导率分别为242.15、143.54和110.07 W/(m·K),显然,相比于Mg和Zn而言,Al是更为优异的导电材料和导热材料。
表3 Al、Mg、Zn的电导率计算值与实测值[26~28]及电子热导率
Table 3
图3
图4
图4
Al、Mg和Zn的电子热导率随温度变化曲线
Fig.4
Variations of electronic thermal conductivity with temperature for Al, Mg, and Zn
2.3 声子热导率
表4 Al、Mg和Zn的热力学参数计算值与实测值[7,28,30~33]与声子热导率
Table 4
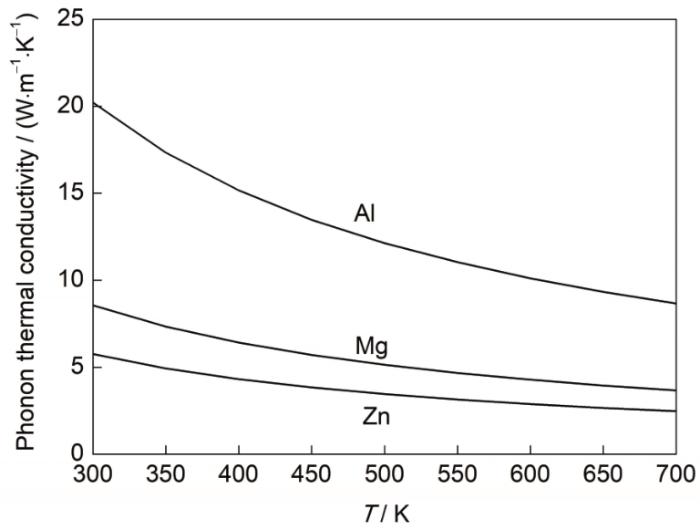
3种材料的声子热导率随温度的变化关系如图5所示。随着温度的升高,声子热导率均表现出明显的下降趋势。这是因为随着温度的上升,材料内部晶格振动加剧,声子与声子之间的散射作用增加,从而导致声子热阻增加,声子热导率降低。3种金属声子热导率的差异性主要是由原子间的结合力不同所导致的。
图5
图5
Al、Mg和Zn的声子热导率随温度变化曲线
Fig.5
Variations of phonon thermal conductivity with temperature for Al, Mg, and Zn
2.4 总热导率
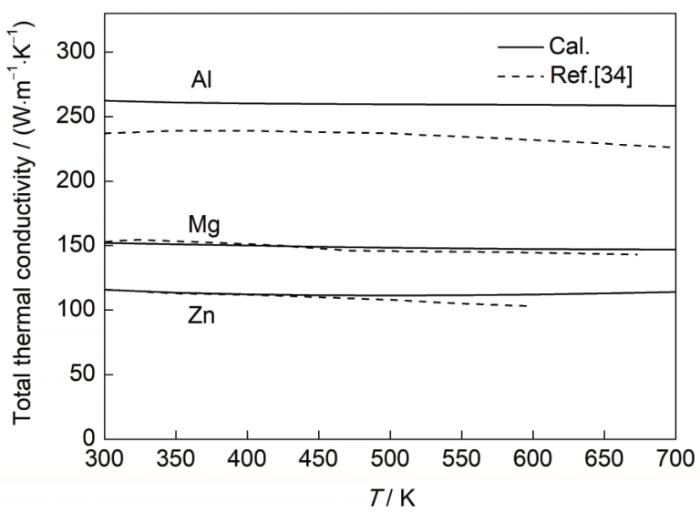
图6为300~700 K温度区间内总热导率与实测值[34]的对比。其中,实线为计算得到的材料的总热导率,虚线表示实测值[34]。结果显示,计算的总热导率变化曲线与实测值吻合良好。另外,Al热导率的计算值与实测值存在微小的偏差,这是因为第一性原理的计算只考虑了材料内部电子、声子之间的相互作用,而实际工程材料中广泛存在大量的晶界、位错与缺陷等,会进一步增加材料内部电子与声子的散射,从而降低材料的热导率。随着温度的升高,3种金属的总热导率均没有发生明显的变化。这是因为在该温度范围内,材料的电子热导率基本不变,声子热导率虽然随温度升高而有所降低,但对整体的影响较小。因此,在该温度区间内,材料的总热导率变化较小,而且3种材料的总热导率也表现出了与电导率一样的规律,即Al > Mg > Zn。
图6
3 分析讨论
对于金属或合金而言,电导率与电子热导率密切相关。随着温度升高,Al、Mg、Zn这3种金属的电导率均呈现出明显的下降趋势。这是因为,金属原子的最外层电子与原子核的结合力弱,很容易摆脱原子核的束缚而变成自由电子,大量自由电子在金属中发生定向运动会产生电流,从而使材料导电。原子在晶体内部会按照一定的几何形式规则排列,并在固定的位置上作高频率的热振动。随着温度的升高,原子振动幅度增大,对自由电子的阻碍作用增加,因此金属材料的电导率随着温度的上升迅速下降。Al的电导率明显高于Mg和Zn,这与金属材料的价电子数目相关。Al、Mg和Zn 3种金属的电子排布规律分别为3s23p1、3s2和3d104s2,Al的价电子数目为3,Mg与Zn的价电子数目都是2。因此在相同条件下,Al晶体中自由电子浓度较高,在相同的外电场作用下产生的电流更大。Mg与Zn的价电子数目相同,但Mg的电导率高于Zn的电导率,这是因为Mg的原子半径较大。一般地,在金属材料中,原子半径越大,原子核对核外电子的束缚作用越小,而Mg的原子半径大于Zn,更容易失去其核外电子,因此相同温度下Mg的电导率要高于Zn的电导率。
其中,
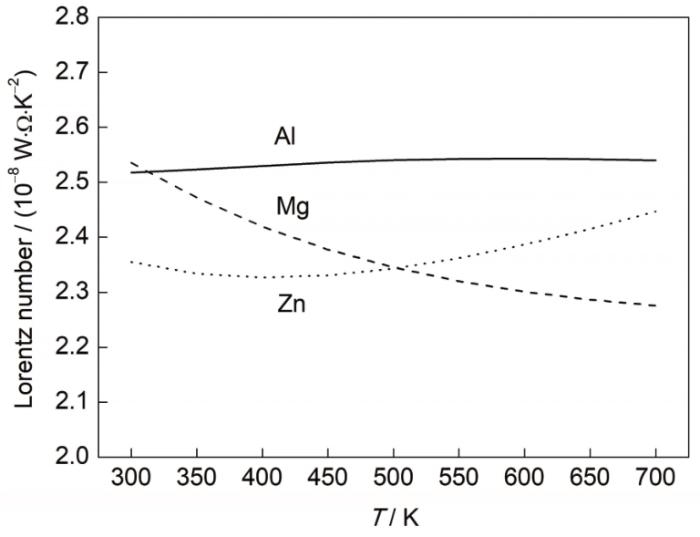
图7为计算得到的Al、Mg、Zn金属材料在不同温度下的Lorenz数。可以看到,3种金属的Lorenz数基本都接近于其理论数值(2.45 × 10-8 W·Ω/K2),波动范围在± 5%之间。对于金属而言,Lorenz数之所以发生变化是由于电子在电场和温度场作用下的散射机制不同造成的。在外加电场作用下,电子的Fermi分布倾向于集体偏离平衡状态,要想使电子回归平衡状态,就需要对电子产生大角度散射;然而在温度场作用下,声子除了大角度散射以外,还存在小角度散射。声子只需要提供给电子很小的能量,就可以使电子在Fermi面附近发生跃迁,即发生小角散射,使系统在温度场作用下回归平衡状态[13,36]。在300~700 K温度区间内,声子的能量较高,具有大的波矢,不管是电场还是温度场基本都以大角散射为主,因此Lorenz数基本不随温度而变化(稳定在标准Lorenz数附近)。本计算结果也证实了Wiedemann-Franz定理在该温度区间的合理性。
图7
图7
Al、Mg和Zn的Lorenz数与温度的关系曲线
Fig.7
Variations of Lorenz number with temperature for Al, Mg, and Zn
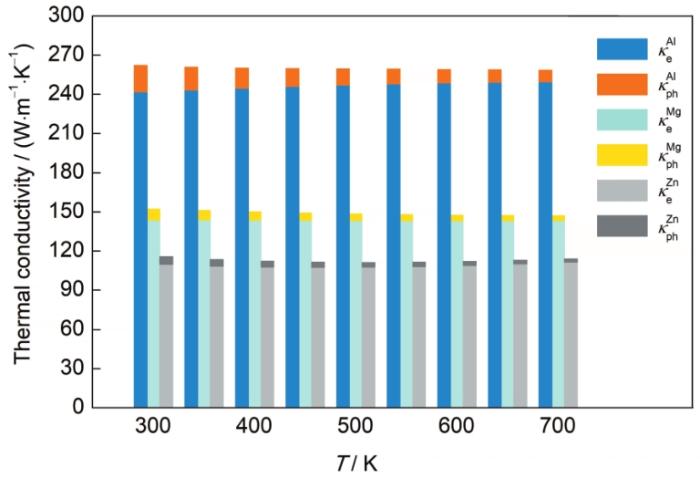
金属材料中,电子与声子对总热导率的贡献存在明显的差异。图8的统计结果表明,在300~700 K温度区间内任何温度下,材料的电子热导率都显著高于声子热导率。这是因为对于金属材料,相比于声子而言,自由电子是更为有效的载流子,并且随着温度的升高,原子围绕晶格位点的振动幅度增大,导致电子与声子以及声子与声子之间的散射几率增加,产生较高的热阻,降低材料的热导率。一般地,纯金属材料中对声子热导率影响最大的是声子与声子之间的碰撞过程。声子之间的相互碰撞分为2种情况:一种是2个声子碰撞之后产生第3个声子,声子的动量不发生改变,这个过程称为正规碰撞过程(normal process)或者N过程;另一种情况是碰撞后声子的动量发生改变,这个过程称为倒逆过程(umklapp process)或者U过程[37]。根据这2种碰撞情况的定义可知,只有U过程的声子散射会产生热阻。一般情况下,随着温度的升高,声子能量增加,声子之间的大角度散射几率升高,U过程的声子散射加剧,导致声子热导率的降低。Yang等[38]对CoSb3的低温热导率研究发现,在300 K温度以上,该材料声子碰撞的U过程占主导作用。
图8
图8
不同温度下Al、Mg、Zn的电子热导率与声子热导率对比
Color online
Fig.8
Comparisons of electron thermal conductivity and phonon thermal conductivity of Al, Mg, and Zn at different temperatures (
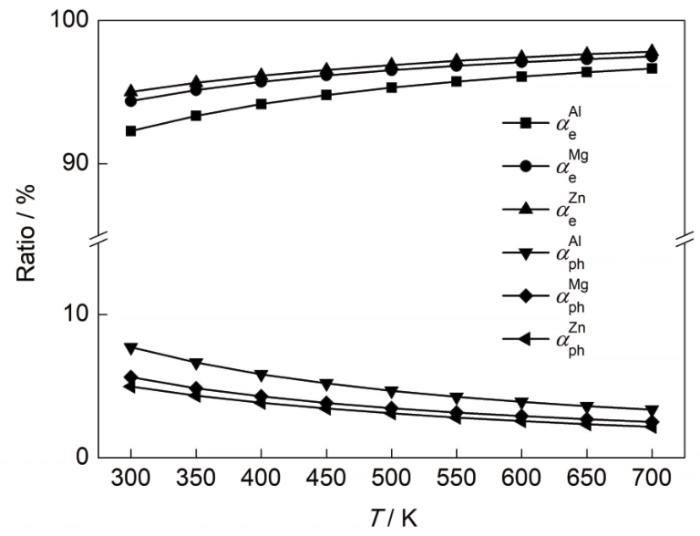
电子与声子热导率对总热导率的贡献比率如图9所示。3种金属材料中,Al的声子热导率对总热导率贡献较高,最高时可接近8%,这与材料的晶体结构和原子质量密切相关。Al属于fcc结构,初基原胞内只包含有一个Al原子,而Mg和Zn均属于六方结构,初基原胞内包含3个原子,相比Mg和Zn,Al晶格振动时产生的简正模数目较少,声子之间的散射几率较小,因此Al的声子热导率较高。此外,由于Mg的原子质量比Zn小,Mg晶体内的晶格振动产生的声子速率较高,声子热导率较高。随着温度的升高,金属材料的声子热导率占总热导率的比值明显下降。这是因为在该温度区间内,温度增加引起声子之间U过程的散射作用加剧,导致声子热阻增大,而电子热导率变化不大,因此声子热导率对总热导率的贡献比例随温度升高逐渐降低。
图9
图9
不同温度下Al、Mg、Zn的电子与声子热导率占总热导率比值
Fig.9
Ratios of electron thermal conductivity and phonon thermal conductivity to the total thermal conductivity for Al, Mg, and Zn at different temperatures (
4 结论
(1) 引入常弛豫时间近似计算金属材料的电子热导率,并将Birch-Murnaghan状态方程与Debye模型代入Slack方程来计算材料的声子热导率,能够明显提高材料热导率的计算效率。计算结果与实验测量值吻合良好,验证了计算方法的准确性。
(2) Al、Mg、Zn 3种金属的总热导率在300~700 K温度内变化不大,其中Al的热导率最大,Mg次之,Zn最小。
(3) Al、Mg、Zn 3种金属材料的Lorenz数在300~700 K温度区间内基本不随温度变化,始终稳定在2.45 × 10-8 W·Ω/K2 (标准Lorenz数)附近。
(4) 在Al、Mg、Zn 3种金属材料的热输运过程中,电子始终发挥着最主要的作用,并且随着温度的升高,声子热导率占总热导率的比率逐渐降低。
参考文献
Texture and mechanical properties of superplastically deformed magnesium alloy rod
[J].
Thermal enhancement from heat sinks by using perforated fins
[J].
Predicted interfacial thermal conductance and thermal conductivity of diamond/Al composites with various interfacial coatings
[J].
Research on the extrusion technology of magnesium alloy radiator
[J].
镁合金散热器挤压工艺研究
[J].
Thermal conductivity of metals and alloys
[J].
First principal study of thermal conductivity of Cu/Fe/Al and their alloys
[D].
关于金属Cu、Fe、Al及其合金热导率的第一性原理研究
[D].
Thermal conductivity of metal from first principles calculations and its application in aluminum
[J].
金属热导率的第一性原理计算方法在铝中的应用
[J].
Decompose the electron and phonon thermal transport of intermetallic compounds NiAl and Ni3Al by first-principles calculations
[J].
Effects of transport direction and carrier concentration on the thermoelectric properties of AgIn5Te8: A first-principles study
[J].
Influence of the relaxation time approximation on first principle study of transport coefficients in thermoelectric material PbTe
[D].
BoltzTraP. A code for calculating band-structure dependent quantities
[J].
Charge carrier mobility in hybrid halide perovskites
[J].
Maximally localized Wannier functions for entangled energy bands
[J].
High throughput combinatorial method for fast and robust prediction of lattice thermal conductivity
[J].
The thermal conductivity of nonmetallic crystals
[J].
High-throughput computational screening of thermal conductivity, Debye temperature, and Grüneisen parameter using a quasiharmonic Debye model
[J].
The compressibility of media under extreme pressures
[J].
Thermoelectric transport properties of silicon: Toward an ab initio approach
[J].
Ab initio calculation of the linewidth of various phonon modes in germanium and silicon
[J].
AFLOWLIB.ORG: A distributed materials properties repository from high-throughput ab initio calculations
[J].
Effect of Zr content on the structure and properties of commercial aluminum
[D].
Zr含量对工业纯铝组织性能的影响
[D].
Effect of grain size on low-temperature electrical resistivity and thermal conductivity of pure magnesium
[J].
Resistivity of single crystal zinc
[J].
Thermodynamic properties of Al, Ni, NiAl, and Ni3Al from first-principles calculations
[J].
Determination of the mechanical properties of extruded pure magnesium during tension-tension low-cycle fatigue using ultrasonic testing
[J].
The absolute X-ray scattering factor of magnesium
[J].
Considerations on the bulk modulus of pure metals
[J].
Ueber die Wärme-Leitungsfähigkeit der Metalle
[J].
Thermal behavior of pure magnesium and binary magnesium alloys
[D].
纯镁和二元镁合金的导热行为研究
[D].
Influence of electron-phonon interaction on the lattice thermal conductivity of Co1-xNixSb3
[J].