绿色环保是现代能源与电力工业发展的重要趋势,降低铁芯损耗和噪音成为亟需解决的问题[1,2,3,4]。取向硅钢是制作变压器铁芯的关键材料,分为普通取向硅钢(CGO)和高磁感取向硅钢(HiB),高磁感取向硅钢具有更高晶粒取向度,磁感更高、铁损更低且磁致伸缩系数更小。提高取向硅钢晶粒取向度和减薄板厚规格可有效降低铁损。随着生产技术不断完善,高磁感取向硅钢晶粒取向度已逐渐接近极限[5],而进一步减薄钢板厚度会大幅提高生产成本和技术难度。高磁感取向硅钢二次再结晶晶粒粗大,通过激光刻痕在钢板表面引入局部残余应力,作为“人工晶界”细化沿轧向的主畴间距进而降低异常损耗,已成为高磁感取向硅钢降低铁损的常用工艺方法。如果兼顾取向硅钢晶粒取向与尺寸以及激光刻痕参数等因素的综合影响,总铁损降幅可达到10%~15%[6,7,8]。
激光在刻痕线附近产生残余应力和塑性变形以及刻痕线间张力,除细化主畴进而降低铁损外,亦会显著影响取向硅钢的磁致伸缩行为[9,10]。刻痕取向硅钢磁致伸缩主要来自2方面:一是取向偏差角引起180°主畴壁间的横向畴在磁化过程中湮灭和重现产生磁致伸缩[11,12,13];二是刻痕区及附近区域(影响区)的局部应力封闭畴引发的磁致伸缩[6,14]。横向畴数量由取向偏差角和涂层张力共同决定[15,16],刻痕影响区应力封闭畴体积则由刻痕参数决定[17]。Redikultsev等[18]发现激光刻痕能够降低取向硅钢磁致伸缩系数。Fujikura等[19]发现激光刻痕参数范围选择对取向硅钢的磁致伸缩系数产生重要影响,刻痕能量密度过高或刻痕间距过小导致磁致伸缩系数提高,并提出通过合理控制横向畴与封闭畴可使总磁致伸缩系数达到最低值。
目前,激光刻痕对取向硅钢磁致伸缩系数的影响规律仍无定论,不过可归因于激光刻痕取向硅钢的磁畴结构由刻痕工艺、取向偏差角和涂层张力等因素的交互作用。Tabrizi[17]提出激光刻痕取向硅钢的磁致伸缩系数为刻痕影响区封闭畴和临近区域内横向畴所引发磁致伸缩系数的加和,虽基于单晶磁畴观测结果计算了激光刻痕取向硅钢的磁致伸缩系数,但无法实现取向偏差角和刻痕参数等多因素作用下磁畴结构与磁致伸缩系数的预测。现有主畴结构的计算模型,是综合了取向偏差角引发杂散磁场能、表面磁荷引发退磁场能以及磁畴结构能量最小化原理,用以预测取向偏差角、涂层应力以及机械刻痕等因素的影响规律[20,21]。但由于激光刻痕复杂的应力分布和磁畴结构,尚未构建起考虑取向偏差角与刻痕参数等多参数条件下磁畴结构和磁致伸缩系数的计算方法。
本工作基于刻痕影响区的应力分布特征,提出激光刻痕取向硅钢退磁状态下的磁畴结构,引入刻痕与取向偏差角间的交互作用,通过磁畴结构能量最小化,计算刻痕条件下取向硅钢磁畴结构与磁致伸缩系数;并进一步提出取向分布条件下的磁致伸缩系数计算模型,研究刻痕参数对取向硅钢磁畴结构与磁致伸缩行为的影响机制及刻痕参数优化方法。
1 计算模型
式中,Elancet为柳叶畴系统总能量;Kc为磁晶各向异性参数;β为晶粒易磁化轴[001]方向与板面的取向偏差角;VL为表面柳叶畴体积分数;μ*为相对磁导率;t为板厚;WL为表面柳叶畴长度;Ww为表面柳叶畴宽度;Dw为主畴宽度;γ180和γ90为畴壁能,其中γ180=2(AsKc)1/2,γ90=(AsKc)1/2,As为刚度常数;λ100为单晶<100>方向的磁致伸缩系数;σu为涂层张力。式中,第1项为表面杂散磁场能,第2~4项分别为180°畴壁能、90°畴壁能和磁弹性能。
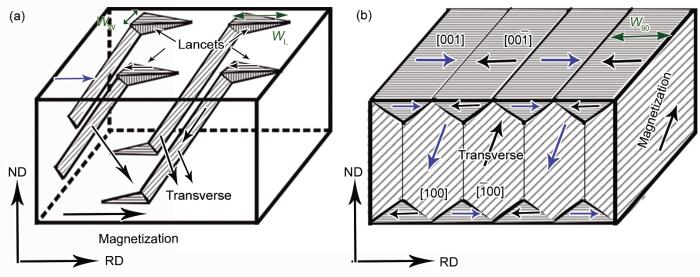
激光刻痕条件下,刻痕影响区形成以应力封闭畴为主的磁畴结构,包含内部横向畴和表面封闭畴,如图1b所示。则在激光刻痕影响区内的应力封闭畴能量为:
图1
图1
取向硅钢磁畴结构模型,包括取向偏差角产生的柳叶畴和横向畴及压应力产生的封闭畴
Fig.1
Models of domain structures in grain-oriented silicon steel (WL—length of lancet domain, Ww—width of lancet domain, W90—width of closure domain, ND—normal direcition, RD—rolling direcrtion)
(a) lancet domain and transverse domain (b) stress closure domain
刻痕影响区局部残余应力形成封闭畴的同时,应力封闭畴和刻痕区域的杂散磁场导致钢板表面杂散磁场降低,进而影响柳叶畴与横向畴数量。因此,本工作提出在具有激光刻痕时的磁畴能量计算中,需要考虑引入刻痕影响区的应力封闭畴、刻痕区杂散磁场能及取向偏差角产生的退磁能等能量的交互影响。则激光刻痕取向硅钢总能量为:
式中,Eg为总能,EstT为激光刻痕后的总杂散磁场能,Emain为总180°主畴壁能,E90为总90°畴壁能,EetL为总磁弹性能。EstT包括取向偏差角引发的表面磁荷杂散磁场能(式(4)第1项)、刻痕局部区域的杂散磁场能[20]和封闭畴表面杂散磁场能(式(4)第2项)。EstL为柳叶畴产生的杂散磁场能,可忽略不计。VC为应力封闭畴体积分数,Bs为饱和磁感应强度,μ0为真空磁导率。刻痕影响区特征与刻痕能量密度(Ea)的关系通过激光热辐射方程和弹塑性热应力分析确定[27,28]。应力封闭畴结构特征利用式(2)进行求解。因此,根据式(3)~(7)中能量最小化求解的主畴与柳叶畴结构,综合考虑了激光刻痕引入应力封闭畴磁畴结构和杂散磁场能对横向畴数量的影响,可反映刻痕与取向偏差角对磁畴结构的综合作用。
式中,λtot为整体磁致伸缩系数,λtransverse和λclosure分别为横向畴和应力封闭畴产生的磁致伸缩系数,Bm为瞬时磁感应强度,VT为横向畴体积分数,WC为刻痕影响区的应力封闭畴宽度。
式(8)中VT利用柳叶畴的尺寸进行求解[26],VC和WC由式(2)中刻痕影响区应力封闭畴结构求解得到。因此,本工作综合考虑激光刻痕参数和取向偏差角对应力封闭畴与横向畴结构的影响,提出了反映刻痕参数与取向偏差角交互作用的磁致伸缩系数计算模型。
本工作计算所用的物理参数[10]如下:Kc=3.62×104 J/m2,As=1.51×10-11 J/m,μ0=4π×10-7 A·m,Bs=2.03 T;t=0.23 mm,σu=5~15 MPa,σc=10~40 MPa,D2=0.1 mm。其中,为表征Ea的影响,选取Dp=4~5 mm。为了表征Dp的影响,Dp选取范围为2~10 mm。刻痕方式采用连续刻痕,刻痕线平行于取向硅钢板横向。
2 计算结果
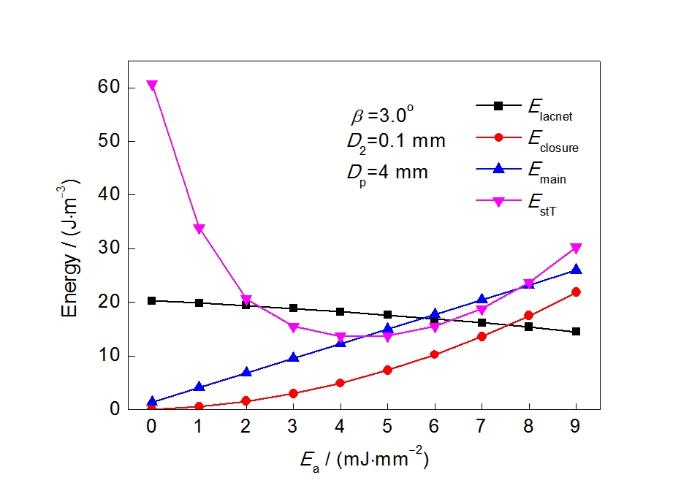
图2为刻痕影响区应力封闭畴能量Eclosure、柳叶畴与横向畴能量Elancet、总180°畴壁能Emain和总杂散磁场能EstT随Ea的变化关系。其中,β=3°,Dp=4 mm,D2=0.1 mm。Eclosure随Ea的提高而增大,表明Ea提高导致应力封闭畴数量增加。Elancet随Ea的提高而减小,是由于应力封闭畴的形成降低了取向偏差产生的退磁能。Emain随着Ea的提高而增大,表明Ea提高导致主畴细化。EstT随着Ea的提高先降低后提高,这可归因于应力封闭畴形成、柳叶畴和横向畴减小和主畴细化等磁畴结构间的交互作用。其中,取向偏差产生的杂散磁场能因刻痕影响区应力封闭畴形成和主畴细化而减小,刻痕区内的杂散磁场能随刻痕能量密度的提高而增大。
图2
图2
不同磁畴能量和刻痕区杂散磁场能与刻痕能量密度(Ea)的关系
Fig.2
Domain energies (Emain, Elancet, Eclosure) and stray field energy (EstT) as a function of laser energy density (Ea) (Emain—energy of 180° domain wall, Elancet—energy of lancet domain system, Eclosure—energy of closure domain system, β—orientation deviation angle, Dp—laser-scribing spacing, D2—laser-scribed width)
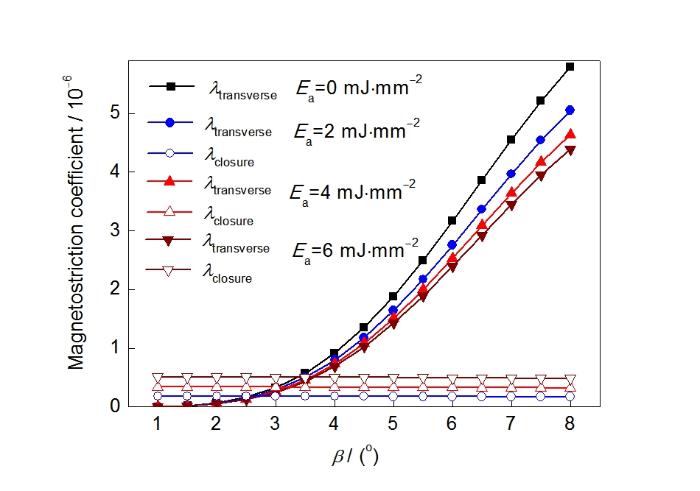
图3为不同Ea下横向畴和应力封闭畴引发的磁致伸缩系数随β的变化。横向畴产生的磁致伸缩系数,随β的增大而明显增加,随Ea提高而降低且降低幅度逐渐减小。应力封闭畴产生的磁致伸缩系数,随Ea增强而提高。其中,低取向偏差角(β<3°)时横向畴产生的磁致伸缩系数很小,而在高取向偏差角(β≥3°)时磁致伸缩系数明显增大。对比2种磁畴结构产生的磁致伸缩系数,低取向偏差角下磁致伸缩系数主要由应力封闭畴数量决定,磁致伸缩系数随Ea提高而增大;而高取向偏差角下磁致伸缩系数主要由横向畴数量决定,随Ea提高而减小。
图3
图3
刻痕条件下横向畴和应力封闭畴产生的磁致伸缩系数随取向偏差角的变化
Fig.3
Dependence of magnetostriction coefficients on β under different Ea (λtransverse—magnetostriction coefficient induced by transverse domain, λclosure—magnetostriction coefficient induced by closure domain)
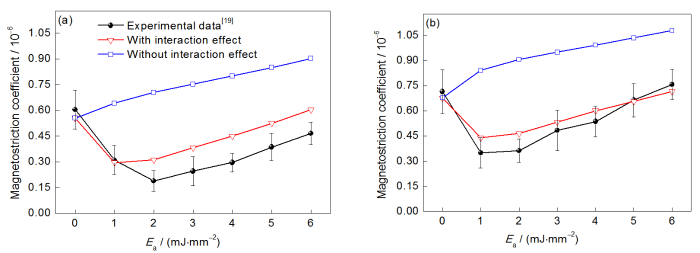
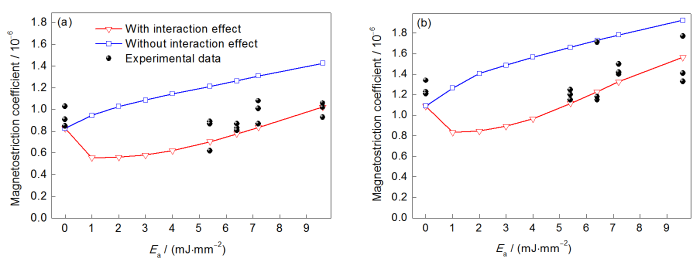
实际上,尽管取向硅钢成品板为单一Goss织构,但各晶粒取向间仍存在一定差异。因此,有必要进一步研究取向偏差角呈现分布特征时的磁致伸缩系数。图4为取向偏差角分布条件下取向硅钢磁致伸缩系数随Ea变化的计算结果。其中,利用正态分布表征取向偏差角分布,平均取向偏差角β取3.0°,D2=0.1 mm,Dp=5 mm,σu=15 MPa。不考虑刻痕与取向偏差角产生横向畴间的交互作用时,磁致伸缩系数随Ea提高而单调增大。考虑刻痕对取向偏差角产生横向畴间的交互作用时,磁致伸缩系数随Ea提高呈先减小后增大的规律,且均显著低于不考虑交互作用的情况。由Ea对横向畴产生磁致伸缩系数的影响可知,当刻痕导致应力封闭畴体积引发的磁致伸缩系数的增幅超过横向畴降低引发磁致伸缩的降幅时,总磁致伸缩系数随Ea提高而增大,反之则减小。
图4
图4
不同磁感应强度下取向硅钢磁致伸缩系数随Ea的变化
Fig.4
Magnetostriction coefficients as a function of Ea under the magnetic induction intensity Bm=1.7 T (a) and Bm=1.9 T (b) (B8—magnetic induction intensity at external magnetic field of 800 A/m. The parameters for measurement and calculation are Dp=5 mm, B8=1.93 T, β= 3.0°, D2=0.1 mm)
图5
图5
B23P095取向硅钢在不同磁感应强度下磁致伸缩系数随Ea的变化
Fig.5
Magnetostriction coefficients of grain-orientated silicon steel B23P095 as a function of Ea under Bm=1.7 T (a) and Bm=1.9 T (b) (Dp=4 mm, B8=1.92 T, β= 3.5°, D2=0.1 mm)
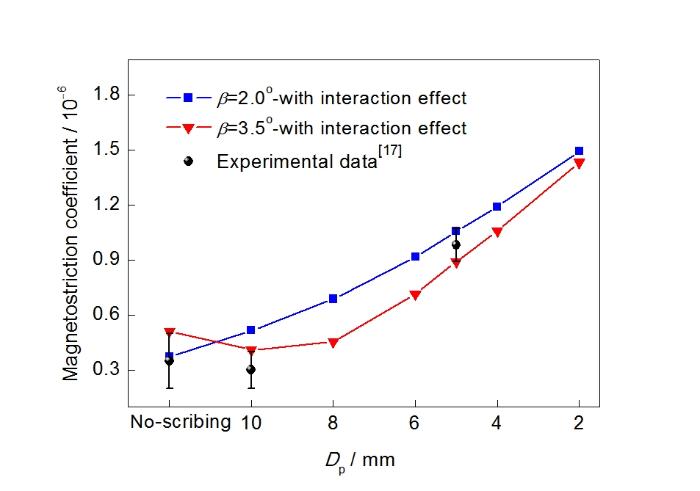
刻痕间距是影响铁损和磁致伸缩系数的重要参数。减小刻痕间距可细化主畴宽度而降低铁损[29],而刻痕间距对磁致伸缩系数的优化通过影响刻痕区应力封闭畴和横向畴数量实现[17]。对平均取向偏差角分别为2.0°和3.5°的0.3 mm厚取向硅钢,计算不同刻痕间距下的磁致伸缩系数,结果如图6所示。其中,Ea=6 mJ/mm2,D2=0.1 mm,D1=0.05 mm,σu=10 MPa。不同取向偏差角取向硅钢的磁致伸缩系数随刻痕间距变化表现出不同趋势。取向偏差角为2.0°时,磁致伸缩系数随刻痕间距减小单调增加;取向偏差角为3.5°时,磁致伸缩系数随刻痕间距减小先降低后增大。低取向偏差角时,横向畴体积分数较小,刻痕区杂散磁场减少横向畴的效应低于刻痕对应力封闭畴增加的效应。因此,取向偏差角为2.0°时(低取向偏差角),磁致伸缩系数随Dp减小表现为单调增加;取向偏差角为3.5°时(高取向偏差角),较大体积分数的横向畴随Dp的减小而减少,刻痕区杂散磁场降低横向畴数量效应提高,但进一步降低Dp时,应力封闭畴增多增大,磁致伸缩系数的效应凸显,磁致伸缩系数随刻痕间距增大呈现出先降低后增大的规律。
图6
图6
不同取向偏差取向硅钢磁致伸缩系数随刻痕线间距的变化
Fig.6
Magnetostriction coefficients as a function of Dp for different β (Sheet thickness 0.3 mm, laser-scribing depth 0.05 mm, tensile force of coating 10 MPa, laser-scribed depth D1=0.05 mm, Ea=6 mJ/mm2, D2=0.1 mm)
表1 刻痕间距变化时取向硅钢磁致伸缩系数的计算结果与实验数据对比
Table 1
Dp mm | Vtransverse[17] % | Vclosure[17] % | λmeasured[17] 10-6 | λcalculated* 10-6 | λcalculated** 10-6 |
|---|---|---|---|---|---|
| 0 | - | - | -0.1~-0.4 | 0 | 0.51 |
| 5 | 0.27 | 8.20 | 0.9~1.1 | 1.25 | 0.85 |
| 10 | 0.135 | 2.44 | 0.2~0.4 | 0.33 | 0.29 |
3 分析讨论
激光刻痕取向硅钢的磁致伸缩,来源于刻痕区残余压应力形成的封闭畴和取向偏差角β产生的横向畴。在不考虑刻痕与取向偏差角交互作用时,应力封闭畴和横向畴引起的磁致伸缩系数之和,与实测值存在明显差距。事实上,刻痕参数改变残余应力,进而影响刻痕区的局部封闭畴结构。同时,刻痕区的局部封闭畴和杂散磁场,也影响取向偏差角产生的横向畴数量。Ea提高,一方面增加了刻痕影响区封闭畴数量,另一方面通过刻痕影响区杂散磁场减少取向偏差产生的横向畴数量。本模型引入刻痕影响区封闭畴能量和杂散磁场能对横向畴特征的影响,使其可以表征刻痕参数与取向偏差角交互作用下的磁致伸缩系数。磁致伸缩系数随Ea增大呈现出先降低后提高的计算结果,与实测相吻合,表明该模型能够准确描述磁畴结构交互作用下取向硅钢磁致伸缩系数的变化规律。
β决定了刻痕条件下哪种90°磁畴结构对磁致伸缩系数起决定作用。β<3°时,刻痕区形成的应力封闭畴数量主导磁致伸缩系数,刻痕参数对横向畴数量影响小;β≥3°时,横向畴数量主导磁致伸缩系数,合适的刻痕参数可有效降低横向畴数量。对于刻痕间距,低偏差角取向硅钢的磁致伸缩系数随刻痕间距减小而增大,较高偏差角取向硅钢的磁致伸缩系数随刻痕间距减小体现为先降低后提高。因此,刻痕参数对磁致伸缩系数的影响,是横向畴减少与应力封闭畴增加的综合效应。对于低噪音要求的激光刻痕取向硅钢,需针对取向硅钢的β分布情况精细优化刻痕参数。
4 结论
(1) 基于激光刻痕参数和取向偏差角对应力封闭畴与横向畴2种90°磁畴结构的影响,提出反映刻痕参数与取向偏差角交互作用的磁畴结构和磁致伸缩系数计算模型,可准确描述激光刻痕条件下取向硅钢的磁致伸缩行为。
(2) 刻痕参数对磁致伸缩系数的影响体现为横向畴减少与应力封闭畴增加的综合效应。取向偏差角决定了激光刻痕条件下磁致伸缩系数是由横向畴还是应力封闭畴主导。随取向偏差角增大,磁致伸缩系数随刻痕间距减小的变化规律由单调提高转变为先降低后提高。