最新录用 | 当期目录 | 过刊浏览 | 热点文章 | 虚拟专辑 | 阅读排行 | 下载排行 | 引用排行 | 期刊订阅

金属学报, 2023, 59(4): 467-477 DOI: 10.11900/0412.1961.2022.00548

综述

层错能对面心立方金属形变机制与力学性能的影响

张哲峰,, 李克强, 蔡拓, 李鹏, 张振军, 刘睿, 杨金波, 张鹏

中国科学院金属研究所 师昌绪先进材料创新中心 沈阳 110016

Effects of Stacking Fault Energy on the Deformation Mechanisms and Mechanical Properties of Face-Centered Cubic Metals

ZHANG Zhefeng,, LI Keqiang, CAI Tuo, LI Peng, ZHANG Zhenjun, LIU Rui, YANG Jinbo, ZHANG Peng

Shi -changxu Innovation Center for Advanced Materials, Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China

通讯作者: 张哲峰，zhfzhang@imr.ac.cn，主要从事金属材料强韧化机制、疲劳与断裂研究

责任编辑: 肖素红

收稿日期: 2022-10-27   修回日期: 2023-01-16  

基金资助: 国家自然科学基金项目(52130002)
国家自然科学基金项目(51901230)

Corresponding authors: ZHANG Zhefeng, professor, Tel:(024)23971043, E-mail:zhfzhang@imr.ac.cn

Received: 2022-10-27   Revised: 2023-01-16  

Fund supported: National Natural Science Foundation of China(52130002)
National Natural Science Foundation of China(51901230)

作者简介 About authors

张哲峰，男，1970年生，研究员，博士

摘要

层错能在面心立方(fcc)金属塑性变形和损伤过程中具有重要作用，本文主要总结了以下研究结果：(1) 随层错能降低，fcc金属滑移方式逐渐从易于交滑移的波状滑移方式转变为平面滑移方式，直至发生变形孪生；(2) 为了理解不同位错密度fcc金属中层错能的变化趋势，采用有效层错能的概念，随位错密度增加，有效层错能也随之升高；(3) 层错能降低不是决定fcc金属形变孪生发生的唯一因素，通过第一原理计算模拟滑移和孪生之间的竞争关系，建立了fcc金属形变孪生临界判据；(4) 通过对高层错能、中等层错能以及低层错能fcc金属疲劳位错组态的实验观察和分析，总结了fcc金属中形成规则驻留滑移带的判定条件；(5) 随Al含量增加，Cu-Al合金层错能降低导致平面滑移程度增加，其拉伸强度和均匀延伸率呈现同步提高趋势；(6) 采用指数应变硬化模型可精确描述Cu-Al合金拉伸加工硬化过程，进而预测了不同合金成分和微观组织状态Cu-Al合金屈服强度-抗拉强度-均匀延伸率之间的定量关系；(7) 随Al含量增加，Cu-Al合金疲劳强度升高；在相同应变幅下，随Al含量增加，其低周疲劳寿命也升高。表明合金成分明显影响fcc金属形变损伤机制及微观缺陷(位错、孪生)演变过程，进而显著影响fcc金属及合金拉伸性能和疲劳性能，这为通过合金设计和制备提高fcc金属力学性能及服役可靠性提供了实验证据和理论基础。

关键词： 面心立方金属; 层错能; 滑移; 孪生; 强度; 塑性; 疲劳强度

Abstract

Stacking fault energy (SFE) can play a crucial role in plastic deformation and damage mechanisms of face-centered cubic (fcc) metals. This study mainly summarized the following results: (1) With the reduction of SFE, the slip mode of fcc metals gradually changes from a facile cross-slip wavy mode to a planar mode until deformation twinning occurs; (2) The concept of effective SFE is applied to investigate the variation of SFE with dislocation density in the fcc metals, with the increase in dislocation density, the effective SFE increases; (3) The reduction of SFE is not the only factor determining the formation of deformation twins in fcc metals. In terms of calculating the competition between simulated slipping and twinning using the first principles, the critical criterion for forming deformation twinning in fcc metals was established; (4) The fatigue dislocation configuration of high-, medium-, and low-SFE fcc metals were analyzed and the judgment conditions for forming regular persistent slip bands (PSBs) are proposed; (5) With the increase in Al content, the SFE of Cu-Al alloy decreases, resulting in a simultaneous increasing trend in the tensile strength and the uniform elongation due to the increasing planar slip degree; (6) The exponential strain-hardening model can accurately describe the tensile strain-hardening process of Cu-Al alloys. The quantitative relationship among yield strength, tensile strength, and uniform elongation of Cu-Al alloy with different alloy compositions and microstructure states was successfully predicted; (7) With the increase in Al content, the fatigue strength of Cu-Al alloy is improved. Increasing Al content at the same strain amplitude will enhance its low-cycle fatigue life. Based on the experimental results above, it is shown that the alloy composition affects the deformation and damage mechanisms, and the evolution process of microscopic defects (dislocations, twins) in fcc metals and alloys. Thus, it drastically affects the tensile and fatigue properties of the fcc metals and alloys. These results provide experimental evidence and a theoretical basis for improving the mechanical properties and service reliability of fcc metals and alloys via alloy designing.

Keywords： face-centered cubic metal; stacking fault energy; slip; twinning; strength; plasticity; fatigue strength

PDF (2222KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张哲峰, 李克强, 蔡拓, 李鹏, 张振军, 刘睿, 杨金波, 张鹏. 层错能对面心立方金属形变机制与力学性能的影响[J]. 金属学报, 2023, 59(4): 467-477 DOI:10.11900/0412.1961.2022.00548

ZHANG Zhefeng, LI Keqiang, CAI Tuo, LI Peng, ZHANG Zhenjun, LIU Rui, YANG Jinbo, ZHANG Peng. Effects of Stacking Fault Energy on the Deformation Mechanisms and Mechanical Properties of Face-Centered Cubic Metals[J]. Acta Metallurgica Sinica, 2023, 59(4): 467-477 DOI:10.11900/0412.1961.2022.00548

面心立方(fcc)金属(如Cu、Ni、Al)在金属材料家族中占有重要一席之地，并且在工业上得到了广泛应用，如钢铁(奥氏体)、铝合金、高温合金、铜合金等。相比于体心立方(bcc)金属(如Mo、W、Ta)和密排六方(hcp)金属(如Ti、Zr、Mg)，fcc金属具有塑性变形容易、可加工性好、低温不易发生脆性断裂等优点[1]，这与fcc金属晶体学特征密切相关。在fcc晶胞中，每个顶点有一个原子，每个面心有一个原子，原子配位数12，滑移面为{111}，滑移方向为<110>，有12个滑移系[2]，这导致其塑性变形与损伤机制表现出与其他2种晶体结构金属材料明显不同的特点。fcc金属是一种理想的模型材料，可用于揭示基本塑性变形、损伤与断裂机制及其对力学性能的影响规律，包括：(1) 如何控制fcc金属塑性变形及微观缺陷(位错、孪生)演化；(2) 如何提高fcc金属力学性能(强度、塑性)；(3) 如何提高fcc金属的疲劳性能(疲劳强度、疲劳寿命)。对几种典型fcc金属(Cu、Cu-Al合金、Cu-Zn合金、不锈钢/孪晶诱导塑性(TWIP)钢、高熵合金、镍基高温合金)的系统研究发现：层错能对fcc金属的塑性变形机制(滑移-孪生过程)具有决定性作用，通过合金设计改变层错能可控制滑移-孪生过程，进而控制其力学性能和疲劳性能。本文以Cu-Al合金为主线，通过改变Al含量实现对层错能的调控，围绕层错能对塑性变形、疲劳损伤机制及力学性能的影响规律展开系统阐述。

1 位错滑移方式转变

fcc金属在拉伸、压缩塑性变形或者低周疲劳过程中，在宏观上表现出不同的表面滑移带形貌(图1a和b)，在微观上也展示出不同的位错组态分布特点(图1c和d)。图1a中表面滑移带比较粗糙，并且应变集中强烈，对应的微观位错也分布集中(图1c)，这种位错运动或者滑移方式被称为“波状”滑移[3]，其变形机制如图1e所示，具有波状滑移行为的金属或合金容易发生交滑移。图1b中表面滑移带呈现出细腻、均匀分布的特征，在微观上位错分布也相对均匀，没有明显的集中现象(图1d)，这种位错滑移方式被称为“平面”滑移[3]，其变形机制如图1f所示，表现出平面滑移的金属或合金不易发生交滑移。通常认为：控制fcc金属波状滑移或平面滑移方式的内在因素是层错能[4,5]，当层错能较高时，通常表现出明显的波状滑移特征，如Al、Ni、Cu等；而当层错能较低时，则表现出均匀分布的平面滑移特征，如Au、Cu-Al合金、Cu-Zn合金等。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   面心立方(fcc)金属典型的滑移方式

Fig.1   Typical slip modes in face-centered cubic (fcc) metals

(a) wavy slip bands (b) planar slip bands

(c) wavy slip dislocation pattern (d) planar slip dislocation pattern

(e) illustration of wavy slip mode (f) illustration of planar slip mode


fcc金属在滑移变形过程中，为了降低能量，<110>/2全位错通常会分解为2根<112>/6 Shockley不全位错，中间夹着一片层错区，由于层错区的形成而产生的额外能量，称之为层错能[1,2]。层错能对fcc金属及其合金的变形机制起决定性作用，因此，测量层错能变得尤为重要，目前已有多种实验方法测量金属的层错能[6~9]，然而所测量的结果却十分分散[10]，这给确定金属层错能带来了困扰。表1[3,7,11]给出了典型fcc金属的层错能。可以看到，不同文献报道的纯Cu的层错能介于40~78 mJ/m2之间，其他金属的层错能也有类似的分散问题。通常层错形成多伴随位错分解，Müllner和Ferreira[12]认为位错应变场的存在会对层错区造成干扰，从而使测量的层错能有别于金属的本征层错能；Pierce等[13]认为应该把金属本征层错能与具体测量的层错能区分开来；Curtze等[14]指出层错能的准确测量应该考虑位错结构的影响。以上研究表明位错组态对层错能具有重要的影响，因此，通过原子尺度模拟可以有效避免实验中的不确定因素，可更直接和客观地考察位错组态对层错能的影响规律。考虑到fcc金属位错分解宽度是描述层错能的一个重要参数，并且分解宽度与层错能计算息息相关，因此，精确测量分解宽度可准确描述位错分解行为并获得可靠的层错能数值。

表1   典型fcc金属层错能数值[3,7,11] (mJ·m-2)

Table 1  Stacking fault energies of typical fcc metals[3,7,11]

ElementRef.[7]Ref.[11]Ref.[3]Range
Al150166166150-166
Ni225128128128-225
Cu70784040-78
Au4545-45
Ag25221616-25

新窗口打开| 下载CSV


最近李克强等[15,16]指出：文献报道的层错能并不是金属的本征层错能，实际位错总是以一定的密度或组态存在，高密度位错之间交互作用更加强烈，势必会对层错能的测量带来影响。根据位错弹性理论，单根位错分解时其分解宽度与本征层错能成反比，进而提出有效层错能(γE)可定义为：

γE=Fi=wi/(πd)
(1)

式中，Fi为不全位错间的交互作用力，wi为位错本征结构特征相关参数，d为位错分解宽度[15,16]。利用 式(1)，在已知d的情况下，可计算得到γE。对于位错列组态，假设位错均匀分布，位错密度(ρ)可以表达为1 / l2 (其中l为位错间距)，进而得到了γE与ρ、本征层错能(γI)之间的定量关系：

γE=wiρ1/2arctanwiρ1/2/γI
(2)

式(2)给出Ag和Cu中以刃位错为例有效层错能与位错密度之间定量关系[15]。可见，随位错密度增加，γE增加，模拟结果与理论预测结果一致。当位错密度趋于零时，γE = γI。如纯Cu中位错密度从1 × 1014 m-2增加到3 × 1016 m-2时，γE从45 mJ/m2增加到78 mJ/m2，这与表1[3,7,11]中Cu的层错能测量范围一致。通常，在利用弱束成像法确定金属层错能时，主要选择金属变形早期阶段，此时对应的位错密度较低，所测的层错能可近似为本征层错能。对于剧烈冷加工的金属，其位错密度在1015~1016 m-2范围，测量的有效层错能势必增加。因此，在实验中测量层错能时，应使金属位错密度尽可能减小，并且以刃型位错为测量对象以近似获得金属的本征层错能。

2 滑移与形变孪生竞争判据

在晶体结构对称性较低、滑移系较少的金属中，当外加应变速率较大或者温度较低时容易发生形变孪生。对于fcc金属，通常认为当层错能较低时容易发生形变孪生[17]，而高层错能金属如Al、Ni则极难发生形变孪生[18,19]。Meyers等[20]提出形变孪生应力与层错能之间呈线性关系，然而，某些fcc金属形变孪生则违背了该判据，例如Ir的层错能要远高于Al，却相对容易观察到形变孪晶[21]；Tadmor和Bernstein[22]基于裂纹尖端模型和位错弹性理论提出一个形变孪生能力判据；随后，Asaro和Suresh[23]基于晶界模型和位错理论提出另一个形变孪生能力判据，然而这2个判据并未体现金属自身的物理性质。

Cai等[24]给出fcc金属中Burgers矢量为b = [1¯10]/2的位错滑移和形变孪生之间的竞争与联系，如图2a[25]所示，b = [1¯10]/2位错滑移开动就是C1位置的原子滑动到C2位置，在滑动过程中会受到临近层B2原子势能的影响，C1位置的原子将沿着势能最小的路径滑动。由于B1和B2中间是势能最低点，C1位置原子应首先滑动到A1位置，然后经A1位置再滑动到C2位置，这样就完成一个完整的滑移过程，此时系统总能量变化趋势如图2b[24]所示。同理，若C1位置的原子滑动到A1位置之后，受到阻力或者受到的驱动力不足以使其从A1位置滑动到C2位置，此时，上一层原子会重复C1到A1的滑动过程，这样形变孪生就启动了，再上一层原子继续重复C1到A1的滑动过程，即形变孪生过程，此时系统总能量变化趋势如图2c[24]所示。基于以上原则采用第一性原理可分别计算不同fcc金属本征性质对形变孪生的影响机制和判据。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   fcc金属滑移与形变孪生竞争示意图[24,25]

Fig.2   Schematic illustrations for competition of slipping and twining

(a) projection of fcc structure on the (111) plane[25] ( b —Burgers vector, bp1 and bp2—partial Burgers vectors)

(b) generalized stacking fault energy (GSFE) variation with a complete slipping[24] (γusf—unstable stacking fault energy, γisf—instinsic stacking fault energy)

(c) GSFE variation with deformation twinning[24] (γutf—unstable twinning fault energy)


在原子滑动过程中系统能量增高，能量随着原子位移变化的曲线称为广义层错能(generalized stacking fault energy，GSFE)曲线，其中，原子由A1位置滑动到C2位置的广义层错能(γSurface[1¯21¯])由下式表达[24]：

γSurface[1¯21¯]=γusf-γisfsinπbp2x
(3)

式中，γusf为不稳定层错能(unstable stacking fault energy)，γisf为内禀层错能(instinsic stacking fault energy)，bp2为原子由A1位置滑动到C2位置的分位错Burgers矢量模，x为滑动参量。C1位置的原子滑动到A1位置后，上一层的C1位置原子再滑动到A1位置的广义层错能(γSurface[2¯11])如下式[24]：

γSurface[2¯11]=γutf-γisfsinπbp1x
(4)

式中，γutf为不稳定孪生能(unstable twinning fault energy)，bp1为原子从C1位置滑动到A1位置的分位错Burgers矢量模。通过滑移和孪生过程分析，可得形变孪生与滑移竞争的临界判据是[24]：

γutfγusf+cosθcosπ3-θ-1×γisfγusf<cosθcosπ3-θ
(5)

式中，θ为滑移方向夹角。令α = γisf / γusf和β = γutf / γusf，方程(5)可以简化为：

β+cosθcosπ3-θ-1×α<cosθcosπ3-θ
(6)

因为0 ≤ θ ≤ π3，所以12 ≤ cosθcosπ3-θ ≤ 2，由此可得fcc金属形变孪生与滑移之间竞争的临界判据为[24]：

γisf / γusf+γutf / γusf<2      or  α+β<2
(7)

式中，α + β = 2是形变孪生与滑移2种竞争机制的临界判据。

为了给出不同fcc金属的形变孪生能力以及难易程度，Cai等[24]分别计算了不同fcc金属关键参数：γisf、γusf和γutf，发现计算的10种金属内禀层错能和实验值[26]比较一致，结合上述判据，图3[25]给出了10种fcc金属的形变孪生能力。图中黑色直线代表临界线α + β = 2，此线右上方区域表示金属易于滑移，左下方区域表示金属易于孪生。进而可以给出不同fcc金属孪生能力，其量化方式是通过其位置与临界线α + β = 2之间的夹角ϕ来度量的，ϕ表示如下[24]：

图3

新窗口打开| 下载原图ZIP| 生成PPT

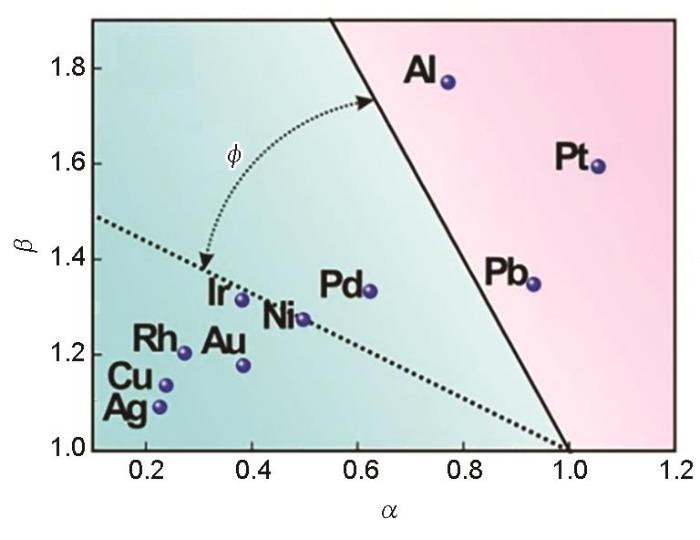
图3   不同fcc金属在α-β坐标系内从滑移过渡到形变孪生的能力比较[25]

Fig.3   Illustration presents the transition from slipping to twinning for various fcc metals in α-β coordinate system (ϕ—angle from α + β = 2, α = γisf / γusf and β = γutf / γusf. The black line is a critical boundary, under which those metals or alloys can form deformation twinning (DT) by the twinning deformation mechanism, while over which these metals or alloys are very difficult to form DT. α + β = 2 is the critical criterion for the two competitive mechanisms between deformation twinning and slipping)[25]


TOR=ϕ=arctanβ-1α-1+π4
(8)

式中，TOR表示晶体取向对形变孪生能力的影响，10种fcc金属形变孪生能力顺序是：Ag > Cu > Rh > Au > Ir > Ni > Pd > Al > Pb > Pt。

3 疲劳位错组态演化规律

众所周知，对于fcc金属循环形变行为的研究起始于对驻留滑移带(persistent slip bands，PSBs)的定义[27]。通常，PSB几乎携带了全部塑性变形，PSB和基体中的塑性应变幅分别为γPSB和γM，可用混合法则来表示晶体承担的平均塑性应变幅(γpl)[28,29]：

γpl=γPSBfPSB+γMfM
(9)

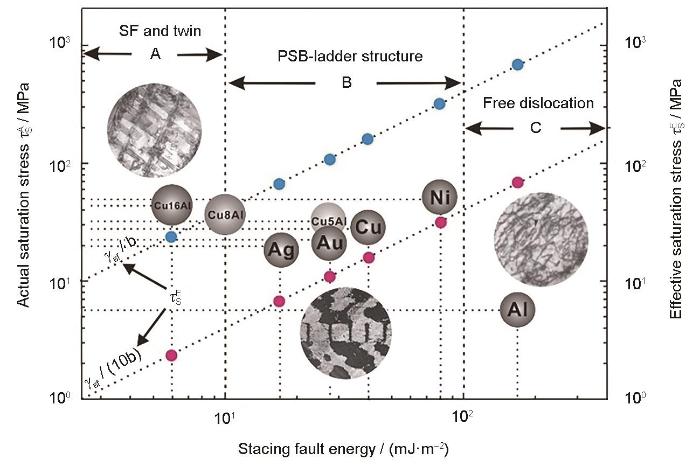
式中，fPSB和fM分别为PSB和基体的体积分数，fM + fPSB = 1。而γPSB和γM则是与塑性应变无关的常数。根据层错能高低，可以将fcc金属分为3类[29]：高层错能金属、中等层错能金属以及低层错能金属，各自代表金属分别是Al (层错能γsf = 166~200 mJ/m2)、Cu (γsf = 40~78 mJ/m2)和Cu-16%Al合金(原子分数，γsf = 6 mJ/m2)。研究[29]表明，Cu、Ni和Ag等中等层错能金属的疲劳位错组态存在极大的共性规律，即总是形成梯状PSB结构；而更高层错能的Al和更低层错能的Cu-Al合金则与之表现出很大差异性，这种差异性集中体现在了PSB梯状结构是否形成上，这主要是层错能改变引起的塑性变形机制不同所致。

基于循环滑移过程对位错偶极子的捕获机制分析，李鹏[29]提出不同fcc金属中形成规则PSB梯状结构，其饱和应力须满足以下判据：

γsf10b<τS<γsfb
(10)

式中，τS是指引起位错组态演化及位错梯形成的有效饱和切应力。将不同fcc金属的层错能和相应的Burgers矢量模b代入到 式(10)中，它们各自形成PSB梯的有效饱和应力区间与实际得到的饱和应力相比，便可直接判断不同fcc金属或合金是否会形成典型PSB梯状结构，如图4[29]所示，其中2条斜线分别代表有效饱和应力的下限和上限：γsf / (10b)和γsf / b，不同fcc金属位错组态的形成被划分为3个区域。对位于B区的fcc金属(如：Ni、Cu或Ag)来说，其实际饱和分切应力(τSA)介于上下限之间，因此，可以形成规则的PSB梯状结构；对于A区的金属来说，τSA通常高于有效分切应力的上限，这类fcc金属中位错组态主要形成层错带结构，如在低Al含量的Cu-Al合金中更倾向于出现类似于Cu中的PSB结构[30]，但当Al含量超过某一值时(比如7% (原子分数)[31])，将形成由偶极子列或层错列构成的驻Lüders带(persistent Lüders band，PLB)结构。C区代表性元素为Al，其饱和切应力为4~5 MPa，但其形成PSB梯状结构所需的有效饱和分切应力则在58~580 MPa范围，此时，位错很难彼此捕获成稳定偶极子段，而是以自由位错运动形式存在，表现为由位错缠杂所构成的团簇结构。上述机制和模型可很好地理解不同fcc金属或合金中疲劳位错组态演化共性规律[29]。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同fcc金属或合金形成规则梯状驻留滑移带与否机理图[29]

Fig.4   Schematic diagram of the formation of persistent slip band ladders or not in different kinds of fcc metals or alloys[29] (γsf—stacking fault energy, b—Burgers vector module, SF—stacking fault, PSB—persistent slip band)


4 孪晶界面疲劳开裂竞争机制

fcc金属在疲劳载荷下，其疲劳损伤主要包括晶粒内部滑移带开裂和各种大角度晶界疲劳开裂[32]。对于fcc多晶体中的退火孪晶界面，在循环载荷下的疲劳开裂则表现出与大角度晶界明显不同的行为和机制。Qu等[33]和Zhang等[34]对Cu-Al和Cu-Zn单相合金多晶体疲劳研究发现：随合金元素(Al或Zn)含量增加或者层错能降低，铜合金中孪晶界面更容易发生疲劳开裂。为了深入认识层错能和晶体取向对孪晶界面疲劳开裂行为与机制的影响，张振军[35]设计了系列Cu-Al和Cu-Zn合金多晶体，通过冷轧和随后退火，获得了平均晶粒尺寸大于100 μm的多晶体，并含有大量退火孪晶界面。通过低周疲劳实验发现：无论是高层错能的纯Cu，还是层错能较低的Cu-10%Zn或Cu-16%Al (原子分数)合金，孪晶界面要么优先滑移带开裂，要么较滑移带更难疲劳开裂[35]，这表明：合金层错能高低不是控制孪晶界面疲劳开裂的唯一因素。

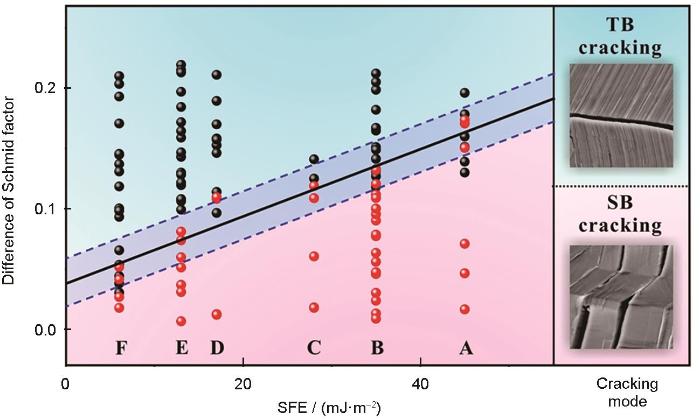
为了客观评价铜合金多晶体层错能和晶体学取向对孪晶界面疲劳开裂的影响规律，考虑到孪晶界面两侧晶体学取向的特殊性，张振军[35]发明了一种滑移形貌法，可用于测量孪晶界面两侧晶粒中滑移带的Schmid因子，通过建立不同孪晶界面两侧滑移带Schmid因子之差、铜合金层错能与孪晶界面疲劳开裂的定量关系，基于6种Cu与铜合金疲劳开裂结果统计(121个案例) (或者孪晶界面疲劳开裂，或者孪晶界面两侧滑移带疲劳开裂)，如图5[35,36]所示，建立了层错能-Schmid因子差坐标下铜合金孪晶界面疲劳开裂与层错能及晶粒取向关系。其中A~F依次代表层错能由高到低的顺序：Cu、Cu-10%Zn、Cu-5%Al、Cu-8%Al、Cu-32%Zn和Cu-16%Al (原子分数)。图中黑点代表在扫描电镜(SEM)照片上观察到孪晶界先于滑移带开裂，红点代表滑移带先于孪晶界疲劳开裂，这清楚地给出了晶粒取向和层错能对孪晶界疲劳开裂行为的综合影响。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   层错能和晶体学取向对滑移带与孪晶界疲劳开裂行为的影响[35,36]

Fig.5   Influences of stacking fault energy (SFE) and crystallographic orientation on the fatigue cracking modes along twin boundaries (TBs) or slip bands (SBs)[35,36] (A: Cu; B: Cu-10%Zn; C: Cu-5%Al; D: Cu-8%Al; E: Cu-32%Zn; F: Cu-16%Al)


5 拉伸强度与塑性制约关系

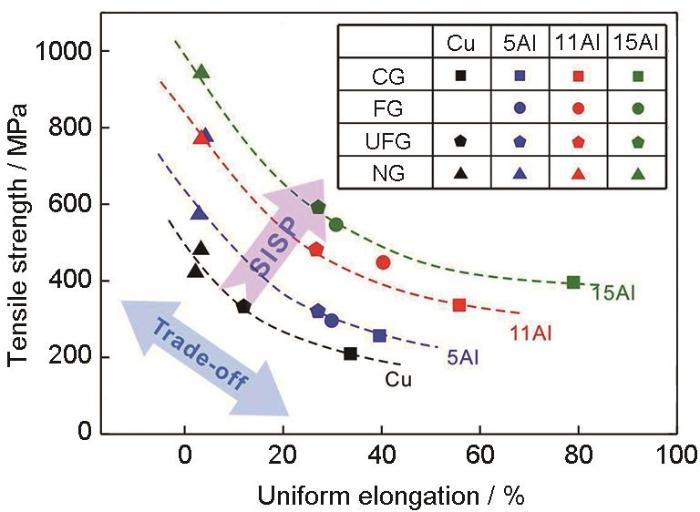
开展多种成分(纯Cu、Cu-5%Al、Cu-11%Al、Cu-15%Al，原子分数)和组织状态(细晶(FG)、超细晶(UFG)、微米晶(MG)、纳米晶(NG))的铜合金拉伸性能实验[37]，结果表明，随合金强度降低，均匀延伸率升高，加工硬化能力得到改善，具有相同合金成分的Cu-Al合金，其强度与塑性之间总是具有明显的倒置关系，如图6[37]所示。随Al含量提高，上述倒置关系曲线向上向右平移，意味着已突破原有合金成分强度-塑性倒置关系限制，并在更高强度-塑性水平建立了新的倒置关系。这种“同步强韧化(synchronously improved strength and plasticity，SISP)”行为普遍存在于Cu-Al合金的不同组织状态下[38]，并在其他fcc金属如Fe-Mn-C-Al[39]、高熵合金[40]中具有共性的规律。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   纯Cu及Cu-Al合金拉伸强度-均匀延伸率倒置关系[37]

Fig.6   Trade-off relation between tensile strength and uniform elongation of pure Cu and Cu-Al alloys with different Al contents and grain sizes[37] (CG—course grain, FG—fine grain, UFG—ultra-fine grain, NG—nano grain, SISP—synchronously improved strength and plasticity)


张哲峰等[41,42]考虑初始组织状态和合金成分对加工硬化的影响，建立了单相金属普适性硬化模型，即指数应变硬化(exponential strain-hardening，ESH)模型，据此推导出单相金属拉伸应力(σ)-应变(ε)的定量关系：

σ=ΘIIn+ησy-ΘIIn-(1-η)σyexp(-nε)
(11)

式中，n为硬化指数，n = Mye2b (其中M为Taylor因子，ye为位错湮灭距离)，反映合金成分的影响；η为初始缺陷对屈服强度(σy)非位错性贡献的比例，反映微观组织的影响；ΘII为第二阶段硬化率。该模型得到了6种合金成分、100余种不同微观组织状态单相Cu-Al合金的拉伸实验验证[42]。

该指数应变硬化模型阐明了单相金属形变过程中一些重要规律：揭示了极限强度、临界强度、真抗拉强度与成分及变形机制之间关系，获得了“屈服强度-抗拉强度-均匀延伸率”之间的定量关系(式(12)~(14))，实现了单相Cu-Al合金拉伸强度、塑性及拉伸应力-应变曲线的定量预测。通过该模型定量揭示了金属材料拉伸强度-塑性同步提升的2个基本原则，即成分优化(提升位错滑移平面性)和组织优化(降低初始高能缺陷)，在铜合金、镍基合金、TWIP钢、高氮钢、316L不锈钢等单相合金中均得到了系统性实验验证[38~43]。其中工程抗拉强度(sn)与σy关系为：

Sn=nΘII+nησyn(1+n)1+nnnΘII-n(1-η)σy1n
(12)

均匀延伸率(en)与σy关系为：

en=(1+n)(ΘII-n(1-η)σy)ΘII+nησy1n-1
(13)

sn与en关系为：

1sn=ηΘII(1+en)n+1+(1+n)(1-η)ΘII(1+en)
(14)

6 疲劳强度与疲劳寿命

以上实验结果表明，随Al含量增加，Cu-Al合金拉伸强度与塑性有同步提高的趋势。为了研究低周疲劳条件下Al含量对Cu-Al合金的影响规律，设计合金成分为Cu、Cu-5%Al、Cu-8%Al和Cu-16%Al (原子分数) 4种材料，在总应变幅为2%、4%、6%、8%和9.5%条件下开展了低周(超低周)疲劳实验[37,44]。研究[37]表明：对于某一固定成分的Cu-Al合金，其循环饱和状态下滞回环随应变幅增加逐渐扩大直至饱和状态。随Al含量变化，相同应变幅下滞回环形状各异，对应循环应力峰值也有所不同[37]。比较不同应变幅下循环应力峰值相连得到的循环应力-应变(CSS)曲线[37]可知，随Al含量增加，循环应力峰值升高，CSS曲线随应变幅增加的上升趋势越明显。

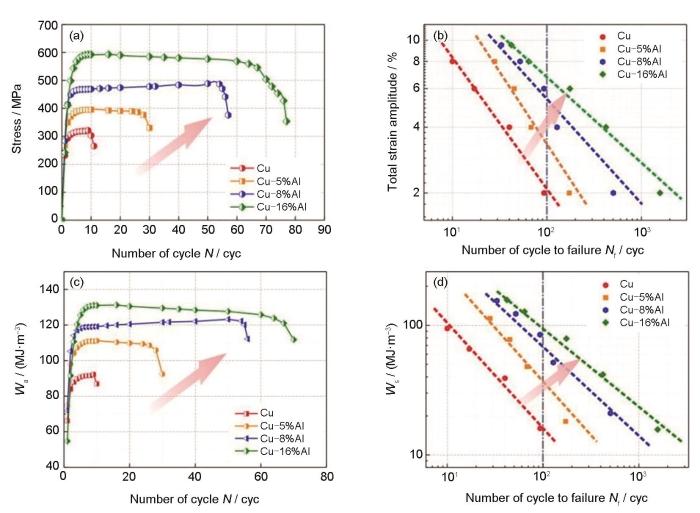
图7[37]为上述Cu-Al合金低周疲劳寿命相关结果，Al含量增加不仅提高了Cu-Al合金循环硬化能力，还延长了低周疲劳寿命，形成了循环应力幅与疲劳寿命同步提高的趋势(图7a[37])。由图7b[37]中的应变-寿命(E-N)曲线可知，随Al含量提高，Cu-Al合金在低周(含超低周[44])寿命范围内，每一应变幅下对应的疲劳寿命均有所增加。根据低周疲劳寿命预测滞回能模型[45]，将滞回能与疲劳寿命建立关系，可得图7c和d[37]。随Al含量增加，同一应变幅下滞回能与循环寿命同步提高；而滞回能-寿命(W-N)曲线也保持了与上述E-N曲线相似的趋势(图7d[37])。可见，无论从应变幅、应力幅还是滞回能角度看，纯Cu与Cu-Al合金低周疲劳性能均随Al含量增加而提高。由于低周疲劳损伤是通过累积不可逆塑性应变的方式实现，因此塑性变形的可逆程度是控制疲劳损伤程度及疲劳寿命高低的关键因素。疲劳后位错组态观察表明：随着Al含量降低，位错交滑移行为被抑制，由波状滑移向平面滑移转变[37]，同时伴随着层错与孪生等平面化程度更高的变形机制出现，使循环塑性变形可逆性大大提高[45]。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   纯Cu及Cu-Al合金低周(含超低周)疲劳基本性能[37]

Fig.7   Fundamental low cycle fatigue (ultra-low cycle fatigue) properties of pure Cu and Cu-Al alloys[37]

(a) cyclic hardening curves (total strain amplitude Δε / 2 = 8.0%)

(b) strain-life (E-N) curves

(c) change of Wa with the number of cycle N (Δε / 2 = 8.0%, Wa—hysteresis energy)

(d) hysteresis energy-life (W-N) curves (Ws—saturated hysteresis energy)


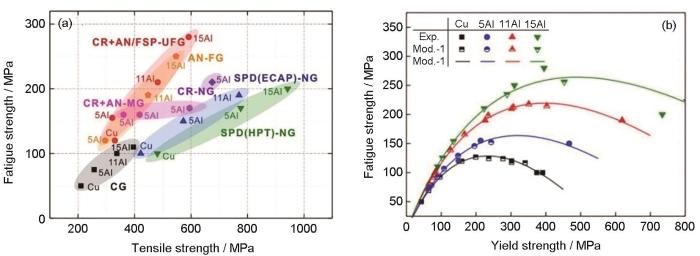
为了认识Al含量对Cu-Al合金高周疲劳性能的影响，开展了不同微观组织和不同Al含量Cu-Al合金高周疲劳实验，结果表明[37,38,46,47]：Cu-Al合金在不同组织状态下呈现出各异的应力-寿命(S-N)曲线特征，且其变化趋势与拉伸性能规律不同，这些S-N曲线相互交叉，最终获得疲劳强度最大值并非是拉伸强度最高的组织状态。图8a[37,38,46,47]以拉伸强度为横坐标，疲劳强度为纵坐标给出了不同Al含量和组织状态Cu-Al合金的疲劳性能汇总数据。可见，(1) 同类组织状态下，疲劳强度随Al含量提高普遍呈增加趋势；(2) 组织状态对疲劳强度的影响规律则较为复杂，组织细化或强化并非总是对应最高的疲劳强度，而拉伸强度处于中等的超细晶状态则表现出最高的疲劳强度，如图8b[38]所示。总之，对于纯Cu及Cu-Al合金，单纯提高其拉伸强度未必导致疲劳强度单调增加，而是在某个强度水平下出现疲劳强度最高值，这与高强钢疲劳强度与拉伸强度呈现出抛物线关系具有一致性[48]，该研究结果为通过合金成分和组织优化实现金属材料抗疲劳设计与制备提供了新的思路。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   纯Cu及Cu-Al合金拉伸强度-疲劳强度关系[37,38,46,47]

Fig.8   Relationships between ultimate tensile strength and fatigue strength of pure Cu and Cu-Al alloys

(a) relationships between fatigue strength and tensile strength (CR—cold rolling, AN—annealing, FSP—friction stir processing, SPD—severe plastic deformation, ECAP—equal channel angular processing, MG—micro grain, HPT—high pressure torsion)[37,38,46,47]

(b) relationships between fatigue strength and yield strength[38]


7 总结与展望

本文通过总结纯Cu和Cu-Al合金等fcc金属形变、损伤机制及其力学性能变化规律，进一步证明可通过改变合金成分调整其层错能，使其变形机制发生变化，如：波状滑移、平面滑移、层错与孪生机制，进而改变或控制其拉伸及疲劳性能。发现层错能大小与位错密度有关，提高位错密度可提高其有效层错能。同时，降低层错能并不是决定fcc金属形变孪生的唯一因素，通过第一性原理计算模拟滑移与孪生行为，发现位错滑移与形变孪生之间存在竞争判据：γisf / γusf + γutf / γusf < 2。通过对具有不同层错能fcc金属疲劳位错组态实验观察和分析，发现fcc金属中形成规则驻留滑移带受其层错能和Burgers矢量控制。

Cu-Al合金随Al含量增加，其拉伸强度和均匀延伸率呈现同步提高趋势；通过指数应变硬化模型可精确描述Cu-Al合金拉伸应力-应变曲线，进而通过建立强度与延伸率之间的定量关系，可实现不同合金成分和微观组织状态Cu-Al合金强度-均匀延伸率关系定量预测。随Al含量增加Cu-Al合金疲劳强度升高，而晶粒从粗晶到细晶、超细晶和纳米晶细化过程中，疲劳强度出现先升高后降低的趋势；在相同应变幅下，随Al含量增加，Cu-Al合金的低周及超低周疲劳寿命逐渐升高，这为通过合金成分设计和组织调控实现高周与低周疲劳性能优化提供了实验证据和思路。

本文主要关注层错能对fcc金属形变、损伤机制及力学性能的影响规律，层错能最核心的作用是通过改变滑移方式(波状滑移与平面滑移)及孪生机制实现对fcc金属力学性能的控制。因此，通过实验测量和计算模拟fcc金属层错能大小，有助于定量描述和分析其变形机制与力学性能之间的定量关系，对合金优化设计和力学性能提高具有重要指导意义。除层错能参数外，短程有序(short-range order，SRO)也是影响fcc金属塑性变形和疲劳损伤机制的一个重要参数[49,50]，它也可以改变fcc金属或合金位错滑移方式、孪生萌生、拉伸强度与塑性、疲劳开裂及疲劳性能[49,50]。近年来高熵合金发展迅猛，尤其是成分复杂的高熵、中熵合金中的位错滑移方式和孪生机制受层错能和短程有序影响更为明显[51]。然而短程有序参数相对难以实验测量和定量描述，这给深入分析短程有序对变形机制和力学性能的定量预测带来一定的困难。

随着高熵合金材料体系向更复杂成分方向发展，文献报道的性能数据呈指数级增长[52]，然而，如何通过高熵合金成分设计提高其强韧性能仍缺少理论指导。对于fcc高熵合金体系，通过计算CoCrNi合金体系的弹性模量、层错能、孪生能力、相稳定性等多种物理参数[53]，结合上述fcc金属变形机制及强韧性能提高的大量实验结果，提出同步提高fcc金属强韧性三原则[53,54]。(1) 弹性模量高：可确保金属原子间结合力足够大，避免解理断裂发生；(2) 层错能低：可提高金属塑性变形均匀性和塑性功；(3) fcc相稳定性：确保不会因发生相变导致脆性断裂。近期研究[55]发现：具有较高弹性模量的CoCrNi系中、高熵合金，在液氦环境下层错能降低，实现了多级协同变形机制，并具有较高的fcc相稳定性，在20 K超低温下获得了超高的断裂韧性(459 MPa·m1/2)。提出金属材料强韧化原则可为筛选、制备具有优异强韧性金属材料提供指导方向，通过与机器学习及第一原理模拟相结合，可避免无休止地盲目实验和计算[56]，为更高效地开发新型强韧性合金提供设计依据。

参考文献

Pan J S, Tong J M, Tian M B. Fundamentals of Materials Science [M]. Beijing: Tsinghua University Press, 2011: 1

[本文引用: 2]

潘金生, 仝健民, 田民波. 材料科学基础 [M]. 北京: 清华大学出版社, 2011: 1

[本文引用: 2]

Anderson P M, Hirth J P, Lothe J. Theory of Dislocations [M]. 3rd Ed., Cambridge: Cambridge University Press, 2017: 1

[本文引用: 2]

Wang Z R.

Cyclic deformation response of planar-slip materials and a new criterion for the wavy-to-planar-slip transition

[J]. Philos. Mag., 2004, 84: 351

DOI      URL     [本文引用: 7]

Lukáš P, Klesnil M.

Cyclic stress-strain response and fatigue life of metals in low amplitude region

[J]. Mater. Sci. Eng., 1973, 11: 345

DOI      URL     [本文引用: 1]

Mughrabi H.

On the current understanding of strain gradient plasticity

[J]. Mater. Sci. Eng., 2004, A387-389: 209

[本文引用: 1]

de Campos M F.

Selected values for the stacking fault energy of face centered cubic metals

[J]. Mater. Sci. Forum, 2008, 591-593: 708

DOI      URL     [本文引用: 1]

Dillamore I L, Smallman R E, Roberts W T.

A determination of the stacking-fault energy of some pure F.C.C. metals

[J]. Philos. Mag., 1964, 9: 517

DOI      URL     [本文引用: 5]

Cockayne D J H, Jenkins M L, Ray I L F.

The measurement of stacking-fault energies of pure face-centred cubic metals

[J]. Philos. Mag., 1971, 24: 1383

DOI      URL    

Stobbs W M, Sworn C H.

The weak beam technique as applied to the determination of the stacking-fault energy of copper

[J]. Philos. Mag., 1971, 24: 1365

DOI      URL     [本文引用: 1]

Reed R P, Schramm R E.

Relationship between stacking-fault energy and X-ray measurements of stacking-fault probability and microstrain

[J]. J. Appl. Phys., 1974, 45: 4705

DOI      URL     [本文引用: 1]

Murr L E. Interfacial Phenomena in Metals and Alloys [M]. Reading: Addison-Wesley, 1975: 1

[本文引用: 5]

Müllner P, Ferreira P J.

On the energy of terminated stacking faults

[J]. Philos. Mag. Lett., 1996, 73: 289

DOI      URL     [本文引用: 1]

Pierce D T, Jiménez J A, Bentley J, et al.

The influence of manganese content on the stacking fault and austenite/ε-martensite interfacial energies in Fe-Mn-(Al-Si) steels investigated by experiment and theory

[J]. Acta Mater., 2014, 68: 238

DOI      URL     [本文引用: 1]

Curtze S, Kuokkala V T, Oikari A, et al.

Thermodynamic modeling of the stacking fault energy of austenitic steels

[J]. Acta Mater., 2011, 59: 1068

DOI      URL     [本文引用: 1]

Li K Q.

Atomistic simulation of the micromechanisms of plastic deformation in face-centered cubic metals

[D]. Shenyang: University of Science and Technology of China (Institute of Metal Research, Chinese Academy of Sciences), 2020

[本文引用: 3]

李克强.

面心立方金属塑性变形微观机制的原子模拟研究

[D]. 沈阳: 中国科学技术大学(中国科学院金属研究所), 2020

[本文引用: 3]

Li K Q, Zhang Z J, Li L L, et al.

Effective stacking fault energy in face-centered cubic metals

[J]. Acta Metall. Sin. (Engl. Lett.), 2018, 31: 873

DOI      [本文引用: 3]

Gray III G T, Kaschner G C, Mason T A, et al.

The influence of interstitial content, temperature, and strain rate on deformation twin formation

[A]. Advances in Twinning. Proceedings International Symposium [C]. 1999 TMS Annual Meeting, 1999: 157

[本文引用: 1]

Chen M W, Ma E, Hemker K J, et al.

Deformation twinning in nanocrystalline aluminum

[J]. Science, 2003, 300: 1275

PMID      [本文引用: 1]

We report transmission electron microscope observations that provide evidence of deformation twinning in plastically deformed nanocrystalline aluminum. The presence of these twins is directly related to the nanocrystalline structure, because they are not observed in coarse-grained pure aluminum. We propose a dislocation-based model to explain the preference for deformation twins and stacking faults in nanocrystalline materials. These results underscore a transition from deformation mechanisms controlled by normal slip to those controlled by partial dislocation activity when grain size decreases to tens of nanometers, and they have implications for interpreting the unusual mechanical behavior of nanocrystalline materials.

Wu X L, Zhu Y T.

Inverse grain-size effect on twinning in nanocrystalline Ni

[J]. Phys. Rev. Lett., 2008, 101: 025503

[本文引用: 1]

Meyers M A, Vöhringer O, Lubarda V A.

The onset of twinning in metals: A constitutive description

[J]. Acta Mater., 2001, 49: 4025

DOI      URL     [本文引用: 1]

Rogers H C, Reed-Hill R E, Hirth J P. Deformation Twinning [M]. New York: Gordon and Breach Science Publishers, 1964: 1

[本文引用: 1]

Tadmor E B, Bernstein N.

A first-principles measure for the twinnability of FCC metals

[J]. J. Mech. Phys. Solids, 2004, 52: 2507

DOI      URL     [本文引用: 2]

Asaro R J, Suresh S.

Mechanistic models for the activation volume and rate sensitivity in metals with nanocrystalline grains and nano-scale twins

[J]. Acta Mater., 2005, 53: 3369

DOI      URL     [本文引用: 1]

Cai T, Zhang Z J, Zhang P, et al.

Competition between slip and twinning in face-centered cubic metals

[J]. J. Appl. Phys., 2014, 116: 163512

DOI      URL     [本文引用: 12]

Cai T.

Computation and simulation for deformation mechanisms of face-centered cubic metals and alloys

[D]. Shenyang: Institute of Metal Research, Chinese Academy of Sciences, 2016

[本文引用: 7]

蔡 拓.

面心立方金属及合金变形机制计算模拟

[D]. 沈阳: 中国科学院金属研究所, 2016

[本文引用: 7]

Wei X M, Zhang J M, Xu K W.

Generalized stacking fault energy in FCC metals with MEAM

[J]. Appl. Surf. Sci., 2007, 254: 1489

DOI      URL     [本文引用: 1]

Mughrabi H.

The cyclic hardening and saturation behaviour of copper single crystals

[J]. Mater. Sci. Eng., 1978, 33: 207

DOI      URL     [本文引用: 1]

Winter A T.

A model for the fatigue of copper at low plastic strain amplitudes

[J]. Philos. Mag., 1974, 30: 719

DOI      URL     [本文引用: 1]

Li P.

Study on the cyclic deformation behavior of face-centered cubic crystals

[D]. Shenyang: Institute of Metal Research, Chinese Academy of Sciences, 2009

[本文引用: 8]

李 鹏.

面心立方晶体循环变形行为研究

[D]. 沈阳: 中国科学院金属研究所, 2009

[本文引用: 8]

Woods P J.

Low-amplitude fatigue of copper and copper-5 at.% aluminium single crystals

[J]. Philos. Mag., 1973, 28: 155

[本文引用: 1]

Wu X M, Wang Z G, Li G Y.

Cyclic deformation and strain burst behavior of Cu-7at.%Al and Cu-16at.%Al single crystals with different orientations

[J]. Mater. Sci. Eng., 2001, A314: 39

[本文引用: 1]

Zhang Z F, Wang Z G.

Grain boundary effects on cyclic deformation and fatigue damage

[J]. Prog. Mater. Sci., 2008, 53: 1025

DOI      URL     [本文引用: 1]

Qu S, Zhang P, Wu S D, et al.

Twin boundaries: Strong or weak?

[J]. Scr. Mater., 2008, 59: 1131

DOI      URL     [本文引用: 1]

Zhang P, Zhang Z J, Li L L, et al.

Twin boundary: Stronger or weaker interface to resist fatigue cracking

[J]. Scr. Mater., 2012, 66: 854

DOI      URL     [本文引用: 1]

Zhang Z J.

Study on the effect of delamination energy on strength-plasticity matching and fatigue behavior of single-phase copper-zinc alloy

[D]. Shenyang: University of Chinese Academy of Sciences (Institute of Metal Research, Chinese Academy of Sciences), 2013

[本文引用: 6]

张振军.

层错能对单相铜锌合金强度塑性匹配及疲劳行为影响研究

[D]. 沈阳: 中国科学院大学(中国科学院金属研究所), 2013

[本文引用: 6]

Zhang Z J, Zhang P, Li L L, et al.

Fatigue cracking at twin boundaries: Effects of crystallographic orientation and stacking fault energy

[J]. Acta Mater., 2012, 60: 3113

DOI      URL     [本文引用: 3]

Liu R.

Study on tensile and fatigue properties of copper-aluminum alloy

[D]. Shenyang: University of Chinese Academy of Sciences (Institute of Metal Research, Chinese Academy of Sciences), 2018

[本文引用: 20]

刘 睿.

铜铝合金拉伸与疲劳性能研究

[D]. 沈阳: 中国科学院大学(中国科学院金属研究所), 2018

[本文引用: 20]

An X H, Wu S D, Wang Z G, et al.

Significance of stacking fault energy in bulk nanostructured materials: Insights from Cu and its binary alloys as model systems

[J]. Prog. Mater. Sci., 2019, 101: 1

DOI      URL     [本文引用: 8]

Yang H K, Tian Y Z, Zhang Z F.

Revealing the mechanical properties and microstructure evolutions of Fe-22Mn-0.6C-(x)Al TWIP steels via Al alloying control

[J]. Mater. Sci. Eng., 2018, A731: 61

[本文引用: 1]

Sun S J, Tian Y Z, Lin H R, et al.

Enhanced strength and ductility of bulk CoCrFeMnNi high entropy alloy having fully recrystallized ultrafine-grained structure

[J]. Mater. Des., 2017, 133: 122

DOI      URL     [本文引用: 2]

Zhang Z F, Shao C W, Wang B, et al.

Tensile and fatigue properties and deformation mechanisms of twinning-induced plasticity steels

[J]. Acta Metall. Sin., 2020, 56: 476

DOI      [本文引用: 1]

With the development of automotive industry, it is necessary to develop advanced high-strength steels for the purpose of lightweight of car. Based on the systematic studies on the strengthening and toughening as well as fatigue design of the twinning-induced plasticity (TWIP) steels, the recent progress in this aspect is summarized and discussed. Among them, the strengthening and toughening mechanisms have been analyzed and further developed in terms of several influencing factors, including compositions, microstructure, strain rate and so on. Furthermore, the low-cycle and high-cycle fatigue behaviors and damage mechanisms were explored. For better understanding the intrinsic fatigue damage mechanism, a new low-cycle fatigue prediction model regarding the hysteresis loop energy during cyclic deformation was introduced. It is found that the energy damage model can well explain and evaluate the fatigue damage mechanism and predict the low-cycle fatigue life of the TWIP steels and other materials. Based on the new fatigue damage model, new TWIP steels with high service performance can be developed by adjusting their deformation and damage mechanisms rationally.

张哲峰, 邵琛玮, 王 斌 等.

孪生诱发塑性钢拉伸与疲劳性能及变形机制

[J]. 金属学报, 2020, 56: 476

DOI      [本文引用: 1]

随着汽车工业的高速发展，以开发先进高强钢为重点的车辆轻量化设计已经成为各大汽车厂商的发展共识。本文基于国内外孪生诱发塑性(TWIP)钢强韧性和抗疲劳设计的成果以及本课题组多年来在该领域的研究工作，系统地总结了TWIP钢的研究现状及最新进展，探讨了影响TWIP钢拉伸性能与变形机制的影响因素，包括合金成分、组织状态、应变速率等。重点介绍TWIP钢的高、低周疲劳性能和微观损伤行为，并提出一种客观评价和预测低周疲劳寿命的方法。从TWIP钢的服役环境和实际应用角度出发，试图为新一代高性能TWIP钢的开发提供新的思路和实验证据。

Zhang Z J, Qu Z, Xu L, et al.

A general physics-based hardening law for single phase metals

[J]. Acta Mater., 2022, 231: 117877

DOI      URL     [本文引用: 2]

Zhang Z J, Qu Z, Xu L, et al.

Relationship between strength and uniform elongation of metals based on an exponential hardening law

[J]. Acta Mater., 2022, 231: 117866

DOI      URL     [本文引用: 1]

Liu R, Zhang Z J, Zhang P, et al.

Extremely-low-cycle fatigue behaviors of Cu and Cu-Al alloys: Damage mechanisms and life prediction

[J]. Acta Mater., 2015, 83: 341

DOI      URL     [本文引用: 2]

Liu R, Zhang Z J, Li L L, et al.

Microscopic mechanisms contributing to the synchronous improvement of strength and plasticity (SISP) for TWIP copper alloys

[J]. Sci. Rep., 2015, 5: 9550

DOI      PMID      [本文引用: 4]

In this study, the concept of "twinning induced plasticity (TWIP) alloys'' is broadened, and the underlying intrinsic microscopic mechanisms of the general TWIP effect are intensively explored. For the first aspect, "TWIP copper alloys'' was proposed following the concept of "TWIP steels'', as they share essentially the same strengthening and toughening mechanisms. For the second aspect, three intrinsic features of twinning: i.e. "dynamic development'', "planarity'', as well as "orientation selectivity'' were derived from the detailed exploration of the deformation behavior in TWIP copper alloys. These features can be considered the microscopic essences of the general "TWIP effect''. Moreover, the effective cooperation between deformation twinning and dislocation slipping in TWIP copper alloys leads to a desirable tendency: the synchronous improvement of strength and plasticity (SISP). This breakthrough against the traditional trade-off relationship, achieved by the general "TWIP effect'', may provide useful strategies for designing high-performance engineering materials.

An X H, Wu S D, Wang Z G, et al.

Enhanced cyclic deformation responses of ultrafine-grained Cu and nanocrystalline Cu-Al alloys

[J]. Acta Mater., 2014, 74: 200

DOI      URL     [本文引用: 4]

Liu R, Tian Y Z, Zhang Z J, et al.

Exploring the fatigue strength improvement of Cu-Al alloys

[J]. Acta Mater., 2018, 144: 613

DOI      URL     [本文引用: 4]

Pang J C, Li S X, Wang Z G, et al.

General relation between tensile strength and fatigue strength of metallic materials

[J]. Mater. Sci. Eng., 2013, A564: 331

[本文引用: 1]

Han D, Zhang Y J, Li X W.

A crucial impact of short-range ordering on the cyclic deformation and damage behavior of face-centered cubic alloys: A case study on Cu-Mn alloys

[J]. Acta Mater., 2021, 205: 116559

DOI      URL     [本文引用: 2]

Zhang Y J, Han D, Li X W.

Improving the stress-controlled fatigue life of low solid-solution hardening Ni-Cr alloys by enhancing short range ordering degree

[J]. Int. J. Fatigue, 2021, 149: 106266

DOI      URL     [本文引用: 2]

Wu Y, Zhang F, Yuan X Y, et al.

Short-range ordering and its effects on mechanical properties of high-entropy alloys

[J]. J. Mater. Sci. Technol., 2021, 62: 214

DOI      [本文引用: 1]

In this letter, we briefly summarize experimental and theoretical findings of formation and characterization of short-range orderings (SROs) as well as their effects on the deformation behavior of high-entropy alloys (HEAs). We show that existence of SROs is a common yet key structural feature of HEAs, and tuning the degree of SROs is an effective way for optimizing mechanical properties of HEAs. In additional, the challenges concerning about formation mechanism and characterization of SROs in HEAs are discussed, and future research activities in this regard are also proposed.

George E P, Curtin W A, Tasan C C.

High entropy alloys: A focused review of mechanical properties and deformation mechanisms

[J]. Acta Mater., 2020, 188: 435

DOI      URL     [本文引用: 1]

Yan J X, Zhang Z J, Zhang P, et al.

Design and optimization of the composition and mechanical properties for non-equiatomic CoCrNi medium-entropy alloys

[J]. J Mater. Sci. Technol., 2023, 139: 232

DOI      [本文引用: 2]

The development of multi-principal element alloys (MPEAs, also called as high- or medium-entropy alloys, HEAs/MEAs) provides tremendous possibilities for materials innovation. However, designing MPEAs with desirable mechanical properties confronts great challenges due to their vast composition space. In this work, we provide an essential criterion to efficiently screen the CoCrNi MEAs with outstanding strength-ductility combinations. The negative Gibbs free energy difference &#x02206;<em>E</em><sub>FCC-BCC</sub> between the face-centered cubic (FCC) and body-centered cubic (BCC) phases, the enhancement of shear modulus <em>G</em> and the decline of stacking fault energy (SFE) <em>&#x003b3;</em><sub>isf</sub> are combined as three requisites to improve the FCC phase stability, yield strength, deformation mechanisms, work-hardening ability and ductility in the criterion. The effects of chemical composition on &#x02206;<em>E</em><sub>FCC-BCC</sub>, <em>G</em> and <em>&#x003b3;</em><sub>isf</sub> were investigated with the first principles calculations for Co<em><sub>x</sub></em>Cr<sub>33</sub>Ni<sub>67-</sub><em><sub>x</sub></em>, Co<sub>33</sub>Cr<em><sub>y</sub></em>Ni<sub>67-</sub><em><sub>y</sub></em> and Co<em><sub>z</sub></em>Cr<sub>66-</sub><em><sub>z</sub></em>Ni<sub>34</sub> (0 &#x02264; <em>x, y</em> &#x02264; 67 and 0 &#x02264; <em>z</em> &#x02264; 66) alloys. Based on the essential criterion and the calculation results, the composition space that displays the negative Gibbs free energy difference &#x02206;<em>E</em><sub>FCC-BCC</sub>, highest shear modulus <em>G</em> and lowest SFE <em>&#x003b3;</em><sub>isf</sub> was screened with the target on the combination of high strength and excellent ductility. In this context, the optimal composition space of Co-Cr-Ni alloys was predicted as 60 at.%-67 at.% Co, 30 at.%-35 at.% Cr and 0 at.%-6 at.% Ni, which coincides well with the previous experimental evidence for Co<sub>55</sub>Cr<sub>40</sub>Ni<sub>5</sub> alloys. The validity of essential criterion is further proved after systematic comparison with numerous experimental data, which demonstrates that the essential criterion can provide significant guidance for the quick exploitation of strong and ductile MEAs and promote the development and application of MPEAs.

Zhang P, Zhang Z F.

Getting tougher in ultracold

[J]. Science, 2022, 378: 947

DOI      PMID      [本文引用: 1]

Certain alloys show exceptional toughness in a liquid helium environment.

Liu D, Yu Q, Kabra S, et al.

Exceptional fracture toughness of CrCoNi-based medium- and high-entropy alloys at 20 kelvin

[J]. Science, 2022, 378: 978

DOI      PMID      [本文引用: 1]

CrCoNi-based medium- and high-entropy alloys display outstanding damage tolerance, especially at cryogenic temperatures. In this study, we examined the fracture toughness values of the equiatomic CrCoNi and CrMnFeCoNi alloys at 20 kelvin (K). We found exceptionally high crack-initiation fracture toughnesses of 262 and 459 megapascal-meters (MPa·m) for CrMnFeCoNi and CrCoNi, respectively; CrCoNi displayed a crack-growth toughness exceeding 540 MPa·m after 2.25 millimeters of stable cracking. Crack-tip deformation structures at 20 K are quite distinct from those at higher temperatures. They involve nucleation and restricted growth of stacking faults, fine nanotwins, and transformed epsilon martensite, with coherent interfaces that can promote both arrest and transmission of dislocations to generate strength and ductility. We believe that these alloys develop fracture resistance through a progressive synergy of deformation mechanisms, dislocation glide, stacking-fault formation, nanotwinning, and phase transformation, which act in concert to prolong strain hardening that simultaneously elevates strength and ductility, leading to exceptional toughness.

Hu Q M, Yang R.

The endless search for better alloys

[J]. Science, 2022, 378: 26

DOI      URL     [本文引用: 1]

Machine learning narrows down the enormous search space for functional materials

/

〈 〉


版权所有 © 《金属学报》编辑部
地址: 沈阳市文化路72号, 中国科学院金属研究所(110016)
电话: +86- 024-23971286 　E-mail: jsxb@imr.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发 技术支持：support@magtech.com.cn