通讯作者:
收稿日期: 2015-07-10
网络出版日期: 2016-03-10
版权声明: 2016 《金属学报》编辑部 《金属学报》编辑部
基金资助:
作者简介:
作者简介: 宋永锋, 男, 1990年生, 硕士生
展开
摘要
制备晶粒尺寸不同的In718合金试样, 采用经验模态分解(EMD)研究超声背散射信号的时频域特征, 分析晶粒尺寸对不同频段固有模态函数(IMF)的影响, 并探求各IMF信号的功率与晶粒尺寸之间的相关性. 结果表明, 原始背散射信号和IMF1信号的频带宽受晶粒尺寸变化影响均不显著; IMF2信号频域分布较为集中, 峰值频率的幅值随晶粒的增大而增大, 其功率与晶粒尺寸相关系数达0.995, 显著高于其它模态, EMD过程实质上滤除了与晶粒尺寸无关的成分. 以充分反映晶粒散射强度的IMF2成分作为晶粒尺寸评价的特征信号, 建立面向In718晶粒尺寸的超声背散射EMD评价模型. 晶粒尺寸实测结果显示, 本方法的灵敏度是传统背散射法的3.7倍; 对2个验证试样的评价误差分别为-3.72%和2.87%, 精度显著高于声速法; 与衰减法相比, 本方法无需厚度信息, 评价结果不受测厚误差的影响; 此外, 相比于金相法具有效率高及无需破坏待测件的优势.
关键词:
Abstract
Superalloy In718 enjoys wide application in such crucial parts as turbine engine disks due to high strength, great toughness and corrosion resistance in different temperature environment. Since the mechanical properties of superalloy In718 are greatly influenced by the grain size, a nondestructive detection method is studied in order to determine the grain size quickly and effectively. In this work, superalloy In718 samples of different grain sizes were produced and the empirical mode decomposition (EMD) method was employed to find the characteristics of the time-frequency domain of the ultrasonic backscattering signals. Then the effects of the grain size over the intrinsic mode function (IMF) of different frequency bands were analyzed to seek the relations between the grain size and the power of the IMF signals. The original backscattering signals and IMF1 (the first IMF) signals barely respond to the change of the grain size because of their wide frequency bandwidths; the distribution of the frequency domain of the IMF2 signals is centralized and the amplitude of the peak frequency increases with the grain size, and the correlation coefficient between the power and the grain size is 0.995, much higher than that of other modes. This method eliminates the components irrelative to the grain size and takes the IMF2 components which fully reflect the intensity of the grain scattering as the characteristic signals of the grain size evaluation to build an ultrasonic backscattering EMD model evaluating the grain size of superalloy In718. The actual measurement results of the grain size show that the sensitivity of this method is 3.7 times over the traditional backscattering method; the evaluation errors over the two verification test samples are -3.72% and 2.87%, apparently more accurate than the ultrasonic velocity method; compared with the attenuation method, this method requires no information of the thickness so that the evaluation results are independent of the thickness measuring error; compared with the metallographic method, this method is more efficient and requires no damage on the components to be evaluated.
Keywords:
In718高温合金具有高强度,优良的热加工性能和高低温环境下的耐腐蚀性, 广泛用于航空涡轮轴发动机涡轮盘,甩油盘,鼓筒轴等各种重要零件[1], 据统计, In718合金制成了现代航空发动机上超过30%的关键零部件[2]. In718的机械性能受晶粒尺寸影响显著, 如晶粒尺寸从2.25 mm细化至0.2 mm时, 其室温下强度极限从751.3 MPa提升至936.7 MPa, 但700 ℃下的延展率从12.1%降至8.17%[3]. 可见, 合理控制晶粒尺寸是制定In718高温合金热加工工艺的关键之一[4], 而晶粒尺寸快速,有效的检出又是其中的基础和前提.
目前晶粒尺寸检测方法可分为有损和无损检测两大类, 有损检测法中金相法利用晶界处化学性质不稳定, 腐蚀形成凹陷显示晶界; 电子背散射衍射(EBSD)法利用各晶粒的取向差异辨识晶粒. 无损评价法则利用晶界处的声阻抗等物理性质的差异测量晶粒尺寸. 有损检测法普遍具有检测精度高的优点, 但制样过程繁琐, 检测效率低且需破坏被测对象. 相比之下, 无损评价法无需破坏被测工件,检测效率高, 因此研究一种能快速有效地检测晶粒尺寸的无损方法具有重要意义. 超声无损评价法具有穿透能力强,灵敏度高等优点, 在晶粒尺寸无损评价中最为常用[5], 国内外学者已开展了大量卓有成效的研究[6~8].
晶粒尺寸对超声波的声速,衰减系数及背散射系数等多个特征量均存在不同程度的影响[9~11]. 其中背散射法具有无需厚度信息,影响测量结果的因素相对较少等优点而受到重视[12]. Margetan[13]用背散射信号品质因素(figure-of-merit, FOM)描述In718晶粒尺寸对超声背散射信号的影响, Panetta等[14]在此基础上结合Thompson-Gray测量模型[15]探求晶粒尺寸对背散射信号的影响规律, 并研究了晶粒尺寸自动测量方法, 但受到单次背散射假设的限制[16], 该方法对粗晶In718材料的测量精度低. 此外, 马世伟和袁康[17]直接将背散射信号强度作为评价晶粒尺寸的特征量, 这种方法简单直观,易于实现. 但背散射信号实质上属于杂波信号, 直接对背散射信号进行时域分析时, 背散射信号所携带的晶粒尺寸信息被噪声淹没, 无法体现与晶粒尺寸的相关性, 导致模型灵敏度不足.
为此, 引入经验模态分解 (empirical mode decomposition, EMD) [18], 通过各固有模态函数(intrinsic mode function, IMF)的时频域特征进一步分析晶粒尺寸对超声背散射信号的影响规律, 探求背散射信号中对晶粒尺寸最敏感的成分, 并以此建立In718晶粒尺寸的超声检测方法, 提高其无损评价的有效性.
实验所采用的锻造态In718合金的成分(质量分数, %)为: Ni 52.37, Fe 19.24, Cr 18.24, Nb 5.20, Mo 3.07, Ti 0.97, Al 0.52, Co 0.15, Si 0.30, Mn 0.007, C 0.04, B 0.004. 首先对In718合金棒材进行线切割, 得到7个试样的坯料. 为使各试样晶粒尺寸梯度化, 用1610BL型高温炉分别对各试样进行固溶处理, 其中No.1~No.5为建模用试样, No.1为锻造态, No.2~No.5分别在960, 980, 1000和1020 ℃固溶处理2 h, 水冷; T1和T2为验证试样, 分别在990和1010 ℃固溶处理2 h, 水冷. 为消除固溶过程产生的应力对超声信号的影响, 对各固溶处理后的试样进行时效处理(720 ℃下保温8 h, 以50 ℃/h的速率随炉冷却至620 ℃保温8 h, 空冷). 由于时效温度较低, 对晶粒尺寸几乎无影响. 接着采用Buehler EcoMet 250型研磨/抛光机进行研磨,抛光, 并采用Kalling's溶液[19]进行腐蚀得到金相试样, 利用DM4000M型金相显微镜(OM)进行组织观察, 按国标GB/T 6394-2002, 用截线法对晶粒尺寸进行测量.
采用Olympus 5072PR 超声脉冲信号发生/接收器和20 MHz的V317-SU-F2.3型水浸纵波聚焦探头组合构成超声脉冲信号接发装置, 通过ADLINK PCIe-9852 高速数据采集卡实现超声信号的采集. 其采样频率为250 MHz, 是探头中心频率的12.5倍, 可确保采样的精确性. 使用DMC2610 PCI总线6轴运动控制卡及六自由度运动平台精确控制水声距, 使超声焦点位于试样中间位置. 采用上述系统分别对No.1~No.5试样进行超声数据采集, 每个试样采集20个超声信号. 图1a和b分别显示了使用脉冲反射法采集超声信号时, 超声在晶界处的散射效应及其产生的超声背散射信号在超声A波中的分布区域.
图1 超声A波信号采集示意图
Fig.1 Schematics of ultrasonic A-wave signal collection (a) backscattering of acoustic beams(b) ultrasonic A-wave signal (t--serial number of sampling points, u(t)--voltage amplitude)
图2 为No.1~No.5试样的OM像. 可见, 固溶处理后晶界变得平直, 经不同温度固溶处理后, 各试样晶粒尺寸均有不同程度的长大: 当试样在960 ℃进行固溶处理时, δ相未溶解, 在钉扎作用的影响下, 晶粒尺寸较原始状态变化很小; 当试样的固溶温度高于980 ℃时晶粒长大较为明显; 当固溶温度达到1020 ℃时, 晶界上的δ相全部溶解, δ相对晶界的束缚被解除, 晶粒长大明显[2]. 经测定, No.1~No.5的平均晶粒尺寸分别为63.6, 68.3, 71.7, 124.8和183.0 μm.
图2 试样No.1~No.5的OM像
Fig.2 OM images of samples No.1 (a), No.2 (b), No.3 (c), No.4 (d) and No.5 (e) (Inset shows the SEM image of δ phase)
从晶粒尺寸梯度分布中选取具有代表性的试样No.1, No.3和No.5, 其超声背散射信号如图3所示. 从图3中可见, 各试样的背散射信号均表现出较强的随机性, 无明显的规律. 采用各试样背散射信号的平均功率作为特征值:
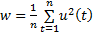
式中, 为背散射信号长度, 为背散射信号的幅值, 为采样点序号. 试样No.1~No.5的背散射信号平均功率分别为0.1107, 0.1030, 0.0941, 0.0762和0.0846 W. 各试样的平均功率的分布规律不明显, 经计算得到各试样背散射信号平均功率与晶粒尺寸的相关性仅为-0.74. 再分析各背散射信号的频域特征, 图4为No.1, No.3和No.5试样背散射信号的频谱图. 从图4可见, 各试样背散射信号的频域分布广泛, 在10~15 MHz的范围内均有一个较明显的峰值, 其它频段幅值并无明显差异. 可见背散射信号中包含了大量不同频段的成分, 由于不同的微观结构只对某些频段表现出高敏感性[20], 直接对背散射信号进行时域分析时, 所携带的晶粒尺寸信息被其它频段的噪声淹没, 弱化了背散射信号与晶粒尺寸的相关性.
图3 试样No.1, No.3和No.5的超声背散射信号
Fig.3 Backscattering signals of samples No.1 (a), No.3 (b) and No.5 (c)
图4 试样No.1, No.3和No.5的背散射信号频谱图
Fig.4 Spectrograms of the backscattering signals of samples No.1 (a), No.3 (b) and No.5 (c) (f--frequency)
对各背散射信号进行经验模态分解[18], 其中试样No.1的背散射信号分解结果如图5所示. 图中s为待分解的背散射信号, IMF1~IMF5对应各阶固有模态函数, r为剩余高阶分量. 各阶IMF的平均功率为:
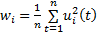
式中, 为IMF阶数, 为第阶IMF幅值. 图6为各阶IMF平均功率与晶粒尺寸的关系. 从图中可见, IMF2平均功率与晶粒尺寸之间表现出较强的正相关性. 进一步算得IMF1~IMF5平均功率与晶粒尺寸的相关系数分别为-0.8182, 0.9954, -0.5779, -0.2686和-0.5741. 可见, IMF2平均功率与晶粒尺寸的相关性显著高于其它模态函数.
图5 试样No.1背散射信号经验模态分解结果
Fig.5 Original backscattering signal (s), the mean intrinsic mode function for five different siftings (IMF1~ IMF5) and the residue (r) of sample No.1
图6 晶粒尺寸与各阶模态函数平均功率的关系
Fig.6 Relationships between the mean power of each IMF and the grain size
为进一步验证上述结果的合理性, 分析各试样模态函数的频域特征. 图7为试样No.1, No.3和No.5的频谱图. 由于IMF4和IMF5中心频率远低于IMF1和IMF2, 其基本情况与IMF3相近, 为保证图像的清晰性, 仅给出IMF1~IMF3的频谱. 由图可知, IMF1的频域分布几乎涵盖了所有模态函数对应的频段, 包含了大量的噪声信号. 相比之下, IMF2的频域分布较为集中, 主要频段均位于10~15 MHz之间, 对应的波长在380~587 μm之间. 各阶模态函数随着阶数增大, 信号中心频率下降明显, IMF3及其它高阶模态函数的波长普遍在1000 μm以上. 可见, 各阶模态函数中IMF2的波长与各试样晶粒尺寸的尺度最为接近.
试样No.1, No.3和No.5的IMF2频谱对比如图8所示. 由图可知, 各试样IMF2
图7 试样No.1, No.3和No.5的模态函数频谱图
Fig.7 Spectrograms of IMF of samples No.1 (a), No.3 (b) and No.5 (c)
图8 试样IMF2信号频谱对比
Fig.8 Spectrograms of the IMF2 components of samples No.1, No.3 and No.5
峰值频率较为接近, 相应幅值随试样晶粒尺寸增大而增大. 可见, 对超声背散射信号进行经验模态分解实质上是对背散射信号进行了滤波处理, 将信号中与晶粒无关的高频和低频成分滤除, 只留下与晶粒尺寸最为相关的IMF2成分.
图9a为5个试样IMF2平均功率与平均晶粒尺寸分布的散点图. 拟合得到的EMD背散射晶粒尺寸评价模型为:

式中, 为平均晶粒尺寸, μm; 为IMF2平均功率, W; 拟合优度R2=0.9921.
为对比验证本方法在In718晶粒尺寸评价的有效性, 将其与衰减法,纵波声速法和传统超声背散射法进行性能的对比分析, 这3种方法的评价模型如图9b~d所示.
其中, 传统背散射评价模型为:
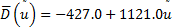
式中, 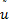
衰减法评价模型为:
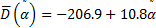
式中, 为纵波衰减系数, Np/m; R2=0.9916.
纵波声速法评价模型为:
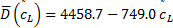
式中, 为纵波声速, km/s; R2=0.9605.
晶粒尺寸从63.6 μm增至183.0 μm时, 将各模型特征量的变化率定义为模型的平均灵敏度系数, 并据此分析各模型的灵敏度差异. EMD背散射模型,传统背散射评价模型,衰减法评价模型和纵波声速法评价模型的平均灵敏度系数分别为90.95%, 24.35%, 44.73%和-2.76%. 可见, 纵波声速法评价模型的平均灵敏度系数最低; 超声背散射EMD模型的灵敏度最高, 是传统背散射评价模型的3.7倍, 是衰减法评价模型的2.0倍.
接着, 对不参与建模的验证试样T1和T2进行分析, 其OM像见图10, 通过金相法测定2试样的平均晶粒尺寸分别为96.7和152.8 μm. 对2个验证试样在不同点位采集20组信号, 分别用4种模型计算其平均晶粒尺寸, 结果如表1所示. 从表中可见, 声速法和传统背散射法的随机误差较大, 与金相法之间最大相对误差分别为7.16%和5.03%, 这是由于声速法拟合优度较低, 且受厚度测量误差影响大. 而传统的背散射模型中, 受第二阶模态以外的其它频段的噪声信号的影响, 导致较大的随机误差. 衰减法和EMD背散射法在稳定性和测量精度方面均达到了较理想的水平, 但EMD方法无需测量待检工件的厚度信息, 对于In718涡轮盘或叶片等厚度测量不便的工件, 评价结果不受测厚误差的影响, 实用性优于衰减法. 另外, EMD背散射法仅需进行超声数据采集和模型计算2个过程, 相比于常用的金相法具有显著的效率优势.
图9 不同的晶粒尺寸评价模型
Fig9 Different models for grain size evaluation
(a) empirical mode decomposition (EMD) backscattering model (b) traditional backscattering model
(c) attenuation model (d) velocity model
(1) 通过超声实验和统计分析可见, 超声背散射信号中主频段为10~15 MHz的第二阶固有模态函数(IMF2)成分对晶粒尺寸响应最敏感.
(2) 针对传统背散射模型灵敏度低的问题, 引入经验模态分解滤除超声背散射信号中的噪声信号, 获得与晶粒尺寸最为相关的IMF2成分.
(3) 以IMF2为特征信号, 建立了In718合金晶粒尺寸的EMD背散射评价模型. 该模型的灵敏度,评价精度显著高于传统背散射模型和声速模型; 且因无需测厚, 相比于衰减模型, 提高了厚度测量不便不准条件下的实用性; 相比于金相法具有评价效率高,无需破坏试样的优势.
The authors have declared that no competing interests exist.

/
| 〈 |
|
〉 |