刘觐, 女, 1988年生, 博士生
以作者前期提出的位错塞积模型为基础, 结合断裂强度与晶粒尺寸的关系, 建立了晶粒细化导致超细晶粒钢总伸长率降低的临界晶粒尺寸的计算模型. 以晶粒尺寸从10 mm减小到0.2 mm为例, 计算结果表明, 钢的总塑性伸长率随着晶粒尺寸的减小首先呈现增加的趋势, 但是当晶粒尺寸减小到大约2.5 mm后, 随着晶粒尺寸的减小, 钢的总伸长率不仅不再增加, 反而出现了显著的降低, 这一结果较好地吻合了近期超细晶粒材料研究的实验现象. 本工作的研究说明, 导致超细晶粒钢伸长率降低的主要机制在于当晶粒细化到一定程度后, 晶界对位错源开动的阻力增大, 由此导致的可动位错数目显著降低使得应变量显著减少.
Based on our earlier preliminary work, a model was developed for prediction of the critical grain size where the plasticity would be decreased as the grain refined. In the model the effect of grain size on the fracture strength was combined. The prediction of the model exhibited that in the range of grain size of 10 mm to 0.2 mm as an example, the total elongation of the steels would be firstly increased. But when the grain size was refined to 2.5 mm and below, the total elongation of the steels was not increased but decreased sharply, which was good agreement with the experimental results published recently. Present work illustrated that the dominant mechanism of the elongation decreased in the ultra-fine grain size materials is due to increase in resistance force of grain boundaries on the dislocation sources resulting in the difficulty of activation of dislocation movements. Its expression would be the decrease of the plastic strain in macro-level.
实现高等级管线钢强韧化的技术关键是利用控轧控冷(thermal mechanical control processing, TMCP)工艺, 通过细化晶粒保证管线钢在高强度的水平下得到良好的低温韧性, 以满足在北极等高寒地区条件下, 管线承受油气输送过程中的冲击疲劳的服役要求[1,2]. 然而, 在整个管线铺设地区, 不可避免地会经过地质条件恶劣的地段. 为了尽可能地保证管线钢在某些极端条件下, 例如地震、滑坡等自然灾害中, 不致由于地质变化导致的管线变形造成的破断, 使得石油、天然气泄漏而造成二次破坏, 就要求管线钢除了能够满足强韧性的使用性能要求之外, 还要具有良好的承受塑性变形的能力[3,4].
大量研究[5,6,7,8,9]已经证明, 当晶粒尺寸细化到一定的范围时, 传统材料学观点中有关材料的塑性随着晶粒的细化而增加的规律已经不再适用于大部分超细晶粒钢. 实验研究的结果[5,6,7,8,9]表明, 当晶粒细化到某一临界值之后, 钢的塑性将随着晶粒尺寸的进一步减小而迅速降低, 钢的加工硬化能力失去, 从而大大降低了钢的变形能力. 因此, 需要进行合理的微观结构设计来提高管线钢的塑性变形能力, 一方面需要细化晶粒保证其具有足够的强度和韧性, 另一方面又需要保证晶粒的细化不导致塑性的降低. 为了实现这一目的, 需要系统地分析晶粒尺寸对钢的塑性变形行为的影响规律和机理, 并确定相应的临界晶粒尺寸, 为新一代管线钢的设计和生产提供技术基础. 目前针对晶粒尺寸减小导致塑性下降这一实验现象的解释已有一些研究工作, 主要分为两类: 一是超细晶粒钢中显著的动态回复作为一种软化机制, 降低了钢的加工硬化率[5,10,11]; 二是超细晶粒钢在变形早期便发生塑性失稳, 将均匀伸长率限制在了很低的水平[11,12]. 但是这些研究主要集中在一些纳米尺度材料的研究[13]和计算研究领域[14,15], 对亚微米级尺度的超细晶粒钢中这种塑性随晶粒尺寸减小而降低的微观物理机理尚缺少系统的分析和深入的研究, 对超细晶粒钢的塑性随晶粒尺寸减小开始迅速减小的“临界晶粒尺寸”也未见有关定量分析计算的模型. 这给实际生产过程中通过设计晶粒尺寸来优化管线钢力学性能的微观结构设计带来了一定的困难. 尽管作者的前期工作提出了利用位错塞积模型[16]为基础来分析晶粒尺寸对应变的影响, 但是分析的基础只是针对一定外加应力条件下材料的变形行为, 没有考虑晶粒尺寸对强度的作用.
本工作结合晶粒尺寸对超细晶粒钢断裂强度的影响, 利用位错运动模型来分析晶粒尺寸对超细晶粒钢拉伸变形时总塑性伸长率的影响. 以X80管线钢为例, 计算了拉伸塑性变形时的塑性随着晶粒尺寸减小由增加转变为迅速减小的临界晶粒尺寸.
材料的总塑性伸长率是断裂强度下材料的应变量, 在一定程度上反映了材料的塑性变形能力. 由于晶粒尺寸的改变会引起材料断裂强度的变化, 因此, 为了分析晶粒尺寸对材料的塑性的影响, 首先需要分析晶粒尺寸对断裂强度的影响. 在Stroh[17]模型的基础上, Smith[18]提出了金属材料中裂纹形核扩展的模型. 根据Smith[18]模型, 微裂纹能够在相邻晶粒中稳定存在的临界外加切应力如下式所示[18]:
式中,
研究[18,19,20,21]表明, 对于多晶体塑性材料, 决定材料断裂强度的主要因素是沿晶界的裂纹扩展, 即晶界是阻碍裂纹扩展的有效障碍[21]. 也就是说, 裂纹即使扩展通过碳化物/铁素体界面, 如果应力不能克服“铁素体晶粒强度”, 那么裂纹将在遇到的第一个铁素体/铁素体晶界处停止. 根据Curry和King[22]的工作, “铁素体晶粒强度”如式(1)所示. 对多晶体材料来说, 由于每个晶粒的取向各不相同, 相同外加应力下, 不同取向晶粒的滑移系上所承受的分切应力是不同的, 其中具有最大取向因子的最软取向晶粒, 外加应力作用在其滑移系上的分切应力是最大的. 因此, 随着外加应力的增加, 最软取向晶粒的滑移系上所承受的分切应力将最先达到
式中,
以X80管线钢为例进行计算. 在计算中, 分别取E=208 GPa[24], v=0.273[25], gs=2.6 J/m[26]和 mmax=0.5[23], 代入式(1)和(2)中进行计算, 得到
断裂时,
式中,
式中,
材料研究工作中通常采用平均取向因子进行计算. 假设多晶体材料具有随机取向的特征, 那么根据晶体学理论, 晶粒在取向空间共有936个具有代表性的取向[29], 因此, 可将取向空间划分为936个微区, 每个微区的特征取向用gi表示, 取向密度权重用f(gi)表示, gi微区的取向因子用 m(gi)表示. 则多晶体的平均取向因子
X80管线钢具有bcc结构, 其常见的滑移系有12个{110}<111>滑移系、12个{112}<111>滑移系和24个{123}<111>滑移系. 由于{123}滑移面上的位错可以通过{110}面与{112}面上滑移的组合完成, 因此, 在计算时忽略{123}<111>上的滑移[30]. 因此, gi取向微区的12个{110}<111>滑移系和12个{112}<111>滑移系上的取向因子是[29]:
式中,
根据式(5)~(7), 便可计算得到材料的
当外加应力达到
式中,
如图2所示, 在平均分切应力
 | Fig.2 Schematic of dislocation pile-up group in a single grain ( td—given applied stress)图2 单个晶粒中的位错塞积示意图 |
根据前期的研究结果, 单个晶粒的位移量与d的关系可以表达为[16]:
式中,
在文献[16]中,
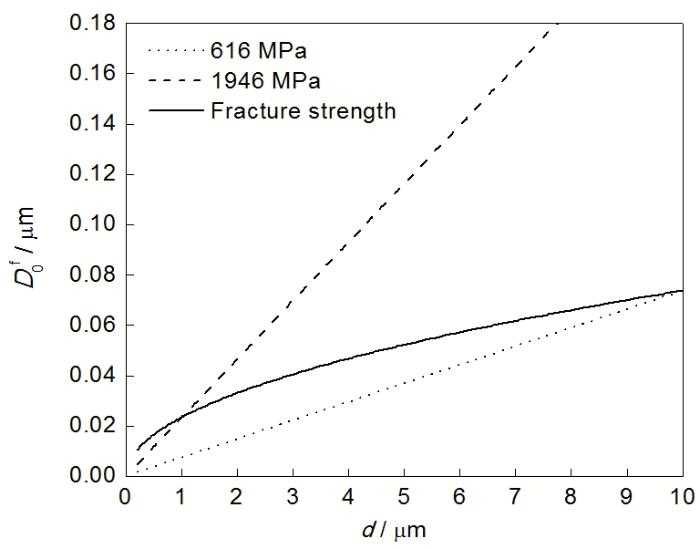 | Fig.3 Relationship between the displacement of a single grain Df0 and d under the corresponding fracture strength图3 相应断裂强度下单个晶粒的位移量 Df0 随d的变化曲线 |
对于给定的晶粒尺寸, 随着拉伸应力的增加, 位错塞积的数目增加, 必然导致单个晶粒塑性变形量的增加. 但是, 如图3中实线所示, 虽然
根据相关研究[16,35], Frank-Read源(FR源)的可开动几率不仅受到作用在FR源上的切应力的影响, 还受到FR源长度与d的比值的影响. 在超细晶粒钢中, 对于一个确定长度的FR源, d越小, 晶界对FR源增殖位错的阻碍作用越显著, 如图4所示.
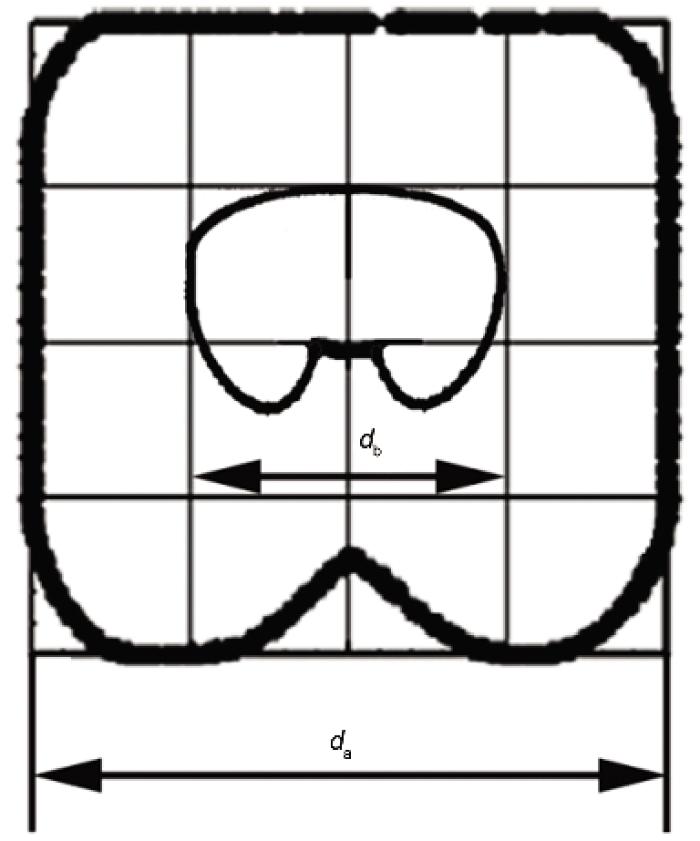 | Fig.4 Schematic of grain boundary blocks the process of Frank-Read source (FR source) emits dislocations (Both da and db represent grain size and da>db)图4 晶界阻碍Frank-Read源(FR源)增殖产生位错的示意图 |
如图4所示, 对于一个确定长度的FR源, 当晶粒尺寸较大时(da), 晶界对FR源增殖位错的阻碍作用较弱, FR源可以放出一个完整的稳定位错圈; 当晶粒尺寸较小时(db), 由于晶界对FR源的阻碍作用显著增加, FR源无法放出一个稳定的位错圈, 使得FR源不能开动.
前期的工作[16]已经建立了多晶体材料中FR源的可开动几率与d和应力的关系. 本工作将
式中,
同样, 以X80管线钢拉伸塑性变形为例, 考虑
以作者前期提出的模型[16]为基础, 综合考虑本工作分析得到的断裂强度与晶粒尺寸的关系, 外加应力等于相应断裂强度时单个晶粒的位移量与晶粒尺寸的关系, 以及位错源可开动几率与晶粒尺寸的关系, 可以计算得到断裂时钢的塑性应变量与晶粒尺寸的关系, 如下式所示:
式中,
将钢断裂时的塑性应变量由真应变转换成工程应变有[36]:
式中,
将X80管线钢的材料参数[25]代入计算, 得到断裂时管线钢的
图7是文献[5,6,9,37~42]报道的1种IF钢(无间隙原子钢)、5种低碳钢和3种TWIP钢(孪生诱导塑性钢)的塑性伸长率与d的关系. 可见, 这些实验数据虽然来自于不同的钢种, 这些超细晶粒钢的制备方法也各不相同, 但是其均匀伸长率
由上述分析可知, 钢的
根据上述分析可知, 这种由于d的减小导致的
本工作以对应断裂强度的总塑性伸长率作为衡量钢的塑性变形能力的参量, 根据钢的断裂强度与晶粒尺寸的关系, 建立了拉伸塑性变形时, 钢的塑性与晶粒尺寸关系的模型. 模型分析计算结果表明, 当晶粒尺寸较大时, 钢的塑性随着晶粒尺寸的减小首先表现出增强的趋势, 但是当晶粒尺寸减小到临界晶粒尺寸之后, 进一步减小晶粒尺寸将导致钢的塑性迅速降低. 根据本工作建立的模型, 计算得到X80管线钢的塑性随晶粒尺寸的减小开始迅速下降的临界晶粒尺寸约为2.5 mm, 与作者前期工作相比, 本工作预测得到的临界晶粒尺寸的数值与实验数据吻合得更好.
Fig.1 Relationship between fracture strength
Fig.2 Schematic of dislocation pile-up group in a single grain ( td—given applied stress)]]>
Fig.3 Relationship between the displacement of a single grain
Fig.4 Schematic of grain boundary blocks the process of Frank-Read source (FR source) emits dislocations (Both da and db represent grain size and da>db)]]>
Fig.5 Relationship between the probability of activated FR sources in polycrystal Ff and d under the applied stress of 616 MPa, 1946 MPa and the corresponding fracture strength]]>
Fig.6 Relationship between the total fracture elongation ef and d]]>
Fig.7 Experimental data of uniform elongation eu or total elongation ef versus d in ultra-fine grain size steels[5,6,9,37~42] (Solid symbols represent eu and hollow symbols represent ef)]]>
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|






