非平衡界面动力学理论

王海丰, 蒲振新, 张建宝

Non-Equilibrium Interface Dynamics Theory

WANG Haifeng, PU Zhenxin, ZHANG Jianbao

图6 非稳态部分拖曳固/液界面动力学过程的摩尔Gibbs自由能示意图

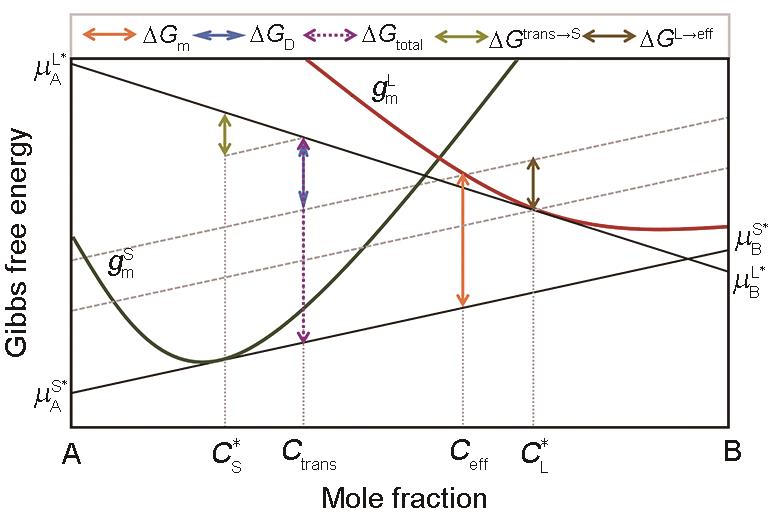
Fig.6 Mole Gibbs free energy diagram for the solid/liquid interface kinetic processes with a partial solute-drag effect under a non-steady-state condition (The total Gibbs free energy dissipated by the interface after solidification of 1 mol liquid is $Δ G_{t o t a l}$ = $(1 - C_{t r a n s}) Δ μ_{A}^{*} + C_{t r a n s} Δ μ_{B}^{*}$ . By translating the tangent of Gibbs free energy curve of solid at $C_{S}^{*}$ to the Gibbs free energy curve of liquid at C_eff, $Δ$ G_total is divided into two parts. The upper one for trans-interface diffusion is $Δ G_{D}$ = $(C_{e f f} - C_{t r a n s}) (Δ μ_{A}^{*} - Δ μ_{B}^{*})$ and latter part for interface migration is $Δ$ G_m = $(1 - C_{e f f}) Δ μ_{A}^{*} + C_{e f f} Δ μ_{B}^{*}$ . The difference in $Δ$ G_D between the steady-state condition and the non-steady-state condition is $Δ G^{t r a n s ‐ S}$ = $(C_{t r a n s} - C_{S}^{*}) (Δ μ_{A}^{*} - Δ μ_{B}^{*})$ , which is the Gibbs free energy dissipated to adjust the actual composition transferred across the interface from $C_{S}^{*}$ to C_trans for trans-interface diffusion. The difference in $Δ$ G_m between the two cases with a full solute-drag effect and with a partial solute-drag effect is $Δ G^{L ‐ e f f}$ = $(C_{L}^{*} - C_{e f f}) (Δ μ_{A}^{*} - Δ μ_{B}^{*})$ , which is the Gibbs free energy dissipated to adjust the liquid composition ahead of the solid/liquid interface from $C_{L}^{*}$ to C_eff for interface migration. It should be pointed out that Hareland et al. ^[30] confused the concepts of C_trans under non-steady-state and C_eff. Furthermore, it is also queried that the definition of C_eff can be stilled be used for a non-steady state condition. For example, there will be a problem when $C_{S}^{*}$ < C_eff < C_trans (C_eff—effective concentration)